1 Introduction

The majority of natural (e.g., polycrystals, wood, and bone) and man-made (e.g., fiber-reinforced composites, concrete, ceramics, and metallic foams) materials are heterogeneous at the micrometer (\(\upmu \)m) length-scale. Heterogeneous materials are referred to materials with different physical properties in terms of their constituents due to the variation in the underlying structure, properties, compositions, etc. Due to unique properties raised from the combination of different phases, heterogeneous materials have gained attention from engineering and scientific communities [7, 14, 16, 18, 32, 35, 56, 61, 62]. As expected, overall physical response of heterogeneous materials at the continuum level is coupled to their underlying microstructure. However, depending on the properties of the underlying constituents and loading conditions, the coupling response could be less pronounced in some materials compared with others. Heterogeneous materials, despite being composed of domains possessing distinct physical properties at the microscale, may be modeled accurately at the macroscale as homogeneous materials by effective (homogenized) material-like properties, [33, 41, 54].

In the case of thermo-mechanical processes, microscale heterogeneity might play a significant role within a length-scale. For example, due to a mismatch in microscale thermal coefficients of expansion, materials subject to high stress or temperature environments (e.g., concrete and bedrock used in nuclear waste storage) exhibit sharp stresses at the macroscopic level [66]. Hence, damage may occur due to induced thermo-mechanical stresses and minimize the operational lifetime of the component. For this reason, efforts have been made to develop more accurate theoretical models to predict material’s physical behavior [8, 17, 30, 45]. The evolution of theoretical models necessitates the development of numerical homogenization methods based on averaging different physical fields to obtain the effective physical properties [25, 27, 42, 58]. The average and the calculation of local field quantities are carried out by solving the underlying physics problem within a so-called representative volume element (RVE) to model the microstructure.

In classical Cauchy continuum mechanics, linear elastic models are based on Hooke’s law that implies a linear relation between Cauchy stress and strain. To include thermal effects, linear elastic models have been extended to account for temperature by adding an extra linear dependency of Cauchy stress, as formulated in Duhamel–Neumann extension in thermomechanics. In problems where the macroscale length scale is several orders of magnitude larger than in the microscale, which is indeed the case in many engineering applications, the aforementioned models are perfectly admissible. However, such models fail to accurately predict the response of the material when the distinction between microscopic and macroscopic length scales is less noticeable [13]. Therefore, generalized continuum theories have been developed to counteract the inability of classical continuum mechanics to account for the microstructural effects [5, 39, 44, 46, 57].

The generalized continuum additionally incorporates higher-order gradients of essential kinematic variables and associated length-scale parameters. The most common application of such models is the strain gradient model, where alongside strain, we have a gradient of strain as an additional state variable [46]. The addition of strain gradient introduces higher-order “hyper” stress as a work conjugate of the strain gradient [15]. However, the extension of the strain gradient models to account for temperature poses new challenges [34]. One approach follows Coleman–Noll rational thermodynamics [64] where only temperature is included in Helmholtz free energy in addition to strain and gradient strain [53]. Another approach includes temperature and gradient of temperature into the Helmholtz free energy, [22, 30, 43]. Unfortunately, both approaches suffer from the lack of experimental data that would provide additional material parameters arising from the inclusion of temperature and gradient of temperature into the Helmholtz free energy. This problem becomes more challenging for models with both temperature and its gradient as two additional variables added in the free energy formulation. Furthermore, another problem that arises from the addition of temperature gradient is an extra time derivative that appears in the flux term. This choice leads to an extension of Fourier’s law into Cattaneo’s equation, where alongside conductivity, there will be an additional parameter coupled with the time derivative of the temperature gradient [48]. Other researchers took a different approach to capture the gradient effects by determining the gradient through elastic and free dilatation [36,37,38]. Specifically, the mutual influence of elastic strain fields and defect fields was determined through free dilatation which is proposed to be interpreted as temperature deformation.

By transitioning from the classical continuum to the generalized continuum, homogenization models move from first-order approaches dealing with strain (displacement first derivative) to second-order approaches dealing with strain and gradient of strain (second derivatives of displacement) [20, 31, 63]. Particularly, the first-order (to be precise, first-gradient) approach requires strict separation of scales, and adherence to the concept of local action negates the ability to capture microscale geometry and deal with localization problems [6]. The second-order approach, by virtue of the generalized continuum, enables us to capture the microscale geometry by introducing length-scale into the material constitutive law [19, 26, 27, 47, 55, 59]. Although applications of the first-order homogenization approaches in thermoelastic problems are abundant in the literature, [12, 51, 71], the second-order homogenization approaches are relatively rare due to above-mentioned problems.

Beside the homogenization method, multi-scale approaches have also been used to perform thermo-mechanical analysis of heterogeneous materials. For instance, FE\(^2\), in which the finite element method is solved at two scales has been introduce [52]. In this approach authors solve the RVE at each Gauss point, which requires high-order continuity of micro/macroscale equations, thus relying on finite element formulation to have at least \(C^1\) continuity in displacement and temperature fields. A significant characteristic of the multiscale asymptotic approach is the ability to avoid continuity requirements owing to the reestablishment of the high-order macroscale derivatives by post-processing. Therefore, some researchers [21, 69] used a second-order asymptotic expansion approach to analyze their coupled thermo-mechanical systems. High-order asymptotic models enables ones to effectively investigate coupled problems by solving periodic functions at the microscale and calculating the macroscale displacement and temperature fields [70]. This work aims to explicitly calculate all the higher-order material terms associated with the generalized continuum model, such as higher-order elastic constants, coupling constants, and parameters associated with temperature.

In the present study, we only include temperature in our model to avoid extending Fourier’s law. In this manner, we analyze the simplest thermo-mechanical model in strain gradient elasticity. We follow the asymptotic homogenization in strain gradient elasticity as introduced in Abali and Barchiesi [2], verified in Yang et al [68], and applied in Vazic et al [65]. To incorporate temperature in the asymptotic homogenization model, we follow existing methods introduced in the literature [23, 24, 60]. In doing so, we have developed a higher-order asymptotic homogenization model for thermoelastic strain gradient materials that accounts for all of the associated higher-order material parameters.

The rest of the paper is organized as follows. The higher-order asymptotic homogenization method and computational implementation are explained in detail in the second section. Numerical results and a discussion of higher-order parameters are presented in the third section, followed by conclusion.

2 Methodology

We follow the asymptotic homogenization method described in Pinho-da Cruz et al. [11]; Abali and Barchiesi [2] and extend it to thermomechanics. In this study, we avoid using variational formulation as this approach is extremely complicated in case of multiphysic models and thus we adopt a classical thermomechanical approach. However, the readers are encouraged to review Giorgio [29] for a variational formulation for one-dimensional linear thermoviscoelasticity. The microstructure is denoted by \({\varvec{y}}\) which is referred to microscale in the rest of the paper; and its corresponding homogenized continuum is denoted by \({\varvec{X}}\), referred as macroscale. Their transformation is handled by a so-called homothetic ratio, \(\epsilon \). Thus, we circumvent a scale separation which enables us to use the same coordinate system for both length-scales. The approach is based on the “known” microscale leading to the “sought after” parameters at the macroscale.

We begin with thermomechanics at microscale and use balance of momentum for calculating the displacement, \({\varvec{u}}\), by a defined stress, \({\varvec{\sigma }}\), under a given (specific) body force, \({\varvec{g}}\), as follows:

$$\begin{aligned} \begin{aligned} \rho ^\text {m}\ddot{u}^\text {m}_i - \sigma ^\text {m}_{ji,j} - \rho ^\text {m}g_i = 0, \end{aligned}\end{aligned}$$
(1)

where we use a comma notation denoting the spatial derivative and \(\rho ^\text {m}\) is the known microscale mass density. Herein and henceforth, we use standard continuum mechanics formulation with summation convention over repeated indices. Similarly, the balance of internal energy reads

$$\begin{aligned} \begin{aligned} \rho ^\text {m}\dot{u}^\text {m}+ q^\text {m}_{i,i} - \rho ^\text {m}r = \sigma ^\text {m}_{ji} (\dot{\varepsilon }^\text {m}_{ij}) , \end{aligned}\end{aligned}$$
(2)

where the specific (per mass) internal energy, u, and heat flux, \({\varvec{q}}\), need to be defined. Source term, r, is the specified internal thermal source. Note that strain used in Eq. (2) is defined in linear form shown below,

$$\begin{aligned} \begin{aligned} \varepsilon ^\text {m}_{ij} = \frac{1}{2}\big ( u^\text {m}_{i,j} + u^\text {m}_{j,i} \big ). \end{aligned}\end{aligned}$$
(3)

Geometric nonlinearities are ignored such that the reference frame is equal as the current frame. Therefore, the rate is simply the partial time derivative in the reference frame that we choose as the known initial (undeformed) configuration. Generalization to higher order is adequate by adopting an energy formulation, which in this case is the specific Helmholtz free energy defined as:

(4)

where \(T^\text {m}\) is the microscale temperature, and \(\eta ^\text {m}\) is the microscale specific entropy. Here, we introduce the first simplification, , indicating that the free energy depends only on the temperature and strain fields. This approach is valid in thermoelasticity and enables us to circumvent any justifications like objectivity (usually done in rational thermodynamics) and use a more direct approach of defining the free energy in an axiomatic manner (as in continuum thermodynamics or in non-equilibrium thermodynamics) where the internal energy is simply defined as an objective quantity. By inserting total derivative of Eq. (4) with respect to time into the Eq. (2), dividing by \(T^\text {m}\), and adopting:

(5)

we can obtain the following relation:

(6)

here the right-hand side (\(\sigma ^\text {m}_{ji} \dot{\varepsilon }^\text {m}_{ij}\)) disappears since there is no dissipative stress in the system (elasticity). After rewriting the heat flux in a straight-forward manner, we obtain the balance of entropy:

$$\begin{aligned} \begin{aligned} \rho ^\text {m}\dot{\eta }^\text {m}+ \Big ( \frac{q^\text {m}_i}{T^\text {m}} \Big )_{,i} - \rho ^\text {m}\frac{r}{T^\text {m}} = -\frac{q_i}{(T^\text {m})^2} T^\text {m}_{,i} . \end{aligned}\end{aligned}$$
(7)

In thermoelasticity, the right-hand side of the Eq. (7) represents the entropy production density which according to the second law of thermodynamics must be positive. This poses a strong condition on the constitutive equation for the heat flux and thus we assume a linear relation called Fourier’s law:

$$\begin{aligned} \begin{aligned} q_i = \kappa ^\text {m}_{ij} T^\text {m}_{,j}. \end{aligned}\end{aligned}$$
(8)

where \(\kappa _{ij}^\text {m}\) is the thermal conductivity. Furthermore, since , we have \(\eta ^\text {m}=\eta ^\text {m}(T^\text {m}, {\varvec{\varepsilon }}^\text {m})\) as a mathematical fact based on Eq. (5)–often it is introduced as a principle of equipresence, but there is no need for such a principle, since there is a mathematical justification for it and we refer the readers to Abali [1] for further details. By summing up the equations for thermoelasticity, we obtain

(9)

In this manner, the whole formulation is reduced to one scalar function, i.e. Helmholtz free energy. As the material obeys Fourier’s law, we model the microscale as a linear thermoelastic material. Thus, we use linear elastic model with a known stiffness tensor, \({\varvec{C}}^\text {m}\), and a thermoelastic interaction, \(\beta ^\text {m}_{ij} = C^\text {m}_{ijkl} \alpha ^\text {m}_{kl}\), with a well-established coefficient of thermal expansion, \({\varvec{\alpha }}^\text {m}\). In this setting, the Helmholtz free energy is modeled in a quadratic form,

(10)

To compare microscale and macroscale Helmholtz free energies, we simplify Eq. (10) by expanding logarithmic temperature function through Taylor expansion as:

$$\begin{aligned} \begin{aligned} \ln \xi = \frac{\xi -1}{\xi } + \frac{(\xi -1)^2}{2\xi ^2} + \cdots \quad \xi \ge \frac{1}{2} \end{aligned}\end{aligned}$$
(11)

where \(\xi = T/T_\text {ref}\). Thus, first expression on the right-hand side of Eq. (10) is expanded to,

$$\begin{aligned} \begin{aligned} -c^\text {m}T^\text {m}\Big [\ln \Big (\frac{T^\text {m}}{T_\text {ref}}\Big ) -1\Big ]&= c^\text {m}T_\text {ref}- \frac{a^\text {m}}{2} (T^\text {m}-T_\text {ref})^2 \end{aligned}\end{aligned}$$
(12)

where specific heat capacity is related to parameter \(a^\text {m}\) defined as:

$$\begin{aligned} \begin{aligned} a^\text {m}= \frac{c^\text {m}}{T^\text {m}} \end{aligned}\end{aligned}$$
(13)

Detailed expansion of the left-hand side of Eq. (12) can be found in “Appendix A”. Combining Eqs. (12) and  (10) leads to:

(14)

Furthermore, the symmetry of the strain tensor leads to minor symmetries of the stiffness matrix \({C^\text {m}_{ijkl}} = {C^\text {m}_{jikl}} = {C^\text {m}_{ijlk}}\), and without loss of generality the symmetry of thermoelastic interaction \({\beta _{ij}^\text {M}} = {\beta _{ji}^\text {M}}\), we obtain

(15)

The equations are closed such that thermoelastic material is modeled at microscale by means of Eq. (5), as follows:

(16)

Furthermore, we consider steady-state condition for temperature and displacement by setting their rate terms equal to zero,

$$\begin{aligned} \bigg ( C^\text {m}_{ijkl} u^\text {m}_{k,l} + \beta ^\text {m}_{ij}(T^\text {m}-T_\text {ref}) \bigg )_{,j} + \rho ^\text {m}g_i= & {} 0 , \nonumber \\ - q^\text {m}_{i,i} - \rho ^\text {m}r= & {} 0 . \end{aligned}$$
(17)

For a homogenized continuum, we employ one axiom that the free energy within the RVE, \(\Omega \), is identical at micro- and macroscale as:

(18)

We can further simplify the analysis by following the mass ratio assumptions:

$$\begin{aligned} \begin{aligned} \rho ^\text {M}\int _\Omega \, \mathrm d V = \int _\Omega \rho ^\text {m}\, \mathrm d V , \ V = \int _\Omega \, \mathrm d V , \rho ^\text {M}= \frac{1}{V} \int _\Omega \rho ^\text {m}\, \mathrm d V , \ \end{aligned}\end{aligned}$$
(19)

2.1 Macroscale

A higher-order macroscale model can be defined by strain \({\varvec{\varepsilon }}^\text {M}\), gradient of strain \(\nabla {\varvec{\varepsilon }}^\text {M}\), and temperature \( T^\text {M}\). In other words, we begin with a specific free energy, , where we use the comma notation as the partial spatial derivative. We emphasize that the microstructure leads to higher order parameters in displacement because of homogenization of the structure [40]; however, we exclude temperature gradient from the free energy. We emphasize that temperature is used in the free energy formulation whereas temperature gradient is used in heat flux. Free energy or equivalently internal energy accommodates terms related to reversible processes, herein, but temperature gradient causes an irreversible process as directly apparent from the entropy production, where this term appears.

We use simplified generalized thermo-mechanical model with a reference thermo-mechanical state, \({\varvec{\varepsilon }}^\text {M}_\text {ref} = 0\), \(\nabla {\varvec{\varepsilon }}^\text {M}_\text {ref} = 0\), and \(T^\text {M}=T^\text {M}_\text {ref}\), and kinematic, balance and constitutive equations are linearized with respect to the reference state. Macroscale Helmholtz free energy, , is then specified as a quadratic form,

(20)

where \({G_{ijklm}^\text {M}}\), \({D_{ijklmn}^\text {M}}\), and \({\gamma _{ijk}^\text {M}}\), are coupling constant, higher-order elastic constants, and higher-order thermoelastic interaction respectively. In the equation above, we have utilized the symmetry of strain, \(\varepsilon ^\text {M}_{ij}=(u^\text {M}_{i,j}+u^\text {M}_{j,i})/2\), that allows us to consider additional minor symmetries \({G^\text {M}_{ijklm}} = {G^\text {M}_{jiklm}} = {G^\text {M}_{ijkml}} = {G^\text {M}_{lmijk}}\) and \({D^\text {M}_{ijklmn}} = {D^\text {M}_{jiklmn}} = {D^\text {M}_{ijkmln}} = {D^\text {M}_{lmnijk}}\), with the usual restrictions for positive definiteness [49, 50], and without loss of generality the symmetry of \({\gamma _{ijk}^\text {M}} = {\gamma _{kji}^\text {M}}\). An analogue to Eq. (9), the governing equations at the macroscale by following a variational formulation [3], read as:

(21)

Now, by using Eq. (20) for the free energy, in the case of steady-state as in Eq. (17), we obtain

$$\begin{aligned} \begin{aligned}&- \bigg ( C^\text {M}_{ijkl} u^\text {M}_{k,l} -\beta ^\text {M}_{ij} (T^\text {M}-T_\text {ref}) + G^\text {M}_{ijklm} u^\text {M}_{k,lm} \bigg )_{,j} \\&\quad + \bigg ( G^\text {M}_{lmijk} u^\text {M}_{l,m} \bigg )_{,jk} - \rho ^\text {M}g_i = 0 , \\&\quad - q^\text {M}_{i,i} + \rho ^\text {M}r = 0. \end{aligned}\end{aligned}$$
(22)

The aim is to find a relation between microscale and macroscale parameters. Specifically, to define such relationship, we start with given parameters in Eq. (17) and obtain the parameters in Eq. (22).

To solve Eq. (22), we introduce a geometric center of the RVE, \(\overset{c}{{\varvec{X}}}\), as follows:

$$\begin{aligned} \overset{c}{{\varvec{X}}} = \frac{1}{V}\int _{\Omega }{\varvec{X}} \, \hbox {d}V \, , \ V = \int _{\Omega } \, \hbox {d}V . \end{aligned}$$
(23)

Assuming displacement and temperature field \({\varvec{u}}^\text {M}\) and \( T ^\text {M}\) are continuous over the microscale, we approximate the macroscale displacement and temperature by a Taylor expansion around the value at the geometric center. Since we assume that the free energy depends on the second gradient of displacement [67] and only on temperature and not its gradient, we truncate higher order terms than quadratic for displacement and higher order terms than linear for temperature.

Macroscopic displacement field and its displacement gradients read:

$$\begin{aligned} u_{i}^\text {M}({\textbf{X}})= & {} u_{i}^\text {M}\vert _{\overset{c}{{\varvec{X}}}} + u_{i,j}^\text {M}\vert _{\overset{c}{{\varvec{X}}}}({X}_j-\overset{c}{X}_j) + \frac{1}{2}u_{i,jk}^\text {M}\vert _{\overset{c}{{\varvec{X}}}}({X}_j-\overset{c}{X}_j)({X}_k-\overset{c}{X}_k)\nonumber \\ u_{i,l}^\text {M}({\textbf{X}})= & {} u_{i,l}^\text {M}\vert _{\overset{c}{{\varvec{X}}}} + u_{i,lk}^\text {M}\vert _{\overset{c}{{\varvec{X}}}}({X}_k-\overset{c}{X}_k)\nonumber \\ u_{i,lm}^\text {M}({\textbf{X}})= & {} u_{i,lm}^\text {M}\vert _{\overset{c}{{\varvec{X}}}}, \end{aligned}$$
(24)

by evaluating parameters \((\cdot )\vert _{\overset{c}{{\varvec{X}}}}\) at the geometric center they are converted to a constant value and thus vanish after derivation. We stress that there is no scale separation such that the gradient at macroscale is used in this expansion by means of the comma notation. Macroscopic temperature field is assumed constant over the RVE leading to

$$\begin{aligned} T ^\text {M}({\textbf{X}}) = T ^\text {M}(\overset{c}{{\varvec{X}}}). \end{aligned}$$
(25)

In Eq. (24), the first and second derivatives of macroscopic deformation field are unknowns. These derivative terms are obtained by spatial averaging and benefiting from the fact that terms evaluated at \(\overset{c}{{\varvec{X}}}\) are constant within \(\Omega \), we can write,

$$\begin{aligned} \begin{aligned}&\langle u_{i,j}^\text {M}\rangle = \frac{1}{V}\int _{\Omega }u_{i,j}^\text {M}\, \hbox {d}V = u_{i,j}^\text {M}\vert _{\overset{c}{X}} + u_{i,jk}^\text {M}\vert _{\overset{c}{X}} \underbrace{\frac{1}{V}\int _{\Omega }(X_k-\overset{c}{X}_k)dV}_{\overset{c}{{\varvec{X}}}-\overset{c}{{\varvec{X}}}\text {= 0}} = u_{i,j}^\text {M}\vert _{\overset{c}{X}}\\&\langle u_{i,jk}^\text {M}\rangle = \frac{1}{V}\int _{\Omega }u_{i,jk}^\text {M}\, \hbox {d}V = u_{i,jk}^\text {M}\vert _{\overset{c}{X}} . \end{aligned} \end{aligned}$$
(26)

Thus Eq. (24) can be rewritten as:

$$\begin{aligned} \begin{aligned} u_{i,j}^\text {M}({\textbf{X}}) = \langle u_{i,j}^\text {M}\rangle + \langle u_{i,jk}^\text {M}\rangle ({X}_k-\overset{c}{X}_k) u_{i,jk}^\text {M}({\textbf{X}}) = \langle u_{i,jk}^\text {M}\rangle \ . \end{aligned} \end{aligned}$$
(27)

We use the axiom in Eq. (18) and replace spatial derivatives of the displacement field with their averages in the macroscale energy definition in Eq. (20). Moreover, spatial averaged terms are constant within the RVE and as such they are taken out of the integral. For the sake of clarity, we write each term of the free energy at macroscale by denoting the corresponding parameter to be determined

$$\begin{aligned} {\varvec{c}}^\text {M}\Rightarrow & {} \int _{\Omega } c^\text {M}T_\text {ref}\, \hbox {d}V = c^\text {M}T_\text {ref}V\nonumber \\ {\varvec{C}}^\text {M}\Rightarrow & {} \int _{\Omega }\frac{1}{2} C_{ijlm}^\text {M}\big (\langle u^\text {M}_{i,j}\rangle + \langle u^\text {M}_{i,jk}\rangle (X_k - \overset{\text {c}}{X}_k)\big )\big (\langle u^\text {M}_{l,m}\rangle + \langle u^\text {M}_{l,mn}\rangle (X_n - \overset{\text {c}}{X}_n)\big ) \, \hbox {d}V \nonumber \\= & {} \frac{1}{2}C^\text {M}_{ijlm}\Big ( \langle u^\text {M}_{i,j}\rangle \langle u^\text {M}_{l,m}\rangle + I_{kn}\langle u^\text {M}_{i,jk}\rangle \langle u^\text {M}_{l,mn}\rangle \Big ) V \nonumber \\ {\varvec{D}}^\text {M}\Rightarrow & {} \int _{\Omega }\frac{1}{2} D^\text {M}_{ijklmn}\langle u^\text {M}_{i,jk}\rangle \langle u^\text {M}_{l,mn}\rangle \, \hbox {d}V = \frac{1}{2}D^\text {M}_{ijklmn} \langle u^\text {M}_{i,jk}\rangle \langle u^\text {M}_{l,mn}\rangle V \nonumber \\ {\varvec{G}}^\text {M}\Rightarrow & {} \int _{\Omega } G^\text {M}_{ijklm}\big (\langle u^\text {M}_{i,j}\rangle + \langle u^\text {M}_{i,jk}\rangle (X_k - \overset{\text {c}}{X}_k)\big )\langle u^\text {M}_{k,lm}\rangle \, \hbox {d}V =G^\text {M}_{ijklm} \langle u^\text {M}_{i,j}\rangle \langle u^\text {M}_{k,lm}\rangle V \nonumber \\ {\varvec{a}}^\text {M}\Rightarrow & {} \int _{\Omega }\frac{1}{2} a^\text {M}\big (T^\text {M}- T_\text {ref}\big )\big (T^\text {M}- T_\text {ref}\big ) \, \hbox {d}V = \frac{1}{2}a^\text {M}\big (T^\text {M}- T_\text {ref}\big )^2V \nonumber \\ {\varvec{\beta }}^\text {M}\Rightarrow & {} \int _{\Omega } \beta ^\text {M}_{ij} \big ( \langle u^\text {M}_{i,j}\rangle + \langle u^\text {M}_{i,jk}\rangle (X_k - \overset{\text {c}}{X}_k) \big )\big (T^\text {M}- T_\text {ref}\big ) \, \hbox {d}V =\beta _{ij}^\text {M}\langle u_{i,j}^\text {M}\rangle \big ( T^\text {M}- T_\text {ref}\big )V\nonumber \\ {\varvec{\gamma }}^\text {M}\Rightarrow & {} \int _{\Omega }\gamma ^\text {M}_{ijk}\langle u_{i,jk}^\text {M}\rangle \big (T^\text {M}- T_\text {ref}\big ) \, \hbox {d}V = \gamma _{ijk}^\text {M}\langle u_{i,jk}^\text {M}\rangle (T^\text {M}- T_\text {ref})V \end{aligned}$$
(28)

where

$$\begin{aligned} \begin{aligned} I_{kn} = \int _{\Omega } (X_{k} - \overset{\text {c}}{X}_{k})(X_{n} - \overset{\text {c}}{X}_{n}) \, \hbox {d}V . \end{aligned}\end{aligned}$$
(29)

Separating above equations and combining parameters with identical combinations of spatial averages, we obtain macroscale deformation energy,

(30)

2.2 Microscale free energy

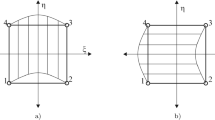
The basic idea behind this method is to transfer between microscale, \({\varvec{y}}\), and macroscale, \({\varvec{X}}\), by means of the so-called homothetic ratio \(\epsilon \). We visualize the meaning of this rather abstract constant in Fig. 1 which is a constant within the RVE.

Fig. 1
figure 1

Scaling from macroscale length L to microscale length l via homothetic ration \(\epsilon \)

Full size image

In our numerical approach, there is one single coordinate system. Thus, we may set \(\epsilon =1\) and model the RVE in real physical dimensions. In general, the homothetic ratio is defined as:

$$\begin{aligned} \underbrace{\epsilon = \frac{l}{L} = \frac{\text {microscale length}}{\text {macroscale length}}}_{\text {Homothetic ratio}} \, , \ \underbrace{ y_j = \frac{1}{\epsilon }(X_j - \overset{c}{X}_j)}_{\text {Local coordinate}} \, , \end{aligned}$$
(31)

\(\longrightarrow y_{i,j} = \delta _{ij}/\epsilon \). Microscale displacement field for the RVE is then expanded with regard to \(\epsilon \) as:

$$\begin{aligned} {\varvec{{\varvec{u}}}}^\text {m}({\varvec{X}}) = \underbrace{\overset{0}{{\varvec{{\varvec{u}}}}}({\varvec{X}},{\varvec{y}}) + \epsilon \overset{1}{{\varvec{{\varvec{u}}}}}({\varvec{X}},{\varvec{y}}) + \epsilon ^2 \overset{2}{{\varvec{u}}}({\varvec{X}},{\varvec{y}}) + \mathcal {O}(\epsilon ^3)}_{\text {Expanded microscale displacement field}} \end{aligned}$$
(32)

where \(\overset{n}{{\varvec{u}}}({\varvec{X}},{\varvec{y}})\) is \({\varvec{y}}\)-periodic. Furthermore, to ensure that temperature within RVE is assumed constant,

$$\begin{aligned} T^\text {m}({\varvec{X}}, {\varvec{y}}) = T^\text {M}({\varvec{X}}) , \end{aligned}$$
(33)

to ensure the \({\varvec{y}}\)-periodicity of a scalar field. By using the chain rule, we obtain the first derivative of (microscale) displacement field,

$$\begin{aligned} \begin{aligned} u^\text {m}_{i,j} = \overset{0}{u}_{i,j} + \frac{1}{\epsilon }\frac{\partial \overset{0}{u}_i}{\partial y_j} + \epsilon \bigg ( \overset{1}{u}_{i,j} + \frac{1}{\epsilon } \frac{\partial \overset{1}{u}_i}{\partial y_j} \bigg ) + \epsilon ^2 \bigg ( \overset{2}{u}_{i,j} + \frac{1}{\epsilon }\frac{\partial \overset{2}{u}_i}{\partial y_j} \bigg ) + \mathcal {O}(\epsilon ^3) . \end{aligned}\end{aligned}$$
(34)

We utilize Eq. (17), use chain rule, and insert Eq. (34),

$$\begin{aligned}{} & {} \Bigg [ {C_{ijkl}^\text {m}}\bigg ( \overset{0}{u}_{k,l} + \frac{1}{\epsilon }\frac{\partial \overset{0}{u}_k}{\partial y_l} + \epsilon \overset{1}{u}_{k,l} + \frac{\partial \overset{1}{u}_k}{\partial y_l} + \epsilon ^2\overset{2}{u}_{k,l} + \epsilon \frac{\partial \overset{2}{u}_k}{\partial y_l} \bigg ) -\beta ^\text {m}_{ij}(T^\text {M}- T_\text {ref})\Bigg ]_{,j} \nonumber \\{} & {} \quad + \frac{1}{\epsilon }\frac{\partial }{\partial y_j}\Bigg [ {C_{ijkl}^\text {m}} \bigg ( \overset{0}{u}_{k,l} + \frac{1}{\epsilon }\frac{\partial \overset{0}{u}_k}{\partial y_l} + \epsilon \overset{1}{u}_{k,l} + \frac{\partial \overset{1}{u}_k}{\partial y_l} + \epsilon ^2\overset{2}{u}_{k,l} + \epsilon \frac{\partial \overset{2}{u}_k}{\partial y_l}\bigg ) -\beta ^\text {m}_{ij}(T^\text {M}- T_\text {ref}) \Bigg ] \nonumber \\{} & {} \quad +\rho ^\text {m}g_i = 0 . \end{aligned}$$
(35)

Comparing coefficients in Eq. (35) of the same order of \(\epsilon \) leads to:

  • \(\epsilon ^{-2}\)

    $$\begin{aligned} \begin{aligned} \frac{\partial }{\partial y_j}\bigg ( {C_{ijkl}^\text {m}} \frac{\partial \overset{0}{u}_k}{\partial y_l}\bigg ) = 0 . \end{aligned}\end{aligned}$$
    (36)

  • \(\epsilon ^{-1}\)

    $$\begin{aligned}{} & {} \Big ({C_{ijkl}^\text {m}} \frac{\partial \overset{0}{u}_k}{\partial y_l}\Big )_{,j} + \frac{\partial }{\partial y_j}({C_{ijkl}^\text {m}} \overset{0}{u}_{k,l}) + \frac{\partial }{\partial y_j}\Big ({C_{ijkl}^\text {m}} \frac{\partial \overset{1}{u}_k}{\partial y_l}\Big )\nonumber \\{} & {} \quad - \frac{\partial }{\partial y_j}\Big (\beta ^\text {m}_{ij}(T^\text {M}- T_\text {ref})\Big )= 0 . \end{aligned}$$
    (37)

  • \(\epsilon ^0\)

    $$\begin{aligned}{} & {} \big ({C_{ijkl}^\text {m}} \overset{0}{u}_{k,l} \big )_{,j} + \Big ({C_{ijkl}^\text {m}} \frac{\partial \overset{1}{u}_k}{\partial y_l}\Big )_{,j} + \frac{\partial }{\partial y_j}\Big ( {C_{ijkl}^\text {m}} \overset{1}{u}_{k,l} \Big ) + \frac{\partial }{\partial y_j}\Big ( {C_{ijkl}^\text {m}} \frac{\partial \overset{2}{u}_k}{\partial y_l} \Big )\nonumber \\{} & {} \quad - \big (\beta ^\text {m}_{ij}T^\text {M}\big )_{,j} + \rho ^\text {m}g_i = 0 . \end{aligned}$$
    (38)

  • \(\epsilon ^1\)

    $$\begin{aligned} \begin{aligned} \bigg [ C^\text {m}_{ijkl} \Big ( \overset{1}{u}_{k,l} + \frac{\partial \overset{2}{u}_k }{\partial y_l} \Big ) \bigg ]_{,j} + \frac{\partial }{\partial y_j} \bigg ( C^\text {m}_{ijkl} \overset{2}{u}_{k,l} \bigg ) = 0 . \end{aligned}\end{aligned}$$
    (39)

  • \(\epsilon ^2\)

    $$\begin{aligned} \begin{aligned} \big ( C^\text {m}_{ijkl} \overset{2}{u}_{k,l} \big )_{,j} = 0 . \end{aligned}\end{aligned}$$
    (40)

Only possible solution for Eq. (36) is to define \(\overset{0}{{\varvec{u}}}\) as a function of \({\varvec{X}}\) because \({\varvec{C}}^\text {m}\) and \({\varvec{\beta }}^\text {m}\) depends on local variable \({\varvec{y}}\). This argumentation leads to,

$$\begin{aligned} \overset{0}{u}_i({\varvec{X}}) = {u}^\text {M}_i({\varvec{X}}) \, . \end{aligned}$$
(41)

We use a separation of variables, Bernoulli Ansatz to rewrite,

$$\begin{aligned} \begin{aligned} \overset{1}{u}_i({\varvec{X}}, {\varvec{y}}) =&u^\text {M}_{a,b}({\varvec{X}}) \varphi _{abi}({\varvec{y}}) - (T^\text {M}({\varvec{X}}) - T_\text {ref}) P_i({\varvec{y}}) \ , \\ \overset{2}{u}_i({\varvec{X}}, {\varvec{y}}) =&u^\text {M}_{a,bc}({\varvec{X}}) \psi _{abci}({\varvec{y}}), \end{aligned}\end{aligned}$$
(42)

where we introduce unknown tensors \({\varvec{\varphi }}\), \({\varvec{\psi }}\), \({\varvec{P}}\) of one rank higher than associated displacement derivatives and temperature field, so that the formulation is general. We emphasize that the temperature is only expanded up to one order less than the displacement. By inserting these into Eq. (37), we acquire

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial y_j}({C_{ijkl}^\text {m}} u^\text {M}_{k,l}) + \frac{\partial }{\partial y_j}\Bigg [{C_{ijkl}^\text {m}} \frac{\partial }{\partial y_l} \Big (u^\text {M}_{a,b} \varphi _{abk} - (T^\text {M}- T_\text {ref}) P_k \Big )\Bigg ] \\ {}&\quad - \frac{\partial }{\partial y_j}\Big [\beta ^\text {m}_{ij}(T^\text {M}- T_\text {ref})\Big ]= 0 \ , \\&u^\text {M}_{a,b} \frac{\partial }{\partial y_j} \Bigg [ C_{ijkl}^\text {m}\Big ( \delta _{ak}\delta _{bl} + \frac{\partial \varphi _{abk}}{\partial y_l} \Big ) \Bigg ] - (T^\text {M}- T_\text {ref}) \frac{\partial }{\partial y_j} \Bigg [ C_{ijkl}^\text {m}\frac{\partial P_k}{\partial y_l} + \beta ^\text {m}_{ij} \Bigg ] = 0 . \end{aligned}\end{aligned}$$
(43)

To obtain general solution of Eq. (43) we need to independently solve the following governing equations

$$\begin{aligned} \frac{\partial }{\partial y_j}\Bigg [\delta _{ak}\delta _{bl} + C^\text {m}_{ijkl}\bigg (\frac{\partial \varphi _{abk}}{\partial y_l} \bigg ) \Bigg ] = 0 . \end{aligned}$$
(44)

in order to obtain \({\varvec{\varphi }}\) and

$$\begin{aligned} \frac{\partial }{\partial y_j}\Bigg ( C^\text {m}_{ijkl}\frac{\partial P_{k}}{\partial y_l} +\beta ^\text {m}_{ij} \Bigg ) = 0 \, . \end{aligned}$$
(45)

to acquire \({\varvec{P}}\). Repeating the same procedure for Eq. (38), we have

$$\begin{aligned} \begin{aligned}&\Bigg [ C_{ijkl}^\text {m}u^\text {M}_{a,b} \delta _{ak}\delta _{bl} + {C_{ijkl}^\text {m}} \frac{\partial }{\partial y_l} \Big ( u^\text {M}_{a,b} \varphi _{abk} - (T^\text {M}- T_\text {ref}) P_k \Big ) \Bigg ]_{,j} \\ {}&+ \frac{\partial }{\partial y_j} \Bigg [ C_{ijkl}^\text {m}\overset{1}{u}_{k,l} + C_{ijkl}^\text {m}\frac{\partial }{\partial y_l} \Big ( u^\text {M}_{a,bc} \psi _{abck} \Big ) \Bigg ] - \big (\beta ^\text {m}_{ij}T^\text {M}\big )_{,j} + \rho ^\text {m}g_i = 0 , \end{aligned}\end{aligned}$$
(46)

which is rewritten

$$\begin{aligned} \begin{aligned}&\Bigg [ u^\text {M}_{a,b} C_{ijkl}^\text {m}\Big ( \delta _{ak}\delta _{bl} + \frac{\partial \varphi _{abk}}{\partial y_l} \Big ) - C_{ijkl}^\text {m}(T^\text {M}- T_\text {ref}) \frac{\partial P_k}{\partial y_l} - \beta ^\text {m}_{ij}T^\text {M}\Bigg ]_{,j} \\ {}&+ \frac{\partial }{\partial y_j} \Bigg [ C_{ijkl}^\text {m}\bigg [ \Big ( u^\text {M}_{a,b} \varphi _{abk} - (T^\text {M}- T_\text {ref})P_k \Big )_{,l} + \frac{\partial }{\partial y_l} \Big ( u^\text {M}_{a,bc} \psi _{abck} \Big ) \bigg ] \Bigg ] + \rho ^\text {m}g_i = 0 , \\&u^\text {M}_{a,bj} C_{ijkl}^\text {m}\Big ( \delta _{ak}\delta _{bl} + \frac{\partial \varphi _{abk}}{\partial y_l} \Big ) - C_{ijkl}^\text {m}T^\text {M}_{,j} \frac{\partial P_k}{\partial y_l} - \beta ^\text {m}_{ij} T^\text {M}_{,j} \\ {}&+ \frac{\partial }{\partial y_j} \Bigg (C_{ijkl}^\text {m}\bigg ( u^\text {M}_{a,bl} \varphi _{abk} - T^\text {M}_{,l} P_k + u^\text {M}_{a,bc} \frac{\partial \psi _{abck}}{\partial y_l} \bigg ) \Bigg ] + \rho ^\text {m}g_i = 0 , \\&u^\text {M}_{a,bc} \Bigg [ \delta _{cj} C_{ijkl}^\text {m}\Big ( \delta _{ak}\delta _{bl} + \frac{\partial \varphi _{abk}}{\partial y_l} \Big ) + \frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m}\Big ( \delta _{lc} \varphi _{abk} + \frac{\partial \psi _{abck}}{\partial y_l} \Big ) \bigg ) \Bigg ] \\&-T^\text {M}_{,a} \Bigg [ C_{iakl}^\text {m}\frac{\partial P_k}{\partial y_l} + \beta ^\text {m}_{ia} + \frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m}\delta _{al} P_k \bigg ) \Bigg ] + \rho ^\text {m}g_i = 0 \ , \end{aligned}\end{aligned}$$
(47)

Furthermore, from Eq. (22), by inserting

$$\begin{aligned} \begin{aligned} \rho ^\text {M}g_i = - C^\text {M}_{ijkl} u^\text {M}_{k,lj} +\beta ^\text {M}_{ij} T^\text {M}_{,j} - G^\text {M}_{ijklm} u^\text {M}_{k,lmj} + G^\text {M}_{lmijk} u^\text {M}_{l,mjk} \end{aligned}\end{aligned}$$
(48)

and using the same cut-off procedure for displacement third derivative and temperature second derivative, we obtain

$$\begin{aligned} \begin{aligned}&u^\text {M}_{a,bc} \Bigg [ \delta _{cj} C_{ijkl}^\text {m}\Big ( \delta _{ak}\delta _{bl} + \frac{\partial \varphi _{abk}}{\partial y_l} \Big ) + \frac{\partial }{\partial y_j} \Bigg ( C_{ijkl}^\text {m}\Big ( \delta _{lc} \varphi _{abk} + \frac{\partial \psi _{abck}}{\partial y_l} \Big ) \Bigg ) \Bigg ] \\&-T^\text {M}_{,a} \Bigg [ C_{iakl}^\text {m}\frac{\partial P_k}{\partial y_l} + \beta ^\text {m}_{ia} + \frac{\partial }{\partial y_j} \bigg ( C_{ijka}^\text {m}P_k \bigg ) \Bigg ] + \frac{\rho ^\text {m}}{\rho ^\text {M}} \Big ( - C^\text {M}_{ijkl} u^\text {M}_{k,lj} +\beta ^\text {M}_{ij} T^\text {M}_{,j} \Big ) = 0 , \end{aligned}\end{aligned}$$
(49)

Rearranging Eq. 49 by separation into the independent parts and enforcing \(T^\text {M}_{,a}=0\) and \(u^\text {M}_{a,bc}=0\) leads to the following equations, respectively.

$$\begin{aligned}{} & {} \frac{\partial }{\partial y_j}\Bigg [ C^\text {m}_{ijkl}\bigg (\frac{\partial \psi _{abck}}{\partial y_l} +\varphi _{abk}\delta _{cl} \bigg ) \Bigg ] + C^\text {m}_{ickl}\bigg (\frac{\partial \varphi _{abk}}{\partial y_l} +\delta _{ak}\delta _{lb} \bigg ) - \frac{\rho ^\text {m}}{\rho ^\text {M}}C^\text {M}_{icab} = 0 \ , \end{aligned}$$
(50)
$$\begin{aligned}{} & {} C_{iakl}^\text {m}\frac{\partial P_k}{\partial y_l} + \beta ^\text {m}_{ia} + \frac{\partial }{\partial y_j} \bigg ( C_{ijka}^\text {m}P_k \bigg ) - \frac{\rho ^\text {m}}{\rho ^\text {M}}\beta ^\text {M}_{ia} = 0 \ , \end{aligned}$$
(51)

Due to our initial assumption in ignoring higher-order temperature terms, Eq. (50) is automatically satisfied. Therefore, we solve Eqs. (44), (45), (50) to determine \({\varvec{\varphi }}\), \({\varvec{P}}\), \({\varvec{\psi }}\), respectively, while honoring \(T^\text {M}_{,a}=0\). By introducing following notations

$$\begin{aligned} \begin{aligned} L_{abij}&= \delta _{ia}\delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \ , \\ N_{abcij}&= \varphi _{abi}\delta _{jc} + \frac{\partial \psi _{abci}}{\partial y_j} \ , \\ Z_{ij}&= \frac{\partial P_{i}}{\partial y_{j}} \ , \end{aligned}\end{aligned}$$
(52)

We need to fulfill

$$\begin{aligned} \begin{aligned} \varphi _{abi} \Leftarrow&\frac{\partial }{\partial y_j}\Bigg ( C^\text {m}_{ijkl} L_{abkl} \Bigg ) = 0 , \\ P_i \Leftarrow&\frac{\partial }{\partial y_j}\Bigg ( C^\text {m}_{ijkl} Z_{kl} +\beta ^\text {m}_{ij} \Bigg ) = 0 , \\ \psi _{abci} \Leftarrow&\frac{\partial }{\partial y_j}\Bigg ( C^\text {m}_{ijkl} N_{abckl} \Bigg ) + C^\text {m}_{ickl} L_{abkl} - \frac{\rho ^\text {m}}{\rho ^\text {M}}C^\text {M}_{icab} = 0 , \end{aligned}\end{aligned}$$
(53)

Equations (42) and  (32) which leads to

$$\begin{aligned} \begin{aligned} u^\text {m}_{i}({\varvec{X}}, {\varvec{y}})&= u^\text {M}_{i}({\varvec{X}}) + \epsilon \Big [ \varphi _{abi}({\varvec{y}})u^\text {M}_{a,b}({\varvec{X}}) - P_{i}({\varvec{y}})( T ^\text {M}({\varvec{X}})- T_\text {ref}) \Big ] \\&+ \epsilon ^2 \Big ( \psi _{abci}({\varvec{y}})u^\text {M}_{a,bc}({\varvec{X}}) \Big ) . \\ u^\text {m}_{i,j}({\varvec{X}}, {\varvec{y}})&= u^\text {M}_{i,j} + \epsilon \Big ( \frac{\partial \varphi _{abi}}{\partial y_j} \frac{1}{\epsilon } u^\text {M}_{a,b} + \varphi _{abi} u^\text {M}_{a,bj} - \frac{\partial P_{i}}{\partial y_j} \frac{1}{\epsilon } ( T ^\text {M}- T_\text {ref}) - P_i T^\text {M}_{,j} \Big ) \\&+ \epsilon ^2 \Big ( \frac{\partial \psi _{abci}}{\partial y_j} \frac{1}{\epsilon } u^\text {M}_{a,bc} + \psi _{abci} u^\text {M}_{a,bcj} \Big ) . \end{aligned}\end{aligned}$$
(54)

To obtain the solution for the microscale free energy and determine the parameters we resort to Eq. 18, where the macroscale energy is given in Eq. (30). We take advantage of the fact that \(T^\text {M}_{,a}=0\) and that third derivative of displacement vanishes. Thus, we obtain the following expression:

$$\begin{aligned} \begin{aligned} u^\text {m}_{i,j} = \bigg (\delta _{ia}\delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \bigg )u^\text {M}_{a,b} - \frac{\partial P_{i}}{\partial y_{j}}( T ^\text {M}- T_\text {ref}) + \epsilon u^\text {M}_{a,bc}\bigg ( \varphi _{abi}\delta _{jc} + \frac{\psi _{abci}}{\partial y_j}\bigg ) \, , \end{aligned}\end{aligned}$$
(55)

with the help of Eq. (27), we acquire

$$\begin{aligned} \begin{aligned} u^\text {m}_{i,j} =&\bigg (\delta _{ia}\delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \bigg )(\langle u_{a,b}^\text {M}\rangle + \epsilon y_{c}\langle u_{a,bc}\rangle ) - \frac{\partial P_{i}}{\partial y_{j}}(T ^\text {M}- T_\text {ref}) \\&+\epsilon \bigg ( \varphi _{abi}\delta _{jc} + \frac{\psi _{abci}}{\partial y_j}\bigg )\langle u^\text {M}_{a,bc}\rangle \, . \end{aligned} \end{aligned}$$
(56)

By introducing

$$\begin{aligned} \begin{aligned} M_{abcij} = y_c L_{abij} + N_{abcij} , \end{aligned}\end{aligned}$$
(57)

and using Eqs. (52),  (56) can be rewritten as:

$$\begin{aligned} u^\text {m}_{i,j} = L_{abij}\langle u_{a,b}^\text {M}\rangle + \epsilon M_{abcij}\langle u_{a,bc}^\text {M}\rangle - Z_{ij}(T ^\text {M}- T_\text {ref}) \end{aligned}$$
(58)

Using the above equation microscale energy becomes

(59)

where

$$\begin{aligned} \begin{aligned} \bar{C}_{abcd}&=\frac{1}{V}\int _{\Omega }C_{ijkl}^\text {m}L_{abij} L_{cdkl} \, \hbox {d}V\\ \bar{G}_{abcde}&=\frac{2\epsilon }{V}\int _{\Omega }C_{ijkl}^\text {m}L_{abij}M_{cdekl} \, \hbox {d}V\\ \bar{\beta }_{ab}&=\frac{2}{V}\int _{\Omega }\Big [C_{ijkl}^\text {m}L_{abij}Z_{kl} - \beta _{ij}^\text {m}L_{abij}\Big ] \, \hbox {d}V\\ \bar{D}_{abcdef}&=\frac{\epsilon ^2}{V}\int _{\Omega }C_{ijkl}^\text {m}M_{abcij}M_{defkl} \, \hbox {d}V\\ \bar{\gamma }_{abc}&=\frac{2\epsilon }{V}\int _{\Omega }\Big [C_{ijkl}^\text {m}M_{abcij}Z_{kl} - \beta _{ij}^\text {m}M_{abcij}\Big ] \, \hbox {d}V\\ \bar{a}&=\frac{1}{V}\int _{\Omega }\Big [C_{ijkl}^\text {m}Z_{ij}Z_{kl} - 2\beta _{ij}^\text {m}Z_{ij}- a^\text {m}\Big ] \, \hbox {d}V\\ \bar{c}&= \frac{2}{V}\int _{\Omega }c^\text {m}\, \hbox {d}V \end{aligned}\end{aligned}$$
(60)

Comparing microscale energy in Eq. 59 to macroscale energy in Eq. 30, we obtain the homogenized values:

$$\begin{aligned} \begin{aligned} C_{ijkl}^\text {M}&= \bar{C}_{ijkl}\\ G_{ijklm}^\text {M}&= \frac{\bar{G}_{ijklm}}{2}\\ \beta _{ij}^\text {M}&= \frac{\bar{\beta }_{ij}}{2}\\ D_{ijklmn}^\text {M}&= \bar{D}_{ijklmn} - C_{ijlm}^\text {M}I_{kn}\\ \gamma _{ijk}^\text {M}&= -\frac{\bar{\gamma }_{ijk}}{2}\\ a^\text {M}&= - \bar{a}\\ c^\text {M}&= \frac{\bar{c}}{2} \end{aligned}\end{aligned}$$
(61)

It should be noted that in Eq. (60), parameters such as thermoelastic interaction \(\bar{\beta }_{ab}\) or coupling constant \(\bar{\gamma }_{ab}\) show the contribution from both mechanical (stiffness matrix) and thermal (thermoelastic interaction) parameters.

3 Heat conduction

For the sake of completeness, we additionally calculate homogenized value of thermal conductivity, \({\varvec{\kappa }}\). We begin with Eq. (22) and Fourier’s law which leads to

$$\begin{aligned} \begin{aligned} \Big ( \kappa _{ij}^\text {m}T _{,j}^\text {m}\Big )_{,i} - \rho ^\text {m}r = 0 \end{aligned}\end{aligned}$$
(62)

Following the same procedure as in Sect. 2.2 and expanding the microscale temperature field for the RVE with the same accuracy up to the first order in \(\epsilon \) as follows:

$$\begin{aligned} T ^\text {m}({\varvec{X}}) = \underbrace{\overset{0}{ T }({\varvec{X}},{\varvec{y}}) + \epsilon \overset{1}{ T }({\varvec{X}},{\varvec{y}}) + \mathcal {O}(\epsilon ^2)}_{\text {Expanded microscale temperature field}} \end{aligned}$$
(63)

We are only interested in expansion up to \(\overset{1}{ T }\), as thermal conductivity contains only gradient of temperature which corresponds to expansion up to and including the first-order. In other words, we start with Fourier’s equation at the microscale and result in Fourier’s equation at the macroscale,

$$\begin{aligned} \begin{aligned} \Big ( \kappa _{ij}^\text {M}T_{,j}^\text {M}\Big )_{,i} - \rho ^\text {M}r = 0 . \end{aligned}\end{aligned}$$
(64)

Hence, we obtain

$$\begin{aligned} \begin{aligned} r = \frac{1}{\rho ^\text {M}} \Big ( \kappa _{ij}^\text {M}T_{,j}^\text {M}\Big )_{,i} \end{aligned}\end{aligned}$$
(65)

Substituting local coordinate \({\varvec{y}}\) into Eq. (63), and taking the first derivatives leads to:

$$\begin{aligned} \begin{aligned} T ^\text {m}_{,j} = \overset{0}{ T }_{,j} + \frac{1}{\epsilon }\frac{\partial \overset{0}{ T }}{\partial y_j} + \epsilon \overset{1}{ T }_{,j} + \frac{\partial \overset{1}{ T }}{\partial y_j} + \mathcal {O}(\epsilon ^2) \ . \end{aligned}\end{aligned}$$
(66)

With Eqs. (66) and  (62), we obtain an asymptotically expanded governing equation:

$$\begin{aligned} \begin{aligned}&\bigg [\kappa ^\text {m}_{ij}\bigg (\overset{0}{ T }_{,j} + \frac{1}{\epsilon }\frac{\partial \overset{0}{ T }}{\partial y_j} + \epsilon \overset{1}{ T }_{,j} + \frac{\partial \overset{1}{ T }}{\partial y_j} + \epsilon ^2\overset{2}{ T }_{,j} + \epsilon \frac{\partial \overset{2}{ T }}{\partial y_j}\bigg )\bigg ]_{,i}\\&+ \frac{1}{\epsilon }\frac{\partial }{\partial y_i}\bigg [\kappa ^\text {m}_{ij}\bigg (\overset{0}{ T }_{,j} + \frac{1}{\epsilon }\frac{\partial \overset{0}{ T }}{\partial y_j} + \epsilon \overset{1}{ T }_{,j} + \frac{\partial \overset{1}{ T }}{\partial y_j} + \epsilon ^2\overset{2}{ T }_{,j} + \epsilon \frac{\partial \overset{2}{ T }}{\partial y_j}\bigg )\bigg ] -\rho ^\text {m}r = 0 \end{aligned} \end{aligned}$$
(67)

Rearranging coefficients with the same order of \(\epsilon \) in Eq. (67) leads to:

  • \(\epsilon ^{-2}\)

    $$\begin{aligned} \frac{\partial }{\partial y_i}\bigg ( {\kappa _{ij}^\text {m}} \frac{\partial \overset{0}{ T }}{\partial y_j}\bigg ) = 0 , \end{aligned}$$
    (68)

  • \(\epsilon ^{-1}\)

    $$\begin{aligned} \bigg ({\kappa _{ij}^\text {m}} \frac{\partial \overset{0}{ T }}{\partial y_j}\bigg )_{,i} + \frac{\partial }{\partial y_i} \Big ( {\kappa _{ij}^\text {m}} \overset{0}{ T }_{,j} \Big ) + \frac{\partial }{\partial y_i}\bigg ( {\kappa _{ij}^\text {m}} \frac{\partial \overset{1}{ T }}{\partial y_j}\bigg ) = 0 , \end{aligned}$$
    (69)

  • \(\epsilon ^0\)

    $$\begin{aligned} \big ({\kappa _{ij}^\text {m}} \overset{0}{ T }_{,j} \big )_{,i} + \bigg ( {\kappa _{ij}^\text {m}} \frac{\partial \overset{1}{ T }}{\partial y_j}\bigg )_{,i} + \frac{\partial }{\partial y_i}\big ( {\kappa _{ij}^\text {m}} \overset{1}{ T }_{,j} \big ) - \rho ^\text {m}r = 0 , \end{aligned}$$
    (70)

Only possible solution for Eq. (68) is to define \(\overset{0}{ T }\) as a function of \({\varvec{X}}\) as \(\kappa ^\text {m}_{ij}\) depends on local variable \({\varvec{y}}\). This observation leads to a straightforward conclusion,

$$\begin{aligned} \overset{0}{ T }({\varvec{X}}) = { T }^\text {M}({\varvec{X}}) , \, \overset{1}{T}({\varvec{X}}, {\varvec{y}}) = -R_j({\varvec{y}}) T^\text {M}_{,j}({\varvec{X}}). \end{aligned}$$
(71)

By imposing Eq. (71) in Eq. (69), we obtain

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial y_i} \bigg ( \kappa ^\text {m}_{ij} T^\text {M}_{,j} - \kappa ^\text {m}_{ij} \frac{\partial R_k }{\partial y_j} T^\text {M}_{,k} \bigg ) = 0 , \\ \frac{\partial }{\partial y_i} \bigg ( \kappa ^\text {m}_{ij} - \kappa ^\text {m}_{ik} \frac{\partial R_j }{\partial y_k} \bigg ) T^\text {M}_{,j} = 0 , \\ \frac{\partial }{\partial y_i} \bigg ( \kappa ^\text {m}_{ij} - \kappa ^\text {m}_{ik} \frac{\partial R_j }{\partial y_k} \bigg ) = 0 , \end{aligned}\end{aligned}$$
(72)

since \(T^\text {M}=T^\text {M}({\varvec{X}})\), solution of the governing equation Eq. (72) is y-periodic function \(R_i\). Inserting Eq. (71) into Eq. (70), we get the following expression:

$$\begin{aligned} \begin{aligned} \Big ( \kappa _{ij}^\text {m}T^\text {M}_{,j} - \kappa _{ip}^\text {m}\frac{\partial R_j}{\partial y_p} T^\text {M}_{,j} \Big )_{,i} - \frac{\partial }{\partial y_i} \Big ( \kappa _{ij}^\text {m}T^\text {M}_{,aj} R_a \Big ) - \rho ^\text {m}r = 0 , \\ \Big ( \kappa _{ij}^\text {m}T^\text {M}_{,j} - \kappa _{ip}^\text {m}\frac{\partial R_j}{\partial y_p} T^\text {M}_{,j} \Big )_{,i} - \frac{\partial }{\partial y_i} \Big ( \kappa _{ij}^\text {m}T^\text {M}_{,aj} R_a \Big ) - \frac{\rho ^\text {m}}{\rho ^\text {M}} \Big ( \kappa _{ij}^\text {M}T^\text {M}_{,j} \Big )_{,i} = 0 , \end{aligned}\end{aligned}$$
(73)

where we have utilized Eq. (65). Since the second gradient in \(T^\text {M}\) is vanished, we obtain

$$\begin{aligned} \begin{aligned} \kappa _{ij}^\text {M}= \rho ^\text {M}\int _\Omega \frac{1}{\rho ^\text {m}} \bigg ( \kappa _{ij}^\text {m}- \kappa _{ip}^\text {m}\frac{\partial R_j}{\partial y_p} \bigg ) \, \hbox {d}V. \end{aligned}\end{aligned}$$
(74)

3.1 Numerical implementation in FEniCS

Calculation of macroscale parameters in Eqs. (61) and  (74) requires the solution of \(P_i\), \(\varphi _{abi}\), \(\psi _{abci}\), and \(R_j\) tensors from Eqs. (45),  (50),  (44), and  (72). To numerically solve these equations, two steps have been taken. First, an RVE, \(\Omega \), with periodic boundary conditions has been created in Salome [9]. The solutions of y-periodic fields, \(P_i\), \(\varphi _{abi}\), \(\psi _{abci}\), and \(R_j\), requires periodicity condition to be satisfied, thus each surface and their corresponding surface must have an identical discretization. This was achieved through projection method in Salome. Second, the weak form is implemented in a Python code to be solved by an open-source packages developed by the FEniCS project [10]. The weak form is obtained by the standard variational formulation by multiplying the governing equation by an arbitrary test function and integrating by parts to reduce the regularity condition of the discrete functions. Discretization for the finite element method (FEM) is established by polynomial form functions with Galerkin method, where the same functional forms are used for both approximate solution and the test functions. For representing a vector, for example, \(P_i\) in 2D \(i=1,2\), we use the Hilbertian Sobolev space, \({\mathscr {H}}^n\) of polynomial order, n,

$$\begin{aligned} \begin{aligned} {\mathscr {V}} =\Bigg \{ \big \{ P_1, P_2 \big \} \in [ {\mathscr {H}}^{n}(\Omega ) ]^\text {DOF} : \big \{ P_1, P_2 \big \} = \text {given} \ \forall {\varvec{x}} \in \partial \Omega _\text {D} \Bigg \} . \end{aligned}\end{aligned}$$
(75)

hence, we use standard (continuous) Lagrange elements in the FEM [72]. As known in the Galerkin approach, we use the same type of a functional space for test functions,

$$\begin{aligned} \begin{aligned} \bar{{\mathscr {V}}} =\Bigg \{ \big \{ \updelta w_1, \updelta w_2 \big \} \in [ {\mathscr {H}}^{n}(\Omega ) ]^\text {DOF} : \big \{ \updelta w_1, \updelta w_2 \big \} = 0 \ \forall {\varvec{x}} \in \partial \Omega _\text {D} \Bigg \} , \end{aligned}\end{aligned}$$
(76)

where we skip testing the solution at Dirichlet boundaries, \(\Omega _\text {D}\), with the known solution. The computational domain, \(\Omega \), is the image of the RVE with the Dirichlet type boundary conditions, \(\Omega _\text {D}\) imposed as periodic boundaries for all fields.

This calculation is done by solving the corresponding weak forms for governing equations in Eqs. (45),  (50),  (44), and  (72), respectively,

$$\begin{aligned} P_i\Leftarrow & {} \int _\Omega \Bigg ( C^\text {m}_{ijkl}\frac{\partial P_{k}}{\partial y_l} +\beta ^\text {m}_{ij} \Bigg ) \updelta w_{i,j} \, \hbox {d}V = 0 , \nonumber \\ \psi _{abci}\Leftarrow & {} \int _\Omega \Bigg [ -\bigg ( C^\text {m}_{ijkl} \frac{\partial \psi _{abck}}{\partial y_l} + C^\text {m}_{ijkl} \varphi _{abk}\delta _{cl} \bigg ) \updelta w_{i,j} + C^\text {m}_{ickl}\bigg (\frac{\partial \varphi _{abk}}{\partial y_l} +\delta _{ak}\delta _{lb} \bigg ) \updelta w_i \nonumber \\{} & {} - \frac{\rho ^\text {m}}{\rho ^\text {M}}C^\text {M}_{icab} \updelta w_i \Bigg ] \, \hbox {d}V = 0, \nonumber \\ \varphi _{abi}\Leftarrow & {} \int _\Omega C^\text {m}_{ijkl}\bigg (\frac{\partial \varphi _{abk}}{\partial y_l} +\delta _{ak}\delta _{bl} \bigg ) \updelta w_{i,j} \, \hbox {d}V = 0 , \nonumber \\ R_j\Leftarrow & {} \int _\Omega \bigg ( \kappa ^\text {m}_{ij} - \kappa ^\text {m}_{ik} \frac{\partial R_j }{\partial y_k} \bigg ) \updelta w_{j,i}= 0 . \end{aligned}$$
(77)

Solutions of these fields are then used to construct the macroscale parameters as illustrated in Fig. 2.

Fig. 2
figure 2

Workflow describing model initialization and solution of the model in FEniCS Solver

Full size image

4 Case studies

In this section, we purposefully selected two case studies to verify and illustrate the importance of homogenized parameters introduced in this paper.

  • Case study I is a homogeneous bulk material (Fig. 3a) to verify that higher-order parameters vanish due to homogeneity, \({\mathbb {G}}^\text {M}=0\), \({\mathbb {D}}^\text {M}=0\), and \(\mathbb {\gamma }^\text {M}=0\).

  • Case study II is defined as a porous material where three distinct geometries with exact porosity are investigated (Fig. 3b–d). These cases were carefully designed for comparison with our previous work on higher-order homogenization in which only the mechanical response of porous structures was extensively investigated [65].

Fig. 3
figure 3

Schematic of the RVEs used in case studies I and II: a homogeneous, b circular pore, c uniformly distrusted pores, and d) randomly distributed pores. All porous RVEs have 20% porosity

Full size image

The material used in all cases is aluminum, with a linear elastic constitutive model at the microscale. Figure 4 illustrates a Scanning Electron Microscopy (SEM) of aluminum foam highlighting the underlying porous structures.

Fig. 4
figure 4

Micrograph of the solid-gas eutectic solidification (Gasar) aluminium foam Gergely [28]

Full size image

Table 1 shows the properties used in these cases. It should be noted that the temperature \(T^\text {M}\) is set equal to 400 K in both cases studies and was used to calculate \(a^\text {M}\).

Table 1 Material data for aluminium from Özdemir et al [52]
Full size table

For a better representation of parameters, we use Voigt’s notation. In the case of stiffness tensor, the matrix notation reads

$$\begin{aligned} \begin{aligned} C^\text {M}_{ijkl} \hat{=} C^\text {M}_{AB} = \begin{pmatrix} C^\text {M}_{1111} &{} C^\text {M}_{1122} &{} C^\text {M}_{1112} \\ C^\text {M}_{2211} &{} C^\text {M}_{2222} &{} C^\text {M}_{2212} \\ C^\text {M}_{1211} &{} C^\text {M}_{1222} &{} C^\text {M}_{1212} \\ \end{pmatrix}, \end{aligned}\end{aligned}$$
(78)

where \(A=\{1,2,3\}\) are used to replace \(ij=\{11,22,12\}\). Similarly, we use \(\theta =\{1,2,3,4,5,6\}\) instead of \(ijk=\{111, 112, 221, 222, 121, 122\}\) such that we have:

$$\begin{aligned}{} & {} \begin{aligned} G^\text {M}_{ijklm}&\hat{=} G^\text {M}_{A\theta } = \begin{pmatrix} G^\text {M}_{11111} &{} G^\text {M}_{11112} &{} G^\text {M}_{11221} &{} G^\text {M}_{11222} &{} G^\text {M}_{11121} &{} G^\text {M}_{11122} \\ G^\text {M}_{22111} &{} G^\text {M}_{22112} &{} G^\text {M}_{22221} &{} G^\text {M}_{22222} &{} G^\text {M}_{22121} &{} G^\text {M}_{22122} \\ G^\text {M}_{12111} &{} G^\text {M}_{12112} &{} G^\text {M}_{12221} &{} G^\text {M}_{12222} &{} G^\text {M}_{12121} &{} G^\text {M}_{12122} \end{pmatrix} \end{aligned} \end{aligned}$$
(79)
$$\begin{aligned}{} & {} \begin{aligned} D^\text {M}_{ijklmn}&\hat{=}\, D^\text {M}_{\theta \gamma } = \begin{pmatrix} D^\text {M}_{111111} &{} D^\text {M}_{111112} &{} D^\text {M}_{111221} &{} D^\text {M}_{111222} &{} D^\text {M}_{111121} &{} D^\text {M}_{111122} \\ D^\text {M}_{112111} &{} D^\text {M}_{112112} &{} D^\text {M}_{112221} &{} D^\text {M}_{112222} &{} D^\text {M}_{112121} &{} D^\text {M}_{112122} \\ D^\text {M}_{221111} &{} D^\text {M}_{221112} &{} D^\text {M}_{221221} &{} D^\text {M}_{221222} &{} D^\text {M}_{221121} &{} D^\text {M}_{221122} \\ D^\text {M}_{222111} &{} D^\text {M}_{222112} &{} D^\text {M}_{222221} &{} D^\text {M}_{222222} &{} D^\text {M}_{222121} &{} D^\text {M}_{222122} \\ D^\text {M}_{121111} &{} D^\text {M}_{121112} &{} D^\text {M}_{121221} &{} D^\text {M}_{121222} &{} D^\text {M}_{121121} &{} D^\text {M}_{121122}\\ D^\text {M}_{122111} &{} D^\text {M}_{122112} &{} D^\text {M}_{122221} &{} D^\text {M}_{122222} &{} D^\text {M}_{122121} &{} D^\text {M}_{122122} \end{pmatrix} , \end{aligned} \end{aligned}$$
(80)
$$\begin{aligned}{} & {} \begin{aligned} \gamma ^\text {M}_{ijk}&\hat{=}\, \gamma ^\text {M}_{Ak} = \begin{pmatrix} \gamma ^\text {M}_{111} &{} \gamma ^\text {M}_{112} \\ \gamma ^\text {M}_{221} &{} \gamma ^\text {M}_{222} \\ \gamma ^\text {M}_{121} &{} \gamma ^\text {M}_{122} \\ \end{pmatrix} . \end{aligned} \end{aligned}$$
(81)

4.1 Case study I: bulk structure

In the case of homogeneous bulk system shown in Fig. 3a, we expect to retrieve classical continuum mechanics solution where higher-order parameters will vanish and homogenized parameters \({{\mathbb {C}}^\text {M}}\) and \({\mathbb {\beta }^\text {M}}\) have the same values as the microscale values.

$$\begin{aligned} C^\text {M}_{AB}= & {} \begin{pmatrix} 84165.6 &{} 27774.7 &{} 0.0 \\ 27774.7 &{} 84165.6 &{} 0.0 \\ 0.0 &{} 0.0 &{} 28195.5\\ \end{pmatrix} \text {MPa}\ , \ \beta ^\text {M}_{ij} = \begin{pmatrix} -2.64 &{} 0.0 \\ 0.0 &{} -2.64 \\ \end{pmatrix} \text {MPa/K} , \end{aligned}$$
(82)
$$\begin{aligned} G^\text {M}_{A\theta }= & {} \begin{pmatrix} 0.0 &{} 0.0 &{} 0.0&{} 0.0 &{} 0.0 &{} 0.0 \\ 0.0 &{} 0.0 &{} 0.0&{} 0.0 &{} 0.0 &{} 0.0 \\ 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 \end{pmatrix} \text {N/mm} , \end{aligned}$$
(83)
$$\begin{aligned} \gamma ^\text {M}_{Ak}= & {} \begin{pmatrix} 0.0 &{} 0.0\\ 0.0 &{} 0.0\\ 0.0 &{} 0.0\\ \end{pmatrix} \text {N/K} , \end{aligned}$$
(84)
$$\begin{aligned} D^\text {M}_{\theta \gamma }= & {} \begin{pmatrix} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0\\ 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0\\ 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0\\ 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0\\ 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0\\ 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 &{} 0.0 \end{pmatrix} \text {N} , \end{aligned}$$
(85)
$$\begin{aligned} \kappa ^\text {M}_{ij}= & {} \begin{pmatrix} 247.0 &{} 0.0 \\ 0.0 &{} 247.0 \\ \end{pmatrix} \text {W/mK} , \end{aligned}$$
(86)

According to Eq. (60), heat capacity \(c^\text {M}\) follows the rule of mixture, while associated parameter \(a^\text {M}\) is related to \(c^\text {M}\) through the Eq. (13).

$$\begin{aligned} c^\text {M}= 0.9\, , \,a^\text {M}= 0.00225 = \frac{0.9}{400} \end{aligned}$$
(87)

4.2 Case study II: porous structure

We emphasize that the higher-gradient is often neglected in composite materials. During the classical homogenization by volume averaging, thermoelastic parameters are obtained in the similar fashion as presented in this paper. However, the differences between this work and the classical homogenization is in higher-order parameters where their significance depends on the chosen length-scale (please refer to the numerical study presented in Abali et al. [4]).

4.2.1 RVE with a single circular pore

In the case of a single centrally located pore as shown in Fig. 3b, we observe cubic material behavior by inspecting the stiffness tensors components, \(C^\text {M}_{11} = C^\text {M}_{22}\). As we assumed constant temperature, the thermoelastic interaction, \({\mathbb {\beta }^\text {M}}\), is solely a function of geometry. In other words, it affects only the volumetric component of thermal strain. Higher-order parameters \({{\mathbb {G}}^\text {M}}\) and \({\mathbb {\gamma }^\text {M}}\) are close to zero due to the centro-symmetry of the RVE with one centrally located pore. However, as one can see, the higher-order parameters manifest in tensor \({{\mathbb {D}}^\text {M}}\).

$$\begin{aligned} C^\text {M}_{AB}= & {} \begin{pmatrix} 49935.8 &{} 14164.6 &{} 0.0 \\ 14164.6 &{} 49935.9 &{} 0.0 \\ 0.0 &{} 0.0 &{} 13570.9 \\ \end{pmatrix} \text {MPa} , \ \beta ^\text {M}_{ij} = \begin{pmatrix} -1.51 &{} 0.0 \\ 0.0 &{} -1.51 \\ \end{pmatrix} \text {MPa/K} , \end{aligned}$$
(88)
$$\begin{aligned} G^\text {M}_{A\theta }= & {} \begin{pmatrix} -0.7 &{} 1.0 &{} -8.7 &{} -0.7 &{} -1.2 &{} 0.0\\ -0.2 &{} 0.3 &{} -2.5 &{} -2.6 &{} -4.2 &{} -0.1\\ -0.7 &{} -1.1 &{} 0.0 &{} -0.2 &{} 0.3 &{} -2.3&{} \end{pmatrix} \text {N/mm} , \end{aligned}$$
(89)
$$\begin{aligned} \gamma ^\text {M}_{Ak}= & {} \begin{pmatrix} 0.0 &{} 0.0\\ 0.0 &{} 0.0\\ 0.0 &{} 0.0 \end{pmatrix} \text {N/K} , \end{aligned}$$
(90)
$$\begin{aligned} D^\text {M}_{\theta \gamma }= & {} \begin{pmatrix} -1351.692 &{} -782.368 &{} -327.905 &{} -0.001 &{} -0.002 &{} 0.003\\ -782.368 &{} 2006.51 &{} 626.348 &{} 0.0 &{} 0.001 &{} 0.0\\ -327.905 &{} 626.348 &{} -37.827 &{} 0.0 &{} 0.0 &{} -0.002\\ -0.001 &{} 0.0 &{} 0.0 &{} -1351.697 &{} -782.372 &{} -327.905\\ -0.002 &{} 0.001 &{} 0.0 &{} -782.372 &{} 2006.502 &{} 626.349\\ 0.003 &{} 0.0 &{} -0.002 &{} -327.905 &{} 626.349 &{} -37.816 \end{pmatrix} \text {N} , \end{aligned}$$
(91)
$$\begin{aligned} \kappa ^\text {M}_{ij}= & {} \begin{pmatrix} 205.9 &{} 0.0 \\ 0.0 &{} 205.9 \\ \end{pmatrix} \text {W/mK} , \end{aligned}$$
(92)

Similar to case I, \(c^\text {M}\) and \(a^\text {M}\) can be calculated from Eqs. (60) and  (13) respectively.

$$\begin{aligned} c^\text {M}= 0.72 = (1-20\%)\times 0.9\, , \,a^\text {M}= 0.0018 = \frac{0.72}{400} \end{aligned}$$
(93)

4.2.2 RVE with uniformly distributed pores

In the case of uniformly distributed pores as shown in Fig. 3c, we observe similar stiffness tensor as the one reported in a case with a single pore. This is simply due to the fact that the porosity was kept the same in both RVEs. As it was mentioned before the stiffness tensor depends on the porosity and the higher-order parameters depend on the homothetic ratio \(\epsilon \). Thus, higher-order parameters are able to account for the RVE size.

$$\begin{aligned} C^\text {M}_{AB}= & {} \begin{pmatrix} 50009.6 &{} 14182.9 &{} 0.0 \\ 14182.9 &{} 50009.8 &{} 0.0 \\ 0.0 &{} 0.0 &{} 13625.3 \\ \end{pmatrix} \text {MPa} , \ \beta ^\text {M}_{ij} = \begin{pmatrix} -1.51 &{} 0.0 \\ 0.0 &{} -1.51 \\ \end{pmatrix} \text {MPa/K} , \end{aligned}$$
(94)
$$\begin{aligned} G^\text {M}_{A\theta }= & {} \begin{pmatrix} 0.1 &{} 1.2 &{} -3.2 &{} 0.2 &{} -0.5 &{} -0.8 \\ 0.0 &{} 0.3 &{} -0.9 &{} 0.6 &{} -1.8 &{} -2.8 \\ 0.1 &{} -0.5 &{} -0.7 &{} 0.1 &{} 0.3 &{} -0.9 \end{pmatrix} \text {N/mm} , \end{aligned}$$
(95)
$$\begin{aligned} \gamma ^\text {M}_{Ak}= & {} \begin{pmatrix} 0.0 &{} 0.0\\ 0.0 &{} 0.0\\ 0.0 &{} 0.0 \end{pmatrix} \text {N/K} , \end{aligned}$$
(96)
$$\begin{aligned} D^\text {M}_{\theta \gamma }= & {} \begin{pmatrix} -338.017 &{} -194.6 &{} -81.655 &{} -0.002 &{} -0.038 &{} -0.015\\ -194.6 &{} 500.881 &{} 155.739 &{} 0.026 &{} 0.001 &{} 0.003\\ -81.655 &{} 155.739 &{} -9.859 &{} 0.001 &{} -0.031 &{} -0.007\\ -0.002 &{} 0.026 &{} 0.001 &{} -337.971 &{} -194.617 &{} -81.662\\ -0.038 &{} 0.001 &{} -0.031 &{} -194.617 &{} 500.888 &{} 155.733\\ -0.015 &{} 0.003 &{} -0.007 &{} -81.662 &{} 155.733 &{} -9.817 \end{pmatrix} \text {N} , \end{aligned}$$
(97)
$$\begin{aligned} \kappa ^\text {M}_{ij}= & {} \begin{pmatrix} 206.0 &{} 0.0 \\ 0.0 &{} 206.0 \\ \end{pmatrix} \text {W/mK} , \end{aligned}$$
(98)
$$\begin{aligned} c^\text {M}= & {} 0.72 = (1-20\%)\times 0.9\, , \,a^\text {M}= 0.0017 \approx \frac{0.72}{400} \end{aligned}$$
(99)

4.2.3 RVE with randomly distributed pores

In the case of randomly distributed pores as shown in Fig. 3d, the microscale structure creates an anisotropic material behavior at the macroscale, shown by non-zero off-diagonal values in \({\mathbb {C}}^\text {M}\). Thermoelastic interaction, \(\mathbb {\beta }^\text {M}\), is again a function of geometry similar to both single and uniformly distributed pore case. However, this randomness in the structure manifest in the shear components of the thermal strain compared with previous cases. Moreover, higher-order parameters \({{\mathbb {G}}^\text {M}}\) and \({\mathbb {\gamma }^\text {M}}\) are no longer zeros as the random distribution breaks the centro-symmetry of the RVE. The \({{\mathbb {D}}^\text {M}}\) is also affected by the random distribution of the pores. A quick comparison between this case with the single pore and uniform distributed pores reveals an anisotropic behavior due to the randomness of the structure. The results for all of the parameters are shown below.

$$\begin{aligned} C^\text {M}_{AB}= & {} \begin{pmatrix} 48494.4 &{} 15572.7 &{} 738.1 \\ 15572.7 &{} 48305.7 &{} 124.8 \\ 738.1 &{} 124.8 &{} 14880.7 \\ \end{pmatrix} \text {MPa}, \ \beta ^\text {M}_{ij} = \begin{pmatrix} -1.51 &{} -0.02 \\ -0.02 &{} -1.51 \\ \end{pmatrix} \text {MPa/K} , \end{aligned}$$
(100)
$$\begin{aligned} G^\text {M}_{A\theta }= & {} \begin{pmatrix} 7.8 &{} -27.2 &{} 2.6 &{} 277.8 &{} -136.3 &{} 13.4\\ -38.6 &{} 519.1 &{} 28.9 &{} -131.0 &{} -340.6 &{} 19.1\\ -4.5 &{} -21.3 &{} 30.2 &{} -29.0 &{} 15.5 &{} -207.0 \end{pmatrix} \text {N/mm} , \end{aligned}$$
(101)
$$\begin{aligned} \gamma ^\text {M}_{Ak}= & {} \begin{pmatrix} 0.00256 &{} 0.01498\\ 0.01204 &{} 0.01823\\ -0.00324 &{} 0.00612 \end{pmatrix} \text {N/K} , \end{aligned}$$
(102)
$$\begin{aligned} D^\text {M}_{\theta \gamma }= & {} \begin{pmatrix} -862.421 &{} -396.974 &{} -49.151 &{} -175.055 &{} 222.629 &{} 71.895\\ -396.974 &{} 981.41 &{} 204.585 &{} 201.93 &{} -154.281 &{} 49.659\\ -49.151 &{} 204.585 &{} -160.335 &{} 137.948 &{} 46.779 &{} -111.412\\ -175.055 &{} 201.93 &{} 137.948 &{} -640.54 &{} -354.525 &{} -1.8\\ 222.629 &{} -154.281 &{} 46.779 &{} -354.525 &{} 919.989 &{} 94.141\\ 71.895 &{} 49.659 &{} -111.412 &{} -1.8 &{} 94.141 &{} -273.504 \end{pmatrix} \text {N} , \end{aligned}$$
(103)
$$\begin{aligned} \kappa ^\text {M}_{ij}= & {} \begin{pmatrix} 206.0 &{} 0.0 \\ 0.0 &{} 206.0 \\ \end{pmatrix} \text {W/mK} , \end{aligned}$$
(104)
$$\begin{aligned} c^\text {M}= 0.72= & {} (1-20\%)\times 0.9\, , \,a^\text {M}= 0.0017 \approx \frac{0.72}{400} \end{aligned}$$
(105)

5 Conclusion

In this paper, we first introduced a theoretical framework for generalized thermomechanics through asymptotic homogenization and we then discussed how it was numerically implemented within FEniCS open-source computing platform. This model incorporates microstructural effects through higher-order thermal and mechanical material parameters at the macroscale. On the mechanical side, we considered stiffness matrix \({\mathbb {C}}^\text {M}\) and higher-order parameters \({\mathbb {D}}^\text {M}\) and \({\mathbb {G}}^\text {M}\), while on the thermal side, we accounted for thermoelastic interaction \(\mathbb {\beta }^\text {M}\) and higher-order parameter \(\mathbb {\gamma }^\text {M}\). All macroscale thermal and mechanical parameters are explicitly computed by assuming a linear thermoelastic material behavior at the microscale.

As mentioned above, FEniCS platform was used to solve the partial differential equations generated from the homogenization procedure. The methodology was verified by using a case study with homogeneous microstructure where the influence of higher-order parameters vanished and homogeneous parameters were recovered. Moreover, a porous materials with different RVEs (i.e., single pore, uniform and randomly distributed pores) were studied. These cases showed that thermoelastic interaction \(\mathbb {\beta }^\text {M}\) has a similar sensitivity to pore morphology as the stiffness matrix \({\mathbb {C}}^\text {M}\) while higher-order thermal parameters \(\mathbb {\gamma }^\text {M}\) mirror the response of the higher-order mechanical parameter \({\mathbb {G}}^\text {M}\) as both of them are linearly dependent on the size of the RVE and have the same behavior with respect to the centro-symmetry of the RVE. Even though these numerical results for thermal parameters still need an in-depth numerical analysis and experimental data for validation, this theoretical framework and its numerical implementation serves as a means to future research for a better understanding of the interplay between microscale morphology and thermo-mechanical material parameters.