1 Introduction

Metal-forming technologies and processes offer a variety of options to influence a product’s final properties. The evocation and adjustment of internal stresses by calibration of forming conditions has been shown in [7, 9, 39, 42, 48, 52, 78]. In particular, hot bulk forming offers the opportunity to use the interactions of thermal, chemical and metallurgical parameters to influence residual stresses. For instance, based on specific cooling strategies, compressive residual stresses shall be induced on the surface, which are assumed to improve the final component’s properties, e.g., higher resistance with respect to fatigue cracking and surface abrasion.

Following the definitions in [25, 40, 85, 86], stresses existing in a closed system in absence of outer forces or moments but fulfill mechanical equilibrium, are called residual stresses. They are typically distinguished into three types, which are characterized by the scale they act on. Thus, residual stresses of first type refer to a certain macroscopic section of the component or the average of some grains, while residual stresses of second and third type are defined on one grain or a number of atoms, respectively. As a consequence, the latter two types can be interpreted as deviations of the stress amplitudes from the first type and are often referred to as microscopic residual stresses. Since residual stresses of second type influence the macroscopic residual stresses of first type, which are most important with regard to the final component’s properties, close attention has to be paid to the microscopic residual stress evolution.

In current research, a focus is dedicated to the distinction between the different types of residual stresses both in experiments and numerical simulations. Early experimental measurements are presented, e.g., in [14, 53], which take into account the scale separation of macroscopic and microscopic residual stresses. A multiscale analysis of residual stresses arising from a thermo-mechanical problem is given in [18]. More recent works show a great variety of applications. In [22], a multiscale self-consistent model regarding the effects of second and third type residual stresses on the Bauschinger effect at the macroscopic level is given. The work of [23] concerns a methodology to quantify the magnitude of the microscopic residual stresses with spectroscopy for ceramics, while [91] gives a predictive model for macroscopic and microscopic residual stresses considering thermo-mechanical effects. Moreover, in [10], an approach for the computation of microscopic residual stresses for single-phase materials is proposed. Different attempts using multiscale models are, e.g., [89] or [60], in which a crystal plasticity finite element model is used. [71] computes macroscopic and phase-specific residual stresses for a deep drawing process of lean duplex steels. The consequence of microstructural residual stresses on the mechanical behavior of additively manufactured steels is described, e.g., in [8]. For further recent investigations in the research field of residual stresses in production technology see [84].

Residual stresses can be evoked by solid–solid phase transformation, for which different numerical models have been discussed in the last decades. For example, in [37, 72, 76], volume fractions of the occurring phases are introduced to distinguish between the kinetics of the phases. Early thermo-mechanical approaches have been given in [15, 30,31,32,33]. A description of the principles of general phase transformation can be found in [34, 35, 38], among others, while [36] focuses especially on martensitic transformation. [13] proposes a continuum mechanical formulation, whereas the work of [59] shows the experimental side, which can be compared to simulations as done, e.g., by [3]. A phenomenological approach has been proposed in [41], and the use of crystal plasticity has been formulated in [61]. Another possibility to describe phase transformation is the application of the Phase-Field Theory as done for instance in [51, 62,63,64], relying on [55, 56], which characterize the phase transformation on the atomic lattice. In order to illustrate the austenite-to-martensite phase transformation on atomic scale, the so-called Bain groups can be applied. They describe the lattice shearing from an initial austenitic to martensitic unit cell. The fundamental work is proposed in [1, 2], and further applications can be found in [50] or [6].

In view of the definition of residual stress of first, second and third type, the application of a multi-scale method is reasonable to account for residual stress acting on different scales. The direct micro-macro transition approach for computational homogenization has been in the focus of research in the last decades. The classical description of the so-called \(\hbox {FE}^2\)-method is proposed in [11, 12, 16, 17, 27, 43, 45,46,47, 49, 65, 66, 74, 75, 81, 82], in which various aspects such as suitable boundary conditions or different mathematical treatments are discussed. The thermo-mechanical coupling in two-scale problems is presented in [57, 58, 68, 79, 80]. Further multi-physics models, such as magnetic-, electric- or ferroelectric-mechanical coupling, are treated in, e.g., [28, 67, 88].

This contribution is based on the approach presented in [83]. Therein, macroscopic residual stresses in a hot bulk formed part are analyzed using a two-scale model with focus on aspects of numerical simulation. In the present contribution, a microstructural analysis is performed to describe the evolution of microscopic residual stresses arising from the austenite-to-martensite transformation in the same process using an extended two-scale model. The paper is structured as follows. After introduction, Sect. 2 briefly introduces the experimental and numerical studies, which serve as input data. Afterwards, in Sect. 3, the two-scale finite element model with the associated macroscopic and microscopic boundary value problem is presented. The application of the proposed framework to the cooling process of the hot bulk formed part is described in Sect. 4. The results are evaluated regarding the microscopic stress evolution in particular. The paper is concluded in Sect. 5.

2 Experimental setup and martensite transformation

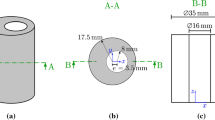
In the focus of the study is a cylindrical specimen with an eccentric hole, the dimensions are defined in Fig. 1. The eccentricity of \(d_x=3.5~\text {mm}\) is chosen in order to provoke inhomogeneous stress distributions following [73]. This specimen is treated in a hot bulk forming process with subsequent cooling as illustrated in Fig. 2. First, it is heated to above \(1000\,\, {}^\circ \text {C}\) in a thermobox, such that full austenitization and a residual stress-free state is achieved. After some holding time, the height is reduced by approximately 50%, still inside the thermobox. Subsequently, the thermobox is removed and the cylinder is cooled in water down to room temperature of \(20\,^\circ \text {C}\) in \(80\,\text {s}\). Afterwards, mechanical measurements are taken regarding the residual stresses of first type near the surface, which can be validated using macroscopic simulations. For these simulations, the MSC.marc solver of the commercial FE software Simufact.forming 14 is utilized to model the experimental setup numerically. Details on the experimental processing and macroscopic material simulations can be found in [4, 5].

Fig. 1
figure 1

Dimensions of considered cylindrical specimen with eccentric hole, \(d_x=3.5\,\text {mm}\), adopted from [83]

Full size image

In this contribution only the cooling process detached from forming is of interest. Required temperature-dependent material parameters, namely bulk modulus \(\kappa \), shear modulus \(\mu \), heat conduction coefficient k, heat expansion coefficient \(\alpha _{\text {T}}\), the product of specific heat capacity and density \(c_\rho \), the yield strength y and the linear hardening parameter h, are determined using JMatPro [24] based on the chemical composition of the considered alloy 1.3505 (100Cr6) given in Table 1. Details on the preparation of the material data are given in Appendix A.1.

Table 1 Chemical composition of the investigated steel alloy 1.3505 used for material data generation with JMatPro
Full size table
Fig. 2
figure 2

Schematic representation of the three process steps, namely heating, forming and cooling, adopted from [83]

Full size image

2.1 Martensite formation

The hot formed and austenitized state of the specimen is taken as the initial state, i.e., \(t=0\,\text {s}\) as illustrated in Fig. 2. It can be considered as stress-free due to the prevalent high temperature. The considered chromium-alloyed steel 1.3505 (100Cr6) in this state consists of a face-centered cubic austenitic lattice. Fast cooling in water below the martensitic start temperature \(\theta _{\text {Ms}}\) leads to a diffusionless phase transformation to martensite, which consists of body-centered tetragonally transformed unit cells. This rearrangement of the atomic lattice is accompanied by a volume expansion of the unit cells, cf. [50]. In the following, a value of 2% is taken into account following the work of [54].

For the evolution of the martensitic volume fraction \(c^{\text {M}}\) in regions below the martensitic start temperature \(\theta _{\text {Ms}}\), the exponential form of the Koistinen–Marburger equation is evaluated, see [26, 29, 87]

$$\begin{aligned} c^{\text {M}} = 1-\exp {\Bigl (-\frac{\theta _{\text {Ms}}-\theta }{\theta _{\text {M0}}}\Bigr )}. \end{aligned}$$
(1)

Therein, \(\theta _{\text {M0}}\) is a temperature independent material parameter, which differs for different alloy compositions. Based on simulative data from the Institute of Forming Technology and Machines (IFUM) at LU Hannover, namely martensitic start temperature \(\theta _{\text {Ms}} = 185\,^\circ \text {C}\) and final process quantities, i.e., room temperature (RT) \(\theta _{\text {RT}} = 20\,^\circ \text {C}\) and the martensitic volume fraction at room temperature \(c^{\text {M}}_{\text {RT}}=0.87\), the alloy-dependent parameter \(\theta _{\text {M0}}\) can be determined by rearranging Eq. (1), i.e.,

$$\begin{aligned}&c^{\text {M}}_{\text {RT}} = 1-\exp {\Bigl (-\frac{\theta _{\text {Ms}}-\theta _{\text {RT}}}{\theta _{\text {M0}}}\Bigr )}\quad \Leftrightarrow \quad \theta _{\text {M0}} = -\frac{\theta _{\text {Ms}}-\theta _{\text {RT}}}{\ln (1- c^{\text {M}}_{\text {RT}})}. \end{aligned}$$
(2)

On the basis of the experiments and macroscopic simulations with Simufact at IFUM mentioned in Sect. 2, the temperature evolution on the outer and inner lateral surface can be illustrated in dependence of the cooling time, cf. Fig. 3. By evaluation of Eq. (1), the related evolution of the martensitic volume fraction on the lateral surface can be illustrated as well. Details on the material modeling of the austenite-to-martensite phase transformation are summarized in Appendix A.2.

Fig. 3
figure 3

Temperature evolution on outer and inner lateral surface and related martensitic volume fraction based on Eq. (1)

Full size image

3 Two-scale finite element simulation

In the case of micro-heterogeneous materials, the direct micro-macro transition approach can be utilized to incorporate microscopic characteristics into the Finite Element Method, see, e.g., [46, 47, 65, 66, 75]. This two-scale computational homogenization scheme takes into account microstructural phenomena in order to compute the macroscopic material behavior. Thereby, the material law of the macroscopic boundary value problem (bvp) is replaced by suitable averages of the solution of microscopic bvps in each macroscopic integration point. In the following, all macroscopic quantities are marked by \({\bar{\bullet }}\), while microscopic quantities remain unmarked, i.e., \(\bullet \).

3.1 Macroscopic boundary value problem

Considering small strains, it holds for the macroscopic body \({\bar{\mathcal {B}}}\in {\mathbb {R}}^2\) that the macroscopic strains are defined as the symmetric gradient of the macroscopic displacements, i.e., \({\bar{{\varvec{\varepsilon }}}} = \nabla _s{\bar{{{{\varvec{u}}}}}}\) with \(\nabla _s\bullet =\frac{1}{2}(\nabla \bullet +\nabla ^\text {T}\bullet )\). For the solution of a thermo-mechanical bvp, the balance of momentum and the balance of energy neglecting outer forces and acceleration terms

$$\begin{aligned} \text {div}\,{\bar{{\varvec{\sigma }}}}={\varvec{0}}\quad \text { and }\quad {\bar{c}}_\rho \,\dot{{\bar{\theta }}}+{\bar{\theta }}\,{\bar{r}} +\text {div}\,{\bar{{{{\varvec{q}}}}}}=0, \end{aligned}$$
(3)

respectively, are taken into account. The occurring macroscopic quantities are the Cauchy stress \({\bar{{\varvec{\sigma }}}}\), the product of specific heat capacity and density, \({\bar{c}}_\rho \), the temperature \({\bar{\theta }}\) and its rate \(\dot{{\bar{\theta }}}\), the cumulative macroscopic heat supply \({\bar{r}}\) and the heat flux vector \({\bar{{{{\varvec{q}}}}}}\). The macroscopic heat flux vector is assumed to equal \({\bar{{{{\varvec{q}}}}}} = -{\bar{k}}\,{\text {grad}}{\bar{\theta }}\) with non-negative heat conduction coefficient \({\bar{k}}\). Since internal heat sources or sinks are neglected, it holds \({\bar{r}}=0\).

Boundary conditions have to be defined for the macroscopic boundary value problem based on the displacement vector \({\bar{{{{\varvec{u}}}}}}\), the macroscopic traction vector \({\bar{{{{\varvec{t}}}}}}\), the macroscopic temperature \({\bar{\theta }}\) and the heat flux on the boundary \({\bar{q}}_0\), i.e.,

(4)

Therein, \({\bar{{{{\varvec{n}}}}}}\) denotes the outer normal on the macroscopic boundary \(\partial \bar{{\mathcal {B}}}\). In general, it has to be fulfilled that

(5)

3.2 Microscopic boundary value problem

On the microscale, a two-dimensional body \(\mathcal {B}\in {\mathbb {R}}^2\) is defined by a representative volume element (RVE), see [20, 21, 90]. Due to the assumed scale separation of macro- and microscale, we consider a steady-state temperature on the microscale without spatial variations within \(\mathcal {B}\). Thus, the microscopic temperature is assumed to be constant in an RVE in each time step, i.e., \(\theta ={\bar{\theta }}\), leading to an isothermal bvp on the microscale. However, the temperature influences the material parameter in the microscopic constitutive equations, see Appendix A.1, and therefore plays an important role on the microscale. Neglecting outer forces and acceleration terms, the balance of momentum \(\mathrm{div}\,\, {\varvec{\sigma }}= {\varvec{0}}\) is considered the microscopic Cauchy stress tensor denoted by \({\varvec{\sigma }}\).

In order to derive microscopic boundary conditions, the Hill–Mandel condition is taken into account, see [21]. It states that the macroscopic stress power is equivalent to the volumetric average of the microscopic stress power, such that it holds

$$\begin{aligned} {\bar{{\varvec{\sigma }}}}:\dot{{\bar{{\varvec{\varepsilon }}}}} = \frac{1}{V_\mathcal {B}}\int _{\mathcal {B}}{\varvec{\sigma }}:{\dot{{\varvec{\varepsilon }}}}\,\text {d}v. \end{aligned}$$
(6)

Therein, \(V_\mathcal {B}\) describes the microscopic volume of the body \(\mathcal {B}\), and \({\dot{{\varvec{\varepsilon }}}}\) and \(\dot{{\bar{{\varvec{\varepsilon }}}}}\) are the microscopic and macroscopic strain rate, respectively. From Eq. (6), different types of boundary conditions can be derived, see, e.g., [66]. In this contribution, periodic boundary conditions are considered, which rely on the decomposition

$$\begin{aligned} {{{\varvec{u}}}}={\bar{{\varvec{\varepsilon }}}}\cdot {{{\varvec{x}}}}+{\tilde{{{{\varvec{w}}}}}},\quad {\tilde{{{{\varvec{w}}}}}}^+ ={\tilde{{{{\varvec{w}}}}}}^-,\quad {{{\varvec{t}}}}^+=-{{{\varvec{t}}}}^- \end{aligned}$$
(7)

with microscopic traction vector \({{{\varvec{t}}}}\) and position vector \({{{\varvec{x}}}}\in \mathcal {B}\). Moreover, \(\bullet ^+\) and \(\bullet ^-\) are quantities at periodically associated points of the boundary of the RVE. The fluctuations of the displacement field are denoted by \({\tilde{{{{\varvec{w}}}}}}\), such that it holds that \({\varvec{\varepsilon }}={\bar{{\varvec{\varepsilon }}}}+{\tilde{{\varvec{\varepsilon }}}}\) with \({\tilde{{\varvec{\varepsilon }}}}=\nabla _s{\tilde{{{{\varvec{w}}}}}}\). Due to the isothermal process in the RVE, no thermal boundary conditions have to be defined. Analogously to the additive decomposition of the strains into a homogeneous and a fluctuation part, a split of the stress tensor can be motivated, i.e.,

$$\begin{aligned} {\varvec{\sigma }}={\bar{{\varvec{\sigma }}}}+{\tilde{{\varvec{\sigma }}}}\quad \text {with}\quad {\bar{{\varvec{\sigma }}}} =\frac{1}{V}\int _{V_\mathcal {B}}{\varvec{\sigma }}\,\mathrm {d}v. \end{aligned}$$
(8)

3.3 Elasto-plastic material model

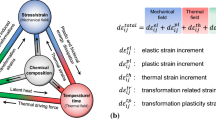
For the material model describing elasto-plastic behavior, we consider the free energy function \(\psi \) which can be divided into mechanical, namely elastic and plastic parts, a thermal and a coupling term. The free energy depends on the elastic strain tensor \({\varvec{\varepsilon }}^{\text {e}}\), the strain-like variable e and the temperature \(\theta \), see [44, 70],

$$\begin{aligned} \psi ({\varvec{\varepsilon }}^{\text {e}},e;\theta )=&\underbrace{ \frac{1}{2}\kappa \,({\text {tr}}{\varvec{\varepsilon }}^{\text {e}})^2+\mu \,\Vert {\text {dev}}{\varvec{\varepsilon }}^{\text {e}}\Vert ^2}_{\text {elastic}}+\,\underbrace{\frac{1}{2}\,h\,e^2}_{\text {plastic}}\,\nonumber \\&-\, \underbrace{c_\rho \,\bigl (\theta \ln \frac{\theta }{\theta _0}-\theta +\theta _0\bigr )}_{\text {thermal}}\,- \underbrace{3\,\alpha _{\text {T}}\,\kappa \,(\theta -\theta _0){\text {tr}}{\varvec{\varepsilon }}^{\text {e}}}_{\text {coupling}}, \end{aligned}$$
(9)

with \({\varvec{\varepsilon }}={\varvec{\varepsilon }}^\text {e}+{\varvec{\varepsilon }}^\text {p}\) and \({\text {dev}}\) as deviatorical operator. Therein, \(\kappa \) denotes the bulk modulus, \(\mu \) the shear modulus, h the linear hardening parameter, \(c_\rho \) the product of specific heat capacity and density, \(\theta _0\) the initial temperature and \(\alpha _{\text {T}}\) the heat expansion coefficient. The microscopic stresses \({\varvec{\sigma }}\) can be derived from the free energy function as

$$\begin{aligned} {\varvec{\sigma }}= \frac{\partial \psi }{\partial {\varvec{\varepsilon }}^\text {e}}\,=\,\kappa \,{\text {tr}}{\varvec{\varepsilon }}^\text {e}\,\mathbf{1}\,+\,2\mu \,{\text {dev}}{\varvec{\varepsilon }}^{\text {e}}\,-\,3\alpha _{\text {T}}\,\kappa \,(\theta -\theta _0)\mathbf{1}, \end{aligned}$$
(10)

which considers the stress response on the microscale based on the steady temperature \(\theta ={{\bar{\theta }}}\). Moreover, a von Mises yield criterion

$$\begin{aligned} \Phi = \Vert {\text {dev}}{\varvec{\sigma }}\Vert \,-\,\sqrt{\frac{2}{3}}\,y\,\le \,0\quad \text {with}\quad y = y_0+\beta \end{aligned}$$
(11)

is chosen following [69], in which y represents the yield stress, which depends on the strain-like variable e and the temperature \(\theta \). In this context, e is to be interpreted as accumulated plastic strains defined for computation time t in dependence of the plastic strain rate \({\dot{{\varvec{\varepsilon }}}}^p\) as

$$\begin{aligned} e = \int _0^t \sqrt{\frac{2}{3}}\,\Vert {\dot{{\varvec{\varepsilon }}}}^p({\hat{t}})\Vert \,\text {d}{\hat{t}}. \end{aligned}$$
(12)

It holds that y is related to the initial yield stress \(y_0\) by the so-called stress-like work conjugate \(\beta =\partial _{e}\psi \).

As transition from microscale to macroscale, a homogenization scheme has to be applied for the mechanical variables, namely the macroscopic stresses \({\bar{{\varvec{\sigma }}}}\), the macroscopic strains \({\bar{{\varvec{\varepsilon }}}}\) and the mechanical part  of the macroscopic tangent moduli. These macroscopic quantities can be computed by appropriate averages over the associated microscopic quantities, for detail see, e.g., [66].

Furthermore, the averaging scheme to obtain the macroscopic bulk modulus \({\bar{\kappa }}\), the macroscopic heat expansion coefficient \({\bar{\alpha }}_\text {T}\), the macroscopic heat conduction coefficient \({\bar{k}}\) and the product of macroscopic specific heat capacity and macroscopic density, \({\bar{c}}_\rho \), is defined as

$$\begin{aligned} {\bar{\bullet }} = c^\text {M}\bullet _\text {M}(\theta )+c^\text {A}\bullet _\text {A} (\theta ),\quad \text {for}\quad \bullet \in \{\kappa ,\alpha _\text {T},k,c_\rho \}. \end{aligned}$$
(13)

This Voigt average is interpreted as upper bound of the material parameters, while Reuss bounds serve as lower bound. For a first setup of the computational model, the simple Voigt averaging scheme is chosen. More physically realistic approximations are, e.g., the Mori–Tanaka model or the self-consistent method, see, e.g., [19].

Besides a macroscopic mechanical part based on the mechanical tangent moduli , the stiffness matrix \({{\bar{{{\varvec{K}}}}}}\) also contains the thermo-mechanical coupling terms, i.e., \({{\bar{{{\varvec{K}}}}}}_{{{{\varvec{u}}}}\theta }\) and \({{\bar{{{\varvec{K}}}}}}_{\theta \theta }\), resulting from a discretized form of the balance of energy, cf. Eq. (3). Due to considered one-way coupled problem, the second thermo-mechanical coupling term \({{\bar{{{\varvec{K}}}}}}_{\theta {{{\varvec{u}}}}}\) is neglected. Since no mechanical outer forces are applied, its influence is diminishing.

(14)

4 Numerical analysis

Based on the previously presented material model and the numerical study in [83], an extended numerical simulation model using the finite element analysis program FEAP, cf. [77], is established. A two-scale boundary value problem (bvp) is defined as combination of a 2D bvp on the macroscale and a microscopic 2D bvp attached to each macroscopic integration point, following Sect. 3, to perform an investigation regarding the stress evolution. Due to the absence of outer forces, those stresses can be interpreted as residual stresses. On the macroscale, the main focus lies on the tangential stress distribution since these stresses are most relevant with respect to life time or strength of the component. On the microscale, the aim is to analyze the fluctuation part of the microscopic stress tensor \({\tilde{{\varvec{\sigma }}}}\) as introduced in Eq. (8) to study the microscopic residual stress distribution.

4.1 Setup of the boundary value problem

The two-dimensional model considers a cross section of the three-dimensional geometry in Fig. 1 located at \(x_3=\frac{h}{2}\). However, we are using the undeformed shape of the cylindrical geometry. It takes into account plane strain conditions for the two-dimensional approximation of the associated three-dimensional problem. To set up the two-scale boundary value problem, the symmetry of geometry and loadings concerning the \(x_1\)-axis of the considered cross section is exploited, see Fig. 1. Consequently, the displacement boundary condition \({\bar{u}}_{x_2}=0\text { on }\partial \bar{{\mathcal {B}}}_{{{\varvec{u}}}}\) is applied to all nodes at \(x_2=0\), cf. Fig. 4. The inner and outer lateral surface is in contact with cooling medium water and hence is directly exposed to the cooling. Here, thermal boundary conditions are applied on \(\partial \bar{{\mathcal {B}}}_\theta \), which are shown in Fig. 3 for outer and inner lateral surface. Due to the symmetry, the heat flux at \(x_2=0\) vanishes, i.e., boundary condition \({\bar{q}}_0=0\) on \(\partial \bar{{\mathcal {B}}}_{{{\varvec{q}}}}\) is applied. Following the analysis of discretization and time step size in [83], the macroscopic geometry is discretized with 20 nine-noded quadrilateral finite elements in radial direction. Relative to that, less finite elements are chosen in circumferential direction. Later investigations will be made for three radial regions, which are marked with I, II and III in Fig. 4, for different wall thicknesses of the cylindrical slice. In these regions, the element size in circumferential direction is reduced, as shown in Fig. 4.

Fig. 4
figure 4

Two-scale boundary value problem to numerically simulate the cooling process. A two-dimensional slice of the cylindrical specimen in combination with two-dimensional boundary value problems to depict the austenite-to-martensite transformation is considered. On the macroscale, the boundary conditions \(u_{x_2}=0\) on \(\partial {{\bar{\mathcal {B}}}}_{{{\varvec{u}}}}\), \({\bar{q}}_0=0\) on \(\partial \bar{{\mathcal {B}}}_{{{\varvec{q}}}}\), \({\bar{{{{\varvec{t}}}}}}=\mathbf{0}\) on \(\partial \bar{{\mathcal {B}}}_{{{\varvec{t}}}}\) and \({\bar{\theta }}\) on \(\partial \bar{{\mathcal {B}}}_\theta \) as given in Fig. 3 are applied. The final phase distribution is given on the microscale with austenite in gray and martensite in red. Regions I, II and III with microscopic investigation points are marked in green

Full size image
Fig. 5
figure 5

Macroscopic temperature \({\bar{\theta }}\) in \(^\circ \text {C}\) and microscopic phase fractions of austenite (white) and martensite (red) after (a) \(t = 9\,\text {s}\) and (b) \(t = 12\,\text {s}\)

Full size image

For the underlying microstructure, the representative volume element (RVE) is chosen to be an artificial structure, which is shown on the right side of Fig. 4. The structured finite element mesh is built of \(30\times 30\) four-noded quadrilateral finite elements, see [83]. Details on the modeling of phase transformation and the consideration of the dependency of the material parameters of austenite and martensite on the temperature can be found in Appendix A and further details in [83]. On the microscale the material modeling considers an elasto-plastic behavior as described in Sect. 3.3. In Fig. 4, red indicates martensitic regions and gray denotes austenitic grains. For the analysis regarding the microstructure, nine macroscopic integration points are evaluated in detail. Those are in the middle and at both ends of regions I, II and III. Points near the outer surface are marked by \(\bigtriangleup \), points near the inner surface by and points in the middle of each region by \(\bigtriangledown \), see Fig. 5a.

4.2 Evolution of phase fractions on microscale

As stated in Sect. 2.1, the fast cooling in water results in a diffusionless phase transformation from austenite to martensite. In the two-scale simulation, the phase transformation is computed based on the macroscopic temperature, which is passed onto the microscale in each integration point. Since the cooling is applied on the lateral surface and the outer lateral surface cools slightly faster than the inner one, the phase transformation starts earlier there, cf. Fig. 5a at positions \(\bigtriangleup \). It can be seen that martensite already started to form, indicated by the regions colored in red in the RVEs, in all three regions I, II and III at \(\bigtriangleup \), whereas at \(\bigtriangledown \) and \(\square \), the white-colored RVEs indicate a fully austenitic state.

With ongoing cooling process, the temperature falls below the martensitic start temperature also at the inner lateral surface, position , and martensite starts to form there as well, see Fig. 5b. Due to the small wall thickness of region II relative to regions I and III, one observes a faster heat conduction to the middle of the region, where the phase transformation has already started. Figure 6a shows a nearly homogeneous temperature distribution on the macroscale. The martensitic volume fraction has nearly reached its final value in all nine points. The final distribution is given in Fig. 6b.

Fig. 6
figure 6

Macroscopic temperature \({\bar{\theta }}\) in \(^\circ \text {C}\) and microscopic phase fractions of austenite (white) and martensite (red) after (a) \(t = 20\,\text {s}\) and (b) \(t = 80\,\text {s}\)

Full size image

4.3 Relation of phase transformation to stress evolution on microscale

Figure 7 analyzes region III point \(\bigtriangleup \) with respect to the microstructural state of phases and resulting stresses. Therefore, the microscopic mechanical pressure term \(p=\frac{1}{3}{\text {tr}}{\tilde{{\varvec{\sigma }}}}\) is taken into account. One sees that with initialization of the austenite-to-martensite phase transformation, cf. Fig. 7a, the first elements are switched to be martensitic. In those regions, compressive stresses occur which are a consequence of the surrounding material hindering the volumetric expansion of the martensite. With ongoing cooling process and increasing martensitic volume fraction, more microscopic elements are switched from austenite to martensite. Thus, in those switched martensitic elements compressive stresses evolve, while elements, which remain austenitic, show tensile stresses, cf. Fig. 7b and c, due to the direct interaction with neighboring expanding areas. Finally in Fig. 7d, at the end of the cooling process, the lastly switched martensitic elements show compressive stresses and the remaining austenitic regions tensile stresses.

Fig. 7
figure 7

Evolution of microscopic phase transformation and relation to stress evolution in MPa on the RVE attached to region III point \(\bigtriangleup \) after (a) \(t = 8.8\,\text {s}\) at the beginning of the martensitic transformation, (b) \(t = 12\,\text {s}\), (c) \(t = 20\,\text {s}\) and (d) \(t = 80\,\text {s}\)

Full size image

Please note that the underlying microstructure is defined by a structured mesh and the switch from austenite to martensite is done in a random process in this computational approach. A more realistic approach, taking into account the spatial morphology of martensite additionally, can be realized using, e.g., phase-field models. Here, the representation based on the phase fraction properties gives a first insight to the interplay between austenite and martensite on the microscopic level.

4.4 Quadratic measures of microscopic stress fluctuations on macroscale

In addition to the distribution of the microscopic stresses over an RVE, see Sect. 4.3, in this section we especially consider their representation at the macroscale. According to Eq. (8), the fluctuations of the stresses are defined as \({\tilde{{\varvec{\sigma }}}}={\varvec{\sigma }}-{\bar{{\varvec{\sigma }}}}\). By definition, the volume average of the microscopic fluctuations over the complete RVE is equal to zero. In order to be able to show their influence on the macroscopic level, quadratic measures \(\langle \bullet ^2\rangle \) of the stress fluctuations, the deviatoric part of the fluctuations and the pressure term are defined. With \(i,j\in \,\{1,2,3\}\) it holds that

$$\begin{aligned} {\left\langle {\tilde{\sigma }}^2_{ij}\right\rangle }&= \frac{1}{V_\mathcal {B}}\int _\mathcal {B}{\tilde{\sigma }}^2_{ij}\, \text {d}v=\frac{1}{V_\mathcal {B}}\int _\mathcal {B}(\sigma _{ij}-{\bar{\sigma }}_{ij})^2\, \text {d}v,\nonumber \\ {\left\langle ({\text {dev}}{\tilde{{\varvec{\sigma }}}})_{ij}^2\right\rangle }&=\frac{1}{V_\mathcal {B}} \int _\mathcal {B}({\text {dev}}{\tilde{{\varvec{\sigma }}}})_{ij}^2\,\text {d}v,\nonumber \\ {\langle p^2\rangle }&=\frac{1}{V_\mathcal {B}}\int _\mathcal {B}(\frac{1}{3}{\text {tr}}{\tilde{{\varvec{\sigma }}}})^2\,\text {d}v\, \end{aligned}$$
(15)

with \({\text {dev}}{{\tilde{{\varvec{\sigma }}}}}={\varvec{\sigma }}-\frac{1}{3}{\text {tr}}{\tilde{{\varvec{\sigma }}}}\mathbf{1}\) and \(p=\frac{1}{3}{\text {tr}}{\tilde{{\varvec{\sigma }}}}\). Dragging the root of the quantities in Eq. (15) results in normed quantities, namely

$$\begin{aligned} \Vert {\tilde{\sigma }}_{ij}\Vert&= \sqrt{ \left\langle {\tilde{\sigma }}_{ij}^2 \right\rangle } \nonumber ,\\ \Vert ({\text {dev}}{\tilde{{\varvec{\sigma }}}})_{ij}\Vert&= \sqrt{\left\langle ({\text {dev}}{\tilde{{\varvec{\sigma }}}})_{ij}^2\right\rangle },\nonumber \\ \Vert p\Vert&= \sqrt{\left\langle p^2\right\rangle }. \end{aligned}$$
(16)

Thus, it is possible to display and evaluate quantities related to the microscopic stress fluctuations macroscopically. In particular, the tangential part of residual stresses near the surfaces is a decisive issue for the durability and wear resistance of a component. Consequently, the macroscopic representation of the tangential part of the fluctuation measures from Eqs. (15) and (16) should be investigated. To calculate these, the angle \(\alpha \) is needed, which is defined by the location of the associated macroscopic integration point of interest with respect to the \(x_1\)-\(x_2\)-coordinate system in Fig. 8. It describes the rotation of the original \(x_1\)-\(x_2\)-coordinate system to a \(x_1^\prime \)-\(x_2^\prime \)-coordinate system, whose \(x_2^\prime \)-axis points in tangential direction.

Fig. 8
figure 8

Rotation of coordinate system by angle \(\alpha \) to compute tangential fluctuation of stresses on microscale

Full size image

Based on the angle \(\alpha \), a rotation matrix \({{{\varvec{R}}}}\) for the mapping of quantities from the \(x_1\)-\(x_2\)-coordinate system to the \(x_1^\prime \)-\(x_2^\prime \)-coordinate system results. The tangential part of the microscopic fluctuations \({\tilde{\sigma }}_\text {tang}\) results from the second main diagonal entry (22) of the mapped microscopic stress fluctuation, i.e.,

$$\begin{aligned} {\tilde{\sigma }}_\text {tang}={\tilde{\sigma }}_{x_2^\prime x_2^\prime }=\Bigl ({{{\varvec{R}}}}\cdot {\varvec{\sigma }}\cdot {{{\varvec{R}}}}^\text { T}-{{{\varvec{R}}}}\cdot {\bar{{\varvec{\sigma }}}}\cdot {{{\varvec{R}}}}^\text {T}\Bigr )_{x_2^\prime x_2^\prime }\quad \text {with}\quad {{{\varvec{R}}}}= \begin{pmatrix} \cos \alpha &{}-\sin \alpha &{}0\\ \sin \alpha &{}\cos \alpha &{}0\\ 0&{}0&{}1\end{pmatrix}. \end{aligned}$$
(17)

By means of an additional quadratic measure, analogous to the treatment in Eqs. (15) and (16), the fluctuations of the stresses can also be represented on the macroscopic level. It is defined as

$$\begin{aligned} \Vert {\tilde{\sigma }}_\text {tang}\Vert = \sqrt{\left\langle {\tilde{\sigma }}_\text {tang}^2\right\rangle } \quad \text {with}\quad \left\langle {\tilde{\sigma }}_\text {tang}^2\right\rangle \,= \frac{1}{V_\mathcal {B}}\int _\mathcal {B}{\tilde{\sigma }}_\text {tang}^2\,\text {d}v. \end{aligned}$$
(18)

4.4.1 Interpretation of microscopic residual stress on macroscale

Figure 9 shows the evolution of different components of the macroscopic averaged measures. In the following the considered quantities are \(\Vert p\Vert \), \(\Vert {\tilde{\sigma }}_{11}\Vert \), \(\Vert ({\text {dev}}{\tilde{\sigma }})_{11}\Vert \) and \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \). In order to achieve better comparability, the scales of all four plots are set to the same range. Definitions of regions I, II and III are given in Fig. 4.

Fig. 9
figure 9

Macroscopic measures, namely \(\Vert p\Vert \), \(\Vert {\tilde{\sigma }}_{11}\Vert \), \(\Vert ({\text {dev}}{\tilde{\sigma }})_{11}\Vert \) and \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \) in MPa after (a) \(t = 9\,\text {s}\) (b) \(t = 12\,\text {s}\), (c) \(t = 20\,\text {s}\) and (d) \(t = 80\,\text {s}\)

Full size image

It can be seen that all four plots at one fixed time t qualitatively show the same behavior. Before the temperature steps below the martensitic start temperature, all four macroscopic quantities are equal to zero. This resembles that no phase transformation occurs on the microscale, since this would induce microscopic fluctuations of stress. After nine seconds of cooling time, the phase transformation has just been initiated near the outer surface, see Fig. 9a. Thus, all four examined quantities differ from zero near the outer surface. With ongoing cooling, the area increases in which microscopic fluctuations are measured, see Fig. 9b. After 12 s of cooling time, the phase transformation has been initiated at the inner lateral surface as well as in region II. The material in the bulk of regions III and I is cooled later, such that still no influence of the microscopic fluctuations can be observed. After 20 s nearly homogeneous values for all four quantities are obtained, see Fig. 9c. The final values at the end of the cooling process are shown in Fig. 9d. At the end of the cooling process, the volume fractions of austenite and martensite are the same for every macroscopic integration point. Thus, we see nearly homogeneous distributions for all four measures with a slight increase near the lateral surfaces. Quantitatively, the deviatorical measure \(\Vert ({\text {dev}}{\tilde{\sigma }})_{11}\Vert \) shows lower stress values than the fluctuation measure \(\Vert {\tilde{\sigma }}_{11}\Vert \) or \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \). Furthermore, the pressure term \(\Vert p\Vert \) exceeds the fluctuation measure \(\Vert {\tilde{\sigma }}_{11}\Vert \) and \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \), respectively.

4.4.2 Interpretation of microscopic tangential residual stress on micro- and macroscale

As continuation of Sect. 4.4.1, in the following the focus is laid on the tangential part of the microscopic stress fluctuations and its representation on micro- and macroscale. Therefore in the following, we consider the tangential part of the fluctuations of the stresses on the microscale \({\tilde{\sigma }}_{\text {tang}}\) and their quadratic measure \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \) on the macroscale.

Fig. 10
figure 10

Tangential part of stress fluctuations \({\tilde{\sigma }}_{\text {tang}}\) in MPa on microscale and their quadratic measure \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \) in MPa on the macroscale after (a) \(t = 9\,\text {s}\) and (b) \(t = 12\,\text {s}\)

Full size image

On the microscale the stress evolution starts with the austenite-to-martensite phase transformation as discussed in Sect. 4.3. The microscopic elements, which are switched to martensite, show high compressive stresses, see Fig. 10a. On the other hand, elements in between show low values or even tensile stresses. Because the phase transformation starts at the outer surface, only at position \(\bigtriangleup \) microscopic fluctuations in all three regions I, II and III can be observed. On the macroscale, the quadratic measure \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \) varies from zero in those regions close to the outer surface. This shows that the selected fluctuation measure is able to display information of the residual stresses of second and third type on the macroscale.

After 12 s of cooling time, cf. Fig. 10b, all examined integration points, except regions I and III at position \(\bigtriangledown \), show fluctuation of stresses \({\tilde{\sigma }}_{\text {tang}}\), which differ from zero. For example, if we look more closely at region III, we see that there are no fluctuations at position \(\bigtriangledown \). Here, the temperature is still above the martensitic start temperature, see Fig. 5b. At position \(\square \) the phase transformation has only started. Thus, the values of the stress fluctuations are lower than at position \(\bigtriangleup \). This is also confirmed by the macroscopic measure, see Fig. 10b.

Fig. 11
figure 11

Tangential part of stress fluctuations \({\tilde{\sigma }}_{\text {tang}}\) in MPa on microscale and their quadratic measure \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \) in MPa on the macroscale after (a) \(t = 20\,\text {s}\) and (b) \(t = 80\,\text {s}\)

Full size image

Figure 11a shows that the phase transformation now takes place everywhere as indicated by the stress development on both scales. The final distribution of \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \) on the macroscale is nearly homogeneous, since in all macroscopic integration points the same phase fraction is present, see Fig. 11b. However, fluctuations of the microscopic tangential residual stresses can be seen in the RVEs. All RVEs seem to have similar states of residual stresses.

4.5 Interpretation of residual stresses of different types on macroscale

Residual stresses are known to influence the wear and fatigue behavior of a component. In order to improve its properties, it seems reasonable to aim for compressive residual stresses near the surface. Thereby, the durability can be enhanced and the component’s life time can be extended, e.g., in case of fatigue cracking. Thus, this section analyzes the macroscopic tangential stress evolution \({\bar{\sigma }}_\text {tang}\) during the cooling process. In Figs. 12 and 13 it is linked to the quadratic measure \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert \) of the tangential part of the stress fluctuations, defined in Eq. (17). Since no outer forces are applied, cf. Fig. 4, the occurring tangential stresses can be interpreted as residual stresses of first type and the quadratic measure as a measure of the microscopic residual stress influence on macroscale. By definition of this measure, we do not distinguish between positive and negative values of stress fluctuations. Instead, the absolute value is taken into account, such that the averaged microscopic residual stress amplitude is displayed.

Fig. 12
figure 12

Tangential residual stresses of first type \({\bar{\sigma }}_\text {tang}\) in MPa and macroscopic measure of microscopic tangential residual stresses \(\Vert {\tilde{\sigma }}_\text {tang}\Vert \) in MPa after (a) \(t = 5\,\text {s}\), (b) \(t = 9\,\text {s}\), (c) \(t = 12\,\text {s}\) and (d) \(t = 20\,\text {s}\)

Full size image
Fig. 13
figure 13

(a) Tangential residual stresses of first type \({\bar{\sigma }}_\text {tang}\) in MPa and macroscopic measure of microscopic tangential residual stresses \(\Vert {\tilde{\sigma }}_\text {tang}\Vert \) in MPa after \(t=80\,\text {s}\) and (b) with different color scaling

Full size image

On the macroscale, the cooling of the lateral surfaces evokes tensile stresses due to thermal contraction in regions near the surface, see Fig. 12a. Since no phase transformation occurs on microscale, the microscopic stress measure does not differ from zero. After the austenite-to-martensite phase transformation is initiated on the microscale, we observe compressive stresses near the outer surface on the macroscale for \({\bar{\sigma }}_\text {tang}\), cf. Fig. 12b. They result from the superposition of stresses due to thermal contraction and the volume expansion due to phase transformation. The quadratic measure shows high values in regions where the phase transformation occurs.

With ongoing cooling process, this behavior can still be observed as shown in Fig. 12c and d. Regions, in which \(\Vert {\tilde{\sigma }}_\text {tang}\Vert \) equals zero, here the bulk material in Fig. 12c, do not undergo phase transformation yet. At \(t=20\,\text {s}\) in Fig. 12d we see that the phase transformation has been initiated in the whole component, since it holds \(\Vert {\tilde{\sigma }}_{\text {tang}}\Vert >0\) everywhere. At the end of the examined process, we see a nearly homogeneous distribution of the quadratic measure \(\Vert {\tilde{\sigma }}_\text {tang}\Vert \), cf. Fig. 13a. With different color scaling as given in Fig. 13b, you can see that the left side shows higher values than the right side of the component. This study shows that, in contrast to the heterogeneous distribution of the macroscopic tangential stresses \({{\bar{\sigma }}}_\text {tang}\) which are related to the residual stresses of first type, see Fig. 13, the stress fluctuations related to the other both types do not depend on their associated macroscopic position. The final distribution of \({\bar{\sigma }}_\text {tang}\) illustrates that tensile stress occur near the surface of the cylindrical component. In contrast, the bulk material shows compressive stresses. Since a targeted stress state with compressive stresses near the lateral surface is desirable to improve, e.g., the components strength, it is inevitable to make adoptions on the cooling process, i.e., changing the cooling rate or the route itself.

5 Conclusion

In this contribution, the cooling process of a hot bulk formed part has been examined with respect to macro- and microscopic residual stress evolution. Therefore, a section of a cylindrical specimen with eccentric hole has been investigated using a two-scale finite element simulation. Aside from the macroscopic tangential stresses, which are known to be most relevant with respect to the component’s properties such as live time or strength, special attention has been paid to the microscale and its stress evolution. In order to enable the examination of microscopic residual stresses and to analyze their influence on the macroscopic residual stresses, quadratic measures have been based on the stress fluctuations. Therewith, we showed the possibility to depict the impact of the austenite-to-martensite phase transformation on the evoked residual stress distribution on micro- and macroscale.

The chosen quadratic measures do not account for the sign of the microscopic stress fluctuations, i.e., compressive and tensile stresses. In order to be able to distinguish between tension and compression, however, it is inevitable to consider this. This has to be adopted in future works. Furthermore, the material model should be extended to divide the microscopic residual stresses into residual stresses of second and third type.

This publication also considers a structured mesh with a randomized phase transformation process on the microscale. In future steps, a more physically motivated microstructure has to be considered to validate the findings. Moreover, a three-dimensional model of the complete specimen should be combined with a three-dimensional microstructure to study the relevance of the third dimension with respect to the stress and temperature evolution. In order to establish compressive stresses near the surface, the cooling process itself has to be modified. This targeted residual stress state can help to achieve higher strength and longer life time. Thereto, additional phases such as bainite, pearlite or ferrite have to be studied and added to the material model, such that the processing of different cooling routes becomes possible, since then it cannot be guaranteed that the process itself is still diffusionless. In addition, experimental validation and calibration of the results are essential to verify the predictive capability of the model with respect to residual stresses and to prompt any modifications.