A new numerical approach to the solution of PDEs with optimal accuracy on irregular domains and Cartesian meshes—part 2: numerical simulations and comparison with FEM

Abstract

A new numerical approach for the time-dependent wave and heat equations as well as for the time-independent Poisson equation developed in Part 1 is applied to the simulation of 1-D and 2-D test problems on regular and irregular domains. Trivial conforming and non-conforming Cartesian meshes with 3-point stencils in the 1-D case and 9-point stencils in the 2-D case are used in calculations. The numerical solutions of the 1-D wave equation as well as the 2-D wave and heat equations for a simple rectangular plate show that the accuracy of the new approach on non-conforming meshes is practically the same as that on conforming meshes for both the Dirichlet and Neumann boundary conditions. Moreover, very small distances ($0.1 h - 10^{-9}h$ where h is the grid size) between the grid points of a Cartesian mesh and the boundary do not decrease the accuracy of the new technique. The application of the new approach to the 2-D problems on an irregular domain shows that the order of accuracy is close to four for the wave and heat equations and is close to five for the Poisson equation. This is in agreement with the theoretical results of Part 1 of the paper. The comparison of the numerical results obtained by the new approach and by FEM shows that at similar 9-point stencils, the accuracy of the new approach on irregular domains is two orders higher for the wave and heat equations and three orders higher for the Poisson equation than that for the linear finite elements. Moreover, the new approach yields even much more accurate results than the quadratic and cubic finite elements with much wider stencils. An example of a problem with a complex irregular domain that requires a prohibitively large computation time with the finite elements but can be easily solved with the new approach is presented.

Appendix A. The summary of the new numerical approach developed in Part 1 of the paper.

The wave and heat equations in domain $\Omega$ can be uniformly written as:

$$\begin{aligned} \frac{\partial ^n u}{\partial t^n} - \bar{c} \nabla ^2 u = f , \end{aligned}$$

(A.1)

where $n=2$ and $\bar{c}=c^2$ for the wave equation as well as $n=1$ and $\bar{c}=a$ for the heat equation, c is the wave velocity, a is the thermal diffusivity, $f (\mathbf{x}, t)$ is the loading term and u is the field variable. The Poisson equation in domain $\Omega$ has the following form:

$$\begin{aligned} \nabla ^2 u = f . \end{aligned}$$

(A.2)

The Neumann boundary conditions $\mathbf{n} \cdot \bigtriangledown u = g_1$ on $\Gamma ^t$ and the Dirichlet boundary conditions $u=g_2$ on $\Gamma ^u$ are applied where $\mathbf{n}$ is the outward unit normal on $\Gamma ^t$ and $\Gamma ^t$ and $\Gamma ^u$ denote the boundaries with the Dirichlet and Neumann boundary conditions, respectively. The initial conditions are $u (\mathbf{x}, t=0) =g_3$, $v (\mathbf{x}, t=0) =g_4$ in $\Omega$ for the wave equation and $u (\mathbf{x}, t=0) =g_3$ in $\Omega$ for the heat equation where $g_i$ ($i=1,2,3,4$) are the given functions.

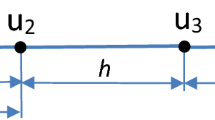
1.1 Appendix A.1. The stencil equations for the 1-D wave equation

The following 3-point stencils on conforming and non-conforming uniform meshes are used:

$$\begin{aligned} h^2 ({m_1} {\ddot{u}^{\mathrm{num}}_{A-1}}+{m_2} {\ddot{u}^{\mathrm{num}}_{A}}+{m_3}{\ddot{u}^{\mathrm{num}}_{A+1}}) + c^2({k_1} {u^{\mathrm{num}}_{A-1}}+{k_2} {u^{\mathrm{num}}_{A}}+{k_3}{u^{\mathrm{num}}_{A+1}}) = \bar{f} + \bar{f}^{Neum} , \end{aligned}$$

(A.3)

where the case of zero loading $f = \bar{f} = 0$ is considered below, $A=2,\ldots ,N-1$, N is the total number of grid points (Fig. 1). The coefficients $m_j$ and $k_j$ ($j=1,2,3$) are determined in Part 1 from the minimization of the local truncation error and are given: a) by Eq. (15) of Part 1 for the internal nodes $A=3,\ldots ,N-2$ located far from the boundary ($\bar{f}^{Neum} =0$); b) by Eq. (14) of Part 1 for the nodes $A=2,N-1$ located close to the boundary with the Dirichlet boundary conditions ($\bar{f}^{Neum} =0$); c) by Eq. (29) of Part 1 for the nodes $A=2,N-1$ located close to the boundary with the Neumann boundary conditions (for the Neumann boundary conditions, $\bar{f}^{Neum} = f_1$ where $f_1$ is determined by Eq. (30) of Part 1). The coefficients $m_1=k_1=0$ are zero in Eq. (29) of Part 1; i.e., the 2-node stencils, Eq. (A.3) with $m_1=k_1=0$, are used for the points located close to the boundary with the Neumann boundary conditions.

1.2 Appendix A.2. The stencil equations for the 2-D wave and heat equations

Fig. 27

The spatial locations of the degrees of freedom $u_{i,j}$ ($i = A-1, A, A+1$, $j = B-1, B, B+1$) that contribute to the 9-point uniform stencil for the internal degree of freedom $u_{A,B}$ located far from the boundary

Fig. 28

The spatial locations of the degrees of freedom $u_{i,j}$ ($i = A-1, A, A+1$, $j = B-1, B, B+1$) that contribute to the 9-point nonuniform stencil for the internal degree of freedom $u_{A,B}$ located close to the boundary with the Dirichlet boundary conditions

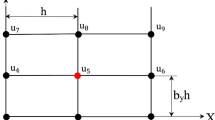
The following 9-point stencils on Cartesian meshes are used:

$$\begin{aligned}&h^2 \left\{ m_1 \frac{d^n u^{\mathrm{num}}_{(A-1),(B-1)}}{dt^n} + m_2 \frac{d^n u^{\mathrm{num}}_{A,(B-1)}}{dt^n} + m_3 \frac{d^n u^{\mathrm{num}}_{(A+1),(B-1)}}{dt^n} + {m_4} \frac{d^n u^{\mathrm{num}}_{(A-1),B}}{dt^n} + {m_5} \frac{d^n u^{\mathrm{num}}_{A,B}}{dt^n}\right. \nonumber \\&\quad \left. + m_6 \frac{d^n u^{\mathrm{num}}_{(A+1),B}}{dt^n} + m_7 \frac{d^n u^{\mathrm{num}}_{(A-1),(B+1)}}{dt^n} + m_8 \frac{d^n u^{\mathrm{num}}_{A,(B+1)}}{dt^n} + m_9 \frac{d^n u^{\mathrm{num}}_{(A+1),(B+1)}}{dt^n} \right\} \nonumber \\&\quad +\bar{c} \{ k_1 u^{\mathrm{num}}_{(A-1),(B-1)} + k_2 u^{\mathrm{num}}_{A,(B-1)} + k_3 u^{\mathrm{num}}_{(A+1),(B-1)} + {k_4} u^{\mathrm{num}}_{(A-1),B} + {k_5} u^{\mathrm{num}}_{A,B} \nonumber \\&\quad + k_6 u^{\mathrm{num}}_{(A+1),B} + k_7 u^{\mathrm{num}}_{(A-1),(B+1)} + k_8 u^{\mathrm{num}}_{A,(B+1)} + k_9 u^{\mathrm{num}}_{(A+1),(B+1)} \} = \bar{f}_{A,B} + \bar{f}_{A,B}^{Neum} , \end{aligned}$$

(A.4)

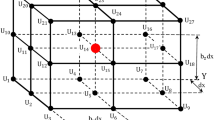
where $\bar{f}_{A,B} = 0$ in the case of zero load $f=0$ and $\bar{f}_{A,B}$ is defined by Eq. (45) of Part 1 for nonzero load $f \ne 0$, the superscript n in the time derivative in Eq. (A.4) and the material parameter $\bar{c}$ are $n=1$ and $\bar{c}=a$ for the heat equation as well as $n=2$ and $\bar{c}=c^2$ for the wave equation. The coefficients $m_j$ and $k_j$ ($j=1,2,\ldots ,9$) along with the coefficients $l_i$ ($i=1,2,3,4$) used for the Neumann boundary conditions (see below) are determined from the minimization of the local truncation error and are: a) given by Eq. (39) of Part 1 for the internal nodes located far from the boundary (Fig. 27) and $\bar{f}_{A,B}^{Neum} =0$; b) calculated by the solution of 17 linear algebraic equations $b_p=0$ for $p=1,2,\ldots , 11,13,14,15,17,20,26$ ($b_p$ are given by Eq. (C.1) of Part 1) for the nodes located close to the boundary with the Dirichlet boundary conditions (see Fig. 28) and $\bar{f}_{A,B}^{Neum}=0$; c) calculated by the solution of 6 linear algebraic equations given by Eq. (52) of Part 1 (as well as Eqs. (C.2) and (A.2) of Part 1) for the nodes located close to the boundary with the Neumann boundary conditions and $\bar{f}_{A,B}^{Neum}=\bar{c} h (l_1 g_1(x_1,y_1,t)+l_2 g_1(x_2,y_2,t)+l_3 g_1(x_3,y_3,t))+ h^3 l_4 \frac{\partial ^n g_1(x_2,y_2,t) }{\partial t^n}$ where $x_i, y_i$ ($i=1,2,3$) are the coordinates of 3 boundary points (Fig. 29) and $g_1(x_i, y_i, t)$ expresses the Neumann boundary conditions. The coefficients $m_7=k_7=0$ for the stencil in Fig. 29 are zero; i.e., the 8-node cut stencils, Eq. (A.4) with $m_7=k_7=0$, are used for the points located close to the boundary with the Neumann boundary conditions.

Fig. 29

The spatial locations of the degrees of freedom $u_{i,j}$ ($i = A-1, A, A+1$, $j = B-1, B, B+1$) that contribute to the 8-point cut stencils for the internal degrees of freedom $u_{A,B}$ and $u_{A,B+1}$ located close to the boundary with the Neumann boundary conditions. $\bullet$ designates the 8 nodes contributing to the stencil equation

1.3 Appendix A.3. The stencil equations for the 2-D Poisson equation

Nine-node stencils for the degree of freedom $u^{\mathrm{num}}_{A,B}$ of the time-independent Poisson equation can be obtained from Eq. (A.4) with $\bar{c}=1$ and $m_j= 0$ ($j=1,2,\ldots ,9$) as follows:

$$\begin{aligned}&k_1 u^{\mathrm{num}}_{(A-1),(B-1)} + k_2 u^{\mathrm{num}}_{A,(B-1)} + k_3 u^{\mathrm{num}}_{(A+1),(B-1)} + {k_4} u^{\mathrm{num}}_{(A-1),B} + {k_5} u^{\mathrm{num}}_{A,B} \nonumber \\&\quad + k_6 u^{\mathrm{num}}_{(A+1),B} + k_7 u^{\mathrm{num}}_{(A-1),(B+1)} + k_8 u^{\mathrm{num}}_{A,(B+1)} + k_9 u^{\mathrm{num}}_{(A+1),(B+1)} = \bar{f}_{A,B} + \bar{f}_{A,B}^{Neum} , \end{aligned}$$

(A.5)

where $\bar{f}_{A,B} = 0$ in the case of zero load $f=0$ and $\bar{f}_{A,B}$ is defined by Eq. (D.1) of Part 1 for nonzero load $f \ne 0$. The coefficients $k_j$ ($j=1,2,\ldots ,9$) along with the coefficients $l_i$ ($i=1,2,3,4$) used for the Neumann boundary conditions (see below) are determined from the minimization of the local truncation error and are: a) given by Eq. (58) of Part 1 for the internal nodes located far from the boundary (Fig. 27) and $\bar{f}_{A,B}^{Neum} =0$; b) calculated by the solution of 8 linear algebraic equations $b_p=0$ for $p=1,2,\ldots , 8$ ($b_p$ are given by Eq. (C.3) of Part 1) for the nodes located close to the boundary with the Dirichlet boundary conditions (see Fig. 28) and $\bar{f}_{A,B}^{Neum}=0$; c) calculated by the solution of 11 linear algebraic equations $b_p=0$ for $p=1,2,\ldots , 11$ ($b_p$ are given by Eq. (C.4) of Part 1) for the nodes located close to the boundary with the Neumann boundary conditions and $\bar{f}_{A,B}^{Neum}=\bar{c} h (l_1 g_1(x_1,y_1)+l_2 g_1(x_2,y_2)+l_3 g_1(x_3,y_3))+ +l_4 g_1(x_4,y_4)$ where $x_i, y_i$ ($i=1,2,3,4$) are the coordinates of 4 boundary points (Fig. 29), and $g_1(x_i, y_i)$ expresses the Neumann boundary conditions. The coefficients $k_7=0$ for the stencil in Fig. 29 are zero; i.e., the 8-node stencils, Eq. (A.5) with $k_7=0$, are used for the points located close to the boundary with the Neumann boundary conditions.