The numerical solution of the 3D Helmholtz equation with optimal accuracy on irregular domains and unfitted Cartesian meshes

Abstract

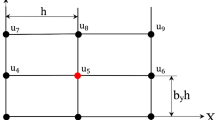
Here, we extend the optimal local truncation error method (OLTEM) recently developed in our papers to the 3D time-independent Helmholtz equation on irregular domains. Trivial unfitted Cartesian meshes and simple 27-point discrete stencil equations are used for 3D irregular domains. The stencil coefficients for the new approach are assumed to be unknown and are calculated by the minimization of the local truncation error of the stencil equations. This provides the optimal order of accuracy of the proposed technique. At similar 27-point stencils, the accuracy of OLTEM is two orders higher for the Dirichlet boundary conditions and one order higher for the Neumann boundary conditions compared to that for linear finite elements. The numerical results for irregular domains also show that at the same number of degrees of freedom, OLTEM is even much more accurate than high-order (up to the fifth order) finite elements with much wider stencils. Compared to linear finite elements with similar 27-point stencils, at accuracy of 0.1% OLTEM decreases the number of degrees of freedom by a factor of greater than 1000. This leads to a huge reduction in computation time. The new approach can be equally applied to the Helmholtz and screened Poisson equations.

Appendices

Appendix 1: The coefficients $b_p$ used in Eq. (10) in Sect. 2.2

The first five coefficients $b_p$ ($p=1,2,\ldots ,5$) used in Eq. (10) are presented below. All coefficients $b_p$ used in Eq. (10) are given in the attached files ‘b-coeff-1.pdf’ and ‘b-coeff-1.nb’.

Eq. (10):

$$\begin{aligned} b_{1}= & {} k_{1}+k_{10}+k_{11}+k_{12}+k_{13}+k_{14}+k_{15}+k_{16}\\&+k_{17}+k_{18}+k_{19}+k_{2}+k_{20}+k_{21}+k_{22}+k_{23}\\&+k_{24}+k_{25}+k_{26}+k_{27}+k_{3}+k_{4}+k_{5}+k_{6}+k_{7}+k_{8}+k_{9}\\ b_{2}= & {} -d_{1} k_{1}-d_{10} k_{10}+d_{12} k_{12}-d_{13} k_{13}\\&+d_{15} k_{15}-d_{16} k_{16}+d_{18} k_{18}-d_{19} k_{19}+d_{21} k_{21}-d_{22} k_{22}+d_{24} k_{24}\\&-d_{25} k_{25}+d_{27} k_{27}+d_{3} k_{3}-d_{4} k_{4}+d_{6} k_{6}-d_{7} k_{7}+d_{9} k_{9} \\ b_{3}= & {} b_{y} (-d_{1} k_{1}-d_{10} k_{10}-d_{11} k_{11}-d_{12} k_{12}\\&+d_{16} k_{16}+d_{17} k_{17}+d_{18} k_{18}-d_{19} k_{19}-d_{2} k_{2}\\&-d_{20} k_{20}-d_{21} k_{21}+d_{25} k_{25}+d_{26} k_{26}+d_{27} k_{27}\\&-d_{3} k_{3}+d_{7} k_{7}+d_{8} k_{8}+d_{9} k_{9}) \\ b_{4}= & {} b_{z} (-d_{1} k_{1}+d_{19} k_{19}-d_{2} k_{2}+d_{20} k_{20}\\&+d_{21} k_{21}+d_{22} k_{22}+d_{23} k_{23}+d_{24} k_{24}+d_{25} k_{25}+d_{26} k_{26}\\&+d_{27} k_{27}-d_{3} k_{3}-d_{4} k_{4}-d_{5} k_{5}-d_{6} k_{6}\\&-d_{7} k_{7}-d_{8} k_{8}-d_{9} k_{9}) \\ b_{5}= & {} b_{y} (d_{1}^2 k_{1}+d_{10}^2 k_{10}-d_{12}^2 k_{12}-d_{16}^2 k_{16}\\&+d_{18}^2 k_{18}+d_{19}^2 k_{19}-d_{21}^2 k_{21}-d_{25}^2 k_{25}\\&+d_{27}^2 k_{27}-d_{3}^2 k_{3}-d_{7}^2 k_{7}+d_{9}^2 k_{9}). \end{aligned}$$

Appendix 2: The coefficients $b_p$ used in Eq. (10) for the Neumann boundary conditions in Sect. 2.3

The first five coefficients $b_p$ ($p=1,2,\ldots ,5$) used in Eq. (10) are presented below. All coefficients $b_p$ used in Eq. (10) are given in the attached files ‘b-coeff-2.pdf’ and ‘b-coeff-2.nb’.

Equation (10):

$$\begin{aligned} b_{1}= & {} k_{1}+k_{10}+k_{11}+k_{12}+k_{13}+k_{14}+k_{15}+k_{16}+k_{17}+k_{18}+k_{19}+k_{2}+k_{20}\\&+k_{21}+k_{22}+k_{23}+k_{24}+k_{25}+k_{26}+k_{27}+k_{3}+k_{4}+k_{5}+k_{6}+k_{7}+k_{8}+k_{9}\\ b_{2}= & {} -d_{1} k_{1}-d_{10} k_{10}+d_{12} k_{12}-d_{13} k_{13}+d_{15} k_{15}-d_{16} k_{16}+d_{18} k_{18}-d_{19} k_{19}\\&+d_{21} k_{21}-d_{22} k_{22}+d_{24} k_{24}-d_{25} k_{25}+d_{27} k_{27}+d_{3} k_{3}-d_{4} k_{4}+d_{6} k_{6}-d_{7} k_{7}\\&+d_{9} k_{9}+{\bar{k}}_{1} n_{1,1}+{\bar{k}}_{10} n_{1,10}+{\bar{k}}_{11} n_{1,11}+{\bar{k}}_{12} n_{1,12}+{\bar{k}}_{13} n_{1,13}+{\bar{k}}_{14} n_{1,14}+{\bar{k}}_{15} n_{1,15}\\&+{\bar{k}}_{16} n_{1,16}+{\bar{k}}_{17} n_{1,17}+{\bar{k}}_{18} n_{1,18}+{\bar{k}}_{19} n_{1,19}+{\bar{k}}_{2} n_{1,2}+{\bar{k}}_{20} n_{1,20}+{\bar{k}}_{21} n_{1,21}\\&+{\bar{k}}_{22} n_{1,22}+{\bar{k}}_{23} n_{1,23}+{\bar{k}}_{24} n_{1,24}+{\bar{k}}_{25} n_{1,25}+{\bar{k}}_{26} n_{1,26}+{\bar{k}}_{27} n_{1,27}+{\bar{k}}_{3} n_{1,3}+{\bar{k}}_{4} n_{1,4}\\& +{\bar{k}}_{5} n_{1,5}+{\bar{k}}_{6} n_{1,6}+{\bar{k}}_{7} n_{1,7}+{\bar{k}}_{8} n_{1,8}+{\bar{k}}_{9} n_{1,9} \\ b_{3}= & {} b_{y} (-d_{1} k_{1}-d_{10} k_{10}-d_{11} k_{11}-d_{12} k_{12}+d_{16} k_{16}+d_{17} k_{17}+d_{18} k_{18}-d_{19} k_{19}-d_{2} k_{2}\\&-d_{20} k_{20}-d_{21} k_{21}+d_{25} k_{25}+d_{26} k_{26}+d_{27} k_{27}-d_{3} k_{3}+d_{7} k_{7}+d_{8} k_{8}+d_{9} k_{9})\\&+{\bar{k}}_{1} n_{2,1}+{\bar{k}}_{10} n_{2,10}+{\bar{k}}_{11} n_{2,11}+{\bar{k}}_{12} n_{2,12}+{\bar{k}}_{13} n_{2,13}+{\bar{k}}_{14} n_{2,14}+{\bar{k}}_{15} n_{2,15}\\&+{\bar{k}}_{16} n_{2,16}+{\bar{k}}_{17} n_{2,17}+{\bar{k}}_{18} n_{2,18}+{\bar{k}}_{19} n_{2,19}+{\bar{k}}_{2} n_{2,2}+{\bar{k}}_{20} n_{2,20}+{\bar{k}}_{21} n_{2,21}+{\bar{k}}_{22} n_{2,22}\\&+{\bar{k}}_{23} n_{2,23}+{\bar{k}}_{24} n_{2,24}+{\bar{k}}_{25} n_{2,25}+{\bar{k}}_{26} n_{2,26}+{\bar{k}}_{27} n_{2,27}+{\bar{k}}_{3} n_{2,3}+{\bar{k}}_{4} n_{2,4}\\&+{\bar{k}}_{5} n_{2,5}+{\bar{k}}_{6} n_{2,6}+{\bar{k}}_{7} n_{2,7}+{\bar{k}}_{8} n_{2,8}+{\bar{k}}_{9} n_{2,9} \\ b_{4}= & {} b_{z} (-d_{1} k_{1}+d_{19} k_{19}-d_{2} k_{2}+d_{20} k_{20}+d_{21} k_{21}+d_{22} k_{22}+d_{23} k_{23}+d_{24} k_{24}\\&+d_{25} k_{25}+d_{26} k_{26}+d_{27} k_{27}-d_{3} k_{3}-d_{4} k_{4}-d_{5} k_{5}-d_{6} k_{6}-d_{7} k_{7}-d_{8} k_{8}-d_{9} k_{9})\\&+{\bar{k}}_{1} n_{3,1}+{\bar{k}}_{10} n_{3,10}+{\bar{k}}_{11} n_{3,11}+{\bar{k}}_{12} n_{3,12}+{\bar{k}}_{13} n_{3,13}+{\bar{k}}_{14} n_{3,14}+{\bar{k}}_{15} n_{3,15}+{\bar{k}}_{16} n_{3,16}\\&+{\bar{k}}_{17} n_{3,17}+{\bar{k}}_{18} n_{3,18}+{\bar{k}}_{19} n_{3,19}+{\bar{k}}_{2} n_{3,2}+{\bar{k}}_{20} n_{3,20}+{\bar{k}}_{21} n_{3,21}+{\bar{k}}_{22} n_{3,22}\\&+{\bar{k}}_{23} n_{3,23}+{\bar{k}}_{24} n_{3,24}+{\bar{k}}_{25} n_{3,25}+{\bar{k}}_{26} n_{3,26}+{\bar{k}}_{27} n_{3,27}+{\bar{k}}_{3} n_{3,3}+{\bar{k}}_{4} n_{3,4}+{\bar{k}}_{5} n_{3,5}\\&+{\bar{k}}_{6} n_{3,6}+{\bar{k}}_{7} n_{3,7}+{\bar{k}}_{8} n_{3,8}+{\bar{k}}_{9} n_{3,9} \\ b_{5}= & {} b_{y} (d_{1}^2 k_{1}-d_{1} {\bar{k}}_{1} n_{1,1}+d_{10}^2 k_{10}\\&-d_{10} {\bar{k}}_{10} n_{1,10}-d_{11} {\bar{k}}_{11} n_{1,11}-d_{12}^2 k_{12}-d_{12} {\bar{k}}_{12} n_{1,12}-d_{16}^2 k_{16}\\&+d_{16} {\bar{k}}_{16} n_{1,16}+d_{17} {\bar{k}}_{17} n_{1,17}+d_{18}^2 k_{18}+d_{18} {\bar{k}}_{18} n_{1,18}+d_{19}^2 k_{19}-d_{19} {\bar{k}}_{19} n_{1,19}\\&-d_{2} {\bar{k}}_{2} n_{1,2}-d_{20} {\bar{k}}_{20} n_{1,20}-d_{21}^2 k_{21}-d_{21} {\bar{k}}_{21} n_{1,21}-d_{25}^2 k_{25}+d_{25} {\bar{k}}_{25} n_{1,25}\\&+d_{26} {\bar{k}}_{26} n_{1,26}+d_{27}^2 k_{27}+d_{27} {\bar{k}}_{27} n_{1,27}-d_{3}^2 k_{3}-d_{3} {\bar{k}}_{3} n_{1,3}-d_{7}^2 k_{7}+d_{7} {\bar{k}}_{7} n_{1,7}+d_{8} {\bar{k}}_{8} n_{1,8}+d_{9}^2 k_{9}\\&+d_{9} {\bar{k}}_{9} n_{1,9})-d_{1} {\bar{k}}_{1} n_{2,1}-d_{10} {\bar{k}}_{10} n_{2,10}+d_{12} {\bar{k}}_{12} n_{2,12}-d_{13} {\bar{k}}_{13} n_{2,13}+d_{15} {\bar{k}}_{15} n_{2,15}\\ &-d_{16} {\bar{k}}_{16} n_{2,16}+d_{18} {\bar{k}}_{18} n_{2,18}-d_{19} {\bar{k}}_{19} n_{2,19}+d_{21} {\bar{k}}_{21} n_{2,21}-d_{22} {\bar{k}}_{22} n_{2,22}+d_{24} {\bar{k}}_{24} n_{2,24}\\&-d_{25} {\bar{k}}_{25} n_{2,25}+d_{27} {\bar{k}}_{27} n_{2,27}+d_{3} {\bar{k}}_{3} n_{2,3}-d_{4} {\bar{k}}_{4} n_{2,4}+d_{6} {\bar{k}}_{6} n_{2,6}\\&-d_{7} {\bar{k}}_{7} n_{2,7}+d_{9} {\bar{k}}_{9} n_{2,9}. \end{aligned}$$