1 Introduction

Potential vorticity (PV) theory, with its mathematical elegance and completeness, has increasingly attracted the attention of dynamicists. Research on PV has deepened our understanding of various atmospheric phenomena, primarily because of its invertibility and conservation (e.g., Hoskins et al. 1985). Application of PV theory to synoptic meteorology has revealed the dynamic mechanisms of many complex weather events. Earlier related studies mostly focused on the redistribution of atmospheric interior PV (e.g., Hoskins et al. 1985), in which the impacts of PV redistribution on the general circulation (e.g., Hoskins et al. 2003; Hoskins 2015; Liu et al. 2007; Luo et al. 2018a, b; Ortega et al. 2018; Xie et al. 2020) and severe weather (e.g., Wu et al. 1995; Wu and Cai 1997; Ma et al. 2022; Zhang et al. 2021a) are of primary interest.

Climate is the cumulative impact of weather over a certain period, e.g., month, season, year, decade or longer. Over long periods, energy generation and dissipation of the atmospheric system are prominent. Because the PV equation explicitly includes the impacts of diabatic heating and frictional dissipation on PV development, it is convenient and instructive to use the PV equation to study climate and its variations. With regard to climate, the features of the source and budget of the atmospheric PV have evoked great interests. For example, Haynes and McIntyre (1987, 1990) introduced the concept of PV density or PV substance, and proposed the impermeability theorem of PV that suggests PV is conserved over a closed isentropic surface. Based on the impermeability theorem, Hoskins (1991) proposed a three-fold division of the atmosphere: the Overworld, Middleworld, and Underworld. The “Overworld” is the region encompassed by isentropic surfaces that are everywhere above the tropopause. The “Middleworld” is the region with isentropic surfaces crossing the tropopause but not striking the Earth’s surface. The “Underworld” is the region with isentropic surfaces intercepting the Earth’s surface. He further illustrated that global atmospheric PV is changeable in the Underworld, but constant above the Underworld. Bretherton and Schӓr (1993) envisioned the impermeability theorem in terms of the so-called effective velocity, and proved that a particle of PV density or PV substance that moves with effective velocity always remains on the same isentropic surface. These findings imply that changes in globally integrated atmospheric PV depend solely on the PV flux on the Earth’s surface (e.g., Sheng et al. 2021). Recently, a number of relevant data analysis regarding the source of Earth’s surface PV has been published (e.g., Ma et al. 2019, 2022; Sheng et al. 2021, 2022; Zhang et al. 2021b).

The PV generated near the Earth’s surface can be transported to the interior of the atmosphere, even from one hemisphere to the other. If the global atmospheric domain that is above the Underworld were covered by a lid of a potential temperature surface and divided into two hemispheric atmospheric domains by a vertical boundary along the equator, then because the PV flux cannot penetrate the upper lid, the hemispheric Earth’s surface and vertical cross section along the equator become two effective boundaries through which the penetrating PV flux determines the changes in hemispheric PV. Over the long term, the integrated surface PV flux should be compensated by the integrated cross-equatorial PV flux (CEPVF). The CEPVF at the equatorial vertical cross section can therefore be considered as a monitor through which the behavior of the surface PV flux can be detected. Because surface PV flux is related to surface air temperature (SAT), diagnosing the variation of CEPVF might further help improve understanding of SAT variation. However, the features and climatological effects related to the integrated CEPVF have received little attention in the meteorological literature. The major objective of this study is to explore the features of the CEPVF and its connection to climate with focus on the SAT of the Northern Hemisphere (NH).

SAT is a vital basic variable in atmospheric science. Variations in SAT have pronounced effects on agriculture, socioeconomic development, and societal activities (Chen and Wu 2018). Spring marks the transition from winter into summer, and it is the season for crops, vegetation recovery, and snowmelt (Chen et al. 2019). Any change in SAT over Eurasia during boreal spring could exert prominent influence on ecosystem recovery (Labat et al. 2004; Wang et al. 2011; Chen et al. 2019). In particular, SAT over Eurasia during boreal spring could connect atmospheric anomalies of the preceding winter and subsequent Asian summer monsoon activity (Ogi et al. 2003; Chen and Wu 2018) by changing the land–sea thermal contrast (Liu and Yanai 2001; D'Arrigo et al. 2006), in which the snow cover provides a memory effect (Ogi et al. 2003; Chen et al. 2016). Therefore, the linkage between CEPVF and SAT over the mid–high latitudes of Eurasia during boreal spring is a specific focus of this study.

The remainder of the paper is organized as follows. Section 2 presents the data, method and theory. Section 3 presents the CEPVF climatology. Section 4 analyzes the interannual relationship between the integrated CEPVF and SAT over the mid–high latitudes of Eurasia during boreal spring and its possible mechanism. Section 5 examines the possible forcing factors of the CEPVF. Finally, the summary and discussion are provided in Sect. 6.

2 Data, method, and theory

2.1 Data

This study uses monthly mean SAT data from the MERRA2 reanalysis product (Rienecker et al. 2011; Lucchesi 2012; https://disc.gsfc.nasa.gov/datasets?project=MERRA-2) and sea surface temperature (SST) data from the COBE SST dataset (Ishii et al. 2005; https://psl.noaa.gov/data/gridded/data.cobe.html). The averaged SST anomalies of the NINO34 index (defined by the region: 5° S–5° N, 120°–170° W), which are used to represent the El Niño–Southern Oscillation (ENSO) condition, are obtained from the following web address: https://psl.noaa.gov/data/climateindices/list/.

PV and PV flux as defined in Eqs. (1) and (3), respectively, involve the product of various variables and therefore the contribution of the transient process might not be represented properly in monthly mean data. To address this problem, we use 3-hourly instantaneous data on the pressure level obtained from MERRA2 to calculate PV and PV flux. The variables include air temperature, zonal wind, and meridional wind.

The research period of this study is 1980–2017. The horizontal resolution of all MERRA2 data is 1.25° × 1.25°. The horizontal resolution of the SST data is 1° × 1°. Climatic mean values calculated over December, January, and February (DJF), March, April, and May (MAM), June, July, and August (JJA), and September, October, and November (SON) are used to represent the conditions of boreal winter, spring, summer, and autumn, respectively.

2.2 Method

Besides the common correlation analysis, regression analysis and composite analysis, the partial correlation is also used in this study to investigate the correlation between the two variables under study by excluding the impact from a third variable. The partial correlation is calculated as follows:

$$r_{12,3} = \frac{{r_{12} - r_{13} r_{23} }}{{\sqrt {(1 - r_{13}^{2} )(1 - r_{23}^{2} )} }},$$

where r12 is the correlation coefficient between variables 1 and 2, r13 is the correlation coefficient between variables 1 and 3, and r23 is the correlation coefficient between variables 2 and 3. The coefficient r12,3 is the partial correlation coefficient between variable 1 and variable 2 with variable 3 removed (Zar 2010).

The linear trend and decadal variation (more than 9 years) of the data are removed to highlight interannual variability.

2.3 Theory

2.3.1 PV, PV budget equation, and PV flux

Here, W is defined as PV per unit volume, the PV density or PV substance. The expression of W in the general form (Haynes and McIntyre 1987, 1990; Bretherton and Schӓr 1993) is as follows:

$$W = \vec{\zeta }_{a} \cdot \nabla \theta ,$$
(1)

where \(\vec{\zeta }_{a}\) is the 3D absolute vorticity vector, and \(\theta\) is potential temperature. The budget equation for PV can be expressed in the conservation form as follows (Haynes and McIntyre 1987, 1990):

$$\frac{\partial W}{{\partial t}} = - \nabla \cdot \vec{J},$$
(2)

with the “PV flux”

$$\vec{J} = \vec {V}_{e} W = \vec{V} W - \vec{ \zeta}_{a} \dot{\theta } - \vec {F}_{\zeta } \theta ,$$
(3)

in which \(\vec{V}\) is the 3D wind vector, \(\dot{\theta } = \frac{d\theta }{{dt}}\) is diabatic heating rate, \(\vec{F} = (F_{x} ,F_{y} )\) is frictional force, \(\vec {F}_{\zeta }\) is the vorticity of frictional force, and

$$\vec {V}_{e} = \vec{J} /W = \vec{V} - (\vec{ \xi}_{a} \dot{\theta } + \vec {F}_{\zeta } \theta )/W$$

is effective velocity. According to Bretherton and Schӓr (1993), because

$$\frac{\partial \theta }{{\partial t}} + \vec{V}_{e} \cdot \nabla \theta \equiv 0,$$

the effective velocity \(\vec {V}_{e}\) is parallel to \(\theta\) surface. Therefore, following Eq. (3), the PV flux \(\vec{ J }\) is directed along isentropic surfaces without penetration, which represents an alternative way of envisioning the impermeability theorem.

Because the divergence of curl is zero, substituting Eq. (1) into Eq. (2) and choosing the form of \(\vec{ J }\) that satisfies Eq. (2) gives (Bretherton and Schӓr 1993)

$$\frac{{\partial \vec{ \xi }_{a} \theta }}{\partial t} = - \vec{ J } .$$
(4)

By integrating Eq. (4) over the given period \(\Delta t\) and adopting the following definition:

$$\vec{J_s} = - \vec{ \xi }_{a} \theta ,$$
(5)

we obtain

$$\vec {J_s} = \int_{{t_{0} }}^{{t_{0} + \Delta t}} {\vec{ J} } dt + \user2{C }=\int_{{t_{0} }}^{{t_{0} + \Delta t}} ({\vec {V}}_{e} W )dt + \user2{C},$$
(6a)

where C is a time-independent constant field. The flux \(\vec{J_s}\) can be considered the temporally accumulated PV flux over a given period (\(\Delta t\)) with a different unit to PV flux \(\vec{J}\). From Eq. (5), we can also obtain

$$W = - \nabla \cdot (\vec{J_s}).$$
(6b)

On the basis of Eq. (6b), and through mimicking the atmospheric convergence \(C = - \nabla \cdot \vec{V}\), in which \(\vec{ V}\) is the atmospheric circulation, the accumulated PV flux \(\vec{J_s}\) can be referred to as PV circulation (hereafter, PVC). From Eq. (6a), we can see PVC represents the cumulative effects of the transient PV flux. From Eqs. (2) and (6b), we can also discern the difference between \(\vec{J_s}\) and \(\vec{ J}\). For a specific domain enclosed by boundary A, its gross PV is determined by the sum of the cross-A PVC \(\vec{J_s}\), whereas its gross PV generation is determined by the sum of the cross-A PV flux \(\vec{ J}\). In simple terms, the convergence of \(\vec{J_s}\) is PV itself (Eq. 6b), whereas the convergence of \(\vec{ J }\) is the local PV generation (Eq. 2).

2.3.2 Gross PV budget in the atmosphere

We define a theta surface (\(\theta_{T}\)) above the Underworld as the top of the atmosphere that is under investigation. Because flux \(\vec{ J }\) at \(\theta_{T}\) is parallel to the \(\theta_{T}\) surface, there is no flux \(\vec{ J }\) perpendicular to the \(\theta_{T}\) surface (Bretherton and Schӓr 1993; Schneider et al. 2003). Integrating the PV budget equation (Eq. 2) globally from the Earth’s surface to the \(\theta_{T}\) surface and using Gauss’s theorem, we obtain the following:

$$\frac{\partial }{\partial t}\iiint\limits_{global} Wdv\; = - \iiint\limits_{global} {\nabla \cdot (\vec{ J} )}dv\; = \; - \iint\limits_{globalsurf} {\vec{ J}\cdot {\overrightarrow {ds}} }.$$
(7a)

If the domain is confined to the NH, then we have

$$\frac{\partial }{\partial t}\iiint\limits_{NH} Wdv\; = - \iiint\limits_{NH} {\nabla \cdot (\vec{J} )}dv\; = \; - \iint\limits_{NHsurf} {\vec{ J}\cdot {\overrightarrow {ds}} } + \iint\limits_{{{\varvec{EQ}}}} {CEPVFds},$$
(7b)

in which \(ds = dxdh\) with h ranging from the surface to \(\theta_{T}\), and

$$CEPVF = \vec{J }\cdot {\vec {j}} \; = J^{y} ,$$
(7c)

which is the meridional component of PV flux across the equatorial vertical section and represents cross-equatorial PV transport. The superscript indicates the vector component. Equation (7a) indicates that the budget of globally integrated PV is determined solely by the Earth’s surface PV flux, which is consistent with previous studies (Haynes and McIntyre 1987, 1990; Hoskins 1991; Schneider et al. 2003).

Equation (7b) indicates that CEPVF also contributes to the PV budget in the NH. Because the PV budget is balanced in the NH in terms of the long-term mean (Eq. 7b), the integrated CEPVF can be regarded as a monitor from which the integrated surface PV flux conditions can be detected. The surface PV flux is related to the surface thermal conditions (Eq. 3), which means that CEPVF is closely linked to the surface thermal conditions.

2.3.3 PV flux and cross-equatorial PV flux in a pressure coordinate system

Most reanalysis data are archived in a pressure coordinate system. For hydrostatic large-scale motion, the pressure coordinate analogue of vorticity may be written as follows (Sheng et al. 2021):

$$\vec {\zeta}_{a} = \frac{\partial v}{{\partial p}}\;\vec{i} - \frac{\partial u}{{\partial p}}\;\vec{j}\; - \; \left(f + \frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}} \right) \;\vec{k},$$

where \((u,v)\) is the horizontal wind vector, and the lowercase letter vectors \((\vec {i} ,\vec { j} ,\vec {k} )\) indicate unit vectors pointing eastward, northward, and downward, respectively.

Then, the component form of PVC (\(\vec{J_s}\)) can be written as follows:

$$\vec {J_s} = - \vec {\zeta}_{a} \theta = (J_{s}^{x} , \, J_{s}^{y} , \, J_{s}^{p} ) = - \frac{\partial v}{{\partial p}}\theta \;\vec{i} + \frac{\partial u}{{\partial p}}\theta \;\vec{j}\; + \;\left(f + \frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}\right)\theta \;\vec{k},$$
(8a)

in which

$$J_{s}^{x} = - \frac{\partial v}{{\partial p}}\theta ,\;\;J_{s}^{y} = \frac{\partial u}{{\partial p}}\theta , \, J_{s}^{p} = (f + \zeta )\theta .$$
(8b)

From Eqs. (6a), (7c), and (8b), we can obtain the following important relation:

$$\Delta \int_{{t_{0} }}^{{t_{0} + \vartriangle t}} {CEPVF \, } dt = \Delta J_{s}^{y} = \Delta \left(\frac{\partial u}{{\partial p}}\theta \right),$$
(9)

where \(\Delta\) indicates the temporal change or time variation. Equation (9) means that the temporal variation of CEPVF over a given period is determined substantially by the variation of vertical shear in the zonal wind weighted by potential temperature.

The PV flux \(\vec{ J }\) (Eq. 3) consists of advective flux (\(\vec{ J_a}\); the first term), heating flux (the second term), and friction flux (the third term). The effect of friction always tends to offset a change in PV but it cannot alter the sign of PV change. In simple terms, friction makes the eventual observed change more moderate than it would be otherwise. The effect of friction is usually confined in the surface layer, as is discussed in Sect. 4.2.3, but it is neglectable in the free atmosphere. In the following analysis concerning the free atmosphere, we do not further investigate the effect of friction in relation to CEPVF.

Along the equator, the heating flux is smaller than the advective flux after integrating vertically over the equator (table not shown), and it tends to slightly offset the advective flux. Moreover, the correlation coefficient between the annual mean integrated advective flux and the sum of both the annual mean integrated advective and heating fluxes is as high as 0.92, passing the 0.01 significance level. This indicates that CEPVF is dominated by advective flux. Thus, we first consider only the advective flux in calculating CEPVF for the free atmosphere.

The meridional component of PV flux in Eq. (3) therefore gives

$$CEPVF = \vec {J_a} \cdot \vec {j} \; = J^{y} = vW.$$
(10)

From Eq. (10), the vertically and zonally integrated CEPVF along the equator can be expressed as follows:

$$\left\{ {CEPVF} \right\} = \int\limits_{EQ} {\int_{pt}^{ps} {CEPVF\;dpdx} } = \int\limits_{EQ} {\int_{pt}^{ps} {vW\;dpdx} } .$$
(11)

From Eq. (11), a CEPVF index, namely CEPVFI, is defined as the normalized time series of {CEPVF}:

$$CEPVFI = \left\{ {CEPVF} \right\}^{\prime } /\sigma ,$$
(12)

where \(\sigma\) is the standard deviation of {CEPVF} and \( \left\{ {CEPVF} \right\}^{\prime }\) is the {CEPVF} anomaly. A positive (negative) CEPVFI value corresponds to anomalous net northward (southward) CEPVF over the equatorial section. Since the climate mean CEPVF is negative (will be shown in Fig. 1), the positive (negative) anomalous CEPVF also implies less (more) southward CEPVF.

Fig. 1
figure 1

Climatic mean distribution of cross-equatorial PV flux (CEPVF) along the equator in a MAM, b JJA, c SON, and d DJF. Unit: 10−7 kg−1 K m2. Black shading indicates land

Full size image

Because the 380 K isentropic surface is near the tropopause over the equator (Wilcox et al. 2012), and because the 100 hPa isobaric surface almost overlaps the 380 K isentropic surface at the equator, the 100 hPa isobaric surface can be considered the tropical tropopause at the equator. Calculation shows that the correlation between the CEPVFI when the upper integral boundary is set at 100 hPa and 380 K successively is as strong as 0.91, exceeding the 0.01 significance level (figure not shown). Furthermore, because the raw data are based on an isobaric surface, directly employing pressure coordinates can avoid extrapolation and interpolation errors. Thus, to focus on the signal in the troposphere in a pressure coordinate system, the upper integral boundary (pt in Eq. 11) is chosen as 100 hPa in this study.

3 Climatology of cross-equatorial PV flux

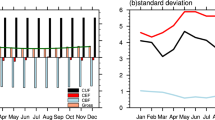
Several important climatological features of CEPVF in different seasons are presented in Fig. 1. These features, which appear in all seasons, include two layers with strong southward CEPVF: one in the upper layer within 200–100 hPa and the other in lower layer within 1000–850 hPa; strong southward CEPVF occurring preferentially around the land in the lower layer; and negative CEPVF dominating over the entire equatorial section, which is the most interesting phenomenon.

The CEPVF is linked with the meridional wind and PV. Zhao and Lu (2020) investigated the vertical structure of cross-equatorial flow (meridional wind). Their results clearly showed two layers in the distribution of cross-equatorial flow with absolute maxima at 200–100 and 1000–700 hPa. High PV in the atmosphere is also concentrated in both the upper layer (Hoskins et al. 1985) and the lower layer (Sheng et al. 2021; Zhao and Ding 2009). Thus, the two layers of CEPVF (Fig. 1) do make sense because they are the product of the meridional wind and PV; however, it remains unclear why negative CEPVF is dominant over the entire equatorial section.

It might be conjectured that PV reverses sign across the equator with positive values to the north and negative values to the south. At the equator, a northerly wind (v < 0) brings positive PV (PV > 0) into the Southern Hemisphere (SH), while a southerly wind (v > 0) brings negative PV (PV < 0) into the NH. In both cases, CEPVF is always negative. Therefore, negative CEPVF is observed over almost the entire equatorial section. The equatorial cross section of the distribution of PV and the meridional wind is shown in Fig. 2. In all seasons, in the areas with red dots (v > 0), PV is mostly negative (PV < 0), whereas in the areas without dots (v < 0), PV is mostly positive (PV > 0). This configuration verifies the physical process, as documented above, that a northerly wind (v < 0) brings positive PV (PV > 0) into the SH, while a southerly wind (v > 0) brings negative PV (PV < 0) into the NH. This physical process can also be seen in Hoskins et al. (2020) and Hoskins and Yang (2021, see their Fig. 1c). Thus, these results indicate that it is this configuration that results in the overwhelming negative CEPVF over the equatorial section. However, certain areas of positive values do exist (Fig. 1) where the climatological meridional wind and PV have opposite signs, e.g., the region with positive values in the upper level shown in Fig. 1b, c. Because CEPVF is a combination of mean and transient eddy processes, these positive values imply that the transient eddy process also contributes to CEPVF, and thus the relevant physical implication deserves further study.

Fig. 2
figure 2

Same as Fig. 1 but for PV per unit volume. Unit: 10−7 K m s kg−1. Red dots indicate southerly wind (v > 0) and areas without dots indicate northerly wind (v < 0)

Full size image

The climatological annual cycle of the {CEPVF} and its standard deviation in each season are shown in Fig. 3a, b, respectively. The positive {CEPVF} component is very small and negative CEPVF dominates the {CEPVF} (Fig. 3a), which is consistent with Fig. 1. The negative {CEPVF} indicates that in terms of the climatological mean there is net PV transport from the NH to the SH. The {CEPVF} shows a semiannual cycle with absolute minima in April and November and absolute maxima in January and July. This semiannual cycle is consistent with the cycle of cross-equatorial mass exchange (Zhang et al. 2008). The value of the standard deviation of {CEPVF} peaks in MAM (Fig. 3b), reaches a trough in DJF, and is intermediate in JJA and SON. This means the strongest (weakest) interannual variability of {CEPVF} occurs in boreal spring (winter).

Fig. 3
figure 3

a Climatological annual cycle of {CEPVF}. Unit: 104 K m Pa s−1. Yellow, gray, and black bars indicate northward, southward, and total CEPVF along the equator, respectively. b Nondimensional {CEPVF} standard deviation in different seasons

Full size image

4 Cross-equatorial PV flux and SAT over Eurasia during boreal spring

As documented in Sect. 2.3, because CEPVF is closely related to surface PV flux in the climatological mean state (Eq. 7b), and because surface PV flux is related to surface SAT (Eq. 3), there should be close linkage between CEPVF and SAT. This is shown to be true in data analyses, particularly in relation to boreal spring. In this section, we show this interannual connection between {CEPVF} and SAT over the mid–high latitudes of Eurasia during boreal spring when the interannual variability of {CEPVF} is the strongest (Fig. 3b) and discuss its possible mechanism.

4.1 Relationship between CEPVF and SAT

The variation of the CEPVFI (Eq. 12) during boreal spring is shown in Fig. 4a. A positive (negative) value of the CEPVFI indicates net anomalous PV transport from the SH (NH) to the NH (SH). The CEPVFI shows strong interannual variability with the variation exceeding one standard deviation in 10 of the 38 years. A regression map of SAT against the CEPVFI over the mid–high latitudes of the Eurasian continent is presented in Fig. 4b, which shows a broad uniform negative pattern over the mid–high latitudes of Eurasia. Embedded within this broad uniform pattern are three significant negative centers: the Mediterranean region, the area southwest of Lake Baikal, and the far east of Russia. This finding indicates that a positive (negative) phase of the CEPVFI corresponds to cooling (warming) over Eurasia. This pattern bears close resemblance to the first empirical orthogonal function (EOF) mode of SAT over Eurasia during boreal spring that was revealed by Chen et al. (2016, see their Fig. 1a). Examination of the correlation between the CEPVFI and the time series of the first EOF mode of SAT indicates that the correlation coefficient reaches 0.36, exceeding the 0.05 significance level. This indicates that CEPVF is related closely to SAT over the mid–high latitudes of Eurasia during boreal spring. However, how CEPVF variation is related to SAT over the northern Eurasian continent remains unclear and requires further investigation.

Fig. 4
figure 4

a Normalized time series of spring CEPVFI. b Regression coefficients of SAT against the CEPVFI during boreal spring (shading, °C). Areas exceeding the 0.05 significance level are highlighted by black dots. Three centers of negative SAT are evident along the black line

Full size image

4.2 Possible mechanism

4.2.1 CEPVF, general circulation, and meridional PVC at the equator

To understand the physical process via which the {CEPVF} is related to SAT, we first investigate the distribution of anomalous CEPVF along the equatorial section. The correlation between the CEPVFI and CEPVF along the equator is shown in Fig. 5a. It is evident that anomalous CEPVF over the equatorial Pacific is predominantly northward (southward) above (below) 700 hPa (Fig. 5a). Conversely, CEPVF over the equatorial Indian Ocean is southward (northward) in the upper (lower) layer.

Fig. 5
figure 5

Distribution of correlation coefficients between the CEPVFI and a \(J_{{}}^{y}\) and b \(J_{s}^{y}\) (shading) and the latitudinal circulation (vectors) along the equatorial section during boreal spring. Vectors exceeding the 0.05 significance level are shown. Areas exceeding the 0.05 significance level are highlighted by black dots. c Regression of variation of \(J_{s}^{y}\): term A (red dashed line), term B (green solid line), and term C (blue solid line) on CEPVFI along the equator at 300 hPa. Unit: 10−1 m K s−1 Pa−1. The result regarding term B is multiplied by 100 for clarity. d Same as c except for 850 hPa

Full size image

The correlation map between the CEPVFI and meridional component of the PVC (\(J_{s}^{y}\); Eq. 8b) is shown in Fig. 5b. Figure  5b bears marked resemblance to the vertical structure of anomalous CEPVF shown in Fig. 5a, which is also in accordance with Eq. (9). The vertical structure with northward CEPVF in the upper level and compensatory southward CEPVF in the lower level over the equatorial Pacific is very clear (Fig. 5b). Moreover, the inverse vertical structure over the equatorial Indian Ocean is also prominent. This anomalous CEPVF pattern (Fig. 5b) revealed by the CEPVFI is consistent with the first EOF mode on \(J_{s}^{y}\) over the equatorial section, and the correlation coefficient of their time series reaches 0.68, passing the 0.01 significance level (figure not shown), which indicates that the CEPVFI could well capture the dominant mode of variation of CEPVF. A more interesting characteristic is that the structure shown in Fig. 5b is less chaotic than that in Fig. 5a. This is mainly because the PVC (\(\vec {J_s}\)) is the time-integrated \(\vec{J}\) (Eq. 6a), which has the high-frequency information filtered out. It should be noted that the convergence of \(\vec{J}\) represents the generation of W, whereas the convergence of \(\vec {J_s}\) is equals to W itself. The similarity between Fig. 5a and b thus becomes natural. It should also be noted that certain differences remain between Fig. 5a and b. This is mainly because \(\vec{ J }\) is approximated to the advective PV flux, whereas \(\vec {J_s}\) includes the total effect of advection, diabatic heating, and friction. Despite this difference, the similarity between Fig. 5a and b confirms that flux \(\vec{J}\) and flux \(\vec {J_s}\) are consistent in depicting the variation of CEPVF.

The nature of \(J_{s}^{y}\) is the vertical shear of the zonal wind weighted by potential temperature. From the definition of \(J_{s}^{y}\) (Eq. 8b), the transitional area with the zero contour in Fig. 5b corresponds to the maximum or minimum zonal wind. As can be seen, the regions of maximum and minimum zonal wind are located in the lower layer near 700 hPa over the equatorial Pacific and Indian Ocean, respectively. Consequently, over the Pacific, the \(J_{s}^{y}\) is positive above the maximum zonal wind but negative below, whereas over the Indian Ocean, the \(J_{s}^{y}\) is negative above the minimum zonal wind but positive below. The above results indicate that the variation of CEPVF is mainly related to the anomalous zonal circulation along the equator.

This result can be verified using the following linear temporal expansion of the meridional component of PVC (Eq. 8b):

$$ \frac{{\Delta J_{s}^{y} }}{A} = \Delta \left(\frac{\partial u}{{\partial p}}\theta \right) \approx \frac{{\frac{\partial u}{{\partial p}}\cdot \Delta \theta }}{B} + \frac{\left(\Delta \frac{\partial u}{{\partial p}}\right) \cdot \theta }{C},$$

which means that the temporal variations of CEPVF (term A) are induced by the variations of potential temperature (term B) and the zonal circulation (term C). The regression of terms A (red dashed line), B (green solid line), and C (blue solid line) on the CEPVFI along the equator at 300 and 850 hPa are shown in Fig. 5c, d, respectively. Because the regression of term B (green line) on CEPVFI is very small, it is multiplied by 100 for clarity in the figure. It is evident that term A along the equator matches well with term C at both upper (Fig. 5c) and lower (Fig. 5d) levels, further confirming that the temporal variation of CEPVF is determined substantially by changes of the zonal circulation along the equator.

Wu and Meng (1998) found strong coupling between the monsoonal zonal circulation over the equatorial Indian Ocean and the Walker circulation over the Pacific. The coupling system operates very much like a pair of gears running on the equatorial Indian Ocean and Pacific (denoted as GIP), and the “gearing point” of the two cells is located near the Maritime Continent. When one cell rotates clockwise, the other rotates anticlockwise. The direction of this gearing with a clockwise (anticlockwise) Walker circulation over the Pacific and anticlockwise (clockwise) monsoonal zonal circulation over the equatorial Indian Ocean is defined as positive (negative). Wu and Meng (1998) demonstrated that the GIP is linked closely to ENSO. The circulation shown in Fig. 5b is in accordance with the negative GIP reported in their study, which suggests that CEPVF might be associated with ENSO.

4.2.2 CEPVF, PV, and PVC

Because the convergence of PVC (\(\vec {J_s}\)) is directly related to PV itself (Eq. 6b), whereas the convergence of PV flux (\(\vec{ J}\)) represents PV generation (Eq. 2), for clear and intuitive illustration of the variation of PV itself we consider PVC in the following analysis. The distributions of the correlation coefficients between the CEPVFI and PV as well as horizontal PVC at different levels are presented in Fig. 6. Generally, in high-latitude regions, the PV distribution exhibits an equivalent barotropic structure, whereas in the tropics, both PV and horizontal PVC in the upper troposphere are out of phase with their counterparts in the lower troposphere. Corresponding to the positive phase of the CEPVFI, northward CEPVF can be seen clearly over the Pacific at 200 hPa (Fig. 6a). This northward CEPVF converges anomalous PV to the north of the equator, compensating the reduction of PV in situ. Meanwhile, southward CEPVF is also significant over the Maritime Continent and the Indian Ocean. The southward PVC over the Indian Ocean transfers PV toward the equator, corresponding to the formation of a belt of PVC divergence associated with negative PV over the north of the Tibetan Plateau (TP). This belt of divergence exudes PV that is conducive to the formation of positive PV over the mid–high latitudes of Eurasia (Eq. 6b). It is further found that the broad pattern of positive PV bears close resemblance to the SAT pattern shown in Fig. 4b, suggesting connection between SAT anomalies and PV anomalies. The broad pattern of positive PV with three nodes over the Eurasian continent exhibits an equivalent barotropic structure that intrudes downward to 500 hPa (Fig. 6b).

Fig. 6
figure 6

Distribution of correlation coefficients between CEPVFI and PV (shading) and horizontal \(\vec {J_s}\) (vectors) at a 200, b 500, and c 850 hPa during boreal spring. Areas exceeding the 0.05 significance level are highlighted by black dots. Vectors exceeding the 0.05 significance level are plotted. The blue line denotes the TP topographic boundary of 3000 m

Full size image

The signal of horizontal PVC over the equator at 500 hPa is weaker than at 200 hPa, especially over the Indian Ocean. However, the three positive PV centers over Eurasia are very clear and the flux vector is significant (Fig. 6b). The horizontal PVC at 850 hPa (Fig. 6c) is opposite that in the upper level (Fig. 6a) along the equator, which is in accordance with Fig. 5b. Although the three positive PV centers are not clear over the mid–high latitudes of Eurasia at this lower level, the in situ divergence of the PVC vectors is prominent.

It is worth noting that near the equator over the Pacific sector PV is positive to the north and negative to the south at 850 hPa, and that this is reversed at 500 and 200 hPa (Fig. 6). This is because part of the PV (\(- (f - \partial u/\partial y) \cdot \partial \theta /\partial p\)) changes its sign across the equator, particularly if the maximum/minimum zonal wind is located at the equator. The intensified equatorial westerly flow in the lower troposphere and easterly flow above 600 hPa over the Pacific sector (Fig. 5b) thus contribute to the anomalous PV distribution there. To the west of the Maritime Continent, for the same reason, PV is negative to the north and positive to the south at 850 and 500 hPa, and the situation is reversed at 200 hPa (Fig. 6). It is because the equatorial westerly flow dominates below 400 hPa in this sector, whereas an easterly flow prevails aloft (Fig. 5b).

To further reveal the characteristics of the broad positive PV pattern in the mid–high latitudes over the Eurasian continent shown in Fig. 6a, the meridional vertical section crossing the central positive PV center (averaged over 70°–105° E) embedded in this broad PV pattern is presented in Fig. 7. The correlation coefficients between the CEPVFI and both PVC and PV are displayed. Because the positive vertical direction is downward in pressure coordinates, mimicking the vertical pressure velocity (\(\omega\)), the vertical component of PVC (\(J_{s}^{p}\)) is multiplied by (− 1) for intuitively plotting. Corresponding to the positive phase of the CEPVFI, in the tropical area below 300 hPa, positive PV exists to the south of the equator and negative PV exists to the north. This is because the prevailing equatorial zonal wind below 300 hPa in the Indian Ocean sector is easterly (Fig. 5b), resulting in cyclonic vorticity to the south of the equator and anticyclonic vorticity to the north. In both the NH and SH, the PVC is downward in the region of positive PV but upward in the region of negative PV. This is because, according to the definition (Eq. 8b), the vertical component of PVC multiplied by (− 1) (\(- J_{s}^{p} = - (f + \zeta )\theta\)) possesses the opposite sign to PV in a hydrostatic atmosphere.

Fig. 7
figure 7

Distribution of correlation coefficients between the CEPVFI and the 70°–105° E mean PV circulation (\(J_{s}^{y}\); − \(J_{s}^{p}\)) (vectors) and PV (shading). Areas exceeding the 0.05 significance level are highlighted by black dots. Vectors exceeding the 0.05 significance level are plotted

Full size image

A remarkable feature evident in Fig. 7 over the TP is the significant area of divergence (convergence) of PVC associated with negative (positive) PV in the upper troposphere above (below) 400 hPa. Diagnosis of the correlation between the CEPVFI and diabatic heating shows that in the area over the TP (28°–40° N, 80°–105° E), the area-averaged diabatic heating increases (decreases) with height below (above) 300 hPa (figure not shown). Positive and negative PV is then generated in the lower layer and upper layer, respectively. This explains at least partly why PV distribution is positive in the lower layer and negative in the upper layer over the TP. The divergence of PVC over the TP connects CEPVF to the SH and transports PV to high latitudes, which is conducive to the formation of a notable positive PV column over the mid–high latitudes of Eurasia (Eq. 6b). Specifically, the divergence over the TP is related to the two gyres of PVC: one to its south and the other to its north. The southern one crosses the equator into the SH in the upper layer and returns to the NH in the lower layer, whereas the northern one moves northward into the higher latitudes, converging and intruding PV downward to the north of the TP, leading to increasing PV over the entire column in the mid–high latitudes of Eurasia. Finally, the positive PV column with an equivalent barotropic structure is formed over the mid–high latitudes of Eurasia.

4.2.3 PV, SAT, and surface feedback

To further reveal how the equivalent barotropic PV column is retained and how it is related to the in situ cold SAT, the vertical cross section of the correlation between the CEPVFI and both PV and potential temperature (along the black line in Fig. 4b) is shown in Fig. 8. Corresponding to the positive phase of the CEPVFI, three equivalent barotropic positive PV columns (Fig. 8) are located at positions coincident with the three cold SAT centers. Based on the PV-θ mechanism (Hoskins et al. 1985, 2003), isentropes in the troposphere will be vertically “sucked” toward a positive PV anomaly, which means the isentropes bow downward (upward) in the upper (lower) layer. As upward (downward) bowing of isentropes indicates a cold (warm) atmosphere, the three equivalent barotropic positive PV columns therefore lead to the broad uniform pattern of cold SAT shown in Fig. 4b.

Fig. 8
figure 8

Distribution of correlation coefficients between the CEPVFI and potential temperature (contours; solid (dashed) lines indicate positive (negative) values) and PV (shading) along the black line displayed in Fig. 1b during boreal spring. The black vertical dashed lines indicate the negative SAT centers displayed in Fig. 4b. Areas exceeding the 0.05 significance level are highlighted by black dots

Full size image

As predicted by the PV-θ mechanism, an outstanding common feature (Fig. 8) is that a warm (cool) anomaly appears in each column above (below) 300 hPa. Recalling that the PV source is at the Earth’s surface, at the boundary surface, the vertical PV transport due to flux \(\vec {J_s}\) is \(\vec {J_s} \cdot \vec {n} \approx \int_{{t_{0} }}^{{t_{0} + \vartriangle t}} {( - f\dot{\theta } - F_{\zeta } \theta )} dt\), which depends on both heating and friction, where \(\vec{n}\) is an upward unit vector. Because a cold surface favors a local anticyclone circulation (Thorpe 1985; Hoskins et al. 1985), the atmosphere then exerts anticyclonic stress on the Earth, and the Earth reacts to the atmosphere by producing cyclonic torque, generating positive PV. Moreover, surface cooling over a cold surface also contributes to the generation of positive PV, which in return contributes to the formation of the lower part of the positive PV column over the cold surface, as presented in Fig. 8.

According to the thermal wind relation, a region with cold SAT and a cold air column above can generate a cyclonic vertical shear circulation. Conversely, a warm anomaly in the upper positive PV column should correspond to an anticyclonic vertical shear circulation. Consequently, a maximum anomalous cyclone circulation should exist in the middle column at around 300 hPa. Because the column is warm aloft and cold below, the static stability should also be maximized in the middle layer. Therefore, the positive PV can extend from the lower layer to the middle layer, as shown in Fig. 8. In return, the PV in the positive barotropic PV columns can further maintain the “warm aloft and cold below” thermal structure of the column due to the PV-θ mechanism. Consequently, the broad uniform pattern of cold SAT shown in Fig. 4b is retained at an equilibrium state attributable to positive feedback between the atmospheric circulation and surface cooling.

The above discussion reveals that the significant connection between CEPVF and SAT over the mid–high latitudes of Eurasia is sustained via the PVC, the PV-θ mechanism, and the surface feedback involving friction, diabatic cooling, and the atmospheric circulation.

5 Possible forcing factors of the CEPVF

The anomalous CEPVF is related closely to the vertical distribution of anomalous zonal circulation over the equator (Eq. 9), and therefore any factors inducing the anomalous equatorial zonal circulation could drive the CEPVF. Because ENSO events have strong effect on the zonal circulation (Bjerknes 1969), ENSO as a strong signal of air–sea interaction along the equator could be a driver of CEPVF. The correlation coefficient between the spring CEPVFI and the preceding winter NINO34 index is as high as 0.62 (figure not shown), and the correlation coefficient between the spring CEPVFI and the current spring NINO34 index is as high as 0.67, as shown in Fig. 9a, both passing the 0.01 significance level and indicating a strong relation between ENSO and CEPVF. The correlation between NINO34 and the meridional component of the PVC (\(J_{s}^{y}\)) is shown in Fig. 9b. In the warm phase of ENSO (Fig. 9b), descending motion is observed over the Maritime Continent, and anomalous westerly and easterly winds are observed in the lower level over the equatorial Pacific and equatorial Indian Ocean, respectively, presenting a negative GIP pattern (Wu and Meng 1998). The CEPVF induced by the warm phase of ENSO is very similar to the CEPVF revealed by the CEPVFI (Fig. 5b). This confirms that ENSO is an important forcing factor of CEPVF.

Fig. 9
figure 9

a Normalized time series of the CEPVFI, NINO34 index, and TSAI during boreal spring. b Same as Fig. 5b but for the spring NINO34 index. c Same as Fig. 5b but for the TSAI index

Full size image

In addition to ENSO, by employing the partial correlation between the CEPVFI and SST with the spring NINO34 index removed, we found another significant forcing signal of the tropical South Atlantic uniform SST mode (TSAM, Fig. 10), which is characterized as SST anomalies with the same sign over the region (30° S–0°, 40° W–10° E). This mode is a major EOF pattern for tropical South Atlantic variability (Huang et al. 2004). The time series of the area-averaged SST in the blue box in Fig. 10 is defined as the TSAM index (TSAI, shown in Fig. 9a) to represent tropical South Atlantic forcing. The correlation coefficient between the TSAI and the leading EOF time series of the SST in the blue box is as high as 0.99 (figure not shown), indicating that the following results are insensitive to the definition of the SST index. The correlation coefficient between the spring TSAI and the spring CEPVFI is 0.35, passing the 0.05 significance level. However, the correlation coefficient between the spring TSAI and the spring NINO34 index is as low as − 0.016, failing the significance test (Fig. 9a). This implies that variation of SST in the tropical South Atlantic is unrelated to ENSO during boreal spring, which is consistent with both Chang et al. (2006) and Kucharski et al. (2007). The TSAM and ENSO therefore can be considered two independent forcing factors that drive CEPVF during boreal spring. As can be seen from Fig. 9c, a significant zonal circulation related to the TSAM is observed around the Maritime Continent, and the induced CEPVF that is concentrated around the Maritime Continent is significant.

Fig. 10
figure 10

Distribution of partial correlation coefficients between the CEPVFI and SST with the spring NINO34 index removed. The area covered by the blue box is (30° S–0°, 40° W–10° E). Areas exceeding the 0.05 significance level are highlighted by black dots. The solid blue line denotes the TP topographic boundary of 3000 m

Full size image

To evaluate the relative roles of the two forcing factors, a regression equation is constructed as CEPVFI* = 0.68(spring NINO34) + 0.36(TSAI) through multiple regression analysis, as shown in Fig. 11a. The correlation between the CEPVFI and the CEPVFI* reconstructed by the spring NINO34 index and the TSAI is 0.75, passing the 0.01 significance level. The explained variance contributed by the NINO34 index and TSAI is approximately 45% and 13% of the total, respectively. Because the NINO34 index and TSAI are unrelated, the total variance explained by these two forcing factors is approximately 58%. These results indicate that the effects of ENSO and the TSAM largely dominate the variation of the CEPVFI.

Fig. 11
figure 11

a Normalized time series of the CEPVFI (red line) and CEPVFI* (blue line) during boreal spring. b Composite SAT differences between strong positive (greater than 1 standard deviation) and negative (less than − 1 standard deviation) ENSO phases during boreal spring. c As in b but for the TSAI. Areas exceeding the 0.1 significance level are highlighted by white dots

Full size image

Because the CEPVF-related zonal circulation induced by ENSO is different to that of the TSAM, the contributions of these two factors to the anomalous SAT should be different. To separate the contributions of ENSO and the TSAM to the anomalous SAT associated with the CEPVFI, Fig. 11 also presents the composite SAT differences between the strong positive (greater than 1 standard deviation) and strong negative (less than − 1 standard deviation) NINO34 index (Fig. 11b) and TSAI (Fig. 11c). ENSO (Fig. 11b) is mainly responsible for the overall cooling over the mid–high latitudes of Eurasia. There are three evident cooling centers, i.e., over the Mediterranean region, northwest of Lake Baikal, and the far east of Russia, similar to the pattern of anomalous SAT induced by the CEPVFI shown in Fig. 4b, except that the center near Lake Baikal is shifted further northward. The TSAM (Fig. 11c) is mainly responsible for the cooling center to the south of Lake Baikal. The two independent forcing factors together largely contribute to the emergence of the wide-ranging cooling pattern related to the CEPVFI over the mid-latitudes of Eurasia.

6 Summary and discussion

6.1 Summary

The change in globally integrated atmospheric PV depends solely on PV flux on the Earth’s surface, which is the lower boundary of the global domain. For the NH domain, the equatorial vertical section becomes another boundary, and the CEPVF becomes another boundary condition for the change of gross PV in the NH. Because the integrated surface PV flux associated with surface thermal conditions is balanced climatologically by the CEPVF (see Eqs. 3 and 7b), the CEPVF is therefore related closely to the thermal conditions of the Earth’s surface. The results of this study highlight that it is the atmospheric PVC (\(\vec {J_s}\), Eq. 8a) that links the CEPVF to the tropical forcing and extratropical SAT response at the Earth’s surface.

In addition to theoretical analysis, this study explored the climatological mean features of the CEPVF and focused on the correlation between CEPVF and SAT anomalies over the mid–high latitudes of Eurasia during boreal spring on the interannual time scale. The major results concerning the relationship between CEPVF and SAT are shown schematically in Fig. 12 and summarized as follows.

  1. (1)

    Climatologically, overwhelming negative CEPVF largely dominates the entire equator, indicating that net PV is transported from the NH to the SH. We highlight that the physical process of a northerly wind (v < 0) bringing positive PV (PV > 0) and a southerly wind (v > 0) bringing negative PV (PV < 0) dominates the distribution of the CEPVF.

  2. (2)

    A CEPVF index, namely the CEPVFI, is defined as the normalized time series of the zonally and vertically integrated CEPVF over the equator. On the interannual time scale, the positive phase of the CEPVFI is closely related to the variation of SAT, particularly the significant cooling over the mid–high latitudes of Eurasia, through the PVC, PV-θ mechanism, and surface feedback, as indicated schematically in Fig. 12. The CEPVF over the equatorial Indian Ocean corresponds to the formation of a belt of divergence of PV over the north of the TP, which transfers PV toward the equator and contributes to the broad positive PV in the upper troposphere over the mid–high latitudes of Eurasia (Fig. 12a). The positive PV intrudes downward into the lower layer and forms three positive PV columns (Fig. 12b). Finally, owing to the PV-θ mechanism, the isentropes in the lower troposphere bow upward within these equivalent barotropic positive PV columns, leading to overall cold SAT over the mid–high latitudes of Eurasia (Fig. 12b, c). In return the cold surface and its cooling feedback to the atmosphere via surface friction and the diabatic process produce positive PV in the lower troposphere within the PV column. Through cooperation with the thermal wind relation, therefore, the cold SAT and the positive PV aloft are maintained at an equilibrium state.

  3. (3)

    Because CEPVF is intrinsically proportional to a function of \(- \frac{\partial u}{{\partial p}}\) (Eq. 9), the variation of CEPVF can result from the change of the zonal circulation over the equator (Fig. 5c, d). Two independent forcing factors, namely ENSO and the TSAM, are identified as the main drivers of the CEPVF associated with the zonal circulation (Fig. 12c). Together, ENSO and the TSAM explain approximately 58% of the CEPVFI variance, of which ENSO accounts for approximately 45% and the TSAM accounts for approximately 13%. Owing to the differences in CEPVF induced by ENSO and the TSAM, the contributions of these two factors to the anomalous SAT differ. A warm ENSO is mainly responsible for the overall cold SAT over the mid–high latitudes of Eurasia, while a warm TSAM is mainly responsible for the cold SAT to the south of Lake Baikal. In combination, ENSO and the TSAM jointly explain a large proportion of the CEPVFI variance, and they influence a major part of the variation of SAT associated with the CEPVF during boreal spring.

Fig. 12
figure 12

Schematic showing the CEPVF influence on SAT over the mid–high latitudes of Eurasia during boreal spring. a PV (shading) and horizontal PV flux (vectors) at 200 hPa, b cross section of PV (shading) and potential temperature (contours), and c SST over oceans and SAT over land. Yellow vectors indicate the zonal circulation over the equator. d Logic diagram summarizing the findings of this study. The upper row with red boxes indicates physical nodes in this study, and the lower row with blue boxes indicates the foundation between these nodes

Full size image

Simplistically, with reference to Fig. 12d, we argue that once heating forcing (e.g., ENSO) appears over the tropics (A), the zonal circulation along the equator will change (B). This process represents manifestation of the consensus that anomalous heating could induce anomalous zonal circulation (e.g., Bjerknes 1969). According to Eq. (9), anomalous zonal circulation (B) will induce anomalous CEPVF (C). Because PV is equal to the convergence of PVC (Eq. 6b), changes in CEPVF (C) at the equatorial boundary of the NH will stimulate adjustment of PVC within the NH, leading to change in PV over the NH (D). Finally, in response to the PV-θ mechanism (Hoskins et al. 1985, 2003) and owing to surface feedback associated with surface friction and diabatic cooling, anomalous cold SAT over the mid–high latitudes of Eurasia (E) is retained.

6.2 Discussion

On the basis of the results of this study, it may be speculated that the physical nature of the equilibrium linkage between CEPVF and extratropical SAT is mainly a manifestation of the response of extratropical SAT to tropical forcing that induces anomalous CEPVF. In this linkage, the CEPVF is much like a monitor through which the impacts of various tropical signals (including but not limited to ENSO and the TSAM) on extratropical SAT can be comprehensively detected. In this process, the PVC is like a bridge through which tropical forcing communicates with extratropical SAT. There are numerous frameworks through which to view the general circulation; however, the necessity to understand the behavior of the atmosphere demands that we seek an increasing array of diagnostic tools (Hoskins 1991). This study sheds new light on the connection between the tropical and mid–high-latitude circulations. Owing to the existence of the easterly wind in the tropics, it is difficult to explain how tropical signals could cross the easterly wind belt and affect the extratropical circulation within the framework of Rossby waves. The perspective of PVC provides a relatively direct and simple connection between the tropics and the mid–high latitudes.

Although the tropical forcing factors that could drive the variability of zonal circulation associated with CEPVF anomalies are physically defensible (e.g., Bjerknes 1969) and statistically significant, numerical sensitivity experiments should be conducted in future to further explore the detailed roles of ENSO and the TSAM in driving the zonal circulation associated with CEPVF anomalies. In addition to boreal spring, the climatological effects related to CEPVF in different seasons should be studied carefully to establish the connection between CEPVF and certain well-known extratropical forcing (e.g., the Arctic Oscillation, Arctic Sea ice, and South Asian high) and further deepen our insight into climate dynamics.