1 Introduction

Potential vorticity (PV), proposed by the pioneers Rossby (1940) and Ertel (1942), has become an illuminating tool for investigating atmospheric flows. By virtue of the conservation and invertibility of PV, the effects of atmospheric PV anomaly on the general circulation structure (e.g., Hoskins et al. 1985; Hoskins 1991, 1997; Xie et al. 2020), ozone (Danielsen 1968; Folkins and Appenzeller 1996; Sandhya et al. 2015), and occurrence of rainstorms (e.g., Wu et al. 2020) and severe weather (e.g., Wu and Cai 1997; Zhang et al. 2021; Ma et al. 2022) are well recognized in the literature.

Meanwhile, Haynes and McIntyre (1987, 1990) proposed the impermeability theorem and suggested that the isentropic surface is impermeable to the PV per unit volume. This seminal work revealed that (1) the net flux vector of PV per unit volume that they proposed (hereafter the HM flux vector) is parallel to the isentropic surface and (2) that the convergence/divergence of the HM flux vector determines the local time derivative of PV or PV generation. Because the isentropic surfaces are closed in the upper and middle levels of the atmosphere and only intersect with the Earth’s surface, such seminal theory has evoked strong interest in PV generation at the Earth’s surface (e.g., Hoskins 1991; Ma et al. 2019; Yu et al. 2019; Sheng et al. 2021), whereas there has been little interest in the atmospheric upper boundary (will be defined in the following) covered by a closed surface.

The variation in the HM flux vector relates to the variation in PV generation. When considering the variation in the PV itself, Sheng et al. (2022) introduced an intuitive vector referred to as the PV circulation (PVC) vector (\(\overrightarrow {{J_{C} }}\) revisited in the following Eq. 2), whose convergence directly leads to the PV itself. The PVC provides a clear picture of the link between the cross-equator PV transport and the Eurasian surface air temperature anomalies (Sheng et al. 2022). Although the impermeability of HM flux vector is well understood, it remains unclear whether the PVC can cross the isentropic surface. Considering an ideal case that a space enclosed by an isentropic surface with constant \(\theta_{0}\), one can have \(\mathop{{\iint}}\limits_{{\theta_{0} }} {\overrightarrow {{J_{C} }} \cdot \overrightarrow {ds} } = \theta_{0} \mathop{{\iint}}\limits_{{\theta_{0} }} {\overrightarrow {{\zeta_{a} }} \cdot \overrightarrow {ds} } \equiv 0\). This implies two things (1) either PVC vectors (\(\overrightarrow{{J_{C}}}\)) are tangential to isentropic surfaces at every point or (2) there can be cross-isentropic PVC provided the net inflow is equal to net outflow. However, a space in a realistically three-dimensional atmosphere cannot be enclosed by a constant \(\theta_{0}\) surface because potential temperature increases with height in the realistic atmosphere. Therefore, we still don’t know exactly whether the PVC or the integral PVC can cross the isentropic surface. Furthermore, in the Northern Hemisphere (NH), if the PVC can cross the atmospheric upper boundary covered by an isentropic surface, it remains a question how the cross-upper boundary PVC flux (CUF) interacts with the cross-equator PVC flux (CEF). This paper addresses these two issues.

Besides the fundamental features of the PVC integrated over the NH, we focus on the CUF and its relation to the CEF. The remainder of the paper is structured as follows. Section 2 presents the data and diagnostics. Section 3 presents the main results. Section 4 presents a summary and discussion.

2 Data and diagnostics

2.1 Data

The monthly mean zonal wind, meridional wind, and air temperature at pressure level are obtained from MERRA2 (Rienecker et al. 2011; Gelaro et al. 2017). The monthly 2-m wind, 2-m air temperature, and surface pressure, which are used to represent the atmospheric bottom conditions, are also obtained from MERRA2. The data at the 380-K isentropic surface used in this study are interpolated from the pressure level data of MERRA2. All data have a horizontal resolution of 0.625° × 0.5° (longitude × latitude). The research period is 1980–2020.

The normalized 50-hPa zonal mean wind averaged across 5° S–5° N is used to define the quasi-biennial oscillation (QBO) index (QBOI; Yamazaki et al. 2020). A westerly (easterly) QBO phase is identified when the QBOI is larger (less) than zero. Boreal winter refers to the December, January, and February.

2.2 Diagnostics

The PV per unit volume (W), PV density, or PV substance in flux form (Bretherton and Schär 1993; Sheng et al. 2022) is

$$W = \nabla \cdot (\overrightarrow {{\zeta_{a} }} \theta )$$
(1)

where \(\overrightarrow {{\zeta_{a} }}\) and \(\theta\) are the three-dimensional absolute vorticity vector and potential temperature, respectively.

Revisiting Sheng et al. (2022), by means of the vector \(\overrightarrow {{J_{C} }}\) expressed as

$$\overrightarrow {{J_{C} }} = - \overrightarrow {{\zeta_{a} }} \theta$$
(2)

we have

$$W = - \nabla \cdot (\overrightarrow {{J_{C} }} )$$
(3)

Through mimicking the atmospheric convergence \(C = - \nabla \cdot (\overrightarrow {V} )\), where \(\overrightarrow {V}\) is three-dimensional wind representing the general circulation, the vector \(\overrightarrow {{J_{C} }}\) is referred to as PVC (i.e., PV circulation). The PVC has an intuitive nature that the convergence of PVC leads to positive PV (Eq. (3)) and vice versa.

2.2.1 Theoretical proof that the PVC can cross the isentropic surface

The impermeability theorem of PV (Haynes and McIntyre 1987, 1990) suggests that the HM flux vector, which contributes to the local time derivative of PV, is parallel to the isentropic surface. Here, we show that different from the traditional HM flux vector, the PVC forming PV itself (Eq. (3)) can cross the isentropic surface.

Our proof relies on the idea of Bretherton and Schär (1993). If a particle moving with effective velocity (\(\overrightarrow {{V_{e} }}\)) has constant \(\theta\) (\(d\theta /dt = 0\)), then \(\overrightarrow {{V_{e} }}\) is parallel to the isentropic surface. Otherwise, \(\overrightarrow {{V_{e} }}\) is nonparallel to the isentropic surface.

Following Bretherton and Schär (1993), the effective velocity is defined as

$$\overrightarrow {{V_{e} }} = \overrightarrow {A} /W$$
(4)

where \(\overrightarrow {A}\) is an arbitrary vector with the units of the time derivative in Eq. (2). By choosing \(\left\{ \begin{gathered} \overrightarrow {A} = \overrightarrow {{A_{0} }} = \partial \overrightarrow {{J_{C} }} /\partial t \hfill \\ \overrightarrow {{V_{e} }} = \overrightarrow {{V_{e} (A_{0} )}} = \overrightarrow {{A_{0} }} /W \hfill \\ \end{gathered} \right.\) and using Eqs. (1), (2), and (4) into the following equation, we have

$$\frac{d\theta }{{dt}} = \frac{\partial \theta }{{\partial t}} + \overrightarrow {{V_{e} (A_{0} )}} \cdot \nabla \theta = \frac{\partial \theta }{{\partial t}} + \frac{{\partial \overrightarrow {{J_{C} }} /\partial t}}{W} \cdot \nabla \theta = - \theta \frac{{\partial \ln \left| {\overrightarrow {{\zeta_{a} }} } \right|}}{\partial t}\not \equiv 0$$
(5)

Equation (7) suggests that a particle moving with a specified velocity \(\overrightarrow {{V_{e} (A_{0} )}}\) has a changing \(\theta\); i.e., \(\overrightarrow {{V_{e} (A_{0} )}}\) is nonparallel to the isentropic surface, and so is \(\overrightarrow {{A_{0} }}\) according to Eq. (4). Consequently, as the time integral of \(\overrightarrow {{A_{0} }}\), the PVC vector (Eq. (2)) is nonparallel to the isentropic surface. In other words, the PVC vector can cross the isentropic surface.

2.2.2 PVC in pressure coordinates

Based on Eq. (2), the component form of the PVC vector for commonly used pressure level data is (Sheng et al. 2022)

$$\overrightarrow {{J_{C} }} = (J_{C}^{x} , \, J_{C}^{y} , \, J_{C}^{p} ) = - \frac{\partial v}{{\partial p}}\theta \;\vec{i} + \frac{\partial u}{{\partial p}}\theta \;\vec{j}\; + \;\left(f + \frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}\right)\theta \;\vec{k}$$
(6)

where

$$J_{C}^{x} = - \frac{\partial v}{{\partial p}}\theta \;$$
(7a)
$$J_{C}^{y} = \frac{\partial u}{{\partial p}}\theta$$
(7b)

and

$$\, J_{C}^{p} = \;\left(f + \frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}\right)\theta$$
(7c)

In Eqs. (4) and (5), \((u,v)\) are the horizontal wind with the units of m s−1; \(f\) is the Coriolis parameter with the units of s−1; and \((\overrightarrow {i} ,\overrightarrow {j} ,\overrightarrow {k} )\) is the unit vector pointing eastward, northward, and downward, respectively. The positive directions of the PVC vector are eastward, northward, and downward.

2.2.3 Gross PV in the NH

Following Sheng et al. (2022), we select the pressure surface \(p_{T}\), where \(p_{T} = p(\theta_{T} )\) and \(\theta_{T}\) is 380-K, as the upper boundary of the atmosphere under investigation. Such an upper boundary lies at the intersection of Overworld and Middleworld (Hoskins 1991) and covers the entire NH’s troposphere and encapsulates approximately 90% of the atmospheric mass. The derivation and conclusion still hold when other \(\theta_{T}\), for example, 370-K and 390-K, are selected. Integrating Eq. (3) in the NH domain enclosed by the atmospheric upper boundary (i.e., \(p(\theta_{T} )\) surface), the lateral boundary (i.e., the cross-section along the equator), and the atmospheric bottom boundary (i.e., the Earth’s surface) and adopting the Gauss divergence theorem, we have the gross PV in the NH:

$$\begin{gathered} {\iiint\limits_{NH} Wdv} = \iiint\limits_{NH} { - \nabla \cdot (\overrightarrow {{J_{C} }} )}dxdydp \hfill \\ Gross\;\;\;\; = \iint\limits_{upper} { - J_{C}^{p} \overrightarrow {k} \cdot ( - \overrightarrow {k} )dxdy + \oint\limits_{eq} {\int_{{p_{T} }}^{{p_{S} }} { - J_{C}^{y} \overrightarrow {j} } } \cdot ( - \overrightarrow {j} )dxdp + }\iint\limits_{bot} { - J_{C}^{p} \overrightarrow {k} \cdot (\overrightarrow {k} )dxdy} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\; = \underline{{\iint\limits_{upper} {J_{C}^{p} dxdy}}} + \underline{{\oint\limits_{eq} {\int_{p_{T}}^{p_{S}} {J_{C}^{y} } } dxdp}} + \underline{{\iint\limits_{bot} { - J_{C}^{p} dxdy}}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;CUF\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;CEF\;\;\;\;\;\;\;\;\;\;\;\;\;\;CBF \hfill \\ \end{gathered}$$
(8)

where \(p_{S}\) and \(p_{T}\) are the pressures at the Earth’s surface and atmospheric upper boundary, respectively. The terms in Eq. (8) denote the gross PV, CUF (i.e. cross-upper boundary PVC flux), CEF (i.e. cross-equator PVC flux), and cross-bottom PVC flux (CBF) in order. Equation (8) indicates that the gross PV in the NH depends solely on the total flux of PVC crossing the atmospheric upper boundary, bottom, and cross-section along the equator. Positive CUF, CEF, and CBF contribute to the positive gross PV and indicate that the integrated PVC vector crossing the corresponding boundary is downward, northward, and upward, respectively. The CUF risks being neglected owing to the inertia of conventional thinking of the impermeability theorem. However, according to the conclusion derived in Sect. 2.2.1, it is noted that the PVC can cross the atmospheric upper boundary and thus the CUF cannot be neglected.

Applying the Stokes curl theorem to the CUF term in Eq. (8), we further obtain

$$CUF = \iint\limits_{upper} {J_{C}^{p} dxdy = }\iint\limits_{upper} {(f + \zeta )\theta \;dxdy = }\;\;\theta_{T} \oint\limits_{eq} {u_{T} dx} + \theta_{T} \iint\limits_{upper} {f\;dxdy}$$
(9)

where \(\zeta = \frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}\) is the relative vorticity and \(u_{T}\) is the zonal wind at the \(p(\theta_{T} )\) surface along the equator.

Because \(\frac{\partial u}{{\partial p}}\) and \(\theta\) are integrable, and because \(\theta\) is positive and decrease with pressure monotonously, the second mean value theorem for integrals can be used here. Applying the second mean value theorem for integrals to the CEF term in Eq. (8), we have

$$CEF = \oint\limits_{eq} {\int_{{p_{T} }}^{{p_{S} }} {J_{C}^{y} } } dxdp = \oint\limits_{eq} {\theta_{T} \int_{{p_{T} }}^{\xi } {\frac{\partial u}{{\partial p}}} } dpdx = - \theta_{T} \oint\limits_{eq} {u_{T} } dx + \theta_{T} \oint\limits_{eq} {u_{\xi } } dx$$
(10)

where \(u_{\xi }\) is the zonal wind at a certain interior point (\(\xi\)) within the cross-section along the equator.

From Eq. (8), the CBF term is

$$CBF = \iint\limits_{bot} { - J_{C}^{p} dxdy = }\iint\limits_{bot} { - (f + \zeta )\theta \;dxdy}$$
(11)

Considering a time anomaly (indicated by a prime), Eqs. (9)–(11) become

$$CUF^{\prime } = \left( {\iint\limits_{{upper}} {(f + \zeta )\theta _{T} dxdy}} \right)^{\prime } = \;\left( {\theta _{T} \oint\limits_{{eq}} {u_{T} dx} } \right)^{\prime }$$
(12)
$$CEF^{\prime } = \left( {\oint\limits_{{eq}} {\theta _{T} \int_{{p_{T} }}^{\xi } {\frac{{\partial u}}{{\partial p}}} } dpdx} \right)^{\prime } = \left( { - \theta _{T} \oint\limits_{{eq}} {u_{T} dx} } \right)^{\prime } \; + \left( {\theta _{T} \oint\limits_{{eq}} {u_{\xi } } dx} \right)^{\prime }$$
(13)

and

$$CBF^{\prime} = \;\left(\iint\limits_{bot} { - (f + \zeta )\theta \;dxdy}\right)^{\prime }$$
(14)

The positive (negative) phase of CUF, CBF, and CEF is identified when the \(CUF^{\prime}\), \(CBF^{\prime}\), and \(CEF^{\prime}\) is larger (less) than zero, respectively.

3 Results

Figure 1a presents the climatological annual cycle of the terms listed in Eq. (8). The climatological gross PV (orange bar) in the NH is reasonably a steady positive value throughout the year. Despite some small differences in March, October, and November, the gross PV almost overlaps the sum (green line) of the CUF, CBF, and CEF, which is in accordance with the theoretical conclusion derived from Eq. (8) and confirms that the climatological gross PV in the NH is determined by the PVC crossing the atmospheric upper boundary, atmospheric bottom, and cross-section along the equator. The climatological CEF is small. Therefore, the positive climatological gross PV in the NH is largely held by the sum of the CUF and CBF. The climatological CUF and CBF are respectively positive and negative, suggesting that the climatological PVC inflows from the atmospheric upper boundary and outflows from the atmospheric bottom. A comparison of the absolute values of the CUF and CBF indicates that, in a climatic sense, the CUF plays a fundamental role in forming the positive basic state of the gross PV in the NH.

Fig. 1
figure 1

(a) Climatological annual cycles of the CUF (black), CBF (blue), CEF (red), and gross PV (orange) in the NH. Unit: 1012 m2 K s−1. The green line indicates the sum of the CUF, CBF, and CEF. The CEF (red) is amplified by a factor of 10 for display. (b) Annual cycles of the standard deviations of the CUF (black), CBF (blue), and CEF (red). Unit: 1010 m2 K s−1

Full size image

Figure 1b presents the standard deviations of the CUF, CBF, and CEF. The variability of CUF and CEF is larger than that of CBF. This feature is expected in that the atmospheric eddies which favor the PV transport tend to appear aloft. Another noteworthy feature in Fig. 1b is that although the climatological value (Fig. 1a) of the CEF is smaller than that of the CUF, their standard deviations (Fig. 1b) are comparable. Recalling Eqs. (9), (12), and (13), because the CUF (Eq. (9)) contains a considerable constant value (\(\theta_{T} \iint\limits_{upper} {f\;dxdy}\)), which contributes nothing to the variation in the CUF (Eq. (12)), and because the variations in the CUF (Eq. (12)) and CEF (Eq. (13)) both relate to the zonal wind along the equator at the atmospheric upper boundary, the comparable variations of the CUF and CEF are natural.

Although the variation of CBF is relatively small (Fig. 1b), it is very important to the gross PV variation (e.g., Hoskins 1991; Sheng et al. 2021; Sheng et al. 2022). In shedding light on the importance of CBF, we adopt the Monte Carlo bootstrapping method to estimate the probability density function of the gross PV anomaly in the NH during the positive and negative phases of the sum of the CUF and CEF (Fig. 2a) and the CBF (Fig. 2b). The resampling process is executed 100,000 times. Figure 2a indicates that in the different phases of the sum of the CUF and CEF, the probability density functions of the mean annual gross PV anomaly in the NH overlap and are not separate from each other. The correlation coefficient between the gross PV in the NH and the sum of the CUF and CEF is as weak as 0.07. However, during the different phases of the CBF (Fig. 2b), the probability density functions are significantly separate from each other. In the positive CBF phase, the gross PV anomaly tends to be positive significantly. In the negative CBF phase, the gross PV anomaly tends to be negative. The correlation coefficient between the CBF and gross PV is 0.57, passing the student’s t-test at a significance level of 0.01. These results suggest that although the anomalous CUF and CEF are prominent (Fig. 1b), their total effect contributes little to the gross PV anomaly (Fig. 2a). The gross PV anomaly is significantly determined by the CBF anomaly (Fig. 2b). The conclusion remains unchanged when the resampling process is repeated 10,000 times, suggesting that the drawn conclusion is insensitive to the sample size and is statistically robust.

Fig. 2
figure 2

Probability density function (colored line) and average (vertical dashed line) of the mean annual gross PV anomaly in the NH estimated from 100,000 bootstrapped samples in the positive (red) and negative (blue) phases of (a) the mean annual sum of the CUF and CEF and (b) the mean annual CBF. The shading indicates the 95% confidence interval

Full size image

To further investigate why the total effect of the CUF and CEF with individually large variability hardly contributes to the variation in gross PV in the NH, we present the annual cycle of the correlation coefficients between the CUF and CEF in Fig. 3. Strong negative values are evident throughout the year. All these values pass the student’s t-test at a significance level of 0.01. The negative correlation coefficients suggest a cancellation of the effects of the CUF and CEF. When the CUF anomaly contributes positively to the gross PV in the NH, the CEF anomaly tends to make a negative contribution and vice versa. Through such cancellation (Fig. 3) and comparable standard deviations of CEF and CUF (Fig. 1b), the total effect of the CUF and CEF contributes hardly anything to the variation in the gross PV in the NH (Fig. 2a).

Fig. 3
figure 3

Annual cycle of correlation coefficient between the CUF and CEF

Full size image

The aforementioned cancellation is intrinsically rooted in the PV dynamics. We see that the anomalous zonal wind integrated along the equator at the atmospheric upper boundary (\(\;(\theta_{T} \oint\limits_{eq} {u_{T} dx)}^{\prime }\)) contributes positively to the CUF anomaly (Eq. (12)) but negatively to the CEF (Eq. (13)). Therefore, such a cancellation holds reasonably. In this relation, the zonal wind along the equator at the atmospheric upper boundary plays a decisive role.

In the physical sense, such a cancellation sheds light on an implied atmospheric process that the PVC inflowing (outflowing) from the atmospheric upper boundary would outflow (inflow) from the cross-section along the equator. Figure 4 is a schematic diagram of this conceptual model. In the westerly phase (Fig. 4a), the zonal wind anomaly along the equator at the atmospheric upper boundary induces the positive vorticity anomaly at the atmospheric upper boundary of the NH according to the Stokes curl theorem (Eq. (12)) and therefore leads to the anomalous downward PVC (Eq. (7c)), which results in the positive CUF anomaly (Eq. (12)). Meanwhile, the zonal wind anomaly increasing with height tends to induce a positive vertical shear anomaly and thus leads to the anomalous southward PVC (Eq. (7b)), which results in the negative CEF anomaly (Eq. (13)). Consequently, the integrated PVC would inflow from the atmospheric upper boundary and outflow from the cross-section along the equator. For the same reason, in the easterly phase (Fig. 4b), the PVC would outflow from the atmospheric upper boundary and inflow from the cross-section along the equator.

Fig. 4
figure 4

Schematic diagram of the integrated PVC flux at the NH’s atmospheric upper boundary and the cross-section along the equator in the (a) westerly phase and (b) easterly phase of the zonal wind anomaly along the equator at the atmospheric upper boundary. Gray vectors indicate the zonal wind anomaly along the equator at the atmospheric upper boundary. Colored vectors represent the PVC anomaly. The brown ball represents the Earth

Full size image

The conceptual model presented in Fig. 4 is shown to be true in the following application regarding the QBO data analyses. The QBO is a prominent signal in the tropical stratosphere, and it features that the alternate easterlies and westerlies descend prominently from the upper stratosphere to the tropopause (Rao et al. 2021). Figure 5a and b present the probability density functions of the CUF (Fig. 5a) and CEF (Fig. 5b) estimated from Monte Carlo bootstrapped samples for the different phases of QBO in boreal winter. Both in the westerly (red shading) and easterly (blue shading) QBO phases, the probability density functions of the CUF (Fig. 5a) and CEF (Fig. 5b) are clearly separated. The correlation coefficients between the QBOI and the CUF and CEF reach 0.54 and − 0.79, passing the student’s t-test at a significance level of 0.01. These results suggest that the zonal wind anomaly of the QBO leads to the significantly anomalous CUF and CEF. Specifically, the anomalous CUF (Fig. 5a) is positive in the westerly QBO phase and negative in the easterly QBO phase. Meanwhile, the anomalous CEF (Fig. 5b) is negative in the westerly QBO phase and positive in the westerly QBO phase.

Fig. 5
figure 5

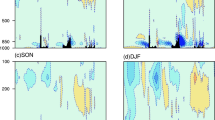
Probability density function (colored line) and average (vertical dashed line) of the (a) CUF and (b) CEF estimated from 100,000 bootstrapped samples in the westerly (red) and easterly (blue) QBO phase during the concurrent boreal winter. The shading indicates the 99% confidence interval. (c) Regressed vertical PVC (shading) at the upper boundary (380-K) and the horizontal PVC (vectors) integrated from the Earth’s surface to the upper boundary on the QBOI during the concurrent boreal winter. Areas exceeding a significance level of 0.05 are indicated by white dots. Vectors exceeding a significance level of 0.05 are shown

Full size image

Figure 5c is a map of the regressed vertical PVC (shading) at the upper boundary (i.e. \(p_{T} = p(\theta_{T} )\) and \(\theta_{T}\) is 380-K) and horizontal PVC (vector) integrated below the upper boundary on the QBOI during the boreal winter. In the westerly QBO phase, the positive vertical PVC (shading) is prominent at the upper boundary. We average vertical PVC (shading) over the upper boundary in the NH and find that the value is greater than zero, which means that the integrated vertical PVC is downward. The horizontal PVC (vector) integrated below the upper boundary is significantly southward. The easterly QBO phase corresponds to the opposite situation. This result suggests that during the westerly (easterly) QBO phase, the integrated PVC is crossing the upper boundary downward (upward) in the NH and is crossing the cross-section along the equator southward (northward). All the results of the QBO data analyses verify the conceptual model proposed in Fig. 4.

4 Summary and discussion

4.1 Summary

Before summarizing the results of the paper, we stress that the present study is not the first to propose the concept of PVC. Following previous work (Sheng et al. 2022), new findings regarding PVC in the NH were presented in this study as summarized below.

  1. (1)

    In contrast to the traditional PV flux proposed by Haynes and McIntyre (1987, 1990), the PVC is theoretically proven to be able to cross the isentropic surface. The gross PV in the NH is determined by the sum of CUF, CEF, and CBF. In terms of climate, because the CEF is small, the climatological gross PV in the NH is largely controlled by the total effect of the CUF and CBF. The CUF, which is prone to being neglected owing to the inertia of conventional thinking of the impermeability theorem, plays a fundamental role in forming the basic state of the gross PV with a positive value in the NH.

  2. (2)

    In terms of variation, there is a cancellation, rooted intrinsically in the PV dynamics, between the CUF and CEF. Therefore, although the CUF and CEF are more variable than the CBF, the total effect of the CUF and CEF contributes little to the variation of the gross PV in the NH. The variation of gross PV in the NH is largely determined by the CBF.

  3. (3)

    The analysis of PV dynamics inspired by the above cancellation sheds light on a seminal atmospheric process (Fig. 4) in which the zonal wind anomaly plays a decisive role. In the westerly (easterly) phase of the anomalous zonal wind integrated along the equator at the atmospheric upper boundary, anomalous PVC inflowing (outflowing) from the atmospheric upper boundary in the NH would outflow (inflow) from the cross-section along the equator. This atmospheric process is evident in different QBO phases.

4.2 Discussion

The result (Fig. 4) of this study suggests that anomalous PVC inflowing (outflowing) from the atmospheric upper boundary in the NH would outflow (inflow) from the cross-section along the equator into the Southern Hemisphere. This PVC thinking provides a novel understanding of how the signal in the NH affects the Southern Hemisphere through the cross-section along the equator. Moreover, Fig. 4 shows that the anomalous PVC at the atmospheric upper boundary is linked to the anomalous PVC at the lateral boundary below. This also provides a new way for understanding the interaction between the upper- and lower-level. If the atmosphere of interest shrinks to a domain enclosed by a polar cap bounded by a latitude circle (gray shading in Fig. 6), the above discussion regarding the PVC can be generalized to see how the polar vertical PVC anomaly interacts with the mid- and high-latitude horizontal PVC anomaly and how the upper- and lower-level signals around the polar region interact with each other. Further relevant works are well worth conducting.

Fig. 6
figure 6

Same as Fig. 4, but the investigated atmosphere (gray shading) shrinks to a domain enclosed by a polar cap bounded by a latitude circle (dashed white line). The ellipse-colored red (cyan) indicates a positive (negative) vorticity anomaly

Full size image

If the selection of \(\theta_{T}\) in this study is far from the 380-K, for example, 600-K or 700-K, the results (Figs. 1, 2, 3) obtained from the data analyses will change to some extent. However, the theoretical derivation, the schematic diagram (Fig. 4), and the qualitative conclusion will still hold because these are the intrinsic results of the PV dynamics and are independent of the selection of the upper boundary.

The gross PV (bar in Fig. 1a) does not keep a constant value throughout the year. Since the variation of gross PV is determined by the PV generation at the Earth’s surface (Hoskins 1991; Ma et al. 2019; Sheng et al. 2021), in JJA (DJF) when the surface heating (cooling) is strong in the NH, the decreasing (increasing) of diabatic heating with height tends to lead a relatively small (large) gross PV (Fig. 1a) according to the PV budget equation (\(\partial W/\partial t \sim - (f + \zeta )\partial \dot{\theta }/\partial p \sim (f + \zeta )\partial \dot{\theta }/\partial z\), in which \(\dot{\theta }\) is diabatic heating rate). However, compared with the climate value of the gross PV (Fig. 1a), the seasonal variation of the gross PV (Fig. 1a) and the standard deviation (Fig. 1b, two orders of magnitude smaller) of the gross PV are very small. This result suggests that the gross PV is quasi-conserved. The issue regarding the conservation of PV is not the focus of this study, but this deserves further study.