Response of convective systems to the orbital forcing of the last interglacial in a global nonhydrostatic atmospheric model with and without a convective parameterization

Abstract

Nonhydrostatic Icosahedral Atmospheric Model (NICAM) coupled with a slab ocean model was applied to a paleoclimate research for the first time. The model was run at a horizontal resolution of 56 km with and without a convective parameterization, given the orbital parameters of the last interglacial (127,000 years before present). The simulated climatological mean-states are qualitatively similar to those in previous studies reinforcing their robustness, however, the resolution of this model enables to represent the narrow precipitation band along the southern edge of the Tibetan Plateau. A particular focus was given to convectively coupled disturbances in our analysis. The simulated results show a greater signal of the Madden–Julian Oscillation and weakening of the moist Kelvin waves. Although the model's representation of the boreal summer intraseasonal oscillation in the present-day simulations is not satisfactory, a significant enhancement of its signal is found in the counterpart of the last interglacial. The density of the tropical cyclones decreases over the western north Pacific, north Atlantic and increases over the south Indian Ocean and south Atlantic. The model's performance is generally better when the convective parameterization is used, but the tropical cyclones are better represented without the convective parameterization. Additional simulations using the low-resolution topography reveals that the better representation of the Tibetan Plateau enhances the boreal summer Asian monsoon and its impact is similar and comparable to that of the orbital parameters over the south Asia and the Indian Ocean.

1 Introduction

In the early stages of the history of paleoclimate simulations, an atmospheric general circulation model (AGCM) had been a useful tool, which was run, given fixed sea surface temperatures (SSTs), or coupled with a slab ocean model, and was able to explain broad characteristics of the periods under consideration, using the limited computer resources available at this stage (Braconnot et al. 2000; Joussaume et al. 1999; Kutzbach and Guetter 1986; Kutzbach and Otto-Bliesner 1982; Manabe and Broccoli 1985 and mony others).

Thanks to the development in computer technology which has been going on in recent decades, we can now couple it with an oceanic GCM and run simulations for even a several thousand years to obtain a quasi-equilibrium state of the atmosphere–ocean coupled system or reproduce a millennial-scale variation (e.g. Clark et al. 2020), which opened up a new age of paleoclimate studies.

Another way to exploit this growing computing power is to increase the model resolution. Throughout the history of the paleoclimate simulations, the horizontal grid spacing of the most of the AGCMs continued to be on the order of 100 km. Within the range of this resolution, the AGCMs use the hydrostatic approximation in their governing equation, a balance between gravity and the vertical pressure gradient force, to remove sound waves and thereby make the model's time step much longer. In addition, the AGCMs need to employ convective parameterizations to account for the effect of an ensemble of cumulus convection whose lateral size is a few to ten kilometers.

In recent years, global nonhydrostatic atmospheric models (GNHM) began to be used for decades of simulations (Roberts et al. 2019), which no longer use the hydrostatic approximation. Under a horizontal resolution of the order of 1 km, the model would become a cloud resolving model, capable of resolving the bulk characteristics of deep moist convection. However, the use of this resolution is still too costly in climate science, and the model is run at much lower resolutions ranging from 7 to 56 km, depending on the available computer resources.

The horizontal resolution of 5–50 km is called a gray-zone, in which the model is unable to resolve deep convection, but it is also inappropriate to use a conventional convective parameterization, as its underlying assumptions no longer hold (e.g. Arakawa and Wu 2013). Despite some unrealistic behaviors and the lack of a solid theoretical basis, most of models continue to use a convective parameterization, and in practice still give good results (Caldwell et al. 2019; Cherchi et al. 2019; Mizuta et al. 2012; Roberts et al. 2018, 2019). The behavior of the conventional convective parameterization at the gray-zone is considered justified if it is responding to multi-grid 100 km-scale forcing. However, the development of scale-aware convective parameterization applicable to the gray-zone is desirable and it is currently underway in many research groups (e.g. Arakawa and Wu 2013; Kwon and Hong 2017).

On the other hand, a research group using Nonhydrostatic Icosahedral Atmospheric Model (NICAM; Kodama et al. 2021; Satoh et al. 2008, 2014, 2017, 2018; Tomita and Satoh 2004) has been running simulations at the gray-zone, mainly 14 km as well as 7 km in limited runs, without using any convective parameterizations. The model at this resolution is sometimes referred to as a cloud permitting model rather than a cloud resolving, but they demonstrated that the model was able to produce a reasonable mean-state (Kodama et al. 2015) as well as convectively coupled tropical disturbances including the moist Kelvin waves (Nasuno et al. 2007, 2008; Tomita et al. 2005), Madden–Julian Oscillation (MJO; Kikuchi et al. 2017; Miura et al. 2007; Miyakawa et al. 2014; Nasuno et al. 2009; Takasuka and Satoh 2020; Yoshizaki et al. 2012 and many others), Boreal Summer Intraseasonal Oscillation (BSISO; Kikuchi et al. 2017; Nakano and Kikuchi 2019) and tropical cyclones (Fudeyasu et al. 2008; Satoh et al. 2015; Yamada et al. 2017, 2019 and many others).

Furthermore, NICAM run at 28 and 56 km resolutions without any convective parameterizations are able to give qualitatively similar results to those obtained at 14 km, though there is a number of clear advantages in the 14 km resolution (Kodama et al. 2021; Takasuka et al. 2018). Why and how this resolution, by far coarser than that of the cloud resolving model, give such behaviors is an interesting question that has not yet been fully explained. Although the simulated convection is the spurious one occurring in the virtual world and does not exist in reality, discrete dynamical systems with cloud microphysics appear to not alter their behavior within this range of resolutions qualitatively. Another possible explanation is that the simulated convection crudely represents aggregated mesoscale convection which does occur in reality under certain circumstances, thus the low-resolution GNHM gives an atmospheric circulation driven by the always-aggregated convection.

This study is an attempt to apply a GNHM to a paleoclimate study, for the first time with NICAM. Due to limited availability of computer resources both in node-hours and storages, we use the model at 56 km resolution, anticipating that the results have a similarity to those at much higher resolution. Questions addressed in this study are as follows. (1) Is the performance of the low-resolution GNHM sufficient for paleoclimate simulations? (2) What are strengths and weaknesses of using the low-resolution GNHM in paleoclimate studies compared to conventional AGCMs? (3) Should we use the convective parameterization in paleoclimate simulations with the low-resolution GNHM? (4) What are strengths and weaknesses of using the convective parameterization as compared to not using it? By answering these questions, we can establish the methodology to use the low-resolution GNHM in future paleoclimate simulations. We run simulations with and without the convective parameterization. Unlike the cases at the gray-zone resolution, the underlying assumptions of the conventional convective parameterization are considered to be marginally valid at 56 km, and the use of the parameterization is entirely appropriate.

Since a strength of the GNHM is widely considered to be its representation of convectively coupled disturbances, we choose a warm period as a target of the first paleoclimate simulation, specifically 127,000 years before present in the last interglacial, hereafter referred to as 127 ka. It is characterized by perihelion close to the boreal summer solstice and a large value of eccentricity in the earth's orbital parameters. This configuration of the earth's orbit greatly enhances the seasonal variation of the insolation in the northern hemisphere, leading to warmer boreal summer. Both geological sources and model simulations suggest that it resulted in significant warming at northern high latitudes, reduction in the sea ice and enhancement of the Asian–African monsoon (Lunt et al. 2013; Otto-Bliesner et al. 2021). The period gained an attention particularly from a viewpoint of polar responses and climate-ice sheet interactions as an example to be compared with those of the future climate change, and has been discussed in the IPCC assessment reports (Jansen et al. 2007; Masson-Delmotte et al. 2013). 127 ka was chosen as one of the periods to be compared in the Paleoclimate Modeling Intercomparison Project Phase 4 (PMIP4; Kageyama et al. 2018; Otto-Bliesner et al. 2017).

Many modelling studies on the last interglacial using the atmosphere–ocean coupled general circulation model (AOGCM) have been made with the changes of the orbital parameters and greenhouse gases (Fischer and Jungclaus 2010; Guarino et al. 2020; Kubatzki et al. 2000; Langebroek and Nisancioglu 2014; Montoya et al. 1998; Nikolova et al. 2013; Otto-Bliesner et al. 2013, 2020; Pedersen et al. 2017; Williams et al. 2020; Zheng et al. 2020), some of which add fresh water input (Clark et al. 2020; Govin et al. 2012) and an interactive vegetation model (O'ishi et al. 2021). These simulations were made with the grid-spacing of the atmosphere ranging from 5.6° at the lowest to 1° at the highest. The examples of the high resolution models among these are FGOALS-f3 (1°; Zheng et al. 2020), CESM2 (1°; Otto-Bliesner et al. 2020) and EC-Earth3 (1.1°; Pedersen et al. 2017).

Reconstructions from geological sources indicate that the global mean sea level at 127 ka was at least 5 m higher than the present (Dutton et al. 2015; Jansen et al. 2007; Masson-Delmotte et al. 2013). From ice-core records (Steig et al. 2015) and standalone ice sheet model simulations (DeConto and Pollard 2016), a major contributor to this rise is arguably considered to be deglaciation of the West Antarctic ice sheet. However, since the purpose of this study is to test the performance of the NICAM for the first time in paleoclimate simulations, we ignore these effects in the surface boundary conditions of 127 ka at this time and change only the orbital parameters, making idealized simulations to see a clean response to the stronger seasonal variation of the northern hemispheric insolation. A simple slab ocean model is used to crudely represent the response of SSTs.

In addition to the mean-state of select variables, this study analyzes convectively coupled disturbances including equatorial waves, intraseasonal oscillations and tropical cyclones. To the best of our knowledge, this study is the first work showing changes in the equatorial waves and intraseasonal oscillations such as the MJO and BSISO in paleoclimate simulations.

The MJO is the dominant variability in the tropical atmosphere on time scales shorter than a season (Lau and Waliser 2012; Madden and Julian 1971, 1972; Zhang 2005, 2013). It is a planetary-scale eastward-propagating convective envelope confined along the equator, which typically grows over the Indian Ocean and migrates to the western Pacific. It becomes a seed developing into a tropical cyclone, when other environmental conditions are favorable (Bessafi and Wheeler 2006; Hall et al. 2001; Higgins and Shi 2001; Liebmann et al. 1994; Maloney and Hartmann 2000; Mo 2000 and many others). The surface wind bursts induced by the MJO over the western Pacific are considered to be potential triggers and inhibitors of El Niño-Southern Oscillation (ENSO) events (Lau 2012).

While the MJO manifests itself throughout the year, the BSISO emerges only during boreal summer. It has a more complex spatial structure and propagation pattern than the MJO. Growing as a zonally elongated planetary-scale convective envelope over the near-equatorial Indian Ocean, it begins to propagate both northward and eastward concurrently, and then forms northwest-southeast-tilted band of convection (Annamalai and Slingo 2001; Goswami 2012; Lau and Chan 1986; Lawrence and Webster 2001). It is the dominant intraseasonal variability in this season and affects onset and break phases of the Indian monsoon.

Although the equatorial waves and intraseasonal oscillations rarely catch the interest of paleoclimatologists, they are important for deep understanding of the Indian monsoons, tropical cyclones and ENSO, which are of greater interest for many climate researchers. Furthermore, the simulated behaviors of these disturbances in the past climate with different boundary conditions can be subjects of interest for tropical meteorologists, because they provide test cases for the theories of the waves and oscillations which are still in progress and dispute.

Section 2 of this paper describes the model and the setup of the simulations. Results are presented in Sect. 3, followed by a summary and discussion in Sect. 4.

2 Model and setup

We use NICAM version 16. The details of the model for this version are given in Kodama et al. (2021). It presented a model description and results submitted to the High Resolution Model Intercomparison Project (HighResMIP) v1.0 (Haarsma et al. 2016) which is one of the projects endorsed by the Coulpled Model Intercomparison Project Phase 6 (CMIP6). The governing equation of the dynamical core is a fully compressible nonhydrostatic system. Its discretization is made with a finite volume method on a quasi-uniform grid configuration which is based on an icosahedral grid mesh, but modified to obtain greater uniformity by spring dynamics method (Tomita et al. 2002). The average interval of the horizontal grid mesh is 55.8 km. The model has 38 layers from the surface to the model top height of 36.7 km in a terrain-following z-coordinate where z is height from the surface. Sound waves are treated separately with a split-explicit integration scheme (Klemp and Wilhelmson 1978).

The cloud microphysics is represented by a single-moment scheme with six water categories including water vapor, cloud liquid, cloud ice, rain, snow and graupel (Roh and Satoh 2014; Roh et al. 2017; Tomita 2008). The vertical component of turbulent eddy fluxes is calculated by a first-order turbulence closure model (Nakanishi and Niino 2006; Noda et al. 2010), while using the bulk formula for the surface fluxes. The radiative transfer is based on a two-stream k-distribution scheme with 111 channels. An orographic gravity wave drag is employed (McFarlane 1987). The land surface model is the Minimal Advanced Treatments of Surface Interaction and Runoff (MATSIRO; Takata et al. 2003), which has five soil layers for temperature and soil moisture as well as three snow layers above the surface.

In order to reduce the computational cost and avoid an extra bias caused by introducing interactive aerosols, the model used in this work does not predict aerosols. In addition, unlike Kodama et al. (2021), our model does not use the present-day offline aerosols for the calculation of the cloud microphysics and radiative processes. For simplicity, it is assumed that there are no aerosols in the atmosphere and the number concentration of cloud particles is uniformly set to a constant value of 50 cc⁻¹ over the entire globe. Freezing of cloud particles occurs entirely based on temperature. This is to avoid an inconsistency caused by the use of the present-day aerosol distribution for the simulations of the paleoclimate.

We use a simple slab ocean model similar to McFarlane et al. (1992) which predicts SSTs, sea ice mass, snow over sea ice and the snow temperature by solving the heat balance between the ocean, sea ice, snow and atmosphere. The predicted SSTs and sea ice mass are nudged to the present-day climatological values with a relaxation time of 7 days. The reference SSTs and sea ice mass are created using a dataset of the HadISST version 1 (Rayner et al. 2003) from 1979 to 1999 and the ensemble mean of the CMIP3 models respectively. Heating by ocean current is not explicitly considered, but the nudging term crudely substitutes for its role. A depth of the slab ocean is uniformly set to 15 m over the globe. The main purpose of using this slab ocean model is to improve the performance of NICAM in terms of the simulated mean-state and variability of the precipitation (see Kodama et al. 2015, 2021) by representing a short-term variation of the SSTs due to an interaction with the atmosphere in a simplified manner, rather than to represent a realistic ocean mixed layer.

The integration was continued for 6 years including a spin-up period of one year and the last 5 years are analyzed. The initial values of the atmosphere and ocean are set up using 0:00 (GMT) 1 January 2016 of the National Centers for Environmental Prediction (NCEP) FNL Operational Model Global Tropospheric Analysis (Kanamitsu et al. 2002). The land variables are taken and interpolated from the last 5-year climatology of a 10-year simulation using the low-resolution NICAM with a grid size of 220 km (Kodama et al. 2021).

The orbital parameters are set to the values specified by the PMIP4 protocol (Otto-Bliesner et al. 2017; Table 1). Large differences are seen in the eccentricity and the angle between autumn equinox and perihelion. The perihelion comes in June at 127 ka, while it comes in January at 0 ka. Figure 1 shows the difference of the insolation at 127 ka from that at 0 ka calculated with these parameters. Here and hereafter, we use the Gregorian calendar and the vernal equinox is fixed on 21 March in both of the 0 and 127 ka simulations. Due to the larger eccentricity and the timing of the perihelion close to the boreal summer solstice, the northern (southern) hemispheric insolation is significantly enhanced (reduced) in June (January). The larger eccentricity leads to the higher angular velocity of the earth around the perihelion and the earlier timing of the autumn equinox, which results in the significant warming (cooling) of the southern (northern) hemisphere around the beginning of October (September). We did not apply the calendar adjustments proposed by Bartlein and Shafer (2019), since the main goal of this work is to see the overall features of the first simple sensitivity test of paleoclimate simulations with NICAM, not a rigorous quantitative evaluation nor comparison with proxies and other models, and it is unlikely that the calendar adjustments affect the conclusions of this work qualitatively.

Table 1 Orbital parameters

Fig. 1

Difference of the downward shortwave radiation at the top of the atmosphere in the 127 ka simulations from that in 0 ka counterparts. The unit is ${\mathrm{Wm}}^{-2}$. Created from the daily mean outputs

For the concentration of greenhouse gases, we use the preindustrial values for all the simulations including those of 127 ka, and the values are taken from the preindustrial setting of the PMIP4 protocol (Table 2). The actual values for 127 ka are slightly different from those of the preindustrial period (Table 1 in Otto-Bliesner et al. 2017), but the impact of the difference is considered to be quite small. The other boundary conditions such as solar constant, geography, ice sheet and vegetation maps are the same as those in the present-day simulation. With this setting, we examine a pure response to the orbital parameters.

Table 2 Concentration of greenhouse gases

Table 3 shows a list of simulations. We performed simulations with and without a convective parameterization for orbital parameters of 0 and 127 ka. For the convective parameterization, we adopt Chikira and Sugiyama (2010), hereafter referred to as the CS scheme, which has been used in the version 5 and 6 of the Model for Interdisciplinary Research on Climate (MIROC; Tatebe et al. 2019; Watanabe et al. 2010). The CS scheme is a mass-flux scheme with multiple cloud types characterized by vertically varying entrainment rates. It can naturally represent the effect of tropospheric moisture on moist convection without empirical triggering schemes through larger entrainment of environmental air near the cloud base (Chikira and Sugiyama 2010). It gives much better representation of the monsoon (Kim et al. 2011), the equatorial waves including the MJO (Chikira 2014; Chikira and Sugiyama 2013), BSISO (Sperber et al. 2013) and tropical cyclones (Mori et al. 2013) compared to MIROC3, the older version of MIROC which uses a different convective parameterization.

Table 3 List of experiments

Usually, deep convection originates from a convective boundary layer (CBL) which has larger values of moist static energy compared to the counterpart above the CBL. However, deep convection can sometimes originate from levels above the CBL. That typically occurs at night and in the early morning over land when strongly cooled near-surface air is overridden by relatively warmer air. Ding and Randall (1998) developed a convective parameterization which accounts for multiple levels as a source for the convection. Although the scheme does not show large changes in the spatial pattern of the global precipitation in their AGCM simulation, it tends to increase the precipitation of the ITCZs over land. In particular, the elevated convection occurs more frequently over North Africa and South Asia in boreal summer compared to the other regions. About 20% of the incidence of moist convection had elevated sources over these regions. Chikira et al. (2006) implemented the convective scheme of Ding and Randall (1998) in their model and applied it to the climate of 6000 years ago (6 ka). They found that the scheme greatly enhances the precipitation over North Africa and South Asia in boreal summer of 6 ka and strengthens the northward shift of the ITCZs. Thus, it is important to represent this effect in the simulation of 127 ka as well.

In the CS scheme described in Chikira and Sugiyama (2010), convection originates from the lowest model layer, so it does not account for the elevated convection. However, accounting for all the possible model levels for the convective sources requires a large computational cost. Thus, in order to represent the elevated convection in a simplified way, we modified the CS scheme so that convection originates from a layer with maximum moist static energy below 700 m from the surface. Generally, the model has 4 layers below this altitude. Although this scheme does not represent convection originating from layers above 700 m, it does represent the typical elevated convection originating from a warm layer overriding the cold near-surface air at night and in the early morning over land. According to Chikira et al. (2006), this type of convection is the one which plays an important role in the enhancement of the northward shift of the ITCZ in the 6 ka simulation.

As seen in Table 3, we performed another set of simulations named LR0k and LR127k. Since the resolution of the model adopted in this work is higher than that of most of the other models which have been used in the paleoclimate simulations, we are interested in the role of the small-scale topography. In particular, since the simulation of 127 ka is characterized by the enhanced Asian monsoon, the realistic representation of the Tibetan Plateau is considered to be important in the simulation of the present-day monsoon and its change at 127 ka.

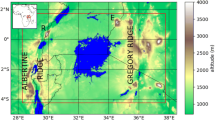
Figure 2a, b shows the observed topography from GTOPO30, the default topographies used in NICAM with 56 km. In order to avoid a numerical instability associated with the effect of a steep topography on the terrain-following vertical coordinate, the topography used in NICAM is created by smoothing out the GTOPO30 data through an iterative application of a hyper-diffusion filter until the maximum gradient of the terrain reaches a threshold value of 0.01 (elevation change per unit horizontal distance).

Fig. 2

a Observed topography from GTOPO30. b Default topography used in NICAM. c Low-resolution topography used in LR0k and LR127k. e, f Error of the elevation in b, c against GTOPO30 respectively. d Difference of b from c. The unit is $\mathrm{m}$. For a, the original resolution of 30 arc seconds (approximately 1 km) was converted to $0.5^\circ \times 0.5^\circ$ mesh by taking area average. Note that the green color in a–c just means the elevation is higher than 0 m. The elevation sometimes becomes higher than the sea level over the ocean because of the diffusion filter. The range of the color bar in d is different from e and f

We created the low resolution topography by applying a threshold value of 0.005 in the diffusion filter, which is quite similar to the one usually used for atmospheric models of 200 km resolution (Fig. 2c). We use it in LR0k and LR127k, while the default counterpart is used for the other simulations. Note that the horizontal resolution in all the simulations is the same (56 km). As seen in Fig. 2e, f, the error of the elevation is significantly reduced around the Tibetan Plateau in the default topography compared to that of the low-resolution counterpart.

3 Results

3.1 Mean-state

Figures 3a–c and 4a–c show December–February (DJF) and June–August (JJA) mean precipitation in CTL0k, CP0k and the observation from the Global Precipitation Climatology Project (GPCP) version 2.2 (Adler et al. 2003). The amount of the peak precipitation over the major convergence zones in CTL0k is twice as large as that in the observation. Note that Kodama et al. (2021) shows that the use of higher resolutions such as 14 km lead to reduced precipitation of the convergence zones without convective parameterizations, thus this defect derives from the coarse resolution adopted in this work. However, the locations of the convergence zones are well reproduced especially in JJA. Due to the explicit representation of deep convection with the extremely coarse grid cells, CTL0k tends to give large blobs of precipitation and a spotty pattern remains even in the 5-year mean precipitation. On the other hand, the precipitation in CP0k is much smoother. The amount of the peak precipitation over the convergence zones is 1.5 times as large as that in the observation, which is still overestimated, but better than that in CTL0k. Figures 3d and 4d show that CP0k reduces the overly produced precipitation in CTL0k and gives more precipitation in the surrounding regions, which generally leads to a better distribution of the precipitation. However, CP0k has a weakness that the peak precipitation predominant over the western Pacific to the east of the Philippines is obscured in boreal summer. In both CTL0k and CP0k, the narrow rain band along the southern edge of the Tibetan Plateau in boreal summer is well reproduced (Fig. 4a, b).

Fig. 3

DJF mean precipitation in a CTL0k, b CP0k and c GPCP. d Difference of the DJF mean precipitation in CP0k from that in CTL0k. The unit is ${\text{mm day}}^{-1}$

Fig. 4

Same as Fig. 3, but for JJA

The zonally averaged seasonal mean precipitation is shown in Fig. 5. Both CTL0k and CP0k reproduces the observed precipitation very well in the mid and high latitudes. The precipitation is largely overestimated over the tropics and the bias of CP0k is smaller than that of CTL0k. The globally averaged annual mean precipitation in CTL0k, CP0k and GPCP is 3.03, 2.98 and 2.67 ${\text{mm day}}^{-1}$ respectively. The bias of the global and zonal mean precipitation is smaller than that in the peak precipitation over the convergence zones, which means that instead of producing excessive precipitation in the convergence zones, it underestimates the weak precipitation over the other regions.

Fig. 5

DJF (top-left), MAM (top-right), JJA (bottom-left) and SON (bottom-right) mean precipitation in CTL0K (blue), CP0k (red) and GPCP (black). The unit is ${\text{mm day}}^{-1}$

Table 4 shows the globally averaged annual mean radiation imbalance at the top of the atmosphere in each of the simulations. Both of the CTL0k and CP0k have a large net positive imbalance. Although our model is coupled with the slab ocean model, the SSTs are nudged to the present-day values. Thus, the extra radiative energy absorbed on the surface due to this imbalance is consumed by the nudging term and does not cause severe problems for the purpose of this study. In general, NICAM largely underestimates low and middle level clouds (e.g. Kodama et al. 2015), which causes an underestimation of the outgoing shortwave radiation by about 16 ${\mathrm{Wm}}^{-2}$ and the outgoing longwave radiation (OLR) by 2 ${\mathrm{Wm}}^{-2}$. Our result is consistent with that of the HighResMIP simulations of NICAM (Fig. 5c, d in Kodama et al. 2021). The imbalance is slightly smaller in CP0k, but the difference is very small. The globally averaged annual, JJA and DJF mean surface temperatures in each of the simulations are also shown in Table 4 as well as that of reanalysis data. Generally, the global mean surface temperature is well reproduced in both of the simulations. CP0k tends to produce slightly higher temperatures, which appears to derive from smaller cloudiness (not shown).

Table 4 Globally averaged annual mean radiation imbalance at the top of the atmosphere (TOA) and globally averaged surface temperatures (Annual, JJA and DJF mean) in each of the simulations

Figure 6 shows the June–September (JJAS) mean precipitation in CTL127k and CP127k and their difference from those in the corresponding 0 ka simulations. Over North Africa, the Intertropical Convergence Zone (ITCZ) shifts northward. Over South Asia, the narrow rain band along the southern edge of the Tibetan Plateau is intensified. There is a large reduction over the Bay of Bengal, the South China Sea and the western Pacific and an increase along the equator over the eastern Indian Ocean and the Maritime Continent. These features are qualitatively similar to those in the previous studies (Otto-Bliesner et al. 2021). There is no big difference in the overall features between CTL127k and CP127k, which is rather surprising considering that the model represents the convective processes in a totally different way in each of the simulations. The reduction over the western Pacific in CP127k is much smaller than that in CTL127k, which appears to correspond to the smaller climatological precipitation in this region. Since the original mean precipitation is overestimated in CTL0k, its change is also likely to be large, so the result of CTL127k should be interpreted carefully.

Fig. 6

(Top) precipitation averaged from June to September in a CTL127k and b CP127k. (Bottom) difference of the precipitation averaged during the same months in c CTL127k and d CP127k from that in CTL0k and CP0k respectively. The unit is ${\text{mm day}}^{-1}$. The purple lines indicate the contours for the elevation of the model surface corresponding to 3000 m, showing the area of the Tibetan Plateau

Figure 7a, b shows the changes in the JJAS mean surface temperatures at 127 ka compared to those at 0 ka. In most areas, the change in the SSTs is within $\pm 1^\circ{\rm C}$, which is considered to be partly caused by nudging of the SSTs to the climatological values of the present climate in the slab-ocean model. On the other hand, there is a significant increase in the surface temperatures over the continents. The temperature rise is particularly high in arid regions where latent heat fluxes cannot respond to balance the enhanced insolation, while the temperature decreases in areas where the precipitation increased. The JJAS mean sea level pressure (SLP) significantly decreases over the continents corresponding to the large temperature increase (Fig. 7c, d). The SLP rises over the east China sea, northern Pacific, which is interpreted as a dynamical response to the reduced SLP over the continents and explains the reduction of the precipitation in these regions.

Fig. 7

(Top) Difference of the JJAS mean surface temperatures in a CTL127K and b CP127k from those in CTL0k and CP0k respectively. (Bottom) Difference of the JJAS mean SLP in c CTL127K and d CP127k from those in CTL0k and CP0k respectively. The unit is K for a, b and hPa for c, d. The purple lines indicate the contours for the elevation of the model surface corresponding to 3000 m, showing the area of the Tibetan Plateau

Figure 8 focuses on the SST changes with a shading range adjusted accordingly. It is noteworthy that a large temperature rise is seen over the Bay of Bengal, South China sea and Philippine Sea where the precipitation is significantly reduced. On the other hand, the warming along the equator over the eastern Indian Ocean, western Pacific and the oceans around the Maritime Continent is relatively moderate despite the significant increase in the precipitation there. These facts indicate that the intensification of the precipitation along the equator is the effect of dynamical forcing deriving from the other region.

Fig. 8

Difference of the JJAS mean SSTs in a CTL127k and b CP127k from those in CTL0k and CP0k respectively. The unit is K

The globally averaged JJA mean surface temperatures in 127 k simulations increase, while the DJF counterparts decrease (Table 4). These changes appear to cancel out and give almost no change in the globally averaged annual mean surface temperatures.

Figure 9a–d shows the time-latitude section of the climatological daily mean precipitation averaged over the longitudinal range of North Africa. The differences of the precipitation in 127 ka simulations from that in 0 ka simulations are also shown in Fig. 9e, f. In both CTL127k and CP127k, the African ITCZ begins to shift more northward compared to that in the 0 ka counterparts in June and reaches its maximum latitude in July and August, intruding into the present-day Sahara desert which extends north of $20^\circ$ N. After October, the ITCZ recedes to the south more quickly and shifts more southward until March than that at 0 ka.

Fig. 9

a–d Time-latitude section of the climatological daily mean precipitation zonally averaged between 10° W and 30° E in each of the simulations. e, c Minus a. f, d Minus b. The unit is ${\text{mm day}}^{-1}$

Figure 10 shows that in terms of the July–August mean precipitation and annual precipitation averaged over the longitudinal range of North Africa, the degree of the northward intrusion of the precipitation at 127 ka is quite similar between CTL127k and CP127k. The previous study shows that the elevated convection discussed in Sect. 2 tends to occur preferentially over the northern half of the ITCZ during boreal summer and enhances its northward shift over North Africa (Chikira et al. 2006). The modification in the convective scheme to allow the elevated convection is considered to help enhance the northward shift of the ITCZ in CP127k, while its effect is directly represented by the dynamical core and microphysics scheme in CTL127k. The similarity of the distribution between CTL127k and CP127k gives us a confidence that the modification in the convective scheme described in Sect. 2 is adequately working.

Fig. 10

(Left) July–August mean precipitation and (right) annual precipitation zonally averaged between 10° W and 30° E. Solid and dashed lines indicate 0 ka and 127 ka simulations respectively. Blue and red lines indicate CTL and CP simulations respectively. Black lines indicate GPCP. The unit is ${\text{mm day}}^{-1}$ for the left panel and ${\text{mm year}}^{-1}$ for the right panel

3.2 Variability

3.2.1 Coherence squared

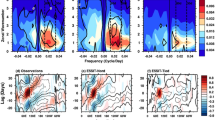
Figure 11 shows the coherence squared and phase difference for the OLR and zonal winds at 850 hPa in each of the simulations, aligned with those created using the observed daily mean OLR of the National Oceanic and Atmospheric Administration (NOAA) Advanced Very High Resolution Radiometer (AVHRR; Liebmann and Smith 1996) and the zonal winds at 850 hPa of the NCEP-National Center for Atmospheric Research (NCAR) reanalysis (Kalnay et al. 1996) from 1979 to 2011. The procedure of the computation follows Hendon and Wheeler (2008). The latitudinal range of the computation is 15° S–15  N. The coherence squared indicates the degree to which the two variables are correlated at a given wavenumber and frequency. Hereafter, the combination of observations and reanalyses is referred to as “observation” for convenience.

Fig. 11

Coherence squared (color) and phase difference (vectors) for the (top) symmetric and (bottom) antisymmetric components of OLR and zonal velocity at 850 hPa in c, d CTL0k and e, f CP0k. a, b Same as c, d and e, f but uses the observed OLR of NOAA AVHRR and the zonal winds at 850 hPa of NCEP reanalysis from 1979 to 2011. Upward arrows in each pixel indicate that the variables are in phase, and right-pointing arrows indicate that the OLR is leading the zonal velocity by a quarter cycle. Dispersion curves of the even and odd meridional mode-numbered equatorial waves for the three equivalent depths of 12, 25, 50 m in Matsuno (1966) are indicated by black lines. IG, ER, EIG and MRG denotes inertio-gravity, equatorial Rossby, Eeastward inertio-gravity and Mixed Rossby-gravity waves. The unit of frequency is cycles per day

The observation shows a significant signal of the MJO around wavenumber 1–3 and frequency 20–80 days in the symmetric components, whose frequency is lower than that of Kelvin waves for a given wavenumber. CTL0k lacks the strong signal of the MJO, and the peak signal erroneously appears on the dispersion curves of the Kelvin waves in wavenumber 1–2. CP0k clearly shows much improved distribution of the signal, though it has a bias toward smaller wavenumber and higher frequency.

CTL0k also has unrealistically strong signals in the symmetric component where frequency is shorter than 10 days and wavenumber is negative, while CP0k does not. Both CTL0k and CP0k show unrealistic noisy signals to the higher-frequency side of the dispersion curves of the Kelvin waves in the symmetric component and the lower-frequency side of the dispersion curves of the eastward inertio-gravity (EIG) and mixed Rossby-gravity (MRG) waves in the antisymmetric component, but these biases are moderate in CP0k compared to those in CTL0k. Both CTL0k and CP0k fails to represent the signals of the EIG and MRG waves as well as that of the MJO in the antisymmetric component.

Figure 12 is the same as Fig. 11, but for 127 ka simulations. The outstanding feature in CP127k is the greater signal of the MJO both in the symmetric and antisymmetric components than that in CP0k. In addition, the signal of the Kelvin waves weakens in CP127k compared to that in CP0k. The similar differences in both the MJO and Kelvin waves are seen between CTL127k and CTL0k as well.

Fig. 12

Same as Fig. 11 but for a, b CTL127k and c, d CP127k

3.2.2 Lag correlation

Figure 13 shows the time-longitude sections of the lag correlation for the precipitation and zonal winds at 850 hPa against those over the eastern Indian Ocean (10° S–5  N, 75° E–100° E) as a reference area respectively in each of the simulations. In advance of computing the correlation, the datasets were bandpass-filtered for 20–100 days to focus on the MJO and then latitudinally averaged between 10° S and 10  N. For comparison, the same plot using the observed precipitation of the Global Precipitation Climatology Project (GPCP) and zonal winds of the NCEP-NCAR reanalysis is shown in Fig. 14a.

Fig. 13

Time-longitude sections of the lag correlation of the precipitation (shading) and the zonal winds (contour) at 850 hPa against those averaged over the eastern Indian Ocean (10 S–5  N, 75 E–100 E) as a reference area in a CTL0k, b CTL127k, c CP0k and d CP127k. The datasets were first bandpass-filtered for 20–100 days and then latitudinally averaged between 10° S and 10° N

Fig. 14

a Same as Fig. 13, but for the observed precipitation of the GPCP and the zonal winds at 850 hPa of the NCEP-NCAR reanalysis. b Same as a, but Time-latitude section against the same reference area. In b, the datasets during the boreal summer period were first bandpass-filtered for 20–100 days and then longitudinally averaged between 80° E and 100° E. The period of the datasets is from 1996 to 2005

The observation shows vigorous and steady eastward propagation of the convective area due to the MJO 60° E to 150° E and − 5 to 10 days, accompanied by the westerly and easterly zonal winds to the west and east respectively. CP0k succeeds in representing this eastward propagation, though its signal is weaker than that of the observation. CP127k exhibits more distinct eastward propagation than CP0k, consistent with the enhanced signal of the MJO in the coherence squared. On the other hand, in both CTL0k and CTL127k, the eastward propagation is unclear and the propagation is too fast, suggesting that its dynamics is closer to that of the Kelvin waves.

Figure 15 shows the lag correlation for the same variables against the same reference area as in Fig. 13, but is the time-latitude sections. Here, only the data during the boreal summer was used and bandpass-filtered for 20–100 days to focus on the BSISO, which was then longitudinally averaged between 80° E and 100° E. For comparison, the same plot using the observed precipitation of the GPCP and zonal winds of the NCEP-NCAR reanalysis is shown in Fig. 14b.

Fig. 15

Same as Fig. 14b but for a CTL0k, b CTL127k, c CP0k and d CP127k

The observation shows clear propagation of the convective area in both northward and southward directions from the equator up to 20° N and 20° S respectively with an intraseasonal time-scale. The convective area is accompanied by the easterly winds on the polar side and westerly winds on the equatorial side. The one propagating northward comprises a part of the overall horizontal time-evolution of the BSISO which has both northward and eastward propagating components.

CTL0k reproduces the northward propagation, though it has weaknesses that the convection diminishes around 10° N and the propagation speed is overestimated. The southward propagation of the convection is totally lacking in CTL0k, though the zonal winds clearly propagate southward. CP0k fails to represent the steady northward propagation of the convection. Instead, the broad convective area standing around 10° S–10° N from − 10 to 10 days abruptly jumps to 15 N° around 10 days. The southward propagation is slightly better compared to CTL0k, but it is significantly weaker than that in the observation.

CTL127k gives a similar pattern to that in CTL0k in terms of the convection. The southward propagation clearly seen in the zonal winds of CTL0k weakens in CTL127k. It is quite impressive that CP127k gives the convective area steadily propagating both northward and southward as seen in the present-day observation, though the southward propagation of the zonal winds are unclear compared to that in CP0k.

3.2.2.1 Tropical cyclone

Here, we analyze the features of the tropical cyclones (TC) represented in each of the simulations. The simulated TCs are compared with the best-track datasets compiled by the International Best Track Archive for Climate Stewardship (IBTrACS; Knapp et al. 2010) from 1980 to 2014, which is comprised of the data from the World Meteorological Organization (WMO) Regional Specialized Meteorological Centers, Tropical Cyclone Warning Centers and other national agencies. See Appendix for the method to detect the TCs.

Figure 16 shows the spatial distribution of the TC genesis densities for IBTrACS and each of the simulations, defined as the number of the TCs per year generated in $5^\circ \times 5^\circ$ grid boxes. The TCs are counted only when it developed into the TC in a given grid box and not when it just moved through the box. Figure 17 adds more information on its interannual variation and statistics for seven ocean basins. Figure 16 might give an impression that the overall density of the simulated TCs are too low and noisy, but it is mainly because the duration of the simulated period is too short, despite the number of the TCs has very strong interannual variability and the period of the IBTrACS datasets is 35 years. Note that longer simulation would give a more smooth and widespread blue area (from 0 to 0.2 in number per year).

Fig. 16

TC genesis density for a IBTrACS and the b–e simulations. The density is defined as the number of the TCs per year generated in $5^\circ \times 5^\circ$ grid boxes. The period of the IBTrACS is from 1980 to 2014. The dotted lines separate the seven ocean basins

Fig. 17

The number of TC genesis over each of the ocean basin. The seven ocean basins are delineated in the previous figure. The circles and crosses indicate the annual number of the TC genesis in each year of the simulations and their five-year means respectively, where blue and red correspond to 0 and 127 k simulations respectively. The boxplots in the left-most part of the panels indicate the interannual variability of the TC genesis in IBTrACS. The values under the simulation names are p-values based on Welch's t test. Note that the scale of the values at each of the panels is different

CTL0k gives reasonable genesis density over the western north Pacific and north Indian Ocean. The basin-mean genesis density appears to be reasonable over the north Atlantic, but the model totally fails to represent the peak density seen in IBTrACS around 10° N. CTL0k considerably underestimates the density over the eastern north Pacific and south Indian Ocean, and overestimates it over the south Pacific to some extent. CP0k gives the lower genesis density over the western north Pacific, north Atlantic and south Pacific than CTL0k. The lower densities over the western north Pacific and south Pacific are considered to be associated with the reduction of the precipitation in CP0k compared to that in CTL0k (Figs. 3d, 4d).

In CTL127k, the genesis density decreases over the western north Pacific and north Atlantic with significance levels of more than 99%, whereas it increases over the south Indian Ocean with a significance level of about 97%. CP127k also shows a decrease over the north Atlantic with a significance level of about 96%, and an increase over the south Indian Ocean, though its significance level (91%) is not sufficiently high. A decrease is seen over the western north Pacific, however, unlike CTL127k, it is very small and is not statistically significant. In contrast to CTL127k, CP127k shows an increase in the genesis density over the south Pacific with a significance level of 96%.

Figures 18 and 19 are same as Figs. 16 and 17 respectively, but for the TC existence density. Unlike the genesis density, the TCs are counted when it exists in the grid boxes, regardless of whether it was born in or moved through the boxes. Strengths and weaknesses of the simulated results as well as its change in 127 ka simulations are overall similar to those of the TC genesis densities. The significance levels for the changes over the north Atlantic are considerably lower than those for the genesis density, while those for the south Indian Ocean are slightly higher. The significance level for the increase over the south Pacific in CP127k is slightly lower than that for the genesis density. Unlike the genesis density, the increase in the existence density over the south Atlantic in CTL127k is significant with 95% level. Figure 18b, c shows that the number of TCs over this basin increases only to the south of 20° S, suggesting that the cyclones detected as TCs with the aforementioned criteria in this area contain extratropical cyclones which have a similar structure to that of the tropical cyclones.

Fig. 18

Same as Fig. 16, but for the TC existence density. The density is defined as the number of TCs per year existing in $5^\circ \times 5^\circ$ grid boxes

Fig. 19

Same as Fig. 17, but for the number of the TC existence over each of the ocean basins

Due to the horizontal resolution which is low to represent realistic TCs, the model is unable to represent strong TCs whose maximum wind velocity exceeds 45 $\mathrm{m s}^{-1}$ in both of the CTL and CP simulations, which makes it rather meaningless to discuss the change in its intensity.

3.2.2.2 Effect of small-scale topography

Figure 20 shows the difference of the JJAS mean precipitation in the CTL simulations from the LR counterparts. In both of the 0 and 127 ka simulations, the precipitation increases along the southern edge of the Tibetan Plateau. From here to the south, a wave-like pattern of the precipitation extending east and west is seen, which appears to propagate southward. The reduction in the precipitation around 15° N is larger in the 0 ka simulation compared to the 127 ka counterpart. The precipitation significantly increases around the equator over the Indian Ocean.

Fig. 20

Difference of the JJAS mean precipitation in a CTL0k and b CTL127k from LR0k and LR127k respectively. The purple lines indicate the contours for the elevation of the model surface corresponding to 3000 m in CTL0k, showing the area of the Tibetan Plateau. The unit is ${\text{mm day}}^{-1}$. The purple lines indicate the contours for the elevation of the default model surface corresponding to 3000 m, showing the area of the Tibetan Plateau

Figure 21 shows the difference of the JJAS mean dry static energy (DSE), moisture and moist static energy (MSE) at a height of 2 m from the surface in the CTL simulations from those of the LR simulations. The DSE increases around $85^\circ$ E and $32^\circ$ N which corresponds to the elevated area in the default topography compared to the low-resolution counterpart (Fig. 2d). On the other hand, the DSE decreases over the southern foot of the Tibetan Plateau which corresponds to the narrow area of the reduced elevation extending east and west in the default topography. As for the moisture, it significantly decreases over the elevated area of the Tibetan Plateau due to the colder temperature there and increases over the southern foot of the Plateau with the reduced elevation which is warmer than that of the low-resolution topography.

Fig. 21

Difference of the JJAS mean a dry static energy, b moisture and c moist static energy at a height of 2 m from the surface in CTL0k from those of LR0k respectively. d–f Same as a–c but for the difference of CTL127k from LR127k. The unit is ${10}^{3}{\mathrm{Jkg}}^{-1}$. Note that moisture is also shown in the unit of energy per unit mass. The purple lines indicate the contours for the elevation of the default model surface corresponding to 3000 m, showing the area of the Tibetan Plateau

The changes in the DSE and moisture are in opposite directions over the interior and surrounding regions of the Tibetan Plateau. Overall, the change in the moisture overcomes that of the DSE, and the MSE shows a decrease along the edge of the Tibetan Plateau and an increase over the southern foot of the Plateau (Fig. 21c, f). The location of the increased precipitation along the southern edge of the Tibetan Plateau corresponds to the region with the reduced MSE of the surface air, which means that the enhanced precipitation is not caused by enhanced energy of the surface air. Figure 21c also shows that the change in the MSE of the surface air is quite small over the Indian Ocean, which suggests that the change in the precipitation over the Indian Ocean is caused by some forcing on the free troposphere, not by that on the surface air.

Figure 22 shows the latitude-height sections of the JJAS mean diabatic heating of all the physical processes and wind velocity zonally averaged between $80^\circ$ E and $100^\circ$ E. An outstanding difference of the diabatic heating in the 127 ka simulations from that in their 0 ka counterparts is the weakening of the heating around $15^\circ$ N in the middle troposphere, which corresponds to the reduced precipitation over the Bay of Bengal seen in Fig. 6c.

Fig. 22

Latitude-height sections of the JJAS mean diabatic heating [${\text{K day}}^{-1}$] of all the physical processes (color) and wind velocity (vector) zonally averaged between $80^\circ$ E and $100^\circ$ E in a CTL0k, b LR0k, d CTL127k and e LR127k. c and f are a minus b and d minus e respectively. The wind vectors are shown using the meridional velocity in the unit of $\mathrm{m s}^{-1}$ and the vertical velocity in the unit of ${\text{hPa h}}^{-1}$ where the vector length of 1 ${\text{hPa h}}^{-1}$ is set to that of $1 \mathrm{m s}^{-1}$. The vector lengths corresponding to given velocities are shown at the upper-right of each of the panels

As for the difference of the CTL simulations from the LR counterparts, the upward motion adjacent to the southern slope of the Tibetan Plateau around $28^\circ$ N is significantly strengthened in both of the 0 and 127 ka simulations (Fig. 22c, f). The wind appears to follow the slope of the terrain which is steeper in the default topography than that in the low-resolution counterpart, explaining the greater upward motion in the default topography. This upward motion should lead to enhanced destabilization of the atmosphere and more intense convective activity in this area. Compared to the 0 ka simulations, 127 ka counterparts show the larger enhancement of the diabatic heating reaching to a higher altitude (Fig. 22c, f), which is considered to be caused by the increased moisture transport from the south and more vigorous convective activity. This mechanism of the precipitation caused by the forced lifting in this region in the present-day climate is supported by studies using satellite observations and reanalysis data (Fu et al. 2018; Shrestha et al. 2012).

Figure 23 shows the latitude-height sections of the JJAS mean temperature and geopotential height zonally averaged between $80^\circ$ E and $100^\circ$ E as increments from the areal means of $20^\circ$ S–$40^\circ$ N and $80^\circ$ E–$100^\circ$ E. The temperature is higher over the continent particularly in the lower troposphere due to the insolation of this season in all the simulations. Corresponding to this temperature structure, the geopotential height is lower in the lower troposphere over the continent, but higher over the Indian Ocean. That induces the southerly winds near the surface due to the frictional convergence over the entire Indian Ocean and the south India (Fig. 22), which also creates the dynamically-forced terrain-following upward motion at the southern slope of the Tibetan Plateau.

Fig. 23

Latitude-height sections of the JJAS mean (color) temperature [K] and geopotential height [m] zonally averaged between $80^\circ$ E and $100^\circ$ E as increments from the areal means of $20^\circ$ S–$40^\circ$ N and $80^\circ$ E–$100^\circ$ E in a CTL0k, b LR0k, d CTL127k and e LR127k. c and f are a minus b and d minus e respectively

Figure 23c, f show an increase in temperature over the top of the Tibetan Plateau with the default topography due to the elevated surface, consistent with Fig. 21a, d and also a decrease near the southern slope of the plateau caused by the dynamically-forced upward motion. The warmer temperature over the Tibetan Plateau creates the higher geopotential height in the upper troposphere aloft, which leads to the relatively lower geopotential height to the south of 25° N in the upper troposphere. The lower geopotential height in the upper troposphere then leads to the higher geopotential height in the lower troposphere and induces greater downward motion and weaker diabatic heating. The remarkable weakening of the diabatic heating in the middle troposphere around $15^\circ$ N in the 0 ka simulations (Fig. 22c) corresponds to the large diabatic heating at the same location in the CTL0k and LR0k (Fig. 22a, b). The reason for the weaker reduction of the heating at the same location in the 127 ka simulations (Fig. 22f) is considered to be the already weaker diabatic heating in the CTL127k and LR127k (Fig. 22d, e), further reduction of which is difficult to occur.

Wu et al. (2012) set up simulations to decompose the effect of the Tibetan Plateau on the atmosphere into that of topography and surface heating. By turning off the sensible heat fluxes over the Tibetan Plateau in boreal summer, they demonstrated that the surface heating over the plateau plays an important role in creating the narrow precipitation band along the southern edge of the plateau by sucking up the near-surface air from the south along the slope. Considering their result, the intensification of the narrow precipitation along the southern edge of the plateau in CTL0k and CTL127k compared to LR0k and LR127k is considered to be enhanced by the warmer temperature over the plateau due to the elevated surface as well as the steeper slope of the plateau discussed above.

Figure 22c, f show that the weakening of the diabatic heating as well as the downward motion is occurring in multiple locations, which are around $15^\circ$ N and $25^\circ$ N in the 0 ka simulations, $10^\circ$ N, $20^\circ$ N and $25^\circ$ N in the 127 ka counterparts. A very strong downward counter flow is also seen in the lower troposphere around $23^\circ$ N. The atmospheric response to the enhanced narrow diabatic heating around 28° N appears to propagate southward and create the wave-like structure which is also seen in Fig. 20.

4 Summary and discussion

This study applied the global nonhydrostatic atmospheric model NICAM to a paleoclimate research for the first time. Although this model is usually used at 14 km and higher resolution, we adopted 56 km due to the limited computer resources, anticipating that the simulated results had a similarity to those at much higher resolution. This study explored a methodology to use the low-resolution GNHM in future paleoclimate simulations and examined its strengths and weaknesses.

Since convective parameterization is usually considered to be necessary for the grid-spacing of 56 km, simulations were run with and without a convective parameterization where the treatment of the convective sources was altered to better represent convection originating from above the CBL. We also performed simulations with a low-resolution topography to understand the strength of its high resolution counterpart.

The last interglacial, 127 ka, was chosen as a target of the simulations, which is characterized by the amplification of the seasonal variation of the northern hemispheric insolation and the enhanced Asian-African monsoon. As a first step, we set up idealized simulations where only orbital parameters were changed to those of 127 ka and a simple slab ocean model was used to represent the response of the SSTs.

Since one of the strengths of NICAM is considered to be its representation of convectively coupled disturbances, we analyzed the equatorial waves, intraseasonal oscillations and tropical cyclones as well as the mean-state of the select variables.

In the mean-state, the present-day simulation gives largely overestimated precipitation over almost all the convergence zones without the convective parameterization. The use of the convective parameterization reduces the precipitation over the convergence zones and gives more precipitation over the surrounding area, making the result closer to that in the observation in both of the amount and spatial pattern. One weakness of the use of the convective parameterization is the underestimation of the precipitation over the western Pacific. With the 56 km resolution, the model succeeds in representing the narrow precipitation band along the southern edge of the Tibetan Plateau which is blurred in models with lower resolutions.

In the 127 ka runs during boreal summer, the narrow precipitation band along the southern edge of the Tibetan Plateau is intensified. A large reduction is seen over the Bay of Bengal, the South China Sea and the western Pacific, while a large increase is seen over the eastern Indian Ocean and the Maritime continent. The ITCZ shifts northward over North Africa. This result is qualitatively similar to that in the previous studies and support its robustness. It is rather interesting that the overall pattern is not much different between the runs with and without the convective parameterization, while the method to represent deep convection is totally different. Since the precipitation is largely overestimated without the convective parameterization, its change tends to be also larger compared to the one with the convective parameterization. However, the degree of the northward intrusion of the small precipitation over the Sahara desert is quite similar between the runs with and without convective parameterization.

The MJO is well represented with the convective parameterization in the present-day simulation. Without the parameterization, the model fails to represent it in the range of the adequate wave number and frequency. In the 127 ka run, the signal of the MJO intensifies in terms of both of the coherence squared and lag correlation. Detailed analysis is still necessary to explain the underlying mechanism. A possible factor is the increase in the mean precipitation over the Indian Ocean. It should be accompanied by a change in the moisture profile, greater moisture in the lower to middle troposphere, which is known to be a favorable condition for the amplification and maintenance of the MJO (Chikira 2014). Another interesting change in the equatorial waves is the weakening of the Kelvin waves in the 127 ka runs, whose mechanism also needs to be explored in future studies.

The northward propagation of the convective area during boreal summer as a part of the BSISO in the present-day simulation is weak in the model compared to the observation. It is slightly better in the run without the convective parameterization. However, the 127 ka run with the convective parameterization shows a considerable strengthening of the northward propagation as well as the southward counterpart, which is not evident enough in the run without the convective parameterization. In terms of the lag correlation, the magnitude of the BSISO in the 127 ka run is comparable to the one in the present-day observation. Although the model's representation of the BSISO in the present-day simulation is not satisfactory, this is an interesting change in terms of the theory of the BSISO. A possible reason for the intensification is the increase in the precipitation over the Indian Ocean, from where the convection starts to propagate northward, but is underestimated in the model. In addition, Jiang et al. (2004) demonstrated the importance of the basic-state vertical shear of zonal winds in the northward propagation of convection in their theory. Since the enhanced Asian monsoon in the 127 ka run leads to the strengthening of the wind shear over the Indian Ocean, its effect is a possible factor to be explored in future studies.

The representation of the genesis and existence densities of the tropical cyclones are slightly better without the convective parameterization. The use of the convective parameterization tends to reduce both of the genesis and existence densities and underestimate them compared to those of the IBTrACS. The underestimation over the western Pacific is particularly notable, which appears to be associated with the underestimated mean precipitation in this region during boreal summer.

Since the period of the integration in this study is only five years, the large interannual variation of the tropical cyclones makes it rather difficult to discuss its changes in the 127 ka simulations with sufficient statistical significance. However, a decrease in the existence density over the western north Pacific, north Atlantic and an increase over the south Indian Ocean and south Atlantic in the 127 ka run are statistically significant with 99, 92, 99 and 95% levels respectively, if the convective parameterization is not used. The use of the convective parameterization gives the same tendency, but with lower significance levels. It appears that the direction of these changes is consistent with that in the mean precipitation.

Additional simulations using the low-resolution topography revealed that the precipitation along the southern edge of the Tibetan Plateau is intensified during the Asian summer monsoon season with the increased resolution of the topography in both of the 0 and 127 ka simulations. From here to the south, a wave-like pattern of the precipitation extending east and west is seen. The precipitation significantly increases around the equator over the Indian Ocean. This response is similar and comparable to that to the orbital parameters of the 127 ka, but limited to the south Asia and Indian Ocean.

During the Asian summer monsoon season, the lower-tropospheric temperature increases over the continent and the southerly winds are generated near the surface by the frictional convergence over the Indian Ocean and south India, which collide with the southern edge of the Tibetan Plateau and create the upward motion. The steeper slope at the edge of the plateau with the default topography leads to the greater upward motion, destabilization and more intense convection in this area, compared to those with the low-resolution topography.

The temperature increases over the Tibetan Plateau due to the elevated surface in the default topography and creates higher geopotential height in the upper troposphere aloft. Then, the higher geopotential height in the upper troposphere over the plateau leads to the relatively lower geopotential height in the upper troposphere, higher geopotential height in the lower troposphere, greater downward motion and reduced diabatic heating to the south of the plateau. Considering the previous study which demonstrated the importance of the boreal summer surface heating over the Tibetan plateau in intensifying the precipitation along the southern edge of the plateau (Wu et al. 2012), the increased temperature over the plateau is also considered to play a role in invigorating the precipitation along the southern edge of the plateau by sucking up the near-surface air from the south along the slope and enhancing the upward motion there. Thus, the cause of the intensification of the precipitation along the southern edge of the plateau is two-fold, steeper slope at the edge and warmer temperature over the plateau.

The effect of boreal summer monsoonal heating on the atmospheric circulation has been well discussed in many previous studies (e.g. Gill 1980; Rodwell and Hoskins 1996; Sashegyi and Geisler 1987). They generally showed that external heating similar to that of the boreal summer monsoon induces an upward motion around the heated area and its effect propagates mainly westward and southward creating a downward motion there. It is speculated that the narrow diabatic heating along the southern edge of the Tibetan Plateau excites linear atmospheric modes which has a large meridional wave number and the wave-like pattern seen to the south of the Tibetan Plateau reflects the existence of these modes (Fig. 20). We also speculate that the enhanced precipitation around the equator over the Indian Ocean is a remote effect of the changes near the Tibetan Plateau, not the cause of the suppression of the precipitation around $15^\circ$ N, since we do not see other strong factors to enhance the precipitation there.

We did not run LR simulations with the convective parameterization due to limited computer resources. However, we expect that the results will be similar even if the convective parameterization is used, considering the fact that the response of the mean-state to the orbital parameters is quite similar between CTL127k and CP127k (Fig. 6a–d).

This study confirms that the use of the convective parameterization is generally helpful for the low-resolution GNHM and its application to paleoclimate researches. However, the model's performance depends on the convective parameterization in use which has its own unique strengths and weaknesses. In our case, the representation of the tropical cyclones was better without the convective parameterization, but it may change with other convective parameterization and by future improvements.

In this work, we used a simple slab ocean model where the SSTs were nudged to those of the present-day climatology as a first step. Thus, our results are not very suitable yet for detailed comparison with other models and proxies (Otto-Bliesner et al. 2021; Scussolini et al. 2019). We are planning to run simulations using the SSTs calculated by an atmosphere–ocean coupled model, which is more suitable for the comparison, but may change some of the conclusions documented in this section. The use of interactive aerosols is another subject to be made in future works.

Appendix

The method to detect TCs is similar to the one adopted in Yamada et al. (2017) and the analysis is performed using the 6 hourly snapshots. First, grid points are searched on which the SLP is 0.5 hPa lower than the mean SLP over the surrounding $7^\circ \times 7^\circ$ grid boxes. These grid points become candidates for the center of the TCs. Next, these candidate grids are regarded as the real centers of the TCs only when they satisfy all of the following criteria. (1) The maximum wind at a height of 10 m over the surrounding $3^\circ \times 3^\circ$ exceeds $17.5 {\mathrm{ms}}^{-1}$. (2) The maximum relative vorticity at 850 hPa exceeds $3.5\times {10}^{-5}{ \mathrm{s}}^{-1}$. (3) The vertical temperature structure exhibits a marked warm core, that is, the sum of temperature deviations at 300, 500 and 700 hPa exceeds 9 K. Here, the temperature deviation is defined as the difference between the temperature at the candidate grid and the mean temperature over the surrounding $7^\circ \times 7^\circ$ grid boxes. (4) The duration of the existence of the TC exceeds 36 h. (5) The TC is formed between 45° S–45° N. The locations of the TC genesis is defined as the grid point where all of the above criteria are satisfied for the first time.

IBTrACS contains the positions and maximum winds of cyclones. We regard the cyclones as TCs when their maximum wind exceeds $17.5 {\mathrm{ms}}^{-1}$. The locations of the TC geneses are defined as the grid points where the maximum winds first exceed $17.5 {\mathrm{ms}}^{-1}$. The maximum winds provided by IBTrACS is time-averaged values, where the period of the average is different depending on the agencies which furnished their best-track datasets. Thus, we use only the datasets provided by the National Hurricane Center (North Atlantic and eastern North Pacific; Jarvinen et al. 1984) and the Joint Typhoon Warning Center (western North Pacific, north Indian Ocean and Southern Hemisphere; Chu et al. 2002) among those provided by IBTrACS, because both centers use 1 min for the period to average the maximum winds.