1 Introduction

1.1 Benchmark artifacts in additive manufacturing

The design of structural components is limited by the manufacturing processes currently available. Additive manufacturing offers large possibilities which have not been achieved by conventional technologies like milling or casting. This freedom of structural design can be exploited via topology optimization (TO) in order to conceive nearly arbitrary structural functions through design requirements which are simple to formulate [1].

A critical path of designing additively manufactured structures is to assess the quality of geometric and material properties under the condition of rapidly melted and solidified material [2,3,4]. This can be achieved via benchmark artifacts which represent critical elements of the quality measure [5,6,7,8], e.g., dimensional accuracy or surface roughness. Benchmark artifacts combine various elements for quality assessment into a single, integral test specimen, hence keeping manufacturing and testing effort low.

Conventionally, a batch of test specimens is fabricated together with the reference part and tested according to ASTM E8 [9] to characterize the quality based on structural properties. Taylor et al. [8] conceived a benchmark artifact that included standardized tensile rods as witness specimens to be tested separately after fabrication. Due to a limited design space, these witness specimens had to be resized to smaller dimensions than specified by the standard. Until now no integral benchmark artifact has been proposed in order to assess the quality of additively manufactured components regarding mechanical properties. It is crucial for an efficient quality characterization to further generalize the notion of benchmark artifacts independently from usual standards. Multiple quality measures must be represented here by a single benchmark artifact. The topology is a priori unknown for this artifact and has to be automatically found by optimization.

1.2 Topology optimization

Topology optimization (TO) has a wide use today, e.g., in the aircraft or automotive industry [1, 10]. Research accelerated in the late 80 s and early 90 s with a typical optimization problem of minimum structural compliance. Gradient methods were established together with an interpolation scheme of artificial intermediate densities by Bendsøe [11], which is now called the Solid Isotropic Material with Penalization (SIMP) [12]. The structure is represented here by a ground element grid with an element-wise distribution of the so-called “density” which stands for an interpolated material volume and stiffness. Each element density has an influence on the objective function in the form of structural compliance. Sensitivities to the element densities are used as gradient information for the optimization, commonly carried out via the Method of Moving Asymptotes [10, 13]. The SIMP method has been proven to render results for conventional minimum compliance problems reliably and fast.

1.2.1 Approaches with evolutionary methods and multi-objective formulations

Other TO approaches in terms of minimum compliance comprise evolutionary methods with heuristic structural element deletion, which is also known as Evolutionary Structural Optimization (ESO) [14], or its bidirectional form (BESO) with element deletion and addition [15, 16]. Especially the ESO approach has been criticized due to its non-reliable structural results and unpredictable breakdown [10, 17]. Several shortcomings could be attenuated by the BESO method. Despite the term “evolutionary”, the ESO method cannot be classified as evolutionary algorithm (EA) as it does not include concepts like population, selection, or mutation [18].

EAs were especially applied to TO together with problem formulations which were more complex than the minimum compliance problem. Multi-objective optimization problems cannot be readily handled by the SIMP approach as it typically involves only a single objective function. Madeira et al. [19] investigated a multi-objective minimum compliance problem regarding multiple load cases by means of genetic algorithms, a subtype of EA. Optimal solutions were generated as a set of Pareto-optimal structural individuals, the so-called Pareto front. Kunakote and Bureerat [20] analyzed various EA with advanced objective functions. Pareto fronts were characterized by the hypervolume indicator [21] and a distance measure from a reference solution, called the generational distance.

Furthermore, the SIMP approach has its limitations considering complex objective functions. Hamza et al. [22] define the shape complexity to be minimized by TO. There are no analytical derivations for the sensitivity of shape complexity which means that non-gradient methods like EA have to be applied. Another complex problem formulation with a lack of sensitivity information was presented by Guirguis and Aly [23] who involve implicit structure representations using level-set methods [24] together with objectives close to application, e.g., the welding effort.

1.2.2 Stresses

Since the early investigations on minimum compliance problems via TO, additional stresses were considered due to finite material properties. Yang and Chen [25] performed a basic study of stress constraints in TO with minimum compliance by means of the SIMP method. Particular challenges were identified as, first, the highly non-linear behavior of stress constraints with respect to the design variables and, second, the inherently high number of constraints as stresses are a local quantity. The first could be counteracted by a small move limit within the optimization process. The latter was relaxed by a global maximum stress function in form of the Kreisselmeier–Steinhauser function [26] and the p-norm function. Due to this continuous form, the maximum stress is always slightly underestimated and has to be renormalized [27, 28]. Duysinx and Bendsøe [29] described singularities occurring with stress-based constraints and zero element densities. They proposed the continuation method with a stepwise reduction of the minimum quasi-zero density in form of a sufficiently small positive value. Le et al. [28] proposed a method for local stress control to counteract insufficient results by a global maximum stress function. TO was carried out by minimizing a p-norm formulation of structural stresses. More general structural representations regarding stress constraints were investigated in terms of level-set methods [30, 31]. Stresses were considered in the TO literature as constraints or as objective functions [32].

For benchmark artifacts which characterize critical mechanical properties of a manufactured reference part, specific target stress states need to be reproduced by the specimen topology for a proper quality assessment. Target stress states are seen as pre-defined states the benchmark artifact has to incorporate. To the best of the authors’ knowledge, target stress states, however, have not yet been investigated with TO.

1.3 Objective and concept of this study

The main objective of the presented study is to give an essential contribution to establish TO with target stress states. It provides the basis for further investigations on generating benchmark artifacts for the quality assessment of additively manufactured components with multiple pre-defined stresses and realistic non-trivial topologies.

Therefore, a new method is introduced which is able to generate a benchmark artifact in the form of a structure reproducing arbitrary pre-defined stresses, i.e., target stress states, under a sufficiently simple loading condition, e.g., a uniaxial tensile state. This paper gives insight into a minimal formulation of the TO problem in order to demonstrate a viable set of constraints and objective functions for a plausible reference solution. Both structural volume and the error of target stress state are minimized by evolutionary algorithms in a multi-objective formulation. Furthermore, solutions of non-trivial target stress states close to application are discussed.

This paper is structured as follows: In order to demonstrate the behavior of the proposed method, an initial basic approach is investigated in Sect.  2 and problem adaptations are derived to improve the TO solution (Sect.  3). These adaptations are used for different, non-trivial target stress states which are close to application (Sect. 4). Afterward comparisons with gradient-type optimization algorithms are made for an appropriate assessment of the current approach in Sect. 5. Finally, results and implications for further investigations are discussed (Sect. 6). All symbols used throughout this paper are summarized in Table 1.

Table 1 Symbols introduced within this paper
Full size table

2 Basic approach

2.1 Problem formulation

It is generally possible to derive key requirements for a benchmark artifact in form of a test specimen described in Sect. 1.1:

  1. (1)

    Manufacturing and testing effort are reduced if there is a single, integral specimen.

  2. (2)

    Results of the specimen tests have to represent critical quality measures of the additively manufactured reference part. The quality measures are formulated as critical stresses which occur in the reference part and hence must similarly be present in the specimen.

  3. (3)

    The specimen volume must be minimum for low material and manufacturing cost.

In the following, these requirements are transferred to a general multi-objective formulation of the optimization problem

$${\text{minimize}}\,\, {\varvec{f}}\left({\varvec{c}}\right) \text{subject to}\,\, {\varvec{g}}\left({\varvec{c}}\right)\le 0\text{,}$$
(1)

where \({\varvec{f}}\left({\varvec{c}}\right)={\left({f}_{1}\left({\varvec{c}}\right),{f}_{2}\left({\varvec{c}}\right)\right)}^{\mathrm{T}}\in {\mathbb{R}}^{2}\) and \({\varvec{g}}\left({\varvec{c}}\right)={\left({g}_{1}\left({\varvec{c}}\right),{g}_{2}\left({\varvec{c}}\right),\dots ,{g}_{m}\left({\varvec{c}}\right)\right)}^{\mathrm{T}}\in {\mathbb{R}}^{m}\) are objective and constraint vectors, respectively. Vector \({\varvec{c}}={\left({c}_{1},{c}_{2},\dots ,{c}_{n}\right)}^{\mathrm{T}}\in {\mathbb{R}}^{n}\) represents the design variables.

According to requirements (2) and (3), the objective functions are the relative structural volume

$${f}_{1}\left({\varvec{c}}\right)=V\left({\varvec{c}}\right)=\frac{{\int }_{\Omega }\rho ({\varvec{x}},{\varvec{c}})d{\varvec{x}}}{{\int }_{\Omega }d{\varvec{x}}}$$
(2)

and the error of stress state

$${f}_{2}\left({\varvec{c}}\right)=\Delta \sigma \left({\varvec{c}}\right)=\underset{{\varvec{x}}\in {\Omega }_{\mathit{TSS}}}{\mathrm{max}}\Vert {{\varvec{\sigma}}}_{a}\left({\varvec{x}},{\varvec{c}}\right)-{{\varvec{\sigma}}}_{0}({\varvec{x}})\Vert \text{,}$$
(3)

respectively. Here \(\rho\) stands for the structural density in TO which scales proportionally with material stiffness \(E\) and determines the material distribution [12]. A density of \(\rho =1\) indicates the full presence of material with the full stiffness \({E}_{0}\) while \(\rho =0\) stands for the absence of material. Intermediate values can be interpreted as porous material or, in 2D, as linearly scaled material thicknesses, both with the intermediate stiffness \(E=\rho {E}_{0}\) [11, 33]. The value \(\Omega\) represents the structural domain with spatial coordinates \({\varvec{x}}\), \({{\varvec{\sigma}}}_{a}\) the actual stress state, and \({{\varvec{\sigma}}}_{0}\) the pre-defined target stress state (TSS). The expression \(\Vert \cdot \Vert\) specifies the Euclidean vector norm. In the basic approach, constraints are only set for structural failure: The structural area with the TSS has to be the critical quality measure in the benchmark artifact and hence must fail first. That is why this TSS should ensure the least factor of safety (FoS) \(S\):

$${g}_{1}\left({\varvec{c}}\right)=\underset{{\varvec{x}}\in {\Omega }_{\mathit{TSS}}}{\mathrm{max}}S\left({\varvec{x}},{\varvec{c}}\right)-\underset{{\varvec{x}}\in\Omega \backslash {\Omega }_{\mathit{TSS}}}{\mathrm{min}}S\left({\varvec{x}},{\varvec{c}}\right)\le 0\text{.}$$
(4)

The quantity \({\Omega }_{\mathit{TSS}}\) describes the area of the TSS, while \(\Omega \backslash {\Omega }_{TSS}\) stands for the entire structural domain except the TSS area (cf. Fig. 1a).

Fig. 1
figure 1

Domain \(\Omega\) with area \({\Omega }_{TSS}\) of target stress state \({{\varvec{\sigma}}}_{0}\) and neighborhood \({\Omega }_{N}\): a general shape, b grid shape specific to basic approach with width \({l}_{x}\) and length \({l}_{y}\). Definition of general stress state \({\varvec{\sigma}}\)

Full size image

2.1.1 Specific problem and reference solution

Based on the general problem, a specific formulation is proposed in form of a simple two-dimensional, gridded structural domain \(\Omega\) (cf. Fig. 1b). It is quadratic, and evenly divided in a ground element grid with 11 × 11 elements. The element densities \({\rho }_{i}\) serve as design variables \({\varvec{c}}=\left({\rho }_{i}\right)\) with \(0<{\rho }_{\mathrm{min}}\le {\rho }_{i}\le 1\) and \(i=1,\dots ,{n}_{e}\). The number of elements and thus the number of design variables is \({n}_{e}=121\). A minimum density \({\rho }_{\mathrm{min}}\) is required to avoid the singularity problem observed for stress-related TO problems [29]. Each element thickness \({t}_{i}\) is calculated via its density \({\rho }_{i}\):

$${t}_{i}={{t}_{0}}{{\rho }_{i}}$$
(5)

for the element indices \(i=1,\dots ,{n}_{e}\). There is a main element (ME) at the structural midpoint representing \({\Omega }_{TSS}\). The neighbor elements (NE) are defined as all eight elements surrounding the ME.

Due to the structural discretization, the objective function values are calculated according to Eqs. (2) and (3) as

$${f}_{1}\left({\varvec{c}}\right)=V=\frac{\sum_{i}{\rho }_{i}}{{n}_{e}}$$
(6)

and

$${f}_{2}\left({\varvec{c}}\right)=\Delta \sigma =\Vert {{\varvec{\sigma}}}_{a,ME}\left({\varvec{c}}\right)-{{\varvec{\sigma}}}_{0}\Vert \text{,}$$
(7)

where \({{\varvec{\sigma}}}_{a,ME}\) represents the actual stress state in the ME. In two dimensions, all stress states are defined coordinate-wise as \({\varvec{\sigma}}={\left({\sigma }_{xx},{\sigma }_{yy},{\tau }_{xy}\right)}^{\mathrm{T}}\). The constraint \({g}_{1}\) has the specific form

$${g}_{1}\left({\varvec{c}}\right)={S}_{ME}\left({\varvec{c}}\right)-\underset{i\in\Omega \backslash {\Omega }_{\mathit{TSS}}}{\mathrm{min}}{S}_{i}\left({\varvec{c}}\right)\le 0 \text{,}$$
(8)

where \({S}_{ME}\) is the FoS in the ME and \({S}_{i}\) with \(i\in\Omega \backslash {\Omega }_{TSS}\) describe the FoS of all elements except the ME. The problem formulation only with constraint \({g}_{1}\) is defined as the basic approach A as it includes the basic formulation of the objectives and a minimal set of constraints.

The specific problem incorporates a simple testing load in form of a uniaxial tensile force distributed over the upper boundary. At the lower boundary, the nodal \(y\) displacement is set to zero. One node at the lower boundary is additionally fixed in \(x\) direction so that no rigid body motion is possible. If all densities \({\rho }_{i}\) are equal, the boundary conditions permit a pure tensile state throughout the structural domain. For the present study, width and height of the structural domain \(\Omega\) are set to \({l}_{x}=100 \,{\text{mm}}\) and \({l}_{y}=100 \,{\text{mm}}\) with a reference element thickness of \({t}_{0}=1 \,{\text{mm}}\). The minimum density is set to \({\rho }_{\mathrm{min}}={10}^{-2}\). The tensile force at the upper boundary is \({F}_{y}=1 \,{\text{kN}}\) and the TSS is set to the trivial form \({{\varvec{\sigma}}}_{0}={\left(0, 50, 0\right)}^{\mathrm{T}} \,{\text{MPa}}\).

The advantage of the proposed specific formulation of the optimization problem is that there is an analytically derivable reference solution (RS): For both objective functions \({f}_{1}\) and \({f}_{2}\) as well as the constraint \({g}_{1}\), an even density distribution \(\rho \left({\varvec{x}}\right)\equiv {\rho }_{RS}={f}_{1}\) is expected. On the one hand, it is suboptimal for the ME to get lighter than the other elements because the stresses increase and thus the FoS becomes overly low. The other elements prefer getting lighter too. On the other hand, it is not possible for the ME to get denser without keeping the FoS less than that of the other elements. An actual tensile stress state for the RS of \({{\varvec{\sigma}}}_{a}={\left(0,{F}_{y}/\left({\rho }_{RS}{t}_{0}{l}_{x}\right),0\right)}^{\mathrm{T}}\) can be calculated. The reference Pareto front results in the form

$${f}_{2,\mathrm{ref}}\left({f}_{1}\right)=\frac{{F}_{y}}{{f}_{1}{t}_{0}{l}_{x}}-{\sigma }_{0,yy}$$
(9)

with \({\rho }_{\mathrm{min}}\le {f}_{1}\le {f}_{1,\mathrm{ref},\mathrm{max}}\). Densities of the RS are limited because

$${f}_{1}\left({f}_{2,\mathrm{ref}}=0\right)={f}_{1,\mathrm{ref},\mathrm{max}}=\frac{{F}_{y}}{{\sigma }_{0,yy}{t}_{0}{l}_{x}}$$
(10)

according to Eq. (9). The upper limit of the relative structural volume has the value \({f}_{1,\mathrm{ref},\mathrm{max}}=0.2\). There is a theoretical maximum error of stress state of \({f}_{2,\mathrm{ref},\mathrm{max}}=950 \,{\text{MPa}}\) in the case that all element densities are the minimum \({\rho }_{\mathrm{min}}\). Table 2 lists all relevant parameters for the basic problem formulation.

Table 2 Parameter values of the basic topology optimization approach with a target stress state
Full size table

2.2 Optimization method

2.2.1 Evolutionary algorithms and GEOpS2

Gradient-based TO methods like SIMP have been used extensively for stress-based problems [25, 27,28,29,30, 34, 35]. Gradient information can be efficiently involved via analytically derived sensitivity information. Nevertheless, original forms of the constraints, e.g., in Eq. (8) can be directly handled via EA. That means that the direct, local form of stress-based optimization can be applied. Gradient-based TO methods only use global [25, 29] or regional [28] approximations for stress evaluation in order to reduce the calculation effort for sensitivity analysis which is not necessary in the present approach. In this study, several modifications of the basic problem are investigated. Results are readily compared and a better understanding is achieved due to the direct approach of EA. Moreover, EA permit a broader perspective of e.g., expanding the number of objective functions, the type of design variables, and non-linear, anisotropic material models with defects due to additive manufacturing. Therefore, it is believed that EA are more appropriate throughout this study for establishing TO with pre-defined target stress states by means of simple examples.

Multi-objective optimization was carried out on Eq. (1) by means of GEOpS2 [36], a robust in-house optimization tool based on EA, which already has been successfully applied to complex optimization problems [37, 38].

Optimization runs involved 200 parent individuals with 420 children in a population. GEOpS2 uses genetic algorithms, evolution strategies, the Montecarlo method, and differential evolution for children generation. Table 3 shows the parameters involved with children generation. Selection was achieved by means of the NSGA-II algorithm [39] with only children involved.

Table 3 Methods and parameter values for children generation
Full size table

Optimization stopped if 50,000 generations were calculated or the objective function values did not change less than 10−6 during 5000 generations. A total of five identical optimization runs were performed for a single configuration to cover statistical variations in the results.

2.2.2 Constraints

Constraints \({\varvec{g}}\) were applied by a simple one-step penalty method. For a better compatibility with results from gradient-type optimization methods, penalized objective functions \({{\varvec{f}}}_{\mathrm{pen}}({\varvec{c}})\) remained continuous and differentiable via

$${f}_{\mathrm{pen},i}\left({\varvec{c}}\right)={f}_{i}\left({\varvec{c}}\right)\cdot \prod_{j=1}^{m}\left(1+q{g}_{\mathrm{pen},j}^{2}\left({\varvec{c}}\right)\right)$$
(11)

with \(i=1,\dots ,n\) and

$${g}_{\mathrm{pen},j}\left({\varvec{c}}\right)=\left\{\begin{array}{l}0\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,{\text{for}}\,\, {g}_{j}\left({\varvec{c}}\right)\le 0\text{,}\\ {g}_{j}\left({\varvec{c}}\right)\,\,\, {\text{for}} \,\,{g}_{j}\left({\varvec{c}}\right)>0\text{.}\end{array}\right.$$
(12)

The parameter \(q\) is a penalty factor set to \(q={10}^{8}\). Penalization by means of Eq. (11) is carried out with non-dimensional values of \({g}_{\mathrm{pen},j}\) in order to avoid unit problems.

2.2.3 Finite element analysis

The objective function values in Eqs. (6) and (7) as well as the constraint in Eq. (8) were evaluated by structural analysis. For this purpose, the in-house finite element (FE) solver FiPPS2 was used. FE analysis involved linear deformations and quadratic 8-node shell elements. Element densities \({\rho }_{i}\) were varied via shell thickness while material properties internally stayed constant.

Stresses for the formulation of \({f}_{2}\) arose from element integration points and were averaged over the element. In order to analyze the FoS of each element for \({g}_{1}\), the von Mises stress \({\sigma }_{M}\) was compared without loss of generality to the yield strength of aluminum \({\sigma }_{Y}=270 \,{\text{MPa}}\) by means of

$${S}_{i}=\frac{{\sigma }_{Y}}{{\sigma }_{M,i}}=\frac{{\sigma }_{Y}}{\sqrt{{\sigma }_{xx,i}^{2}+{\sigma }_{yy,i}^{2}-{\sigma }_{xx,i}{\sigma }_{yy,i}+3{\tau }_{xy,i}^{2}}}$$
(13)

with the element index \(i=1,\dots ,n_e\).

2.2.4 Evaluation of optimization results

All Pareto-optimal results of the multi-objective optimization were combined to the Pareto front. Based on an arbitrary reference point in \(({f}_{1},{f}_{2})\) space, the hypervolume indicator (HVI) [20, 21] in the relative form

$$HVI=\frac{1}{{f}_{\mathrm{1,0}}\,{f}_{\mathrm{2,0}}}\sum_{k=1}^{{n}_{P}}\left({f}_{\mathrm{1,0}}-{f}_{1,k}\right)\left({f}_{2,k-1}-{f}_{2,k}\right)$$
(14)

served as a comparative performance measure. The quantity \({{\varvec{f}}}_{k}={\left({f}_{1,k},{f}_{2,k}\right)}^{\mathrm{T}}\) for \(k=1,\dots ,{n}_{P}\) with the number \({n}_{P}\) of parent individuals stands for the \(k\)-th point in the minimization Pareto front ordered by ascending \({f}_{1}\) and descending \({f}_{2}\). The reference point \({{\varvec{f}}}_{0}={\left({f}_{\mathrm{1,0}},{f}_{\mathrm{2,0}}\right)}^{\mathrm{T}}\) was set to \({{\varvec{f}}}_{0}={\left(1, 950 \,{\text{MPa}}\right)}^{\mathrm{T}}\). Values of \({\varvec{f}}\) greater than the reference point \({{\varvec{f}}}_{0}\) were not included in Eq. (14). The RS exhibits an HVI of about 0.968. This value was calculated numerically by means of \({n}_{P}=200\) data points evenly distributed over the interval \({f}_{1}\in [{\rho }_{\mathrm{min}},0.2]\).

Moreover, the generational distance (GD) [20] in the relative form

$$GD=\frac{1}{{n}_{P}}\sum_{k=1}^{{n}_{P}}\Delta {f}_{\mathrm{min},k}$$
(15)

with

$$\Delta {f}_{\mathrm{min},k}=\left\{\begin{array}{l}\frac{{f}_{2,k}-{f}_{2,\mathrm{ref}}\left({f}_{1,k}\right)}{{f}_{\mathrm{2,0}}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for}} \,\,{f}_{1,k}\le {f}_{1,\mathrm{ref},\mathrm{max}}\text{,}\\ \sqrt{{\left(\frac{{f}_{1,k}-{f}_{1,\mathrm{ref},\mathrm{max}}}{{f}_{\mathrm{1,0}}}\right)}^{2}+{\left(\frac{{f}_{2,k}}{{f}_{\mathrm{2,0}}}\right)}^{2}} \,\,\,\,\,\,\,\,{\text{for}}\,\, {f}_{1,k}>{f}_{1,\mathrm{ref},\mathrm{max}}\end{array}\right.$$
(16)

was used to quantify deviations from the RS in Eq. (9). Convergence was assessed by means of the histories of minimum objective values over optimization generations.

2.2.5 Workflow

The optimization method involves an optimization model based on the formulation generally described in Sect. 2.1 and the optimizer GEOpS2. Objective values and constraints depend on the results of the structural analysis with FiPPS2, which is carried out in each objective function call. Optimization results were finally evaluated regarding the Pareto front, histories of minimum objective function values, HVI, GD, and the element density distribution of the structural individuals. Figure 2 gives an overview of the workflow of the proposed optimization method. More details about the optimization model routine and its interfaces to GEOpS2 and FiPPS2 are depicted in Fig. 3.

Fig. 2
figure 2

Proposed optimization method: optimizer GEOpS2 carries out the numerical topology optimization. The optimization model interacts with finite element solver FiPPS2 and generates objective function values \({\varvec{f}}\). Stopping criteria are checked after each generation

Full size image
Fig. 3
figure 3

Workflow of the optimization model. Bold arrows at the top and the bottom represent the interface with the overall optimization process

Full size image

2.3 Optimization results

Figure 4 shows the optimization results of the basic approach A according to the specific formulation. The Pareto front apparently cannot reach the RS. The history of both objective function values is displayed in Fig. 5. The values apparently decrease even for a high number of generations. Thus, the convergence behavior of the optimization appears to be limited.

Fig. 4
figure 4

Pareto fronts of the basic approach A after 50,000 generations. Five identical optimization results (opt.) are displayed versus the reference solution (ref.)

Full size image
Fig.5
figure 5

History of the minimum objective function values of the basic approach A

Full size image

Although low errors of the stress state \(\Delta \sigma <{10}^{-4} \,{\text{MPa}}\) are achieved for values of about \(V=0.3\dots 0.4\) (cf. Fig. 4), there are nearly random element densities \({\rho }_{i}\) for all individuals as shown in Fig. 6. The individual with the largest \(V\) exhibits densities of up to \({\rho }_{i}=0.540\). Due to the constraint \({g}_{1}\), the ME has a small density \({\rho }_{i}\) for all individuals which facilitates the largest FoS in this element.

Fig. 6
figure 6

Typical structural solutions of the basic approach A: a Low relative structural volume \(V=0.0695\) and high error of stress state \(\Delta \sigma =195.6 \,{\text{MPa}}\) (optimization 2). b Intermediate \(V=0.1811\) and \(\Delta \sigma =21.6 \,{\text{MPa}}\) (optimization 3). c High \(V=0.292\) and low \(\Delta \sigma =3.75\cdot {10}^{-5} \,{\text{MPa}}\) (optimization 1)

Full size image

The highest HVI is 0.921 (optimization 2) compared to 0.968 of the RS (cf. Fig. 7) while the least GD reaches a value of 0.0321 (optimization 1). It is noticeable that the GD does not decrease monotonously over the optimization process. Especially optimization 2 exhibits a considerable peak at around generation 29,000. This can be ascribed to the optimization method which finds new Pareto-optimal individuals with the lowest relative structural volume but a relatively high error of stress state. Consequently, the GD increases while a new least objective function value has been found (cf. Fig. 5, upper part).

Fig. 7
figure 7

History of the hypervolume indicator (HVI) and the generational distance (GD) of the basic approach A

Full size image

3 Adapted approach

Since the basic approach A cannot produce results which resemble the RS, further modifications have to be included. An adapted approach is presented in this section in which constraints \({\varvec{g}}\), the formulation of objective functions \({\varvec{f}}\), and the design space \({\varvec{c}}\) are extended. Table 4 gives an overview of all single modifications that are presented in the following sections.

Table 4 Overview of modifications in the adapted approach
Full size table

3.1 Modified constraints

A promising possibility to enhance the convergence behavior of the optimization is to relax the active constraints. This can be done by searching the minimum FoS not only in the TSS domain \({\Omega }_{TSS}\) but also in its neighborhood \({\Omega }_{N}\) represented by the NE. Hence, the constraint in a modification B can be stated as

$${g}_{1,B}=\underset{{\Omega }_{\mathit{TSS}}\cup {\Omega }_{N}}{\mathrm{max}}S\left({\varvec{c}}\right)-\underset{\Omega \backslash \left({\Omega }_{\mathit{TSS}}\cup {\Omega }_{N}\right)}{\mathrm{min}}S\left({\varvec{c}}\right)\text{.}$$
(17)

In order to ensure a valid stress state and to avoid numerical dependencies, the stresses in the ME and its NE have to be as even as possible. That is why the modification C is introduced which limit the standard deviation of the actual stress states \({{\varvec{\sigma}}}_{a}\) of the ME and its NE. An additional constraint is given for the elements in \({\Omega }_{TSS}\cup {\Omega }_{N}\) by

$${g}_{2,C}=\sqrt{\frac{1}{{n}_{e,N}}{\sum }_{k=1}^{{n}_{e,N}}{\Vert {{\varvec{\sigma}}}_{a,k}-{{\varvec{\sigma}}}_{a,ME}\Vert }^{2}}-{\sigma }_{\varepsilon ,\mathrm{lim}}$$
(18)

with \({n}_{e,N}\) as the number of elements including ME and NE, \({{\varvec{\sigma}}}_{a,k}\) as the actual stress state in element \(k\), and \({{\varvec{\sigma}}}_{a,ME}\) as the actual stress state of the ME. In the following, the limit is set to \({\sigma }_{\varepsilon ,\mathrm{lim}}=5 \,{\text{MPa}}\).

3.1.1 Optimization results

Figure 8 shows the Pareto fronts of all optimizations with modifications B and C. Compared to the basic approach A (cf. Fig. 4), only structural individuals with high relative volumes of greater than \(V=0.2\) are generated. Single individuals reach very low errors of stress state \(\Delta \sigma\) in both modifications. Lower HVI and higher GD than in the basic approach indicate a hampering influence of the additional constraints (cf. Table 5).

Fig. 8
figure 8

Pareto fronts of modifications B and C after 50,000 generations. Five identical optimization results are displayed versus the reference solution

Full size image
Table 5 Minimum objective function values, hypervolume indicator (HVI), and generational distance (GD) for the basic approach A and modifications B, and C after 50,000 generations
Full size table

Modification B exhibits larger variations between each optimization run. The structural solution with the least error of stress state \(\Delta \sigma\) is illustrated in Fig. 9a. The central area of the ME and its NE is dominated by low-density elements. The overall density distribution appears to be more even and to have higher values than in the basic approach.

Fig. 9
figure 9

Structural solutions with least errors of stress state: a Modification B, \(V=0.424\), \(\Delta \sigma =3.32\cdot {10}^{-8} \,{\text{MPa}}\) (optimization 1). b Modification C, \(V=0.303\), \(\Delta \sigma =5.88\cdot {10}^{-7} \,{\text{MPa}}\) (optimization 4)

Full size image

The additional constraint in modification C apparently leads to elements with nearly equal densities in the ME with neighbors (cf. Fig. 9b). The outer structure has in return a distribution with a density range larger than the basic approach.

3.2 Modified objective functions

Another way to enhance the optimization results is modifying the basic formulation of the objective functions. Only the objective function \({f}_{2}\) is changed in a way so that the error of stress state is assessed slightly differently. It is intended that optimization results are fully comparable to the basic approach and effectively no new optimization problem was formulated. In modification D, both domains \({\Omega }_{TSS}\) and \({\Omega }_{N}\) are included into calculating \(\Delta \sigma\) by the averaged p2-norm

$${f}_{2,D}\left({\varvec{c}}\right)=\Delta \sigma =\sqrt{\frac{1}{{n}_{e,N}}{\sum }_{k=1}^{{n}_{e,N}}{\Vert {{\varvec{\sigma}}}_{a,k}\left({\varvec{c}}\right)-{{\varvec{\sigma}}}_{0}\Vert }^{2}}\text{.}$$
(19)

3.2.1 Optimization results

Figure 10 presents the Pareto fronts of all optimization runs for modification D. Individuals are achieved with low relative volume \(V\) similar to the basic approach. Least errors of stress state \(\Delta \sigma\) stay significantly higher. Resulting individuals of modification D with the least error of stress state \(\Delta \sigma\) are shown in Fig. 11a. The Pareto fronts of modification D resemble the RS better than modifications B and C (cf. Fig. 8). Solutions with lower \(\Delta \sigma\) tend to values of \(V\) less than in modifications B and C but still greater than the expected minimum at \(V=0.2\). There are individuals which outperform the Pareto front of the RS, which appears generally implausible in light of the derivation in Sect. 2.1 and indicates that the modified objective function \({f}_{2}\) is not fully equivalent to the basic formulation. To this effect, appendix A gives a more detailed explanation.

Fig.10
figure 10

Pareto fronts of modification D after 50,000 generations. Five identical optimization results are displayed versus the reference solution

Full size image
Fig. 11
figure 11

Structural solutions with least errors of stress state: a Modification D, \(V=0.268\), \(\Delta \sigma =0.493 \,{\text{MPa}}\) (optimization 3). b Modification C + E, \(V=0.208\), \(\Delta \sigma =1.668\cdot {10}^{-4} \,{\text{MPa}}\) (optimization 2). c Modification C + D + E, \(V=0.1993\), \(\Delta \sigma =0.253 \,{\text{MPa}}\) (optimization 2)

Full size image

It is believed that implausible solutions in modification D are highly grid-dependent and will not play an important role when further refining the structural representation of the benchmark artifact (cf. appendix A).

3.3 Modified design space

Modification E extends the design space by a scaling factor \({w}_{\rho }\in \left[{10}^{-2},{10}^{2}\right]\) which acts on all given densities \({\rho }_{i}\). That means that the new design space has one more design variable than the original one. This approach is supposed to generate more structural solutions close to the RS.

This modification involves density healing by writing density values back to the domain limits \([{\rho }_{\mathrm{min}},1]\) if they were violated.

3.3.1 Optimization results

Modification E achieves very good approximations of the RS, indicated by a high HVI close to the reference value of 0.968 (cf. Table 6). Objective function values decrease with a high convergence rate as shown in Fig. 12 exemplarily. This modification is the only one that did not exploit the maximum number of 50,000 generations, but converged earlier. Thus, low values for \({f}_{1}\) and \({f}_{2}\) have been obtained.

Table 6 Minimum objective function values, hypervolume indicator (HVI), and generational distance (GD) for the modifications D, E, C + E, and C + D + E after 50,000 generations
Full size table
Fig. 12
figure 12

History of the minimum objective function values of modification E

Full size image

3.4 Combined modifications

Despite high variations in the least values of \({f}_{1}\) and \({f}_{2}\) for all optimization runs, the reference Pareto front is met very well for the combinations C + E and C + D + E (cf. Fig. 13). The combined modifications C + E achieved the analytic minimum of \(\Delta \sigma\) at \(V=0.2\) with low deviations in \(V\). The additional modification D seems to reduce the variation of feasible solutions since the Pareto fronts are considerably narrower as shown in Fig. 10b. Thus, higher minimum objective values \({f}_{1}\) and \({f}_{2}\) are obtained (cf. Table 6). Due to larger deviations of \(V\) close to the minimum \(\Delta \sigma\) at \(V=0.2\), the GD values are more scattered with a high standard deviation. Figure 11b and c prove that the expected structural RS could be achieved very well in both combinations.

Fig. 13
figure 13

Pareto fronts of modifications C + E and C + D + E after 50,000 generations. Five identical optimization results are displayed versus the reference solution

Full size image

4 Problem formulation close to application

While Sects. 2 and 3 described a problem formulation with a trivial pre-defined tensile TSS, this section uses stress states different from the global tensile loading of the benchmark artifact. This step generalizes the purpose of the artifact to reproduce arbitrary pre-defined stresses under a common testing load.

4.1 Adaptations to the problem formulation

Compressive stress \({{\varvec{\sigma}}}_{0}={\left(-50, 0, 0\right)}^{\mathrm{T}} \,{\text{MPa}}\) and shear stress \({{\varvec{\sigma}}}_{0}={\left(0, 0, 50\right)}^{\mathrm{T}} \,{\text{MPa}}\) are now considered as non-trivial pre-defined TSS. All \(y\) displacements of the nodes at the upper boundary of the FE model are now coupled in order to achieve a uniform boundary condition especially for asymmetric solutions. Specimen areas with zero density are expected so that stress relaxation is necessary to avoid stress singularities [28, 29]. Therefore, minimum density is set to \({\rho }_{\mathrm{min}}={10}^{-6}\) and element stresses and FoS are not considered for densities lower than a limit \({\rho }_{\mathrm{lim}}={10}^{-2}\). Other parameters for optimization remain the same as in the basic approach.

4.2 Expected topologies

In contrast to the trivial tensile TSS in Sects. 2 and 3, there is no exact reference solution for the TSS considered in this section. Only plausible expected topologies can be assumed as shown in Fig. 14. Besides the minimum objective function values achieved, expected topologies are used for a qualitative validation of the optimization results.

Fig. 14
figure 14

Expected topologies for non-trivial target stress states (highlighted): a Compressive target stress. b Shear target stress

Full size image

4.3 Optimization results

Figure 15 illustrates results with non-trivial TSS for the basic approach A. While there is no clear topology for the optimization solutions with compressive TSS (cf. Fig. 15a), shear TSS form a plausible topology on grid-level rudimentarily. It is expected that this solution highly depends on the element grid resolution.

Fig. 15
figure 15

Structural solutions with least errors of stress state for basic approach A: a Compressive target stress, \(V=0.382\), \(\Delta \sigma =5.66\cdot {10}^{-3} \,{\text{MPa}}\) (optimization 2). b Shear target stress, \(V=0.233\), \(\Delta \sigma =0.01391 \,{\text{MPa}}\) (optimization 2)

Full size image

The combined modification C + E yielded results for the trivial tensile TSS closest to the reference solution. So it was identified as most efficient in that case. It is depicted in Fig. 16, that modification C + E also leads to optimization solutions for non-trivial TSS that resemble the expected topologies in large part. However, solutions do not seem to be generated robustly as it also produces solutions with a density distribution close to a uniform plate (cf. Fig. 16a). Furthermore, errors of stress state are noticeably high with values of up to \(\Delta \sigma =47.7 \,{\text{MPa}}\). Table 7 reveals that the main stress component of the target stress is principally achieved—even though on a considerably lower level. The main part of the errors may be ascribed to the large tensile component still present.

Fig. 16
figure 16

Structural solutions with least errors of stress state for modification C + E, which was most efficient for the tensile target stress state: a Compressive target stress, \(V=0.899\), \(\Delta \sigma =45.9 \,{\text{MPa}}\) (optimization 1). b Compressive target stress, solution with plausible topology, \(V=0.610\), \(\Delta \sigma =47.7 \,{\text{MPa}}\) (optimization 3). c Shear target stress, \(V=0.623\), \(\Delta \sigma =44.4 \,{\text{MPa}}\) (optimization 3)

Full size image
Table 7 Minimum objective function values, according actual stress states of the main element, and hypervolume indicator (HVI) for the basic approach A and modifications C + E and C + D + E with non-trivial target stress states after 50,000 generations
Full size table

The combined modification in the form C + D + E was identified to yield more stable optimization results while featuring a slightly different formulation of the objective function (cf. Eq. (19)). Topologies are closer to the expected solutions in Fig. 14 than with the combined modification C + E (cf. Fig. 17). Topologies with compressive TSS exhibit again high errors of larger than \(\Delta \sigma =49.8 \,{\text{MPa}}\) as shown in Table 7. In contrast, shear TSS can be achieved particularly better.

Fig. 17
figure 17

Structural solutions with least errors of stress state for modification C + D + E: a Compressive target stress, \(V=0.736\), \(\Delta \sigma =49.9 \,{\text{MPa}}\) (optimization 3). b Shear target stress, \(V=0.396\), \(\Delta \sigma =16.10 \,{\text{MPa}}\) (optimization 2)

Full size image

Minimum objective function values together with the HVI are summarized in Table 7. For compressive TSS, combination C + D + E has minimum values for \({f}_{1}\) higher than combination C + E. This partially confirms results from trivial tensile TSS in Sect. 3.4that modification D reduces the variation of optimization results (cf. Fig. 13). In contrast, modification D has a positive effect on minimum objective values \({f}_{2}\) for shear TSS, as already seen in the actual stress state of the main element.

Histories of minimum objective function values \({f}_{1}\) and \({f}_{2}\) for non-trivial TSS and the combined modification C + D + E are shown in Fig. 18. Minimum \({f}_{1}\) exhibits very small decreases for high generation numbers with both TSS. Also minimum \({f}_{2}\) retains nearly the same value. Shear TSS facilitate a constant decrease in minimum \({f}_{2}\) thus constantly improving the error of stress state \(\Delta \sigma\). It is clear that no convergence is achieved especially for optimization runs 2, 3, and 5 (cf. Fig. 18b, bottom).

Fig. 18
figure 18

History of the minimum objective function values for non-trivial target stress states with modification C + D + E: a Compressive target stresses. b Shear target stresses

Full size image

5 Comparison with gradient methods

5.1 Gradient-type optimization approach

In this section, gradient-type algorithms are applied to the optimization problem formulated in Eq. (1). Non-trivial TSS from Sect. 4 are considered. Results are compared to the respective optimization with EA. Optimizations investigated for the following comparison of EA and gradient-type algorithms include the basic formulation (A) and basically those modifications that generated plausible results in Sect. 4. Modification E with a global density scaling factor \({w}_{\rho }\) represents a mechanism to change element densities simultaneously. It appears to be helpful especially for EA as a heuristic optimization method with stochastic differential element density changes. It is believed that simultaneous, directional density changes are inherent to gradient-based optimization methods and a scaling factor \({w}_{\rho }\) is not necessary for comparison.

5.1.1 Adapted optimization problem

All applied optimization algorithms only permit a single objective function \({f}_{SO}\). Therefore, both objective functions \({f}_{1}\) and \({f}_{2}\) from multi-objective optimization are combined to

$${f}_{SO}={w}_{1}{f}_{1}+{w}_{2}{f}_{2}$$
(20)

with the weighting factors \({w}_{1}=10\) and \({w}_{2}=1\). Units are neglected for evaluating \({f}_{SO}\). Constraints are penalized by means of a six-step penalty method according to the basic formulation as in Eq. (11) with a sequence of \(q\in \left\{{\mathrm{1,10,10}}^{2},{10}^{3},{10}^{4},{10}^{8}\right\}\).

Gradient-based optimization runs start from uniform initial element density distribution with \(V=0.1\). These density distributions do not necessarily fulfill all optimization constraints at the beginning. In order to exhibit a non-zero gradient information at every point of the design space, the discontinuous minimum function in Eq. (8) is replaced by the continuous Kreisselmeier–Steinhauser function [25, 26]

$$\mathrm{min}\,{S}_{i}\left({\varvec{c}}\right) \to -\frac{1}{r}\mathrm{ln}{\sum }_{i}\mathrm{exp}\left(-r{S}_{i}\left({\varvec{c}}\right)\right)$$
(21)

with \(r=10\).

FoS for low element densities are penalized via

$${S}_{i,\mathrm{pen}}\left({\rho }_{i}\right)=\left\{\begin{array}{l}{S}_{i}\left({\rho }_{i}\right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,{\text{for}}\,\,\, {\rho }_{i}\ge {\rho }_{\mathrm{lim}}\text{,}\\ {S}_{i}\left({\rho }_{i}\right)+q{\left({\rho }_{\mathrm{lim}}-{\rho }_{i}\right)}^{2} \,\,\,{\text{for}}\,\,\, {\rho }_{i}<{\rho }_{\mathrm{lim}}\text{.}\end{array}\right.$$
(22)

as a continuous and differentiable form of stress relaxation [28, 29]. Index \(i\) represents the considered elements. The penalty factor \(q\) is set to \(q={10}^{5}\). Equation (22) has the purpose to discard the FoS of elements with very low densities through high penalization. With that, these elements are not wrongly critical for the constraint in Eq. (8).

5.1.2 Optimization algorithms

The optimization library NLopt [40] offers a wide variety of algorithms from which four gradient-based ones are selected: LBFGS [41], MMA [13], SLSQP [42], and TNewton [43]. The optimization model subroutine is designed in a way that different optimizers can be connected easily. For the investigations in this section, the same model was optimized by gradient-based methods in NLopt replacing evolutionary algorithms in GEOpS2 (cf. Fig. 2).

Relative function value and argument tolerances are both set to 10–7. Optimization stops if changes fall below this value. Algorithms LBFGS, MMA, SLSQP, and TNewton are limited to a maximum iteration number of 50,000.

5.1.3 Sensitivity analysis

Efficiency is not prioritized in the actual study. That is why sensitivities are calculated by means of forward difference quotients with an absolute interval length of 10–8.

Nevertheless, sensitivities for Eqs. (7) and (8) are derived for an easier classification of the actual problem. If \({f}_{2}\left({\varvec{c}}\right)={f}_{2}\left({{\varvec{\sigma}}}_{a,ME}\left({\varvec{c}}\right)\right)\), then the derivative with respect to the design variable \({\varvec{c}}\) is

$$\frac{\partial {f}_{2}}{\partial {\varvec{c}}}=\frac{\partial {f}_{2}}{\partial {{\varvec{\sigma}}}_{a,ME}}\frac{\partial {{\varvec{\sigma}}}_{a,ME}}{\partial {\varvec{c}}}\text{,}$$
(23)

where the last term contains well-known sensitivities of the stress components as described by Holmberg et al. [34] and Deng et al. [35]. With \({g}_{1}\left({\varvec{c}}\right)={g}_{1}\left({S}_{ME}\left({\varvec{c}}\right),{S}_{i}\left({\varvec{c}}\right)\right)\) and \(i\in\Omega \backslash {\Omega }_{TSS}\) sensitivities result in

$$\frac{\partial {g}_{1}}{\partial {\varvec{c}}}=\frac{\partial {g}_{1}}{\partial {S}_{ME}({\varvec{c}})}\frac{\partial {S}_{ME}}{\partial {\varvec{c}}}+{\sum }_{i}\frac{\partial {g}_{1}}{\partial {S}_{i}({\varvec{c}})}\frac{\partial {S}_{i}}{\partial {\varvec{c}}}\text{.}$$
(24)

It is obvious, that \(\partial {g}_{1}/\partial {\varvec{c}}\) not only depends on \({\varvec{c}}\) but also on the specific position of the ME, i.e., the specific element in the FE model. Thus, sensitivities can only be evaluated analytically if target stresses are determined in a subdomain \({\Omega }_{TSS}\) that is constant throughout optimization. Calculation of FoS always includes element stresses \({\varvec{\sigma}}\), so that

$$\frac{\partial {S}_{j}}{\partial {\varvec{c}}}=\frac{\partial {S}_{j}}{\partial {{\varvec{\sigma}}}_{j}}\frac{\partial {{\varvec{\sigma}}}_{j}}{\partial {\varvec{c}}}$$
(25)

with \(j\) as the index of considered elements. Again, sensitivities of stress components are already described in literature [34, 35]. Possible efficient solution methods involve the adjoint method provided that the number of actual constraints stays low [34].

5.2 Optimization results and comparison to evolutionary algorithms

All results from gradient-based TO are listed in Table 8 and compared to the solution from EA by means of GEOpS2. Gradient TO reaches feasible solutions only with the basic approach A. It seems that the additional constraint in modification C is too strict for proper solution generation. The TSS is achieved very well for the basic approach A and modification C by nearly all gradient TO algorithms. Especially results of minimum \({f}_{1}\) and \({f}_{2}\) from modification C and C + D are overall better than in optimizations with EA, although no feasible solutions have been found. Results from EA tend to exhibit higher specimen volumes \(V\) than from gradient-based algorithms. This trend attenuates when the TSS is also achieved better by means of EA with modification C + D and target shear stresses.

Table 8 Comparison of optimization by means of different gradient-based optimization algorithms and evolutionary algorithms (GEOpS2): objective function values and iteration/generation number
Full size table

Maximum iteration numbers are displayed in Table 8 as well. Very high numbers in EA indicates, that the overall calculation effort is much higher for TO with EA than with gradient-based algorithms. This finding can be put in perspective by the fact that EA enable global optimization with a considerably better final solution finding in the presence of several constraints.

Figure 19 presents feasible structural solutions from gradient-based TO with the basic approach A. The algorithm SLSQP offered the least single-objective function value \({f}_{SO}\) while meeting all constraints properly. Structural solutions for compressive and shear TSS are shown in Fig. 19a and c, respectively. They resemble the expected topologies in Fig. 14 rather less well and hint at basic features only at the grid element scale. Especially for target compressive stresses, the algorithm MMA offers a clearer structural solution close to the expected one (cf. Fig. 19b).

Fig. 19
figure 19

Structural solutions of gradient-based optimization with target compressive and shear stress states: a Modification A with algorithm SLSQP, target compressive stress, \(V=0.246\), \(\Delta \sigma =8.99\cdot {10}^{-4} \,{\text{MPa}}\) (least objective function value \({f}_{SO}\)). b Modification A with algorithm MMA, target compressive stress, solution with plausible topology, \(V=0.363\), \(\Delta \sigma =7.02\cdot {10}^{-4} \,{\text{MPa}}\). c Modification A with algorithm SLSQP, target shear stress, \(V=0.155\), \(\Delta \sigma =0.1052 \,{\text{MPa}}\) (least objective function value \({f}_{SO}\))

Full size image

6 Discussion and outlook

6.1 Appropriate formulation of the optimization problem

A method for topology optimization was presented that incorporates a pre-defined stress state, i.e., a target stress state, by means of evolutionary algorithms. Both the error \(\Delta \sigma\) of the target stress state and the relative structural volume \(V\) were minimized. In a first step, various extensions and modifications on constraints, objective functions, and the design space were investigated for a trivial tensile TSS in order to find a solution which resembles the reference solution available for this formulation. The RS was defined as a solution with all equal element densities. The regarding Pareto front was derived to the form in Eq. (9).

The basic approach A without any modifications, as described in Sect. 2, is not able to generate solutions in the expected form: Densities have a wide range and a stochastic distribution. Additional constraints as in modifications B and C seem to impair the convergence behavior. As a result, Pareto fronts stay in a region of high \(V\) whereas the basic approach A reaches yet a much larger portion of the objective function space. One reason for this may be that more element densities are indirectly controlled by the FoS (modification B) or the stresses (modification C) and design possibilities become less for the outer element densities.

A modified objective function in modification D is aimed at involving not only the central ME but also its NE by merging all local actual stress states to a single error formulation. It was intended not to modify the overall optimization problem but to achieve better results that are comparable to the basic approach A. Densities in the considered area of the ME with its NE tend to be more even but the outer distribution stays similarly stochastic as the solution of the basic approach A. Modification D also exhibits implausible solutions which are better than the RS leading to very low GD values. As it can be ascribed to the discrete element grid (cf. appendix A), this modification is not generally discarded.

The density scaling factor \({w}_{\rho }\) introduced for modification E improves the solution quality of the optimization considerably with Pareto fronts close to the RS and fast convergence. The reason may lie in the feature of \({w}_{\rho }\) to favor solutions with low density variation. It seems that the optimization approach can utilize this feature well so that objective function values converge very fast. It is thus believed that two modifications are at least necessary for optimizing a benchmark artifact in the way presented in this study: On the one hand, the neighborhood of the ME must be constrained so that a smooth transition between the stresses of adjacent elements is obtained. On the other hand, the design space has to be extended in order to favor solutions with an even density distribution. A modified formulation of the objective function as in modification D is optional and has advantages in generating robust results (cf. Sect. 4.3).

6.2 Transfer to real benchmark artifacts

Findings from the optimization problem with trivial tensile TSS were successfully transferred to problems with non-trivial TSS, which are closer to application and can be related to real benchmark artifacts more easily. On the one hand, non-trivial TSS are achieved well by the basic approach A and less accurately for the combined modifications C + E and C + D + E (cf. Table 7). On the other hand, plausible topologies are only reliably found if both ME and NE are considered in the formulation of the objective functions (modification D) and the constraints (modification C). This indicates, that the basic approach A generates results that are highly grid-dependent and difficult to interpret. Modifications D and E help to mitigate grid-dependency.

Displacement views in Fig. 20 unveil two basic mechanisms each for compressive and shear TSS that help to generate the pre-defined stresses: On the one hand, the compressive stress state can be ascribed to the structural O-shape as clearly depicted in the expected topology in Fig. 14a and lightly indicated in Fig. 20a. The global tensile load is redirected by the diagonal bar structures in the corners of the design space in order to compress the horizontal middle structure. Furthermore, dense structural parts in the middle left and right ensure, that the transverse contraction in this area is less than above and below. Relative horizontal displacements to the middle area are the result. On the other hand, shear stress is produced in the middle area by two shifted legs primarily via eccentric loading (cf. Fig. 20b). In addition, slightly slanted parts of the legs produce a load shift in \(x\) direction that distorts the middle area horizontally.

Fig. 20
figure 20

Displacements of structural solutions with least errors of stress state for modification C + D + E. The deformed area of target stress states is framed by dashed lines: a Compressive target stress, \(V=0.736\), \(\Delta \sigma =49.9 \,{\text{MPa}}\) (optimization 3), scale factor 1000. b Shear target stress, \(V=0.396\), \(\Delta \sigma =16.10 \,{\text{MPa}}\) (optimization 2), scale factor 100. Functional cut-outs are marked by dotted ellipses

Full size image

Structural solutions of TO as shown in Fig. 14 seem not only to minimize stresses but also include specific functionalities. These do not directly influence overall material stiffness or stresses, as it is seen in classical TO with minimum compliance and stress constraints. For example, the structural solution with target shear stress, as displayed in Fig. 20b, must offer a stiff, vertical main leg but also must feature a well-defined cut-out to facilitate leg bending and the subsequent \(x\) displacement. Similar structural features have been reported for TO with compliant mechanisms [44]. Consequently, pre-defined TSS can be considered a class of TO problem which uses compliant mechanisms to achieve a quantitatively specific functional target.

Geometry interpretation is a pivotal challenge for transferring the TO results to real structural parts. Especially intermediate material densities must be converted into discrete material. Previous approaches use micro-voids [11], density thresholding or contouring [12], and lattice structures adapted to requirements of additive manufacturing [45]. In this study, geometries of benchmark artifacts are proposed by means of simple material contouring based on the expected functionality. Examples of geometry derivation are shown in Fig. 21. Due to the fact that TO solutions exhibit intermediate densities, the final benchmark artifact geometry must be further post-processed in order to fulfill both the objective in Eq. (7) and the primary constraint in Eq. (8).

Fig. 21
figure 21

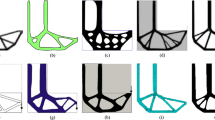
Transfer of structural solutions to real benchmark artifacts in terms of material contouring. Resulting geometry as a combination of the optimized topology and a standard tensile test specimen according to ISO 6892–1 [46]: a Compressive target stress. b Shear target stress

Full size image

Additional steps for improvement may reduce uncertainties in geometry derivation of real benchmark artifacts. They include mesh-independent structural parametrizations with a high-resolution element grid, penalization of intermediate densities in a SIMP-like manner, and elastic boundary conditions close to the final specimen geometry. Moreover, the optimization results may be improved by manufacturability constraints in order to generate topologies that are easier to be produced by additive manufacturing [1, 47]. Last, influences of the specific TSS value \({{\varvec{\sigma}}}_{0}\) and the constraint limit \({\sigma }_{\varepsilon ,\mathrm{lim}}\) on the structural solution should be investigated, as these parameters were defined rather arbitrarily in the actual study.

6.3 Optimization performance compared to gradient methods

Gradient methods achieved overall good results in reaching the TSS even for non-trivial formulations, which were better than in optimizations with EA. The MMA algorithm generated a topology close to the expected one for compressive TSS. However, feasible structural solutions were found via gradient-based algorithms only for the basic approach A. Modifications in the formulation of the constraints (C) or the objective functions (D) hence could not be handled appropriately. It is assumed that pre-defined stresses lead to highly non-convex objective functions due to non-linear relationships between design variables and the error of pre-defined stresses [25]. Gradient-based optimization only finds local optima which lie close to the initial guess. In this way, it cannot be guaranteed that a feasible solution is found by gradient-based algorithms. Nevertheless, a very small iteration number compared to optimization with EA indicates that TO can be performed generally much more efficiently by gradient methods, as already reported by Guirguis et al. [48].

EA generated feasible solutions throughout owing to a global optimization approach. Furthermore, the exact local form of the primary constraint in Eq. (8) was considered in contrast to the continuous approximation in terms of Eq. (21) for the gradient-based approach. This was possible for EA with no additional effort as sensitivity calculation was not necessary. However, a low convergence rate was observed. Even in the modifications with the fastest convergence at least about 10,000 generations are necessary to prove that a steady solution has been found. It is known from literature that TO with EA does not feature fast convergence or convergence at all [10, 20]. Generated results must be therefore seen as optimized approximations rather than optimal solutions. Moreover, EA can hardly handle a large number of design variables [20, 22]. Both lead to slow optimization and rather large-spread results. Moreover, EAs involve shortcomings in terms of a strongly limited number of design variables. Especially high-resolution element grids only can go along with a grid-independent structural parametrization with rather less design variables. In addition, multiple optimization runs are necessary in TO via EA in order to ensure a proper solution finding process in view of inherent heuristic methods. Together with a low convergence, calculation effort stays considerably high.

The TO problem presented in the actual study describes a special case of the general formulation in Sect. 2.1. This special case may serve as a basis for further investigations of problems regarding an advanced application which includes more objective functions, discrete design variables, and non-linear, anisotropic material models especially for additive manufacturing. For example, gradient-based TO methods have limitations if the position of the TSS is optimized as well. EA promises to find proper solutions even for complex formulations of objective functions and constraints. Advanced problem formulations will furthermore foreground trade-offs between Pareto-optimal structural solutions from an engineering perspective, e.g., where small errors of stress state are prioritized over small specimen volumes. This kind of trade-off is only possible with a multi-objective formulation of the TO problem which is currently not fully approachable by means of classical gradient-based methods.

A future perspective could be to combine reliable solution finding of optimization with EA and efficient sizing of element densities by means of gradient-type methods. EA would suggest partially converged structural solutions as a precursor to an efficient finalization with gradient methods. The calculation effort would be clearly lower than with EA alone but could still utilize its global optimization properties. Robust and efficient solution finding of realistic shapes will make an essential contribution to an application of the proposed TO method to benchmark artifacts for additively manufactured components.