Abstract
Setup-related aspects of background-oriented schlieren (BOS) experiments are discussed focusing on a sensitivity parameter S, which represents the relation between light deflection and resulting BOS signal, and the geometric blur. An analytic expression for the geometric blur by means of the circle of confusion (CoC) was derived which shows a proportional relation to the sensitivity factor S. The theoretical findings were validated in a reference experiment using generic distortions in glass plates. It was found that the filtering effect of the blur decreases the maximum background shift and its influence can be expressed with a blur loss factor B, which depends on the size of the CoC in relation to the investigated object. Multiplying the setup sensitivity S with the blur loss B results in the effective sensitivity \(S _{{\rm eff}}\) that determines the maximum achievable BOS signal of a schlieren object. For the investigated reference objects, the maximum effective sensitivity \(S _{{\rm eff}}\) was found to occur at CoC sizes in the object domain from 2.5 to 3.8 times the extent of the investigated objects. A step-by-step method is proposed for designing BOS experiments to obtain a maximum signal strength. The design parameters are further discussed specifically in regard to rotor tip vortex visualization, for which a variety of previously reported experiments are compared. A simple prediction method for the BOS signal of blade tip vortices is proposed and validated with experimental data from a rotor test stand. The application of the method to rotor systems of different size shows the requirement for increasingly higher sensitivity values for visualizing vortices of small-scale rotors.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
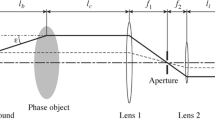
Density-based visualization techniques are a well-known and widely used tool for flow field diagnostics. A more recent development is the background-oriented schlieren technique (BOS), which was demonstrated in early publications by Dalziel et al. (2000), Raffel et al. (2000a, b), and Richard et al. (2000). A general review on the technical details and different applications is provided by Raffel (2015). Like other schlieren techniques, the BOS method is based on a changing refraction of light rays due to spatial density gradients in the flow field. Schlieren objects are imaged, usually with a digital camera, in front of a background pattern, which results in displacements (\(u _{{\rm d}}\), \(v _{{\rm d}}\)) of the pattern in the image plane. The background shift between the measurement image and an undisturbed reference image with no density gradient between camera and background is evaluated. The most common evaluation technique is based on a moving-window cross-correlation as is also used for particle image velocimetry (PIV). The principle of a standard BOS setup is illustrated in Fig. 1 for a vertical density gradient \(\partial \rho / \partial y\) resulting in a displacement \(v _{{\rm d}}\). It analogously applies to horizontal gradients \(\partial \rho / \partial x\) (\(u _{{\rm d}}\)). With the phase object located between camera and background, the light rays are deflected by an angle \(\varepsilon _y\). It can be expressed after Venkatakrishnan and Meier (2004) by
which comprises an integration of refractive index gradients along the line of sight z. The refractive index depends on the fluid density, and the relation is given for gaseous media by the Gladstone–Dale equation \(n=G\rho +1\), where G is the Gladstone–Dale constant (Raffel 2015). The visualization of specific phase objects works best if they are spatially restricted and surrounded by medium with an otherwise homogeneous refractive index \(n_{\infty }\).
An application for which BOS can be used is the visualization of vortices. For example, it has been frequently applied and adapted by the helicopter groups at DLR Göttingen and NASA Ames, to investigate rotor blade tip vortices (Raffel et al. 2014; Gardner et al. 2019). A sample result of an EC 135 in forward flight from Wolf et al. (2022) is shown in Fig. 2.
Due to its relatively simple application and the possibility to use natural backgrounds (see Hargather and Settles (2010)), the technique is well suited compared to other techniques for full-scale measurements (Raffel et al. 2000a; Heineck et al. 2010; Schairer et al. 2013; Bauknecht et al. 2014b; Raffel et al. 2014; Bauknecht et al. 2014a, 2017b; Tritschler et al. 2019; Bauknecht et al. 2019; Schwarz et al. 2020). The density differences within a blade tip vortex are relatively small compared to other flow features for which schlieren techniques are commonly used, such as temperature gradients or shock waves. Therefore, it is important for a successful measurement to optimize both the signal and the noise level. Based on our practical experiences with the application of BOS to vortex visualization, this paper aims to give an overview over the essential design parameters and to provide a guideline for choosing the geometrical parameters for a setup with the goal of achieving a maximum signal.
Principle of a standard BOS setup, after Bauknecht et al. (2014b)
BOS image of an EC 135 in forward flight, measured by Wolf et al. (2022)
The first part of the paper comprises an analytical discussion of the two key setup parameters sensitivity and geometric blur. The second part deals with an experiment that was conducted with reference objects of different sizes and strengths. They were recorded with a variety of different BOS setups in order to transfer the theoretical considerations to actual BOS recordings. Based on the results, a suggestion for a step-by-step guideline for setting up a BOS-system is derived.
In the third part, the specifics of the application of BOS on helicopter blade tip vortices are discussed based on experiments at the rotor test facility in Göttingen (RTG). The BOS signals of blade tip vortex recordings are compared to theoretical predictions based on the Vatistas vortex model. An overview on typical setups for rotor blade tip vortex visualizations is given along with signal strengths that can be expected for a number of relevant rotor systems.
2 Theoretical evaluation of sensitivity and resolution
The correlation of measurement and reference image yields a displacement field (\(u _{{\rm d}}\), \(v _{{\rm d}}\)), as sketched in Fig. 1 for vertical displacements \(v _{{\rm d}}\). Whether the investigated phase object can be detected in the displacement field depends on both the displacement magnitude and the spatial resolution with which the object is sampled. These two quantities are substantially dependent on the sensitivity and the geometric blur that the setup yields.
2.1 Sensitivity
The background displacement \(v _{{\rm d}}\) can be expressed as
and depends on the deflection angle \(\varepsilon _y\), inherent to the density object, as well as the geometric and opto-geometric parameters of the setup. These consist of the focal length of the lens f, the distance between object and background \(Z_D\) and the distance between lens and density variation \(Z_A\) (see Fig. 1). The setup-related parameters can be summarized in the setup-specific sensitivity factor
The general implications discussed in different publications (Goldhahn and Seume 2007; Hargather and Settles 2012; Gojani et al. 2013; Raffel 2015; Rajendran et al. 2020) are that the sensitivity can be increased by increasing the focal length and by positioning the object closer to the camera (Raffel 2015; Hargather and Settles 2012). It is typically stated that the amount to which the object can be moved closer to the camera is limited by the need to keep the object in reasonable focus. The plane of focus is typically located at the background to ensure best contrast (Hargather and Settles 2012; Raffel 2015).
However, when planning an experiment, the size of the field of view (FOV) is often a predefined boundary condition. The focal length that is needed to achieve a certain FOV size \(L _{{\rm FOV}}\) at a distance \(Z_A\) with a camera sensor size \(L _{{\rm sensor}}\) can be calculated by
For non-square camera sensors, either the horizontal (x) or vertical (y) extents of both FOV and sensor need to be applied. For simplicity, we will not differentiate between the different axes in the following. When applying Eqs. 4 to 3, a relation which is rarely stated explicitly (see, for example, Hargather and Settles (2012)) can be derived: for a fixed FOV size and a given setup length \(Z_B=Z_A+Z_D\), a variation of \(Z_A\) leads to a maximum sensitivity S at \(Z_A/Z_B=0.5\). To illustrate this, the resulting normalized sensitivity values are shown in Fig. 3a for different overall setup lengths \(Z_B\). When the setup length \(Z_B\) is increased at a constant ratio of \(Z_A/Z_B\), lenses with a higher focal length are required, which results in a higher sensitivity factor S.
2.2 Spatial resolution
The two main factors that limit the spatial resolution of BOS measurements are the geometric blur of the recorded schlieren object and the interrogation window (IW) size that is used in the correlation. The effect of IW size has been analyzed in a number of studies (Goldhahn and Seume 2007; Vinnichenko et al. 2012; Gojani and Obayashi 2012). Broadly speaking, to increase the spatial resolution, the IW size should be chosen as small as possible. This minimum size is limited by a minimum number of resolvable background structures that an interrogation window should comprise to avoid increasing errors due to invalid correlation results. When using a dot pattern, a minimum value of 7–10 dots is suggested by Vinnichenko et al. (2012), while Gojani and Obayashi (2012) recommend a minimum number of 4–5 dots. This is in agreement with the effective number of at least 5 particle images per interrogation window that is recommended by Raffel et al. (2018) for particle image velocimetry (PIV). The optimum dot diameter is typically chosen to cover around 3 pixels. With a typical dot density, an IW size of 12 \(\times\) 12 pixels comprises about 6 dots. Since the effect of IW size on resolvable object size has been thoroughly investigated both in respect to PIV and also to BOS (Richard et al. 2006; Kähler et al. 2012; Gojani and Obayashi 2012; Vinnichenko et al. 2012), it will not be the focus of the present discussion. It has to be mentioned that besides correlation methods also optical flow algorithms can be used to derive the background shift (Atcheson et al. 2009; Smith et al. 2017). However, in test evaluations with synthetic BOS images using different optical flow algorithms we found it difficult to automatically achieve the same resolution and accuracy of a 12x12 window cross-correlation.
The other key parameter for the achievable spatial resolution of a BOS system is the geometric blur of the recorded schlieren object, which is inherent to the BOS technique. It is often stated that the imaged object has to be maintained in sufficient focus. A quantitative discussion of the effect, however, is found only in few publications (Raffel 2015; Gojani et al. 2013). Rajendran et al. (2019) recently provided a Ray Tracing tool that allows the generation of synthetic BOS images of a density object which takes into account the effect of geometric blur. Since such methods are computationally expensive, a rough estimation of the image blur prior to the setup of an experiment can be useful. In traditional photography, the image blur is specified by the “circle of confusion” (CoC) (Greenleaf 1950), which describes the blur spot that is created in the camera image plane by an imaged singular point. Commonly, a maximum permissible CoC size is used to determine the depth of field (DOF) for a camera setup.
The equations given by Greenleaf (1950) can be used to inversely determine the resulting CoC for an imaged schlieren object at a distance \(Z_D\) from the focus plane:
This quantity corresponds to the geometric blur that is stated in a different formulation by Raffel (2015). The circle of confusion is proportional to the inverse of the f-number \(f_{\#}\) and increases with the square of the focal length f. Combined with Eqs. 3 and 4, Eq. 5 can be expressed as
This means that the CoC size and thus, the blur of an imaged schlieren object is linearly related to the setup sensitivity S, as is depicted in Fig. 3b for different aperture settings. For a given sensitivity S of a setup, \(f_{\#}\) is thus the main parameter that allows modification of the minimal feature size that can be resolved. This means that the ratio of \(Z_A/Z_B\) is in itself not a measure for the object blur since the same sensitivity S, and thus, circle of confusion size (at a given f-number) can be obtained with a different combination of \(Z_A/Z_B\) and focal length f.
In order to relate the geometric blur to the investigated object, the CoC can be transferred to the object domain by
\(\text {CoC} _{{\rm object}}\) is used in the following discussion to compare the setup-inherent blur characteristic to the recorded objects.
3 Reference object experiment
3.1 Setup
To analyze the influence of setup sensitivity S and geometric blur on actual BOS data, reference schlieren objects were recorded with a variety of BOS setups. The reference objects consisted of elongated indentations of different depth (\(0.5{-}5\,\mu\)m) and width (\(2{-}10\) mm) that were polished into soda lime glass plates. The disturbances were designed to produce an artificial phase object similar to a blade tip vortex, which is the main target for BOS investigations at the helicopter group at DLR Göttingen. Fiducial markers were added to the glass plates in order to align the schlieren objects in the different recordings. A Phantom Veo 640 L camera with a sensor consisting of 2560 \(\times\) 1600 pixels was used, equipped with lenses of focal lengths between \(f = 50\) mm and \(f = 500\) mm. For each lens, the glass plates were recorded at distance ratios \(Z_A/Z_B\) of 0.7, 0.5, and 0.3, if the closest focusing distance allowed for it. The different setups covered ranges of \(Z_B\) between 0.5 m and 11.4 m and featured sensitivities from \(S = 17\) mm to \(S = 366\) mm. The FOV size was kept approximately constant in the different setups at about 160 mm \(\times\) 100 mm resulting in a resolution of 16 pixels per mm in the measurement plane.
The camera was focused on a background that consisted of retro-reflective foil printed with randomly placed dots of either 0.4 mm or 1 mm diameter depending on the ratio \(Z_A/Z_B\), so that for each setup the dots corresponded to an imaged size between 3.4 and 5 pixels. The background was illuminated with 4 LED spots, and the exposure times of the camera were varied between \(50\,\mu \text {s}\) and \(1000\,\mu \text {s}\) in order to achieve a similar intensity of the background images in the different setups. A sample setup is depicted in Fig. 4. A multipass algorithm was used with square cross-correlation windows starting at 48 \(\times\) 48 pixels and reducing in size to the final value of 12 \(\times\) 12 pixels. It was found that the spatial resolution of this final IW size was sufficiently small that a variation in IW size to 8 \(\times\) 8 or 16 \(\times\) 16 pixels did not significantly affect the resulting displacement profiles. No additional smoothing or data improvement was used. For each setup, an average displacement field from 20 individual correlation results was derived. The data were analyzed using DaVis 10.1 from LaVision (2019).
A sample BOS recording of a glass plate containing an optical disturbance is shown in Fig. 5a; the zoomed-in region shows the shifted dot pattern in the region of the optical distortion. Figure. 5b depicts the result of the correlation of the measurement image with the undisturbed background. To correct for slight misalignment of the plate and for a varying angle at which the light rays pass through the surface depending on their distance from the optical axis, linear shift profiles were extracted from the undisturbed parts of the glass plate and subtracted from the displacement field. The color map indicates the horizontal background displacement \(u _{{\rm d}}\) in pixels. Due to the curved surface in horizontal direction, the light is deflected in opposite directions depending on the gradient of the glass surface. In the center of the groove, the light passes the disturbance object without refraction.
3.2 Discussion
Profiles of the horizontal background displacement \(u _{{\rm d}}\) along the horizontal (x) axis were extracted and averaged in the marked area between the gray lines in Figs. 5a, b along y. Sample profiles are shown in Figs. 6 and 7. To characterize the displacement profiles, values for the maximum displacement (average of positive and negative peak value, \(u _{{\rm d, max}}\)), the separation distance between the positive and negative peak \(\Delta x/2\) and the peak broadness in terms of the full width at half maximum (FWHM) were extracted. The resulting values are listed in Table 1 for the four different optical disturbances that were used. The values were derived with the setup featuring the lowest sensitivity of \(S=16.7\) mm and thus, the smallest geometric blur with \(\text {CoC} _{{\rm object}}=0.87\) mm.
The profiles that are depicted in Fig. 6 were recorded with settings that result in a similar sensitivity between \(S= 62 - 73\) mm and at a constant aperture setting of \(f_{\#}=16\). Despite the different lenses and ratios of \(Z_A/Z_B\), the profiles are in good agreement not only with regard to the maximum signal \(u _{{\rm d, max}}\) but also with regard to their spatial shape. This illustrates the significance of the sensitivity parameter S, since it is, along with \(f_{\#}\), the main parameter determining the BOS signal of a given schlieren object. The similarity of the profiles also underlines the direct relation between sensitivity S and geometric blur (for a given \(f_{\#}\)).
Horizontal displacement profiles \(u _{{\rm d}}\) of object no. 2 for different f-numbers at \(S=97\,\text {mm}\) (a) and different sensitivities at \(f_{\#}=16\) (b). In addition, the data for \(S=17\,\text {mm}\) were scaled up proportionally to the sensitivity S and subsequently filtered with a Gaussian filter
The effect of a change in geometric blur is illustrated in Fig. 7a, which comprises displacement profiles that were recorded with the same setup but different aperture settings. A smaller \(f_{\#}\) results in an increased CoC (see Eqs. 5–7). This leads to a “smearing” of the signal and thus a broadening of the profile and corresponding reduction in the maximum signal strength \(u _{{\rm d, max}}\). At \(f_{\#}=5.6\) and \(\text {CoC} _{{\rm object}}=18.4\) mm, the maximum signal corresponds to 21% of the maximum signal measured at the highest investigated f-number of \(f_{\#}=22\) with \(\text {CoC} _{{\rm object}}=4.1\) mm.
When increasing the setup sensitivity S at a constant f-number, the background displacement for a given light deflection angle \(\varepsilon _y\) increases (Eq. 2). Simultaneously, the geometric blur increases (Eq. 7), which leads to counteracting effects on the maximum signal when the CoC size reaches a size in the range of the recorded object. This can be observed in Fig. 7b in which displacement profiles captured with different setup sensitivities ranging from 17 mm to 132 mm (at \(f_{\#}=16\)) are depicted. The lowest sensitivity of \(S=17\) mm results in the smallest CoC size of \(\text {CoC} _{{\rm object}}=0.87\) mm with which the object can be sampled with the highest spatial resolution. With increasing sensitivity S, the maximum signal \(u _{{\rm d, max}}\) increases up to \(S=97\) mm, while the simultaneously increasing geometric blur broadens the profiles and smears the spatial details. When increasing the sensitivity above \(S=100\) mm, the effect of blur becomes more dominant and results in a decreasing maximum signal (visible in the peak value of the negative background displacement). The effect of geometric blur can be simulated by applying a suitable filter function to an unblurred signal. This unblurred signal was approximated for the data in Fig. 7b by scaling up the signal at \(S=17\,\)mm in proportion to the higher sensitivities. Subsequently, a Gaussian filter with a window size \(N _{{\rm filter}}\) corresponding to the respective \(\text {CoC} _{{\rm object}}\) size was applied using the MATLAB function “gausswin.” A width factor \(w=1.8\) was used resulting in a standard deviation of \(\sigma _{{\rm filter}}=(N _{{\rm filter}}-1)/2w\). The resulting scaled and filtered profiles are included in Fig. 7b as dashed lines. Since the peak values and the shapes of the computed profiles show a good agreement with the measured data, the chosen filter based on the \(\text {CoC} _{{\rm object}}\) size seems to model the effect of geometric blur well.
The threshold for which the growing CoC prevents a further increase in the maximum signal depends on the size and the shape of the recorded object. To investigate this in more detail, maximum displacement values \(u _{{\rm d, max}}\) for the different setups and different sized disturbances are shown in Fig. 8 over the sensitivity values S of the corresponding setups. It can be seen that for each investigated glass plate, the measured pixel shift initially increases nearly linear with increasing sensitivity S. However, as already visible in Fig. 7b, for each object a maximum displacement value is reached and a further increase in the sensitivity factor S leads to a decrease in the maximum signal. This is due to the \(\text {CoC} _{{\rm object}}\) size reaching a critical value \(\text {CoC} _{{\rm lim}}\) at which its filtering effect outweighs the effect of increasing sensitivity S and thus, limits the achievable maximum signal. For the present reference data, this value is reached at a size of \(\text {CoC} _{{\rm lim}}\) between 2.5 and 3.8 times the extent of the investigated objects, in terms of the FWHM (see Table 1). The corresponding ratios of the limiting circle of confusion size \(\text {CoC} _{{\rm lim}}\) and the structure size are included in Table 1. It has to be noted though that due to the sparse sampling of sensitivities in the range \(S>145\) mm, only a coarse estimation of \(\text {CoC} _{{\rm lim}}\) can be given for disturbance no. 3 and 4. Nonetheless, the data show that for the investigated distortion object, a maximum signal is reached at a certain setup sensitivity S. This means that the setup sensitivity factor S alone is not sufficient to predict the maximum signal \(u _{{\rm d, max}}\) of a schlieren object with given deflection angle \(\epsilon\). If the lens geometry causes a non-negligible blur in the imaging of the object, an additional “blur loss” factor B must be taken into account. When adapting Eq. 2, which represents the displacement of an individual light ray according to the pinhole model, to include the effect of blur when using a finite aperture, the maximum background displacement caused by the object calculates to
The product of setup sensitivity S and blur loss B can be regarded as “effective sensitivity” \(S _{{\rm eff}}= S \cdot B\).
To obtain a more general indication on the blur loss connected to the imaging of a certain schlieren object, the factor B can be computed by using the described filtering approach that showed to adequately model the effect of geometric blur according to Fig. 7b. When applying a filter with increasing size to the signal profile of reference object no. 2 (at \(S=17\,\)mm, blue line in Fig. 7b) the maximum signal decreases progressively. By dividing the maximum of the filtered signal by the maximum of the unfiltered input signal, the blur loss factor B depicted as red dashed line in Fig. 9 is obtained. Multiplying this blur loss B with the setup sensitivity S, which increases linear with \(\text {CoC} _{{\rm object}}\), results in the effective sensitivity \(S _{{\rm eff}}\). The corresponding values for \(S _{{\rm eff}}\), normalized with its maximum, are depicted as solid red line. The values based on the filtering approach agree well with the measured values, which are included as red markers and correspond to the data in Fig. 8 normalized with the maximum of a fit to the data. In addition to the values obtained for glass plate reference object no. 2, the approach was also applied to the background displacement obtained for a blade tip vortex (dashed and solid black lines), which will be discussed in more detail in the next section of the paper (see Fig. 13c). When analyzing the normalized effective sensitivity \(S _{{\rm eff}}\), it can be found that opposed to the reference object no maximum value exists. Instead, \(S _{{\rm eff}}\) approaches a plateau at a \(\text {CoC} _{{\rm object}}\) size of about 5 times the core radius \(r _{{\rm c}}\) of the vortex. This different behavior shows that the blur loss is dependent on the shape of the schlieren object and the exact size of \(\text {CoC} _{{\rm lim}}\) at which the maximum signal is reached cannot be generalized.
Blur loss factor B and resulting normalized effective sensitivity \(S _{{\rm eff}}=S \cdot B\) over ratio of \(\text {CoC} _{{\rm object}}\) to object size (either FWHM or \(r _{{\rm c}}\)). Included are data for reference object no. 2 and for a sample blade tip vortex (see Fig. 13c)
Process for determining the minimum resolvable structure size depicting a 3-bar element of the resolution target (a) a corresponding blurred sample recording of the same excerpt (b), a vertical intensity profile through the image as indicated by dashed red line (c), and the determined minimum structure sizes \(s _{{\rm min}}\) for all setups (d)
The blur does not only affect the maximum signal strength but also the achievable spatial resolution and thus, limits the minimum size of an object that can still be resolved. There are different ways to define the spatial resolution of an optical system. In general, the minimum resolvable object size is the minimum distance, at which two individual points can be separated from each other. Several criteria can be used to decide if points can still be distinguished from one another based on the contrast of the recorded object, such as the Rayleigh and the Sparrow criteria (see, for example, Lasch and Naumann (2006)). In the current investigation, the USAF 1951 3-Bar resolution target was used to measure the optical resolution (see MIL-STD-150A,“photographic lenses”). The target is constituted by elements that consist of three horizontal and three vertical bars. The size of the bars in each element series varies in logarithmic steps. The array of horizontal bars for such an element is depicted in Fig. 10a along with a sample image of the pattern that was recorded with a sensitivity of \(S = 36.6\) mm and a corresponding \(\text {CoC} _{{\rm object}}\) of 2.01 mm (Fig. 10b). For this specific setup, the depicted bar element was the smallest for which the three bars could still be distinguished and corresponds to a bar width of 1.06 mm. The lower limit to which the bar elements are still resolvable was determined based on intensity profiles through the pattern, as indicated by the dashed red line in Fig. 10b. The corresponding profile is depicted in Fig. 10c. The three minima that correspond to the individual stripes are still detectable. The contrast \(C=(I_{1}-I_2)/I_1+I_2\) at which two neighboring bright (\(I_{1}\)) and dark bars (\(I_2\)) could just be separated varied between 3% and 12% (6.4% in average). The contrast level for the smallest detectable structure therefore lay somewhere between the Rayleigh and the Sparrow criterion (see Lasch and Naumann (2006)).
Figure 10d depicts the detected minimum structure sizes that could be resolved with the different setups over the respective calculated \(\text {CoC} _{{\rm object}}\) sizes. The minimum resolvable structure size \(s _{{\rm min}}\) corresponds to roughly half the CoC size in the object domain, as indicated by the dashed line:
This was also found by Braukmann et al. (2021). The limitation of the spatial resolution has to be kept in mind when setting up an experiment. If the focus is on details of the spatial object structure or if several closely spaced objects need to be distinguished, this can constrain the maximum suitable CoC size below the value of \(\text {CoC} _{{\rm lim}}\) at which the maximum signal is achieved.
As a result of the discussed considerations, we suggest the following approach for setting up a BOS-system in order to achieve the maximum signal:
-
1.
Determine the desired FOV for the recorded object. The maximum FOV size is limited in order to maintain the spatial resolution and depends on the spatial accuracy with which the object is to be resolved. An estimation can be done based on the number of interrogation windows to spatially sample the object. When setting the background dot size to match the value of about 3 pixels on the camera chip, an interrogation window size of 12 pixels is still sufficient to contain about 5 dots. In the following, a sample calculation is performed based on the parameters of the glass plate experiment. E.g.: The object of a size of 2.4 mm is to be resolved with 13 vectors at an IW size of 12 \(\times\) 12 pixels and an overlap of 75%. This results in a required resolution of \(13 \cdot 12/4 = 39\) pixels per 2.4 mm and thus 16.25 pixels per mm. With the camera used for the glass plate experiments with a sensor size of 2560 \(\times\) 1600, this results in a FOV size of 158 mm \(\times\) 98 mm.
-
2.
Check the maximum f-number that can be used to still achieve sufficient contrast with the available light and the required exposure time. E.g.: In case of the glass plate measurement, \(f_{\#}=16\) was chosen.
-
3.
Use the maximum allowable \(\text {CoC} _{{\rm object}}\) to determine the setup sensitivity factor S using Eq. 7. Based on the investigated reference objects, a \(\text {CoC} _{{\rm object}}\) size of \(2 - 3\) times the structure size seems suitable to obtain the maximum signal, although schlieren objects with different shapes (such as blade tip vortices) may allow for larger \(\text {CoC} _{{\rm object}}\) sizes without signal loss. E.g.: For the structure size of 2.4 mm, a maximum allowable size of \(\text {CoC} _{{\rm object}}=2\cdot 2.4\,\text {mm}=4.8\,\text {mm}\) is determined. With a chip size of 25.6 mm \(\times\) 16 mm, the above stated FOV size, and \(f_{\#}\), the desired setup sensitivity calculates to: \(S= 4.8\,\text {mm} \cdot 16 \cdot (1+\frac{25.6\,\text {mm}}{158\,\text {mm}})=89.2\) mm.
-
4.
Choose the values of \(Z_A\) and \(Z_D\) to match the chosen sensitivity S (Eq. 2). The minimum overall distance \(Z_B\) at a given sensitivity S is achieved for \(Z_A/Z_B=0.5\). Other values may be better suited due to geometric constraints in the experiment. In general, it is better to achieve a given sensitivity value S with a longer focal length rather than a shorter one due to the requirement of paraxial recording. After Gojani et al., the size of the recorded background domain should be smaller than 50% of the distance \(Z_B\), for the paraxial approximation to be applicable within an accuracy of 1% (Gojani et al. 2013). In practice, if the distance \(Z_D\) can be chosen freely, \(Z_A\) can be set first, based on the desired FOV size and the available lenses/space (Eq. 4). In the next step, \(Z_D\) can be set to match the desired sensitivity S according to \(Z_D=(Z_A-f)/(\frac{f}{S}-1)\). E.g.: When assuming a focal length of \(f=180\) mm for the sample calculation, \(Z_A\) equates to \(Z_A=180\,{\text {mm}}\cdot (158\,{\text {mm}}+25.6\,{\text {mm}})/25.6\,{\text {mm}}=1291\,{\text {mm}}\) and thus \(\hbox { }\ Z_D=(1291\,{\text {mm}}-180\,{\text {mm}})/\) \((180\,{\text {mm}}/89.2\,{\text {mm}}-1)=1091\,{\text {mm}}\).
-
5.
Determine the optimum background dot size based on the sensor properties and the background magnification to image the dots with a size of about 3 pixels on the sensor. E.g.: In case of the sample calculation, this results in a dot size of 0.34 mm.
4 Application of BOS to blade tip vortices
BOS is frequently used by the helicopter group at DLR Göttingen and other groups as a method to investigate rotor blade tip vortices. In the following, an overview over the setup parameters of past BOS experiments for blade tip vortex visualization is given with the purpose to provide reference values for orientation when setting up future experiments. In addition, a simple method is proposed to estimate the expected BOS signal dependent on the rotor and setup parameters which is validated with experimental data gained on a rotor test stand. The method is subsequently applied to a number of differently sized rotor systems.
4.1 Comparison of previous BOS experiments for blade tip vortex visualization
BOS has been used in the past to visualize blade tip vortices on a variety of rotor systems from sub-scale rotors to full-scale helicopters in free flight. The setup parameters (as far as mentioned) that were used in various published studies are listed in Table 2 sorted with increasing focal length of the used lenses. If a value range is reported in multi-camera setups, the average value is stated. The overall setup lengths span from \(Z_B=5.2\) m in laboratory investigations (Bauknecht 2016; Braukmann et al. 2018) to 1100 m in full-scale helicopter measurements in the Swiss Alps (Bauknecht et al. 2017b). The calculated sensitivities range from \(S=44\) mm (Raffel et al. 2000b, a) to \(S=468\) mm (Bauknecht 2016; Braukmann et al. 2018). In most of the used setups, the investigated rotor was positioned somewhere between \(Z_A=0.3\,Z_B\) and \(Z_A=0.7\,Z_B\). The interrogation windows used for evaluating the recorded images were sized between 8 and 20 pixels.
In addition to the BOS system parameters, selected parameters of the used rotors are listed to relate the setups to the investigated vortices in terms of their size and their strength. The resulting total vortex circulation \(\Gamma _{{\text v}}\) at a large radial distance is approximated with \(\Gamma _{{\text v}}= (C_T/\sigma ) 2\Omega R c\) for ideally twisted blades (Leishman 2016), using the thrust coefficient \(C_T\), the solidity \(\sigma\), the rotational frequency \(\Omega\), the rotor radius R, and the chord length c. The vortex core radius \(r _{{\text c}}\) is estimated with \(r _{{\text c}}= 0.04\,c\), which seems to be a reasonable assumption for typical blade loadings based on previous studies such as, for example, Ramasamy and Leishman (2006). Braukmann et al. (2020) measured core radii in the range of \(r_{{\text{c}}} = 0.018{\mkern 1mu} c{\text{ }} - 0.048{\mkern 1mu} c\) depending on blade pitch for a vortex age of \(\psi =25^\circ\). These values, however, only reflect young blade tip vortices. Especially for large vortex Reynolds numbers \(Re _{{\text v}}\le 10^5\), the vortex cores grow significantly with increasing age. Schwarz et al. (2020) reported \(r _{{\text c}}=0.07\,c-0.14\,c\) for full-scale helicopter vortices in ground proximity at a vortex age around \(\psi =540^\circ\). The estimated values for \(\Gamma _{{\text v}}\) and \(r _{{\text c}}\) are meant to give a rough guide to help with the classification of the corresponding measurements.
The spatial resolution of the respective vortices is indicated in Table 2 in terms of pixels as well as in relation to the circle of confusion size \(\text {CoC} _{{\rm object}}\) and the interrogation window size. For investigations that aimed at the visualization of large parts of the vortex system (Bauknecht et al. 2014b, 2017b, 2019, 2014a), the pixels per core radius range from 2.59 to 8.64. Investigations with the focus more on detailed regions of individual vortex filaments feature resolutions from 21.9 to 81.9 pixels per core radius (Schairer et al. 2013; Braukmann et al. 2021; Bauknecht 2016; Braukmann et al. 2018). This means that for large fields of view the interrogation window size is often larger than the core radii of the investigated vortices. This introduces an additional filtering effect that can be approximated similar to the assessment of the geometric blur (see Fig. 9). If the interrogation window size \(\text {IW} _{{\rm object}}\) (transferred to the object domain) is larger than the circle of confusion \(\text {CoC} _{{\rm object}}\), this effect dominates the loss in maximum signal.
The calculated geometric blur spans from \(\text {CoC} _{{\rm object}}=0.21\,r _{{\rm c}}\) to \(\text {CoC} _{{\rm object}}=5.37\,r _{{\rm c}}\). Based on the considerations from the previous section, the blur loss factor B can be determined depending on the ratio \(\text {CoC} _{{\rm object}}/ r _{{\rm c}}\). For blade tip vortices, the factor is given by the black dashed line in Fig. 9. By multiplying it with the setup sensitivity factor S, the effective sensitivity \(S _{{\rm eff}}= S \cdot B\) can be calculated. At \(\text {CoC} _{{\rm object}}/r _{{\rm c}}=4\) about 90% of the effective sensitivity \(S _{{\rm eff}}\) and thus of the maximum achievable signal are reached and a further increase in S does not yield a substantial increase in signal. For cases in which the IW size is larger than the circle of confusion, the ratio \(\text {IW} _{{\rm object}}/r _{{\rm c}}\) is used instead of \(\text {CoC} _{{\rm object}}/r _{{\rm c}}\) to predict the signal loss B. Since state-of-the-art correlation algorithms often use Gaussian weighting functions, the curve that was derived for B based on a Gauss filter to model the geometric blur can be applied analogously for a first approximation. The resulting values for \(S _{{\rm eff}}\) are included in the last column of Table 2.
It should be noted that maximizing the signal is not always necessary and if a high spatial resolution is desired it can be expedient to use lower setup sensitivities S in order to decrease geometric blur. Additionally, the experimental implementation can be dictated by geometric constraints which do not allow to choose the sensitivity freely.
4.2 Vortex signal prediction
When setting up an experiment, it can be useful to have an indication of the expected signal strength. In the past, efforts have been made to develop tools for BOS signal prediction. Rajendran et al. (2019) developed a ray tracing tool to generate synthetic BOS images from a density object (buoyancy driven turbulence). Such a tool, however, requires a considerable amount of computational effort (according to Rajendran et al. (2019) about 1 billion rays are required to render a single PIV image). In the following, a relatively simple methodology based on a theoretical density distribution within the vortices is described, which was recently applied by Braukmann et al. (2021), where further details can be found. The approach is based on the density distribution \(\rho\) along the radial coordinate r that results from the swirl velocity according to the Vatistas vortex model from 2015 (Vatistas et al. 2015). It is an extension of the Vatistas model from 1991 (Vatistas et al. 1991). In the vortex model, the swirl velocity distribution \(V_{{\theta }}\) over the radial coordinate r is given:
\(V_{\theta ,\text {max}}\) represents the maximum swirl velocity and is located at the core radius \(r _{{\rm c}}\). The turbulence factor \(\beta\) can be varied according to the vortex properties, with a higher \(\beta\) representing a higher turbulence level in the vortex. Additionally, the model comprises an integer swirl shape parameter \(n _{{\rm v}}\).
Bagai and Leishman (1993) developed an approach to derive the density distribution from the swirl velocity. Based on the ideal gas law, they stated the connection between the swirl velocity and the density distribution for an inviscid, stationary, two-dimensional vortex:
The formulation contains the specific heat ratio of air \(\gamma\), the ambient air pressure \(p_{\infty }\), and the ambient air density \(\rho _{\infty }\). While Bagai & Leishman assumed isentropic flow, Braukmann et al. (2021) found that the conditions within the core of a blade tip vortex can be better approximated by assuming isothermal flow. This corresponds to a polytropic exponent of \(n _{{\rm p}}=1\) instead of \(n _{{\rm p}}=\gamma =1.4\) for the isentropic case. When replacing \(\gamma\) with \(n _{{\rm p}}=1\) in Eq. 11, integrating both sides of the equation with respect to r gives.
The constants of integration can be determined by using the boundary condition \(\rho (r) \rightarrow \rho _{\infty }\) for \(r\rightarrow \infty\). Braukmann et al. (2021) derived the integral \(\int {V_{{\theta }}^2/r\text {d}r}\) for the Vatistas 2015 model (Eq. 10) with a swirl shape parameter of \(n _{{\rm v}}=1\):
It can be used in combination with Eq. 12 to obtain the density distribution based on the swirl velocity.
Figure 11 qualitatively illustrates the density distribution within a blade tip vortex and the deflection \(\varepsilon\) of a sample light ray passing through the vortex. The cause for this deflection is a change in refractive index which can be calculated for gaseous media according to the Gladstone–Dale equation \(n=G\rho +1\). The deflection \(\epsilon\) can then be calculated after Venkatakrishnan and Meier (2004) according to Eq. 1.
For the current consideration, the light is assumed to pass the vortex parallel and perpendicular to the vortex axis, as illustrated in Fig. 11. The deflections each of the initially parallel beams experiences are integrated along the direction of propagation (z). The resulting overall deflection angle \(\varepsilon\) depends on the radial position r. For the Vatistas 2015 model with \(n _{{\rm v}}=1\), the maximum deflection occurs at a radial position of \(r=0.70\,r _{{\rm c}}\). Using a setup-specific sensitivity factor S, as defined in Eq. 2, theoretical image displacements (\(u _{{\rm d}}\), \(v _{{\rm d}}\)) can be calculated.
4.3 Comparison with test rotor data
To validate the BOS signal estimation method for vortices, experimental data from the DLR rotor test stand (RTG) are used. The details of the experiment are provided by Braukmann et al. (2021). The investigated four-bladed rotor had a rotor radius of \(R=0.65\) m and a chord length of \(c=72\) mm with a negative linear blade twist of \(-9.3^\circ\) along the span. The rotor was equipped with a swashplate that allowed the investigation of cyclic pitch cases. The rotor was operated at a rotational frequency of \(\Omega = 148.28\) rad/s (23.6 Hz) with a mean root pitch angle of \(23.7^\circ\), resulting in a thrust of \(T=236\) N. The optical measurement techniques PIV and BOS were applied simultaneously, which allows to relate the BOS signal of the vortices directly to the instantaneously recorded vortex parameters such as the vortex circulation \(\Gamma _{{\rm v}}\), core radius \(r _{{\rm c}}\) and maximum swirl velocity \(V_{\theta ,{\text {max}}}\) that were determined based on the velocity data from PIV.
The BOS system consisted of a PCO.dimax S4 CMOS camera that was equipped with a Tamron lens with a focal length of \(f=300\) mm. The camera was positioned at a distance of \(Z_A=3.82\) m from the measurement volume and at \(Z_B=7.69\) m from the background, which resulted in a sensitivity factor of \(S=155\) mm (see also values from Braukmann et al. (2021) in Table 2). The geometric layout of the setup is sketched in Fig. 12a according to Braukmann et al. (2020).
Sketch of the BOS system at the rotor test stand (a), sample displacement image containing three vortices (b) (both from Braukmann et al. (2020)), and displacement profiles \(u _{{\rm d}}\) perpendicular to vortex axis for a sample test point (c)
A retroreflective foil with a random dot pattern of 1 mm diameter per dot was recorded. The background was illuminated by an LED array that was positioned close to the camera to maximize the recorded light intensity and thus, allow for a high aperture setting of f/32. This resulted in a circle of confusion size in the object domain of \(\text {CoC} _{{\rm object}}=4.47\) mm, which is \(0.6 - 2.2\) times the experimentally measured core radius \(r _{{\rm c}}\). Based on the blur analysis in the previous section (Fig. 9), it can be assumed that for this ratio of CoC to object size, the loss of maximum signal due to blur is still comparatively small (2% − 22%).
A sample result of the BOS system from Braukmann et al. (2020) is shown in Fig. 12b. The color levels indicate the total background displacement \(\sqrt{u _{{\rm d}}^2+v _{{\rm d}}^2}\) in pixels. In the shown perspective, the axial inflow comes from the left side, whereas the rotor hub is located on the right side outside of the image frame. The blades move through the FOV from top to bottom.
Two regions with a high background displacement occur on both sides of the vortex center. The zoomed-in region in Fig. 12b shows the displacement vectors, which are pointing towards the vortex center. For each test point, 200 images were recorded. Individual displacement profiles were extracted perpendicular to the vortex axis and are depicted in Fig. 12c for a sample test point (gray lines). The profiles were subsequently averaged (blue line), and a spline fit was applied to detect the peak values and locations (blue markers).
Radial profiles of swirl velocity (a), density (b) and pixel shift on the camera sensor (c) for a sample vortex. Included are the measured data from PIV (a) and BOS (c) as well as the predictions based on the Vatistas model (Vatistas et al. 2015) when specifying \(V_{\theta ,{\text {max}}}\) and \(r _{{\rm c}}\)
Comparison of measured BOS signal and computed pixel shift based on Vatistas model (\(\beta =1\)) (Vatistas et al. 2015) for blade tip vortices with varying circulation \(\Gamma _{{\rm v}}\)
The velocity data that were simultaneously recorded with PIV was used to extract vortex parameters, as described by Braukmann et al. (2021). A measured radial swirl velocity profile for a sample blade tip vortex is depicted in Fig. 13a with black triangles (\(\blacktriangle\)). The extracted core radii \(r _{{\rm c}}\), and maximum swirl velocity \(V_{\theta ,{\text {max}}}\) were used to additionally calculate swirl velocity profiles according to the Vatistas model (Eq. 10, Vatistas et al. (2015)). In Fig. 13a, the red and blue lines represent resulting velocity profiles derived using different turbulence factors \(\beta\). For the fully laminar case (\(\beta =1\)), the swirl velocity farther outwards is underpredicted, whereas \(\beta =1.15\) represents the case that best approximates the swirl velocity and thus, the vortex circulation at \(r/c>0.5\).
Density distributions are derived by combining Eqs. 13 and 11 and solving them for \(\rho\). The resulting profiles for \(\beta =1\) and \(\beta =1.15\) are shown in Fig. 13b. The density distribution is foremost dependent on the swirl velocity within the vortex core. Since the turbulence factor does not significantly change the velocity profile in the core, the density curves for both depicted turbulence factors are relatively similar.
Based on the computed density and on the geometric parameters of the BOS setup (Eqs. 1 and 2), theoretical image displacements \(u _{{\rm d}}\) were calculated and are shown in Fig. 13c. Additionally, the experimentally determined background shift on the camera sensor is included (\(\blacktriangle\)). The maximum BOS signal (\(u _{{\rm d, max}}\)) from the prediction compares well with the experimental data. The peak position in the experimental data is at a slightly larger radial coordinate than in the prediction. This is likely a result of the blur, which was not accounted for in the predicted signal. With a ratio of \(\text {CoC} _{{\rm object}}/ r _{{\rm c}}=1.5\), the maximum signal would also be decreased by 12% according to Fig. 9. The nonetheless good agreement between measured and predicted signal could be a result of the maximum swirl velocity \(V_{\theta ,{\text {max}}}\) being also slightly underestimated due to the filtering effect of the finite interrogation windows in PIV. A similar observation was made by Braukmann et al. (2021). It can also be observed that the turbulence factor \(\beta\) has only negligible influence on the predicted maximum BOS signal.
To expand the comparison, vortices that were created at different blade pitch angles (\(24^\circ \pm 6^\circ\) at the blade root) during a cyclic pitch period are analyzed. The corresponding vortex circulation ranged from \(\Gamma _{{\rm v}}\approx 1-3.25\) m\(^2\)/s. Again, the parameters \(r _{{\rm c}}\) and \(V_{\theta ,{\text {max}}}\) were determined from PIV measurements and used to calculate a predicted BOS signal. Figure 14 depicts the maximum background displacements \(u _{{\rm d, max}}\) from both the predictions and the corresponding BOS measurements. The deviation between the measured and predicted signal is lower than 22% for all recorded vortices. The average difference is 0.012 pixels, corresponding to less than 8 % of the measured signal.
The data indicate that the applied method allows for a plausible estimation of the expected BOS signal. When planning a BOS setup for vortex visualization, this can help determining the minimum sensitivity S that is needed to achieve a detectable signal. Indications on the value of this threshold vary in different publications. The accuracy of sub-pixel resolution depends on the used cross-correlation algorithm and is stated with 0.04 pixels (Scarano and Riethmuller 1999), 0.05 pixels (Kähler et al. 2016), or 0.1 pixel (Goldhahn and Seume 2007; Hargather and Settles 2012).
It has to be noted that the accuracy of the signal prediction depends on the knowledge of the core radius and more importantly the maximum swirl velocity of the vortex. If the maximum swirl velocity is not known, a vortex model based on the vortex circulation can be used for a coarse estimation. This will be discussed more closely in the next section, with the aim of predicting BOS signals for rotor systems where only the basic rotor parameters are known.
4.3.1 BOS signal estimation using basic rotor parameters
When planning a BOS setup to visualize blade tip vortices of a certain rotor, the blade tip vortex parameters \(r _{{\rm c}}\) and \(V_{\theta ,{\text {max}}}\) are often not known and can only be estimated. The core radius \(r _{{\rm c}}\) is influenced by the tip shape and grows with increasing vortex age depending on the vortex Reynolds number. Ramasamy and Leishman presented a vortex model that predicts the core radius growth for different wake ages and Reynolds numbers (Ramasamy and Leishman 2007). Based on their reported data, a core radius of \(r _{{\rm c}}\approx 0.04\,c\) for young blade tip vortices (\(\psi <45^\circ\)) seems to be a reasonable assumption and fits the current vortex data. Based on the thrust of a rotor, a vortex circulation can be estimated assuming ideally twisted blades by \(\Gamma _{{\rm v}}=2\Omega Rc \left( \frac{C_T}{\sigma }\right)\) (see also estimated values for \(r _{{\rm c}}\) and \(\Gamma _{{\rm v}}\) in Table 2). Based on the vortex circulation and the core radius, different vortex models can be used to calculate radial swirl velocity profiles. While the Lamb–Oseen (L–S) model assumes a completely laminar interior flow (Lamb 1932), the transitional Ramsamy–Leishman (R–L) vortex model takes into account the vortex Reynolds number (Ramasamy and Leishman 2006, 2007). Additionally, the Vatistas model can be adapted to use the vortex circulation as input. In the following, this was done by assuming the total vortex circulation to be equal to the circulation at \(r=0.65c\) resulting in \(V_{\theta }(0.65c)=\frac{\Gamma _{{\rm v}}}{2\pi (0.65c)}\). When substituting this in Eq. 10, a maximum swirl velocity can be calculated based on \(\Gamma _{{\rm v}}\) that is then used as input to derive swirl velocity profiles.
Swirl velocity profiles (a) and resulting BOS signal (b) derived with different vortex models when using the vortex circulation \(\Gamma _{{\rm v}}\) as input. Included are the Vatistas model for different turbulence factors \(\beta\) and core radii \(r _{{\rm c}}\) (Vatistas et al. 2015), the Lamb–Oseen model (Lamb 1932), and the Ramasamy–Leishman model (Ramasamy and Leishman 2007)
Velocity profiles resulting from the different models when using the measured circulation at \(r=0.65c\) as input are depicted in Fig. 15a. The resulting predicted BOS signals (derived with numerical integration for the R–L and L–S model) are shown in Fig. 15b. The maximum swirl velocity and thus, the magnitude of the BOS signal significantly depend on the used vortex models. While the maximum swirl velocity is overestimated by the L-S-model, the R-L model underpredicts the maximum swirl velocity for the present vortex Reynolds number of \(Re _{{\rm v}}=1.36\cdot 10^5\). The best approximation is achieved using the Vatistas model. However, the predicted maximum swirl velocity is relatively sensitive to the chosen values of \(r _{{\rm c}}\) and \(\beta\) as indicated by the blue (\(\beta =1.0-1.3\)) and red (\(r _{{\rm c}}=0.03\,c-0.05\,c\)) curve bundles. This indicates that a BOS signal prediction based on an approximated vortex circulation can only provide a rough estimate.
However, an easily derived guiding value can be helpful when planning an experiment. Therefore, the described signal prediction scheme was applied to a variety of rotor systems ranging from sub-scale test rotors that were used in past rotor wake investigations to full-scale helicopters as large as the CH53 with a rotor radius of \(R=12\) m. In each case, the Vatistas model with a turbulence factor of \(\beta =1.1\) and a core diameter of \(r _{{\rm c}}=0.04\,c\) was used for consistency.
Theoretical values for the vortex circulation \(\Gamma _{{\rm v}}\) were calculated based on the thrust and the geometric parameters of the rotors that are given in the corresponding publications. If a technical description of a helicopter instead of an experimental investigation is referenced (\(\boxed {18}\), \(\boxed {22}\), \(\boxed {23}\)), the thrust is based on the helicopters maximum takeoff weight (MTOW). The sensitivities \(S _{{\rm 0.05}}\) that would be required to achieve a maximum background displacement of 0.05 pixels were calculated, which corresponds to the minimum displacement value than can be detected with state-of-the-art correlation algorithms according to Kähler et al. (2016). The resulting sensitivities \(S _{{\rm 0.05}}\) for each rotor are plotted in Fig. 16 over the estimated vortex circulation \(\Gamma _{{\rm v}}\). For this sample calculation, a pixel size of \(10\,\mu \text {m}\) as a typical value for high-speed cameras is assumed. The rotor sizes are indicated by the different markers. For full-scale helicopters with circulation values \(\Gamma _{{\rm v}}> 5\) m\(^2\)/s, sensitivity values around \(S=50\) mm or less are sufficient to achieve the desired signal. It has to be noted though that the expected signal depends on the vortex core radius, which increases with vortex age, especially for high vortex Reynolds numbers (Ramasamy and Leishman 2006). For the visualization of older vortices, higher sensitivity values S are required. For scaled-down model rotor systems with lower vortex circulations, the required sensitivity increases. To capture vortices with \(\Gamma _{{\rm v}}< 0.6\) m\(^2\)/s, usually setup sensitivities of 200 mm and above are required. Since the maximum achievable effective sensitivity \(S _{{\rm eff}}\) (see Fig. 9) and thus the maximum BOS signal is limited by geometric blur, this means that for these small-scale rotors it can be difficult to reach the desired background shift of 0.05 pixels. It has to be noted though that these considerations apply only when the line of sight of the BOS camera is oriented perpendicular to the vortex axis. A larger deflection is achieved if the direction of the light rays runs more parallel to the vortex axis. When recording a helical blade tip vortex system, this is typically the case at the farther outboard parts of the curved vortex filaments. This can be observed, for example, in Fig. 17, which shows the vortex system around a model helicopter during takeoff (for setup parameters see Bauknecht et al. (2019)). It is visualized using the divergence operator of the background displacement field. While the more inboard parts of the older vortices are increasingly hard to detect, the outboard sections can still clearly be tracked as the approach the ground plane. This effect can allow for a successful vortex visualization with setup sensitivities below the nominally required value. It is also important to keep in mind that the required sensitivity depends on the physical pixel size of the camera. For example, the result shown in Fig. 17 was recorded using a Nikon D7100 DSLR camera with a pixel size of \(3.91\,\mu \text {m}\). This reduces the required sensitivity to \(S=70\) mm instead of \(S=180\) mm required for a pixel size of \(10\,\mu \text {m}\).
In summary, a signal estimation can help to assess the suitability of BOS for a certain blade tip vortex measurement and to specify the geometric layout. It allows to determine if the maximum achievable effective sensitivity \(S _{{\rm eff}}\) is sufficient for the specific purpose or whether the signal is strong enough that the system does not have to be tuned for maximum sensitivity, which would reduce the geometric blur.
Vortex system around a model helicopter during takeoff, for setup parameters see Bauknecht et al. (2019)
5 Conclusions
Basic parameters for the design of a BOS system were analyzed, and a methodology for achieving a maximum signal from a given schlieren object was presented. Emphasis was placed on the relation between the sensitivity of a setup S and the inherent geometric blur that “smears” the signal and thus limits both the spatial resolution and the maximum achievable signal. The theoretical considerations were applied and validated based on results from a reference experiment using glass plates with generic distortions of different strength and spatial extent. The following conclusions were drawn:
-
The geometric setup sensitivity parameter S connects the light deflection due to a schlieren object to the physical background shift on the camera sensor under the assumption of the pinhole camera model. For a fixed field of view size, it is maximized when the object is positioned half way between camera and background.
-
The sensitivity factor S is directly linked to the geometric blur with which the object is recorded. Increasing the sensitivity S results in a proportional increase in the geometric blur, given the f-number, FOV, and chip size are kept constant. An identical BOS signal is created for the same S value, independent of the combination of geometric and lens parameters that are chosen to achieve the respective sensitivity S. This was confirmed by comparing shift profiles of reference glass objects that were obtained with different BOS setups.
-
The reference experiment showed that the maximum achievable signal is limited due to geometric blur. The blur-induced signal loss can be modeled using a filter with the size of the circle of confusion in the object domain. A blur loss factor B was derived for different CoC sizes in relation to the object size. By multiplying this factor with the setup sensitivity S, an effective sensitivity \(S _{{\rm eff}}\) can be calculated, which is a measure for the maximum achievable signal in a real BOS recording influenced by blur. For the investigated reference objects, the maximum signal was found at CoC sizes in the object domain of about 2.5 to 3.8 times the extent of the investigated objects. A further increase in the setup sensitivity S, and thus, CoC was found to reduce the effective sensitivity \(S _{{\rm eff}}\) resulting in a lower BOS signal. The exact change in effective sensitivity as a function of CoC size depends on the particular schlieren object. For blade tip vortices, for example, an asymptotic approach to an upper limit can be observed.
-
The minimum structure size that can still be resolved with a specific setup was determined using a USAF 3-Bar resolution target. It was found to roughly correspond to 50% of the CoC size in the object domain. The discussed principles were used to develop a step-by-step method for setting up a BOS experiment in order to achieve a maximum signal.
In addition to the general characteristic parameters of a BOS setup, the specifics of its application for the measurement of blade tip vortices were discussed. This contained an overview over vortex measurements that are reported in the previous literature and the description of a simple methodology to predict the BOS signal of a certain vortex. The resulting conclusions can be summarized as follows:
-
For a number of previous BOS measurements of blade tip vortices, sensitivity values and circle of confusion sizes were calculated based on the reported setup data. The calculated sensitivity values range from \(S=44\) mm to \(S=468\) mm while the calculated geometric blur covers circle of confusion sizes in the object domain from 0.2 to 5.4 times the estimated vortex core radius.
-
To predict the BOS signal of a tip vortex, density distributions based on velocity profiles from the Vatistas Vortex model are calculated. The assumption of isothermal flow within the vortex was used. The scheme was validated based on BOS and PIV data recorded at the rotor test stand Göttingen for a variety of blade tip vortices. Using the measured maximum swirl velocity and the core radius as input, the prediction agreed well with the measured data showing an average difference of less than 8 % of the measured signal.
-
The prediction scheme was adapted to be used with basic rotor parameters from which a vortex circulation value is estimated. Although it was shown that signal estimation based on circulation involves a fairly large degree of uncertainty, this method can be used to obtain a rough estimate of the signal to be expected for a particular rotor system. The application to a number of rotors showed that for full-scale helicopter vortices, typically a sensitivity factor of 50 mm is sufficient to achieve a detectable background shift. For scaled model rotors, the required sensitivity increases, making it increasingly difficult to visualize vortices with a circulation of less than \(\Gamma _{{\rm v}}< 0.5\)m/s\(^2\).
Availability of data and materials
The used data can be provided by the authors on request.
Abbreviations
- B :
-
Blur loss factor
- c :
-
Blade chord length (m)
- C :
-
Contrast
- CoC:
-
Circle of confusion (m)
- \(\text {CoC} _{{\rm object}}\) :
-
Circle of confusion in object domain (m)
- \(\text {CoC} _{{\rm lim}}\) :
-
\(\text {CoC} _{{\rm object}}\) size at maximum signal (m)
- \(C_T\) :
-
Thrust coefficient, \(C_T = T/(\rho \pi \Omega ^2 R^4)\)
- f :
-
Focal length (m)
- \(f_{\#}\) :
-
F-number
- G :
-
Gladstone–Dale constant (m\(^3\)/kg)
- \(I_{1}\),\(I_{2}\) :
-
Intensities of USAF target bars (counts)
- IW:
-
Interrogation window (pixel)
- \(\text {IW} _{{\rm object}}\) :
-
IW size in object domain (m)
- \(L _{{\rm FOV}}\) :
-
Field of view size (m)
- \(L _{{\rm sensor}}\) :
-
Camera sensor size (m)
- n :
-
Refractive index
- \(n_{\infty }\) :
-
Refractive index of ambient air
- \(n _{{\rm p}}\) :
-
Polytropic exponent, \(n _{{\rm p}}=1\)
- \(n _{{\rm v}}\) :
-
Vatistas swirl shape parameter
- \(N_b\) :
-
Number of blades
- \(N _{{\rm filter}}\) :
-
Size of filter window
- p :
-
Pressure (Pa)
- \(p_{\infty }\) :
-
Ambient air pressure (Pa)
- r :
-
Radial coordinate (m)
- \(r _{{\rm c}}\) :
-
Vortex core radius (m)
- R :
-
Rotor radius (m)
- \(Re _{{\rm v}}\) :
-
Vortex Reynolds number, \(Re _{{\rm v}}\) = \(\Gamma _{{\rm v}}/ \nu\)
- \(s _{{\rm min}}\) :
-
Minimum resolvable structure size (m)
- S :
-
Setup-specific sensitivity factor (m)
- \(S _{{\rm eff}}\) :
-
Effective sensitivity factor (m), \(S _{{\rm eff}}=S \cdot B\)
- \(S _{{\rm 0.05}}\) :
-
Required sensitivity for \(u _{{\rm d}}=0.05\) pixels (m)
- T :
-
Rotor thrust (N)
- \(u _{{\rm d}},v _{{\rm d}}\) :
-
Background displacements in x, y direction (pixels)
- \(u _{{\rm d, max}}\) :
-
Maximum background displacement (pixels)
- \(V_{{\theta }}\) :
-
Swirl velocity around vortex center (m/s)
- \(V_{\theta ,{\text {max}}}\) :
-
Maximum swirl velocity (m/s)
- w :
-
Width factor of Gauss filter
- x, y, z :
-
Coordinates in the reference frame (m)
- \(Z_A\) :
-
Distance camera lens to density object (m)
- \(Z_B\) :
-
Distance camera lens to background (m)
- \(Z_D\) :
-
Distance density object to background (m)
- \(\beta\) :
-
Turbulence factor
- \(\gamma\) :
-
Specific heat ratio of air
- \(\Gamma\) :
-
Circulation (m\(^2\)/s)
- \(\Gamma _{{\rm v}}\) :
-
Vortex circulation at large distances (m\(^2\)/s)
- \(\epsilon\) :
-
Deflection angle (\(^\circ\))
- \(\epsilon _y\) :
-
Deflection angle in y-direction (\(^\circ\))
- \(\nu\) :
-
Kinematic viscosity (m\(^2\)/s)
- \(\rho\) :
-
Air density (kg/m\(^3\))
- \(\rho _{\infty }\) :
-
Ambient air density (kg/m\(^3\))
- \(\sigma\) :
-
Rotor solidity, \(\sigma =N_bc\)/\(\pi R\)
- \(\sigma _{{\rm filter}}\) :
-
Standard deviation off Gauss filter
- \(\psi\) :
-
Vortex age (\(^{\circ }\))
- \(\Omega\) :
-
Angular velocity of the rotor (rad/s)
References
Atcheson B, Heidrich W, Ihrke I (2009) An evaluation of optical flow algorithms for background oriented Schlieren imaging. Exp Fluids 46(3):467–476. https://doi.org/10.1007/s00348-008-0572-7
Bagai A, Leishman JG (1993) Flow visualization of compressible vortex structures using density gradient techniques. Exp Fluids 15(6):431–442. https://doi.org/10.1007/BF00191786
Barthélemy JP, von Reth RD, Beziac G (1991) Organization and technical status of the NH90 european helicopter programme. In: 17th European Rotorcraft Forum, Berlin, Germany
Bauknecht A (2016) Characterization of blade tip vortices on large-scale rotors. PhD thesis, Leibniz Universität Hannover
Bauknecht A, Ewers B, Wolf CC, Leopold F, Yin J, Raffel M (2014) Three-dimensional reconstruction of helicopter blade-tip vortices using a multi-camera BOS system. Exp Fluids. https://doi.org/10.1007/s00348-014-1866-6
Bauknecht A, Merz CB, Raffel M, Landolt A, Meier AH (2014) Blade-tip vortex detection in maneuvering flight using the background-oriented Schlieren technique. J Aircr 51(6):2005–2014. https://doi.org/10.2514/1.C032672
Bauknecht A, Ewers B, Schneider O, Raffel M (2017) Blade tip vortex measurements on actively twisted rotor blades. Exp Fluids. https://doi.org/10.1007/s00348-017-2312-3
Bauknecht A, Merz CB, Raffel M (2017) Airborne visualization of helicopter blade tip vortices. J Vis 20(1):139–150. https://doi.org/10.1007/s12650-016-0389-z
Bauknecht A, Schwarz C, Raffel M, Mailänder S (2019) Flow measurement techniques for rotor wake characterization on free-flying helicopters in ground effect. In: AIAA science and technology forum and exposition, San Diego, CA, USA, AIAA 2019–2107. https://doi.org/10.2514/6.2019-2107
Braukmann JN, Bauknecht A, Wolf CC, Raffel M (2018) Towards density reconstruction of helicopter blade tip vortices from high-speed background-oriented Schlieren data. In: Heller G, Krämer E, Wagner C, Bansmer S, Radespiel R, Semaan R, Dillmann A (eds) New results in numerical and experimental fluid mechanics XI. Springer, Berlin, pp 375–385
Braukmann JN, Wolf CC, Goerttler A, Raffel M (2020) Blade tip vortex system of a rotor with cyclic pitch. AIAA J 58(7):2869–2880. https://doi.org/10.2514/1.J058678
Braukmann JN, Goerttler A, Wolf CC, Schwarz C, Raffel M (2021) Combining simultaneous density and velocity measurements of rotor blade tip vortices under cyclic pitch conditions. Exp Fluids. https://doi.org/10.1007/s00348-021-03281-w
Dalziel SB, Hughes GO, Sutherland BR (2000) Whole-field density measurements by ‘synthetic Schlieren’. Exp Fluids 28(4):322–335. https://doi.org/10.1007/s003480050391
Gardner A, Wolf C, Raffel M (2019) Review of measurement techniques for unsteady helicopter rotor flows. Progress Aerospace Sci. https://doi.org/10.1016/j.paerosci.2019.100566
Gojani AB, Obayashi S (2012) Assessment of some experimental and image analysis factors for background-oriented Schlieren measurements. Appl Opt 51(31):7554–7559. https://doi.org/10.1364/AO.51.007554
Gojani AB, Kamishi B, Obayashi S (2013) Measurement sensitivity and resolution for background oriented Schlieren during image recording. J Visualization 16(3):201–207. https://doi.org/10.1007/s12650-013-0170-5
Goldhahn E, Seume J (2007) The background oriented Schlieren technique: sensitivity, accuracy, resolution and application to a three-dimensional density field. Exp Fluids 43(2):241–249. https://doi.org/10.1007/s00348-007-0331-1
Greenleaf AR (1950) Photographic optics. Macmillan, New York
Hargather MJ, Settles GS (2010) Natural-background-oriented Schlieren imaging. Exp Fluids 48(1):59–68. https://doi.org/10.1007/s00348-009-0709-3
Hargather MJ, Settles GS (2012) A comparison of three quantitative Schlieren techniques. Opt Lasers Eng 50(1):8–17. https://doi.org/10.1016/j.optlaseng.2011.05.012
Heineck JT, Kushner LK, Schairer ET, Walker LA (2010) Retroreflective background oriented schlieren (RBOS) as applied to full-scale UH-60 blade tip vortices. In: American Helicopter Society aeromechanics specialists’ conference, San Francisco, CA, USA
Kähler CJ, Scharnowski S, Cierpka C (2012) On the resolution limit of digital particle image velocimetry. Exp Fluids 52(6):1629–1639. https://doi.org/10.1007/s00348-012-1280-x
Kähler CJ, Astarita T, Vlachos PP, Sakakibara J, Hain R, Discetti S, La Foy R, Cierpka C (2016) Main results of the 4th international PIV challenge. Exp Fluids. https://doi.org/10.1007/s00348-016-2173-1
Kutz BM, Keßler M, Krämer E (2013) Experimental and numerical examination of a helicopter hovering in ground effect. CEAS Aeronaut J 4(4):397–408. https://doi.org/10.1007/s13272-013-0084-x
Lamb H (1932) Hydrodynamics. Cambridge University Press, Cambridge
Lasch P, Naumann D (2006) Spatial resolution in infrared microspectroscopic imaging of tissues. Biochimica et Biophysica Acta (BBA) - Biomembranes 1758(7):814–829. https://doi.org/10.1016/j.bbamem.2006.06.008
Lee TE, Leishman JG, Ramasamy M (2010) Fluid dynamics of interacting blade tip vortices with a ground plane. J Am Helicopter Soc. https://doi.org/10.4050/JAHS.55.022005
Leishman JG (2016) Principles of helicopter aerodynamics, 2nd edn. Cambridge University Press, New York
Light JS (1993) Tip vortex geometry of a hovering helicopter rotor in ground effect. J Am Helicopter Soc 38(2):34–42. https://doi.org/10.4050/JAHS.38.34
Lößle F, Kostek A, Schwarz C, Schmid R (2021) Experimental measurement of a UAV rotor’s acoustic emission. In: Heller G, Krämer E, Wagner C, Dillmann A (eds) New Results in Numerical and Experimental Fluid Mechanics XIII. Springer International Publishing, Berlin, pp 387–396
Milluzzo JI, Leishman JG (2017) Vortical sheet behavior in the wake of a rotor in ground effect. AIAA J 55(1):24–35. https://doi.org/10.2514/1.J054498
Milluzzo JI, Sydney A, Rauleder J, Leishman JG (2010) In-ground-effect aerodynamics of rotors with different blade tips. In: American Helicopter Society 66th annual forum, Phoenix, AZ, USA
Raffel M (2015) Background-oriented schlieren (BOS) techniques. Exp Fluids. https://doi.org/10.1007/s00348-015-1927-5
Raffel M, Richard H, Meier GEA (2000a) On the applicability of background oriented optical tomography for large scale aerodynamic investigations. Exp Fluids 28(5):477–481. https://doi.org/10.1007/s003480050408
Raffel M, Tung C, Richard H, Yu Y, Meier GEA (2000b) Background oriented stereoscopic schlieren (BOSS) for full-scale helicopter vortex characterization. In: 9th international symposium on flow visualization, Edinburgh, UK
Raffel M, Heineck JT, Schairer E, Leopold F, Kindler K (2014) Background-oriented schlieren imaging for full-scale and in-flight testing. J Am Helicopter Soc. https://doi.org/10.4050/JAHS.59.012002
Raffel M, Willert CE, Scarano F, Kähler C, Wereley ST, Kompenhans J (2018) () Particle image velocimetry: a practical guide, 3rd edn. Cham. https://doi.org/10.1007/978-3-319-68852-7
Rajendran LK, Bane SPM, Vlachos PP (2019) PIV/BOS synthetic image generation in variable density environments for error analysis and experiment design. Meas Sci Technol. https://doi.org/10.1088/1361-6501/ab1ca8
Rajendran LK, Bane SPM, Vlachos PP (2020) Uncertainty amplification due to density/refractive index gradients in background-oriented Schlieren experiments. Exp Fluids. https://doi.org/10.1007/s00348-020-02978-8
Ramasamy M, Leishman JG (2004) Interdependence of diffusion and straining of helicopter blade tip vortices. J Aircr 41(5):1014–1024. https://doi.org/10.2514/1.3364
Ramasamy M, Leishman JG (2006) A generalized model for transitional blade tip vortices. J Am Helicopter Soc 51(1):92–103. https://doi.org/10.4050/1.3092881
Ramasamy M, Leishman JG (2007) A Reynolds number-based blade tip vortex model. J Am Helicopter Soc 52(3):214–223. https://doi.org/10.4050/JAHS.52.214
Ramasamy M, Yamauchi GK (2017) Using model-scale tandem-rotor measurements in ground effect to understand full-scale CH-47D outwash. J Am Helicopter Soc. https://doi.org/10.4050/JAHS.62.012004
Ramasamy M, Gold NP, Bhagwat MJ (2010) Rotor hover performance and flowfield measurements with untwisted and highly-twisted blades. In: 36th European rotorcraft forum, Paris, France
Rauleder J, Leishman JG (2014) Flow environment and organized turbulence structures near a plane below a rotor. AIAA J 52(1):146–161. https://doi.org/10.2514/1.J052315
Rauleder J, Leishman JG (2014) Particle-fluid interactions in rotor-generated vortex flows. Exp Fluids. https://doi.org/10.1007/s00348-014-1689-5
Richard H, Raffel M, Rein M, Kompenhans J, Meier GEA (2000) Demonstration of the applicability of a background oriented schlieren (BOS) method. In: 10th international symposium on applications of laser techniques to fluid mechanics, Lisbon, Portugal
Richard H, Bosbach J, Henning A, Raffel M, van der Wall B (2006) 2C and 3C PIV measurements on a rotor in hover condition. In: 13th international symposium on applications of laser techniques to fluid mechanics, Lisbon, Portugal
Scarano F, Riethmuller ML (1999) Iterative multigrid approach in PIV image processing with discrete window offset. Exp Fluids 26(6):513–523. https://doi.org/10.1007/s003480050318
Schairer E, Kushner LK, Heineck JT (2013) Measurements of tip vortices from a full-scale UH-60A rotor by retro-reflective background oriented schlieren and stereo photogrammetry. In: American Helicopter Society 69th annual forum, Phoenix, AZ, USA
Schwarz C, Bauknecht A, Mailänder S, Raffel M (2019) Wake characterization of a free-flying model helicopter in ground effect. J Am Helicopter Soc. https://doi.org/10.4050/JAHS.64.012010
Schwarz C, Bauknecht A, Wolf CC, Coyle A, Raffel M (2020) A full-scale rotor-wake investigation of a free-flying helicopter in ground effect using BOS and PIV. J Am Helicopter Soc. https://doi.org/10.4050/JAHS.65.032007
Smith NT, Heineck JT, Schairer ET (2017) Optical flow for flight and wind tunnel background oriented Schlieren imaging. In: 55th AIAA aerospace sciences meeting, Gravepine, TX, USA
Tritschler JK, Milluzzo JI, Holder JM (2019) Performance effects of hover in-ground-effect over sloped terrain. In: Vertical flight society 75th annual forum, Philadelphia, PA, USA
Vatistas GH, Kozel V, Mih WC (1991) A simpler model for concentrated vortices. Exp Fluids 11(1):73–76. https://doi.org/10.1007/BF00198434
Vatistas GH, Panagiotakakos GD, Manikis FI (2015) Extension of the n-vortex model to approximate the effects of turbulence. J Aircr 52(5):1721–1725. https://doi.org/10.2514/1.C033238
Venkatakrishnan L, Meier GEA (2004) Density measurements using the background oriented Schlieren technique. Exp Fluids 37(2):237–247. https://doi.org/10.1007/s00348-004-0807-1
Vinnichenko NA, Uvarov A, Y PY (2012) Accuracy of background oriented schlieren for different background patterns and means of refraction index reconstruction. In: 15th international symposium on flow visualization, Minsk, Belarus
Wadcock AJ, Ewing LA, Solis E, Potsdam M, Rajagopalan G (2008) Rotorcraft downwash flow field study to understand the aerodynamics of helicopter brownout. In: American Helicopter society southwest region technical specialists’ meeting, Dallas-Fort Worth, TX, USA
Wolf CC, Braukmann JN, Stauber W, Schwermer T, Raffel M (2019) The tip vortex system of a four-bladed rotor in dynamic stall conditions. J Am Helicopter Soc. https://doi.org/10.4050/JAHS.64.022005
Wolf CC, Schwarz C, Kaufmann K, Gardner AD, Michaelis D, Bosbach J, Schanz D, Schröder A (2019) Experimental study of secondary vortex structures in a rotor wake. Exp Fluids. https://doi.org/10.1007/s00348-019-2807-1
Wolf CC, Weiss A, Schwarz C, Braukmann JN, Koch S, Raffel M (2022) Wake unsteadiness and tip vortex system of full-scale helicopters in ground effect. J Am Helicopter Soc 67(1):1–17. https://doi.org/10.4050/JAHS.67.012010
Acknowledgements
The current investigation was conducted within the framework of the DLR project “URBAN Rescue”. The authors would like to thank C.C. Wolf, A.D. Gardner, and M. Raffel for their insightful input and for fruitful discussions. Furthermore, the authors deeply appreciate the support by M. Krebs.
Funding
Open Access funding enabled and organized by Projekt DEAL. The work was carried out and funded as part of the DLR project “URBAN Rescue”.
Author information
Authors and Affiliations
Contributions
Both authors contributed to the manuscript text, prepared the figures and reviewed the manuscript.
Corresponding author
Ethics declarations
Ethical approval
This declaration is not applicable.
Conflict of interest
The authors have no competing interests as defined by Springer, or other interests that might be perceived to influence the results and/or discussion reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schwarz, C., Braukmann, J.N. Practical aspects of designing background-oriented schlieren (BOS) experiments for vortex measurements. Exp Fluids 64, 67 (2023). https://doi.org/10.1007/s00348-023-03602-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-023-03602-1