Abstract
A methodology for a posteriori uncertainty quantification of pressure data retrieved from particle image velocimetry (PIV) is proposed. It relies upon the Bayesian framework, where the posterior distribution (probability distribution of the true velocity, given the PIV measurements) is obtained from the prior distribution (prior knowledge of properties of the velocity field, e.g., divergence-free) and the statistical model of PIV measurement uncertainty. Once the posterior covariance matrix of the velocity is known, it is propagated through the discretized Poisson equation for pressure. Numerical assessment of the proposed method on a steady Lamb–Oseen vortex shows excellent agreement with Monte Carlo simulations, while linear uncertainty propagation underestimates the uncertainty in the pressure by up to 30 %. The method is finally applied to an experimental test case of a turbulent boundary layer in air, obtained using time-resolved tomographic PIV. Simultaneously with the PIV measurements, microphone measurements were carried out at the wall. The pressure reconstructed from the tomographic PIV data is compared to the microphone measurements. Realizing that the uncertainty of the latter is significantly smaller than the PIV-based pressure, this allows us to obtain an estimate for the true error of the former. The comparison between true error and estimated uncertainty demonstrates the accuracy of the uncertainty estimates on the pressure. In addition, enforcing the divergence-free constraint is found to result in a significantly more accurate reconstructed pressure field. The estimated uncertainty confirms this result.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Particle image velocimetry (PIV) is nowadays recognized as a reliable tool for the determination of the instantaneous static pressure in two- or three-dimensional flow fields (van Oudheusden 2013). The main advantage of the PIV-based pressure reconstruction with respect to conventional pressure probes (e.g., pressure transducers or microphones) is the instantaneous 2D or 3D pressure field determination, without the need of an expensive design and manufacturing of models where densely distributed sensors are installed (Ragni et al. 2011). PIV-based pressure measurements are made possible for applications where probes cannot be installed, such as microaerial vehicles (Tronchin et al. 2015). Additionally, they convey a quantitative visualization of the flow structures responsible for the aerodynamic forces acting on the model. Industrial tests typically require pressure information, for the evaluation of forces. Pressure fluctuations are important when dealing with fatigue studies and aeroacoustic source measurements (Haigermoser 2009; Liu and Katz 2013; Pröbsting et al. 2013).
The computation of the pressure field relies upon PIV measurement of the velocity and acceleration. Provided appropriate boundary conditions, it is conventionally performed by spatial integration of the pressure gradient or by solution of the Poisson equation, though recently alternative methods have been investigated as well (Auteri et al. 2015; Neeteson and Rival 2015). The formulation of the problem in terms of the Poisson equation is often employed because it limits accumulation of errors in the reconstructed pressure (van Oudheusden 2013). Applying the divergence operator to the momentum equation and assuming incompressible flow, the Poisson equation for pressure follows:
To solve Eq. 1, appropriate boundary conditions on the pressure (Dirichlet) or its spatial gradient (Neumann) must be specified. It is important to remark that, although no temporal derivative appears in Eq. 1, its boundary conditions are time dependent and require the computation of the flow acceleration at the boundary of the computational domain. In practice, the discretization of Eq. 1 results in an algebraic system of equations:
which is then solved. A is a discrete representation of the Laplace operator, obtained, for example, by finite differences and \({\mathbf{f}}\) will be referred to as the source term.
When solving Eq. 2 to determine the static pressure field, several factors contribute to the overall uncertainty. According to van Oudheusden (2013), the most relevant for the accuracy of the reconstructed pressure field are:
-
the accuracy of the underlying velocity data;
-
the spatial and temporal resolutions, which affect the accuracy of velocity derivatives;
-
the approach used to evaluate the velocity material acceleration (Eulerian or Lagrangian approach);
-
the boundary conditions;
-
the pressure gradient integration procedure;
-
for PIV-based pressure reconstruction of planar PIV data, application of a 2D model to a 3D flow.
As a result, the uncertainty of the static pressure is a complex function of the parameters above. Quantifying the uncertainty of the pressure measurement is of primary importance for the determination of a confidence interval where the true pressure value lies. Furthermore, it constitutes the basis for estimating the uncertainty of the aerodynamic forces (e.g., lift and drag) acting on a model.
Several works have focused on evaluating the contribution of the above mentioned factors to the error of the reconstructed pressure. For example, de Kat and van Oudheusden (2012) derived an analytical expression of the error of the material acceleration for both Eulerian and Lagrangian approaches. In both approaches, the laser pulse separation \(\Updelta t\) has opposite effects on truncation and random error. Increasing \(\Updelta t\) increases truncation error, but decreases the relative random error. Furthermore, the error of the material acceleration is typically smaller when it is calculated with the Lagrangian approach. Violato et al. (2011) introduced a criterion for the selection of the minimum and maximum \(\Updelta t\) that accounts for the maximum allowed error on the material acceleration and the effect of the out-of-plane displacement of the particles. The authors found that the Lagrangian approach features a random error about 1.5 times smaller than that estimated for the Eulerian approach. The difference between the two approaches is less pronounced when looking at the resulting pressure field, due to the error suppression during the pressure gradient integration. Several schemes for the integration of the pressure gradient have been proposed, including the space-marching integration (Baur and Köngeter 1999), the omnidirectional integration (Liu and Katz 2006) and the Poisson equation for pressure (Gurka et al. 1999). In de Kat and van Oudheusden (2010), a comparative assessment of pressure integration methods is conducted. Although the upshot was that the integration method has minor impact, and only the space-marching approach is clearly inferior, their conclusions were based on statistical analysis and not on the instantaneous pressure uncertainty. In fact, no quantitative information about the uncertainty of computed pressure fields was provided in these early studies. In later studies by de Kat and van Oudheusden (2012) and de Kat and Ganapathisubramani (2013), quantitative information was provided. They used Gaussian vortices for their numerical verification. Charonko et al. (2010) reported that the error of the velocity field has a major influence on the accuracy of the reconstructed pressure. In their work, the pressure result became ‘unusable’ as soon as very small levels of random error were introduced. Extensive data post-processing was required to reduce the velocity error and make accurate pressure reconstructions feasible. However, Murai et al. (2007) reported that a fairly simple smoothing of the velocity data is sufficient for accurate pressure results. Charonko et al. (2010) also investigated the effect of off-axis measurement and out-of-plane velocity. They found that schemes performing well in 2D conditions continued to do so for misalignments up to 30°. de Kat and van Oudheusden (2012) showed that the response to misalignments follows a cosine relation.
In turbulent flows, PIV-based pressure reconstruction presents two major challenges: the small magnitude of the pressure fluctuations and the large dynamic range (Ghaemi and Scarano 2013; Joshi et al. 2014). Ghaemi et al. (2012) conducted time-resolved PIV (TR-PIV) measurements to investigate the pressure fluctuations in a turbulent boundary layer at \(Re_{\theta }=2400\). The agreement between the PIV-based pressure and that measured by a surface microphone was evaluated via the cross-correlation coefficient, which was equal to 0.6. The probability density functions of the two signals agreed up to 3 kHz for tomographic PIV data and up to 1 kHz for planar data. Similarly Pröbsting et al. (2013) carried out the PIV-based pressure reconstruction in a turbulent boundary layer at \(Re_{\theta }=730\). The data were validated by comparison with a surface microphone and with DNS data. Also in this case, the PIV-based pressure signal showed fair agreement with the microphone signal, but the cross-correlation coefficient between the two did not exceed 0.6. Despite the relatively high correlation coefficient achieved, those studies opened several doubts on the accuracy of the PIV-based pressure reconstruction. Acoustic emissions of the flow over a rectangular cavity were investigated by Koschatzky et al. (2011). The fluctuating pressure fields computed from TR-PIV were used as input for the prediction of the sound emission. The authors found that the PIV-based pressure data and the direct pressure measurement at the cavity walls had a similar frequency spectrum. The main frequency tone and the first harmonic were correctly captured, but the amplitude was significantly underestimated. The PIV measurement uncertainty strongly influenced the reconstructed pressure at locations with weak pressure fluctuations.
From the discussion above, it emerges that PIV-based pressure is often highly inaccurate due to the many error sources that contribute to the total error. As a result, quantifying the uncertainty of the reconstructed pressure is of primary importance to the future use of this method. Furthermore, a posteriori uncertainty quantification could be used to inform the choice of experimental and post-processing parameters, along with the pressure reconstruction approach, to maximize the precision of the pressure field. The present work discusses the mathematical framework for the uncertainty propagation from the velocity field to the pressure field. It is formulated from a Bayesian perspective, to allow the measurement uncertainty of the velocity field from PIV to be naturally combined with prior knowledge of the velocity field (e.g., divergence-free) (Wikle and Berliner 2007). Therefore, it is suitable for the quantification of the random uncertainty of pressure, which stems from the random uncertainty of the velocity. A number of a posteriori approaches have recently been proposed to quantify the PIV measurement uncertainty. Sciacchitano et al. (2015) have provided a comparison of these methods. The present framework can also propagate the uncertainty of the velocity spatial and temporal derivatives, when information on the latter is available. The uncertainty due to the application of a 2D model to a 3D flow—i.e., pressure from planar PIV—is not addressed here. We refer to Charonko et al. (2010) and de Kat and van Oudheusden (2012), who investigated the error resulting from applying planar PIV in a 3D flow.
The outline of this paper is as follows: Sect. 2 introduces the proposed methodology. Section 3 presents a numerical assessment with an analytical test case, where the proposed method is compared with Monte Carlo simulations and linear uncertainty propagation (JCGM 2008). Section 4 applies the method to the turbulent boundary layer experiment done by Pröbsting et al. (2013), where microphone measurements are available to assess the PIV-based pressure field and the usefulness of the confidence intervals obtained from the present uncertainty quantification method. Conclusions are drawn in Sect. 5.
2 Methodology
The method to propagate the uncertainty from the velocity field to the pressure field is split into three successive steps and explained in their respective sections:
-
characterize the uncertainty in the velocity field \({\mathbf{u}}\) (Sect. 2.1);
-
propagate the uncertainty from the velocity field to the source term \({\mathbf{f}}\) (Sect. 2.2);
-
propagate the uncertainty from the source term to the pressure field \({\mathbf{p}}\) (Sect. 2.3).
Section 2.4 illustrates the complete methodology for a simple one-dimensional example. The uncertainty of a variable will be expressed through a probability density function (pdf) \(\rho \left( \cdot \right)\).
2.1 The velocity field uncertainty
To characterize the uncertainty in the velocity field, we do not have to solely rely on the PIV measurement uncertainty. First of all, we may have some additional knowledge about the underlying velocity field. Secondly, factors other than the PIV measurement uncertainty contribute to the overall uncertainty of the pressure field, as listed in Sect. 1. The Bayesian framework provides a mathematically and statistically consistent formulation for combining measurements with prior knowledge. Ultimately, we are interested in the probability distribution of the true velocity field \({\mathbf{u}}\) conditioned on the measured velocity field \({\mathbf{u}}_{\text {PIV}}\). This can be expressed through the pdf \(\rho \left( {\mathbf{u}}|{\mathbf{u}}_{\text {PIV}}\right)\). It is known as the posterior. By Bayes’ rule,
where \(\rho _0\left( {\mathbf{u}}\right)\) is the prior and represents the uncertainty in the velocity field before including any measurements. The term \(\rho \left( {\mathbf{u}}_{\text {PIV}}|{\mathbf{u}}\right)\) represents the measurements conditioned on the true velocity field. As general as it is, Eq. 3 is not straightforward to use for general probability density functions. A number of simplifications will therefore be made. Firstly, the pdfs are assumed to be Gaussian. Therefore, the complete pdf can be described in terms of its mean \({\mathbb{E}}\left( \cdot \right)\) and covariance \({\varSigma }\left( \cdot \right)\). Assuming a Gaussian process may seem like a limiting assumption, but in fact this leads to a general framework for approximating arbitrary fields (Rasmussen 2004). In the following, we will refer to it as Gaussian process regression (GPR). In the field of PIV, Gunes et al. (2006) and de Baar et al. (2014) used GPR to interpolate velocity fields, though they did not exploit the posterior covariance of the method.
2.1.1 The prior on the velocity field
We discretize the velocity field at n spatial locations of interest \({\mathbf{x}}\in {\mathbb{R}}^{d\cdot n}\). This gives a vector \({\mathbf{u}}\in {\mathbb{R}}^{d\cdot n}\), describing the d-dimensional velocity components at these locations. Due to the assumption of Gaussian processes and the discretization, we have the following multivariate normal distribution:
with \(\pmb {\mu }_0\) and P the prior mean and prior covariance matrix, respectively. We start the discussion with the prior mean \(\pmb {\mu }_0\in {\mathbb{R}}^{d\cdot n}\). For simplicity, we assume each velocity component to be a constant field. This is not a limiting simplification since the complexity of the field that can be reconstructed is determined by the prior covariance used. The prior covariance matrix is defined as:
where \(\tau ^2\) is the prior variance and \(r^{ij}\) represents the (scaled) distance between \({\mathbf{x}}^i\) and \({\mathbf{x}}^j\):
where \(\theta _k\) is the correlation length in the direction k. \(\phi \left( r^{ij}\right)\) is a covariance function and represents the correlation between \({\mathbf{x}}^i\) and \({\mathbf{x}}^j\). It is a function only of their separation by the assumption of a stationary process (Rasmussen 2004). The covariance function is 1 at distance 0 and at infinitely large distance it should approach 0. In other words, at infinite distance the behavior of the two points is uncorrelated. Gaussians are popular covariance functions. In the present paper, however, we use the Wendland function with smoothness \(C^4\) (Wendland 2005):
where \(+\) indicates that \(\left( 1-r^{ij}\right) _+^6=0\) for \(r^{ij}\ge 1\). The Wendland function is a good approximation to a Gaussian function. Due to its compact support, it results in a sparse covariance matrix, leading to savings in memory and computational time when inverting it.
Ultimately, one can either setup a prior covariance matrix for each velocity component independently, as was done by de Baar et al. (2014), or a single covariance matrix that constrains the velocity components according to mass conservation (the divergence-free or solenoidal constraint) (Azijli and Dwight 2015). The details can be found in these works. Whichever method is used, two parameters result that need to be determined, namely the prior variance \(\tau ^2\) from Eq. 4 and the correlation length \(\theta _k\) from Eq. 5. They can either be specified a priori or through a maximum likelihood optimization. Azijli and Dwight (2015) followed the a priori approach. This was possible because the PIV data had sufficient spatial resolution. de Baar et al. (2014) followed the optimization route since their PIV data had insufficient spatial resolution.
2.1.2 The PIV measurement uncertainty model
With m measurements, we define the vector \({\mathbf{u}}_{\text {PIV}}\in {\mathbb{R}}^{d\cdot m}\) at the measurement locations \({\mathbf{x}}_{\text {PIV}}\in {\mathbb{R}}^{d\cdot m}\). We can take \({\mathbf{x}}={\mathbf{x}}_{\text {PIV}}\) (i.e., \(n=m\)), in which case we will obtain the pressure field on the same mesh as the PIV field. Or we can take n larger than m, in which case we attempt to obtain the pressure field on a finer mesh. The measurement uncertainty is also assumed to come from a Gaussian distribution, where the mean represents the bias error and the standard deviation represents the random error (Sciacchitano et al. 2015). Once quantified, the estimate of the bias error can be subtracted from the measurements. Therefore, the measurements
can be represented as a multivariate Gaussian distribution, where \(\pmb {\epsilon }\sim {\mathcal{N}}\left( {\mathbf{0}},R\right)\) is the measurement error of the velocity field, assumed to be Gaussian noise with zero mean and covariance matrix R. The matrix H maps the velocities from \({\mathbf{x}}\) to \({\mathbf{x}}_{\text {PIV}}\). In the most general case, H would represent an arbitrary interpolation matrix (representing, for example, polynomial or radial basis function interpolation). In the present work, the measurement locations are taken to be a subset of the locations of interest; therefore, H is a Boolean matrix. In particular, if \({\mathbf{x}}={\mathbf{x}}_{\text {PIV}}\) then H is the identity matrix, giving
This situation where the pressure field is evaluated at the same locations where the velocity measurements are available is the most common (van Oudheusden 2013), but our framework allows generalization.
2.1.3 The posterior on the velocity field
Having defined the prior and carried out the measurements, they are combined to obtain the posterior distribution. The prior and likelihood are both Gaussian distributed, and since all operators defined are linear, the posterior is Gaussian distributed as well with mean and covariance given by (Wikle and Berliner 2007):
respectively. In the present paper, we will also consider the situation where we construct the pressure field by completely relying on the PIV data, i.e., no prior knowledge is taken into account and the velocity is only assumed to be known at the locations coming from the measurements. Mathematically, this can be expressed by taking \(P=\tau ^2I\), where \(\tau =\infty\), and \(H=I\). Equation 7 becomes
The term \(\tau ^2I\left( R+\tau ^2I\right) ^{-1}\) becomes I for infinitely large prior variance, so Eq. 9 reduces to
The posterior covariance from Eq. 8 becomes
With the prior variance approaching infinity, Eq. 11 can be rewritten to reveal
In words, Eqs. 10 and 12 state that the posterior mean and covariance are equal to the measured velocity field and measurement uncertainty, respectively. This makes sense intuitively, but it is important that it also follows naturally from the framework.
2.2 Propagating uncertainties to the source term
The posterior distribution of the velocity (see Eqs. 7, 8) must be propagated through \({\mathbf{f}}\) to obtain the mean \({\mathbb{E}}\left( {\mathbf{f}}\right)\) and covariance \({\varSigma }\left( {\mathbf{f}}\right)\) of the source term. However, this is not straightforward since \({\mathbf{f}}\), derived from the Navier–Stokes equations, has a nonlinear dependence on the velocity. We consider two options to obtain the mean and covariance of the source term.
The first is through carrying out Monte Carlo simulations (Metropolis and Ulam 1949), a popular method for uncertainty propagation. Briefly, random realizations from the posterior distribution \(\rho \left( {\mathbf{u}}|{\mathbf{u}}_{\text {PIV}}\right)\) are generated. In practice, a random realization with the required covariance structure specified by \({\varSigma }\left( {\mathbf{u}}|{\mathbf{u}}_{\text {PIV}}\right)\) can be obtained by computing the Cholesky decomposition
followed by multiplying L with a vector containing uncorrelated random realizations from a standard Gaussian distribution (Gibbs 2011). Subsequently, for each realization the source term \({\mathbf{f}}\) is then evaluated. From this one can construct \({\mathbb{E}}\left( {\mathbf{f}}\right)\) and \({\varSigma }\left( {\mathbf{f}}\right)\).
The second method enables exact uncertainty propagation in contrast to the Monte Carlo method. A closer look at the Navier–Stokes equations reveals that the nonlinear term contains a product of at most two variables. As a result, it is possible to calculate the expected value and covariance exactly. For generality, we define four random variables a, b, c and d. For the expected value, one can use the definition of covariance:
where \(\sigma \left( a,b\right)\) represents the covariance between a and b. For the covariance between two products of random variables ab and cd, Bohrnstedt and Goldberger (1969) derived the following expression:
Equation 13 is valid irrespective of the distributions of a and b, since it is simply a rewrite of the definition of covariance. Equation 14 on the other hand is valid only if the distributions are Gaussian. Indeed, this is what we have done in the present work. The source term, however, is no longer Gaussian distributed.
It is important to state that this exact method is only possible if the material acceleration is evaluated with respect to a stationary reference frame, i.e., the Eulerian approach. If the Lagrangian approach is used, products arise with more than two random variables. Brown and Alexander (1991) derived general expressions for the covariance of a product of n random variables with a product of m random variables. However, these contain higher-order moments. If they cannot be determined, they need to be neglected, resulting in an approximation. The Monte Carlo method can straightforwardly be applied no matter which approach is used.
2.3 Uncertainty in the pressure field
The discretization error arising from solving the discrete system in Eq. 2 contributes to the overall uncertainty in the calculated pressure. This error can be reduced by interpolating the measurements onto a finer numerical mesh, which is possible with GPR, and then solving the (larger) resulting system. However, there is a moment where the interpolation error starts to dominate, thereby limiting the total error reduction. Fortunately, with GPR the interpolation is accompanied by confidence intervals through the posterior covariance matrix \({\varSigma }\left( {\mathbf{u}}|{\mathbf{u}}_{\text {PIV}}\right)\). The interpolation error is therefore included in the pressure field uncertainty, provided that the system is solved on a sufficiently fine mesh.
The mean and covariance for the pressure follow straightforwardly from the identities of the expected value and covariance since the Laplace operator given by the left-hand side of Eq. 2, is a linear operator:
Figure 1 summarizes the steps involved to propagate the uncertainty from the velocity to the pressure field.
2.4 A one-dimensional example
We use a simple one-dimensional example to clarify each step of the proposed methodology. Extension to two- and three-dimensional problems is relatively straightforward and will be explained in Sects. 3 and 4, covering the synthetic test case and the experimental data, respectively. Consider the following one-dimensional example:
Equation 17 is similar to the Poisson equation Eq. 1 in that the second derivative of the pressure is taken and the right-hand side is nonlinear in the velocity u. For simplicity, we do exclude the dimensions from the variables considered. The problem is completed with Dirichlet boundary conditions. If we take
it can be verified that the pressure is
We take six uniformly distributed measurement locations (\(m=6\)) but discretize the velocity at 41 points to illustrate the ability of GPR to interpolate the measurement points (\(n=41\)).
For the prior mean, we assume the zero vector, so \(\pmb {\mu }_0= 0\). The prior covariance matrix is set up according to Eq. 4, where we have used the Wendland function from Eq. 6 as the covariance function. The correlation length \(\theta\) and the prior variance \(\tau ^2\) are found using a cross-validation approach (Viana et al. 2009) and are set to 2 and 0.48, respectively. The black dots in Fig. 2a are the true function evaluations at the n locations of interest. The thick blue line represents the prior mean. The bottom plot in Fig. 2a shows the prior variance, scaled with \(\tau ^2\).
One-dimensional example. a True function evaluations (black dots), observations (red crosses), prior mean (blue line), prior variance scaled with \(\tau ^2\) (black line); b posterior mean (blue line), posterior variance scaled with prior variance \(\tau ^2\) (black line). The variables are left dimensionless
Measurement noise is included, with a variance of \(\sigma ^2= 2.5\times 10^{-5}\). It is assumed that the measurement uncertainty at the locations are uncorrelated with each other, therefore \(R=\sigma ^2I\), where I is the identity matrix. Since there are 6 uniformly distributed measurement locations and the state contains 41 uniformly distributed points, the observation operator \(H\in {\mathbb{R}}^{6\times 41}\) is simply a Boolean matrix with \(H^{ij}=1\) at \(j=8i-7\;(i=1,2,\ldots ,6)\) and \(H^{ij}=0\) everywhere else.
With all the relevant components defined, we can calculate the posterior mean and covariance with Eqs. 7 and 8, respectively. Figure 2b shows the results. Starting with the mean (top plot): combining the prior and measurements we obtain a posterior that agrees well with the true function evaluations. Proceeding to the bottom plot, the posterior variance is strongly decreased with respect to the prior variance from the bottom plot in Fig. 2a. Also, we can clearly see a decrease in the variance at the measurement locations and an increase in between. Indeed, the measurements are informative and the larger the distance from them, the larger the uncertainty in the reconstruction. Note that the variance is not decreasing to zero at the measurement locations, since we included measurement noise with a variance of \(\sigma ^2= 2.5\times 10^{-5}\).
To illustrate how the exact propagation method presented in Sect. 2.2 compares with Monte Carlo simulations, we refer to Fig. 3a, b. They show how the random velocity error eventually propagates into the pressure. The difference with the two figures is due to the accuracy of the pressure measurements at the boundaries. In Fig. 3a, it is assumed that the pressure can be measured with perfect accuracy. In Fig. 3b, we have taken standard deviations of \(1\times 10^{-4}\) and \(5\times 10^{-4}\) for the pressure measurements at the left and right boundaries, respectively.
One-dimensional example. Exact standard deviation of calculated pressure (black line), and Monte Carlo results using N realizations. a Perfect pressure measurements at boundaries, b assuming \(\sigma _p=1 \times 10^{-4}\) at \(x=0\) and \(\sigma _p=5 \times 10^{-4}\) at \(x=1\). The variables are left dimensionless
Finally, we shift our focus to Sect. 2.3 on the influence of discretization and interpolation errors. In the absence of measurement noise (\(\sigma =0\)) and measurements available at all locations (\(m=n\)), the error reduces with a finer mesh (larger n or decreasing mesh distance h), as illustrated by the red line in Fig. 4. Since we used second-order finite difference schemes to discretize the differential operators, we observe second-order convergence. However, with measurements only available at the six locations (\(m=6\)), GPR can be used to interpolate the measurements onto the finer mesh. Indeed, it is common in PIV measurements of turbulent flows that not all scales are resolved. The magenta line in Fig. 4 illustrates the plateau that occurs once the interpolation error starts to dominate the discretization error, thereby hindering the initial monotonic decrease in the total error. With the blue line, we have included the measurement noise: The initial decrease and the plateau are still present; however, as expected we observe the influence of the noise and a larger final error.
One-dimensional example. Root-mean-square error (rmse) of the reconstructed pressure as a function of mesh size \(h=1/(n-1)\). When \(m = n, \sigma =0\), the observations are available at all points, without measurement noise; when \(m = 6\), the observations are available at six equally spaced points and interpolated onto a stencil with spacing h. Specifically, \(m = 6\), \(\sigma \ne 0\) represents six equally spaced observations, with \(\sigma ^2=2.5 \times 10^{-5}; m = 6, \sigma =0\) represents six equally spaced observations, without measurement noise; ‘estimated’ is the estimated error following from Eq. 16 when \(\sigma ^2=2.5\times 10^{-5}\). The variables are left dimensionless
In the above discussion, we were able to calculate the error since we know the true pressure. In practice though, the true pressure is unknown and we aim to estimate it, which is of course the goal of the present work. The black line in Fig. 4 represents the estimated error resulting from solving Eq. 16 and shows that it is a good approximation of the true error, thereby illustrating the ability of the method to also include the interpolation error in the error estimate.
3 Numerical verification
The proposed numerical procedure for uncertainty quantification of PIV-based pressure reconstruction is compared to a reference solution obtained using the Monte Carlo method with 10, 000 samples. The Monte Carlo simulation employs exactly the same statistical models as our proposed approach, so that in this section we are verifying only the numerical procedure, and not the statistical modeling. The considered flow field is a two-dimensional incompressible Lamb–Oseen vortex (de Kat and van Oudheusden 2012; de Kat and Ganapathisubramani 2013). In a polar reference system with radius r and azimuthal angle \(\theta\) the analytical expressions of azimuthal velocity \(V_{\theta }\) and radial velocity \(V_r\) are, respectively:
where \({\varGamma }\) is the vortex circulation, \(\nu\) is the kinematic viscosity, and t is time. A steady simulation is conducted with \(t=1\;\text {s}\). The values of dynamic viscosity and density are set to \(\mu =2.4\times 10^{-7}\;\text {Pa}\,\text {s}\) and \(\rho =1.2\;\text {kg/m}^3\), respectively, yielding a kinematic viscosity \(\nu =2.0\times 10^{-7}\;\text {m}^2/\text {s}\). The vortex circulation is \({\varGamma }=0.02\;\text {m}^2/\text {s}\). The analytical expression of the pressure field is obtained from integration of the Navier–Stokes equations in polar coordinates, yielding:
where Ei is the exponential integral function. The square domain has a size of \(20\;\text {mm}\), and the center of the vortex coincides with the center of the domain at \(\left( x,y\right) =\left( 0,0\right)\). The domain is divided into 50 grid points in both horizontal and vertical directions, resulting in a grid spacing \(d=0.4\;\text {mm}\). The analytical velocity and pressure field are illustrated in Fig. 5; the pressure in the vortex core is \(p_{\text {core}} =-9.78\;\text {Pa}\). To simulate noise in the velocity measurements, zero-mean white Gaussian noise is added to the two velocity components, with a standard deviation ranging from 0 to 30 % of the maximum velocity magnitude \(V_{\text {mag}}\): \(R=U^2I\), where \(U=\alpha V_{\text {mag}}\). \(\alpha\) is between 0 and 0.30. The pressure field is reconstructed from the velocity data using the Poisson equation approach with pure Dirichlet boundary conditions. The pressure at the boundary of the measurement domain is computed via the incompressible flow momentum equation, i.e., the Bernoulli equation.
For all values of noise level, the standard uncertainty of the reconstructed pressure is evaluated with two approaches: (1) the Bayesian framework presented in Sect. 2; (2) linear uncertainty propagation (Wieneke and Sciacchitano 2015). In the latter approach, it is assumed that the two velocity components have the same uncertainty U and that the velocity errors are uncorrelated in space, which is true for the current simulation, but not in typical PIV experiments due to the finite interrogation window size. The expression of the uncertainty of the pressure evaluated by the linear uncertainty propagation reads as:
The uncertainty results from both approaches are compared with the results obtained by Monte Carlo simulations. The results at the center of the vortex are shown in Fig. 6: The pressure error increases linearly from 0.3 to 10 % of \(p_{\text {core}}\) as the uncertainty of the velocity is increased. The Bayesian framework and linear uncertainty propagation reproduce the linear behavior of the uncertainty. However, the linear approach underestimates the uncertainty by about 30 % with respect to the Monte Carlo results, whereas the agreement between the Bayesian framework and Monte Carlo results is excellent. For illustration purposes, we show the comparison between the standard deviation computed with the different methods. Figure 7a illustrates the standard deviation of the pressure error obtained via Monte Carlo simulations for the case where the standard deviation of the added noise is 15 % of the velocity magnitude; the pressure error is below 1 % outside the vortex core and increases up to 4 % in the vortex center. The Bayesian framework for uncertainty propagation (Fig. 7b) shows excellent agreement with the Monte Carlo results. The linear error propagation, however (Fig. 7c), significantly underestimates the uncertainty. It is noted that the pressure errors obtained here are lower than those reported by de Kat and van Oudheusden (2012) for a very similar test case. The difference between the two results is attributed to the choice of the boundary conditions for the pressure computation. In our work, we set Dirichlet boundary conditions over the entire boundary. Conversely, de Kat and van Oudheusden (2012) applied Dirichlet boundary conditions over the lower edge and Neumann boundary conditions over the remaining edges. Also, we use the pressure Poisson equation (see Eq. 1) under the assumption of 2D flow, whereas de Kat and van Oudheusden (2012) use a 2D Poisson formulation of 3D flow. This formulation allows them to assess the influence of a 3D flow in 2D pressure evaluation.
Lamb–Oseen vortex. Comparison between the standard deviation of the pressure error from Monte -Carlo simulations (a), the Bayesian framework (b) and linear uncertainty propagation (c). The results are normalized with \(|p_{\text {core}}|\) and in percentage. The noise level on the velocity: 15 % of the maximum velocity magnitude
4 Application to experimental data
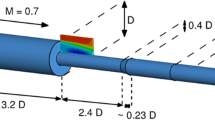
The experimental test case considered is a fully developed turbulent boundary layer over a flat plate in air, obtained using time-resolved tomographic PIV. The experiments were carried out by Pröbsting et al. (2013). The PIV acquisition frequency was 10 kHz, and 1500 instantaneous velocity fields were collected. The free stream velocity was 10 m/s, so assuming incompressible flow is justified. The size of the reconstructed volume was \(19.7\times 4.2\times 41.3\,\text {mm}^3\). Further details of the experimental parameters are reported in Pröbsting et al. (2013). This experiment is particularly useful for the present paper since microphone measurements were conducted simultaneously with the tomo-PIV measurements. Specifically, a pinhole microphone was located at the wall. According to Pröbsting et al. (2013) and Ghaemi et al. (2012), the uncertainty of the microphone does not exceed 500 μ Pa, which is approximately 0.05 % of the measured pressure fluctuations. The microphone measurements can therefore be used as a reliable ground truth, enabling the possibility to assess the usefulness of the proposed uncertainty propagation method. The assessment is done in the following way: The instantaneous error at time instant \(t_i\) is defined as the difference between the pressure from the microphone \(p_{\text {mic}}\) and the PIV-based pressure \(p_{\text {PIV}}\), evaluated at the microphone location \({\mathbf{x}}_{\text {mic}}\):
With the uncertainty propagation method described in the present paper, the standard deviation of the PIV-based pressure at location \({\mathbf{x}}_j\) and time instant \(t_i\) follows from the pressure covariance matrix, given by Eq. 16:
\({\varSigma }_i^{jj}\) represents the jth diagonal term of the covariance matrix at time instant \(t_i\). When evaluated at the microphone location, we will denote Eq. 23 as \(\hat{\delta }_{\text {mic}}\). With the expanded uncertainty \(U=k\hat{\delta }_{\text {mic}}\), a certain percentage of \(|\pmb {\delta }|\) should be smaller than U. Timmins et al. (2012) referred to this as the ‘uncertainty effectiveness.’ Assuming a Gaussian distribution, a 68.3 % confidence level is obtained when \(k=1\) and 95 % when \(k=1.96\) (Coleman and Steele 2009). Figure 8 illustrates the definitions we have introduced.
To carry out the uncertainty propagation, we start out with identifying the prior. Two cases are distinguished: (1) we completely rely on the PIV measurement and take no prior physical knowledge into account. Therefore, the posterior mean and covariance are simply the PIV field (Eq. 10) and its uncertainty (Eq. 12), respectively; (2) realizing the flow is incompressible, we enforce the divergence-free constraint by applying a solenoidal filter (Azijli and Dwight 2015). The solenoidal filter is linear; therefore, the posterior distribution will remain Gaussian distributed (Fig. 9).
Proceeding to the measurements, the uncertainty of the PIV field is expressed through the observation error covariance matrix R. A number of methods are nowadays available to calculate a posteriori the uncertainty from PIV (Sciacchitano et al. 2015). However, since the particle images were not available at the moment of the calculation, we have used a different method. Considering that the flow velocity should be divergence-free, we use the measured spurious velocity divergence as an estimator for the uncertainty in the velocity field. This has already been observed by others (Scarano and Poelma 2009; Violato 2013). In the present paper, we use the following approach: we apply the solenoidal filter to the PIV data \({\mathbf{u}}_{\text {PIV}}\), rendering an analytically divergence-free velocity field \({\mathbf{u}}_{\text {sol}}\). Figure 10 shows the streamwise velocity at the center plane before (top) and after (bottom) applying the solenoidal filter at one time instant. The difference between \({\mathbf{u}}_{\text {PIV}}\) and \({\mathbf{u}}_{\text {sol}}\) is an approximation of the true error. With 1500 samples, the variance of the error in time is taken as an approximation for the variance of the measurement uncertainty, i.e., the diagonal terms in the observation error covariance matrix R. Figure 11 shows pdfs of \({\mathbf{u}}_{\text {PIV}}-{\mathbf{u}}_{\text {sol}}\) for the 1500 samples at two locations, namely the microphone location (bottom) and the upper side of the measurement domain directly above the microphone (top). The pdfs look approximately Gaussian, so our assumption of a Gaussian distribution for the PIV measurement uncertainty seems acceptable. Comparing the top plots with their bottom counterparts, notice the increase in variance of the bottom plots, indicating a larger measurement uncertainty closer to the wall. To investigate this further, Fig. 12 shows the standard uncertainty of each velocity component at the center plane. We clearly see a spatially varying measurement uncertainty for each velocity component. In particular, we observe that the uncertainty increases closer to the wall. The PIV data were processed with a \(32\times 16\times 32\) interrogation window with 75 % overlap. Due to the use of overlapping windows, the measurement error will be spatially correlated. Mathematically, the off-diagonal terms of the observation error covariance matrix R are unequal to zero. Wieneke and Sciacchitano (2015) investigated how the spatial correlation of the measurement uncertainty depends on the overlap and interrogation window sizes using Monte Carlo simulations. From their analysis, they found correlation values for different grid spacings. Rather than directly inserting them into R, we have approximated these values by fitting the Wendland function from Eq. 6 through them. This ensures that R will be numerically positive definite; therefore, the matrix can be inverted (Wendland 2005).
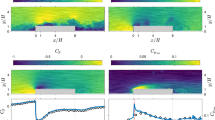
Pressure time series obtained with the microphone (red) and PIV (black). \(\delta\) is the boundary layer thickness, \(u_{\infty }\) is the free stream velocity, \(q_{\infty }\) is the free stream dynamic pressure and p′ the pressure fluctuation. The gray regions represent the estimated uncertainty, where the bounds are \(p_{\text {PIV}}\left( {\mathbf{x}}_{\text {mic}},t_i\right) \pm k\hat{\delta }_{\text {mic}}\left( t_i\right)\), where \(k=1\)
The boundary conditions we impose are the same as applied by Pröbsting et al. (2013), namely Dirichlet at the top boundary and Neumann at all other boundaries. We use both the Eulerian and the Lagrangian approaches to evaluate the material acceleration. According to Violato et al. (2011), the Lagrangian approach should result in a more accurate reconstructed pressure field, since the boundary layer flow is a convection dominated type of flow. Whether this is indeed true should not only follow from comparison with the microphone measurement, but is also expected to be represented by a smaller uncertainty in the reconstructed pressure. To propagate the uncertainties, we carry out Monte Carlo simulations using 100 realizations. This is the number suggested by Houtekamer and Mitchell (1998) in the context of the Ensemble Kalman Filter, which is practically a Monte Carlo version of the Kalman Filter for nonlinear systems.
Following Pröbsting et al. (2013), Fig. 9 shows the pressure time series for a subset of the data. The red lines in the plots are the microphone signal. The results are normalized with the free stream dynamic pressure \(q_{\infty }\approx 60\) Pa. The fluctuations of the microphone signal are of the order of 2 % of the free stream dynamic pressure, which is around 1.2 Pa. The black lines in Fig. 9 are the PIV-based pressure signals. The results represent four cases. From top to bottom: without applying the prior knowledge of divergence-free velocity fields through the solenoidal filter and using the Eulerian approach; without the prior knowledge using the Lagrangian approach; including the solenoidal prior and using the Eulerian approach; including the solenoidal prior and using the Lagrangian approach. From the figure, we can already deduce the observations made by Violato et al. (2011), namely that the Lagrangian approach results in more accurate pressure reconstruction than the Eulerian approach, and the observations made by Azijli and Dwight (2015) that using the solenoidal prior improves the pressure reconstruction.
In addition to the PIV-based pressure signals, we have also plotted the estimated uncertainty. The bounds of the gray region are \(p_{\text {PIV}}\left( {\mathbf{x}}_{\text {mic}},t_i\right) \pm k\hat{\delta }_{\text {mic}}\left( t_i\right)\), where we have taken for the coverage factor \(k=1\), so an 68.3 % confidence level for a Gaussian distribution. We have not plotted the 95 % confidence level (\(k=1.96\)) since it would obscure the figures. Already from the plots, we can observe that the bounds indeed become tighter when switching from the Eulerian to the Lagrangian approach and when including the solenoidal prior.
Table 1 quantifies these observations. First of all, it shows the standard deviation (std) of the error \(\delta\) between the microphone and PIV-based reconstruction. The errors range from 1.2 Pa without the solenoidal prior and the Eulerian approach to approximately 0.6 Pa when using the solenoidal prior together with the Lagrangian approach. The focus of the present work is how the estimated uncertainty compares with this. The rightmost column of Table 1 shows the standard deviation of the approximated error \(\hat{\delta }_{\text {mic}}\), averaged over the 1500 fields in time. First of all, we notice the excellent agreement between the true and estimated errors. In addition, we observe that switching from the Eulerian to the Lagrangian approach indeed results in a decrease in the estimated uncertainty. The uncertainty is further decreased when including the prior knowledge of divergence-free velocity fields. Table 2 shows the results for the uncertainty effectiveness for the 68.3 and 95 % confidence levels. In conclusion, the approximated error that follows from the uncertainty propagation method is indeed useful, given that the uncertainty effectiveness is close to the theoretical value. We used coverage factors corresponding to a Gaussian distribution. Though the velocity uncertainties we started out with were Gaussian, due to the nonlinearity of the Navier–Stokes equations the pressure need not be Gaussian distributed anymore. A Gaussian distribution is known to have skewness 0 and a kurtosis of 3. Since we used Monte Carlo simulations to propagate the uncertainties, we have the full probability distributions of the pressure. The skewness and kurtosis of the velocity at the microphone location were 0.034 and 3.02, respectively, since we used a finite number of random realizations, i.e., 100. Table 3 shows the resulting values for the pressure distributions, extracted from the position of the microphone in the PIV field. There is indeed a departure from the Gaussian observable, though not considerable. Therefore, it is acceptable to use the Gaussian coverage factors.
To appreciate how the PIV measurement uncertainty propagates to the calculated pressure field, we refer to Fig. 13. It shows the standard uncertainty of the reconstructed pressure field as a function of the distance from the wall where the microphone is located. As we move away from the wall, the uncertainty decreases. Compare this with Fig. 12, which shows the standard uncertainty of the PIV measurement. Similarly, we notice a decrease in the standard uncertainty with increasing distance from the wall.
5 Conclusions
The present work proposed a methodology for the a posteriori quantification of the uncertainty of pressure data retrieved from PIV measurements. The approach relies upon the Bayesian framework, where the posterior distribution (probability distribution of the true velocity, given the PIV measurements) is obtained from the prior distribution (prior knowledge of the velocity, e.g., within a certain bound or divergence-free) and the distribution representing the PIV measurement uncertainty. Once the covariance matrix of the velocity is known, it is propagated through the Poisson equation. Provided the velocity uncertainty is Gaussian and the Eulerian approach is used, the uncertainty can be calculated exactly. Otherwise, Monte Carlo simulations can be used. Numerical assessment of the method on a steady Lamb–Oseen vortex showed excellent agreement of the propagated uncertainty with Monte Carlo simulations, while linear uncertainty propagation underestimates the uncertainty of the pressure by up to 30 %. The method was finally applied to an experimental test case of a turbulent boundary layer in air, obtained using time-resolved tomographic PIV. The pressure reconstructed from tomographic PIV data was compared to the surface measurement conducted by a microphone to determine the actual error of the former. The PIV uncertainty was quantified by applying a solenoidal filter to remove spurious divergence. In addition, spatial correlation of the PIV uncertainty was included. It was found that close to the wall, the velocity uncertainty increases, most likely due to the increased velocity gradient closer to the wall. This was observed to be propagated into the pressure field as well. The comparison between actual and approximated error showed the effectiveness of the proposed method for uncertainty quantification of pressure data from tomographic PIV experiments. The Lagrangian approach resulted in more accurate reconstructed pressure fields than the Eulerian approach, reducing the errors from approximately 2 % of the free stream dynamic pressure to approximately 1.5 %. Also, enforcing the divergence-free constraint was found to result in a more accurate reconstructed pressure field, eventually reducing the errors to 1 %. Both observations also followed from the uncertainty quantification through a decrease in the estimated uncertainty. In addition, the estimated errors were in excellent agreement with the actual error of the pressure.
References
Auteri F, Carini M, Zagaglia D, Montagnani D, Gibertini G, Merz C, Zanotti A (2015) A novel approach for reconstructing pressure from PIV velocity measurements. Exp Fluids 56(2):1–16
Azijli I, Dwight RP (2015) Solenoidal filtering of volumetric velocity measurements using Gaussian process regression. Exp Fluids 56(11):198
Baur T, Köngeter J (1999) PIV with high temporal resolution for the determination of local pressure reductions from coherent turbulence phenomena. In: 3rd Int Symp on PIV
Bohrnstedt GW, Goldberger AS (1969) On the exact covariance of products of random variables. J Am Stat Assoc 64(328):1439–1442
Brown D, Alexander N (1991) The analysis of the variance and covariance of products. Biometrics 47(2):429–444
Charonko JJ, King CV, Smith BL, Vlachos PP (2010) Assessment of pressure field calculations from particle image velocimetry measurements. Meas Sci Technol 21(10)
Coleman HW, Steele WG (2009) Experimentation, validation, and uncertainty analysis for engineers. Wiley, Hoboken
de Baar JH, Percin M, Dwight RP, van Oudheusden BW, Bijl H (2014) Kriging regression of PIV data using a local error estimate. Exp Fluids 55(1):1650
de Kat R, van Oudheusden BW (2010) Instantaneous planar pressure from PIV: analytic and experimental test-cases. In: Proceedings of the 15th international symposium on applications of laser techniques to fluid mechanics, Lisbon, Portugal
de Kat R, van Oudheusden B (2012) Instantaneous planar pressure determination from PIV in turbulent flow. Exp Fluids 52(5):1089–1106
de Kat R, Ganapathisubramani B (2013) Pressure from particle image velocimetry for convective flows: a taylors hypothesis approach. Meas Sci Technol 24(2):024,002
Ghaemi S, Ragni D, Scarano F (2012) PIV-based pressure fluctuations in the turbulent boundary layer. Exp Fluids 53(6):1823–1840
Ghaemi S, Scarano F (2013) Turbulent structure of high-amplitude pressure peaks within the turbulent boundary layer. J Fluid Mech 735:381–426
Gibbs BP (2011) Advanced Kalman filtering, least-squares and modeling: a practical handbook. Wiley, Hoboken
Gunes H, Sirisup S, Karniadakis GE (2006) Gappy data: to Krig or not to Krig? J Comput Phys 212(1):358–382
Gurka R, Liberzon A, Hefetz D, Rubinstein D, Shavit U (1999) Computation of pressure distribution using PIV velocity data. In: 3rd International workshop on PIV, Santa Barbara
Haigermoser C (2009) Application of an acoustic analogy to PIV data from rectangular cavity flows. Exp Fluids 47(1):145–157
Houtekamer PL, Mitchell HL (1998) Data assimilation using an ensemble Kalman filter technique. Mon Weather Rev 126(3):796–811
JCGM (2008) Guide to the expression of uncertainty in measurement
Joshi P, Liu X, Katz J (2014) Effect of mean and fluctuating pressure gradients on boundary layer turbulence. J Fluid Mech 748:36
Koschatzky V, Moore P, Westerweel J, Scarano F, Boersma B (2011) High speed PIV applied to aerodynamic noise investigation. Exp Fluids 50(4):863–876
Liu X, Katz J (2006) Instantaneous pressure and material acceleration measurements using a four-exposure PIV system. Exp Fluids 41(2):227–240
Liu X, Katz J (2013) Vortex-corner interactions in a cavity shear layer elucidated by time-resolved measurements of the pressure field. J Fluid Mech 728:417–457
Metropolis N, Ulam S (1949) The Monte Carlo method. J Am Stat Assoc 44(247):335–341
Murai Y, Nakada T, Suzuki T, Yamamoto F (2007) Particle tracking velocimetry applied to estimate the pressure field around a Savonius turbine. Meas Sci Technol 18(8):2491
Neeteson NJ, Rival DE (2015) Pressure-field extraction on unstructured flow data using a voronoi tessellation-based networking algorithm: a proof-of-principle study. Exp Fluids 56(2):1–13
Pröbsting S, Scarano F, Bernardini M, Pirozzoli S (2013) On the estimation of wall pressure coherence using time-resolved tomographic PIV. Exp Fluids 54(7):1–15
Ragni D, Van Oudheusden B, Scarano F (2011) Non-intrusive aerodynamic loads analysis of an aircraft propeller blade. Exp Fluids 51(2):361–371
Rasmussen CE (2004) Gaussian processes in machine learning. In: Advanced lectures on machine learning. Springer, Berlin, pp 63–71
Scarano F, Poelma C (2009) Three-dimensional vorticity patterns of cylinder wakes. Exp Fluids 47(1):69–83
Sciacchitano A, Neal DR, Smith BL, Warner SO, Vlachos PP, Wieneke B, Scarano F (2015) Collaborative framework for PIV uncertainty quantification: comparative assessment of methods. Meas Sci Technol 26(7):074,004
Timmins B, Wilson B, Smith B, Vlachos P (2012) A method for automatic estimation of instantaneous local uncertainty in particle image velocimetry measurements. Exp Fluids 53(4):1133–1147
Tronchin T, David L, Farcy A (2015) Loads and pressure evaluation of the flow around a flapping wing from instantaneous 3D velocity measurements. Exp Fluids 56(1):1–16
van Oudheusden B (2013) PIV-based pressure measurement. Meas Sci Technol 24(3):1–32
Viana FA, Haftka RT, Steffen V Jr (2009) Multiple surrogates: how cross-validation errors can help us to obtain the best predictor. Struct Multidiscip Optim 39(4):439–457
Violato D (2013) 3D flow organization and dynamics in subsonic jets: aeroacoustic source analysis by tomographic PIV. Ph.D. Thesis, TU Delft, Delft University of Technology
Violato D, Moore P, Scarano F (2011) Lagrangian and eulerian pressure field evaluation of rod-airfoil flow from time-resolved tomographic PIV. Exp Fluids 50(4):1057–1070
Wendland H (2005) Scattered data approximation, vol 17. Cambridge University Press, Cambridge
Wieneke B, Sciacchitano A (2015) PIV uncertainty propagation. In: 11th Int Symp on PIV-PIV15
Wikle C, Berliner M (2007) A Bayesian tutorial for data assimilation. Phys D 230(1):1–16
Acknowledgments
We thank Dr. Stefan Pröbsting for providing the data set of the turbulent flat plate boundary layer in air.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Azijli, I., Sciacchitano, A., Ragni, D. et al. A posteriori uncertainty quantification of PIV-based pressure data. Exp Fluids 57, 72 (2016). https://doi.org/10.1007/s00348-016-2159-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-016-2159-z