Lagrangian and Eulerian pressure field evaluation of rod-airfoil flow from time-resolved tomographic PIV

Abstract

This work investigates the rod-airfoil air flow by time-resolved Tomographic Particle Image Velocimetry (TR-TOMO PIV) in thin-light volume configuration. Experiments are performed at the region close to the leading edge of a NACA0012 airfoil embedded in the von Kármán wake of a cylindrical rod. The 3D velocity field measured at 5 kHz is used to evaluate the instantaneous planar pressure field by integration of the pressure gradient field. The experimental data are treated with a discretized model based on multiple velocity measurements. The time separation used to evaluate the Lagrangian derivative along a fluid parcel trajectory has to be taken into account to reduce precision error. By comparing Lagrangian and Eulerian approaches, the latter is restricted to shorter time separations and is found not applicable to evaluate pressure gradient field if a relative precision error lower than 10% is required. Finally, the pressure evaluated from tomographic velocity measurements is compared to that obtained from simulated planar ones to discuss the effect of 3D flow phenomena on the accuracy of the proposed technique.

1 Introduction

The knowledge of accurate methods to evaluate pressure fields from PIV measurements has become of high interest in many fluid dynamic investigations.

Aeroacoustic predictions of flows interacting with body-surfaces (Haigermoser 2009; Koschatzky et al. 2010; Lorenzoni et al. 2009) is a recent field where the aforementioned methods are applied to time-resolved PIV to extract the body-surface pressure distribution which is used to predict the instantaneous far-field acoustic pressure by means of Curle’s analogy (1955). Higher accuracy in the pressure evaluation from PIV would lead to more reliable PIV-based sound predictions to be used together with computational aeroacoustics CAA (Crighton 1993), sensors and microphone arrays (Brooks and Humphreys 2003).

Liu and Katz (2006) developed a scheme to evaluate the instantaneous pressure distribution by integrating the material acceleration computed from four-exposure PIV data which enabled to map the instantaneous planar pressure field. Measurements of material acceleration in turbulent flows were also done earlier by Voth et al. (1998) and La Porta et al. (2000) using particle tracking technique. In the investigation of the instantaneous pressure field around a square-section cylinder by time-resolved stereo-PIV, de Kat et al. (2008) demonstrated the accuracy of the pressure determination scheme (Gurka et al. 1999) following an Eulerian approach.

The PIV technique was used for noise investigation by Seiner (1998) who, in the study of jet noise, applied two-point velocity correlation to evaluate Lighthill turbulent stress tensor. Schröder et al. (2004) investigated the noise-producing flow structures in the wake of a flat plate with elliptic leading edge by space–time correlations of the fluctuating z-component of the vorticity field. The explicit use of acoustic analogies for sound prediction with time-resolved PIV was done by Haigermoser (2009) for cavity noise studies and, later, by Koschatzky et al. (2010).

For the rod-airfoil benchmark configuration (Jacob et al. 2004), Henning et al. (2009) recently investigated the mechanism of sound generation by means of simultaneous planar PIV in the near-field and phased-microphone-array measurements in the far-field. Cross-correlation between the acoustic pressure and velocity or vorticity fluctuations (Henning et al. 2008) was applied to characterize flow structures involved in noise production. From the temporal evolution of the cross-correlation coefficient, the authors suggested that the source region was located by the leading edge of the airfoil. With a similar experimental approach, the far-field aeroacoustic of the rod-airfoil configuration was investigated by Lorenzoni et al. (2009) who reported a favorable comparison for the tonal component between microphone measurements and predictions based on Curle’s acoustic analogy (1955) applied to time-resolved planar PIV (TR PIV).

A number of issues have emerged from some of the mentioned studies. Except for computational approaches, no account has been made of the 3-D features in the flow due to intrinsic limitation of the planar two- and three-component PIV technique. In the investigation of the rod-airfoil flow, Lorenzoni et al. (2009) stated that a noise prediction more accurate than that obtained assuming 2-D flow could be achieved if 3-D flow effects are taken into account. Also, in the same investigation, the low temporal resolution limited the accuracy of the evaluated instantaneous pressure, as well as of the pressure time rate of change, which is of prior importance for the evaluation of Curle’s aeroacoustic analogy. Furthermore, the question of whether the pressure gradient should be estimated from either an Eulerian (Baur and Kongeter 1999) or a Lagrangian approach (Liu and Katz 2006) has not been fully answered and experimentally verified.

By this work, tomographic particle image velocimetry technique (Elsinga et al. 2006; Schröder et al. 2008), in thin-volume configuration, enabling to fully describe the velocity gradient tensor, is applied to study the 3-D flow pattern of a rod-airfoil system similar to that investigated by Lorenzoni et al. (2009). To discuss the 3-D flow effects neglected in the work by Lorenzoni et al. (2009), pressure and material acceleration on the measurement domain midplane are compared to those evaluated from planar PIV. Furthermore, the measurements are performed at high time resolution in order to apply a multi-step technique (Moore et al. 2010) based on Liu and Katz (2006) scheme for an accurate evaluation of Lagrangian derivatives.

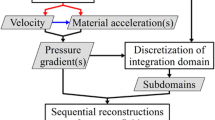
The work includes a brief theoretical background of a Lagrangian approach to evaluate the instantaneous planar pressure distribution from TR-TOMO PIV. The relation between the time separation and the precision and the truncation errors is recalled. Furthermore, the Lagrangian approach for material derivative evaluation is compared to the Eulerian one in terms of precision error at different values of the time interval. A criterion restricting the relative precision error to 10% on the material velocity derivative is given and, under such conditions, the instantaneous planar pressure evaluated from tomographic velocity fields is compared to that obtained from synchronous planar PIV velocity fields to discuss 3-D flow effects in rod-airfoil flow. At present time, limiting the precision error on the material acceleration to a value of 10% represents a realistic estimate for well-controlled PIV experiments.

2 Theoretical background

2.1 Pressure field evaluation

Curle’s aeroacoustic analogy (1955), an extension of Lighthill’s theory (1952), accounts for the noise production from solid objects interacting with an unsteady flow. In the analytical formulation for low Mach number, the acoustic pressure fluctuation in the far-field region is a function of the time rate of change of the pressure fluctuation integral on the surface of the body caused by the interaction with the flow. This means that the surface pressure distribution has to be measured in time to evaluate the pressure fluctuation in the acoustic domain.

The instantaneous pressure field p can be inferred from the measurement of the time-resolved velocity field according to the incompressible ($\rho\,=\,\hbox{const}$) Navier Stokes equations

$$ \nabla p = -\rho \left(\frac{D{\bf V}}{D t} + \nu \nabla^2 {\bf V} \right), $$

(1)

where

$$ \frac{D {\bf V}}{D t} = \frac{\partial {\bf V}}{\partial t} + \left({\bf V} \cdot \nabla\right) {\bf V} $$

(2)

is the material acceleration. This can be computed either by means of Eq. (2) with an Eulerian approach, as proposed by Baur and Kongeter (1999), or with the Lagrangian approach (Liu and Katz 2006). The suitability of both schemes for the accurate evaluation of the pressure gradient distribution is currently under discussion (de Kat and van Oudheusden 2010), of which an experimental study is provided in the present paper.

Also, the pressure gradient spatial integration in a planar domain has been approached in different ways. Liu and Katz (2006) proposed an omni-directional virtual boundary integration algorithm, instead van Oudheusden et al. (2007) used a direct 2D integration technique based on the work of Baur and Kongeter (1999). Later, the same authors, referring to the work of Gurka et al. (1999), reverted to the use of Poisson equation,

$$ \nabla^{2}p=-\rho \nabla \cdot \left ( \frac{D {\bf V}}{D t} + \nu \nabla^2 {\bf V} \right ) $$

(3)

which has demonstrated superior accuracy and showed to be less prone to localized error propagation (de Kat et al. 2008). In the latter Neumann boundary conditions

$$ \nabla p=-\rho \frac{D {\bf V}}{D t} $$

(4)

are applied, whereas Dirichlet conditions are assigned where p is known either by a direct measurement or by invoking Bernoulli’s equation in region of steady and irrotational flow:

$$ p-p_{{\hbox{ref}}}=\frac{1}{2}\rho\left(\left|{\bf V}_{{\hbox{ref}}}^{2}\right|-\left|{\bf V}^{2}\right| \right). $$

(5)

The evaluation of the sound source integral of the Curle’s analogy (1955) would require the measurement of the surface pressure distribution along the entire airfoil span. However, despite the fact that thin-volume TOMO PIV enables the velocity measurement over a limited airfoil span-wise, it is relevant to evaluate the effect of the 3D-flow features on the pressure field, which is obtained under the hypothesis of 2D flow if based on planar PIV measurements. Furthermore, the scheme used for the evaluation of the material velocity derivative is studied in relation to the measurement accuracy. Therefore, experiments need to be conducted at sufficiently high temporal resolution in order to be able to decouple the effects of the latter from the above ones.

The material derivative evaluation along a fluid particle trajectory can be performed only if the time evolution of three-component velocity vector is measured inside a volume, such as obtained by TR-TOMO PIV. In particular, between two time instants t ₁ and t ₂, the 3-D trajectory $\Upgamma$ (see Fig. 1) can be reconstructed only between P ₂ and P ₃, that is inside the measurement domain $x_{V}\times y_{V}\times z_{V}$. On the other hand, the reconstruction of $\widehat{P_{1}P_{2}}$ and $\widehat{P_{3}P_{4}}$ is done respectively using the measurement performed on adjacent fluid particle trajectories $\Upgamma ''$ and $\Upgamma '$ that are inside the measurement volume when $\Upgamma$ is, respectively, still or already out (see trajectory projections $\Upgamma^{\prime\prime}_{XZ}$ and $\Upgamma^{\prime}_{XZ}$). Thus, for a planar measurement, the reconstruction of 3D-flow trajectories is not possible (Liu and Katz 2006).

Fig. 1

Three-dimensional fluid particle trajectory $\Upgamma$ (continuous black line) and its projections on plane x-y and x-z. In gray the domain of measurement

Substituting (2) in (1), it follows that the planar pressure gradient reads as

$$ \frac{\partial p}{\partial x}=-\rho \left[ \frac{\partial u} {\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} \right] $$

(6)

$$ \frac{\partial p}{\partial y}=-\rho \left[ \frac{\partial v} {\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} \right]. $$

(7)

In the above equations, the viscous term is not included as commonly assumed in other studies at Re > 10³ (Haigermoser 2009; de Kat et al. 2009; Koschatzky et al. 2010; Lorenzoni et al. 2009).

It is observed that planar measurements of 3D flow, providing two- or three-component velocity vector fields, result in an approximated evaluation of the planar pressure gradient distribution. On the contrary, tomographic ones return the complete velocity vector and the complete velocity gradient tensor, in turn enabling the determination of the pressure gradient under more general hypotheses.

2.2 Material derivative evaluation

2.2.1 Lagrangian approach

The Lagrangian evaluation of the material derivative along a fluid particle trajectory $\Upgamma$ is performed calculating the first order velocity difference:

$$ \frac{D {\bf V}}{D t}({\bf x}, {t_{0}}) \approx \frac{({\bf V}_{2} - {\bf V}_{1} )}{(t_{2}-t_{1})}=\frac{\Updelta{\bf V}}{\Updelta t} $$

(8)

In the equation above, ${\bf V}_{1} = {\bf V}({\bf x}_{1}, t_{1})$ and ${\bf V}_{2}={\bf V}({\bf x}_{2}, t_{2})$ are the fluid particle velocities at subsequent time instants and $\Updelta t$ is referred to as temporal separation.

The material derivative evaluation along a fluid particle trajectory is performed by two subsequent steps: the reconstruction of the fluid particle trajectory and the evaluation of velocity finite difference. Therefore, each of these two operations is a possible source of precision and truncation errors.

Figure 2a illustrates the effect of the time separation $\Updelta t$ between two subsequent velocity measurements on the trajectory reconstruction in terms of truncation error. Considering vector V ₁ and V ₅ to reconstruct the trajectory, then, according to the reconstruction by central scheme

$$ {\bf x}_{5}={\bf x}_{K}+{\bf V}_{3} \frac{\Updelta t_{15} }{2} $$

(9)

$$ {\bf x}_{1}={\bf x}_{K}-{\bf V}_{3} \frac{\Updelta t_{15} }{2}, $$

(10)

the truncation error is $\overline{HK}(O(\Updelta t^{2})$). When the time separation between velocity measurements is shorter, which is for example the case of V ₂ and V ₄, the truncation error reduces to $\overline{H'K}$.

Fig. 2

(a) Fluid particle traveling across the measurement domain (in gray); (b) uncertainty of velocity measurements; Lagrangian velocity variations: (c) $\Updelta t=2 \delta t$ and (d) $\Updelta t=4 \delta t$

In the same way, if a short temporal separation is employed, also the material derivative evaluation benefits of low truncation error.

Considering that PIV measurement uncertainty on the displacement field is $\mu=0.1\,\hbox{pixel}$ (Willert and Gharib 1999), the velocity uncertainty, indicated in Fig. 2b with a circle, is given by

$$ \varepsilon_{V}=\frac{\mu \cdot pxs}{\delta t}, $$

(11)

where pxs is the pixel or voxel size in physical units and δt is the pulse separation time.

The evaluation of the trajectory and the velocity variation will be affected by precision error. When the latter is computed with a short temporal separation, for example by means of V ₂ and V ₄, it is likely that its magnitude is comparable to the velocity uncertainty (see Fig. 2c) therefore yielding high relative precision error in the material derivative. Higher temporal separations, instead, typically lead to larger velocity variations (see Fig. 2d) and, consequently to more accurate evaluations of the Lagrangian acceleration.

The effect of the time separation on the precision and the truncation errors is inverse: to define the time separation to be used in practical application, it is now proposed a criterion limiting the total error affecting the material derivatives.

The total error on the material derivative is given by the sum of precision ε _p and truncation error ε _t . The precision error is defined by

$$ \varepsilon_{p}=\left ( \frac{D {\bf V}}{D t} \right )_{{\hbox{measured}}} - \left ( \frac{D {\bf V}}{D t} \right )_{{\hbox{actual}}} $$

(12)

In relative terms, the above reads as

$$ \varepsilon_{r}=\frac{\left ( \frac{D {\bf V}}{D t} \right )_{{\hbox{measured}}} - \left ( \frac{D {\bf V}}{D t} \right )_{{\hbox{actual}}}}{\left ( \frac{D {\bf V}}{D t} \right )_{{\hbox{actual}}}}. $$

(13)

Recalling the velocity uncertainty ε _V , the relative precision error can be estimated as

$$ \varepsilon_{r}=\frac{\varepsilon_{V}/\Updelta t}{\left ( D {\bf V}/D t \right )_{{\hbox{ref}}}} $$

(14)

where $\left ( D {\bf V}/D t \right )_{{\hbox{ref}}}$ is the value of reference for the material derivative.

Considering that dominant flow structures are responsible for the largest pressure variation at the airfoil surface, from dimensional analysis, it is obtained that

$$ D {\bf V}/D t=O \left ( U_{\infty}f_{{\hbox{shed}}}\right ) $$

(15)

where U _∞ and f _shed are, respectively, the free-stream velocity and the shedding frequency of Kármán vortices.

The criterion to employ on the material acceleration reads as

$$ \varepsilon_{r}\le10\%, $$

(16)

from which

$$ \varepsilon_{p}\le0.1 U_{\infty}f_{\hbox{{shed}}}. $$

(17)

Recalling Eq. (14), it is obtained the minimum time separation to evaluate the Lagrangian acceleration:

$$ \Updelta t_{{\hbox{min}}}=\frac{1}{0.1}\frac{\varepsilon_{V}}{f_{{\hbox{shed}}}U_{\infty}}. $$

(18)

A conservative estimate of ε _V for TOMO-PIV experiments can be inferred from the a-posteriori analysis by Scarano and Poelma (2009) who reported 0.1 voxels of error for x and y displacement, and 0.15 voxels for the z one.

On the other hand, the time separation must not be longer than a maximum value $\Updelta t_{{\hbox{max}}}$, the time needed by a fluid particle to cross the measurement domain along the thickness z _V :

$$ \Updelta t_{\hbox{{max}}}\approx\frac{z_{V}}{|w|} $$

(19)

where |w| is the typical value of the out-of-plane velocity. A conservative estimate of |w| is given in Lorenzoni et al. (2009) who found that w is 25% maximum of the free-stream velocity. When the time separation does not satisfy (19), as, for example, in the case of $\Updelta t=6\delta t$ (see vectors V′₁ and V′₅ in Fig. 2a), the Lagrangian tracking cannot be performed since the fluid particle exits the domain.

When the acquisition frequency is $f\ge\frac{1}{\Updelta t_{{\hbox{min}}}}$, the method based on multiple velocity measurements (Moore et al. 2010) can be employed to reduce the truncation error in the trajectory evaluation as well as to take advantage of long time separation such to reduce the relative precision error in the material acceleration. In fact, if the material acceleration is for example computed with a time separation of 4δt (see Fig. 3 where δt = 1/f), by the multi-step method, the trajectory is reconstructed using V ₂ and V ₄ in addition to V ₁ and V ₅. Hence, compared to the single-step approach, the truncation error is $\overline{HK}$ instead of $\overline{H'K'}$, which, in general terms means that, when $\Updelta t=N/f$, the use of the multi-step approach reduces the truncation error of a factor N.

Fig. 3

Comparison between single-step and multi-step method for trajectory evaluation

2.2.2 Eulerian approach

The Eulerian evaluation of the material derivative through Eq. (2) is subjected to a different treatment of the error propagation, and the criterion for an accurate measurement is here compared to that defined for the Lagrangian approach.

According to Nyquist–Shannon sampling theorem, the smallest flow scale of wavelength λ that is resolved by PIV measurements is

$$ \lambda \approx 2l $$

(20)

where l is the dimension of the smallest interrogation window employed for the cross-correlation.

Considering also that the flow structures are convected by the mean flow U _conv, as illustrated in Fig. 4, the material acceleration can be accurately evaluated if the time separation $\Updelta t$ is such that

$$ \Updelta t \leq C \frac{2l}{U_{{\hbox{conv}}}}. $$

(21)

Fig. 4

Convected vortex at three subsequent time instants

In the above, the constant C must be chosen between 0 and 1 to ensure that both the Eulerian acceleration and the advection term of Eq. (2) are evaluated on the same flow structure. In particular, in order to linearly approximate the velocity gradient with low truncation error $O(\Updelta x)$, C must be smaller than 0.25 (see Fig. 4).

In many practical situations, however, the time requirement expressed in Eq. (21) and the condition of velocity variation measurability of Eq. (18) are conflicting and they cannot be respected at the same time.

3 Experimental set up

Experiments are carried out in the open test section of a low-speed wind tunnel ($0.4\times 0.4\,\hbox{m}^{2}$) at the Aerodynamic Laboratories of TU Delft Aerospace Engineering Department.

A Plexiglas NACA0012 airfoil of 0.1m chord length c is horizontally placed at zero incidence 0.104 m in the wake of a cylindrical rod ($d =0.01\,\hbox{m}$), which is 0.195 m far from the wind tunnel exit (see Fig. 5). The rod and the airfoil are in line with each other.

Fig. 5

Sketch of the rod-airfoil configuration

The configuration is tested for a nominal free-stream velocity of 5 m/s, yielding a Reynolds number of 3500 on the rod diameter. The regime of flow motion past a rod is referred to as shear layer transition (Williamson 1996). Kármán vortices are shed from the rod with a frequency of 100 Hz, which corresponds to a highly tonal noise generated by the interaction of the vortex on the airfoil leading edge (Table 1).

Table 1 Experimental conditions

The thin-light volume is formed at the leading edge of the quarter span section of the airfoil on the side of cameras, section still immersed in the inner core of the wind tunnel jet (see Fig. 6). A knife-edge slit is added in the path of the laser light sheet to cut the low intensity lobes from the light profile and create a 3-mm-thickness sheet. The imaged particle concentration is 0.06 particles per pixel (ppp) corresponding to 5 particles/$\hbox{mm}^{3}$.

Fig. 6

Sketch of rod-airfoil tomographic experiment set up

Four high-speed cameras, subtending a solid angle of $35\times35\,\hbox{deg}^{2}$, record 12-bit images of tracer particles and the objective numerical aperture is set for a focal depth matching the light sheet thickness. Sheimpflug adapters are used to align the focal plane with the midplane of the illuminated volume. Sequences of 5,000 image quadruplets are acquired in continuous mode at 5 kHz, yielding a normalized sampling rate of f ^* = 50, where f ^* is the ratio between acquisition and shed frequency (Table 2).

Table 2 Experimental settings

3.1 Tomographic reconstruction

The MART algorithm (Herrmann and Lent, 1976), which is implemented in LaVision Davis 7.4, is used to reconstruct the 3D-light intensity field. A total of 5 iterations of the algorithm are performed with a diffusion parameter of 0.5 for the first three.

Prior to the volume reconstruction, the 3D calibration function is corrected by the volume self-calibration to minimize the disparity fields, decreasing in the calibration error from a typical value of 0.5–0.1 pixel (Wieneke 2008). The accuracy of the reconstruction object is improved by means of image pre-processing with background intensity removal and non-linear subsliding minimum subtraction (11 × 11 kernel size).

Volumes of $50 \times 50 \times 3\,\hbox{mm}^{3}$ discretized with 831 × 831 × 50 voxels are then obtained applying a pixel to voxel ratio of 1. The resulting voxel size is 59 $10^{-3}\,\hbox{mm}/\hbox{vox}$.

The a-posteriori evaluation is made by means of the analysis of the reconstructed object intensity levels. The particle average peak intensity in a cross-section of the volume is displayed in Fig. 7 (left) from which it can be deduced that light is concentrated within 50 voxels (≈3 mm) at a slight angle with respect to the calibration plane. The reconstructed region is sketched along the boundaries of the illuminated region. The peak intensity profile is extracted and normalized (Fig. 7 right), yielding a signal-to-noise ratio (SNR) above 2 within a thickness of 30 voxels (1.8 mm) where, therefore, the measurement is considered reliable.

Fig. 7

Left: reconstructed particle peak intensity distribution averaged along y-axis (black box indicates the reconstructed region); right: normalized particle peak intensity <E^*> profile along z-axis to indicate the signal-to-noise ratio

3.2 3D-Vector field computation

Three-dimensional particle field motion is computed by spatial cross-correlation of pairs of reconstructed volumes with VODIM software (Volume Deformation Iterative Multigrid, developed at TU Delft), an extension to volumetric intensity fields of the window deformation technique for planar cross-correlation (Scarano and Riethmuller 2000). Interrogation boxes of size decreasing from of 201 × 201 × 21 to 47 × 47 × 19 and 75% overlap between adjacent interrogation boxes produce a velocity field measured over a grid of 66 × 66 × 6 points. At the given particle concentration, an average of 50 particles are counted within the smallest interrogation box.

Data processing is performed by in parallel with a dual quad-core Intel Xeon processors at 2.66 GHz with 8 GB RAM memory requiring 2 and 2.5 min for the reconstruction of a pair of objects and 3D cross-correlation, respectively. Noisy fluctuations of the velocity vectors are reduced by applying a space–time regression, a second-order polynomial least-square fit over a kernel of 5 spatio-temporal samples (Scarano and Poelma 2009).

3.3 Pressure field determination

As the velocity domain is rather thin (just 6 measurement points along z-axis), the Lagrangian evaluation of the material derivative and, as consequence that of the pressure, is done on the mid z-plane of the domain where it is less likely that the fluid particles exit the domain at a given $\Updelta t_{\hbox{{min}}}<\Updelta t<\Updelta t_{\hbox{{max}}}$ (see Sect. 2.2.1). In particular, the integration is performed on the third z-plane where regions affected by measurement noise are avoided. In Fig. 8, the integration domain is sketched and the Neumann and the Dirichlet boundary conditions are specified.

Fig. 8

Boundary condition of Neumann (dashed line) and Dirichlet (solid line). In gray the measurement domain

4 Results

A total of 100 shedding cycles are determined, each of which is described by 50 samples, ten times higher than the sampling rate used by Lorenzoni et al. (2009).

The spatial sampling rate of the velocity field, on the other hand, is 1.4 vectors/mm along x and y-direction and 3.4 vectors/mm along z, resulting from non-cubic interrogation boxes.

With respect to the reference velocity V _ref of 16 voxels at point (x/c =  −0.24, y/c =  −0.4), the velocity measurement uncertainty is 1%. In the following, V _ref will be referred to as U _∞.

4.1 Velocity field

In the region in front of the airfoil ($x/c \le 0;0.04 \le y/c \le -0.08$, Fig. 9), the mean flow is characterized by a decrease of u-velocity component leading to the stagnation point where the vertical velocity component rises in magnitude identifying a region of upward acceleration and one of downward. Flow symmetry is observed for the w-component which is affected by measurement errors not exceeding 1% of U _∞. From contours of turbulent kinetic energy,

$$ k=\frac{1}{2}\left( \sqrt{\overline{u^{\prime 2}}}+\sqrt{\overline {v^{\prime 2}}}+\sqrt{\overline {w^{\prime 2}}} \right) $$

(22)

(see Fig. 9), intense turbulent motion is detected ahead of the airfoil in the region corresponding to the von Kármán wake shed from the rod.

Fig. 9

Mean velocity components and normalized turbulent kinetic energy on the midplane

The wake is constituted by counter-rotating vortices which interact with the airfoil leading edge, as shown in the sequence of snapshots of Fig. 13 (first row) by contours of the out-of-plane vorticity component. Time instant t is normalized with respect to the shedding period T yielding t* = t/T.

Measurements performed in the region corresponding to the laser shadow (in gray, see Fig. 9) are not reliable and therefore are avoided from the analysis. Additionally, velocity derivatives are not performed near by the boundaries of the measurement domain since velocity vectors are typically affected by noise (in gray, see Fig. 13).

4.2 Material velocity derivative

From dimensional analysis discussed in Sect. 2.2.1, it results that, in order to limit the relative precision error to 10% maximum, ensuring that the z-displacement of the trajectory is shorter than z _v  = 30 voxels, the time separation to be used for the Lagrangian evaluation of the material acceleration must be chosen between 0.6 and 1.5 ms, according to Eqs. (18 and 19). In contrast, with respect to the estimation proposed in Sect. 2.2.2, when the Eulerian approach is used, the time separation must not be larger than 0.3 ms. This conflicts with the condition of velocity measurability, $\Updelta t\ge 0.6\,\hbox{ms}$ (see Eq. (18)), and it leads to material acceleration affected by 20% in precision error.

Time separation constraints estimated for both the approaches are now verified by an a-posteriori analysis. Using the standard deviation $\sigma_{\Updelta u}$ as an estimate of the typical velocity variation within $\Updelta t,\left (\frac{DV}{Dt} \right )_{\hbox{{ref}}}$ of Eq. (14) can be rewritten as

$$ \left (\frac{DV}{Dt} \right )_{\hbox{{ref}}} \approx \frac{\left ( \Updelta V \right )_{\hbox{{ref}}}}{\Updelta t} \approx \frac{\sigma_{\Updelta u}} {\Updelta t} $$

(23)

In the above, velocity variations are evaluated along fluid particle trajectories when the approach is Lagrangian, or at fixed point when it is Eulerian.

4.2.1 Lagrangian approach: a-posteriori analysis

Considering point B(x/c = −0.077; y/c = −0.033) as representative of the region of intense turbulent motion ($\frac{k} {U_{\infty}}=0.15$, see Fig. 9). In voxel units, the standard deviation evaluated within a time interval of $1/f=0.2\,\hbox{ms}$ is 0.29 voxels. Therefore, it would result material acceleration affected by 34% of relative precision error. On the contrary, to restrict this to values not larger than 10%, according to Eq. (14), where $\left (\frac{DV}{Dt} \right)_{\hbox{{ref}}}$ is given by Eq. (23), the time separation must be sufficiently large to have $\sigma_{\Updelta u}\geq$ 1 voxel. This is measured for $\Updelta t \ge0.8\,\hbox{ms}$, which is in agreement with the estimation made a-priori by Eq. (18).

Considering the Euclidean norm |w′| of the mean and the fluctuating value of the w-velocity component,

$$ |w'|=\sqrt{\bar{w}^{2}+w^{\prime 2}}, $$

(24)

as an estimate of the out-of-plane motion at point B. Typically, fluid particles move of 30 voxels along z-direction in a time interval of 3.4 ms. However, to avoid the evaluation of the trajectory by velocity vectors at domain border, as affected by noise, the maximum time separation is reduced to 1.5 ms, which leads to typical z-displacements of 15 voxels. In the legend of Fig. 10 (top), standard deviation of velocity variation $\sigma_{\Updelta u}$ and |w′| are reported, in voxel unit, for each time separation.

Fig. 10

Time histories and corresponding probability density function of x-component of material velocity acceleration at point B using different time separation: (top) Lagrangian approach with MS scheme; (center) Lagrangian approach with LO and MS scheme; (bottom) comparison between the Lagrangian MS and the Eulerian approach

In Fig. 10 (top), the time history of x-component material velocity derivative at point B is plotted for time separation ranging between 0.2 and 3.2 ms. While for $\Updelta t=0.2\,\hbox{ms}$ and 0.4 ms, strong oscillations are exhibited because of $\sigma_{\Updelta u}$ typically smaller than 1 voxel, when the time separation is larger than 0.8 ms, such as 1.2 ms, the Lagrangian derivative features trends gradually smoother meaning of a decreasing relative precision error. The effect of $\Updelta t$ on the trend of the Lagrangian velocity derivative can be also observed from the plot of probability density function: longer time separations leads to narrower Gaussian distributions as consequence of smoother trends.

For $\Updelta t\geq 1.5\,\hbox{ms}$, e.g. $\Updelta t=$ 2.4 and 3.2 ms which are not accepted because leading to z-displacement larger than z _v /2, rising truncation error is observed, for example, between 0 and 3 ms (see Fig. 10 top).

For the present investigation, the time separation is chosen to be 1.2 ms which, at point B, leads to a relative precision error of 8%. This, however, increases to 26% at point A (x/c = 0.023; y/c = −0.028, $\sigma_{\Updelta u}=0.38\,\hbox{vox}$), which is representative of the region out of the Kármán wake and where the turbulent activity is 66% lower compared to that at point B (see Fig. 9). In Fig. 11, relative precision error at point A and B is plotted against time separation.

Fig. 11

Relative precision error on the material derivative evaluated by the Lagrangian approach (MS)

The time history of the Lagrangian velocity derivative computed by single-step scheme (LO) and by the multi-step scheme (MS) proposed Moore et al. (2010) is illustrated in Fig. 10 (center). The two approaches lead to very similar results. This results from the velocity time resolution which is sufficiently high that the use of the multi-step scheme does not lead to a reduction in the truncation error of the evaluated trajectories. Under such a condition, therefore, it is possible to decouple the investigation of the time separation on material derivative and pressure fields from that focused on the effects of flow three-dimensionality.

4.2.2 Eulerian approach: a-posteriori analysis

In an a-posteriori analysis of the time separation to employ in the Eulerian approach, the convection velocity U _conv (see Eq. (21)) can be estimated by the local mean velocity component $\bar{u}$. This, at point B is, in voxel units, 10.5 voxels leading to a maximum time separation of 0.4 ms which confirms the a-priori estimation discussed in Sect. 2.2.2. However, since the typical velocity variation measured within 0.4 ms is $\sigma_{\Updelta u}=0.65\,\hbox{voxels}$, the material acceleration is affected by 15% precision error. To comply with the condition restricting the relative precision error to 10%, it would be requested to employ a separation time not smaller than 1ms which is clearly in contrast to the condition (21).

4.2.3 Comparison

Compared with the minimum time separation allowed for the Lagrangian approach, that maximum for the Eulerian one is two times shorter yielding material acceleration with a relative precision error at point B 1.5 times larger than that estimated for the Lagrangian approach.

In Fig. 10 (bottom), the time history of the material acceleration at point B computed by both Eulerian and Lagrangian approach is plotted for time separation of 0.4 and 1.2 ms. Curves corresponding to the shortest $\Updelta t$ show a marked jigsaw-like behavior that are characterized by similar trend and statistical dispersion. When the material acceleration is calculated using $\Updelta t=$ 1.2 ms, as condition (21) is not satisfied, the Eulerian approach provides a noisy solution with standard deviation 25% larger than that corresponding to the Lagrangian one. Still, while in this case a decrease in $\sigma_{\Updelta u \slash \Updelta t}$ of 27% is observed when passing from a $\Updelta t=$ 0.4 to 1.2 ms, for the Eulerian approach, the reduction is of 14%.

In Fig. 13 (second and third row), a sequence of instantaneous contours of material acceleration is shown for both the Lagrangian and the Eulerian case. In the region of the Kármán wake and in that by the leading edge, as already seen at point B (Fig. 10 bottom), the Eulerian evaluation leads to noisy fields where, compared to the Lagrangian one, no flow-structure convection is detected.

4.3 Pressure field determination

The last step of the procedure consists in the spatial integration of Eq. (3) on the mid z-plane. In Fig. 14 (first row), the sequence of pressure fluctuation contours corresponding to those of vorticity is depicted to highlight the relation between cinematic and thermodynamic field. They are evaluated by means of the Lagrangian approach employing multi-step scheme with $\Updelta t=1.2\,\hbox{ms}$.

Compared to those obtained by the Lagrangian method, the pressure fields evaluated by means of the Eulerian approach with $\Updelta t= 0.4\,\hbox{ms}$, as illustrated in Fig. 14 (first and second row), show differences in the contour patterns, although less marked than those observed for the material derivative (Fig. 13). To have a more quantitative understanding of the influence of the two approaches on the pressure field, the pressure time histories at point B corresponding to those of material acceleration of Fig. 10 (bottom) are plotted in Fig. 12. Similarly to what observed for the material acceleration, when a time separation of 0.4 ms is employed, both the approaches lead to oscillating results with comparable values of standard deviation. In the Lagrangian approach, an increase in $\Updelta t$ from 0.4 to 1.2 ms leads to a reduction in standard deviation of the pressure signal of 30%, similarly to what observed for the material acceleration. By contrast, in case of the Eulerian approach, the drop is of 25%, which is approximately the double of the reduction observed for the corresponding material acceleration. This smoothing effect might be due to the integration method, on which no further investigation has been conducted within this paper.

Fig. 12

Time histories and corresponding probability density function of pressure fluctuation at point B resulting form the Lagrangian (MS) and the Eulerian approach

Fig. 13

Sequence of instantaneous out-of-plane vorticity component contours with velocity vectors in a convective frame of reference u = 0.2U _∞ (first row); contours of material acceleration inferred from 3D velocity field by means of the Lagrangian approach$@\,\Updelta t=$ 1.2 ms (second row) and the Eulerian approach$@\,\Updelta t=$ 0.4 ms (third row)

Fig. 14

Sequence of instantaneous pressure fluctuation contours inferred from 3D velocity field by means of the Lagrangian approach$@\,\Updelta t=$ 1.2 ms (first row) and the Eulerian approach$@\,\Updelta t=$ 0.4 ms (second row)

4.4 3-D flow effects

A synchronous planar and tomographic PIV measurement is simulated in order to evaluate 3-D flow effects on the pressure field. Volumes of 831 × 831 × 17 voxels, corresponding to $50 \times 50 \times 1\,\hbox{mm}^{3}$ are extracted from the central z-position of the reconstructed tomographic objects. The imaged particle intensity levels are summed along z in a Gaussian way and are cross-correlated with interrogation windows of size identical to the x-y dimensions of the interrogation boxes (see Sect. 3.2). An average of 50 particles are counted in the smallest interrogation window.

A Lagrangian approach is used to evaluate the material acceleration. This, however, is evaluated along the projection of particle trajectories on the measurement plane, as only two velocity components can be measured by planar PIV.

Three- and two-dimensional-based material acceleration and pressure fluctuation show similar pattern, as illustrated in Fig. 15 where the flow quantities are plotted along y/c = −0.125 at t* = 0.72 (see Figs. 13 and 14). In general, the similarity is observed at each point of the integration plane and for all the time instants.

Fig. 15

Material acceleration (left) and pressure fluctuation (right) inferred from 3D and 2D velocity field at y/c=−0.125

To further investigate the effect of flow 3-D on the Lagrangian approach, tomographic PIV data of a cylinder wake at Re = 540 are used. The attention is focused upon a subregion of 61 × 48 × 27 measurement points containing a vortex, which is located 5 cylinder diameters (d _R ) downstream. Details of the experiment are given in Scarano and Poelma (2009).

Compared to TOMO-PIV measurements obtained in thin-light volume configuration, the ones performed on the cylinder wake enable the evaluation of the pressure field also on planes which are not aligned with the dominant flow direction. As each shedding cycle is sampled approximately 9 times, the evaluation of the material acceleration is performed by single-step scheme (LO) without any substantial rise in truncation error (see Sect. 4.2.1). The pressure field is integrated on the planes y/d _R  = 5 and z/d _R  = 0 using the corresponding planar subsets of two-component velocity (respectively called as 2Dy and 2Dz) and the tomographic data (3D). 2Dy-, 2Dz- and 3D-based material acceleration and pressure field are compared along the intersection of the aforementioned planes (see Fig. 16). In case of 2Dy subset, errors are typically smaller than 20% similarly to what observed for the rod-airfoil flow. In contrast, if the planar subset is not parallel with the y-plane, which is the dominant direction of flow, the error increases, meaning of a larger influence of the out-of-plane velocity component on the trajectory reconstruction. On plane z/d _R  = 0, for example, the 2D-based evaluation lead to an error of 100%. Similar behavior is observed for the pressure field which is integrated assigning boundary condition of Dirichlet $\Updelta p=$ 0 at point (x/d _R  = 4.71, y/d _R  = 5, z/d _R  = 0) and Neumann along the domain boundaries. Moreover, 3D-based pressure fluctuation evaluated on plane y/d _R  = 5 and on plane z/d _R  = 0 (respectively 3Dy and 3Dz, see Fig. 16 right) show small differences, as a result of the error introduced by the pressure integration method.

Fig. 16

Cylinder wake vortex: 3D- and 2D-based material acceleration (left) and pressure (right) along streamwise direction

5 Conclusions

This paper describes an experiment performed on a rod-airfoil flow by means of TR-TOMO PIV in thin-light volume configuration. Being a 3-D measurement technique, TR-TOMO PIV, when performed at time rate of sampling sufficiently high, enables the detection of the unsteady and the 3-D nature of the turbulent flow motions typical of the rod-airfoil configuration. In fact, unlike planar measurements where only two velocity components are available, it provides all the velocity information for the Lagrangian evaluation of the instantaneous pressure field.

A criterion restricting the relative precision error to 10% on the Lagrangian velocity derivative is proposed to determine the time separation in which performing the evaluation along the particle trajectories. The effect of $\Updelta t$ on the material derivative is analyzed in terms of relative precision error, and 1.2 ms is finally chosen. On the other hand, when an Eulerian approach is employed, the time separation is limited to 0.4 ms in order to evaluate the Eulerian acceleration and the advection term on the same flow scales. Under such a condition, the method yields a relative precision error of 15%.

Material velocity derivative and pressure fluctuation evaluated from tomographic measurements in a Lagrangian manner feature patterns similar to those obtained from planar ones as long as the measurement plane is aligned with the dominant flow direction. Instead, if the condition of alignment is no longer satisfied, which means that the out-of-plane velocity component becomes not negligible with respect to the others, the Lagrangian approach based on planar measurements leads to an erroneous evaluation of the material acceleration and the pressure field.

Further investigations are needed to quantify the effects of the pressure integration method.

In the present study, noise prediction by means of Curle’s analogy is not performed because flow velocity measurements are available on a limited portion of the airfoil surface. Nevertheless, the demonstration of the necessary steps for a Lagrangian evaluation of the pressure fluctuation field based on TR-TOMO PIV velocity data suggests that further investigations are needed to extend the process up to the determination of the source term of Curle’s analogy. This combined with TR-TOMO PIV has the potential to be a powerful tool to predict noise, to identify the source of sound and to understand the noise generation mechanism.