Abstract
Laser-induced incandescence at high-repetition rates can in principle be used to resolve the temporal evolution of soot processes. The intrusive character of this technique, however, requires due care of historical effects associated with multiple exposures of individual soot particles to laser light. On the other hand, repetitive heating and cooling opens up an independent, acoustic detection channel. We illustrate a photo-acoustic soot volume fraction measurement, and show that the comparison to simultaneously recorded laser-induced incandescence provides qualitative information on soot growth. Experiments are performed on a propane-fueled, co-flow stabilized diffusion flame, and signals are collected at varying heights above the burner deck. Results show a clear correlation between the laser-induced incandescence and photo-acoustic signals; small deviations are interpreted as a qualitative indicator for the particle size.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Laser-induced incandescence (LII) is one of the few optical techniques suited for in situ studies of soot in combustion. It is a relatively brute force technique, and, contrary to many other optical diagnostics, cannot be considered as non-intrusive. The basic principle of LII is rapid heating of particles by means of a short, intense laser pulse, and recording the increased incandescence. Typically, only a small part of the full spectral range of the incandescence is recorded; this reduces the risk of interference by stray laser light or inadvertent laser-induced fluorescence, but also aggravates the dependence on particle temperature. By integrating the LII signal over time a measure of the soot volume fraction is obtained, whereas the decay of the incandescence over time contains information on the primary particle size.
In principle, LII can be implemented using high-repetition rate excitation and detection, to follow the soot volume fraction evolution over time in non-stationary combustion processes, like they occur in, e.g., internal combustion engines [1,2,3]. The intrusiveness of LII, however, now requires extra caution in the interpretation of the LII signal. When the contents of the probe volume are not refreshed between consecutive excitation laser pulses, the same soot volume will be probed multiple times. Since it is well known that soot particles are considerably modified by the excitation in an LII experiment [4, 5], it is unlikely that a single soot particle will respond identically upon multiple exposures [6]. However, excitation at high-repetition rates renders another, independent detection method feasible, viz. acoustic detection, of which only a limited number of reports are published to date [7, 8]. Sending high-frequency laser pulse trains through a sooting flame will produce a sound wave that is easily detectable by a microphone, or even by ear. This method of generating a photo-acoustic (PA) signal is illustrated in Fig. 1. In the absence of sublimation, achieved by selecting a sufficiently low fluence, conduction is the major heat loss channel for laser-heated soot [9], and the sound is associated with the repetitive heating and cooling of the gas surrounding the excited soot particles.
Both the increased luminescence intensity and the sound intensity will depend on the local soot volume fraction in the probe volume. This information, however, is presented in different forms. The acoustical signal strength is a measure for the energy lost by the heated soot particles to the surrounding gas, whereas the optical signal is due to light emission in a certain wavelength band. In this paper, we present an experimental comparison of laser-induced incandescence and photo-acoustic measurements on a sooting diffusion flame stabilized by a co-flow of the air. We will argue that the acoustic signal is in fact a more direct representative for the soot volume fraction than the induced incandescence. A direct comparison of the acoustical and optical signals reveals small differences, which can be related to soot particle size. In the following, we will briefly describe the physics behind LII and PA, and the experimental setup. Subsequently, the laser-induced incandescence and photo-acoustic soot measurements on a propane diffusion flame at 5 kHz repetition rate are presented and discussed.
2 Theory
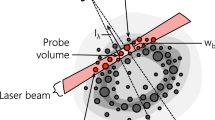
The idea of LII as a tool for soot diagnostics was introduced by Melton [10], who laid the foundation for a computational model that can be used to predict the LII signal. Over the following years, this model has been discussed and refined by various authors [11, 12]. We will consider only a limited model here following parts of the treatment by Michelsen et al. [12]. Figure 1 depicts the main heat transfer mechanisms during and after laser heating, being absorption and conduction. These mechanisms will determine the particle temperature evolution, and have distinctive dependencies on particle size [13]: a feature that is utilized when determining volume fractions and particle sizes. A simplified form of the differential equation Melton proposed is expressed by
where \(\dot{U}_{\mathrm{{int}}}\) is the rate of change in internal energy of a soot particle, \(\dot{Q}_{\mathrm{{abs}}}\) is the rate of absorption of laser light, \(\dot{Q}_{\mathrm{{con}}}\) is the conduction rate from particle to ambient gas, \(\dot{Q}_{\mathrm{{sub}}}\) is the heat loss rate due to sublimation of carbon from the particle surface, and \(\dot{Q}_{\mathrm{{rad}}}\) is the rate of energy loss by thermal radiation. All heat fluxes have been taken as positive, and their sign in (1) determines whether it is a loss or a gain term. The radiation term is often neglected in the energy balance, since its contribution to the cooling rate is several orders of magnitude smaller than the conduction losses.
Equation (1) merely states that the rate of change in internal energy is equal to the net amount of heat transfer to the soot particle, a fundamental consequence of the first law of thermodynamics. The rate of change of the internal energy is directly related to the rate of change of the particle temperature via
where \(\rho _\mathrm{{s}}\) and \(c_\mathrm{{s}}\) are the density and specific heat capacity of the soot particle, respectively. D is the particle diameter and \(\dot{T}\) is the temperature rise rate. Substitution of (1) into (2) provides an expression for the temperature rise rate:
where we have neglected cooling due to thermal radiation. The absorption of laser light, relevant only during an excitation laser pulse, is expressed by
where \(\eta _{\mathrm{{abs}}}\) is the absorption efficiency of a soot particle and \(\dot{F}\) is the temporal profile of laser fluence. For particles in the Rayleigh regime \((\frac{\pi D}{\lambda _{\mathrm{{ex}}}} \ll {1})\) [14], the absorption efficiency is computed using
Here, E(m) is the absorption function, and \(\lambda _{\mathrm{{ex}}}\) is the laser excitation wavelength. From (4) and (5), it follows that particles in the Rayleigh regime absorb laser energy at a rate proportional to their volume.
Although radiative heat losses are often neglected in the heat balance of a soot particle, it is the broadband thermal radiation that ultimately forms the LII signal. The spectral radiance of a black body is described by Planck’s law:
where h is the Planck constant, c is the speed of light in vacuum, \(\lambda\) is the radiation wavelength and \(k_\mathrm{{B}}\) is the Boltzmann constant.
Detection of the LII signal with a typical intensified camera is essentially an integration of Plancks law over a certain spectral detection band, time interval, and particle size distribution. Yet, soot is not a perfect black body, and thus, the spectral emissivity has to be taken into account. In addition, the spectral sensitivity and solid angle of the detection system limit the collection of signal. The resulting detected LII signal is expressed by
where \(\varDelta \lambda\) is the wavelength detection band (largely determined by the selection of filters), \(\varDelta t\) is the time interval of detection, \(\chi (\lambda )\) is the quantum efficiency of the detection equipment, \(\varOmega\) is the solid angle of detection, and \(\sigma (D)\) is the soot particle size distribution. The spectral emissivity \(\epsilon (\lambda )\) is expressed similarly to the absorption efficiency as
Substitution of (8) into (7), and assuming a narrow size distribution \(\sigma (D)\), in turn yields the proportionality:
where \(N_\mathrm{{p}}\) is the particle number density. The proportionality in (9) holds as long as the particle temperature is independent of its diameter. This is readily achieved using prompt, short detection intervals (i.e., ideally detect only during the laser pulse) and applying a sufficiently low laser fluence, such that the particle temperature remains well below 4000 K, and hence, cooling due to excessive sublimation is prevented [15].
To circumvent issues from shot-to-shot variations in laser intensity, Melton nonetheless applied a high fluence allowing sublimation to reduce the influence of these variations. Despite that this eased the interpretation of LII images, it did introduce difficulties for inferring soot volume fraction information. As the particles are exposed to a lot of laser energy, sublimation becomes increasingly influential in the heat balance, inducing significant temperature variations between particles of different sizes. Notably, it is the increasing cooling rate of smaller particles that endows the LII signal with a bias towards larger particle sizes [13]. Melton analyzed this feature and arrived at an alternate proportionality expressed by
where x is dependent on the choice of detection wavelength, and was determined to be
Here, \(\lambda _{\mathrm{{c}}}\) is the center wavelength (in nm) of the detection band. Hence, detection towards the red part of the spectrum can effectively reduce the bias in proportionality of the collected signal and soot volume fraction. Note that this deviation from an exact volume dependence arises from the detection step in LII. The photo-acoustic signal, on the other hand, is proportional to the pressure rise associated with the temperature rise of the ambient gas. Without any dependence on the wavelength of radiative emission, the acoustical signal exhibits a more direct relation with soot volume fraction. As long as conduction is the major heat loss channel for laser-heated particles, all heat input essentially ends up in the ambient gas. From (4) and (5), we can, therefore, expect the PA signal to be strictly proportional to the soot volume fraction.
Of course, there are some caveats to consider. First, microphones detect pressure variations, the amplitude of which depend on the cooling rate. Under atmospheric conditions, however, the characteristic cool-down time (the rate at which the particles dump the energy absorbed from the laser beam into the ambient gas) is always much smaller (in the order of 1 µs [16]) than the sound period. The sound wave frequency, of course, is equal to the laser pulse repetition rate (5 kHz in this case). The acoustic excitation can, therefore, be considered as instantaneous, independent of particle size. Second, the LII bias towards larger particles can be reduced using large detection wavelengths. This has several drawbacks. The experiment becomes more sensitive to background radiation by soot outside of the probe volume, intensified cameras are increasingly less sensitive, and the risk of fluorescence interference by mainly \(\hbox {C}_2\) (Swan bands) and polycyclic aromatic hydrocarbons increases. The latter can in turn be largely prevented using an Nd:YAG at its fundamental wavelength, as was done in this work. Moreover, in this particular case, there is information in the bias when compared to the photo-acoustic signal, so in fact, we use blue filtering to increase the bias. Following the approach of Mueller and Martin [17], the relation between LII signal and particle temperature for the detection system used in this work has been assessed, and was found to exhibit an approximate \(\hbox {T}^{14}\) dependence. It is thus expected that small variations in temperature between particles of different size classes result in considerable differences in radiation yield. Finally, it is not entirely clear what the effect of sublimation will be. Some of the absorbed energy is then lost on breaking bonds, and will contribute neither to the optical nor to the acoustical signal. Most of the experiments reported in this paper are performed at low fluence, so as to avoid sublimation.
3 Experiment
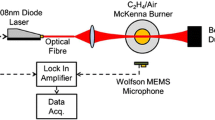
A schematic overview of the experimental setup is shown in Fig. 2. The laser was synchronized to the camera using a Stanford DG535 delay generator. The delay was set to exactly the period of the camera frame rate, resulting in a laser repetition rate that is half the frame rate of the camera. Synchronization of camera and laser system was further fine-tuned for prompt detection using a fast photodiode (Thorlabs DET10A/M). The 5/10 kHz approach allows to alternatingly collect LII images and background images, and hence enables individual correction for background luminosity for each laser shot. Each background luminosity image is simply subtracted from the preceding raw LII image, leaving only the laser-induced signal. A power meter was used to measure the average power output of the laser at regular intervals during a measurement series, using a flip mirror. Note that laser power information is thus not available for each individual shot.
3.1 Laser system
A diode-pumped Nd:YAG laser which is capable of repetition rates up to 10 kHz (Edgewave IS8II) is employed in the experiments. To reduce the influence of crosstalk from laser-induced fluorescence, the doubling crystal was removed from the laser, and it was used at its fundamental wavelength (1064 nm). A repetition rate of 5 kHz is selected for all measurements. With a full power capability of 70 W at the applied repetition rate, maximum energy amounts to 14 mJ per pulse. The width and height of the rectangular beam equal 8 and 3 mm, respectively, yielding a laser fluence of 0.058 \(\mathrm{{J}}/\mathrm{{cm}}^{2}\) at full power. Fluence was adjusted by controlling the diode current, which affects the laser pulsewidth. Temporal laser profiles were measured using a fast photodiode at various power settings, and the results are shown in Fig. 3, where it can be seen that the pulse width amounts to about 8 ns at full power. For simultaneous collection of LII and PA signals, no additional optics were used, and the laser was operated at full power. In some of the experiments treated in Sect. 4, however, the laser beam was focussed to increase fluence further. This will be stated where appropriate. The spatial beam profile is specified as top-hat along its width, while the opposite direction is showing a Gaussian intensity distribution.
3.2 Detection equipment
An 8-bit CMOS camera (Lambert HiCam 5000) fitted with a 50 mm Nikon AF Nikkor f/1.4 objective lens were used for LII imaging. The camera has a built-in second generation S20 intensifier that is capable of gating times down to 40 ns. Prompt detection (i.e., recording is started at the arrival of the laser pulse) with a 40 ns intensifier gate was applied in all measurements. Most of the background luminosity is rejected by a 450 nm short wave pass filter. The maximum frame size of the camera is \(512 \times 512\) pixels, but this setting only allows for a maximum frame rate of 5 kHz. Reducing the height of the frame provides the possibility of increasing the frame rate. A frame size of \(512 \times 256\) pixels was used, running at a frame rate of 10 kHz.
For collection of photo-acoustic signals, a Knowles EK23033 electret microphone was used, which was wired to a signal preamplifier and connected to a LeCroy WaveRunner 44MXi-S sampling oscilloscope. The microphone converts pressure differences to a voltage. The preamplifier in turn increases signal strength by a factor of 50. To be able to subtract background noise from the laser-induced signal, a reference measurement is taken without laser for each setting. A Fast Fourier Transform (FFT) is performed directly on the oscilloscope during the measurements. Only the intensity at 5 kHz originating from the laser-induced sound wave is used for further data analysis. Interpolation of the FFT spectrum is done to obtain the peak intensity at 5 kHz. The frequency response of the microphone is, therefore, not of importance, as the relative sound intensity is not biased by frequency-dependent differences in sensitivity. Each measurement point is run three times, and for each run, an average signal from 100 samples is taken from the scope. A similar procedure is applied to the LII measurements, where an ensemble average is taken over 100 consecutively collected images. LII and PA signals are recorded simultaneously at each location, so that the probe volume for both measurements is always exactly the same.
Figure 4 shows the FFT spectrum of a typical acoustical measurement. A distinct peak is seen at 5 kHz, corresponding to the laser-induced sound. A second peak is seen around 3.5 kHz, which was identified to be caused by the co-flow of air through the burner. Additional background signal is seen over the whole spectrum, although weak in intensity. A small peak at 10 kHz is attributed to the second harmonic of the fundamental 5 kHz excitation frequency. Obviously, the pulsed excitation process will not result in a purely sinusoidal sound wave, which explains the presence of higher harmonics.
3.3 Diffusion flames
Initial exploratory experiments were performed on a simple candle flame, as shown in Fig. 5a. These experiments served to identify potential multiple exposure effects when performing high-speed measurements on sooting diffusion flames. Thereafter, simultaneous LII and PA signals were collected on a more sophisticated diffusion flame burner (Fig. 5b), the flame of which is stabilized by a co-flow of the air. A schematic overview of the burner, including geometrical data, is shown in Fig. 6. Propane at high pressure is fed to the burner via a pressure regulator, and the flame height is manually controlled at 65 mm above the burner deck by adjusting the admitted fuel flow. Pressurized air at eight bar is administered to the co-flow channel. Flow homogenization is established by passing the air through several grids and porous materials before exiting at the burner deck. A glass cylinder shields the flame from ambient disturbances.
When operated at full power, the laser used in this work is able to considerably modify the appearance of a flame, as evidenced in Fig. 5. These images are made using a consumer DSLR (Nikon D7000) camera; details of exposure are shown in the images. Both recordings are taken under an approximate \(45^\circ\) angle with the laser beam, although at different orientations. In Fig. 5a, the laser beam passes the camera from the side, whereas in Fig. 5b, the beam travels towards the camera. Soot particles hit by a focused laser beam are essentially blown to pieces, giving rise to a strong decrease in flame luminosity, also in the region above the probe volume. Increased luminescence is observed only in illuminated regions of the flame, where laser intensity is low enough so as to only heat the soot, rather than destroy it. Interestingly, the strong temperature dependence of the soot luminosity amplifies small irregularities in the laser beam intensity profile, notably visible in Fig. 5b. Because these spatial beam non-uniformities are shown here to have a significant impact on the increased incandescence yield, they can easily dominate the structure observed in Fig. 5b. The combination of a sooting flame and DSLR camera can quickly provide some qualitative insight in the spatial laser beam profile, without the need for an expensive beam profiler.
4 Results
4.1 Multiple exposure effects
During a measurement, the laser probes a dynamic equilibrium in the flame. Fresh soot particles continuously are supplied at the bottom of the probe volume. Subsequently, they are hit several times by laser pulses, while they traverse the probe volume, eventually leaving it at the top. Thus, the recorded, quasi-steady signal is made up of contributions by both fresh and aged soot particles. To obtain a representative measurement, we need to know the effect of aging.
The convection speed of burning gases in a candle flame was determined by means of soot vaporization velocimetry, essentially introduced by Seitzmann et al. [18]. For this experiment, the position of the camera was changed, indicated by the shaded pictogram in Fig. 2, and the laser beam was strongly focused using a spherical lens. The idea is already illustrated in Fig. 5a. At high power, the laser burns away the soot that it hits, leaving a soot-free channel downstream. By suddenly switching off the laser, this channel is filled again with luminous soot particles by convection. This process can be followed by high-speed imaging, and the convection velocity can be estimated from the filling rate; see Fig. 7, where high-speed recordings of flame luminescence are depicted after the laser is shut down. Images are post-processed with a color map showing high and low intensities in red and blue, respectively. The height was determined by imaging a grid at the position of the flame. For the candle flame at ambient conditions, we find a speed of \(0.68 \pm 0.016\) m/s. Although this convection speed is not directly applicable to the co-flow burner, we argue that, due to the pressurized gas flow of the burner, its velocity is presumably higher. As a consequence, multiple exposure effects will be less significant.
Exploratory experiments on the candle flame were continued to assess the impact of multiple exposure effects. With a probe volume height of 3 mm and a laser repetition rate of 5 kHz, the convection speed found above implies that soot particles in the candle flame experience about 22 laser pulses while traversing the probe volume. Figure 8 shows how the quasi-equilibrium situation is reached. The laser is continuously pumped by diodes, but initially, the Q-switch is disabled by a trigger inhibit function on the delay generator. At \(t=0\), the Q-switch is suddenly activated, and the LII signal (integrated over the probe volume) is recorded for the subsequent individual pulses. This experiment is performed for various fluences at a constant full power setting of the laser (fluence is increased by focusing the laser beam). The results are compared in Fig. 8, normalized to the LII signal induced by the 10th laser shot. After only about 5–6 laser pulses, the system is seen to have reached a quasi-steady state. At low fluence, this state is reached following an initial rise of the LII signal, whereas at high fluence, it is the culmination of a decaying trend. Our interpretation of the trends in Fig. 8 is based on a balance between soot sublimation and ambient gas heating. At low fluence, the soot is heated relatively modestly, but otherwise essentially unmodified by the laser. After each laser pulse it cools down, thereby heating the ambient gas. The next laser pulse, therefore, finds the soot at a slightly higher initial temperature, and is thus able to also heat the soot to a slightly higher final temperature, resulting in increased luminescence. This continues until a new equilibrium has been reached [19]. At high laser fluence, the aforementioned heating also occurs, but now, the soot particles are (at least partly) destroyed by the laser, which reduces the luminescence yield. For the subsequent measurements on the co-flow burner, a fluence of \(0.058\;\mathrm{{J}}/\mathrm{{cm}}^{2}\) was selected. This corresponds to running the laser at full power with no additional optics affecting the laser beam. Although the fluence of individual pulses is thereby set at \(0.058\;\mathrm{{J}}/\mathrm{{cm}}^{2}\), the effective fluence is expected to be higher, because local gas heating plays a role in the final temperature that particles reach.
4.2 Relative soot growth
Figure 9 shows the fluence dependence of the PA signal. A linear relationship appears to exist between low fluences and PA signal, corroborated by the linear fit to the measurement data. This is expected behavior, since the intensity of the photo-acoustic signal depends on the increase in sensible heat (i.e., internal energy) of the soot particles, assumed that all laser-induced heat is transferred from particle to gas. The increase in internal energy in turn is directly proportional to laser fluence, as can be seen from (4) and (5).
Interestingly, at a fixed fluence, it turns out that the LII and PA signals, recorded simultaneously, do not behave the same in all regions of the flame. Figure 10 depicts the PA and LII signals as a function of height above the burner exit (HAB); both are normalized to their (peak) value at HAB = 40 mm. An obvious correlation is observed between the two signals, but a systematic deviation remains. The origin of this deviation can at least partially be ascribed to the 40 ns gate time, which is relatively long compared to the 8 ns laser pulse (FWHM). For this reason, conduction dominates the energy balance of the soot particles for 80% of the detection time, and temperature differences between particles of varying sizes arise. As previously discussed, the bias of proportionality between LII signal and soot volume fraction is caused by temperature variations for particles of different sizes in the probe volume.
The PA signal, on the other hand, does relate proportionally to the soot volume fraction, as it is a direct measure of the amount of absorbed energy. Thus, the difference in observed signals can be attributed to the unequal particle size dependence of the PA and the LII signals. Indeed, soot particles are expected to vary in size as a function of HAB, and the systematic deviation between the PA and LII signals can be used to extract more information about this variation. To illustrate this, the data from Fig. 10 are plotted against each other (rather than as a function of HAB) in Fig. 11. From the analysis of Sect. 2, it follows that the normalized signals can be written as
Particle number density and particle size at the reference HAB are \(N_0\) and \(D_0\), respectively. Of course, there will be a size distribution rather than a single one, but that is irrelevant for the argument. Thus, we can expect a relation between the normalized signals given by
According to Meltons expressions from (10) and (11), the constant x has a value of approximately 0.35 for the detection range used in the current measurements. Yet, Melton derived this expression from high fluence measurements, and it might, therefore, not be fully applicable here. In the absence of excessive sublimation, the value of x is expected to be lower than 0.35, for conduction is the only mechanism resulting in particle temperature differences during LII detection. In addition, as previously stated, we apply blue filtering to increase the bias as much as possible. Equation (14) implies that the LII signal will be lower than the PA signal when the particles are smaller than the reference particle size, and vice versa when the particles are larger.
Figure 11 illustrates the normalized LII signal as a function of the normalized PA signal, for the same measurement, as presented in Fig. 10. Each dot corresponds to a specific HAB, and the black solid line indicates the trend that would be seen if the normalized LII and PA signals were equal. As both signals are normalized to 40 mm HAB, their values are necessarily equal for that measurement point. The results show that the LII signal is lower than the PA signal until the normalization point is reached. Thereafter, the LII signal surpasses the PA signal. According to (14), this is a result of the primary particle size increasing along the measurement range in the flame. It must be noted that the last 10 mm in the tip of the flame have not been measured. These points were omitted due to flame instabilities in the tip of the flame when high-repetition rate laser heating was applied, rendering it impossible to collect useful signals. It is likely that the particles will eventually decrease in size in this part of the flame due to oxidation, but definitive conclusions cannot be drawn. Still, it is indeed possible to derive qualitative information on soot growth from differences in the LII and PA signals. As compared to LII, the PA detection channel is cheap and flexible, and less sensitive to the cooling process of laser-heated soot, at least for the low fluence applied here. This provides a more direct measure for the soot volume fraction. A clear downside of the PA detection method is the lack of spatial resolution.
5 Conclusion
Photo-acoustic detection of laser-heated soot is shown to be a suitable technique for soot volume fraction measurement. As with LII, an independent calibration is required to obtain quantitative results. A photo-acoustic measurement is simpler and cheaper than LII (no camera needed), but the result is integrated over the whole illuminated volume, whereas planar LII provides additional spatial information. Photo-acoustic measurement, in combination with time-integrated LII, can be used to obtain qualitative information on the soot particle size.
Further investigation is needed to explore the particle sizing capability of the described method. As previously mentioned, the deviation from an exact volume dependence of the incandescence signal originates solely from the detection procedure. More specifically, the selection of optical filters and camera gating time is expected to influence the observed difference between the PA and LII signals as a function of HAB. The LII signal becomes less sensitive to particle size changes when the detection band is shifted to the red part of the spectrum. The camera gating time is also thought to affect the bias of the LII signal towards larger particles, as the share of conduction in the time-integrated signal increases when longer gating times are applied.
References
J. Sjöholm, R. Wellander, H. Bladh, M. Richter, P.-E. Bengtsson, M. Alden, SAE Int. J. Engines 4, 1607–1622 (2011)
I.G. Boxx, O. Heinold, K.P. Geigle, Exp. Fluids 56, 3 (2015). https://doi.org/10.1007/s00348-014-1865-7
P.C. Bakker, R.C. Willems, N.J. Dam. SAE Paper 2016-01-0725 (2016)
R.L. Vander Wal, T.M. Ticich, A.B. Stephens, Appl. Phys. B 67, 115–123 (1998)
E. Cenker, A. Bennett, W.L. Roberts, Aerosol Sci. Technol 51(12), 1354–1367 (2017)
J.B. Michael, P. Venkateswaran, C.R. Shaddix, T.R. Meyer, Appl. Optics 54, 3331–3344 (2015)
G.S. Humphries, J. Dunn, M.M. Hossain, M. Lengden, I.S. Burns, J.D. Black, Appl. Phys. B 119, 709–715 (2015)
H.A. Beck, R. Niessner, C. Haisch, Anal. Bioanal. Chem. 375, 1136–1143 (2003)
B. Mewes, J.M. Seitzman, Appl. Optics 36, 709–717 (1997)
L.A. Melton, Appl. Optics 23, 2201–2208 (1984)
C. Schulz, B.F. Kock, M. Hofmann, H. Michelsen, S. Will, B. Bougie, R. Suntz, G. Smallwood, Appl. Phys. B 83, 333–354 (2006)
H.A. Michelsen, F. Liu, B.F. Kock, H. Bladh, A. Boiarciuc, M. Charwath, T. Dreier, R. Hadef, M. Hofmann, J. Reimann, S. Will, P.-E. Bengtsson, H. Bockhorn, F. Foucher, K.-P. Geigle, C. Moinaïm-Rousselle, C. Schulz, R. Stirn, B. Tribalet, R. Suntz, Appl. Phys. B 87, 503–521 (2007)
H. Bladh, J. Johnsson, P.-E. Bengtsson, Appl. Phys. B 90, 109–125 (2008)
H. Moosmüller, W.P. Arnott, J. Air Waste Manage. Assoc. 59, 1028–2031 (2009)
H.A. Michelsen, J. Chem. Phys. 118, 7012–7045 (2003)
F. Goulay, P.E. Schrader, X.López Yglesias, H.A. Michelsen, Appl. Phys. B 112, 287–306 (2013)
C.J. Mueller, G.C. Martin. SAE Paper 2002-01-1631 (2002)
J.M. Seitzman, R.T. Wainner, P. Yang, Optics Lett. 24, 1632–1634 (1999)
E. Nordström, N.-E. Olofsson, J. Simonsson, J. Johnsson, H. Bladh, P.-E. Bengtsson, Proc. Comb. Inst. 35, 3707–3713 (2015)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the topical collection “Laser-Induced Incandescence”, guest edited by Klaus Peter Geigle and Stefan Will.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Willems, R.C., Bakker, P.C. & Dam, N.J. Laser-induced incandescence versus photo-acoustics: implications for qualitative soot size diagnostics. Appl. Phys. B 125, 138 (2019). https://doi.org/10.1007/s00340-019-7248-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00340-019-7248-2