Preparation, characterization and magnetic properties of Sm_0.95Ho_0.05FeO₃ nanoparticles and their application in the purification of water

Abstract

Sm_0.95Ho_0.05FeO₃ was successfully prepared in a single phase using the citrate combustion method. The investigated sample was characterized using X-ray diffraction (XRD), a high-resolution transmission electron microscope (HRTEM) and X-ray photoemission spectroscopy (XPS). XRD confirmed that the sample was synthesized in an orthorhombic phase with an average crystallite size of 12 nm. HRTEM indicated that the sample was prepared in the nanoscale with an average particle size of 18 nm. XPS was used to identify the chemical bonds, binding energies and core levels of Sm_0.95Ho_0.05FeO₃. The magnetic properties were studied using a vibrating sample magnetometer and DC magnetic susceptibility using Faraday’s method. The sample has an antiferromagnetic behavior with weak ferromagnetic components. The presence of magnetic Ho³⁺ ions in the SmFeO₃ sample causes the magnetic exchange interaction between the 2p orbital of Fe³⁺ and the 4d sub-shell of Ho³⁺ ions. The dependence of pH value on the removal efficiency of Pb²⁺ from water was studied. The maximum Pb²⁺ removal efficiency of the Ho-doped SmFeO₃ nano perovskite is 26% at pH = 5 and 99% at pH = 8. The Freundlich, Langmuir and Temkin isotherms were studied to understand the adsorption mechanism. The Temkin adsorption isotherm best fitted with the experimental data.

1 Introduction

Rare earth orthoferrite (RFeO₃) has attracted attention due to its interesting physical and chemical properties, such as multiferroicity, magnetic properties, spin–phonon coupling, catalytic properties, an abnormal dielectric constant, magnetization reversal at very low temperatures, a high Neel temperature (T_N) above room temperature and a high dielectric constant [1,2,3,4,5,6]. Many applications for ABO₃ orthoferrites have been developed, including energy storage devices, spintronics, heavy metal and dye removal from wastewater, and chemical sensors [7,8,9,10,11]. Rare earth orthoferrites usually have a distorted orthorhombic structure with the Pbnm space group [6, 8, 12]. In this structure, the rare earth cation R³⁺ has 12 coordination numbers, while Fe ions coordinate with six O²⁻ anions, forming FeO₆ octahedra [13, 14]. The tilting and distortion of FeO₆ affect the ionic radii of rare earth cations. The distortion of FeO₆ increases by decreasing the rare earth ionic radii due to the R–O bond length and bond angle change.

SmFeO₃ is one of the rare earth orthoferrite materials. It has attracted great attention from researchers due to its properties, such as the antiferromagnetic properties with weak ferromagnetism, the highest spin reorientation transition temperature (470 K), the particle size-affected dielectric constant and piezoelectricity at room temperature [14]. The magnetic properties of SmFeO₃ originate from three magnetic interactions, i.e., rare earth–rare earth (R³⁺–R³⁺), rare earth–iron (R³⁺–Fe³⁺) and iron–iron (Fe³⁺–Fe³⁺) interactions [1, 15].

The change in A-site cation radius affects the distortion of the perovskite structure and the tilting of the FeO₆ octahedron. The doping of rare earth ions at the A site has an impact on the magnetic properties of SmFeO₃. Liu [16] studied the effect of nonmagnetic La ion doping on the magnetic properties of SmFeO₃. Because the Sm spins are in a frustrated state, the magnetic anisotropy energy and exchange bias of Sm_1−xLa_xFeO₃ rise slightly for x = 0.05 and then fall by increasing the La content by more than 0.05. Praveena et al. [15] prepared Sm_1−xCa_xFeO₃ where x = 0, 0.25, 0.5, 0.75 and 1 using the sol–gel method at low temperatures. As Ca²⁺ increases, a significant enhancement in remnant magnetization (M_r) and coercivity (H_c) is observed. The magnetic properties of the Sm_1−xCa_xFeO₃ samples were improved due to the destruction of the spin cycloid with Sm.

Heavy metal pollution is an international issue that is growing with the development of modern industry. The sources of lead in the environment are ceramic printing industries, battery manufacturing, ammunition and acid metal plating [17]. The presence of the toxic heavy metal lead in water has great harmful effects on the human body, so it is one of the most worrying problems [18, 19]. High lead exposure has been reported to have a number of negative health impacts on children, including neurotoxicity [20], low IQ [21, 22], poor mental development [23], low quantitative skills [24], and learning difficulties. For adults, lead exposure has health consequences such as diabetes, renal disease [25] and cognitive dysfunction from early childhood exposure [26].

There are many conventional methods for the removal of heavy metal ions, such as membrane filtration, chemical precipitation, reverse osmosis, ultrafiltration and flotation. The adsorption method is more effective for heavy metal ion removal due to its properties such as simplicity, cost-effectiveness, no sludge formation and good regeneration capacity [27,28,29]. Adsorption occurs due to the physical or chemical attraction of lead ions to the surface of the adsorbent [30].

Perovskites are effective materials for heavy metal removal owing to their properties such as high stability, low price, high surface energy, and absorptivity, catalytic, electronic, magnetic and optical characteristics [28]. One of the main advantages of using magnetic materials (i.e., perovskite) for heavy metal removal is the easy separation from the solution by an external magnet. Some of the perovskite samples that were used for heavy metal removal are La_0.85Ce_0.15FeO₃ [8], CeCoO₃ [31], LaFeO₃ [32], and LaAlO₃ [33]. Meanwhile, the removal of lead ions from water by using Sm_0.95Ho_0.05FeO₃ nanocomposites has not been reported yet. Therefore, this work demonstrated the use of Ho-doped SmFeO₃ nanoparticles to eliminate lead from aqueous solutions.

In this work, Sm_0.95Ho_0.05FeO₃ was synthesized using a simple citrate combustion method. The aim of this study is to study the phase formation, morphology and magnetic behavior of Sm_0.95Ho_0.05FeO₃. The other goal is to examine the ability of the investigated sample to remove lead from water. The effect of pH value on the removal efficiency of pb²⁺ ions from water was studied.

2 Experimental work

2.1 Preparation of nanocomposites

Sm_0.95Ho_0.05FeO₃ was synthesized by the citrate combustion method. The precursor metal nitrates (purity 99.9% Sigma-Aldrich) were mixed in stoichiometric ratios with citric acid as a fuel. The citric acid/nitrate ratio is equal to 1. The pH of the solution was adjusted to 7 using the ammonia solution. The solution was heated on the hot plate until a highly viscous liquid was formed. The viscous liquid swelled and auto-ignited as it was heated further, resulting in a fluffy powder. This preparation method is low cost, simple, and quick. The sample was ground well for 1 h using an agate mortar to obtain a powder. The sample was sintered at 500 °C for 2 h with a heating/cooling rate of 4 degrees/min in air. Figure 1 illustrates the flowchart of the preparation of Ho-doped SmFeO₃.

Fig. 1

Flowchart for the preparation of Sm_0.95Ho_0.05FeO₃

2.2 Sample characterizations and measurements

The sample was well ground into powder before being subjected to the following characterizations. X-ray diffraction (XRD, Bruker advance D8 diffractometer, λ = 1.5418 Å) was used to study the structure of the investigated sample, Sm_0.95Ho_0.05FeO₃. The crystalline phases of the sample were identified using the International Centre for Diffraction Data (ICDD) card number 74-1474.

A certain amount of the sample was suspended in deionized water by using an ultrasonicator for 30 min before the characterization using HRTEM. The surface morphology of Ho-doped SmFeO₃ was characterized using a transmission electron microscope (HRTEM, JEOL-2100) operated at 200 kV. The surface chemical composition of the investigated sample was measured using the X-ray photoelectron spectrometer (XPS) via K-ALPHA (Thermo Fisher Scientific, USA).

The magnetic behavior of the Ho-doped perovskite SmFeO₃ was studied using a vibrating sample magnetometer and DC magnetic susceptibility using the Faraday method [34]. The magnetic susceptibility of the investigated sample was measured by introducing a cylindrical glass tube with a small amount of powdered sample at the point of maximum gradient.

2.3 Heavy metal removal

2.3.1 Effect of pH value

A lead ion solution of concentration (100 ppm) was prepared from pure lead nitrate to determine the heavy metal ion removal efficiency of the Sm_0.95Ho_0.05FeO₃ sample. A working solution (50 ppm) was prepared by diluting the above solution. A few 250-mL flasks containing 50 ppm lead ion solution and 0.02 g of the investigated sample were used. By using ammonia and diluted nitric acid solutions, the pH values of lead solutions were adjusted from 3 to 8. The resultant solutions were stirred at 25 °C using an electric shaker (Orbital Shaker SO1) at 200 rpm for 1 h. By using a 0.2-μm syringe filter, 10 mL of the supernatant solutions was filtered. Inductively coupled plasma spectrometry (ICP, Prodigy7) was used to calculate the concentration of pb²⁺ ions in the filtrated solution.

The metal ion removal efficiency (η) and the equilibrium adsorption capacity (q) were calculated according to the following equations [35]:

$$ \eta = \frac{{C_{i} - C_{{\text{e}}} }}{{C_{i} }} \times 100, $$

(1)

$$ q = \frac{{\left( {C_{i} - C_{{\text{e}}} } \right)V}}{m}, $$

(2)

where C_i and C_e are the initial and final concentrations (mg/L) of the metal ion solution, respectively, while m is the mass of the adsorbent and V is the volume of Pb (II) solution.

3 Results and discussion

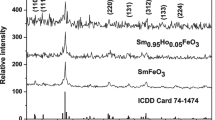
XRD was used to examine the crystalline structure of the prepared sample, Sm_0.95Ho_0.05FeO₃. Figure 2 shows the XRD pattern of the investigated sample. All the diffraction peaks are indexed with the ICCD card number 74-1474. Sm_0.95Ho_0.05FeO₃ has been synthesized in a single-phase orthorhombic structure with space group Pbnm. Major diffracted peaks (110), (111), (112), (220), (131), (312), (133) and (224) were observed in the XRD pattern at 2θ values of 22.96, 25.66, 32.51, 47.05, 53.38, 58.88, 63.97 and 69.88, which indicates the sample has an orthorhombic phase. The high-intensity peak (112) observed at 2θ indicates the growth direction of Sm_0.95Ho_0.05FeO₃. The values of lattice parameters were calculated on the basis of the orthorhombic structure according to the following equation:

$$ \frac{1}{{d^{2} }} = \frac{{h^{2} }}{{a^{2} }} + \frac{{k^{2} }}{{b^{2} }} + \frac{{l^{2} }}{{c^{2} }}. $$

(3)

Fig. 2

XRD of the sample Sm_0.95Ho_0.05FeO₃

The average crystallite size was estimated using Scherer’s equation [36] and is reported in Table 1. The value of the crystallite size (12.1 nm) indicates that the sample was synthesized in the nano scale.

$$ D = \frac{0.94\lambda }{{\beta \cos \theta }}. $$

(4)

Table 1 Experimental lattice parameters: crystallite size (D), unit cell volume (V), theoretical density (D_x) and tolerance factor (t)

The theoretical density of the investigated sample was calculated using the following equation:

$$ D_{x} = \frac{ZM}{{NV}}, $$

(5)

where Z = 4 is the number of molecules per unit cell, N is Avogadro's number, M is the molecular weight, and V is the unit cell volume.

The Goldsmith perovskite tolerance factor (t) measures the lattice mismatch between the ions of the perovskite materials [37]. The highest value of t is equal to 1 for a cubic perovskite structure. The value of the tolerance factor was calculated according to the following equation:

$$ t = \frac{{r_{{\text{A}}} + r_{{\text{O}}} }}{{\sqrt 2 \left( {r_{{{\text{Fe}}}} + r_{{\text{O}}} } \right)}}, $$

(6)

where r_A, r_B, and r_O are the ionic radii of the A, B, and oxygen ions, respectively. The A-site ionic radius can be calculated according to the equation $r_{{\text{A}}} = \, 0.95r_{{{\text{Sm}}}}^{3 + } + \, 0.05 r_{{{\text{Ho}}}}^{3 + }$. The tolerance factor value of the investigated sample is 0.8786, which indicates that the sample has an orthorhombic structure. The tolerance factor is less than one due to the lattice distortion arising from the tilting of <FeO₆> octahedral structure.

Figure 3 illustrates the EDX energy spectra of Sm_0.95Ho_0.05FeO₃. The atomic percentages (at%) and weight percentages (wt%) of the Fe, O, Sm, and Ho elements are illustrated in the inset table in Fig. 3. The experimental at% and wt% were obtained from EDX, while the theoretical values were calculated from the chemical formula Sm_0.95Ho_0.05FeO₃. The small variation of weight and atomic percentages between the experimental and theoretical values is due to oxygen deficiency, which can be advantageous for heavy metal removal from water.

Fig. 3

EDX for the Sm_0.95Ho_0.05FeO₃ sample. The inset table shows the weight percentage (wt%) and atomic percentage (at%) of the elements O, Sm, Fe, and Ho

Figure 4a, b illustrates the HRTEM images of the investigated nanoparticles at different scales. The average particle size of Sm_0.95Ho_0.05FeO₃ is 18 nm, which confirms that the sample was synthesized in the nanoscale. The nanoparticles are agglomerated due to the magnetic properties of the sample. Figure 4b includes an inset of the selected area electron diffraction (SAED) pattern. The bright rings in the SAED indicate that the sample was synthesized in good crystalline form. The SAED pattern also illustrated that the prepared Sm_0.95Ho_0.05FeO₃ nanoparticles are polycrystalline in nature.

Fig. 4

HRTEM of the sample Sm_0.95Ho_0.05FeO₃

The XPS characterization was carried out to verify the chemical composition and valence state of the Sm_0.95Ho_0.05FeO₃ nanoparticles. The wide-range XPS survey spectra of Sm_0.95Ho_0.05FeO₃ nanoparticles are illustrated in Fig. 5a. The peaks of different elements such as Sm, Ho, Fe, O, and C have been identified. The C 1s peak is observed at 287.21 eV, which is used as a charge reference to rectify the binding energy of the XPS spectra [38]. Figure 5a illustrates that there is no secondary phase from holmium metal or oxide. Therefore, Ho was substituted at the expense of the Sm site and maintained the perovskite structure in a single phase as a result obtained from XRD data. The XPS peak of Ho 4d at a binding energy of 160.79 eV due to the presence of Ho³⁺ is shown in Fig. 5b [39,40,41]. The Ho 4d spectrum is obvious in a small range of scan spectra as a result of the very small quantity of Ho in Sm_0.95Ho_0.05FeO₃ perovskite.

Fig. 5

XPS spectra of Sm_0.95Ho_0.05FeO₃: a a wide scan and b narrow scans of Ho 4d signals

The magnetic parameters of orthoferrite depend on many factors, such as the composition, the cation preference occupation, purity, homogeneity and surface to volume ratio [1]. The magnetic properties of Sm_0.95Ho_0.05FeO₃ were studied by using the hysteresis loop and Faraday’s law. The magnetic hysteresis loop of the investigated perovskite is illustrated in Fig. 6 at room temperature. The values of the maximum magnetization (M_s), the coercive field (H_c) and the remnant magnetization (M_r) are listed in Table 2. The hysteresis loop has a small area with nonlinearity, a very small coercive field, and remnant magnetization. The non-saturation behavior of the magnetic loop shows the dominance of its antiferromagnetic character. The hysteresis loop has S-shape, which indicates the presence of an antiferromagnetic order with weak ferromagnetic components [1]. The super exchange interactions are presented between the magnetic ions Fe³⁺, Ho³⁺ and Sm³⁺ ions, while the weak ferromagnetism originates from canted antiferromagnetic spins in the investigated sample. The anisotropy constant value is calculated from the following equation [42] and reported in Table 2.

$$ K = \frac{{H_{{\text{C}}} \times M_{{\text{S}}} }}{0.96}, $$

(7)

where H_c is the coercivity, K is the magnetic anisotropy constant and M_s denotes saturation magnetization. The weak anisotropy of Sm_0.95Ho_0.05FeO₃ is due to the non-collinearity (canting) of spins on their surface [42].

Fig. 6

Room temperature M–H loops of the investigated sample at room temperature

Table 2 The values of the maximum magnetization (M_m), remanence magnetization (M_r), the coercive field (H_c), anisotropy constant (K), M–H loop area and squareness ratio for Sm_0.95Ho_0.05FeO₃

Ateia et al. [14] used the citrate auto-combustion method to prepare SmFeO₃ and found that the saturation magnetization was 0.639 emu/g. In the present study, the maximum magnetization of Ho-doped SmFeO₃ increased four times that of SmFeO₃ as a result of the substitution of Ho³⁺ ions (10.3 μ_B) instead of Sm³⁺ ions (1.6 μ_B) [43]. Due to lattice distortion caused by the difference in ionic radii of Ho³⁺ (1.015 Å) and Sm³⁺ (1.079 Å), the magnetization of SmFeO₃ is increased by substituting Ho³⁺ ions for Sm³⁺ ions [44].

The dependence of the molar magnetic susceptibility (χ_M) on the absolute temperature T (K) is illustrated in Fig. 7 for the investigated sample Sm_0.95Ho_0.05FeO_3. The χ_M values decrease as the temperature increases to the Néel temperature. Figure 7 confirms the AFM behavior of the Ho-doped SmFeO₃ sample with weak ferromagnetic components [45, 46]. The values of magnetic constants such as Curie temperature (T_c), Curie–Weiss constant (θ), Curie constant (C) and the effective magnetic moment (μ_eff) are calculated and reported in Table 3. Introducing the Ho³⁺ ions into the sample increases the magnetization due to the presence of new magnetic interactions between Ho³⁺–Ho³⁺ and Ho³⁺–Sm³⁺ interactions. By introducing Ho³⁺ ions into SmFeO₃, the distortion increased, as illustrated in the tolerance factor, leading to changes in the bond lengths of Fe–O and Sm–O. The structure distortion, the bond angle and the bond length all strongly affect the super exchange interaction [47]. The presence of magnetic Ho³⁺ ions in the investigated sample causes the magnetic exchange interaction between the 2p orbital of Fe³⁺ and the 4d sub-shell of Ho³⁺ ions [48].

Fig. 7

The dependence of the molar magnetic susceptibility on the absolute temperature for Sm_0.95Ho_0.05FeO₃ at different magnetic field intensities

Table 3 Calculated magnetic constants: Curie temperature (T_c), Curie constant (C), Curie–Weiss constant (θ) and the effective magnetic moment (μ_eff)

The interaction between the adsorbent and the adsorbate depends on many factors, such as the pH value of the solution [8]. The pH value determines the adsorbent's net surface charge, the type of adsorbed species and the degree of ionization [49]. In aqueous solutions, iron oxides are hydrated and form FeOH groups, which cover their surfaces. Depending on the pH value of the solution, the hydroxylated sites on the surface can react with H⁺ or OH⁻ ions from dissolved acids or bases, and positive (FeOH₂⁺) or negative (FeO⁻) charges are produced on the surface of perovskite [17].

$$ \begin{aligned} & {\text{FeOH}} + {\text{OH}}^{ - } = {\text{FeO}}^{ - } + {\text{H}}_{2} {\text{O,}} \\ & {\text{FeOH}} + {\text{H}}^{ + } = {\text{FeOH}}_{2}^{ + } . \\ \end{aligned} $$

Figure 8 shows the dependence of the adsorption efficiency of the removal of Pb²⁺ heavy metal ions on the pH solution. Since there are more H⁺ ions in the solution when the pH is very low, H⁺ and heavy metal ions compete for the same active sites on the adsorbent, which results in a low removal efficiency. As pH rises, the sample surface acquires a negative sign and the adsorption of lead ions increases. In this case, electrostatic interactions dominate the adsorption process. Figure 8 illustrates that the optimum pH value for precipitate Pb²⁺ is pH = 5. At a high pH value (pH = 8), Pb²⁺ ions precipitate as hydroxide, which is unfavorable for the adsorption process [50].

Fig. 8

Effect of pH on the adsorption efficiency of Pb²⁺ ions

The adsorption isotherm gives more information about the mechanism of adsorption between the investigated sample and the lead ion liquid phase. In the present work, Langmuir, Freundlich and Temkin isotherm models were studied for the absorption efficiency of lead ions on Sm_0.95Ho_0.05FeO₃.

The Langmuir, Freundlich and Temkin isotherm models [51, 52] were applied to explain the equilibrium adsorption of the pb²⁺ ion on Sm_0.95Ho_0.05FeO₃ nanoparticles. Equations (8)–(10) express the Langmuir, Freundlich and Temkin isotherm models, respectively.

$$ \frac{{C_{{\text{e}}} }}{{q_{{\text{e}}} }} = \frac{1}{{q_{{\text{m}}} K_{{\text{L}}} }} + \frac{{C_{{\text{e}}} }}{{q_{{\text{m}}} }}, $$

(8)

$$ q_{{\text{e}}} = \, K_{{\text{f}}} C_{{\text{e}}}^{\frac{1}{n}} , $$

(9)

$$ q_{{\text{e}}} = \frac{RT}{{b_{{\text{T}}} }} \ln K_{{\text{T}}} + \frac{RT}{{b_{{\text{T}}} }} \ln C_{{\text{e}}} , $$

(10)

where C_e is the equilibrium metal concentration (mg/L), q_m and K_L are the Langmuir constants associated with maximum adsorption capacity (mg/g), K_f is the Freundlich constant, $\frac{1}{n}$ is the adsorption intensity, T is the absolute temperature (K), R is the common gas constant (0.008314 kJ/mol K), $\frac{1}{{b_{{\text{T}}} }}$ is the Temkin constant related to the heat of sorption (kJ/mol) and $K_{{\text{T}}}$ is the Temkin constant related to adsorption capacity (L/g).

Figure 9 illustrates the relationship between ln q_e and ln C_e which agrees with the Freundlich isotherm model_. The values of 1/n and K_f were calculated from the slope and the intercept of the best fit line in Fig. 9. The dependence of C_e/q on C_e according to the Langmuir isotherm model is illustrated in Fig. 10. Adsorbent–adsorbate interactions are taken into account in the Temkin isotherm. Figure 11 illustrates the linear plot between q_e and lnC_e according to the Temkin isotherm model. The constants $\frac{1}{{b_{{\text{T}}} }}$ and $K_{{\text{T}}}$ can be determined from the slope and intercept, respectively.

Fig. 9

Linear fit of experimental data of the adsorption of Pb²⁺ according to the Freundlich isotherm model

Fig. 10

Linear fit of experimental data of the adsorption of Pb²⁺ using the Langmuir adsorption isotherm model

Fig. 11

Temkin adsorption isotherm model of the adsorption of Pb²⁺ on Sm_0.95Ho_0.05FeO₃ nanoparticles

Table 4 shows the values of the correlation coefficient (R²) for the Langmuir, Freundlich and Temkin isotherm models. The Temkin isotherm has an R² of 0.9453. Thus, the Temkin adsorption isotherm best fitted with the experimental data.

Table 4 The correlation coefficient (R²) of different isotherm models

4 Conclusions

The X-ray diffraction analysis ensures Sm_0.95Ho_0.05FeO₃ was synthesized in a single-phase orthorhombic structure. The average particle size of the investigated sample is 18 nm. The bright rings in the SAED indicate that the sample was synthesized with good crystalline nature. XPS illustrated that Ho was substituted at the expense of Sm and maintained the perovskite structure in a single phase. Sm_0.95Ho_0.05FeO₃ has antiferromagnetic properties with a maximum magnetization equal to 2.5467 emu g⁻¹. Introducing the Ho³⁺ ions into the sample increases the magnetization due to the presence of new magnetic interactions between Ho³⁺–Ho³⁺ and Ho³⁺–Sm³⁺ interactions. Ho-doped SmFeO₃ can act as a heavy metal pb²⁺ adsorber from wastewater. The optimum removal efficiency of lead ions from water is 26% by Sm_0.95Ho_0.05FeO₃. The Temkin adsorption isotherm is the best description of the adsorption of the Pb²⁺ ion from water.