Strong Symmetry Breaking in Coupled, Identical Lengyel–Epstein Oscillators via Folded Singularities

Abstract

We study pairs of symmetrically coupled, identical Lengyel-Epstein oscillators, where the coupling can be through both the fast and slow variables. We find a plethora of strong symmetry breaking rhythms, in which the two oscillators exhibit qualitatively different oscillations, and their amplitudes differ by as much as an order of magnitude. Analysis of the folded singularities in the coupled system shows that a key folded node, located off the symmetry axis, is the primary mechanism responsible for the strong symmetry breaking. Passage through the neighborhood of this folded node can result in splitting between the amplitudes of the oscillators, in which one is constrained to remain of small amplitude, while the other makes a large-amplitude oscillation or a mixed-mode oscillation. The analysis also reveals an organizing center in parameter space, where the system undergoes an asymmetric canard explosion, in which one oscillator exhibits a sequence of limit cycle canards, over an interval of parameter values centered at the explosion point, while the other oscillator executes small amplitude oscillations. Other folded singularities can also impact properties of the strong symmetry breaking rhythms. We contrast these strong symmetry breaking rhythms with asymmetric rhythms that are close to symmetric states, such as in-phase or anti-phase oscillations. In addition to the symmetry breaking rhythms, we also find an explosion of anti-phase limit cycle canards, which mediates the transition from small-amplitude, anti-phase oscillations to large-amplitude, anti-phase oscillations.

1 Introduction

Symmetry breaking arises in physics, chemistry, biology, mathematics, and other areas of science and engineering whenever a model or system possesses a symmetry, but a solution of the model or a state of the system does not reflect that symmetry. Symmetry breaking can take a myriad of forms (Anderson 1972; Beekman et al. 2019; Collins and Stewart 1993; Golubitsky and Stewart 2004; Gross 1996; Li and Bowerman 2010; Mainzer 1997; Stewart 1999). For systems of coupled oscillators, symmetry breaking famously can involve clusters of oscillators exhibiting coherent (or synchronized) behavior, with other clusters exhibiting incoherent (or desynchronized) behavior, forming chimeras, see, for example, (Kuramoto and Battogtokh 2002; Abrams and Strogatz 2004; Motter 2010; Kemeth et al. 2018). Chimeras occur both in large systems of coupled oscillators and in small systems. One goal of current research is to understand minimal chimeras, i.e., conditions under which a minimal number of oscillators can exhibit chimeras or chimera-like modes of activity (Kemeth et al. 2018; Panaggio et al. 2016; Hart et al. 2016; Maistrenko et al. 2017; Wojewoda et al. 2016; Burylko et al. 2022; Awal et al. 2019).

In pairs of symmetrically coupled identical oscillators, rhythms may be called strong symmetry breaking rhythms when the amplitudes of the two oscillators are substantially different or when the two oscillators exhibit qualitatively different types of dynamics. Such rhythms have recently been discovered in pairs of symmetrically coupled, identical oscillators of fast–slow type (Awal et al. 2019; Awal and Epstein 2021, 2020; Awal et al. 2023), including van der Pol oscillators and Lengyel-Epstein oscillators. Asymmetric rhythms in which the amplitudes of the oscillators differ substantially have also been observed in Wiehl et al. (2021).

Examples of strong symmetry breaking rhythms include those in which one oscillator exhibits small-amplitude oscillations (SAOs) while the other undergoes large-amplitude oscillations (LAOs). These two modes of oscillation have substantially different amplitudes and are qualitatively different, since the SAOs are oscillations that are close to a steady state of an individual oscillator, while the LAOs are classical relaxation oscillations consisting of long segments near widely separated states in alternation with rapid jumps between them. Other examples of strong symmetry breaking include rhythms in which one oscillator exhibits SAOs while the other displays mixed-mode oscillations (MMOs). Each MMO consists of one or more LAOs and one or more SAOs, so that the amplitude of the oscillator exhibiting MMOs is substantially larger than that of the other oscillator, and they are also of qualitatively different types. There also exist strong symmetry breaking rhythms in which one oscillator exhibits SAOs, while the other undergoes limit cycle canards (LCCs). These strong symmetry breaking rhythms are labeled SAO-LAO, SAO-MMO, and SAO-LCC rhythms, respectively (Awal et al. 2023).

Strong symmetry breaking contrasts with asymmetric rhythms in which pairs of identical oscillators are close to a symmetric state of the symmetrically coupled system. Such asymmetric rhythms arise, for example, when two identical oscillators are close to being either in-phase or anti-phase. Examples include the asymmetric spiking and asymmetric bursting rhythms in the Butera model of the pre-Bötzinger complex presented in Chapter 5 of Roberts (2018) and in Roberts et al. (2015), as well as asymmetric rhythms that are near in-phase states in coupled van der Pol oscillators in a study of the role maximal canards play in synchronization of relaxation oscillators in Ersöz et al. (2017). Also, asymmetric states that are close to symmetric states are known to exist in other, more general systems of coupled oscillators.

Symmetry breaking has also been reported recently in pairs of identical FitzHugh–Nagumo equations (Pedersen et al. 2022). A pitchfork bifurcation of limit cycles is studied, and it is shown how coupling two spiking cells can lead to bursting. The burst events are MMOs, even though neither planar oscillator can exhibit MMOs by itself. The system features a cusp point, and a particular folded node gives rise to the MMOs. The variables $u_\parallel = \tfrac{1}{2}(u_1 + u_2)$ and $u_\perp = \tfrac{1}{2}(u_1-u_2)$ are used, and one can measure the symmetry breaking using $u_\perp$.

In this article, we analyze strong symmetry breaking rhythms in a pair of coupled, identical Lengyel-Epstein (LE) oscillators, and we use the theory of folded singularities (Takens 1976; Szmolyan and Wechselberger 2001; Wechselberger 2005) to understand the mechanisms responsible for the strong symmetry breaking.

1.1 Symmetrically Coupled, Identical Lengyel–Epstein Oscillators

The LE model is a paradigm relaxation oscillator in chemistry, where it describes temporal oscillations and Turing pattern formation in the chlorine dioxide-iodine-malonic acid (CDIMA) reaction (Lengyel et al. 1990) and in the chlorite-iodide-malonic acid (CIMA) reaction (Lengyel and Epstein 1991). See also (Haim et al. 2015; Jang et al. 2004; Jensen et al. 1994). It has an activator, u, corresponding to the concentration of the iodine-containing species, and an inhibitor, v, representing the concentration of the chlorine-containing species. The equations governing the time evolution of the species concentrations are

$$\begin{aligned} \begin{aligned} {\dot{u}}&= a-u-\frac{4uv}{1+u^2} =: f(u,v)\\ {\dot{v}}&= \beta \left( u-\frac{uv}{1+u^2} \right) =: \beta g(u,v). \end{aligned} \end{aligned}$$

(1.1)

Here, the overdot denotes the derivative with respect to time t, $a>0$ is a parameter related to the initial reactant concentrations, $\beta \ge 0$ is a small parameter that measures the separation of time scales, u is the fast activator variable, and v is the slow inhibitor variable.

We focus on the parameter regime in which (1.1) is the prototype of a classical relaxation oscillator; so we consider $a> 3\sqrt{3} \approx 5.19615$. For these values of a, the fast nullcline

$$\begin{aligned} \{ f=0 \} = \left\{ v = \frac{1}{4u} (a-u)\left( 1+u^2\right) \right\} \end{aligned}$$

(1.2)

is a cubic-like curve that consists of three branches (see Fig. 1). There are two attracting branches, where the derivative

$$\begin{aligned} \left. \frac{\partial f}{\partial u} \right| _{\{ f=0 \} } = -\frac{a-a u^2+2 u^3}{u\left( 1+u^2\right) } \end{aligned}$$

is negative. In between, there is a repelling branch along which the derivative is positive. In the (u, v) phase plane, the fast nullcline is a cubic-like critical manifold of (1.1) with $\beta =0$ (Fig. 1). There are two fold points, $L_{\pm }$, with $u,v>0$. Here, the subscripts indicate that the u-coordinate of $L_-$ is smaller than the u-coordinate of $L_+$. On each of the three open branches, the critical manifold is normally hyperbolic, but the fold points are non-hyperbolic. (For completeness, we note that with $0< a < 3\sqrt{3}$, the fast nullcline consists of only one branch with negative slope, so that all of the equilibria in the first quadrant are attracting fixed points of the fast subsystem. Hence, classical relaxation oscillations do not occur with $0<a<3\sqrt{3}$).

Fig. 1

Phase plane of a single Lengyel-Epstein oscillator. The LCCs exist in an exponentially small parameter interval of a values that are $\mathcal {O}(\beta )$ close to the value of $a_c$ (recall (1.5)), where the slow nullcline (red curve, $g=0$) intersects the fast nullcline (blue curve, $f=0$) at a fold point (blue marker, $\tfrac{\partial f}{\partial u} = 0$). The headless/jump-back canards (magenta and green) are separated from the canards with head/jump-away canards (cyan, orange, and purple) by the maximal canard (black). The LCCs facilitate the transition from a fixed point to a relaxation oscillation (yellow)

Single LE oscillators (1.1) have an equilibrium at

$$\begin{aligned} (u_{\textrm{e}},v_{\textrm{e}}) = \left( \frac{a}{5}, 1+\frac{a^2}{25} \right) \end{aligned}$$

(1.3)

where the fast nullcline intersects the slow nullcline ($g(u,v)=0$). This equilibrium undergoes a Hopf bifurcation at

$$\begin{aligned} a_H=\frac{5}{6}\left( \sqrt{60+\beta ^2}+ \beta \right) , \end{aligned}$$

(1.4)

at which the equilibrium transitions from being stable to unstable. Also, there is a canard point precisely when the equilibrium lies at the left fold point, i.e., to leading order at

$$\begin{aligned} (u_c,v_c,a_c) = \left( \sqrt{\frac{5}{3}}, \frac{8}{3}, 5 \sqrt{\frac{5}{3}} \right) , \end{aligned}$$

(1.5)

where we note that $5\sqrt{\frac{5}{3}}=6.454972\ldots$. See Fig. 1. The asymptotic expansion of $a_c$ is $a_c(\beta )=5\sqrt{\frac{5}{3}} + 5\beta +\mathcal {O}\left( \beta ^2\right)$.¹ Hence, in the parameter regime $a>3\sqrt{3}$, single LE oscillators can exhibit the full spectrum of different types of oscillations characteristic of planar fast–slow systems, including SAOs, LCCs, and LAOs. Moreover, the canard point $a_c(\beta )$ also serves as one of the two main organizing centers for the coupled system, as we show below.

The main model studied in this article is a pair of symmetrically coupled, identical LE oscillators:

$$\begin{aligned} {} \begin{aligned} {\dot{u}}_1 = a - u_1 - \frac{4u_1 v_1}{1 + u_1^2} + d_u(u_2 - u_1),\\ {\dot{v}}_1 = \beta \biggr (u_1 -\frac{u_1 v_1}{1 + u_1^2} + d_v(v_2 - v_1)\biggr ), \\ {\dot{u}}_2 = a - u_2 - \frac{4u_2 v_2}{1 + u_2^2} - d_u(u_2 - u_1), \\ {\dot{v}}_2 = \beta \biggr (u_2 - \frac{u_2 v_2}{1 + u_2^2} - d_v(v_2 - v_1)\biggr ). \end{aligned} \end{aligned}$$

(1.6)

Here, $d_{u}$ represents the coupling strength for the activator species u, and $d_v$ represents the coupling strength of the inhibitor species v. A schematic of the coupling is shown in Fig. 2. The coupling is symmetric, and (1.6) is invariant under the interchange of the labels on the oscillators, $u_1 \rightarrow u_2, \quad v_1 \rightarrow v_2,$ as may be seen directly from the coupling schematic and from the system (1.6). That is, if $(u_1(t),v_1(t),u_2(t),v_2(t))$ is a solution of (1.6), then $(u_2(t),v_2(t),u_1(t),v_1(t))$ is another solution obtained by reflection across the axis of symmetry $\{ u_1=u_2, v_1=v_2 \}$. Further information about the coupled model (1.6), including the equilibria, the Hopf bifurcations, and the branches of classical in-phase (IP) and anti-phase (AP) rhythms, is presented in Sect. 2.

Fig. 2

Reciprocal coupling scheme of(1.6)

In the $(u_1,v_1,u_2,v_2)$ phase space, the coupled system (1.6) has a two-dimensional critical surface $S_0$, which is the Cartesian product of the fast nullclines of the individual oscillators. On this critical surface/manifold, which may be referred to as a Cartesian product quilt (Awal et al. 2023), there are a number of key points that are classified mathematically as folded singularities. In general fast–slow systems, these key points were first studied in Takens (1976), and over the past two decades they have been studied extensively in many fast–slow systems, see for example (Szmolyan and Wechselberger 2001; Wechselberger 2005; Dumortier and Roussarie 1996; Brøns et al. 2006; Krupa and Wechselberger 2010; Mitry et al. 2013; Vo and Wechselberger 2015; de Maesschalck et al. 2021).

1.2 Principal Results

In this article, we build on the brief introduction of some asymmetric rhythms of (1.6) presented in Sect. 4 of Awal et al. (2023).

We begin by analyzing the different types of folded singularities in (1.6), determining where they exist in parameter space, and the bifurcations they undergo (see Sect. 3). We show that there is a key folded node (FN), near the local minima of the fast nullclines of both oscillators – but off the symmetry axis of (1.6) – which is the main mechanism responsible for the strong symmetry breaking. Orbits that enter into the neighborhood of this FN are guided through the neighborhood by its strong-, weak-, and secondary canards. We show that the location of this key FN and the orientation of its canards on and near the quilt can guide the orbits in a manner that splits the oscillators, i.e., strongly breaks the symmetry, with one constrained to remain of small amplitude and the other guided to make a fast, large-amplitude excursion.

The simplest strong symmetry breaking rhythms created by this FN are $0^2 1^0$ SAO-LAO rhythms, in which one oscillator exhibits two SAOs per period while the other undergoes a full relaxation limit cycle (see Sect. 4). These rhythms arise when the orbits in phase space make a simple pass each period through the neighborhood of the key FN, near either its strong or weak canard. We show that in both cases the dynamics induced by these canards of the FN lead to the splitting between the directions the two oscillators subsequently go in phase space, i.e., to the strong symmetry breaking. Moreover, we determine the relative order in time in which the SAOs and the up and down jumps of the LAO occur, as that also depends on the passage through the neighborhood of the FN.

The $0^2 1^0$ SAO-LAO rhythms are at the base of a family of strong symmetry breaking $0^s 1^0$ rhythms, with $s \ge 2$. We show that these arise for parameter values such that the key FN off the symmetry axis also has secondary canards, which rotate about the weak canard of the FN (see Sect. 4). The number of secondary canards of this FN point and the number of rotational sectors they induce are determined by the eigenvalue ratio of this point (Wechselberger 2005; Brøns et al. 2006). Then, in turn, the number of SAOs the orbit exhibits is determined by the rotational sector of the FN that the orbit enters.

Next, we show analytically that there is a second organizing center for the coupled system (1.6) at $a=a_\textrm{asym,c}(\beta )$, where an asymmetric canard explosion takes place (see Appendix E and especially formula (E.1)). That is, for each value of the parameter a in a small neighborhood centered on $a_{\textrm{asym,c}}(\beta )$, there exist strong symmetry breaking SAO-LCC rhythms in which the amplitude of one oscillator remains small, while the other oscillator exhibits LCCs. The LCCs vary with the parameter, just as in the case of a single LE oscillator, in a sequence of “headless” ducks, maximal “headless” ducks, and ducks with heads. This is the sequence in which relaxation oscillations are born, through a canard explosion, and the novelty here is that one of the oscillators can undergo this sequence while the other remains of small amplitude, despite the fact that they are identical and coupled symmetrically through both the fast and the slow variables. We use the method of geometric desingularization to carry out the analysis and derive the formula for $a_{\textrm{asym,c}}(\beta )$, which is shown to agree with the results of numerical simulations to within the asymptotic order of the calculation.

Following this derivation, we show that in a neighborhood of $a_\textrm{asym,c}(\beta )$ in parameter space, system (1.6) exhibits strong symmetry breaking $0^{s_1} 1^{s_2}$ SAO-MMO rhythms (see Sect. 5). In these rhythms, one oscillator makes $s_1$ SAOs each period (just as for the SAO-LAO rhythms), while the second oscillator exhibits an MMO each period, which consists of one LAO and $s_2$ SAOs. These exist stably for a broad range of integers $s_1$ and $s_2$. Moreover, for these, we study how the strong symmetry breaking is also made possible here by the canards of the same FN point, which lies off the symmetry axis.

After presenting the results about the strong symmetry breaking rhythms, the key folded singularity that makes them possible, and the asymmetric canard explosion that acts as an organizing center, we present a number of new weak symmetry breaking rhythms for system (1.6) (see Sect. 6). These are close to AP LAO and AP MMO rhythms. We show how pairs of FNs are responsible for creating these rhythms. Also, we contrast these dynamics with the strong symmetry breaking rhythms, emphasizing the differences between the numbers of key folded singularities involved, how the orbits pass through their neighborhoods, and how their canards are oriented and guide the orbits. Moreover, these types of weak symmetry breaking rhythms, close to IP and AP rhythms, will also exist in other symmetrically coupled, identical fast–slow oscillators that have FNs on their critical surfaces.

In addition to the key FN off the symmetry axis, there are some folded saddle (FS) points—both on and off the symmetry axis—which play important roles in forming asymmetric rhythms. Folded saddle points (Mitry et al. 2013) have strong canards that guide orbits across the fold curves of the critical surface, from a stable branch to an unstable branch. We find that an FS point off the symmetry axis acts as an important lane marker on the Cartesian product quilt for certain strong symmetry breaking SAO-LAO and SAO-MMO rhythms. Also, there is an FS point on the symmetry axis, and its strong canard acts as a separatrix relevant to the formation of weak symmetry breaking rhythms.

The analysis of the coupled LE model (1.6) also brings to light two new phenomena of independent interest. First, we discover a new type of explosion of LCCs, in which pairs of identical fast–slow oscillators are in AP and simultaneously undergo a canard explosion. This explosion of AP LCCs occurs over an open interval of parameter values, and it is a generic bifurcation. This contrasts with the situation for single planar fast–slow oscillators (and by default also for coupled identical in-phase oscillators), where the explosion of IP LCCs occurs in an exponentially narrow interval of parameter values. Moreover, this type of explosion of AP LCCs is found to mediate the transition from AP SAO-SAO rhythms to AP LAO-LAO rhythms, and it exists in other coupled, identical fast–slow oscillators, as well, including in identical van der Pol oscillators coupled symmetrically through the fast variables (as can be shown using the same approach as used here). Second, not only does the model (1.6) have bifurcation curves corresponding to each of the main known types of folded saddle-node (FSN) bifurcations, including the FSN’s of types I, II, and III (Krupa and Wechselberger 2010; Vo and Wechselberger 2015; Roberts 2018; Roberts et al. 2015), but it also has a pitchfork bifurcation in which a folded singularity changes stability and two new folded singularities emerge.

Bifurcation diagrams were computed using the numerical continuation software AUTO (Doedel et al. 2007). Maximal canards were computed in AUTO by solving appropriate two-point boundary value problems (Desroches et al. 2010). Numerical simulations were performed using Matlab’s built-in nonstiff ODE solver ode113. Independent confirmation was obtained using Mathematica’s built-in ODE solvers with stiffness switching enabled.

Table 1 List of abbreviations used in this article

2 Equilibria, Hopf Bifurcations, and Classical IP and AP Rhythms

In this section, we briefly report on the equilibria of the symmetrically coupled LE model (1.6), on Hopf bifurcations, and on the branches of IP and AP rhythms that emerge from these Hopf bifurcations. Most of these results are expected. They serve as reference points in the study of strong symmetry breaking rhythms, and they are useful for understanding the observed multistability of rhythms in the system. The new phenomena are the AP LCCs and the explosion in which they occur (see Fig. 3c–e).

Exchanging the first and second equations in system (1.6), we write it as

$$\begin{aligned} \begin{aligned} {\dot{u}}_1&= a-u_1-\frac{4u_1v_1}{1+u_1^2} + d_u \left( u_2-u_1 \right) =: f(u_1,v_1) + d_u \left( u_2-u_1 \right) \\ {\dot{u}}_2&= a-u_2-\frac{4u_2v_2}{1+u_2^2} - d_u \left( u_2-u_1 \right) =: f(u_2,v_2) - d_u \left( u_2-u_1 \right) \\ {\dot{v}}_1&= \beta \left( u_1-\frac{u_1v_1}{1+u_1^2} + d_v \left( v_2-v_1 \right) \right) =: \beta \left[ g(u_1,v_1) + d_v \left( v_2-v_1\right) \right] \\ {\dot{v}}_2&= \beta \left( u_2-\frac{u_2v_2}{1+u_2^2} - d_v \left( v_2-v_1 \right) \right) =: \beta \left[ g(u_2,v_2) - d_v \left( v_2-v_1\right) \right] . \end{aligned} \end{aligned}$$

(2.1)

This system possesses either one or three equilibria, depending on parameters. We distinguish them by whether or not they lie on the axis of symmetry $\{ u_1=u_2, v_2=v_1 \}$. The symmetric equilibrium is

$$\begin{aligned} E_{\textrm{symm}} = \left\{ (u_1,u_2,v_1,v_2) = \left( \frac{a}{5}, \frac{a}{5}, 1+ \frac{a^2}{25}, 1+\frac{a^2}{25} \right) \right\} , \end{aligned}$$

(2.2)

recall (1.3). It exists for all positive values of the parameters $(a,d_u,d_v)$.

There are also two non-symmetric equilibria. These are given by

$$\begin{aligned} E_{ns} = \left\{ u_1 = \frac{a}{5} \mp \frac{\sqrt{ap (50d_v(5+2d_u) + a p )}}{5p}, u_2 = \frac{a}{5} \pm \frac{\sqrt{ap (50d_v(5+2d_u) + a p)}}{5p} \right\} ,\nonumber \\ \end{aligned}$$

(2.3)

where $v_1$ and $v_2$ can be calculated (see (3.2), for example), and the quantity p is

$$\begin{aligned} p=p(a,d_u,d_v)= 5(5+2d_u) - 2a d_v (3-2d_u). \end{aligned}$$

These non-symmetric equilibria exist provided the parameters satisfy $ap (50d_v(5+2d_u) + ap) \ge 0.$ They are created in pitchfork bifurcations from the symmetric state $E_{\textrm{symm}}$ at

$$\begin{aligned} a_{\textrm{PF}} = \frac{5}{4d_v} \cdot \left[ \frac{5+2d_u \pm \sqrt{(5+2d_u)(5+2d_u+16d_v^2(3-2d_u))}}{3-2d_u} \right] . \end{aligned}$$

(2.4)

The pitchfork bifurcations occur for all $0 \le d_u < \frac{3}{2}$ and $0\le d_v$. Also, in the limit $d_u,d_v \rightarrow 0$, the non-symmetric equilibria approach $u=0$ and $u=\tfrac{2a}{5}$, respectively.

The characteristic equation of the Jacobian matrix of (2.1) evaluated at $E_{\textrm{symm}}$ is

$$\begin{aligned} \left( \lambda ^2 - q_1 \lambda + q_2\right) \left( \lambda ^2 -\left( q_1-2q_3\right) \lambda +\left( q_2-2q_4\right) \right) =0, \end{aligned}$$

(2.5)

where $q_1=f_u+\beta g_v$ and $q_2=\beta (f_u g_v - f_v g_u)$ are the trace and determinant, respectively, of the Jacobian of a single LE oscillator, and $q_3=d_u+\beta d_v$ and $q_4=\beta \left( d_v (f_u-d_u) + d_u(g_v-d_v)\right)$ arise due to the coupling. The derivation of the characteristic equation is given in Appendix A.

Hence, $E_{\textrm{symm}}$ undergoes two types of Hopf bifurcations. The first Hopf bifurcation is at

$$\begin{aligned} a_{\textrm{H,IP}} = \frac{5}{6} \left( \sqrt{60+\beta ^2} + \beta \right) = 5 \sqrt{\frac{5}{3}} + \frac{5}{6} \beta + \mathcal {O}\left( \beta ^2\right) \end{aligned}$$

(2.6)

(recall (1.4)), and it is supercritical for all sufficiently small $\beta$. At $a=a_{\textrm{H,IP}}$, the first factor in the characteristic equation vanishes, independently of the coupling strengths. This corresponds to where the singular Hopf bifurcation of the single LE oscillator occurs. Here, IP SAO-SAO rhythms emerge from $E_{\textrm{symm}}$. As illustrated by the red branch in the bifurcation diagram of Fig. 3, the IP SAO-SAO rhythms are stable until the nearly vertical segment of the branch is reached, where they lose stability. Then, in a narrow parameter interval centered about $a=a_c$, an explosion of IP LCCs occurs. The IP oscillators behave as a single LE oscillator, and hence the canard point for the explosion of IP LCCs is the same as the canard point for a single LE oscillator, recall (1.5). Finally, for larger a, the oscillators undergo stable, classical IP LAO-LAO rhythms. (For further illustration of some parameter values for which the equilibrium $E_{\textrm{symm}}$, the IP SAO-SAO rhythms, and the IP LAO-LAO rhythms are stable, see Appendix B and the data in Table 3.)

Fig. 3

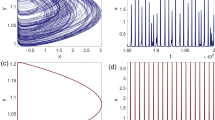
a Branches of IP rhythms (red) and AP rhythms (blue) of (1.6). These branches emanate from the symmetric equilibrium $E_{\textrm{symm}}$ (black) at $a_{\textrm{H,IP}}$ and $a_{\textrm{H,AP}}$, respectively (black dots in the inset), see (2.6) and (2.7). Stable rhythms are represented by solid curves, and unstable rhythms by dashed curves. Panels b–e show sequences of orbits along various segments of the IP and AP branches. b IP LCCs observed along the segment of the red branch corresponding to the IP canard explosion (star markers in the inset) at $a_c=5\sqrt{\frac{5}{3}}=6.454972...$, recall (1.5) These are the classical LCCs of a single LE oscillator. c AP LCCs observed along the lower segment of the AP branch (diamond markers in (a)). d A different set of AP LCCs, observed along the upper segment (mustaches in (a)). e Additional AP LCCs, observed along the middle segment of the AP branch (soccer balls in (a)). Here, $d_u = 8 \times 10^{-4}, d_v = 0.5$ and $\beta = 0.001$. Also, u represents both $u_1$ and $u_2$, and v represents both $v_1$ and $v_2$. For the AP rhythms, the trajectories in the phase space are the same, but the two oscillators are half a period out of phase along the trajectories

The second Hopf bifurcation of $E_{\textrm{symm}}$ is induced by the coupling terms. It occurs at

$$\begin{aligned} \begin{aligned} a_{\textrm{H,AP}}&= \frac{5\beta + 5\sqrt{\beta ^2 + 4\left( 3-2d_u-2\beta d_v\right) \left( 5+2d_u+2 \beta d_v\right) }}{2\left( 3-2d_u-2\beta d_v\right) }, \\&= 5 \sqrt{\frac{5+2d_u}{3-2d_u}} + \frac{5\left( 15-4d_u-4d_u^2+16 d_v \sqrt{15-4d_u-4d_u^2}\right) }{2(3-2d_u)\left( 15-4d_u-4d_u^2\right) } \beta +\mathcal {O}\left( \beta ^2\right) , \end{aligned} \end{aligned}$$

(2.7)

provided $0\le d_u<3/2$ and that $\beta$ is sufficiently small. At $a=a_{\textrm{H,AP}}$, the second factor in the characteristic Eq. (2.5) vanishes, and the value of the bifurcation parameter depends on the coupling strengths $d_u$ and $d_v$.

This Hopf bifurcation is subcritical for all $\mathcal {O}(1)$ values of $d_v$ (see, e.g., Fig. 3). A branch of AP SAO-SAO rhythms emerges from $E_{\textrm{symm}}$ (corresponding to the lower blue branch in Fig. 3a). These AP SAO-SAO rhythms are (jump-back) canard cycles, a.k.a. ducks without heads (see the black and red solutions in Fig. 3c).

As the AP branch is continued for larger values of a (diamond markers), a new type of canard explosion is discovered. In particular, the AP rhythms undergo a sequence of LCCs (see the green, blue, and magenta solutions in Fig. 3c), until they become stable or unstable AP LAO-LAO rhythms, depending on parameters (e.g., for small $d_v$ they are stable, and for large $d_v$, including $d_v = 0.5$, they are unstable).

A canard explosion of AP LCCs has not been observed before. In the four-dimensional space of solutions of (1.6), the explosion of AP LCCs occurs over a wide range of a values, as shown in 3c. This contrasts with the situation for single (and IP) LE oscillators, where the canard explosion is confined to an exponentially narrow interval. This is a reflection of the fact that, in systems with two (or more) slow variables, they are created by the canards of folded singularities, and hence the canard phenomenon is generic and occurs on larger open parameter sets.

Continuing further along the blue AP branch in Fig. 3a, the solutions develop an additional small-amplitude canard cycle (Figs. 3d, e, corresponding to the mustache and soccer ball markers in (a), respectively).

Remark 1

Using the information about the folded singularities found in Sect. 3, one can further understand these AP LCC and AP LAO rhythms. The geometric deconstructions are presented in Appendix C, since they are of independent interest, and so that the focus of the article stays on the strong symmetry breaking and other asymmetric rhythms of (1.6).

Remark 2

As we shall see in Sect. 3.5, $a_{\textrm{H,AP}}$ is also the singular Hopf bifurcation associated with the FSN II of the symmetric folded singularity and the symmetric ordinary singularity. The FSN II of these symmetric singularities occurs at $a = 5 \sqrt{\frac{5+2d_u}{3-2d_u}}$.

3 Geometric Singular Perturbation Theory Analysis of the Coupled LE Model

In this section, we present the geometric singular perturbation analysis of the symmetrically coupled LE model (2.1), by studying the fast subsystem, the critical manifold and its fold curves, and the patches of the Cartesian product quilts (Sect. 3.1), the slow system (Sect. 3.2), the folded singularities (Sect. 3.3), and their bifurcations (Sects. 3.5 and 3.6). We also present the full geometry of the local dynamics and canards induced by FNs (Sect. 3.4), since there is an FN that is the primary mechanism responsible for the strong symmetry breaking observed in the main rhythms studied in this article. The reader interested in these strong symmetry breaking rhythms could go directly to Sect. 4 after reading Sects. 3.1–3.4.

3.1 Fast Subsystem

By taking the limit $\beta \rightarrow 0$ in (2.1), we obtain the fast subsystem

$$\begin{aligned} \begin{aligned} {\dot{u}}_1&= f(u_1,v_1) + d_u \left( u_2-u_1 \right) \\ {\dot{u}}_2&= f(u_2,v_2) - d_u \left( u_2-u_1 \right) . \end{aligned} \end{aligned}$$

(3.1)

Here, $v_1$ and $v_2$ are constant. Throughout this section, for notation, we write $\textbf{f}= (f(u_1,v_1),f(u_2,v_2))$, and $\frac{\partial f}{\partial u_i}$ and $\frac{\partial f}{\partial v_i}$ will denote the partial derivatives of $f(u_i,v_i)$ with respect to $u_i$ and $v_i$, for $i=1,2$. Further, $D_\textbf{u} \textbf{f}$ and $D_\textbf{v} \textbf{f}$ denote the $2 \times 2$ Jacobian matrices with respect to $\textbf{u} = (u_1,u_2)$ and $\textbf{v} = (v_1,v_2)$.

Equilibria of the fast subsystem determine the critical manifold,

$$\begin{aligned}{} & {} S = \left\{ v_{1S} = \frac{1}{4u_1} \left( 1+u_1^2 \right) \left( a-u_1+d_u (u_2-u_1) \right) , \,\, \right. \nonumber \\{} & {} \left. v_{2S} = \frac{1}{4u_2} \left( 1+u_2^2 \right) \left( a-u_2-d_u (u_2-u_1) \right) \right\} . \end{aligned}$$

(3.2)

The critical manifold S is a two-dimensional surface in the four-dimensional $(u_1,u_2,v_1,v_2)$ space, which may be thought of as a quilt; see Fig. 4. It is subdivided into multiple patches based on the eigenvalues of the Jacobian of the fast subsystem evaluated at the points on S,

$$\begin{aligned} D_\textbf{u} \textbf{f} + d_u C = \begin{bmatrix} \frac{\partial f}{\partial u_1} - d_u &{} d_u \\ d_u &{} \frac{\partial f}{\partial u_2} - d_u \end{bmatrix}, \end{aligned}$$

(3.3)

where $C = \begin{bmatrix} -1 &{} 1 \\ 1 &{} -1 \end{bmatrix}$ is the coupling matrix.

Fig. 4

Projection of the critical manifold $S=S_a \cup S_s \cup S_r \cup L$ onto a the $(u_1,u_2,v_1)$ phase space and b the $(u_1,u_2)$ phase plane. The (blue) attracting patches $S_a$ are separated from the (yellow) saddle patch $S_s$ by the fold set L (black curves). Similarly for the (yellow) saddle and (red) repelling patches $S_r$. The gaps between the blue and red patches, through which the yellow patch is connected, increase with $d_u$. Here, $a=6.55$ and $d_u = 0.1$

In analyzing the Jacobian, we first observe that $D_\textbf{u} \textbf{f} + d_u C$ is symmetric at all points on S. Hence, the eigenvalues of the fast subsystem are real at all points on S, and S contains only stable and unstable nodes, saddles, and saddle-nodes. We write $S_a$ for the patch of S on which the equilibria are stable nodes; $S_s$ is the patch consisting of saddles; and $S_r$ is the patch consisting of unstable nodes. See Fig. 4.

Second, we observe that the boundaries of these patches are given by the subset of S on which the Jacobian has zero determinant. This is called the fold set

$$\begin{aligned}{} & {} L = \left\{ (\textbf{u},\textbf{v}) \in S: \det \left( D_\textbf{u} \textbf{f} +d_u C\right) = 0 \right\} \nonumber \\{} & {} \quad = \left\{ (\textbf{u},\textbf{v}) \in S: \frac{\partial f}{\partial u_1} \frac{\partial f}{\partial u_2} - d_u \left( \frac{\partial f}{\partial u_1} + \frac{\partial f}{\partial u_2} \right) = 0 \right\} . \end{aligned}$$

(3.4)

In general, one of the eigenvalues changes sign along a fold curve in L, see the black curves in Fig. 4. Overall,

$$\begin{aligned} S = S_a \cup S_s \cup S_r \cup L. \end{aligned}$$

(3.5)

Moreover, depending on the system parameters, the set $S_r$ may be empty (see Remark 4).

Third, we observe that since the eigenvalues of the Jacobian are real, there is no mechanism purely in the fast subsystem for delayed Hopf bifurcations. Hence, the mechanism that generates the small oscillations in the rhythms must be encoded in the slow subsystem, to which we now turn.

3.2 Slow Subsystem

In this section, we work with the coupled LE system (2.1) in the slow time variable ${\tilde{t}}=\beta t$. The reduced problem, or slow subsystem, is given by the differential-algebraic system

$$\begin{aligned} \begin{aligned} \textbf{0}&= \textbf{f}(\textbf{u},\textbf{v}) + d_u C \textbf{u} \\ \frac{{\text {d}}{} \textbf{v}}{{\text {d}}{\tilde{t}}}&= \textbf{g}(\textbf{u},\textbf{v}) + d_v C \textbf{v}, \end{aligned} \end{aligned}$$

(3.6)

where $\textbf{g}=(g(u_1,v_1),g(u_2,v_2))$. Differentiating the algebraic constraints with respect to ${\tilde{t}}$ and multiplying by the adjoint matrix gives

$$\begin{aligned} \begin{aligned} \det \left( D_\textbf{u} \textbf{f} + d_u C\right) \frac{{\text {d}}{} \textbf{u}}{{\text {d}}{\tilde{t}}}&= -{\text {adj}} \left( D_\textbf{u} \textbf{f}+d_u C \right) D_\textbf{v} \textbf{f} \left( \textbf{g}+d_v C \textbf{v} \right) \\ \frac{{\text {d}}{} \textbf{v}}{{\text {d}}{\tilde{t}}}&= \textbf{g} + d_v C \textbf{v}, \end{aligned} \end{aligned}$$

(3.7)

where all functions are evaluated along the critical manifold S. The reduced flow (3.7) is singular along the fold set L. We desingularize via the transformation ${\text {d}}{\tilde{t}} = \det \left( D_\textbf{u} \textbf{f} + d_u C\right) \, {\text {d}}\tau$, which gives the desingularized reduced system valid on S,

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}u}{{\text {d}}\tau }&= -{\text {adj}} \left( D_\textbf{u} \textbf{f} + d_u C \right) D_\textbf{v} \textbf{f} \left( \textbf{g} +d_v C \textbf{v} \right) \\ \frac{{\text {d}}{} \textbf{v}}{{\text {d}}\tau }&= \det \left( D_\textbf{u} \textbf{f} + d_u C\right) \left( \textbf{g} + d_v C \textbf{v} \right) . \end{aligned} \end{aligned}$$

(3.8)

In components, the desingularized reduced system is

$$\begin{aligned} \frac{{\text {d}}u_1}{{\text {d}}\tau }= & {} F_1(u_1,u_2):= \left( d_u - \frac{\partial f}{\partial u_2} \right) \frac{\partial f}{\partial v_1} \left( g(u_1,v_1) \right. \nonumber \\{} & {} \left. + d_v (v_2-v_1) \right) + d_u \frac{\partial f}{\partial v_2} \left( g(u_2,v_2) - d_v(v_2-v_1) \right) \nonumber \\ \frac{{\text {d}}u_2}{{\text {d}}\tau }= & {} F_2(u_1,u_2):= d_u \frac{\partial f}{\partial v_1} \left( g(u_1,v_1) + d_v (v_2-v_1) \right) \nonumber \\{} & {} + \left( d_u - \frac{\partial f}{\partial u_1} \right) \frac{\partial f}{\partial v_2} \left( g(u_2,v_2) - d_v(v_2-v_1) \right) \nonumber \\ \frac{{\text {d}}v_1}{{\text {d}}\tau }= & {} \det \left( D_\textbf{u} \textbf{f} + d_u C\right) \left( g(u_1,v_1) + d_v (v_2-v_1) \right) \nonumber \\ \frac{{\text {d}}v_2}{{\text {d}}\tau }= & {} \det \left( D_\textbf{u} \textbf{f} + d_u C\right) \left( g(u_2,v_2) - d_v (v_2-v_1) \right) . \end{aligned}$$

(3.9)

This system is a self-contained system of equations for the dynamics on S. (Note that on S, one has $F_1\vert _S =F_1(u_1,u_2)$ and $F_2\vert _S=F_2(u_1,u_2)$, since $v_1=v_{1S}(u_1,u_2)$ and $v_2=v_{2S} (u_1,u_2)$). The desingularized reduced system (3.9) is the system that we study now to find the folded singularities.

3.3 Folded Singularities of the Coupled LE Model

The folded singularities, M, of (2.1) are solutions of the system of three algebraic equations in two unknowns given by

$$\begin{aligned} F_1 = 0, \ \ \ \ F_2 = 0, \ \ \ \ \det \left( D_\textbf{u} \textbf{f} + d_u C\right) = 0. \end{aligned}$$

(3.10)

They are distinct from the equilibria (or ordinary singularities) of (3.9), which are the equilibria $E_{\textrm{symm}}$ and $E_{ns}$ of the original model (2.1), recall (2.2) and (2.3). Hence, one also requires $\frac{\partial f}{\partial u} \vert _S \ne 0$ in order for a solution to be a folded singularity.

We reduce these three conditions to two independent conditions, as follows. At folded singularities, the matrix $D_\textbf{u} \textbf{f} + d_u C$ has linearly dependent rows, since $\det \left( D_\textbf{u} \textbf{f} + d_u C\right) = 0$. Hence, the adjoint has linearly dependent columns. Let $A_1$ and $A_2$ denote the columns of ${\text {adj}} \left( D_\textbf{u} \textbf{f} + d_u C\right)$. Then, at folded singularities, the algebraic conditions $F_1 = 0$ and $F_2 = 0$ can be rewritten as a single condition,

$$\begin{aligned} \begin{bmatrix} F_1 \\ F_2 \end{bmatrix}= & {} A_1 \left( \frac{\partial f}{\partial v_1} (g(u_1,v_1)+d_v(v_2-v_1)) + \kappa \frac{\partial f}{\partial v_2} (g(u_2,v_2)-d_v(v_2-v_1)) \right) \\= & {} \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \end{aligned}$$

where $\kappa = - \frac{\partial f}{\partial u_1}/\frac{\partial f}{\partial u_2}$. Hence, the folded singularities may be found among the solutions $(u_1,u_2)$ of the following system of two equations:

$$\begin{aligned} \begin{aligned} \frac{\partial f}{\partial u_1} \frac{\partial f}{\partial v_2} (g(u_2,v_2)-d_v(v_2-v_1)) - \frac{\partial f}{\partial u_2} \frac{\partial f}{\partial v_1} (g(u_1,v_1)+d_v (v_2-v_1))&= 0 \\ \frac{\partial f}{\partial u_1} \frac{\partial f}{\partial u_2} - d_u \left( \frac{\partial f}{\partial u_1} + \frac{\partial f}{\partial u_2} \right)&= 0. \end{aligned} \end{aligned}$$

(3.11)

Here, the second equation is precisely the third condition in (3.10).

Finally, those solutions of (3.11) at which $\frac{\partial f}{\partial u_1} = 0$ or $\frac{\partial f}{\partial u_2} = 0$ are ordinary singularities (equilibria). Hence, they are not included among the set of folded singularities. Therefore, the folded singularities of (2.1) are precisely those solutions of (3.11) at which

$$\begin{aligned}{} & {} \left( u_1^2-1\right) \left( a+d_u\left( u_2-u_1\right) \right) -2u_1^3 \ne 0 \nonumber \\{} & {} \quad \text { and } \quad \left( u_2^2-1\right) \left( a-d_u\left( u_2-u_1\right) \right) -2u_2^3 \ne 0. \end{aligned}$$

(3.12)

Following the classification of the ordinary singularities into either symmetric or non-symmetric (Sect. 3), we distinguish here between the folded singularities, $M_s$, that exist on the symmetry axis $\{ u_1 = u_2, v_1= v_2 \}$ and the folded singularities, $M_{ns}$, that exist away from it (i.e., that are non-symmetric). From Eqs. (3.9)(a) and (b) and condition (3.12), we find that the symmetric folded singularities are solutions of $2 d_u - \frac{\partial f}{\partial u} \vert _S =0$, that is

$$\begin{aligned} c(u) = a- a u^2 +2u\left( d_u+u^2+d_u u^2\right) = 0. \end{aligned}$$

(3.13)

Analysis of this condition reveals that there are exactly two symmetric folded singularities $M_s$ in the positive $(u_1,u_2)$ quadrant provided

$$\begin{aligned} \begin{aligned} a&> \frac{1}{\sqrt{2}} \sqrt{27+72d_u+44d_u^2+\sqrt{(1+2d_u)(9+10d_u)}(9+10d_u)}, \\&= \frac{3+2d_u + \sqrt{9+28d_u+20d_u^2}}{2} \sqrt{\frac{ 3+4d_u + \sqrt{9+28d_u+20d_u^2}}{2(1+d_u)}} \\&= 3\sqrt{3} + 4 \sqrt{3} d_u - \frac{2}{3\sqrt{3}}d_u^2 + \mathcal {O}\left( d_u^3\right) \end{aligned} \end{aligned}$$

(3.14)

The derivation of this result proceeds as follows. First, we observe that the cubic $c(u)=a- a u^2 +2u\left( d_u+u^2+d_u u^2\right)$ in (3.13) has up to two turning points, and that $u>0$ at both of these turning points (when they exist) for $a \ge 0$ and $d_u \ge 0$. This implies at least two of the three real roots of c(u) have positive u values. Next, the constant term in the function c(u) is a negative multiple of the product of its roots. This implies one root must have opposite sign to the other two. Hence, when the parameters are such that there are three real roots, two of those roots lie in the domain $u>0$. Finally, the inequality in (3.14) is obtained by finding the condition such that the two positive roots of c(u) coincide.

The folded singularities, which are given by the solutions of (3.11) that satisfy the condition (3.12), may be classified based on the eigenvalues of the linearization of the desingularized reduced system (3.9). The generic types of folded singularities are FN, FS, and FF (folded foci), corresponding to eigenvalues of the linearization with the same sign, opposite signs, and nonzero imaginary parts, respectively. Various types of ordinary and folded singularities are illustrated in Fig. 5. The symmetric folded singularities lie on the diagonal $\{u_1=u_2 \}$ at the boundaries between the saddle sheets and the repelling sheets. The non-symmetric folded singularities come in pairs and are symmetrically disposed with respect to the diagonal.

A non-symmetric FN on the boundary of the lower left patch $S_a$ turns out to be the main mechanism responsible for the strong symmetry breaking in the rhythms studied here. Hence, in Sect. 3.4 we review the salient aspects of the geometry induced by FNs. Then, a systematic bifurcation study of the folded singularities and their dependence on system parameters is presented in Sects. 3.5 and 3.6.

Remark 3

Folded singularities are not equilibria of the coupled system (1.6). Rather, they are points at which the desingularized system (3.9) may become regular via a zero over zero, l’Hopital rule type cancellation. Such cancellations are precisely what permits solutions on one branch of S, say an attracting branch $S_a$, to continue past the fold set L onto an adjacent patch, e.g., a saddle or repelling patch, $S_s$ or $S_r$, and spend long times near them despite their being unstable. Hence, folded singularities are the gateway mechanisms responsible for the creation of the canard solutions and rhythms studied here.

Remark 4

The condition (3.14) on the existence of the symmetric folded singularities is also the condition such that the repelling sheet $S_r$ is non-empty. Furthermore, since this is a condition on the geometry of the critical manifold, it is independent of $d_v$.

Fig. 5

Singularities of the coupled LE model (1.6) in a the chemically relevant part of the phase plane, and b in a neighborhood of the symmetric equilibrium, $E_{\textrm{symm}}$. The folded singularities lie at the intersections of the (black) fold curves with the (blue) $F_1 = 0$ and (red) $F_2 = 0$ nullclines. The black, dashed, diagonal line is the axis of symmetry. The two symmetric folded singularities are both FS. The non-symmetric folded singularities are FN, FS, and FF. Here, $a=6.55, d_u = 0.1$, and $d_v = 0.5$

3.4 Local Dynamics Around an FN Singularity

Canard solutions have been shown to play key roles in shaping the dynamics of a wide range of physical systems. The canard dynamics of a FN singularity are particularly important in the creation of SAOs such as in the bursting electrical activity of human beta-cells (Battaglin and Pedersen 2021), the El Niño-Southern Oscillation (Roberts et al. 2016), and arrhythmogenesis in cardiac muscle cells (Kimrey et al. 2022). The canards of FSs have been shown to play the role of a firing threshold manifold in a model of an excitable neuron (Mitry et al. 2013), and have also been demonstrated to be the mechanism for spike-adding in parabolic bursting models (Desroches et al. 2016). Here, we outline the salient features of the canard dynamics of a FN in the context of the coupled LE system.

In the singular limit ($\beta \rightarrow 0$), a FN singularity possesses a (singular) strong canard and a (singular) weak canard. The subset of the attracting sheet of the critical manifold enclosed by the singular strong canard and the fold curve is the funnel of the FN. Solutions in the funnel are known as singular candidates, and they can connect the attracting sheet of the critical manifold (such as a patch $S_a$) to a saddle sheet (such as a patch $S_s$) or a repelling sheet (such as $S_r$) (Brøns et al. 2006; Kuehn 2015).

For $0<\beta \ll 1$, these features of the FN persist and perturb to nearby structures of similar types (Szmolyan and Wechselberger 2001; Wechselberger 2005, 2012). The singular strong canard perturbs to a nearby solution called the primary strong canard, $\gamma _s$. Similarly, the singular weak canard perturbs to a nearby solution called the primary weak canard, $\gamma _w$ (Szmolyan and Wechselberger 2001). A major difference for nonzero $\beta$ is that, of the singular candidates, only finitely many will persist as a connection between an attracting manifold and a saddle manifold. These solutions that connect the attracting and saddle manifolds are the maximal canards, and they include the primary strong and primary weak canards. The other maximal canard solutions that connect the attracting and saddle manifolds are known as secondary canards (Wechselberger 2005). For a fixed parameter set, the number of maximal canard solutions can be predicted using the eigenvalues, $\lambda _s<\lambda _w<0$, of the FN. Let $\mu = \lambda _w/\lambda _s$ denote the eigenvalue ratio. Then, provided that $\mu$ is bounded away from zero and that $\mu ^{-1}$ is not an integer, the number of secondary canards is

$$\begin{aligned} \left\lfloor \frac{1-\mu }{2\mu } \right\rfloor , \end{aligned}$$

(3.15)

where $\lfloor \cdot \rfloor$ is the floor function (Brøns et al. 2006).

Fig. 6

The strong, weak, and secondary canards of the FN, along with the rotational sectors they define. a The primary strong and primary weak canards, $\gamma _s$ and $\gamma _w$, of the FNs. Both FNs have eigenvalue ratio $\mu \approx 0.187$. Hence, for each FN, there are also two secondary canards, $\gamma _1$ and $\gamma _2$, by (3.15). Together, these canard solutions are the boundaries on the attracting manifold of the rotational sectors, $R_j$, $j=0,1,2,3$. Solutions in sector $R_j$ exhibit j small oscillations about the weak canard in an $\mathcal {O}\left( \sqrt{\beta }\right)$ neighborhood of the FN. b A solution with initial condition (square marker) in sector $R_0$. It transitions through the neighborhood of the FN without rotation. c A solution with initial condition (triangle marker) in sector $R_1$. It executes one small oscillation near the FN. d A solution with initial condition (diamond marker) in sector $R_2$. It executes two small oscillations near the FN. e A solution with initial condition (pentagon marker) in sector $R_{\max } = R_3$. It executes three small oscillations near the FN. Here, $a=6.5, d_u = 0.15, d_v = 0.5$, and $\beta = 0.001$

The primary strong canard and the secondary canards partition the attracting manifold into sectors, $R_j$ for $j = 0, 1, \ldots , s_{\max }$, where $s_{\max } = \left\lfloor \tfrac{\mu +1}{2\mu } \right\rfloor ,$ as illustrated in Fig. 6a; see also (Brøns et al. 2006; Desroches et al. 2010). (Note: $\left\lfloor \tfrac{\mu + 1 }{2\mu } \right\rfloor = \left\lfloor \tfrac{1-\mu }{2\mu } + 1 \right\rfloor$). The first rotational sector, $R_1$, is the subset of the attracting manifold enclosed by the primary strong canard, $\gamma _s$, and the first secondary canard, $\gamma _1$. Solutions with initial conditions in the sector $R_1$ will execute one small oscillation in an $\mathcal {O}\left( \sqrt{\beta }\right)$ neighborhood of the FN (Fig. 6b). The axis of rotation for the oscillation is the primary weak canard. More generally, the rotational sector $R_j$ is delimited by $\gamma _{j-1}$ and $\gamma _j$ for $j=1,2,\ldots , s_{\max }$, where $\gamma _0 = \gamma _s$ and $\gamma _{s_{\max }} = \gamma _w$. Solutions in sector $R_j$ exhibit j small oscillations around the weak canard in an $\mathcal {O}\left( \sqrt{\beta }\right)$ neighborhood of the FN (Fig. 6c–e, where $j=1,2,3,$ respectively). Thus, the strong canard is the local phase space separatrix that divides between solutions that will exhibit local oscillations near the FN and solutions that will pass by without any rotations. The secondary canards further subdivide the phase space based on the rotational properties of solutions.²

At $\mathcal {O}(1)$ distances from the FN, the secondary canards, $\gamma _j$ for $j=1,2,\ldots , s_{\max }-1$, are $\mathcal {O}\left( \beta ^{(1-\mu )/2}\right)$ close to the strong canard. Thus, the secondary canards collapse onto the strong canard in the singular limit $\beta \rightarrow 0$ and conversely, emanate from the strong canard as $\beta$ is increased from zero (Brøns et al. 2006). Since the secondary canards are closely spaced around the strong canard, this implies that the sub-maximal rotational sectors, $R_j$ for $j=1,2,\ldots , s_{\max }-1$, have widths of size $\mathcal {O}\left( \beta ^{(1-\mu )/2}\right)$, and that the largest sectors are the zero-rotation sector $R_0$ and the maximal rotation sector $R_{\max }$. Hence, the most common asymmetric rhythms have either zero canard-induced SAOs or the maximal number of canard-induced SAOs.

Remark 5

For the subset of the attracting manifold between the weak canard and a small neighborhood of the fold curve, the number of rotations can be either $s_{\max }$ or $s_{\max }-1$, depending on the value of the eigenvalue ratio $\mu$; for examples, see Figs. 12 and 17 of Vo et al. (2012) and Fig. 9 of Krupa et al. (2008).

3.5 Bifurcations of the Folded Singularities

In this subsection, we present the main bifurcations of the symmetric and non-symmetric folded singularities. We observe that some of these bifurcations involve both folded and ordinary singularities.

The symmetric folded singularities can undergo an FSN I in which a pair of folded singularities (one FS and one faux FN, denoted by fFN) collide and annihilate each other along the fold set L. For the coupled LE model, there is a FSN I of the symmetric folded singularities when

$$\begin{aligned} a_{\textrm{FSN I}} = \frac{1}{2} \left( 3+2d_u + \sqrt{9+28d_u+20d_u^2} \right) \sqrt{\frac{ 3+4d_u + \sqrt{9+28d_u+20d_u^2}}{2(1+d_u)}}.\nonumber \\ \end{aligned}$$

(3.16)

This is precisely the SN bifurcation in which the symmetric folded singularities on the boundary between $S_s$ and $S_r$ disappear together, along with the patch $S_r$. See the red FSN I curve in Fig. 7 and recall the condition (3.14).

Next, there is an FSN II of the symmetric ordinary singularity $E_s$ and a symmetric folded singularity at

$$\begin{aligned} a_{\textrm{FSN II}} = 5 \sqrt{\frac{5+2d_u}{3-2d_u}}. \end{aligned}$$

(3.17)

In this FSN II bifurcation, $E_s$ crosses over the fold curve L and exchanges stability with a symmetric folded singularity. Hence, this bifurcation may also be thought of as a hybrid transcritical bifurcation of an ordinary singularity and a folded singularity. (See the black curve between regions III and IV in Fig. 7).

There is an FSN III of the symmetric ordinary singularity $E_s$ and the non-symmetric folded singularities at $a = 5 \sqrt{5/3}$. In this FSN III, a pair of non-symmetric folded singularities emerge from the symmetric equilibrium $E_s$. This FSN III bifurcation at $a = 5 \sqrt{5/3}$ is independent of the coupling strengths, and it is located at $a_c$, the same value as the canard point of the single LE oscillator. (See the black FSN III line in Fig. 7). This type of FSN III is of the type first discovered in Roberts (2018), Roberts et al. (2015). In particular, it corresponds to subcase 4 of the FSN III family from Section 7.1 of Roberts (2018); see also Roberts et al. (2015), where the same type of FSN III is discussed in the context of a coupled system of respiratory neurons in the pre-Bötzinger complex. It may also be thought of as a hybrid pitchfork bifurcation in which an ordinary singularity changes stability and a pair of folded singularities are created.

Finally, there is a pitchfork bifurcation of folded singularities, in which a pair of non-symmetric folded singularities bifurcate out of a symmetric folded singularity. We label this pitchfork bifurcation of folded singularities $\hbox {PF}_{\textrm{M}}$. To the best of our knowledge, this type of bifurcation has not yet been studied. A parametric representation of the curve along which this pitchfork bifurcation of folded singularities occurs in the $(a,d_u)$ plane is given by

$$\begin{aligned} \begin{aligned} a_{\mathrm{PF_M}}&= \frac{5u+10u^3-3u^5+u\sqrt{25+80u^2+62u^4-48u^6+9u^8}}{2\left( 1+u^2\right) }, \\ d_u&= \frac{\left( u^2-1\right) \sqrt{25+80u^2+62u^4-48u^6+9u^8}-9u^2 -5+9u^4-3u^6}{4\left( 1+u^2\right) ^2}, \end{aligned}\nonumber \\ \end{aligned}$$

(3.18)

where $\sqrt{\tfrac{5}{3}}< u < \sqrt{3}$ so that $d_u >0$. (See the green $\hbox {PF}_{\textrm{M}}$ curve in Fig. 7). This $\hbox {PF}_{\textrm{M}}$ curve is independent of $d_v$. Moreover, at $a=3\sqrt{3}$, it tangentially intersects the FSN I curve (3.16), in which the symmetric folded singularities $M_s$ on the boundary between $S_s$ and $S_r$ are created/annihilated. Finally, at $a = 5\sqrt{\frac{5}{3}}$, it tangentially intersects the FSN III curve.

Remark 6

FSN II bifurcations can also occur when a non-symmetric ordinary singularity, $E_{ns}$, merges with a folded singularity. However, we omit the analytical conditions for these, because the resulting FSN II bifurcations occur when one of $u_1$ or $u_2$ is negative, and hence have no chemical relevance.

3.6 Summary: Folded Singularities and Their Bifurcations

In this subsection, we summarize the main chemically relevant folded singularities (i.e., those with $u \ge 0$ and $v \ge 0$) and their bifurcations in the $(a,d_u)$ parameter plane for a representative value of $d_v$. See Fig. 7 and Table 2. Similar bifurcation diagrams and tables are obtained for other small values of $d_v$.

Fig. 7

Bifurcations of the desingularized reduced system. a $(a,d_u)$ bifurcation diagram for $d_v = 0.5$, showing the curves of FSN I-III and $\hbox {PF}_{\textrm{M}}$, as well as the degenerate FN (DFN) curve (recall Sect. 3.5). FNs occur in the blue shaded regions. Hence, regions Va, Vb, Vc, and VIIa may support MMOs, and these are of primary interest for finding strong symmetry breaking rhythms. The configuration shown in Fig. 5 corresponds to a point in region Vb. Representative configurations of the $(u_1,u_2)$ phase plane are shown in b and c in the cases where the repelling sheet, $S_r$, and the symmetric folded singularities, $M_s^{\ell /u}$, do not exist (b), and do exist (c). Panel b/c corresponds to the blue cross/blue shield marker in (a). These markers lie on opposite sides of the red FSN I curve

The vertical black line at $a = 5\sqrt{\frac{5}{3}}$ is the locus of FSN III bifurcations in which a pair of non-symmetric folded singularities coincide with the symmetric equilibrium $E_s$. The red curve, given by Eq. (3.16), corresponds to the locus of FSN I bifurcations of the symmetric folded singularities. This curve separates the regions of parameter space for which $S_s$ is empty (above the red curve) and $S_s$ is non-empty (below the red curve). The green curve, given by Eq. (3.18), corresponds to the locus of pitchfork bifurcations of folded singularities in which a pair of non-symmetric folded singularities coincides with the symmetric folded singularity. This green curve intersects the vertical black FSN III curve tangentially at $a = 5\sqrt{\frac{5}{3}}$, and it intersects the red FSN I curve tangentially at $a = 3\sqrt{3}$. The black curve given by $a_{\textrm{FSNII}} = 5 \sqrt{\frac{5+2d_u}{3-2d_u}}$ corresponds to the locus of FSN II bifurcations in which the symmetric equilibrium $E_s$ intersects one of the symmetric folded singularities. This curve intersects the red FSN I curve (3.16) tangentially at the point $(a,d_u) = \left( \sqrt{5\left( 8+\sqrt{89}\right) }, \tfrac{1}{4}\left( \sqrt{89}-7\right) \right)$. The cyan curve is the locus of points for which the non-symmetric folded singularity is a DFN. In the interior of the region enclosed by the cyan curve, the folded singularities are FF. Below the cyan curve, the folded singularities are FNs. The magenta curve is the locus of points for which the non-symmetric folded singularity is a DFN.

Table 2 For each regions I–VII, the table shows the types of symmetric folded singularities $M_s^{\ell ,u}$ and non-symmetric folded singularities $M_{ns}^{\ell ,m,u}$, as well as which patch the symmetric equilibrium $E_{\textrm{symm}}$ is on.

The bifurcation curves divide the $(a,d_u)$ plane into distinct regions, based on the geometry of the critical manifold, the number of folded singularities, and their classifications:

Region I:

Left of the vertical (black) FSN III line at $a_c = 5\sqrt{\frac{5}{3}}$ and above the (red) FSN I curve (3.16).

Region II:

Bounded by the vertical black FSN III line at $a_c = 5\sqrt{\frac{5}{3}}$, a segment of the blue DFN curve, and the red FSN I curve (3.16).

Region III:

Enclosed by the red FSN I curve (3.16), the vertical black FSN III line at $a = 5\sqrt{\frac{5}{3}}$, and the black FSN II curve $a_{\textrm{FSNII}} = 5 \sqrt{\frac{5+2d_u}{3-2d_u}}$. This region is further partitioned into two subregions, IIIa and IIIb, one on either side of the organizing center at $(a,d_u) = \left( \sqrt{5\left( 8+\sqrt{89}\right) }, \tfrac{1}{4}\left( \sqrt{89}-7\right) \right)$, where the red FSN I curve is tangent to the black FSN II curve.

Region IV:

Bounded above by the black FSN II curve $a_{\textrm{FSNII}} = 5 \sqrt{\frac{5+2d_u}{3-2d_u}}$ and by the blue DFN curve.

Region V:

Enclosed by the vertical black FSN III line at $a_c = 5\sqrt{\tfrac{5}{3}}$ and the blue DFN curve. This region has three subregions (Va, Vb, and Vc), separated by the red FSN I and black FSN II curves.

Region VI:

Enclosed by the red FSN I curve (3.16), the green FSN III curve (3.18), and the vertical black FSN III line at $a_c = 5\sqrt{\frac{5}{3}}$.

Region VII:

Enclosed by the green $\hbox {PF}_M$ curve (3.18). This region is subdivided into two smaller regions by the blue DFN curve.

We now list the singularities in each region and their types. To do so, we introduce the following notation with reference to Fig. 5. In Fig. 5a, there are two symmetric folded singularities and six non-symmetric folded singularities. We label the symmetric folded singularities as $M_s^{\ell }$ and $M_s^{u}$, corresponding to the lower ($\ell$) and upper (u) symmetric folded singularities, respectively. For the non-symmetric folded singularities, we first note that there is reflection symmetry in the diagonal line $\left\{ u_1 = u_2\right\}$, so that we may focus on just the upper left half of the plane. We call the non-symmetric folded singularity with the smallest $(u_1,u_2)$-coordinates $M_{ns}^{\ell }$, with $\ell$ denoting lower, see FN in Fig. 5 for example. The non-symmetric folded singularity with moderate-size $(u_1,u_2)$-coordinates is labeled as $M_{ns}^m$, with m denoting middle, and is a FS in Fig. 5. Finally, the non-symmetric folded singularity with large $(u_1,u_2)$-coordinates is $M_{ns}^u$, with u denoting upper, see FF in Fig. 5), for example.

Overall, regions Va, Vb, Vc, and VIIa (shaded in blue in Fig. 7a) are of most interest for the strong symmetry breaking rhythms studied in this article. System (1.6) has non-symmetric FNs in these regions. Hence, whether an oscillator exhibits SAOs LAOs, or MMOs is determined by how the orbit passes through the neighborhood relative to the canards of the FN. These FNs lie off the symmetry axis $(u_1=u_2, v_1=v_2)$, and we will see that their strong and weak canards are oriented so that a strong asymmetry develops between the two oscillators as the orbit is guided by them.. In particular, the orientations of the strong and weak canards of such an FN guide the orbits so that one oscillator can stay close to its local minimum for the remainder of the period while the other can make a large excursion. In this manner, the amplitude of oscillations exhibited by one oscillator can remain small during the entire period, while that of the other becomes large, resulting in strong symmetry breaking.

Remark 7

As will be shown, some of the SAOs in strong symmetry breaking rhythms are induced by return mechanisms, as the orbit makes a short, fast jump from one patch to another, instead of by canards. Hence, it may also be possible to create other symmetry-breaking rhythms using this mechanism.

4 Strong Symmetry Breaking SAO-LAO Rhythms and the Key FN Primarily Responsible for them

In this section, we study strong symmetry breaking SAO-LAO rhythms. They are denoted $0^s 1^0$, where s is the number of SAOs made by oscillator 1 per period while oscillator 2 exhibits one LAO. Representative $0^2 1^0$ rhythms are studied in Sect. 4.1 (see Figs. 8a and 9a). There, we also identify the non-symmetric FN primarily responsible for the strong nature of the symmetry breaking. Then, in Sect. 4.2, we study the branch of stable $0^2 1^0$ rhythms in parameter space, showing how these SAO-LAOs emerge from asymmetric canard explosions of SAO-LCC rhythms. Finally, in Sect. 4.3, we extend the results to $0^s 1^0$ rhythms for $s\ge 2$.

4.1 Two representative SAO-LAO Symmetry Breaking Rhythms

For the first representative asymmetric $0^2 1^0$ SAO-LAO rhythm, shown in Fig. 8, the orbit enters the funnel of the FN in the maximal rotation sector ($R_{\max }$) and stays close to the weak canard, $\gamma _w$, of this FN during its passage through the neighborhood. In fact, it is so close to $\gamma _w$ that the SAOs are below the visible threshold. Then, when it leaves the neighborhood of this FN, the orbit passes right of the equilibrium $E_{\textrm{symm}}$ as shown in the inset, and oscillator 1 remains near its local minimum, while oscillator 2 is forced to make a fast up-jump and begin its LAO.

Fig. 8

A representative asymmetric $0^2 1^0$ rhythm. a Time series. Oscillator 1 (blue) exhibits two SAOs and oscillator 2 (red) an LAO per period. b Projection of the orbit (black) into the $(u_1,u_2)$ plane. At the local minimum of $u_1$ (red ducky), the orbit enters the funnel of the non-symmetric FN, close to its weak canard $\gamma _w$ (dashed blue curve). It remains close to $\gamma _w$, crossing the fold curve L (black curve) near $L_{1-}$ and $L_{2-}$ (cyan ducky) in quick succession, just right of $E_{\textrm{symm}}$. There, oscillator 2 makes its fast up-jump, while oscillator 1 remains near its minimum. Hence, the amplitudes of the oscillators split into large (red) and small (blue) due to the passage through the neighborhood of FN, which makes it primarily responsible for the strong symmetry breaking. Subsequently, the orbit lands on the upper (yellow) saddle sheet (blue ducky) and follows the true canard, $\gamma _t$, of the upper FS as $u_1$ slowly reaches the maximum of its SAO (green ducky). Hence, the first maximum in oscillator 1 occurs after the up-jump in oscillator 2. Finally, the orbit makes a short hop over to the stable (blue) sheet $S_a$ (yellow ducky) and then oscillator 2 jumps back down to complete its LAO (red ducky). The influence of the upper FS point on the orbit is described below. Note the different scales on the axes. Because oscillator 1 exhibits SAOs, the dynamics in the $u_1$ direction lie near the branch of the fold set L near $L_{1-} \approx \{ u_1 = 1.29 \}$. Here, $a=6.47, d_u=8 \times 10^{-4}$, and $d_v = 0.5$ (region Vc of Fig. 7), with $\beta = 0.001$

Next, during the plateau portion of the LAO of oscillator 2 (between the blue and green duckies), the orbit lies close to the true canard (red) of the upper FS (near the blue ducky). The length of this plateau portion is determined by how close the orbit is to that canard of the FS point when it approaches the upper branch. Moreover, we observe that, during this portion, oscillator 1 continues to stay near its local minimum. Finally, oscillator 1 makes a small jump back to its left attracting branch (to near the yellow ducky), and then oscillator 2 makes the down-jump of its LAO. In this manner, oscillator 1 remains near its local minimum for the entire period, and only undergoes SAOs, while oscillator 2 makes both its fast up and down jumps with the slow segments in between, hence exhibiting its entire LAO.

For this first representative rhythm, passage through the neighborhood of the FN point is what first causes the orbits of the two oscillators to separate and their amplitudes to become distinct. The weak canard $\gamma _w$ of the FN guides the orbit across the portion $L_{2-}$ of the fold curve, where the amplitude of oscillator 1 remains small, and that of oscillator 2 must become large, since it must jump up to its right branch. In this manner, the FN is the primary mechanism responsible for the strong symmetry breaking between the two oscillators, since the large split in the amplitudes is initiated during the passage through the neighborhood of the FN. We note that the upper FS also influences the dynamics, but its role is limited to the plateau portion where oscillator 2 already has large amplitude (as described above).

We also observe that, for these parameter values, the key non-symmetric FN has an eigenvalue ratio of $\mu \approx 0.0672$, which implies that for $0 < \beta \ll 1$ this FN not only has strong and weak canards, but it also has six secondary canards by (3.15), and $R_{\textrm{max}}=R_7$. (These secondary canards do not play a role in the attractor shown in Fig. 8, but they do for other initial conditions, causing oscillator 2 to undergo MMOs with small-amplitude rotations about the weak canard $\gamma _w$).

Fig. 9

A second representative asymmetric $0^2 1^0$ rhythm, and the non-symmetric FN primarily responsible for the strong symmetry breaking. a Time series: oscillator 1 (blue) undergoes SAOs while oscillator 2 (red) exhibits LAOs. b Deconstruction in the $(u_1,u_2)$ phase plane. The orbit (black) stays close to the strong canard $\gamma _s$ (blue, double arrows) of FN, as it passes through the neighborhood. Then, (cyan ducky) it bends back and makes a small, fast jump back to the yellow sheet (blue ducky). Note that this small, fast jump passes above the fold curve $L_{1-}$ and the symmetric (lower) FS point, and hence FS has no direct impact on the orbit. Then, the up-jump occurs (to the upper attracting sheet, green ducky), in which $u_2$ begins its relaxation oscillation. Subsequently, the orbit slowly drifts back to a neighborhood of $L_{2+}$, and, near the yellow ducky, the orbit returns to the lower attracting blue sheet and completes its cycle. Overall, passage through the neighborhood of the FN close to $\gamma _s$, and the subsequent small, fast jump back of oscillator 1 to its left branch, causes the amplitude of oscillator 1 to remain small, while that of oscillator 2 must become large, since the orbit lands (blue ducky) on the other side of $L_{2-}$. Here, oscillator 1 has its first SAO well before the up-jump of oscillator 2, since the orbit is near the strong canard of the FN. Note the differences in the scales on the two axes. Here, $a=6.54, d_u = 8 \times 10^{-4}, d_v = 1.0588$ with $\beta = 0.003$. The singular geometry corresponds to region Vc of Fig. 7

In the second representative asymmetric $0^2 1^0$ rhythm, shown in Fig. 9, the orbit enters (near the red ducky) the funnel of the FN and passes directly through the $R_0$ rotation sector, very close to the strong canard, $\gamma _s$ of the FN. This is in contrast with the situation for the first representative rhythm, where the passage is near the weak canard of the FN point. Hence, along the orbit of the second rhythm, oscillator 2 does not exhibit any small-amplitude rotations before its fast up-jump. Indeed, for the parameter values here, oscillator 2 cannot exhibit the SAOs needed to make an MMO, and instead exhibits an LAO. This is because, for the parameters here, the non-symmetric FN has an eigenvalue ratio of $\mu \approx 0.568$ and, hence, there are no secondary canards (by (3.15)), i.e., the only canards associated to it are its strong and weak canards. Further along, the orbit stays close to the strong canard to just before $L_{2-}$ (cyan ducky). However, before oscillator 2 reaches its local minimum on $L_{2-}$, the orbit makes a small, fast jump back to the saddle sheet to a point above $L_{2-}$ (blue ducky), passing above the fold curve $L_{1-}$ and the symmetric FS. Hence, oscillator 1 performs one SAO and is already back on its left attracting branch before the up-jump in oscillator 2 has even begun. Moreover, oscillator 1 remains near its left attracting branch for the rest of the period (including as it makes its second, shorter SAO), while oscillator 2 undergoes its entire relaxation oscillation.

In this manner, the key FN makes the strong symmetry breaking possible also for this second representative rhythm. Its strong canard guides the orbit through to the other side, until the small, fast jump back occurs. Hence, oscillator 1 remains near its minimum and oscillator 2 is forced to make a fast up-jump.

Finally, we observe that in these rhythms, the occurrence of the first maximum of the SAO of oscillator 1 relative to the LAO of oscillator 2 is determined by the structural difference in whether the orbit follows closely the strong or the weak canard of the FN. For the first representative $0^2 1^0$ rhythm, the peak in oscillator 1 occurs after the fast jump up in oscillator 2 (see the inset in Fig. 8a). This is because, after the up-jump, the true canard of the FS off the symmetry axis (near the blue ducky) acts as the lane marker guiding the orbit, while oscillator 1 slowly reaches its local maximum and oscillator 2 is on its upper stable branch. As a result, the local maximum of $u_1$ occurs after the up-jump in $u_2$, as does the second SAO. This contrasts with the dynamics observed for the second representative $0^2 1^0$ rhythm, where the first SAO occurs before the up-jump in $u_2$ since the orbit is near the strong canard of the FN.

Remark 8

For the parameters corresponding to these rhythms, the fold set L, recall (3.4), lies close to the folds, $L_{1\pm }$ and $L_{2\pm }$, of the individual oscillators, which are straight lines. The gaps between the blue and red patches are small, since $d_u$ is small here. Hence, we use the labels $L_{1\pm }$ and $L_{2\pm }$ to indicate the segments of L that are close to the fold curves of these individual oscillators.

4.2 Branches of Strong Symmetry Breaking SAO-LAO Rhythms Created Primarily by the same FN

The asymmetric $0^2 1^0$ rhythms presented in the previous subsection lie on the same branch of $0^2 1^0$ rhythms in the parameter space. We now study the dynamics along this branch as a function of the bifurcation parameter a. For all of the orbits, the same FN is again the primary mechanism responsible for the strong symmetry breaking, since the split between the amplitudes of the oscillators occurs during the passage through the neighborhood of that FN.

For the given parameter set, the (green) branch of $0^2 1^0$ rhythms forms an isola. The full isola, with its various segments, is shown in Fig. 10a. One sees that the green isola consists of a left nearly vertical segment (inset in Fig. 10a), a snaking plateau with many segments (inset in Fig. 11a), a right nearly vertical segment (inset in Fig. 12a), and a lower plateau joining the two nearly vertical segments. (We note that the main frames in Figs. 10a, 11a, and 12a are identical, for reference, but the plots in the insets show magnifications of the different segments of the isola.) The stable segment of the $0^2 1^0$ isola lies on the snaking plateau and is delimited by a saddle-node bifurcation and a period-doubling bifurcation. The other segments of the green isola, including the two nearly vertical segments on which the asymmetric canard explosions occur, represent unstable orbits.

Fig. 10

The primary asymmetric canard explosion leading to $0^2 1^0$ SAO-LAO rhythms. a The entire isola (green) of $0^2 1^0$ rhythms, with its many segments, as a function of the bifurcation parameter a: loci of stable orbits (solid curve) and unstable orbits (dashed curve, with equal spaces between dashes; note some spaces are covered by markers). The isola comes close to, but does not touch, the Hopf point (black dot). Inset (ai) shows a magnification of the segment of the isola corresponding to the left asymmetric canard explosion of SAO-LCC rhythms centered at $a=6.461823$, along with the sequence of colored squares that denote the orbits shown (black, red, green, navy blue, purple, yellow, and cyan). b Projection of solutions into the $(u_1,u_2)$ plane corresponding to the square markers in the inset (ai). These solutions closely follow the weak canard, $\gamma _w$, of the non-symmetric FN. The inset in b shows an enlargement of the region near the intersection of $L_{1-}$ and $L_{2-}$. (Note the difference in the scales on the axes). The corresponding time series for the red, blue, and cyan orbits are shown in panels (c), (d), and (e), respectively. The SAOs of oscillator 1 are shown in black, and the rhythms of oscillator 2 are shown in red, blue, and cyan. c Time series of a SAO-LCC rhythm in which oscillator 2 exhibits a jump-back canard (i.e., a headless duck). d Time series of a SAO-LCC rhythm in which oscillator 2 exhibits the maximal canard. e Time series of a SAO-LCC rhythm in which oscillator 2 exhibits a jump-away canard (i.e., a duck with head). Here, $d_u = 8 \times 10^{-4}, d_v = 0.5$, and $\beta =0.001$. Rhythms observed along the other segments of the green isola are illustrated below

Fig. 11

Asymmetric $0^2 1^0$ SAO-LAO rhythms for $d_u = 8 \times 10^{-4}, d_v = 0.5$, and $\beta =0.001$. a Same bifurcation diagram as in Fig. 10a. (ai) Upper half of the snaking branch. (aii) Lower half of the snaking branch. b Growth of the orbit segments that follow the true canard, $\gamma _t$, of the FS (diamonds in (aii): red, brown, olive green). c Growth of the SAOs near $L_{1-}$ and $L_{2-}$ (stars in (aii): green and navy blue). d Replacement of a canard-induced SAO with an SAO induced by a fast jump from the lower saddle sheet to the lower attracting sheet (triangles in (ai): blue, indigo, orange). e Change in the return mechanism (hats in (ai): orange, olive, lime-green). The ducky colors have been chosen in part for the contrast with the colors of the patches

Fig. 12

The second asymmetric canard explosion of the $0^2 1^0$ SAO-LAO rhythms, for the same parameter values as in Fig. 10. The same FN is the key mechanism responsible for the strong symmetry breaking here also, since—after the orbit passes through the neighborhood of the FN—the amplitude of oscillator 1 remains small while oscillator 2 makes an LCC. a Same diagram as shown in Fig. 10a, but with inset (ai) showing a magnification of the rightmost asymmetric canard explosion, and the sequence of colors denoting the orbits shown (black, red. green, navy blue, yellow, and cyan). b Projection of the orbits on the $(u_1,u_2)$ plane of the solutions corresponding to the turtle markers. These solutions closely follow the secondary canard, $\gamma _1$, of the same FN. The time series of the red, green, and yellow orbits are shown in panels (c), (d), and (e), respectively. The short segments on which the oscillators rapidly jump down correspond to SAOs that are induced by the fast returns, while the small bumps midway between these are canard-induced SAOs. The latter occur because the orbit enters the funnel of the FN in the rotation sector $R_1$, between the strong canard $\gamma _s$ and the first secondary canard $\gamma _1$, close to $\gamma _1$. Hence, it makes one rotation about $\gamma _w$. Note that the SAOs of oscillator 1 are shown in black to better contrast with the colored rhythms of oscillator 2 and that the scales on the axes are different

We now describe the properties of the solutions along the three main segments of this isola. Each segment is indicated by different markers: squares (Fig. 10); diamonds, stars, triangles, hats (Fig. 11); and turtles (Fig. 12). Also, within the snaking portion of the isola (Fig. 11), we use a color gradient for the markers (as indicated in the caption) to show the progression of orbits as the parameter a is varied. In this manner, one may continue from the end of one segment to the beginning of the next.

We begin with the left, nearly vertical segment of the $0^2 1^0$ isola, which occurs at $a \approx 6.461823$ (inset (ai) in Fig. 10a with square markers). It corresponds to an asymmetric canard explosion in which oscillator 1 exhibits two SAOs per event while oscillator 2 grows from an SAO to an LAO, via a family of LCCs. Moreover, it occurs $\mathcal {O}\left( \beta ^2\right)$ close to the analytically predicted $a_{\textrm{asym,c}} \approx 6.461791$, see formula (E.1) for $a_{\textrm{asym,c}}(\beta )$ in Appendix E.

Solutions (at each of the square markers along this nearly vertical segment of the $0^2 1^0$ isola) are compared to the underlying singular limit structures in the $(u_1,u_2)$ phase plane in Fig. 10b. There are five folded singularities in the region of phase space where the asymmetric canard explosion occurs. There is a symmetric FS near the intersection of $L_{1-}$ and $L_{2-}$ see the inset of panel (b)). Its true canard (red, single arrow) coincides with the axis of symmetry. The remaining folded singularities are non-symmetric. The FNs have strong canards, $\gamma _s$ (blue, double arrows), and weak canards, $\gamma _w$ (blue, dashed, single arrow). There is a non-symmetric FS at the boundary between the upper attracting and saddle sheets, with true and faux canards, $\gamma _t$ and $\gamma _f$, respectively. The other non-symmetric folded singularity near the intersection of $L_{1-}$ and $L_{2-}$ is an FS (however it has no direct influence on the dynamics of the rhythm shown).

The $0^2 1^0$ rhythms along the asymmetric canard explosion in Fig. 10(ai) closely follow the weak canard, $\gamma _w$, of the non-symmetric FN on L near $L_{1-}$ (Fig. 10b). Starting with the black orbit (black square in (a)), both oscillators exhibit SAOs around their respective lower folds, i.e., around $L_{1-}$ and $L_{2-}$. For parameters further up the vertical green branch (see the inset (ai)), the LCCs are such that oscillator 2 follows its unstable branch on the saddle sheet for progressively longer times (red and green orbits) until it reaches the maximal canard (blue orbit), which reaches a neighborhood of $L_{2+}$. The associated time series in Fig. 10c, d show that oscillator 1 stays small amplitude while oscillator 2 grows in amplitude. As the solution continues to move further up the green vertical branch, oscillator 2 exhibits fast jumps in the $u_2$ direction onto the upper blue attracting sheet. These fast jumps to the upper blue attracting sheet occur closer and closer to $L_{2-}$ as the LP point on the vertical branch is reached (magenta, yellow, and cyan orbits). The time series show that, for these jump-away canards, oscillator 2 has grown to a relaxation oscillator (Fig. 10e). For these rhythms, the same FN is the mechanism that creates the strong symmetry breaking.

Next, the plateau portion of the $0^2 1^0$ isola consists of four distinct segments, distinguished by diamond, star, triangle, and hat markers (Figs. 11ai, aii). The part of the snaking plateau with the diamond markers contains the stable segment of the $0^2 1^0$ isola, and it is enclosed by the saddle-node (LP) and period-doubling (PD) bifurcation points. The solutions corresponding to the diamond markers are shown in Fig. 11b. The key singularities involved in these rhythms are the non-symmetric FN on $L_{1-}$ and the uppermost non-symmetric FS on $L_{1-}$. Starting on the lower attracting sheet, the solutions follow the weak canard, $\gamma _w$, of the non-symmetric FN on $L_{1-}$ up to a neighborhood of the location where $L_{1-}$ and $L_{2-}$ meet. There, the solutions jump to the upper saddle sheet, where they then follow the true canard, $\gamma _t$, of the upper non-symmetric FS for long times. Then, the solutions jump in the $u_1$ direction away from the saddle sheet and return to the lower attracting sheet via relaxation dynamics.

The solutions corresponding to the star markers in Fig. 11aii are shown in Fig. 11c. Starting on the lower attracting sheet, the solutions lie in the rotational sector enclosed by the secondary canards, $\gamma _1$ and $\gamma _2$, of the non-symmetric FN on $L_{1-}$. Consequently, the solutions exhibit two SAOs as they pass near the FN in the neighborhood of the intersection of $L_{1-}$ and $L_{2-}$. Then, there is a fast jump in the $u_2$ direction to the upper saddle sheet. There, the solutions slowly drift toward the fold curve $L_{2+}$, where they then execute a fast jump in the $u_2$ direction down to the lower saddle sheet. From there, the solutions then return to the lower attracting sheet, and the cycle repeats. Also, in this manner, the FN is again the mechanism for the strong symmetry breaking, since the amplitude of oscillator 1 remains small while oscillator 2 executes an LAO after the passage through the neighborhood of the FN.

Remark 9

The green solution in Fig. 11c immediately executes its fast $u_1$ jump back to the lower attracting sheet, whereas the blue solution spends some time drifting along the saddle sheet away from $L_{1-}$ before it makes its fast $u_1$ jump leftward. This difference arises because the green orbit lands on one side of the saddle slow manifold, whereas the blue orbit lands on the other side.

The solutions corresponding to the triangle markers in Fig. 11ai are shown in Fig. 11d. The blue solution here has the same deconstruction as the blue rhythm from Fig. 11c. That is, the solution lies in the rotational sector enclosed by the secondary canards, $\gamma _1$ and $\gamma _2$, of the non-symmetric FN and hence exhibits two SAOs near the FN. As the parameter a is increased, the landing point of the orbit on its downward $u_2$ jump moves closer to the saddle slow manifold until it eventually crosses the saddle slow manifold and the orbits simply jump left to the attracting blue sheet without any rightward $u_1$ excursions on the saddle sheet (compare the light blue and dark blue rhythms). Moreover, as the parameter a is increased, the solution moves through the maximal secondary canard $\gamma _1$, which causes the amplitudes of the SAOs to grow. Additionally, after the solution has passed through $\gamma _1$, the second SAO is no longer canard-induced but is due to a fast transition from the lower saddle sheet to the lower attracting sheet (compare the SAOs of the dark blue and orange orbits, for instance).

The solutions corresponding to the hats in Fig. 11ai are shown in Fig. 11e. As the parameter a is varied along this part of the $0^2 1^0$ isola, the changes in the dynamics occur due to the positions of the solutions relative to the upper and lower saddle slow manifolds. The up-jump in the $u_2$ direction for the orange solution puts it to the left of the saddle slow manifold, so it immediately jumps left to the upper attracting sheet. The olive solution, on the other hand, lands close enough to the upper saddle slow manifold that it is able to follow the saddle slow manifold for long times before exhibiting a fast jump in the $u_1$ direction. Eventually, the solutions are able to follow the upper saddle sheet for long enough that they encounter the fold curve $L_{2+}$, which causes them to switch their direction of fast jump to the $u_2$ direction and they jump down to the lower saddle sheet (e.g., see the lime-green rhythm). A similar sequence is seen for the solutions on this lower saddle sheet, with solutions either jumping left to the lower attracting sheet or exhibiting long excursions to the right before they execute their fast $u_1$-jump back to the lower attracting sheet.

Finally, the green $0^2 1^0$ isola has another nearly vertical segment at $a \approx 6.465513$ (Fig. 12ai). This second nearly vertical segment corresponds to an asymmetric canard explosion of a different type from that studied in Fig. 10. The solutions (Fig. 12b) along this part of the $0^2 1^0$ branch lie in the $R_1$ rotational sector (between $\gamma _s$ and $\gamma _1$), and they closely follow the maximal secondary canard $\gamma _1$ of the non-symmetric FN on L (near $L_{1-}$). The black solution (corresponding to the black turtle in (ai)) exhibits a small oscillation in the neighborhood of the intersection of $L_{1-}$ and $L_{2-}$. This SAO carries the solution from the blue attracting sheet to the red repelling sheet. There, a fast jump occurs in the $u_1$ direction that takes the solution to the yellow saddle sheet, followed by a fast jump in the $u_2$ direction that takes the solution back to the attracting sheet. Throughout the period, the amplitudes stay small. This black orbit may be thought of as a small headless duck.

As the vertical green branch in (ai) is traversed, the LCC closely follows $\gamma _1$ for progressively longer times on the repelling sheet (red and green trajectories in (b)) before the $u_1$ and $u_2$ jumps return the solution to the attracting sheet. This corresponds to a growth of the amplitude of oscillator 2 (Fig. 12c, d) until the maximal headless duck is attained (given approximately by the green orbit). Further up the bifurcation curve in (ai), after the maximal canard is reached, there is a switch in the return mechanism. For the blue, magenta, yellow, and cyan solutions, the escape from the secondary canard occurs via an up-jump in the $u_2$-direction. These orbits may be thought of as ducks with heads. Finally, along this segment, the orbit exhibits a more traditional relaxation-type excursion back to the blue attracting sheet. For these solutions, the time series of oscillator 2 exhibits more classic relaxation-type oscillations (Fig. 12e).

4.3 Extension to $0^s 1^0$ SAO-LAO rhythms with $s\ge 2$

The $0^2 1^0$ SAO-LAO orbits studied in this section are the first in a family of $0^s 1^0$ SAO-LAO rhythms with $s\ge 2$. In each of the rhythms in this family, oscillator 1 exhibits s SAOs per period, while oscillator 2 undergoes one relaxation oscillation (i.e., LAO). For example, $0^3 1^0$ rhythms are observed with $\beta =0.01$, $d_u=0.00088$, $d_v=0.155172$, and $6.5149 \le a \le 6.5364$.

For each of these $0^s 1^0$ rhythms, $s-1$ of the SAOs that oscillator 1 makes are induced by the canards of the same non-symmetric FN, and the other SAO is induced by the return mechanism. The orbits of these rhythms enter the funnel region of the FN. In particular, they enter between the $\gamma _{s-2}$ and $\gamma _{s-1}$ secondary canards, close to the latter. Hence, they make $s-1$ oscillations about the weak canard $\gamma _w$, i.e., they make $s-1$ canard-induced SAOs.

The plateaus of stable $0^s 1^0$ SAO-LAO rhythms terminate at one end in period doubling bifurcations (see, for example, Fig. 10a for $s=2$). The $0^s 1^0$ rhythm becomes unstable, and a new stable SAO-LAO rhythm is observed consisting of two different $0^s 1^0$ events in alternation, which we label as an $(0^s 1^0)_2$ SAO-LAO rhythm. Moreover, for parameter values near the period-doubling bifurcation, these two different $0^s 1^0$ events are close to the unstable $0^s 1^0$ rhythm. As the parameter is varied, the differences between the two events grow until there is another period-doubling bifurcation to a $(0^s 1^0)_4$ rhythm, and so forth. We explored in detail the case with $s=3$, where we observed the period doubling sequence up to a branch of stable $(0^3 1^0)_{16}$ SAO-LAO rhythms (for example, by varying $d_u$ from 0.00620407 to 0.00880550 with $a = 6.54$, $\beta = 0.01$, and $d_v = 0.155172$).

We also observed alternating rhythms that exhibit two events per period, an $0^{s_1}1^0$ SAO-LAO event and an $0^{s_2} 1^1$ SAO-MMO event. For these, the returns to the funnel of the non-symmetric FN alternate between the $R_0$ and $R_1$ rotational sectors.

5 Strong Symmetry Breaking SAO-MMO rhythms

In this section, we present SAO-MMO rhythms of (1.6) with strong symmetry breaking. Denoted by $0^{s_1} 1^{s_2}$ for integers $s_1, s_2 \ge 1$, oscillator 1 exhibits $s_1$ small amplitude oscillations per period, and the MMO that oscillator 2 exhibits each period consists of one LAO and $s_2$ SAOs. In parameter space, these SAO-MMO rhythms occur naturally close to the asymmetric canard explosion $a_{\textrm{asym,c}}(\beta )$ (recall (E.1)) analyzed in Appendix E. A partial bifurcation diagram showing the stable branches of a selection of these asymmetric rhythms is shown in Fig. 13. Also, as we will show in this section, the same non-symmetric FN studied in Sect. 4 is responsible for the strong symmetry breaking, by making it possible for oscillator 1 to maintain small amplitude during the entire period while oscillator 2 exhibits an MMO each period.

Fig. 13

a Families of strong symmetry breaking SAO-MMO rhythms (black, red, blue, magenta, cyan, and orange curves) in a small, $\mathcal {O}\left( \beta ^{3/2} \right)$ neighborhood of the leftmost asymmetric canard explosion of the (green) $0^2 1^0$ branch, recall $a_{\textrm{asym,c}}(\beta )$ from (1.5). Only the stable plateaus from each SAO-MMO branch have been shown. b Zoom on an interval of a values corresponding to some SAO-MMO rhythms for which both $s_1$ and $s_2$ are large. Inset: further zoom on some small plateaus of such stable SAO-MMO branches. Here, $d_u=8\times 10^{-4}, d_v=0.5$, and $\beta =0.001$

With an exception, each labeled plateau of stable SAO-MMO rhythms in Fig. 13 belongs to a distinct isola. The exception involves the two magenta $0^{14}1^8$ plateaus on the left side of Fig. 13a, which belong to the same isola, and there may be other such pairs of plateaus not shown. These plateaus of stable, strong symmetry breaking SAO-MMO rhythms appear, numerically, to densely fill the parameter interval shown. In the gaps where no isolas have been drawn, e.g., between the magenta $0^{14}1^8$ branch and the blue $0^{44} 1^{24}$ branch, the attractor is observed numerically to be an asymmetric $0^{s_1} 1^{s_2}$ SAO-MMO in which both $s_1$ and $s_2$ are large. The stable plateaus for these particular families are especially narrow and have been omitted from Fig. 13. (The numerical continuation encounters non-convergence issues here. Coordinate and parameter scalings together with transformations would be required to resolve this continuation issue, but we leave this for future work). Plateaus of stable $0^{s_1} 1^{s_2}$ SAO-MMO rhythms with low values of $s_1$ and $s_2$ were also observed for larger values of $d_v$ (see, e.g., case 5 of Table 3).

Fig. 14

A strong symmetry breaking $0^6 1^3$ SAO-MMO rhythm. The same FN studied for the SAO-LAO rhythms is also responsible here for the strong symmetry breaking. a Time series showing that oscillator 1 (blue) exhibits six small-oscillations per period while oscillator 2 (red) exhibits a $1^3$ MMO in each period. b Projection of the solution into the $(u_1,u_2)$ phase plane. c Magnified view of the SAOs near the intersection of $L_{1-}$ and $L_{2-}$. The non-symmetric FNs each have a singular strong canard $\gamma _s$ (blue, double arrows) and a singular weak canard (blue, single arrow). The symmetric FS has a true canard that coincides with the axis of symmetry and forms a heteroclinic connection with the symmetric equilibrium, $E_{\textrm{symm}}$. The dynamics of the orbit in the neighborhood of these FN and FS is complex due to the fact that the singularities are close to two different bifurcations. There is also a non-symmetric FS, which possesses true and faux canards, $\gamma _t$ and $\gamma _f$, respectively. The orbit has a segment near the true canard (blue to green ducky), leading to oscillator 1 attaining the maximum of its largest SAO. Here, $a = 6.46174, d_u = 8 \times 10^{-4}, d_v = 0.5$ (corresponding to region Vc of Fig. 7), and $\beta =0.001$. Note the different scales on the axes

The deconstruction of a representative stable, strong symmetry breaking $0^6 1^3$ SAO-MMO rhythm is shown in Fig. 14. For this rhythm, oscillator 1 exhibits six SAOs per period while oscillator 2 exhibits a $1^3$ MMO every period (Fig. 14a). The projection of the solution into the $(u_1,u_2)$ phase plane shows that the dynamics are concentrated around the branch of the fold set L near $L_{1-}$ (Fig. 14b).

Starting at the red ducky, the solution lies in the funnel of the non-symmetric FN on L near $L_{1-}$. In this funnel, the solution drifts toward the FN (red to cyan ducky), close to its weak canard. It follows $\gamma _w$ from the attracting sheet to the saddle sheet, past the symmetric equilibrium, and onto the repelling sheet. Here, the canard dynamics of the non-symmetric FN, the canard dynamics of the symmetric FS, and the dynamics of the symmetric equilibrium produce the complex array of SAOs seen in Fig. 14c.

After the SAOs near the non-symmetric FN and the symmetric FS have been completed, the solution jumps up to a neighborhood of the upper saddle manifold (blue ducky). In the process, the amplitude of oscillator 2 has become large, while that of oscillator 1 remains small. From there, the solution follows the true canard of the FS up to the green ducky (in the same manner as for the second $0^21^0$ SAO-LAO rhythm) where it jumps back to the upper attracting manifold (yellow ducky). The solution then quickly reaches a neighborhood of the fold $L_{2+}$ and executes a fast $u_2$-jump down to the lower attracting manifold. This down-jump brings the solution back to the red ducky and completes the cycle.

In Fig. 14, the parameter values are in region Vc of Fig. 7, and they are such that the eigenvalue ratio of the non-symmetric FNs is $\mu \approx 0.0432$, which is $\mathcal {O}\left( \sqrt{\beta }\right)$ and close to zero. Hence, the system is close to bifurcation. In fact, the system is close to two different bifurcations of singularities. Namely, the system is extremely close to a FSN II (Krupa and Wechselberger 2010), because the symmetric FS and symmetric equilibrium $E_{\textrm{symm}}$ are almost coincident. This pair of folded and ordinary singularities undergoes a transcritical bifurcation on the FSN II curve in Fig. 7, and the number of maximal canards associated to a FN near this bifurcation is estimated to be $\mathcal {O}\left( \beta ^{-1/2} \right)$ (Krupa and Wechselberger 2010). In addition, the system is also close (but not as close) to an FSN III (Roberts 2018), because the (key) non-symmetric FN (and its mirror image in the axis of symmetry) and the symmetric equilibrium are close together. These three singularities merge on the vertical black FSN III curve in Fig. 7, and the number of maximal canards induced by the FN in this case is estimated to be $\mathcal {O}\left( \beta ^{-1/2} \right)$, see Section 7.4.5 of (Roberts 2018).

In summary, we have shown that system (1.6) has strong symmetry breaking $0^{s_1} 1^{s_2}$ SAO-MMO rhythms for many pairs $(s_1,s_2)$. In parameter space, the plateaus of stable segments along the branches of all these rhythms lie close to the asymmetric canard explosion at $a_\textrm{asym,c}(\beta )=6.454972\ldots$, recall (E.1). Dynamically, the orbits of these SAO-MMOs are similar in several respects to the second representative $0^2 1^0$ SAO-LAO rhythm, especially in that they are close to the weak canard during the passage through the neighborhood of the FN. The main difference is that here the key FN is much closer to the symmetric FS and fixed point, $E_{\textrm{symm}}$, so that the FN has multiple rotation sectors here, and one observes rhythms in which oscillator 1 can have multiple SAOs while oscillator 2 has many SAOs as part of its MMO.

Remark 10

While the dynamics near FSN II and FSN III points have each been studied individually, there have been no studies of a system in which both bifurcations occur almost simultaneously. This is beyond the scope of this article, and we leave it as an open problem for coupled oscillator systems.

6 Weak Symmetry Breaking Rhythms in (1.6)

Rhythms exhibiting weak symmetry breaking have also been observed in the coupled LE model (1.6). Each of these rhythms is a small perturbation of a symmetric state of the coupled oscillators.

The dynamics of these rhythms are also shepherded by the folded singularities and their associated canards. However, there are typically more folded singularities involved for each rhythm than there are for the strong symmetry breaking rhythms, since the symmetric rhythms to which the weak symmetry breaking rhythms are close can involve twice as many folded singularities.

6.1 Canardioids

The first example of a weak symmetry breaking rhythm is a canardioid, which lies close to a $1^3$ AP rhythm. It is shown in Fig. 15, along with its deconstruction.

Fig. 15

A weak symmetry breaking canardioid. a Time series. Oscillators 1 (blue) and 2 (red) exhibit nearly AP quasiperiodic $1^3$ rhythms. Overall, the orbit lies close to a symmetric $1^3$ AP rhythm. b Projection onto the $(u_1,u_2)$ plane. c Enlargement showing the key components of the deconstruction of the canardioid. The non-symmetric FNs have an eigenvalue ratio of $\mu \approx 0.568$, so that only the strong and weak canards exist. The strong canards of these FNs (blue, double arrow) and the true canard of the symmetric FS (red, single arrow) are the main lane markers guiding the trajectory. Also shown are the sectors, $R_0$ and $R_{\textrm{max}}=R_1$. After the orbit enters a sector $R_0$ (e.g., near the green ducky), it will pass through the neighborhood of the FN and then make a large excursion near the symmetry axis. Instead, after the orbit enters a sector $R_1$ (e.g., near the cyan or red ducky), it will pass through the neighborhood of the FN and then make an SAO (e.g., to the yellow ducky). Here, $a=6.54, d_u=8 \times 10^{-4}, d_v=1.0588,$ and $\beta =0.014$. The singular geometry here corresponds to region Vc of Fig. 7. d Persistence of the singular strong canards (blue) as primary strong canards for $\beta = 0.0025$ (orange), $\beta = 0.005$ (light blue), $\beta = 0.01$ (magenta), and $\beta = 0.014$ (green)

The projection into the $(u_1,u_2)$ phase plane (Fig. 15b and the enlargement in Fig. 15c) show the weak symmetry breaking. For this rhythm, there are six singularities in the neighborhood of where the SAOs occur (Fig. 15b, c). There is a pair of non-symmetric FNs on L near $L_{1-}$ and $L_{2-}$, a symmetric FS at the boundary between the red repelling sheet and the yellow saddle sheet (whose strong canard lies on the symmetry line, acting as a separatrix), a pair of non-symmetric FSs, and the symmetric equilibrium $E_{\textrm{symm}}$.

For the non-symmetric FNs, the eigenvalue ratio is $\mu \approx 0.568$, so that by (3.15) only the strong and weak canards persist for small, nonzero $\beta$. Hence, each FN has a pair of rotational sectors $R_0$ and $R_1$, dividing the attracting manifold of the symmetrically coupled system into four distinct sectors. The zero-rotation sector $R_0$ of the non-symmetric FN on L near $L_{1-}$ is the region bounded above by the axis of symmetry and below by the primary strong canard of that FN. Solutions with initial conditions in this sector encounter the fold curve and then exhibit a fast jump in the $u_1$-direction, without executing any small oscillations around the weak canard of that FN. Similarly, the zero-rotation sector $R_0$ of the other non-symmetric FN, on L near $L_{2-}$, is the region bounded below by the axis of symmetry and above by the strong canard of that FN. Solutions in this region exhibit fast jumps in the $u_2$-direction. Then, the $R_1$ rotational sector of the non-symmetric FN on L near $L_{1-}$ is the region of the attracting manifold below (enclosed by) the strong canard. Solutions with initial conditions in this region undergo one rotation around the weak canard of this FN before leaving the neighborhood. Similarly, solutions with initial conditions in the $R_1$ rotational sector enclosed by the strong canard of the FN on L near $L_{2-}$ execute one small oscillation around that FN before they leave the neighborhood.

The canardioid dynamics can be understood in terms of these four sectors. (See the deconstruction of the canardioid in Fig. 15b and the enlargement in Fig. 15c). Starting at the red ducky, the solution lies in the $R_1$ sector of the FN on L near $L_{1-}$. As such, the solution is able to move slowly beyond the attracting patch ($S_a$, blue), through a corner of the saddle patch ($S_s$, yellow), and onto the repelling patch ($S_r$, red) for some time (red to yellow ducky). During this time, oscillators 1 and 2 both move to being near their repelling branches, but their amplitudes remain relatively small, near their local minima. Then, the repulsion causes the solution to execute a short fast $u_1$-jump to the left to the saddle patch (yellow to blue ducky), during which oscillator 1 moves back to the left (stable) side of its local minimum. This is followed by a short, fast jump back to the attracting manifold (blue to green ducky), during which oscillator 2 moves back to the left (stable) side of its local minimum. The return to the attracting manifold injects the solution into the $R_0$ rotational sector of the same FN. The solution thus passes through the neighborhood of the FN without exhibiting any canard dynamics and makes a large-amplitude excursion instead (green ducky to well beyond the yellow ducky). This large-amplitude excursion is responsible for the rightmost part of the heart-shape in Fig. 15b.

The leftmost part of the heart-shaped orbit is created in a similar manner, but with the roles of the two oscillators reversed. After the solution completes the rightmost part, it eventually returns to the attracting patch and lands in the $R_1$ sector of the other non-symmetric FN on L near $L_{2-}$ (cyan ducky). From there, the solution undergoes a similar sequence—with the roles of oscillators 1 and 2 reversed—leading to an SAO near that FN followed by a large-amplitude excursion for $u_2$, during which time oscillator 1 makes SAOs. This LAO of oscillator 2 forms the upper (leftmost) part of the heart-shaped orbit. Since the entire orbit traces out a curve that is heart-shaped, we refer to it as a canardioid. Overall, the canardioid is close to being a $1^3$ AP rhythm, i.e., it is a weak symmetry breaking rhythm.

The unfolding of the strong canard for various values of $\beta$ is shown in Fig. 15d. As $\beta$ is decreased from the value used for frames (a)–(c), the primary strong canards move further from the axis of symmetry. Hence, the $R_0$ sectors get larger, and the set of initial conditions leading to large-amplitude excursions gets proportionally larger. This shows how the relative sizes of $R_0$ and $R_1$ change with $\beta$.

Remark 11

The rhythms shown in Figs. 9 and 15 both have segments in the zero rotation sector $R_0$ of the non-symmetric FN. However, in the former, the orbit enters very close to the strong canard $\gamma _s$, at the boundary of $R_0$ with $R_1$, so that orbit subsequently returns to the attracting patch, the amplitude of oscillator 1 remains small, and there is strong symmetry breaking. In contrast, the latter orbit enters further away from $\gamma _s$, in the middle of $R_0$, and hence the orbit stays near the symmetry line, the amplitudes of both oscillators become large, and there is weak symmetry breaking.

6.2 Weak Symmetry Breaking AP MMO-MMO Rhythms

Another example of weak symmetry breaking in (1.6) is the butterflied canardioid. A representative example is shown in Fig. 16. The deconstruction of the butterflied canardioid in the $(u_1,u_2)$ plane (Fig. 16b) reveals that it is asymmetric, and that it is a small perturbation of an AP MMO-MMO.

Fig. 16

A weak symmetry breaking butterflied canardioid in (1.6). It is close to an AP $1^1$ MMO rhythm. a Time series. Oscillators 1 (blue) and 2 (red) exhibit periodic $1^1$ MMOs that are close to being in AP. b Projection into the $(u_1,u_2)$ plane. Each non-symmetric FN has eigenvalue ratio $\mu \approx 0.104$ so that there are four secondary canards by (3.15) in addition to the primary strong and weak canards. The strong canard (blue, $\gamma _s$), first secondary canard (red, $\gamma _1$), and second secondary canard (green, $\gamma _2$) have been computed. c The MMO for oscillator 2 is canard-induced, because the orbit falls into the $R_1$ rotational sector between $\gamma _s$ and $\gamma _1$. d The MMO for oscillator 1 is not canard-induced. Instead, the global return projects the orbit onto the saddle manifold, and the subsequent jump back to the attracting sheet induces a small oscillation. Here, $a=6.6, d_u = 2 \times 10^{-4}, d_v=0.155$, and $\beta = 0.01$. The singular geometry for this example corresponds to region Vc of Fig. 7

There are seven singularities (see Fig. 16b): two symmetric FSs, the symmetric equilibrium, two non-symmetric FNs, and two non-symmetric FSs. The FNs each have an eigenvalue ratio of $\mu \approx 0.104$. Hence, by (3.15), there will be four secondary canard solutions that persist for sufficiently small $\beta$, as well as the primary strong and primary weak canards. The strong canard, $\gamma _s$, and secondary canards, $\gamma _1$ and $\gamma _2$, are shown for each FN in Fig. 16c, d. Recall that the maximal canards partition the attracting manifold into sectors: solutions that enter the sector $R_j$, enclosed by $\gamma _j$ and $\gamma _{j+1}$ for $j=0,1,2,3,4$, exhibit j oscillations in the neighborhood of the FN.

The deconstruction of the butterflied canardioid proceeds as follows. Starting at the red ducky, the solution is in the $R_0$ sector of the FN on L near $L_{1-}$ (Fig. 16d). The solution flows toward $L_{1-}$ and proceeds to execute a fast jump in the $u_1$ direction toward the lower right attracting manifold (Fig. 16b, red to yellow ducky). The solution quickly reaches a neighborhood of the fold $L_{1+}$ and jumps back in the $u_1$ direction to the lower left attracting manifold (yellow to green ducky). The solution lands in the sector $R_1$ of the other FN on L, near $L_{2-}$. Consequently, the solution exhibits a canard-induced oscillation in the neighborhood of that other FN about its weak canard (with $u_2$ exhibiting an oscillation and $u_1$ increasing monotonically), before it jumps up in the $u_2$ direction (green to blue ducky). The solution then exhibits a fast $u_2$ jump down to the lower saddle manifold (blue to magenta ducky). The repulsion of the saddle manifold then induces another fast jump in the $u_1$ direction to the lower left attracting manifold. This returns the solution to the $R_0$ sector of the FN on L near $L_{1-}$.

From the deconstruction, we see that the asymmetry in the rhythm comes from the local dynamics around the two non-symmetric FNs. The MMOs exhibited by oscillator 2 are canard-induced (Brøns et al. 2006), with the SAOs generated by the canard dynamics of the FN on $L_{2-}$. The MMOs exhibited by oscillator 1, on the other hand, are entirely due to the return mechanism, and they have segments near the symmetry axis. The SAOs in the MMOs of oscillator 1 come from the small, fast jump from the lower saddle manifold to the lower left attracting manifold.

Period-doubling of MMO-MMO rhythms has also been observed. This is similar to the period-doubling of MMO rhythms observed in single oscillators, such as, for example, in models of pituitary lactotroph cells (see figures 2-5 in (Vo et al. 2012)), only here there is an asymmetry between the coupled oscillators.

7 Conclusions and Discussion

In this article, we analyzed strong symmetry breaking rhythms in pairs of symmetrically coupled, identical Lengyel-Epstein oscillators (1.6). These include families of $0^s 1^0$ SAO-LAO, SAO-LCC, and $0^{s_1} 1^{s_2}$ SAO-MMO rhythms. The amplitudes and behaviors of the two oscillators differ substantially.

The analysis of these rhythms has been based on the folded singularities of (1.6), as well as on the dynamics induced by their canards (see the summary of the main folded singularities given in Fig. 7 and Table 2). The locations of the folded singularities have been determined as functions of system parameters (Eqs. (3.11) and (3.12)), and their bifurcations have been determined (Sect. 3.5). FSN I–III bifurcations arise, as does a new pitchfork bifurcation in which a folded singularity changes stability and two new folded singularities are created.

An FN that lies on the fold curve L between the lower left attracting $S_a$ and saddle sheet $S_r$, off the symmetry axis (see Sect. 3.4), was identified as the primary mechanism for the creation of the strong symmetry breaking rhythms. The strong, weak, and secondary canards of this FN guide the orbits in the four-dimensional phase space, splitting the oscillators in such a way that the amplitude of oscillator 1 remains small for the entire period, while oscillator 2 makes a large excursion.

For the family of strong symmetry breaking $0^s 1^0$ SAO-LAO rhythms, passage near the strong or the weak canard of this FN causes the orbit of oscillator 1 to stay near its local minimum for the entire period and oscillator 2 to make its LAO, as illustrated in Figs. 8 and 9 (for $s=2$). Furthermore, the analysis in Sect. 4 shows that, for orbits that pass near the strong canard of the FN, the up-jump in oscillator 2 occurs after the first SAO of oscillator 1, whereas for orbits that pass through the neighborhood near the weak canard, oscillator 2 jumps before oscillator 1. Also, of the s SAOs that oscillator 1 exhibits during each period, typically $s-1$ of them are induced by canards of the FN, while the other SAO occurs during the passage near the true canard of the upper FS point, and is hence a return-induced SAO, recall Sect. 4.2. In some rhythms, as, for example, in some $0^3 1^0$ rhythms, there is a tiny SAO that oscillator 1 undergoes just after the down jump of oscillator 2 is completed. The branches of stable SAO-LAO rhythms end in period-doubling bifurcations, and the numerical evidence indicates that the sequence follows the Feigenbaum scenario.

Explosions of strong symmetry breaking SAO-LCC rhythms were also discovered and analyzed. As illustrated in Fig. 10, oscillator 1 exhibits SAOs while oscillator 2 exhibits LCCs. Analysis based on the method of geometric desingularization (App. E) led to the asymptotic formula for the point $a_{\textrm{asym,c}}(\beta )$ at which this explosion is centered, (E.1), and good agreement was found between the numerically observed value at which the explosion occurs and the analytical prediction. This asymmetric canard explosion is the bifurcation sequence by which the SAO-LAO rhythms are created (Fig. 10a). Two other explosions of asymmetric SAO-LCC rhythms were also observed (Figs. 11 and 12). Moreover, this phenomenon should arise in other systems of coupled fast–slow oscillators that have canards.

We observe families of $0^{s_1} 1^{s_2}$ SAO-MMO strong symmetry breaking rhythms (recall Fig. 13) just to the left of this strong symmetry breaking canard explosion in parameter space. The same non-symmetric FN is the primary mechanism making these possible, as well, as illustrated in Fig. 14. The orbit in phase space is in the $s_2 - 1$ rotation sector $R_{s_2 - 1}$ of this FN. Hence, typically $s_2-1$ of oscillator 2’s SAOs in the MMO are canard-induced; the other occurs during the passage near the true canard of the upper FS, and is hence return-induced. The number of secondary canards, which is given by (3.15), determines how many rotation sectors are in the funnel of the FN, and the asymptotic estimates of the widths of the rotation sectors help determine how likely each of the different strong symmetry breaking orbits is to be found.

For the strong symmetry breaking orbits, the main effect of increasing the coupling strength $d_u$ may be understood as follows. Starting with $d_u$ small and values of a just to the right of $a_{\textrm{asym,c}}$, one observes stable SAO-LAO rhythms, since one is just to the right of the asymmetric canard explosion. Then, for larger values of $d_u$ (with the other parameters fixed), one observes SAO-MMO rhythms of varying complexity. For larger values of $d_u$, the nearly vertical segment where the asymmetric canard explosion occurs shifts rightward in a (by formula (E.1)). Thus, in the simulations with a unaltered, one is now in the parameter regime to the left of that canard explosion, which is densely filled with the stable plateaus of neighboring SAO-MMO isolas (recall Fig. 13). Numerical simulations confirm the analytical result that, for larger values of $d_u$, one observes $0^{s_1} 1^{s_2}$ rhythms with larger values of $s_1$ and $s_2$.

The theories of folded singularities and geometric desingularization are developed as asymptotic theories, valid here for $\beta$ sufficiently small, and various of the comparisons to the theory have been done by performing simulations for sequences of values of $\beta$. To supplement the theory, it is also of interest to fix the reaction rates, coupling strengths, and initial conditions for (1.6), and perform simulations for a sequence of small values of $\beta$. The results are reported in Appendix D, where we note that kinetics parameters are chosen there to be the same as those in Case 6 of Table 3.

We contrast the dynamics of strong symmetry breaking rhythms with those of other, asymmetric rhythms of (1.6) that are close to IP and AP symmetries, see Sect. 6. For example, asymmetric rhythms dubbed canardioids (Figs. 15 and 16) lie close to AP MMO-MMO rhythms. More folded singularities are involved in making these rhythms possible (than for strong symmetry breaking rhythms), since they are close to symmetric states.

During the course of this study, we discovered an explosion of AP LCCs (recall Sect. 2 and Fig. 3). While these AP LCC rhythms have anti-phase symmetry, they are of independent interest, and they mediate the transition between AP SAO-SAO rhythms and AP LAO-LAO rhythms, in analogy to how classical IP LCC-LCC orbits mediate the transition between IP SAO-SAO rhythms and IP LAO-LAO rhythms. As shown in App. C using the same method employed throughout this article, we found that the AP LCCs of the headless duck type are created by a pair of non-symmetric FNs and follow their strong canards (Fig. 17b). AP LCCs of the type ducks with heads occur further along this branch (see the green and blue orbits in Fig. 3c), completing the explosion of AP LCCs. Even further along the branch, the AP LCCs are guided by the true canards of a pair of non-symmetric FSs (Fig. 17c). The true and faux canards of the symmetric FS also play important roles. Furthermore, the dependence of these rhythms on the folded singularity canards shows why the explosion of AP LCCs occurs over a relatively large range of parameter values, as opposed to the exponentially narrow interval over which the explosion of IP LCCs occurs in (1.6).

We expect that the method employed here, of using geometric singular perturbation theory and identifying the folded singularities and their bifurcations, to study a pair of identical LE oscillators (1.6) coupled through both the slow and fast variables can also be applied to other pairs of coupled, planar, fast–slow relaxation oscillators, such as the van der Pol model.

The approach based on Cartesian product quilts and folded singularities that we introduced in Awal et al. (2023) and further develop here is expected to have a number of natural extensions that are also useful for strong symmetry breaking in more general symmetrically coupled, identical fast–slow oscillators, including oscillators with one (or more) fast variables and two (or more) slow variables, as well as to strong symmetry breaking in systems of three or more identical coupled oscillators.

We end with a few open problems. It is of interest to determine how the SAO-MMO rhythms are organized. Might there be a hierarchy of Farey sequences? So far, we have only found rhythms of these types in which oscillator 2 has one LAO or MMO event per period. Are there also SAO-MMO rhythms with two or more LAO or MMO events per period, as is the case for single oscillators with two (or more) slow variables and one (or more) fast variables and FN points. (Here, we note that the rhythms in Figure 5.1 vary in the fifth decimal place, and hence we think the search for rhythms with two or more LAO or MMO events per period -if they exist- is challenging and the stability intervals might be even narrower). Also, within the rich cluster of $0^{s_1} 1^{s_2}$ orbits in which oscillator 2 has just one LAO or MMO event per period, how are the various plateaus organized?

Appendices

A Derivation of the Characteristic Equation (2.5)

In this appendix, we present a brief derivation of the characteristic Eq. (2.5) for the Jacobian matrix of system (2.1) linearized about $E_{\textrm{symm}}$. The Jacobian matrix has the following block form:

$$\begin{aligned} D\textbf{f} = \begin{bmatrix} \textbf{f}_\textbf{u} \textbf{I} + d_u C &{} \textbf{f}_\textbf{v} \textbf{I} \\ \beta \textbf{g}_\textbf{u} \textbf{I} &{} \beta \textbf{g}_\textbf{v} \textbf{I} + \beta d_v C \end{bmatrix}, \end{aligned}$$

(A.1)

where all the derivatives are evaluated at $E_{\textrm{symm}}$, $\textbf{I}$ is the $2\times 2$ identity matrix, and we recall that $C = \begin{bmatrix} -1 &{} 1 \\ 1 &{} -1 \end{bmatrix}$ is the coupling matrix. Hence, because the $2 \times 2$ blocks commute, the determinant is

$$\begin{aligned}{} & {} \textrm{det} \left[ D\textbf{f} - \lambda I\right] = \textrm{det} \left[ (\textbf{f}_\textbf{u} -\lambda )(\beta \textbf{g}_\textbf{v} - \lambda )\textbf{I} + \beta d_v (\textbf{f}_\textbf{u}-\lambda )C + d_u (\beta \textbf{g}_\textbf{v} -\lambda )C \right. \nonumber \\{} & {} \left. \quad + \beta d_u d_v C^2 - \beta \textbf{f}_\textbf{v} \textbf{g}_\textbf{u} \textbf{I} \right] . \end{aligned}$$

(A.2)

Then, using the fact that $C^2 = -2C$ and grouping the terms, one finds that $\textrm{det} \left[ D\textbf{f} - \lambda I\right]$ is given by:

$$\begin{aligned} \textrm{det}\left[ \lambda ^2 \textbf{I} - (\textbf{f}_\textbf{u}+\beta \textbf{g}_\textbf{v}) \lambda \textbf{I} - (d_u + \beta d_v)\lambda C +\beta (\textbf{f}_\textbf{u}{} \textbf{g}_\textbf{v}- \textbf{f}_\textbf{v} \textbf{g}_\textbf{u})\textbf{I} +\beta (d_v \textbf{f}_\textbf{u} + d_u \textbf{g}_\textbf{v} -2d_u d_v)C \right] . \end{aligned}$$

Next, we recall the notation introduced in Sect. 2, $q_1= (\textbf{f}_\textbf{u} + \beta \textbf{g}_\textbf{v})$ and $q_2=\beta (f_u g_v - f_v g_u)$ are the trace and determinant, respectively, of the Jacobian of a single LE oscillator, and $q_3=d_u+\beta d_v$ and $q_4=\beta (d_v (f_u-d_u) + d_u(g_v-d_v))$ arise due to the coupling. Hence,

$$\begin{aligned} \textrm{det} \left[ D\textbf{f} - \lambda I\right] = \textrm{det} \left[ \lambda ^2 \textbf{I} - \lambda \left( q_1 \textbf{I} + q_3 C\right) + q_2 \textbf{I} + q_4 C \right] . \end{aligned}$$

(A.3)

Finally, we observe that the $2 \times 2$ matrix in (A.3) is of the form $\begin{bmatrix} \alpha &{} \gamma \\ \gamma &{} \alpha \end{bmatrix}$, and we use the algebraic relation $\alpha ^2 -\gamma ^2=(\alpha +\gamma )(\alpha -\gamma )$ when evaluating this determinant to arrive at

$$\begin{aligned} \textrm{det} [ D\textbf{f} - \lambda \textbf{I} ] = \left( \lambda ^2 -q_1 \lambda + q_2\right) \left( \lambda ^2 -\left( q_1 - 2 q_3\right) \lambda +\left( q_2-2q_4\right) \right) . \end{aligned}$$

This yields (2.5).

B Multistability in (1.6)

In this appendix, we briefly discuss some of the multistability observed in system (1.6), which is indicated by the bifurcation diagrams shown in Sects. 2–5. For example, Fig. 3 shows that, for a representative pair of values $(d_u,d_v)$, stable IP LAO-LAO rhythms exist over a broad range of values of the bifurcation parameter a, and this is also the case for a large regime in the $(d_u,d_v)$ parameter plane (data not shown). Over different parts of these intervals, other stable rhythms co-exist, such as $0^{s_1} 1^0$ SAO-LAO rhythms and $0^{s_1} 1^{s_2}$ SAO-MMO rhythms, as shown in the bifurcation diagrams in Figs. 10a and 13. This type of multistability was also observed in pairs of identical van der Pol oscillators coupled only through the slow variables, see Awal et al. (2023).

Table 3 Rhythms varying a, with the other parameters fixed at $d_u=8.1\times 10^{-4}$, $d_v=1.0588$, and $\beta =0.01$ and initial conditions fixed at $(u_1,v_1)=(0.63,2.82)$ and $(u_2,v_2)=(3.27,2.70)$

To further illustrate the multistability, we carry out direct numerical integration varying the parameter a, and keeping the other parameters fixed. The results are shown in Table 3. The symmetric steady state $E_{\textrm{symm}}$ is stable (case 1) until $a_{\textrm{H,IP}}$, where the family of stable SAO-SAO rhythms (case 2) is created. The SAO-SAO states undergo period doubling (case 3) just before the canard point $a_c$. For values of a greater than $a_c$, the given initial condition lies in the basin of attraction of either the stable IP LAO-LAO rhythm or the stable SAO-LAO or SAO-MMO rhythms (cases 4-7). The initial condition fixed in these simulations is in different basins of attraction as a varies, but the basins exist over the range. The numerical integration was carried out using MATLAB ODE solver 113 for ODEs with absolute and relative tolerances of $1\times 10^{-9}\ \text {and}\ 1\times 10^{-12}$, respectively.

The period doubling observed in case 3 appears to follow the classical Feigenbaum scenario. For the doubling from p2 to p4, one finds 4.703 (approximately), and for the doubling from p4 to p8, one finds approximately 4.696, where for reference we recall that the Feigenbaum constant is 4.6692.... Similar period doubling results were observed for other parameter sets (data not shown).

C Canard Explosion of the Antiphase Rhythms

In this appendix, we deconstruct the AP rhythms and describe their bifurcations in terms of the folded singularities and their associated canards. The focus is on the novel explosion of AP LCCs.

We start by recalling that the AP rhythms lie along the dashed blue curve in the bifurcation diagram shown in Fig. 3a. The key branches of AP rhythms are also shown here in Fig. 17a. The AP rhythms (black curve) emerge from the subcritical AP Hopf bifurcation at $a_{\textrm{H,AP}}$ (black marker) of the symmetric equilibrium state $E_{\textrm{symm}}$. The AP curve has three segments separated by fold bifurcations, which are labeled as $\hbox {LP}_1$ and $\hbox {LP}_2$. Recall from Sect. 2 that there is a novel type of canard explosion that occurs along the lowermost segment of the AP curve. Also, we recall that for this parameter set, all of the AP rhythms are unstable. However, it is possible to tune the parameters so that parts of the AP branch become stable (e.g., with $d_v = 0.05$ the uppermost segment of the AP branch is stable).

Fig. 17

a Bifurcations of the AP solutions with respect to a for $d_u=8 \times 10^{-4}, d_v = 0.5$, and $\beta = 0.001$. Insets: magnifications of $\hbox {LP}_1$ and $\hbox {LP}_2$. The remaining panels show solutions in the $(u_1,u_2)$ plane. b AP LCC (left diamond in (a)) that closely follows the strong canards of the FNs. c AP LCC (right diamond in (a)) that closely follows the true canards of the non-symmetric FSs. d Comparison of solutions before (solid black) and after (dashed black) the $\hbox {LP}_1$ bifurcation (magenta/green triangles in (a)). e Representative AP LCC rhythm from the uppermost branch of the AP curve (red mustache in (a)). f Mechanism for the $\hbox {LP}_2$ bifurcation. Before/after the bifurcation, the solution (solid/dashed black) lies outside/inside the funnel (see the gold/cyan stars in (a)). g Representative AP LCC rhythm from the innermost branch of the AP curve (black soccer ball in (a))

To understand the AP rhythms, we briefly describe the geometry of the system in the $(u_1,u_2)$ plane and identify the key singularities. (This also helps keep the appendix relatively self-contained.) The critical manifold consists of six patches, with four attracting sheets, $S_a$ (blue) in the corners, one continuously connected saddle sheet, $S_s$ (yellow) surrounding the attracting sheets, and a repelling sheet, $S_r$ (red) in the interior. (For small $d_u$, the saddle sheet is almost the cross product of four disjoint saddle sheets, and the gap between the attracting and repelling sheets is very small).

There are eight singularities involved in the dynamics and bifurcations of the AP rhythms:

• The symmetric equilibrium $E_{\textrm{symm}}$: lies on $S_r$ for all a values for which the AP rhythms exist.

• Symmetric FS: lies near the intersection of $L_{1-}$ and $L_{2-}$. Its true canard coincides with the axis of symmetry and is shown in Fig. 17b–g as a solid red line. Its faux canard is shown as a dashed red curve.

• Non-symmetric FN/FF: lies at the boundary between the lower attracting and lower saddle sheets. Depending on parameters, it may be a FN or a FF. When it is a FN, its strong canard is shown as a blue curve.

• Non-symmetric FS: lies at the boundary between the saddle and repelling sheets. Its true canard is shown as a red curve, and it connects the saddle and repelling manifolds.

• Non-symmetric FS: lies at the boundary between the upper attracting and upper saddle sheets. Its true canard is shown as a green curve (to distinguish it from the true canards of the other FSs).

For each of the non-symmetric folded singularities listed above, there is a mirror singularity obtained by reflection across the diagonal line $\{ u_1 = u_2 \}$.

With the geometry of the system laid out, we now deconstruct the AP rhythms. Starting near the AP Hopf bifurcation $a_{\textrm{H,AP}}$ on the lowermost AP branch, the solutions (Fig. 17b, black curve) are small-amplitude AP canard cycles. The slow segments on the saddle sheets closely follow the strong canards (Fig. 17b, blue curves) of the non-symmetric FNs, and the fast jumps (double arrows) mediate the transitions between the different branches of the saddle slow manifolds. In the (u, v) phase plane, these are AP headless ducks (see the black and red orbits in Fig. 3c). Since these solutions trace out segments of unstable saddle slow manifolds, they must be unstable.

As the parameter a is increased along the lowermost AP branch, the AP canard cycles grow in amplitude until they reach the AP maximal canard (see the red solution in Fig. 3c). Then, as a is further increased, the slow segments of the solution eventually switch from closely following the strong canards of the non-symmetric FNs to closely following the true canards of the non-symmetric FSs (Fig. 17c). Subsequently, the slow segments of the solution stay close to the true canards (red curve) of the non-symmetric FSs. (This FS mechanism allows the solutions to traverse the saddle slow manifold for long times without the need for a FN, which is necessary since the non-symmetric FN becomes a FF at $a \approx 6.69$.) An example of these AP LCCs, which are ducks with heads, is given by the green curve in Fig. 3c.

As a is further increased along the lowermost AP branch, the fast jumps eventually project the orbits onto the faux canard (dashed red curve) of the symmetric FS. The solution follows the faux canard toward the symmetric FS for some time before jumping away and executing a large-amplitude excursion (Fig. 17d, solid black curve). As a is increased toward the saddle-node bifurcation $\hbox {LP}_1$ in Fig. 17a, the solution follows the faux canard of the symmetric FS for longer times up to some maximal distance (approximately corresponding to when the orbit reaches the fold curves $L_{1-}/L_{2-}$). The a-value for which the solution traces the faux canard the maximal distance corresponds to the saddle-node bifurcation at $\hbox {LP}_1$. After the saddle-node bifurcation $\hbox {LP}_1$, the AP branch turns around and the solutions escape the faux canard by jumping back toward the attracting manifold and then executing their large-amplitude excursions (Fig. 17d, dashed black curve).

Along the uppermost segment of the AP branch, the AP solutions consist of an LAO followed by an SAO, as illustrated by the curves in the (u, v) phase plane in Fig. 3d (and marked by the corresponding mustaches). Starting at the peak of the orbit near the uppermost non-symmetric FS, there is a slow drift along the upper saddle sheet that closely follows the true canard of the non-symmetric FN (Fig. 17e, green curve). This is followed by a fast jump down to the lower saddle sheet. On this saddle sheet, there is short segment of slow drift to the right, which is then followed by a fast jump back to left to the lower attracting sheet. This slow drift and fast jump back are responsible for the SAO observed in the AP solutions. Moreover, the fast jump projects the solution into the region enclosed by the true canard (red diagonal line) of the symmetric FS and the strong canard (blue curve) of the lower non-symmetric FN. Since the orbit lands outside the funnel of the FN, there are no canard dynamics, and the solution drifts toward the fold $L_{1-}$, where it then jumps toward the rightmost non-symmetric FS. The rest of the orbit is then obtained by symmetry across the line $\{ u_1=u_2 \}$.

As a is decreased toward the saddle-node bifurcation at $\hbox {LP}_2$, the slow segments of the solutions on the lower attracting manifold approach the strong canards of the non-symmetric FNs (Fig. 17f, solid black curve). At the saddle-node bifurcation $\hbox {LP}_2$, the slow segments of the solutions land precisely on the strong canards. After the bifurcation has occurred, the AP solutions enter the funnel of the non-symmetric FNs but remain close to the strong canard itself (Fig. 17f, dashed black curve). As such, solutions on the innermost part of the AP branch have slow segments that closely follow the strong canards of the non-symmetric FNs, and slow segments that closely follow the true canards of the outermost non-symmetric FSs (Fig. 17g). Representative rhythms are illustrated in Fig. 3e.

D Results from Numerical Simulations Varying $\beta$

In this appendix, we briefly report on some results observed in numerical simulations of Eq. (1.6) as the parameter $\beta$ is varied, while the other parameters are fixed. The results are reported in Table 4. The observed strong symmetry breaking rhythms are SAO-LAO rhythms (cases 3, 5, and 6). Weak symmetry breaking states are seen in Case 9; as $\beta$ is taken closer to the upper end of this range, the asymmetric rhythms are successively close to AP $(1^3)_4$, $(1^3)_2$, and $1^3$ rhythms, respectively, where the subscript denotes the number of different $1^3$ events per period. There are also symmetric states, including AP MMO rhythms (case 1), IP SAO rhythms, and the ubiquitous IP LAO rhythms (cases 2, 4, and 7).

Table 4 Rhythms varying $\beta$, with the other parameters fixed at $a = 6.54$, $d_u = 8.1\times 10^{-4}$, and $d_v=1.0588$, and the initial conditions fixed at $(u_1, v_1) = (0.63, 2.82), (u_2, v_2) = (3.27, 2.70)$

E Analysis of the Asymmetric Canard Explosion that Consists of Broken-Symmetry SAO-LCC Rhythms

In this appendix, we use the method of geometric desingularization (a.k.a. the blow-up method) to analyze the asymmetric canard explosion of system (1.6) in which one oscillator (taken to be oscillator 2 here) undergoes an explosion of LCCs while the other exhibits SAOs. We show analytically that, for $d_u=\mathcal {O}(\beta ^2)$ and $d_v=\mathcal {O}(\beta )$, the asymmetric canard explosion is given asymptotically in $0< \beta \ll 1$ by

$$\begin{aligned} a_{\textrm{asym,c}}(\beta ) = 5 \sqrt{\frac{5}{3}} + 5 \beta + \frac{4}{3} \sqrt{\frac{5}{3}} d_u + \frac{2}{3}\sqrt{\frac{5}{3}} \beta d_v + \frac{153\sqrt{15}}{64} \beta ^2 +\mathcal {O}(\beta ^3). \end{aligned}$$

(E.1)

This analysis confirms the numerical observations of the asymmetric canard explosion shown in Fig. 10. Numerical simulations of (1.6) with parameters set at $\beta =0.001$, $d_u=0.0008$, and $d_v=0.5$ show that the asymmetric canard explosion point occurs at $a=6.46182$. This agrees to within $\mathcal {O}(\beta ^2)$ of the value of $a_\textrm{symm,c}(0.001)=6.46179...$ predicted by (E.1), as expected based on the order of the remainder terms in the asymptotic expansion. Note that the analytic prediction matches the numerically computed location of the asymmetric canard explosion quite well, despite (i) $d_v$ being $\mathcal {O}(1)$ in Fig. 10, whereas the analysis requires it to be $\mathcal {O}(\beta )$, and (ii) the branch being computed in Fig. 10(ai) is the asymmetric explosion of the $0^21^0$ branch, whereas the analysis pertains to the asymmetric explosion of the $0^1 1^0$ rhythms. This is because, even though there are two SAOs in the $0^21^0$ rhythms, those SAOs scale similarly to the $0^1 1^0$ rhythm that the following blow-up and Melnikov analysis is based on. Moreover, in the $0^2 1^0$ rhythms, only one of the SAOs is created by passage through the FN point. The other SAO is created by the slow passage near the true canard $\gamma _t$ of the upper non-symmetric FS point, during the segment where oscillator 2 is on its right/upper branch (as shown in Fig. 8 and as is the case for the orbits shown in the left, near-vertical segment of the explosion in Fig. 10). Hence, the local analysis for the asymmetric canard explosion is the same for the two types of orbits, since they have the same local dynamics near FN. Also, we note that the linear dependence of $a_{\textrm{asym,c}}(\beta )$ on $d_u$ and $d_v$ at leading order agrees with the results observed numerically.

Asymmetric canard explosions were first observed in Awal et al. (2023) for pairs of coupled, identical van der Pol oscillators, with coupling only through the slow variable. The analysis here shows that the method developed in Awal et al. (2023) is more widely applicable to including fast–slow systems with coupling in both variables. (Also, the opposite situation in which oscillator 1 undergoes an explosion of LCCs while oscillator 2 exhibits SAOs, may be found using the same analysis, with the scalings of the two oscillators switched.)

1.1 E.1 Blow-up Transformation

We start by recalling from (1.5) that the parameter value at which a single LE oscillator undergoes a canard explosion is $(u_c,v_c,a_c)= \left( \sqrt{\frac{5}{3}}, \frac{8}{3}, 5\sqrt{\frac{5}{3}}\right)$. With this as a point of reference, it is useful to translate the dependent variables and the a parameter so that the canard point is at the origin:

$$\begin{aligned} u_1=u_c+{\bar{u}}_1, \ \ \ v_1=v_c+{\bar{v}}_1, \ \ \ u_2=u_c+{\bar{u}}_2, \ \ \ v_2=v_c+{\bar{v}}_2, \ \ \ a =a_c+{\bar{a}}. \end{aligned}$$

Also, we observe that the asymmetric canard explosion occurs for small values of $d_u$ and $d_v$, and so we rescale these as $d_u=\beta ^2 {\bar{d}}_u$ and $d_v=\beta {\bar{d}}_v$. Hence, the coupled system (1.6) becomes

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}{\bar{u}}_1}{{\text {d}}t}&= f(u_c+{\bar{u}}_1,v_c+{\bar{v}}_1) + \beta ^2 {\bar{d}}_u ({\bar{u}}_2 - {\bar{u}}_1)\\ \frac{{\text {d}}{\bar{v}}_1}{{\text {d}}t}&= \beta \biggr (g(u_c+{\bar{u}}_1,v_c+{\bar{v}}_1) + \beta {\bar{d}}_v({\bar{v}}_2 - {\bar{v}}_1)\biggr ) \\ \frac{{\text {d}}{\bar{u}}_2}{{\text {d}}t}&= f(u_c+{\bar{u}}_2,v_c+{\bar{v}}_2) - \beta ^2 {\bar{d}}_u ({\bar{u}}_2 - {\bar{u}}_1)\\ \frac{{\text {d}}{\bar{v}}_2}{{\text {d}}t}&= \beta \biggr (g(u_c+{\bar{u}}_2,v_c+{\bar{v}}_2) - \beta {\bar{d}}_v({\bar{v}}_2 - {\bar{v}}_1)\biggr ), \end{aligned} \end{aligned}$$

(E.2)

where we recall that $f(u,v)=a-u-\frac{4uv}{1+u^2}$ and $g(u,v)=u-\frac{uv}{1+u^2}$. (Note that here it is convenient to keep the original ordering of the equations, as in (1.6).)

With $\beta =0$, the origin $({\bar{u}}_1,{\bar{v}}_1,{\bar{u}}_2,{\bar{v}}_2)=(0,0,0,0)$ is a nilpotent point of (E.2), with a quadruple eigenvalue at zero. Hence, it is useful to apply the method of geometric desingularization (a.k.a. the blow-up method), which blows up the origin into a topological hemisphere. This desingularization effectively acts as a microscope, magnifying the flow near the nilpotent point to be a flow on and near a hemisphere, where the degeneracies in the original system are lifted, and all of the orbits can readily be distinguished and analyzed with classical invariant manifold theory.

We introduce the time-dependent small quantity $r=r(t) \ge 0$, scale the dependent variables with the appropriate powers of r, and elevate the small parameter $\beta$ to the status of a variable, by setting:

$$\begin{aligned}{} & {} {\bar{u}}_1 = \frac{1}{5}{\bar{a}} + r^4 x_1, \, {\bar{v}}_1 = {\bar{v}}_{1,S}({\bar{u}}_1) + \frac{1}{\sqrt{2}}\left( \frac{5}{3}\right) ^{1/4} r^5 y_1, {\bar{u}}_2 = \frac{5}{2} r x_2, \nonumber \\{} & {} \quad {\bar{v}}_2 = \frac{25}{8} r^2 y_2, \,\beta = r^2 {\hat{\beta }}. \end{aligned}$$

(E.3)

Therefore, the new dependent variables are $x_1,y_1,x_2,y_2,$ and ${\hat{\beta }}$. Also, we scale the parameter ${\bar{a}}$ as

$$\begin{aligned} {\bar{a}} = r^2 \phi _1 + r^4 \phi _2 + \cdots , \end{aligned}$$

(E.4)

where the $\phi _i, i=1,2,\ldots$, are parameters whose values will be determined in the course of the analysis. We recall the formula for the critical manifold (3.2), which in the rescaled variables (with $\beta =0$) is

$$\begin{aligned} {\bar{v}}_{i,S}({\bar{u}})=\frac{8 {\bar{a}} + 2 \sqrt{15} {\bar{a}}{\bar{u}} + 2 \sqrt{15}{\bar{u}}^2 + 3 {\bar{a}}{\bar{u}}^2 -3{\bar{u}}^3}{4\left( \sqrt{15} + 3 {\bar{u}}\right) }, \ \ \ \ i =1,2. \end{aligned}$$

With the transformations (E.3) and (E.4) of the variables and the parameters, the origin in (E.2) is blown up into the 4-sphere, $S^4 = \left\{ x_1^2 + y_1^2 + x_2^2 + y_2^2 + {\hat{\beta }}^2 = 1 \right\} ,$ which is embedded in ${\mathbb R}^5$. For ${\bar{u}}_1$ and ${\bar{v}}_1$, the powers of r in (E.3) are determined by how close oscillator 1 is observed to stay near the canard point, at the local minimum of the fast nullcline ${\bar{v}}_1={\bar{v}}_{1,S}({\bar{u}}_1)$, during the entire time in which oscillator 2 exhibits its LCCs. For ${\bar{u}}_2$ and ${\bar{v}}_2$, the powers of r in (E.3) are the same as those used in the analysis of the LCCs in the canard explosion of a single, uncoupled LE oscillator. The relative powers of r reflect the fact that the fast nullcline of oscillator 2 is locally parabolic, so that ${\bar{u}}_2$ and ${\bar{v}}_2$ are scaled linearly and quadratically in r, respectively, as is also the case in other fast–slow planar systems such as the coupled, identical van der Pol oscillators studied in Awal et al. (2023). Furthermore, the various constants in (E.3) are chosen so that the coefficients in the final system are well balanced.

Now, since there is no one single coordinate chart that can be used to study the full dynamics on and near the entire upper hemisphere, we proceed as in the method of geometric desingularization by examining the flow in different charts. Here, for system (E.2), we use the following charts:

$$\begin{aligned} \begin{aligned} K_{\text {entry/exit}}&=\{ y_2 = 1 \} \qquad {\text{(Entry }}/{\text {exit}} \; {\text { chart)}} \\ \ K_{\textrm{resc}}&=\{ {\hat{\beta }} = 1 \} \qquad {\text{(Rescaling }} \; {\text {or}} \; {\text {Central}} \; {\text {chart)}} \end{aligned} \end{aligned}$$

(E.5)

We emphasize that the charts $K_{\text {entry/exit}}$ and $K_{\textrm{resc}}$ are sufficient for studying the canard dynamics on and near the upper hemisphere. A characterization of the full dynamics on and near the upper hemisphere would require us to study the dynamics in additional coordinate charts.

1.2 E.2 Dynamics in the Central Chart and Derivation of (E.1)

In the rescaling (or central) chart $K_{\textrm{resc}}$, the change of variables is given by setting ${\hat{\beta }}=1$ in (E.3):

$$\begin{aligned}{} & {} {\bar{u}}_1 = \frac{1}{5}\left( r^2 \phi _1 + r^4 \phi _2 +\cdots \right) + r^4 x_1, \nonumber \\{} & {} \quad {\bar{v}}_1 = {\bar{v}}_{1,S}({\bar{u}}_1) + \frac{1}{\sqrt{2}}\left( \frac{5}{3}\right) ^{1/4} r^5 y_1, {\bar{u}}_2 = \frac{5}{2} r x_2, \nonumber \\{} & {} \quad {\bar{v}}_2 = \frac{25}{8} r^2 y_2, \beta = r^2, \end{aligned}$$

(E.6)

per the definition of chart $K_{\textrm{resc}}$. Let $\omega =\frac{3^{1/4} 5^{3/4}}{2\sqrt{2}}$. With these variables, system (E.2) becomes

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}x_1}{{\text {d}}t}&= r\left[ -\omega y_1 + \frac{5}{2} {\bar{d}}_u x_2 \right] + \mathcal {O}\left( r^2\right) , \\ \frac{{\text {d}}y_1}{{\text {d}}t}&= r \left[ \omega x_1 + \frac{5}{2} \omega {\bar{d}}_v y_2 - \frac{1}{\omega } {\bar{d}}_v \phi _1 \right] + \mathcal {O}\left( r^2\right) , \\ \frac{{\text {d}}x_2}{{\text {d}}t}&= r\left[ \frac{5\sqrt{15}}{8}\left( x_2^2 - y_2 \right) + \frac{2}{5} \phi _1 \right] +\mathcal {O}\left( r^2\right) \\ \frac{{\text {d}}y_2}{{\text {d}}t}&= r x_2 + \mathcal {O}\left( r^2\right) . \end{aligned} \end{aligned}$$

As a final step, we desingularize this vector field by employing the rescaled time variable:

$$\begin{aligned} {\tilde{t}}_2 = \omega r t, \end{aligned}$$

and we also rescale $x_2$ and $y_2$ so that the system is in its simplest form for finding the asymmetric canard point at the heart of the canard explosion:

$$\begin{aligned} {\tilde{x}}_1=x_1, \ \ \ {\tilde{y}}_1=y_1, \ \ \ {\tilde{x}}_2 = \omega x_2, \ \ \ {\tilde{y}}_2 = \frac{5\sqrt{15}}{8} y_2. \end{aligned}$$

Hence, the vector field we study in the rescaling chart is:

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}{\tilde{x}}_1}{{\text {d}}{\tilde{t}}_2}&= -{\tilde{y}}_1 + \frac{4}{\sqrt{15}} {\bar{d}}_u {\tilde{x}}_2 + \mathcal {O}(r), \\ \frac{{\text {d}}{\tilde{y}}_1}{{\text {d}}{\tilde{t}}_2}&= {\tilde{x}}_1 + \frac{4}{5\sqrt{15}} {\bar{d}}_v (5 {\tilde{y}}_2 - 2 \phi _1) + \mathcal {O}(r), \\ \frac{{\text {d}}{\tilde{x}}_2}{{\text {d}}{\tilde{t}}_2}&= {\tilde{x}}_2^2 - {\tilde{y}}_2 + \frac{2}{5} \phi _1 + \mathcal {O}(r), \\ \frac{{\text {d}}{\tilde{y}}_2}{{\text {d}}{\tilde{t}}_2}&= {\tilde{x}}_2 + \mathcal {O}(r). \end{aligned} \end{aligned}$$

(E.7)

This is the main vector field we study in chart $K_{\textrm{resc}}$.

For small values of r, the full system (E.7) is a perturbation of the $r=0$ system:

$$\begin{aligned} \frac{{\text {d}}{\tilde{x}}_1}{{\text {d}}{\tilde{t}}_2}= & {} -{\tilde{y}}_1 + \frac{4}{\sqrt{15}} {\bar{d}}_u {\tilde{x}}_2, \nonumber \\ \frac{{\text {d}}{\tilde{y}}_1}{{\text {d}}{\tilde{t}}_2}= & {} {\tilde{x}}_1 + \frac{4}{5\sqrt{15}} {\bar{d}}_v (5 {\tilde{y}}_2 - 2 \phi _1), \nonumber \\ \frac{{\text {d}}{\tilde{x}}_2}{{\text {d}}{\tilde{t}}_2}= & {} {\tilde{x}}_2^2 - {\tilde{y}}_2 + \frac{2}{5} \phi _1, \nonumber \\ \frac{{\text {d}}{\tilde{y}}_2}{{\text {d}}{\tilde{t}}_2}= & {} {\tilde{x}}_2. \end{aligned}$$

(E.8)

Crucially, one observes that the $({\tilde{x}}_2,{\tilde{y}}_2)$ subsystem of (E.8) is independent of the variables ${\tilde{x}}_1$ and ${\tilde{y}}_1$. In fact, in the full system (E.7), the $({\tilde{x}}_2,{\tilde{y}}_2)$ subsystem is independent of ${\tilde{x}}_1$ and ${\tilde{y}}_1$ up to and including terms of $\mathcal {O}(r^5)$. Hence, we first analyze the $({\tilde{x}}_2,{\tilde{y}}_2)$ subsystem of (E.8) and then consider the full system (E.7) as a small-amplitude perturbation.

The $({\tilde{x}}_2,{\tilde{y}}_2)$ subsystem of (E.8) is a one-degree-of-freedom Hamiltonian system, with

$$\begin{aligned} H({\tilde{x}}_2,{\tilde{y}}_2) = \frac{1}{2} e^{-2{\tilde{y}}_2} \left( -{\tilde{x}}_2^2 + {\tilde{y}}_2 + \frac{1}{2} - \frac{2\phi _1}{5} \right) \end{aligned}$$

(E.9)

and non-canonical form

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}{\tilde{x}}_2}{{\text {d}}{\tilde{t}}_2}&= e^{2{\tilde{y}}_2} \frac{\partial H}{\partial {\tilde{y}}_2}, \\ \frac{{\text {d}}{\tilde{y}}_2}{{\text {d}}{\tilde{t}}_2}&= - e^{2{\tilde{y}}_2} \frac{\partial H}{\partial {\tilde{x}}_2}. \end{aligned} \end{aligned}$$

(E.10)

In chart $K_{\textrm{resc}}$, the LCC solutions of (1.6) are represented in the limit $r=0$ by the following parabolic solution of (E.10):

$$\begin{aligned} \Gamma = ({\tilde{x}}_2,{\tilde{y}}_2)=\left( \frac{1}{2} {\tilde{t}}_2, \frac{1}{4}{\tilde{t}}_2^2 - \frac{1}{2} + \frac{2\phi _1}{5} \right) , \ \ \ {\tilde{t}}_2 \in (-\infty ,\infty ). \end{aligned}$$

This solution is a heteroclinic orbit of (E.10), connecting two points at infinity. When the $({\tilde{x}}_2,{\tilde{y}}_2)$ plane is projected on the hemisphere, one observes that $\Gamma$ connects two points on the equator. In fact, it lies in the transverse intersection of a center-stable manifold, $C_a$, and a center-unstable manifold, $C_r$, on the invariant hemisphere $\{ r=0 \}$. (We determine what these center-stable and center-unstable manifolds are in Appendix E.3 and show that the special solution $\Gamma$ lies in their intersection in Appendix E.4.)

Remark E.1

We determine the $({\tilde{x}}_1,{\tilde{y}}_1)$ components of the special solution $\Gamma$ by solving the forced linear system

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}{\tilde{x}}_1}{{\text {d}}{\tilde{t}}_2}&= -{\tilde{y}}_1 + \frac{4}{\sqrt{15}} {\bar{d}}_u {\tilde{x}}_2, \\ \frac{{\text {d}}{\tilde{y}}_1}{{\text {d}}{\tilde{t}}_2}&= {\tilde{x}}_1 + \frac{4}{5\sqrt{15}} {\bar{d}}_v (5 {\tilde{y}}_2 - 2 \phi _1). \end{aligned} \end{aligned}$$

The solution

$$\begin{aligned} \begin{bmatrix} {\tilde{x}}_1({\tilde{t}}_2) \\ {\tilde{y}}_1({\tilde{t}}_2) \end{bmatrix} = \begin{bmatrix} \tfrac{\sqrt{15}{\tilde{x}}_1(0)-2({\tilde{d}}_u+2{\tilde{d}}_v)}{\sqrt{15}} &{} -{\tilde{y}}_1(0) \\ {\tilde{y}}_1(0) &{} \tfrac{\sqrt{15}{\tilde{x}}_1(0)-2({\tilde{d}}_u+2{\tilde{d}}_v)}{\sqrt{15}} \end{bmatrix} \begin{bmatrix} \cos {\tilde{t}}_2 \\ \sin {\tilde{t}}_2 \end{bmatrix} + \begin{bmatrix} \tfrac{2{\bar{d}}_u+4{\bar{d}}_v-{\bar{d}}_v {\tilde{t}}_2^2}{\sqrt{15}} \\ \tfrac{2({\bar{d}}_u+{\bar{d}}_v) {\tilde{t}}_2}{\sqrt{15}} \end{bmatrix} \end{aligned}$$

consists of a simple harmonic oscillator with a forced response that is, at most, quadratic in ${\tilde{t}}_2$.

Now, we determine the parameter values for which the center-unstable and center-stable manifolds in system (E.7) intersect transversely with $0<r \ll 1$. This is achieved using Melnikov theory. In particular, the splitting distance between the center-unstable and center-stable manifolds as measured on the hyperplane $\{ {\tilde{x}}_2=0\}$ is

$$\begin{aligned} D(r) = D_1 r + D_2 r^2 + D_3 r^3 + D_4 r^4 + D_5 r^5 + \mathcal {O}(r^6). \end{aligned}$$

(E.11)

Here,

$$\begin{aligned} \begin{aligned} D_1&= \frac{\omega }{5} \int _{-\infty }^\infty \nabla H \cdot \left( {\tilde{x}}_2 {\tilde{y}}_2 - 7 {\tilde{x}}_2^3, {\tilde{x}}_2^2 - {\tilde{y}}_2 \right) ^T \vert _\Gamma \,d{\tilde{t}}_2 = - \frac{3}{25} \omega e^{1 - \frac{4\phi _1}{5}} \sqrt{\frac{\pi }{2}} (\phi _1-5), \\ D_2&= \int _{-\infty }^\infty \nabla H \cdot \left( \frac{\sqrt{15}}{8} {\tilde{x}}_2^2 (5 {\tilde{x}}_2^2 + {\tilde{y}}_2) + \frac{2\phi _2}{5}, \frac{1}{8}\sqrt{\frac{3}{5}}({\tilde{x}}_2{\tilde{y}}_2 - 7 {\tilde{x}}_2^3) \right) ^T \vert _\Gamma \, d{\tilde{t}}_2 = 0, \\ D_3&= \frac{\omega }{40\sqrt{15}} \int _{-\infty }^\infty \nabla H \cdot \left( -{\tilde{x}}_2 (64{\hat{d}}_u + 165 {\tilde{x}}_2^4 +105 {\tilde{x}}_2^2 {\tilde{y}}_2, \frac{1}{5}(375 {\tilde{x}}_2^4 + 75 {\tilde{x}}_2^2 {\tilde{y}}_2 \right. \\&\left. \quad + 64 {\bar{d}}_v (-5 {\tilde{y}}_2 + 2 \phi _1)) \right) ^T \vert _\Gamma \, d{\tilde{t}}_2 \\&= \frac{\omega }{320\sqrt{15}} e^{1-\frac{4\phi _1}{5}}\sqrt{\frac{\pi }{2}} (975+256 {\bar{d}}_u + 128 {\bar{d}}_v + 138 \phi _1), \\ D_4&= \int _{-\infty }^\infty \nabla H \cdot \left( \frac{15}{64}{\tilde{x}}_2^6 + \frac{75}{64}{\tilde{x}}_2^4 {\tilde{y}}_2 + \frac{2}{25}{\bar{d}}_u \phi _1, -\frac{3}{64} {\tilde{x}}_2^3(11 {\tilde{x}}_2^2 + 7 {\tilde{y}}_2) \right) ^T \vert _\Gamma \, d{\tilde{t}}_2 =0, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} D_5&= \frac{3\omega }{64} \int _{-\infty }^\infty \nabla H \cdot \left( {\tilde{x}}_2^5(17{\tilde{x}}_2^2 -11 {\tilde{y}}_2), {\tilde{x}}_2^6 + 5 {\tilde{x}}_2^4 {\tilde{y}}_2 + \frac{512}{1875}{\bar{d}}_v \phi _1^2 + \frac{1024}{75\sqrt{15}}{\bar{d}}_v \phi _2 \right) ^T \vert _\Gamma \, d{\tilde{t}}_2 \\&= \frac{3\omega }{64} e^{1- \frac{4\phi _1}{5}} \sqrt{\frac{\pi }{2}} \left( -\frac{105}{16} + \frac{39\phi _1}{16} + \frac{512}{1875} {\bar{d}}_v \phi _1^2 + \frac{1024}{75\sqrt{15}} \ {\bar{d}}_v \phi _2 \right) . \end{aligned} \end{aligned}$$

Hence, for all sufficiently small values of $r>0$, D(r) has simple zeroes for

$$\begin{aligned} \begin{aligned} \phi _1&= 5 + \frac{1}{192}\sqrt{\frac{5}{3}} \left( 1665 + 256 {\bar{d}}_u + 128{\bar{d}}_v\right) r^2 + \mathcal {O}(r^4), \\ \phi _2&= -\frac{\sqrt{15}}{2} + \mathcal {O}(r^2). \end{aligned} \end{aligned}$$

In turn, recalling the scalings of ${\bar{a}}$, $\beta$, $d_u$, and $d_v$, we find that D(r) has simple zeroes for

$$\begin{aligned} {\bar{a}} = 5 \beta + \frac{4}{3}\sqrt{\frac{5}{3}} d_u + \frac{2}{3}\sqrt{\frac{5}{3}} \beta d_v + \frac{153\omega ^2}{40} \beta ^2 + \mathcal {O}(\beta ^3). \end{aligned}$$

Finally, translating this result for the simple zeroes back to the original parameter $a= a_c +{\bar{a}}$, one finds that the asymmetric canard explosion is centered at

$$\begin{aligned} a_{\textrm{asym,c}}(\beta ) = 5 \sqrt{\frac{5}{3}} + 5 \beta + \frac{4}{3} \sqrt{\frac{5}{3}} d_u + \frac{2}{3}\sqrt{\frac{5}{3}} \beta d_v + \frac{153\sqrt{15}}{64}\beta ^2 + \mathcal {O}(\beta ^3), \end{aligned}$$

for $d_u=\mathcal {O}(\beta ^2)$ and $d_v=\mathcal {O}(\beta )$, which is precisely formula (E.1).

1.3 E.3 Dynamics in the Entry/Exit Chart

The Melnikov calculation performed in Appendix E.2 determines the parameters for which there is an intersection of the center-stable and center-unstable manifolds, $C_a$ and $C_r$. Here, we examine the nature of these manifolds and determine where they originate from. The analysis here and in Appendix E.4 closely follows the approach in Szmolyan and Wechselberger (2001).

In the entry/exit chart $K_{\mathrm{entry/exit}}$, the blow-up transformation is given by setting $y_2 = 1$ in (E.3):

$$\begin{aligned} \begin{aligned} {\overline{u}}_1&= \frac{1}{5} r_{1E}^2 \beta _{1E} \phi _1+r_{1E}^4 x_{1E} + \cdots , \,\,\, {\overline{v}}_1 = {\overline{v}}_{1,S}({\overline{u}}_1) + \frac{1}{\sqrt{2}}\left( \frac{5}{3} \right) ^{1/4} r_{1E}^5 y_{1E}, \\ {\overline{u}}_2&= \frac{5}{2} r_{1E} x_{2E}, \,\,\, {\overline{v}}_2 = \frac{25}{8} r_{1E}^2, \,\,\, \beta = r_{1E}^2 \beta _{1E}. \end{aligned} \end{aligned}$$

Here, the subscript E is used to distinguish the new variables $(x_{1E},x_{2E},y_{1E}r_{1E},\beta _{1E})$ in the entry/exit chart from the variables in the rescaling chart. The distinction will be important especially in the transformations between coordinate charts carried out in Appendix E.4. However, here in this subsection, we drop the subscript E to declutter the notation.

Transformation and desingularization by a factor of $r_1$ (i.e., rescaling time as ${\tilde{t}}_1 = r_1 t$) gives the dynamics in the entry/exit chart $K_{\mathrm{entry/exit}}$ as

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}x_1}{{\text {d}}{\tilde{t}}_1}&= -\omega y_1 + \mathcal {O}(r_1,\beta _1), \\ \frac{{\text {d}}x_2}{{\text {d}}{\tilde{t}}_1}&= \frac{5\sqrt{15}}{8} \left( x_2^2-1 \right) + \mathcal {O}(r_1, \beta _1), \\ \frac{{\text {d}}y_1}{{\text {d}}{\tilde{t}}_1}&= \beta _1 \left( \omega x_1 - \frac{5}{2} x_2 y_1 + \mathcal {O}(r_1,\beta _1) \right) , \\ \frac{{\text {d}}r_1}{{\text {d}}{\tilde{t}}_1}&= r_1^2 \beta _1 \left( \frac{1}{2}x_2+\mathcal {O}(r_1,\beta _1) \right) , \\ \frac{{\text {d}}\beta _1}{{\text {d}}{\tilde{t}}_1}&= -\beta _1^2 \left( x_2 + \mathcal {O}(r_1) \right) . \end{aligned} \end{aligned}$$

(E.12)

This system has two invariant subspaces, $\{ r_1 = 0 \}$ and $\{ \beta _1 = 0 \}$.

The dynamics in the invariant subspace $\{ r_1 = 0 \} \cap \{ \beta _1 = 0 \}$ is given by

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}x_1}{{\text {d}}{\tilde{t}}_1}&= -\omega y_1, \\ \frac{{\text {d}}x_2}{{\text {d}}{\tilde{t}}_1}&= \frac{5\sqrt{15}}{8} \left( x_2^2-1 \right) , \\ \frac{{\text {d}}y_1}{{\text {d}}{\tilde{t}}_1}&= 0. \end{aligned} \end{aligned}$$

This system possesses a line, $L_{a,1} = \left\{ (x_1, -1, 0,0,0) \right\}$, of normally hyperbolic attracting equilibria with nonzero eigenvalue $\lambda _a = -\tfrac{5 \sqrt{15}}{4}$. Similarly, the system possesses a line, $L_{r,1} = \left\{ (x_1,1,0,0,0) \right\}$, of normally hyperbolic repelling equilibria with nonzero eigenvalue $\lambda _r = \frac{5\sqrt{15}}{4}$.

The dynamics in the invariant hyperplane $\{ \beta _1 = 0 \}$ are given by

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}x_1}{{\text {d}}{\tilde{t}}_1}&= -\omega y_1 + \mathcal {O}(r_1), \\ \frac{{\text {d}}x_2}{{\text {d}}{\tilde{t}}_1}&= \frac{5\sqrt{15}}{8} \left( x_2^2-1 \right) + \mathcal {O}(r_1), \\ \frac{{\text {d}}y_1}{{\text {d}}{\tilde{t}}_1}&= 0, \\ \frac{{\text {d}}r_1}{{\text {d}}{\tilde{t}}_1}&= 0. \end{aligned} \end{aligned}$$

(E.13)

For this system, there are normally hyperbolic surfaces, $S_{a,1}$ and $S_{r,1}$, of equilibria that emanate from the lines $L_{a,1}$ and $L_{r,1}$, respectively. The surfaces $S_{a,1}$ and $S_{r,1}$ correspond to the attracting and repelling sheets of the critical manifold (of oscillator 2). On $S_{a,1}$ and $S_{r,1}$, the nonzero eigenvalues are $\mathcal {O}(r_1)$ perturbations of the nonzero eigenvalues $\lambda _a$ and $\lambda _r$, respectively.

The dynamics in the invariant hyperplane $\{ r_1 = 0 \}$ are given by

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}x_1}{{\text {d}}{\tilde{t}}_1}&= -\omega y_1 + \mathcal {O}(\beta _1), \\ \frac{{\text {d}}x_2}{{\text {d}}{\tilde{t}}_1}&= \frac{5\sqrt{15}}{8} \left( x_2^2-1 \right) + \mathcal {O}(\beta _1), \\ \frac{{\text {d}}y_1}{{\text {d}}{\tilde{t}}_1}&= \beta _1 \left( \omega x_1 - \frac{5}{2} x_2 y_1 + \mathcal {O}(\beta _1) \right) , \\ \frac{{\text {d}}\beta _1}{{\text {d}}{\tilde{t}}_1}&= -\beta _1^2 x_2. \end{aligned} \end{aligned}$$

(E.14)

The lines $L_{a,1}$ and $L_{r,1}$ are equilibria of this system with triple-zero eigenvalue and one nonzero eigenvalue. Consequently, there exist 3D center manifolds, $C_{a,1}$ and $C_{r,1}$, of the lines $L_{a,1}$ and $L_{r,1}$.

With the analysis above, we can draw the following conclusions about the blown-up system (E.12). First, there exists an attracting 4D center manifold, $M_{a,1}$, of the line, $L_{a,1}$, of equilibria. The center manifold $M_{a,1}$ contains the surface, $S_{a,1}$, of equilibria, as well as the center manifold $C_{a,1}$. Moreover, for $r_1, \beta _1$, and $|x_1|$ sufficiently small, the center manifold $M_{a,1}$ has a graph representation, i.e., $x_2 = h_a(x_1,y_1,r_1,\beta _1)$ for some function $h_a$. Additionally, the branch of the center manifold $C_{a,1}$ in $r_1 = 0$ is unique for $x_2<0$. Similarly, there exists a repelling 4D center manifold, $M_{r,1}$, of the line, $L_{r,1}$, of equilibria. The center manifold $M_{r,1}$ contains the surface, $S_{r,1}$, of equilibria, as well as the center manifold $C_{r,1}$. Moreover, for $r_1, \beta _1$, and $|x_1|$ sufficiently small, the center manifold $M_{r,1}$ has a graph representation, i.e., $x_2 = h_r(x_1,y_1,r_1,\beta _1)$ for some function $h_r$. Finally, the branch of the center manifold $C_{r,1}$ in $r_1 = 0$ is unique for $x_2>0$.

1.4 E.4 Connecting the Dynamics Between the Two Charts

In Appendix E.2, we determined the parameters for which an intersection between a center-stable manifold, $C_a$, and a center-unstable manifold, $C_r$, would persist. In Appendix E.3, we determined the center manifolds of the lines of equilibria $L_{a,1}$ and $L_{r,1}$. Here, we show that the center manifolds $C_{a,1}$ and $C_{r,1}$ from the entry/exit chart are precisely the center-stable and center-unstable manifolds that intersect in the rescaling chart. To distinguish between objects in these charts, we include an E or C subscript corresponding to the entry/exit and central charts, respectively. That is, the variables in the entry/exit chart are $(x_{1E},x_{2E},y_{1E},r_{1E},\beta _{1E})$ and the variables in the central chart are $(x_{1C},x_{2C},y_{1C},y_{2C},r_{2C})$.

The following transition maps, defined for $y_{2C}>0$ and $\beta _{1E}>0$, respectively, enable one to transport solutions from one chart to another:

$$\begin{aligned} \begin{aligned}&\left( x_{1E}, x_{2E}, y_{1E}, r_{1E},\beta _{1E} \right) = \kappa _{CE}(x_{1C},x_{2C},y_{1C},y_{2C},r_{2C})\\&\quad = \left( \frac{x_{1C}}{y_{2C}^2}, \frac{x_{2C}}{\sqrt{y_{2C}}}, \frac{y_{1C}}{y_{2C}^{5/2}}, r_{2C} \sqrt{y_{2C}}, \frac{1}{y_{2C}} \right) , \\&\left( x_{1C}, x_{2C}, y_{1C}, y_{2C}, r_{2C} \right) = \kappa _{EC}(x_{1E}, x_{2E}, y_{1E}, r_{1E},\beta _{1E}) \\&\quad = \left( \frac{x_{1E}}{\beta _{1E}^2}, x_{2E} \sqrt{\beta _{1E}}, \frac{y_{1E}}{\beta _{1E}^{5/2}}, \frac{1}{\beta _{1E}}, r_{1E} \sqrt{\beta _{1E}} \right) . \end{aligned} \end{aligned}$$

That is, $\kappa _{CE}$ is the change of coordinates that maps objects from the central chart to the entry/exit chart, and $\kappa _{EC}$ is the change of coordinates that takes objects from the entry/exit chart and transports them to the central chart.

We use $\kappa _{CE}$ to determine where the special solution $\Gamma$ from the central chart ends up in the entry/exit chart as $t \rightarrow \pm \infty$ (recalling also that t was rescaled there). To do this, we calculate the limit

$$\begin{aligned} \lim _{t \rightarrow \infty } \kappa _{CE}(\Gamma (t)) = (0,1,0,0,0), \end{aligned}$$

which is a point on the line $L_{r,1}$ of equilibria. By calculating the tangent vector, $\lim _{t \rightarrow \infty } \tfrac{\frac{\text {d}}{{\text {d}}t} \kappa _{CE}(\Gamma (t))}{\Vert \frac{\text {d}}{{\text {d}}t} \kappa _{CE}(\Gamma (t))\Vert }$, of the special solution in the entry/exit chart at the point (0, 1, 0, 0, 0), it can be shown that $\kappa _{CE}(\Gamma )$ lies in the tangent space of the center manifold $C_{r,1}$. Similarly, we find that

$$\begin{aligned} \lim _{t \rightarrow -\infty } \kappa _{CE}(\Gamma (t)) = (0,-1,0,0,0), \end{aligned}$$

which is a point on the line $L_{a,1}$ of equilibria. As before, it can be shown, by calculating the tangent vector, $\lim _{t \rightarrow -\infty } \tfrac{\frac{{\text {d}}}{{\text {d}}t} \kappa _{CE}(\Gamma (t))}{\Vert \frac{{\text {d}}}{{\text {d}}t} \kappa _{CE}(\Gamma (t))\Vert }$, of the special solution in the entry/exit chart at the point $(0,-1,0,0,0)$ that $\kappa _{CE}(\Gamma )$ lies in the tangent space of the center manifold $C_{a,1}$.

Thus, the special orbit $\Gamma$ from the central chart emanates from a point on $L_{a,1}$ along the unique part of the center manifold $C_{a,1}$ in $r_1=0, \beta _1>0$ in chart $K_\mathrm{entry/exit}$. It then moves across the hemisphere and terminates at a point on $L_{r,1}$ along the unique part of the center manifold $C_{r,1}$ in $r_1 = 0, \beta _1 >0$ in chart $K_{\mathrm{entry/exit}}$. Since the center manifolds $C_{a,1}$ and $C_{r,1}$ can be extended along the special solution $\Gamma$, it follows that $\Gamma$ corresponds to the intersection of the center manifolds across the sphere $S^5$.