Geometric analysis of mixed-mode oscillations in a model of electrical activity in human beta-cells

Abstract

Human pancreatic beta-cells may exhibit complex mixed-mode oscillatory electrical activity, which underlies insulin secretion. A recent biophysical model of human beta-cell electrophysiology can simulate such bursting behavior, but a mathematical understanding of the model’s dynamics is still lacking. Here we exploit time-scale separation to simplify the original model to a simpler three-dimensional model that retains the behavior of the original model and allows us to apply geometric singular perturbation theory to investigate the origin of mixed-mode oscillations. Changing a parameter modeling the maximal conductance of a potassium current, we find that the reduced model possesses a singular Hopf bifurcation that results in small-amplitude oscillations, which go through a period-doubling sequence and chaos until the birth of a large-scale return mechanism and bursting dynamics. The theory of folded node singularities provide insight into the bursting dynamics further away from the singular Hopf bifurcation and the eventual transition to simple spiking activity. Numerical simulations confirm that the insight obtained from the analysis of the reduced model can be lifted back to the original model.

1 Introduction

Glucose-induced insulin secretion from pancreatic beta-cells involves electrical activity, which leads to opening of voltage-gated $\hbox {Ca}^{2+}$ channels and exocytosis of insulin-containing granules [1, 13, 28]. Mouse beta-cells provide the typical experimental material for the study of electrical behavior underlying insulin release, and decades of studies have shown that the membrane voltage of mouse beta-cells exhibit bursting oscillations composed of active phases of action potential firing from a plateau interspersed by silent, hyperpolarized phases. This behavior, and complex variations of it, are believed to underlie pulsatile insulin release [4, 13, 33]. Mathematical modeling has played an important role in unraveling the mechanisms underlying the complex electrophysiological behavior of mouse beta-cells [4, 22, 30], and these models represent a prototypical example of so-called square-wave bursters that can be studied as a slow-fast system using time-scale separation [3, 26].

More recently an increasing number of studies have been performed on human beta-cells, which show similarities but also important electrophysiological differences to their counterpart from mice [5, 19, 25, 28]. Human beta-cells typically show spiking or very fast bursting, with about half of the cell population exhibiting each type of behavior. In contrast to square-wave bursting observed in mouse beta-cells, bursting in human beta-cells is often characterized by an active phase with very few and small oscillations around a depolarized plateau [2, 5, 19, 27]. This behavior resembles activity in certain pituitary cells and has been coined pseudo-plateau bursting [31]. Such bursting electrical activity has been proposed to evoke more hormone release than simple action potential firing [24, 32, 35], and is therefore of biophysical relevance.

A decade ago the first mathematical model of human beta-cell electrophysiology was developed [23]. This model and its descendants [17, 18, 20, 27] can simulate both spiking and fast bursting activity. However, so far no mathematical analysis of this model, in particular with respect to the dynamics underlying pseudo-plateau bursting, has been performed. Inspired by analysis of models exhibiting pseudo-plateau bursting in pituitary cells [31, 36], we speculate that mixed-mode oscillations (MMOs) due to folded singularities orchestrate pseudo-plateau bursting in models of human beta-cells. We refer to MMOs as complex patterns that arise in dynamical systems, in which Small Amplitude Oscillations (SAO) and Large Amplitude Oscillations (LAO) are interspersed [3, 6, 9]. Similar studies have been performed for MMOs in neurons [29, 34, 37] and cardiac cells [14, 15, 38]; see also [3, 7, 9] and references therein. However, the present work is the first to provide insight into MMOs in human beta-cells, which has relevance for our understanding of the control of insulin release.

2 Theoretical background

In the following sections we will reduce the original model of electrical activity in human beta-cells [23] to a three-dimensional model that will allow us to apply MMO theory. In this section we outline this theory, mainly following Desroches et al. [9].

We consider the three-dimensional fast-slow system of singularly perturbed ordinary differential equations

$$\begin{aligned} \begin{aligned} \epsilon \dot{x}&= f(x,y,z)\, ,\\ \dot{y}&= g_1(x,y,z)\, ,\\ \dot{z}&= g_2(x,y,z)\, , \end{aligned} \end{aligned}$$

(1)

with $f, g_1, g_2$ sufficiently smooth functions and a small parameter $0 < \epsilon \ll 1$. Let t denote the independent variable of (1) and $\dot{x}$ the derivative of x with respect to t. In this system x is the fast variable and y, z are the slow variables, and t is referred to as the slow time scale.

By switching to the fast time scale $\tau = t/\epsilon$, one obtains the equivalent system

$$\begin{aligned} \begin{aligned} x'&= f(x,y,z)\, ,\\ y'&= \epsilon g_1(x,y,z)\, ,\\ z'&= \epsilon g_2(x,y,z)\, , \end{aligned} \end{aligned}$$

(2)

where $x'$ denotes the derivative of x with respect to $\tau$ . As $\epsilon \rightarrow 0$ the trajectories of (2) converge during fast epochs to solutions of the fast subsystem or layer equations

$$\begin{aligned} \begin{aligned} x'&= f(x,y,z)\,,\\ y'&= 0\, ,\\ z'&= 0\, , \end{aligned} \end{aligned}$$

(3)

implying that the fast flow is almost horizontal, following the principal direction of the fast variable x.

Conversely during slow epochs trajectories of (1) converge to solutions of the slow subsystem or reduced problem:

$$\begin{aligned} \begin{aligned} 0&= f(x,y,z)\, ,\\ \dot{y}&= g_1(x,y,z)\, ,\\ \dot{z}&= g_2(x,y,z)\, , \end{aligned} \end{aligned}$$

(4)

which is a system of differential-algebraic equations.

Geometric singular perturbation theory (GSPT) is used to understand the dynamics of the full systems (1) and (2) for $\epsilon > 0$ from the (singular) fast and slow subsystems (3) and (4). The algebraic equation in (4) defines the so-called critical manifold

$$\begin{aligned} S : = \lbrace \left( x,y,z \right) : f(x,y,z)=0 \rbrace \, , \end{aligned}$$

(5)

and the slow flow determined by (4) is constrained to lay on this manifold. S is supposed to be a smooth manifold. Note that the points of S are equilibrium points for the layer equations (3).

GSPT guarantees that normally hyperbolic invariant manifold S persists as locally invariant slow manifolds $S_\epsilon$ of the full problem (1) for sufficiently small $\epsilon$. Moreover the restriction of the flow of (1) to $S_\epsilon$ is a small smooth perturbation of the flow of the reduced problem (4) [10]. Normal hyperbolicity is often difficult to verify when there is only a single time scale. However, in our slow-fast setting, S consists entirely of equilibria (of the layer equations (3)) and therefore the requirement of normal hyperbolicity of a compact subset $S_0 \subset S$ is satisfied as soon as all $p \in S_0$ are hyperbolic equilibria, i.e., if $f_x: =\partial f / \partial x$ is uniformly bounded away from the imaginary axis for all $p \in S_0$. In that case the critical manifold $S_0$ is normally hyperbolic.

GSPT breaks down at points on the critical manifold where normal hyperbolicity fails. This happens at points on S where their projection onto the space of slow variables is singular, i.e., on the fold lines L, defined as the set of equilibria of (3) with a zero eigenvalue,

$$\begin{aligned} L : = \lbrace \left( x,y,z \right) \in S : f_x(x,y,z)=0 \rbrace \, . \end{aligned}$$

The stability of points $p \in S$ as equilibria of the layer problem (3) depends on the sign of $f_x$: the fold lines divide the critical manifold S into attracting sheets $S_a$ (where $f_x<0$) and repelling sheets $S_r$ (where $f_x>0$). The critical manifold S is assumed to be (locally) a folded surface, i.e.,

$$\begin{aligned} S = S_a \cup L \cup S_r\, , \end{aligned}$$

(6)

and we suppose $f_{xx} \ne 0$ for every point on the fold line L, i.e.,

$$\begin{aligned} L : = \lbrace \left( x,y,z \right) \in S : f_x(x,y,z)=0, f_{xx}(x,y,z) \ne 0 \rbrace . \end{aligned}$$

(7)

This condition ensures that S has a fold, and not a deflection tangent, in L.

Without loss of generality, we assume that $\left. f_z(p) \right| _{p \in L} \ne 0$ holds locally. It follows by the implicit function theorem that S is locally given as a graph $z=\phi (x,y)$. Hence the reduced problem (4) can be projected onto the (x, y)-plane, yielding

$$\begin{aligned} \left. \begin{aligned} - f_x \dot{x}&= f_y g_1 + f_z g_2 \\ \dot{y}&= g_1 \end{aligned} \right| _{z=\phi (x,y)}\ , \end{aligned}$$

(8)

where the first equation is obtained by differentiating the algebraic equation $f=0$ (which generates the folded surface) with respect to t. Indeed, this equation is no longer necessary after imposing the equivalent constraint $z=\phi (x,y)$; conversely its derivative allows us to make explicit the evolution of the fast variable on the slow manifold S.

Finally, desingularization (i.e. rescaling time by $dt = - f_x dt'$) removes the singular term on the fold and gives the desingularized system

$$\begin{aligned} \left. \begin{aligned} \dot{x}&= f_y g_1 + f_z g_2 \\ \dot{y}&= - f_x g_1 \end{aligned} \right| _{z=\phi (x,y)}\ . \end{aligned}$$

(9)

The desingularized system (9) is equivalent to the original one (8) on the attracting sheets $S_a$ but has opposite orientation on the repelling sheets $S_r$ due to the time rescaling: for every point $p \in S_a$ we have by definition $f_x(p) < 0$, hence rescaling time by the factor $-f_x(p) > 0$ does not change the orientation; conversely, $-f_x(p)$ is negative on $S_r$ and thus changes the direction of the flow.

Singularities of the desingularized system (9), i.e., points where $\dot{x}=\dot{y}=0$, can be classed as ordinary or folded. Ordinary singularities are true equilibria on S of the initial system (1) where $g_1$ is vanishing (and $g_2=0$ as well, since $f_y$ and $f_z$ are nonvanishing in the vicinity of L). Folded singularities, on the other hand, are points along the fold lines L (hence where $f_x=0$) where $\left. f_y g_1 + f_z g_2 \right| _{z=\phi (x,y)}$ equals zero. These are characterized as folded saddles, nodes or foci based on the eigenvalues $\sigma _s$ and $\sigma _w$ of the Jacobian J of (9) evaluated at the folded singularity. We use notation so that $|\sigma _s|\ge |\sigma _w|$ and denote $\sigma _s$ and $\sigma _w$ the strong and weak eigenvalue, respectively.

2.1 Canards

The trajectories of the slow flow that lie along the eigendirections of a folded saddle, or a folded node, connect the two sheets of the critical manifold through the folded singularity in finite time. In these points the slow flow switches from incoming to outgoing. Such solutions are called singular canards and their persistence under small perturbations can give rise to complex dynamics. We call the singular canard corresponding to the strong (respectively weak) eigendirection the strong (respectively weak) singular canard $\tilde{\gamma }_s$ (respectively $\tilde{\gamma }_w$).

For the case of a folded node, the strong singular canard $\tilde{\gamma }_s$ and the fold curve L bound sector of trajectories that cross from $S_a$ to $S_r$ by passing through the folded node. This sector is called the funnel of the folded node, and the funnel contains necessarily the weak singular canard. In the system we are going to study, the relevant folded singularities are attracting folded nodes.

Singular canards persist under small perturbations $\epsilon \,{>}\,0$, and their perturbation are simply denoted canards. In geometric terms, a canard corresponds to the intersection of the manifold $S_{a,\epsilon }$ and $S_{r,\epsilon }$ extended by the flow to the vicinity of the folded singularity [9]. Canards are not unique since the corresponding invariant manifolds $S_{a,\epsilon }$ and $S_{r,\epsilon }$ are not unique. For a fixed choice of the invariant manifolds we call their intersections maximal canards. Maximal canards can be seen as perturbations of singular canards that preserve the original behaviour. The singular canard $\tilde{\gamma }_s$ (the strong canard) always perturbs to a maximal canard $\gamma _s$, and in general, the singular canard $\tilde{\gamma }_w$ (the weak canard) also perturbs to a maximal canard $\gamma _w$ [6, 9]. We call $\gamma _s$ and $\gamma _w$ primary canards. In addition to these, there are other maximal canards, which we call secondary canards. The presence of secondary canards divides the sector between primary maximal canards $\tilde{\gamma }_w$ and $\tilde{\gamma }_s$ into subsectors. Furthermore, trajectories within each subsector will be forced to take a certain number of turns around $\tilde{\gamma }_w$ when passing through the folded node resulting in SAOs [6, 9].

Fig. 1

Different behavior in the 7D model depending on the maximal whole-cell hERG conductances. Hyperpolarization at high hERG conductance ($g_{\mathrm{{hERG}}}=0.8$ nS/pF; a), “spiking” action potential firing at $g_{\mathrm{{hERG}}}=0.5$ nS/pF (b), and bursting electrical activity at low hERG conductance ($g_{\mathrm{{hERG}}}=0.13$ nS/pF; c). The columns show membrane potential V, L-type CaV inactivation gating variable $h_{\mathrm{{CaL}}}$ and hERG activation variable $m_{\mathrm{{hERG}}}$. Parameters as in the article by Pedersen [23] except $g_{\mathrm{{KV}}}=0.25$ nS/pF and $h_{\mathrm{{hERG}}}=0.4$

3 MMOs in a model of human beta-cells

Our starting point is a slightly modified version of the Hodgkin–Huxley type model of electrical activity in human beta-cells [23]. Briefly, this seven-dimensional nonlinear model represents the dynamics of the beta-cell membrane potential V, which is controlled by currents (normalized to cell capacitance) through a set of ion channels. Channel gating operating on different time scales makes the dynamics highly nontrivial and different kinds of dynamical patterns can be observed depending on the model parameters. In the following we refer to this model as the 7d-model. Further details and biophysical motivation can be found in the original paper [23]. For completeness we provide the equations of the model.

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}\, V}{\mathrm{d}t}&= - I_{\mathrm{{total}}} \\&= - ( I_{K_V}+I_{KATP}+I_{BK}+I_{hERG}+I_{CaT}\\&\quad +I_{CaL}+I_{CaPQ}+I_{Na}+I_{leak} ),\\ \frac{\mathrm{d}\, m_{K_V}}{\mathrm{d}t}&= \frac{m_{K_V,\infty }(V)-m_{K_V}}{\tau _{mKV}(V)},\\ \frac{\mathrm{d}\, m_{BK}}{\mathrm{d}t}&= \frac{m_{BK,\infty }(V)-m_{BK}}{\tau _{mBK}},\\ \frac{\mathrm{d}\, m_{hERG}}{\mathrm{d}t}&= \frac{m_{hERG,\infty }(V)-m_{hERG}}{\tau _{mhERG}},\\ \frac{\mathrm{d}\, h_{CaT}}{\mathrm{d}t}&=\frac{h_{CaT,\infty }(V)-h_{CaT}}{\tau _{hCaT}},\\ \frac{\mathrm{d}\, h_{CaL}}{\mathrm{d}t}&=\frac{h_{CaL,\infty }(V)-h_{CaL}}{\tau _{hCaL}},\\ \frac{\mathrm{d}\, h_{Na}}{\mathrm{d}t}&= \frac{h_{Na,\infty }(V)-h_{Na}}{\tau _{hNa}}, \end{aligned} \end{aligned}$$

(10)

with currents

$$\begin{aligned} \begin{aligned} I_{K_V}&= g_{K_V} \, m_{K_V} \, (V-V_K), \\ I_{\mathrm{{KATP}}}&= g_{KATP} \, (V-V_K), \\ I_{\mathrm{{BK}}}&= \left( -(I_{\mathrm{{CaT}}}+I_{\mathrm{{CaL}}}+I_{\mathrm{{CaPQ}}}) + B_{\mathrm{{BK}}}\, \right) \\&\quad \times \bar{g}_{\mathrm{{BK}}} \, m_{\mathrm{{BK}}} \, (V-V_{K}),\\ I_{\mathrm{{hERG}}}&= g_{\mathrm{{hERG}}} \, m_{\mathrm{{hERG}}} \, h_{\mathrm{{hERG}}} \, (V-V_{K}),\\ I_{\mathrm{{CaT}}}&=g_{\mathrm{{CaT}}} \, m_{CaT,\infty }(V) \, h_{CaT} \, (V-V_{Ca}),\\ I_{\mathrm{{CaL}}}&=g_{\mathrm{{CaL}}} \, m_{CaL,\infty }(V) \, h_{CaL} \, (V-V_{Ca}),\\ I_{\mathrm{{CaPQ}}}&=g_{\mathrm{{CaPQ}}} \, m_{CaPQ,\infty }(V) \, (V-V_{Ca}),\\ I_{Na}&=g_{\mathrm{{Na}}} \, m_{Na,\infty }(V) \, h_{Na} \, (V-V_{Na}),\\ I_{\mathrm{{leak}}}&= g_{\mathrm{{leak}}} \, (V-V_{\mathrm{{leak}}}), \end{aligned} \end{aligned}$$

(11)

and steady-state activation ($m_{X,\infty }$) and inactivation ($h_{X,\infty }$) functions of the form

$$\begin{aligned} \begin{aligned} m_{X,\infty }(V)&= \left( 1+\exp { \left( \frac{V-V_{mX}}{n_{mX}} \right) } \right) ^{-1},\\ h_{X,\infty }(V)&= \left( 1+\exp { \left( \frac{V-V_{hX}}{n_{hX}} \right) } \right) ^{-1}.\\ \end{aligned} \end{aligned}$$

(12)

Finally, the voltage-dependent time scale of $m_{K_V}$ is

$$\begin{aligned} \begin{aligned} \tau _{{{mKV}}} ={\left\{ \begin{array}{ll} \tau _{{ {mKV}},0} + 10 \;\text {ms} \cdot \exp {\left( -\frac{V+20\,\mathrm{mV}}{6 \, \text {mV}} \right) } \\ \qquad \qquad \qquad \qquad \qquad \qquad \quad \text{ if } \; V >- 26.6 \; \text {mV} ,\\ \tau _{{mKV},0} + 30 \; \text {ms} \qquad \qquad \quad \quad \text{ otherwise. } \end{array}\right. }\\ \end{aligned} \end{aligned}$$

(13)

The model reproduces the three main types of electrical behavior seen in human beta-cells: silence characterized by the absence of action potential generation, spiking activity consisting of individual action potentials, and pseudo-plateau bursting where small action potentials fire from a depolarized plateau (Fig. 1). Changing the maximal conductance of the hERG potassium current, $g_{hERG}$, suffices to switch between the different types of behavior. In the following we are mainly interested in understanding the dynamics of pseudo-plateau bursting.

3.1 Model reduction

To apply the theory exposed in Sect. 2 we reduce the initial 7D-model to a 3-dimensional system. Based on the time scales shown in Table 1 we divide the variables into three categories (fast, medium and slow). The (fast) variable V is excluded from this analysis since all the other variables depend on it.

Table 1 Characterization of variables according to their time scales. Note that $\tau _{mKV}(V)$ depends on V, and the range of its values is given

Fig. 2

Projection of the 7D-model simulations (blue curves) from Fig. 1 with spiking ($g_{\mathrm{{hERG}}}=0.5$ nS/pF; panels Aa,Ab,Ac) or bursting ($g_{\mathrm{{hERG}}}=0.13$ nS/pF; Ba,Bb,Bc) for the fast variables $h_{\mathrm{{CaT}}}$ (Aa,Ba), $h_{Na}$ (Ab,Bb) and $m_{BK}$ (Ac,Bc). The red curves show the corresponding steady-state functions

Fig. 3

Projection onto the $(h_{\mathrm{{CaL}}}, m_{\mathrm{{KV}}})$-plane of the 7D-model simulations (blue curves) from Fig. 1 with spiking ($g_{\mathrm{{hERG}}}=0.5$ nS/pF; panel A) or bursting ($g_{hERG}=0.13$ nS/pF; B). The red line is the approximation (14). The dashed rectangle indicate the region corresponding to the active phase where the approximation is adequate

For the fastest variables we use quasi steady-state approximations as frequently done for Hodgkin-Huxley types models. From a mathematical point of view, this implies that these variables should be approximated by their steady-state functions. Simulations shown in Fig. 2 confirm that the quasi steady-state approximation is reasonable for the three fast variables $h_{\mathrm{{CaT}}}$, $h_{\mathrm{{Na}}}$, $m_{\mathrm{{BK}}}$.

The medium-fast variables $h_{\mathrm{{CaL}}}$ and $m_{\mathrm{{KV}}}$ are not well approximated by their steady-state functions and we use another widely applied approach due to Fitzhugh [11]. Since the two variables have similar timescales, we plot $m_{\mathrm{{KV}}}$ versus $h_{\mathrm{{CaL}}}$, and fit the curve with a linear function. As seen in Fig. 3, for the case of bursting, which is our main interest, an adequate fit for the active phase is given by

$$\begin{aligned} m_{\mathrm{{KV}}}(h_{\mathrm{{CaL}}}) = -0.125\, h_{CaL} + 0.13. \end{aligned}$$

(14)

We thus obtain the three-dimensional system (from now on we use h and m in place of $h_{\mathrm{{CaL}}}$ and $m_{\mathrm{{hERG}}}$, respectively),

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}\, V}{\mathrm{d}t}&= - I_{\mathrm{{Total}}}\left( V,h,m\right) ,\\ \frac{\mathrm{d}\, h}{\mathrm{d}t}&= \frac{h_\infty (V)-h}{\tau _h} ,\\ \frac{\mathrm{d}\, m}{\mathrm{d}t}&= \frac{m_\infty (V)-m}{\tau _m}. \end{aligned} \end{aligned}$$

(15)

We denote this system the 3D model. Simulations show that the three types of dynamics (hyperpolarization, spiking, bursting) present in the original 7D model are preserved in this model (Fig. 4).

Fig. 4

Simulations for the 3D-model (15) for different values of $g_{\mathrm{{hERG}}}$. No electrical activity (hyperpolarization) for $g_{hERG}=0.5$ nS/pF (a), spiking activity for $g_{\mathrm{{hERG}}}=0.4$ nS/pF (b) and bursting activity for $g_{\mathrm{{hERG}}}=0.16$ nS/pF (c)

3.2 Geometric singular perturbation theory

The characteristic time constant for the V equation in (15) is the reciprocal of the maximal conductance normalized to cell capacitance, i.e.,

$$\begin{aligned} \tau _V = 1/\max \{g_X\} = 1/g_{Na} = 2.5 \text { ms.} \end{aligned}$$

(16)

We conclude that V is the fastest variable and, after scaling of time, rewrite the system in the form studied in Section 2, with $\tilde{t} = t/\tau _m$, $\epsilon =1/(g_{Na}\tau _m)=0.025$ and $\tilde{I}=I/g_{Na}$,

$$\begin{aligned} \begin{aligned} \epsilon \frac{\mathrm{d}V}{\mathrm{d}\tilde{t}}&= - \tilde{I}_{\mathrm{{Total}}}\left( V,h,m\right) =: f(V,h,m)\, ,\\ \frac{\mathrm{d}h}{\mathrm{d}\tilde{t}}&= \frac{\tau _m}{\tau _h}({h_\infty (V)-h}) =: g_1(V,h)\, ,\\ \frac{\mathrm{d}m}{\mathrm{d}\tilde{t}}&= {m_\infty (V)-m} =: g_2(V,m). \end{aligned} \end{aligned}$$

(17)

This allows us to apply GSPT to our 3d-model to understand the mechanism organizing pseudo-plateau bursting, which is observed for example with $g_{\mathrm{{hERG}}}=0.16$ nS/pF (Fig. 4).

We remark that $g_2$ (respectively $g_1$) does not depend on h (respectively m) and that the dependence on m (respectively h) is linear. In addition, f is linear with respect to both h and m, and has the form

$$\begin{aligned} f(V) = A(V) - m\, g_{hERG}\,B(V) - h\, C(V) \end{aligned}$$

(18)

for appropriate functions A, B, C. Note that the form (18) is rather general for Hodgkin–Huxley-type, conductance-based models.

It follows from the above that when we solve $f=0$ in order to calculate the folded surface S defined in (5), we can find m as an explicit function of V and h, i.e.,

$$\begin{aligned} m = \phi \left( V,h \right) := \frac{A(V)-h\, C(V)}{ g_{\mathrm{{hERG}}}\,B(V)}. \end{aligned}$$

(19)

Fold curves are obtained by asking $f_V=0$, which yields

$$\begin{aligned} h=\psi \left( V \right) := \frac{A'(V) B(V) - A(V) B'(V)}{B(V) C'(V) - B'(V)C(V)}, \end{aligned}$$

(20)

after imposing (19). Note that the fold curve does not depend on $g_{hERG}$.

We proceed with the analysis by studying system (17) in the limit case when $\epsilon \rightarrow 0$. We project the system onto the critical manifold, described by the (V, h) coordinates, and find the slow desingularized problem of the form of (9),

$$\begin{aligned} \begin{aligned} \dot{V}&= f_h g_1 + f_m g_2, \\ \dot{h}&= - f_V g_1, \end{aligned} \end{aligned}$$

(21)

evaluated at $m=\phi (V,h)$. Using (17), (18) and (19) this system becomes

$$\begin{aligned} \begin{aligned} \dot{V}&= - \frac{\tau _m}{\tau _h}C(V)(h_{\infty }(V)-h) \\&\quad - \big ({g_{hERG}\,B(V)\, m_{\infty }(V) - (A(V)-h\,C(V)\big )},\\ \dot{h}&= - \frac{\tau _m}{\tau _h}({h_{\infty }(V)-h})\\&\quad \times \big (A'(V) - \frac{A(V)-h\,C(V)}{B(V)} B'(V) - h\, C'(V)\big ) . \end{aligned} \end{aligned}$$

(22)

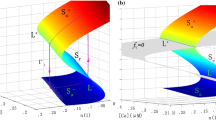
We analyzed this system by performing symbolic calculations in Mathematica (Wolfram Research, Inc., version 12.1.1.0). The resulting expressions were then evaluated numerically. For standard parameters and $g_{hERG}=0.16$ nS/pF, the desingularized system (22) has three equilibria at points where $\dot{V} = 0$ and at least one of $f_V$ and $g_1$ is vanishing. Two of these are plotted in Fig. 5, while the third one is out of the range of $h \in (0,1)$; this latter is a folded focus, and hence it is of no interest for the analysis of canards [9] and for the dynamics of the system.

The other two equilibria of the desingularized system are an attractive folded node and a saddle. The saddle is a real equilibrium of system (17) since it is not on the fold and $g_1 = 0$ (and $g_2 = 0$ as well, see Section 2). On the other hand, the attractive folded node lies on one of the fold curves and therefore represents the point where the canard trajectories go from the attractive manifold $S_a$ to the repelling one $S_r$ (see Fig. 5). The singular canards and the consequent funnel (shadowed gray region) limited by the strong singular canard and the fold curve on the attractive manifold $S_a$ are shown in Fig. 5, together with the simulation previously computed in Fig. 4, projected onto the 2d-plane $(V,h_{CaL})$. The trajectory enters the funnel and starts oscillating around the weak singular canard passing through the folded node. The system is attracted towards the saddle equilibrium and is then, after a few oscillations, pushed away from the saddle in the unstable eigendirection. Finally the global return mechanism yields a LAO and permits the system to repeat the cycle.

Fig. 5

Analysis of the desingularized system and simulations of the 3d model using default parameters, and $g_{hERG} = 0.16$ nS/pF. Fold curves are plotted in green, and the attracting and repelling sheets are indicated by $S_a$ and $S_r$, respectively. The blue point indicates the folded node while the red one is the ordinary saddle equilibrium. The eigenvector directions of the two singularities are plotted with the corresponding colors, and using dashed thick and dotted lines for the strong and weak eigenvectors, respectively. In particular, the strong ($\tilde{\gamma }_s$) and weak ($\tilde{\gamma }_w$) singular canards correspond to the blue dashed thick and dotted lines, respectively. The funnel of the folded node is indicated by the shaded grey region. The projection of the simulation of the 3d model is shown by the black curve

3.2.1 Maximal Canards

We now go into greater details for the study of the system for $\epsilon >0$. Recall that $S_a$ and $S_r$ are perturbed to attractive and repelling slow manifolds $S_{a,\epsilon }$ and $S_{r,\epsilon }$, and that maximal canards appear in the vicinity of the folded node as the intersections of $S_{a,\epsilon }$ and $S_{r,\epsilon }$. Further, secondary canards split the funnel—more precisely they split the sector of secondary canards—into subsectors. When the solution of the system enters the funnel, it enters in one of these specific subsectors, which are determined by the primary and secondary maximal canards.

Fig. 6

A: Portions of the slow attracting ($S_{a,\epsilon }$, red) and repelling ($S_{r,\epsilon }$, blue) manifolds for $g_{hERG}=0.16$ nS/pF with superimposed maximal canards ($\gamma _1$ in green and $\gamma _2$ in magenta) and the $1^2$ MMO solution of the 3d-model from Fig. 4 (black) superimposed. B: As panel A, but for $g_{hERG}=0.18$ nS/pF with $1^1$ MMOs. C: The intersection of the structures in panel A with the plane defined by $m=0.35$. The red and blue curves represent the intersection with $S_{a,\epsilon }$ and $S_{r,\epsilon }$, respectively. Maximal canards correspond to the crossings of the two curves. The strong canard $\gamma _s$ (cyan square) is highlighted in addition to $\gamma _1$ (green triangle) and $\gamma _2$ (magenta downward-pointing triangle). The black cross indicates the point where the $1^2$ MMO solution of the 3d-model intersects the plane defined by $m=0.35$ in the fold region. D: As panel C, but for $g_{hERG}=0.18$ nS/pF

We find $S_{a,\epsilon }$ (respectively $S_{r,\epsilon }$) by evolving the 3d-model forward (respectively backward) in time starting from points of a line on $S_a$ (respectively $S_r$) at some distance from the fold. Such points are $\epsilon$-close to the slow manifold, and are rapidly attracted to $S_{a,\epsilon }$ (respectively $S_{r,\epsilon }$) in forward (respectively backward) time. Our approach can be seen as a simplified alternative to finding the intersections of the slow manifolds by defining an appropriate Boundary Value Problem [8].

Figure 6A shows these geometric structures for $g_{hERG}=0.16$ nS/pF, corresponding to the dynamics simulated in Fig. 4. As predicted by the theory, $S_{a,\epsilon }$ and $S_{r,\epsilon }$ are twisted and intersect in twisting curves (maximal canards). This fact is more clearly seen when plotting the intersection between $S_{a,\epsilon }$, respectively $S_{r,\epsilon }$, and a plane defined by m being constant (Fig. 6C). These intersections define two curves in the plane, and their crossings correspond to the maximal canards. The solution to the 3d-model (black) enters the region near the folded node along the attracting sheet in the section between the first ($\gamma _1$) and the second ($\gamma _2$) secondary canards, and hence perform two SAOs before leaving the fold region. The return mechanism, which yields a large amplitude oscillation, then reinjects the system into the funnel and the dynamics is repeated, resulting in $1^2$ mixed-mode oscillations. In contrast, for $g_{hERG}=0.18$ nS/pF, the return mechanism injects the system into the section between the strong canard $\gamma _s$ and first secondary canard $\gamma _1$ (Fig. 6BD). Therefore the system performs only one SAO during the passage through the fold region and thus exhibits $1^1$ MMOs.

3.3 Bifurcations

We now aim to understand how changes in $g_{\mathrm{{hERG}}}$ lead to different dynamical patterns. The relation between $g_{\mathrm{{hERG}}}$ and the folded singularity can be found from imposing $\dot{V}=0$ in (22) with $h(V)=\Psi (V)$ and solving for $g_{hERG}$. Similarly, the curve of the full system equilibrium is found by isolating $g_{hERG}$ from $\frac{\mathrm{d}V}{\mathrm{d}\tilde{t}}=0$ in (17) with $m=m_{\infty }(V)$ and $h=h_{\infty }(V)$, i.e., by solving $\phi (V,h_{\infty }(V))=m_{\infty }(V)$. As shown in Fig. 7 these curve intersect at approximately $(0.06 \text { nS/pF},$-25.3$\text { mV})$, and thus a folded saddle-node (FSN) of type II [9] is present at these values. For all other values of $g_{hERG}$, the folded singularity is a saddle. For $g_{\mathrm{{hERG}}}<0.06$ nS/pF, the full system equilibrium is stable, corresponding to a permanently depolarized state, and located on the attracting sheet of the slow manifold.

Fig. 7

Overview of the behavior of the 3d-model when $g_{\mathrm{{hERG}}}$ changes. Panel A: For low values of $g_{\mathrm{{hERG}}}$ the model has stable equilibriums indicated by the full curve. At $g_{\mathrm{{hERG}}}\approx 0.11$ nS/pF the system undergoes a supercritical Hopf bifurcation (HB) and the equilibrium becomes an unstable saddle-focus (dotted curve). The dash-dotted line indicates the location of the folded node. This curve intersects the branch of equilibriums at $g_{\mathrm{{hERG}}}\approx 0.06$ nS/pF where a folded saddle-node (FSN) of type II is present, as shown in the upper inset (corresponding to the gray horizontal strip in the main figure). The blue points show maxima and minima for the attractive orbits originating from the HB. The stable limit cycle born in the HB undergoes a period-doubling (PD) cascade to chaos as shown in the lower inset (corresponding to the gray vertical strip in the main figure). At $g_{\mathrm{{hERG}}}\approx 0.1537$ nS/pF, an abrupt transition to MMOs occurs, as indicated by the gap in the diagram in the lower inset (red triangle). Following transitions through windows of apparent chaotic behavior, regular $1^2$ and $1^1$ MMOs are present for large intervals of $g_{\mathrm{{hERG}}}$, as indicated, until only $1^0$ large-scale oscillations corresponding to spiking appear for $g_{\mathrm{{hERG}}}>0.21$ nS/pF. Panel B shows the maximum number of SAOs calculated from (23) as a function of $g_{\mathrm{{hERG}}}$

It is known that a singular Hopf Bifurcation is often occurring near FSN of type II [9, 12]. Indeed, by calculating the eigenvalues of the full-system equilibriums, we find a Hopf bifurcation (HB) at $g_{hERG}=0.1095$ nS/pF. This HB is supercritical. We performed a scan over a range of $g_{hERG}$ values to follow the limit cycle born in the HB. Fig. 7 shows the numerically calculated maximum and minimum values. We see that the system goes through a period-doubling cascade as $g_{hERG}$ increases, entering chaos, which is interrupted at $g_{hERG}\approx 0.1537$ nS/pF where a sharp transition of the lowest minimum occurs. This bifurcation, which leads to MMOs, is most likely due to the intersection of the unstable manifold of the saddle-focus and the repelling sheet of the slow manifold [12, 21].

Fig. 8

The analysis for the 3d-model provides insight into the 7D-model. A simulated orbit (black) of the 7d-model (from Fig. 1) is projected onto $(V, h_{\mathrm{{Ca}}}, m_{\mathrm{{hERG}}})$ space and compared to the geometric structures found for the analysis of the 3d-model with $g_{\mathrm{{hERG}}} = 0.16$ nS/pF: The critical manifold composed of the attracting ($S_a$) and repelling ($S_r$) sheets separated by the fold curves (green curve) is shown with the folded node (blue point) and the saddle (red). The computed orbit shows small oscillations starting near the folded node that spiral around the weak singular canard (blue line) before escaping towards the other fold curve. A relaxation-like return mechanism takes the system back to the attracting sheet $S_a$, yielding the first peak seen in the simulation in Fig. 1. $S_a$ is then followed towards the upper fold and the events repeat.

As $g_{\mathrm{{hERG}}}$ increases further, the MMOs become regular $1^2$ oscillations, followed by a transition to $1^1$ MMOs, and finally regular $1^0$ spiking with no SAOs, as indicated in Fig. 7. These transitions can be understood from the return mechanism re-injecting the system into different sectors of the folded-node funnel (see Section 3.2.1 and Fig. 6 regarding $g_{\mathrm{{hERG}}}=0.16$ nS/pF versus $g_{\mathrm{{hERG}}}=0.18$ nS/pF) until it misses the funnel and relaxation-type spiking oscillations appear. Thus, as $g_{hERG}$ increases, the SAO-generating mechanism shifts from being based on dynamics associated with the singular HB to being organized by canards and the twisted slow manifolds around the folded node. In addition, the maximal number of canard-induced SAOs, which can be calculated from the ratio $\mu$ of the eigenvalues of the folded node as [6, 9]

$$\begin{aligned} \mathrm{{SAO}}_{\mathrm{{max}}} = \left\lfloor \frac{\mu - 1}{2} \right\rfloor , \end{aligned}$$

(23)

where $\lfloor \, \cdot \, \rfloor$ denotes the floor function, decreases as $g_{\mathrm{{hERG}}}$ increases (Fig. 7, lower panel).

4 Discussion

Bursting electrical activity has been proposed to evoke more hormone release than simple action potential firing by increasing the influx of calcium [24, 32, 35], and it is therefore important to understand the mechanisms that drive this kind of electrical behaviour. Pseudo-plateau bursting, as observed in human beta-cells [2, 5, 19, 27] and reproduced by the mathematical model studied here [23], can be seen as MMO dynamics and thus studied with the theory of folded singularities as done in this work.

To perform the mathematical analysis we performed a series of approximations to reduce the system to a 3d-model, which exhibited the same kind of qualitative patterns as the 7d-model. It is natural to ask whether the analysis performed for the 3d-model can be lifted back to the original model. Indeed, as shown in Fig. 8, the simulated dynamics of the 7d-model appears to be organized by the structure found for the 3d-model. When projected onto the $(V, h_{Ca}, m_{hERG})$ space, the 7d-system approaches the folded node found for the 3d-model and performs SAO around the weak canard. It then approaches the saddle point located on the repelling sheet before spiralling away. A global return mechanism takes the orbit back to the attracting sheet and the cycle is repeated.

In simulations of the original model [23], as well as in the reduced 3D-model presented here, qualitative changes from spiking to bursting to silent electrical behavior are seen as the hERG conductance $g_{\mathrm{{hERG}}}$ is reduced (Figs. 1 and 4). The same kind of qualitative changes can be seen for other modifications to the parameters of the potassium currents in the model [23]. Based on the analysis performed here, we propose that these changes can be understood as follows. Starting from a permanently depolarized state, increasing (hyperpolarizing) potassium current moves the equilibrium from the attracting to the repelling sheet of the slow manifold, passing through a FSN of type II. As the potassium conductance, here $g_{hERG}$, increases further, the depolarized equilibrium loses stability in a singular Hopf bifurcation. Following intervals with regular and chaotic oscillations, bursting in the form of MMOs appear when the chaotic attractor is destroyed when the unstable manifold of the saddle-focus and the repelling sheet of the slow manifold intersect. As the potassium conductance increases further the MMOs are organized mainly by the folded node, and when the return mechanism no longer inject the orbit into the funnel of the folded node, relaxation-type spiking oscillations appear. Eventually, the equilibrium moves to the other attracting sheet of the slow manifold and the system becomes stable and hyperpolarized.

Although our analysis of the 3D model appears to capture the dynamics of the 7D model satisfactorily, some discrepancies may be observed. For example, the 7D model may exhibit $1^3$ MMOs (Fig. 1), which were not observed in the 3D model when scanning through different $g_{\mathrm{{hERG}}}$ values (Fig. 7). This is likely due to the model simplifications. Indeed, the approximation (14) is not very accurate, and misses for example the final oscillation of the active phase at $(h_{\mathrm{{CaL}}},m_{\mathrm{{KV}}})\approx (0.4, 0.14)$, see Fig. 3. Future studies could analyze the 4d model $(V,h_{\mathrm{{CaL}}},m_{\mathrm{{KV}}}, m_{\mathrm{{hERG}}})$ as a 1 fast – 3 slow variable system. Concerning the 3D model, it may be seen as a three timescale problem [16], in particular in case the time-constant for $m_{\mathrm{{hERG}}}$ is increased compared to the (biophysically realistic) value used here. Such an analysis is left for future work.

Concluding, we have shown an example of how advanced mathematical analysis based on geometric singular perturbation theory can provide insight into a complex but biologically realistic mathematical models of electrical activity underlying insulin release in humans.