Morrey’s Conjecture for the Planar Volumetric-Isochoric Split: Least Rank-One Convex Energy Functions

Abstract

We consider Morrey’s open question whether rank-one convexity already implies quasiconvexity in the planar case. For some specific families of energies, there are precise conditions known under which rank-one convexity even implies polyconvexity. We will extend some of these findings to the more general family of energies $W{:}{\text {GL}}^+(n)\rightarrow \mathbb {R}$ with an additive volumetric-isochoric split, i.e.

$$\begin{aligned} W(F)=W_{\mathrm{iso}}(F)+W_{\mathrm{vol}}(\det F)={\widetilde{W}}_{\mathrm{iso}}\bigg (\frac{F}{\sqrt{\det F}}\bigg )+W_{\mathrm{vol}}(\det F)\,, \end{aligned}$$

which is the natural finite extension of isotropic linear elasticity. Our approach is based on a condition for rank-one convexity which was recently derived from the classical two-dimensional criterion by Knowles and Sternberg and consists of a family of one-dimensional coupled differential inequalities. We identify a number of “least” rank-one convex energies and, in particular, show that for planar volumetric-isochorically split energies with a concave volumetric part, the question of whether rank-one convexity implies quasiconvexity can be reduced to the open question of whether the rank-one convex energy function

$$\begin{aligned} W_{\mathrm{magic}}^{+}(F)=\frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}-\log \frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}+\log \det F=\frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}+2\log \lambda _{\mathrm{min}} \end{aligned}$$

is quasiconvex. In addition, we demonstrate that under affine boundary conditions, $W_{\mathrm{magic}}^+(F)$ allows for non-trivial inhomogeneous deformations with the same energy level as the homogeneous solution, and show a surprising connection to the work of Burkholder and Iwaniec in the field of complex analysis.

1 Introduction

One of the major open problems in the calculus of variations is Morrey’s problem in the planar case. The open question is whether or not rank-one convexity implies quasiconvexity. Morrey (1952, 2009) conjectured that this is not the case in general and indeed the result by Šverák (1992b) settles the question for the case $n\ge 3$. On the other hand, in the one-dimensional case, all four notions of convexity are equivalent. For the last nearly thirty years, impressive progress on the problem has been made (Kawohl and Sweers 1990; Harris et al. 2018; Faraco and Szekelyhidi 2008; Pedregal and Sverak 1998; Sebestyen and Szekelyhidi 2015; Müller 1999) without, however, leading to a full solution. While researchers coming from the area of nonlinear elasticity in general seem to believe that Morrey’s conjecture is true also in the planar case, i.e. that rank-one convexity does not imply quasiconvexity, researchers with a background in conformal and quasiconformal analysis (Astala et al. 2008) tend to believe in the truth of the opposite implication (Iwaniec 1982). In conformal analysis, this conclusion would imply a number of far-reaching conjectures which are themselves deemed reasonable at present.

Nonlinear elasticity is concerned with energies W defined on the group of matrices with positive determinant ${{\,\mathrm{GL}\,}}^{\!+}(n)=\left\{ F\in \mathbb {R}^{n\times n}|\det F>0\right\}$, while the general case of Morrey’s question considers scalar functions W defined on the linear space $\mathbb {R}^{n\times n}$. It is conceivable that the answer to the planar Morrey’s conjecture depends on whether one focuses on ${{\,\mathrm{GL}\,}}^{\!+}(2)$ or $\mathbb {R}^{2\times 2}$. Assuming that an example for Morrey’s conjecture in ${{\,\mathrm{GL}\,}}^{\!+}(2)$ can be found, it is also not immediately clear how such an example might be generalized to the $\mathbb {R}^{2\times 2}$-case (although it is tempting to believe that this is always possible). The precise statement of Morrey’s conjecture also depends on the invariance properties one requires for the energy W and the domain of definition. Different versions of Morrey’s conjecture include the following, all of which currently remain open:

• Morrey I: Let $W:\mathbb {R}^{n\times n}\rightarrow \mathbb {R}$ (with no further invariance requirement). If W is rank-one convex, then W is not necessarily quasiconvex. For $n\ge 3$ (W being continuous), this statement on the class of all real-valued functions as originally considered by Morrey (1952) has been conclusively settled by Sverak’s famous counterexample (Šverák 1992b).

• Morrey II: Let $W:\mathbb {R}^{2\times 2}\rightarrow \mathbb {R}$ be continuous and left/right-${{\,\mathrm{SO}\,}}(2)$ invariant (objective and hemitropic). If W is rank-one convex, then W is not necessarily quasiconvex.

• Morrey III: Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ be left-${{\,\mathrm{SO}\,}}(2)$ invariant (objective, frame-indifferent) and right-${{\,\mathrm{O}\,}}(2)$ invariant (isotropic). If W is rank-one convex, then W is not necessarily quasiconvex.

• Morrey IV: Let $W:\mathbb {R}^{2\times 2}\rightarrow \mathbb {R}$ be left-${{\,\mathrm{SO}\,}}(2)$ invariant (objective, frame-indifferent) and right-${{\,\mathrm{O}\,}}(2)$ invariant (isotropic). If W is rank-one convex, then W is not necessarily quasiconvex.

• Morrey V: Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ and $W(F)\rightarrow \infty$ as $\det F\rightarrow 0$ be left/right-${{\,\mathrm{SO}\,}}(2)$ invariant (objective and hemitropic). If W is rank-one convex, then W is not necessarily quasiconvex.

Astala et al. (2012) and their groups try to disprove Morrey II to prove various conjectures in the context of complex analysis. It is conceivable, however, that Morrey II is false, while Morrey III is true. Similarly, Morrey III may also be false with Morrey II being true. There is no clear connection between the two statements: in Morrey III the domain of definition is smaller, but then rank-one convexity needs only to hold true on a smaller set as compared to Morrey II. The role of invariance requirements (isotropic versus hemitropic) or general anisotropy is also open.

The restriction to ${{\,\mathrm{GL}\,}}^{\!+}(2)$ and isotropy in Morrey III is advantageous because the check of rank-one convexity can be based on a version of Knowles/Sternberg conditions (Knowles and Sternberg 1976, 1978) operating only on the representation of the elastic energy in terms of singular values. The rank-one convexity condition on $\mathbb {R}^{2\times 2}$ was also completely settled by Hamburger (1987), Aubert (1995). Nevertheless, it seems that one has to choose a favourable representation first and then use an adapted criterion. Quasiconvexity on the other hand is notoriously difficult to prove or disprove. A straightforward sufficient condition is Sir John Ball’s polyconvexity condition (Ball 1976). One of the advantages of polyconvexity is that it is both suitable for ${{\,\mathrm{GL}\,}}^{\!+}(2)$ and $\mathbb {R}^{2\times 2}$ and that there are sharp characterizations of polyconvexity in the ${{\,\mathrm{GL}\,}}^{\!+}(2)$ and isotropic case (Dacorogna 2008; Šilhavý 1997; Mielke 2005).

Apparently, even for $n\ge 3$, there is no isotropic example to Morrey I to be found in the literature. A common method to approach Morrey’s conjecture is to discuss a specific family of energies, e.g. purely volumetric or isochoric energies (cf. Sects. 2.1 and 2.2), to find an often simple relation between the different notions of convexity. We will extend these findings to a much more involved class of energies with an additive volumetric-isochoric split (2.1) and follow the concept of “least” rank-one convex energies, i.e. functions that are as weakly rank-one convex as possible, to serve as canonical candidates. Focusing on energies with a concave volumetric part we show that the rank-one convex function

$$\begin{aligned} W_{\mathrm{magic}}^+(F)= & {} \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}-\log \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}+\log \det F\nonumber \\= & {} \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}+2 \log \lambda _{\hbox {min}}\end{aligned}$$

with $\lambda _{\hbox {max}}\ge \lambda _{\hbox {min}}>0$ as the ordered singular values of the deformation gradient $F=\nabla \varphi$ suffices as the sole candidate for this class of functions. The question of quasiconvexity for $W_{\text {magic}}^+(F)$ closes Morrey’s conjecture for all volumetric-isochorically split energies with a concave volumetric part, cf. Theorem 4.1, giving the following alternatives:

• If $W_{\text {magic}}^+$ is not quasiconvex, then Morrey’s conjecture III is true.

• If $W_{\text {magic}}^+$ is quasiconvex, then no example of Morrey’s conjecture III can be found in the class of volumetric-isochoric split energies with a concave volumetric part, i.e. in this class, rank-one convexity equals quasiconvexity.¹

In a sequel of this work (Voss et al. 2021a) we will numerically investigate the quasiconvexity of $W_{\text {magic}}^+(F)$.

1.1 Basic Definitions of Convexity Properties

Definition 1.1

The energy function $W:\mathbb {R}^{n\times n}\rightarrow \mathbb {R}\cup \{+\infty \}$ is quasiconvex if and only if

$$\begin{aligned}&\int _\Omega W(F_0+\nabla \vartheta (x))\,{\text {d}x}\ge \int _\Omega W(F_0)\,{\text {d}x}=|\Omega |\cdot W(F_0)\nonumber \\&\quad \text {for all }F_0\in \mathbb {R}^{n\times n},\;\vartheta \subset W_0^{1,\infty }(\Omega ;\mathbb {R}^n) \end{aligned}$$

(1.1)

for any domain $\Omega \subset \mathbb {R}^n$ with Lebesgue measure $|\Omega |$. The energy is strictly quasiconvex if inequality (1.1) is strict.

While quasiconvexity is sufficient to ensure weak lower semi-continuity of the energy functional, it has the simple disadvantage of being almost impossible to prove or disprove. This led to the introduction of sufficient and necessary conditions for quasiconvexity.

Definition 1.2

The energy function $W:\mathbb {R}^{n\times n}\rightarrow \mathbb {R}\cup \{+\infty \}$ is polyconvex if and only if there exists a convex function $P:\mathbb {R}^{m(n)}\rightarrow \mathbb {R}\cup \{+\infty \}$ with

$$\begin{aligned} W(F)=P\big (F,{{\,\mathrm{adj}\,}}_2(F),\cdots ,{{\,\mathrm{adj}\,}}_n(F)\big )\qquad \text {for all}\quad F\in \mathbb {R}^{n\times n} \end{aligned}$$

(1.2)

with ${{\,\mathrm{adj}\,}}_i(F)\in \mathbb {R}^{n\times n}$ as the matrix of the determinants of all $i\times i-$minors of F and $m(n) :=\sum _{i=1}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) ^2$. The energy is strictly polyconvex if there exists a representation P which is strictly convex.

In particular, for the planar case $n=2$, the energy $W:\mathbb {R}^{2\times 2}\rightarrow \mathbb {R}\cup \{+\infty \}$ is polyconvex if and only if there exists a convex mapping $P:\mathbb {R}^{2\times 2}\times \mathbb {R}\cong \mathbb {R}^5\rightarrow \mathbb {R}\cup \{+\infty \}$ with

$$\begin{aligned} W(F)=P(F,\det F)\qquad \text {for all}\quad F\in \mathbb {R}^{2\times 2}\,. \end{aligned}$$

Whereas polyconvexity provides a sufficient criterion for quasiconvexity, rank-one convexity is introduced as a necessary condition.

Definition 1.3

The energy $W:\mathbb {R}^{n\times n}\rightarrow \mathbb {R}\cup \{+\infty \}$ is rank-one convex if and only if

$$\begin{aligned}&W(t \, F_1+(1-t)\,F_2)\le t\,W(F_1)+(1-t)\,W(F_2)\qquad \text {for}\nonumber \\&{{\,\mathrm{rank}\,}}(F_1-F_2)=1\,,\quad t\in (0,1)\, \end{aligned}$$

(1.3)

If the energy is two times differentiable, global rank-one convexity is equivalent to the Legendre–Hadamard ellipticity condition

$$\begin{aligned} D^2W(F).(\xi \otimes \eta ,\xi \otimes \eta )\ge 0 \qquad \text {for all}\quad F\in \mathbb {R}^{n\times n},\;\xi ,\eta \in \mathbb {R}^n \end{aligned}$$

(1.4)

which expresses the ellipticity of the Euler–Lagrange equations ${{\,\mathrm{Div}\,}}DW(\nabla \varphi )=0$ associated to the variational problem

$$\begin{aligned} I(\varphi )=\int _\Omega W(\nabla \varphi (x))\,{\text {d}x}\rightarrow \min \, \end{aligned}$$

(1.5)

The energy is strictly rank-one convex if inequality (1.3) is strict.

Overall, for any $W:\mathbb {R}^{n\times n}\rightarrow \mathbb {R}\cup \{+\infty \}$ we have the well known hierarchy (Ball 1976; Dacorogna 2008)

$$\begin{aligned} \text {polyconvexity}\quad \implies \quad \text {quasiconvexity}\quad \implies \quad \text {rank-one convexity}. \end{aligned}$$

(1.6)

In nonlinear elasticity theory, energy functions are more naturally defined on ${{\,\mathrm{GL}\,}}^{\!+}(n)$ instead of $\mathbb {R}^{n\times n}$, since a non-positive determinant of the deformation gradient $F=\nabla \varphi$ would correspond either to an infinite compression ($\det F=0$) or to a change of orientation ($\det F<0$) within the modelled physical body, both of which are deemed mechanically implausible.

Definition 1.4

A function $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow \mathbb {R}$ is called quasi-/poly-/rank-one convex if the function

$$\begin{aligned} {\widehat{W}}:\mathbb {R}^{n\times n}\rightarrow \mathbb {R}\cup \{+\infty \}\,,\quad {\widehat{W}}(F)={\left\{ \begin{array}{ll} W(F) &{}\text {if }\;F\in {{\,\mathrm{GL}\,}}^{\!+}(n)\,,\\ +\infty &{}\text {if }\;F\notin {{\,\mathrm{GL}\,}}^{\!+}(n)\,, \end{array}\right. } \end{aligned}$$

is quasi-/poly-/rank-one convex. A function $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow \mathbb {R}$ is called convex if there exists a convex function ${\widehat{W}}:\mathbb {R}^{n\times n}\rightarrow \mathbb {R}$ such that ${\widehat{W}}(F)=W(F)$ for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$.

2 The Additive Volumetric-Isochoric Split

Next, we discuss the general family of planar energies $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}\cup \{\infty \}$ with additive combinations of conformally invariant (isochoric) energies on the one hand, and area-dependent (volumetric) energies (also called the additive volumetric-isochoric split) on the other hand:

$$\begin{aligned} W(F)=W_{\text {iso}}(F)+W_{\text {vol}}(\det F)=\underbrace{{\widetilde{W}}_\text {iso}\bigg (\frac{F}{\sqrt{\det F}}\bigg )}_{{\text {conformally invariant}}}+\underbrace{W_{\text {vol}}(\det F)}_{\quad {\text {purely area-dependent in 2D}}}. \end{aligned}$$

(2.1)

It is already known that for purely isochoric energies (cf. Sect. 2.2) as well as purely volumetric energies (cf. Sect. 2.1) rank-one convexity already implies polyconvexity (and thereby quasiconvexity). Thus, it is suggestive to inquire whether the same conclusion can be reached for additive combinations or not.

The additive volumetric-isochoric split itself is a natural finite extension of isotropic linear elasticity, i.e.

$$\begin{aligned} W_\text {lin}(\nabla u)&=\mu \Vert {{\,\mathrm{sym}\,}}\nabla u \Vert ^{2} +\frac{\lambda }{2}({{\,\mathrm{tr}\,}}\nabla u)^{2}=\mu \Vert {{\,\mathrm{dev}\,}}_{n}{{\,\mathrm{sym}\,}}\nabla u \Vert ^{2} +\frac{\kappa }{2}({{\,\mathrm{tr}\,}}\nabla u)^{2}\,,\nonumber \\ \sigma ^\text {lin}&=DW_\text {lin}(\nabla u)=2\mu \,{{\,\mathrm{dev}\,}}_{n}{{\,\mathrm{sym}\,}}\nabla u+\kappa \,{{\,\mathrm{tr}\,}}(\nabla u)\,\mathbb {1}. \end{aligned}$$

(2.2)

The right-hand side of the energy is automatically additively separated into pure infinitesimal shape change and infinitesimal volume change of the displacement gradient $\nabla u$, with a similar additive split of the linear Cauchy stress tensor into a deviatoric part and a spherical part, depending only on the shape change and volumetric change, respectively.

This type of energy functions is often used for modeling slightly incompressible material behaviour (Ciarlet 1988; Hartmann and Neff 2003; Favrie et al. 2014; Ogden 1978; Charrier et al. 1988) or when otherwise no detailed information on the actual response of the material is available (Simo 1988; Gavrilyuk et al. 2016; Ndanou et al. 2017). In the nonlinear regime, this split is not a fundamental law of nature for isotropic bodies (as it is in the linear case) but rather introduces a convenient form of the representation of the energy. Formally, this split can also be generalized to the anisotropic case, where it shows, however, some severe deficiencies (Federico 2010; Murphy and Rogerson 2018) from a modeling point of view.²

A primary application of the volumetric-isochoric split is the adaptation of incompressible hyperelastic models to (slightly) compressible materials in arbitrary dimension $n\ge 2$: For any given isotropic function³$W_{\text {inc}}:{{\,\mathrm{SL}\,}}(n)\rightarrow \mathbb {R}$, an elastic energy potential W of the form (2.1) can be constructed by simply setting

$$\begin{aligned} W(F) = W_{\text {inc}}\biggl (\frac{F}{\root n \of {\det F}}\biggr ) + f(\det F) = W_{\text {inc}}\big ({\widehat{I}}_1,\dotsc ,{\widehat{I}}_{n-1}\big ) + f(\det F) \end{aligned}$$

with an appropriate function $f:\mathbb {R}_+\rightarrow \mathbb {R}$, where ${\widehat{I}}_1,\dotsc ,{\widehat{I}}_{n-1}$ denote the principal invariants of $\frac{F}{\root n \of {\det F}}$. Common examples of such energy functions include the compressible Neo-Hooke and the compressible Mooney–Rivlin model (Ogden 1983).

A typical example of the volumetric-isochoric format is the geometrically nonlinear quadratic Hencky energy (Neff et al. 2016; Hencky 1928; Sendova and Walton 2005; Martin et al. 2019)

$$\begin{aligned} W_{\mathrm{H}}(F)&=\mu \Vert {{\,\mathrm{dev}\,}}_n\log V \Vert ^2+\frac{\kappa }{2}\left( {{\,\mathrm{tr}\,}}\log V\right) ^2,\qquad V=\sqrt{FF^T},\nonumber \\ \tau _{\mathrm{H}}&=2\mu {{\,\mathrm{dev}\,}}_n\log V+\kappa {{\,\mathrm{tr}\,}}(\log V)\cdot \mathbb {1}=2\mu \log \frac{V}{\root 3 \of {\det V}}+\kappa \log \det F\cdot \mathbb {1}\end{aligned}$$

(2.3)

as well as its physically nonlinear extension, the exponentiated Hencky-model (Neff et al. 2015a; Neff and Ghiba 2016)

$$\begin{aligned} W_{\mathrm{eH}}&=\frac{\mu }{k}e^{k\Vert {{\,\mathrm{dev}\,}}_n\log V \Vert ^2}+\frac{\kappa }{2{\widehat{k}}}e^{{\widehat{k}}\left( {{\,\mathrm{tr}\,}}\log V\right) ^2}\,,\nonumber \\ \tau _{\mathrm{eH}}&=2\mu e^{k\Vert {{\,\mathrm{dev}\,}}_n\log \,V\Vert ^2}\cdot {{\,\mathrm{dev}\,}}_n\log V+\underbrace{\kappa e^{{\widehat{k}}\left( {{\,\mathrm{tr}\,}}\log V\right) ^2}{{\,\mathrm{tr}\,}}(\log V)\cdot \mathbb {1}}_{=\kappa e^{{\widehat{k}}\left( \log \det F\right) ^2}\log \det F\cdot \mathbb {1}}\,, \end{aligned}$$

(2.4)

which has been used for stable computation of the inversion of tubes (Nedjar et al. 2018), the modeling of tire-derived material (Montella et al. 2016) or applications in bio-mechanics (Schroder et al. 2018). It is well known that (2.3) and (2.4) are overall not rank-one convex (Neff et al. 2015a) and indeed there does not exist any elastic energy depending on $\Vert {{\,\mathrm{dev}\,}}_n\log V \Vert ^2$, $n\ge 3$ that is rank-one convex (Ghiba et al. 2015a). The situation is, surprisingly, completely different in the planar case: For $n=2$, the energy in Eq. (2.4) is not only rank-one convex, but even polyconvex (Neff et al. 2015b; Ghiba et al. 2015b) if $k\ge \frac{1}{8}$.

2.1 Purely Volumetric Energies

For some types of energies $W:\mathbb {R}^{2\times 2}\rightarrow \mathbb {R}$, precise conditions are known under which rank-one convexity implies polyconvexity and therefore quasiconvexity (Müller 1999; Ball 2002). One specific family of energies for which the relation between rank-one convexity and polyconvexity is already known is that of purely volumetric energies $W(F)=f(\det F)$. This class describes fluid-like material behaviour, i.e. shape change is not penalized at all.

Lemma 2.1

(Dacorogna (2008)) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ be of the form $W(F)=f(\det F)$ with $f:\mathbb {R}_+\rightarrow \mathbb {R}$. The following are equivalent:

• (i) W is polyconvex,

• (ii) W is quasiconvex,

• (iii) W is rank-one convex,

• (iv) f is convex on $(0,\infty )$.

The same holds for the so-called Hadamard material (Dacorogna 2008; Ball and Murat 1984; Grabovsky and Truskinovsky 2019; Dantas 2006):

Lemma 2.2

(Dacorogna (2008)) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow \mathbb {R}$ of the form $W(F)=\Vert F \Vert ^\alpha +f(\det F)$ with $f:\mathbb {R}_+\rightarrow \mathbb {R}$ and $1\le \alpha <2n$. The following are equivalent:

• (i) W is polyconvex,

• (ii) W is quasiconvex,

• (iii) W is rank-one convex,

• (iv) f is convex on $(0,\infty )$.

2.2 Purely Isochoric Energies

In a recent contribution (Martin et al. 2017), we present a similar statement for isochoric energies, also called conformally invariant energies, i.e. functions $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ with

$$\begin{aligned} W(AFB) = W(F) \qquad \text {for all}\quad A,B\in {{\,\mathrm{CSO}\,}}(2)\,, \end{aligned}$$

(2.5)

where

$$\begin{aligned} {{\,\mathrm{CSO}\,}}(2):=\mathbb {R}^+\cdot {{\,\mathrm{SO}\,}}(2)=\{aR\in {{\,\mathrm{GL}\,}}^{\!+}(2) \,|\,a\in (0,\infty )\,,\; R\in {{\,\mathrm{SO}\,}}(2)\} \end{aligned}$$

(2.6)

denotes the conformal special orthogonal group. This requirement can equivalently be expressed as

$$\begin{aligned}&W(R_1F)=W(F)=W(FR_2)\,,\quad W(aF)=W(F) \quad \nonumber \\&\text {for all}\quad R_1,R_2\in {{\,\mathrm{SO}\,}}(2)\,,\; a\in (0,\infty )\,, \end{aligned}$$

(2.7)

i.e. left- and right-invariance under the special orthogonal group ${{\,\mathrm{SO}\,}}(2)$ and invariance under scaling. An energy W satisfying $W(aF)=W(F)$ is more commonly known as isochoric. Following Astala et al. (2008), we introduce the (nonlinear) distortion function or outer distortion

$$\begin{aligned} \mathbb {K}:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}\,,\qquad \mathbb {K}(F):=\frac{1}{2}\frac{\Vert F \Vert ^2}{\det F}=\frac{\lambda _1^2+\lambda _2^2}{2\lambda _1\lambda _2}=\frac{1}{2}\left( \frac{\lambda _1}{\lambda _2}+\frac{\lambda _2}{\lambda _1}\right) , \end{aligned}$$

(2.8)

where $\Vert \,.\, \Vert$ denotes the Frobenius matrix norm with $\Vert F \Vert ^2=\sum _{i,j=1}^2 F_{ij}^2$ as well as the linear distortion or (large) dilatation

$$\begin{aligned} K(F):{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}\,,\qquad K(F)=\frac{{\varvec{|}}F{\varvec{|}}^2}{\det F}=\frac{\lambda ^{2}_{\mathrm{max}}}{\lambda _{\mathrm{min}} \lambda _{\mathrm{max}}}=\frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\,, \end{aligned}$$

(2.9)

where ${\varvec{|}}F{\varvec{|}}=\sup _{\Vert \xi \Vert =1}\Vert F\xi \Vert _{\mathbb {R}^2}=\lambda _{\hbox {max}}$ denotes the operator norm (i.e. the largest singular value) of F.

Lemma 2.3

(Martin et al. 2017) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ be conformally invariant. Then there exist uniquely determined functions $g:\mathbb {R}_+\times \mathbb {R}_+\rightarrow \mathbb {R}$, $h:\mathbb {R}_+\rightarrow \mathbb {R}$, ${\widehat{h}}:[1,\infty )\rightarrow \mathbb {R}$ and $\Psi :[1,\infty )\rightarrow \mathbb {R}$ such that

$$\begin{aligned} W(F) = g(\lambda _1,\lambda _2) = h\left( \frac{\lambda _1}{\lambda _2}\right) = {\widehat{h}}(K(F)) = \Psi (\mathbb {K}(F)) \end{aligned}$$

(2.10)

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with (not necessarily ordered) singular values $\lambda _1,\lambda _2$. Furthermore,

$$\begin{aligned} h(t)=h\left( \frac{1}{t}\right) ,\quad g(x,y)=g(y,x) \quad \text { and }\quad g(ax,ay)=g(x,y) \end{aligned}$$

(2.11)

for all $a,t,x,y\in (0,\infty )$.

Note that the isotropy requirement (2.11) implies that h is already uniquely determined by its values on $[1,\infty )$. While we do distinguish between $\lambda _1,\lambda _2$ as the non-ordered singular values and $\lambda _{\hbox {max}}\ge \lambda _{\hbox {min}}$ as the ordered singular values, we will interchange h and ${\widehat{h}}$ to simplify some notations here because $h(t)={\widehat{h}}(t)$ for all $t\ge 1$.

Lemma 2.4

(Martin et al. 2017) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ be conformally invariant, and let $g:\mathbb {R}_+\times \mathbb {R}_+\rightarrow \mathbb {R}$, $h:\mathbb {R}_+\rightarrow \mathbb {R}$ and $\Psi :[1,\infty )\rightarrow \mathbb {R}$ denote the uniquely determined functions with

$$\begin{aligned} W(F) = g(\lambda _1,\lambda _2) = h\left( \frac{\lambda _1}{\lambda _2}\right) = \Psi (\mathbb {K}(F)) \end{aligned}$$

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with singular values $\lambda _1,\lambda _2$, where $\mathbb {K}(F)=\frac{1}{2}\frac{\Vert F \Vert ^2}{\det F}$. Then the following are equivalent:

• (i) W is polyconvex,

• (ii) W is quasiconvex,

• (iii) W is rank-one convex,

• (iv) g is separately convex,

• (v) h is convex on $(0,\infty )$,

• (vi) h is convex and non-decreasing on $[1,\infty )$.

3 Least Rank-One Convex Candidates

We aim to discuss Morrey’s conjecture in this setting, i.e.:

• Is every rank-one convex energy with an additive volumetric-isochoric split in 2D already quasiconvex?

Our approach to this question is based on identifying volumetric-isochorically split energies which are, in a cetain sense, extremal (Fenchel and Blackett 1953; Šverák 1992a) among the rank-one convex functions. To this end, we consider the set of coupled one-dimensional inequalities from Theorem 3.2, which are equivalent to rank-one convexity, and find those functions for which equality holds in at least one case; due to this extremal property, we will refer to these functions as “least” rank-one convex.⁴ In Sect. 4, this allows us to reduce the above question to a single function for the case of a convex volumetric part, while mutliple least rank-one convex energies with a non-convex volumetric part are identified in Sect. 5. A summary of our approach is shown in Fig. 2 on p. 21.

3.1 Rank-One Convexity

For objective and isotropic planar energies with additive volumetric-isochoric split, there exists a unique representation (Martin et al. 2017, Lemma 3.1)

$$\begin{aligned} W(F)&=h\bigg (\frac{\lambda _1}{\lambda _2}\bigg )+f(\lambda _1\lambda _2)\,,\quad h,f:\mathbb {R}_+\rightarrow \mathbb {R}\,,\nonumber \\ h(t)&=h\bigg (\frac{1}{t}\bigg )\qquad \text {for all}\quad t\in (0,\infty )\,, \end{aligned}$$

(3.1)

where $\lambda _1,\lambda _2>0$ denote the singular values of F and h, f are given real-valued functions. In view of Lemmas 2.2 and 2.4 it is now tempting to believe that rank-one convexity conditions on $W_{\text {iso}}$ and $W_{\text {vol}}$ also allow for a sort of split and can be reduced to separate statements on h and f. However, this is not even the case in planar linear elasticity, where $W_\text {lin}$ from Eq. (2.2) is rank-one convex in the displacement gradient $\nabla u$ if and only if $\mu \ge 0$ and $\mu +\kappa \ge 0$. This means that rank-one convexity of $W_\text {lin}$ implies that $W_\text {iso}^\text {lin}$ is rank-one convex, whereas $W_\text {vol}^\text {lin}$ might not be rank-one convex, since e.g. $\kappa <0$ is allowed. We are therefore prepared to expect some coupling in the conditions for h and f.

For rank-one convexity on ${{\,\mathrm{GL}\,}}^{\!+}(2)$, (Knowles and Sternberg 1976, 1978) (see also Šilhavý 1997, p. 308) established the following important and useful criterion.

Lemma 3.1

(Knowles and Sternberg 1976, 1978, cf. Šilhavý 1997; Parry 1995; Dacorogna 2001; Šilhavý 1999, 2002; Aubert and Tahraoui 1987; Aubert 1995) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ be an objective-isotropic function of class $C^2$ with the representation in terms of the singular values of the deformation gradient F given by $W(F)=g(\lambda _1,\lambda _2)$, where $g\in C^2(\mathbb {R}_+^2,\mathbb {R})$. Then W is rank-one convex if and only if the following five conditions are satisfied:

• (i)       $\displaystyle g_{xx}\ge 0 \text { and } g_{yy}\ge 0\qquad \text {for all}\quad x,y\in (0,\infty )\,,$(separate convexity)

• (ii)       $\displaystyle \frac{xg_x-yg_y}{x-y}\ge 0\qquad \text {for all}\quad x,y\in (0,\infty )\,, x\ne y\,,$(Baker–Ericksen inequalities)

• (iii)       $\displaystyle g_{xx}-g_{xy}+\frac{g_x}{x}\ge 0\quad \text {and}\quad g_{yy}-g_{xy}+\frac{g_y}{y}\ge 0\qquad \text {for all}\quad x,y\in (0,\infty )\,,\; x=y\,,$

• (iv)       $\displaystyle \sqrt{g_{xx}\,g_{yy}}+g_{xy}+\frac{g_x-g_y}{x-y}\ge 0\qquad \text {for all}\quad x,y\in (0,\infty )\,,\; x\ne y\,,$

• (v)       $\displaystyle \sqrt{g_{xx}\,g_{yy}}-g_{xy}+\frac{g_x+g_y}{x+y}\ge 0\qquad \text {for all}\quad x,y\in (0,\infty )\,.$

Furthermore, if all the above inequalities are strict, then W is strictly rank-one convex.

In a recent contribution (Voss et al. 2021b) we applied the criterion by Knowles and Sternberg to volumetric-isochorically split energies: using weakened regularity assumptions (Martin et al. 2020) the following conditions can be established.

Theorem 3.2

(Voss et al. 2021b; Martin et al. 2020) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ be an objective-isotropic function with

$$\begin{aligned} W(F)={\widehat{g}}(\lambda _{\hbox {max}},\lambda _{\hbox {min}})={\widehat{h}}\left( \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}\right) +f(\lambda _{\hbox {max}}\lambda _{\hbox {min}})\qquad \text {for all}\quad F\in {{\,\mathrm{GL}\,}}^{\!+}(2) \end{aligned}$$

and ordered singular values $\lambda _{\hbox {max}}\ge \lambda _{\hbox {min}}$, where ${\widehat{h}}\in C^2((1,\infty );\mathbb {R})$ and $f\in C^2(\mathbb {R}_+;\mathbb {R})$. We write $h:\mathbb {R}_+\rightarrow \mathbb {R}$ with $h(t):={\widehat{h}}(t)$ for $t\ge 1$ and $h(t):={\widehat{h}}\bigl (\frac{1}{t}\bigr )$ for $t<1$. Let

$$\begin{aligned} h_0=\inf _{t\in (1,\infty )}t^2h''(t)\qquad \text {and}\qquad f_0=\inf _{z\in (0,\infty )}z^2f''(z)\,. \end{aligned}$$

Then W is rank-one convex if and only if

• (1)       $\displaystyle h_0+f_0\ge 0\,,$      (separate convexity)

• (2)       $\displaystyle h'(t)\ge 0\,,$      (Baker–Ericksen inequality)

• (3)       $\displaystyle \frac{2t}{t-1}h'(t)-t^2h''(t)+f_0\ge 0$   or   $\displaystyle a(t)+\left[ b(t)-c(t)\right] f_0\ge 0\,,$

• (4)       $\displaystyle \frac{2t}{t+1}h'(t)+t^2h''(t)-f_0\ge 0$   or   $\displaystyle a(t)+\left[ b(t)+c(t)\right] f_0\ge 0$

for all $t>1$, where

$$\begin{aligned} a(t)&=t^2(t^2-1)h'(t)h''(t)-2th'(t)^2,\qquad b(t)=(t^2+3)h'(t)+2t(t^2+1)h''(t)\,,\\ c(t)&=4t\bigl (h'(t)+th''(t)\bigr ). \end{aligned}$$

3.2 The Volumetric Part f(z)

Theorem 3.2 yields:

Lemma 3.3

Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ be a rank-one convex isotropic energy function with an additive volumetric-isochoric split $W(F)=h\bigl (\frac{\lambda _1}{\lambda _2}\bigr )+f(\lambda _1\lambda _2)$. Then h is convex on $(0,\infty )$ or f is convex on $(0,\infty )$.

Proof

The separate convexity condition 1) in Theorem 3.2 implies

$$\begin{aligned} h_0+f_0\ge 0\quad \implies \quad&h_0\ge 0\quad \text {or}\quad f_0\ge 0\nonumber \\ \Longleftrightarrow \quad&t^2h''(t)\ge 0\quad \text {for all }t\in (1,\infty )\quad \text {or}\quad z^2f''(z)\ge 0\quad \text {for all }z\in (0,\infty )\nonumber \\ \Longleftrightarrow \quad&h''(t)\ge 0\quad \text {for all }t\in (1,\infty )\quad \text {or}\quad f''(z)\ge 0\quad \text {for all }z\in (0,\infty )\,. \end{aligned}$$

(3.2)

The invariance property $h(t)=h\big (\frac{1}{t}\big )$ of the isochoric part h yields

$$\begin{aligned} h'(t)&=\frac{\text {d}}{\text {d}t}h(t)=\frac{\text {d}}{\text {d}t}h\left( \frac{1}{t}\right) =-\frac{1}{t^2}h'\left( \frac{1}{t}\right) , \end{aligned}$$

(3.3)

$$\begin{aligned} h''(t)&=\frac{\text {d}}{\text {d}t}h'(t)=\frac{\text {d}}{\text {d}t}\left[ -\frac{1}{t^2}h'\left( \frac{1}{t}\right) \right] =\frac{2}{t^3}h'\left( \frac{1}{t}\right) +\frac{1}{t^4}h''\left( \frac{1}{t}\right) . \end{aligned}$$

(3.4)

Thus for arbitrary $s\in (0,1)$ the monotonicity condition 2) in Theorem 3.2 implies $h''(s)\ge 0$ as well if $h''(t)\ge 0$ for all $t\in (1,\infty )$. $\square$

Lemma 3.3 states that rank-one convexity of an energy with a volumetric-isochoric split always implies the global convexity of h nor f. Thus if neither h or f are convex, the sum $W(F)=h\bigl (\frac{\lambda _1}{\lambda _2}\bigr )+f(\lambda _1\lambda _2)$ is not rank-one convex. On the other hand, if h and f are both convex, the energy is already polyconvex as the sum of two individual polyconvex energies (cf. Lemmas 2.1 and 2.4). Therefore, for our purpose it is sufficient to consider the two subclasses

$$\begin{aligned} {\mathfrak {M}}_+&:=\left\{ W(F)=h\biggl (\frac{\lambda _{1}}{\lambda _{2}}\biggr )+f(\lambda _{1}\lambda _{2})\;|\;h:(1,\infty )\rightarrow \mathbb {R}\text { is convex}\right\} \end{aligned}$$

(3.5)

and

$$\begin{aligned} {\mathfrak {M}}_-&:=\left\{ W(F)=h\biggl (\frac{\lambda _{1}}{\lambda _{2}}\biggr )+f(\lambda _{1}\lambda _{2})\;|\;f:\mathbb {R}_+\rightarrow \mathbb {R}\text { is convex}\right\} \end{aligned}$$

(3.6)

where either f or h are convex. The conditions in Theorem 3.2 contain several different expressions related to the isochoric part h(t), while $f_0=\inf _{z\in (0,\infty )}z^2f''(z)$ occurs exclusively for the volumetric term. We utilize this observation to reduce the volumetric parts of the sets ${\mathfrak {M}}_+$ and ${\mathfrak {M}}_-$ to a single function for all least rank-one convex representatives:

Lemma 3.4

Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ be a two-times differentiable isotropic energy function with a volumetric-isochoric split

$$\begin{aligned} W(F)=h\biggl (\frac{\lambda _1}{\lambda _2}\biggr )+f(\lambda _1\lambda _2) \end{aligned}$$

that is rank-one convex but not quasiconvex. Then there exists a constant $c\in \mathbb {R}$ so that the energy

$$\begin{aligned} W_0(F):=h\biggl (\frac{\lambda _1}{\lambda _2}\biggr )+c\log (\lambda _1\lambda _2) \end{aligned}$$

(3.7)

is rank-one convex but not quasiconvex, as well.

Proof

Both energies have the same isochoric part, but different volumetric parts. We set⁵

$$\begin{aligned} c:=-f_0=-\inf _{z\in (0,\infty )}z^2f''(z)\,,\qquad {\widetilde{f}}(z):=c\log (z)\,. \end{aligned}$$

(3.8)

Then

$$\begin{aligned} {\widetilde{f}}_0=\inf _{z\in (0,\infty )}z^2{\widetilde{f}}''(z)=\inf _{z\in (0,\infty )}z^2\left( -\frac{c}{z^2}\right) =-c=f_0\,. \end{aligned}$$

Thus the conditions in Theorem 3.2 are identical for both energies and they share the same rank-one convexity behaviour. Therefore, $W_0(F)$ is rank-one convex. Regarding the quasiconvexity, we consider the difference between the two energies

$$\begin{aligned} W^*(F):=W(F)-W_0(F)=f(\lambda _1\lambda _2)-c\log (\lambda _1\lambda _2) \, {=}{:}\, f^*(\lambda _1\lambda _2)\,. \end{aligned}$$

(3.9)

The energy $W^*(F)$ is a purely volumetric energy with $f_0^*=f_0-{\widetilde{f}}_0=0$. Thus ${f^*}''(z)\ge 0$ for all $z\in (0,\infty )$, i.e. $f^*$ is convex and in particular $W^*(F)$ is quasiconvex (cf. Lemma 2.1). If $W_0(F)$ is quasiconvex, then the sum $W(F)=W_0(F)+W^*(F)$ of two individual quasiconvex functions is quasiconvex as well, which contradicts the initial assumption that W(F) is not quasiconvex. $\square$

Equation (3.9) shows that every rank-one convex function W(F) with a volumetric-isochoric split can be rewritten as the sum of two individual rank-one convex energies

$$\begin{aligned} W(F)= & {} h\biggl (\frac{\lambda _1}{\lambda _2}\biggr )+f(\lambda _1\lambda _2)=h\biggl (\frac{\lambda _1}{\lambda _2}\biggr )+c\log (\lambda _1\lambda _2)+f^*(\lambda _1\lambda _2)\nonumber \\= & {} W_0(F)+W^*(F)\,. \end{aligned}$$

(3.10)

The second part $W^*(F)=f^*(\det F)$ is a purely volumetric energy, i.e. rank-one convexity already implies quasiconvexity, while the first part $W_0(F)$ maintains the isochoric part h(t). In other words, Lemma 3.4 states that if there exists a volumetric-isochorically split energy W(F) that is rank-one convex but not quasiconvex, then there exists a function $W_0(F)=h\bigl (\frac{\lambda _1}{\lambda _2}\bigr )+c\log (\lambda _1\lambda _2)$ that is rank-one convex but not quasiconvex as well.

Since multiplying with an arbitrary constant $\alpha \in \mathbb {R}_+$ has no effect on the convexity behaviour of the energy function, we can also set $c=\pm 1$ without loss of generality. We reduce the two subclasses ${\mathfrak {M}}_+$ and ${\mathfrak {M}}_-$ of volumetric-isochorically split energies to two new sets

$$\begin{aligned} {\mathfrak {M}}_+^*&:=\left\{ W(F)=h\biggl (\frac{\lambda _1}{\lambda _2}\biggr )+\log (\lambda _1\lambda _2)\;|\;h:(1,\infty )\rightarrow \mathbb {R}\text { is convex}\right\} \end{aligned}$$

(3.11)

and

$$\begin{aligned} {\mathfrak {M}}_-^*&:=\left\{ W(F)=h\biggl (\frac{\lambda _1}{\lambda _2}\biggr )-\log (\lambda _1\lambda _2)\;|\;h:(1,\infty )\rightarrow \mathbb {R}\text { is not convex}\right\} . \end{aligned}$$

(3.12)

4 Subclass ${\mathfrak {M}}_+$: Convex Isochoric Part

We focus on volumetric-isochorically split energies which have a convex isochoric part h(t) together with a non-convex volumetric part $f(\det F)=\log \det F$, i.e. $W\in {\mathfrak {M}}_+^*$. It is possible to reduce the whole class ${\mathfrak {M}}_+^*$ and thereby ${\mathfrak {M}}_+$, to a single rank-one convex representative $W_{\text {magic}}^+(F)$ (cf. Theorem 4.1) as the only candidate to check for quasiconvexity to answer Morrey’s questions for all energies with a volumetric-isochoric split and a convex isochoric part.

This candidate is found by searching for energy functions that satisfy inequality conditions of Theorem 3.2 by equality. We start with the first inequality which is the most important condition due to its equivalence to separate convexity:

$$\begin{aligned} 1)&h_0+f_0\ge 0\,,\qquad h_0=\inf _{t\in (1,\infty )}t^2h''(t)\qquad \text {and}\qquad f_0=\inf _{z\in (0,\infty )}z^2f''(z)\,.&\end{aligned}$$

(4.1)

We consider the case of equality for all $t\ge 1$. For every $W\in {\mathfrak {M}}_+^*$, the volumetric part is given by $f(z)=\log z$, which implies

$$\begin{aligned} f_0=\inf _{z\in (0,\infty )}z^2f''(z)=\inf _{z\in (0,\infty )}z^2 \frac{-1}{z^2}=-1\,,\nonumber \\ \end{aligned}$$

and we compute

$$\begin{aligned} t^2h''(t)-1=0\quad \Longleftrightarrow \quad h''(t) =\frac{1}{t^2}\quad \Longleftrightarrow \quad h(t)=-\log t+at+b\,. \end{aligned}$$

(4.2)

The constant $b\in \mathbb {R}$ is negligible regarding any convexity property and thus we set $b=0$. We determine the other constant $a\in \mathbb {R}$ by testing the remaining convexity conditions and choose the constant a so that these inequalities are satisfied as non-strictly as possible to obtain our first least rank-one convex candidate. In this way, the monotonicity condition 2) of Theorem 3.2 is given by

$$\begin{aligned} -\frac{1}{t}+a\ge 0\qquad \text {for all}\quad t\ge 1\qquad \Longleftrightarrow \qquad a\ge 1\,. \end{aligned}$$

(4.3)

Next, condition 3a) of Theorem 3.2,

$$\begin{aligned} \frac{2t}{t-1}\frac{at-1}{t}-t^2\frac{1}{t^2}-1\ge 0\qquad \Longleftrightarrow \qquad \frac{2(a-1)t}{t-1}\ge 0\qquad \text {for all}\quad t\ge 1\,, \end{aligned}$$

(4.4)

is satisfied for all $a\ge 1$ while condition 4a) of Theorem 3.2,

$$\begin{aligned} \frac{2t}{t+1}\frac{at-1}{t}+t^2\frac{1}{t^2}+1\ge 0\qquad \Longleftrightarrow \qquad \frac{2(a+1)t}{t+1}\ge 0\qquad \text {for all}\quad t\ge 1\,, \end{aligned}$$

(4.5)

is satisfied for $a\ge -1$. The two remaining conditions 3b) and 4b) of Theorem 3.2 are satisfied for $a\ge 1$ and $a\ge 3-2\sqrt{2}$, respectively. Putting all conditions together, we conclude that the case $a=1$ should be considered optimal and results in a least rank-one convex candidate. Overall, our canonical candidate is $h(t)=t-\log t$, which corresponds to the energy function

The energy $W_{\text {magic}}^+(F)$ satisfies the conditions 1) and 3a) by equality for all $t\ge 1$, conditions 2) and 3b) for $t=1$. We show that this function is the single representative for the energy class ${\mathfrak {M}}_+$ regarding the question of quasiconvexity.

Theorem 4.1

The following are equivalent:

• (i) There exists a two-times differentiable isotropic energy $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ with a volumetric-isochoric split

  $$\begin{aligned} W(F) = h\biggl (\frac{\lambda _1}{\lambda _2}\biggr )+f(\lambda _1\lambda _2) \end{aligned}$$

  (4.7)

  such that h is convex, i.e. $W\in {\mathfrak {M}}_+$, and W is rank-one convex but W is not quasiconvex.

• (ii) The rank-one convex function $W_{\text {magic}}^+(F):{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ with

  $$\begin{aligned} W_{\text {magic}}^+(F):=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} - \log \left( \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}\right) + \log \det F \end{aligned}$$

  (4.8)

  with singular values $\lambda _{\hbox {max}}\ge \lambda _{\hbox {min}}$ of F is not quasiconvex.

Proof

Using Theorem 3.2, we can directly prove the rank-one convexity of $W_{\text {magic}}^+$. We calculate

$$\begin{aligned}&h_0=\inf _{t\in (1,\infty )}t^2h''(t)=\inf _{t\in (1,\infty )}t^2\frac{1}{t^2}=1\,,\\&\quad \qquad f_0=\inf _{z\in (0,\infty )}z^2f''(z)=\inf _{z\in (0,\infty )}z^2\left( -\frac{1}{z^2}\right) =-1\,, \end{aligned}$$

• 1)       $\displaystyle h_0+f_0=1-1\ge 0\,,\checkmark$

• 2)       $\displaystyle h'(t)=1-\frac{1}{t}\ge 0$   for all $t\ge 1\,,\checkmark$

• 3a)       $\displaystyle \frac{2t}{t-1}h'(t)-t^2h''(t)+f_0=\frac{2t}{t-1}\frac{t-1}{t}-1-1=0\ge 0\,,\checkmark$

• 4a)       $\displaystyle \frac{2t}{t+1}h'(t)+t^2h''(t)-f_0=\frac{2t}{t+1}\frac{t-1}{t}+1+1$$=2\left( \frac{t-1}{t+1}+1\right) =\frac{4t}{t+1}\ge 0\checkmark$

By definition $W_{\text {magic}}^+\in {\mathfrak {M}}_+$. i.e. (ii) $\implies$ ((i). Starting with W(F) from (i), we use Lemma 3.4 to reduce the class of energies from ${\mathfrak {M}}_+$ to ${\mathfrak {M}}_+^*$. Thus there exists a constant $c>0$ so that the energy

$$\begin{aligned} W_0(F)=h\biggl (\frac{\lambda _1}{\lambda _2}\biggr )+c\log (\lambda _1\lambda _2) \end{aligned}$$

is rank-one convex but not quasiconvex. Without loss of generality, we set $c=1$, because multiplying with an arbitrary positive constant has no effect on the convexity behaviour of the energy, and change h accordingly. We consider the difference

$$\begin{aligned} W^*(F):=W_0(F)-W_{\text {magic}}^+(F)= h(t)-t+\log t{=}{:}{\widetilde{h}}(t)\,,\qquad t=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}\,, \end{aligned}$$

(4.9)

which is a purely isochoric energy. We show that $W^*(F)$ itself is quasiconvex. For this, we study the first two conditions of Theorem 3.2 for the rank-one convex energy

$$\begin{aligned} W_0(F)=W^*(F)+W_{\text {magic}}^+(F)={\widetilde{h}}(t)+t-\log t+\log \det F\,. \end{aligned}$$

We compute $\displaystyle f_0=\inf _{z\in (0,\infty )}z^2\frac{-1}{z^2}=-1$ and

• (i) $\displaystyle h_0+f_0=\inf _{t\in (1,\infty )}t^2\left( {\widetilde{h}}''(t)+\frac{1}{t^2}\right) -1={\widetilde{h}}_0\ge 0\qquad \implies \qquad {\widetilde{h}}''(t)\ge 0$   for all $t\in (1,\infty )$.

• (ii) $h'(t)\ge 0$ for all $t\ge 1$   and    ${\widetilde{h}}'(t)=h'(t)-1+\frac{1}{t}$ for $t=1$ it holds    ${\widetilde{h}}'(1)=h'(1)-1+1=h'(1)\ge 0$.

Thus ${\widetilde{h}}(t)$ is convex for all $t\ge 1$ and non-decreasing at $t=1$. Both together imply ${\widetilde{h}}'(t)\ge {\widetilde{h}}'(1)\ge 0$ for all $t\ge 1$, i.e. the mapping $t\mapsto {\widetilde{h}}(t)$ is non-decreasing on $[1,\infty )$. By Lemma 2.4, the isochoric energy $W^*(F)={\widetilde{h}}\bigl (\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}\bigr )$ is quasiconvex. The sum of two individual quasiconvex functions is again quasiconvex; hence the non-quasiconvexity of $W_0(F)=W^*(F)+W_{\text {magic}}^+(F)$ requires that $W_{\text {magic}}^+(F)$ is already non-quasiconvex. $\square$

Remark 4.2

Theorem 4.1 can also be stated as the equivalence between the quasiconvexity of $W_{\text {magic}}^+$ and the implication

$$\begin{aligned} W \text { rank-one convex} \quad \implies \quad W \text { quasiconvex}\qquad \qquad \text {for all}\quad W\in {\mathfrak {M}}_+\,, \end{aligned}$$

i.e. for all energies with an additive volumetric-isochoric split and a convex isochoric part.

Due to the use of the ordered singular values $\lambda _{\hbox {max}}\ge \lambda _{\hbox {min}}$ instead of the unsorted singular values $\lambda _1,\lambda _2$ of F, the representation $h:\mathbb {R}_+\rightarrow \mathbb {R}$ of the isochoric part is not smooth at $t=1$ in general. Nevertheless, for the candidate $W_{\text {magic}}^+$ we have

$$\begin{aligned} h(t)={\left\{ \begin{array}{ll}t-\log t &{}\text {if }\;t\ge 1\,,\\ \frac{1}{t}+\log t &{}\text {if }\;t\le 1\,,\end{array}\right. } \end{aligned}$$

(4.10)

which implies $h\in C^2(\mathbb {R}_+;\mathbb {R})$ because

$$\begin{aligned} \lim _{t\searrow 1}h'(t)&=\lim _{t\rightarrow 1}1-\frac{1}{t}=0=\lim _{t\rightarrow 1}-\frac{1}{t^2}+\frac{1}{t}=\lim _{t\nearrow 1}h'(t)\,,\\ \lim _{t\searrow 1}h''(t)&=\lim _{t\rightarrow 1}\frac{1}{t^2}=1=\lim _{t\rightarrow 1}\frac{2}{t^3}-\frac{1}{t^2}=\lim _{t\nearrow 1}h''(t)\,. \end{aligned}$$

Although Theorem 4.1 reduces the question of whether ${\mathfrak {M}}_+$ contains a rank-one convex, non-quasiconvex function to the very particular question of whether $W_{\text {magic}}^+(F)$ is quasiconvex, the latter still remains open at this point (cf. Sect. 6). We note, however, that the stronger condition of polyconvexity is indeed not satisfied for $W_{\text {magic}}^+(F)$

Lemma 4.3

The energy $W_{\text {magic}}^+(F)=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} - \log \bigl (\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}\bigr ) + \log \det F$ is not polyconvex.

Proof

Every polyconvex function $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ must grow at least linear for $\det F\rightarrow 0$ (Dacorogna 2008, Cor. 5.9). This can be motivated by the following: If W(F) is polyconvex, there exists a (not necessarily unique) representation $P:\mathbb {R}^{2\times 2}\times \mathbb {R}_+\rightarrow \mathbb {R}$ with $W(F)=P(F,\det F)$ which is convex. We consider the hyperplane attached to P at $(\mathbb {1},1)$. Convexity in $\mathbb {R}^{2\times 2}\times \mathbb {R}_+$ implies that P is bounded below from its hyperplane. On the contrary,

$$\begin{aligned} \lim _{\lambda \rightarrow 0}P(\lambda \mathbb {1},\lambda ^2)=\lim _{\lambda \rightarrow 0}W_{\text {magic}}^+(\lambda \mathbb {1})=\lim _{\lambda \rightarrow 0}\frac{\lambda }{\lambda }+2\log \lambda =-\infty \end{aligned}$$

is unbounded. Thus $W_{\text {magic}}^+(F)$ cannot be polyconvex. $\square$

To summarize, the question whether an energy $W\in {\mathfrak {M}}_+$ exists which is rank-one convex but not quasiconvex or not, i.e. rank-one convexity always implies quasiconvexity, can be reduced to the specific question of quasiconvexity of the single energy function $W_{\text {magic}}^+(F)$. In this sense, our candidate represents an extreme point of ${\mathfrak {M}}_+$, i.e. it is the single least rank-one convex function of this subclass. Moreover, our energy $W_{\text {magic}}^+(F)$ is non-polyconvex, which is necessary to serve as a possible example for Morrey’s conjecture.

5 Subclass ${\mathfrak {M}}_-$: Convex Volumetric Part

We continue with volumetric-isochorically split energies which have a non-convex isochoric part h(t) together with a convex volumetric part $f(\det F)=-\log \det F$, i.e. $W\in {\mathfrak {M}}_-^*$. This time, the question of whether an energy $W\in {\mathfrak {M}}_-$ exists which is rank-one convex but not quasiconvex is much more involved and cannot be reduced to the matter of quasiconvexity of a single extreme representative. Nevertheless, we give a few candidates which are analogous to $W_{\text {magic}}^+\in {\mathfrak {M}}_+$.

Again, following the concept of least rank-one convex functions, we are looking for energies that cannot be split additively into two non-trivial functions which are both individually rank-one convex. For this, we take the four inequalities of Theorem 3.2 characterizing rank-one convexity and consider the corresponding differential equations, i.e. energies which only fulfill these inequalities conditions by equality. However, a function does not have to satisfy all four conditions non-strictly to be a least rank-one convex candidate; recall that the energy $W_{\text {magic}}^+(F)$ as the single representative of ${\mathfrak {M}}_+$ satisfies conditions 1) and 3a) by equality for all $t\ge 1$ and condition 2) for $t=1$ but is not optimal for the remaining inequalities.

As a method to find candidates for least rank-one convex functions of ${\mathfrak {M}}_-$, we examine each condition characterizing rank-one convexity separately and search for equality for all $t\ge 1$. Thus we are capable of finding very interesting energies, e.g. a function which is nowhere strictly separately convex or satisfies another inequality condition by equality. However, due to their dependence on $t\ge 1$ this approach does not cover all possible extreme cases of ${\mathfrak {M}}_-$. An energy can already be a least rank-one convex candidate if it satisfies one or more inequality conditions non-strictly for a single $t\ge 1$ and not all $t\ge 1$ as described above (cf. Sect. 5.2). Besides, conditions 3) and 4) allow for even more involved combinations because of their internal case-by-case distinction.

5.1 Obtaining $W_{\text {magic}}^-$

We start with the first inequality of Theorem 3.2, which is the most important condition due to its equivalence to separate convexity:

$$\begin{aligned} 1)&h_0+f_0\ge 0\,,\qquad h_0=\inf _{t\in (1,\infty )}t^2h''(t)\qquad \text {and}\qquad f_0=\inf _{z\in (0,\infty )}z^2f''(z)\,.&\end{aligned}$$

(5.1)

We consider the case of equality for all $t\ge 1$. For every $W\in {\mathfrak {M}}_-^*$, the volumetric part is given by $f(z)=-\log z$, which implies

$$\begin{aligned} f_0=\inf _{z\in (0,\infty )}z^2f''(z)=\inf _{z\in (0,\infty )}z^2\frac{1}{z^2}=1\,, \end{aligned}$$

and we compute

$$\begin{aligned} t^2h''(t)+1=0\quad \Longleftrightarrow \quad h''(t)=-\frac{1}{t^2}\quad \Longleftrightarrow \quad h(t)=\log t+at+b\,. \end{aligned}$$

(5.2)

The constant $b\in \mathbb {R}$ is negligible regarding any convexity property and thus we set $b=0$. We determine the other constant $a\in \mathbb {R}$ by testing the remaining convexity conditions and choose the constant a so that these inequalities are satisfied as non-strictly as possible to obtain our first least rank-one convex candidate. In this way, the monotonicity condition 2) of Theorem 3.2 is given by

$$\begin{aligned} \frac{1}{t}+a\ge 0\qquad \text {for all}\quad t\ge 1\qquad \Longleftrightarrow \qquad a\ge 0\,. \end{aligned}$$

(5.3)

Next, condition 3a) of Theorem 3.2,

$$\begin{aligned} \frac{2t}{t-1}\frac{1+at}{t}+t^2\frac{1}{t^2}+1\ge 0\qquad \Longleftrightarrow \qquad \frac{2(a+1)t}{t-1}\ge 0\qquad \text {for all}\quad t\ge 1\,, \end{aligned}$$

(5.4)

is satisfied for all $a\ge -1$ while condition 4a) of Theorem 3.2,

$$\begin{aligned} \frac{2t}{t+1}\frac{1+at}{t}-t^2\frac{1}{t^2}-1\ge 0\qquad \Longleftrightarrow \qquad \frac{2(a-1)t}{t+1}\ge 0\qquad \text {for all}\quad t\ge 1\,, \end{aligned}$$

(5.5)

is satisfied for $a\ge 1$. The two remaining conditions 3b) and 4b) of Theorem 3.2 are never satisfied for $a\ne 1$. Putting all conditions together, we conclude that the case $a=1$ yields a least rank-one convex function. Overall, our canonical candidate regarding equality in condition 1) of Theorem 3.2 for all $t\ge 1$ is $h(t)=t+\log t$, which corresponds to the energy function

an analogous candidate to $W_{\text {magic}}^+\in {\mathfrak {M}}_+$. The energy $W_{\text {magic}}^-(F)$ satisfies condition 1), 4a) and 4b) non-strict for all $t\ge 1$, conditions 2) in the limit $t\rightarrow \infty$ but is not optimal for the remaining inequalities. Contrary to the discussion in the last section, where we showed that $W_{\text {magic}}^+$ is as the single least rank-one convex candidate for the energy class ${\mathfrak {M}}_+$, the same is not true for $W_{\text {magic}}^-(F)$, i.e. it exists several distinct least rank-one convex energies for the class ${\mathfrak {M}}_-$.

5.2 Obtaining $W_\text {smooth}$

We continue with the second condition of Theorem 3.2, which is equivalent to the Baker–Ericksen inequalities, and consider the limit case

$$\begin{aligned} 2)\quad h'(t)=0\qquad \text {for all}\quad t\ge 1. \end{aligned}$$

(5.7)

The only solution to this differential equation is the constant function $h(t)=c$ which provides the purely volumetric energy $W(F)=c-\log \det F$. Thus we have no (non-trivial) least rank-one convex candidate corresponding to the monotonicity condition 2).

Before we continue to work with the more involved conditions 3) and 4), we will consider an alternative variant to produce more least rank-one convex energies utilizing the fact that an energy function can be least rank-one convex without satisfying one single condition non-strict for all $t\in (1,\infty )$. Starting with $W_{\text {magic}}^-(F)$, we can weaken the monotonicity condition 2) by waiving the requirement of being nowhere strictly separately convex. However, we have to ensure that the energy remains non-strictly separately convex for one $t\in [1,\infty ]$. Thus we are looking for a new function h(t) which is less monotone but slightly more convex then the expression $t+\log t$. We choose the ansatz

$$\begin{aligned} h(t)=at+\frac{b}{t}+\log t\,,\qquad a,b\in \mathbb {R} \end{aligned}$$

(5.8)

and with the first two conditions of Theorem 3.2 we compute

$$\begin{aligned} 1)&h_0+f_0&=\inf _{t\in (0,\infty )}t^2\left( \frac{2b}{t^3}-\frac{1}{t^2}\right) +1=\inf _{t\in (0,\infty )}\frac{4b}{t}\ge 0\qquad \Longleftrightarrow \qquad b\ge 0\,,&\\ 2)&h'(t)&=a-\frac{b}{t^2}+\frac{1}{t}\ge 0\qquad \Longleftrightarrow \qquad a\ge 0\quad \text {and}\quad b\le a+1\,.&\end{aligned}$$

We are interested in the limit case $b=a+1$ so that $h'(1)=0$, i.e. the function is not strictly monotone for $t=1$. The second limit case $a=0$ would reestablish $W_{\text {magic}}^-(F)$. Note that the separate convexity condition is only non-strict in the limit case $t\rightarrow \infty$. We evaluate the remaining conditions and choose the remaining constant $a\ge 0$ accordingly. Then

$$\begin{aligned} 3a)\quad&\frac{2t}{t-1}\left( a-\frac{a+1}{t^2}+\frac{1}{t}\right) -t^2\left( 2\frac{a+1}{t^3}-\frac{1}{t^2}\right) +1\ge 0\quad \Longleftrightarrow \quad \nonumber \\&2(a+1)\ge 0\quad \text {for all}\quad t\ge 1\,, \end{aligned}$$

which is satisfied for $a\ge -1$ which is already ensured by conditions 2). Lastly, we compute

$$\begin{aligned} 4a)\quad&\frac{2t}{t+1}\left( a-\frac{a+1}{t^2}+\frac{1}{t}\right) +t^2\left( 2\frac{a+1}{t^3}-\frac{1}{t^2}\right) -1\ge 0\quad \Longleftrightarrow \quad \nonumber \\&2\frac{at-t+a+1}{t+1}\ge 0\quad \text {for all}\quad t\ge 1 \end{aligned}$$

which is fulfilled for $a\ge 1$. For the case $0\le a\le 1$ the remaining condition

$$\begin{aligned} 4b)&2\frac{1+t+3t^2-t^3+a(1+t+3t^2+3t^3)}{t^2}\ge 0\qquad \text {for all}\quad t\ge 1&\end{aligned}$$

(5.9)

is satisfied for $a\ge \frac{1}{3}$. Overall, $a=\frac{1}{3}$ yields the least rank-one convex candidate with the isochoric term $h(t)=\frac{t}{3}+\frac{4}{3t}+\log t$ which generates

The energy $W_\text {smooth}(F)$ is strictly rank one convex for all $t\in (1,\infty )$, but unlike $W_{\text {magic}}^-(F)$, it is only a least rank-one candidate in the sense that it is non-strictly separately convex for $t\rightarrow \infty$ and satisfies condition 2) of Theorem 3.2 by equality for $t=1$.

5.3 Obtaining $W_\text {3b}$

We generate a third candidate using our original method with focus on the last two inequalities of Theorem 3.2 and start with condition

$$\begin{aligned} 3a)&\frac{2t}{t-1}h'(t)-t^2h''(t)+1=0\qquad \Longleftrightarrow \qquad h''(t)=\frac{2}{t(t-1)}h'(t)+\frac{1}{t^2}\,.&\end{aligned}$$

(5.11)

We solve the differential equation by adding a particular solution to the associated homogeneous equation:

$$\begin{aligned}&h'(t)&=x_h(t)+x_p(t)\qquad \text {with}\qquad x_p(t)=\frac{1-t}{t^2}\qquad \text {and} \end{aligned}$$

(5.12)

$$\begin{aligned}&x_h'(t)&=2\left( \frac{1}{t-1}-\frac{1}{t}\right) x_h(t)\nonumber \\\Longleftrightarrow & {} \log x_h(t)&=2\left( \log |t-1|-\log t\right) +c\nonumber \\\Longleftrightarrow & {} x_h(t)&=c\left( \frac{t-1}{t}\right) ^2\,. \end{aligned}$$

(5.13)

Thus

$$\begin{aligned} h'(t)= & {} c\left( 1-\frac{2}{t}+\frac{1}{t^2}\right) -\frac{1}{t}+\frac{1}{t^2}\quad \Longleftrightarrow \quad \nonumber \\ h(t)= & {} c\left( t-2\log t-\frac{1}{t}\right) -\log t-\frac{1}{t}+b\,. \end{aligned}$$

(5.14)

However, the monotonicity condition

$$\begin{aligned} h'(t)=\frac{c(t-1)^2-(t-1)}{t^2}\ge 0\quad \Longleftrightarrow \quad c\ge \frac{1}{t-1}\quad \text {for all}\quad t>1 \end{aligned}$$

(5.15)

cannot be satisfied in the limit $t\rightarrow 1$. Thus there does not exist a rank-one convex candidate which satisfies condition 3a) by equality for all $t>1$. We continue with condition

$$\begin{aligned} 4a)&\quad \frac{2t}{t+1}h'(t)+t^2h''(t)-1=0\qquad \Longleftrightarrow \qquad h''(t)=-\frac{2}{t(t-1)}h'(t)+\frac{1}{t^2}\,.&\end{aligned}$$

(5.16)

Again, we solve the differential equation by adding a particular solution to the associated homogeneous equation:

$$\begin{aligned}&h'(t)&=x_h(t)+x_p(t)\quad \text {with}\quad x_p(t)=-\frac{t+1}{t^2}\quad \text {and} \end{aligned}$$

(5.17)

$$\begin{aligned}&x_h'(t)&=2\left( \frac{1}{t+1}-\frac{1}{t}\right) x_h(t)\nonumber \\\Longleftrightarrow & {} \log x_h(t)&=2\left( \log (t+1)-\log t\right) +c\nonumber \\\Longleftrightarrow & {} x_h(t)&=c\left( \frac{t+1}{t}\right) ^2. \end{aligned}$$

(5.18)

Thus

$$\begin{aligned} h'(t)= & {} c\left( 1+\frac{2}{t}+\frac{1}{t^2}\right) -\frac{1}{t}-\frac{1}{t^2}\quad \Longleftrightarrow \quad \nonumber \\ h(t)= & {} c\left( t+2\log t-\frac{1}{t}\right) -\log t+\frac{1}{t}+b\,. \end{aligned}$$

(5.19)

We set $b=0$ and determine $c\in \mathbb {R}$ by evaluating the remaining rank-one convexity conditions. The separate convexity condition 1) yields

$$\begin{aligned} h_0&=\inf _{t\in (1,\infty )}t^2h''(t)=t^2\left[ c\left( -\frac{2}{t^3} -\frac{2}{t^2}\right) +\frac{2}{t^3}+\frac{1}{t^2}\right] \nonumber \\&=\inf _{t\in (1,\infty )}2(1-c)\frac{1}{t}+1-2c \ge -1\,. \end{aligned}$$

(5.20)

In the case $c\ge 1$, the infimum is attained at $t=1$ and

$$\begin{aligned} 3-4c\ge -1\qquad \Longleftrightarrow \qquad c\le 1\,. \end{aligned}$$

For the case $c\le 1$, the infimum is at $t\rightarrow \infty$ and

$$\begin{aligned} 1-2c\ge -1\qquad \Longleftrightarrow \qquad c\le 1\,. \end{aligned}$$

Thus $c\le 1$. The monotonicity condition

$$\begin{aligned} 2)&h'(t)=\frac{c(t+1)^2-(t+1)}{t^2}\ge 0\qquad \Longleftrightarrow \qquad c\ge \frac{1}{t+1}\qquad \text {for all}\quad t\ge 1&\end{aligned}$$

(5.21)

is satified for $c\ge \frac{1}{2}$. The remaining condition 3a) leads to

$$\begin{aligned}&\frac{2t}{t-1}\frac{c(t+1)^2-(t+1)}{t^2}-\left[ c\left( -\frac{2}{t^3}-\frac{2}{t^2}\right) +\frac{2}{t^3}+\frac{1}{t^2}\right] +1\ge 0\nonumber \\&\Longleftrightarrow 2\frac{c(t+1)^2-(t+1)}{t(t-1)}+2(c-1)\frac{t+1}{t}\ge 0\nonumber \\&\Longleftrightarrow \frac{c(t+1)^2-(t+1)+(c-1)(t+1)(t-1)}{t-1}\ge 0\nonumber \\&\Longleftrightarrow \frac{c(2t^2+2t)-t^2-t}{t-1}\ge 0\nonumber \\&\Longleftrightarrow 2c-1 \quad \ge 0\quad \Longleftrightarrow \quad c\ge \frac{1}{2}\,. \end{aligned}$$

(5.22)

Thus we can consider the two borderline cases

$$\begin{aligned} c=\frac{1}{2}:\qquad h(t)=\frac{1}{2}\left( t+\frac{1}{t}\right) ,\qquad \text {and}\qquad c=1:\qquad h(t)=t+\log t.\nonumber \\ \end{aligned}$$

(5.23)

However, the first function

$$\begin{aligned} h\left( \frac{\lambda _1}{\lambda _2}\right) =\frac{1}{2}\left( \frac{\lambda _1}{\lambda _2} +\frac{\lambda _2}{\lambda _1}\right) =\frac{\lambda _1^1+\lambda _2^2}{2\lambda _1\lambda _2}=\frac{\Vert F \Vert ^2}{2\det F}=\mathbb {K}(F) \end{aligned}$$

(5.24)

is already polyconvex and therefore not suitable to provide an example for Morrey’s question with respect to volumetric-isochorically split energies. The second part $h(t)=t+\log t$ is already known as the isochoric part of $W_{\text {magic}}^-(F)$.

We consider the condition

$$\begin{aligned} 3b)&t^2(t^2-1)h'(t)h''(t)-2th'(t)^2+(t^2-4t+3)h'(t)+2t(t-1)^2h''(t)=0\,.&\end{aligned}$$

(5.25)

With the support of Mathematica, the only solution that also satisfies the remaining inequalities turns out to be

$$\begin{aligned} h(t)&{=}\frac{1}{2ct}\left[ 1+\sqrt{4ct+(1+t)^2}{+}t^2-2(1+2\sqrt{1+c})t{+}\sqrt{1+2(1+2c)t+t^2}\right] \nonumber \\&\quad +2\log \left( 2(1+c+\sqrt{1+c})\right) \nonumber \\&\quad +\log t-\log \left( 1-2c+t+\sqrt{4ct+(1+t)^2}\right) \nonumber \\&\quad -\log \left( 1+(1+2c)t+\sqrt{4ct+(1+t)^2}\right) \end{aligned}$$

(5.26)

with an arbitrary constant $c>0$. The condition 1) is non-strict in the limit $t\rightarrow \infty$ and condition 2) is non-strict for $t=1$ which is a similar behaviour to that of $W_\text {smooth}(F)$. In the case of $c=1$, condition 4a) is non-strict in the limit $t\rightarrow \infty$ and we obtain

$$\begin{aligned} h(t)= & {} \frac{1}{2t}\left( 1+t^2+(1+t)\sqrt{1+6t+t^2}\right) -\log t\nonumber \\&+\log \left( 1+4t+t^2+(1+t)\sqrt{1+6t+t^2}\right) \end{aligned}$$

(5.27)

as our new least rank-one convex candidate. Note that the relation

$$\begin{aligned} h(t)&=\frac{1}{2}\left( t+\frac{1}{t}+\sqrt{2+t^2+\frac{1}{t^2}+6\left( t+\frac{1}{t}\right) }\right) \\&\quad +\log \left( 4+t+\frac{1}{t}+\sqrt{2+t^2+\frac{1}{t^2}+6\left( t+\frac{1}{t}\right) }\right) =h\left( \frac{1}{t}\right) \end{aligned}$$

implies that h is smooth at $t=1$. Together with the volumetric part $f(z)=-\log z$ we arrive at

which is equivalent to

$$\begin{aligned}&W_\text {3b}(F)=\mathbb {K}(F)+\sqrt{\mathbb {K}^2(F)+3\mathbb {K}(F)}\\&+\log \left( 2+\mathbb {K}(F)+\sqrt{\mathbb {K}^2(F)+3\mathbb {K}(F)}\right) +\log 2-\log \det F\,. \end{aligned}$$

For the last differential equation of Theorem 3.2,

$$\begin{aligned} 4b)&t^2(t^2-1)h'(t)h''(t)-2th'(t)^2+(t^2+4t+3)h'(t)+2t(t+1)^2h''(t)=0\,, \end{aligned}$$

(5.29)

we use Mathematica again, but this time the already known candidate $W_{\text {magic}}^-(F)$ is the only solution which also satisfies the remaining conditions as a least rank-one convex candidate.

5.4 Comparison

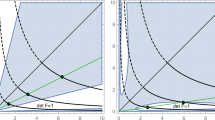
Overall, we have obtained three energy function $W_{\text {magic}}^-(F), W_\text {smooth}(F)$ and $W_\text {3b}(F)$ which satisfy different conditions of Theorem 3.2 by equality (cf. Table 1, Fig. 1). We use them as least rank-one convex representatives of ${\mathfrak {M}}_-$.

Table 1 All three candidates $W_{\text {magic}}^-(F),W_\text {smooth}(F)$ and $W_\text {3b}(F)\in {\mathfrak {M}}_-$ satisfy different conditions of Theorem 3.2 non-strictly; the $\equiv$ indicates equality for all $t\ge 1$

Fig. 1

Visualization of the isochoric part $h:\mathbb {R}_+\rightarrow \mathbb {R}$ with $h(t)=h\bigl (\frac{1}{t}\bigr )$ of the three candidates $W_{\text {magic}}^-, W_\text {smooth}$ and $W_\text {3b}\in {\mathfrak {M}}_-$. The non-convex regions of h are shown by the dashed lines

Unfortunately, we cannot show yet that we identified all least rank-one convex energies in the class ${\mathfrak {M}}_-$. Similar to Sect. 5.2, it is possible to construct more least rank-one convex energies, in the sense that they satisfy at least one inequality condition of Theorem 3.2 non-strictly for an arbitrary $t\in [1,\infty )$ or in the limit $t\rightarrow \infty$ by choosing a different ansatz than equation (5.8). Therefore, it is not sufficient to test these three candidates for quasiconvexity and conclude the quasiconvexity behaviour for the whole energy class ${\mathfrak {M}}_-$. This has the following reasons: First, we only considered the case where the isochoric part satisfies one of the conditions 3a) and 4a) for all $t\ge 1$ or 3b) and 4b) for all $t\ge 1$. This is a more restrictive constraint than needed for rank-one convexity, e.g. it would be sufficient if an energy satisfies condition 3a) for some interval $I\subset \mathbb {R}_+$ and condition 3b) for the remaining part $\mathbb {R}_+\setminus I$. It is only necessary that for every $t\ge 1$ one of the two conditions 3a) or 3b) (and 4a) or 4b) respectively) is satisfied.

It is not clear how to decide which of our three energies $W_{\text {magic}}^-,\,W_\text {smooth},\,W_\text {3b}$ is the best candidate for Morrey’s conjecture because each energy is already least rank-one convex in the sense of satisfying one inequality condition of Theorem 3.2 non-strictly. Thus the difference between two least rank-one convex candidates is neither a rank-one convex nor a rank-one concave function, e.g. the transition from $W_{\text {magic}}^-$ to $W_\text {smooth}$ is done by adding the isochoric part $h(t)=\frac{4}{3}\frac{1}{t}-\frac{2}{3}t$ which is convex but monotone decreasing. An energy function can also be non-rank-one convex and non-concave simultaneously at some $F_0\in {{\,\mathrm{GL}\,}}^{\!+}(2)$, similar to a saddle point. This makes it very challenging, if not impossible, to find a single weakest rank-one convex candidate for ${\mathfrak {M}}_-$.

Still, with separate convexity as the most important part of rank-one convexity, it is reasonable to start with the candidate $W_{\text {magic}}^-(F)$ and check for quasiconvexity. Our first (negative) result in this respect is the following.

Proposition 5.1

The energy

$$\begin{aligned} W_{\text {magic}}^-:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}\,,\quad W_{\text {magic}}^-(F)= & {} \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} + \log \left( \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} \right) - \log (\lambda _{\mathrm{max}} \lambda _{\mathrm{min}})\nonumber \\= & {} \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} - 2\log (\lambda _{\hbox {min}})\,. \end{aligned}$$

is polyconvex.

Proof

We check for polyconvexity with a Theorem due to Šilhavý (2002), Proposition 4.1 (see also Mielke 2005, Theorem 4.1) for energy functions in terms of the (ordered) singular values. It states that any $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ of the form

$$\begin{aligned} W(F) = {\widehat{g}}\big (\lambda _{\hbox {max}},\lambda _{\hbox {min}}\big ) \qquad \text {for all} F\in {{\,\mathrm{GL}\,}}^{\!+}(2)\quad \text {with singular values }\lambda _{\hbox {max}}\ge \lambda _{\hbox {min}}\nonumber \\ \end{aligned}$$

(5.30)

is polyconvex if and only if for every $\gamma _1\ge \gamma _2>0$, there exists

$$\begin{aligned} c\in \left[ -\frac{f_1-f_2}{\gamma _1-\gamma _2}\,,\; \frac{f_1+f_2}{\gamma _1+\gamma _2} \right] ,\quad f_i = \frac{\text {d}}{\text {d}\gamma _i}{\widehat{g}}(\gamma _1,\gamma _2)\,, \end{aligned}$$

(5.31)

such that for all $\nu _1\ge \nu _2>0$,

$$\begin{aligned} {\widehat{g}}(\nu _1,\nu _2) \ge {\widehat{g}}(\gamma _1,\gamma _2) + f_1(\nu _1-\gamma _1) + f_2(\nu _2-\gamma _2) + c(\nu _1-\gamma _1)(\nu _2-\gamma _2)\,.\nonumber \\ \end{aligned}$$

(5.32)

The energy $W_{\text {magic}}^-$ can be expressed in the form (5.30) with ${\widehat{g}}$ such that

$$\begin{aligned} {\widehat{g}}(x,y) = \frac{x}{y} - 2\log (y) \end{aligned}$$

for $x>y>0$. In particular, for $\gamma _1\ge \gamma _2>0$,

$$\begin{aligned} f_1&= \frac{\text {d}}{\text {d}\gamma _1}{\widehat{g}}(\gamma _1,\gamma _2) = \frac{\text {d}}{\text {d}\gamma _1}\left[ \frac{\gamma _1}{\gamma _2} - 2\log (\gamma _2) \right] = \frac{1}{\gamma _2}\,,\nonumber \\ f_2&= \frac{\text {d}}{\text {d}\gamma _2}{\widehat{g}}(\gamma _1,\gamma _2) = \frac{\text {d}}{\text {d}\gamma _2}\left[ \frac{\gamma _1}{\gamma _2} - 2\log (\gamma _2)\right] = -\frac{2}{\gamma _2} - \frac{\gamma _1}{\gamma _2^2} = -\frac{2\gamma _2+\gamma _1}{\gamma _2^2}\,. \end{aligned}$$

(5.33)

Now, for any given $\gamma _1\ge \gamma _2>0$, choose

$$\begin{aligned} c = \frac{f_1+f_2}{\gamma _1+\gamma _2} = \frac{\frac{1}{\gamma _2}-\frac{2\gamma _2+\gamma _1}{\gamma _2^2}}{\gamma _1+\gamma _2} = \frac{\frac{-\gamma _2-\gamma _1}{\gamma _2^2}}{\gamma _1+\gamma _2} = - \frac{1}{\gamma _2^2}\cdot \frac{\gamma _1+\gamma _2}{\gamma _1+\gamma _2} = -\frac{1}{\gamma _2^2}\,. \end{aligned}$$

In order to establish the proposition, it suffices to show that for any $\nu _1\ge \nu _2>0$,

$$\begin{aligned} 0&\le {\widehat{g}}(\nu _1,\nu _2) - {\widehat{g}}(\gamma _1,\gamma _2) - f_1(\nu _1-\gamma _1) - f_2(\nu _2-\gamma _2) - c(\nu _1-\gamma _1)(\nu _2-\gamma _2)\nonumber \\&= \frac{\nu _1}{\nu _2} - 2\log (\nu _2) - \frac{\gamma _1}{\gamma _2} + 2\log (\gamma _2) - f_1(\nu _1-\gamma _1) - f_2(\nu _2-\gamma _2) - c(\nu _1-\gamma _1)(\nu _2-\gamma _2)\nonumber \\&= \frac{\nu _1}{\nu _2} - \frac{\gamma _1}{\gamma _2} + 2\log \left( \frac{\gamma _2}{\nu _2}\right) - \frac{1}{\gamma _2}\cdot (\nu _1-\gamma _1) + \frac{2\gamma _2+\gamma _1}{\gamma _2^2}\cdot (\nu _2-\gamma _2) + \frac{1}{\gamma _2^2}\cdot (\nu _1-\gamma _1)(\nu _2-\gamma _2)\nonumber \\&= \frac{\nu _1}{\nu _2} - \frac{\gamma _1}{\gamma _2} + 2\log \left( \frac{\gamma _2}{\nu _2}\right) - \frac{\nu _1}{\gamma _2} + \frac{\gamma _1}{\gamma _2} + \frac{1}{\gamma _{2}^{2}}\cdot \bigl ( (2\gamma _2+\gamma _1)(\nu _2-\gamma _2) + (\nu _1-\gamma _1)(\nu _2-\gamma _2) \bigr )\nonumber \\&= \frac{\nu _1}{\nu _2} - \frac{\nu _1}{\gamma _2} + 2\log \left( \frac{\gamma _2}{\nu _2}\right) + \frac{1}{\gamma _2^2}(2\gamma _{2}+\nu _1)(\nu _2-\gamma _2)\nonumber \\&= \nu _1\cdot \left( \frac{1}{\nu _2} - \frac{1}{\gamma _2} + \frac{\nu _2-\gamma _2}{\gamma _{2}^{2}} \right) + 2\log \left( \frac{\gamma _2}{\nu _2}\right) + \frac{1}{\gamma _2^2}\cdot 2\gamma _2\cdot (\nu _2-\gamma _2)\nonumber \\&= \nu _1\cdot \frac{\gamma _{2}^{2}-\gamma _2\nu _2+\nu _2^2-\gamma _2\nu _2}{\gamma _{2}^{2}\nu _2} + 2\log \left( \frac{\gamma _2}{\nu _2}\right) + \frac{2(\nu _2-\gamma _2)}{\gamma _2}\nonumber \\&= \nu _1\cdot \frac{(\gamma _2-\nu _2)^2}{\gamma _{2}^{2}\nu _2} + 2\log \left( \frac{\gamma _2}{\nu _2}\right) + 2\frac{\nu _2}{\gamma _2} - 2\,. \end{aligned}$$

(5.34)

Since $\nu _1\ge \nu _2>0$ by assumption,

$$\begin{aligned}&\nu _1\cdot \frac{(\gamma _2-\nu _2)^2}{\gamma _2^2\nu _2} + 2\log \left( \frac{\gamma _2}{\nu _2}\right) + 2\frac{\nu _2}{\gamma _2} - 2\nonumber \\&\quad \ge \nu _2\cdot \frac{(\gamma _2-\nu _2)^2}{\gamma _2^2\nu _2} + 2\log \left( \frac{\gamma _2}{\nu _2}\right) + 2\frac{\nu _2}{\gamma _2} - 2\nonumber \\&\quad = \frac{\gamma _2^2-2\gamma _2\nu _2+\nu _2^2}{\gamma _2^2} + 2\log \left( \frac{\gamma _2}{\nu _2}\right) + 2\frac{\nu _2}{\gamma _2} - 2\nonumber \\&\quad = 1 + \left( \frac{\nu _2}{\gamma _2} \right) ^2 - 2\frac{\nu _2}{\gamma _2} + 2\log \left( \frac{\gamma _2}{\nu _2}\right) + 2\frac{\nu _2}{\gamma _2} - 2\nonumber \\&\quad = \left( \frac{\nu _2}{\gamma _2} \right) ^2 + 2\log \left( \frac{\gamma _2}{\nu _2}\right) - 1 \;=\; \left( \frac{\nu _2}{\gamma _2} \right) ^2 - \log \left( \left( \frac{\nu _2}{\gamma _2}\right) ^2\right) - 1 \;\ge \; 0\,, \end{aligned}$$

(5.35)

where the final inequality holds since $t\ge 1+\log (t)$ for all $t>0$. $\square$

Fig. 2

Overview of the reduction from Morrey’s question for the class of isotropic planar energies with an additive volumetric-isochoric split to the question whether or not the least rank-one convex candidates are quasiconvex. For energies with a convex isochoric term h(t) it is sufficient to test the non-polyconvex candidate $W_{\text {magic}}^+$. Energies with a non-convex isochoric term h(t) cannot be reduced to a single candidate ($W_{\text {magic}}^-,\;W_\text {smooth},\;W_\text {3b},\ldots$) and it remains to show whether or not there exists a non-polyconvex representative

6 Connection to the Burkholder Functional

Recall that quasiconvexity of $W_{\text {magic}}^+(F)$ would imply quasiconvexity for all rank-one convex energies with an additive volumetric-isochoric split and a convex isochoric part, while proving the opposite would lead to an example of Morrey’s conjecture.

Definition 6.1

For an energy function $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow \mathbb {R}$, we define its Shield transformation (Shield 1967; Ball 1977) as

$$\begin{aligned} W^\#:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow \mathbb {R}\,,\qquad W^\#(F)=\det (F)\cdot W(F^{-1})\,. \end{aligned}$$

(6.1)

Lemma 6.2

Let $W,W_1,W_2:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow \mathbb {R}$. Then

• (i) $W^{\#\#}=W$,

• (ii) $W_1\le W_2$ if and only if $W_1^\#\le W_2^\#$,

• (iii) W is rank-one convex if and only if $W^\#$ is rank-one convex,

• (iv) W is $C_0^\infty$-quasiconvex if and only if $W^\#$ is $C_0^\infty$-quasiconvex,$^{6}$

• (v) W is polyconvex if and only if $W^\#$ is polyconvex.

Proof

The equality

$$\begin{aligned} W^{\#\#}(F) = \det (F)\cdot W^\#(F^{-1}) = \det (F)\cdot [\det (F^{-1})\cdot W((F^{-1})^{-1})] = W(F) \end{aligned}$$

directly establishes (i). Now, if $W_1\le W_2$, i.e. $W_1(F)\le W_2(F)$ for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$, then

$$\begin{aligned} W_1^\#(F) = \det (F)\cdot W_1(F^{-1}) \le \det (F)\cdot W_2(F^{-1}) = W_2^\#(F) \end{aligned}$$

which, combined with (i), establishes (ii). Finally, the invariance of rank-one convexity, quasiconvexity⁶ and polyconvexity under the Shield transformation are well known (Ball 1977, Theorem 2.6), and the equivalence can thus be inferred from i).

$\square$

Note that (classical) convexity of W is not equivalent to the convexity of $W^\#$ for dimension $n\ge 2$; for example, the constant mapping $W\equiv 1$ is convex, whereas $W^\#(F)=\det F$ is not. Furthermore, in the one-dimensional case, the invariance of the convexity properties can be expressed as the equivalence

$$\begin{aligned} f:\mathbb {R}_+\rightarrow \mathbb {R}\,\, \text {is convex}\quad \Longleftrightarrow \quad f^\#:\mathbb {R}_+\rightarrow \mathbb {R}\,,\quad f^\#(t) = t\cdot f\left( \frac{1}{t}\right) \quad \text {is convex}\,, \end{aligned}$$

which is related to the study of so-called reciprocally convex functions (Merkle 2004, Lemma 2.2) and, for $f\in C^2(\mathbb {R}_+)$, follows directly from the equality

$$\begin{aligned} \frac{\text {d}^2}{\text {d}t^2}\left[ t\cdot f\left( \frac{1}{t}\right) \right] = \frac{\text {d}}{\text {d}t}\left[ f\left( \frac{1}{t}\right) - \frac{1}{t}f'\left( \frac{1}{t}\right) \right] = \frac{1}{t^3}f''\left( \frac{1}{t}\right) ,\qquad t>0\,. \end{aligned}$$

Applying now the Shield transformation, we show a surprising connection between our candidate $W_{\text {magic}}^+(F)$ and the work of Iwaniec in the field of complex analysis and the so-called Burkholder functional. Using the connection $\mathbb {C}^2\cong \mathbb {R}^{2\times 2}$ we arrive at a much more general settings of functions $W:\mathbb {R}^{2\times 2}\rightarrow \mathbb {R}$ without a volumetric-isochoric split defined on the linear space $\mathbb {R}^{2\times 2}$ instead ${{\,\mathrm{GL}\,}}^{\!+}(2)$.

6.1 The Burkholder Functional

In the following, we sketch an alternative approach to obtain the energy candidate

$$\begin{aligned} W_{\text {magic}}^+(F)=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}-\log \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}+\log \det F=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}+ 2\log \lambda _{\hbox {min}}\,. \end{aligned}$$

(6.2)

Theorem 6.3

(Iwaniec 2002, 1999, Proposition 5.1) The function

$$\begin{aligned} W_\mathrm{{IW}}^-:\mathbb {R}^{n\times n}\rightarrow \mathbb {R}\,,\qquad W_\mathrm{{IW}}^-(F)=\underbrace{|1-\frac{n}{p} |}_{{=}{:}c}\,{\varvec{|}}F{\varvec{|}}^p-{\varvec{|}}F{\varvec{|}}^{p-n}\det F \end{aligned}$$

(6.3)

is rank-one convex for all $p\ge \frac{n}{2}$. Furthermore, the factor $c=|1-\frac{n}{p} |$ is the smallest possible constant for which this statement is true.

Here ${\varvec{|}}F{\varvec{|}}:=\sup _{\Vert \xi \Vert =1}\Vert F\xi \Vert _{\mathbb {R}^2}=\lambda _{\hbox {max}}$ denotes the operator norm (i.e. the largest singular value) of F. The function $W_{\mathrm{IW}}^-$ is homogeneous of degreee p, i.e. $W(\alpha F)=\alpha ^pW(F)$, but it is a non-polynomial function due to its dependence⁷ on ${\varvec{|}}F{\varvec{|}}$. Moreover, the function is not isotropic but only hemitropic⁸ (not right-${{\,\mathrm{O}\,}}(2)$-invariant).

We continue with the planar case ($n=2$) and restrict the investigation to $p\ge 2$:

$$\begin{aligned} W_{\text {IW}}^-(F)&=|\underbrace{1-\frac{2}{p}}_{>0} |\,{\varvec{|}}F{\varvec{|}}^p-{\varvec{|}}F{\varvec{|}}^{p-2}\det F=\left[ -\det F+\left( 1-\frac{2}{p}\right) {\varvec{|}}F{\varvec{|}}^2\right] {\varvec{|}}F{\varvec{|}}^{p-2}\,. \end{aligned}$$

(6.4)

Let us define

$$\begin{aligned} B_p(F)\,:=\,\frac{p}{2}W_{\mathrm{IW}}^-(F)&=-\left[ \frac{p}{2}\det F+\left( 1-\frac{p}{2}\right) {\varvec{|}}F{\varvec{|}}^2\right] {\varvec{|}}F{\varvec{|}}^{p-2}\,, \end{aligned}$$

(6.5)

where

$$\begin{aligned} B_p(F)&=-\left( \frac{p}{2}\det F+\left( 1-\frac{p}{2}\right) \lambda _{\hbox {max}}^2\right) \lambda _{\hbox {max}}^{p-2}=-\frac{p}{2}\det F\lambda _{\hbox {max}}^{p-2}-\frac{2-p}{2}\lambda _{\hbox {max}}^p\nonumber \\&=-\frac{p}{2}\det F\left( \frac{\Vert F \Vert ^2+\sqrt{\Vert F \Vert ^4-4(\det F)^2}}{2}\right) ^\frac{p-2}{2}\nonumber \\&\quad -\frac{2-p}{2}\left( \frac{\Vert F \Vert ^2+\sqrt{\Vert F \Vert ^4-4(\det F)^2}}{2}\right) ^\frac{p}{2} \end{aligned}$$

(6.6)

is also known as the Burkholder functional⁹ (Burkholder 1988; Astala et al. 2012). It is already established that the function $B_p$ is rank-one convex and satisfies a quasiconvexity property at the identity $F=\mathbb {1}$ in the case of smooth non-positive integrands (Astala et al. 2012, Theorem 1.2), namely if $\vartheta \subset C_0^\infty (\Omega ;\mathbb {R}^2)$ and $B_p(\mathbb {1}+\nabla \vartheta (x))\le 0$ for all $x\in \Omega$, then

$$\begin{aligned} \int _\Omega B_p(\mathbb {1}+\nabla \vartheta (x))\,{\text {d}x}\ge \int _\Omega B_p(\mathbb {1})\,{\text {d}x}=-|\Omega |\,,\qquad p\ge 2\,. \end{aligned}$$

(6.7)

Lemma 6.4

(Burkholder 1988) The function $B_p:\mathbb {R}^{2\times 2}\rightarrow \mathbb {R}$ with

$$\begin{aligned} B_p(F)=-\left[ \frac{p}{2}\det F+\left( 1-\frac{p}{2}\right) {\varvec{|}}F{\varvec{|}}^2\right] {\varvec{|}}F{\varvec{|}}^{p-2},\qquad p\ge 2\,, \end{aligned}$$

is rank-one convex.

Proof

For the convenience of the reader, we add the proof from Burkholder (1988): We use the connection to complex analysis $\mathbb {R}^{2\times 2}\cong \mathbb {C}^2$ (cf. “Appendix”) where we identify

$$\begin{aligned} F(z,w):=\begin{pmatrix} \Re z+\Re w &{} \Im w -\Im z\\ \Im z+\Im w &{} \Re z-\Re w \end{pmatrix} \end{aligned}$$

(6.8)

and transform the Burkholder function $B_p(F)$ to a function $L_p:\mathbb {C}\times \mathbb {C}\rightarrow \mathbb {R}$ with

$$\begin{aligned} L_p(z,w)=\left( |z |-(p-1)|w |\right) \left( |z | +|w |\right) ^{p-1}. \end{aligned}$$

(6.9)

Then $B_p(F(z,w))=-L_p(z,w)$ and, for rank-one matrices $\xi \otimes \eta$ with $\xi ,\eta \in \mathbb {R}^2$, we find

$$\begin{aligned} B_p(F(z,w)+t\xi \otimes \eta )=-L_p(z+th,w+tk)\,, \end{aligned}$$

(6.10)

where

$$\begin{aligned} \begin{pmatrix} \xi _1\eta _1 &{} \xi _1\eta _2\\ \xi _2\eta _1 &{} \xi _1\eta _2 \end{pmatrix}=\begin{pmatrix} \Re h+\Re k &{} \Im k -\Im h\\ \Im h+\Im k &{} \Re h-\Re k \end{pmatrix}\quad \Longleftrightarrow \quad \begin{matrix} \Re h=\frac{1}{2}\left( \xi _1\eta _1+\xi _2\eta _2\right) ,&{}\Re k=\frac{1}{2}\left( \xi _1\eta _1-\xi _2\eta _2\right) ,\\ \Im h=\frac{1}{2}\left( \xi _2\eta _1-\xi _1\eta _2\right) ,&{}\Im k=\frac{1}{2}\left( \xi _1\eta _2+\xi _2\eta _1\right) . \end{matrix} \end{aligned}$$

In addition, for rank-one matrices with this definition,

$$\begin{aligned} 4|h |^2&=|2\Re h |^2+|2\Im h |^2=(\xi _1\eta _1+\xi _2\eta _2)^2+(\xi _2\eta _1-\xi _1\eta _2)^2\nonumber \\&=\xi _1^2\eta _1^2+2\xi _1\eta _1\xi _2\eta _2+\xi _2^2\eta _2^2+\xi _2^2\eta _1^2-2\xi _2\eta _1\xi _1\eta _2+\xi _1^2\eta _2^2\nonumber \\&=\xi _1^2\eta _1^2+\xi _1^2\eta _2^2+\xi _2^2\eta _1^2+\xi _2^2\eta _2^2\nonumber \\&=\xi _1^2\eta _1^2-2\xi _1\eta _1\xi _2\eta _2+\xi _2^2\eta _2^2+\xi _1^2\eta _2^2+2\xi _1\eta _2\xi _2\eta _1+\xi _2^2\eta _1^2\nonumber \\&=(\xi _1\eta _1-\xi _2\eta _2)^2+(\xi _1\eta _2+\xi _2\eta _1)^2\nonumber \\&=|2\Re k |^2+|2\Im k |^2=4|k |^2\qquad \implies \qquad |h |=|k |. \end{aligned}$$

(6.11)

Now the rank-one convexity of $B_p(F)$ follows from the concavity of $-L_p(z+th,w+tk)$ (cf. Burkholder 1988, Eq. (1.14)), i.e. the observation that for all $z,w,h,k\in \mathbb {C}$ with $|k |\le |h |$ the mapping

$$\begin{aligned} t\mapsto -L_p(z+th,w+tk) \end{aligned}$$

(6.12)

is concave on $\mathbb {R}$. $\square$

The function of Burkholder plays an important role in the martingale study of the Beurling-Ahlfors operator (cf. “Appendix”) where several open questions (in particular an important conjecture of Iwaniec and Martin 1993) could be answered by showing that $B_p(F)$ is quasiconvex.

In case of $p=2$ the energy function $B_2(F)$ is a null Lagrangian since

$$\begin{aligned} B_2(F)=-\left[ \det F+\left( 1-1\right) {\varvec{|}}F{\varvec{|}}^2\right] {\varvec{|}}F{\varvec{|}}^{2-2}=-\det F\,. \end{aligned}$$

(6.13)

Therefore, the expression $B_p(F)- B_2(F)$ has the same convexity behaviour as $B_p$ itself and we can formally compute the derivative with respect to p. We define

$$\begin{aligned} B_\star (F)&:=\lim _{p\searrow 2}\frac{ B_p(F)- B_2(F)}{p-2}=\frac{\text {d}}{\text {d}p}B_p(F)|_{p=2}\nonumber \\&=\frac{\text {d}}{\text {d}p}\left[ \left( -\frac{p}{2}\det F+\left( \frac{p}{2}-1\right) {\varvec{|}}F{\varvec{|}}^2\right) e^{(p-2)\log {\varvec{|}}F{\varvec{|}}}\right] _{p=2}\nonumber \\&=-\frac{1}{2}\det F+\frac{1}{2}{\varvec{|}}F{\varvec{|}}^2+\left( -\det F+0\right) \log {\varvec{|}}F{\varvec{|}}\nonumber \\&=-\frac{1}{2}\left( 1+2\log {\varvec{|}}F{\varvec{|}}\right) \det F+\frac{1}{2}{\varvec{|}}F{\varvec{|}}^2\nonumber \\&=-\frac{1}{2}\left( 1+\log \big ({\varvec{|}}F{\varvec{|}}^2\big )\right) \det F+\frac{1}{2}{\varvec{|}}F{\varvec{|}}^2. \end{aligned}$$

(6.14)

The function $B_\star$ remains globally rank-one convex and quasiconvex at the identity.¹⁰ If we restrict $B_\star$ to ${{\,\mathrm{GL}\,}}^{\!+}(2)$, we may now calculate its Shield transformation (Astala et al. 2012)

$$\begin{aligned} B^\#_\star (F)&=\det F\cdot B_\star (F^{-1})=\det F\left[ -\frac{1}{2}\left( 1+\log \big ({\varvec{|}}F^{-1}{\varvec{|}}^2\big )\right) \det (F^{-1})+\frac{1}{2}{\varvec{|}}F^{-1}{\varvec{|}}^2\right] \nonumber \\&=-\frac{1}{2}-\log {\varvec{|}}F^{-1}{\varvec{|}}+\frac{1}{2}\det F{\varvec{|}}F^{-1}{\varvec{|}}^2\nonumber \\&=-\frac{1}{2}-\log \left( \frac{{\varvec{|}}F{\varvec{|}}}{\det F}\right) +\frac{1}{2}\det F\frac{{\varvec{|}}F{\varvec{|}}^2}{(\det F)^2}\nonumber \\&=-\frac{1}{2}-\log {\varvec{|}}F{\varvec{|}}+\log \det F+\frac{1}{2}\frac{{\varvec{|}}F{\varvec{|}}^2}{\det F}\,, \end{aligned}$$

(6.15)

where we have used that in the two-dimensional case,

$$\begin{aligned} {\varvec{|}}F^{-1}{\varvec{|}}=\frac{1}{\lambda _{\hbox {min}}}=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}\lambda _{\hbox {max}}}=\frac{{\varvec{|}}F{\varvec{|}}}{\det F}\,. \end{aligned}$$

Omitting the additive constant $-\frac{1}{2}$ in Eq. (6.15), which has no effect on the convexity behaviour, we arrive at

$$\begin{aligned} B^\#_\star (F)+\frac{1}{2}&=\frac{1}{2}\frac{{\varvec{|}}F{\varvec{|}}^2}{\det F}-\log {\varvec{|}}F{\varvec{|}}+\log \det F\nonumber \\&=\frac{1}{2}\frac{\lambda _{\hbox {max}}^2}{\lambda _{\hbox {max}}\lambda _{\hbox {min}}}-\log \lambda _{\hbox {max}}+\log (\lambda _{\hbox {max}}\lambda _{\hbox {min}}) \nonumber \\&=\frac{1}{2}\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} +\log \lambda _{\hbox {min}}=\frac{1}{2}W_{\text {magic}}^+(F)\,. \end{aligned}$$

(6.16)

In particular, Lemma 6.2 and Theorem 6.3 also imply that $W_{\text {magic}}^+(F)$ is rank-one convex.

An overview of the relation between our energy candidate $W_{\text {magic}}^+(F)$ and the Burkholder functional $B_p(F)$ is visualized in Fig. 3. Again, while we try to find an example to settle Morrey’s question, i.e. show that our energy function $W_{\text {magic}}^+(F)$ is not quasiconvex, in the topic of martingale study, it is sought to prove that $B_p(F)$ is quasiconvex to positively affirm some estimates in function theory, see “Appendix” for more information.

Fig. 3

Connection between the Burkholder functional $B_p(F)$ and our energy candidate $W_{\text {magic}}^+(F)$ as a chance to check Morrey’s conjecture, where ${\varvec{|}}F{\varvec{|}}=\sup _{\Vert \xi \Vert =1}\Vert F\xi \Vert _{\mathbb {R}^2}=\lambda _{\hbox {max}}$ denotes the operator norm (i.e. the largest singular value) of F

7 Radially Symmetric Deformations

Radial deformations play an important role for planar quasiconvexity. For isotropic materials, it seems reasonable that any global minimizer under radial boundary conditions is radial, but such a symmetry statement may cease to hold for non-convex nonlinear problems¹¹ (Brock et al. 1996). A deformation is radial if there exists a function $v:[0,\infty )\rightarrow \mathbb {R}$ such that

$$\begin{aligned} \varphi (x)=v(\Vert x \Vert )\frac{x}{\Vert x \Vert }\qquad \text {with}\quad v(0)=0\,. \end{aligned}$$

(7.3)

In that case,

$$\begin{aligned} \nabla \varphi (x)&=\frac{v(\Vert x \Vert )}{\Vert x \Vert }\mathbb {1}_2 +\left( \frac{v'(\Vert x \Vert )\frac{x}{\Vert x \Vert }\Vert x \Vert -v(\Vert x \Vert )\frac{x}{\Vert x \Vert }}{\Vert x \Vert ^2}\right) \otimes x\nonumber \\&=\frac{v(\Vert x \Vert )}{\Vert x \Vert }\mathbb {1}_2+\left( v'(\Vert x \Vert )-\frac{v(\Vert x \Vert )}{\Vert x \Vert }\right) \frac{1}{{\Vert x \Vert }^2}x\otimes x\,, \end{aligned}$$

(7.1)

with the singular values of $\nabla \varphi (x)$ given by

$$\begin{aligned} \lambda _1=v'(\Vert x \Vert )\,,\qquad \lambda _2=\frac{v(\Vert x \Vert )}{\Vert x \Vert }\,. \end{aligned}$$

(7.4)

Using mappings of this type, it is possible to construct an extensive class of inhomogeneous deformations for which the energy value of $W_{\text {magic}}^+$ is identical to that of the homogeneous deformation (cf. Lemma 7.3). In particular, this implies that the homogeneous solution to the energy minimization problem is neither unique nor stable.

First, however, it is important to note that radial mappings cannot serve as a counterexample to Morrey’s conjecture, since rank-one convexity of an energy is already sufficient for a homogeneous mapping to be energetically optimal among all radial deformations.

Lemma 7.1

(Ball 1987) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ be an isotropic, objective and separately convex energy function and $g(\lambda _1,\lambda _2)=W(F)$ with $\lambda _1,\lambda _2$ as the singular values of F. If $F_0\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ is a homogeneous radial mapping, i.e. $F_0=\lambda \mathbb {1}$ with $\lambda \in \mathbb {R}_+$, then

$$\begin{aligned} \int _{B_1(0)}W(\nabla \varphi (x))\,{\text {d}x}\ge \int _{B_1(0)}W(F_0)\,{\text {d}x}=\pi g(\lambda ,\lambda ) \end{aligned}$$

(7.5)

for all radial deformations $\varphi$ of the form (7.2) with $\varphi |_{\partial B_1(0)}(x)=F_0x$.

Proof

For the homogeneous radial deformation gradient of the form $F_0=\lambda \mathbb {1}$, we compute

$$\begin{aligned} \int _{B_1(0)}W(\lambda \mathbb {1}){\text {d}x}_1{\text {d}x}_2=2\pi \int _0^1 r g\left( \lambda ,\lambda \right) {\text {d}r}=2\pi g\left( \lambda ,\lambda \right) \left[ \frac{r^2}{2}\right] _0^1=\pi g(\lambda ,\lambda )\,. \end{aligned}$$

(7.6)

For an arbitrary radial deformation $\varphi (x)=v(\Vert x \Vert )\frac{x}{\Vert x \Vert }=g\left( v'(\Vert x \Vert ),\frac{v(\Vert x \Vert )}{\Vert x \Vert }\right)$, we write

$$\begin{aligned}&\int _{B_1(0)}W(\nabla \varphi (x_1,x_2))\,{\text {d}x}_1{\text {d}x}_2=\int _{B_1(0)}g(\lambda _1,\lambda _2)\,{\text {d}x}_1{\text {d}x}_2\nonumber \\&=\int _0^{2\pi }\int _0^1 g\left( v',\frac{v}{r}\right) r{\text {d}r}\text {d}\vartheta =2\pi \int _0^1 r g\left( v',\frac{v}{r}\right) {\text {d}r}\,. \end{aligned}$$

Separate convexity of g in the first argument ensures

$$\begin{aligned} g(x_2,y)\ge g(x_1,y)+(x_2-x_1)g_x(x_1,y)\qquad \text {for all}\quad x_1,x_2,y\in \mathbb {R}\,. \end{aligned}$$

Setting symbolically $x_1=y=\frac{v}{r}$ and $x_2=v'$ implies

$$\begin{aligned} g\left( v',\frac{v}{r}\right)&\ge g\left( \frac{v}{r},\frac{v}{r}\right) +\left( v'-\frac{v}{r}\right) g_x\left( \frac{v}{r},\frac{v}{r}\right) . \end{aligned}$$

(7.7)

Thus we compute

$$\begin{aligned} \int _{B_1(0)}W(\nabla \varphi (x_1,x_2))\,{\text {d}x}&=2\pi \int _0^1 r g\left( v',\frac{v}{r}\right) {\text {d}r}\nonumber \\&\ge 2\pi \int _0^1 r\left[ g\left( \frac{v}{r},\frac{v}{r}\right) +\left( v'-\frac{v}{r}\right) g_x\left( \frac{v}{r},\frac{v}{r}\right) \right] {\text {d}r}\nonumber \\&\overset{{(*)}}{=}2\pi \int _0^1 \frac{\text {d}}{\text {d}r}\left[ \frac{r^2}{2} g\left( \frac{v(r)}{r},\frac{v(r)}{r}\right) \right] {\text {d}r}\nonumber \\&=\pi \left[ r^2 g\left( \frac{v(r)}{r},\frac{v(r)}{r}\right) \right] _0^1=\pi g(\lambda ,\lambda ) \end{aligned}$$

(7.8)

with $\lambda =v(1)$ and $v(0)=0$. Equality $(*)$ follows from

$$\begin{aligned}&\frac{\text {d}}{\text {d}r}\left[ \frac{r^2}{2} g\left( \frac{v(r)}{r},\frac{v(r)}{r}\right) \right] =r g\left( \frac{v(r)}{r},\frac{v(r)}{r}\right) +r^2g_x\left( \frac{v(r)}{r},\frac{v(r)}{r}\right) \left( \frac{v'(r)}{r}-\frac{v(r)}{r^2}\right) \nonumber \\&\quad =r\left[ g\left( \frac{v(r)}{r},\frac{v(r)}{r}\right) +\left( v'(r)-\frac{v(r)}{r}\right) g_x\left( \frac{v(r)}{r},\frac{v(r)}{r}\right) \right] , \end{aligned}$$

(7.9)

where we used the equality $g_x(\lambda ,\lambda )=g_y(\lambda ,\lambda )$; note that $g(\lambda _1,\lambda _2)=g(\lambda _2,\lambda _1)$ due to the isotropy of W. Overall,

$$\begin{aligned} \int _{B_1(0)}W(\nabla \varphi (x_1,x_2))\,{\text {d}x}\ge \pi g(\lambda ,\lambda )=\int _{B_1(0)}W(F_0)\,{\text {d}x}\,. \end{aligned}$$

$\square$

7.1 Expanding and Contracting Deformations

In general, non-trivial radial deformations do not have the same energy value as the homogeneous deformation $\varphi _0(x)=\lambda x$, especially if the energy is strictly separately convex. However, there exist non-trivial examples for the Burkholder energy $B_p(F)$ as well as for the energy $W_{\text {magic}}^+(F)$ for which equality holds. In order to construct such deformations, we first consider the general class of radial functions with $v(0)=0$ and $v(R)=R$ which keep the center point and exterior radius constant. More specifically, we consider the subclasses of expanding and contracting functions

$$\begin{aligned} {\mathcal {V}}_R:=&\left\{ v\in C^1([0,R])\,\big |\,v(0)=0\,,\;v(R)=R\,,\; \frac{v(r)}{r}\ge v'(r)\ge 0\quad \forall \; r\in [0,R]\right\} , \end{aligned}$$

(expanding)

$$\begin{aligned} {\mathcal {V}}_R^{-1}=&\left\{ v\in C^1([0,R])\,\big |\,v(0)=0\,,\;v(R)=R\,,\; v'(r)\ge \frac{v(r)}{r}\ge 0\quad \forall \; r\in [0,R]\right\} , \end{aligned}$$

(contracting)

for which the order of the singular values $\lambda _{\hbox {min}}$ and $\lambda _{\hbox {max}}$ remains fixed.¹² The class ${\mathcal {V}}_R$ of expanding functions can be described by radial functions for which the gradient of the tangent in a point (r, v(r)) is smaller then the gradient of the secant of the origin with (r, v(r)) for any $r\in [0,R]$ as shown in Fig. 4.

In contrast, the class ${\mathcal {V}}_R^{-1}$ of contracting functions contains any radial functions v such that the gradient of the tangent in a point (r, v(r)) is larger than the gradient of the secant of the origin with (r, v(r)) for any $r\in [0,R]$ as shown in Fig. 4. The connection between ${\mathcal {V}}_R$ and ${\mathcal {V}}_R^{-1}$ is given by the inverse function theorem: For an arbitrary $v\in {\mathcal {V}}_R$ with $r\mapsto v(r)$ and its inverse function $v^{-1}\in {\mathcal {V}}_R^{-1}$ with $t\mapsto v^{-1}(t)$, we find

$$\begin{aligned}&v^{-1}(t)=\frac{1}{v'\big (v^{-1}(t)\big )} \ge \frac{v^{-1}(t)}{t} \nonumber \\&\Longleftrightarrow \quad \frac{t}{v^{-1}(t)}\ge v'\big (v^{-1}(t)\big )\quad \Longleftrightarrow \quad \frac{v(r)}{r}\ge v'(r)\,. \end{aligned}$$

(7.10)

Fig. 4

Left: Visualization of an expanding radial function $v_1\in {\mathcal {V}}_R$ with $v_1(r)>r$. Right: Visualization of a contracting radial function $v_2\in {\mathcal {V}}_R^{-1}$ with $v_2(r)<r$ which is the inverse of $v_1$

Lemma 7.2

(Astala et al. 2012) The energy value of the Burkholder energy is constant on the class of expanding functions ${\mathcal {V}}_R$, i.e.

$$\begin{aligned} \int _{B_R(0)}B_p(\nabla \varphi )\,{\text {d}x}=\int _{B_R(0)}B_p(\mathbb {1})\,{\text {d}x}\end{aligned}$$

(7.11)

for all radial deformations $\varphi (x)=v(\Vert x \Vert )\frac{x}{\Vert x \Vert }$ with $v\in {\mathcal {V}}_R$, where $B_R(0)$ denotes the ball with radius R and center 0.

Proof

For $v\in {\mathcal {V}}_R$ we have $\lambda _{\hbox {max}}=\frac{v(\Vert x \Vert )}{\Vert x \Vert }\ge v'(\Vert x \Vert )=\lambda _{\hbox {min}}\ge 0$ and calculate

$$\begin{aligned} \int _{B_R(0)}-B_p(\nabla \varphi )\,{\text {d}x}&=\int _{B_R(0)}\frac{p}{2}\frac{v'(\Vert x \Vert )v(\Vert x \Vert )^{p-1}}{\Vert x \Vert ^{p-1}}+\frac{2-p}{2}\frac{v(\Vert x \Vert )^p}{\Vert x \Vert ^p}\,{\text {d}x}\nonumber \\&=2\pi \int _0^R\left( \frac{p}{2}\frac{v'(r)v(r)^{p-1}}{r^{p-1}}+\frac{2-p}{2}\frac{v(r)^p}{r^p}\right) r\,{\text {d}r}\nonumber \\&=\pi \int _0^R p\frac{v'(r)v(r)^{p-1}}{r^{p-2}}+(2-p)\frac{v(r)^p}{r^{p-1}}\,{\text {d}r}\nonumber \\&=\pi \int _0^R\frac{\text {d}}{\text {d}r}\left[ \frac{v(r)^p}{r^{p-2}}\right] {\text {d}r}=\pi \left[ \frac{v(R)^p}{R^{p-2}}-\lim _{r\rightarrow 0}\frac{v(r)^p}{r^{p-2}}\right] _0^R=\pi R^2\nonumber \\&=\int _{B_R(0)}1\,{\text {d}x}=\int _{B_R(0)}-B_p(\mathbb {1})\,{\text {d}x}\,. \end{aligned}$$

(7.12)

$\square$

The following lemma establishes an analogous result for the function $W_{\text {magic}}^+$ with

$$\begin{aligned} W_{\text {magic}}^+(F)=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}-\log \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}+\log \big (\lambda _{\hbox {max}}\lambda _{\hbox {min}}\big )=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}+2\log \lambda _{\hbox {min}}\,. \end{aligned}$$

(7.13)

Lemma 7.3

The energy value of $W_{\text {magic}}^+$ is constant on the class of contracting functions ${\mathcal {V}}_R^{-1}$, i.e.

$$\begin{aligned} \int _{B_R(0)}W_{\text {magic}}^+(\nabla \varphi )\,{\text {d}x}=\int _{B_R(0)}W_{\text {magic}}^+(\mathbb {1})\,{\text {d}x}\end{aligned}$$

(7.14)

for all radial deformations $\varphi (x)=v(\Vert x \Vert )\frac{x}{\Vert x \Vert }$ with $v\in {\mathcal {V}}_R^{-1}$.

Proof

We first extend Lemma 7.2 to the function $B_\star :{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ with

$$\begin{aligned}&B_\star (F)=\lim _{p\searrow 2}\frac{B_p(F)-B_2(F)}{p-2}=\frac{\text {d}}{\text {d}p}B_p(F)|_{p=2}\\&\quad =-\frac{1}{2}\left( 1+\log \big ({\varvec{|}}F{\varvec{|}}^2\big )\right) \det F+\frac{1}{2}{\varvec{|}}F{\varvec{|}}^2, \end{aligned}$$

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$, where $B_2(F)=\det F$; note that $B_2$ is a null Lagrangian. For expanding deformations defined by ${\mathcal {V}}_R$, we find

$$\begin{aligned} \int _{B_R(0)}B_\star (\nabla \varphi )\,{\text {d}x}&=\int _{B_R(0)}\lim _{p\searrow 2}\frac{B_p(\nabla \varphi )-B_2(\nabla \varphi )}{p-2}\,{\text {d}x}\\&=\lim _{p\searrow 2}\frac{1}{p-2}\int _{B_R(0)}B_p(\nabla \varphi )-B_2(\nabla \varphi )\,{\text {d}x}\\&=\lim _{p\searrow 2}\frac{1}{p-2}\int _{B_R(0)}B_p(\mathbb {1})-B_2(\mathbb {1})\,{\text {d}x}=\int _{B_R(0)}B_\star (\mathbb {1})\,{\text {d}x}\,, \end{aligned}$$

thus the energy potential of $B_\star$ is indeed constant on the class ${\mathcal {V}}_R$. Next, recall that $B_\star$ and $W_{\text {magic}}^+$ are related via the Shield transformation, i.e. that $B_\star ^\#(F)=\frac{1}{2}\bigl (W_{\text {magic}}^+(F)-1\bigr )$ for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$, and that for every expanding radial deformation $\varphi$, its inverse mapping $\varphi ^{-1}$ is a contracting radial deformation, i.e. that for every $v(r)\in {\mathcal {V}}_R^{-1}$ there exists a unique $w(r)\in {\mathcal {V}}_R$ with $w=v^{-1}$. We can therefore apply the general formula

$$\begin{aligned} \int _\Omega W\big (\nabla \varphi (x)\big )\,{\text {d}x}= & {} \int _{\varphi (\Omega )} W\big (\big [\nabla _\xi (\varphi ^{-1})(\xi )\big ]^{-1}\big )\det \nabla _\xi \varphi ^{-1}(\xi )\,{\text {d}\xi }\nonumber \\= & {} \int _{\varphi (\Omega )} W^\#\big (\nabla _\xi (\varphi ^{-1})(\xi )\big )\,{\text {d}\xi }\end{aligned}$$

(7.15)

to $\varphi (\Omega )=\Omega =B_R(0)$ to find

$$\begin{aligned} \int _{B_R(0)}W_{\text {magic}}^+(F_v)\,{\text {d}x}= & {} \int _{B_R(0)}2B_\star (F_w)+1\,{\text {d}x}\nonumber \\= & {} \int _{B_R(0)}2B_\star (\mathbb {1})+1\,{\text {d}x}=\int _{B_R(0)}W_{\text {magic}}^+(\mathbb {1})\,{\text {d}x}\,, \end{aligned}$$

(7.16)

where $F_v$ and $F_w$ are the deformation gradients corresponding to v(r) and $w(r)=v^{-1}(r)$, respectively. $\square$

Both the radial deformations $\varphi (x)=v(\Vert x \Vert )\frac{x}{\Vert x \Vert }$ defined by $v\in {\mathcal {V}}_R$ in Lemma 7.2 and $v\in {\mathcal {V}}_R^{-1}$ in Lemma 7.3 can be extended by Astala et al. (2012)

• (i) Choosing any $F_0=\lambda Q$ instead of $\mathbb {1}$ for arbitrary $\lambda >0$ and $Q\in {{\,\mathrm{SO}\,}}(2)$,

• (ii) Choosing any point $z_0\in \Omega$ instead of the origin,

• (iii) Combining multiple separate balls $B_{R_i}(z_i)$ with $\bigcap _{i}B_{R_i}(z_i)=\emptyset$,

• (iv) Inductively adding more balls $B_{r}(z_0')$ which are contained in a previous ball $B_{R}(z_0)$ under the assumption that the contracting deformation of the outer ball $B_{R}(z_0)$ maintains $F_0=\lambda Q$ at the boundary of the inner ball $B_{r}(z_0')$,

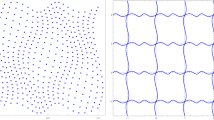
to construct an overall non-radially symmetric deformation (cf. Fig. 5) with the same energy level as the homogeneous deformation.

Fig. 5

Circular packing of several balls with various contracting mappings to achieve an overall non-symmetric deformation, also called piecewise radial mapping. Note that for the right-hand figure, the contraction in the “outer” circles need to satisfy the conditions stated in (iv) above

8 Summary

The class of planar energy functions with an additive volumetric-isochoric split, i.e. functions on ${{\,\mathrm{GL}\,}}^{\!+}(2)$ of the form

$$\begin{aligned} W(F)= & {} h\bigg (\frac{\lambda _1}{\lambda _2}\bigg )+f(\lambda _1\lambda _2)\,,\qquad h,f:\mathbb {R}_+\rightarrow \mathbb {R}\,,\nonumber \\ h(t)= & {} h\bigg (\frac{1}{t}\bigg )\quad \text {for all }\;t\in (0,\infty )\,, \end{aligned}$$

(8.1)

where $\lambda _1,\lambda _2>0$ denote the singular values of F and h, f are given real-valued functions, proves to be a rather interesting subject in the context of Morrey’s conjecture: On the one hand, if neither h nor f is convex, then W is not rank-one convex; on the other hand, convexity of both f and h already implies that W is quasiconvex.

Investigating the remaining cases, we first focused on functions with a convex isochoric part h. In that case, Theorem 4.1 shows that the question whether or not rank-one convexity implies quasiconvexity can be reduced to the question whether the particular (rank-one convex) function $W_{\text {magic}}^+:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow \mathbb {R}$ with

$$\begin{aligned} W_{\text {magic}}^+(F)=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} - \log \left( \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}\right) + \log \det F=\frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}}+2\log \lambda _{\hbox {min}}\end{aligned}$$

(8.2)

is quasiconvex. While $W_{\text {magic}}^+$ is not polyconvex according to Lemma 4.3, determining whether or not $W_{\text {magic}}^+$ is indeed quasiconvex remains an open problem at this point.

The case of volumetric-isochorically split functions with a convex volumetric part f appears to be more involved: In Sect. 5, we identified three “least” rank-one convex functions $W_{\text {magic}}^-(F),\,W_\text {smooth}(F),$ and $W_\text {3b}(F)$, none of which is currently known to be quasiconvex. A comprehensive overview for candidates with an additive volumetric-isochoric split is given in Fig. 2.

8.1 Symmetry and Stability

The energy potential $W_{\text {magic}}^+$ also exhibits a number of interesting properties regarding the relation between symmetry and stability: According to Lemma 7.3, $W_{\text {magic}}^+$ is constant for the non-trivial class of contracting radially symmetric deformations, i.e. $W_{\text {magic}}^+$ allows for inhomogeneous deformations whose energy level is equal to the homogeneous one. This implies that the homogeneous solution to the energy minimization problem is neither unique nor stable.

As shown in Fig. 5, it is thereby possible to construct a non-symmetrical microstructure for the fully isotropic energy potential $W_{\text {magic}}^+$ even if the applied boundary conditions are fully symmetrical. This is in stark contrast to the linear convex case, where such symmetrically posed problems generally yield symmetric solutions; in practice, this observation allows for certain simplifications (e.g. by reducing calculations to any quarter of a cylinder) of symmetric linear problems. However, in the nonlinear non-convex case, it is even possible for a symmetrically stated problem (cf. Eq. (7.1)) to not have a stable symmetric solution at all (Brock et al. 1996). This phenomenon, which is exhibited by the energy function $W_{\text {magic}}^+$ as well, demonstrates a “preference of disorder over order” which can occur in non-(strictly-)quasiconvex problems.

Note that due to Lemma 7.1, radially symmetric deformations cannot be energetically favourable compared to the affine solution even under the weaker assumption of separate convexity. Additionally, in an intriguing article by Kawohl and Sweers (1990), it is shown that the simple assumption $\varphi (x,y)=\varphi (-x,y)$ for the test function $\varphi \in W_0^{1,\infty }(\Omega )$ on the domain $\Omega =(-1,1)^2$ is enough for the transition from rank-one convexity to quasiconvexity. Thus in general, the break of symmetry plays an essential role in stability and, in particular, must be taken into account for the minimization of potentially non-quasiconvex energies.

Appendix: Complex Analysis

As indicated in Sect. 6, the energy function $W_{\text {magic}}^+$ has an intriguing connection to the work of Iwaniec in the field of complex analysis and Burkholder’s martingale theory. Here, we briefly discuss the conversion of the energy $W_{\text {magic}}^+(F)$ into complex notation.

Generally, we now consider a complex-valued function ${\textit{f}}:U\subset \mathbb {C}\rightarrow \mathbb {C}$ with $z\mapsto {\textit{f}}(z)$. (Note that this function ${\textit{f}}$ should not be mistaken with the volumetric part $f:\mathbb {R}_+\rightarrow \mathbb {R}$ used in the additive volumetric-isochoric split.) It is common to use the complex vector $(\partial _z{\textit{f}},\partial _{\overline{z}}{\textit{f}})$ to describe the derivative of a non-holomorphic function on $\mathbb {C}$ instead of the deformation gradient $F=D{\textit{f}}(z)\in \mathbb {R}^{2\times 2}$. Thus we need to rephrase any energy function on $\mathbb {R}^{2\times 2}$ or on ${{\,\mathrm{GL}\,}}^{\!+}(2)$ as a mapping $L:\mathbb {C}\times \mathbb {C}\rightarrow \mathbb {R}$ and consider the corresponding minimization problem

$$\begin{aligned} \min _{{\textit{f}}:U\rightarrow \mathbb {C}}\int _U L(\partial _z{\textit{f}},\partial _{\overline{z}}{\textit{f}})\,{\text {d}z}\,. \end{aligned}$$

(A.1)

On the other hand, we can always translate $(z,w)\mapsto L(z,w)$ to a real-valued function $W:\mathbb {R}^{2\times 2}\rightarrow \mathbb {R}$ using the identity

$$\begin{aligned} \partial _z{\textit{f}}(z)&=\frac{1}{2}\left( \partial _x-i\partial _y\right) \left[ u(x,y)+iv(x,y)\right] =\frac{1}{2}\left[ \partial _xu+\partial _yv+i\left( \partial _xv-\partial _yu\right) \right] \,, \end{aligned}$$

(A.2)

$$\begin{aligned} \partial _{\overline{z}}{\textit{f}}(z)&=\frac{1}{2}\left( \partial _x+i\partial _y\right) \left[ u(x,y)+iv(x,y)\right] =\frac{1}{2}\left[ \partial _xu-\partial _yv+i\left( \partial _xv+\partial _yu\right) \right] \end{aligned}$$

(A.3)

to compute the corresponding deformation gradient $F=D{\textit{f}}(z)$, i.e. using the isomorphism

$$\begin{aligned}&\bigl (z(F),w(F)\bigr ) =\begin{pmatrix} F_{11}+F_{22} &{} F_{11}-F_{22}\\ i(F_{21}-F_{12}) &{} i(F_{21}+F_{12}) \end{pmatrix}\nonumber \\&\quad \Longleftrightarrow \quad F(z,w)=\begin{pmatrix} \Re z+\Re w &{} \Im w -\Im z\\ \Im z+\Im w &{} \Re z-\Re w \end{pmatrix}. \end{aligned}$$

(A.4)

Example A.1

We consider $L:\mathbb {C}\times \mathbb {C}\rightarrow \mathbb {R}$ with

$$\begin{aligned} L(z,w)=|z |^2-|w |^2 \end{aligned}$$

(A.5)

and compute

$$\begin{aligned} L(\partial _z{\textit{f}},\partial _{\overline{z}}{\textit{f}})&=|\partial _z{\textit{f}} |^2-|\partial _{\overline{z}}{\textit{f}} |^2\nonumber \\&=\left| \frac{1}{2}\left[ \partial _xu{+}\partial _yv {+} i\left( \partial _xv-\partial _yu\right) \right] \right| ^2-\left| \frac{1}{2}\left[ \partial _xu-\partial _yv+i\left( \partial _xv+\partial _yu\right) \right] \right| ^2\nonumber \\&=\frac{1}{4}\left[ \left( \partial _xu+\partial _yv\right) ^2+\left( \partial _xv-\partial _yu\right) ^2-\left( \partial _xu-\partial _yv\right) ^2-\left( \partial _xv+\partial _yu\right) ^2\right] \nonumber \\&=\frac{1}{4}\left[ \partial _xu^2+2\partial _xu\partial _yv+\partial _yv^2+\partial _xv^2-2\partial _xv\partial _yu+\partial _yu^2\right. \nonumber \\&\;\left. -\partial _xu^2+2\partial _xu\partial _yv-\partial _yv^2-\partial _xv^2-2\partial _xv\partial _yu-\partial _yu^2\right] \nonumber \\&=\frac{1}{2}\left[ \partial _xu\partial _yv-\partial _xv\partial _yu+\partial _xu\partial _yv-\partial _xv\partial _yu\right] \nonumber \\&=\partial _xu\partial _yv-\partial _xv\partial _yu=J_{\textit{f}}(z)\,. \end{aligned}$$

(A.6)

Thus we can identify the complex mapping $L(z,w)=|z |^2-|w |^2$ with the isotropic energy function

$$\begin{aligned} W(F)=F_{11}F_{22}-F_{12}F_{21}=\det F\,. \end{aligned}$$

(A.7)

Similarly, since

$$\begin{aligned} |\partial _z{\textit{f}} |^2+|\partial _{\overline{z}}{\textit{f}} |^2&=\left| \frac{1}{2}\left[ \partial _xu+\partial _yv+i\left( \partial _xv-\partial _yu\right) \right] \right| ^2{+}\left| \frac{1}{2}\left[ \partial _xu-\partial _yv {+}i\left( \partial _xv+\partial _yu\right) \right] \right| ^2\nonumber \\&=\frac{1}{4}\left[ \left( \partial _xu+\partial _yv\right) ^2+\left( \partial _xv-\partial _yu\right) ^2+\left( \partial _xu-\partial _yv\right) ^2+\left( \partial _xv+\partial _yu\right) ^2\right] \nonumber \\&=\frac{1}{4}\left[ \partial _xu^2+2\partial _xu\partial _yv+\partial _yv^2+\partial _xv^2-2\partial _xv\partial _yu+\partial _yu^2\right. \nonumber \\&\;\left. +\partial _xu^2-2\partial _xu\partial _yv+\partial _yv^2+\partial _xv^2+2\partial _xv\partial _yu+\partial _yu^2\right] \nonumber \\&=\frac{1}{2}\left[ \partial _xu^2+\partial _yv^2+\partial _xv^2+\partial _yu^2\right] =\partial _xu^2+\partial _yv^2, \end{aligned}$$

(A.8)

we identify $L(z,w)=|z |^2+|w |^2$ with $W(F)=\frac{1}{2}\Vert F \Vert ^2$.

Analogous computations yield the representations

$$\begin{aligned} |z |^2&=\frac{1}{2}\left[ \left( |z |^2+|w |^2\right) +\left( |z |^2-|w |^2\right) \right] =\frac{1}{4}\Vert F \Vert ^2+\frac{1}{2}\det F\,,\nonumber \\ |w |^2&=\frac{1}{2}\left[ \left( |z |^2+|w |^2\right) -\left( |z |^2-|w |^2\right) \right] =\frac{1}{4}\Vert F \Vert ^2-\frac{1}{2}\det F\,,\nonumber \\ |z ||w |&=\sqrt{\frac{1}{4}\Vert F \Vert ^2+\frac{1}{2}\det F}\cdot \sqrt{\frac{1}{4}\Vert F \Vert ^2-\frac{1}{2}\det F}=\frac{1}{4}\sqrt{\Vert F \Vert ^4-4(\det F)^2}\nonumber \\ \left( |z |+|w |\right) ^2&= |z |^2+|w |^2+2|z ||w | = \frac{1}{2}\Vert F \Vert ^2+\frac{2}{4}\sqrt{\Vert F \Vert ^4-4(\det F)^2}\nonumber \\&= \frac{\Vert F \Vert ^2+\sqrt{\Vert F \Vert ^4-4(\det F)^2}}{2} = {\varvec{|}}F{\varvec{|}}^2 = \lambda _{\hbox {max}}^2\,,\nonumber \\ |z | -|w |&= \frac{|z |^2-|w |^2}{|z |+|w |}=\frac{\det F}{\lambda _{\hbox {max}}}=\lambda _{\hbox {min}}\,,\nonumber \\ \mathbb {K}(F)&= \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} = \frac{|z | +|w |}{|z | -|w |}\,,\nonumber \\ K(F)&= \frac{\Vert F \Vert ^2}{2\det F} = \frac{|z |^2+|w |^2}{|z |^2-|w |^2}\,, \end{aligned}$$

(A.9)

which can be used to to convert the energy

$$\begin{aligned} W_{\text {magic}}^+(F)= & {} \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} - \log \frac{\lambda _{\hbox {max}}}{\lambda _{\hbox {min}}} + \log \det F = K(F)+2\log \lambda _{\hbox {min}}\nonumber \\= & {} \frac{|z | +|w |}{|z | -|w |}+2\log \left( |z |-|w |\right) \end{aligned}$$

(A.10)

to a mapping $L:\mathbb {C}\times \mathbb {C}\rightarrow \mathbb {R}$; note that $|z |>|w |$ holds for arbitrary $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ because¹³$|z |-|w |=\det F>0$.

As indicated in Sect. 6, the Burkholder functional¹⁴

$$\begin{aligned} B_p(F)=-\left[ \frac{p}{2}\det F+\left( 1-\frac{p}{2}\right) {\varvec{|}}F{\varvec{|}}^2\right] {\varvec{|}}F{\varvec{|}}^{p-2} \,, \end{aligned}$$

(A.11)

with $p\ge 2$ and

$$\begin{aligned} {\varvec{|}}F{\varvec{|}} =\lambda _{\hbox {max}}= \sqrt{\frac{\Vert F \Vert ^2+\sqrt{\Vert F \Vert ^4-4(\det F)^2}}{2}} \end{aligned}$$

(A.12)

denoting the operator norm, plays an important role in complex analysis. Its representation as a complex mapping $L_p:\mathbb {C}\times \mathbb {C}\rightarrow \mathbb {R}$ can be computed via

$$\begin{aligned} -B_p(F)&=\left[ \frac{p}{2}\det F+\left( 1-\frac{p}{2}\right) {\varvec{|}}F{\varvec{|}}^2\right] {\varvec{|}}F{\varvec{|}}^{p-2}\nonumber \\&=\left[ \frac{p}{2}\left( |z |^2-|w |^2\right) +\left( 1-\frac{p}{2}\right) \left( |z | +|w |\right) ^2\right] \left( |z | +|w |\right) ^{p-2}\nonumber \\&=\frac{1}{2}\left[ p|z |^2-p|w |^2+(2-p)\left( |z |^2+2|z ||w | +|w |^2\right) \right] \left( |z | +|w |\right) ^{p-2}\nonumber \\&=\left[ |z |^2+(2-p)|z ||w |+(1-p)|w |^2\right] \left( |z | +|w |\right) ^{p-2}\nonumber \\&=\left( |z |-(p-1)|w |\right) \left( |z | +|w |\right) ^{p-1}{=}{:}L_p(z,w) \,. \end{aligned}$$

(A.13)

In addition to its connection to Morrey’s conjecture (cf. Sect. 6), the Burkholder functional $B_p(F)$, or rather its complex representation $L_p(z,w)$, plays an important role in martingale inequalities and the Beurling-Ahlfors transform (also called complex Hilbert transform) $S:L^p(\mathbb {C})\rightarrow L^p(\mathbb {C})$, defined as the singular integral

$$\begin{aligned} (S\omega )(z)=-\frac{1}{\pi }\iint _\mathbb {C}\frac{\omega (\xi )}{(z-\xi )^2}\,{\text {d}\xi }\,,\qquad \omega \in L^p(\mathbb {C})\,. \end{aligned}$$

(A.14)

One primary aim in function theory is determining the p-norm

$$\begin{aligned} \Vert S \Vert _{p}=\sup _{\omega \in L^p(\mathbb {C})}\frac{\Vert S(\omega ) \Vert _p}{\Vert \omega \Vert _p}\,,\qquad 1<p<\infty \end{aligned}$$

of the Beurling transform. A yet unsolved conjecture of Iwaniec (1982), Iwaniec and Martin (1993), Iwaniec (2002) states that

$$\begin{aligned} \Vert S \Vert _{p} = p^\star - 1 = {\left\{ \begin{array}{ll}p-1 &{}\text {if }\;2\le p<\infty \,,\\ \frac{1}{p-1} &{}\text {if }\;1<p\le 2\,.\end{array}\right. } \end{aligned}$$

(A.15)

We can shorten the notation in (A.15) by introducing $p^\star =\max (p,p')$ with $\frac{1}{p}+\frac{1}{p'}=1$ for arbitrary $p>1$. It is already known (Iwaniec and Martin 1993) that $\Vert S \Vert _{p}\ge p^\star - 1$ as well as $\Vert S \Vert _{p}\le C_n(p^\star - 1)$, where the constant $C_n$ is at best exponential in n. Burkholder (1988) proved that the inequality

$$\begin{aligned}&|z |^p -(p^\star -1)^p|w |^p \le \alpha _p\left( |z |-(p^\star -1)|w |\right) \left( |z | +|w |\right) ^{p-1},\nonumber \\&\alpha _p=p\left( 1-\frac{1}{p^\star }\right) ^{p-1}, \end{aligned}$$

(A.16)

holds for all $p>1$. In the case $p\ge 2$, we can identify Burkholder’s functional $L_p(z,w)$ in complex notion with the right hand side of (A.16). The term on the left-hand side,

$$\begin{aligned} V(z,w) = |z |^p -(p^\star -1)^p|w |^p \,, \end{aligned}$$

(A.17)

plays an important role in sharp estimates for martingales (Burkholder 1988). To prove Iwaniec’s conjecture (A.15), the expression (Astala et al. 2015)

$$\begin{aligned} \Vert S({\textit{f}}) \Vert _p\le (p^\star -1)\Vert {\textit{f}} \Vert _p\,,\qquad 1<p<\infty \end{aligned}$$

(A.18)

must be shown to hold for all ${\textit{f}}\in L_p(\mathbb {C})$. With the identity (cf. Banuelos and Lindeman 1997) $\displaystyle S\circ \frac{\partial }{\partial {\overline{z}}}=\frac{\partial }{\partial z}$, the above inequality is equivalent to

$$\begin{aligned} \Vert \partial _z{\textit{f}} \Vert _p\le (p^\star -1)\Vert \partial _{\overline{z}}{\textit{f}} \Vert _p\,,\qquad {\textit{f}}\in C_0^\infty (\mathbb {C})\,, \end{aligned}$$

(A.19)

which shows a direct connection to the mapping $V:\mathbb {C}\times \mathbb {C}\rightarrow \mathbb {R}$ in Eq. (A.17). The conjecture of Iwaniec would follow (Banuelos and Lindeman 1997) from

$$\begin{aligned} \mathop {\iint }\limits _{\mathbb {C}} L_p(\partial _z {\textit{f}},\partial _{\overline{z}}{\textit{f}})\,{\text {d}\xi }\le 0\qquad \forall \;{\textit{f}}\in C_0^\infty (\mathbb {C})\,. \end{aligned}$$

(A.20)

This inequality is the motivation for the claim of quasiconcavity of $L_p(z,w)$, i.e. quasiconvexity of the Burkholder functional $B_p(F)$, as a sufficient but not necessary statement to ensure Iwaniec’s conjecture (Davis et al. 2011). In fact, inequality (A.20) is equivalent to quasiconcavity of $L_p$ at 0 (Banuelos 2010). In an older work of Baernstein and Montgomery-Smith (2011) they present some first numerical evidence in favour of inequality (A.20) up to machine precision, using a $2N^2$ real dimensional space splitting the unit square $[0,1]^2$ into triangles to approximate $L_p(z,w)$ by piecewise linear functions (with N ranging from 6 to 100).