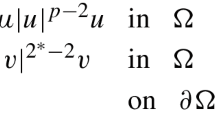High perturbations of quasilinear problems with double criticality

Abstract

This paper is concerned with the qualitative analysis of solutions to the following class of quasilinear problems

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _{\Phi }u=f(x,u) &{}\quad \text {in } \Omega ,\\ u=0 &{}\quad \text {on }\partial \Omega , \end{array} \right. \end{aligned}$$

(P)

where $\Delta _{\Phi }u=\mathrm{div}\,(\varphi (x,|\nabla u|)\nabla u)$ and $\Phi (x,t)=\int _{0}^{|t|}\varphi (x,s)s\,ds$ is a generalized N-function. We assume that $\Omega \subset {\mathbb {R}}^N$ is a smooth bounded domain that contains two open regions $\Omega _N,\Omega _p$ with ${\overline{\Omega }}_N \cap {\overline{\Omega }}_p=\emptyset$. The features of this paper are that $-\Delta _{\Phi }u$ behaves like $-\Delta _N u$ on $\Omega _N$ and $-\Delta _p u$ on $\Omega _p$, and that the growth of $f:\Omega \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ is like that of $e^{\alpha |t|^{\frac{N}{N-1}}}$ on $\Omega _N$ and as $|t|^{p^{*}-2}t$ on $\Omega _p$ when |t| is large enough. The main result establishes the existence of solutions in a suitable Musielak–Sobolev space in the case of high perturbations with respect to the values of a positive parameter.

1 Introduction

In this paper we study the existence of solutions for the following class of quasilinear problems

where $\Omega \subset {\mathbb {R}}^N$ ($N \ge 2$) is a smooth bounded domain, $\Delta _{\Phi }u=\mathrm{div}\,(\varphi (x,|\nabla u|)\nabla u)$ is the $\Phi$-Laplace operator, where $\Phi (x,t)=\int _{0}^{|t|}\varphi (x,s)s\,ds, \varphi : \Omega \times [0,+\infty ) \rightarrow [0,+\infty )$ and $f: \Omega \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ are continuous functions that satisfy some hypothesis that will be mentioned later on.

Before proceeding further, let us go through some known results associated to the $\Phi$-Laplace equations. In the recent past, the study of such equations concerning the existence theory has been a research topic of considerable interest. This nonhomogeneous differential operator extends the standard p-Laplace operator, the variable exponent p-Laplace operator, the weighted p-Laplace operator, and the p, q-Laplace operator.

When $\Phi$ is independent of x, solutions of problem (P) are investigated in the Orlicz–Sobolev space [40], and we refer the reader to Alves et al. [4], Alves et al. [5], Fukagai et al. [26], Carvalho et al. [13], Fukagai and Narukawa [27], Harjulehto and Hästö [32], and their references for the study of such PDEs. When $\Phi$ also depends on x, we are led to study the problems in variable exponent Sobolev spaces [22, 36] or in Musielak–Sobolev spaces [17, 33, 38, 40]. Differential equations in variable exponent Sobolev spaces have been studied extensively in the last years, most part of them involving the p(x)-Laplacian operator, see Alves and Barreiro [2], Alves and Ferreira [3], Alves and Souto [6], Alves and Rădulescu [7], Chabrowski and Fu [16], Fan and Zhang [24], Fan [25], Rădulescu and Repovš [41] and the references therein. However, differential equations in general Musielak–Sobolev spaces have been studied very little, see for instance, Azroul et al. [8], Benkirane and Sidi El Vally [11], Fan [23], Liu and Zhao [37], Wang and Liu [43] and the references therein.

In the present paper we will apply some recent results involving Musielak–Sobolev spaces to study the existence of nontrivial solutions for problem (P).

We now state our main hypotheses on the functions $\Phi$ and $\varphi$:

$(\varphi _1)$:

For each $x \in \Omega$, $\varphi (x,.)$ is a $C^1$ function in the interval $(0,+\infty )$.

$(\varphi _2)$:

$\varphi (x,t)$, $\partial _{t}(\varphi (x,t)t)>0$, for $x \in \Omega$ and $t>0$.

$(\varphi _3)$:

There exist $1<p<N<q<p^*$ such that

$$\begin{aligned} p\le \frac{\varphi (x,|t|)|t|^{2}}{\Phi (x,|t|)}\le q,\quad \text{ for } \ x \in \Omega \ \text{ and } \ t \not = 0. \end{aligned}$$

Using some ideas developed by Fukagai et al. [26], we can show that if $\varphi$ satisfies conditions $(\varphi _1){-}(\varphi _3)$, then $\Phi$ is a generalized N-function.

The complementary function ${\widetilde{\Phi }}$ associated with $\Phi$ is given by the Legendre transformation, that is,

$$\begin{aligned} {\widetilde{\Phi }}(x,s) = \max _{t\ge 0}\{ st - \Phi (x,t)\}, \quad x \in \Omega \ \text{ and } \ s \in {\mathbb {R}}. \end{aligned}$$

(1.1)

The functions $\Phi$ and ${\widetilde{\Phi }}$ are complement of each other and ${\widetilde{\Phi }}$ is also a generalized N-function.

Hereafter, we also assume that for some constant $d_1$,

$(\varphi _4)$:

$\inf _{x \in \Omega }\Phi (x,1)=d_1>0$.

$(\varphi _5)$:

For each $t_0 \not =0$, there is $c_0>0$ such that

$$\begin{aligned} \frac{\Phi (x,t)}{t} \ge c_0 \quad \text{ and } \quad \frac{{\tilde{\Phi }}(x,t)}{t} \ge c_0 \qquad \text{ for } \ t \ge t_0 \ \text{ and } \ x \in \Omega . \end{aligned}$$

The conditions $(\varphi _1){-}(\varphi _5)$ are very important in our approach, because they permit to conclude that both the Musielak–Orlicz space $L^{\Phi }(\Omega )$ and the Musielak–Sobolev space $W^{1,\Phi }(\Omega )$ are reflexive and separable Banach spaces; see Sect. 2 for more details.

Next, we will state more conditions on the function $\varphi$. Hereafter, we will suppose that there are three smooth domains $\Omega _N, \Omega _q, \Omega _p \subset \Omega$ with nonempty interior such that

$$\begin{aligned} \Omega =\Omega _N \cup \Omega _q \cup \Omega _p \end{aligned}$$

and there is $\delta >0$ such that

$$\begin{aligned} (\overline{\Omega _N})_{\delta } \cap (\overline{\Omega _p})_{\delta }=\emptyset . \end{aligned}$$

Hereafter, if $A \subset \Omega$, we denote by $A_\delta$ to be the $\delta$-neighbourhood of A restricted to $\Omega$, that is,

$$\begin{aligned} A_\delta =\{x \in \Omega \,:\, \mathrm{dist}\,(x,A)<\delta \}. \end{aligned}$$

Associated with the sets $\Omega _N, \Omega _q$ and $\Omega _p$, we will consider three continuous functions $\eta _N,\eta _q,\eta _p:{\overline{\Omega }} \rightarrow [0,1]$ satisfying:

$$\begin{aligned} \eta _N(x)= & {} 1, \quad \forall x \in \overline{\Omega _N}, \\ \eta _p(x)= & {} 1, \quad \forall x \in \overline{\Omega _p}, \end{aligned}$$

and

$$\begin{aligned}&\eta _q(x)=1, \quad \forall x \in \Omega _q= {\Omega } {\setminus } \overline{(\Omega _N \cup \Omega _p)},\\&\eta _N(x)=0,\quad \forall x \in (\overline{\Omega _N})^c_{\delta }, \quad \eta _p(x)=0, \quad \forall x \in (\overline{\Omega _p})^c_{\delta },\\&\eta _q(x)>0, \quad \forall x \in (\overline{\Omega _q})_{\delta },\quad \eta _q(x)=0,\quad \forall x \in (\overline{\Omega _q})^c_{\delta } \end{aligned}$$

and for some positive constant $c_4$,

$$\begin{aligned} \eta _q(x)\le c_4 \text {dist}(x, \partial (\Omega _q)_{\delta } \cap \Omega _p)^{l}, \quad \forall x \in \overline{\Omega _p} \cap (\Omega _q)_{\delta }, \end{aligned}$$

where $l>q$ and $\text {dist}(x, \partial (\Omega _q)_{\delta } \cap \Omega _p)=\inf \{|x-y|\,:\,y \in \partial (\Omega _q)_{\delta } \cap \Omega _p\}$.

We assume that the continuous function $f:{\overline{\Omega }} \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ has one of the following forms:

or

where $\lambda$ is a positive parameter, $\alpha >0$, $p^*>r>q>N>p>\frac{N}{2}$, $\beta >q$, where $p^*=\frac{Np}{N-p}$, $g:{\overline{\Omega }} \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ and ${\tilde{\eta }}_q: {\bar{\Omega }}\rightarrow [0,1]$ are continuous functions such that

$$\begin{aligned} {\tilde{\eta }}_q(x)=1, \quad \forall x \in \Omega _q= {\Omega } {\setminus } \overline{(\Omega _N \cup \Omega _p)} \end{aligned}$$

and

$$\begin{aligned} {\tilde{\eta }}_q(x)=0, \quad \forall \,x \in (\overline{\Omega _q})^c_{\delta /2}. \end{aligned}$$

Related to the function g, we assume the following conditions

for some $q_1>q$ and there is $\theta >q$ such that

where $G(x,t)=\int _{0}^{t}g(x,s)\,ds$, for $t \in {\mathbb {R}}$.

With these notations, we are ready to mention our last conditions on $\varphi$. If f is the form $(f_1)$, we assume for each $t>0$ the following:

$(\varphi _6)$:

$\varphi (x,t) \ge t^{N-2}, \quad \text{ for } \quad x \in \Omega _N \quad \text{ and } \quad c_1 t^{N-2} \ge \varphi (x,t), \quad x \in \Omega _N {\setminus } \overline{(\Omega _q)_{\delta }}.$

$(\varphi _7)$:

$\varphi (x,t) \ge \tau _1(x)t^{q-2}, \quad \text{ for } \quad x \in (\Omega _q)_{\delta }$ where $\tau _1:{\overline{\Omega }} \rightarrow {\mathbb {R}}$ is a continuous function satisfying:

$$\begin{aligned} \tau _1(x)>0, \quad \forall x \in (\Omega _q)_{\delta } \qquad \text{ and } \qquad \tau _1(x)=0, \quad \forall x \in ((\Omega _q)_{\delta })^c. \end{aligned}$$

$(\varphi _8)$:

$\tau _2(x)t^{q-2}+c_2t^{p-2} \ge \varphi (x,t) \ge t^{p-2}, \quad x \in \Omega _p$ where $\tau _2:\overline{\Omega _p} \rightarrow {\mathbb {R}}$ is a nonnegative continuous function satisfying:

$$\begin{aligned} \tau _2(x)\le c_3 \mathrm{dist}(x, \partial (\Omega _q)_{\delta } \cap \Omega _p)^{s}, \quad \forall x \in \overline{\Omega _p} \cap (\Omega _q)_{\delta } \end{aligned}$$

for some $s>q$ and

$$\begin{aligned} \tau _2(x)=0, \quad \forall x \in \overline{\Omega _p} {\setminus } \overline{(\Omega _q)_{\delta }}, \end{aligned}$$

for some constants $c_i>0$ with $i=1,2,3.$

Now, if f is the form $(f_2)$ we make a little adjustment in the condition $(\varphi _6)$ of the following way:

$(\varphi _6)$:

$\varphi (x,t) \ge t^{N-2}, \quad \text{ for } \ x \in \Omega _N.$

As a model of a function that satisfies the conditions $(\varphi _1)-(\varphi _8)$ is the function $\varphi :{\Omega } \times [0,+\infty ) \rightarrow [0,+\infty )$ defined by

$$\begin{aligned} \varphi (x,t)=\eta _N(x)t^{N-2}+\eta _{q}(x)t^{q-2}+\eta _{p}(x)t^{p-2}, \quad \forall \,(x,t) \in {\Omega } \times [0,+\infty ) \end{aligned}$$

(1.2)

and so,

$$\begin{aligned} \Phi (x,t)=\frac{\eta _N(x)}{N}|t|^{N}+\frac{\eta _{q}(x)}{q}|t|^{q}+\frac{\eta _{p}(x)}{p}|t|^{p}, \quad \forall \, (x,t)\in {\Omega } \times {\mathbb {R}}. \end{aligned}$$

(1.3)

The reader is invited to observe that according to model (1.3), the operator $\Delta _{\Phi }$ has different behaviors in the region $\Omega$, it behaves like $\Delta _p$ in one region and $\Delta _N$ in another disjoint region, where the nonlinearity f behaves like $|t|^{p^{*}-2}t$ and $e^{|u|^\frac{N}{N-1}}$ respectively, and so, the problem (P) has double criticality. This type of phenomena is very interesting, because we will work in the same problem with two types of nonlinearity that bring to the problem a lost of compactness, and in this case, we need to control these terms by doing simultaneously two different types of estimates. More precisely, in the present paper we will apply the Concentration Compactness Lemma due to Lions in $W^{1,p}(\Omega _p)$ found in Medeiros [21, Lemma 3.1], to get good estimate involving the integrals with the function $|t|^{p^*}$, while we will use a version of the Trudinger–Moser inequality in $W^{1,N}(\Omega _N)$ by Cianchi [18], see Lemma 3.3, to obtain a control in the integrals involving the exponential growth. One difficulty that appears in our study is that we do not know if the trace of the functions on $\partial {\Omega }_p$ and $\partial \Omega _N$ are zero, hence we must use results that are applied in the study of problem with Neumann boundary conditions. We believe that this is the first article where this type of doubly criticality is studied in the literature.

An important fact that we would like to point out is that our study is strongly related to the double-phase problems that have received a special attention in the last years. As mentioned in [7], the study of non-autonomous functionals characterized by the fact that the energy density changes its ellipticity and growth properties according to the point that has been continued by Mingione et al. [10, 19, 20], Bahrouni et al. [9], Cencelj et al. [14], Gasiński and Winkert [29, 30], Papageorgiou et al. [39], Zhang and Rădulescu [45], etc. These contributions are in relationship with the work of Zhikov [46, 47], which describe the behavior of phenomena arising in nonlinear elasticity. In fact, variational problems with nonstandard integrands were introduced at the beginning of the 1980’s and were studied in the context of averaging and the Lavrent’ev phenomenon. Zhikov provided models for strongly anisotropic materials in the context of homogenisation. In particular, he considered the following model functional

$$\begin{aligned} {{\mathcal {P}}}_{p,q}(u) :=\int _\Omega (|Du|^p+a(x)|Du|^q)dx,\quad 0\le a(x)\le L,\ 1<p<q, \end{aligned}$$

(1.4)

where the modulating coefficient a(x) dictates the geometry of the composite made of two differential materials, with hardening exponents p and q, respectively. In our case, the functions $\eta _N(x), \eta _p(x)$ and $\eta _q(x)$ work like function a(x) in the papers due to Zhikov.

Our main result establishes the existence of solutions to problem (P) in the case of high perturbations, that is, for large values of the positive parameter $\lambda$.

Theorem 1.1

Assume $(g_1)$, $(g_2)$ and $(\varphi _1){-}(\varphi _8)$. Then, if either $(f_1)$ or $(f_2)$ holds, there exists $\lambda ^*>0$ such that problem (P) has a nontrivial solution for all $\lambda \ge \lambda ^*$.

The proof of Theorem 1.1 is done via Variational Methods, more precisely we have used the mountain pass theorem without (PS) condition found in Willem [44] to establish our main results, although we face several difficulties. As mentioned above, due to the exponential critical behavior, we establish several auxiliary results (Lemmas 3.4, 3.5 and Corollary 3.6) of Moser-Trudinger type which captures the nonzero Dirichlet boundary value Sobolev functions and become very useful in our setting. To handle the critical exponent term, we use a Lions concentration compactness principle (Lemma 3.1) for the nonzero Dirichlet boundary value Sobolev functions.

This paper is organised as follows. In Sect. 2, we make a brief review about the Musielak–Orlicz and Musielak–Sobolev spaces, while in Sect. 3 we discuss some technical results that are crucial to overcome the lost of compactness involving the terms with critical growth and exponential critical growth. Finally, in Sect. 4, we prove our main result.

2 A brief review about the Musielak–Sobolev spaces

In this section, we recall some results on Musielak–Orlicz and Musielak–Sobolev spaces. For more details we refer to [17, 23, 32, 38] and their references.

Let $\Omega \subset {\mathbb {R}}^N$ be a smooth bounded domain and $\Phi (x,t)=\int _{0}^{|t|}\varphi (x,s)s\,ds$ be a generalized N-function, that is, for each $t \in {\mathbb {R}}$, the function $\Phi (., t)$ is measurable, and for a.e. $x \in \Omega$, the function $\Phi (x, .)$ is an N-function. For the reader’s convenience, we recall that a continuous function $A : {\mathbb {R}} \rightarrow [0,+\infty )$ is an N-function if

(i):

A is convex.

(ii):

$A = 0 \Leftrightarrow t = 0$.

(iii):

$\lim _{t\rightarrow 0}\frac{A(t)}{t}=0$ and $\lim _{t\rightarrow +\infty }\frac{A(t)}{t}= +\infty$ .

(iv):

A is even.

The Musielak–Orlicz space $L^{\Phi }(\Omega )$ is defined by

$$\begin{aligned} L^{\Phi }(\Omega )=\left\{ u:\Omega \rightarrow {\mathbb {R}} \left| \,u\text { is measurable and }\,\,\exists \, \tau >0 \,\, \text{ such } \text{ that } \,\, \int _{\Omega }\Phi \left( x,\frac{|u|}{\tau }\right) \,dx<+\infty \right. \right\} \end{aligned}$$

endowed with the Luxemburg norm

$$\begin{aligned} \left| u\right| _{\Phi }=\inf \left\{ \lambda >0\left| \,\int _{\Omega }\Phi \left( x,\frac{|u|}{\lambda }\right) \,dx \le 1\right. \right\} . \end{aligned}$$

We say that an N-function $\Phi$ satisfies the weak $\Delta _{2}$-condition, denote by $\Phi \in \Delta _{2}$, if there are $K>0$ and a nonnegative function $h \in L^{1}(\Omega )$ such that

$$\begin{aligned} \Phi (x,2t) \le K\Phi (x,t) + h(x)\quad \text{ for } \ x \in \Omega \ \text{ and } \ t\in {\mathbb {R}}, \end{aligned}$$

When $h=0$, we say that $\Phi$ satisfies the $\Delta _{2}$-condition. Arguing as in [40, Theorem 4.4.4], it follows that $\Phi$ satisfies the $\Delta _{2}$-condition if, and only if,

$$\begin{aligned} \sup _{(x,t) \in \Omega \times (0,+\infty )}\frac{\varphi (x,|t|)|t|^2}{\Phi (x,|t|)}<+\infty . \end{aligned}$$

Moreover, an important inequality involving $\Phi$ and its complementary function ${\tilde{\Phi }}$ (see (1.1)) is a Young’s type inequality given by

$$\begin{aligned} st \le \Phi (x,s) + {\widetilde{\Phi }}(x,t), \quad x \in \Omega \ \text{ and } \ \forall s, t\ge 0. \end{aligned}$$

(2.1)

Using the above inequality, it is possible to prove a Hölder type inequality, that is,

$$\begin{aligned} \Big | \int _{\Omega }uvdx \Big | \le 2 \Vert u \Vert _{\Phi }\Vert v \Vert _{{\widetilde{\Phi }}}\quad \forall \,u \in L^{\Phi }(\Omega ) \ \text{ and } \ \forall \,v \in L^{{\widetilde{\Phi }}}(\Omega ). \end{aligned}$$

Arguing as in [26], if $(\varphi _3)$ holds, we derive that

$$\begin{aligned} \frac{q}{q-1}\le \frac{{\tilde{\varphi }}(x,|t|)|t|^2}{{\tilde{\Phi }}(x,|t|)} \le \frac{p}{p-1}, \quad x \in \Omega \ \text{ and } \ t \not =0, \end{aligned}$$

where

$$\begin{aligned} {\tilde{\Phi }}(x,t)=\int _0^{|t|}{\tilde{\varphi }}(x,s)s\,ds, \end{aligned}$$

and

$$\begin{aligned} {\tilde{\varphi }}(x,s)=\sup \{t\,:\,\varphi (x,t)t \le s\}, \quad x \in {\overline{\Omega }} \ \text{ and } \ s\ge 0. \end{aligned}$$

Hence, if ($\varphi _3$) holds, we have ${\tilde{\Phi }}$ also satisfies the $\Delta _{2}$-condition.

Arguing as in [26, Lemma A2], it is possible to prove that $\Phi$ and ${\tilde{\Phi }}$ satisfy the following inequality

$$\begin{aligned} {\tilde{\Phi }}(x,\varphi (x,t)t) \le \Phi (x,2t), \quad x \in \Omega \ \text{ and } \ t \ge 0. \end{aligned}$$

(2.2)

The condition ($\varphi _3$) is very interesting, because following the ideas of [26, Lemmas 2.1 and 2.5], it is possible to prove the following: Setting the functions

$$\begin{aligned} \xi _{0}(t)= & {} \min \{t^{p},t^q\}, \quad \xi _{1}(t)=\max \{t^{p},t^q\}, \quad \xi _{3}(t)=\min \{t^{\frac{p}{p-1}},t^{\frac{q}{q-1}}\} \quad \text{ and }\\ \xi _{4}(t)= & {} \max \{t^{\frac{p}{p-1}},t^{\frac{q}{q-1}}\}, \end{aligned}$$

we have

$$\begin{aligned} \xi _0(s)\Phi (x,t)\le & {} \Phi (x,st) \le \xi _1(s)\Phi (x,t) \quad \text{ for } \ s,t \ge 0, \end{aligned}$$

(2.3)

$$\begin{aligned} \xi _0(|u|_\Phi )\le & {} \int _{\Omega }\Phi (x,|u|)\,dx \le \xi _1(|u|_\Phi ) \quad \text{ for }\ u \in L^{\Phi }(\Omega ), \end{aligned}$$

(2.4)

$$\begin{aligned} \xi _3(s){\tilde{\Phi }}(x,t)\le & {} {\tilde{\Phi }}(x,st) \le \xi _4(s){\tilde{\Phi }}(x,t) \quad \text{ for } \ s,t \ge 0, \end{aligned}$$

(2.5)

and

$$\begin{aligned} \xi _3(|u|_{{\tilde{\Phi }}}) \le \int _{\Omega }{\tilde{\Phi }}(x,|u|)\,dx \le \xi _4(|u|_{{\tilde{\Phi }}}) \quad \text{ for }\ u \in L^{{\tilde{\Phi }}}(\Omega ). \end{aligned}$$

(2.6)

The Musielak–Sobolev space $W^{1,\Phi }(\Omega )$ can be defined by

$$\begin{aligned} W^{1,\Phi }(\Omega )=\left\{ u\in L^{\Phi }(\Omega )\left| \,\left| \nabla u\right| \in L^{\Phi }(\Omega )\right. \right\} \end{aligned}$$

with the norm

$$\begin{aligned} \left\| u\right\| _{1,\Phi }=\left| u\right| _{\Phi }+\left| \nabla u\right| _{\Phi }. \end{aligned}$$

The conditions $(\varphi _1){-}(\varphi _5)$ ensure that the spaces $L^{\Phi }(\Omega )$ and $W^{1,\Phi }(\Omega )$ are reflexive and separable Banach spaces, for more details see [23, Propositions 1.6 and 1.8]. In what follows, $W_0^{1,\Phi }(\Omega )$ is defined as the closure of $C_0^{\infty }(\Omega )$ in $W_0^{1,\Phi }(\Omega )$ with respect to the above norm. Moreover, $\Vert u\Vert =|\nabla u|_{\Phi }$ is a norm in $W_0^{1,\Phi }(\Omega )$, and if $(\varphi _1){-}(\varphi _5)$ holds, by [31, Lemma 5.7], $\Vert \,\,\Vert$ is equivalent to the norm $\Vert u\Vert _{1,\Phi }$ in $W_0^{1,\Phi }(\Omega )$.

As a consequence of (2.4) we have the lemma below that will be used later on.

Proposition 2.1

The functional $\rho :W_0^{1,\Phi }(\Omega ) \rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \rho (u)=\int _{\Omega } \Phi (x,|\nabla u|)\,dx, \end{aligned}$$

(2.7)

has the following properties : 

(i):

If $\left\| u\right\| \ge 1$, then $\left\| u\right\| ^{p}\le \rho (u)\le \left\| u\right\| ^{q}$.

(ii):

If $\Vert u\Vert \le 1,$ then $\left\| u\right\| ^{q}\le \rho (u)\le \left\| u\right\| ^{p}$.

In particular,  $\rho (u)=1$ if and only if $\left\| u \right\| =1$ and if $(u_n) \subset W_0^{ 1,\Phi }( \Omega ),$ then $\left\| u_{n}\right\| \rightarrow 0$ if and only if $\rho ( u_{n}) \rightarrow 0$.

Remark 1

For the functional $\xi :L^{\Phi }(\Omega )\rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} \xi (u)=\int _{\Omega }\Phi (x,|u|)\,dx\text {,} \end{aligned}$$

the conclusion of Proposition 2.1 also holds, for example, if $(u_n) \subset L^{\Phi }( \Omega )$, then $\left| u_{n}\right| _{\Phi }\rightarrow 0$ if and only if $\xi (u_{n})\rightarrow 0$.

From the definition of $W^{1,\Phi }(\Omega )$ and properties of $\Phi$, we have the continuous embedding

$$\begin{aligned} W^{1,\Phi }(\Omega ) \hookrightarrow W^{1,q}(({\Omega }_q)_{\omega }) \end{aligned}$$

for all $\omega \in (0,\delta )$ and the compact embedding

$$\begin{aligned} W^{1,q}(({\Omega }_q)_\delta ) \hookrightarrow C(\overline{(\Omega _q)_{\omega }}), \end{aligned}$$

because $q>N$, from where it follows that

$$\begin{aligned} W^{1,\Phi }(\Omega ) \hookrightarrow C(\overline{(\Omega _q)_{\omega }}), \end{aligned}$$

(2.8)

is compact, which is crucial in our approach.

Next we would like to state our last result found in [23, Theorem 2.2], which says the operator $-\Delta _{\Phi }: W_0^{1,\Phi }(\Omega ) \rightarrow (W_0^{1,\Phi }(\Omega ))^*$ belongs to the Class $(S_+)$.

Lemma 2.2

Assume the conditions $(\varphi _1){-}(\varphi _8)$. If $u_n \rightharpoonup u$ in $W_0^{1,\Phi }(\Omega )$ and

$$\begin{aligned} \lim _{n \rightarrow +\infty }\int _{\Omega }\langle \varphi (x,|\nabla u_n|)\nabla u_n, \nabla u_n- \nabla u\rangle \,dx=0, \end{aligned}$$

then $u_n \rightarrow u$ in $W_0^{1,\Phi }(\Omega )$.

3 Some technical results

The main goal of this section is to recall and prove some technical results that are crucial in the proof of our main result. Since we are going to work with double criticality, which involves the exponential critical growth and the critical growth $p^*$, the next two results are crucial in our approach. The first one is a Concentration Compactness Lemma due to Lions for $W^{1,p}(\Theta )$ explored in Medeiros [21], where $\Theta \subset {\mathbb {R}}^N$ is a smooth bounded domain .

Lemma 3.1

Let $(u_n)$ be a sequence in $W^{1,p}(\Theta )$ with $1<p<N$ and $u_n \rightharpoonup u$ in $W^{1,p}(\Theta )$. If

• (i) $|\nabla u_n|^{p} \rightarrow \mu$ weakly-$^*$ in the sense of measure,  and

• (ii) $|u_n|^{p^*} \rightarrow \nu$ weakly-$^*$ in the sense of measure, 

then for at most a countable index set J,  we have

$$\begin{aligned} \left\{ \begin{array}{l} (\text {a})\quad \nu =|u|^{p^*}+\sum _{j \in J}\nu _j \delta _{x_j},\,\nu _j \ge 0.\\ (\text {b})\quad \mu \ge |\nabla u|^{p}+\sum _{j \in J}\mu _j \delta _{x_j},\,\mu _j \ge 0.\\ (\text {c})\quad \text{ If } \,\, x_j \in \Theta , \,\, \text{ then } \quad S_p\nu _j^{\frac{p}{p^*}} \le \mu _j.\\ (\text {d})\quad \text{ If } \,\, x_j \in \partial \Theta , \,\, \text{ then } \quad \frac{S_p}{2^{p/N}}\nu _j^{\frac{p}{p^*}} \le \mu _j, \end{array} \right. \end{aligned}$$

where $p^*=\frac{Np}{N-p}$ and $S_p$ denotes the best constant of the embedding $D^{1,p}({\mathbb {R}}^N) \hookrightarrow L^{p^*}({\mathbb {R}}^N)$ given by

$$\begin{aligned} S_p= \inf _{ {\small { \begin{array}{l} u \in D^{1,p}({\mathbb {R}}^N) \\ u \not =0 \end{array}}}} \frac{ \int _{{\mathbb {R}}^N}|\nabla u|^{p}\,dx}{\left( \int _{{\mathbb {R}}^N}|u|^{p^*}\,dx\right) ^{\frac{p}{p^*}}}. \end{aligned}$$

(3.1)

The proof of the above lemma follows by combining the arguments explored in Struwe [42, Chapter I, Section 4] and the following Cherrier’s inequality [15] below.

Lemma 3.2

Let $\Theta \subset {\mathbb {R}}^N$ be a smooth bounded domain and $p \in (1,N)$. Then for each $\tau >0,$ there is $M_{\tau }>0$ such that

$$\begin{aligned} \left[ \frac{S_p}{2^{\frac{p}{N}}}-\tau \right] \Vert u\Vert ^{p}_{L^{p^*}(\Theta )} \le \Vert \nabla u\Vert ^{p}_{L^{p}(\Theta )}+M_{\tau }\Vert u\Vert ^{p}_{L^{p}(\Theta )}, \quad \forall \,u \in W^{1,p}(\Theta ). \end{aligned}$$

The second result that we would like to point out is a version of Trundiger–Moser inequality in $W^{1,N}(\Theta )$ due to Cianchi [18, Theorem 1.1].

Lemma 3.3

Let $\Theta \subset {\mathbb {R}}^N$ be a smooth bounded domain for $N \ge 2$ and $u \in W^{1,N}(\Theta )$. Then,  there is a constant $C(\Theta )>0$ such that

$$\begin{aligned} \int _{\Theta }e^{\alpha _N\left( \frac{|u-u_{\Theta }|}{\Vert \nabla u\Vert _{L^{N}(\Theta )}}\right) ^{N'}}\,dx \le C(\Theta ), \end{aligned}$$

(3.2)

where $N'=\frac{N}{N-1},$ $u_{\Theta }=\frac{1}{|\Theta |}\int _{\Theta }u\,dx$ is the mean value of u in $\Theta ,$ $\alpha _N=N\left( \frac{w_N}{2}\right) ^{\frac{1}{N}}$ and $w_N$ is the volume of sphere $S^{N-1}$. The integral on the left-hand of (3.2) is finite for each $u \in W^{1,N}(\Theta )$ even if $\alpha _N$ is replaced by any other small positive number, but no inequality of type (3.2) can hold with a large constant in the place of $\alpha _N$.

From Lemma 3.3, for each $u \in W^{1,N}(\Theta )$, we have

$$\begin{aligned} e^{t|u|^{N'}} \in L^{1}(\Theta ), \quad \forall \,t \ge 0. \end{aligned}$$

(3.3)

For the reader interested in Trudinger–Moser inequality for functions in $W^{1,N}(\Theta )$, we would like to cite the papers due to Adimurthi and Yadava [1], Kaur and Sreenadh [35] and their references.

As a consequence of Lemma 3.3, we have the following two results.

Lemma 3.4

Given $t >1$ and $\alpha >0,$ there is $r \in (0,1)$ and $C=C(t,r,N)>0$ such that

$$\begin{aligned} \sup \left\{ \int _{\Theta }e^{t\alpha |u|^{N'}}\,dx\,:\, u \in W^{1,N}(\Theta ), \,\, \Vert \nabla u\Vert _{L^{N}(\Theta )}\le r \quad \text{ and } \quad \Vert u\Vert _{L^{1}(\Theta )} \le r \right\} \le C. \end{aligned}$$

(3.4)

Proof

Note that if $u \in W^{1,N}(\Theta )$, we have

$$\begin{aligned} \int _{\Theta }e^{t\alpha |u|^{N'}}\,dx \le e^{t2^{N'}\alpha |u_{\Theta }|^{N'}}\int _{\Theta }e^{t2^{N'}\alpha |u-u_{\Theta }|^{N'}}\,dx. \end{aligned}$$

Since

$$\begin{aligned} |u_{\Theta }| \le \frac{1}{|\Theta |}\int _{\Theta }|u|\,dx \le \frac{r}{|\Theta |} \end{aligned}$$

it follows that

$$\begin{aligned} \begin{array}{ll} \int _{\Theta }e^{t\alpha |u|^{N'}}\,dx &{}\le K \int _{\Theta }e^{t2^{N'}\alpha \Vert \nabla u\Vert ^{N'}_{L^{N}(\Theta )}\left( \frac{|u-u_{\Theta }|}{\Vert \nabla u\Vert _{L^{N}(\Theta )}}\right) ^{N'}}\,dx \\ &{} \le K \int _{\Theta }e^{t2^{N'}\alpha r^{N'}\left( \frac{|u-u_{\Theta }|}{\Vert \nabla u\Vert _{L^{N}(\Theta )}}\right) ^{N'}}\,dx, \\ \end{array} \end{aligned}$$

where $K=e^{t2^{N'}\alpha \left( \frac{r}{|\Theta |}\right) ^{N'}}$. Fixing r of such way that $t2^{N'}\alpha r^{N'} \le \alpha _N$, the result follows by employing Lemma 3.3. $\square$

Lemma 3.5

Let $\alpha >0$ and $(u_n) \subset W^{1,N}(\Theta )$ be a sequence satisfying $\Vert \nabla u_n\Vert ^{N'}_{L^{N}(\Theta )}\le \frac{\tau }{2^{N'}}\frac{\alpha _N}{\alpha }$ and $\Vert u_n\Vert _{L^{1}(\Theta )} \le M$ for some $\tau \in (0,1)$ and $M>0$. Then,  there is $t >1$ with $t \approx 1$ such that

$$\begin{aligned} \sup _{n \in {\mathbb {N}}}\int _{\Theta }e^{t\alpha |u_n|^{N'}}\,dx<+\infty . \end{aligned}$$

(3.5)

Hence,  the sequence $f_n(x)=e^{\alpha |u_n(x)|^{N'}}$ is a bounded sequence in $L^{t}(\Theta )$.

Proof

Arguing as in Lemma 3.4, we get

$$\begin{aligned} \int _{\Theta }e^{t\alpha |u|^{N'}}\,dx \le K \int _{\Theta }e^{t2^{N'}\alpha \Vert \nabla u_n\Vert ^{N'}_{L^{N}(\Theta )}\left( \frac{|u_n-(u_n)_{\Theta }|}{\Vert \nabla u_n\Vert _{L^{N}(\Theta )}}\right) ^{N'}}\,dx, \end{aligned}$$

where $K=e^{t2^{N'}\alpha \left( \frac{M}{|\Theta |}\right) ^{N'}}$ and so,

$$\begin{aligned} \int _{\Theta }e^{t\alpha |u|^{N'}}\,dx \le K \int _{\Theta }e^{t \tau \alpha _N \left( \frac{|u_n-(u_n)_{\Theta }|}{\Vert \nabla u_n\Vert _{L^{N}(\Theta )}}\right) ^{N'}}\,dx. \end{aligned}$$

As $\tau \in (0,1)$, we can take $t >1$ with $t \approx 1$ of such way that $t \tau \in (0,1)$, and the result follows again by using Lemma 3.3. $\square$

As a consequence of Lemma 3.5, we have the corollary below.

Corollary 3.6

Let $(u_n) \subset W^{1,N}(\Theta )$ be a sequence as in Lemma 3.5. If $u_n(x) \rightarrow u(x)$ a.e. in $\Theta ,$ then $f_n \rightharpoonup f$ in $L^{t}(\Theta )$ where $f(x)=e^{\alpha |u(x)|^{N'}},$ that is, 

$$\begin{aligned} \int _{\Theta }f_n \varphi \,dx \rightarrow \int _{\Theta }f \varphi \,dx, \quad \forall \,\varphi \in L^{t'}(\Theta ), \end{aligned}$$

where $\frac{1}{t}+\frac{1}{t'}=1$.

Our next result will help us to conclude that the energy functional associated with problem (P) is $C^{1}(W_0^{1,\Phi }(\Omega ),{\mathbb {R}})$. Since it follows as in Bezerra do Ó, Medeiros and Severo [12, Proposition 1], we will omit its proof.

Lemma 3.7

Let $(u_n) \subset W^{1,N}(\Theta )$ be a sequence such that $u_n \rightarrow u$ in $W^{1,N}(\Theta )$ for some $u \in W^{1,N}(\Theta )$. Then,  for some subsequence,  still denoted by itself,  there is $v \in W^{1,N}(\Theta )$ such that : 

• (i) $u_n(x) \rightarrow u(x)$ a.e. in $\Theta$.

• (ii) $|u_n(x)| \le v(x)$ a.e. in $\Theta$ for all $n \in {\mathbb {N}}$.

The energy functional $I:W_0^{1,\Phi }(\Omega ) \rightarrow {\mathbb {R}}$ associated to problem (P) is given by

$$\begin{aligned} I(u)=\int _{\Omega }\Phi (x,|\nabla u|)\,dx-\int _{\Omega }F(x,u)\,dx, \end{aligned}$$

where $F(x,t)=\int _{0}^{t}f(x,s)\, ds, \, t \in {\mathbb {R}}$.

Lemma 3.8

The functional I belongs to $C^{1}(W_0^{1,\Phi }(\Omega ),{\mathbb {R}})$ and

$$\begin{aligned} I'(u)v=\int _{\Omega }\varphi (x,|\nabla u|)\nabla u\nabla v\,dx-\int _{\Omega }f(x,u)v\,dx, \quad \forall u,v \in W_0^{1,\Phi }(\Omega ). \end{aligned}$$

Proof

In what follows we will only do the proof by supposing that f is of the type $(f_1)$, because the type $(f_2)$ can be done of a similar way. Note that functional I can be written of the form

$$\begin{aligned} I(u)=\Psi _0(u)-\Psi _1(u)-\Psi _2(u)-\Psi _3(u) \end{aligned}$$

where

$$\begin{aligned} \Psi _0(u)= & {} \int _{\Omega }\Phi (x,|\nabla u|)\,dx, \\ \Psi _1(u)= & {} \int _{(\Omega _q)_{\delta /2}}F(x,u)\,dx, \\ \Psi _2(u)= & {} \lambda \int _{\Omega _N {\setminus } (\Omega _q)_{\delta /2}}F_1(x,u)\,dx, \end{aligned}$$

where $F_1(x,t)=\int _{0}^{t}|s|^{\beta -2}se^{\alpha |s|^{N'}}\,ds$, and

$$\begin{aligned} \Psi _3(u)=\frac{1}{p^*}\int _{\Omega _p {\setminus } (\Omega _q)_{\delta /2}}|u|^{p^*}\,dx. \end{aligned}$$

Since for each $x \in \Omega$, we have $\Phi (x,.) \in C^{1}([0,+\infty ),[0,+\infty ))$, a well known argument ensures that $\Psi _0 \in C^{1}(W_0^{1,\Phi }(\Omega ),{\mathbb {R}})$ with

$$\begin{aligned} \Psi _0'(u)v=\int _{\Omega }\varphi (x,|\nabla u|)\nabla u\nabla v\,dx, \quad \forall u,v \in W_0^{1,\Phi }(\Omega ). \end{aligned}$$

Now, by $(\varphi _6){-}(\varphi _8)$, we know that the space $W_0^{1,\Phi }(\Omega )$ is continuously embedded into $C(\overline{(\Omega _q)_{\delta /2}}), W^{1,\Phi }(\Omega _N{\setminus } (\Omega _q)_{\delta /2})$ and $W^{1,\Phi }(\Omega _p{\setminus } (\Omega _q)_{\delta /2})$. Therefore, it is easy to prove that the functionals $\Psi _1,\Psi _2$ and $\Psi _3$ also belong to $C^{1}(W_0^{1,\Phi }(\Omega ),{\mathbb {R}})$ with

$$\begin{aligned} \Psi '_1(u)v= & {} \int _{(\Omega _q)_{\delta /2}}f(x,u)v\,dx, \quad \forall \,u,v \in W_0^{1,\Phi }(\Omega ), \\ \Psi '_2(u)v= & {} \lambda \int _{\Omega _N {\setminus } (\Omega _q)_{\delta /2}}|u|^{\beta -2}ue^{\alpha |u|^{N'}}v\,dx, \quad \forall \,u,v \in W_0^{1,\Phi }(\Omega ) \end{aligned}$$

and

$$\begin{aligned} \Psi _3'(u)v=\int _{\Omega _p {\setminus } (\Omega _q)_{\delta /2}}|u|^{p^*-2}uv\,dx, \quad \forall u,v \in W_0^{1,\Phi }(\Omega ). \end{aligned}$$

This proves the desired result. Here, Lemma 3.7 plays an important rule in the proof that $\Psi _2$ belongs to $C^{1}(W_0^{1,\Phi }(\Omega ),{\mathbb {R}})$ $\square$

Next, our goal is to prove that I satisfies the mountain pass geometry and the well known (PS) condition.

Lemma 3.9

The functional I satisfies the mountain pass geometry for $\lambda \ge 1,$ that is, 

• (a) There are $r, \rho >0$ such that

  $$\begin{aligned} I(u) \ge \rho \quad \text{ for } \ \Vert u\Vert =r. \end{aligned}$$

• (b) There is $\psi \in W_0^{1,\Phi }(\Omega ) {\setminus } {\overline{B}}_r(0),$ independent of $\lambda \ge 1,$ such that $I(\psi )<0$.

Proof

In what follows we will assume that f is of the type $(f_1)$, because if $(f_2)$ holds the argument is similar. In fact when f is of the type $(f_2)$ the result follows for any $\lambda >0$. As in the proof of Lemma 3.8, we are going to write I of the form

$$\begin{aligned} I(u)=\int _{\Omega }\Phi (x,|\nabla u|)\,dx-\Psi _1(u)-\Psi _2(u)-\Psi _3(u), \quad \forall \,u \in W_0^{1,\Phi }(\Omega ). \end{aligned}$$

The embedding (2.8) together with the definition of f and $(g_1)$ ensures that if r is small, we have

$$\begin{aligned} \int _{(\Omega _q)_{\delta /2}}|F(x,u)|\,dx \le C \int _{(\Omega _q)_{\delta /2}}(|u|^{q_1}+|u|^{\beta }+|u|^{p^*})\,dx , \quad \text{ for } \ \Vert u\Vert =r, \end{aligned}$$

for some positive constant C and $q_1>q$. Here, we have used the fact that $\beta ,p^*>q$. Thus,

$$\begin{aligned} \Psi _1(u) \le C(\Vert u\Vert ^{q_1} + \Vert u\Vert ^{\beta }+\Vert u\Vert ^{p^*}) \end{aligned}$$

(3.6)

for some $C>0$.

From definition of $\Psi _2$, f, (3.3) and Hölder inequality, we get

$$\begin{aligned} \Psi _2(u) \le \lambda \left( \int _{\Omega _N}|u|^{2\beta }\,dx\right) ^{\frac{1}{2}}\left( \int _{\Omega _N}e^{2\alpha |u|^{N'}} \,dx\right) ^{\frac{1}{2}}. \end{aligned}$$

Fixing $\Vert u\Vert =r$ with r small enough, the Lemma 3.4 guarantees that

$$\begin{aligned} \sup \left\{ \int _{\Omega _N}e^{t\alpha |u|^{N'}}\,dx\,:\, \Vert u\Vert \le r \right\} \le C. \end{aligned}$$

Hence

$$\begin{aligned} \Psi _2(u) \le C|u|_{L^{2\beta }(\Omega _N)}^{\beta } \le C_1\Vert u\Vert ^{\beta }. \end{aligned}$$

(3.7)

Now, a direct argument shows that

$$\begin{aligned} \Psi _3(u) \le C_2\Vert u\Vert ^{p^*}. \end{aligned}$$

(3.8)

From (3.7) and (3.8),

$$\begin{aligned} I(u) \ge \int _{\Omega }\Phi (x,|\nabla u|)\,dx-C\Vert u\Vert ^{\beta }-C_1\Vert u\Vert ^{q_1}-C_2\Vert u\Vert ^{p^*}, \quad \text{ for } \ \Vert u\Vert =r. \end{aligned}$$

Now, applying Proposition 2.1(ii) for r small enough, we find

$$\begin{aligned} I(u) \ge \Vert u\Vert ^{q}-C\Vert u\Vert ^{\beta }-C_3\Vert u\Vert ^{q_1}-C_4\Vert u\Vert ^{p^*}, \quad \text{ for } \ \Vert u\Vert =r. \end{aligned}$$

Now, (a) follows by using the fact that $\beta ,q_1,p^* >q$.

In order to prove (b), as $\lambda \ge 1$, note that

$$\begin{aligned} f(x,t) \ge |t|^{\beta -2}t, \qquad \forall x \in \Omega _N {\setminus } \overline{(\Omega _q)_{\delta }} \quad \text{ and } \quad t \ge 0. \end{aligned}$$

From this, fixing a nonnegative function $w \in C_{0}^{\infty }(\Omega _N {\setminus } \overline{(\Omega _q)_{\delta }}) {\setminus } \{0\}$ and $t>0$ we find

$$\begin{aligned} I(t w) \le \frac{t^Nc_1}{N}\int _{\Omega _N}|\nabla w|^{N}\,dx-\frac{t^{\beta }}{\beta }\int _{\Omega _N}|w|^{\beta }\,dx. \end{aligned}$$

As $\beta >N$,

$$\begin{aligned} I(t w) \rightarrow -\infty \quad \text{ when } \ t \rightarrow +\infty , \end{aligned}$$

and so, (b) follows with $\psi =tw$ and t being large enough. $\square$

In the sequel, we denote by d the mountain pass level associated with I, that is,

$$\begin{aligned} d=\inf _{h \in \Gamma }\max _{t \in [0,1]}I(h(t)) \ge \rho >0 \end{aligned}$$

where

$$\begin{aligned} \Gamma =\left\{ \gamma \in C([0,1],W_0^{1,\Phi }(\Omega ))\,:\, \gamma (0)=0 \quad \text{ and } \quad \gamma (1)=\psi \right\} , \end{aligned}$$

and $\psi$ was given in Lemma 3.9.

By using the mountain pass theorem found in Willem [44, Theorem 1.15], there is a $(PS)_d$ sequence $(u_n) \subset W_0^{1,\Phi }(\Omega )$ for I, that is,

$$\begin{aligned} I(u_n) \rightarrow d \quad \text{ and } \quad I'(u_n) \rightarrow 0 \qquad \text{ as }\ n \rightarrow +\infty . \end{aligned}$$

(3.9)

Lemma 3.10

The sequence $(u_n)$ is bounded in $W_0^{1,\Phi }(\Omega )$.

Proof

Setting $\chi =\min \{\theta ,\beta ,p^*\}>q$, it follows by definition of f that

$$\begin{aligned} 0<\chi F(x,t)\le f(x,t)t, \quad \forall (x,t) \in \Omega \times ({\mathbb {R}} {\setminus } \{0\}), \end{aligned}$$

(3.10)

which says that f satisfies the famous Ambrosetti–Rabinowitz condition. Since $(u_n)$ is a $(PS)_d$ sequence for I, there are $C_1,C_2>0$ such that

$$\begin{aligned} I(u_n)-\frac{1}{\chi }I'(u_n)u_n \le C_1+C_2\Vert u_n\Vert , \quad \forall \,n \in {\mathbb {N}}. \end{aligned}$$

(3.11)

From definition of I and $(\varphi _3)$,

$$\begin{aligned} I(u_n)-\frac{1}{\chi }I'(u_n)u_n\ge & {} \int _{\Omega }\Phi (x,|\nabla u_n|)\,dx-\frac{1}{\chi }\int _{\Omega }\varphi (x,|\nabla u_n|)|\nabla u_n|^2\,dx \\\ge & {} \left( 1-\frac{q}{\chi }\right) \int _{\Omega }\Phi (x,|\nabla u_n|)\,dx. \end{aligned}$$

Therefore,

$$\begin{aligned} \left( 1-\frac{q}{\chi }\right) \int _{\Omega }\Phi (x,|\nabla u_n|)\,dx \le C_1+C_2\Vert u_n\Vert , \quad \forall n \in {\mathbb {N}}. \end{aligned}$$

If $\Vert u_n\Vert \ge 1$, then Proposition 2.1(i) leads to

$$\begin{aligned} \left( 1-\frac{q}{\chi }\right) \Vert u_n\Vert ^{p}\le C_1+C_2\Vert u_n\Vert , \quad \forall \,n \in {\mathbb {N}}, \end{aligned}$$

from where it follows the boundedness of $(u_n)$, finishing the proof. $\square$

Since $W_0^{1,\Phi }(\Omega )$ is reflexive and $(u_n) \subset W_0^{1,\Phi }(\Omega )$ is a bounded sequence, we assume that for some subsequence, still denoted by itself, there is $u \in W_0^{1,\Phi }(\Omega )$ such that

$$\begin{aligned} u_n \rightharpoonup u \quad \text{ in } \ W_0^{1,\Phi }(\Omega ), \end{aligned}$$

and

$$\begin{aligned} u_n(x) \rightarrow u(x) \quad \text{ a.e. } \text{ in } \ \Omega . \end{aligned}$$

Lemma 3.11

There is $\lambda ^*>1,$ such that for $\lambda \ge \lambda ^*,$ it holds

$$\begin{aligned} d <\left( 1-\frac{q}{\chi }\right) \min \left\{ \frac{1}{N}\left( \frac{\alpha _N}{2^{N'}\alpha }\right) ^{N-1}, \frac{1}{p} {S_p^{\frac{N}{p}}}\right\} , \end{aligned}$$

where $\chi =\min \{\theta ,\beta ,p^*\}$.

Proof

Taking a nonnegative function $\psi \in C_{0}^{\infty }(\Omega _N {\setminus } \overline{(\Omega _q)_{\delta }}) {\setminus } \{0\}$ and $t>0$ as in the proof of Lemma 3.9, we obtain

$$\begin{aligned} I(t\psi ) \le \frac{t^Nc_1}{N}\int _{\Omega _N}|\nabla \psi |^{N}\,dx-\frac{\lambda t^{\beta }}{\beta }\int _{\Omega _N}|\psi |^{\beta }\,dx. \end{aligned}$$

A direct computation gives

$$\begin{aligned} \max _{t \in [0,+\infty )}I(t\psi ) \le \frac{1}{\lambda ^{\frac{N}{\beta -N}}}\left( \frac{1}{N}-\frac{1}{\beta }\right) \frac{\left( c_1\Vert \nabla \psi \Vert _{L^{N}(\Omega _N)}^{N}\right) ^{\frac{\beta }{\beta -N}}}{\left( \Vert \psi \Vert ^{\beta }_{L^{\beta }(\Omega _N)}\right) ^{\frac{N}{\beta -N}}}. \end{aligned}$$

Therefore, fixing the path $\gamma _1(s)=s\psi$ for $s \in [0,1]$, we have $\gamma _1 \in \Gamma$, and so,

$$\begin{aligned} d \le \max _{s \in [0,1]}I(\gamma _1(s))\le \max _{t \in [0,+\infty )}I(t\psi ) \le \frac{1}{\lambda ^{\frac{N}{\beta -N}}}\left( \frac{1}{N}-\frac{1}{\beta }\right) \frac{\left( c_1\Vert \nabla \psi \Vert _{L^{N}(\Omega _N)}^{N}\right) ^{\frac{\beta }{\beta -N}}}{\left( \Vert \psi \Vert ^{\beta }_{L^{\beta }(\Omega _N)}\right) ^{\frac{N}{\beta -N}}}. \end{aligned}$$

Now, choosing $\lambda ^*>0$ of such way that for all $\lambda \ge \lambda ^*$, we have

$$\begin{aligned} \frac{1}{\lambda ^{\frac{N}{\beta -N}}}\left( \frac{1}{N}-\frac{1}{\beta }\right) \frac{\left( c_1\Vert \nabla \psi \Vert _{L^{N}(\Omega _N)}^{N}\right) ^{\frac{\beta }{\beta -N}}}{\left( \Vert \psi \Vert ^{\beta }_{L^{\beta }(\Omega _N)}\right) ^{\frac{N}{\beta -N}}} <\left( 1-\frac{q}{\chi }\right) \min \left\{ \frac{1}{N}\left( \frac{\alpha _N}{2^{N'}\alpha }\right) ^{N-1}, \frac{1}{p} {S_p^{\frac{N}{p}}}\right\} . \end{aligned}$$

Therefore,

$$\begin{aligned} d< \left( 1-\frac{q}{\chi }\right) \min \left\{ \frac{1}{N}\left( \frac{\alpha _N}{2^{N'}\alpha }\right) ^{N-1}, \frac{1}{p} {S_p^{\frac{N}{p}}}\right\} , \quad \,\forall \lambda \ge \lambda ^*, \end{aligned}$$

which shows the desired result. $\square$

Corollary 3.12

The sequence $(u_n)$ satisfies

$$\begin{aligned} \limsup _{n \rightarrow +\infty }\Vert \nabla u_n\Vert _{L^{N}(\Omega _N)}^{\frac{N}{N-1}}< \frac{\alpha _N}{2^{N'} \alpha }. \end{aligned}$$

Then,  without lost of generality,  we can assume that there is $\tau \in (0,1)$ such that

$$\begin{aligned} \Vert \nabla u_n\Vert _{L^{N}(\Omega _N)}^{\frac{N}{N-1}} \le \frac{\tau \alpha _N}{2^{N'} \alpha }, \quad \forall n \in {\mathbb {N}}. \end{aligned}$$

Proof

First of all, we must recall that

$$\begin{aligned} I(u_n)-\frac{1}{\chi }I'(u_n)u_n=d+o_n(1)\Vert u_n\Vert +o_n(1), \end{aligned}$$

from where it follows that

$$\begin{aligned} d+o_n(1)\Vert u_n\Vert +o_n(1)\ge & {} \int _{\Omega }\left( (\Phi (x,|\nabla u_n|)-\frac{1}{\chi }\varphi (x,|\nabla u_n|)|\nabla u_n|^{2}\right) \,dx \\\ge & {} \frac{1}{N}\left( 1-\frac{q}{\chi }\right) \int _{\Omega _N}|\nabla u_n|^{N}\,dx. \end{aligned}$$

Hence, by Lemma 3.11,

$$\begin{aligned} \limsup _{n \rightarrow +\infty }\frac{1}{N}\left( 1-\frac{q}{\chi }\right) \int _{\Omega _N}|\nabla u_n|^{N}\,dx \le d< \min \left( 1-\frac{q}{\chi }\right) \left\{ \frac{1}{N}\left( \frac{\alpha _N}{2^{N'}\alpha }\right) ^{N-1},\frac{1}{p}S_p^{\frac{N}{p}}\right\} \end{aligned}$$

leading to

$$\begin{aligned} \limsup _{n \rightarrow +\infty }\int _{\Omega _N}|\nabla u_n|^{N}\,dx < \left( \frac{\alpha _N}{2^{N'}\alpha }\right) ^{N-1}, \end{aligned}$$

which proves the lemma. $\square$

Lemma 3.13

The functional I verifies the $(PS)_d$ condition.

Proof

In what follows, we will assume that f is of the type $(f_1)$. Moreover, let us set

$$\begin{aligned} P_n=\int _{\Omega }\langle \varphi (x,|\nabla u_n|)\nabla u_n, \nabla u_n- \nabla u\rangle \,dx, \end{aligned}$$

that is,

$$\begin{aligned} P_n=I'(u_n)u_n+\int _{\Omega }f(x,u_n)u_n\,dx-I'(u_n)u-\int _{\Omega }f(x,u_n)u\,dx. \end{aligned}$$

Consequently

$$\begin{aligned} P_n=\int _{\Omega }f(x,u_n)u_n\,dx-\int _{\Omega }f(x,u_n)u\,dx+o_n(1). \end{aligned}$$

From the definition of f together with embedding (2.8),

$$\begin{aligned} \lim _{n \rightarrow +\infty }\int _{\Omega }{\tilde{\eta }}_q(x)g(x,u_n)u_n\,dx= & {} \lim _{n \rightarrow +\infty }\int _{\Omega }{\tilde{\eta }}_q(x)g(x,u_n)u\,dx \\= & {} \int _{\Omega }{\tilde{\eta }}_q(x)g(x,u)u\,dx, \\ \lim _{n \rightarrow +\infty }\int _{\Omega {\setminus } \Omega _N}{\eta }_N(x)|u_n|^{\beta }e^{\alpha |u_n|^{N'}}\,dx= & {} \int _{\Omega {\setminus } \Omega _N}{\eta }_N(x)|u|^{\beta }e^{\alpha |u|^{N'}}\,dx, \\ \lim _{n \rightarrow +\infty }\int _{\Omega {\setminus } \Omega _N}{\eta }_N(x)|u_n|^{\beta -2}u_{n}ue^{\alpha |u_n|^{N'}}dx= & {} \int _{\Omega {\setminus } \Omega _N}{\eta }_N(x)|u|^{\beta }e^{\alpha |u|^{N'}}\,dx, \\ \lim _{n \rightarrow +\infty }\int _{\Omega {\setminus } \Omega _p}{\eta }_p(x)|u_n|^{p^*}\,dx= & {} \int _{\Omega {\setminus } \Omega _p}{\eta }_p(x)|u|^{p^*}\,dx, \end{aligned}$$

and

$$\begin{aligned} \lim _{n \rightarrow +\infty }\int _{\Omega {\setminus } \Omega _p}{\eta }_p(x)|u_n|^{p^*-2}u_nu\,dx=\int _{\Omega {\setminus } \Omega _p}{\eta }_p(x)|u|^{p^*}\,dx. \end{aligned}$$

Consequently

$$\begin{aligned} P_n= & {} \lambda \int _{\Omega _N}|u_n|^{\beta }e^{\alpha |u_n|^{N'}}\,dx-\lambda \int _{\Omega _N }|u_n|^{\beta -2}u_nue^{\alpha |u_n|^{N'}}\,dx + \int _{\Omega _p}|u_n|^{p^*}\,dx \\&-\int _{\Omega _p}|u_n|^{p^*-2}u_nu\,dx\,dx+o_n(1). \end{aligned}$$

By Corollary 3.12, the sequence $(u_n)$ satisfies

$$\begin{aligned} \Vert \nabla u_n\Vert _{L^{N}(\Omega _N)}^{N'} \le \frac{\tau \alpha _N}{2^{N'} \alpha }, \quad \forall n \in {\mathbb {N}}, \end{aligned}$$

for some $\tau \in (0,1)$. Employing Corollary 3.6, there is $t>1$ and $t \approx 1$ such that the sequence $h_n(x)=e^{\alpha |u_n(x)|^{N'}}$ is weakly convergent to $h(x)=e^{\alpha |u(x)|^{N'}}$ in $L^{t}(\Omega _N)$ , that is,

$$\begin{aligned} \int _{\Omega _N}h_n \varphi \,dx \rightarrow \int _{\Omega _N}h \varphi \,dx, \quad \forall \varphi \in L^{t'}(\Omega _N), \end{aligned}$$

(3.12)

where $t'=\frac{t}{t-1}$. As

$$\begin{aligned} |u_n|^{\beta } \rightarrow |u|^{\beta } \quad \text{ in } \ L^{t'}(\Omega _N) \end{aligned}$$

it follows that

$$\begin{aligned} \int _{\Omega _N}h_n |u_n|^{\beta } \,dx \rightarrow \int _{\Omega _N}h |u|^\beta \,dx, \end{aligned}$$

that is,

$$\begin{aligned} \int _{\Omega _N}|u_n|^{\beta }e^{\alpha |u_n|^{N'}} \,dx \rightarrow \int _{\Omega _N}|u|^{\beta }e^{\alpha |u|^{N'}} \,dx. \end{aligned}$$

Now, using the fact that

$$\begin{aligned} |u_n|^{\beta -2}u_nu \rightarrow |u|^{\beta } \quad \text{ in } \ L^{t'}(\Omega _N) \end{aligned}$$

we also derive that

$$\begin{aligned} \int _{\Omega _N}|u_n|^{\beta -2}u_nue^{\alpha |u_n(x)|^{N'}} \,dx \rightarrow \int _{\Omega _N}|u|^{\beta -2}uue^{\alpha |u(x)|^{N'}}\,dx. \end{aligned}$$

The above analysis ensures that

$$\begin{aligned} \lim _{n \rightarrow +\infty }\int _{\Omega _N}|u_n|^{\beta }e^{\alpha |u_n(x)|^{N'}}\,dx=\lim _{n \rightarrow +\infty }\int _{\Omega _N}|u_n|^{\beta -2}u_nue^{\alpha |u_n(x)|^{N'}}\,dx=\int _{\Omega _N}|u|^{\beta }e^{\alpha |u|^{N'}}\,dx, \end{aligned}$$

and then,

$$\begin{aligned} P_n=\int _{\Omega _p}|u_n|^{p^*}\,dx-\int _{\Omega _p}|u_n|^{p^*-2}u_nu\,dx+o_n(1). \end{aligned}$$

By [34, Lemma 4.8],

$$\begin{aligned} \lim _{n \rightarrow +\infty }\int _{\Omega _p}|u_n|^{p^*-2}u_nu\,dx=\int _{\Omega _p}|u|^{p^*}\,dx, \end{aligned}$$

then

$$\begin{aligned} P_n=\int _{\Omega _p}|u_n|^{p^*}\,dx-\int _{\Omega _p}|u|^{p^*}\,dx+o_n(1). \end{aligned}$$

Now, we are going to use the Concentration Compactness Lemma 3.1 to the sequence $(u_n) \subset W^{1,p}(\Omega _p)$. From $(\varphi _7)$, for each open ball $B \subset (\Omega _q)_{\delta }$ we have that the embedding $W^{1,\Phi }(\Omega ) \hookrightarrow C({\overline{B}})$ is compact, then as $(u_n)$ is a bounded (PS) for I, it is possible to prove that for some subsequence there holds

$$\begin{aligned} \int _{B}\langle \varphi (x,|\nabla u_n|)\nabla u_n, \nabla u_n- \nabla u\rangle \,dx \rightarrow 0. \end{aligned}$$

Since from $(\varphi _6){-}(\varphi _8)$, the embedding $W^{1,\Phi }(B) \hookrightarrow L^{\Phi }(B)$ is compact, the last limit together with the $\Delta _2$-condition implies that

$$\begin{aligned} u_n \rightarrow u \quad \text{ in } \ W^{1,\Phi }(B). \end{aligned}$$

Now, recalling that the embedding $W^{1,\Phi }(B) \hookrightarrow W^{1,p}(B)$ is continuous, we derive that

$$\begin{aligned} u_n \rightarrow u \quad \text{ in } \ W^{1,p}(B), \end{aligned}$$

from where it follows that $x_i \in \overline{\Omega _p} {\setminus } (\Omega _q)_{\delta }$ for all $i \in J$. Now, our goal is proving that J must be a finite set. Have this in mind, we will consider $J=J_1 \cup J_2$ where

$$\begin{aligned} J_1=\{i \in J\,:\,x_i \in \overline{\Omega _p} {\setminus } \overline{(\Omega _q)_{\delta }} \} \end{aligned}$$

and

$$\begin{aligned} J_2=\{i \in J\,:\,x_i \in \partial (\Omega _q)_{\delta } \cap \Omega _p \}. \end{aligned}$$

If $i \in J_1$, the condition $(\varphi _8)$ says that $c_2t^{p-2} \ge \varphi (x,t) \ge t^{p-2}$ for $x \in \overline{\Omega _p} {\setminus } \overline{(\Omega _q)_{\delta }}$. This fact permits to repeat the same arguments explored in [28, Lemma 2.3] to conclude that $J_1$ is finite. Now, if $i \in J_2$, the situation is more subtle and we must be careful. In what follows let us consider ${\tilde{\psi }} \in C_{0}^{\infty }({\mathbb {R}}^N)$ such that

$$\begin{aligned} {\tilde{\psi }} \equiv 1 \quad \text{ on } \ B(0,1)\qquad \text{ and } \qquad {\tilde{\psi }} \equiv 0 \quad \text{ on }\ B(0,2)^c. \end{aligned}$$

For each $\epsilon >0$, we set

$$\begin{aligned} \psi (x)={\tilde{\psi }}({(x-x_i)}/{\epsilon }), \quad \forall x \in {\mathbb {R}}^N. \end{aligned}$$

Since $(u_n)$ is a bounded sequence in $W^{1,\Phi }(\Omega )$, the sequence $(\psi u_n)$ is also bounded in $W^{1,\Phi }(\Omega )$, and so, $I'(u_n)\psi u_n=o_n(1)$. Hence,

$$\begin{aligned} \int _{\Omega }\varphi (x,|\nabla u_n|)\nabla u_n \nabla (\psi u_n)\,dx=\int _{\Omega }{\tilde{\eta }}_q(x)g(x,u_n)\psi u_n\,dx+\int _{\Omega }\eta _p(x)|u_n|^{p^*}\psi \,dx+o_n(1). \end{aligned}$$

Now, given $\xi >0$, the Young’s inequality (2.1) combined with (2.2) and $\Delta _2$-condition gives

$$\begin{aligned} \int _{\Omega } |\varphi (x,|\nabla u_n|)|\nabla u_n||u_n||\nabla \psi |\,dx \le \xi \int _{\Omega }\Phi (x,|\nabla u_n|)\,dx +C_{\xi }\int _{\Omega }\Phi (x,|\nabla \psi ||u_n|)\,dx, \end{aligned}$$

for some $C_\xi >0$. Note that by $(\varphi _8)$,

$$\begin{aligned} \int _{\Omega }\Phi (x,|\nabla \psi ||u_n|)\,dx \le C_1\left( \int _{B(x_i,2\epsilon )}|\nabla \psi |^p||u_n|^p\,dx+\int _{B(x_i,2\epsilon )}\tau _2(x)|\nabla \psi |^q||u_n|^q\,dx \right) . \end{aligned}$$

By Hölder inequality

$$\begin{aligned} \limsup _{n \rightarrow +\infty }\int _{B(x_i,2\epsilon )} |u_n|^p|\nabla \psi |^p\,dx \le C_2\left( \int _{B(x_i,2\epsilon )}|u|^{p^*}\,dx\right) ^{\frac{N-p}{N}} \end{aligned}$$

from where it follows that

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\left[ \limsup _{n \rightarrow +\infty }\int _{B(x_i,2\epsilon )} |u_n|^p|\nabla \psi |^p\,dx\right] \le \lim _{\epsilon \rightarrow 0} C_2\left( \int _{B(x_i,2\epsilon )}|u|^{p^*}\,dx\right) ^{\frac{N-p}{N}}=0. \end{aligned}$$

(3.13)

Arguing as above, we also have

$$\begin{aligned} \limsup _{n \rightarrow +\infty }\int _{\Omega }\tau _2(x)|u_n|^q|\nabla \psi |^q\,dx \le \left( \int _{B(x_i,2\epsilon )}\left| \tau _2^{\frac{1}{q}}(x)\nabla \psi \right| ^{\frac{qp^*}{p^*-q}}\,dx \right) ^{\frac{p^*-q}{p^*}}\left( \int _{B(x_i,2\epsilon )}|u|^{p^*} \,dx\right) ^{\frac{q}{p^*}}. \end{aligned}$$

By change of variable,

$$\begin{aligned} \int _{B(x_i,2\epsilon )}\left| \tau _2^{\frac{1}{q}}(x)\nabla \psi \right| ^{\frac{qp^*}{p^*-q}}\,dx= & {} \left( \frac{1}{\epsilon }\right) ^{\frac{qp^*}{p^*-q}}\int _{B(0,2)}\left| \tau _2^{\frac{1}{q}}(\epsilon x+x_i)\nabla {\tilde{\psi }}\right| ^{\frac{qp^*}{p^*-q}}\,dx \\ \\\le & {} C_5\left( \frac{1}{\epsilon }\right) ^{\frac{qp^*}{p^*-q}} \int _{B(0,2)}\left| \tau _2^{\frac{1}{q}}(\epsilon x+x_i)\right| ^{\frac{qp^*}{p^*-q}}\,dx . \end{aligned}$$

Since $x_i \in \partial (\Omega _q)_{\delta } \cap \Omega _p$, it follows that

$$\begin{aligned} \tau _2(\epsilon x+x_i) \le c_3\epsilon ^{s}|x|^{s} \end{aligned}$$

and

$$\begin{aligned} \int _{B(x_i,2\epsilon )}\left| \tau _2^{\frac{1}{q}}(x)\nabla \psi \right| ^{\frac{qp^*}{p^*-q}}\,dx \le C_6\epsilon ^{\frac{(s-q)p^*}{p^*-q}}. \end{aligned}$$

As $s>q$, it follows that

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\left[ \limsup _{n \rightarrow +\infty }\int _{\Omega }\tau _2(x)|u_n|^q|\nabla \psi |^q\,dx \right] =0. \end{aligned}$$

(3.14)

Now, the boundedness of $(u_n)$ in $W^{1,\Phi }(\Omega )$ together with Proposition 2.1, (3.13) and (3.14) ensures that

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\left[ \limsup _{n \rightarrow +\infty }\int _{\Omega }|\varphi (x,|\nabla u_n|)|\nabla u_n||u_n||\nabla \psi |\,dx \right] \le \xi C, \end{aligned}$$

for some $C>0$. Since $\xi >0$ is arbitrary, we can deduce that

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\left[ \limsup _{n \rightarrow +\infty }\int _{\Omega }|\varphi (x,|\nabla u_n|)|\nabla u_n||u_n||\nabla \psi |\,dx \right] =0. \end{aligned}$$

The last limit together with the fact that $\varphi (x,t) \ge t^{p-2}$ for $x \in \Omega _p$ permit to conclude as in [28, Lemma 2.3], that $J_2$ is also finite. Consequently, J is a finite set. However, in order to conclude the proof of the lemma, we need to show that J is in fact an empty set. Seeking by a contradiction, assume that there is $i \in J$. In this case, the argument explored in [28] also says for us that

$$\begin{aligned} \nu _i \ge {S_p^{\frac{N}{p}}}. \end{aligned}$$

Hence, by Lemma 3.1(d),

$$\begin{aligned} \mu _i \ge {S_p^{\frac{N}{p}}}. \end{aligned}$$

As $|\nabla u_n|^{p} \rightarrow \mu$ weakly-$^*$ in the sense of measure, we have

$$\begin{aligned} \liminf _{n \rightarrow +\infty }\int _{\Omega _p}|\nabla u_n|^{p}\,dx \ge \mu _i \end{aligned}$$

and so,

$$\begin{aligned} \liminf _{n \rightarrow +\infty }\int _{\Omega _p}|\nabla u_n|^{p}\,dx \ge {S_p^{\frac{N}{p}}}. \end{aligned}$$

Now, using once more the equality

$$\begin{aligned} I(u_n)-\frac{1}{\chi }I'(u_n)u_n=d+o_n(1)\Vert u_n\Vert +o_n(1), \end{aligned}$$

we get

$$\begin{aligned} d+o_n(1)\Vert u_n\Vert +o_n(1) \ge \frac{1}{p}\left( 1-\frac{q}{\chi }\right) \int _{\Omega _p}|\nabla u_n|^{p}\,dx. \end{aligned}$$

Taking the limit of $n \rightarrow +\infty$, we find the inequality below

$$\begin{aligned} d \ge \frac{1}{p}\left( 1-\frac{q}{\chi }\right) {S_p^{\frac{N}{p}}} \end{aligned}$$

that contradicts the Lemma 3.11, showing that $J=\emptyset$. Thereby, by Lemma 3.1(a), $\nu =|u|^{p^*}$ and

$$\begin{aligned} \int _{\Omega _p}|u_n|^{p^*}\,dx \rightarrow \int _{\Omega _p}|u|^{p^*}\,dx, \end{aligned}$$

implying that $P_n=o_n(1)$, that is,

$$\begin{aligned} \lim _{n \rightarrow +\infty }\int _{\Omega }\langle \varphi (x,|\nabla u_n|)\nabla u_n, \nabla u_n- \nabla u\rangle \,dx=0. \end{aligned}$$

Now, it is enough to apply Lemma 2.2 to finish the proof. $\square$

4 Proof of the main result

Proof of Theorem 1.1 completed

First of all, we recall that Lemmas 3.9 and 3.13 showed that the energy functional I satisfies the mountain pass geometry and the $(PS)_d$ condition on space $W_0^{1,\Phi }(\Omega )$. Hence, there is a nontrivial critical point $u \in W_0^{1,\Phi }(\Omega )$ of I such that

$$\begin{aligned} u_n \rightarrow u \quad \text{ in } \ W_0^{1,\Phi }(\Omega ), \end{aligned}$$

and so,

$$\begin{aligned} I(u)=d>0 \quad \text{ and } \quad I'(u)=0, \end{aligned}$$

finishing the proof. $\square$