Abstract
We investigate the distance function \(\varvec{\delta }_{K}^{\phi }\) from an arbitrary closed subset K of a finite-dimensional Banach space \( (\mathbf {R}^{n}, \phi ) \), equipped with a uniformly convex \( \mathscr {C}^{2} \)-norm \( \phi \). These spaces are known as Minkowski spaces and they are one of the fundamental spaces of Finslerian geometry (see Martini et al. in Expo Math 19:97–142, 2001, https://doi.org/10.1016/S0723-0869(01)80025-6). We prove that the gradient of \(\varvec{\delta }_{K}^{\phi }\) satisfies a Lipschitz property on the complement of the \(\phi \)-cut-locus of K (a.k.a. the medial axis of \(\mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K\)) and we prove a structural result for the set of points outside K where \(\varvec{\delta }_{K}^{\phi }\) is pointwise twice differentiable, providing an answer to a question raised by Hiriart-Urruty (Am Math Mon 89:456–458, 1982, https://doi.org/10.2307/2321379). Our results give sharp generalisations of some classical results in the theory of distance functions and they are motivated by critical low-regularity examples for which the available results gives no meaningful or very restricted informations. The results of this paper find natural applications in the theory of partial differential equations and in convex geometry.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For the basic notation we refer the reader to Sect. 2.1.
Suppose \( K \subseteq \mathbf {R}^{n} \) is a closed set and \(\phi \) is a uniformly convex norm on \(\mathbf {R}^{n}\); cf. 2.8. Our central object of study is the \(\phi \)- distance function
We investigate in detail the set of points where \(\varvec{\delta }_{K}^{\phi }\) is not differentiable and then also the set of points where it is not pointwise twice differentiable. Define
A basic and fundamental result in the theory of distance functions asserts what follows.
Theorem 1.1
(\(\mathcal {C}^{1,1}\)-regularity) If \( K \subseteq \mathbf {R}^{n} \) is an arbitrary closed set, then \( \varvec{\delta }_{K}^{\phi } \) is \( \mathcal {C}^{1} \) with a locally Lipschitz gradient on the open subset \( U := \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}\big (K \cup \mathop {\mathrm {Clos}}\Sigma ^{\phi }(K)\big ) \).
This result can be deduced employing general results from the theory of Hamilton–Jacobi equations (see [31, Theorem 15.1] or [16]). Indeed, for a general closed set K it is well known that \(\varvec{\delta }_{K}^{\phi } \) is a locally semiconcave function on \( \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \) and it satisfies, in a viscosity sense, the Eikonal equation \( \phi ^*({{\,\mathrm{grad}\,}}u) =1 \) on \( \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \) (where \(\phi ^*\) is the dual norm of \(\phi \) as defined in 2.7); see [8, 31, 45]. For the Euclidean norm Theorem 1.1 can also be obtained using a purely geometric argument (see [17, 4.8]).
Of course, the conclusion of the theorem can be improved if we know that K is at least a \( \mathcal {C}^2 \)-submanifold. In fact, in this case \( \varvec{\delta }_{K}^{\phi } \) is at least of class \(\mathscr {C}^{2}\) on the open subset U and \(\mathop {\mathrm {Clos}}\Sigma ^{\phi }(K)\) is a set of \( \mathscr {L}^{n} \)-measure zero; if K is a \( \mathcal {C}^{2,1} \)-submanifold, then \(\mathop {\mathrm {Clos}}\Sigma ^{\phi }(K)\) is a set of locally finite \( \mathscr {H}^{n-1} \)-measure; see [12, 28, 32, 33, 36]. A sufficient condition that guarantees \( \mathscr {L}^{n} (\mathop {\mathrm {Clos}}\Sigma (K)) =0 \) for closed \( \mathcal {C}^{1,1} \)-hypersurfaces K in terms of the inner radius of curvature is given in [35, Theorem 4.1]. Moreover, if K is a closed \( \mathcal {C}^1 \)-hypersurface, then [35, Theorem 1.3] provides a necessary and sufficient condition for a point \( x \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \) to lie in \( \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}\mathop {\mathrm {Clos}}(\Sigma (K)) \).
On the other hand, it turns out that the \( \mathcal {C}^2 \)-regularity is a critical hypothesis; indeed the second named author has shown, in [41], that for a convex open subset \( \Omega \) with \( \mathcal {C}^{1,1} \)-boundary the set \( \mathop {\mathrm {Clos}}\Sigma ^{\phi }(\mathbf {R}^{n} {{\,\mathrm{\sim }\,}}\Omega ) \) might have non empty interior in \( \Omega \); moreover, for a typical (in the sense of Baire Category) convex open subset \( \Omega \) with \( \mathcal {C}^1 \)-boundary we have that \(\Sigma ^{\phi }(\mathbf {R}^{n} {{\,\mathrm{\sim }\,}}\Omega ) \) is dense in \( \Omega \). There exist even closed \(\mathcal {C}^{1, \alpha } \)-hypersurfaces K such that \( \Sigma ^{\phi }(K) \) is dense in all of \( \mathbf {R}^{n} \); see [41, Corollary 2.9]. In all these examples one can choose \( \phi \) to be the Euclidean norm. Therefore, the set U defined in 1.1 might easily be empty even if \( K = \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}\Omega \) and \( \Omega \) is a convex open subset with \( \mathcal {C}^{1} \) boundary, or might reduce to a small tubular neighbourhood around K if \( \Omega \) has a \( \mathcal {C}^{1,1} \) boundary. Consequently Theorem 1.1 provides no (or very limited) information in these situations. On the other hand it is well known that the gradient of \( \varvec{\delta }_{K}^{\phi } \) is a continuous map on its domain \( \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}(K \cup \Sigma ^{\phi }(K)) \). Therefore, it is a natural to ask for a characterisation of the largest set on which the gradient of \( \varvec{\delta }_{K}^{\phi } \) satisfies a Lipschitz condition. We identify that set in Theorem 1.4, providing an effective sharp generalization of Theorem 1.1 that is applicable in the aforementioned critical low-regularity cases.
Besides its central role in Theorem 1.1, the set \( \Sigma ^{\phi }(K) \) has been extensively studied in the last decades. Indeed, if we define the \(\phi \)- nearest point projection \(\varvec{\xi }_{K}^{\phi }\) to be the multivalued function (see 2.11 and 2.28) mapping a point \(x \in \mathbf {R}^{n}\) into the set
then it is well known that \( \Sigma ^{\phi }(K) \) is precisely the set of points \( x \in \mathbf {R}^{n} \sim K \) where \(\varvec{\xi }_{K}^{\phi }(x) \) is not a singleton. It is remarkable that \( \Sigma ^{\phi }(K) \) can be always covered by countably many \( \mathcal {C}^2 \)-hypersurfaces (see [23, 44]); moreover upper bounds on its Hausdorff measure are known (see [1]). Lower bounds and results on the propagation of the non-differentiability points can be obtained from [3, 4, 14]. The topological properties of the set \( \Sigma ^{\phi }(K) \) in a Euclidean or Riemannian setting are studied in [5, 13, 30].
Since \(\varvec{\delta }_{K}^{\phi }\) is locally semiconcave outside K, it is a natural question to investigate the set of points \( x \in \mathbf {R}^{n} \sim K \) where \( \varvec{\delta }_{K}^{\phi } \) is pointwise twice differentiable, which means the set of points where the function admits a second-order Taylor polynomial; see 2.22. Thus, we consider the set
A classical theorem on the twice differentiability of convex functions of Alexandrov (see [7]) readily implies the following result.
Theorem 1.2
If \( K \subseteq \mathbf {R}^{n} \) is an arbitrary closed set, then \( \mathscr {L}^{n} (\Sigma ^{\phi }_2(K)) =0 \).
The example in 4.19 shows that the dimension of the set \( \Sigma ^{\phi }_2(K) \) might be exactly n even if K is a closed convex body with \( \mathcal {C}^{1,1} \)-boundary. On the other hand, it is natural to ask about the structure of \( \Sigma ^{\phi }_2(K) \) for a general closed set K; however, nothing is known in the literature. The problem, in the Euclidean setting, goes back at least to [26] (see last paragraph on page 458). We remark that the set of twice-differentiability points of the \(\phi \)-distance function \(\varvec{\delta }_{K}^{\phi }\) corresponds to the set of differentiability points of the \( \phi \)-nearest point projection \(\varvec{\xi }_{K}^{\phi }\); see 2.41(e). Only if K is convex sharp results are available, that describe the structure of \( \Sigma ^\phi _2(K) \) in terms of the unit \( \phi \)- normal bundle of K. This is defined for an arbitrary closed set \( K \subseteq \mathbf {R}^{n} \) as

We recall that \( N^{\phi }(K) \) is a Borel and countably \((n-1)\)-rectifiable subset of \(\mathbf {R}^{2n}\); cf. [15, Lemma 5.2], see [18, 3.2.14(2)] for the notion of rectifiability.
Theorem 1.3
Suppose \( K \subseteq \mathbf {R}^{n} \) is convex. Then there exists \( Z \subseteq N^\phi (K) \) with \( \mathscr {H}^{n-1} (Z) =0 \) such that
In particular, for \( \mathscr {H}^{n-1} \) almost all \((a, \eta ) \in N^\phi (K) \) the distance function \(\varvec{\delta }_{K}^{\phi } \) is pointwise twice differentiable at all points of the ray \( \{ a + r \eta : 0< r < +\infty \} \).
The exceptional set Z cannot be excluded. In fact, even if \( \phi \) is the Euclidean norm, there exist convex bodies K with \( \mathcal {C}^{1,1} \) boundaries such that the set Z is dense in \( N^{\phi }(K) \) with Hausdorff dimension \( n-1 \); see 4.19. Indeed, the construction of the \( \mathcal {C}^{1,1} \)-convex hypersurface in Theorem 4.19 shows that one can choose Z to be somewhat arbitrarily complicated. In the Euclidean setting Theorem 1.3 is a classical fact in convex geometry; see [42]. The general anisotropic version in Theorem 1.3 can be proved employing Theorem 1.1 and following a similar argument. We also remark that for \( n =2 \) Theorem 1.3 can be deduced from a more general statement in [10]. See also [27] for related results.
Our Theorem 1.5 extends Theorem 1.3 to arbitrary closed sets and it gives the first answer to the question of Hiriart-Urruty, providing a new insight into the structure of \( \Sigma ^{\phi }_2(K) \).
1.1 The main results of the present paper
In addition to the notions already introduced in the previous section, we introduce here a few additional definitions and facts. Here \( K \subseteq \mathbf {R}^{n} \) is always an arbitrary closed set. The \(\phi \)- reach of K is the function \(\varvec{r}_{K}^{\phi }: N^{\phi }(K) \rightarrow (0, + \infty ]\) given by
Simple arguments show that \( \varvec{r}_{K}^{\phi } \) is upper semicontinuous; see 2.35. Moreover, we define \({{\,\mathrm{Cut}\,}}^{\phi }(K)\), the \( \phi \)-cut locus of K, by
In view of this last definition, the number \(\varvec{r}_{K}^{\phi }(a,\eta )\) can be seen as the \( \phi \)- distance from the cut locus of K in direction \(\eta \); indeed, this function plays a central role in the seminal work [28], where it is proved to be Lipschitz continuous provided K is a smooth submanifold, and in other papers on the subject; see for instance [12, 32]. Note that (see Remark 4.1)
We notice also that \( \mathscr {L}^{n} ({{\,\mathrm{Cut}\,}}^{\phi }(K)) = 0 \); see Remark 4.4. Since \( \Sigma ^{\phi }(K) \) might not be nowhere dense, the same is true for \( {{\,\mathrm{Cut}\,}}^\phi (K) \). Observe that \(\varvec{\xi }_{K}^{\phi }\) induces a natural fibration
Our goal is to study regularity properties of \(\varvec{\delta }_{K}^{\phi } \) on \(\mathbf {R}^{n} {{\,\mathrm{\sim }\,}}({{\,\mathrm{Cut}\,}}^{\phi }(K) \cup K)\). To this end we look at the sets of points of \( \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}({{\,\mathrm{Cut}\,}}^{\phi }(K) \cup K) \) with a uniform positive relative \( \phi \)-distance to the cut-locus; in other words, we consider the sets
Notice that \(\mathbf {R}^{n} {{\,\mathrm{\sim }\,}}({{\,\mathrm{Cut}\,}}^{\phi }(K) \cup K) = \bigcup _{\sigma >1} K_{\sigma } \) but \( K_{\sigma } \) might have empty interior for every \(\sigma > 1\).
Our first result asserts that \( {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi } \) is locally Lipschitz continuous on the sets \( K_{\sigma } \), which is a sharp generalisation of Theorem 1.1. More precisely we prove the following result.
Theorem 1.4
(Lipschitz estimates for the gradient) Suppose \(\phi : \mathbf {R}^{n} \rightarrow \mathbf {R}\) is a uniformly convex norm of class \(\mathscr {C}^{2}\) away from the origin, \(K \subseteq \mathbf {R}^{n}\) is closed, \(1< \sigma < \infty \), \(0< s< t < \infty \), and
Then \( {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi } | K_{\sigma ,s,t} \) is Lipschitz continuous.
The restriction “\(\sigma \rho \le \varvec{r}_{K}^{\phi }(a, \eta )\)” cannot be avoided since the Lipschitz constant of \({{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }\) may explode near points of \({{\,\mathrm{Cut}\,}}^{\phi }(K)\); cf. 4.2. Observe that if \(x \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}\bigl ( \mathop {\mathrm {Clos}}\Sigma ^{\phi }(K) \cup K \bigr )\), then x has positive distance from \({{\,\mathrm{Cut}\,}}^{\phi }(K) \); hence, Theorem 1.4 includes Theorem 1.1 as a special case; moreover, it is sharp in terms of specifying the set of points where a Lipschitz condition for \({{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }\) holds. There are two main difficulties in proving 1.4. The first one arises from the fact that \( {{\,\mathrm{Cut}\,}}^{\phi }(K) \) might be dense in \( \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \) and consequently it does not seem to be possible to rely on general results for Hamilton–Jacobi equations as for Theorem 1.1. The second difficulty comes from working with a possibly non-Euclidean norm. In fact, if \( \phi \) is the Euclidean norm then the proof of Theorem 1.4 follows rather directly from the geometric argument originally found by Federer for sets of positive reach in [17], see [40, 3.10(1)]. However, this argument is not applicable if \( \phi \) is not the Euclidean norm, in which case one needs a considerably more sophisticated approach, based on a careful analysis of the geometric properties of the \( \phi \)-balls (which occupies the entire Sect. 3). In fact this analysis allows to show that the \( \phi \)-nearest point projection \( \varvec{\xi }_{K}^{\phi } \) onto K satisfies the asserted Lipschitz property. Recalling the well known relation between \( \varvec{\xi }_{K}^{\phi } \) and \( {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi } \) (see Lemma 2.41(c))
we get the conclusion of 1.4. Notice that uniform convexity and regularity of the norm for \( n\ge 3 \) are crucial to obtain the Lipschitz property in Theorem 1.4; see the last section in [10].
The second goal of this paper is to extend Theorem 1.3 to arbitrary closed sets. In case of convex sets the reach function satisfies \( \varvec{r}_{K}^{\phi }(a, \eta ) = + \infty \) for every \((a, \eta )\in N^\phi (K) \) and consequently \( {{\,\mathrm{Cut}\,}}^\phi (K) = \varnothing \). This is a very special situation given by the assumption of convexity; indeed, even if we consider \( \mathcal {C}^{1,1} \) convex hypersurfaces the reach function might be discontinuous on a dense set and the cut-locus might not be nowhere dense; see 2.37. This suggests that a generalization of Theorem 1.3 to non-convex sets requires a careful analysis of the behaviour of \( \varvec{r}_{K}^{\phi } \) and the connection with the points of differentiability of \( \varvec{\xi }_{K}^{\phi } \). This can be done considering the new reach-type function (recall (7))

for \((a, \eta )\in N^\phi (K)\). It holds that \(0 \le \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \le \varvec{r}_{K}^{\phi }(a, \eta ) \) for every \( (a, \eta )\in N^\phi (K)\); see Remark 4.10. However simple examples show that there exist closed sets K for which \( \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) < \varvec{r}_{K}^{\phi }(a, \eta ) \) for some \( (a, \eta ) \in N^\phi (K) \); cf. 4.17. If K is a closed set such that the \(\phi \)-tubular neighbourhood \( \{ x : \varvec{\delta }_{K}^{\phi }(x) < \rho \} \) of radius \( \rho > 0 \) does not intersect \( \Sigma ^{\phi }(K) \), then \( \varvec{r}_{K}^{\phi }(a, \eta ) \ge \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \ge \rho \) for every \( (a, \eta )\in N^\phi (K) \); cf. Lemma 4.16.
Employing the reach function \( \underline{\varvec{r}_{K}^{\phi }} \) we obtain the following result on the structure of the \( \Sigma ^{\phi }_2(K) \) for an arbitrary closed set K.
Theorem 1.5
Suppose \(K \subseteq \mathbf {R}^{n}\) is closed. Then
-
(a)
\( {{\,\mathrm{Cut}\,}}^\phi (K) \subseteq \Sigma ^{\phi }_2(K) \).
-
(b)
If \((a, \eta )\in N^\phi (K) \) and there exists \( 0< r < \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \) such that \( a + r\eta \notin \Sigma ^\phi _2(K) \), then \( a + s\eta \notin \Sigma ^\phi _2(K) \) for every \( 0< s < \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \).
-
(c)
\( \mathscr {H}^{n-1} \bigl ( \{ (a, \eta ): \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) < \varvec{r}_{K}^{\phi }(a,\eta ) \} \bigr ) =0 \).
-
(d)
there exist \( Z \subseteq N^\phi (K) \) with \( \mathscr {H}^{n-1} (Z) =0 \) and a residual set
$$\begin{aligned} R \subseteq \bigl \{ a + r\eta : \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \le r < \varvec{r}_{K}^{\phi }(a, \eta ) \bigr \} \end{aligned}$$such that
$$\begin{aligned} \Sigma ^{\phi }_2(K) \setminus {{\,\mathrm{Cut}\,}}^\phi (K) = \bigl \{ a + r\eta : 0< r < \underline{\varvec{r}_{K}^{\phi }}(a,\eta ), \; (a, \eta ) \in Z \bigr \} \cup R. \end{aligned}$$
In particular, for \( \mathscr {H}^{n-1} \) almost all \((a, \eta ) \in N^\phi (K) \) the distance function \(\varvec{\delta }_{K}^{\phi } \) is pointwise twice differentiable at all points of the line segment \( \{ a + r \eta : 0< r < \varvec{r}_{K}^{\phi }(a, \eta ) \} \).
We do not know whether \(R = \{ a + r \eta : \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \le r < \varvec{r}_{K}^{\phi }(a, \eta ) \}\); this is left as an open problem. In Remark 4.18 we show, however, that
The proof of Theorem 1.5 is based on the Lipschitz property proved in Theorem 1.4 and on some general estimates for the pointwise principal curvatures of level sets of \(\varvec{\delta }_{K}^{\phi } \) (these level sets might not even be topological manifolds but they admit a natural notion of pointwise curvature; see 2.44). Moreover, results on the preservation of the density points under bilipschitz transformations (see [11]) and on the approximate differentiability of multivalued functions (see 2.38) are used in a crucial way.
1.2 Applications
Here we briefly mention a couple of different applications of the results of the present paper.
Pointwise regularity and gradient Lipschitz estimates for solutions of the Eikonal equation Suppose \( \Omega \subseteq \mathbf {R}^{n} \) is an arbitrary open set, \( \phi \) is a uniformly convex \( \mathcal {C}^2 \)-norm and \( \phi ^*(u) = \sup \{ u \bullet v : \phi (v) =1 \} \). It is well known that \( \varvec{\delta }_{K}^{\phi } \) is the unique viscosity solution of the following Eikonal equation on \( \Omega \)
If \( \partial \Omega \) is hypersurface of class at least \( \mathcal {C}^2 \), then the local structure of this solution has been extensively studied and it is by now very well understood (see the references cited at the beginning of this introduction). On the other hand, as already explained, if \( \partial \Omega \) is not \( \mathcal {C}^2 \) then such a solution can have a very complicated (in particular dense!) singular set (see [41]) and many classical results in the theory do not give an insight about its local structure. In this direction our results in Theorems 1.4 and 1.5 provide a new and rather sharp description of the structure of the solutions of the Eikonal equation for arbitrary domains.
Steiner formula and curvature measures in uniformly convex finite dimensional Banach spaces One of the original motivation of the second author for the present work is to provide results that can be used to advance the theory of convex and integral geometry in Minkowski spaces; see [27]. In [25] Theorems 1.4 and 1.5 are used to prove the Steiner formula for arbitrary closed sets in a uniformly convex Banach space (Minkowski space); thus, extending the same formula previously obtained in [24] in the Euclidean space. The Steiner formula is then used as a starting point to develop the theory of curvature measures for sets of positive reach in a Minkowski space.
2 Preliminaries
2.1 Notation
We follow traditional well established and widely accepted conventions and notations typical for geometric measure theory. For convenience of the reader we briefly describe them here. We use the following symbols
- \(\mathbf {R}\):
-
set of real numbers;
- \(\overline{\mathbf {R}} = \mathbf {R}\cup \{ -\infty , +\infty \}\):
-
extended reals;
- \(\mathbf {Z}_+\):
-
set of positive integers;
- \(\varnothing \):
-
the empty set;
- \(\mathscr {H}^d\):
-
the \(d\)-dimensional Hausdorff measure;
- \(\mathscr {L}^n\):
-
the Lebesgue measure over \(\mathbf {R}^n\);
- \(\varvec{\alpha }(k)\):
-
Lebesgue measure of the unit ball in \(\mathbf {R}^k\);
- \(\mathbf {S}^{n-1}\):
-
the unit Euclidean sphere in \(\mathbf {R}^n\);
- \(x \bullet y\):
-
the inner product of two vectors x and y in a Euclidean space;
- |x|:
-
the norm of a vector x in a normed vectorspace;
- \(A {{\,\mathrm{\sim }\,}}B\):
-
set-theoretic difference of two sets A and B;
- \(\mathop {\mathrm {Clos}}A\):
-
closure of a subset A of a topological space;
- \({{\,\mathrm{Int}\,}}{A}\):
-
interior of a subset A of a topological space;
- \(\partial {A} = \mathop {\mathrm {Clos}}A {{\,\mathrm{\sim }\,}}{{\,\mathrm{Int}\,}}{A}\):
-
topological boundary of a subset A of a topological space;
- \({{\,\mathrm{dmn}\,}}f\):
-
domain of a function f;
- \(f[A ]\):
-
the image of a set \(A \subset {{\,\mathrm{dmn}\,}}f\) under the function f;
- \({{\,\mathrm{im}\,}}f\):
-
the image of a function f, i.e., \({{\,\mathrm{im}\,}}f = f [{{\,\mathrm{dmn}\,}}f ]\);
- \(\mathrm {D}f\):
-
derivative of a function f defined on a subset of a normed vectorspace; cf. 2.23;
- \({{\,\mathrm{grad}\,}}f\):
-
gradient of a real-valued function f defined on a subset of a Euclidean space;
- \(A+B = \{ a+b : a \in A \,, b \in B \}\):
-
algebraic sum of subsets A and B of a vectorspace;
- \({{\,\mathrm{Hom}\,}}(X,Y)\):
-
vectorspace of linear maps of type \(X \rightarrow Y\);
- \(\Lambda x\) or \(\langle x \,, \Lambda \rangle \):
-
the value of a linear map \(\Lambda \) on a vector \(x \in {{\,\mathrm{dmn}\,}}\Lambda \);
- \(\mathbf {U}^{\phi }(x,r) = \{ z : \phi (z-x) < r \}\):
-
open ball with respect to a norm \(\phi \);
- \(\mathbf {B}^{\phi }(x,r) = \{ z : \phi (z-x) \le r \}\):
-
closed ball with respect to a norm \(\phi \);
- f|A:
-
restriction of a function f to the set \(A \subseteq {{\,\mathrm{dmn}\,}}f\);
- \(\nabla f(x)\):
-
the set of subgradients of a convex function f at \(x \in {{\,\mathrm{dmn}\,}}f\); cf. 2.20 and 2.21;
- \({T}_\natural \):
-
the linear orthogonal projection onto a linear subspace T of a Euclidean space;
- \(T^{\perp }\):
-
the orthogonal complement of a linear subspace T of a Euclidean space;
- \([ A \ni x \mapsto f(x)]\):
-
an unnamed function defined on A whose value at \(x \in A\) is f(x);
 :
:-
the restriction of a measure \(\mu \) to a set A; cf. [18, 2.1.2];
- \({{\,\mathrm{Tan}\,}}(S,x)\):
-
tangent cone at x of a subset S of a normed vectorspace; cf. [18, 3.1.21];
- \({{\,\mathrm{Nor}\,}}(S,x)\):
-
normal cone at x of a subset S of a Euclidean space; cf. [18, 3.1.21];
Given \(k \in \mathbf {Z}_+\) and \(0< \alpha < 1\) we shall say that a function f is of class \(\mathscr {C}^{k,\alpha }\) if the \(k^{\mathrm {th}}\) derivative \(\mathrm {D}^kf\) exists and satisfies the Hölder condition with exponent \(\alpha \); cf. [18, 3.1.11 and 5.2.1]. We say that f is of class \(\mathscr {C}^{k}\) if \(\mathrm {D}^kf\) is just continuous.
Remark 2.1
We study several notions depending on the norm \(\phi \), whose name is always in the superscript. In case \(\phi \) is the standard Euclidean norm on \(\mathbf {R}^{n}\) we omit it in the notation so, e.g., if \(x \in \mathbf {R}^{n}\) and \(0< r < \infty \), then \(\mathbf {U}(x,r)\) denotes an open Euclidean ball in \(\mathbf {R}^{n}\).
We now introduce some classical functions
-
Hausdorff densities of a Radon measure \(\mu \) at x
$$\begin{aligned}&\varvec{\Theta }^{*n}(\mu ,x) = \limsup _{r \downarrow 0} \frac{\mu (\mathbf {B}(x,r))}{\varvec{\alpha }(n)r^{n}} \,, \qquad \varvec{\Theta }^{n}_{*}(\mu ,x) = \liminf _{r \downarrow 0} \frac{\mu (\mathbf {B}(x,r))}{\varvec{\alpha }(n)r^{n}} \,, \\&\text {and} \quad \varvec{\Theta }^{n}(\mu ,x) = \varvec{\Theta }^{*n}(\mu ,x) \quad \text {whenever }\varvec{\Theta }^{*n}(\mu ,x) = \varvec{\Theta }^{n}_{*}(\mu ,x) \,; \end{aligned}$$ -
dilations
$$\begin{aligned} \varvec{\mu }_{r}(x) = rx \quad \text {whenever }r \in \mathbf {R}\text { and }x \text { is a vector} \,; \end{aligned}$$ -
translations
$$\begin{aligned} \varvec{\tau }_{a}(b) = a + b \quad \text {whenever }a \text { and }b \text { are vectors in a vectorspace }X \,; \end{aligned}$$ -
the identity map on a set X
$$\begin{aligned} \mathbf {I}_{X}(x) = x \quad \text {whenever }x \in X \,. \end{aligned}$$
Remark 2.2
Without introducing any new symbols (in order not to make the notation too heavy) we find that given a function f defined on a subset of a normed vectorspace
\({{\,\mathrm{dmn}\,}}\mathrm {D}f\) is the set of differentiability points of f.
Remark 2.3
We shall repeatedly make use of the following simple fact. If f is a real valued function defined on a subset of a Euclidean space X, \(x \in {{\,\mathrm{dmn}\,}}\mathrm {D}^2 f\), and \(u,v \in X\), then
Remark 2.4
We adopt the convention that “\(C_{x.y}(a,b,c)\)” refers to the object (e.g. constant) defined in item (lemma, theorem, corollary, remark) x.y under the name ”C”, where a, b, c should be substituted for parameters of x.y in order of their occurrence. For instance, if v is a vector such that \(\phi (v) = 1\), then \(M_{{3.7}}(\tfrac{1}{2},v)\) is the manifold constructed by employing 3.7 with \(\tfrac{1}{2}\) and v in place of “\(\varepsilon \)” and “\(\eta \)”.
2.2 Basic concepts
Definition 2.5
We say that a norm \(\phi : X \rightarrow \mathbf {R}\) is strictly convex if for all \(a,b \in X\)
Remark 2.6
In the sequel, unless otherwise specified, \(n\) shall be a fixed positive integer, X will be a vectorspace of dimension \(n\), and \(\phi : X \rightarrow \mathbf {R}\) will be a strictly convex norm on X of class \(\mathscr {C}^{2}\) away from the origin. Of course, X shall be isomorphic with \(\mathbf {R}^{n}\) but, whenever we write X instead of \(\mathbf {R}^{n}\), we want to emphasise that there might not be a natural choice of a Euclidean structure on X.
Definition 2.7
Whenever X is equipped with a scalar product and \(\phi : X \rightarrow \mathbf {R}\) is a norm we define the conjugate norm \(\phi ^{*} : X \rightarrow \mathbf {R}\) by the formula
Definition 2.8
(cf. [15, 2.12, 2.13]) Assume X is equipped with a Euclidean structure. We say that \(\phi : X \rightarrow \mathbf {R}\) is a uniformly convex norm if it is a norm and there exists \(\gamma > 0\) such that the function \(\bigl [ X \ni x \mapsto \phi (x) - \gamma |x| \bigr ]\) is convex.
Remark 2.9
[cf. [15, 2.32]] If \(\phi \) is a uniformly convex norm of class \(\mathscr {C}^{2}\) away from the origin, then \(\phi ^{*}\) is also a uniformly convex norm of class \(\mathscr {C}^{2}\) away from the origin. Moreover, \({{\,\mathrm{grad}\,}}\phi ^{*}|S^*\) is the inverse of \({{\,\mathrm{grad}\,}}\phi |S\), where \(S = \partial \mathbf {B}^{\phi }(0,1)\) and \(S^* = \partial \mathbf {B}^{\phi ^{*}}(0,1)\).
Definition 2.10
Given a closed set \( K \subseteq X \) we define
Definition 2.11
A map of the type \(f : X \rightarrow \mathbf {2}^{Y}\) shall be called Y- multivalued. In case \(x \in X\) and f(x) is a singleton, we abuse the notation and write f(x) to denote the unique member of f(x).
Definition 2.12
Let f be a Y-multivalued function on X and \( A \subseteq X \). Then we denote with f|A the Y-multivalued map on X defined as
Definition 2.13
Let f be a Y-multivalued function on X and \( A \subseteq X \). Then we define the inverse \( f^{-1} \) of f as the X-multivalued map on Y as
Definition 2.14
Suppose \(K \subseteq X\) is closed and \(\varvec{\xi }_{K}^{\phi } : X \rightarrow \mathbf {2}^{K}\) is the \(\phi \)-nearest point projection onto K characterised by (2).
The Cahn–Hoffman map of K associated to \(\phi \) is the multivalued map \(\varvec{\nu }_{K}^{\phi } : X {{\,\mathrm{\sim }\,}}K \rightarrow \mathbf {2}^{\partial \mathbf {B}^{\phi }(0,1)}\) defined by the formula
Remark 2.15
It will be useful to notice that \(\varvec{\xi }_{K}^{\phi }(x)\) is a compact subset of X for every \(x \in X\).
Remark 2.16
Since \(\phi \) is a norm, one readily checks that if \( a \in K \), \( v \in X \) and \( \varvec{\delta }_{K}^{\phi } (a+v) = \phi (v) \), then \( \varvec{\delta }_{K}^{\phi }(a+tv) = t \phi (v) \) for every \( 0 \le t \le 1 \).
Remark 2.17
It has been observed in [15, 2.38(g)], using strict convexity of \(\phi \), that if \( a \in K \), \( u \in \partial \mathbf {U}^{\phi }(0,1) \), \( 0< t < \infty \) and \( \varvec{\delta }_{K}^{\phi }(a+tu) = t \), then \( \varvec{\xi }_{K}^{\phi }(a+su) \) is a singleton and \(\varvec{\xi }_{K}^{\phi }(a+su) = \{a\}\) for every \( 0< s <t \).
Definition 2.18
(cf. [38, p. 213]) Let \(f : X \rightarrow \overline{\mathbf {R}}\) and \(x,v \in X\). The one-sided directional derivative of f at x with respect to v is defined to be
whenever the limit exists in \(\overline{\mathbf {R}}\).
Remark 2.19
If f is a convex function and x is a point with \(f(x) \in \mathbf {R}\), then \( f'(x;v) \) exists for every \( v \in X \); cf. [38, Theorem 23.1].
Definition 2.20
(cf. [38, p. 214–215 and Theorem 23.2]) Suppose \(f : X \rightarrow \overline{\mathbf {R}}\) is convex and \(x \in X\) is such that \(f(x) \in \mathbf {R}\). We say that \( \zeta \in X \) is a subgradient of f at x if
The set of all subgradients of f at x is denoted by \(\nabla f(x)\).
Remark 2.21
Since the symbol “\(\partial {}\)” is used in this paper for the topological boundary of a set and, on grounds of set theory, functions are sets it would introduce ambiguities if we used the standard notation “\(\partial f\)” for the subgradient mapping of f; hence, we decided to denote it “\(\nabla f\)”.
In the next definition we use the notion of a polynomial function which is formally defined in [18, 1.10.4].
Definition 2.22
Let X, Y be normed vectorspaces and f be a function mapping a subset of X into Y. We say that f is pointwise differentiable of order k at x if there exist: an open set \(U \subseteq X\) such that \(x \in U \subseteq {{\,\mathrm{dmn}\,}}f\) and a polynomial function \(P : X \rightarrow Y\) of degree at most k such that \(f(x) = P(x)\) and
Whenever this holds P is unique and the pointwise differential of order i of f at x, for \(i = 1, \ldots ,k\), is defined by \({{\,\mathrm{pt}\,}}\mathrm {D}^i f(x) = \mathrm {D}^i P(x) \). As usual \({{\,\mathrm{pt}\,}}\mathrm {D}^1 f(x) = {{\,\mathrm{pt}\,}}\mathrm {D}f(x)\).
Remark 2.23
The notion of pointwise differentiability of order 1 coincides with the classical notion of differentiability so \({{\,\mathrm{pt}\,}}\mathrm {D}= \mathrm {D}\); cf. [18, 3.1]. A summary of known facts about pointwise differentiability for functions can be found, e.g., in [34, §2].
Remark 2.24
If f is a \(\mathbf {R}\)-valued convex function on an open subset U of X then \(\nabla f(x)\) is non empty for every \(x \in U\); cf. [38, Theorem 23.4]. Moreover, f is differentiable of order 1 at x if and only if \(\nabla f(x)\) is a singleton; cf. [38, 25.1].
We need to extend the concept of continuity and differentiability to multivalued maps.
Definition 2.25
[cf. [46, Definition 2]] Let X and Y be normed vectorspaces and T be a Y-multivalued map defined on X. We say that T is weakly continuous at \(a \in X\) if and only if \(T(a) \ne \varnothing \) and for each \(\varepsilon > 0\) there exists \(\delta > 0\) such that
If, additionally, T(a) is a singleton, then we say that T is continuous at a.
Remark 2.26
We notice that if \(T(y) = \varnothing \) for \(y \in \mathbf {B}(x,\delta ) {{\,\mathrm{\sim }\,}}\{x\}\) then T is continuous at x. On the other hand, we remark that studying the map \(\varvec{\xi }_{K}^{\phi }\) we do not need to worry about such strange behaviour. Moreover, in 2.41(f) we prove that \(\varvec{\xi }_{K}^{\phi }\) is weakly continuous on the whole of \(\mathbf {R}^n\). Obviously, \(\varvec{\xi }_{K}^{\phi }(x)\) is a singleton for all \(x \in X\) if and only if K is convex.
Remark 2.27
Note that weakly continuous multivalued functions may carry connected sets into disconnected sets. Consider, e.g., the function \(f : \mathbf {R}\rightarrow \mathbf {2}^{\mathbf {R}}\) given by \(f(t) = \{-1\}\) if \(t < 0\), \(f(t) = \{ 1 \}\) if \(t > 0\), and \(f(0) = \{ -1 \,, 0 \,, 1 \}\); then, f is weakly continuous in the sense of 2.25. Another example is \(\varvec{\xi }_{K}^{\phi }\) which is weakly continuous on the whole of \(\mathbf {R}^{n}\) regardless of the choice of the closed set \(K \subseteq \mathbf {R}^{n}\); in particular, when K is disconnected; cf. 2.41(f).
Definition 2.28
[cf. [46, Definition 3]] Let X, Y be finite dimensional normed vectorspaces and T be a Y-multivalued map defined on X. We say that T is differentiable at \(a \in X\) if and only if T(a) is a singleton and there exists a linear map \(L : X \rightarrow Y\) such that for any \(\varepsilon > 0\) there exists \(\delta > 0\) satisfying
The set of all such L is denoted by \(\mathrm {D}T(a)\). In case \(\mathrm {D}T(a)\) is a singleton, we say that T is strongly differentiable at a.
Remark 2.29
Note that it might happen that \(T(y) = \varnothing \) for some \(y \in \mathbf {B}(x,\delta )\). Actually, if \(T(x) \ne \varnothing \) and there exists \(\delta > 0\) such that \(T(y) = \varnothing \) for \(y \in \mathbf {B}(x,\delta ) {{\,\mathrm{\sim }\,}}\{x\}\), then T is differentiable at x with \(\mathrm {D}T(x) = {{\,\mathrm{Hom}\,}}(X,Y)\). On the other hand if, e.g., \(\dim X = n\) and  , then \(\mathrm {D}T(x)\) is a singleton.
, then \(\mathrm {D}T(x)\) is a singleton.
Remark 2.30
Let P and Q be two multivalued functions and \( x \in \mathbf {R}^{n} \). If P is differentiable at x and Q is differentiable at P(x) then the multivalued function R given by
is differentiable at x.
Definition 2.31
Let \( K \subseteq \mathbf {R}^{n} \) be closed. For \(x \in \mathbf {R}^{n}\) define \( \varvec{\rho }^{\phi }_{K}: \mathbf {R}^n \rightarrow \overline{\mathbf {R}} \cap \{t : 1 \le t \le \infty \} \) as
whenever \( x \in \mathbf {R}^n \) and \( a \in \varvec{\xi }_{K}^{\phi }(x) \).
Remark 2.32
Definition 2.31 is well posed, since 2.17 gives that if \( \varvec{\xi }_{K}^{\phi }(x) \) is not a singleton, then
The following Lemma will be used in Sect. 4.
Lemma 2.33
For every closed set \( K \subseteq \mathbf {R}^n \) the function \( \varvec{\rho }^{\phi }_{K} \) is upper semicontinuous and satisfies
Moreover, \( {{\,\mathrm{Cut}\,}}^\phi (K) = \mathbf {R}^n \cap \{x : \varvec{\rho }^{\phi }_{K}(x) = 1\} \).
Proof
Let \(x_0, x_1, x_2, \ldots \in \mathbf {R}^{n}\) and \(\beta \in \mathbf {R}\) be such that \(\lim _{i \rightarrow \infty } x_i = x_0\), \(\phi (x_i - x_0) < 1\) for \(i \in \mathbf {Z}_+\), and \(\lim _{i \rightarrow \infty } \varvec{\rho }^{\phi }_{K}(x_i) > \beta \). Since \(\varvec{\delta }_{K}^{\phi }\) is continuous we have \(\lim _{i \rightarrow \infty } \varvec{\delta }_{K}^{\phi }(x_i) = \varvec{\delta }_{K}^{\phi }(x_0)\) and we may assume \(\varvec{\delta }_{K}^{\phi }(x_i) < \varvec{\delta }_{K}^{\phi }(x_0) + 1\) for \(i \in \mathbf {Z}_+\). Choose \(a_i \in \varvec{\xi }_{K}^{\phi }(x_i)\) for \(i \in \mathbf {Z}_+\). Since \(\{a_i : i \in \mathbf {Z}_+\} \subseteq \mathbf {B}^{\phi }(x_0,\varvec{\delta }_{K}^{\phi }(x_0) + 2)\) we may, possibly choosing a subsequence, assume that \(\lim _{i \rightarrow \infty } a_i = a_0\) and then \(a_0 \in \varvec{\xi }_{K}^{\phi }(x_0)\) by continuity of both \(\varvec{\delta }_{K}^{\phi }\) and \(\phi \). Assume further that \(\varvec{\rho }^{\phi }_{K}(x_i) \ge \beta \) for \(i \in \mathbf {Z}_+\). Recalling the definition of \(\varvec{\rho }^{\phi }_{K}\) we obtain
hence, \(\varvec{\rho }^{\phi }_{K}(x_0) \ge \beta \). Since this holds for any \(\beta \in \mathbf {R}\) satisfying \(\lim _{i \rightarrow \infty } \varvec{\rho }^{\phi }_{K}(x_i) > \beta \), we see that \(\lim _{i \rightarrow \infty } \varvec{\rho }^{\phi }_{K}(x_i) \le \varvec{\rho }^{\phi }_{K}(x_0)\) and we conclude that \( \varvec{\rho }^{\phi }_{K} \) is upper semicontinuous.
Suppose \( x \in \mathbf {R}^{n+1} \), \( a \in \varvec{\xi }_{K}^{\phi }(x) \) and \( 0 < t \le \varvec{\rho }^{\phi }_{K}(x) \) and we prove that \(\varvec{\rho }^{\phi }_{K}(x) = t \varvec{\rho }^{\phi }_{K}(a + t (x-a)) \). Evidently, if \(\varvec{\rho }^{\phi }_{K}(x) = \infty \), then \(\varvec{\rho }^{\phi }_{K}(a + t (x-a)) = \infty \) for all \(0< t < \infty \) and the assertion is true. Therefore, we assume \(1 \le \varvec{\rho }^{\phi }_{K}(x) < \infty \) and define \( y = a + t(x-a) \). Notice that \( \varvec{\delta }_{K}^{\phi }(y) = t \varvec{\delta }_{K}^{\phi }(x) \) and \( a \in \varvec{\xi }_{K}^{\phi }(y) \). Since
Noting that \(x = a + \frac{1}{t}(y-a)\), \( \varvec{\rho }^{\phi }_{K}(y) \ge \frac{1}{t} \), and \( a \in \varvec{\xi }_{K}^{\phi }(y) \), we can apply the inequality in (9), replacing x and t with y and \( \frac{1}{t} \) respectively, to obtain the reverse inequality; hence, equality.
Finally the assertion about the cut locus follows directly from the definition of \( \varvec{\rho }^{\phi }_{K} \). \(\square \)
Lemma 2.34
Suppose \( K \subseteq \mathbf {R}^n \) is closed, \( \sigma > 1 \), \( K_\sigma = \{ x : \varvec{\rho }^{\phi }_{K}(x) \ge \sigma \} \sim K \) and the \( \mathbf {R}^n \)-multivalued function \( h_t \) is defined as
Then the map \( h_t|K_\sigma \) is a homeomorphism onto \( K_{\sigma /t} \) with \( (h_t|K_\sigma )^{-1} = h_{1/t}| K_{\sigma /t} \) for every \( 0< t < \sigma \).
Proof
Since \( t \varvec{\rho }^{\phi }_{K}(h_t(x)) = \varvec{\rho }^{\phi }_{K}(x) \ge \sigma \) for every \( x \in K_\sigma \) by Lemma 2.33, we get that \( h_t[K_\sigma ] \subseteq K_{\sigma /t} \). Let \( y \in K_{\sigma /t} \) and define \( x = h_{1/t}(y)\). Since \(\varvec{\xi }_{K}^{\phi }(y)\) is a singleton we can write \(x = \varvec{\xi }_{K}^{\phi }(y) + \frac{1}{t}(y - \varvec{\xi }_{K}^{\phi }(y)) \). Notice that \( \varvec{\xi }_{K}^{\phi }(x) = \varvec{\xi }_{K}^{\phi }(y) \) and \(\frac{1}{t}\varvec{\rho }^{\phi }_{K}(x) = \varvec{\rho }^{\phi }_{K}(y) \ge \frac{\sigma }{t} \), again by Lemma 2.33. We conclude that \( x \in K_\sigma \) and, by a direct computation, \( h_t(x) = y \). It follows that \( h_t \circ h_{1/t} = \mathbf {I}_{K_{\sigma /t}} \) and \( h_t[K_\sigma ] = K_{\sigma /t} \).
Since \( 0< \frac{1}{t} < \frac{\sigma }{t} \) we apply the statement proved in the last paragraph with t and \( \sigma \) replaced by \( \frac{1}{t} \) and \( \frac{\sigma }{t} \) respectively to infer that \( h_{1/t} \circ h_{t} = \mathbf {I}_{K_\sigma } \) and \( h_{1/t}[K_{\sigma /t}] = K_\sigma \). This proves that \( h_t|K_\sigma \) is an homeomorphism onto \( K_{\sigma /t} \). \(\square \)
The next lemma provides an alternative description of the normal bundle \(N^\phi (K)\) defined in (4) and the reach function defined in (5).
Lemma 2.35
For every closed set \( K \subseteq \mathbf {R}^n \) the function \(\varvec{r}_{K}^{\phi }: N^\phi (K) \rightarrow \mathbf {R} \cap \{t : 0 < t \le \infty \}\) is upper semicontinuous. Moreover,
and
Proof
Assume this is not true, so that for each \(i \in \mathbf {Z}_+\) there is \((a_i,u_i) \in N^{\phi }(K)\) such that
Let \(s \in \mathbf {R}^{}\) be such that
Since \(\varvec{r}_{K}^{\phi }(a,u) < s\) we can find \(b \in K\) such that \(\phi ((a+su) - b) < s\). Let \(\varepsilon \in \mathbf {R}^{}\) be such that
Let \(i \in \mathbf {Z}_+\) be so big that \(\phi (a_i - a) \le 2^{-3} \varepsilon \) and \(\phi (u_i - u) \le 2^{-3} s^{-1} \varepsilon \). Then
Since \(\varvec{r}_{K}^{\phi }(a_i,u_i) \ge s\) we get a contradiction
The second part of the statement follows mechanically from the definitions. \(\square \)
Remark 2.36
Notice that in [15, Remark 5.6] we erroneously claim that \(\varvec{r}_{K}^{\phi }\) is lower semicontinuous which is obviousy wrong but, fortunatelly, does not affect other results of [15] since we only need the fact that \(\varvec{r}_{K}^{\phi }\) is a Borel function there.
Remark 2.37
The function \( \varvec{r}_{K}^{\phi } \) can fail to be continuous even if K is a compact convex \( \mathcal {C}^{1,1} \) hypersurface. In fact in [41] we show that there exists a compact and convex \( \mathcal {C}^{1,1} \)-hypersurface K such that \( \mathop {\mathrm {Clos}}(\Sigma (K)) \) has non empty interior. Noting that N(K) is the classical unit normal bundle of K and consequently it is compact, we infer that if \(\varvec{r}_{K}^{}\) was continuous then \( {{\,\mathrm{Cut}\,}}(K) \) would be compact; consequently \( \mathop {\mathrm {Clos}}(\Sigma (K)) = {{\,\mathrm{Cut}\,}}(K) \) and \( \mathscr {L}^{n} ({{\,\mathrm{Cut}\,}}(K)) > 0 \) which is incompatible with Remark 4.4.
2.3 Auxiliary results
The following lemma shows that if \(A \subseteq \mathbf {R}^{n}\) is a set of points at which a multivalued function f satisfies a Lipschitz condition, a is a density points of A, and f|A is differentiable at a, then f is differentiable at a. It is a variant of a classical result stating that a Lipschitz function that is approximately differentiable at a point is classically differentiable at that point; cf. [18, 3.1.5].
Lemma 2.38
Assume

Then f is strongly differentiable at a.
Proof
Since a is a density point of A we see that f|A is strongly differentiable at a and \(\mathrm {D}f(a) = \{L\}\) for some \(L \in {{\,\mathrm{Hom}\,}}(\mathbf {R}^{n},\mathbf {R}^{n})\); cf. 2.29. Let \(\varepsilon > 0\). Choose \(0< \delta < \varepsilon \) such that
Let \(c \in \mathbf {B}(a,\delta )\) and \(y \in f(c)\). Set \(r = |c-a|\) and choose \(b \in A\) such that \(|c-b| = \varvec{\delta }_{A}^{}(c) \le r\). Clearly \(\mathbf {B}(c,|c-b|) \subseteq \mathbf {B}(a,2r)\) and \({ \mathscr {L}^{n} }\,{\mathbf {B}(c,|c-b|)} = \varvec{\alpha }(n) |c-b|^{n}\); hence,
Since \(b \in A\) we obtain
\(\square \)
The next lemma is a classical result in convex analysis.
Lemma 2.39
If \( U \subseteq \mathbf {R}^{n} \) is an open convex set, \( f : U \rightarrow \mathbf {R}^{} \) is a convex function and \( x \in U \), then the following three statements are equivalent.
-
(a)
f is pointwise differentiable of order 2 at x.
-
(b)
The multivalued map \(\nabla f\) is differentiable at x.
-
(c)
There is at least one function \(g : U \rightarrow \mathbf {R}^{n}\) such that \(g(y) \in \nabla f(y)\) for every \(y \in U\) and g is differentiable at x.
If (a), (b), and (c) hold, then
Proof
Clearly \(\nabla f(y) \ne \varnothing \) for all \(y \in U\) because f is convex and 2.24. The proof that (a) implies (c) is contained in [2, p. 495] (and attributed to Fitzpatrick). For the proof that (c) implies (b) and (b) implies (a), one can look in [9]. In fact, first we notice that f is "zweimal differenzierbar in p" in the sense of [9, 4.2] if and only if \( \nabla f \) is differentiable at p in the sense of 2.28; then we look at [9, 4.3] and [9, 4.8] respectively. \(\square \)
Definition 2.40
Suppose \( U \subseteq \mathbf {R}^{n}\) is open. We say that a function \( g : U \rightarrow \mathbf {R}^{} \) is semiconcave if and only if there exists \(\kappa \ge 0\) such that the function \(g(y) - (\kappa /2) |y|^{2}\) is concave.
The following lemma collects few facts on the continuity, differentiability, and convexity properties of \(\varvec{\delta }_{K}^{\phi }\) and \( \varvec{\xi }_{K}^{\phi } \) for an arbitrary closed set K.
Lemma 2.41
Let \( K \subseteq \mathbf {R}^{n} \) be a closed set. Then the following statements hold.
-
(a)
\((\varvec{\delta }_{K}^{\phi })'(x;v) = \inf \ \bigl \{ {{\,\mathrm{grad}\,}}\phi (x-y) \bullet v : y \in \varvec{\xi }_{K}^{\phi }(x) \bigr \} \) for every \( v \in \mathbf {R}^{n} \) and \( x \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \).
-
(b)
For each \( x \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \) there exists an open neighbourhood \( U \subseteq \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \) of x such that \( \varvec{\delta }_{K}^{\phi }|U \) is semiconcave.
-
(c)
\( \varvec{\delta }_{K}^{\phi } \) is differentiable at \( x \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \) if and only if \( \varvec{\xi }_{K}^{\phi }(x) \) is a singleton, in which case
$$\begin{aligned} {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }(x) = {{\,\mathrm{grad}\,}}\phi (x - \varvec{\xi }_{K}^{\phi }(x)) \,, \quad \varvec{\xi }_{K}^{\phi }(x) = x - \varvec{\delta }_{K}^{\phi }(x){{\,\mathrm{grad}\,}}\phi ^{*}({{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }(x)) \,. \end{aligned}$$ -
(d)
If \( \varvec{\delta }_{K}^{\phi } \) is differentiable at \( x \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \) then \( \varvec{\delta }_{K}^{\phi } \) is differentiable at \( \varvec{\xi }_{K}^{\phi }(x) + t(x-\varvec{\xi }_{K}^{\phi }(x)) \) for \( 0< t < \varvec{\rho }^{\phi }_{K}(x) \) with
$$\begin{aligned} {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }(x) = {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi } \bigl ( \varvec{\xi }_{K}^{\phi }(x) + t(x-\varvec{\xi }_{K}^{\phi }(x)) \bigr ) \,. \end{aligned}$$ -
(e)
\(\varvec{\delta }_{K}^{\phi }\) is pointwise differentiable of order 2 at \(x \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K\) if and only if \(\varvec{\xi }_{K}^{\phi }\) is differentiable at x in the sense of 2.28, in which case
$$\begin{aligned} {{\,\mathrm{pt}\,}}\mathrm {D}^2\varvec{\delta }_{K}^{\phi }(x)(u,v) = \mathrm {D}({{\,\mathrm{grad}\,}}\phi \circ \varvec{\nu }_{K}^{\phi })(x)(u) \bullet v \quad \text {for } u, v \in \mathbf {R}^{n} \,. \end{aligned}$$ -
(f)
\(\varvec{\xi }_{K}^{\phi }\) is weakly continuous in the sense of 2.25.
Proof
The assertions (a) and (b) correspond to [45, Corollary to Theorem 3*] and [45, Theorem 5], respectively.
We prove (c). If \( \varvec{\xi }_{K}^{\phi }(x) \) is a singleton, then for every \( v \in \mathbf {R}^{n} \) the partial derivative of \(\varvec{\delta }_{K}^{\phi }\) at x with respect to v exists and equals \({{\,\mathrm{grad}\,}}\phi (x-\varvec{\xi }_{K}^{\phi }(x)) \bullet v\) by (a). Since \(\varvec{\delta }_{K}^{\phi }\) is Lipschitz continuous with Lipschitz constant 1 by [15, Lemma 2.38(a)] and \((\varvec{\delta }_{K}^{\phi })'(x;\varvec{\nu }_{K}^{\phi }(x)) = 1\) by [15, Lemma 2.32(c)] we conclude that \(\varvec{\delta }_{K}^{\phi }\) is differentiable at x using [19, 2.4, 2.5]. On the other hand if \(\varvec{\xi }_{K}^{\phi }(x)\) is not a singleton then \( \varvec{\delta }_{K}^{\phi } \) is not differentiable at x by a result of Konjagin [29] (see also [45, Proposition 2]).
Assertion (d) follows from (c) and 2.17.
To prove (e) we observe that for \( x \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \) there exist, by (b), a constant \( \kappa > 0 \), an open neighbourhood U of x, and a convex function \( V : U \rightarrow \mathbf {R}^{} \) such that
Moreover, we observe, using (a), that if \( \xi : U \rightarrow \mathbf {R}^{n} \) is a function such that \( \xi (y) \in \varvec{\xi }_{K}^{\phi }(y) \) for every \( y \in U \), then \( \kappa y-{{\,\mathrm{grad}\,}}\phi (y-\xi (y)) = \kappa y - {{\,\mathrm{grad}\,}}\phi \big (\varvec{\delta }_{K}^{\phi }(y)^{-1}(y - \xi (y))\big ) \in \nabla V(y) \). Therefore, we conclude from 2.39 that \( \varvec{\delta }_{K}^{\phi } \) is pointwise differentiable of order 2 at x if and only if \( \varvec{\xi }_{K}^{\phi } \) is differentiable at x. The displayed equation in (e) also follows from the postscript of 2.39.
Finally we prove (f). The argument used in [15, 2.38(b)], which proves the statement for the restriction of \( \varvec{\xi }_{K}^{\phi } \) to the set of points where it is single-valued, also works in the general case of (f). For completeness we provide a proof. By contradiction we assume there are \( x \in \mathbf {R}^{n} \), \( \varepsilon > 0 \) and two sequences \(x_{i}\in \mathbf {R}^{n} \) and \(a_{i}\in K\) such that \( x_{i} \rightarrow x \), \( a_{i} \in \varvec{\xi }_{K}^{\phi }(x_{i}) \) and \( |a_{i} - b| \ge \varepsilon \) for every \( b \in \varvec{\xi }_{K}^{\phi }(x) \) and for every \( i \ge 1 \). Noting that
and
for every \( i \ge 1 \), it follows that \(\{a_{i}: i \ge 1 \}\) is a bounded sequence and consequently we can assume \( a_{i} \rightarrow a \) for some \( a \in K \). Then
It follows that \(|a_{i} - a| \ge \varepsilon \) for every \( i \ge 1 \), which is in contradiction with \( a_{i} \rightarrow a \). \(\square \)
Remark 2.42
Continuity properties of \(\varvec{\xi }_{K}^{\phi }|U\) will be studied more carefully in 3.2 in case \(\phi \) is strictly convex and in 3.9 in case \(\phi \) is uniformly convex.
Lemma 2.43
Assume T is an hyperplane in \(\mathbf {R}^{n}\), \( \alpha \in T \), \( f : T \rightarrow T^{\perp } \) is function continuous at \( \alpha \), \( a = \alpha + f(\alpha ) \), \( A = \{ \chi + f(\chi ): \chi \in T \} \) and \( {{\,\mathrm{Tan}\,}}(A,a) \subseteq T \). Then f is differentiable at \( \alpha \), \(\mathrm {D}f(\alpha ) = 0\), and \( {{\,\mathrm{Tan}\,}}(A,a) = T \).
Proof
We prove that \(\mathrm {D}f(\alpha )\) exists and equals zero. If \(\limsup _{T \ni \chi \rightarrow \alpha } |f(\chi ) - f(\alpha )| \cdot |\chi - \alpha |^{-1} > 0\), then we could find a sequence \(\chi _j \in T\) such that \(\chi _j \rightarrow \alpha \), \((\chi _j - \alpha ) \cdot |\chi _j - \alpha |^{-1} \rightarrow w \in T\), and \((f(\chi _j) - f(\alpha )) \cdot |\chi _j - \alpha |^{-1} \rightarrow v \in T^{\perp }\) with \(v \ne 0\) as \(j \rightarrow \infty \); hence, setting \(v_j = \chi _j + f(\chi _j)\) we would obtain \((v_j - a) \cdot |v_j - a|^{-1} \rightarrow w \in {{\,\mathrm{Tan}\,}}(A,a)\) as \(j \rightarrow \infty \) and \(T_\natural ^\perp w \ne 0\) which would contradict \( {{\,\mathrm{Tan}\,}}(A,a) \subseteq T \) by the definition of tangent cone; cf. [18, 3.1.21]. \(\square \)
The following Lemma follows rather directly from classical implicit function theorems for Lipschitz and semiconcave functions. In the next lemma, given \( x \in \mathbf {R}^{n} \), \( \epsilon , \delta > 0 \), and a linear space \(T \subseteq \mathbf {R}^{n}\), we make use of cylinders aligned to T defined the following way
Moreover, we recall from Lemma 2.41 that
Lemma 2.44
Suppose K is a closed subset of \( \mathbf {R}^{n+1} \), \( r > 0 \), \( x \in S^{\phi }(K,r) \), \( \varvec{\delta }_{K}^{\phi } \) is differentiable at x, \( \nu = {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }(x)/|{{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }(x)| \) and \( T = \mathbf {R}^{n} \cap \{ v : v \bullet \nu =0 \} \).
Then \( T = {{\,\mathrm{Tan}\,}}(S^{\phi }(K,r),x) \) and there are \( \epsilon , \delta > 0 \) and a semiconcave function \( f : T \rightarrow \mathbf {R}\) such that f is differentiable at \( {T}_\natural x \) with \( \mathrm {D}f({T}_\natural x) =0 \),
and
Moreover, if \( \varvec{\delta }_{K}^{\phi } \) is pointwise differentiable of order 2 at x then f is pointwise differentiable of order 2 at \( {T}_\natural x \) and
Proof
We notice that \(\varvec{\delta }_{K}^{\phi } \) is locally semiconcave on \( \mathbf {R}^{n} \sim K \) by Lemma 2.41(b). Since \( \varvec{\delta }_{K}^{\phi } \) is differentiable at x and \( {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }(x) \ne 0 \), noting Remark 2.24 and [22, Remark 1.4], we see that we can apply [22, Theorem 3.3] to find \( \epsilon , \delta > 0 \) and a semiconcave function \( f : T \rightarrow \mathbf {R}\) such that (10) and (11) hold.Footnote 1 Since \( \varvec{\delta }_{K}^{\phi } \) is differentiable at x, then \( {{\,\mathrm{Tan}\,}}(S^\phi (K,r), x) \subseteq T \). Therefore, the first part of the conclusion follows from Lemma 2.43.
Assume now that \( \varvec{\delta }_{K}^{\phi } \) is pointwise differentiable of order 2 at x and \( x =0 \). Setting \(\zeta = \chi + f(\chi )\nu \), we notice that \(\mathrm {D}\varvec{\delta }_{K}^{\phi }(0)(\zeta ) = f(\chi ) |{{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }(0)|\) so
which means that f is pointwise differentiable of order 2 at 0 with
\(\square \)
Lemma 2.45
Suppose T is a hyperplane in \(\mathbf {R}^{n}\), \( f : T \rightarrow T^\perp \) is a function of class \(\mathscr {C}^{2}\) such that \( f(0)=0 \) and \( \mathrm {D}f(0) =0 \), \( \Sigma = \{\chi + f(\chi ): \chi \in T\} \), and \( \eta : \Sigma \rightarrow \mathbf {S}^{n-1} \) is a function of class \(\mathscr {C}^{1}\) such that \( \eta (x) \in {{\,\mathrm{Nor}\,}}(\Sigma ,x)\) for \( x \in \Sigma \). Then
Proof
Noting that \( \eta (\chi + f(\chi )) \bullet (u + \mathrm {D}f(\chi )u) =0 \) for \( u \in T \) and \( \chi \in T \), we differentiate this relation with respect to \( \chi \) at 0. \(\square \)
3 Lipschitz estimates
In this section we consider an abstract Minkowski space \((X,\phi )\) of dimension \(n\) and we are defining a Euclidean structure on X to fit our problem. For this reason we choose to denote the space with “X” rather than “\(\mathbf {R}^{n}\)” since the latter refers to a space with a predefined Euclidean structure which is of no use to us. The operator norm of a bilinear map \(\Lambda : X \times X \rightarrow X\) with respect to \(\phi \) is defined as in [18, 1.10.5], i.e.,
Once the Euclidean structure on X is defined we shall use the symbol \(\Vert \Lambda \Vert \) to denote the operator norm of \(\Lambda \) with respect to that Euclidean structure.
Definition 3.1
(cf. [17, 4.1]) Let \(K \subseteq X\) be closed. We define the set of points with unique nearest point
We start by showing that \(\varvec{\xi }_{K}^{\phi }\) is uniformly continuous on certain sets. Later, in 3.9 and 3.10, we bootstrap this regularity to Lipschitz continuity. Uniform continuity is obtained for strictly convex norms \(\phi \), while Lipschitz continuity requires uniform convexity and \(\mathscr {C}^{2}\) regularity of \(\phi \).
Lemma 3.2
Assume
Then there exists \(\omega _{\lambda } : \mathbf {R}\rightarrow \mathbf {R}\) such that \(\lim _{t \downarrow 0} \omega _{\lambda }(t) = 0\) and
Proof
For \(0 \le t < \infty \) define
Observe that strict convexity of \(\phi \) yields
Indeed, assume \(\limsup _{t \downarrow 0} \omega _{\lambda }(t) = \delta \). Find sequences \(X \cap \{ a_j : j \in \mathbf {Z}_+\}\) and \(X \cap \{ b_j : j \in \mathbf {Z}_+\}\) such that \((a_j,b_j) \in K_{\lambda }(1/j)\), \(\phi (a_j - b_j) \ge \delta - 1/j\), \(\lim _{j \rightarrow \infty } a_j = a_0\) and \(\lim _{j \rightarrow \infty } b_j = b_0\) with \(\phi (a_0) = \lambda \), \(\phi (b_0) \ge \lambda \), \(\phi (b_0 - a_a) \ge \delta \), \(\phi (z_0 - (1 - 1/\lambda )a_0) \le 1\). Then
which implies that \(a_0 = b_0\) and \(\delta = 0\) by 2.5.
Let \(x \in K_{\lambda } \subseteq \mathrm {Unp}^{\phi }(K)\), \(y \in X\). Choose
Clearly we have
Since \((x-c)/r = (1 - 1/\lambda )a\) we obtain
Because \(x \in K_{\lambda }\) we know also that \(\phi ({\bar{a}} - c) < \phi ({\bar{b}} - c)\); hence,
This shows that \((a,b) \in K_{\lambda }(t)\) so \(\phi (a-b) \le \omega _{\lambda }(t)\) and \(\phi ({\bar{a}} - {\bar{b}}) \le r \omega _{\lambda }(t)\). \(\square \)
Corollary 3.3
Assume \(\phi \) is strictly convex, \(K \subseteq X\) is closed, \(0< s< t < \infty \), \(1< \lambda < \infty \), and
Then \(\varvec{\xi }_{K}^{\phi }|K_{\lambda ,s,t}\) is uniformly continuous.
Remark 3.4
This provides an alternative proof that \(\varvec{\xi }_{K}^{\phi } | \mathrm {Unp}^{\phi }(K)\) is continuous; cf. [15, 2.42].
Remark 3.5
Assume that X is a finite dimensional vectorspace equipped with a strictly convex and continuously differentiable (away from the origin) norm \(\phi : X \rightarrow \mathbf {R}\). We define
Note that whenever \(\eta \in S\) the map \(\pi (\eta )\) is a projection onto \({{\,\mathrm{Tan}\,}}(S,\eta )\) such that
Lemma 3.6
Consider the situation as in 3.5. Let \(0< \varepsilon < 1\) and set
Then \(\pi (\eta ) | S \cap \mathbf {B}^{\phi }(\eta ,R)\) is injective whenever \(\eta \in S\).
Proof
Assume that for some \(\eta \in S\) the map \(\pi (\eta )|S \cap \mathbf {B}^{\phi }(\eta ,R)\) is not injective. Set
and let \(\xi ,\zeta \in D\) be such that \(\pi (\eta ) \xi = \pi (\eta ) \zeta \); hence, \(\xi -\zeta \in \ker \pi (\eta ) = {{\,\mathrm{span}\,}}\{\eta \}\). Assume \(\phi (\xi -\eta ) \le \phi (\zeta -\eta )\). If \(\eta = \xi \), then \(\zeta = -\eta \) and \(\phi (\zeta -\eta ) = 2 > 1\) which cannot happen because \(\zeta \in D\) and \(R \le 1\). Let \(P = {{\,\mathrm{span}\,}}\{ \eta \,, \xi \}\). Then \(\zeta = \xi + \lambda \eta \) for some \(\lambda \in \mathbf {R}\) and we get
Let \(\gamma : \mathbf {R}\rightarrow S \cap P\) be such that
Set \(A = {{\,\mathrm{im}\,}}\gamma |[0,1]\). Since \(\xi - \zeta \in {{\,\mathrm{span}\,}}\{\eta \}\) we see that both \(\xi \) and \(\eta \) are on the same side of the line \({{\,\mathrm{span}\,}}\{\eta \}\) in P. Therefore, the Monotonicity Lemma [37, Proposition 31] yields that \([[0,1] \ni t \mapsto \phi (\gamma (t) - \eta )]\) is a strictly increasing function and we know that \(\phi (\zeta -\eta ) \le R\); thus, we have \(\phi (\gamma (t) - \eta ) \le R\) for all \(t \in [0,1]\) and
Let \(w \in P\) and \(\omega \in P^*\) be such that w and \(\eta \) are linearly independent, \(\omega (w) = 1\), and \(\omega (\eta ) = 0\). Define the function \(f : \mathbf {R}\rightarrow \mathbf {R}\) by
Note that \(f(1) - f(0) = \omega (\zeta -\xi ) = 0\) so \(f(1) = f(0)\) and, by the mean value theorem, there exists \(t_0 \in [0,1]\) such that
Set \(\nu = \gamma (t_0)\). Since \(\gamma '(t_0) \in {{\,\mathrm{Tan}\,}}(S,\nu )\) we see that \(\eta \in {{\,\mathrm{Tan}\,}}(S,\nu )\) and \(\pi (\nu ) \eta = \eta \) so
but \(\nu \in A \subseteq D\) so this contradicts the choice of R. \(\square \)
Remark 3.7
Consider the situation as in 3.5 and assume \(\phi \) is of class \(\mathscr {C}^{2}\) away from the origin. Let \(\varepsilon \in (0,1)\) and \(\eta \in S\). Set \(R = R_{{3.6}}(\varepsilon )\), \(T = {{\,\mathrm{Tan}\,}}(S,\eta )\), and \(M = S \cap \mathbf {B}^{\phi }(\eta ,R)\). Since \(\pi (\eta )|M\) is injective and M is compact we see that \(\pi (\eta )|M\) is a homeomorphism between M and \(A = \pi (\eta ) [M ]\subseteq T\). Set
Since \(\phi \) is of class \(\mathscr {C}^{2}\) we see that M is a manifold of class \(\mathscr {C}^{2}\) and \(H : C \rightarrow M\) is of class \(\mathscr {C}^{2}\),
Differentiating the equation
we get
however, if \(u,v \in T = {{\,\mathrm{im}\,}}\pi (\eta )\), then \(\mathrm {D}\pi (\eta )uv \in \ker \pi (\eta ) = {{\,\mathrm{span}\,}}\{\eta \}\) by (13) and for all \(x \in S \cap C\) we also have \(\mathrm {D}H(x)\eta = 0\); hence
Since T is tangent at \(\eta \in S\) to the level-set S of \(\phi \) we have \(\mathrm {D}\phi (\eta ) u = 0\) whenever \(u \in T\); thus, differentiating (12) twice and recalling that \(\phi (\eta ) = 1\) and \(\xi (\eta ) = \eta \) we obtain
Remark 3.8
In 3.9 we prove that \(\varvec{\xi }_{K}^{\phi }\) is Lipschitz continuous on each of the sets \(K_{\lambda ,s,t} = \{ x : \varvec{\rho }^{\phi }_{K}(x) \ge \lambda \,, s \le \varvec{\delta }_{K}^{\phi }(x) \le t \}\) defined for \(0< s< t < \infty \) and \(1< \lambda < \infty \). Since the proof is a bit technical we briefly describe the main idea. For \(x \in K_{\lambda ,s,t}\) and \(y \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K\) with \(\phi (x-a) \le \varepsilon \) we set \(a = \varvec{\xi }_{K}^{\phi }(x)\) and choose any \(b \in \varvec{\xi }_{K}^{\phi }(y)\). First we find a point c for which \(T = {{\,\mathrm{Tan}\,}}(\partial {\mathbf {B}^{\phi }(x,\varvec{\delta }_{K}^{\phi }(x))},a) = {{\,\mathrm{Tan}\,}}(\partial {\mathbf {B}^{\phi }(y,\varvec{\delta }_{K}^{\phi }(y))},c)\). For this point we have \(\phi (a-c) \le 2 \phi (x-y)\); see (17). Then we choose \(e \in \partial {\mathbf {B}^{\phi }(y,\varvec{\delta }_{K}^{\phi }(y))}\) and \(d \in \partial {\mathbf {B}^{\phi }(a+\lambda (x-a),\lambda \varvec{\delta }_{K}^{\phi }(x))}\) which have the same orthogonal (with respect to the Euclidean structure induced by \(\mathrm {D}^2 \phi (a-x)\)) projections onto T as a and b respectively; see Fig. 1. We represent \(\partial {\mathbf {B}^{\phi }(a+\lambda (x-a),\lambda \varvec{\delta }_{K}^{\phi }(x))}\) and \(\partial {\mathbf {B}^{\phi }(y,\varvec{\delta }_{K}^{\phi }(y))}\) locally around a and c as graphs over T of functions \(g_w\) and \(g_u\) of class \(\mathscr {C}^{2}\) using 3.6. Employing 3.2 we can find \(\varepsilon > 0\) which guarantees that d, e, and b fit on the graphs of \(g_w\), \(g_y\), and \(g_y\) respectively. Let q be the signed distance from T such that \(q(x-a) > 0\). The crucial point of the proof is in the estimates (21) and (22), where we use the second order Taylor formulas for \(g_w\) and \(g_y\) to compare (both ways) the heights \(q(d-a)\), \(q(e-c)\), and \(q(b-c)\) with \(\lambda ^{-1}|{T}_\natural (d-a)|^2\), \(|{T}_\natural (a-c)|^2\), and \(|{T}_\natural (b-c)|^2\) respectively up to errors expressed in terms of the modulus of continuity of \(\mathrm {D}^2 H\), where H comes from 3.7. Analysing the situation presented on Fig. 1 we obtain an estimate of the form
which, using the comparison mentioned before, is translated into
where \(\Delta _1\) and \(\Delta _2\) can be made arbitrarily close to 1 by adjusting \(\varepsilon \) depending on the modulus of continuity of \(\mathrm {D}^2 H\). This leads to the estimate (24) of the form
where, again, \(\Delta _4\) is close to 1 given \(\varepsilon \) is small enough; hence, the last term may be absorbed on the left-hand side. Since \(|{T}_\natural (b-a)| \approx |b-a|\) and \(|{T}_\natural (c-a)| \approx |x-y|\) we get the conclusion.
Theorem 3.9
Consider the situation as in 3.5. Assume
There exist \(\varepsilon = \varepsilon (\lambda ,\phi ,\varvec{\delta }_{K}^{\phi }(x))\) and \(\Gamma = \Gamma (\lambda ,\phi )\) such that
Proof
Clearly we can assume \(a \ne b\) and \(y \in X {{\,\mathrm{\sim }\,}}K\). Define
Note for the record (see Fig. 1)
Recall 2.4 and define
Let \(q \in X^*\) be such that \(q(\eta ) = -1\) and \(\ker q = T\). Note that \(\mathrm {D}^2 \phi (\eta )(\eta ,\eta ) = 0\) by one-homogeneity of \(\phi \). Let \( B : X \times X \rightarrow \mathbf {R}\) be the bilinear form such that
By our assumption on \(\mathrm {D}^2 \phi (\eta )\) the map B defines a scalar product on X. In the sequel of this proof we shall assume the Euclidean structure on X comes from B. In particular, we shall use the notations
Let \(\omega _{\lambda }\) be the map obtained from 3.2. Set
where the operator norm of the bilinear map \(\mathrm {D}^2 H(\zeta ) - \mathrm {D}^2 H(\chi ) : X \times X \rightarrow X\) is taken with respect to the Euclidean structure on X defined by (14). Choose \(\varepsilon \in \mathbf {R}\) so that
Assume \(\phi (x-y) \le \varepsilon \). Note that
Set \(E = {T}_\natural [C ]\) and define
so that
Recall that \(H = H \circ {T}_\natural \) and \(a-x,c-y \in \ker {T}_\natural = T^{\perp } = {{\,\mathrm{span}\,}}\{\eta \}\). Set
and observe that
Recalling 3.7 we see that
thus, since \(|\eta | = 1\) and \(q(-\eta ) = 1\) the Taylor formula [18, 3.1.11, p. 220] yields
Repeating the above computation twice with \(g_y\), c, e and \(g_y\), c, b in place of \(g_w\), a, d we get
Consequently, using (18), (19), and (20)
and
hence,
Recalling (16), (17), \(\phi (x-y) \le \varepsilon \), \(\varvec{\rho }^{\phi }_{K}(x) \ge \lambda \) and using 3.2 we obtain
Employing (15), (16), and noting that
we obtain
hence; plugging these estimates to (24) yields
Note that \(|{T}_\natural (a-c)| \le 2 \varepsilon \Delta _1 \le \min \{r_x,r_y\}\) by (15) and (16). In case \(q(a-c) \ge 0\) we combine (25), (23), (22), (20) to get
If \(q(a-c) < 0\), then \(q(b-a) = q(b-c) + q(c-a) \ge 0\) and we get by (18), (19), (21), (25)
As a result the final estimate of (26) holds regardless of the sign of \(q(a-c)\). Employing (17)
where \(\Gamma = 2 \Delta _1 (\tfrac{12\lambda }{\lambda - 1} + 2 + \tfrac{ (12\lambda )^2}{(\lambda - 1)^2})\). \(\square \)
Corollary 3.10
Assume \(\phi \) is uniformly convex, \(K \subseteq X\) is closed, \(0< s< t < \infty \), \(1< \lambda < \infty \), and
Then there exists \(\Gamma \in \mathbf {R}\) depending only on s, t, \(\lambda \), and \(\phi \) such that
In particular, \(\varvec{\xi }_{K}^{\phi }|K_{\lambda ,s,t}\) is Lipschitz continuous.
Proof
Assume \(a \in K_{\lambda ,s,t}\), \(b \in \mathbf {R}^{n}\), \(y \in \varvec{\xi }_{K}^{\phi }(b)\), \(x \in \varvec{\xi }_{K}^{\phi }(a)\), and \(\varvec{\delta }_{K}^{\phi }(b) \le t\). Let \(\varepsilon = \varepsilon _{3.9}(\lambda ,\phi ,s)\). If \(\phi (a-b) \le \varepsilon \), then the conclusion follows from 3.9. In case \(\phi (a-b) > \varepsilon \), we have
\(\square \)
Remark 3.11
Observe that the bound for the Lipschitz constant of \(\varvec{\xi }_{K}^{\phi }|K_{\lambda ,s,t}\) obtained in 3.9 explodes with \(\lambda \rightarrow 1^+\). This is in accordance with 4.2.
Proof of Theorem 1.4
Since
by 2.41(c) we obtain the claim directly from 3.10. \(\square \)
4 Twice differentiability points
In this section we prove Theorem 1.5. Recall that \(\varvec{r}_{K}^{\phi }\) was defined by (5), pointwise differentiability in 2.22, \(\phi \)-cut locus \({{\,\mathrm{Cut}\,}}^{\phi }(K)\) by (6), and singular sets \(\Sigma ^{\phi }(K)\) and \(\Sigma ^{\phi }_2(K)\) in (1) and (3).
Remark 4.1
It is well known, and follows from 2.17, 2.41(c) and [21, Theorem 3B], that
Remark 4.2
Consider the parabola \(K = \{ (x,x^2) : x \in \mathbf {R}\}\) with centre of curvature at the point \(a = (0,\frac{1}{2}) \in \mathbf {R}^2\). Then \(a \in {{\,\mathrm{Cut}\,}}(K) \cap \mathrm {Unp}^{}(K)\). We look at the behaviour of \(\varvec{\xi }_{K}^{}\) on the line \(\{ (x,\frac{1}{2}) : x \in \mathbf {R}\}\). Whenever \(0< x < 8^{-1/2}\), setting \(b = (2x,\frac{1}{2})\), we have \(\varvec{\xi }_{K}^{}(b) = (\sqrt{x},x)\); hence, \(\varvec{\xi }_{K}^{}\) is not differentiable at a and \(\varvec{\delta }_{K}^{}\) is not pointwise differentiable of order 2 at a. Note also that \(\varvec{\xi }_{K}^{}\) is not even Lipschitz continuous in any neighbourhood of a. On the other hand 2.41(c) yields differentiability of \(\varvec{\delta }_{K}^{}\) at a (which can also be checked by direct computation). We conclude \(a \in \Sigma _2(K) {{\,\mathrm{\sim }\,}}\Sigma (K)\). In 4.3 we prove that this is a generic situation for points in \({{\,\mathrm{Cut}\,}}(K) \cap \mathrm {Unp}^{}(K)\).
Lemma 4.3
Assume \(K \subseteq \mathbf {R}^{n}\) is closed, \( x \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \), and \( \varvec{\delta }_{K}^{\phi } \) is pointwise differentiable of order 2 at x.
Then \( \varvec{\rho }^{\phi }_{K}(x)> 1 \). In particular \( {{\,\mathrm{Cut}\,}}^{\phi }(K) \subseteq \Sigma ^{\phi }_2(K)\).
Proof
Define \(r = \varvec{\delta }_{K}^{\phi }(x) \), \( \nu = \varvec{\nu }_{K}^{\phi }(x) \), \( a = \varvec{\xi }_{K}^{\phi }(x) \) and \( T = \mathbf {R}^{n} \cap \{ v : v \bullet {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }(x) \} \). We use 2.44 to find \( r_1 > 0 \) and a continuous function \( f : T \rightarrow T^\perp \) which is pointwise twice differentiable at \( {T}_\natural x \) with \( \mathrm {D}f({T}_\natural x) = 0 \) such that, defining \( M = \{\chi + f(\chi ) : \chi \in T \} \) and \( U = \mathbf {U}^{\phi }(x,r_1)\), it holds \( U \cap S^{\phi }(K,r) = U \cap M \). Decreasing \(r_1 > 0\) if necessary, we infer from the pointwise twice differentiability of f in \( {T}_\natural x \) that there exists a polynomial function \( P : T \rightarrow T^\perp \) of degree at most 2 such that
Decreasing \(r_1 > 0\) even more, we can assume also that \( U {{\,\mathrm{\sim }\,}}S^{\phi }(K,r) \) is the union of two connected and disjointed open sets \( U^- \) and \( U^+ \) such that
Since \( \mathbf {U}^{\phi }(a,r) \cap S^{\phi }(K,r) = \varnothing \) we infer \( U \cap \mathbf {U}^{\phi }(a,r) \subseteq U^- \). Moreover, it follows from (27) that there exists \( s > 0 \) such that \(\mathbf {U}^{\phi }(x + s \nu ,s) \subseteq U^+ \) (notice \( s < r_1 \)) and
Choose \( 0< \epsilon < \frac{r_1}{4} \). The continuity of \( \varvec{\xi }_{K}^{\phi } \) and \( \varvec{\delta }_{K}^{\phi } \) at x implies that there exists \( 0< \delta < \epsilon \) such that \( \phi (b-a) < \epsilon \) and \( \phi (b-y) < r + \epsilon \) for every \( b \in \varvec{\xi }_{K}^{\phi }(y) \) and for every \( y \in \mathbf {U}^{\phi }(x,2\delta ) \). Define \( y = x + \delta \nu \), choose \( b \in \varvec{\xi }_{K}^{\phi }(y) \) and let \( \tau = \sup \{ t : 0 \le t \le 1, \; \phi (y + t(b-y) - a) > r \} \). Notice
Therefore, \(y + \tau (b-y) \in U \cap \mathbf {B}^{\phi }(a,r) \subseteq \mathop {\mathrm {Clos}}U^- \cap U \). Since \( y \in U^+ \) we infer there exists \( 0 < t \le \tau \) such that \( y + t (b-y) \in S^{\phi }(K,r) \). Defining \( z = y + t (b-y) \) and noting that \( \phi (z-b) = \phi (x-a) \) and \( \phi (y-z) \ge \phi (y-x) \) by (28), we infer
whence we conclude that \( a \in \varvec{\xi }_{K}^{\phi }(y) \) and consequently \( \varvec{\rho }^{\phi }_{K}(x) > 1 \). \(\square \)
Remark 4.4
Since \( \mathscr {L}^{n} (\Sigma ^{\phi }_2(K)) =0 \) by the Alexandrov theorem [7], it follows that
In a Riemannian setting a conclusion analogous to Lemma 4.3 is contained in [6]. A proof of \( \mathscr {L}^{n} ({{\,\mathrm{Cut}\,}}^\phi (K)) =0\) along different lines can be found in the proof of [15, Theorem 5.9, Claim 1], see also [15, Remark 5.10].
In the next result the classical notion of approximate lower limit of a function plays a central role. Let us first recall this definition.
Definition 4.5
[cf. [18, 2.9.12]] Let \(\rho : \mathbf {R}^{n} \rightarrow \mathbf {R}\) be a function. The approximate lower limit of \( \rho \) at x is defined as

Remark 4.6
If \( \rho \) is \( \mathscr {L}^n \)-measurable, then \({{\,\mathrm{ap}\,}}\liminf _{y \rightarrow x} \rho (y) \ge \sigma \in \mathbf {R}\) if and only if

The approximate lower limit of an arbitrary function always defines a Borel function. This fact can be proved using an argument similar to those of [39, Lemma 5.1].
Lemma 4.7
Suppose \( f : \mathbf {R}^n \rightarrow \overline{\mathbf {R}} \) is an arbitrary function and let \( \underline{f} : \mathbf {R}^n \rightarrow \overline{\mathbf {R}}\) be defined as
Then \( \underline{f} \) is a Borel function.
Proof
For every \( t \in \mathbf {R} \) we define \( F_t = \{x : f(x) < t\} \) and we set
for \( t \in \mathbf {R} \), \( i \in \mathbf {Z}_+ \) and \( r > 0 \). Then we prove that the set \( W_{t, i, r} \) is a closed subset of \( \mathbf {R}^n \) for every \( t \in \mathbf {R} \), \( i \in \mathbf {Z}_+ \) and \( r > 0 \). Choose a sequence \( y_k \in W_{t, i, r} \) that converges to \( y \in \mathbf {R}^n \). Noting that
we conclude from [18, 2.1.5]
and \( y \in W_{t, i, r} \). Fix now \( \sigma \in \mathbf {R} \), an increasing sequence \(t_j\) converging to \( \sigma \), and a countable dense subset D of \( \mathbf {R} \). Noting that
we conclude that \( \{x : \underline{f}(x) \ge \sigma \} \) is a Borel subset of \( \mathbf {R}^n \); hence, \( \underline{f} \) is a Borel function. \(\square \)
We consider now the approximate lower envelope of \( \varvec{\rho }^{\phi }_{K} \) (see Definition 2.31).
Definition 4.8
For a closed set \( K \subseteq \mathbf {R}^n \) we define the function \( \underline{\varvec{\rho }^{\phi }_{K}} : \mathbf {R}^n \rightarrow \mathbf {R} \) as
Remark 4.9
Clearly \( 1 \le \underline{\varvec{\rho }^{\phi }_{K}}(x) \le \limsup _{y \rightarrow x} \varvec{\rho }^{\phi }_{K}(y) \le \varvec{\rho }^{\phi }_{K}(x)\) for \( x \in \mathbf {R}^{n}\) by Lemma 2.33.
Remark 4.10
Let \((a, \eta )\in N^\phi (K) \). If there exists \( 0< r < \varvec{r}_{K}^{\phi }(a, \eta ) \) and \( \sigma > 1 \) with \( \underline{\varvec{\rho }^{\phi }_{K}}(a+r\eta ) \ge \sigma \), then it follows from Remarks 4.6 and 4.9 and Lemma 2.35 that
Therefore it follows from the definition in (8) that \( \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \le \varvec{r}_{K}^{\phi }(a, \eta ) \) for every \((a, \eta )\in N^\phi (K) \).
We recall the following notation: if \( K \subseteq \mathbf {R}^n \) is a closed set and \( \sigma \ge 1 \) we set
If \( \sigma > 1 \) then \( K_\sigma \subseteq \mathbf {R}^n {\setminus } (K \cup {{\,\mathrm{Cut}\,}}^\phi (K)) \) and \( K_1 = \mathbf {R}^n \sim K \). Compare the next Lemma with Lemma 2.33.
Lemma 4.11
For every closed set \( K \subseteq \mathbf {R}^n \) the function \( \underline{\varvec{\rho }^{\phi }_{K}} \) is a Borel function and it satisfies
for \( x \in \mathbf {R}^{n+1} \sim K \) with \( \underline{\varvec{\rho }^{\phi }_{K}}(x) > 1 \) and \( 0< t < \underline{\varvec{\rho }^{\phi }_{K}}(x) \).
Proof
The function \( \underline{\varvec{\rho }^{\phi }_{K}} \) is a Borel function by Lemma 4.7.
Let \( h_t \) be defined as in Lemma 2.34 for all \( t \in \mathbf {R} \). Suppose \( x \in \mathbf {R}^n \sim K \), \(\sigma = \underline{\varvec{\rho }^{\phi }_{K}}(x) > 1 \) and \( 0< t < \sigma \). We choose \( 0< \epsilon < \frac{\varvec{\delta }_{K}^{\phi }(x)}{2} \) and we notice that
and, with the help of Lemma 2.34,
Then we infer from Corollary 3.10 and Lemma 2.34 that \( h_{t}| K_{\sigma } \cap \mathbf {B}^\phi (x, \epsilon ) \) is a bi-Lipschitz homeomorphism. Since  , we employ [11, Theorem 1] to conclude that
, we employ [11, Theorem 1] to conclude that

Noting that \( \underline{\varvec{\rho }^{\phi }_{K}}(h_t(x)) \ge \underline{\varvec{\rho }^{\phi }_{K}}(x)/t > \sup \{1, 1/t\} \), we can apply the inequality in (29), with x and t replaced by \( h_t(x) \) and \( \frac{1}{t} \) respectively, to obtain the desired conclusion. \(\square \)
Lemma 4.12
Suppose
Then the following statements hold.
-
(a)
\( {{\,\mathrm{im}\,}}\mathrm {D}\varvec{\nu }_{K}^{\phi }(x) \subseteq T \).
-
(b)
\( \mathrm {D}\varvec{\nu }_{K}^{\phi }(x)(\varvec{\nu }_{K}^{\phi }(x)) = \mathrm {D}\varvec{\xi }_{K}^{\phi }(x)(\varvec{\nu }_{K}^{\phi }(x)) =0 \).
-
(c)
There exists a basis \( v_1, \ldots , v_{n-1} \) of T of eigenvectors of \( \mathrm {D}\varvec{\nu }^\phi _K(x)| T \in {{\,\mathrm{Hom}\,}}(T,T) \) and the eigenvalues \( \chi _{1} \le \cdots \le \chi _{n-1} \) of \(\mathrm {D}\varvec{\nu }_{K}^{\phi }(x)|T \) are real numbers such that
$$\begin{aligned} \frac{1}{(1-\lambda )\varvec{\delta }_{K}^{\phi }(x)}\le \chi _{i} \le \frac{1}{\varvec{\delta }_{K}^{\phi }(x)} \,. \end{aligned}$$ -
(d)
\(\mathrm {D}h_t(x)\) is an isomorphism of \(\mathbf {R}^{n}\) for every \( 0< t < \lambda \).
-
(e)
If \( \sigma > 1 \) the \( \mathbf {R}^n \)-multivalued map \( h_{1/t} \) is strongly differentiable at \( h_t(x) \) for every \( 0< t < \sigma \).
-
(f)
If \(\sigma > 1\), then \( \varvec{\delta }_{K}^{\phi } \) is pointwise differentiable of order 2 at \(h_t(x)\) whenever \(0< t < \sigma \).
Proof
Note that \(\lambda > 1\) and \(1 \le \sigma \le \lambda \) by Lemma 4.3 and Remark 4.9 and also that \(\varvec{\nu }_{K}^{\phi }\) is differentiable at x by 2.41(e). We choose a function \( \xi : \mathbf {R}^{n} \rightarrow \mathbf {R}^{n} \) such that \( \xi (y) \in \varvec{\xi }_{K}^{\phi }(y) \) for \( y \in \mathbf {R}^{n} \) and we define
Employing 2.41(e)(c) we notice that \( \eta \) is differentiable at x,
since \( |\eta (y)| = 1 \) for every \( y \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K\). Moreover, we compute
whence we conclude that \( \mathrm {D}\eta (x)|T \in {{\,\mathrm{Hom}\,}}(T,T) \) is self-adjoint. Recalling 2.9 we notice that
for \( y \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K \). Henceforth,
Since \( \mathrm {D}{{\,\mathrm{grad}\,}}\phi ^{*}(v)v = 0\) and \( \mathrm {D}{{\,\mathrm{grad}\,}}\phi ^{*}(v) \) is self-adjoint for \( v \in \mathbf {R}^{n} {{\,\mathrm{\sim }\,}}\{0\} \), we conclude that
whence we deduce that \( {{\,\mathrm{im}\,}}\mathrm {D}{{\,\mathrm{grad}\,}}\phi ^{*}(v) \subseteq \{ u : u \bullet v =0 \} \) for \( v \ne 0 \), \( {{\,\mathrm{im}\,}}\mathrm {D}\nu (x) \subseteq T \), and \( \mathrm {D}{{\,\mathrm{grad}\,}}\phi ^{*}(\eta (x))|T \in {{\,\mathrm{Hom}\,}}(T,T) \) is a positive definite self-adjoint linear map. In particular, we established (a) and, moreover, it follows from (32) and [15, 2.25] that the eigenvalues of \( \mathrm {D}\nu (x)|T \) are real numbers.
To prove (b) we notice by 2.17 that the equations
hold for \( 0 < t \le 1 \) and we differentiate with respect to t at \( t = 1 \).
We now check the estimate claimed in (c) for the eigenvalues of \( \mathrm {D}\varvec{\nu }_{K}^{\phi }(x)|T \). Assume \(x=0\) and \(\lambda = \varvec{\rho }^{\phi }_{K}(0) > 1\). Define
and observe that \( W_1 \subseteq \{ y : \varvec{\delta }_{K}^{\phi }(y) < r \} \), \( W_2 \subseteq \{y : \varvec{\delta }_{K}^{\phi }(y) > r \} \) and \(0 \in \partial W_1 \cap \partial W_2 \cap S^{\phi }(K,r) \). Notice that \( {{\,\mathrm{Tan}\,}}(S^{\phi }(K,r), 0) = {{\,\mathrm{Tan}\,}}(\partial W_1, 0) = {{\,\mathrm{Tan}\,}}(\partial W_2, 0) \). Using 2.44, we find an open set V containing 0 and three functions \( f : T \rightarrow T^\perp \), \( f_1 : T \rightarrow T^\perp \) and \( f_2 : T \rightarrow T^\perp \) such that \( f_1 \) and \( f_2 \) are of class \(\mathscr {C}^{2}\), f is pointwise differentiable of order 2 at 0, \( f(0) = f_1(0)= f_2(0)=0 \), \(\mathrm {D}f(0) = \mathrm {D}f_1(0) = \mathrm {D}f_2(0) =0 \),
and \( f_1(\chi ) \bullet \eta (0) \le f(\chi )\bullet \eta (0) \le f_2(\chi ) \bullet \eta (0)\) for \( \chi \in {T}_\natural [V ]\). In particular,
Let \( \eta _i : \partial W_i \rightarrow \mathbf {S}^{n-1} \) be the exterior unit normal function of \( W_i \) for \(i \in \{1,2\}\). Then \( \eta _1(0) = \eta (0) = - \eta _2(0) \) and we use 2.44 in combination with (30), (31), and 2.45 to infer
To conclude we use the argument from the third paragraph of the proof of [15, 2.34]. First, we find a positive definite self-adjoint map \( C \in {{\,\mathrm{Hom}\,}}(T,T) \) such that \( \mathrm {D}{{\,\mathrm{grad}\,}}\phi (\eta (0))|T = C \circ C \); then we observe, using [15, 2.33], that
whence we deduce, employing (33)
Noting that \( C \circ \mathrm {D}\eta (0) \circ C \) is a self adjoint map with the same eigenvalues as \( \mathrm {D}\nu (0) = \mathrm {D}{{\,\mathrm{grad}\,}}\phi (\eta (0)) \circ \mathrm {D}\eta (0) \) we finally obtain the estimate in (c).
We turn to the proof of (d). Let \( 0< t < \lambda \) and assume \( t \ne 1 \) (notice that \( h_1 = \mathbf {I}_{\mathbf {R}^n} \)). By contradiction, if there was \(v \ne 0\) with \(\mathrm {D}h_t(x)v = 0\), then it would follow that
and, noting that \(\varvec{\nu }_{K}^{\phi }(x) \bullet {{\,\mathrm{grad}\,}}\varvec{\delta }_{K}^{\phi }(x) = \phi (\varvec{\nu }_{K}^{\phi }(x)) = 1\) and \( v = w + \kappa \varvec{\nu }_{K}^{\phi }(x) \) for some \( w \in T \) and \( \kappa \in \mathbf {R}^{} \), we could employ (b) to compute
whence we would deduce from (a) that \( \kappa =0 \), \( w \ne 0 \) and
which would contradict one of the estimates in (c): in case \(0< t < 1\), we have \((1-t)^{-1} > 1\) and if \(1< t < \lambda \), then \((1-t)^{-1} < (1-\lambda )^{-1}\).
Finally, we prove (e) and (f). Let \( \sigma > 1 \) and \( 0< t < \sigma \). We define the \( \mathbf {R}^n \)-multivalued maps (see Definition 2.12) T and S by
Then T is continuous at \( h_t(x) \) and \( S = T^{-1} \) by Lemma 4.11 (see Definition 2.13). Moreover, since  , it follows from Remark 2.29 that S is strongly differentiable at x with \( \mathrm {D}S(x) = \mathrm {D}h_t(x) \) and it follows from Lemma 4.11 that
, it follows from Remark 2.29 that S is strongly differentiable at x with \( \mathrm {D}S(x) = \mathrm {D}h_t(x) \) and it follows from Lemma 4.11 that

We apply [46, Lemma 2] to conclude that T is differentiable at \( h_t(x) \) and, noting the Lipschitz property of \( h_{1/t} \) over \( K_{\sigma /t} \) that can be deduced from Corollary 3.10, we can use Lemma 2.38 to conclude that \( h_{1/t} \) is strongly differentiable at \( h_t(x) \). Therefore \( \varvec{\xi }_{K}^{\phi } \) is strongly differentiable at \( h_t(x) \) and \( \varvec{\delta }_{K}^{\phi } \) is pointwise differentiable of order 2 at \( h_t(x) \) by Lemma 2.41(e). \(\square \)
Remark 4.13
The proof of (c) shows the following fact. Suppose \( \xi : \mathbf {R}^n \rightarrow \mathbf {R}^n \) is an arbitrary function such that \( \xi (y)\in \varvec{\xi }^\phi _K(y) \) for \( y \in \mathbf {R}^{n} \) and
Then \(\mathrm {D}(\nabla \phi )(\eta (x))|T \) and \( \mathrm {D}\eta (x)|T \) are self-adjoint maps in \( {{\,\mathrm{Hom}\,}}(T,T) \),
The next Lemma clarifies the relation between the function \( \underline{\varvec{\rho }^{\phi }_{K}} \) and the function \( \underline{\varvec{r}_{K}^{\phi }} \).
Lemma 4.14
Suppose \( K \subseteq \mathbf {R}^n \) is closed and \( (a, \eta )\in N^\phi (K) \). Then the following statements are equivalent.
-
(a)
\( \underline{\varvec{\rho }^{\phi }_{K}}(a + r \eta ) > 1 \) for some \( r > 0 \),
-
(b)
\( \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) > 0 \),
-
(c)
\( \underline{\varvec{\rho }^{\phi }_{K}}(a+r\eta ) > 1 \) for every \( 0< r < \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \).
If (a), (b) or (c) holds, then
Proof
It follows from the definition of \( \underline{\varvec{r}_{K}^{\phi }} \) that (a) implies (b) and it is obvious that (c) implies (a). It remains to prove that (b) implies (c) and the equality in (34). Let \( 0< r < \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \) and choose \( \sigma > 1 \) and \( 0< s < \varvec{r}_{K}^{\phi }(a, \eta ) \) such that

It follows that \( \underline{\varvec{\rho }^{\phi }_{K}}(a + s \eta ) \ge \sigma > 1 \) and employing Lemma 4.11 we conclude that
Since \( \frac{r}{s} < \sigma \), choosing \( t = \frac{r}{s} \) we obtain
Letting \(\sigma s \) approach \(\underline{\varvec{r}_{K}^{\phi }}(a, \eta )\), we infer from (35) that \( \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \le r \underline{\varvec{\rho }^{\phi }_{K}}(a +r \eta ) \) for \( 0< r < \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \).
Finally if \( 0< r < \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \), then \( \underline{\varvec{\rho }^{\phi }_{K}}(a+r\eta ) > 1 \),

It follows that \( r\underline{\varvec{\rho }^{\phi }_{K}}(a + r\eta )\le \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \) and the proof is complete. \(\square \)
Lemma 4.14 implies the Borel measurability of the reach function \( \underline{\varvec{r}_{K}^{\phi }} \).
Lemma 4.15
For every closed set \( K \subseteq \mathbf {R}^n \) the function \( \underline{\varvec{r}_{K}^{\phi }} \) is a Borel function.
Proof
Let \( \lambda > 0 \) and choose a sequence \(r_i \downarrow 0 \) such that \( r_i < \lambda \) for every \( i \ge 1 \). It follows from Lemma 4.14 that
whence we infer from Lemma 4.11 that \( \{\underline{\varvec{r}_{K}^{\phi }} \ge \lambda \} \) is a Borel subset of \( N^\phi (K) \). \(\square \)
Lemma 4.16
Suppose \( K \subseteq \mathbf {R}^n \) is a closed set, \( \rho > 0 \), \( U =\{ x : \varvec{\delta }_{K}^{\phi }(x) < \rho \} \), and \( U \cap \Sigma ^{\phi }(K) = \varnothing \).
Then \(\underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \ge \rho \) for every \( (a, \eta )\in N^\phi (K) \). In particular, if K is convex then \( \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) = + \infty \) for every \((a, \eta ) \in N^\phi (K) \).
Proof
First we notice that \( \mathop {\mathrm {Clos}}{{\,\mathrm{Cut}\,}}^\phi (K) \cap U = \varnothing \) by Remark 4.1. It follows that
and \( N^\phi (K) = \{(\varvec{\xi }_{K}^{\phi }(x), \varvec{\nu }_{K}^{\phi }(x)) : x \in U\} \). Using Lemma 2.35 we obtain that \( \varvec{\delta }_{K}^{\phi }(x) \varvec{\rho }^{\phi }_{K}(x) \ge \rho \) for every \( x \in U \) and we infer that
for every \( x\in U \) and the conclusion follows. \(\square \)
Remark 4.17
Let \((e_1,e_2)\) be the standard basis of \(\mathbf {R}^{2}\) and set \( x_k = 2^{-k} \) for \(k \in \mathbf {Z}_+\). Then
Define
Let \( a > 0 \). Evidently \( \varvec{\rho }^{}_{K}(ae_2) = \infty \) and \( (0, e_2) \in N(K) \). We shall prove that \( \underline{\varvec{\rho }^{}_{K}}(ae_2) < \infty \) and infer that
Define \( c_k = \frac{x_k + x_{k+1}}{2} \) to be the centre of the segment in \(\mathbf {R}\) joining \( x_{k+1} \) and \( x_k \). Moreover, let \( Q_k \) be the 2-dimensional square with centre in \( c_k e_1 + a e_2 \) and side-length \( \frac{x_k - x_{k+1}}{2} = 2^{-k-2} \) and let \( T_k \) be the 2-dimensional triangle with vertices in \( x_{k+1}e_1 \), \( x_k e_1 \), and \( c_k e_1 + 2a e_2 \). Clearly, there exists \(k_0 \in \mathbf {Z}_+\) depending only on a such that \( Q_k \subseteq T_k \) for \(k \in \mathbf {Z}_+\) with \(k \ge k_0\). Noting that
one infers that there is \(k_1 \ge k_0\) depending only on a such that for \( k \in \mathbf {Z}_+\) with \(k \ge k_1\) there holds
Consequently,
Now, for \(k \ge k_1\) we get
and conclude that  ; hence, \(\underline{\varvec{\rho }^{}_{K}}(ae_2) \le 6\).
; hence, \(\underline{\varvec{\rho }^{}_{K}}(ae_2) \le 6\).
Finally, we prove that \( \varvec{\xi }_{K}^{\phi } \) is not differentiable at \( a e_2 \) for each \( a > 0 \). Assume that there exists \(L = \mathrm {D}\varvec{\xi }_{K}^{} (ae_2)\in {{\,\mathrm{Hom}\,}}(\mathbf {R}^2,\mathbf {R}^2)\). Since \( \varvec{\xi }_{K}^{}(ae_2) = 0 \) and \( \varvec{\xi }_{K}^{}(ae_2 + x_ke_1) = x_k e_1 \) for \(k \in \mathbf {Z}_+\) it must be \(L e_1 = e_1\). However, \( \varvec{\xi }_{K}^{}(ae_2 + c_ke_1) = \{x_k e_1, x_{k+1}e_1\} \) for \( k \in \mathbf {Z}_+\) and
Proof of Theorem 1.5
Notice that the statement in (a) is proved in Lemma 4.3. The statement in (b) follows combining Lemma 4.14 with Lemma 4.12(f).
Define \(\mathbf {R}_{+} = \{ t : 0< t < \infty \}\) and for \( t \in \mathbf {R}_{+} \) the function \(f_t : \mathbf {R}^{n} \times \mathbf {R}^{n} \rightarrow \mathbf {R}^{n}\) by the formula \(f_t(a, \eta ) = a + t \eta \) whenever \(a,\eta \in \mathbf {R}^{n}\). Next, define \( g: \mathbf {R}^n \sim (K \cup {{\,\mathrm{Cut}\,}}^\phi (K)) \rightarrow N^\phi (K) \) by \( g(x)= (\varvec{\xi }_{K}^{\phi }(x), \varvec{\nu }_{K}^{\phi }(x)) \) for \( x \in \mathbf {R}^n \sim (K \cup {{\,\mathrm{Cut}\,}}^\phi (K))\). Corollary 3.10 yields
Moreover, for every \( t \in \mathbf {R}_{+} \) it follows from Lemma 2.35
We turn to the proof of (c). Set \( B = (\mathbf {R}^{n} {{\,\mathrm{\sim }\,}}K) \cap \{ x : \underline{\varvec{\rho }^{\phi }_{K}}(x) < \varvec{\rho }^{\phi }_{K}(x) \} \). Since \( \varvec{\rho }^{\phi }_{K} \) is a Borel function by 2.33 and \(\underline{\varvec{\rho }^{\phi }_{K}}\) is \( \mathscr {L}^{n} \) measurable by Lemma 4.11 we see that B is \( \mathscr {L}^{n} \) measurable and it follows from [18, 2.9.13] that \( \mathscr {L}^{n} (B) = 0\); hence, the coarea formula [18, 3.2.11] yields a set \(J \subseteq \mathbf {R}_{+}\) such that \( \mathscr {L}^{1} (\mathbf {R}_{+} {{\,\mathrm{\sim }\,}}J) = 0\) and
For \(t \in \mathbf {R}_{+}\) define
Since \( f_t[W_t ]\subseteq B \cap S^{\phi }(K,t) \) for \( t \in \mathbf {R}_{+} \) by Lemma 4.14, it follows that
Since \( g [K_{\lambda } \cap f_t[W_t ]]= g [K_{\lambda } \cap S^{\phi }(K,t) ]\cap W_t \) for \( \lambda > 1 \) and \( t \in \mathbf {R}_{+} \), we conclude from (37) and (36) that
Since \(W_t = \bigcup \{ W_t \cap g [K_{\lambda } \cap S^{\phi }(K,t) ]: 1 < \lambda \in \mathbf {Q}\}\), it follows that \( \mathscr {H}^{n-1} (W_t) =0 \) for \( \mathscr {L}^{1} \) almost all \( t \in \mathbf {R}_{+} \). Noting that \( W = \bigcup _{t > 0}W_t \) and \( W_t \subseteq W_s \) for \( s \le t \), we infer \( \mathscr {H}^{n-1} (W) = 0\).
We finally prove (d). Define
If \( (a, \eta ) \in N^\phi (K) {{\,\mathrm{\sim }\,}}Z \), then there exists \( 0< s < \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \) such that \( \varvec{\delta }_{K}^{\phi } \) is pointwise twice differentiable at \( a + s \eta \). Since \(\underline{\varvec{\rho }^{\phi }_{K}}(a + s \eta )> 1\) and \( \underline{\varvec{\rho }^{\phi }_{K}}(a + s \eta ) = s^{-1} \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) > 1 \) by Lemma 4.14, we infer from 4.12(f) that \( \varvec{\delta }_{K}^{\phi } \) is pointwise twice differentiable at \( a + t \eta \) for all \( 0< t < \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \).
Consequently, it remains to show that \( \mathscr {H}^{n-1} (Z) = 0\). This can be done with an argument similar as in the proof of (c). Since \( \mathscr {L}^{n} (\Sigma ^{\phi }_2(K)) =0 \) it follows from coarea formula [18, 3.2.11] that there is \(I \subseteq \mathbf {R}_{+}\) such that \( \mathscr {L}^{1} (\mathbf {R}_{+} {{\,\mathrm{\sim }\,}}I) = 0\) and
We define \(Z_{t} = Z \cap \{ (a, \eta ): t < \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \} \) for \( t \in \mathbf {R}_{+} \). Noting that \(f_t [Z_t ]\subseteq \Sigma ^{\phi }_2(K) \cap S^{\phi }(K,t)\) for \( t > 0 \), we infer that
Since \( g[K_{\lambda } \cap f_t [Z_t ]]= g [K_{\lambda } \cap S^{\phi }(K,t) ]\cap Z_t \) for \( \lambda > 1 \) and \( t > 0 \), we conclude that
It follows that \( \mathscr {H}^{n-1} (Z_t) =0 \) for \( \mathcal {L}^1 \) almost all \( t > 0 \). Noting that \( Z = \bigcup _{t > 0}Z_t \) and \( Z_t \subseteq Z_s \) for \( s \le t \), we see that \( \mathscr {H}^{n-1} (Z) =0 \). \(\square \)
Remark 4.18
Recalling the set B from the proof above and noting that
we conclude that \(\mathscr {L}^n(\{a + r\eta : \underline{\varvec{r}_{K}^{\phi }}(a, \eta ) \le r <\varvec{r}_{K}^{\phi }(a, \eta )\}) = 0\).
The following theorem shows that even in the case of convex bodies with \( \mathcal {C}^{1,1} \)-boundaries, the dimension of the set Z in the statement (d) can be precisely \( n-1 \). See also [45, Theorem 1] for a similar construction.
Theorem 4.19
There exists a convex set \( K \subseteq \mathbf {R}^{2} \) with \( \mathscr {C}^{1,1} \) boundary and a dense set \( S \subseteq \partial {K} \) such that
-
(a)
\( \mathscr {H}^{1} (S) =0 \) and \( \mathscr {H}^{s} (S) = + \infty \) for all \( s < 1 \),
-
(b)
\( \mathscr {H}^{1} (N(K)|S) =0 \) and \( \mathscr {H}^{s} (N(K)|S) = + \infty \) for all \( s < 1 \),
-
(c)
\( \varvec{\xi }_{K}^{}|S^{\phi }(K,r) \) is not differentiable at \( a + r u \) for all \( r > 0 \) and \( (a,u) \in N(K)|S \).
In particular, both \( \Sigma _2(K) \) and the set of points where \( \varvec{\delta }_{K}^{} \) is not directionally differentiable are dense in \( \mathbf {R}^{2} {{\,\mathrm{\sim }\,}}K \) with Hausdorff dimension 2.
Proof
We choose a dense \( G_\delta \)-set \( G \subseteq \mathbf {R}\) with \( \mathscr {L}^{1} (G) = 0 \) and \( \mathscr {H}^{s} (G) = + \infty \) for all \( s < 1 \). Then Zahorski theorem (see [43] or [20]) ensures the existence of non-decreasing Lipschitz function \( f : \mathbf {R}\rightarrow \mathbf {R}\) such that f is not differentiable at each point of G and it is differentiable at each point of \( \mathbf {R}{{\,\mathrm{\sim }\,}}G \). Let g be a primitive of f and notice that g is a \( \mathscr {C}^{1,1} \) convex function. Let
Evidently K is a convex set with \( \mathscr {C}^{1,1} \) boundary, \( \mathscr {H}^{1} (S)=0 \) and \( \mathscr {H}^{s} (S) = + \infty \) for every \( s < 1 \). If \(\eta : \partial {K} \rightarrow \mathbf {S}^{1} \) is the exterior unit normal of K then
whence we infer that \( \eta \) is not differentiable at each point of S and it is differentiable at all poáints of \(\partial {K} {{\,\mathrm{\sim }\,}}S\). Moreover, we notice that the map \( \phi : \partial {K} \rightarrow N(K) \), defined by \( \phi (z) = (z, \eta (z)) \) for \( x \in \partial {K} \), is a bilipschitz homeomorphism and \( N(K)|S = \phi (S) \). Therefore, (b) holds.
To check (c) we assume that \( \varvec{\xi }_{K}^{}|S^{\phi }(K,r) \) is differentiable at \( a+ ru \) for some \( r > 0 \) and \( (a,u) \in N(K)|S \). We notice that \( \varvec{\xi }_{K}^{}| S^{\phi }(K,r) \) is a bilipschitz homeomorphism onto \( \partial {K} \) with
Therefore, \( \mathrm {D}(\varvec{\xi }_{K}^{}|S^{\phi }(K,r))(a+ ru) : {{\,\mathrm{Tan}\,}}(S^{\phi }(K,r),a + ru) \rightarrow {{\,\mathrm{Tan}\,}}(\partial {K},a) \) is a linear homeomorphism and \((\varvec{\xi }_{K}^{}|S^{\phi }(K,r))^{-1}\) is differentiable at a. This contradicts the fact that \( \eta \) is not differentiable at a. \(\square \)
Availability of data and material
Not applicable.
Change history
27 August 2022
Missing Open Access funding information has been added in the Funding Note.
Notes
At a first sight we can only deduce from [22, Theorem 3.3] that there exist \( \epsilon , \delta > 0 \), an hyperplane \( S \subseteq \mathbf {R}^{n} \) and a semiconcave function \( f : S \rightarrow \mathbf {R}\) such that (10) and (11) with S replaced by T. However, closer inspection of the proof of [22, Theorem 3.3] reveals that we can choose \( S = T \), as the existence of a lipschitzian function \( f : T \rightarrow \mathbf {R}\) which satisfies (10) for some \( \epsilon , \delta > 0 \) directly follows from Clarke implicit function theorem.
References
Alberti, G., Ambrosio, L., Cannarsa, P.: On the singularities of convex functions. Manuscripta Math. 76(3–4), 421–435 (1992). https://doi.org/10.1007/BF02567770
Abatzoglou, T.: Finite-dimensional Banach spaces with a.e. differentiable metric projection. Proc. Am. Math. Soc. 78(4), 492–496 (1980). https://doi.org/10.2307/2042418
Albano, P., Cannarsa, P.: Structural properties of singularities of semiconcave functions. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 28(4):719–740 (1999). http://www.numdam.org/item?id=ASNSP_1999_4_28_4_719_0
Albano, P., Cannarsa, P.: Propagation of singularities for solutions of nonlinear first order partial differential equations. Arch. Ration. Mech. Anal. 162(1), 1–23 (2002). https://doi.org/10.1007/s002050100176
Albano, P., Cannarsa, P., Nguyen, K.T., Sinestrari, C.: Singular gradient flow of the distance function and homotopy equivalence. Math. Ann. 356(1), 23–43 (2013). https://doi.org/10.1007/s00208-012-0835-8
Albano, P.: On the cut locus of closed sets. Nonlinear Anal. 125, 398–405 (2015). https://doi.org/10.1016/j.na.2015.06.003
Alexandroff, A.D.: Almost everywhere existence of the second differential of a convex function and some properties of convex surfaces connected with it. Leningrad State Univ. Ann. [Uchenye Zapiski] Math. Ser. 6, 3–35 (1939)
Asplund, E.: Differentiability of the metric projection in finite-dimensional Euclidean space. Proc. Am. Math. Soc. 38, 218–219 (1973). https://doi.org/10.2307/2038801
Bangert, V.: Analytische Eigenschaften konvexer Funktionen auf Riemannschen Mannigfaltigkeiten. J. Reine Angew. Math. 307, 309–324 (1979). https://doi.org/10.1515/crll.1979.307-308.309
Bárány, I., Hug, D., Schneider, R.: Affine diameters of convex bodies. Proc. Am. Math. Soc. 144(2), 797–812 (2016). https://doi.org/10.1090/proc12746
Buczolich, Z.: Density points and bi-Lipschitz functions in \({ R}^m\). Proc. Am. Math. Soc. 116(1), 53–59 (1992). https://doi.org/10.2307/2159293
Crasta, G., Malusa, A.: The distance function from the boundary in a Minkowski space. Trans. Am. Math. Soc. 359(12), 5725–5759 (2007). https://doi.org/10.1090/S0002-9947-07-04260-2
Cannarsa, P., Peirone, R.: Unbounded components of the singular set of the distance function in \({{\mathbb{R}}}^n\). Trans. Am. Math. Soc. 353(11), 4567–4581 (2001). https://doi.org/10.1090/S0002-9947-01-02836-7
Cannarsa, P., Yifeng, Yu.: Singular dynamics for semiconcave functions. J. Eur. Math. Soc. (JEMS) 11(5), 999–1024 (2009). https://doi.org/10.4171/JEMS/173
De Rosa, A., Kolasiński, S., Santilli, M.: Uniqueness of critical points of the anisotropic isoperimetric problem for finite perimeter sets. Arch. Ration. Mech. Anal. 238(3), 1157–1198 (2020). https://doi.org/10.1007/s00205-020-01562-y
Fathi, A.: Regularity of \(C^1\) solutions of the Hamilton–Jacobi equation. Ann. Fac. Sci. Toulouse Math. (6) 12(4):479–516 (2003). http://afst.cedram.org/item?id=AFST_2003_6_12_4_479_0
Federer, H.: Curvature measures. Trans. Am. Math. Soc. 93, 418–491 (1959)
Federer, H.: Geometric Measure Theory. Die Grundlehren der mathematischen Wissenschaften, Band 153. Springer-Verlag New York Inc., New York (1969)
Fitzpatrick, S.: Differentiation of real-valued functions and continuity of metric projections. Proc. Am. Math. Soc. 91(4), 544–548 (1984). https://doi.org/10.2307/2044798
Fowler, T., Preiss, D.: A simple proof of Zahorski’s description of non-differentiability sets of Lipschitz functions. Real Anal. Exchange 34(1):127–138 (2009). http://projecteuclid.org/euclid.rae/1242738925
Fremlin, D.H.: Skeletons and central sets. Proc. Lond. Math. Soc. (3) 74(3), 701–720 (1997). https://doi.org/10.1112/S0024611597000233
Fu, J.H.G.: Tubular neighborhoods in Euclidean spaces. Duke Math. J. 52(4), 1025–1046 (1985). https://doi.org/10.1215/S0012-7094-85-05254-8
Hajłasz, P.: On an old theorem of Erdős about ambiguous locus. Colloq. Math. (2022). https://doi.org/10.4064
Hug, D., Last, G., Weil, W.: A local Steiner-type formula for general closed sets and applications. Math. Z. 246(1–2), 237–272 (2004). https://doi.org/10.1007/s00209-003-0597-9
Hug, D., Santilli, M.: Curvature measures and soap bubbles beyond convexity. Preprint arXiv:2204.04909
Hiriart-Urruty, J.-B.: Unsolved problems: at what points is the projection mapping differentiable? Am. Math. Mon. 89(7), 456–458 (1982). https://doi.org/10.2307/2321379
Hug, D.: Measures, Curvatures and Currents in Convex Geometry. Habilitationsschrift. Albert-Ludwigs-Universität, Freiburg (1999). https://doi.org/10.6094/UNIFR/167349
Itoh, J., Tanaka, M.: The Lipschitz continuity of the distance function to the cut locus. Trans. Am. Math. Soc. 353(1), 21–40 (2001). https://doi.org/10.1090/S0002-9947-00-02564-2
Konjagin, S.V.: Approximation properties of arbitrary sets in Banach spaces. Dokl. Akad. Nauk SSSR 239(2), 261–264 (1978)
Lieutier, A.: Any open bounded subset of rn has the same homotopy type as its medial axis. Comput. Aided Des. 36, 1029–1046 (2004)
Lions, P.-L.: Generalized Solutions of Hamilton–Jacobi Equations, Volume 69 of Research Notes in Mathematics. Pitman (Advanced Publishing Program), Boston–London (1982)
Li, Y., Nirenberg, L.: The distance function to the boundary, Finsler geometry, and the singular set of viscosity solutions of some Hamilton–Jacobi equations. Commun. Pure Appl. Math. 58(1), 85–146 (2005). https://doi.org/10.1002/cpa.20051
Li, Y., Nirenberg, L.: Regularity of the distance function to the boundary. Rend. Accad. Naz. Sci. XL Mem. Mat. Appl. (5) 29, 257–264 (2005)
Menne, U.: Pointwise differentiability of higher order for sets. Ann. Glob. Anal. Geom. 55(3), 591–621 (2019). https://doi.org/10.1007/s10455-018-9642-0
Miura, T.: A characterization of cut locus for \(C^1\) hypersurfaces. NoDEA Nonlinear Differ. Equ. Appl. 23(6), 60 (2016). https://doi.org/10.1007/s00030-016-0413-y
Mantegazza, C., Mennucci, A.C.: Hamilton–Jacobi equations and distance functions on Riemannian manifolds. Appl. Math. Optim. 47(1), 1–25 (2003). https://doi.org/10.1007/s00245-002-0736-4
Martini, H., Swanepoel, K.J., Weiß, G.: The geometry of Minkowski spaces—a survey. I. Expo. Math. 19(2), 97–142 (2001). https://doi.org/10.1016/S0723-0869(01)80025-6
Rockafellar, R.T.: Convex Analysis. Princeton Mathematical Series, vol. 28. Princeton University Press, Princeton (1970)
Santilli, M.: Rectifiability and approximate differentiability of higher order for sets. Indiana Univ. Math. J. 68(3), 1013–1046 (2019). https://doi.org/10.1512/iumj.2019.68.7645
Santilli, M.: Fine properties of the curvature of arbitrary closed sets. Ann. Mat. Pura Appl. (4) 199(4), 1431–1456 (2020). https://doi.org/10.1007/s10231-019-00926-w
Santilli, M.: Distance functions with dense singular sets. Commun. Partial Differ. Equ. 46(7), 1319–1325 (2021). https://doi.org/10.1080/03605302.2021.1871623
Schneider, R.: Convex Bodies: The Brunn–Minkowski Theory, Volume 151 of Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge (2014). (expanded edition)
Zahorski, Z.: Sur l’ensemble des points de non-dérivabilité d’une fonction continue. Bull. Soc. Math. France 74:147–178 (1946). http://www.numdam.org/item?id=BSMF_1946__74__147_0
Zajíček, L.: On the differentiation of convex functions in finite and infinite dimensional spaces. Czechoslovak Math. J. 29(3), 340–348 (1979)
Zajíček, L.: Differentiability of the distance function and points of multivaluedness of the metric projection in Banach space. Czechoslovak Math. J. 33(2), 292–308 (1983)
Zajíček, L.: On differentiation of metric projections in finite-dimensional Banach spaces. Czechoslovak Math. J. 33(3), 325–336 (1983)
Funding
Open access funding provided by Universitá degli Studi dell’Aquila within the CRUI-CARE Agreement. The research of Sławomir Kolasiński was supported by the National Science Centre Poland Grant no. 2016/23/D/ST1/01084 (years 2017-2021).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Code availability
Not applicable.
Additional information
Communicated by Yoshikazu Giga.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kolasiński, S., Santilli, M. Regularity of the distance function from arbitrary closed sets. Math. Ann. 386, 735–777 (2023). https://doi.org/10.1007/s00208-022-02407-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-022-02407-7


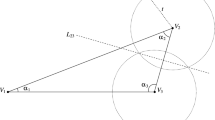

 :
: