Skip to main content
SpringerLink
Log in

Gromov hyperbolicity of the Hilbert distance

  • Published:
Annals of Global Analysis and Geometry Aims and scope Submit manuscript

Abstract

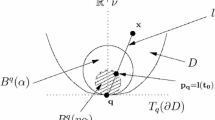
In this paper, we investigate Bonk–Schramm pseudodistances on bounded domains in \({\mathbb {R}}^n\) with \({\mathcal {C}}^2\)-smooth boundary. We use them to propose an alternative proof of the Gromov hyperbolicity of strongly convex domains in \({\mathbb {R}}^n\), emphasizing the similarities between the Kobayashi distance and the Hilbert distance and unifying the results in Balogh and Bonk (Comment Math Helv 75:504–533, 2000), Karlsson and Noskov (Enseign Math II 48:73–89, 2002). This approach is inspired by the works of Bonk and Schramm (Geom Funct Anal 10:266–306, 2000), Balogh and Bonk (Comment Math Helv 75:504–533, 2000) and Blanc-Centi (Math Z 263:481–498, 2009).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Balogh, Z.M., Bonk, M.: Gromov hyperbolicity and the Kobayashi metric on strictly pseudoconvex domains. Comment. Math. Helv. 75(3), 504–533 (2000)

    Article  MathSciNet  Google Scholar 

  2. Blanc-Centi, I.: On the Gromov hyperbolicity of the Kobayashi metric on strictly pseudoconvex regions in the almost complex case. Math. Z. 263, 481–498 (2009)

    Article  MathSciNet  Google Scholar 

  3. Bonk, M., Schramm, O.: Embeddings of Gromov hyperbolic spaces. Geom. Funct. Anal 10, 266–306 (2000)

    Article  MathSciNet  Google Scholar 

  4. Brooks, J.N., Strantzen, J.B.: Blaschke’s rolling theorem in \({\mathbb{R}}\). Mem. Amer. Math. Soc. 405,(1989)

  5. Colbois, B., Verovic, P.: Hilbert geometry for strictly convex domains. Geometriae Dedicata 105, 29–42 (2004)

    Article  MathSciNet  Google Scholar 

  6. Delgado, J.A.: Blaschke’s theorem for convex hypersurfaces. J. Differ. Goem. 14, 489–496 (1979)

    MathSciNet  MATH  Google Scholar 

  7. Ghys, E., de la Harpe, P.: Sur les groupes hyperboliques d’apres Mikhael Gromov Progr. Math., vol. 83. Birkhauser, Boston (1990)

    Book  Google Scholar 

  8. Gromov, M., Lafontaine, J., Pansu, P.: Structures métriques pour les variétés riemanniennes. Cedic/F. Nathan, Paris (1981)

    Google Scholar 

  9. Karlsson, A., Noskov, G.: The Hilbert metric and Gromov hyperbolicity. Enseign. Math. II(48), 73–89 (2002)

    MathSciNet  MATH  Google Scholar 

  10. Koutroufiotis, D.: On Blaschke’s rolling theorems. Arch. Math. 23, 655–660 (1972)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University Monastir Institut préparatoire aux etudes, d’ingénieur de Monastir, 5000, Monastir, Tunisia

    Fathi Haggui & Houcine Guermazi

Authors
  1. Fathi Haggui
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Houcine Guermazi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fathi Haggui.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Haggui, F., Guermazi, H. Gromov hyperbolicity of the Hilbert distance. Ann Glob Anal Geom 61, 235–251 (2022). https://doi.org/10.1007/s10455-021-09809-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10455-021-09809-x

Keywords

Mathematics Subject Classification

Search

Navigation