Abstract
We formulate and prove finite dimensional analogs for the classical Balian–Low theorem, and for a quantitative Balian–Low type theorem that, in the case of the real line, we obtained in a previous work. Moreover, we show that these results imply their counter-parts on the real line.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 A Balian–Low type theorem in finite dimensions
Let \(g\in L^2(\mathbb {R})\). The Gabor system generated by g with respect to the lattice \(\mathbb {Z}^2\) is given by
The classical Balian–Low Theorem [3, 4, 9, 21] states that if the Gabor system G(g) is an orthonormal basis, or a Riesz basis, in \(L^2(\mathbb {R})\), then g must have much worse time-frequency localization than what the uncertainty principle permits. The precise formulation is as follows (see [7] for a detailed discussion of the proof and its history).
Theorem A
(Balian, Battle, Coifman, Daubechies, Low, Semmes) Let \(g \in L^2(\mathbb {R})\). If G(g) is an orthonormal basis or a Riesz basis in \(L^2(\mathbb {R})\), then
We note that by Parseval’s identity, condition (2) is equivalent to saying that we must have either
That is, these integrals are considered infinite if the corresponding functions are not absolutely continuous, or if they do not have a derivative in \(L^2\).
In the last 25 years, the Balian–Low theorem inspired a large body of work in time-frequency analysis, including, among others, a non-symmetric version [6, 12, 13, 23], an amalagam space version [19], versions which discuss different types of systems [10, 17, 18, 23], versions not on lattices [8, 16], and a quantified version [24]. The latter result will be discussed in more detail in the second part of this introduction.
Although it provides for an excellent “rule of thumbs” in time-frequency analysis, the Balian–Low theorem is not adaptable to many applications since, in realistic situations, information about a signal is given by a finite dimensional vector rather than by a function over the real line. The question of whether a finite dimensional version of this theorem holds has been circling among researchers in the area.Footnote 1 In particular, Lammers and Stampe pose this as the “finite dimensional Balian–Low conjecture” in [20]. Our main goal in this paper is to answer this question in the affirmative.
Let \(N\in \mathbb {N}\) and denote \(d=N^2\). We consider the space \(\ell _2^d\) of all functions defined over the cyclic group \(\mathbb {Z}_d:=\mathbb {Z}/d\mathbb {Z}\) with the normalization,
To motivate this normalization, let g be a continuous function in \(L^2(\mathbb {R})\) and put \(b(j) = g({j}/{N})\), \(j\in \mathbb {Z}\cap [-N^2/2,N^2/2)\). That is, the sequence \(b \in \ell _2^d\) consists of samples of the function g, at steps of length 1 / N over the interval \([-N/2, N/2]\). Then, for “large enough” N, the above \(\ell ^2\) norm can be interpreted as a Riemann sum approximating the \(L^2(\mathbb {R})\) norm of g. Note that in Sect. 2, we define the finite Fourier transform \({\mathcal {F}}_d\) so that it is unitary on \(\ell _2^d\).
Let \(N\mathbb {Z}_d\) denote the set \(\{ N k : k \in \mathbb {Z}\}\) modulo d. For \(b\in \ell _2^d\), the Gabor system generated by b with respect to \((N\mathbb {Z}_d)^2\), is given by
We point out that, with the choice \(b(j) = g(j/N)\), the discrete Gabor system \(G_d(b)\) yields a discretization of the Gabor system G(g) restricted to the interval \([-N/2,N/2)\).
To formulate the Balian–Low theorem in this setting, we use a discrete version of condition (3). To this end, we denote the discrete derivative of a function \(b=\{b(j)\}_{j=0}^{d-1}\in \ell _2^d\) by
and put
where the infimum is taken over all sequences \(b\in \ell _2^d\) for which the system \(G_d(b)\) is an orthonormal basis in \(\ell _2^d\). We note that for the choice \(b(j) = g(j/N)\), samples of the derivative of g at the points j / N are approximated by \(N\Delta b\). Therefore, the expression inside of the infimum is a discretization of the integrals in the condition (3). Our finite dimensional version of the Balian–Low theorem, that answers the finite Balian–Low conjecture in the affirmitive, may now be formulated as follows.
Theorem 1.1
There exist constants \(c,C>0\) so that, for all integers \(N \ge 2\), we have
In particular, \(\alpha (N)\rightarrow \infty \) as N tends to infinity.
Remark 1.2
Theorem 1.1 also holds in the case that the infimum in \(\alpha (N)\) is taken over all \(b\in \ell _2^d\) for which the system \(G_d(b)\) is a basis in \(\ell _2^d\) with lower and upper Riesz basis bounds at least A and at most B, respectively. In this case, the constants c, C in Theorem 1.1 depend on A and B. (For a precise definition of the Riesz basis bounds see Sect. 2). The dependence on the Riesz basis bounds is necessary, in the sense that it can not be replaced by a dependence on the \(\ell _2^d\) norm of b (see Remark 4.3).
Remark 1.3
The classical Balian–Low theorem (Theorem A) follows as a corollary of Theorem 1.1, as we show in Sect. 6.
Remark 1.4
By restricting to \(N \ge N_0\), for large \(N_0\), the constants in the above theorem improve. Indeed, combining Proposition 4.1 with Remarks 4.4 and 4.6, respectively, we obtain the asymptotic bounds
1.2 A finite dimensional quantitative Balian–Low type theorem
In [22], F. Nazarov obtained the following quantitative version of the classical uncertainty principle: Let \(g\in L^2(\mathbb {R})\) and \( {\mathfrak {Q}},{\mathfrak {R}}\subset \mathbb {R}\) be two sets of finite measure, then
In [24], we obtained the following quantitative Balian–Low theorem, which is a modest analog of Nazarov’s result for generators of Gabor orthonormal bases and, more generally, Gabor Riesz bases.
Theorem B
(Nitzan, Olsen) Let \(g \in L^2(\mathbb {R})\). If G(g) is an orthonormal basis or a Riesz basis then, for every \(Q,R>1\), we have
where the constant \(C>0\) depends only on the Riesz basis bounds of G(g).
This quantitative version of the Balian–Low theorem implies the classical Balian–Low theorem (Theorem A), as well as several extensions of it, including the non-symmetric cases and the amalgam space cases referred to above. Here, we prove the following finite dimensional version of this theorem.
Theorem 1.5
There exists a constant \(C>0\) such that the following holds. Let \(N \ge {350}\), and let \(b \in \ell _2^d\) (where \(d=N^2\)) be such that \(G_d(b)\) is an orthonormal basis in \(\ell _2^d\). Then, for all positive integers \(Q, R \in [1, N/{30}]\), we have
Remark 1.6
The comments made in Remarks 1.2 and 1.3 hold also for Theorem 1.5 (see Theorem 5.3 and Sect. 6.3, respectively).
Remark 1.7
The conditions appearing in Theorem 1.5 are not optimal, but rather, these conditions were chosen to avoid a cumbersome presentation. In particular, we point out that a more delicate estimate in Lemma 5.1, or the use of a different function, will improve the condition \(N \ge {350}\). Some modifications in the proof of Lemma 5.2 will improve this condition as well. In addition, a careful analysis of the proof will allow one to improve each one of the conditions \(N \ge {350}\) and \(Q,R \le N/{30}\) at the expense of making the constant C smaller. In fact, any two of the previous conditions can be improved at the cost of the third.
1.3 Finite dimension Balian–Low type theorems over rectangular lattices
The conclusions of the classical Balian–Low theorem (Theorem A) and its quantitative version (Theorem B), still hold if we replace Gabor systems over the square lattice \(\mathbb {Z}^2\) by Gabor systems over the rectangular lattices \(\lambda \mathbb {Z}\times \frac{1}{\lambda }\mathbb {Z}\), where \(\lambda >0\). Indeed, this is immediately seen by making an appropriate dilation of the generator function g. In the finite dimensional case, however, such dilations are in general not possible. The question of which finite rectangular lattices allow Balian–Low type theorems therefore has an interest in its own right. We address this in the extensions of Theorems 1.1 and 1.5 formulated below.
Let \(M,N\in \mathbb {N}\) and denote \(d=MN\). We consider the space \(\ell _2^{(M,N)}\) of all functions defined over the cyclic group \(\mathbb {Z}_d:=\mathbb {Z}/d\mathbb {Z}\) with normalization
This non-symmetric normalization is motivated by the fact that if g is a continuous function in \(L^2(\mathbb {R})\) and \(b(j) = g({j}/{ M} )\), \(j\in \mathbb {Z}\cap [-MN/2,MN/2)\), then the above \(\ell ^2\)-norm can be interpreted as a Riemann sum for the \(L^2(\mathbb {R})\) norm of g over the interval \([-N/2, N/2]\). Note that in Sect. 7, we define the finite Fourier transform \({\mathcal {F}}_{(M,N)}\) so that it is a unitary operator from \(\ell _2^{(M,N)}\) to \(\ell _2^{(N,M)}\).
Let \(b\in \ell _2^{(M,N)}\). The Gabor system generated by b with respect to \(M\mathbb {Z}_{d} \times N\mathbb {Z}_{d}\) is given by
We point out that making the choice \(b(j) = g(j/M)\), the discrete Gabor system \(G_{(M,N)}(b)\) yields a 1 / M–discretization of the Gabor system G(g) restricted to \([-N/2,N/2]\).
To formulate the discrete Balian–Low theorem in this setting, we put
where the infimum is taken over all sequences \(b\in \ell _2^{(M,N)}\) for which the system \(G_{(M,N)}(b)\) is an orthonormal basis in \(\ell _2^{(M,N)}\). We note that for the choice \(b(j) = g(j/M)\), the expression inside of the infimum is a discretization of the integrals in condition (3).
We are now ready to formulate the extensions of Theorems 1.1 and 1.5 to Gabor systems over rectangles.
Theorem 1.8
There exist constants \(c,C>0\) so that, for all integers \(M,N \ge 2\), we have
In particular, \(\alpha (M,N)\rightarrow \infty \) as \(\min \{M,N\}\) tends to infinity.
Theorem 1.9
There exists a constant \(C>0\) such that the following holds. Let \(M,N \ge {350}\), and let \(b \in \ell _2^{(M,N)}\) be such that \(G_{(M,N)}(b)\) is an orthonormal basis in \(\ell _2^{(M,N)}\). Then, for all positive integers \(Q \le N/{30}\), \( R \le M/{16}\), we have
We point out that Remarks 1.2 and 1.6 also hold for Theorems 1.8 and 1.9, respectively. That is, these theorems can be extended to generators of general bases with the constants depending only on the Riesz basis bounds. Remark 1.7 also holds in this case.
1.4 The structure of the paper
In Sect. 2 we discuss some preliminaries, in particular the finite and continuous Zak transform. In Sect. 3 we present two improved versions of a lemma that we first proved in [24]. These results quantify the discontinuity of the argument of a quasi-periodic function. In Sect. 4, we apply these lemmas to prove Theorem 1.1, while in Sect. 5, we use them to prove Theorem 1.5. In Sect. 6, we show how the Balian–Low theorem (Theorem A) and its quantitative version (Theorem B) can be obtained from their finite dimensional analogs. Finally, in Sect. 7 we discuss Theorems 1.8 and 1.9. We give only a sketch of a proof for Theorem 1.8, as the proofs in the rectangular case are very similar to the proofs in the square lattice case.
2 Preliminaries
2.1 Basic notations, and the continuous and finite Fourier transforms
Throughout the paper, we usually denote by f a function defined over the real line, and by g a function defined over the real line which is a generator of a Gabor system. Similarly, we usually denote by a a discrete function in \(\ell ^d_2\), and by b a function in \(\ell ^d_2\) which is a generator of a Gabor system.
For \(f \in L^1(\mathbb {R})\), and with the usual extension to \(f \in L^2(\mathbb {R})\), we use the Fourier transform
We let \({\mathcal {S}}(\mathbb {R})\) denote the Schwartz class of functions \(\phi \) which are infinitely many times differentiable, and that satisfy \(\sup _{t \in \mathbb {R}} |t^k \phi ^{(\ell )}(t)| < \infty \) for all \(k, \ell \in \mathbb {N}\).
Recall from the introduction that for \(N\in \mathbb {N}\) and \(d=N^2\), we denote by \(\ell _2^d\) the space of all functions defined over the cyclic group \(\mathbb {Z}_d:=\mathbb {Z}/d\mathbb {Z}\) with the normalization
For \(a \in \ell _2^d\), we use the finite Fourier transform
With the chosen normalization, the finite Fourier transform is unitary on \(\ell _2^d\). We define the periodic convolution of \(a, b \in \mathbb {C}^d\), by
and note the convolution relation \({\mathcal {F}}_d(a *b) = {\mathcal {F}}_d (a) \cdot {\mathcal {F}}_d (b)\). Observe that, for the choice \(a(j) = f(j/N)\), the discrete Fourier transforms and convolutions yield natural discretizations of their respective counterparts on \(\mathbb {R}\).
Also, recall that for a sequence \(a\in \ell _2^d\), we denote the discrete derivative by \(\Delta a(j) = a(j+1) - a(j)\). From time to time, we encounter sequences depending on more than one variable, say \(a\big (k + \psi (s)\big )\) where \(\psi \) is some function depending on the integer s. In this case, we write \(\Delta _{(s)}\) if we want to indicate that the difference is to be taken with respect to s. That is, \(\Delta _{(s)} a\big (k+ \psi (s)\big ) = a\big (k + \psi (s+1)\big ) - a\big (k + \psi (s)\big )\).
We will also consider functions \(W : \mathbb {Z}^2_d \rightarrow \mathbb {C}\) for which we use the notations
Finally, we let \(\ell _2([0,N-1]^2)\) denote the space of sequences supported on \(\mathbb {Z}^2 \cap [0,N-1]^2\) with norm
where, as usual, \(d=N^2\). We note that this normalization can be related to the process of sampling an \(L^2\) function over \([0, 1]^2\), on the vertices of squares of side length 1 / N, and computing the corresponding Rieman sum.
2.2 The continuous and finite Zak transforms
On \(L^2(\mathbb {R})\), the Zak transform is defined as follows.
Definition 2.1
Let \(f \in L^2(\mathbb {R})\). The continuous Zak transform of f is given by
We summarise the basic properties of the continuous Zak transform in the following lemma. Proofs for these properties, as well as further discussion of the Zak transform, can be found, e.g., in [14, Chapter 8].
Lemma 2.2
Let \(f \in L^2(\mathbb {R})\). The following hold.
-
i.
The Zak transform is quasi-periodic on \(\mathbb {R}^2\) in the sense that
$$\begin{aligned} Zf(x+1,y) = \mathrm {e}^{2\pi \mathrm {i}y} Zf(x,y) \quad \text {and} \quad Zf(x,y+1) = Zf(x,y). \end{aligned}$$(11)In particular, this means that the function Zf is determined by its values on \([0,1]^2\).
-
ii.
The Zak transform is a unitary operator from \(L^2(\mathbb {R})\) onto \(L^2([0,1]^2)\).
-
iii.
The Zak transform and the Fourier transform satisfy the relation
$$\begin{aligned} Z ({\mathcal {F}}f)(x,y) = \mathrm {e}^{2\pi \mathrm {i}xy} Zf(-y,x). \end{aligned}$$ -
iv.
For \(\phi \in {\mathcal {S}}(\mathbb {R})\), the Zak transform satisfies the convolution relation
$$\begin{aligned} Z (f *\phi ) = Z (f) *_1 \phi , \end{aligned}$$where the subscript of \(*_1\) indicates that the convolution is taken with respect to the first variable of the Zak transform.
Next, we discuss a Zak transform for \(\ell _2^d\) which appears in, e.g., [2].
Definition 2.3
Let \(N\in \mathbb {Z}\) and set \(d=N^2\). The finite Zak transform of \(a\in \ell _2^d\), with respect to \((N\mathbb {Z}_d)^2\), is given by
Note that with this definition, \(Z_d(a)\) is well-defined as a function on \(\mathbb {Z}_d^2\) (that is, it is d-periodic separately in each variable).
The basic properties of the finite Zak transform mirror closely those of the continuous Zak transform and are stated in the following lemma. Parts (i), (ii) and (iii) of this Lemma can be found as Theorems 1, 3 and 4 in [2]. Part (iv) follows immediately from the definitions of the Zak transform and the convolution.
Lemma 2.4
Let \(N\in \mathbb {N}\), \(d=N^2\) and \(a \in \ell _2^d\). Then the following hold.
-
(i)
The function \(Z_d(a)\) is N-quasi-periodic on \(\mathbb {Z}_d^2\) in the sense that
$$\begin{aligned} \begin{aligned} Z_d(a)(m + N,n)&= \mathrm {e}^{2\pi \mathrm {i}\frac{n}{N}}Z_d(a)(m,n), \\ Z_d(a)(m,n+N)&= Z_d (a)\,(m,n). \end{aligned} \end{aligned}$$(12)In particular, \(Z_d(a)\) is determined by its values on the set \(\mathbb {Z}^2 \cap [0,N-1]^2\).
-
(ii)
The transform \(Z_d\) is a unitary operator from \(\ell _2^d\) onto \(\ell _2 ([0,N-1]^2)\).
-
(iii)
The finite Zak transform and the finite Fourier transform satisfy the relation
$$\begin{aligned} Z_d ({\mathcal {F}}_d a)(m,n) = \, \mathrm {e}^{2\pi \mathrm {i}\frac{mn}{d}} Z_d(a) (-n,m). \end{aligned}$$(13) -
(iv)
The finite Zak transform satisfies the convolution relation
$$\begin{aligned} Z_d (a *\phi ) = Z_d(a) *_1 \phi ,\qquad a, \phi \in \ell _2^d. \end{aligned}$$where the subscript of \(*_1\) indicates that the convolution is taken with respect to the first variable of the finite Zak transform.
Remark 2.5
We will make use of a somewhat more general property than the N-quasi periodicity. Namely, we will be interested in functions \(W : \mathbb {Z}^2_d \rightarrow \mathbb {C}\) satisfying
where \(\eta \) is a unimodular constant. In particular, we note that if a function is N-quasi-periodic then any translation of it satisfies the relations (14). For easy reference to this property we will call a function satisfying it N-quasi-periodic up to a constant.
We will make use of the following lemma, which is a finite dimensional analog of inequality (16) from [24].
Lemma 2.6
Let \(N\in \mathbb {N}\) and \(d=N^2\). Suppose that \(a, \phi \in \ell _2^{d}\) and \(k\in \mathbb {N}\), then it holds that
Proof
For a function \(a\in \ell _2^d\), write \(\Delta _ka(n)=a(n+k)-a(n)\). Property (iv) of Lemma 2.4 implies that \(\Delta _k Z_d(a *\phi )=Z_d(a)*_1(\Delta _k \phi )\). The result now follows by applying the triangle inequality to \(\sum |\Delta _k \phi |\). \(\square \)
2.3 Gabor Riesz bases and the Zak transform
A system of vectors \(\{f_n\}\) in a separable Hilbert space H is called a Riesz basis if it is the image of an orthonormal basis under a bounded and invertible linear transformation \(T:H\mapsto H\). Equivalently, the system \(\{f_n\}\) is a Riesz basis if and only if it is complete in H and satisfies the inequality
for all finite sequences of complex numbers \(\{c_n\}\), where A and B are positive constants. The largest A and smallest B for which (16) holds are called the lower and upper Riesz basis bounds, respectively. We note that every basis in a finite dimensional space is a Riesz basis.
The proof for Part (i) of the following proposition can be found, e.g., in [14, Corollary 8.3.2(b)], while part (ii) can be found in [2, Theorem 6].
Proposition 2.7
-
(i)
Let \(g\in L^2(\mathbb {R})\). Then, G(g) is a Riesz basis in \(L^2(\mathbb {R})\) with Riesz basis bounds A and B if and only if \(A\le |Zg(x,y)|^2\le B\) for almost every \((x,y)\in [0,1]^2\).
-
(ii)
Let \(N\in \mathbb {N}\), \(d=N^2\) and \(b\in \ell _2^d\). Then, \(G_d(b)\) is a basis in \(\ell _2^d\) with Riesz basis bounds A and B if and only if \(A\le |Z_d(b)(m,n)|^2\le B\) for all \((m,n) \in [0,N-1]^2 \cap \mathbb {Z}^2\).
2.4 Relating continuous and finite signals
In the introduction, we motivated our choices of normalizations by relating finite signals to samples of continuous ones. In this subsection, we formulate this relation precisely.
Fix \(N \in {\mathbb {N}}\) and let \(d=N^2\). For a function f in the Schwartz class \({\mathcal {S}}(\mathbb {R})\) and a continuous N-periodic function h, we define their N-periodisation and N-samples, respectively, by
First we relate these operators to the Fourier transform and the Zak transform via Poisson–type formulas. We note that part (i) of the following proposition is stated without proof in [1].
Proposition 2.8
For f in the Schwartz class \({\mathcal {S}}(\mathbb {R})\), the following hold.
-
(i)
For every \(N\in \mathbb {N}\) and \((m,n)\in \mathbb {Z}^2\), we have
$$\begin{aligned} Z_{d} (S_N {P_N f})(m,n) = Zf(m/N, n/N). \end{aligned}$$(17) -
(ii)
For every \(N\in \mathbb {N}\), we have
$$\begin{aligned} {\mathcal {F}}_{d}S_N P_N f = S_N P_N {\mathcal {F}} f. \end{aligned}$$(18)
Proof
(i): Since \(f \in {\mathcal {S}}(\mathbb {R})\), we can change the order of summation in the expression for \(Z_d(S_N P_N f)(m,n)\). This immediately yields the formula.
(ii): Observe that part (i) holds for both f and \({\mathcal {F}}f\). With this, in combination with parts (iii) of Lemmas 2.2 and 2.4, the proof of part (ii) follows. \(\square \)
Remark 2.9
-
(i)
Although Proposition 2.8 is formulated for functions in the Schwartz class \({\mathcal {S}}(\mathbb {R})\), it is readily checked that it holds for all functions \(f \in L^2(\mathbb {R})\) which satisfy both \(\sup _{t \in \mathbb {R}} |t^2 f(t)| < \infty \) and \(\sup _{\xi \in \mathbb {R}} |\xi ^2 {{\hat{f}}}(\xi )| < \infty \).
-
(ii)
In Sect. 6, we extend Proposition 2.8 to \(f \in L^2(\mathbb {R})\).
The following lemma relates the discrete and continuous derivatives.
Lemma 2.10
Let \(f\in L^2(\mathbb {R})\) be a function that satisfies the condition of Remark 2.9(i), and denote \(a=S_NP_Nf\). Then,
Proof
The inequality follows by applying the Fundamental Theorem of Calculus to the differences \(\Delta a_j\) and then applying the triangle inequality. \(\square \)
3 Regularity of the Zak transforms
Essentially, this paper is about the regularity of Zak transforms (or rather, their lack of such). In this section, we formulate a few lemmas in this regard.
3.1 ‘Jumps’ of quasi-periodic functions on \(\mathbb {Z}_d^2\)
It is well known that the argument of a quasi-periodic function on \(\mathbb {R}^2\) cannot be continuous (see, e.g., [14, Lemma 8.4.2]). In [24, Lemma 1], we show that such a function has to ‘jump’ on all rectangular lattices (see Remark 3.2, below). The latter lemma is finite dimensional in nature. For easy reference we formulate it below. To this end, we use the notation
to denote that
Lemma 3.1
Fix integers \(K,L\ge 2\). Let \(\gamma \in \mathbb {C}\) and let H be a function on \(([0,K] \times [0,L]) \cap \mathbb {Z}^2\) that satisfies
Then, there exist \((i,j)\in ([0,K-1] \times [0,L-1]) \cap \mathbb {Z}^2\) such that
or
Remark 3.2
From time to time, we refer to functions satisfying conditions such as (19) or (20) as having ‘jumps’. This notion of ‘jumps’ is imprecise and merely meant to be descriptive, and will depend on the context of the given situation.
Remark 3.3
Note that for \(K=L=N\), the argument of an N-quasi-periodic up to a constant function (see (14)) satisfies the conditions of Lemma 3.1.
3.2 ‘Jumps’ of quasi-periodic functions on subsets of \(\mathbb {Z}_d^2\)
In this subsection, we extend Lemma 3.1 to show that it also holds when the function is restricted to certain subsets of \(\mathbb {Z}_d^2\), which we want to treat as if they were sublattices of \(\mathbb {Z}_d^2\), even if they, strictly speaking, are not. To this end, for integers \(K,L \in [2,N]\), we define the functions
where [a] denotes the integer part of a. Note that \(\sigma _K=\omega _L=N\). We can now state the following lemma.
Lemma 3.4
Fix positive integers \(N \ge {9}\), \(K,L\in [2,N]\), and denote \(d=N^2\). Let W be a function defined over \(\mathbb {Z}_d^2\) that is N-quasi-periodic up to a constant (see (14)). Denote by H any branch of the argument of W, so that \(W= |W| \mathrm {e}^{2\pi \mathrm {i}H}\). Then, there exist \((s,t) \in ([0,K-1]\times [0,L-1]) \cap \mathbb {Z}^2\) so that either
or
Proof
Suppose that (14) holds for W with the constant \(\eta =e^{2\pi i \gamma }\). We start by modifying the argument \(H(\sigma _{s}, \omega _{t})\) of W to obtain a function that satisfies the conditions of Lemma 3.1. To this end, for \((s,t)\in \mathbb {Z}^2\), set \(h_{s,t} = H(\sigma _{s}, \omega _{t})\), and define a function \(\Phi (s,t)\) on \(([0,K]\times [0,L]) \cap \mathbb {Z}^2\) as follows:
We note that since \(\omega _L=N\), and H is the argument of a function that is N-periodic in the second variable, we have
Therefore, \(\Phi (s,L)=\Phi (s,0)\) (mod 1) for every \(s\in [0,K] \cap \mathbb {Z}\). It follows that \(\Phi \) satisfies the conditions of Lemma 3.1 on \(([0,K]\times [0,L]) \cap \mathbb {Z}^2\), and, as a consequence, there exists a point \((s,t) \in ([0,K-1]\times [0,L-1]) \cap \mathbb {Z}^2\) so that either
hold. The jumps for \(h_{s,t}\) now follow from the jumps of \(\Phi \). Indeed, if the jump is in the vertical direction, or if it is in the horizontal direction at a point (s, t) with \(s \le K-2\), then this is immediate from the definition of \(\Phi \). If the jump is in the horizontal direction, at a point (s, t) with \(s = K-1\), then we note that, since \(\sigma _K = N\), the N-quasi-periodicity up to a constant of W implies that
Since, by definition \(\Phi (K-1,t)=h_{K-1,t}\), it follows that
The lemma now follows from the fact that,
\(\square \)
We obtain the following corollary of Lemma 3.4.
Corollary 3.5
Fix an integer \(N_0 \ge {9}\) and a constant \(A>0\). Let
For any integers \(N \ge N_0\) and \(K,L\in [2,N]\), the following holds (with \(d=N^2\)). If W is an N-quasi periodic function satisfying \(A \le |W|^2\) over the lattice \(\mathbb {Z}^2_d\), then, for every \((u, v) \in \mathbb {Z}_d^2\), there exists at least one point \((s,t)\in ([0,K-1] \times [0,L-1])\cap \mathbb {Z}^2\) such that
where \(\sigma _s, \omega _t\) are defined in (21).
Proof
First, we point out that we define the argument \(\arg (z)\) of a complex number z so that \(z=|z|e^{2\pi i\text {arg}(z)}\). Since any translation of a quasi-periodic function is quasi-periodic up to a constant, as defined in (14), it follows from Lemma 3.4 that on an \(N\times N\) square the argument of W jumps by more than \({{1}/{8}} - 1/N\) in at least one of the inequalities (24) or (25). As the modulus of W is bounded from below by \(\sqrt{A}\), the conclusion now follows from basic trigonometry. \(\square \)
4 A proof for Theorem 1.1
Here we give a proof for Theorem 1.1 in the general Riesz basis case referred to in Remark 1.2. In the first subsection below, we reformulate the theorem in terms of the Zak transform. Using this, we proceed to prove the bound from below, and, finally, we prove the bound from above.
4.1 Measures of smoothness for finite sequences
Fix \(N\in \mathbb {N}\) and set \(d=N^2\). For \(b \in \ell ^d_2\), denote
and
Note that with these notations the quantity \(\alpha (N)\) defined in the introduction satisfies
where the infimum is taken over \(b \in \ell ^d_2\) for which G(b) is an orthonormal basis.
Proposition 4.1
Let \(b\in \ell ^d_2\) be such that \(|Z_d(b)(m,n)|^2\le B\) for all \((m,n)\in \mathbb {Z}_d^2\). Then, for all integers \(N\ge 2\), we have
Proof
We will only prove the right-hand side inequality in (26) since the left-hand side inequality is proved in the same way.
As the finite Zak transform commutes with the difference operation \(\Delta \), that is \(Z_d(\Delta b)= \Delta Z_d(b)\), and the finite Zak transform is unitary from \(\ell _2^d\) to \(\ell _2([0,N-1]^2)\), we find that
Multiplying the above equation by \(d=N^2\), we get
Similarly,
To relate the expression on the right-hand side to \(\Gamma Z_d ( b)\), we use the relation between the finite Fourier transform and the Zak transform (13) to compute
Combining this estimate with (28), and recalling that the Zak transform is N-periodic in the second variable, we find that
where in the last estimate, we used the facts that \(m\le N\) and \(d=N^2\). Multiplying this inequality by \(N^2\), and combining it with (27), the right-hand inequality of (26) follows. \(\square \)
For \(A,B>0\), we put
where the infimums are taken over all \(b\in \ell ^d_2\) for which the system \(G_d(b)\) is a basis with Riesz basis bounds at least A and at most B.
Proposition 4.1 now implies that with the notations above, the following inequality holds for every \(N \in \mathbb {N}\):
In light of this inequality, Theorem 1.1 (as well as the version discussed in Remark 1.2) can be reformulated as follows.
Theorem 4.2
There exist constants \(c,C>0\) so that, for all integers \(N \ge 2\), we have
Remark 4.3
To see that it is necessary to include the the Riesz basis bounds in the definitions of \(\alpha _{A,B}(N)\) and \(\beta _{A,B}(N)\) (and that these bounds cannot be replaced by \(\ell _2^d\) normalization) consider the following example. Let \(h = \mathrm {e}^{-\pi (x-\tau )^2}\) with \(\tau \in (0,1/2) \backslash \mathbb {Q}\). By [11, Lemma 3.40], it follows that Zh has exactly one zero on the unit square located at \((1/2+\tau ,1/2)\). Since the first coordinate of this point is irrational, it follows by Proposition 2.8 that the function \(Z_d(b_{N})\) with \(b_{N} = S_N P_N h\), where \(d=N^2\), does not have a zero on \(\mathbb {Z}_d^2\). Consequently, Proposition 2.7 implies that the finite Gabor system \(G_d(b_N)\) is a basis for \(\ell ^d_2\), though the (lower) Riesz basis bounds of these bases decay as N increases. Straight-forward computations, using only the regularity and decay of the Gaussian, show that there exist constants \(C,D, E>0\), such that the following hold:
-
(i)
\(C \le \Vert b_N\Vert _d\le D\) for every \(N\in \mathbb {N},\) (ii) \(\alpha (b_N,N)\le E\) as \(N \rightarrow \infty \).
This example shows that the constant c in Theorem 1.1 depends on the lower Riesz basis bounds in the definition of \(\alpha _{A,B}(N)\). Similarly, it may be shown that C depends on the upper Riesz basis bound.
4.2 Proof for the lower bound in Theorem 4.2
Proof
Given \(N\ge {9}\), we set \(d=N^2\) and let \(J\in \mathbb {N}\) be such that \(2^J\le N<2^{J+1}\). Fix \(j\in [0,J-1] \cap \mathbb {Z}\). Let \(\sigma ^{(j)}_t\) and \(\omega ^{(j)}_t\) be as defined in (21) with \(K_j=L_j=2^{J-j}\). That is,
We note that
where both the infimum and supremum are taken over all \(t\in \mathbb {Z}\). Indeed, to see this, consider separately the cases \(N=2^J\) and \(N>2^J\), and use the fact that all of the numbers involved in these inequalities are integers.
For \(u,v \in [0,2^j-1] \cap \mathbb {Z}\), write
Note that due to (30), if \(u_1\ne u_2\) then \(\mathrm {Lat}_j(u_1) \cap \mathrm {Lat}_j(u_2) = \emptyset \), and if \((u_1,v_1)\ne (u_2,v_2)\) then \(\mathrm {Lat}_j(u_1,v_1) \cap \mathrm {Lat}_j(u_2,v_2) = \emptyset \).
Given \(b\in \ell _2^d\), we denote \(W=Z_d(b)\). Set \(\delta =2\sqrt{A}\sin (\pi /{72})\), then, since \(N\ge {9}\) Corollary 3.5 implies that each of the sets \(\mathrm {Lat}_j(u,v)\) contains a point on which the function W ‘jumps’, i.e., where
Our goal is to collect ‘jumps’ of W that are, in some sense, separated. We do this in an inductive process.
In the first step, let \(j=0\). By Corollary 3.5, there exists a point \((m_0,n_0)\) in \(\mathrm {Lat}_0(0,0)\) so that (31) holds for this point. Let \({\widetilde{S}}_0=S_0 = \{(m_0,n_0)\}\). Next, let \(j=1\). For \(u\in \{0,1\}\), the sets \(\mathrm {Lat}_1(u)\) are disjoint, and so at least one of them does not contain the number \(m_0\). Let \(u^{1}_1 \in \{0,1\}\) be such that the set \(\mathrm {Lat}_1(u_1^1)\) has this property, and, similarly, let \(v^{1}_1\in \{0,1\}\) be such that \(\mathrm {Lat}_1(v^{1}_1)\) does not contain the number \(n_0\). By Corollary 3.5, there exists a point \((m_1,n_1)\) in \(\mathrm {Lat}_{1}(u^{1}_1,v^{1}_1)\) so that (31) holds for this point. Let \(S_1 = \{(m_1,n_1)\}\), and put \(\widetilde{S_1}=S_0\cup S_1\). Note that the two points in \({\widetilde{S}}_1\) do not have the same value in either coordinate.
We now consider the general case. Assume that for some \(1 \le j \le J-2\) we have found sets \(S_j\), \({\widetilde{S}}_j\) and \({\widetilde{S}}_{j-1}\) so that \({\widetilde{S}}_j={\widetilde{S}}_{j-1}\cup S_j\) and
-
i.
\(|{\widetilde{S}}_{j-1}|= |S_j|=2^{j-1}\) and \(|{\widetilde{S}}_j|=2^j\).
-
ii.
Every point in \({S}_j\) satisfies condition (31).
-
iii.
No two points in \({\widetilde{S}}_j\) have the same value in either coordinate.
We now construct the sets \(S_{j+1}\) and \({\widetilde{S}}_{j+1}\). Consider the sets \(\mathrm {Lat}_{j+1}(u)\) for \(u\in [0,2^{j+1}-1] \cap \mathbb {Z}\). These \(2^{j+1}\) sets are disjoint and therefore at least \(2^j\) of them do not contain any of the numbers that are the first coordinates of the points in \({\widetilde{S}}_j\). We let these sets correspond to \(u^{j+1}_k \in [0,2^{j+1}-1] \cap \mathbb {Z}\) for \(1\le k\le 2^j\), and similarly, let \(v^{j+1}_k \in [0,2^{j+1}-1] \cap \mathbb {Z}\), for \(1\le k\le 2^j\), be so that no integer in \(\mathrm {Lat}_{j+1}(v^{j+1}_k)\) coincide with the second coordinate of any point in \({\widetilde{S}}_j\). By Corollary 3.5, there is a point in each of the sets \(\mathrm {Lat}_{j+1}(u^{j+1}_k,v^{j+1}_k)\) so that (31) holds. Let \(S_{j+1}\) be the set containing all these points and let \({\widetilde{S}}_{j+1}={\widetilde{S}}_j\cup S_{j+1}\). Note that \(S_{j+1}\) and \({\widetilde{S}}_{j+1}\) satisfy conditions (i),(ii) and (iii) above, with j replaced by \(j+1\).
Now, for a fixed \(0 \le j \le J-1\), each point \((m,n)\in S_j\) is of the form \((m,n)=(u+\sigma ^{(j)}_{s},v+\sigma ^{(j)}_{t})\) for some \((u,v)\in [0,2^{j}-1]^2 \cap \mathbb {Z}^2\) and \((s,t)\in [0,2^{J-j}-1]^2 \cap \mathbb {Z}^2\). We observe that condition (31) implies the following for such a point (m, n) (where we apply the Cauchy–Schwarz inequality and (30) in the third step):
The last step of the above computation follows by combining the observation that the summands are N-periodic, that is, \(|\Delta W(m,n)| = |\Delta W(m-N,n)|\) and \(|\Gamma W(m,n)| = |\Gamma W(m,n-N)|\), with the fact that, by (30), the number of terms in each sum is bounded by \(2^J\), and therefore also by N.
Since no two points of \({\widetilde{S}}_{J-1}=\cup _{j=0}^{J-1}S_j\) have the same value in either coordinate, and \(|S_j|=2^{j-1}\), we obtain
As \(J+1 \ge \log N/\log 2\), the desired lower inequality now follows. \(\square \)
Remark 4.4
Given the restriction \(N\ge N_0\), it follows from Corollary 3.5 that the \(\delta \) appearing in the last proof may be choosen to be \(\delta = 2\sqrt{A}\sin \pi ({1/8} - 1/N_0)\). Moreover, the inequality \(J+1 \ge \log N/\log 2\) yields
Plugging this into the estimate (32), we find that
For \(N_0={9}\), this yields the estimate \(\beta _{A,B}(N) \ge A\log N/{533}\), while as \(N_0 \rightarrow \infty \) we get that
4.3 Proof for the upper bound in Theorem 4.2
We consider a function that first appeared in [5] (see also [23]). In these references, this function was used for similar purposes as here, namely, to provide examples of generators of orthonormal Gabor systems with close to optimal localisation.
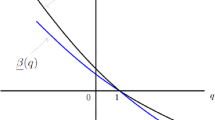
To define the function, we first define the smooth functions \(\phi : \mathbb {R}\rightarrow [0,1]\) and \(\gamma : (0,1] \rightarrow [0,1]\) by
Using these functions, we define (see Fig. 1)
Finally, on \([0,1]^2\), we define the function
which we extend (continuously on \(\mathbb {R}^2{\setminus }\mathbb {Z}^2\)) to a quasi-periodic function on all of \(\mathbb {R}^2\) (in a mild abuse of notation, we also denote the quasi-periodic extension by G(x, y)). Since the finite Zak transform is unitary, it follows that there exists a sequence \(b \in \ell ^d_2\) of unit norm so that
In particular, since G is unimodular, it follows by Proposition 2.7 that the Gabor system \(G_d(b)\) is an orthonormal basis for \(\ell _2^d\).
The following proposition provides the required estimate from above on \(\beta _{1,1}(N)\).
Proposition 4.5
Let b be the sequence defined above. Then, there exists a constant \(C>0\) so that for all \(N \ge 2\) and \(d = N^2\), we have
Proof
In this proof, we denote by C positive constants which may change from line to line. In light of (33), we need to estimate the expression
To estimate (I), we make the following partition of the set \( [0,N-1]^2 \cap \mathbb {Z}^2\):
On \(A_0\), the values of G(m / N, n / N) are constant, so
On \(A_2\), we use the fact that the function G is \(C^\infty \) on \(\mathbb {R}^2 \backslash \mathbb {Z}^2\), and moreover, that on the set \(\{(x,y)\in [0,1]^2:y\ge x\vee x\ge 1/8\}\) both G, and its derivatives, are continuous. Indeed, this means that we are justified in using the Mean Value theorem for \((m,n) \in A_2\) to make the estimate
where \(\mu _{m,n} \in (m/N,(m+1)/N)\) and \(C = C(G) > 0\) is a constant not depending on N. It follows immediately that
On \(A_1\), we do the computation
where \(\mu _{m,n} \in (m/N,(m+1)/N)\) as before. To estimate \((*)\), we compute
This allows the bound
To estimate (II), we consider the corresponding sums over \(A_2\) and over \(B = A_0\cup A_1\). We skip the estimates for \(A_2\), which are completely analogous to the corresponding estimates made above. Instead, we turn our focus to the estimate for B. As above, we begin by using the Mean Value Theorem to write
where \(\nu _{m,n}\in [n/N,(n+1)/N]\). To estimate \((**)\), we compute
This allows the estimate
\(\square \)
Remark 4.6
To determine a bound for the constant C of inequality (34), observe that we can actually choose \(\phi \) to be piecewise linear, and therefore to satisfy \(\Vert \phi '\Vert _\infty ^2 \le 1\). Moreover, observe that
where \(C_0\) is some positive constant. Since the remaining sums over \(A_2\) only contribute to \(C_0\), we conclude that asymptotically,
5 A quantitative Balian–Low type theorem in finite dimensions
In this section, we prove a finite dimensional version of the quantitative Balian–Low inequality. For the most part, we follow the main ideas appearing in our paper [24].
5.1 Auxiliary results
The estimate in the following lemma is not optimal, but rather, chosen to simplify the presentation. We leave the proof, which is straight-forward, to the reader.
Lemma 5.1
Let \(\rho : \mathbb {R}\rightarrow \mathbb {R}\) be the inverse Fourier transform of
Then
Lemma 5.2
Let \(A, B>0\) and \(N\ge {350} \sqrt{B/A}\). There exist positive constants \(\delta =\delta (A)\) and \(C=C(A,B)\) such that the following holds (with \(d=N^2\)). Let
-
(i)
\(Q, R \in \mathbb {Z}\) such that \(1\le Q,R \le (N/{30}) \cdot \sqrt{A/B}\),
-
(ii)
\(\phi ,\psi \in \ell _2^d\) such that \(\sum _n|\Delta \phi (n)|\le 10 R\) and \(\sum _n|\Delta \psi (n)|\le 10 Q\),
-
(iii)
\(b\in \ell _2^d\) such that \(A \le |Z_d (b)|^2 \le B\).
Then, there exists a set \(S\subset ([0,N-1]\cap \mathbb {Z})^2\) of size \(|S|\ge C N^2/ QR\) such that all \((u,v)\in S\) satisfy either
Proof of Lemma 5.2
For the given A and for \(N_0={350}\), let \(\delta _1 = 2\sqrt{A}\sin (\pi /8-\pi /{350})\) be the constant from Corollary 3.5. Notice that the integers Q, R and N satisfy
Therefore, there exist integers K and L that satisfy
We choose K, L to be the smallest such integers.
For \(s,t \in \mathbb {Z}\), let \(\sigma _s\) and \(\omega _t\) be as defined in (21), that is,
Note that \(\sigma _K=\omega _L=N\) and denote \(\Sigma = \inf \{\Delta _{(s)}\sigma _s\}\) and \(\Omega = \inf \{\Delta _{(t)}\omega _t\}\). The conditions on K and L imply that, for some constant \(C_1=C_1(A,B)\),
For \((u,v)\in ([0,\Sigma -1]\cap \mathbb {Z})\times ([0,\Omega -1]\cap \mathbb {Z})\), write
and
Note that if \((u_1,v_1)\ne (u_2,v_2)\) then it follows from the definition of \(\Sigma \) and \(\Omega \) that \(\mathrm {Lat}(u_1,v_1) \cap \mathrm {Lat}(u_2,v_2) = \emptyset \) and \(\mathrm {Lat^*}(u_1,v_1) \cap \mathrm {Lat^*}(u_2,v_2) = \emptyset \). We will show that for each (u, v), either the set \(\mathrm {Lat}(u,v)\) or the set \(\mathrm {Lat^*}(u,v)\) contains a point from \(([0,N-1]\cap \mathbb {Z})^2\) which satisfies condition (35) or (36), respectively. Putting \(C=C_1/2\) our proof will then be complete.
So, fix \((u,v)\in ([0,\Sigma -1]\cap \mathbb {Z})\times ([0,\Omega -1]\cap \mathbb {Z})\). Due to Corollary 3.5, there exists at least one point \((s,t)\in ([0,K-1]\cap \mathbb {Z})\times ([0,L-1]\cap \mathbb {Z})\) such that (24) or (25) hold with \(W= Z_d(b)\).
Assume first that (24) holds. Lemma 2.6, the estimate \(|\Delta _{(s)}\sigma _s|\le 2N/K\), and condition (37), imply that
It follows that either \((u+\sigma _s,v+\omega _t)\) or \((u+\sigma _{(s+1)},v+\omega _t)\) satisfy (35) with \(\delta =\delta _1/20\). It may happen that this chosen point does not belong to \(([0,N-1]\cap \mathbb {Z})^2\), that is, it is of the form \((u+N,v+\omega _t)\). In that case, due to the N-quasi-periodicity of the Zak transform, the point \((u,v+\omega _t)\) satisfies the same inequality, and is in \(([0,N-1]\cap \mathbb {Z})^2\).
Assume now that (25) holds for (u, v) and (s, t). Then (13), the N-quasi-periodicity of \(Z_d(b)\), and the estimate \(|\Delta _{(t)}\omega _t|\le {2N/L}\), imply that
On the other hand, as in the previous case, we have
It follows that either \((N-v-\omega _t,u+\sigma _s)\) or \((N-v-\omega _{(t+1)},u+\sigma _s)\) satisfy (36) with \(\delta =\delta _1/40\). It may happen that this chosen point is the point \((-v,u+\sigma _s)\). In that case, due to the N-quasi-periodicity of the Zak transform, the point \((N-v,u+\sigma _s)\) satisfies the same inequality, and is in \(([0,N-1]\cap \mathbb {Z})^2\). \(\square \)
5.2 A proof for Theorem 1.5
We are now ready to prove Theorem 1.5. In fact, we prove the more general version referred to in Remark 1.6 which we formulate as follows:
Theorem 5.3
Let \(A,B>0\). There exists a constant \(C=C(A,B)>0\) so that the following holds. Let \(N \ge {350} \sqrt{B/A}\) and let \(b \in \ell _2^d\) (where \(d=N^2\)) be such that \(G_d(b)\) is a basis in \(\ell _2^d\) with Riesz basis bounds A and B. Then, for all positive integers \(1 \le Q, R \le ( N/{30})\cdot \sqrt{A/B}\), we have
Proof of Theorem 1.5
Let \(\rho : \mathbb {R}\rightarrow {\mathbb {R}}\) be as in Lemma 5.1 and put \(\Phi (t) = R \rho (Rt)\) and \(\Psi (t) = Q \rho ( Qt)\). Denote \(\phi = S_N P_N \Phi \) and \(\psi = S_N P_N \Psi \). By Lemma 2.10, in combination with Lemma 5.1, it follows that \(\sum _n|\Delta \phi (n)|\le {10} R\) and \(\sum _n|\Delta \psi (n)|\le {10} Q\). As a consequence, the integers Q, R and N, as well as the functions \(\phi ,\psi \) and b, all satisfy the requirements of Lemma 5.2.
As \(Q,R < N/2\), by Proposition 2.8, and Remark 2.9(i), we have \(0\le {\mathcal {F}}_d\phi , {\mathcal {F}}_d\psi \le 1\) over \(\ell _2^d\). Moreover, we also have \({\mathcal {F}}_d\phi (j)=1\) for \(j\in [0, RN/2] \cup [N^2- RN/2+1,N^2]\) and \({\mathcal {F}}_d\psi (j)=1\) for \(j\in [0, QN/2] \cup [N^2- QN/2+1,N^2]\). It therefore follows from Lemma 5.2, and the fact that both the finite Zak transform and the finite Fourier transform are unitary, that, for some constant \(C>0\),
The result now follows by applying a suitable time-frequency translate to the sequence b. \(\square \)
6 Applications to the continuous setting
In this section we show that both the classical and quantitative Balian–Low theorems follow from their finite dimensional analogs.
6.1 Relating continuous and finite signals – revisited
We start by extending Proposition 2.8 to the space \(L^2(\mathbb {R})\). We do this in four steps. In the first, we introduce some additional notations. To this end, fix \(N\in \mathbb {N}\), \(N\ge 2\), and let \(d=N^2\).
Step I: By \((L^2[0,1/N]^2)^d\), we denote the space of all d-tuples \(\{ \phi (j)\}_{j=0}^{d-1}\) with function entries \(\phi (j) \in L^2([0, {1}/{N}]^2)\), equipped with the norm given by
Note that the factor N appears in the norm in order to take the measure of [0, 1 / N] into account. Similarly, by \((L^2[0,1/N]^2)^{N\times N}\), we denote the space of all \(N\times N\) matrices \(\{ \phi (j,k)\}_{j,k=0}^{N-1}\) with function entries \(\phi (j,k) \in L^2([0, {1}/{N}]^2)\), equipped with norm given by
(The reader should note the different in normalisations used in (38) and (39).)
Step II: We consider functions h(u, v; t) defined over \([0, {1}/{N}]^2\times \mathbb {R}\), that are N-periodic with respect to the variable t, and are such that, for every fixed \(t_0\), the restriction \(h(u,v;t_0)\) is well defined almost everywhere and belongs to \(L^2([0,1/N]^2)\). Observe that the operator
trivially satisfies
Above, we understand the notations \({\mathcal {F}}_d S_N h\) and \(Z_d S_N h\) to mean that \({\mathcal {F}}_d\) and \(Z_d\) operate on \(S_Nh\) with respect to the variable j with (u, v) being considered fixed.
Step III: Let \(f\in L^2(\mathbb {R})\). For \((u,v)\in [0, {1}/{N}]^2\), we define the function
and formally put
Note that if f is in the Schwarz class \({\mathcal {S}}(\mathbb {R})\), then the function \(h(u,v;t):=P_N {f}_{(u,v)}(t)\) satisfies the conditions on h(u, v; t) described in Step II. The following lemma shows that this is true for all \(f\in L^2(\mathbb {R})\).
Lemma 6.1
For \(f\in L^2(\mathbb {R})\), let \(f_{(u,v)} (t)\) be the function defined above. Then, for every fixed \(t_0 \in \mathbb {R}\), we have
That is, the series defining \(P_N f_{(u,v)}(t_0)\) converges in the norm of \(L^2([0,1/N]^2)\).
Proof
Use the fact that \(\{\sqrt{N}\mathrm {e}^{2\pi \mathrm {i}N\ell v}\}_{\ell \in \mathbb {Z}}\) is an orthonormal basis over [0, 1 / N]. \(\square \)
It follows that, for \(f\in L^2(\mathbb {R})\), the operator \(S_NP_Nf_{(u,v)}\) is well defined and that conditions (40), (41), (42) hold with \(h (u,v;t)=P_Nf_{(u,v)}(t)\).
Step IV: For f in \(L^2(\mathbb {R})\), we understand the notations \({\mathcal {F}} f_{(u,v)}(t)\) and \(Z f_{(u,v)}(t)\) to mean that the Fourier transform and the Zak transform are taken with respect to the variable t, with (u, v) being fixed. Since \({\mathcal {S}}(\mathbb {R})\) is dense in \(L^2(\mathbb {R})\), we obtain the following extension of Proposition 2.8.
Proposition 6.2
Let \(f\in L^2(\mathbb {R})\). Then, the following hold.
-
(i)
For all \(N\in \mathbb {N}\) and \((m,n)\in \mathbb {Z}^2\), we have
$$\begin{aligned} Z_{d} (S_N {P_N f_{(u,v)}})(m,n) = Zf_{(u,v)}(m/N, n/N), \end{aligned}$$(43)where the equality holds in the sense of \({L^2([0,{1}/{N}]^2)}\).
-
(ii)
For all \(N\in \mathbb {N}\), we have
$$\begin{aligned} {\mathcal {F}}_{d}S_N P_N {f_{(u,v)}} = S_N P_N {\mathcal {F}} f_{(u,v)}, \end{aligned}$$(44)where the equality holds in the sense of \((L^2[0,{1}/{N}]^2)^d\).
Proof
First, Proposition 2.8 implies that (43) and (44) hold for \(f \in {\mathcal {S}}(\mathbb {R})\) pointwise everywhere. Since \({\mathcal {S}}(\mathbb {R})\) is dense in \(L^2(\mathbb {R})\), it is enough to show that the four operators implicitly defined by the left and right-hand sides of (43) and (44) are isometric (in fact, they are unitary). This easily follows by using the fact that \(\{\sqrt{N}\mathrm {e}^{2\pi \mathrm {i}N\ell v}\}_{\ell \in \mathbb {Z}}\) is an orthonormal basis over [0, 1 / N]. \(\square \)
In light of Proposition 2.7, we get the following from part (i) of Proposition
Corollary 6.3
Let \(g\in L^2(\mathbb {R})\) be such that the Gabor system G(g) is a Riesz basis in \(L^2(\mathbb {R})\) with lower and upper Riesz basis bounds A and B, respectively. Then, for almost every \((u,v)\in [0,{1}/{N}]^2\), the Gabor system \(G_d(S_NP_N g_{(u,v)})\) is a Riesz basis in \(\ell _2^d\) with lower and upper Riesz basis bounds \({{\widetilde{A}}}\) and \({{\widetilde{B}}}\) satisfying \(A \le {{\widetilde{A}}}\) and \(\widetilde{B} \le B\), respectively.
6.2 The classical Balian–Low theorem
We start with the following lemma which relates the discrete and continuous derivatives of \(L^2(\mathbb {R})\) functions.
Lemma 6.4
Let \(f\in L^2(\mathbb {R})\) and \(N\in \mathbb {N}\). Denote \(F_{(u,v)}=S_NP_Nf_{(u,v)}\). Then,
where the integral on the right-hand side is understood to be infinite if f is not absolutely continuous, or if its derivative is not in \(L^2(\mathbb {R})\).
Proof
Put \(a_u(j,l)=f(u+\frac{j}{N}+ \ell N)\) and fix \(j\in [0,N^2-1] \cap \mathbb {Z}\). Since \(f\in L^2(\mathbb {R})\), we have, with respect to the variable \(\ell \), that \(a_u(j,\ell ) \in \ell _2(\mathbb {Z})\) for almost every u. We compute
where we applied the inequalities \(|a+b|^2\le 2|a|^2+2|b|^2\) and \(|e^{ix}-1|\le |x|\). By the Cauchy-Schwartz inequality, we get
Combining these two estimates, the result follows. \(\square \)
We are now ready to show that the classical Balian–Low theorem (Theorem A) follows from our finite Balian–Low theorem (Theorem 1.1).
Proof of the Classical Balian–Low Theorem
Let \(g\in L^2(\mathbb {R})\) be such that the Gabor system G(g) is a Riesz basis with lower and upper Riesz basis bounds A and B, respectively. For all integers \(N\ge 2\), \(d = N^2\), and \(u,v\in [0,1/N]^2\), we consider the finite dimensional signal \(S_NP_N g_{(u,v)}\). By Corollary 6.3, for almost every \(u,v\in [0,1/N]^2\), this is a basis in \(\ell _2^{d}\) with Riesz basis bounds \({{\widetilde{A}}}\), \({{\widetilde{B}}}\) satisfying \(A \le {{\widetilde{A}}}\) and \({{\widetilde{B}}} \le B\). By Theorem 1.1, (see also Remark 1.2) we have
Integrating both parts with respect to (u, v) over the set \([0, {1}/{N}]^2\), and applying Proposition 6.2 (ii), we get
By Lemma 6.4, we obtain
Finally, letting N tend to infinity, the result follows. \(\square \)
6.3 A quantiative Balian–Low theorem
Discrete and continuous tail estimates are related by the following lemma.
Lemma 6.5
Let \(f\in L^2(\mathbb {R})\) and \(Q,N\in \mathbb {N}\) be such that \(Q\le N\). Denote \(F_{(u,v)}=S_NP_Nf_{(u,v)}\). Then,
Proof
This follows by using the fact that \(\{\sqrt{N}\mathrm {e}^{2\pi \mathrm {i}N\ell v}\}_{\ell \in \mathbb {Z}}\) is an orthonormal basis over [0, 1 / N]. \(\square \)
We are now ready to show that the Quantitative Balian–Low theorem (Theorem B) follows from Theorem 1.5 (or rather, the more general Theorem 5.3).
Proof of the Quantitative Balian–Low Theorem
Let \(g\in L^2(\mathbb {R})\) be such that G(g) is a Riesz basis with lower and upper Riesz basis bounds A and B, respectively, and let Q, R be positive integers. Let \(N\ge {200} \max \{Q,R\}\cdot \sqrt{B/A}\) and set \(d = N^2\). For fixed \(u,v\in \mathbb {R}\), consider the finite dimensional signal \(S_NP_Ng_{(u,v)}\). By Corollary 6.3, for almost every \(u,v\in [0,1/N]^2\), this is a basis in \(\ell _2^{d}\) with Riesz basis bounds \(\widetilde{A}\), \({{\widetilde{B}}}\) satisfying \(A \le {{\widetilde{A}}}\) and \(\widetilde{B} \le B\). By Theorem 5.3 we have
Integrating both terms with respect to (u, v) over the set \([0,{1}/{N}]^2\), and applying Proposition 6.2 (ii), we get
By Lemma 6.5 we obtain,
The result now follows by applying an appropriate translation and modulation to g (note that a translations and modulations of g preserve the Riesz basis properties of G(g)). \(\square \)
7 Balian–Low theorems for Gabor systems over rectangles
In this section, we turn to theorems 1.8 and 1.9. As the proofs are very similar to those of theorems 1.1 and 1.5, respectively, we only provide an outline of the main ideas, and leave it to the reader to fill in the details.
7.1 The finite Zak transforms over rectangles.
Throughout this section, we let \(M,N \in \mathbb {N}\) and denote \(d=MN\). With the normalization
it is readily checked that the Fourier transform is a unitary operator from \(\ell _2^{(M,N)}\) to \(\ell _2^{(N,M)}\) (for the definition av this space, recall (8)).
We use the periodic convolution, defined for \(a,b \in \ell _2^{(M,N)}\), by
This yields the convolution relation \({\mathcal {F}}_{(M,N)}(a *b) = {\mathcal {F}}_{(M,N)} a \cdot {\mathcal {F}}_{(M,N)}b\).
We will also make use of the space \(\ell _2([0,M-1]\times [0,N-1])\), with the normalization
The finite Zak transform for \(a\in \ell _2^{(M,N)}\) is given by
Note that with this definition, \(Z_{(M,N)} (a)\) is well-defined as a function on \(\mathbb {Z}_d^2\) (that is, it is d-periodic separately in each variable).
The basic properties of \(Z_{(M,N)}\) are stated in the following two results (compare with Lemma 2.2 and part (ii) of Proposition 2.7).
Lemma 7.1
Let \(M,N\in \mathbb {N}\) and \(d=MN\). For \(a \in \ell _2^{(M,N)}\), the following hold.
-
(i)
The function \(Z_{(M,N)}(a)\) is (M, N)-quasi-periodic on \(\mathbb {Z}_d^2\) in the sense that
$$\begin{aligned} \begin{aligned} Z_{(M,N)}(a)(m + M,n)&= \mathrm {e}^{2\pi \mathrm {i}\frac{n}{N}}Z_{(M,N)}(a)(m,n), \\ Z_{(M,N)}(a)(m,n+N)&= Z_{(M,N)} (a)(m,n). \end{aligned} \end{aligned}$$(45)In particular, the finite Zak transform is determined by its values on the set \(\mathbb {Z}^2 \cap ([0,M-1]\times [0,N-1])\).
-
(ii)
The transform \(Z_{(M,N)}\) is a unitary operator from \(\ell _2^{(M,N)}\) onto \(\ell _2([0,M-1]\times [0,N-1])\).
-
(iii)
The finite Zak transform and the finite Fourier transform satisfy the relation
$$\begin{aligned} Z_{(N,M)} ({\mathcal {F}}_{(M,N)}a)(n,m) = \, \mathrm {e}^{2\pi \mathrm {i}\frac{mn}{d}} Z_{(M,N)}(a) (-m,n). \end{aligned}$$(46)
Proposition 7.2
Let \(M,N\in \mathbb {N}\) and \(b\in \ell _2^{(M,N)}\). Then the Gabor system \(G_{(M,N)}(b)\), defined in (9), is a basis in \(\ell _2^{(M,N)}\) with Riesz basis bounds A and B, if and only if \(A\le |Z_{(M,N)}(b)(m,n)|^2\le B\) for all \((m,n) \in \mathbb {Z}^2\cap ([0,M-1]\times [0,N-1])\).
7.2 Regularity of the finite Zak transforms over rectangles
Lemma 3.1 is already formulated in a rectangular version. One can obtain a similar analog of Lemma 3.4 with the notations
for integers \(K \in [2,M]\) and \(L \in [2,N]\). Note that, similar to the square case, we have \(\sigma _K=M\) and \(\omega _L=N\). With this we get the following extension of Corollary 3.5.
Corollary 7.3
Fix an integer \(N_0 \ge {9}\) and a constant \(A>0\). Let
For any integers \(M,N \ge N_0\), \(K\in [2,M]\), and \(L\in [2,N]\), the following holds (with \(d=MN\)). Let W be an (M, N)-quasi periodic function over the lattice \(\mathbb {Z}_d^2\) satisfying \(A \le |W(m,n)|^2\), for all \((m,n)\in \mathbb {Z}^2_d\). Then, for every \((u, v) \in \mathbb {Z}_d^2\) there exists at least one point \((s,t)\in ([0,K-1] \times [0,L-1]) \cap \mathbb {Z}^2\) such that
where \(\sigma _s, \omega _t\) are defined in (47).
7.3 A Balian–Low type theorem in finite dimensions over rectangles
For \(b\in \ell ^{(M,N)}_2\), denote
and
Given \(A,B>0\) set
where both infimums are taken over all \(b\in \ell ^{(M,N)}_2\) for which the system \(G_{(M,N)}(b)\) is a basis with lower and upper Riesz basis bounds A and B, respectively. The analog of Proposition 4.1 for the rectangular case gives the inequalities
Theorem 1.8 is a consequence of the following result, which is analogue to Theorem 4.2.
Theorem 7.4
There exist constants \(c,C>0\) so that, for all integers \(M,N \ge 2\), we have
Proof
In what follows we let c, C denote different constants which may change from line to line. Let \(b\in \ell ^{(M,N)}_2\) be so that \(G_{(M,N)}(b)\) is a basis with Riesz basis bounds A and B, and put \(W = Z_{(M,N)}(b)\). To obtain the lower inequality, we first consider the case \(M>N\). Put \(\sigma _s = [s M/N]\), and consider square product sets
Note that similar to (30), it holds that
This implies that, for integers \(0 \le k < [M/N]\), the \(N\times N\) squares \(\mathrm {Lat_k}\) are disjoint as subsets of the \(M \times N\) rectangle \(([0,M-1] \times [0,N-1])\cap \mathbb {Z}^2\). Since, when restricted to each of the square sets \(\{ ( k + \sigma _s, t) : s,t {\in [0,N]\cap Z} \},\) the function W is N–quasi–periodic, it follows by Theorem 4.2 that
By (52), and the Cauchy–Schwarz inequality, we have
where the last step of the above computation follows from the fact that the summands are M-periodic. Plugging this into (53) we get,
Since each of the [M / N ] sets \(\mathrm {Lat}_k\) are disjoint, we may sum up these inequalities to obtain
Dividing by [M / N] on both sides, and using the inequalities \(x/2 \le [x] \le x\) valid for \(x \ge 1\), it follows that
By repeating the same type of argument for the case \(M<N\), the estimate from below in (53) follows.
To obtain the upper inequality in (53), we consider the same function G(x, y) that was used in the proof for Theorem 1.1, and split into two cases as above.
We begin with the case \(M>N\), where it suffices to go through essentially the same computations as in the proof of Proposition 4.5, this time considering a vector \(b \in \ell _2^{(M,N)}\) so that \(Z_{(M,N)}(b)(m,n) = G(m/M,n/N)\), where G is the same function used in square case. With this, we obtain the inequality
for some constant \(C>0\).
We turn to the case \(M<N\). Swapping the roles of m, M and n, N, respectively, it follows that the vector \(b\in \ell _2^{(N,M)}\) which satisfies \(Z_{(N,M)}b(n,m)=G(n/N,m/M)\) is the same as in the above case, whence \(\beta (b,N,M) \le C \log M\). Now, since \(\alpha (b,N,M)=\alpha ({\mathcal {F}}_{(N,M)}b,M,N)\), the relation (50) implies that
In combination, the inequalities (55) and (56) yield the desired upper bound for \(\beta (M,N)\). \(\square \)
Remark 7.5
The quantitative Balian–Low theorem in finite dimensions over finite rectangular lattices (Theorem 1.9) may be proved as in the square case, with the only modification being putting \(\phi = S_{M} P_{N} \Phi \) and \(\psi = S_{N} P_{M} \Psi \).
Notes
For more on other uncertainty principles in the finite dimensional setting, we refer the reader to [15] and the references therein.
References
Auslander, L., Gertner, I., Tolimieri, R.: The discrete Zak transform application to time-frequency analysis and synthesis of nonstationary signals. IEEE Trans. Signal Process. 39, 825–835 (1991)
Auslander, L., Gertner, I., Tolimieri, R.: The Finite Zak Transform and the Finite Fourier Transform. Radar and sonar, Part II, IMA Vol. Math. Appl., vol. 39, pp. 21–35. Springer, New York (1992)
Balian, R.: Un principe d’incertitude fort en théorie du signal ou en mécanique quantique. C. R. Acad. Sci. Paris Sér. II Méc. Phys. Chim. Sci. Unive. Sci. Terre 292(20), 1357–1362 (1981)
Battle, G.: Heisenberg proof of the Balian–Low theorem. Lett. Math. Phys. 15(2), 175–177 (1988)
Benedetto, J.J., Czaja, W., Gadziński, P., Powell, A.M.: The Balian–Low theorem and regularity of Gabor systems. J. Geom. Anal. 13(2), 239–254 (2003)
Benedetto, J.J., Czaja, W., Powell, A.M., Sterbenz, J.: An endpoint \((1,\infty )\) Balian–Low theorem. Math. Res. Lett. 13(2–3), 467–474 (2006)
Benedetto, J.J., Heil, C., Walnut, D.F.: Differentiation and the Balian–Low theorem. J. Fourier Anal. Appl. 1(4), 355–402 (1995)
Bourgain, J.: A remark on the uncertainty principle for hilbertian basis. J. Funct. Anal. 79(1), 136–143 (1988)
Daubechies, I.: The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inform. Theory 36(5), 961–1005 (1990)
Daubechies, I., Janssen, J.E.M.: Two theorems on lattice expansions. IEEE Trans. Inform. Theory 39(1), 3–6 (1993)
Folland, G.B.: Harmonic Analysis in Phase Space. Princeton University Press, Princeton (1989)
Gautam, S.Z.: A critical-exponent Balian–Low theorem. Math. Res. Lett. 15(3), 471–483 (2008)
Gröchenig, K.: An uncertainty principle related to the Poisson summation formula. Stud. Math. 121(1), 87–104 (1996)
Gröchenig, K.: Foundations of Time-Frequency Analysis. Applied and Numerical Harmonic Analysis. Birkhäuser Boston Inc., Boston, MA (2001)
Ghobber, S., Jaming, P.: On uncertainty principles in the finite dimensional setting. Linear Algebra Appl. 435(4), 751–768 (2011)
Gröchenig, K., Malinnikova, E.: Phase space localisation of Riesz bases for \(\ell ^2({\mathbf{R}}^d)\). Rev. Mat. Iberoam. 29(1), 115–134 (2013)
Heil, C., Powell, A.M.: Gabor Schauder bases and the Balian–Low theorem. J. Math. Phys. 47(11), 1–21 (2006)
Heil, C.E., Powell, A.M.: Regularity for complete and minimal Gabor systems on a lattice. Ill. J. Math. 53(4), 1077–1094 (2009)
Heil, C.E.: Wiener Amalgam Spaces in Generalized Harmonic Analysis and Wavelet Theory. ProQuest LLC, Ann Arbor, MI, Thesis (Ph.D.)–University of Maryland, College Park (1990)
Lammers, M., Stampe, S.: The finite Balian–Low conjecture. In: International Conference on Sampling Theory and Applications (SampTA), pp. 139–143 (2015)
Low, F.E.: Complete sets of wave packets. In: DeTar, C., et al. (eds.) A Passion for Physics: Essays in Honor of Geoffrey Chew, pp. 17–22. World Scientific, Singapore (1985)
Nazarov, F.L.: Local estimates for exponential polynomials and their applications to inequalities of the uncertainty principle type. Algebra i Analiz 5(4), 3–66 (1993)
Nitzan, S., Olsen, J.-F.: From exact systems to Riesz bases in the Balian–Low theorem. J. Fourier Anal. Appl. 17(4), 567–603 (2011)
Nitzan, S., Olsen, J.-F.: A quantitative Balian–Low theorem. J. Fourier Anal. Appl. 19(5), 1078–1092 (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Loukas Grafakos.
The first author is supported by NSF Grant DMS-1600726. The second author is partially supported by KVA Grant MG2016-0023.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.