Income inequality and price elasticity of market demand: the case of crossing Lorenz curves

Abstract

This paper extends Ibragimov and Ibragimov (Econ Theory 32:579–587, 2007) in which the effect of changes income inequality on the price elasticity of market demand is characterized for the class of income distribution changes occurring through non-intersecting Lorenz curve shifts. We derive sufficient conditions for increase/decrease in price elasticity of market demand, under general changes in income distribution, allowing Lorenz curves to intersect as they shift. We conclude by drawing out implications of different types of tax policy changes for demand elasticity.

1 Introduction

The relationship between income distribution and economic outcomes such as growth and welfare has been an important area in economic research (see, among others, the discussion in Piketty and Saez 2003; Milanovic 2005, 2011; Atkinson et al. 2011). In this paper, we contribute to an important strand in this literature: on the effects of income distribution and inequality on market demand (see the discussion in Ibragimov and Ibragimov 2007, and references therein). Specifically, we address how changes in the income distribution affect the price elasticity of market demand.

The volume and growth of market demand are important concerns for national governments, particularly so in the current global economic environment. In recent years many governments, facing the need to balance demand growth with fiscal sustainability, have modified their taxation and expenditure programmes. From the policy point of view, it is useful to understand how changes in direct tax schedules work through income distribution and affect market demand elasticity. We address this issue in this paper.

Formal analysis of income and wealth inequality relies on the concepts of Lorenz dominance and majorization (Marshall et al. 2011). These ordering relations enable comparison of disparity among components of vectors (e.g., incomes in a population). Over the past several years, a number of works in the literature have extended the theory and applications for these ordering relations, and (Schur-convex) functions that preserve them (see discussion in Ibragimov et al. 2015; Ibragimov and Prokhorov 2017).

Ibragimov and Ibragimov (2007) consider the market demand function for a good, aggregated from individual demand functions with price and income as arguments. Under the assumption of common preferences, they characterize the changes in price elasticity of market demand following from changes in income distribution. For the limited class of changes in income distribution where increases and decreases in income inequality occur through non-intersecting Lorenz curve shifts, they show how the increase or decrease in the price elasticity of market demand depends on the Schur-convexity/Schur-concavity of the market demand function and convexity/concavity properties of the individual demand functions.

Changes in income distribution where Lorenz curves intersect are far more common than changes in income distribution that take the form of non-intersecting Lorenz curve shifts. One general example is polarization of incomes. Another is the change in the distribution of after-tax income, after changes in tax schedules. For example, when a graduated-rate progressive income tax is replaced by a flat tax, with increased personal exemptions, the new Lorenz curve for after-tax income will intersect the old one. Thus, it is useful to extend the results in Ibragimov and Ibragimov (2007) to income distribution changes where Lorenz curves intersect. We establish sufficient conditions under which price elasticity of market demand increases or decreases under general changes in income distribution, allowing Lorenz curves to intersect as they shift. Our analysis ties in the implications of the type of tax policy changes mentioned above.

The paper is organized as follows: Sect. 2 sets out the concepts and definitions. In Sect. 3, we extend the Ibragimov and Ibragimov (2007) results, determining sufficient conditions under which market demand elasticity for a consumption good increases or decreases with income distribution changes where Lorenz curves intersect. In Sect. 4, the results in Sect. 3 are applied to distributional consequences of direct tax policy. Section 5 concludes. “Appendix 1” summarizes several concepts related to the analysis in the paper. “Appendix 2” contains the proofs of the main results obtained. Section 3 and “Appendix 3” further illustrate implications of the main results in the paper using several commonly used demand functions, such as the Almost Ideal Demand System and demands for necessities, non-necessities and luxury goods.

2 Concepts

Consider a population consisting of K individuals, whose incomes $x_i,$ $i=1,\ldots , K,$ lie in the interval $[0,{\hat{x}}], \; {\hat{x}} < \infty$. Let the K-vector $\mathbf{x } = \left( x_1, \ldots , x_K\right)$ represent the distribution of the total income $T=\sum _{i=1}^K x_i$ in the population. Without loss of generality, we also employ $\mathbf{x }$ to denote its rearrangement in the ascending order: $\left( x_{(1)} \le \cdots \le x_{(K)}\right)$.

Reframing the above set-up in terms of random variables allows us to bring the Lorenz dominance relation into the analysis. Let X be a random variable (r.v.) with a uniform distribution on the set $\{x_1,\ldots , x_K\}:$ $P(X=x_i)=1/K,$ $i=1,\ldots , K.$ Further, let $F_X(x),$ $x\in \mathfrak {R},$ denote the cumulative distribution function (cdf) of X,  and let $\text {F}_{\text {X}}^{-1}(t),$ $t\in (0, 1),$ stand for the corresponding quantile function, that is, $\text {F}_{\text {X}}^{-1}(t)$ is the right continuous inverse distribution function corresponding to $\text {F}_{\text {X}}:$ $\text {F}_{\text {X}}^{-1}(t)=\sup \{x: F(x)\le t\},$ for $0\le t<1,$ and $\text {F}_{\text {X}}^{-1}(1)=\sup \{x: F(x)< 1\},$ for $t=1.$ On this basis, the mean $\mu _{X}$ of X (the average income ${\overline{x}}=(1/K)\sum _{i=1}^K x_i$) is equal to $\mu _{X}=\int _\mathbf{0 }^{1} \text {F}_{\text {X}}^{-1}(t)\hbox {d}t.$

Definition 2.1

(Lorenz 1905; Gastwirth 1971; Marshall et al. 2011) The Lorenz curve $L_{X}(u),$ $u\in [0, 1]$ corresponding to the income distribution $\mathbf{x } = \left( x_1, \ldots , x_n\right)$ (the r.v. X) is defined by¹

$$\begin{aligned} L_{X}(u)=\frac{1}{\mu _{X}}\int _\mathbf{0 }^{u} \text {F}_{\text {X}}^{-1}(t)\hbox {d}t\ \quad \hbox {for} \ 0\le u \le 1. \end{aligned}$$

For the (non-random) income distribution vector $\mathbf{x }$, $L_X(u)$ is the proportion of the total income $\sum _{i=1}^K x_i$ that accrues to the uth fraction of K, cumulated from the lowest end of income with the population ordered by size of income. The Lorenz curve corresponding to $\mathbf{x }$ is the continuous piece-wise linear function that interpolates the points $\left( i/K, \sum _{j=1}^i x_{(j)}/\sum _{j=1}^K x_{(j)}\right) ,\ i=1,2, \ldots , K$, starting with the point (0, 0). The Lorenz curve is the basis for the Lorenz dominance relation, which induces a partial order over income distributions based on the variability or disparity of incomes in the population.

The concept of majorization corresponds to the concept of Lorenz dominance with the difference that while Lorenz dominance relation can be defined as a stochastic relation that applies to random variables, the majorization relation relates to non-random vectors.

Definition 2.2

(Arnold 2007; Marshall et al. 2011) For $\mathbf{x } , \mathbf{y } \in \mathfrak {R}^K$,   $\mathbf {x}$ is said to be majorized by $\mathbf {y}$, ($\mathbf {y}$ majorizes $\mathbf {x}$; $\mathbf {x} \prec \mathbf {y}$),² if $\sum _{i=1}^k {x}_{(i)} \ge \sum _{i=1}^k {y}_{(i)}, \, k= 1, \ldots , K-1$ and $\sum _{i=1}^K {x}_{(i)} = \sum _{i=1}^K {y}_{(i)}$.

The Lorenz order for discrete random variables corresponds to the majorization order (Muirhead 1903; Hardy et al. 1934, 1952; Marshall et al. 2011) which applies to non-random vectors: both relations define the same partial order over the set of possible distributions of a total income, that is, over the set of distributions of the income r.v. X on $[0, {\hat{x}}]$ with the same mean, $\mu _X.$

All commonly used indices of variability, including inequality, concentration, risk, diversity are consistent with the partial order induced by Lorenz dominance/majorization. These indices belong to the family of Schur-convex functions.

Definition 2.3

(Schur 1923; Marshall et al. 2011) A function $\Phi (\mathbf{x }),$ $\mathbf{x }=\left( x_1, \ldots , x_K\right)$ $\in$ ${\mathcal {A}}\subseteq \mathfrak {R}^K$ is said to be Schur-convex on ${\mathcal {A}}$ if $\mathbf {x} ^1, \mathbf {x} ^2\in {\mathcal {A}},$ $\mathbf {x} ^1 \prec \mathbf {x} ^2$ implies that $\Phi (\mathbf {x} ^1) \le \Phi (\mathbf {x} ^2).$ For any interval $I \subseteq \mathfrak {R}$, a continuously differentiable function $\Phi (\mathbf{x }),$ $\mathbf{x }=\left( x_1, \ldots , x_K\right) ,$ is Schur-convex on $I^K$ if and only if it is symmetric (under permutations of arguments) in $(x_1, \ldots x_K)\in I^K$ and

$$\begin{aligned} \left( x_i - x_j\right) \left( \frac{\partial }{\partial x_i} \Phi \left( \mathbf {x} \right) - \frac{\partial }{\partial x_j} \Phi \left( \mathbf {x} \right) \right) \ge 0, \quad \forall \; \mathbf {x} \in I^K. \end{aligned}$$

It is useful to characterize the Schur-convexity of additive functions, e.g., the market demand function for a good that is aggregated from individual demand functions.

Theorem 2.1

(Marshall et al. 2011) For any interval $I \subseteq \mathfrak {R}$, if the function $\phi : I \rightarrow \mathfrak {R}$ is convex, then, for $\mathbf {x} =(x_1,\ldots ,x_K)$:

$$\begin{aligned} \Phi (\mathbf {x} )=\sum _{i=1}^K \phi (x_i) \end{aligned}$$

is Schur-convex on $I^K$. Consequently, $\mathbf {x} ^1, \mathbf {x} ^2\in I^K,$ $\mathbf {x} ^1 \prec \mathbf {x} ^2$ implies $\Phi (\mathbf {x} ^1) \le \Phi (\mathbf {x} ^2)$. Further, if $\phi : I \rightarrow \mathfrak {R}$ is continuous, then Schur-convexity of $\Phi (\mathbf {x} )=\sum _{i=1}^K \phi (x_i)$ on $I^K$ holds if and only if $\phi$ is convex on I.

Hardy et al. (1934) showed the equivalence of a number of ordering relations in the comparison of variability or inequality in any two distributions $\mathbf {x} ^1=(x^1_1,\ldots , x^1_K),$ $\mathbf {x} ^2=(x^2_1,\ldots , x^2_K)$ of the same total $T=\sum _{i=1}^K x^1_i=\sum _{i=1}^K x^2_i$. One such relation in their result (see below) is the Pigou–Dalton principle which states that an order preserving regressive transfer (from a poorer person to a richer person) increases inequality, and an order preserving progressive transfer (from a richer person to a poorer person) decreases inequality. Income transfers between persons are said to be order preserving if they leave the ordering of incomes unaltered.

Theorem 2.2

(Hardy et al. 1934; Marshall et al. 2011) Let $\mathbf {x} ^1=(x^1_1,\ldots , x^1_K), \mathbf {x} ^2=(x^2_1, \ldots , x^2_K) \in \mathfrak {R}^n,$ and let $\sum _{i=1}^K x^i_1=\sum _{i=1}^K x^i_2.$ Further let, as above, $X^1$ and $X^2$ denote r.v.’s with uniform distributions on the sets $\{x^1_1,\ldots , x^1_K\}$ and $\{x^2_1,\ldots , x^2_K\},$ respectively: $P(X^1=x^1_i)=P(X^2=x^2_i)=1/K,$ $i=1,\ldots , K.$ The following conditions are equivalent:

• (i) $\mathbf {x} ^1$ is majorized by $\mathbf {x} ^2:$ $\mathbf {x} ^1 \prec \mathbf {x} ^2$

• (ii) $\mathbf {x} ^1$ is Lorenz dominated by $\mathbf {x} ^2:$ $L_{X^1}(u) \ge L_{X^2}(u)$ for all $u \in (0,1)$

• (iii) $\mathbf {x} ^1$ can be obtained from $\mathbf {x} ^2$ by a non-empty finite sequence of order preserving progressive transfers.

• (iv) $\Phi (\mathbf {x} ^1) = \sum _{i =1}^K \phi (x_i^1) \le \Phi (\mathbf {x} ^2) = \sum _{i =1}^K \phi (x_i^2)$ for every continuous convex function $\phi : \mathfrak {R}\mapsto \mathfrak {R}$.

Any reasonable measure of variability, or inequality, must uphold the Pigou–Dalton principle, and equivalently, be consistent with the partial order induced by Lorenz dominance/majorization. Hence, they must be Schur-convex ($\Phi : [0, {\hat{x}}]^K \rightarrow \mathfrak {R}$ such that $\Phi (\mathbf {x} ^1)\le \Phi (\mathbf {x} ^2)$ for $\mathbf {x} ^1, \mathbf {x} ^2 \in [0, {\hat{x}}]^K$ if $\mathbf {x} ^1$ can be obtained from $\mathbf {x} ^2$ by a non-empty finite sequence of order preserving progressive transfers). In this case, there is less ‘variability’ in distribution $\mathbf{x }^1$ than in distribution $\mathbf{x }^2$, as measured by any Schur-convex function.

The Lorenz dominance / majorization order is partial in that the set of vectors with intersecting Lorenz curves cannot be ordered based on those relations. Our analysis is concerned with the price elasticity implications of general changes in income distribution, allowing Lorenz curves to cross as they shift. We now turn to this.

Income distributions with intersecting Lorenz curves

To proceed, it is useful to relate crossing Lorenz curves with crossing of cdf’s of income distributions (r.v.’s on $[0, {\hat{x}}]$). For any two distributions $\mathbf {x} ^1=(x^1_1,\ldots , x^1_K),$ $\mathbf {x} ^2=(x^2_1,\ldots , x^2_K)$ of the same total income $T=\sum _{i=1}^K x_i^1=\sum _{i=1}^K x_i^2,$ we denote by $X^1$ and $X^2$ the r.v.’s with uniform distributions on the sets $\{x^1_1,\ldots , x^1_K\}$ and $\{x^2_1,\ldots , x^2_K\},$ respectively: $P(X^1=x^1_i)=P(X^2=x^2_i)=1/K,$ $i=1,\ldots , K.$ Further, let $F_{X^1}(x)$ and $F_{X^2}(x)$ denote the cdf’s of the r.v.’s $X^1$ and $X^2,$ and $L_{X^1}(u)$ and $L_{X^2}(u)$ denote the Lorenz curves corresponding to the income distribution vectors $\mathbf {x} ^1$ and $\mathbf {x} ^2$ (the income r.v.’s $X^1$ and $X^2$). The following result on the relationship between the crossing of (continuous) Lorenz curves (Definition 2.1) and the crossing of integrals of cdf’s is useful:

Proposition 2.1

(Chiu 2007) For real vectors $\mathbf {x} ^1=(x^1_1,\ldots , x^1_K),$ $\mathbf {x} ^2=(x^2_1,\ldots , x^2_K)$ with $\sum _{i=1}^K x_i^1=\sum _{i=1}^K x_i^2$ $\big (\hbox {corresponding to r.v.'s} X^1,$ $X^2 \ \hbox {with the same mean}$: $\mu _{X^1}=\mu _{X^2}=(1/K)\sum _{i=1}^K x_i^1=(1/K)\sum _{i=1}^K x_i^2\; \big )$, $L_{X^1}(u)$ crosses $L_{X^2}(u)$ n times first from above if and only if $\int _0^x F_{X^2}(y)dy$ crosses $\int _0^x F_{X^1}(y)dy$ n times first from above.

It follows that if the integrals $\int _0^x F_{X^2}(y)dy$ and $\int _0^x F_{X^1}(y)dy$ do not cross, the corresponding Lorenz curves do not cross. This case where there is a Lorenz dominance relation between the two distributions was analyzed in Ibragimov and Ibragimov (2007).

Now consider the case of the integral $\int _0^x F_{X^2}(y)dy$ crossing $\int _0^x F_{X^1}(y)dy$ once from above. By the above proposition $L_{X^1}(u)$ crosses $L_{X^2}(u)$ once from above. The issue that comes into play when Lorenz curves cross, is the extent of “downside inequality” in one distribution relative to the other. The Lorenz criterion has been supplemented in the literature with the additional principle of “aversion to downside inequality” (Davies and Hoy 1995), equivalently, the principle of “transfer sensitivity” (Shorrocks and Foster 1987), accommodating the analysis of crossing Lorenz curves (see “Appendix A” for the definition of downside inequality and related concepts). The essential idea is that the transfer of any specific amount of income from a poorer to a richer person should be considered more disequalizing, the lower this transfer occurs in the distribution, other things being equal. The “weak” definition of transfer sensitivity requires that inequality reduction resulting from an order preserving progressive transfer of a fixed size between participants the same distance apart should be inversely related to the income of the donor (and recipient). (Weak) transfer sensitivity completes the ordering of intersecting Lorenz curves that cross only once.

Definition 2.4

(Shorrocks and Foster 1987) A Schur-convex function $\Phi$ exhibits transfer sensitivity (downside inequality aversion) if $\Phi (\mathbf {x} ^1) < \Phi (\mathbf {x} ^2)$ whenever the change of distribution from $\mathbf {x} ^1$ to $\mathbf {x} ^2$ (both real K-vectors with the same mean) is a downside inequality increase.

Menezes et al. (1980) and Shorrocks and Foster (1987) showed that additive Schur-convex functions of the type: $\Phi (\mathbf{x })=\sum _{i=1}^K \phi (x_i),$ where $\phi '>0$ and $\phi ''>0,$ are weakly transfer sensitive (equivalently, downside inequality averse) if and only if $\phi '''<0$.³

Shorrocks and Foster (1987) showed that all downside inequality averse, additive Schur-convex functions will agree on the ordering of Lorenz curves that intersect once, if the distribution that has Lorenz curve that crosses the other from above has a lower variance.⁴

Proposition 2.2

(Shorrocks and Foster 1987) Let $\mathbf {x} ^1=(x^1_1,\ldots , x^1_K), \mathbf {x} ^2=(x^2_1,\ldots , x^2_K)$ be real vectors with $\sum _{i=1}^K x^1_i=\sum _{i=1}^K x^2_i,$ and suppose that $L_{X^1}(u)$ crosses $L_{X^2}(u)$ once from above. Then the variance of the r.v. $X^1$ is not greater than the variance of the r.v. $X^2$ ($V(X^1) \le V(X^2)$) if and only if $\Phi (\mathbf {x} ^1)<\Phi (\mathbf {x} ^2)$ for any additive Schur-convex function $\Phi$ exhibiting transfer sensitivity.

For real vectors $\mathbf {x} ^1, \mathbf {x} ^2$ with the same mean income, the condition $\int _0^{{\hat{x}}}\int _0^t[F_{X^2}(y)-F_{X^1}(y)]\hbox {d}y\hbox {d}t \ge 0$ is the same as $V(X^1) \le V(X^2)$ (that is, the variance of the r.v. $X^1$ is not greater than that of the r.v. $X^2$). Based on Proposition 2.2 above, it is easy to compare transfer sensitivity when $V(X^1) \le V(X^2)$. But the result does not help in the case where the distribution with its Lorenz curve crossing that of the other from above has larger variance.

This gap in the ordering of distributions was filled by Chiu (2007), where the result has also been generalized from single-crossing Lorenz curves to multiple-crossing Lorenz curves. Based on Proposition 6.1 (“Appendix 1”), Chiu (2007) showed that relative ranking of two distributions by any additive Schur-convex function $\Phi (\mathbf{x })=\sum _{i=1}^K \phi (x_i)$ is determined by its degree of inequality aversion and its degree of transfer sensitivity (downside inequality aversion). In the special case of single-crossing Lorenz curves, the ratio $-\phi '''/\phi ''$ measures the strength of transfer sensitivity (downside inequality aversion) of the function $\phi$ against its inequality aversion, and determines the Schur-convex function’s ranking of $\mathbf{x }^1$ and $\mathbf{x }^2$.⁵

Proposition 2.3

(Chiu 2007) Suppose $\Phi$ and $\Psi$ are additive Schur-convex functions and, for $\mathbf {x} ^1=(x^1_1,\ldots , x^1_K),$ $\mathbf {x} ^2=(x^2_1, \ldots , x^2_K)$ with $\sum _{i=1}^K x^1_i=\sum _{i=1}^K x^2_i,$ the Lorenz curve $L_{X^1}(u)$ crosses the Lorenz curve $L_{X^2}(u)$ once from above and $V(X^1) > V(X^2)$. Then $(i)\;and\;(ii)$ are equivalent.

• (i) $\Phi (\mathbf {x} ^2) \ge \Phi (\mathbf {x} ^1)$ implies $\Psi (\mathbf {x} ^2) \ge \Psi (\mathbf {x} ^1)$

• (ii) $-\frac{\phi '''(x)}{\phi ''(x)} \le -\frac{\psi '''(x)}{\psi ''(x)}$ for all $x \in [0,{\hat{x}}]$

From the results in Chiu (2007) presented in this section and “Appendix 1”, it follows that the following holds in the case of single-crossing Lorenz curves, where $L_{X^1}(u)$ crosses $L_{X^2}(u)$ once from above and $\mathbf{x }^2$ can be obtained from $\mathbf{x }^1$ by a combination of a downside inequality increase and an inequality decrease due to a sequence of order preserving progressive transfers (called Pigou–Dalton inequality decrease). If $\mathbf{x }^2$ and $\mathbf{x }^1$ map to the same value of an additive Schur-convex function $\Phi$ (i.e., if $\Phi$ is a measure of inequality, $\mathbf{x }^2$ and $\mathbf{x }^1$ are judged “equally unequal”), then another additive Schur-convex function $\Psi$ with $-[\psi '''(x)]/[\psi ''(x)]$ uniformly larger than $-[\phi '''(x)]/[\phi ''(x)]$ will map $\mathbf{x }^2$ to a higher value (“more unequal”) than $\mathbf{x }^1$ (Chiu 2007). We apply these results to characterizing the changes in price elasticity of market demand when income distributions change.

3 Price elasticity of market demand and income distribution

Ibragimov and Ibragimov (2007) consider K consumers and M goods in a market. Let $\Phi _m({\mathcal {P}},\mathbf{x })= \sum _{i=1}^K \phi _{im}({\mathcal {P}}, x_i)$ denote the market demand function for good m, where $\phi _{im}({\mathcal {P}},x_i)$ is the demand function of the ith individual for the good, ${\mathcal {P}}=(p_1,\ldots ,p_M)$ is the vector of prices for the M goods in the economy, and $\mathbf{x }=(x_1,\ldots , x_K)$ is the vector of incomes of the consumers. As in Ibragimov and Ibragimov (2007), throughout the paper, we suppose that all consumers have the same preferences. Thus:

$$\begin{aligned} \phi _{1m}({\mathcal {P}}, x) =\phi _{2m}({\mathcal {P}}, x) = \cdots = \phi _{Km}({\mathcal {P}}, x) = \phi _{m}({\mathcal {P}}, x) \end{aligned}$$

Denote the cross-price elasticity of the aggregate demand on the m-th good with respect to the l-th good’s price by $e_{ml}=\partial \text {log} \Phi _m({\mathcal {P}},\mathbf{x })/\partial \text {log} p_l$. Denote the domain of the function $\phi _m({\mathcal {P}}, x)$ by $S_1 \in R^{M+1}$, and let $S_2 = \{({\mathcal {P}}, \mathbf{x }) = ({\mathcal {P}}, x_1,\ldots , x_K) \in \mathfrak {R}^{M+K} | ({\mathcal {P}}, x_i) \in S_1, \; i = 1,\ldots ,K\}$ be the domain of the function $\Phi _m({\mathcal {P}}, \mathbf{x })$.

Theorem 3.1

(Ibragimov and Ibragimov 2007) Let goods m and l be complements. Then:

• (i) If the functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ are convex with respect to x for $({\mathcal {P}}, x) \in S_1$, then the conditions $({\mathcal {P}},\mathbf {x} ^1),\; ({\mathcal {P}}, \mathbf {x} ^2) \in S_2$ and $\mathbf {x} ^1 \prec \mathbf {x} ^2$ imply $|e_{ml}(\mathbf {x} ^1)| \ge |e_{ml}(\mathbf {x} ^2)|$.

• (ii) If the functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ are concave with respect to x for $({\mathcal {P}}, x) \in S_1$, then the conditions $({\mathcal {P}}, \mathbf {x} ^1),\; ({\mathcal {P}}, \mathbf {x} ^2) \in S_2$ and $\mathbf {x} ^1 \prec \mathbf {x} ^2$ imply $|e_{ml}(\mathbf {x} ^1)| \le |e_{ml}(\mathbf {x} ^2)|$.

Thus, a change in the income distribution will increase or decrease market demand elasticity, depending on whether the individual demand functions $\phi _m({\mathcal {P}}, x)$ and their derivatives are convex or concave in income levels x; equivalently, by Theorem 2.1, on whether the market demand function $\Phi _m({\mathcal {P}},\mathbf{x })$ and its first derivatives are Schur-convex or Schur-concave with respect to vectors $\mathbf{x }$ representing income distributions. The first part of the above Theorem states that the more variable, i.e., unequal, is the distribution of income, the smaller is the cross-price elasticity of demand for the m-th good with respect to the l-th good’s price in absolute value, if the individual demand functions and their derivatives are convex (equivalently, if the market demand function and its first derivatives are Schur-convex). The second part states that the more variable, i.e., unequal, is the distribution of income, the larger is the cross-price elasticity of demand for the m-th good with respect to the l-th good’s price in absolute value, if the individual demand functions and their derivatives are concave (equivalently, if the market demand function and its first derivatives are Schur-concave).

In general, tax (and transfer) policies change income distributions (from $\mathbf{x }^1$ to $\mathbf{x }^2$, say) such that the Lorenz curves of the before and the after income distributions intersect. In order to extend results of the above type to the case of crossing Lorenz curves, we employ the concept of transfer sensitivity (Definition 2.4). Applying this definition to market demand functions, we may say that a market demand function is transfer sensitive (equivalently, downside inequality averse) if the transfer of any specific amount of income from a poorer to a richer person will increase market demand by a greater amount, the lower this transfer occurs in the distribution, other things being equal. Applying the results in Menezes et al. (1980) and Shorrocks and Foster (1987), Schur-convex market demand functions which are additive in individual demand functions with positive first and second derivatives (see Sect. 3) are transfer sensitive / downside inequality averse if and only if they have negative third derivatives. This enables us to characterize the effect on market demand elasticity of changes in income distributions such that Lorenz curves intersect, depending on the sign of the third derivative of the individual demand function.

Admittedly, the behavioural implications of the third derivatives of the demand function are not intuitive. But a number of results in demand analysis have been based on assumptions on the third derivative of demand. Weyl and Fabinger (2013) rely on the third derivative of demand to characterize the pass-through rate of wholesale prices. Ravallion et al. (2000) characterize the behaviour of emissions depending on assumptions on the third derivative of the emissions demand function. In this section and “Appendix 3”, we provide examples of demand functions with positive and negative third derivatives.

3.1 Price elasticities when Lorenz curves intersect (1)

Throughout the rest of the section, $\mathbf{x }^1=(x_1^1,\ldots , x_K^1)$ and $\mathbf{x }^2=(x_1^2,\ldots , x_K^2)$ denote two distributions of the same total income, so that $\sum _{i=1}^K x^1_i=\sum _{i=1}^K x^2_i.$ This implies that the average incomes in the two income distributions are the same, and the means of the corresponding r.v.’s $X^1$ and $X^2$ with uniform distribution on the sets of components of $\mathbf{x }^1$ and $\mathbf{x }^2$ coincide: $\mu _{X^1}=E(X^1)=E(X^2)=\mu _{X_2}.$ Let the Lorenz curve corresponding to the income distribution vector $\mathbf{x }^1$ (the r.v. $X^1$ with uniform distribution on the set of components of $\mathbf{x }^1$) cross that corresponding to the income distribution vector $\mathbf{x }^2$ (the r.v. $X^2$) once from above. We first take the case where the variance $V(X^1)$ of the r.v. $X^1$ is not greater than the variance $V(X^2)$ of $X^2:$ $V(X^1)\le V(X^2).$

Theorem 3.2

Let goods m and l be complements. Then:

• (i) Let the functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ be convex with respect to x, and let $\phi _m'''({\mathcal {P}},x)<0$ and $\partial ^4\phi _m({\mathcal {P}},x)/\partial p_l\partial ^3 x<0$ for $({\mathcal {P}}, x) \in S_1.$ Suppose that $({\mathcal {P}}, \mathbf {x} ^1),\; ({\mathcal {P}}, \mathbf {x} ^2) \in S_2$ are such that the Lorenz curve corresponding to $\mathbf {x} ^1$ crosses that corresponding to $\mathbf {x} ^2$ once from above, and the variance $V(X^1)$ of the r.v. $X^1$ is not greater than the variance $V(X^2)$ of the r.v. $X^2.$ Then $|e_{ml}(\mathbf {x} ^1)| > |e_{ml}(\mathbf {x} ^2)|$.

• (ii) Let the functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ be concave with respect to x,  and let $\phi _m'''({\mathcal {P}},x)>0$ and $\partial ^4\phi _m({\mathcal {P}},x)/\partial p_l\partial ^3 x>0$ for $({\mathcal {P}}, x) \in S_1.$ Suppose that $({\mathcal {P}}, \mathbf {x} ^1),\; ({\mathcal {P}}, \mathbf {x} ^2) \in S_2$ are such that the Lorenz curve corresponding to $\mathbf {x} ^1$ crosses that corresponding to $\mathbf {x} ^2$ once from above, and the variance $V(X^1)$ of the r.v. $X^1$ is not greater than the variance $V(X^2)$ of the r.v. $X^2.$ Then $|e_{ml}(\mathbf {x} ^1)| < |e_{ml}(\mathbf {x} ^2)|$.

When goods m and l are substitutes, these implications are correspondingly reversed.

Proof in “Appendix 2.1”

Thus, under the additional assumptions of Theorem 3.2 for the case of crossing Lorenz curves relative to Theorem 3.1, an increase in downside inequality in the distribution of the income reduces the absolute value of the cross-price elasticity of demand on the m-th good with respect to the l-th good’s price, if the individual demand functions $\phi _m({\mathcal {P}}, x)$ and their derivatives are convex in income levels x (equivalently, if the market demand function $\Phi _m({\mathcal {P}},\mathbf{x })$ and its first derivatives are Schur-convex with respect to income distribution vectors $\mathbf{x }$). Also, under the additional assumptions of Theorem 3.2, an increase in downside inequality in the distribution of income increases the absolute value of the cross-price elasticity of demand for the m-th good with respect to the l-th good’s price, if the individual demand functions and their derivatives are concave (equivalently, if the market demand function and its first derivatives are Schur-concave).

Remark 3.1

Theorem 3.2 generalizes to the case where the condition $\partial ^4\phi _m({\mathcal {P}}, x)/\partial p_l\partial ^3 x \le (\ge ) \; 0$ replaces the corresponding strict inequality conditions.

Proof in “Appendix 2.2”

Corollary 3.1

Consider the own-price elasticity of market demand for any good:

• (i) If the functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_m$ are convex with respect to x for $({\mathcal {P}}, x) \in S_1$, and $\phi _m'''({\mathcal {P}}, x)<0$ and $\partial ^4\phi _m({\mathcal {P}}, x)/\partial p_l\partial ^3 x<0$, then $|e_{mm}(\mathbf {x} ^1)| > |e_{mm}(\mathbf {x} ^2)|$ under the conditions (a) $({\mathcal {P}}, \mathbf {x} ^1),\; ({\mathcal {P}}, \mathbf {x} ^2) \in S_2$, (b) The Lorenz curve corresponding to $\mathbf {x} ^1$ crosses that corresponding to $\mathbf {x} ^2$ once from above, and (c) The variance of $X^1$ is not greater than that of $X^2$.

• (ii) If the functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_m$ are concave with respect to x for $({\mathcal {P}}, x) \in S_1$, and $\phi _m'''({\mathcal {P}}, x)>0$ and $\partial ^4\phi _m({\mathcal {P}}, x)/\partial p_l\partial ^3 x>0$, then $|e_{mm}(\mathbf {x} ^1)| < |e_{mm}(\mathbf {x} ^2)|$ under the same conditions stated above in (i).

Under the assumptions in part (i) of the result above, an increase in downside inequality in the distribution of income will reduce the absolute value of the own-price elasticity of demand if the individual demand functions $\phi _m({\mathcal {P}}, x)$ and their derivatives are convex in income levels x (equivalently, if the market demand function $\Phi _m({\mathcal {P}},\mathbf{x })$ and its first derivatives are Schur-convex with respect to income distribution vectors $\mathbf{x }$). Under the same assumptions, an increase in downside inequality in the distribution of income will reduce the absolute value of the own-price elasticity of the demand if the individual demand functions and their derivatives are concave (equivalently, if the market demand function and its first derivatives are Schur-concave).

3.1.1 Example

Example 3.1

Deaton and Muelbauer (1980) introduced and estimated the Almost Ideal Demand System (AIDS) using data on consumer expenditures in Britain. Consider a market demand function $\Phi _m({\mathcal {P}},\mathbf{x })$ in the AIDS form:

$$\begin{aligned} \Phi _m({\mathcal {P}},\mathbf{x })= & {} Y\left[ \alpha _m+\sum _{j=1}^M \gamma _{mj}\log p_j+\beta _m\left( \frac{\sum _{i=1}^K x_i \log x_i}{Y} \right. \right. \\&\left. \left. -\,\alpha _0 -\sum _{k=1}^M \alpha _k \log p_k -\frac{1}{2}\sum _{j=1}^M\sum _{k=1}^M \gamma _{kj}\log p_k \log p_j\right) \right] \end{aligned}$$

where $Y=\sum _{i=1}^K x_i$, and $\alpha _i, \beta _i,\gamma _{ij}$ are parameters such that $\sum _{k=1}^M \alpha _k=1, \sum _{i=1}^M \gamma _{ij}=$ $\sum _{j=1}^M \gamma _{ij}=$ $\sum _{k=1}^M \beta _{k}$ $=0,$ $\gamma _{ij}=\gamma _{ji}$.

It is obvious that:

$$\begin{aligned} \phi _m({\mathcal {P}},x)= & {} x\left[ \alpha _m+\sum _{j=1}^M \gamma _{mj}\log p_j+\beta _m\left( \frac{x \log x}{K x} \right. \right. \\&\left. \left. -\,\alpha _0-\sum _{k=1}^M \alpha _k \log p_k -\frac{1}{2}\sum _{j=1}^M\sum _{k=1}^M \gamma _{kj}\log p_k \log p_j\right) \right] \end{aligned}$$

and

$$\begin{aligned} \partial \phi _m({\mathcal {P}}, x)/\partial p_l=x\left[ \frac{\gamma _{ml}}{p_l}-\beta _m \frac{\alpha _l}{p_l}-\sum _{k=1}^M \frac{\gamma _{kl}}{p_l}\log p_k\right] . \end{aligned}$$

Therefore: $\phi _m'''({\mathcal {P}},x)=-\beta _m/x^2$ and $\partial ^4 \phi _m({\mathcal {P}}, x)/\partial p_l\partial ^3 x=0$.

When $\beta _m>0$, $\phi _m({\mathcal {P}},x)$ is a convex function and $\phi _m'''({\mathcal {P}},x)<0$. According to the empirical results of Deaton and Muelbauer (1980) presented in Table 1, an increase in downside inequality in the distribution of income would have reduced the absolute value of the own-price elasticity of the demand for clothing, and transport and communications (non-necessities).

When $\beta _m<0$, $\phi _m({\mathcal {P}},x)$ is a concave function and $\phi _m'''({\mathcal {P}},x)>0$. An increase in downside inequality in the distribution of income would have increased the absolute value of the own-price elasticity of the demand for food and housing (necessities).

Table 1 Deaton and Muelbauer (1980) estimates of $\beta _m$ from the almost ideal demand system using annual data on consumer expenditures in Britain over the period 1954 to 1974

Other examples extended from Ibragimov and Ibragimov (2007) are presented in “Appendix 3”.

3.2 Price elasticities when Lorenz curves intersect (2)

We now turn to the case where the variance of the r.v. $X^1$ is larger than the variance of $X^2:$ $V(X^1)>V(X^2),$ again with the Lorenz curve corresponding to $\mathbf{x }^1$ crossing that corresponding to $\mathbf{x }^2$ once from above. Theorem 3.2 is not helpful. Employing Proposition 2.3, it is possible to order the market demand elasticities conditioned on $\mathbf{x }^1$ and on $\mathbf{x }^2$, based on the relative strengths of the degree of transfer sensitivity (downside inequality aversion) and the degree of inequality aversion, pertaining to the demand function. Recall that a more transfer sensitive demand function is one for which the transfer of any specific amount of income from a poorer to a richer person will increase demand by a greater amount, the lower this transfer occurs in the distribution, other things being equal. A more inequality averse demand function is one for which any reduction in inequality through a non-intersecting shift of the Lorenz curve will increase demand by a greater amount, other things being equal.

3.2.1 Demand function for good (m) under different income distributions

Theorem 3.3

Let goods m and l be complements. Let the functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ be convex (concave) with respect to x for $({\mathcal {P}}, x) \in S_1$. Further, let the Lorenz curve corresponding to $\mathbf {x} ^1$ cross that corresponding to $\mathbf {x} ^2$ once from above, and let the variance $V(X^1)$ of the r.v. $X^1$ be greater than the variance $V(X^2)$ of the r.v. $X^2$. Then for $({\mathcal {P}}, \mathbf {x} ^1),\; ({\mathcal {P}}, \mathbf {x} ^2) \in S_2$:

$$\begin{aligned} |e_{ml}(\mathbf {x} ^1)| \ge |e_{ml}(\mathbf {x} ^2)| \end{aligned}$$

if either of the following conditions hold:

• $$\begin{aligned} \Phi _m({\mathcal {P}}, \mathbf {x} ^1)\le & {} \Phi _m({\mathcal {P}}, \mathbf {x} ^2)\\&-\,\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)} \le -\frac{\partial \phi _m'''({\mathcal {P}},x)/\partial p_l}{\partial \phi _m''({\mathcal {P}},x)/\partial p_l} \quad \hbox {for all} \; x \in [0, {\hat{x}}] \end{aligned}$$
• $$\begin{aligned} \partial \Phi _m(P, \mathbf {x} ^1)/\partial p_l\le & {} \partial \Phi _m(P, \mathbf {x} ^2)/\partial p_l\\&-\,\frac{\partial \phi _m'''(P,x)/\partial p_l}{\partial \phi _m''(P,x)/\partial p_l} \le -\frac{\phi _m'''(P,x)}{\phi _m''(P,x)} \quad \hbox {for all} \; x \in [0, {\hat{x}}] \end{aligned}$$

Proof in “Appendix 2.3”

That is, given two income distributions, $\mathbf{x }^1$ and $\mathbf{x }^2$, let $\mathbf{x }^1$ be characterized by a greater degree of downside inequality relative to Pigou–Dalton inequality. Further, let the market demand for good m be larger under $\mathbf{x }^2$ than under $\mathbf{x }^1$, and let the market demand function for good m be characterized by a uniformly smaller ratio $-\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)},$ of third to second derivatives when compared to the corresponding ratio $-\frac{\partial \phi _m'''({\mathcal {P}},x)/\partial p_l}{\partial \phi _m''({\mathcal {P}},x)/\partial p_l}$ of third to second derivatives of the cross derivative of market demand for good m with respect to the price of good l. Then the cross-price elasticity $e_{ml}(\mathbf {x} ^2)$ of market demand for the m-th good with respect to the l-th good’s price under $\mathbf{x }^2$ is smaller than the cross-price elasticity $e_{ml}(\mathbf {x} ^1)$ under $\mathbf{x }^1,$ in absolute value.

The same elasticity comparisons also hold if the cross derivative of market demand for good m with respect to the price of good l is larger under $\mathbf{x }^2$ than under $\mathbf{x }^1,$ and the ratio $-\frac{\partial \phi _m'''(P,x)/\partial p_l}{\partial \phi _m''(P,x)/\partial p_l}$ of third to second derivatives of the cross derivative of market demand for good m, with respect to price of good l is uniformly smaller compared to the ratio $-\frac{\phi _m'''(P,x)}{\phi _m''(P,x)}$ of third to second derivatives of the market demand function for good m.

When goods m and l are substitutes, the conclusions of this result are correspondingly reversed.

Remark 3.2

In Theorem 3.3, if the inequality signs in the conditions in change from $\le$ to $\ge$, then $|e_{ml}(\mathbf {x} ^1)| \le |e_{ml}(\mathbf {x} ^2)|$.

3.2.2 Demand functions for different goods (m) and (n) under different income distributions

Now consider the situation where K consumers in the economy generate demand for goods m and n. Let $\Phi _m({\mathcal {P}},\mathbf{x })=\sum _{i=1}^K \phi _{m}({\mathcal {P}},x_i)$ and $\Psi _n({\mathcal {P}},\mathbf{x })=\sum _{i=1}^K \psi _{n}({\mathcal {P}},x_i)$ be two corresponding market demand functions, and let the cross elasticities of market demands with respect to the price of good l be denoted by $e_{ml}$ and $e_{nl}$, respectively.

Corollary 3.2

Let goods m and l be complements, and let goods n and l be complements as well. Then the following conclusions hold:

• (i) Suppose that $\phi _{m}({\mathcal {P}},x)$ and $\psi _{n}({\mathcal {P}},x)$ are convex (concave) functions on $S_1;$ for $\mathbf {x} ^1 \; \text {and} \; \mathbf {x} ^2 \in S_2$, $L_{X^1}(u)$ crosses $L_{X^2}(u)$ once from above; and the variance of the r.v. $X^1$ is greater than that of the r.v. $X^2:$ $V({X}^1) > V({X}^2).$ Then

  $$\begin{aligned} -\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)} \le -\frac{\psi _n'''({\mathcal {P}},x)}{\psi _n''({\mathcal {P}},x)}, \quad \hbox {for} \; \hbox {all}\; x \in [0, {\hat{x}}] \end{aligned}$$

  is equivalent to:

  $$\begin{aligned}\Phi _m({\mathcal {P}},\mathbf {x} ^2)\ge \Phi _n({\mathcal {P}},\mathbf {x} ^1) \Rightarrow \Psi _m({\mathcal {P}},\mathbf {x} ^2) \ge \Psi _n({\mathcal {P}},\mathbf {x} ^1) \end{aligned}$$

• (ii) Suppose that $\partial \phi _{m}({\mathcal {P}},x)/ \partial p_l$ and $\partial \psi _{n}({\mathcal {P}},x)/ \partial p_l$ are convex (concave) functions on $S_1;$ for $\mathbf {x} ^1 \; \text {and} \; \mathbf {x} ^2 \in S_2$, $L_{X^1}(u)$ crosses $L_{X^2}(u)$ once from above; and the variance of the r.v. $X^1$ is greater than that of the r.v. $X^2:$ $V({X}^1) > V({X}^2).$ Then

  $$\begin{aligned} -\frac{\partial \phi _m'''({\mathcal {P}},x)/ \partial p_l}{\partial \phi _m''({\mathcal {P}},x)/ \partial p_l} \le -\frac{\partial \psi _n'''({\mathcal {P}},x)/ \partial p_l}{\partial \psi _n''({\mathcal {P}},x)/ \partial p_l}, \; \hbox {for} \; \hbox {all}\; x \in [0, {\hat{x}}] \end{aligned}$$

  is equivalent to:

  $$\begin{aligned} \partial \Phi _m({\mathcal {P}},\mathbf {x} ^2)/ \partial p_l\ge \partial \Phi _n({\mathcal {P}},\mathbf {x} ^1)/ \partial p_l \Rightarrow \partial \Psi _m({\mathcal {P}},\mathbf {x} ^2)/ \partial p_l \ge \partial \Psi _n({\mathcal {P}},\mathbf {x} ^1)/ \partial p_l \end{aligned}$$

Proof

Direct application of Proposition 2.3. $\square$

Now consider two income distributions, $\mathbf{x }^1$ and $\mathbf{x }^2$, with $L_{X^1}(u)$ crossing $L_{X^2}(u)$ once from above, and the variance of the r.v. $X^1$ being greater than that of the r.v. $X^2:$ $V(X^1) > V(X^2)$. Whether the change from $\mathbf{x }^1$ to $\mathbf{x }^2$ reduces the value of the $e_{ml}({\mathcal {P}},\mathbf{x })$ depends on the relative strengths of the degree of inequality aversion and the degree of downside inequality aversion of cross-price elasticity. The next theorem shows that even when the cross-price elasticity $e_{ml}$ of $\mathbf{x }^2$ is greater than that of $\mathbf{x }^1,$ the same is also true for another cross-price elasticity $e_{nl}({\mathcal {P}},\mathbf{x })$ if $-\frac{\psi _n'''({\mathcal {P}},x)}{\psi _n''({\mathcal {P}},x)}$ and $-\frac{\partial \psi _n'''({\mathcal {P}},x)/ \partial p_l}{\partial \psi _n''({\mathcal {P}},x)/ \partial p_l}$ are uniformly larger than $-\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)}$ and $-\frac{\partial \phi _m'''({\mathcal {P}},x)/ \partial p_l}{\partial \phi _m''({\mathcal {P}},x)/ \partial p_l}$, respectively.

Theorem 3.4

Let goods m and l be complements, and so too, goods n and l. Suppose that $\phi _{m}({\mathcal {P}},X)$, $\psi _{n}({\mathcal {P}},X),$ $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ and $\partial \psi _n({\mathcal {P}}, x)/\partial p_l$ are convex (concave) functions on $S_1;$ for $({\mathcal {P}},\mathbf {x} ^1) \; \text {and} \; ({\mathcal {P}},\mathbf {x} ^2) \in S_2$, and $L_{X^1}$ crosses $L_{X^2}$ once from above; and $V(X^1) > V(X^2).$ Then (i) and (ii) are equivalent.

• (i) $-\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)} \le -\frac{\psi _n'''({\mathcal {P}},x)}{\psi _n''({\mathcal {P}},x)}; -\frac{\partial \phi _m'''({\mathcal {P}},x)/ \partial p_l}{\partial \phi _m''({\mathcal {P}},x)/ \partial p_l} \le -\frac{\partial \psi _n'''({\mathcal {P}},x)/ \partial p_l}{\partial \psi _n''({\mathcal {P}},x)/ \partial p_l}, \; \text {for all} \; x\in [0, {\hat{x}}]$

• (ii) $e_{ml}(\mathbf {x} ^2) \ge e_{ml}(\mathbf {x} ^1) \Rightarrow e_{nl}(\mathbf {x} ^2) \ge e_{nl}(\mathbf {x} ^1)$

Proof in “Appendix 2.4”

Remark 3.1

If the conditions in Theorem 3.4 hold, it can be said that $e_{nl}$ has a higher degree of “downside inequality aversion relative to inequality aversion” than $e_{ml}$, noting that cross-price elasticity is neither an additive index nor an inequality index.

4 Tax polices, income distributions, and elasticity of market demand

In 2011, the “squeezed middle” was named the Oxford Dictionaries Word Of The Year. The squeezed middle has been variously defined. The Resolution Foundation, a think tank that has been influential in the discussion, has defined it as the 40% of the population that earns less than the median wage but more than the bottom 10% (Resolution Foundation 2013). Changes in economic conditions that squeeze the middle class alone shift the Lorenz curve such that it intersects the original Lorenz curve once from above.

Among various economic changes, tax-benefit systems change the distribution of income. One type of tax policy change that squeezes the middle class with the new Lorenz curve single-crossing the old once from above is a move to a flatter tax system. Mirrlees (1971) showed that optimal tax schedules can be close to linear. While this result is not robust (Tuomala 1990), flat tax systems have been adopted in many countries in Eastern Europe.⁶ We show that a move to flatter taxes, with a higher personal allowance, and a marginal rate that is intermediate between the old lowest and highest marginal rates, can affect market demand elasticities for specific goods, acting through changes in income distribution.⁷

Let $0 \le t(x) < 1$ denote the tax liability on income x. Assuming that t(x) is differentiable, the tax system is progressive if the average tax rate rises with income—$\partial \left( t(x)/x \right) / \partial x > 0$. In this case, the post-tax income distribution Lorenz dominates the pre-tax income distribution (Jakobsson 1971). Suppose the current tax schedule is represented by $t_1(X)$, with a personal allowance set at $A^1$. Consider the effect of changing the tax schedule to $t_j(x), \; j=2,3,\ldots$, with a corresponding personal allowance set at $A^j$. Let $\mathbf{x }^j$ be the income distribution after the application of tax schedule $t_j(x),$ and, as before, let $X^j$ denote the r.v. with a uniform distribution on the components of $\mathbf{x }^j.$

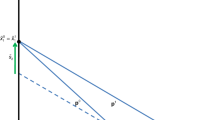
Dardanoni and Lambert (1988) establish that if tax schedules $t_1(x)$ and $t_2(x)$ (not restricted to flat rate schedules or to progressive schedules) generate the same tax revenue, and if $t_2(x)$ crosses $t_1(x)$ twice, first from below, then $L_{X^2}(u)$ would cross $L_{X^1}(u)$ once from above. This will the case when a progressive tax schedule is replaced with a flat rate tax schedule, with a higher personal allowance, and a marginal rate that is intermediate between the old lowest and highest marginal rates. The after-flat-tax Lorenz curve will cross the after-progressive-tax Lorenz curve, once from above: the after-flat-tax income distribution will have less downside inequality than the after-progressive-tax income distribution (Fig. 1).

Fig. 1

The left panel presents the tax schedule: $t_1(x)$, the progressive tax schedule and $t_2(x)$, the flat rate tax schedule. The right panel presents the corresponding Lorenz curves

Proposition 4.1

(Davies and Hoy 2002) For any progressive tax schedule $t_1(x)$, there exist unique flat rate tax schedules $t_l(x)$ and $t_u(x)$ that generate the same tax yield, such that, for any flat rate tax schedule $t_j(x)$:

• (i) The post-tax income distribution after tax schedule $t_j$ Lorenz dominates the post-tax income distribution after the original progressive tax schedule $t_1$ if $t_j<t_l$

• (ii) The post-tax income distribution after tax schedule $t_j$ is Lorenz dominated by the post-tax income distribution after the original progressive tax schedule $t_1$ if $t_j>t_u$

• (iii) The post-tax Lorenz curve after tax schedule $t_j$ crosses the post-tax Lorenz curve after the original progressive tax schedule $t_1$ once from above if $t_l<t_j<t_u$

We now turn to establishing the relationship between tax policy and market demand (consequences of shifting to a flat rate tax from a progressive tax schedule, such that the associated Lorenz curves intersect); that is, for values of $t_j$ where $t_l<t_j<t_u$. Note that, we compare tax systems which generate equal amounts of tax revenue, based on the presumption that behaviour is unaltered by the particular tax system under consideration.

Suppose tax schedules $t_2(x)$ and $t_1(x)$ generate the same tax yield, and $t_2(x)$ crosses $t_1(x)$ twice, first from below— equivalent to the Lorenz curve of $\mathbf{x }^2$ crossing that of $\mathbf{x }^1$ once from above. Depending on the variances of $\mathbf{x }^2$ and $\mathbf{x }^1$, the results in the previous section apply. As we focus on a flat tax schedule, $t_2(x)$, and a progressive tax schedule, $t_1(x)$, the variance of the r.v. $X^2$ is greater than that of the r.v. $X^1$.

Corollary 4.1

Let goods m and l be complements. Suppose tax schedules $t_2(x)$ and $t_1(x)$ generate the same tax yield and $t_2(x)$ crosses $t_1(x)$ twice first from below and $V(X^2) > V(X^1)$. If functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ are convex (or concave) with respect to x for $({\mathcal {P}}, {x}) \in S_1$, for $({\mathcal {P}}, \mathbf {x} ^2),\; ({\mathcal {P}}, \mathbf {x} ^1) \in S_2$ and the following either one condition hold:

• $$\begin{aligned} \Phi _m({\mathcal {P}}, \mathbf {x} ^2)\le & {} \Phi _m({\mathcal {P}}, \mathbf {x} ^1)\\&-\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)} \le -\frac{\partial \phi _m'''({\mathcal {P}},x)/\partial p_l}{\partial \phi _m''({\mathcal {P}},x)/\partial p_l} \; \hbox {for} \; \hbox {all}\; x \in [0, {\hat{x}}] \end{aligned}$$
• $$\begin{aligned} \partial \Phi _m(P, \mathbf {x} ^2)/\partial p_l\le & {} \partial \Phi _m(P, \mathbf {x} ^1)/\partial p_l\\&-\frac{\partial \phi _m'''(P,x)/\partial p_l}{\partial \phi _m''(P,x)/\partial p_l} \le -\frac{\phi _m'''(P,x)}{\phi _m''(P,x)} \; \hbox {for} \; \hbox {all}\; x \in [0, {\hat{x}}] \end{aligned}$$

then $|e_{ml}(\mathbf {x} ^2)| \ge |e_{ml}(\mathbf {x} ^1)|$.

Suppose that a tax reform results in the old tax schedule crossing the new twice first from below and a reduction in the variance of the after-tax income distribution, which leads to more downside inequality and less Pigou–Dalton inequality in the after-tax income distribution among consumers in the economy. Then how the cross-price elasticity changes due to a tax reform depends on the strength of the downside inequality aversion against its own inequality aversion for the market demand function on good m and its derivative with respect to good l.

Corollary 4.2

Let goods m, n and l be complements. Suppose tax schedules $t_2(x)$ and $t_1(x)$ generate the same tax yield and $t_2(x)$ crosses $t_1(x)$ twice first from below and $V({X}^2) > V({X}^1)$. If $\phi _{im}({\mathcal {P}},x)$, $\psi _{in}({\mathcal {P}},x)$, $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ and $\partial \psi _n({\mathcal {P}}, x)/\partial p_l$ are convex (or concave) functions on $S_1$, for $\mathbf {x} ^1 \; and \; \mathbf {x} ^2 \in S_2$, then (i) and (ii) are equivalent.

• (i) $-\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)} \le -\frac{\psi _n'''({\mathcal {P}},x)}{\psi _n''({\mathcal {P}},x)}, -\frac{\partial \phi _m'''({\mathcal {P}},x)/ \partial p_l}{\partial \phi _m''({\mathcal {P}},x)/ \partial p_l} \le -\frac{\partial \psi _n'''({\mathcal {P}},x)/ \partial p_l}{\partial \psi _n''({\mathcal {P}},x)/ \partial p_l}, \; \hbox {for} \; \hbox {all}\; x \in [0, {\hat{x}}]$

• (ii) $e_{ml}(\mathbf {x} ^1) \ge e_{ml}(\mathbf {x} ^2) \Rightarrow e_{nl}(\mathbf {x} ^1) \ge e_{nl}(\mathbf {x} ^2)$

Suppose that a tax reform results in the old tax schedule crossing the new twice first from below and a reduction in the variance of the after-tax income distribution, which leads to more downside inequality and less Pigou–Dalton inequality in the after-tax income distribution among consumers in the economy, and the cross-price elasticity on good m,  $e_{ml},$ of $\mathbf{x }^1$ is greater than that of $\mathbf{x }^2.$ Then the same hold for the cross-price elasticity on good n,  $e_{nl},$ if $-\frac{\psi _n'''({\mathcal {P}},x)}{\psi _n''({\mathcal {P}},x)}$ and $-\frac{\partial \psi _n'''({\mathcal {P}},x)/ \partial p_l}{\partial \psi _n''({\mathcal {P}},x)/ \partial p_l},$ are uniformly larger than $-\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)}$ and $-\frac{\partial \phi _m'''({\mathcal {P}},x)/ \partial p_l}{\partial \phi _m''({\mathcal {P}},x)/ \partial p_l}$, respectively.

5 Conclusions

We characterized the way in which the price elasticity of market demand changes with income distribution, extending the analysis of Ibragimov and Ibragimov (2007), allowing shifting Lorenz curves to intersect. We showed that the increase or decrease in market demand elasticity depends on the Schur-convexity/Schur-concavity as well as an analogue of “downside inequality aversion” of the (homogeneous) individual demand function and its derivative with respect to price.

If the Lorenz curve of one income distribution crosses that of another once from above, and the variance of former is not greater than that of the latter, then there is an increase in downside inequality in moving from the former to the latter. For goods that are complements, if the individual demand function is convex, the change between the former and the latter (increasing or decreasing downside inequality) leads to a change in cross-price elasticity in the opposite direction. If the individual demand function is concave, then the increase or decrease in downside inequality leads to a change in cross-price elasticity in the same direction. If the goods are substitutes, the above patterns are reversed.

Based on these results, we characterized the way in which changes in market demand elasticity are driven by shifts between progressive and flatter tax schedules. The effect depends on the values of the second and third derivatives of both the individual demand function, and its derivative with respect to price. The knowledge of these higher-order derivatives required for the comparative statics results can be obtained from the estimated parameters of the AIDS and other demand systems. Such analysis should be helpful in understanding the effect of a class of direct tax policy changes on market demand elasticity and thus on market demand.

Appendices

Appendix 1: Concepts

In this appendix, we set out some additional concepts, definitions and results related to the analysis in the paper.

A mean-preserving spread (MPS) is defined as any function which, when added to a probability or density function, transfers weight from the centre of the distribution to its tails, without changing the mean. This makes the distribution more heavy-tailed. Similarly, a mean-preserving contraction (MPC) is any function which when added to a probability or density function, shifts weight from tails towards the center of a distribution without altering the mean. It is intuitively clear that any MPS will increase inequality and that any MPC will decrease inequality.

Definition 6.1

(Menezes et al. 1980) The change from the income distribution $\mathbf {x} ^1$ to distribution $\mathbf {x} ^2$ is an MPS—equivalently, a series of regressive transfers (the change from $\mathbf {x} ^2$ to $\mathbf {x} ^1$ is an MPC—equivalently, a series of progressive transfers); if $S(x)=\text {F}_{X^2}(x)-\text {F}_{X^1}(x)$ satisfies the following conditions:

• (i) $\int _0^{{\hat{x}}} S(t)\hbox {d}t=0$

• (ii) $\int _0^x S(t)\hbox {d}t \ge 0$ for all $x \in [0,{\hat{x}}]$ where the inequality is strict for some subintervals within $[0,{\hat{x}}]$

Definition 6.2

(Menezes et al. 1980) A mean-variance-preserving transformation (MVPT) is a combination of an MPS and an MPC that leaves the overall variance unchanged, with the MPS occurring at lower income levels than the MPC.

Definition 6.3

(Menezes et al. 1980) The change from $\mathbf {x} ^1$ to $\mathbf {x} ^2$ is said to be a downside inequality increase if $D(x)=[\text {F}_{X^2}(x)-\text {F}_{X^1}(x)]$ is such that

• (i) $\int _0^{{\hat{x}}} D(t)\hbox {d}t=0$

• (ii) $\int _0^{{\hat{x}}} \int _0^t D(y)\hbox {d}y\hbox {d}t=0$

• (iii) $\int _0^x \int _0^t D(y)\hbox {d}y\hbox {d}t \ge 0$ for all $x \in [0,{{\hat{x}}}]$ and $>0$ for some $x\in [0, {\hat{x}}]$

This is equivalent to $\mathbf{x }^2$ having more downside risk than $\mathbf{x }^1$ as defined by Menezes et al. (1980) in the context of decisions under risk. They argued that any inequality or risk index exhibiting transfer sensitivity (downside inequality aversion) would always assign a higher value to a distribution that has more “downside inequality” or “downside risk” than another, in the sense that the former can be obtained from the latter by a series of mean-variance-preserving transformations (MVPT).

Building on the above concepts and definitions, Chiu (2007) proved the following result, which is helpful in comparing distributions in terms of downside inequality aversion when $V(X^1) > V(X^2)$.

Proposition 6.1

(Chiu 2007) Let $\mathbf {x} ^1=(x^1_1,\ldots , x^1_K), \mathbf {x} ^2=(x^2_1,\ldots , x^2_K)$ be real vectors with $\sum _{i=1}^K x^1_i=\sum _{i=1}^K x^2_i.$ Then:

• (i) $\text {F}_{X^2}(x)-\text {F}_{X^1}(x)=D(x)+C(x)$ where D(x) is a downside inequality increase and C(x) an MPC if and only if $\int _0^{{\hat{x}}} \int _0^t [\text {F}_{X^2}(y)-\text {F}_{X^1}(y)]\hbox {d}y\hbox {d}t <0$, and $\int _x^{{\hat{x}}} \int _0^t [\text {F}_{X^2}(y)-\text {F}_{X^1}(y)]\hbox {d}y\hbox {d}t \le 0$ for all $x \in [0,{{\hat{x}}}]$.

• (ii) $\text {F}_{X^2}(x)-\text {F}_{X^1}(x)=D(x)+S(x)$ where D(x) is a downside inequality increase and S(x) an MPS if and only if $\int _0^{{\hat{x}}} \int _0^t [\text {F}_{X^2}(y)-\text {F}_{X^1}(y)]\hbox {d}y\hbox {d}t >0$, and $\int _0^{x} \int _0^t [\text {F}_{X^2}(y)-\text {F}_{X^1}(y)]\hbox {d}y\hbox {d}t \ge 0$ for all $x \in [0,{{\hat{x}}}]$.

Based on Proposition 6.1, Chiu (2007) showed that relative ranking of two distributions by an inequality index $\Phi$ is determined by its degree of inequality aversion and degree of downside inequality aversion. In the special case of single-crossing Lorenz curves, the function $-\phi '''/\phi ''$ (referred to as “prudence measure”, Kimball 1990) measures the strength of the index’s downside inequality aversion against its inequality aversion and determines the index’s ranking of $\mathbf{x }^1$ and $\mathbf{x }^2.$

Appendix 2: Proof

1.1 Proof of Theorem 3.2

Proof

Part (i): According to Theorem 2.1, from the convexity of functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ with respect to x for $({\mathcal {P}}, x) \in S_1$ it follows that the functions $\Phi _m({\mathcal {P}}, \mathbf{x })=\sum _{i=1}^K \phi _m({\mathcal {P}}, x_i)$ and $\partial \Phi _m({\mathcal {P}}, \mathbf{x })/\partial p_l=\sum _{i=1}^K \partial \phi _m({\mathcal {P}}, x_i)/\partial p_l$ are Schur-convex in $\mathbf{x }$ on $S_2$. If $\partial ^3\phi _m({\mathcal {P}}, x)/\partial ^3 x<0$ and $\partial ^4\phi _m({\mathcal {P}},x)/\partial p_l\partial ^3 x<0$, it follows that $\Phi _m({\mathcal {P}}, \mathbf{x })$ and $\partial \Phi _m({\mathcal {P}}, \mathbf{x })/\partial p_l$ are characterized by downside inequality aversion. By Proposition 2.2, if $L_{X^1}(u)$ crosses $L_{X^2}(u)$ once from above and $V(X^1) \le V(X^2)$, then $\Phi _m(P, \mathbf{x }^1) < \Phi _m({\mathcal {P}}, \mathbf{x }^2)$ and $\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l <\partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l$. It follows that

$$\begin{aligned} e_{ml}(\mathbf{x }^1)= & {} \partial \log \Phi _m({\mathcal {P}},\mathbf{x }^1)/\partial \log p_l= [(\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l)p_l]/\Phi _m({\mathcal {P}}, \mathbf{x }^1)\\< & {} [(\partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l)p_l]/\Phi _m({\mathcal {P}}, \mathbf{x }^2)=e_{ml}(\mathbf{x }^2). \end{aligned}$$

Since the goods m and l are complements ($\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l$ is non-positive), it is true that $|e_{ml}(\mathbf{x }^1)| > |e_{ml}(\mathbf{x }^2)|$.

The proof for part (ii) follows the same argument, with respect to Schur-concave functions. The functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ are concave with respect to x for $({\mathcal {P}}, x) \in S_1$. It follows that the functions $\Phi _m({\mathcal {P}}, \mathbf{x })=\sum _{i=1}^K \phi _m({\mathcal {P}}, x_i)$ and $\partial \Phi _m({\mathcal {P}}, \mathbf{x })/\partial p_l=\sum _{i=1}^K \partial \phi _m({\mathcal {P}}, x_i)/\partial p_l$ are Schur-concave in $\mathbf{x }$ on $S_2$. If $\partial ^3\phi _m({\mathcal {P}},x)/\partial ^3 x>0$ and $\partial ^4\phi _m({\mathcal {P}},x)/\partial p_l\partial ^3 x>0$, then $-\partial ^3\phi _m({\mathcal {P}},x)/\partial ^3 x$ $<0$ and $-\partial ^4\phi _m({\mathcal {P}},x)/\partial p_l\partial ^3 x<0$, and it follows that $-\Phi _m({\mathcal {P}}, \mathbf{x })$ and $-\partial \Phi _m({\mathcal {P}}, \mathbf{x })/\partial p_l$ are characterized by downside inequality aversion. By Proposition 2.2, if $L_{X^1}(u)$ crosses $L_{X^2}(u)$ once from above, and $V(\mathbf{x }^1) \le V(\mathbf{x }^2)$, then $-\Phi _m({\mathcal {P}}, \mathbf{x }^1) < -\Phi _m({\mathcal {P}}, \mathbf{x }^2)$ and $-\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l <-\partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l$ and it follows that $\Phi _m({\mathcal {P}}, \mathbf{x }^1) > \Phi _m({\mathcal {P}}, \mathbf{x }^2)$ and $\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l > \partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l$. Thus:

$$\begin{aligned} e_{ml}(\mathbf{x }^1)= & {} \partial \log \Phi _m({\mathcal {P}},\mathbf{x })/\partial \log p_l=[(\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l)p_l]/\Phi _m({\mathcal {P}}, \mathbf{x }^1)\\> & {} [(\partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l)p_l]/\Phi _m({\mathcal {P}}, \mathbf{x }^2)=e_{ml}(\mathbf{x }^2) \end{aligned}$$

Since the goods m and l are complements, it is true that $|e_{ml}(\mathbf{x }^1)| < |e_{ml}(\mathbf{x }^2)|$. $\square$

1.2 Proof of Remark 3.1

Proof

Part (i): If the functions $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ are convex with respect to x, then $\partial ^3\phi _m({\mathcal {P}}, x)/\partial p_l\partial ^2 x \ge 0$.

If $\partial ^3\phi _m({\mathcal {P}},x)/\partial p_l\partial ^2 x > 0$ and $\partial ^4\phi _m({\mathcal {P}},x)/\partial p_l\partial ^3 x=0$, then $\partial \phi _m({\mathcal {P}},x)/\partial p_l$ can be expressed as $ax^2+bx+f({\mathcal {P}})$ where $a>0$ and b are some constants. As variance of $X^1$ is not greater than that of $X^2$, while their means equal each other, for the additive index, $\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l <\partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l$.

If $\partial ^3\phi _m({\mathcal {P}},x)/\partial p_l\partial ^2 x = 0$, then $\partial \phi _m({\mathcal {P}},x)/\partial p_l$ can be expressed as $ax + g({\mathcal {P}})$, where a is some constant. As the sum over the elements in $\mathbf{x }^1$ are equal to that over elements in $\mathbf{x }^2$, $\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l = \partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l$.

Part (ii): The proof for the concave case follows similar lines. $\square$

1.3 Proof of Theorem 3.3

Proof

The functions $\phi _m({\mathcal {P}}, x)$ and $\partial \phi _m({\mathcal {P}}, x)/\partial p_l$ are convex (concave) with respect to x for $({\mathcal {P}}, x) \in S_1$; hence, the functions $\Phi _m({\mathcal {P}}, \mathbf{x })$ and $\partial \Phi _m({\mathcal {P}}, \mathbf{x })/\partial p_l$ are Schur-convex (Schur-concave) in $\mathbf{x }$ on $S_2$. By Proposition 2.3, if $L_{X^1}(u)$ crosses $L_{X^2}(u)$ once from above, and $V(X^1) > V(X^2)$, then

$$\begin{aligned} -\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)} \le -\frac{\partial \phi _m'''({\mathcal {P}},x)/\partial p_l}{\partial \phi _m''({\mathcal {P}},x)/\partial p_l} \quad \hbox {for all} \; x \in [0, {\hat{x}}] \end{aligned}$$

is equivalent to the stating that:

$$\begin{aligned} \Phi _m({\mathcal {P}}, \mathbf{x }^1) \le \Phi _m({\mathcal {P}}, \mathbf{x }^2) \Rightarrow \partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l \le \partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l. \end{aligned}$$

As $\Phi _m({\mathcal {P}}, \mathbf{x }^1) \le \Phi _m({\mathcal {P}}, \mathbf{x }^2)$, it is true that $\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l \le \partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l$. From this relation, it follows that

$$\begin{aligned}&e_{ml}(\mathbf{x }^1)=\partial \log \Phi _m({\mathcal {P}},\mathbf{x }^1)/\partial \log p_l=[(\partial \Phi _m({\mathcal {P}}, \mathbf{x }^1)/\partial p_l)p_l]/\Phi _m({\mathcal {P}}, \mathbf{x }^1)\\&\quad \le [(\partial \Phi _m({\mathcal {P}}, \mathbf{x }^2)/\partial p_l)p_l]/\Phi _m({\mathcal {P}}, \mathbf{x }^2)=e_{ml}(\mathbf{x }^2). \end{aligned}$$

Since goods m and l are complements, it is true that $|e_{ml}(\mathbf{x }^1)| \ge |e_{ml}(\mathbf{x }^2)|$.

The proof of the rest of the theorem is similar. $\square$

1.4 Proof of Theorem 3.4

Proof

If $L_{X^1}(u)$ crosses $L_{X^2}(u)$ once from above, and $V(X^1) > V(X^2)$, then $\mathbf{x }^2$ can be obtained from $\mathbf{x }^1$ by a combination of a downside inequality increase and a Pigou–Dalton inequality decrease. Suppose $-\frac{\phi _m'''({\mathcal {P}},x)}{\phi _m''({\mathcal {P}},x)} \le -\frac{\psi _n'''({\mathcal {P}},x)}{\psi _n''({\mathcal {P}},x)} \; \text {and} \;-\frac{\partial \phi _m'''({\mathcal {P}},x)/ \partial p_l}{\partial \phi _m''({\mathcal {P}},x)/ \partial p_l} \le -\frac{\partial \psi _n'''({\mathcal {P}},x)/ \partial p_l}{\partial \psi _n''({\mathcal {P}},x)/ \partial p_l} \; \text {for all}\; x \in [0, {\hat{x}}]$. By Corollary 3.2, this is equivalent to stating that: $\Phi _m({\mathcal {P}},\mathbf{x }^2)\ge \Phi _n({\mathcal {P}},\mathbf{x }^1) \Rightarrow \Psi _m({\mathcal {P}},\mathbf{x }^2) \ge \Psi _n({\mathcal {P}},\mathbf{x }^1)$ and $\partial \Phi _m({\mathcal {P}},\mathbf{x }^2)/ \partial p_l\ge \partial \Phi _n({\mathcal {P}},\mathbf{x }^1)/ \partial p_l \Rightarrow \partial \Psi _m({\mathcal {P}},\mathbf{x }^2)/ \partial p_l \ge \partial \Psi _n({\mathcal {P}},\mathbf{x }^1)/ \partial p_l$. It follows from these two implications that:

$$\begin{aligned}&[\partial \Phi _m({\mathcal {P}},\mathbf{x }^2)/ \partial p_l]/\Phi _m({\mathcal {P}},\mathbf{x }^2) \ge [\partial \Phi _n({\mathcal {P}},\mathbf{x }^1)/ \partial p_l]/ \Phi _n({\mathcal {P}},\mathbf{x }^1) \\&\quad \Rightarrow [\partial \Psi _m({\mathcal {P}},\mathbf{x }^2)/ \partial p_l]/\Psi _m({\mathcal {P}},\mathbf{x }^2) \ge [\partial \Psi _n({\mathcal {P}},\mathbf{x }^1)/ \partial p_l]/ \Psi _n({\mathcal {P}},\mathbf{x }^1). \end{aligned}$$

This is equivalent to the statement:

$$\begin{aligned} e_{ml}(\mathbf{x }^2) \ge e_{ml}(\mathbf{x }^1) \Rightarrow e_{nl}(\mathbf{x }^2) \ge e_{nl}(\mathbf{x }^1) \end{aligned}$$

Hence, (i) and (ii) are equivalent. $\square$

Appendix 3: Examples

Example 8.1

Consider the following demand function for an individual good: $\phi _m(p_m,x)=\frac{\alpha x(x-\gamma p_m)}{x+\beta p_m}$, where $\alpha> 0,\beta > 0,\gamma \ge 0$. This is characteristic of demand for luxuries. One has

$$\begin{aligned} \phi _m''(p_m,x)= & {} \frac{2\alpha \beta ^2 p_m^2+2\alpha \gamma \beta p_m^2}{(x+\beta p_m)^3}\\ \phi _m'''(p_m,x)= & {} -3\frac{2\alpha \beta ^2 p_m^2+2\alpha \gamma \beta p_m^2}{(x+\beta p_m)^4}\\ \partial \phi _m''(p_m,x)/\partial p_m= & {} (\gamma +\beta )\frac{4\beta p_m x-2 \beta ^2 p_m^2}{(x+\beta p_m)^4}\\ \partial \phi _m'''(p_m,x)/\partial p_m= & {} (\gamma +\beta )\frac{-12x\beta p_m+12\beta ^2p_m^2}{(x+\beta p_m)^5} \end{aligned}$$

Note that $\phi _m$ satisfies the conditions of part (i) of Corollary 3.1: $\phi _m(p_m, x)$ and $\partial \phi _m(p_m, x)/\partial p_l$ are convex with respect to x;

$\partial ^3\phi _m(p_m,x)/\partial ^3 x <0$, and $\partial ^4\phi _m(p_m,x)/\partial p_l\partial ^3 x<0$ on the set $S_1=\{(p_m,x): x>\beta p_m\}$.

Example 8.2

Consider the following demand function for an individual good: $\phi _m(p_m,\alpha ,\beta ,x)=\alpha x/(x+\beta p_m)$, where $\alpha , \beta >0$. This is characteristic of demand for necessities. One has

$$\begin{aligned} \phi _m''(p_m,x)= & {} -2\frac{\alpha \beta p_m}{(x+\beta p_m)^3}\\ \phi _m'''(p_m,x)= & {} 6\frac{\alpha \beta p_m}{(x+\beta p_m)^4}\\ \partial \phi _m''(p_m,x)/\partial p_m= & {} -2 \beta \alpha \frac{x-\beta p_m}{(x+\beta p_m)^4}\\ \partial \phi _m'''(p_m,x)/\partial p_m= & {} 2 \beta \alpha \frac{3x - 5\beta p_m}{(x+\beta p_m)^5} \end{aligned}$$

Note that $\phi _m$ satisfies the conditions: $\phi _m(P_m, x)$; $\partial \phi _m(P_m, x)/\partial p_l$ are concave with respect to x; $\partial ^3\phi _m(P_m,x)/\partial ^3 x>0$, and $\partial ^4\phi _m(p_m,x)/\partial p_l\partial ^3 x>0$ on the set $S_1=\{(p_m,x): x>5\beta p_m/3\}$.

.