The Intuition Behind Income Effects of Price Changes in Discrete Choice Models, and a Simple Method for Measuring the Compensating Variation

Abstract

Small and Rosen’s (Econometrica 49(1):105–130, 1981) method for measuring consumer surplus using discrete choice models has been widely adopted in public policy analysis. For the case of a price change, the present paper elucidates five theoretical assumptions inherent within Small and Rosen’s measure, and employs indifference maps to demonstrate that this measure is only applicable to the context of a single discrete choice free of non-linear income effects. The paper argues that, where non-linear income effects are present, the aforementioned theoretical assumptions should be relaxed, and the consumption context revised from discrete choice to discrete–continuous demand. Furthermore, the paper proposes a simple analytical method for approximating the expected Hicksian compensating variation in the presence of non-linear income effects, and compares the empirical performance of this method against existing methods using data from Morey et al. (Am J Agric Econ 75(3):578–592, 1993). As well as offering a simple approximation, the proposed method yields insights on the potential range of the compensating variation depending on the extent of switching between choice alternatives, and on the attribution of the compensating variation to the relevant choice alternatives.

1 Introduction

Discrete choice models are routinely commissioned by planning authorities, as a tool for predicting the impacts of policy interventions on demand and welfare. Such interventions may take many forms, but fundamental to economic interests are those which affect prices and/or incomes. Discrete choice models are conventionally estimated on individual-level preference data, whereas planning authorities are focussed more on the preferences of the market or society as a whole. This provokes an interesting question of how discrete choices can be defensibly aggregated, so as to yield market- or societal-level forecasts of quantity demanded and welfare following price and/or income changes.

In what follows, we will conceptualise the interaction between choice and demand in terms of Small and Rosen’s (1981)¹ model of discrete–continuous demand. According to this model, an individual is offered a set of mutually exclusive goods from which he/she is invited to select their preferred good (e.g. choice of recreation site) and, conditional upon that choice, the individual consumes a quantity of a commodity (e.g. number of trips to the chosen site). The principal outcome of S&R’s paper is the derivation of a consumer surplus measure specific to the discrete choice component of the discrete–continuous demand.²

S&R’s consumer surplus measure is defined in terms of the representative consumer (Gorman 1953), and conveniently allows the aggregation of discrete choices across individuals. However, as is widely acknowledged, a limiting property of S&R’s measure is that non-linear income effects³ of price (and lump sum income) changes are excluded. This property straightforwardly ensures path independence (Morey 1984), but is rather strong, and potentially introduces bias into the resulting measure of surplus. Recognising this limitation, a number of contributors (e.g. Hau 1985; Jara-Díaz and Videla 1989, 1990; McFadden 1995; Herriges and Kling 1999; Karlström 1999; Karlström and Morey 2001; Dagsvik and Karlström 2005; de Palma and Kilani 2011) have explored methods for estimating the corresponding Hicksian compensating variation. The attraction of the compensating variation is that, unlike S&R’s measure, it elicits a path independent measure of consumer surplus—even when non-linear income effects are admitted.

Against this background, the present paper will seek to make four contributions:

• 1. Following a brief overview of S&R’s welfare measure and elucidation of its underlying assumptions (Sect. 2), we will translate S&R’s algebraic presentation into a diagrammatic one using indifference maps.

• 2. Using S&R’s model of discrete–continuous demand, we will develop an intuition for modelling linear income effects and/or substitution effects of price changes through the ‘numeraire’ good (Sect. 3). Whilst S&R’s paper devotes only passing comment to the numeraire good, the present paper will show that it plays a crucial role within S&R’s consumer surplus measure.

• 3. With a few exceptions (e.g. Karlström and Morey 2001; de Palma and Kilani 2011), the literature has devoted limited discussion to the intuition behind non-linear income effects in discrete choice consumption contexts. Using S&R’s model of discrete–continuous demand, we will develop an intuition for modelling non-linear income effects of price changes through the conditional demand (Sect. 4).

• 4. Despite the interest in measuring the Hicksian compensating variation, practical application has hitherto been impeded by the computational requirements of the candidate methods. Against this background, we will propose a simple method for approximating the Hicksian compensating variation (also Sect. 4), and illustrate its application using analytical and empirical examples (Sect. 5).

2 Some Preliminary Definitions and Concepts

This section will introduce notation and briefly summarise the standard presentation of S&R’s model of discrete–continuous demand. Readers already initiated in S&R may wish to proceed directly to Sect. 3.

2.1 S&R’s Model of Discrete–Continuous Demand

Following S&R, let us consider the problem of an individual consuming a bundle of three goods, where the first two goods are mutually exclusive, and the third good acts as a numeraire.⁴ More formally, the individual faces the following maximisation problem:

$$\begin{array}{*{20}l} {\text{Max}} \hfill & {u = u\left( {\mathbf{x}} \right)} \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {p_{1} x_{1} + p_{2} x_{2} + x_{n} = y} \hfill \\ {} \hfill & {x_{1} x_{2} = 0} \hfill \\ {} \hfill & {{\mathbf{x}} \ge 0} \hfill \\ \end{array}$$

(1)

where $u$ is direct utility; ${\mathbf{x}} = \left( {x_{1} ,x_{2} ,x_{n} } \right)$ is a bundle comprising the consumed quantities of goods 1, 2 and the numeraire good $n$; ${\mathbf{p}} = \left( {p_{1} ,p_{2} ,1} \right)$ is the associated vector of prices for goods 1, 2 and $n$; and $y$ is income. The price of the numeraire good is set to one, such that the numeraire good and income are normalised to the same units. S&R conceptualised (1) as a problem of discrete–continuous demand, whereby the individual first chooses between goods 1 and 2 according to which yields the greater utility. We denote this choice:

$$u^{*} \left( {\mathbf{x}} \right) = v^{*} \left( {{\mathbf{p}},y} \right) = \tilde{v}_{k} \left( {p_{k} ,y} \right) = {\text{Max}}\left\{ {\tilde{v}_{1} \left( {p_{1} ,y} \right),\tilde{v}_{2} \left( {p_{2} ,y} \right)} \right\}$$

(2)

where $u^{*}$ is the maximum direct utility given income $y$, $v^{*}$ is the maximum indirect utility, $\tilde{v}_{k}$ is the conditional indirect utility, and $k$ indexes the chosen (i.e. utility maximising) good, i.e. $k = 1$ if $\tilde{v}_{1} \ge \tilde{v}_{2}$, or $k = 2$ otherwise.

In the manner of S&R’s Eq. 3.16, let us relate the conditional demand $\tilde{x}_{j}$ (i.e. conditional upon the discrete choice between goods 1 and 2) to the unconditional demand $x_{j}$, as follows:

$$x_{j} \left( {{\mathbf{p}},y} \right) = \delta_{j} \left( {{\mathbf{p}},y} \right)\, \cdot \tilde{x}_{j} \left( {p_{j} ,y} \right)\quad {\text{for}}\;j = 1,2$$

(3)

where $\delta_{j}$ is the uncompensated discrete choice indicator; e.g. $\delta_{1} = 1$ if $k = 1$ (i.e. if $\tilde{v}_{1}^{{}} \left( {p_{1} ,y} \right) \ge \tilde{v}_{2}^{{}} \left( {p_{2} ,y} \right)$, and good 1 is therefore chosen) or $\delta_{1} = 0$ if $k = 2$. S&R also proposed a probabilistic notion of the discrete choice indicator,⁵ re-stating (3) in terms of the expected demand for goods 1 and 2, from the perspective of the representative consumer:

$$x_{j} \left( {{\mathbf{p}},y} \right) = \pi_{j} \left( {{\mathbf{p}},y} \right) \cdot \tilde{x}_{j} \left( {p_{j} ,y} \right)\quad {\text{for}}\;j = 1,2$$

(4)

where $\pi_{j}$ denotes the uncompensated probabilistic demand for good $j$ (i.e. $\sum\nolimits_{j = 1,2} {\pi_{j} \left( {{\mathbf{p}},y} \right) = 1}$).

2.2 Comparative Statics of the Discrete–Continuous Demand

Within the framework of (4), we can examine the comparative statics of the discrete–continuous demand in response to price changes, via the usual apparatus of the Slutsky equation. Batley and Ibáñez (2013a) presented detailed derivations of the Slutsky equation, expanding upon the working in S&R. For present purposes, it will suffice to simply report the outcomes of these derivations, which are as follows for the probabilistic and conditional demands, respectively⁶:

$$\frac{{\partial \pi_{j}^{c} }}{{\partial p_{j} }} = \frac{{\partial \pi_{j} }}{{\partial p_{j} }} + \frac{{\partial \pi_{j} }}{\partial y}x_{j} \quad {\text{for}}\;j = 1,2$$

(5)

$$\frac{{\partial \tilde{x}_{j}^{c} }}{{\partial p_{j} }} = \frac{{\partial \tilde{x}_{j} }}{{\partial p_{j} }} + \frac{{\partial \tilde{x}_{j} }}{\partial y}\tilde{x}_{j} \quad {\text{for}}\;j = 1,2$$

(6)

where $\pi_{j}^{c}$ is the compensated probabilistic demand for good $j$, and $\tilde{x}_{j}^{c}$ is the compensated conditional demand for good $j$. In principle, (5) and (6) give rise to both a substitution effect (i.e. the first component of each summation) and an income effect (i.e. the second component). In practice, however, an income effect (at least a non-linear one) manifests only in the case of the conditional demand (6). This point, which we will justify in Sects. 3 and 4, is fundamental to the present paper.

2.3 Econometric Specification of the Probabilistic Demand

The diagrammatic analysis that follows in subsequent sections will make an important distinction between the discrete–continuous demand [which gives rise to the expected demand (4)] and the restricted case of a single discrete choice (where $\tilde{x}_{j} = 1$ for $j = 1,2$, and (4) simplifies to the probabilistic demand). Mindful of our interest in deriving consumer surplus, it will be important to ensure that the probabilistic demand is consistent with microeconomic theory, and this motivates our adoption of the Random Utility Model (RUM). With reference to Marschak (1960) and Block and Marschak (1960), who conceived RUM, and Daly and Zachary (1978), who formalised RUM in mathematical terms, define:

$$\pi_{j}^{{}} = { \Pr }\left\{ {\tilde{v}_{j}^{{}} \left( {p_{j} ,y} \right) \ge \tilde{v}_{m}^{{}} \left( {p_{m} ,y} \right)} \right\}\quad {\text{for}}\quad j,m = 1,2\quad m \ne j$$

(7)

where $\tilde{v}_{j}^{{}}$ is the conditional indirect utility of good $j$ as before. If we then dissect conditional indirect utility such that $\tilde{v}_{j}^{{}} \left( {p_{j} ,y} \right) = W_{j} \left( {p_{j} ,y} \right) + \varepsilon_{j}^{{}}$, where $W_{j}$ is deterministic utility and $\varepsilon_{j}^{{}}$ is a random term independent of $W_{j}$, and substitute in (7), then we have:

$$\begin{aligned} \pi_{j} & = { \Pr }\left\{ {W_{j} \left( {p_{j} ,y} \right) + \varepsilon_{j}^{{}} \ge W_{m} \left( {p_{m} ,y} \right) + \varepsilon_{m}^{{}} } \right\} \\ & = \varphi \left( {W_{j} \left( {p_{j} ,y} \right) - W_{m} \left( {p_{m} ,y} \right)} \right)\quad {\text{for}}\quad j,m = 1,2\quad m \ne j \\ \end{aligned}$$

(8)

where $\varphi$ is the cumulative density function of $\varepsilon_{m} - \varepsilon_{j}$.

Expanding upon previous work by others (e.g. Hau 1985, 1987; Jara-Díaz and Videla 1990), Batley and Ibáñez (2013a) showed that, in the restricted case of discrete choice, compliance of the expected demand (4) with the fundamental properties of demand functions—i.e. adding-up, negativity, homogeneity and symmetry—calls for five assumptions, as follows⁷:

• Assumption I: unit conditional demand for goods 1 and 2, i.e. $\tilde{x}_{1} = \tilde{x}_{2} = 1$

• Assumption II: for each good, equivalence (in absolute value) between the conditional marginal utilities of income and price, i.e. $- {{\partial W_{1} } \mathord{\left/ {\vphantom {{\partial W_{1} } {\partial p_{1} = {{\partial W_{1} } \mathord{\left/ {\vphantom {{\partial W_{1} } {\partial y}}} \right. \kern-0pt} {\partial y}}}}} \right. \kern-0pt} {\partial p_{1} = {{\partial W_{1} } \mathord{\left/ {\vphantom {{\partial W_{1} } {\partial y}}} \right. \kern-0pt} {\partial y}}}},\; - {{\partial W_{2} } \mathord{\left/ {\vphantom {{\partial W_{2} } {\partial p_{2} = {{\partial W_{2} } \mathord{\left/ {\vphantom {{\partial W_{2} } {\partial y}}} \right. \kern-0pt} {\partial y}}}}} \right. \kern-0pt} {\partial p_{2} = {{\partial W_{2} } \mathord{\left/ {\vphantom {{\partial W_{2} } {\partial y}}} \right. \kern-0pt} {\partial y}}}}$

• Assumption III: the conditional marginal utility of income is common across goods, i.e. ${{\partial W_{1} } \mathord{\left/ {\vphantom {{\partial W_{1} } {\partial y = }}} \right. \kern-0pt} {\partial y = }}{{\partial W_{2} } \mathord{\left/ {\vphantom {{\partial W_{2} } {\partial y}}} \right. \kern-0pt} {\partial y}} = \lambda$

• Assumption IV: the conditional marginal utility of price is common across goods, i.e. ${{\partial W_{1} } \mathord{\left/ {\vphantom {{\partial W_{1} } {\partial p_{1} = }}} \right. \kern-0pt} {\partial p_{1} = }}{{\partial W_{2} } \mathord{\left/ {\vphantom {{\partial W_{2} } {\partial p_{2} }}} \right. \kern-0pt} {\partial p_{2} }} = - \lambda$

• Assumption V: the conditional marginal utility of income is independent of the prices of goods 1 and 2, i.e. ${{\partial \lambda } \mathord{\left/ {\vphantom {{\partial \lambda } {\partial p_{1} = {{\partial \lambda } \mathord{\left/ {\vphantom {{\partial \lambda } {\partial p_{2} = 0}}} \right. \kern-0pt} {\partial p_{2} = 0}}}}} \right. \kern-0pt} {\partial p_{1} = {{\partial \lambda } \mathord{\left/ {\vphantom {{\partial \lambda } {\partial p_{2} = 0}}} \right. \kern-0pt} {\partial p_{2} = 0}}}}$

Given Roy’s identity, some of these assumptions are inter-related, namely: Assumptions I and II each imply the other; Assumptions II and III together imply (but are not implied by) Assumption IV; and Assumptions II and IV together imply (but are not implied by) Assumption III. Thus, there are effectively three independent assumptions, and these assumptions will recur throughout the remainder of this paper.

2.4 Deriving Consumer Surplus from the Discrete–Continuous Demand

Completing our discussion of preliminary concepts, let us consider the change in consumer surplus associated with a given change in price with income held constant. We begin by deriving consumer surplus change from the general model of discrete–continuous demand, before restricting the model to discrete choice.

In general terms, and with reference to (1), consider the change in direct utility between Do-Nothing and Do-Something states (which we denote 0 and 1, respectively):

$$\Delta u = u\left( {{\mathbf{x}}_{{}}^{1} } \right) - u\left( {{\mathbf{x}}_{{}}^{0} } \right)$$

(9)

With reference to (2), we can re-state (9) equivalently in terms of indirect utility:

$$\Delta u = \Delta v = v\left( {{\mathbf{p}}_{{}}^{1} ,y} \right) - v\left( {{\mathbf{p}}_{{}}^{0} ,y} \right)$$

(10)

Substituting from (4), the expected discrete–continuous demand model gives rise to the following analogy to (10):

$$\begin{aligned} & \Delta E\left( v \right) = - \lambda \cdot \int_{{{\mathbf{p}}^{0} }}^{{{\mathbf{p}}^{1} }} {\left( {\sum\nolimits_{j = 1,2} {\pi_{j} \left( {{\mathbf{p}},y} \right) \cdot \tilde{x}_{j} \left( {p_{j} ,y} \right)} } \right)\,d{\mathbf{p}}\quad } \\ & {\text{where}}\quad \pi_{j} \left( {{\mathbf{p}},y} \right) = \pi_{j} \left( {W_{j} \left( {p_{j} ,y} \right) - W_{m} \left( {p_{m} ,y} \right)} \right)\quad {\text{for}}\;j,m = 1,2\quad m \ne j \\ \end{aligned}$$

(11)

and where $\lambda$ denotes the conditional marginal utility of income for the representative consumer.⁸ The change in expected consumer surplus is thus elicited by integrating the expectation of the uncompensated (i.e. Marshallian) demands for goods 1 and 2 with respect to the relevant price change, and transforming the resulting money measure into utils by means of the marginal utility of income, i.e. $\lambda$.

Let us now focus upon the probabilistic demand, which restricts (11) to the case of a single discrete choice (i.e. $\tilde{x}_{j} = 1$ for $j = 1,2$). Referring back to (8), which introduced RUM, deterministic utility is a function of price, but the random term is independent of price. On this basis, the change in expected consumer surplus can be elicited by integrating the uncompensated probabilistic demand with respect to the change in deterministic utility associated with the change in price.

$$\Delta E\left( v \right) = \int_{{W_{j}^{0} }}^{{W_{j}^{1} }} {\pi_{j} \left( {W_{j} \left( {p_{j} ,y} \right) - W_{m} \left( {p_{m} ,y} \right)} \right)} \,dW_{j} \quad {\text{for}}\;j,m = 1,2\quad m \ne j$$

(12)

Since RUM embodies the ‘translational invariance’ property, meaning that only differences in deterministic utility influence probability, and because we are working in the binary case, consumer surplus change can be measured from the perspective of either good 1 or good 2. In the particular case where the random term in (8) is distributed Multivariate Extreme Value (MEV), RUM adopts the logit form, and (12) gives rise to the well-known ‘log sum’ formulation:

$$\Delta E\left( v \right) = \ln \left( {\sum\nolimits_{j = 1,2} {\exp \left( {W_{j} \left( {p_{j}^{1} ,y} \right)} \right)} } \right) - \ln \left( {\sum\nolimits_{j = 1,2} {\exp \left( {W_{j} \left( {p_{j}^{0} ,y} \right)} \right)} } \right)$$

(13)

Batley and Ibáñez (2013a) showed that, given Assumptions I–V, non-linear income effects of price (and lump sum income) changes will be excluded. Furthermore, if linear as well as non-linear income effects are absent, then (13) can be interpreted not only as the expected change in Marshallian consumer surplus, but also as the expected Hicksian compensating variation.

3 The Income Effects of a Price Change in the Discrete Choice Case

From a Marshallian perspective (i.e. admitting income effects of a price change, potentially in a non-linear fashion), the consumer surplus change can be represented as (10). Alternatively, the consumer surplus change can be measured using methods devised by Hicks (1943) and Slutsky (1915), which extract any income effects and in so doing ensure path independence. These measures determine the minimum/maximum quantity of money that must be given to/can be taken from an individual in order to leave him/her at the same utility (in the case of Hicks) or demand (in the case of Slutsky) as before the price increase/decrease. In more formal terms, these measures arise from the following identities, respectively:

$$v\left( {{\mathbf{p}}_{{}}^{1} ,y - h} \right) = v\left( {{\mathbf{p}}_{{}}^{0} ,y} \right)$$

(14)

$${\mathbf{x}}\left( {{\mathbf{p}}_{{}}^{1} ,y - s} \right) = {\mathbf{x}}\left( {{\mathbf{p}}_{{}}^{0} ,y} \right)$$

(15)

where $h$ is the Hicksian compensating variation, and $s$ is the Slutsky compensating variation. Conventionally, $h,s < 0$ in the case of a price increase, and $h,s > 0$ in the case of a price reduction. A focus of the subsequent discussion will be the presence or absence of income effects and, by implication, the distinction between path dependent and path independent measures of consumer surplus change.

3.1 A Diagrammatic Exposition of the Discrete–Continuous Demand Problem

Having introduced S&R’s discrete–continuous demand problem algebraically, the subsequent discussion will translate the algebraic analysis into a diagrammatic one—this exercise will expose some additional features of the problem at hand.

From a deterministic (3) as opposed to probabilistic (4) perspective, it will prove useful to tighten S&R’s commentary around the budget constraint in (1), by re-stating:

$$y = \sum\nolimits_{j = 1,2} {\delta_{j} \cdot } \left( {p_{j} \tilde{x}_{j} + \left. {x_{n} } \right|_{{\delta_{j}^{ + } }} } \right)$$

(16)

This re-statement clarifies that demand for the numeraire will be conditioned by the choice of good 1 or 2, since expenditure on either good may vary, and the numeraire will account for the residual of the budget once this expenditure has been transacted. Whilst not explicitly discussed by S&R, (16) alludes to the key property that, provided the numeraire is infinitely divisible, goods 1 or 2 can be combined with the numeraire to form composite goods.

In the case of a single discrete choice, (16) further simplifies to:

$$y = \sum\nolimits_{j = 1,2} {\delta_{j} \cdot \left( {p_{j} + \left. {x_{n} } \right|_{{\delta_{j}^{ + } }} } \right)}$$

(17)

Conditional upon choosing a single unit of either good 1 or 2, it must then hold that:

$$\frac{y}{{p_{j} }} = \frac{{p_{j} + \left. {x_{n} } \right|_{{\delta_{j}^{ + } }} }}{{p_{j} }}\quad {\text{for}}\;j = 1,2$$

(18)

Clearly, if $\left. {x_{n} } \right|_{{\delta_{j}^{ + } }} > 0$ then ${y \mathord{\left/ {\vphantom {y {p_{j} }}} \right. \kern-0pt} {p_{j} }} > 1$. Furthermore, define:

$$\frac{y}{{\tilde{p}_{j} }} = \frac{{p_{j} + \left. {x_{n} } \right|_{{\delta_{j}^{ + } }} }}{{\tilde{p}_{j} }} = 1\quad {\text{for}}\;j = 1,2$$

(19)

where $\tilde{p}_{j}$ is the conditional price of goods $j = 1,2$, which might otherwise be interpreted as the price of the relevant composite good. That is to say, since the same budget applies to both goods 1 and 2, and the numeraire accounts for any residual of that budget, the choice between goods 1 and 2 can alternatively be conceptualised as choosing between single units of their respective composite goods.

From (19), it must further hold that:

$$\frac{{p_{1} + \left. {x_{n} } \right|_{{\delta_{1}^{ + } }} }}{{p_{2} + \left. {x_{n} } \right|_{{\delta_{2}^{ + } }} }} = \frac{{\tilde{p}_{1} }}{{\tilde{p}_{2} }} = 1$$

Thus, in State 0, it must be the case that the conditional prices of goods 1 and 2 are equal.⁹

Against this background, Figs. 1 and 2 show an indifference map for an individual defined on the dimensions $x_{1}$ and $x_{2}$; the distinction between the two figures is that the first refers to the general case of discrete–continuous demand, whereas the second refers to the restricted case of a single discrete choice.

Fig. 1

Discrete-continuous demand for goods 1 and 2 in response to a price reduction, given a deterministic discrete choice indicator

Fig. 2

Discrete choice for goods 1 and 2 and demand for the numeraire good in response to a price reduction, given a deterministic discrete choice indicator

If we substitute for $x_{1}$ and $x_{2}$ using our discrete–continuous demand model (3), which employs the deterministic discrete choice indicator, then we can represent the indifference maps on the dimensions $\delta_{1} \cdot \tilde{x}_{1}$ and $\delta_{2} \cdot \tilde{x}_{2}$. If we further assume $\left. {x_{n}^{0} } \right|_{{\delta_{j}^{ + } }} = 0$ for $j = 1,2$, such that demand for the numeraire good is zero in State 0, then this will afford us a degree of expositional convenience (but this assumption will be relaxed in the practical applications of Sect. 5). On this basis, define ${\mathbf{x}}^{0} = \left( {x_{1}^{0} ,x_{2}^{0} ,0} \right)$ to be the vector of demands (comprising the quantities of goods 1, 2 and $n$, respectively) at initial prices ${\mathbf{p}}^{0} = \left( {p_{1}^{0} ,p_{2}^{0} ,1} \right)$. If we also assume $x_{1} x_{2} = 0$ as per (1), then consumption is further restricted to one of two specific bundles (i.e. $\delta_{1} = 1$ and $\delta_{2} = 0$ if good 1 is chosen, or vice versa if good 2 is chosen),¹⁰ such that budget will be wholly devoted to:

• Good 1, giving rise to ${\mathbf{x}}^{0} = \left( {\tilde{x}_{1}^{0} ,0,0} \right)$; or

• Good 2, giving rise to ${\mathbf{x}}^{0} = \left( {0,\tilde{x}_{2}^{0} ,0} \right)$.

Since the budget constraint in (1) is specified as an equality, consumption of either bundle will exhaust total budget $y$,¹¹ giving rise to one of the following corner solutions:

$$\tilde{x}_{1}^{0} = \frac{y}{{p_{1}^{0} }},\quad \tilde{x}_{2}^{0} = \frac{y}{{p_{2}^{0} }}$$

(20)

If we now consider a change in prices from ${\mathbf{p}}^{0}$ in the Do-Nothing to ${\mathbf{p}}^{1} = \left( {p_{1}^{1} ,p_{2}^{1} ,1} \right)$ in the Do-Something, entailing a reduction in the price of good 2 with other prices held constant, then feasible consumption of good 2 will increase, whilst feasible consumption of good 1 will remain unchanged, i.e.

$$\tilde{x}_{1}^{1} = \frac{y}{{p_{1}^{1} }} = \tilde{x}_{1}^{0} ,\quad \tilde{x}_{2}^{1} = \frac{y}{{p_{2}^{1} }} > \tilde{x}_{2}^{0}$$

(21)

This case is shown explicitly in Fig. 1, where the initial budget constraint is labelled ${\mathbf{p}}^{0}$, and the new budget constraint following the price reduction is labelled ${\mathbf{p}}^{1}$. That is to say, the reduction in the price of good 2 is represented by the budget constraint pivoting on the allocation $\left( {\tilde{x}_{1}^{0} ,0,0} \right)$, and outwards from $\left( {0,\tilde{x}_{2}^{0} ,0} \right)$ to $\left( {0,\tilde{x}_{2}^{1} ,0} \right)$. The same case is shown implicitly in Fig. 2, where the increased purchasing power arising from the price reduction is represented in terms of increased consumption of the numeraire good—as proxy for increased consumption of good 2. This distinction will be discussed further in what follows.

3.2 The Three Demand Responses

Supported by the above rationale, let us further develop the example of a reduction in the price of good 2, distinguishing between the effects on the discrete choice and the conditional demand respectively. In relating (20) and (21) to S&R’s problem of discrete–continuous demand, we must countenance the possibility that a change in prices may induce a change in preferences in (2), i.e. the utility maximising good $k$ in States 0 and 1 may differ. On this basis, Karlström and Morey (2001) considered three groups of individuals, namely:

• Group A: individuals who choose good 1 both before and after the reduction in the price of good 2;

• Group B: individuals who choose good 2 both before and after the reduction in the price of good 2;

• Group C: individuals who choose good 1 before the reduction in the price of good 2, and good 2 after.

The subsequent sections will consider Groups A, B and C diagrammatically, showing the demand response and compensating variation in each instance.

3.2.1 Group A

With regards to Group A, and drawing reference to both Figs. 1 and 2, consider an individual who chooses good 1 both before, i.e. ${\mathbf{x}}_{A}^{0} = \left( {\tilde{x}_{1}^{0} ,0,0} \right)$, and after, i.e. ${\mathbf{x}}_{A}^{1} = \left( {\tilde{x}_{1}^{1} ,0,0} \right)$, the reduction in the price of good 2. Since $\tilde{x}_{1}^{0} = \tilde{x}_{1}^{1}$ and $\tilde{x}_{2}^{0} = \tilde{x}_{2}^{1} = 0$, the price reduction has no impact on demand (or welfare).

3.2.2 Group B

With regards to Group B, consider an individual who chooses good 2 both before and after the reduction in the price of good 2, i.e. ${\mathbf{x}}_{B}^{0} = \left( {0,\tilde{x}_{2}^{0} ,0} \right)$ and ${\mathbf{x}}_{B}^{1} = \left( {0,\tilde{x}_{2}^{1} ,0} \right)$. With reference to Fig. 1, the increased purchasing power associated with the reduction in $p_{2}$ is entirely devoted to increased conditional demand for good 2, i.e. $\tilde{x}_{2}^{1} > \tilde{x}_{2}^{0}$. On this basis, we can develop a Slutsky decomposition of the price reduction, by tracing the budget constraint applying to the new prices ${\mathbf{p}}_{{}}^{1}$ back to the initial bundle ${\mathbf{x}}_{B}^{0} = \left( {0,\tilde{x}_{2}^{0} ,0} \right)$, using the construct of the dotted budget constraint. Relating this decomposition to the Slutsky equation for the conditional demand (6), the price reduction affects only the demand for good 2, implying that there is zero substitution between goods 1 and 2, and that the increase in demand for good 2 arises from a quasi-linear income effect. Since ${\mathbf{x}}_{B}^{1} = \left( {0,\tilde{x}_{2}^{1} ,0} \right)$ entails a corner solution, the compensating variation $\tilde{s}_{2}$ shown in Fig. 1 employs demand (rather than utility) as the benchmark [i.e. in the manner of (15)], and should therefore be interpreted as the conditional Slutsky compensating variation; the same interpretation applies to Group C in the following sub-section.

With reference to Fig. 2, we can repeat our consideration of Group B but this time imposing $\tilde{x}_{1} = \tilde{x}_{2} = 1$ (i.e. Assumption I), which restricts our model of discrete–continuous demand to a single discrete choice. If the discrete choice between goods 1 and 2 is the extent of the individual’s consumption possibilities, then $y = \tilde{p}_{1} = \tilde{p}_{2}$ must hold in both the Do-Nothing and Do-Something via (17), and the individual will be unable to realise the potential for a compensating variation by consuming additional units of good 2.¹² On the other hand, if in the Do-Something we admit the numeraire good (i.e. $x_{n}^{1} > 0$), then we can via (18) derive an analogy to (21):

$$\tilde{x}_{2}^{1} = \frac{y}{{p_{2}^{1} }} = \frac{{p_{2}^{1} + \left. {x_{n}^{1} } \right|_{{\delta_{2}^{ + } }} }}{{p_{2}^{1} }} = 1 + \frac{{\left. {x_{n}^{1} } \right|_{{\delta_{2}^{ + } }} }}{{p_{2}^{1} }}$$

where good 2 is reconstituted as a composite of the numeraire good, and the numeraire effectively becomes a proxy for the conditional Slutsky compensating variation. Given the reduction in the price of good 2, the individual is able to consume the initial bundle ${\mathbf{x}}_{B}^{0} = \left( {0,1,0} \right)$ with reduced income, and can additionally devote the income saving to consumption of the numeraire good, realising a final bundle ${\mathbf{x}}_{B}^{1} = \left( {0,1,\left. {x_{n}^{1} } \right|_{{\delta_{2}^{ + } }} } \right)$. That is to say, in the event that $\tilde{x}_{2}^{0} = \tilde{x}_{2}^{1} = 1$ becomes a limiting property, the numeraire good can compensate for the inability of the individual to consume additional units of good 2. Therefore, even in the restricted case of a single discrete choice, the individual can—through admission of the numeraire good in the Do-Something—realise the conditional Slutsky compensating variation ($\tilde{s}_{2}$ in Fig. 2) from the reduction in the price of good 2.

3.2.3 Group C

With regards to Group C, consider an individual who chooses good 1 before the reduction in the price of good 2, and good 2 after. Returning to the discrete–continuous case (Fig. 1), the relevant consumption bundles are ${\mathbf{x}}_{C}^{0} = \left( {\tilde{x}_{1}^{0} ,0,0} \right)$ and ${\mathbf{x}}_{C}^{1} = \left( {0,\tilde{x}_{2}^{1} ,0} \right)$. This situation comes with some difficulties of interpretation. One way of interpreting Group C would be to reason that the change in demand from the initial bundle ${\mathbf{x}}_{C}^{0}$ to the new bundle ${\mathbf{x}}_{C}^{1}$ represents a pure substitution effect, but with no compensating variation, since both bundles fall on the new budget constraint under prices ${\mathbf{p}}_{{}}^{1}$. However, the proposition that a price reduction realises no compensating variation might appear less than intuitive. If that were the case, the consumer would have no incentive to switch. With that sentiment in mind, let us develop an alternative interpretation by acknowledging that good 1 was preferred to good 2 at prices ${\mathbf{p}}_{{}}^{0}$. Since good 1 must have been at least as attractive as good 2 at those prices (i.e. $u\left( {\tilde{x}_{1}^{0} ,0,0} \right) \ge u\left( {0,\tilde{x}_{2}^{0} ,0} \right)$), we can trace the budget constraint applying to the new prices ${\mathbf{p}}_{{}}^{1}$ back to the bundle $\left( {0,\tilde{x}_{2}^{0} ,0} \right)$, and reason that, depending on the strength of preference for $\left( {\tilde{x}_{1}^{0} ,0,0} \right)$ over $\left( {0,\tilde{x}_{2}^{0} ,0} \right)$ at prices ${\mathbf{p}}_{{}}^{0}$, the conditional Slutsky compensating variation of the change in prices to ${\mathbf{p}}_{{}}^{1}$ must be within the range zero to $\tilde{s}_{2}$. That is to say, if the individual had been indifferent between $\left( {\tilde{x}_{1}^{0} ,0,0} \right)$ and $\left( {0,\tilde{x}_{2}^{0} ,0} \right)$ at ${\mathbf{p}}_{{}}^{0}$, then the conditional Slutsky compensating variation would be $\tilde{s}_{2}$. On the other hand, if $\left( {\tilde{x}_{1}^{0} ,0,0} \right)$ had been strongly preferred to $\left( {0,\tilde{x}_{2}^{0} ,0} \right)$, then the compensating variation would be closer to zero, consistent with our initial line of reasoning.

If we now restrict Group C to a single discrete choice but admit the numeraire good in the Do-Something (Fig. 2), then the relevant bundles before and after the reduction in the price of good 2 become ${\mathbf{x}}_{C}^{0} = \left( {1,0,0} \right)$ and ${\mathbf{x}}_{C}^{1} = \left( {0,1,\left. {x_{n}^{1} } \right|_{{\delta_{2}^{ + } }} } \right)$ respectively. In an analogous manner to Group B, the conditional Slutsky compensating variation can in this case be realised through the numeraire good (whilst acknowledging that the point of switching remains uncertain).

3.3 Rationalising the Practical Application of S&R’s Consumer Surplus Measure

The previous section has clarified that, for the restricted case of a single discrete choice, any compensating variation of a price change will, in principle, be due to a quasi-linear income effect (Group B) or a pure substitution effect (Group C). Accordingly, there is no conceptual basis for a non-linear income effect. In practice, however, it is important to understand two factors that will influence the magnitude of the aggregate compensating variation across the population; first, the composition of the population in terms of Group B and C individuals, and second, the strength of preference for good 2 over good 1 in the case of Group C individuals. In contrast to Sect. 3.2, which employed the discrete choice indicator [i.e. emanating from (3)], these factors call for the employment of the probabilistic choice indicator [i.e. emanating from (4)].

From a probabilistic perspective, it will again prove useful to tighten S&R’s commentary around the budget constraint in (1), by re-stating:

$$y = \sum\nolimits_{j = 1,2} {\pi_{j} \cdot } \left( {p_{j} \tilde{x}_{j} \left. { + x_{n} } \right|_{{\delta_{j}^{ + } }} } \right)$$

Analogous to the deterministic case, the probabilistic case can thus be conceptualised as a choice between two composite goods (i.e. combining either good 1 or 2 with the numeraire).

Substituting for $x_{1}$ and $x_{2}$ using (4), Fig. 3 shows an indifference map defined on the dimensions $\pi_{1} \cdot \tilde{x}_{1}$ and $\pi_{2} \cdot \tilde{x}_{2}$. If we further assume $\left. {x_{n}^{0} } \right|_{{\delta_{j}^{ + } }} = 0$ for $j = 1,2$, such that demand for the numeraire good is zero in State 0, then this will again afford us a degree of expositional convenience (but this assumption will be relaxed in the practical applications of Sect. 5). On this basis, and in common with Figs. 1 and 2, define ${\mathbf{x}}^{0} = \left( {x_{1}^{0} ,x_{2}^{0} ,0} \right)$ to be the vector of demands (comprising the quantities of goods 1, 2 and $n$, respectively) at initial prices ${\mathbf{p}}^{0} = \left( {p_{1}^{0} ,p_{2}^{0} ,1} \right)$. Unlike Figs. 1 and 2 which imposed the constraint $x_{1} x_{2} = 0$, Fig. 3 effectively relaxes this constraint, thereby allowing consumption of both goods 1 and 2 in combination.¹³ Referring back to Sect. 2.3, Fig. 3 allows the relaxation of Assumptions I and II (i.e. allowing the conditional demand for good 2 to be greater than one) and the relaxation of Assumption IV (i.e. potentially admitting a substitution effect, as will be discussed in what follows).

Fig. 3

Discrete choice for goods 1 and 2 and demand for the numeraire good in response to a price reduction, given a probabilistic discrete choice indicator

Whilst permitting such generality, it will be attractive from an expositional perspective to define State 0 in analogous terms to Fig. 2, such that Fig. 2 can be conceptualised as a restrictive case of Fig. 3. To this end, assume that State 0 entails unit conditional demands for goods 1 and 2 (i.e. $\tilde{x}_{1}^{0} = \tilde{x}_{2}^{0} = 1$, as per Assumption I); given zero demand for the numeraire, this assumption implies that goods 1 and 2 have common prices. Furthermore, assume that goods 1 and 2 have equal probability of being chosen (i.e. $\pi_{1}^{0} = \pi_{2}^{0} = 0.5$), implying that there are no differences in quality between the two goods. Whereas in the deterministic case consumption is restricted to allocations at either extreme of the budget line, the probabilistic case re-conceptualises the budget line as a continuum of possible allocations subject to the choice probabilities adding to one. In other words, the budget line also constitutes an indifference line. Therefore, whilst Fig. 3 assumes $\pi_{1}^{0} = \pi_{2}^{0} = 0.5$ in State 0, any deviation from these probabilities would entail a movement along the budget line. To illustrate, let us now change prices from ${\mathbf{p}}_{{}}^{0}$ to ${\mathbf{p}}_{{}}^{1}$, where State 1 entails a reduction in the price of good 2 with other prices held constant. This provokes the following demand responses:

• First, there is a substitution effect that accounts for an increase in the expected demand for the numeraire good from zero (i.e. the initial normalisation) to $\pi_{2}^{1} \cdot \left( {{{x_{n,se}^{1} } \mathord{\left/ {\vphantom {{x_{n,se}^{1} } {p_{2}^{1} }}} \right. \kern-0pt} {p_{2}^{1} }}} \right)$,¹⁴ and the movement from ${\mathbf{x}}^{0}$ to the intermediate bundle ${\mathbf{x}}^{se}$. This substitution effect can be further decomposed into the movement from ${\mathbf{x}}^{0}$ to ${\mathbf{x}}_{\pi }^{se}$, which accounts for the increase in the probability of choosing good 2 given conditional demands of one unit (i.e. along the line from $\tilde{x}_{1}^{0} = \tilde{x}_{1}^{1} = 1\,$ to $\tilde{x}_{2}^{0} = \tilde{x}_{2}^{1} = 1\,$, such that $\pi_{1}^{1} < \pi_{2}^{1}$), whilst the remainder of the movement to ${\mathbf{x}}^{se}$ accounts for substitution between good 1 and the numeraire. This substitution effect will be driven by Group C individuals.

• Second, there is an income effect specific to the numeraire good. This accounts for a further increase in the expected demand for the numeraire by $\pi_{2}^{1} \cdot \left( {{{x_{n,ie}^{1} } \mathord{\left/ {\vphantom {{x_{n,ie}^{1} } {p_{2}^{1} }}} \right. \kern-0pt} {p_{2}^{1} }}} \right)$, and the movement from ${\mathbf{x}}^{se}$ to the final equilibrium bundle ${\mathbf{x}}^{1}$. Consistent with path independence, the income expansion path ($IEP$) is linear. This income effect will be driven by Group B individuals.

The total demand response in the Do-Something is given by the expected demand for the numeraire good, i.e. $\pi_{2}^{1} \cdot \left( {{{x_{n}^{1} } \mathord{\left/ {\vphantom {{x_{n}^{1} } {p_{2} }}} \right. \kern-0pt} {p_{2} }}} \right) = \pi_{2}^{1} \cdot \left( {\left( {{{x_{n,se}^{1} } \mathord{\left/ {\vphantom {{x_{n,se}^{1} } {p_{2}^{1} }}} \right. \kern-0pt} {p_{2}^{1} }}} \right) + \left( {{{x_{n,ie}^{1} } \mathord{\left/ {\vphantom {{x_{n,ie}^{1} } {p_{2}^{1} }}} \right. \kern-0pt} {p_{2}^{1} }}} \right)} \right)$. Within this, the contribution from the substitution effect can be otherwise interpreted as the expected Slutsky compensating variation. Further to the earlier comment following (13), although non-linear income effects are absent from Fig. 3, the linear income effect represented by the $IEP$ will result in a discrepancy between the expected Slutsky compensating variation and the expected change in Marshallian consumer surplus.

4 The Income Effects of a Price Change in the Discrete Continuous Case

A key point emerging from Sect. 3 is that, in the restricted case of a single discrete choice, there is no facility for non-linear income effects of a price change. Indeed, we have sought to clarify that the method of employing the numeraire good as a proxy for the conditional demands for goods 1 and 2 is appropriate for representing linear income effects or substitution effects of a price change. The numeraire good cannot be similarly employed as a proxy where income effects are non-linear; this is clear from Marshall’s (1920) definition of the numeraire good in the context of partial equilibrium analysis.¹⁵ In order to admit non-linearity, we must instead represent income effects in terms of the (unrestricted) conditional demands for goods 1 and 2, as will now be demonstrated.

4.1 Admitting Non-linear Income Effects of a Price Change

Drawing upon the Slutsky equations (5) and (6), this section will formalise the proposition that non-linear income effects of a price change must be accommodated through the conditional demands, before presenting a diagrammatic illustration. The latter will provide the germ of a practical solution for measuring the compensating variation, which we will develop in Sect. 4.2.2. Let us begin by writing the Slutsky equation for the unconditional (expected) demand as a whole, i.e. combining (5) and (6):

$$\frac{{\partial x_{j}^{c} }}{{\partial p_{j} }} = \left( {\frac{{\partial \pi_{j} }}{{\partial p_{j} }} + \frac{{\partial \pi_{j} }}{\partial y}x_{j} } \right) \cdot \tilde{x}_{j}^{c} + \pi_{j}^{c} \cdot \left( {\frac{{\partial \tilde{x}_{j} }}{{\partial p_{j} }} + \frac{{\partial \tilde{x}_{j} }}{\partial y}\tilde{x}_{j} } \right)\quad {\text{for}}\;j = 1,2$$

(22)

In the context of (22), we will consider the potential for separate income effects of price changes in relation to the probabilistic and conditional demands.

With regards to the probabilistic demand within (22), and making use of the RUM definition (8), let us write the column matrix ${\varvec{\upeta}}$ consisting of the income effects of price changes on goods 1 and 2 (i.e. ${{\partial \pi_{j} } \mathord{\left/ {\vphantom {{\partial \pi_{j} } {\partial y}}} \right. \kern-0pt} {\partial y}} \cdot x_{j}$):

$${\varvec{\upeta}}\left( {\pi_{1} ,\pi_{2} } \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial \pi_{1} }}{{\partial W_{1} }} \frac{{\partial W_{1} }}{\partial y} x_{1} } \\ {\frac{{\partial \pi_{2} }}{{\partial W_{2} }} \frac{{\partial W_{2} }}{\partial y} x_{2} } \\ \end{array} } \right]$$

(23)

If we substitute for the unconditional (expected) demand using (4), acknowledge that ${{\partial \pi_{1} } \mathord{\left/ {\vphantom {{\partial \pi_{1} } {\partial W_{1} = {{\partial \pi_{2} } \mathord{\left/ {\vphantom {{\partial \pi_{2} } {\partial W_{2} }}} \right. \kern-0pt} {\partial W_{2} }}}}} \right. \kern-0pt} {\partial W_{1} = {{\partial \pi_{2} } \mathord{\left/ {\vphantom {{\partial \pi_{2} } {\partial W_{2} }}} \right. \kern-0pt} {\partial W_{2} }}}}$ holds by definition (Daly and Zachary 1978), and impose Assumptions I and III (which apply to the case of a single discrete choice, see Sect. 2.3), then (23) simplifies to:

$${\varvec{\upeta}}\left( {\pi_{1} ,\pi_{2} } \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial \pi_{1} }}{{\partial W_{1} }} \frac{{\partial W_{1} }}{\partial y} \pi_{1} } \\ {\frac{{\partial \pi_{1} }}{{\partial W_{1} }} \frac{{\partial W_{1} }}{\partial y} \pi_{2} } \\ \end{array} } \right]$$

(24)

In this way, (24) gives rise to the case shown in Fig. 3. Provided the numeraire good is present in the Do-Something, any income effects of price changes will be linear (i.e. common to goods 1 and 2), and collectively constrained by the requirement for $\pi_{1} + \pi_{2} = 1$.¹⁶

With regards to the conditional demand within (22), we can repeat the same exercise by writing the column matrix ${\varvec{\upeta}}$ of the income effects of price changes on goods 1 and 2 (i.e. ${{\partial \tilde{x}_{j} } \mathord{\left/ {\vphantom {{\partial \tilde{x}_{j} } {\partial y}}} \right. \kern-0pt} {\partial y}} \cdot \tilde{x}_{j}$):

$${\varvec{\upeta}}\left( {\tilde{x}_{1} ,\tilde{x}_{2} } \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial \tilde{x}_{1} }}{\partial y} \tilde{x}_{1} } \\ {\frac{{\partial \tilde{x}_{2} }}{\partial y} \tilde{x}_{2} } \\ \end{array} } \right]$$

(25)

Unlike (24), (25) imposes no restriction on the prevalence, linearity and magnitude of income effects.

If we now combine (23) and (25), then this gives rise to the more general case of Fig. 4, which shows the change in expected demands arising from a change in prices. In response to a change in prices from ${\mathbf{p}}_{{}}^{0}$ to ${\mathbf{p}}_{{}}^{1}$, entailing a reduction in the price of good 2 with other prices held constant, the individual moves from the initial bundle ${\mathbf{x}}^{0}$ to the final bundle ${\mathbf{x}}^{1}$. This movement can be decomposed as follows.

Fig. 4

Discrete-continuous demand for goods 1 and 2 in response to a price reduction, given a probabilistic discrete choice indicator

• First, there is a substitution effect that accounts for an increase in the expected demand for good 2 from 0.5 in the Do-Nothing¹⁷ to $0.5 + x_{2,se}^{1}$ in the Do-Something, and the movement from ${\mathbf{x}}^{0}$ to the intermediate bundle ${\mathbf{x}}^{se}$. Again, this substitution effect can be further decomposed into the movement from ${\mathbf{x}}^{0}$ to ${\mathbf{x}}_{\pi }^{se}$, which accounts for an increase in the probability of choosing good 2 given conditional demands of one unit, and the remaining movement to ${\mathbf{x}}^{se}$, which accounts for substitution between the conditional demands for goods 1 and 2.

• Second, there are income effects on the conditional demands for both goods 1 and 2. With regards to good 2, this accounts for a further increase in the expected demand by $x_{2,ie}^{1}$, and the movement from ${\mathbf{x}}^{se}$ to the final equilibrium bundle ${\mathbf{x}}^{1}$.

In common with Fig. 3, Fig. 4 allows the relaxation of Assumptions I, II and IV. In contrast to Fig. 3, Fig. 4 also allows the relaxation of Assumption V, which gives rise to a non-linear income expansion path ($IEP$). Summing the two demand responses, the expected demand for good 2 in the Do-Something is given by $x_{2}^{1} = 0.5 + x_{2,se}^{1} + x_{2,ie}^{1}$. This reflects the minimum conditional demand of one unit for both goods 1 and 2 and, provided these goods are infinitely divisible, the potential for additional conditional demand in excess of one.

4.2 Methods for Measuring the Expected Compensating Variation

At long last, we are now equipped to address the primary objective of the paper, which is to inform methods for measuring the compensating variation of a price change in the presence of non-linear income effects. With reference to the Slutsky equation (22), it is important to acknowledge that a price change could, in principle, impact upon either or both of the component parts of the expected demand, namely the probabilistic demand (23) and the conditional demand (25). Previous attempts at measuring the expected compensating variation in the presence of non-linear income effects (e.g. Karlström and Morey 2001) have focussed upon the identity:

$$E\left( {v^{*} \left( {{\mathbf{p}}_{{}}^{1} ,y - h} \right)} \right) = E\left( {v^{*} \left( {{\mathbf{p}}_{{}}^{0} ,y} \right)} \right)$$

(26)

where $v^{*} = {\text{Max}}\left\{ {\tilde{v}_{1} ,\tilde{v}_{2} } \right\}$, $h$ is the Hicksian compensating variation (both unconditionally and conditionally), and the 0 and 1 superscripts denote the states before and after a change in prices with income constant. A common simplifying assumption [e.g. McFadden (1995)] is that the random terms are equal across the two states (i.e. $\varepsilon_{j}^{0} = \varepsilon_{j}^{1}$ for $j = 1,2$); this is consistent with the earlier assumption concerning the independence of the random terms from deterministic utility in (8). The identity (26) has two features which distinguish it from (14). First, it is defined in terms of maximum indirect utility; this reflects the discrete choice context, and the possibility that the chosen good could differ before and after the change in prices (i.e. Group C, Sect. 3.2.3). Second, it is defined in terms of the expectation of maximum indirect utility; this reflects the definition of RUM (8), and the fact that, in identifying the utility-maximising good, the difference in random terms could potentially outweigh the difference in deterministic utilities.

4.2.1 Existing Methods for Measuring the Expected Compensating Variation

Although the literature has proposed a number of methods for estimating the expected Hicksian compensating variation in (26), the contributions of McFadden (1995) and Karlström and Morey (2001) have attracted particular attention.

McFadden’s is a simulation-based method which involves the following steps. First, with reference to (8), a draw $t$ is made of the random term $\varepsilon_{j,t}$ for $j = 1,2$. Second, on the basis of this draw, the quantity $v_{t}^{*} \left( {{\mathbf{p}}_{{}}^{0} ,y} \right)$ is calculated, thereby establishing the maximum utility in State 0. Third, considering goods 1 and 2 separately, the following identity is solved for $\tilde{h}_{j,t}$:

$$W_{j} \left( {p_{j}^{1} ,y - \tilde{h}_{j,t} } \right) + \varepsilon_{j,t} = v_{t}^{*} \left( {{\mathbf{p}}_{{}}^{0} ,y} \right)\quad {\text{for}}\;j = 1,2$$

where $\tilde{h}_{j,t}^{{}}$ is the conditional Hicksian compensating variation for good $j = 1,2$ and draw $t$. Fourth, for each draw, the maximum (for a price reduction, i.e. $h_{t}^{*} = {\text{Max}}\left\{ {\tilde{h}_{1,t} ,\tilde{h}_{2,t} } \right\}$) or minimum (for a price increase) compensating variation is identified. Finally, $h_{t}^{*}$ is enumerated across draws. Although the method yields an exact estimate of the expected Hicksian compensating variation, it entails substantial computation, and practical application has been limited. In an attempt to reduce computational burden, Morey et al. (1993) proposed an approximation to McFadden’s method which solves (26) for a representative consumer; Zhao and Huang’s (2017) recent paper has reconsidered the accuracy of this approximation.

Karlström and Morey’s is an analytical method, which derives the following identity for the expected income $E\left( a \right)$ required in State 1 so as to maintain the expected utility realised in State 0:

$$E\left( a \right) = \sum\nolimits_{j = 1,2} {\left( {\tilde{y}_{jj} \hat{\pi }_{j} - \int_{{y_{jj}^{*} }}^{{\tilde{y}_{jj}^{{}} }} {y\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\pi }_{j} }}{\partial y}dy} } \right)} \quad {\text{for}}\;j,m = 1,2\quad m \ne j$$

(27)

where $\hat{\pi }_{j} = \hat{\pi }_{j} \left( {W_{j} \left( {p_{j}^{1} ,\tilde{y}_{jj}^{{}} } \right) - W_{m} \left( {p_{m}^{1} ,\tilde{y}_{mm}^{{}} } \right)} \right)$ is the probability of choosing good $j$ in a RUM where the deterministic utilities of $j$ and $m$ are a function of their respective prices in State 1 and respective incomes $\tilde{y}_{jj}^{{}}$ and $\tilde{y}_{mm}^{{}}$; $\tilde{y}_{jj}^{{}}$ is the income required in State 1 to maintain the deterministic utility realised in State 0, if good $j$ were chosen in both states (and similarly for $\tilde{y}_{mm}^{{}}$); $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\pi }_{j} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\pi }_{j} \left( {W_{j} \left( {p_{j}^{1} ,y} \right) - W_{m}^{*} } \right)$ is the probability of choosing good $j$ in a RUM where the deterministic utility of $j$ is a function of price in State 1 and income $y$, whilst the deterministic utility of $m$ is given by the maximum of the deterministic utilities for that good across States 0 and 1, i.e. $W_{m}^{*} = {\text{Max}}\left\{ {W_{m} \left( {p_{m}^{0} ,y} \right),W_{m} \left( {p_{m}^{1} ,y} \right)} \right\}$; $y_{jj}^{*} = {\text{Min}}\left\{ {\tilde{y}_{11} ,\tilde{y}_{22} } \right\}$ defines the lower integration limits.

In equipping (27) with some intuition, it may be useful to refer back to Groups A, B and C in Sect. 3.2. The first element on the right-hand side of (27) takes account of Groups A and B; presuming that the same good is chosen in both states, it measures the expected income required in State 1 to maintain the utility arising in State 0. The second element on the right-hand side of (27) takes account of Group C, by acknowledging the possibility that, as prices change, preferences may change. In practice, the conditional Hicksian compensating variation of Group C will fall somewhere between the compensating variations of Group A (i.e. zero) and Group B, hence the integration. Having accounted for the shares of Group A, B and C individuals within the population, and the expected income $m$ required by each group, the expected Hicksian compensating variation is elicited from the identity:

$$E\left( h \right) = y - E\left( a \right)$$

(28)

A limitation of Karlström and Morey’s method is that neither $\hat{\pi }_{j}$ nor $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\pi }_{j}$ can be observed, since they are different RUMs from (8), and additional analysis is therefore required to derive these probabilities. This method, like McFadden’s, has not been widely adopted in practice.¹⁸

4.2.2 A Simple Method for Approximating the Expected Compensating Variation

Having developed an intuition for the expected compensating variation in the presence of non-linear income effects, Sect. 4.1 informs a simple alternative to McFadden’s and Karlström and Morey’s methods, as follows. Since, with reference to the earlier definition of RUM (8), the random terms for goods 1 and 2 are assumed to be independent of prices and income, any change in prices for a given income affects only the deterministic utilities of goods 1 and 2. On this basis, let us take the total derivative of expected maximum utility:

$$dE\left( {v^{*} } \right) = \frac{{\partial E\left( {v^{*} } \right)}}{{\partial W_{1} }}dW_{1} + \frac{{\partial E\left( {v^{*} } \right)}}{{\partial W_{2} }}dW_{2}$$

(29)

Ben-Akiva and Lerman (1985) noted the property that, if the distribution of the random terms is translationally invariant, the partial derivative of $E\left( {v^{*} } \right)$ with respect to the deterministic utility of good $j$ yields the choice probability for that good. On this basis, (29) simplifies to:

$$dE\left( {v^{*} } \right) = \pi_{1} \left( {{\mathbf{p}}^{1} ,y} \right)dW_{1} + \pi_{2} \left( {{\mathbf{p}}^{1} ,y} \right)dW_{2}$$

(30)

The change in expected maximum utility (associated with a change in prices between States 0 and 1) can thus be represented as the expectation (in State 1) of the change (between States 0 and 1) in the deterministic utilities of goods 1 and 2. Comparing against its discrete choice counterpart, note that (30) admits benefits through both goods 1 and 2, whereas (13) effectively admits benefits through the numeraire good only. This reflects the notion of multiple discrete choice in combination with unconstrained conditional demand—and the transition from the exposition of Fig. 3 to that of Fig. 4.

Whilst the identity (30) represents the expected change in Marshallian consumer surplus, it also motivates the Hicksian or Slutsky analogue:

$$E\left( b \right) = \pi_{1}^{c} \left( {{\mathbf{p}}^{1} ,u} \right) \cdot \tilde{b}_{1} + \pi_{2}^{c} \left( {{\mathbf{p}}^{1} ,u} \right) \cdot \tilde{b}_{2}$$

(31)

where $b = h$ and $\tilde{b} = \tilde{h}$, or $b = s$ and $\tilde{b} = \tilde{s}$, depending on whether Hicks’ or Slutsky’s version of the compensating variation is employed, and remembering from (5) that $\pi_{j}^{c}$ represents the compensated probabilistic demand for good $j = 1,2$. Although (31) is intuitively clear, practical implementation is not straightforward, especially as the compensated probabilistic demands are unobservable. The obvious way forward is to employ the uncompensated probabilistic demands as proxies, but since the latter demands are a function of income, this provokes the further question of how the income transactions $\tilde{h}$ and $\tilde{s}$ should be accounted for.

In a forerunner to the simulation method summarised in Sect. 4.2.1, McFadden (1995) proposed the following analytical bounds on the expected Hicksian compensating variation:

$$\sum\nolimits_{j = 1,2} {\pi_{j}^{{}} \left( {{\mathbf{p}}^{0} ,y} \right) \cdot \tilde{h}_{j}^{{}} } \le E\left( h \right) \le \sum\nolimits_{j = 1,2} {\pi_{j}^{{}} \left( {{\mathbf{p}}^{1} ,y - h} \right) \cdot \tilde{h}_{j}^{{}} }$$

(32)

where the lower bound is based on the choice shares in State 0, the upper bound is based on the choice shares in State 1 after the unconditional Hicksian compensating variation has been transacted, and the conditional Hicksian compensating variation is specified independently of the choice shares. Since the upper bound features two distinct notions of the compensating variation—unconditional and conditional, which conceivably inter-relate—practical implementation necessitates ‘…simultaneous or iterative solution of the random utility model for the [compensating variation]’ (McFadden 1995, p. 11); this has been seen as a fundamental weakness of (32). If however we adopt a Slutsky approach to defining the bounds, then this weakness can be readily overcome, as we will now demonstrate.

Drawing reference to Figs. 3 and 4, let us specify the bounds¹⁹:

$$\sum\nolimits_{j = 1,2} {\pi_{j} \left( {{\mathbf{p}}_{{}}^{0} ,y} \right)} \cdot \tilde{s}_{j}^{{{\mathbf{x}}^{0} }} \le E\left( h \right) \le \sum\nolimits_{j = 1,2} {\pi_{j} \left( {{\mathbf{p}}_{{}}^{1} ,y} \right)} \cdot \tilde{s}_{j}^{{{\mathbf{x}}_{\pi }^{se} }}$$

(33)

where $\tilde{s}_{j}^{{{\mathbf{x}}^{0} }}$ and $\tilde{s}_{j}^{{{\mathbf{x}}_{\pi }^{se} }}$ represent alternative measures of the conditional Slutsky compensating variation, arising from the following identities respectively²⁰:

$$\pi_{j} \left( {{\mathbf{p}}^{0} ,y} \right) \cdot W_{j}^{{}} \left( {\tilde{p}_{j}^{0} ,y} \right) = \pi_{j} \left( {{\mathbf{p}}^{0} ,y} \right) \cdot W_{j}^{{}} \left( {\tilde{p}_{j}^{1} ,y - \tilde{s}_{j}^{{{\mathbf{x}}^{0} }} } \right)\quad {\text{for}}\;j = 1,2$$

(34)

$$\pi_{j} \left( {{\mathbf{p}}^{0} ,y} \right) \cdot W_{j}^{{}} \left( {\tilde{p}_{j}^{0} ,y} \right) = \pi_{j} \left( {{\mathbf{p}}^{1} ,y} \right) \cdot W_{j}^{{}} \left( {\tilde{p}_{j}^{1} ,y - \tilde{s}_{j}^{{{\mathbf{x}}_{\pi }^{se} }} } \right)\quad {\text{for}}\;j = 1,2$$

(35)

where:

$$\tilde{p}_{j}^{0} = \hbox{Max} \left\{p_{1}^{0} ,p_{2}^{0} \right\}\quad j = 1,2$$

(36)

$$\tilde{p}_{j}^{1} = \left( {p_{j}^{1} - p_{j}^{0} } \right) + \tilde{p}_{j}^{0} \quad j = 1,2$$

(37)

With reference to (34) and (35), the conditional utilities are functional upon the conditional prices of goods 1 and 2 and the residual budget after the conditional Slutsky compensating variation has been transacted, whilst the probabilities continue to be defined in terms of the unconditional prices and the complete budget. With reference to (36), the conditional price of each good in State 0 is taken to be the maximum of the unconditional prices across both goods—this ensures compliance with (19) in the Do-Nothing. With reference to (37), the conditional price of each good in State 1 is then calculated to reflect the change in the unconditional price for that good, but from the starting point of the conditional price in State 0 (as opposed to from the starting point of the unconditional price).

The identities (34) and (35) are motivated by the observation that, for the case of a single discrete choice, goods 1 and 2 are perfectly substitutable, implying that expected deterministic utility is constant along the relevant budget/indifference lines in Figs. 3 and 4. Moreover, (34) and (35) provide a device for determining where the budget/indifference lines pertaining to States 0 and 1 intersect, thereby identifying allocations of goods 1 and 2 relevant to the Slutsky decomposition of a price change. More specifically, and again drawing upon Groups A, B and C from Sect. 3.2, (34) and (35) yield the conditional Slutsky compensating variation for two polar cases:

• First, (34) pertains to the case where the choice shares remain constant before and after the price change, i.e. Groups A and B only. In other words, any substitution effect takes place through the conditional demand only.

• Second, (35) pertains to the case where goods 1 and 2 are perfectly substitutable and the choice shares exhibit the maximum possible change as price changes, i.e. Groups A, B and C. In other words, any substitution effect takes place primarily through the probabilistic demand, and the conditional demand accounts only for any residual substitution.

As will be apparent from Figs. 3 and 4, neither of the above polar cases is associated with an optimal consumption bundle (i.e. a point of tangency between the relevant budget/indifference lines), and this justifies the interpretation of $\tilde{s}_{j}^{{{\mathbf{x}}^{0} }}$ and $\tilde{s}_{j}^{{{\mathbf{x}}_{\pi }^{se} }}$ as the conditional Slutsky (as opposed to Hicksian) compensating variations.

For a price reduction, we would expect $\tilde{s}_{j}^{{{\mathbf{x}}_{\pi }^{se} }} > \tilde{s}_{j}^{{{\mathbf{x}}^{0} }}$, since if preferences change in response, then the conditional compensating variation of Group C would be greater than zero. Moreover, in the context of discrete–continuous demand, the lower bound of (33) is effectively the Laspeyres price index, whilst the upper bound is effectively the Paasche price index. For the choice shares in State 0, the lower bound gives the change in expenditure associated with the price change in State 1. For the choice shares in State 1, the upper bound does similarly. Since expected deterministic utility is constant along the initial budget/indifference line, the expected Hicksian compensating variation will fall within these bounds.

The key attraction of the simple method (33) is that it can be straightforwardly implemented, using the observed choice shares and calculations of the conditional indirect utilities from the discrete choice model. It could be deployed as a pragmatic approximation to McFadden’s (1995) and Karlström and Morey’s (2001) methods, or alternatively it could be deployed in tandem—since it yields additional insights on the potential range of the Hicksian compensating variation depending on the extent of switching between choice alternatives. Finally, aside from its simplicity, a further attraction of (33) is that it indexes by goods 1 and 2, meaning that—unlike the log sum method—it straightforwardly elicits the contribution of each good to welfare change (Hyman and Daly 2014).

5 Illustrating the Practical Application of the Simple Method

Whilst lending itself to implementation through the discrete choice model, the simple method can in principle accommodate either linear (i.e. Figure 3) or non-linear (i.e. Figure 4) income effects. The present section will expand upon this proposition, by applying (33), (34) and (35) to both the discrete choice and discrete–continuous cases. In application, the distinguishing feature of these cases is the econometric specification of the conditional indirect utility function. That is to say, the discrete choice case should adhere to Assumptions I–V (Sect. 2.3), whilst the discrete–continuous case should relax some or all of Assumptions I–V (Sect. 4.1). This section comprises two sub-sections, the first developing a number of analytical examples, and the second developing an empirical example using real data.

5.1 Analytical Examples

5.1.1 Application of the Simple Method to McFadden (1981)

McFadden’s (1981) ‘residual income’ form is widely applied in practice, and entails the following specification of conditional indirect utility:

$$W_{j} = \beta \cdot \left( {y - p_{j} } \right)\quad {\text{for}}\;j = 1,2$$

(38)

where $\beta$ is a parameter to be estimated. By definition, the specification (38) complies with Assumptions I–V detailed in Sect. 2.3 and, in so doing, excludes non-linear income effects of price changes. Furthermore, (38) implies the presence of the numeraire good, and is consistent therefore with the rationale illustrated in Fig. 3. Applying (38) to (34) and (35), we get:

$$\beta_{{}}^{0} \cdot \left( {y - \tilde{p}_{j}^{0} } \right) = \beta_{{}}^{0} \cdot \left( {y - \tilde{s}_{j}^{{{\mathbf{x}}^{0} }} - \tilde{p}_{j}^{1} } \right)\quad {\text{for}}\;j = 1,2$$

(39)

$$\pi_{j} \left( {{\mathbf{p}}^{0} ,y} \right) \cdot \beta_{{}}^{1} \cdot \left( {y - \tilde{p}_{j}^{0} } \right) = \pi_{j} \left( {{\mathbf{p}}^{1} ,y} \right) \cdot \beta_{{}}^{1} \cdot \left( {y - \tilde{s}_{j}^{{{\mathbf{x}}_{\pi }^{se} }} - \tilde{p}_{j}^{1} } \right)\quad {\text{for}}\;j = 1,2$$

(40)

Assuming the parameters to be common across States 0 and 1 (i.e. $\beta^{0} = \beta^{1} = \beta$), we can simplify (39) and (40), and solve for $\tilde{s}_{j}^{{{\mathbf{x}}^{0} }}$ and $\tilde{s}_{j}^{{{\mathbf{x}}_{\pi }^{se} }}$ respectively:

$$\tilde{s}_{j}^{{{\mathbf{x}}^{0} }} = \left( {\tilde{p}_{j}^{0} - \tilde{p}_{j}^{1} } \right)\quad {\text{for}}\;j = 1,2$$

(41)

$$\tilde{s}_{j}^{{{\mathbf{x}}_{\pi }^{se} }} = \left( {y - \tilde{p}_{j}^{1} } \right) - \frac{{\pi_{j}^{0} }}{{\pi_{j}^{1} }} \cdot \left( {y - \tilde{p}_{j}^{0} } \right)\quad {\text{for}}\;j = 1,2$$

(42)

To illustrate the application of (41) and (42), let us consider a numerical example, involving a reduction in the price of good 2, with other prices held constant (i.e. faithful to Fig. 3). Specifically, let us assume $\beta = 0.1$, $y = 100$, $p_{1}^{0} = p_{1}^{1} = 100$, $p_{2}^{0} = 100$ and $p_{2}^{1} = 95$, such that consumption of the numeraire good is normalised to zero in State 0. Following the price reduction in State 1, however, continued compliance with Assumptions I–V necessitates diversion of the increased purchasing power to the numeraire good.

Assuming the random terms for goods 1 and 2 to be independently and identically distributed Multivariate Extreme Value (MEV), such that RUM is of the binary logit form, it is interesting to compare three alternative methods for measuring the expected change in consumer surplus across States 0 and 1. First, according to the simple method of calculating the lower and upper bounds on the expected Hicksian compensating variation (33)²¹:

$$2.50 \le E\left( h \right) \le 3.11$$

Second, according to the traditional log sum measure (13):

$${{\Delta E\left( v \right)} \mathord{\left/ {\vphantom {{\Delta E\left( v \right)} \lambda }} \right. \kern-0pt} \lambda } = 2.81$$

Third, according to the widely used ‘rule-of-a-half’ (RoH) approximation to consumer surplus change (Lane et al. 1971; Neuburger 1971):

$$RoH = \sum\nolimits_{j = 1,2} {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\left( {p_{j}^{0} - p_{j}^{1} } \right)\left( {\pi_{j}^{0} + \pi_{j}^{1} } \right)} = 2.81$$

In other words, for the case of a single discrete choice, the average of the lower and upper bounds yields both the log sum and RoH measures.²² These results accord with theoretical results first reported by Hicks (1942), and subsequently refined by Diewert (1992) and Hillinger (2001). Given perfect substitution between goods 1 and 2 and the absence of non-linear income effects, we would expect the RoH to equal both the average of the Laspeyres and Paasche price indexes, and the average of the Hicksian compensating and equivalent variations.

At this juncture, it is appropriate to revisit the earlier discussion in Sect. 3.1 around unconditional and conditional prices. Consistent with the diagrammatic exposition of Sects. 3 and 4, the worked example above assumed $y = p_{1}^{0} = p_{2}^{0} = 100$, thus implying the normalisation $\left. {x_{n}^{0} } \right|_{{\delta_{j}^{ + } }} = 0$ for $j = 1,2$. Let us now relax this normalisation by instead assuming $\beta = 0.1$, $y = 100$, $p_{1}^{0} = p_{1}^{1} = 100$, $p_{2}^{0} = 95$ and $p_{2}^{1} = 90$. This case entails the same absolute reduction in the price of good 2 as before, but from a different starting point—given that some consumption of the numeraire good is now introduced in the Do-Nothing. With reference to (36) and (37):

$$\begin{aligned} \tilde{p}_{1}^{0} & = \tilde{p}_{2}^{0} = \hbox{Max} \left\{p_{1}^{0} ,p_{2}^{0} \right\} = 100 \\ \tilde{p}_{1}^{1} & = \left( {p_{1}^{1} - p_{1}^{0} } \right) + \tilde{p}_{1}^{0} = \left( {100 - 100} \right) + 100 = 100 \\ \tilde{p}_{2}^{1} & = \left( {p_{2}^{1} - p_{2}^{0} } \right) + \tilde{p}_{2}^{0} = \left( {90 - 95} \right) + 100 = 95 \\ \end{aligned}$$

Repeating the comparison of alternative measures of the expected change in consumer surplus, we now get the following bounds from the simple method:

$$3.11 \le E\left( h \right) \le 3.66$$

By comparison, the log sum gives ${{\Delta E\left( v \right)} \mathord{\left/ {\vphantom {{\Delta E\left( v \right)} \lambda }} \right. \kern-0pt} \lambda } = 3.39$ and the rule-of-a-half $RoH = 3.38$. Thus, aside from slight rounding error, the average of the lower and upper bounds again yields both the log sum and RoH measures.

5.1.2 Application of the Simple Method to Karlström and Morey (2001)

Karlström and Morey (2001) asserted that the application of a power term to McFadden’s residual income specification offers a means of admitting non-linear income effects of price (and lump sum income) changes, i.e. consistent with the rationale illustrated in Fig. 4. More specifically, Karlström and Morey considered a three-alternative choice set, and specified conditional indirect utility:

$$W_{j} = \beta \cdot \left( {y - p_{j} } \right)^{2} \quad {\text{for}}\;j = 1,2,3$$

(43)

If the three goods exhibit common prices [as should apply conditionally following (19)] then (43) complies with Assumptions I–IV, but not Assumption V, and thus admits non-linear income effects.²³ If however prices are not common (as might apply unconditionally) then Assumptions III and IV are also relaxed. Substituting for (43) in (34) and (35), and solving for the conditional compensating variation, we have:

$$\begin{aligned} \tilde{s}_{j}^{{{\mathbf{x}}^{0} }} & = \left( {\tilde{p}_{j}^{0} - \tilde{p}_{j}^{1} } \right)\quad {\text{for}}\;j = 1,2,3 \\ \tilde{s}_{j}^{{{\mathbf{x}}_{\pi }^{se} }} & = \left( {y - \tilde{p}_{j}^{1} } \right) - \left( {\frac{{\pi_{j}^{0} }}{{\pi_{j}^{1} }} \cdot \left( {y - \tilde{p}_{j}^{0} } \right)^{2} } \right)^{0.5} \quad {\text{for}}\;j = 1,2,3 \\ \end{aligned}$$

Karlström and Morey illustrated the application of (43) within (27) by way of a numerical example; this involved an increase in the price of good 1 between States 0 and 1, with other prices held constant, and the random terms again independently and identically distributed MEV. Specifically, they assumed $\beta = 0.1$, $y = 100$, $p_{1}^{0} = 94.5$, $p_{1}^{1} = 95$, $p_{2}^{0} = p_{2}^{1} = 95$ and $p_{3}^{0} = p_{3}^{1} = 96$. On this basis, and with reference to (28), Karlström and Morey reported:

$$E\left( h \right) = y - E\left( a \right) = 100 - 100.24 = - 0.24$$

Developing the same example using the simple method of calculating the lower and upper bounds on the expected Hicksian compensating variation (33), we get:

$$- 0.27 \le E\left( h \right) \le - 0.17$$

whilst the log sum yields ${{\Delta E\left( v \right)} \mathord{\left/ {\vphantom {{\Delta E\left( v \right)} {\bar{\lambda }^{0} }}} \right. \kern-0pt} {\bar{\lambda }^{0} }} = - 0.26$ (noting that in this case there is a need to average the conditional marginal utility of income across goods), and the rule-of-a-half yields $RoH = - 0.24$.

Karlström and Morey also repeated the same example using an alternative specification of conditional indirect utility:

$$W_{j} = \beta \cdot \left( {y - p_{j} } \right)^{0.5} \quad {\text{for}}\quad j = 1,2,3$$

(44)

In this case, they calculated $E\left( h \right) = - 0.17$, whilst the simple method (33) yields the bounds $- 0.17 \le E\left( h \right) \le - 0.17$, the log sum gives ${{\Delta E\left( v \right)} \mathord{\left/ {\vphantom {{\Delta E\left( v \right)} {\bar{\lambda }^{0} }}} \right. \kern-0pt} {\bar{\lambda }^{0} }} = - 0.16$, and the rule-of-a-half gives $RoH = - 0.17$. The closeness of the alternative measures for these two examples reflects the fact that, whilst non-linear income effects are prevalent, they are trivial in magnitude. This is an implication of the specifications (43) and (44), which impose Assumption I irrespective of the prevailing prices.

5.2 Empirical Examples

Building upon the previous section, this section illustrates the empirical application of the simple method by re-analysing the dataset used by Karlström and Morey (2001) to illustrate their expected compensating variation method.²⁴

5.2.1 Data

The dataset originates from Morey et al. (1993), and entails a sample of 168 Maine fishermen self-reporting salmon fishing trips made to eight rivers (five in the Maine area of the United States and three in Canada) during 1988. In Morey et al., these reported trips were translated into a destination choice model where, for each fishing trip (up to a maximum of fifty during the year), destination was modelled as a function of trip costs (i.e. price) and catch rates (i.e. as an indicator of quality) associated with each site. The choice set also includes the possibility of not making a fishing trip to one of the eight named rivers on a given weekend, thus admitting annual trip rates (to these eight rivers) of less than fifty. Indeed, 13.3 trips on average were made during the year, and the most popular destination was the Penobscot River in the US. Socio-economic variables, such as club membership, age and years of experience, are also included in the dataset.

5.2.2 Model Specification

The original model specification reported in Morey et al. (1993) was a three-level (repeated) nested logit model. Karlström and Morey (2001) consolidated this into a two-level nested logit model, as the original model specification violated global regularity conditions. For our own purposes, we further reduced complexity by restricting the model to the multinomial logit (MNL) specification but—with some qualifications concerning the number of attributes—retained the original specification of the utility functions. More specifically, we included income effects of price changes via the components $\beta_{0} \cdot (y - p_{j} ) + \beta_{1} \cdot (y - p_{j} )^{0.5}$, which embody linear and non-linear income effects respectively. Following earlier discussion in Sect. 5.1.2, note that if the different fishing trips entail common prices (as should apply conditionally), then this specification also complies with Assumptions I–IV, but relaxes Assumption V; if however prices are not common (as might apply unconditionally) then Assumptions III and IV are also relaxed. Whilst our earlier concerns regarding this specification (footnote 23) are relevant, we retained this specification so as to remain faithful to Morey et al’s representation of income effects. One departure from Morey et al. was that we omitted socio-economic and quality variables, so as to align the empirical analysis with the earlier theoretical analysis of Sects. 4 and 5. There would seem to be no reason in principle why the simple method for measuring the compensating variation could not be extended to accommodate quality as well as price changes, but this extension falls beyond the scope of the present paper.

5.2.3 Results

We began the empirical analysis by estimating a simplified MNL model with utility specified to be linear in residual income (i.e. assuming $\beta_{1} = 0$, thereby eliminating the second of the two income effects stated above), but omitting alternative specific constants, quality and other socio-economic variables as previously discussed. The estimation results for this model, referred to as Model (I), are reported in Table 1, where price is associated with a positive coefficient (i.e. $\beta_{0} > 0$) given the ‘residual income’ formulation of utility.

Table 1 Models of destination choice for salmon fishing based on Morey et al. (1993)

Having estimated Model (I) on Morey et al’s data (thereby establishing State 0), we then introduced the policy scenario of a $5 dollar increase in the price of fishing at the Penobscot River only (State 1). Applying this policy scenario to Model (I), we estimated the welfare change using six alternative methods, namely: (1) the log sum method; (2) McFadden’s simulation method; (3) Morey et al’s representative consumer method; (4) Karlström and Morey’s analytical method; (5) the simple bounds method proposed in this paper; and (6) the RoH. More specifically, for each fisherman in the sample, the welfare impact of the price change was calculated for each fishing trip, and then multiplied by fifty to elicit the annual welfare impact.

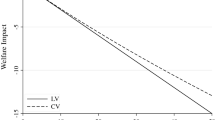
Since Model (I) embodied linear income effects of price changes, the ‘natural’ method for estimating welfare change is the log sum; recall from Sect. 2.4 that the log sum implies Assumptions I–V. Taking the average across the 168 fishermen of the annual welfare loss due to the $5 increase at the Penobscot River, the log sum returns an estimate of $40.71 (see the second column of Table 2). The same estimate is recovered by the Karlström and Morey and Morey et al. methods, whilst the estimates from the McFadden, RoH and simple methods diverge only slightly from the log sum.

Table 2 Expected annual welfare impact (in US$) per fisherman of $5 increase in price of fishing at the Penobscot River, based on Morey et al. (1993)

The next stage of the empirical analysis involved re-estimating the MNL model to incorporate both linear and non-linear income effects of price changes (i.e. relaxing the assumption β₁ = 0), and this is reported as Model (II) in Table 1. Model (II) was then applied as before to estimate the welfare change under State 1 vis-à-vis State 0. Given the presence of non-linear income effects, the log sum is no longer appropriate, and the estimated welfare loss of $53.33 is therefore somewhat of an outlier when compared to the estimates from the other methods. Again, the simple method generates bounds which (with the exception of the log sum) tightly envelope the other welfare estimates but, given the presence of non-linear income effects, the average of the bounds now diverges from the RoH. Moreover, this reflects the general result that we would expect to see: for a price increase (decrease), the log sum overestimates (underestimates) the consumer surplus loss (gain). This is because the log sum underestimates the extent of switching between goods 1 and 2 in the event of a price change.

6 Synthesis and Conclusions

Adopting the presentation by S&R, we introduced a problem of discrete–continuous demand whereby an individual is offered a discrete choice between two mutually exclusive goods; conditional upon that choice, he/she consumes a positive quantity of the chosen good and potentially also a positive quantity of a numeraire good, subject to the constraint of budget. In the context of this problem, we considered the impacts of a price change on demand and consumer surplus, for a range of practical consumption situations. We dissected the separate contributions of the discrete choice and conditional demands to the overall demand response, and we further dissected the demand response into income and substitution effects. A key contribution of S&R was the derivation of a consumer surplus measure specific to the discrete choice component of demand; an example of this measure is the ‘log sum’ measure, which has been applied extensively in public policy analysis. Against this background, we arrive at the following conclusions:

• 1. If Assumptions I–V (Sect. 2.3) are imposed on S&R’s model of discrete–continuous demand, then the model is restricted to a single discrete choice (i.e. conditional demand is fixed at one), and we derive the notion of a probabilistic demand function. This provides a theoretical basis—in terms of microeconomics—for the Random Utility Model (RUM). These assumptions also imply that, if the conditional demand is to comply with the budget condition, then goods 1 and 2 should be reconstituted as composites of the numeraire good, and face common conditional prices.

• 2. S&R’s consumer surplus measure (12) arises from the integration of the probabilistic demand, and is underpinned by Assumptions I–V. Although it is widely acknowledged that (12) excludes non-linear income effects of a price change on goods 1 and 2, we have clarified that, in the absence of the numeraire good, linear income effects and substitution effects are also excluded. If, however, we admit the numeraire good, then this can proxy for both:

  • Quasi-linear income effects; these relate to ‘Group B’ individuals, who do not switch between goods following a price change, and;

  • Substitution effects; these relate to ‘Group C’ individuals, who switch between goods.

  Moreover, in practical implementations of (12), such as the popular ‘log sum’ measure (13), the change in expected consumer surplus associated with a price change will be capitalised entirely in terms of the numeraire good. The magnitude of this surplus will depend upon the proportions of Group B and C individuals within the population, and the relative strength of preferences for goods 1 and 2 in the case of Group C.

• 3. In order to admit non-linear income effects of price (and lump sum income) changes, we must relax some or all of Assumptions I–V, and revert from the discrete choice model, to the model of discrete–continuous demand. More specifically, within the discrete–continuous demand model, we must relax:

  • Assumptions I and II, in order to admit linear income effects of price changes where there is no change in the relative shares of goods 1 and 2.

  • Assumptions I, II and III, in order to admit linear income effects of lump sum income changes where there is a change in the relative shares.

  • Assumptions I, II and IV, in order to admit linear income effects of price changes where there is a change in the relative shares.

  • Assumptions I, II, IV and V, in order to admit non-linear income effects of price changes.

• 4. Recognising the limitations of S&R’s consumer surplus measure, McFadden (1995) and Karlström and Morey (2001) devised methods for measuring the expected Hicksian compensating variation in the presence of non-linear income effects. However, both methods call for significant computational and/or analytical effort following estimation of the discrete choice model, and this perhaps explains why neither method has been widely adopted in practice. The present paper proposed a simple method for approximating the expected Hicksian compensating variation. This entails the derivation of analytical bounds, where one bound is given by the expected Slutsky compensating variation in the event of zero substitution between goods, and the other bound is given by the corresponding measure in the event of maximum substitution between goods. These bounds correspond to the Laspeyres and Paasche price indexes for the context of discrete–continuous demand.

• 5. The attraction of the simple method is that it can be straightforwardly implemented using the observed choice shares and calculations of the conditional indirect utilities. It could be deployed as a pragmatic approximation to extant methods for measuring the expected Hicksian compensating variation, or it could even be deployed in tandem with extant methods. In the latter case, the simple method yields additional insights on the potential range of the Hicksian compensating variation depending on the extent of switching between choice alternatives, as well as on the attribution of the Hicksian compensating variation to the relevant choice alternatives.

• 6. Comparing the simple method for approximating the expected Hicksian compensating variation against the log sum and rule-of-a-half methods, we demonstrated empirically that, for a price increase (decrease), the log sum overestimates (underestimates) the consumer surplus loss (gain).

• 7. Whilst beyond the scope of the present paper, the simple method for measuring the compensating variation could—through the concept of ‘generalised cost’ (McIntosh and Quarmby 1970)—be readily extended to accommodate quality changes as well as price changes. In the case of the residual income formulation of the utility function (as used in Sect. 5), the simple method can also accommodate lump sum income changes, but this extension does not hold for other utility formulations.

At the beginning of this paper, we introduced S&R’s framework of discrete–continuous demand. This framework distinguishes between the consumption choices across different dimensions, and the quantity of consumption along any single dimension, that give rise to the overall observed demand. The paper has shown that, in terms of this framework, any non-linear income effects of a price change will be associated with the quantity of demand conditional upon choice (in the context of the expected demand), and not with choice per se. We conclude that, if non-linear income effects are relevant to the empirical context of application, then the analyst should relax Assumptions I–V, move from a discrete choice framework to a discrete–continuous one, and calculate expected consumer surplus change using a path independent measure such as the one proposed in this paper.