Contribution of GRAV-D airborne gravity to improvement of regional gravimetric geoid modelling in Colorado, USA

Abstract

This paper studies the contribution of airborne gravity data to improvement of gravimetric geoid modelling across the mountainous area in Colorado, USA. First, airborne gravity data was processed, filtered, and downward-continued. Then, three gravity anomaly grids were prepared; the first grid only from the terrestrial gravity data, the second grid only from the downward-continued airborne gravity data, and the third grid from combined downward-continued airborne and terrestrial gravity data. Gravimetric geoid models with the three gravity anomaly grids were determined using the least-squares modification of Stokes’ formula with additive corrections (LSMSA) method. The absolute and relative accuracy of the computed gravimetric geoid models was estimated on GNSS/levelling points. Results exhibit the accuracy improved by 1.1 cm or 20% in terms of standard deviation when airborne and terrestrial gravity data was used for geoid computation, compared to the geoid model computed only from terrestrial gravity data. Finally, the spectral analysis of surface gravity anomaly grids and geoid models was performed, which provided insights into specific wavelength bands in which airborne gravity data contributed and improved the power spectrum.

Introduction

The Earth’s gravity field data provide fundamental information for the geoscientific community. Global gravity field models (GGMs) provide low-frequency information, whereas other data types provide medium, high, and very high-frequency information. Commonly used data types for regional and local gravity field and geoid modelling include: (i) gravity data (airborne, land, marine, and satellite), (ii) gradiometric data (terrestrial, airborne, and satellite), (iii) altimeter data, (iv) deflections of the vertical, (v) digital elevation models (DEMs), and (vi) crustal (density) models. Each data type has its properties and limitations in terms of spatial resolution, covered spectral band, and accuracy. Spatial and spectral resolutions along with approximate accuracy of the main data types used in the regional gravity field and geoid modelling are summarized in Table 1.

Table 1 Spatial and spectral properties with accuracy estimates of the main data types used in the regional gravity field and geoid modelling

Apart from GGMs, which are being improved in terms of accuracy and spatial resolution in recent years due to gravity-dedicated satellite missions, terrestrial (land) gravity is the most widely used data type in geoid modelling. It is sufficiently accurate and reliable, but may also be time-consuming and laborious for collection. Therefore, when larger (e.g. >10,000 $\hbox {km}^2$) or hardly accessible areas (polar areas, mountains, forests, coastal areas, oceans) have to be gravimetrically mapped, airborne gravity practically becomes the only option. First airborne gravimetry tests were performed back in 1958 (Thompson and LaCoste 1960). However, its wider usage began in the early 1990s due to the full operational capability of the Global Positioning System (GPS) and the implementation of carrier-phase differential GPS (DGPS) techniques. This allowed more accurate determination of velocity and acceleration of an airplane, which consequentially enabled the reduction of the errors in collecting data caused by flight dynamics. As a measurement technique, airborne gravimetry is operational and cost-effective; it may map the gravity field with a relatively high spatial resolution (e.g. minimum recoverable half-wavelength $\sim$5 km), but it is prone to different types of errors caused by flight dynamics, weather conditions, sensor characteristics, etc. Generally, the accuracy of airborne gravity data is from 1 to 3 mGal according to root mean square (RMS) for the spatial resolutions of 5 to 15 km. For such data accuracy, the expected accuracy of determined regional geoid models is from 3 and 10 cm, respectively (e.g. Childers et al. 1999).

Airborne gravity data can be used for regional geoid modelling. In the last two decades, several countries performed airborne gravity campaigns to establish, modernize and update their national gravity databases (e.g. USA, Turkey, New Zealand, Australia, Philippines, Mongolia, and Nepal). Airborne gravity data may be beneficial in the context of the modernization of regional and national height reference systems (HRS). Historical tide-gauge/levelling-based HRS may be replaced by gravimetric geoid-based HRS. Airborne gravity data was already used for gravimetric and hybrid (models fitted to a local or regional vertical datum) geoid modelling in many areas worldwide including: North Jutland (Kearsley et al. 1998), Taiwan (Hwang et al. 2007; Hájková 2015), Italy (Barzaghi et al. 2009), United Arab Emirates (Forsberg et al. 2012), South Korea (Jekeli et al. 2013), New Zealand (McCubbine et al. 2017), and East Malaysia (Jamil et al. 2017).

Gravimetric geoid models have a widespread usage in geodesy and geophysics. In geodesy, they are mainly used as reference surfaces (vertical datums) for heights, in realization and unification of HRS (Rummel and Teunissen 1988; Ihde et al. 2017), and in navigation (Groves 2013, p. 64; Teunissen and Montenbruck 2017, p. 35). In geophysics, geoid models are used for studies of the Earth’s interior and ocean dynamics (e.g. Vanicek and Christou 1993).

One of the tasks in regional geoid modelling is the optimal combination of different data types and the estimation of their specific contributions to modelled quantities. Combining airborne gravity data with other data types is a non-straightforward task by itself. First, raw gravity and Global Navigation Satellite System (GNSS) data is collected by sensors onboard aircraft. Then, data is processed in several steps (see, e.g. Childers et al. 1999; Bruton 2000; Olesen 2002; Damiani et al. 2017; Lu et al. 2017):

• 1. Kinematic GNSS data of airplane flight lines is post-processed.

• 2. Timing of gravity and kinematic GNSS data is synchronized.

• 3. Corrections for aircraft motion, meter off-level, and drift are applied.

• 4. Absolute gravity tie is performed.

• 5. Short- and long-wavelength signal components are filtered out.

The output of such processing is filtered gravity values along flight lines. To use such data for geoid modelling, it must be continued from aircraft altitudes (varying from 1 to 10 km) down to the topographic surface or boundary surface (geoid). The solutions of downward continuation (DWC) of airborne gravity both in spatial and spectral domains were proposed by many authors, such as Forsberg (1987), Novák and Heck (2002), Bayoud and Sideris (2003) and Sjöberg and Eshagh (2009). As gravity data coming from several measurement sensors have generally different resolutions, their merging can be performed using the so-called multi-resolution (MR) boundary-value problem (BVP). A theoretical basis for some of the possible methods of solving MR BVP is given in Holota (1995), Schwarz and Li (1997) and Novák et al. (2003). Gravity-to-potential inversion may be done either on the geoid or the topographic surface. The solution on the geoid is Stokes’ BVP, whereas the solution on the topographic surface is Molodensky’s BVP. In any case, to fully exploit the advantages of all available data types, their efficient combination in the regional gravity field modelling remains in research focus with many issues needing to be investigated; see, e.g. Schwarz and Li (1996), Li (2000) and Hwang et al. (2007).

The main motivation of this study is to explore the potential of airborne gravity data to improve the accuracy of a regional gravimetric geoid model in a complex and mountainous study area. Airborne gravity data was acquired within the Gravity for the Redefinition of the American Vertical Datum (GRAV-D) project (Smith 2020). The contribution of airborne gravity data is analysed in spatial and spectral domains. Two main questions are addressed in this study: (i) Does the accuracy of geoid models improve if airborne gravity data is included, compared to the solution computed only with terrestrial gravity data? (ii) How does the inclusion of airborne gravity data affect the gravity anomaly and geoid undulation power spectrums?

Several authors studied the feasibility of airborne gravity data in regional geoid modelling. For instance, Yu-Shen and Hwang (2010) improved the geoid in Taiwan from 9.5 to 8.7 cm compared to GNSS/levelling, Bae et al. (2012) from 6.6 to 5.5 cm in South Korea, and McCubbine et al. (2017) from 4.6 to 3.1 cm in New Zealand. Some authors used the GRAV-D airborne gravity data for geoid modelling in test areas in Texas and Iowa, USA (Smith et al. 2013; Li et al. 2016; Wang et al. 2017; Huang et al. 2019). Results verified expectations regarding improvements of accuracy in geoid models due to the usage of airborne gravity data.

In this study, the computation area was located in the US State of Colorado. Terrestrial and airborne gravity datasets (along with GNSS/levelling) were provided in 2018 by the National Geodetic Survey (NGS) of the US National Oceanic and Atmospheric Administration (NOAA) to all researchers interested in comparison of geoid/quasi-geoid computation methods and determination of the potential values for selected stations. These research initiatives were performed within the International Association of Geodesy (IAG) joint working groups “Strategy for the Realization of the International Height Reference System (IHRS)”and “The 1-cm Geoid Experiment”(Sánchez 2019; Wang and Forsberg 2019). Along with the datasets, the guidelines for computations were prepared and distributed. The guidelines provided a set of required and recommended constant values such as the reference ellipsoid, the value of gravitational constant, directions for treatment of zero- and first-degree coefficients in GGMs, and the equation for computation of atmospheric corrections (Sánchez et al. 2018).

Geoid determination was performed in the following way. First, gravity data was prepared in several processing steps: (i) conversion of input gravity values to surface gravity anomalies, (ii) downward continuation, (iii) outlier detection and removal, and (iv) gridding. After data processing, geoid models were determined using the least-squares (LS) modification of Stokes’ formula with additive corrections. It is designated here as the LSMSA method, although it is also known as the KTH method. The method dates back to 1980s (e.g. Sjöberg 1980, 1981, 1984), and was continually developed since then (e.g. Sjöberg and Bagherbandi 2017, Sects. 4, 5 and 6 Sjöberg 2020). The method uses the stochastically modified Stokes’ formula to compute approximate geoid undulations from the input grid of surface gravity anomalies. Then, corrections accounting for effects of topography, atmosphere, downward continuation, and ellipsoidal approximation are computed and added to the approximate geoid undulations (see Sect. 5).

Data and study area

The datasets used in computations were: (i) 59,303 terrestrial gravity points (geodetic latitude $\varphi$, geodetic longitude $\lambda$, gravity value g, orthometric height H) on the topographic surface, (ii) 283,716 airborne gravity points ($\varphi$, $\lambda$, g, ellipsoidal height $h^{\text {flight}}$) on the flight altitude, and (iii) 509 GNSS/levelling points ($\varphi$, $\lambda$, h, H). The spatial distribution of the datasets is plotted in Fig. 1. The reference frame for 3-D positioning ($\varphi$, $\lambda$, h) is the IGS (International GNSS Service) Reference Frame 2008 (IGS08) (Rebischung et al. 2012), epoch 2005.0, on the Geodetic Reference System 1980 (GRS80) ellipsoid (see Moritz 2000). Spirit-levelled Helmert orthometric heights refer to the North American Vertical Datum 1988 (NAVD88); see Zilkoski et al. (1992).

The airborne gravity dataset—block Mountain South S05—was acquired in 2016 and 2017. The campaign was performed within the GRAV-D project, which started back in 2007 and is led by NGS. One of the main objectives of the project was to gravimetrically map the entire US territory until 2022, in order to establish a new national HRS based on a gravimetric geoid model (Smith and Roman 2010). During the measurement campaign, an aircraft was flying between 5 and 8 km above the topographic surface. It carried the Micro-g LaCoste Turn-key Airborne Gravimetry System (TAGS), which is a beam-type, zero-length spring, gravity sensor fixed to a gyro-stabilized platform. Flight line-spacing was 10 km with crossover lines spaced from 40 to 80 km. The average line length was $\sim$450 km. The spatial resolution of airborne gravity was from 20 to 50 km (i.e. 0.15$^{\circ }$ to 0.5$^{\circ }$), depending on the aircraft’s altitude and velocity. The nominal (average) altitude of 6.3 km for all blocks and lines within the project meant that no feature smaller than 20 km could be resolved. During processing and preparation of raw airborne data, it was filtered three times using a time-domain Gaussian filter with 6$\sigma$ length of 120s (Team 2017), which corresponds to a half-transfer filter length of approximately 100 s.

Fig. 1

Spatial distribution of terrestrial and airborne gravity data (left) and GNSS/levelling points (right)

The block with airborne gravity data covers the area between $34.8^\circ \le \varphi \le 38.3^\circ$, $251.3^\circ \le \lambda \le 258.1^\circ$. However, the areas covered by airborne and terrestrial gravity data did not coincide; there were no airborne data for longitudes between $250^\circ \le \lambda \le 250.8^\circ$ and for latitudes between $38.8^\circ \le \varphi \le 40^\circ$ (see Fig. 1, left). As the main objective of this study was to estimate the specific contribution of airborne gravity to geoid modelling, it did not make much sense to compute and validate geoid models over areas without airborne gravity data. Therefore, geoid models were determined only for the area covered by the airborne gravity data (geoid computation area extents are visible in Fig. 1). Consequently, GNSS/levelling points located in this area were extracted, which meant that from the initially provided 509 GNSS/levelling points only 75 points located within the geoid computation area extents were selected and used for validation of the computed geoid models (see Fig. 1, right).

Preparation of input gravity data

As the LSMSA method was used for geoid modelling, conversion of g-values to surface (Molodensky-type, modern) free-air gravity anomalies $\Delta g_{\text {FA}}$ for both terrestrial and airborne gravity datasets was needed. An alternative approach exists in which gravity disturbances are used, instead of using gravity anomalies; see Hotine (1969), Novák et al. (2001), Novák et al. (2003), Bayoud and Sideris (2003), Sjöberg and Eshagh (2009) and Märdla et al. (2018).

Surface gravity anomalies are defined as the difference between gravity value on the topographic surface $g_P$ and normal gravity value on the telluroid $\gamma _{Q}$ (Hofmann-Wellenhof and Moritz 2005, Eqs. 8-23 and 8-25):

$$\begin{aligned} \Delta g_{\text {FA}} = g_{P} - \gamma _{Q}, \end{aligned}$$

(1)

where $\gamma _{Q}$ was calculated from:

$$\begin{aligned} \gamma _{Q} = \gamma _{0}\left[ 1-2\left( 1+f+m-2 f \sin ^{2} \varphi \right) \frac{H^N}{a}+3\left( \frac{H^N}{a}\right) ^{2}\right] ,\nonumber \\ \end{aligned}$$

(2)

where $\gamma _0$ is the normal gravity value at the surface of the reference ellipsoid (see Eq. 20), a, b, f and GM represent the semi-major axes, semi-minor axes, flattening, and geocentric gravitational constant of the reference ellipsoid GRS80, m is obtained from $\omega ^2a^2b/(GM)$, $\omega$ represents the angular rotation velocity of reference ellipsoid, and $H^N$ is the normal height of the point (the height of the telluroid above the reference ellipsoid). Equation 2 represents an analytical continuation of the normal gravity from the ellipsoid along the surface normal. Conversion from the initially provided orthometric heights H to the required normal heights $H^N$ for all gravity points was performed using the correction term synthesized from the global spherical harmonic (SH) quasi-geoid to geoid separation model (Zeta-to-N-to2160-egm2008) (Survey 2016).

The usage of airborne gravity data is more complex than the usage of terrestrial gravity data due to the necessity of their downward continuation from the flight altitude ($h^\text {flight}$) to the corresponding point on the topographic surface ($h^\text {topography}$); see Sect. 2.3). Therefore, ellipsoidal heights of the topographic surface $h^\text {topography}$ were obtained by summing up interpolated orthometric heights H from the NASA Shuttle Radar Topography Mission (SRTM) Version 3.0 Global 1$^{\prime \prime }$ (SRTMGL1 ver. 003, JPL 2013) DEM and interpolated geoid undulations N from the national hybrid geoid model GEOID18 (Roman and Ahlgren 2019), which was fitted to the NAVD88. This step ensured consistency within the height data associated with the terrestrial gravity data and with the downward-continued airborne gravity data.

The atmospheric correction was calculated using (Wenzel 1985):

$$\begin{aligned}&\delta g_\text {atm}=0.874-9.9 \cdot 10^{-5} H+3.56 \cdot 10^{-9}\nonumber \\&H^{2} \text { in (mGal), for } H \text { in (m)}. \end{aligned}$$

(3)

Calculated values were added to g-values of all points in terrestrial and airborne gravity datasets.

Finally, high-frequency noise, caused mainly by airplane flight dynamics, had to be reduced in all input quantities which entered into the calculation of airborne surface gravity anomalies $\Delta g_{\text {FA}}^\text {airborne}$ (Eq. 1). Therefore, all input quantities were filtered using the same filter applied by the NGS team in preprocessing the airborne gravity data (see Sect. 2).

Outlier detection and removal

The first step in processing the airborne gravity data was bias and outlier detection and removal. The general principle is to subtract all known gravity field contributions in order to obtain a statistically more homogeneous and smoother residual gravity field. Such a residual field typically has 25% to 50% smaller standard deviation than a field represented by free-air gravity anomalies. A mean value of residual field is expected to be around zero mGal. Residual gravity anomalies $\Delta g_{\text {RA}}$ are defined as (Forsberg 1984a):

$$\begin{aligned} \Delta g_{\text {RA}} = \Delta g_{\text {FA}}- \Delta g_{\text {GGM}} - \Delta g_{\text {RTC}}, \end{aligned}$$

(4)

where $\Delta g_{\text {FA}}$ are the surface gravity anomalies (see Eq. 1), $\Delta g_{\text {GGM}}$ are the gravity anomalies inferred from Earth Gravitational Model 2008 (EGM2008, Pavlis et al. 2012), $\Delta g_{\text {RTC}}$ are the residual terrain corrections (RTC). $\Delta g_{\text {GGM}}$ and $\Delta g_{\text {RTC}}$ were computed on the topographic surface for terrestrial gravity data, and on the flight altitude for airborne gravity data. $\Delta g_{\text {RTC}}$ were computed by flat-top prism integration of the vertical gravitational attraction of topographic masses above and below a reference topographic surface (Nagy 1966 and Forsberg 1984a). The constant topographic mass density value of 2670 $\hbox {kg}\cdot \hbox {m}^{-3}$ was used in all computations (e.g. Hinze 2003).

The residual terrain correction $\Delta g_{\text {RTC}}$ was computed using the inner and outer integration radius of 30 and 200 km. The DEMs resolutions in inner and outer zones were $1^{\prime \prime }$ (full resolution of SRTMGL1 DEM) and $1^{\prime }$ (created by averaging the 1$^{\prime \prime }$ version). A reference DEM with the angular resolution of $5^{\prime }$ was obtained by the moving-average technique to match the resolution of the reference field model EGM2008. To preserve consistency, all terms in Eq. 4 were filtered using the same filter which was used in the processing of the airborne gravity data (see Sect. 2).

As the residual gravity field is stripped of long and medium wavelengths (SH degrees from 2 to 2190), as well as short and very short wavelengths (SH degrees from 2190 to $\sim$216,000), it consists mainly of: (i) gravity observation errors, (ii) commission errors of gravity anomalies computed from GGM, (iii) commission errors of RTC gravity anomalies, (iv) local to regional density anomalies due to constant density value, and (v) omission errors. Consequently, such a homogeneous field reveals potential outliers in gravity data and potential areas with systematic errors.

Outlier detection/removal was performed separately for terrestrial and airborne gravity data, using the following procedure:

• 1. Calculation of the median (MED) and the median of absolute deviations (MAD) values from $\Delta g_{\text {RA}}$¹.

• 2. Calculation of the value of normalized MAD (NMAD) by multiplying the MAD value with the factor 1.4826².

• 3. Selection of candidate outliers according to the following criterion: $\Delta g_{\text {RA}}^{\text {candidate}} \notin [$MED − 3$\cdot$NMAD, MED $+$ 3$\cdot$NMAD].

• 4. Removing candidate outliers $\Delta g_{\text {RA}}^{\text {candidate}}$ from the dataset.

• 5. Interpolation of values $\Delta g_{\text {RA}}^{\text {interpolated}}$ for each candidate outlier $\Delta g_{\text {RA}}^{\text {candidate}}$ using triangulation-based linear interpolation (Matlab function griddata). In that way, an interpolated value $\Delta g_{\text {RA}}^{\text {interpolated}}$ is obtained for each candidate outlier $\Delta g_{\text {RA}}^{\text {candidate}}$. [This step was only used for outlier detection, not for gridding the gravity anomalies. This procedure is explained in Sect. 2.5.]

• 6. Calculation of the differences between the interpolated values and values of candidate outliers $\varepsilon =\Delta g_{\text {RA}}^{\text {interpolated}} - \Delta g_{\text {RA}}^{\text {candidate}}$.

• 7. Removal of all values from gravity datasets for which $\varepsilon$ values are larger than the threshold values (limit values which separate outliers and non-outliers). Threshold values were estimated from a cumulative distribution function (CDF) of the absolute values of $\Delta g_{\text {RA}}$ (see Fig. 2). The values were selected as 95% percentiles, and corresponded to 19 mGal for terrestrial gravity data and 12 mGal for airborne gravity data.

Fig. 2

Cumulative distribution function (CDF) of the absolute values of residual gravity anomalies $\Delta g_\text {RA}$ used for the determination of the outlier limits (95% percentiles)

Fig. 3

Gridded residual gravity anomalies $\Delta g_{\text {RA}}$; with outliers (subfigures a and c) and without outliers (subfigures b and d) (mGal)

From the terrestrial and airborne datasets, 744 and 3399 gravity points were removed, respectively. The standard deviation of the residual gravity anomalies after outlier removal was reduced from 8.9 to 7.8 mGal for the terrestrial gravity data, and from 6.6 to 4.5 mGal for the airborne gravity data. Mean values of both gravity datasets were decreased to zero mGal. The gridded residual anomaly field is visualized in Fig. 3³. The gravity field after outlier removal is smoother, without evident biases or areas of larger local anomalies.

The final dataset, which was used in gridding of the surface gravity anomalies (see Sect. 2.5), consisted of 338,876 points, 17% of which were terrestrial and 83% were airborne gravity points. The area covered by the gravity data was approximately 383,000 $\hbox {km}^2$. The average spatial density of all gravity points was 88 points (pts) per 100 $\hbox {km}^{2}$; for terrestrial gravity, it is 15 pts per 100 $\hbox {km}^{2}$ and for airborne gravity 73 pts per 100 $\hbox {km}^{2}$.

Downward continuation of airborne gravity data

DWC is one of the most unstable procedures in the airborne gravity data processing. Due to its inherent numerical instabilities and high-frequency error amplification, it usually requires a regularization using iteration procedures. Several space- and frequency-domain DWC methods have been proposed including: inverse Poisson’s integral equation, least-squares collocation (LSC), direct band-limited approach, normal free-air gradient, analytical DWC, or the semi-parametric method. See, for instance, Novák et al. (2001), Novák and Heck (2002), Kern (2003), and Bayoud and Sideris (2003). In this research, the 3D LSC method (Forsberg 1987) is used as it has many advantages. The method is well-established, straightforward, numerically stable, allows interpolation anywhere in the 3-D space, input data does not have to be gridded nor has to be on the same height. The method was used in several studies; see, e.g. Alberts and Klees (2004), Barzaghi et al. (2009), Goli and Najafi-Alamdari (2011), McCubbine et al. (2017), and Zhao et al. (2018). Global gravity field and topography information were used to remove and restore low- and high-frequency gravity contents before and after DWC. The DWC procedure consisted of the following steps:

• 1. Airborne gravity data preparation.

  • (a) Calculation of $\Delta g_{\text {FA}}^{\text {flight}}$ at the flight altitude (see Eq. 1).

  • (b) Calculation of $\Delta g_{\text {GGM}}^{\text {flight}}$ and $\Delta g_{\text {RTC}}^{\text {flight}}$ effects at the flight altitude.

  • (c) Calculation of $\Delta g_{\text {RA}}^{\text {flight}}$ at the flight altitude by removing $\Delta g_{\text {GGM}}^{\text {flight}}$ and $\Delta g_{\text {RTC}}^{\text {flight}}$ effects (see Eq. 4).

• 2. Terrestrial gravity data preparation.

  • (a) Calculation of $\Delta g_{\text {FA}}^{\text {topography}}$ on the topographic surface.

  • (b) Calculation of $\Delta g_{\text {GGM}}^{\text {topography}}$ and $\Delta g_{\text {RTC}}^{\text {topography}}$ effects on the topographic surface.

  • (c) Calculation of residual gravity anomalies on the topographic surface $\Delta g_{\text {RA}}^{\text {topography}}$ by removing $\Delta g_{\text {GGM}}^{\text {topography}}$ and $\Delta g_{\text {RTC}}^{\text {topography}}$ effects (see Eq. 4).

• 3. Downward continuation of airborne gravity data.

  • (a) Calculation of an empirical covariance function (ECF) using the residual gravity anomalies ($\Delta g_{\text {RA}}^{\text {flight}}$ and $\Delta g_{\text {RA}}^{\text {topography}}$).

  • (b) Determination of the fitting parameters of the logarithmic flat-Earth analytic covariance function (ACF), which has the following form (Forsberg 1987, Eq. 30):

    $$\begin{aligned}&ACF(\Delta g^{x_i,y_i, H_i}, \Delta g^{x_j,y_j, H_j})\nonumber \\&=-f\sum _{k=0}^{3}\alpha _k \ln \left[ D_k + \left[ s^2 + \left( D_k+H_i+H_j \right) ^2 \right] ^\frac{1}{2} \right] \ ,\nonumber \\ \end{aligned}$$

    (5)

    where $\Delta g^{x_i,y_i, H_i}$ and $\Delta g^{x_j,y_j, H_j}$ are pairs of gravity points, x and y are plane (map projection) Easting and Northing coordinates, $H_i$ and $H_j$ are orthometric heights of gravity points, $\alpha _k$ are weight factors (with values $\alpha _0=1$, $\alpha _1=-3$, $\alpha _2=3$, and $\alpha _3=-1$; after Forsberg 1987, Eq. 29), $s=\sqrt{(x_i-x_j)^2+(y_i-y_j)^2}$ is the planar (horizontal) distance between points i and j.

    The auxiliary quantity $D_k$ in Eq. 5 is defined as:

    $$\begin{aligned} D_k=D+kT. \end{aligned}$$

    (6)

    The scale factor f in Eq. 5 is defined as:

    $$\begin{aligned} f=C_0 \log \frac{(D+T)^3(D+3T)}{D(D+2T)^3}. \end{aligned}$$

    (7)

    Values of the variance of gravity anomalies $C_0$, depth of the Bjerhammar sphere D, and the low-frequency attenuation depth factor T, are obtained by fitting the ECF to the ACF. ECF and ACF along with values of the fitting parameters are plotted in Fig. 4.

  • (c) Downward continuation of airborne residual gravity anomalies from the aircraft altitude to the topographic surface using a windowed LSC. Blocks had the size of $1^\circ \times 1^\circ$ with $0.2^\circ \times 0.2^\circ$ overlaps. The size and overlaps of the blocks were selected so that the matrix of normal equations could be inverted on a personal computer. Overlaps allowed smooth transition without edge effects along and between blocks.

• 4. Obtaining downward-continued airborne gravity anomalies at the topographic surface $\Delta g_{\text {FA}}^{\text {topography}}$ by restoring $\Delta g_{\text {GGM}}^{\text {topography}}$ and $\Delta g_{\text {RTC}}^{\text {topography}}$ effects calculated at the topographic surface.

After completing all steps, downward-continued airborne gravity data referred to the topographic surface. As such, all data was ready for gridding (see Sect. 2.5).

Fig. 4

Empirical (ECF) and analytic (ACF) covariance functions used for DWC of the airborne gravity data

Analysis of airborne and terrestrial gravity data errors

The accuracy of gravity data was estimated by performing three procedures: (i) crossover error analysis of airborne gravity data between flight lines, (ii) crossover error analysis between downward-continued airborne gravity values and the corresponding terrestrial gravity values at the topographic surface, and (iii) estimation of data uncertainties by using leave-one-out cross-validation (LOOCV) procedure.

Firstly, 88 airborne points were detected having an identical position at two different (crossing) flight lines. Identical position means that the planar distance between the two points is smaller than 0.00001$^\circ$ ($\sim$1 m). Standard deviation of the crossover error of residual gravity anomalies at the flight altitude was $\sigma _\text {crossover}= 2.2$ mGal. This value is comparable with findings of Zhong et al. (2015), Team (2017), and Huang et al. (2019) who investigated crossover errors of several GRAV-D data blocks. The crossover error indicates the unmodelled noise level of the data, under the assumption that the data noise between tracks is random and uncorrelated.

From crossover error at the flight altitude, the accuracy of downward-continued airborne gravity data was estimated. Generally, the accuracy of downward-continued airborne gravity data consists of the accuracy of the airborne data (at flight altitude) and the accuracy of the DWC procedure. The random error of the DWC procedure was estimated by applying the error propagation law to Poisson’s integral transformation. The error of the DWC procedure was estimated to be $\sigma _\text {DWC}=3$ mGal. Therefore, the accuracy of downward-continued airborne gravity data was estimated to be $\sigma _\text {airborne}=\sqrt{\frac{1}{2}\sigma _\text {crossover}^2 + \sigma _\text {DWC}^2}= 3.4$ mGal.

Secondly, 25 points with identical position in airborne and terrestrial datasets were detected. Estimated standard deviation of the crossover error between downward-continued airborne gravity and terrestrial gravity was 4.3 mGal. The previously estimated value $\sigma _\text {airborne}=3.4$ mGal was used as the accuracy of downward-continued airborne gravity data. An estimated accuracy of the terrestrial gravity data, assuming uncorrelated random errors, was estimated to be $\sigma _\text {terrestrial}=\sqrt{4.3^2-3.4^2} = 2.6$ mGal. Therefore, the accuracy of terrestrial gravity dataset is superior to that of airborne gravity dataset by $\sim$25%.

The mean value of the differences between identical terrestrial and downward-continued airborne points was 0.3 mGal. This indicated that there was a systematic error (bias) present in the airborne gravity data compared to the terrestrial gravity data. A slightly larger systematic error was found in some other studies, such as: Hwang et al. (2007, Table 2), McCubbine (2016, Table 6.5) and Zhao et al. (2018), where mean values of the differences were 1.5, 1.0, and $-$ 1.9 mGal, respectively. The expected impact on the determined geoid undulation caused by the bias of airborne gravity data was estimated using Eq. 2-234 from Heiskanen and Moritz (1967):

$$\begin{aligned} \sigma _{N}=\frac{d}{g} \sigma _{\Delta g}, \end{aligned}$$

(8)

where g is the approximate gravity value at the computation point in [mGal], and d is the integration radius of gravity data around the computation point in (m). For Eq. 8 selected values are: $g\approx 981000$ mGal, $\sigma _{\Delta g}=0.3$ mGal, and $d= 100$ km. So, the expected bias of the determined geoid due to biased airborne gravity data, is $\sigma _{N}\approx$ 3 cm (see Table 5).

Thirdly, instead of using two uniform standard deviation values for gridding of the entire terrestrial and airborne gravity datasets ($\sigma _\text {terrestrial}$ and $\sigma _\text {airborne}$), iterative LOOCV procedure was applied for deriving a priori weights for each point which entered the gridding procedure. Thus, gridding of point gravity anomalies by using LSC interpolation method was expected to be improved (see later, Sect. 2.5). LOOCV is used in applied sciences to estimate how accurately a predictive model may perform. In geodesy, it may be used for the estimation of the medium to high-frequency errors of data (e.g. Saleh et al. 2013; Jiang and Wang 2016). It is an iterative method, wherein each iteration only one point of interest is excluded from the entire dataset, then the value for that excluded point is predicted (interpolated) from the nearest points. The difference between the predicted and excluded value ($\tau =\Delta g_\text {predicted} - \Delta g_\text {excluded}$) may be considered as an accuracy measure. The $1/\tau ^2$ value is taken as the weight of the point since it shall mainly contain the remained medium and high-frequency errors in the data. Long-wavelength errors in the data cancel out in the differences between predicted and excluded point. The LOOCV procedure repeats until weights for all points in the dataset are estimated. Again, the windowed (block-by-block) LSC was used for interpolation, where for each point, all points inside the 1$^\circ \times 1^\circ$ (100 km $\times$ 100 km) area around the excluded point were considered for the interpolation. Residual gravity anomalies were used as input data. Two-dimensional isotropic second-order Markov covariance model was used for the ACFs (Kasper Jr 1971, Eq. 7):

$$\begin{aligned} C(d)=C_{0}\left( 1+\frac{d}{D}\right) e^{\frac{-d}{D}} (\mathrm {mGal}^2) \end{aligned}$$

(9)

where d is the planar distance between points in (km), $C_0$ is the variance of the input gravity anomalies in ($\hbox {mGal}^2$), and D is the correlation length in (km). Two sets of fitting parameters were estimated, one from the terrestrial and one from the airborne gravity data (see Fig. 5).

Fig. 5

Empirical (ECF) and analytic (ACF) covariance functions for terrestrial gravity data (top) and airborne gravity data (bottom) used in LOOCV

Gravity data gridding and spectral analysis

The LSMSA method requires surface gravity anomalies in gridded form. Therefore, after outlier detection and point-wise weight estimation, three grids of surface gravity anomalies were prepared with resolution 1$^{\prime }$, covering the area $34.9^\circ \hbox {N}$ $\le \varphi \le$ 39.9$^\circ$N and 250.1$^\circ$E $\le \lambda \le$257.9$^\circ$E. The first grid was prepared only from the terrestrial gravity data (without the inclusion of available airborne gravity data), the second grid only from the downward-continued airborne gravity data, and the third grid from combined terrestrial and downward-continued airborne gravity data (see Fig. 6). The gridding procedure was again performed in the remove-gridding-restore fashion using residual gravity anomalies ($\Delta g_{\text {RA}}$) as input data, where removed gravity anomalies were restored after gridding. The procedure was as follows: point-wise surface gravity anomalies $\longrightarrow$ point-wise subtraction of the gravity anomalies computed from the GGM and the topography $\longrightarrow$ gridding of $\Delta g_{\text {RA}}$ $\longrightarrow$ grid-wise restoration of the gravity anomalies computed from the GGM and the topography $\longrightarrow$ gridded surface gravity anomalies. The LSC was used as the gridding method, which required a priori stochastic assumptions about the gravity field characteristics. In our case, the interpolation reliability was increased by taking into account the estimated data uncertainty by appending a priori weights for each data point as described in Sect. 2.4. Similar gridding principles were implemented in other studies; see, e.g. Märdla et al. (2017) and Varga (2018). The obtained surface gravity anomaly grids were used as input data in all geoid computations (see Sect. 3).

Fig. 6

Surface gravity anomaly grids used as input data in geoid modelling (mGal)

Fig. 7

Power spectrum of the surface gravity anomaly grids ($\hbox {mGal}^2$)

In the last step, spectral properties of the prepared surface gravity anomalies grids were analysed to check if airborne gravity data could contribute to some specific wavelengths of the geoid with respect to the terrestrial gravity data. There exist several approaches to compute power spectra densities (PSDs) from regional or local gravity datasets; see, e.g. Flury (2006). Here, we estimated degree variances by a procedure based on the Fourier 2D-PSDs by azimuth averaging (Forsberg 1984b). This or a similar method has been applied for estimating the high-frequency part of the spherical harmonic power spectrum from local datasets by Forsberg (1984b), Vassiliou and Schwarz (1987), Flury (2006), Voigt and Denker (2006), Jekeli (2010), Szűcs et al. (2014), and Rexer and Hirt (2015). Our aim was not to investigate PSDs beyond the SH degree 2000, but only in the bandwidth of 2-2000. The degree 2000 has been chosen due to the airborne gravity data line-spacing of 10 km.

Fig. 8

Topography of the study area represented by the SRTMGL1 global DEM (units in (m)), along with 75 GNSS/levelling points, and extents of the gravity data and geoid computation area

We plotted the degree variances of terrestrial, airborne and combined airborne and terrestrial gravity anomalies grids in Fig. 7 as well as the degree variances of gravity anomalies synthesized from EGM2008. Note that we were not able to recover the SH degrees $\le$ 100 due to the limited geographic extent of regional gravity data. Thus, the spectra of both datasets were relatively flat and below the information from GGMs. In the rest of the interval, the degree variances from all three datasets were oscillating around the spectrum of EGM2008. It can be seen that airborne gravity anomalies were significantly more powerful in the bandwidth of 200–1400 compared to only terrestrial gravity anomalies and combined gravity anomalies. The airborne gravity power decreased beyond the SH degree 1400, where parts of the medium- and high-frequency spectrum caused by the topographic gravity signal were not detected by the airborne gravity or were filtered out during data preprocessing. This finding supports the goal of GRAV-D project (see Sect. 2). The signal of the combined grid copied the signal of the airborne gravity data in the bandwidth of 0–850. Thus, we expect that airborne gravity data contribute mainly in the bandwidth of 400–850, which corresponds to the spatial resolution of airborne gravity data from 20 to 50 km.

The signal generated by the combined grid contains more power than the grids based only on terrestrial and airborne gravity data in the bandwidth 1300–1500, while in bandwidth 1500–1750 it has less power than the stronger terrestrial grid. In an ideal case, the signal of combined grids should copy the stronger signal (either airborne or terrestrial data) over the whole bandwidth. Even though the accuracy of resulting combined airborne and terrestrial data geoid at the end showed improvement in accuracy around 20% compared to terrestrial data geoid, PSDs plotted in Fig. 7 indicate that our combination has not been performed optimally from a spectral point of view. Terrestrial and airborne gravity data have been combined in the spatial domain as is described above. We combined 5 times more band-limited airborne points with terrestrial points and PSDs reflect it.

Digital elevation model

For estimating topographic effects on gravity and geoid undulations, a regional DEM was prepared covering the area $33^\circ \hbox {N} \le \varphi \le 42^\circ \hbox {N}$ and $248^\circ \hbox {E} \le \lambda \le 260^\circ \hbox {E}$ with a 1$^{\prime \prime }$resolution (see Fig. 8). The DEM originated from the SRTM (Farr and Kobrick 2000). In this study, SRTMGL1 ver. 003 was used, which was released in 2015 and is considered to be an improved version of previously published versions. The accuracy of the full-resolution DEM over the study area was estimated from the differences between orthometric heights of GNSS/levelling points and DEM-interpolated heights ($\varepsilon = H^\text {GNSS/levelling}-H^\text {DEM}$). The accuracy is described by the mean value (bias) and standard deviation of the differences $\varepsilon$, having values of mean $-$ 2.2  m and $\sigma =3.7$  m. The mean value of $-$ 2.2  m meant that the DEM systematically overestimated elevations in the study area. The RMSE of differences was 4.5 m, which corresponded to an absolute error of 7.4m at 90% confidence. This indicates that the accuracy of this version is better for 54%, compared to 16 m, which is an officially declared absolute error of SRTM DEMs (Rodriguez et al. 2006).

Global geopotential models

GGMs provide information for long wavelengths of the geoid in regional geoid determination. Depending on the availability and quality of other data sources, mainly terrestrial gravity, GGMs’ cut-off degree is usually somewhere between 180 and 250, which corresponds to spatial resolutions between 220 and 160 km. Due to potential spectral overlaps and correlation caused by terrestrial, marine, and altimetric gravity data used in the development of combined GGMs, it is more convenient to use satellite-only GGMs produced solely from gravity-dedicated satellite missions (e.g. GOCE-only or GOCE+GRACE models).

In order to properly compute gravity field functionals from spherical harmonic coefficients (SHC), consistent treatment is needed for spherical/ellipsoidal harmonic representations, GM and R constants, zero- and first-degree terms, and tides. In this analysis, geoid undulations $N_{\text {GGM}}$ were computed by using parameters of the reference ellipsoid GRS80, R and GM from distribution files (with extension *.gfc) of each GGM (usually $R= 6378136.3$ m, $GM= 3986004.415 \times 10^8\,\hbox {m}^3\,\hbox {s}^{-2}$), $G= 6.67259 \times 10^{-11}\,\hbox {m}^3\,\hbox {kg}^{-1}\,\hbox {s}^{-2}$, and $\rho = 2670\,\hbox {kg m}^{-3}$. Heights were synthesized from the global SH digital terrain model DTM2006.0 (Pavlis et al. 2007). The treatment of tides is described in Sect. 3 (see also Eq. 11). The zero-degree term, which accounts for the difference in mass between the GGM and the reference ellipsoid, was calculated using the first term of Eq. 12. Degree-one terms were set to zero, since both validated GGMs and GRS80 (as the reference ellipsoid) are geocentric.

A common procedure for obtaining information about the quality of GGMs is through their comparison with GNSS/levelling points. The procedure starts with the calculation of geoid undulations N or height anomalies $\zeta$ from SHC. Computed GGM-values are then subtracted from values estimated from GNSS/levelling points: $\delta N = N_{\text {GNSS/levelling}}- N_{\text {{GGM}}}$. Differences $\delta N$ indicate the agreement of GGMs over the study area with control data, reflecting the commission and omission errors of GGM, as well as the accuracy of GNSS/levelling data.

Six GGMs were selected for validation purposes, including EGM2008, EIGEN-6S4 (Förste et al. 2015), GOCO05S (Mayer-Gürr 2015), GO-CONS-GCF-2-TIM-R5 (Brockmann et al. 2014), ITU-GGC16 (Akyilmaz et al. 2016), and XGM2016 (Pail et al. 2016). EGM2008 and XGM2016 are combined data models whereas the other models are satellite-only GGMs. The degree $n_ {\text {max}}=280$ was selected for all GGMs as the maximum SH degree, since GOCO05S, GO-CONS-GCF-2-TIM-R5, and ITU-GGC16 do not have degrees beyond this value. For comparison purposes, EGM2008 was also tested up to the maximum SH degree of 2190.

Results of the GGM validation are summarized in Table 2. Differences between the validated models for the selected $n_ {\text {max}}=280$ did not exceed 1 cm in terms of the standard deviation. They had a similar mean value of $-$ 23 cm and standard deviations of 41 cm. The selection of the optimal GGM and $n_{\text {max}}$ is known to be of specific importance for regional gravimetric geoid modelling as the cm-geoid signal has most spectral power for the SH degrees from around 200 to 3000 (Tscherning and Rapp 1974; Schwarz and Li 1996). Therefore, for regional geoid determination, different GGMs and different cut-off degrees should be tested, before deciding an optimal choice. The mean values and standard deviation of the differences between GNSS/levelling and GGM-derived geoid undulations $\delta N$ are $-$ 4 cm and 6.6 cm when EGM2008 is used up to the maximum SH degree. The standard deviation of 6.6 cm can be considered as the optimal accuracy, considering that the orthometric heights are given in the historic HRS NAVD88 and the study area is mountainous.

Gravimetric geoid modelling

The gravimetric geoid models were determined in the equiangular grid with resolution $1^{\prime }\times 1^{\prime }$ (2 km $\times$ 1.5  km) over the territory of 35.2$^\circ$N $\le \varphi \le$ 38$^\circ$N and 251.4$^\circ$E  $\le \lambda \le$ 257.5$^\circ$E. The computation area covered almost 170,000 $\hbox {km}^2$ ($3^{\circ }\times \, 6^{\circ }$), with topography varying between approximately 500 m and 4400 m, mean 1390 m, RMS 1560 m; see Fig. 8. Minimum and maximum altitudes of the GNSS/levelling points used in validation were 1340 m and 3188 m, respectively.

Integral-based geoid determination techniques rely on the solution of the second or third BVPs in which the disturbing potential or geoid undulation is determined by Hotine’s or Stokes’ formulas either from measured gravity disturbances or anomalies continued to a spherical boundary surface. In this study, the geoid computation was performed using the LS modification of Stokes’ kernel with additive corrections (LSMSA) method. This method was developed mainly by L.E. Sjöberg. The LSMSA method was applied for regional geoid modelling in many areas worldwide such as the Nordic-Baltic area (Ellmann 2004; Ågren et al. 2016), Sweden (Ågren et al. 2009), France (Yildiz et al. 2012), Turkey (Abbak et al. 2012) and Croatia (Varga 2018).

In the LSMSA method, surface gravity anomalies and GGM are used for the calculation of the approximate geoid undulation ${\widetilde{N}}$. Afterwards, all other effects are computed separately and added as geoid undulation corrections (e.g. Sjöberg and Bagherbandi 2017, Eq. 6.3a):

$$\begin{aligned} N={\widetilde{N}}+\delta N_{\text {top}}^{\text {comb}}+\delta N_{\text {DWC}}+\delta N_{\text {atm}}+\delta N_{\text {ell}}\ , \end{aligned}$$

(10)

where ${\widetilde{N}}$ is the approximate geoid undulation, $\delta N_{\text {top}}^{\text {comb}}$ is the combined (direct and indirect) topographic correction, $\delta N_{\text {DWC}}$⁴ is the downward-continuation correction, $\delta N_{\text {atm}}$ is the atmospheric correction and $\delta N_{\text {ell}}$ stands for the ellipsoidal correction. A more detailed explanation of the LSMSA method is given in Annex A.

Table 2 Statistics of the differences between GNSS/levelling and GGM derived geoid undulations. Units in (m)

Table 3 Input models and parameters used for geoid modelling

In the LSMSA method, the following parameters had to be selected for performing computations: the form of the modified Stokes’ kernel $S^\text {modif}$ (biased, unbiased, or optimum), integration (truncation) cap radius $\psi$, error variance of input gravity anomalies $C_0$ (the value of the covariance function at $\psi =0^\circ$), modification degree M, and the mean crustal density $\rho _c$. Input models, such as GGM and DEM, had to be chosen as well. Several values of input parameters and models were tested in computations to obtain the optimal solution; see Table 3.

The reference ellipsoid in all computations was GRS80. Following the recommendations of Sánchez et al. (2018), all geoid models were determined in the tide-free (TF) system. Gravity datasets and ellipsoidal heights from GNSS/levelling dataset were in TF system. Some GGMs were distributed in the zero-tide (ZT) system (e.g. GOCO05S), and some in the tide-free system (e.g. EIGEN-6S4). In order to be consistent, GGMs given in the ZT system were converted to the TF system by changing the ${\bar{C}}_{20}$ coefficient to include the zero-frequency (permanent) tide contribution according to Eq. 6.14 in Luzum and Petit (2012):

$$\begin{aligned} {\bar{C}}^\text {TF}_{20}={\bar{C}}^\text {ZT}_{20}+4.173\cdot 10^{-9}. \end{aligned}$$

(11)

All geoid models were determined to be consistent with the IHRS conventional geoid reference potential value $W_0^\mathrm {IHRS}$. Therefore, the zero-degree term was calculated using the generalized Bruns’ formula, and added to the computed gravimetric geoid undulations (Heiskanen and Moritz 1967, Eq. 2–182):

$$\begin{aligned} N_{0}=\frac{GM_{\mathrm {GGM}}-GM_{\mathrm {GRS} 80}}{r \gamma _{0}} -\frac{\Delta W}{\gamma _{0}}, \end{aligned}$$

(12)

where $GM_{\mathrm {GGM}}$ is taken from the used GGM, $GM_{\mathrm {GRS} 80}$ is the constant of the reference GRS80 ellipsoid, r is the geocentric radial distance of the computation point, $\gamma _0$ is normal gravity value of the computation point at the ellipsoid surface, $\Delta W$ is obtained from the difference between the $W_0^{\mathrm {IHRS}}=62{,}636{,}853.4\,\hbox {m}^2\,\hbox {s}^{-2}$ (Sánchez et al. 2016) and the normal potential value on the reference GRS80 ellipsoid $U_0^{\mathrm {GRS} 80}=62{,}636{,}860.85\,\hbox {m}^2\,\hbox {s}^{-2}$. The estimated value of the zero-degree term $N_0$ was $-$ 0.18 m, when following numerical values are used: $GM_{\mathrm {GGM}}=3{,}986{,}004.415 \cdot 10^8\,\hbox {m}^3\,\hbox {s}^{-2}$, $GM_{\mathrm {GRS} 80}= 3{,}986{,}005\cdot 10^{8}\,\hbox {m}^3\,\hbox {s}^{-2}$, $r\approx a_{\mathrm {GRS} 80}= 6{,}378{,}137.0$ m, $\gamma _0 \approx {\bar{\gamma }}_{\mathrm {GRS} 80} =9.798\,\hbox {ms}^{-2}$, and $\Delta W=W_0^{\mathrm {IHRS}}-U_0^{\mathrm {GRS} 80}=-7.45\,\hbox {m}^2\,\hbox {s}^{-2}$.

Results and discussion

Geoid computations with different input parameters (Table 3) resulted in more than five hundred different solutions. Only three solutions, with the smallest standard deviation values of the differences with respect to the GNSS/levelling, were selected for further analysis; one for each gravity anomaly grid (airborne, terrestrial and airborne and terrestrial). Validation of all estimated solutions was performed in the absolute and relative sense. In the absolute sense, the principle was similar to the validation of GGMs (see Sect. 2.7), except that validated values were obtained by interpolating geoid undulations $N_\text {geoid}^\text {int}$ from the grid to the position of each GNSS/levelling point. Then, the geoid undulation differences were estimated using the equation:

$$\begin{aligned} \delta N = N_{\text {GNSS/levelling}}- N_{\text {geoid}}^{\text {interpolated}}, \end{aligned}$$

(13)

which indicated the accuracy of each gravimetric geoid model. Due to unavailability of error estimates for h and N from GNSS/levelling data, they are considered to be error-free in this study. Input models and parameters of the finally selected gravimetric geoid models are given in Table 4.

Table 4 Input parameters and models of the final geoid models

Table 5 Statistics of the differences between geoid undulations at the 75 GNSS/levelling points and geoid undulations interpolated from the computed gravimetric geoid models. Units in (cm)

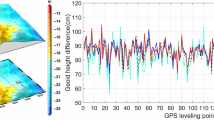
Standard deviation of differences between geoid undulations from control GNSS/levelling points and geoid undulations interpolated from the estimated geoid models exhibited an accuracy improvement of 1.1 cm or 20% when the airborne and terrestrial gravity data was used compared to the solution in which only the terrestrial gravity data was used; see Table 5. Comparing airborne data geoid and terrestrial data geoid, the airborne data geoid had 0.8 cm smaller standard deviation. However, the airborne data geoid had a mean error larger than the terrestrial data geoid, $-$ 2.7 cm compared to $-$ 0.5 cm. This effect might originate from the bias detected in the airborne gravity data (see Table 6) or from aliasing effects caused by ellipsoidal heights, which may be less accurate in the airborne gravity data. By comparing the RMS values of each solution, the improvement of the geoid accuracy was confirmed as the airborne and terrestrial data geoid had the RMS of 5.5 cm, whereas the airborne data geoid had the RMS of 6.3 cm, which represents an improvement of 14%.

Comparisons with the full-power EGM2008, as it matched the GNSS/levelling data best among all validated GGMs (see Table 2), manifested that the agreement of all three geoid models (airborne, terrestrial and airborne and terrestrial) outperformed the agreement of EGM2008. EGM2008 had the largest mean error of $-$ 4.1 cm and the standard deviation of 6.6 cm, whereas the best solution—the airborne and terrestrial data geoid—had the mean error of $-$ 1.4 cm and the standard deviation of 5.4 cm.

In all three cases, ITU-GGC16 model outperformed other tested satellite GGMs. Even though it was developed up to $n_\text {max}= 280$, the best solution was yielded for $n_\text {max}= 210$. The usual practice in regional geoid determination is to truncate GGM at some lower degree than maximum to obtain a better geoid solution, as the SHC after some (i.e. $n>$150) degree are quickly becoming less accurate (see, e.g. Brockmann et al. 2014).

Fig. 9

Absolute values of geoid undulation differences (grid-minus-grid) between the airborne and terrestrial data geoid and terrestrial data geoid

Fig. 9 shows geoid undulation differences between grids of airborne and terrestrial and terrestrial geoids. Areas with the largest discrepancies are those which are mostly influenced by airborne gravity data. Five areas may be visually selected as those with strongest contribution of airborne gravity data, and all five areas are mountainous parts of the study area, where terrestrial gravity data is sparse or even non-existent (see Figs. 1, left and 8). In these areas, the airborne and terrestrial data geoid presents differences in geoid undulations from 4 cm to 16 cm compared to the terrestrial data geoid.

The relative geoid accuracy of the final models was estimated using geoid undulation differences $\Delta N_{ij}$ between the GNSS/levelling points (e.g. Varga 2018, pp. 78):

$$\begin{aligned} \Delta N_{ij} = \frac{[(h^i-H^i)_{\text {GNSS/levelling}} -N^i_{\text {geoid}}]-[(h^j-H^j)_{\text {GNSS/levelling}} -N^j_{\text {geoid}}]}{d_{ij}}\ ,\nonumber \\ \end{aligned}$$

(14)

where i and j are indices of the pair of GNSS/levelling points and $d_{ij}$ is the planar distance between each pair of points in (km). There are $k (k-1)/2$ baselines, where the k is the number of GNSS/levelling points. In our case, k is 75, and the number of baselines is 2775. $\Delta N_{ij}$ was calculated for each baseline. Distances between points were grouped according to provisionally defined distance intervals (e.g. 0–20 km, 20–40 km, 40–60 km, ...). The standard (misclosure) error $\sigma (\Delta N_{ij})$ was calculated as the mean value of the differences $\Delta N_{ij}$ for each distance interval. The standard (misclosure) error is furtherly compared to maximal allowable misclosure errors in two-way precise levelling (0.2 (cm)$\sqrt{d (\text {km}) }$, used in realization of high-order networks of height control points) and with technical levelling (0.5 (cm)$\sqrt{d (\text {km}) }$, used in realization of lower-order networks of height control points). Standard (misclosure) error as an accuracy measure is valuable from the engineering perspective as the gravimetric and hybrid geoid models are used not only for absolute positioning (determination of height in a reference system) but also for height transfer over distances. This geodetic method is known as GNSS/levelling, where the geoid (or quasi-geoid) is used to transfer orthometric (or normal heights) in the height reference system from one place to another. In the past, this was performed exclusively by using spirit, trigonometric or barometric levelling.

Fig. 10

Relative geoid accuracy (cm)

More information about absolute and relative accuracy validation of GGMs and geoid models may be found in Kotsakis and Sideris (1999) and Featherstone (2001).

The relative geoid accuracy comparison is visualized in Fig. 10. As expected, precise levelling is the best method for height transfer over all distances. Technical (lower-order) levelling is better suited for height transfer than GNSS/levelling using the geoid up to distances of 90 km. Then, for increasing distances ($d>100$ km) the airborne and airborne and terrestrial data geoids provide better relative accuracy than technical levelling. When the airborne and terrestrial data geoid models are compared to each other, the terrestrial data geoid has better relative accuracy for distances up to approximately 75 km. For longer distances, the airborne and airborne and terrestrial data geoids are more accurate than the terrestrial data geoid. The airborne and airborne and terrestrial data geoids are also very similar in the relative sense; for some distances, they have larger differences, but this may be due to a very small number of baselines between points in some distance intervals (mainly for distances larger than 300 km).

Fig. 11

Power spectrum of the final geoid models ($\hbox {m}^2$)

The geoid undulation power spectrum is plotted in Fig. 11. Compared to EGM2008, all geoid models have significantly more power in all spectral bands, except for the lower SH degrees between $0<n<40$. All geoid models have practically the same spectrum over the SH degrees $0<n<750$. Above degree 750, the spectrum of the geoid determined from airborne and terrestrial data oscillates around the spectrum of the geoid based on airborne data only and does not reflect the strongest signal of the terrestrial data geoid. This finding is caused by the gravity datasets combination and fully corresponds to the finding from the spectral analysis of the input gravity grids (see Sect. 2.5). We realize by comparing the three curves in Figs. 7 and 11 with the curve related to EGM2008 that in the bandwidth 0 to 900 all regional geoids have significantly more power than the corresponding EGM2008 curve. This is caused by the modified Stokes’ kernel (see Fig. 13) used in the geoid determination, where lower degrees have larger weight, while higher degrees (above 300) have the constant weight value. The modified Stokes’ kernel works like a low-pass filter. We can recognize the same PSDs’ local maxima and minima above 1000 in both figures (see Figs. 7 and 11).

Conclusions

Gravimetric geoid models were determined for the mountainous area in Colorado by using three surface gravity anomaly grids (terrestrial, airborne and airborne and terrestrial).

The main finding is that the geoid based on the airborne and terrestrial gravity data had the highest accuracy, as it had the smallest standard deviation and RMS of geoid undulation differences with respect to GNSS/levelling. Thus, the airborne gravity data improved the accuracy of gravimetric geoid models compared to geoid models computed solely from terrestrial gravity data. The standard deviation of differences between GNSS/levelling and undulations from computed geoid models was 1.1 cm lower for airborne and terrestrial data geoid, compared to the terrestrial data geoid. This is an improvement in geoid accuracy of 20%. Our results are consistent with previous studies from Smith et al. 2013 and Wang et al. 2017, which showed an improved geoid accuracy when GRAV-D airborne gravity was employed.

Fig. 12

Integration of gravity data ($Q_1$, $Q_2$, ..., $Q_N$) within inner zone limited by spherical cap $\sigma _0$ having radius $\psi$ around computation point P

The strongest influence of airborne gravity on the final geoid models is evident in the mountainous parts of the study area, where terrestrial gravity is sparse or even non-existent, which shows that terrestrial and airborne gravity data are complementary.

Relative geoid accuracy for airborne and airborne and terrestrial data geoid is almost similar for most distances; e.g. for baselines of 25 km and 400 km, the standard errors are 4 and 7 cm, respectively. For all distances larger than 75 km, relative geoid accuracy of the terrestrial data geoid is lower by 20% than for airborne and airborne and terrestrial data geoids.

In the spectral domain, airborne and terrestrial gravity anomalies have more power over the SH degrees of 400$<n<$850, which are mostly covered by airborne gravity data. However, the improvement of the airborne and terrestrial data geoid is not visible in the same bandwidth. Beyond this bandwidth, the spectrum of the airborne and terrestrial data geoid model is stronger than the counterpart from airborne gravity data and reflects more the terrestrial gravity data, which helps to increase the power of the geoid models based only on the airborne gravity data. We applied non-optimal weighting during combination of terrestrial and airborne gravity data. It seems that a much larger number of airborne gravity points dominate airborne and terrestrial data geoid model. This effect is also visible in the power spectrum. The problem of the optimal combination of airborne and gravity data remains a topic for future research.

The estimated 1$\sigma$ accuracy of terrestrial and airborne gravity data was 2.6 mGal and 3.4 mGal, respectively. The airborne data geoid was biased by 3 cm with respect to GNSS/levelling, which was caused by the biased airborne gravity data (0.3 mGal).

Windowed least-squares collocation proved to be computationally efficient for the continuation of the large airborne gravity datasets down to the topographic surface, as well as for gridding of scattered gravity values. However, computations had to be optimized. If block size and overlaps between blocks are sufficiently large, and if an identical analytic covariance function is used over the entire area, then biases between blocks are not detectable in the computed geoid models.

Validated GGMs had practically the same agreement with GNSS/levelling for the maximal SH degree $n_\text {max}=280$. However, geoid models computed using different GGMs indicated that the selection of GGM and SH truncation degree is important. Optimal GGM truncation degree has to be numerically tested and determined in order to obtain the best geoid solution. In our case, geoid models obtained by using the satellite-only model ITU-GGC16 as the reference gravity field for low-frequencies of the geoid, with maximal SH $n_\text {max}=210$ and integration cap $\psi =0.7^{\circ }$, resulted in the best agreement with the GNSS/levelling data among all GGMs (including even EGM2008).

The LSMSA geoid modelling method gave competitive results compared to other computation methods and techniques (see also NTIS and GEOF geoid solution in Wang et al. 2021).

Annex A: Geoid modelling method: least-squares modification of Stokes’ formula with additive corrections

The description and mathematical formulation of the LSMSA method are given in this section. LSMSA is a regional gravimetric geoid modelling method which may combine terrestrial and airborne gravity data. The gravity data are integrated within a spherical cap $\sigma _0$ (near-zone contribution) with the far-zone ($\sigma -\sigma _0$) contribution estimated from GGM (see Fig. 12).

Stochastic modifications of the Stokes’ formula use gravity signal and error spectra (estimated from GGMs) to optimize contributions of input gravity data and GGM. The method uses one of the available LS estimators for finding modification parameters $s_n$ by considering errors of all available gravity data, GGM and truncation errors of Stokes’ integral. In this way, truncation errors of data integration, errors of input gravity data and errors of geopotential coefficients are minimized in the LS sense. All terms can be computed by using the following equations; see, e.g. Sjöberg (2003a), Ellmann and Sjöberg (2004), Sjöberg (2004), Ågren et al. (2009), Sjöberg and Bagherbandi (2017):

$$\begin{aligned} {\widetilde{N}}= & {} \frac{R}{4\pi \gamma } \iint \limits _{\sigma _0}S^{L}(\psi )\Delta g \mathrm{d}\sigma _0 + \frac{R}{2\gamma }\sum _{n=2}^{M}b_n\Delta g_n, \end{aligned}$$

(15)

$$\begin{aligned} \delta N_{\text {top}}^{\text {comb}}= & {} -\frac{2 \pi G \rho _c}{\gamma }\left( H_P^2+\frac{2H_P^3}{3R} \right) , \end{aligned}$$

(16)

$$\begin{aligned} \delta N_{\text {DWC}}= & {} \frac{\Delta g_P}{\gamma }H_P+3 \frac{{\tilde{N}}}{r_P}H_P-\frac{1}{2\gamma } \frac{\partial \Delta g}{\partial r} \bigg |_P H_P^2\ \nonumber \\&+\frac{R}{2 \gamma } \sum _{n=2}^{M} b_{n}\left[ \left( \frac{R}{r_{P}}\right) ^{n+2}-1\right] \Delta g_{n} \nonumber \\&+ \frac{R}{4 \pi \gamma } \iint \limits _{\sigma _{0}} S^{L}(\psi )\left[ \frac{\partial \Delta g}{\partial r} \bigg |_Q\left( H_{P}-H_{Q}\right) \right] \mathrm{d}\sigma _{0}, \end{aligned}$$

(17)

$$\begin{aligned} \delta N_{\text {atm}}= & {} -\frac{G R \rho _{a}}{\gamma } \iint \limits _{\sigma _{0}} S^{L}(\psi ) H_{P} \mathrm{d}\sigma _{0}, \end{aligned}$$

(18)

$$\begin{aligned} \delta N_{\text {ell}}= & {} \psi \left[ \left( 0.12-0.38 \sin ^{2} \varphi \right) \Delta g_P+0.17 {\widetilde{N}} \cos ^{2} \varphi \right] ,\nonumber \\ \end{aligned}$$

(19)

where

• P is the computation (evaluation) point, and Q the running (integration) point,

• $\varphi _P$ is the latitude, $r_P=R+H_P$ the geocentric (spherical) radius,

• $H=H_P$ the orthometric height of the computation point,

• $R=(2a+b)/3$ is the mean radius,

• $\gamma = \gamma _0 (P)$ is the normal gravity of the computation point P on the ellipsoid surface ($h=0$) computed using the Somigliana formula (Heiskanen and Moritz 1967, Eq. 2–78):

  $$\begin{aligned} \gamma _0= \frac{a \gamma _e \cos ^2 \varphi + b \gamma _p \sin ^2 \varphi }{\sqrt{a^2 \cos ^2 \varphi + b^2 \sin ^2 \varphi }}, \end{aligned}$$

  (20)

  where a and b are semi-major and semi-minor axes of the reference ellipsoid, $\gamma _e$ and $\gamma _p$ are the normal gravity values at the equator and poles,

• $\sigma _0$ is the spherical cap with the radius $\psi$, which defines the area of integration,

• $\psi =\psi _{PQ}$ is the integration cap radius, the geocentric angle (or angular distance) between the computation P and integration Q points,

• n is the spherical harmonic degree,

• $S^{L}$ is the modified Stokes’ formula up to the modification limit L (Heiskanen and Moritz 1967, Eq. 2-169):

  $$\begin{aligned} S^{L}(\psi )=\sum _{n=2}^{\infty } \frac{2 n+1}{n-1} P_{n}(\cos \psi )-\sum _{n=2}^{L} \frac{2 n+1}{2} s_{n} P_{n}(\cos \psi ), \end{aligned}$$

  (21)

  where the first term is the original spectral form of the Stokes’ formula $S(\psi )$, and $P_n (\cos \psi )$ are the Legendre polynomials.

  Figure 13 shows original (unmodified) and modified spectral-forms of the Stokes’ kernel as a function of the SH degree. The modified (weighted) Stokes’ kernel gradually converges to zero until the selected SH degree, whereas the original Stokes’ function fluctuates around zero. The kernel function $S(\psi )$ in Fig. 13 is computed from the closed-form equation (Heiskanen and Moritz 1967, Eq. 2–164):

  $$\begin{aligned} S(\psi )= & {} \frac{1}{s} - 6s + 1 - 5\cos \psi - 3\cos \psi \ln (s + {s^2}), \nonumber \\&\text {where } s = \sin \frac{\psi }{2}. \end{aligned}$$

  (22)

• L is the maximum (uppermost) SH degree of the modification by arbitrary parameters $s_n$,

• $\Delta g$ is the surface gravity anomaly, defined by Eq. 1,

• $d \sigma$ is an infinitesimal surface element of the unit sphere $\sigma$,

• M is the arbitrarily chosen maximum SH degree of the used GGM,

• $b_n$ is the set of spectral (stochastic) modification coefficients of Stokes’ formula governed by the type of estimator (biased, unbiased, or optimum) (see Table 7),

• $Q_n^L$ are the Molodensky truncation coefficients up to the degree L:

  $$\begin{aligned} Q_{n}^{L}=Q_{n}\left( \psi _{0}\right) -\sum _{k=2}^{L} \frac{2 k+1}{2} s_{k} e_{n k}\left( \psi _{0}\right) , \end{aligned}$$

  (23)

  • with the Molodensky truncation coefficients $Q_n$ defined as:

    $$\begin{aligned} Q_{n}=\int \limits _{\psi _{0}}^{\pi } S(\psi ) P_{n}(\cos \psi ) \sin \psi \mathrm{d} \psi , \end{aligned}$$

    (24)

  • and Paul’s coefficients $e_{nk}$ defined as:

    $$\begin{aligned} e_{n k}=e_{n k}\left( \psi _{0}\right) =\frac{2 k+1}{2} \int \limits _{\psi _{0}}^{\pi } P_{n}(\cos \psi ) P_{k}(\cos \psi ) \sin \psi \mathrm{d} \psi ,\nonumber \\ \end{aligned}$$

    (25)

• $s_n$ are the LS modification parameters, which depend on the stochastic characteristics of the input gravity data, stochastic characteristics of GGM, and integration cap radius.

  $$\begin{aligned} s_{n}=\left\{ \begin{array}{c} s_{n}, \text{ if } 2 \le n \le L, \\ 0, \text{ otherwise. } \end{array}\right. \end{aligned}$$

  (26)

  The values of the $s_n$ parameters are obtained from the following linear system of equations:

  $$\begin{aligned} \sum _{r=2}^{L} a_{k r} s_{r}=h_{k}, \quad k=2,3, \ldots , L, \end{aligned}$$

  (27)

  $a_{kr}$ and $h_k$ are the modification coefficients determined from numerical values of $Q_n$ and $e_{nk}$, gravity anomaly signal degree variances of GGM ($c_n$), error degree variances of GGM ($dc_n$), and error degree variances of the input gravity data ($\sigma _n^2$), where

  $$\begin{aligned} a_{k r}= & {} \sum _{n=2}^{\infty } e_{n k} e_{n r} C_{n}+\delta _{k r} C_{r}-e_{k r} C_{k}-e_{k r} C_{r}, \end{aligned}$$

  (28)
  $$\begin{aligned} h_{k}= & {} \frac{2 \sigma _{k}^{2}}{k-1}-Q_{k} C_{k}+\frac{2 k+1}{2} \sum _{n=2}^{\infty }\left( Q_{n} e_{n k} C_{n}-\frac{2}{n-1} e_{n k} \sigma _{n}^{2}\right) ,\nonumber \\ \end{aligned}$$

  (29)
  $$\begin{aligned} \delta _{k r}= & {} \left\{ \begin{array}{cc} 1 &{} \text{ if } k=r, \\ 0 &{} \text{ otherwise } , \end{array}\right. \nonumber \\\end{aligned}$$

  (30)
  $$\begin{aligned} C_{k}= & {} \sigma _{k}^{2}\left\{ \begin{array}{ll} C_{k} d C_{k} /\left( C_{k}+d C_{k}\right) &{} \text{ if } 2 \le k \le M, \\ C_{k} &{} \text{ if } k>M, \end{array}\right. \end{aligned}$$

  (31)
  $$\begin{aligned} e_{n k}= & {} \frac{2 k+1}{2} e_{n k}\left( \psi _{0}\right) . \end{aligned}$$

  (32)

  More details are given in Ellmann 2005a, Table 1.

• $\Delta g_n$ is the gravity anomaly expanded into a series of Laplace harmonics (Heiskanen and Moritz 1967, p. 97):

  $$\begin{aligned} \Delta g_{n}=\frac{2 n+1}{4 \pi } \iint \limits _{\sigma } \Delta g P_{n}(\cos \psi ) \mathrm{d}\sigma \end{aligned}$$

  (33)

• G is the universal gravitational constant 6.67430 $\times$ 10$^{-11}$ $\hbox {m}^3$ $\hbox {kg}^{-1}$ $\hbox {s}^{-2}$ (Tiesinga et al. 2020),

• $\rho _c$ is the mean crustal density equal to 2670 $\hbox {kg m}^{-3}$ (Hinze 2003),

• $\frac{\partial \Delta g}{\partial r}\bigg |_{P}$ is the vertical gradient of the gravity anomaly at the computation point P, computed from Eq. 2-217 in Heiskanen and Moritz (1967):

  $$\begin{aligned} \frac{R^{2}}{2 \pi } \iint \limits _{\sigma _{0}} \frac{\Delta g_{Q}-\Delta g_{P}}{l_{0}^{3}} d \sigma _0-\frac{2}{R} \Delta g_P, \end{aligned}$$

  (34)

  with the spherical distance between the computation and integration points obtained as $l_0=2 R \sin \frac{\psi }{2}$,

• $\rho _a$ is the density of the atmosphere at the sea level, which is equal to 1.23 $\hbox {kg m}^{-3}$ (see, e.g. Sjöberg 1999).

Fig. 13

Original and modified Stokes’ kernels as a function of the SH degree. Integration cap radius is $\psi =0.7^{\circ }$ as used in the final geoid models

Table 6 Statistics of residual gravity anomalies $\Delta g_{\text {RA}}$ before and after outlier removal (mGal)

Table 7 Stochastic LS estimators of Stokes’ formula (after Ellmann 2005b, Table 1)

The modification parameters $s_n$ and $b_n$ (see Table 7) were estimated using the LS method described in Ellmann (2005a). The procedure consisted of the following steps:

• 1. Determination of the gravity anomaly error variance using the closed-form isotropic reciprocal distance type error degree covariance function (Ellmann 2005a, Eq. 14).

  $$\begin{aligned} \sigma _{n}^{2}=c_{T}(1-\mu ) \mu ^{n}, \quad 0<\mu <1, \end{aligned}$$

  (35)

  where $\mu =0.99899012911838605$ value is found for the terrestrial anomaly correlation length $C(\psi )= 0.1\circ$, and $c_T=\frac{C_0}{\mu ^2}$.

• 2. Determination of the gravity anomaly degree variance and error degree variance ($c_n$ and $d c_n$) according to:

  $$\begin{aligned} {c}_{n}= & {} \frac{(G M)^{2}}{a^{4}}(n-1)^{2} \sum _{m=0}^{n}\left( {\bar{C}}_{nm}^{2}+{\bar{S}}_{nm}^{2}\right) , \end{aligned}$$

  (36)
  $$\begin{aligned} d c_{n}= & {} \frac{(G M)^{2}}{a^{4}}(n-1)^{2} \sum _{m=0}^{n}\left( \sigma _{{\bar{C}}_{n m}}^2+\sigma _{{\bar{S}}_{nm}}^2\right) , \end{aligned}$$

  (37)

  where ${\bar{C}}_{n m}$, ${\bar{S}}_{n m}$, $\sigma _{{\bar{C}}_{n m}}$, and $\sigma _{{\bar{S}}_{n m}}$ are the fully normalized SH coefficients and corresponding standard deviations of the used GGM.

• 3. Determination of the gravity anomaly degree variance of the geopotential coefficients for degrees beyond the cut-off degree of the used GGM. For this, the Tscherning-Rapp analytical covariance model was used (Tscherning and Rapp 1974, pp. 20–22):

  $$\begin{aligned} c_{n}=425.28\cdot 0.999617^{n+2} \frac{(n-1)}{(n-2)(n+24)}. \end{aligned}$$

  (38)

• 4. Determination of Paul’s ($E_{nk}$) and Molodensky’s truncation coefficients ($Q_n$) (Paul 1973 and Hagiwara 1976).

• 5. Determination of the LS modification parameters using the truncated total LS regularization.

• 6. Determination of the coefficients $s_n$ and $b_n$.

• 7. Determination of the modified Stokes’ kernel $S^{L}(\psi )$ across the integration cap $\psi$.

For the detailed explanation of the LSMSA method, interested readers may refer to references specific to the topic, e.g. Sjöberg and Hunegnaw (2000), Ågren (2004), Abbak and Ustun (2014), Ellmann (2004), Ellmann (2005a), Ellmann (2005b) and Sjöberg and Bagherbandi (2017).