Benefits of non-tidal loading applied at distinct levels in VLBI analysis

Abstract

In the analysis of very long baseline interferometry (VLBI) observations, many geophysical models are used for correcting the theoretical signal delay. In addition to the conventional models described by Petit and Luzum (eds) (IERS Conventions, 2010), we are applying different parts of non-tidal site loading, namely the atmospheric, oceanic, and hydrological ones. To investigate their individual contributions, these parts are considered both separately and combined to a total loading. The application of the corresponding site displacements is performed at two distinct levels of the geodetic parameter estimation process (observation and normal equation level), which turn out to give very similar results in many cases. To validate our findings internally, the site displacements are provided by two different data centres: the Earth-System-Modelling group at the Deutsches GeoForschungsZentrum in Potsdam (ESMGFZ, see Dill and Dobslaw, J Geophys Res Solid Earth, 2013. https://doi.org/10.1002/jgrb.50353)] and the International Mass Loading Service [IMLS, see Petrov (The international mass loading service, 2015)]. We show that considering non-tidal loading is actually useful for mitigating systematic effects in the VLBI results, like annual signals in the station height time series. If the sum of all non-tidal loading parts is considered, the WRMS of the station heights and baseline lengths is reduced in 80–90% of all cases, and the relative improvement is about $-\,3.5$% on average. The main differences between our chosen providers originate from hydrological loading.

Introduction

Due to various geophysical processes, the positions of reference points fixed to the Earth’s crust change over time. When estimating the long-term linear motion of these points in the context of terrestrial reference frames (TRF), the instantaneous positions are regularized by subtracting a number of short-term periodic displacements. The conventional displacements are summarized in chapter 7.1 of the International Earth Rotation and Reference Systems Service (IERS) Conventions of 2010 (Petit and Luzum 2010) and include tidal effects at mainly diurnal and semi-diurnal periods.

Displacements by non-tidal loading, however, are usually not applied. The latter is induced by rather local and irregular changes in atmospheric pressure and the mass redistribution of ocean or land water (hydrology). According to Petit and Luzum (2010), the modelling of non-tidal loading is less accurate, and the impact on the geodetic parameters is less significant than for the conventional displacements. In recent years, however, the number of providers for site displacements computed from non-tidal loading has increased (compare, for example, the Global Geophysical Fluid Center (GGFC)), and the quality of the underlying (numerical) models has improved (see, for example, Dill and Dobslaw 2013; Gelaro et al. 2017). In recognition of this progress, the DTRF2014 was the first TRF to include non-tidal loading (compare Seitz et al. 2016, 2020), and the official contributions to the International VLBI Service for Geodesy and Astrometry (IVS¹) must be computed with corrections for non-tidal atmospheric loading. Nevertheless, a general acceptance is not yet achieved.

Atmospheric loading effects have been investigated first by numerous authors (Rabbel and Zschau 1985; van Dam and Wahr 1987; van Dam and Herring 1994; Sun et al. 1995; MacMillan and Gipson 1994; Petrov and Boy 2004; Tregoning and van Dam 2005b; Böhm et al. 2009; Dach et al. 2010, for example), mostly by using VLBI or the Global Navigation Satellite System (GNSS). Afterwards, non-tidal loading generated from the redistribution of water has also been analysed. Eriksson and MacMillan (2014), for example, include hydrological loading next to the atmospheric one in VLBI analysis and find that the application of the corresponding site displacements leads to a significant improvement in the repeatability of vertical station coordinates. Similar results were found by van Dam et al. (2001) or Tregoning et al. (2009) for the Global Positioning System (GPS). Two of the few studies focusing on the application of non-tidal loading created from the redistribution of ocean water are those of Williams and Penna (2011) and van Dam et al. (2012), who observe a corresponding reduction in the scatter of many GPS station height time series. It should be noted that site displacements are also induced by processes not driven by surface loading, like the thermal expansion of antennas or bedrock, for example. While VLBI at least takes care of the former, we will not particularly focus on such effects in this study.

The joint application of the non-tidal loading parts (atmospheric, oceanic, hydrological) in VLBI analysis has been investigated by Schuh et al. (2003), for example. The authors use different combinations of numerical models for the associated site displacements, but although they find several improvements in station height and baseline repeatabilities, no best combination could be identified. MacMillan and Boy (2004), on the other hand, fix specific models for the site displacements and process VLBI experiments with different combinations of the non-tidal loading parts. Both studies, however, do not apply all parts separately. This is finally done by Roggenbuck et al. (2015), who use site displacements provided by the Goddard Space Flight Center (GSFC²) of the National Aeronautics and Space Administration (NASA) and examine the impact on global solutions for Satellite Laser Ranging (SLR), VLBI, and GNSS.

In this paper, we extend the existing research by exploring the application of non-tidal loading at different levels in the parameter estimation process. The straightforward approach of correcting for site displacements at the observation level (OBS) is basically followed by all aforementioned authors. This way, the original (sub-daily) temporal resolution of the site displacements can be exploited. An alternative is the application at normal equation level (NEQ), which is described by Seitz et al. (2020). Session-wise (e.g. average) displacements are computed, which lead to a loss of temporal resolution, but can be used to directly modify the normal equation without any need to recover the observation equation. By examining both levels, we want to determine whether the approximation of OBS by NEQ is a reasonable approach. By restricting ourselves to VLBI, we can cover the impact on a broad range of parameter types (including tropospheric and clock parameters, which are often neglected). By distinguishing all three parts of non-tidal loading (next to their combination), we identify their individual properties and contributions to the results at both levels. And finally, by using two different data sets for the site displacements, we can internally validate our findings and detect discrepancies. All these items also distinguish our work from the most recent study by Männel et al. (2019), who make use of one of the same data sets, but consider the joint application of all non-tidal loading parts at the observation level with respect to VLBI and GNSS.

We do not analyse the application at solution level, which was done by Böhm et al. (2009), for example, although we briefly compare this approach to OBS and NEQ.

As we are producing session-wise VLBI solutions and no long-term TRF, non-elastic loading effects will only be visible in the time series of the estimated station positions. However, we are particularly interested in the impact of elastic non-tidal loading, and other displacing effects are subject to future research.

The paper is organized as follows: in Sect. 2, we describe the used non-tidal loading parts, the data providers, and the properties of the corresponding displacement time series. Section 3 contains the derivation of the individual application levels. In Sect. 4, we provide the results of processing VLBI observations with various combinations of non-tidal loading parts, data providers, and application levels. Section 5 completes the paper with conclusions and an outlook on future research.

Non-tidal loading

Computation of site displacements

We are considering three parts of non-tidal loading:

• 1. non-tidal atmospheric loading (ATM),

• 2. non-tidal oceanic loading (OCE), and

• 3. hydrological loading (HYD).

In all three cases, variations in the distribution of particular masses, basically air and water, lead to deformations of the Earth’s crust and hence to changes in the position of reference points which are fixed to the latter. In the case of ATM, atmospheric circulation moves air masses around the Earth, and the resulting variation of atmospheric pressure deforms the crust (Darwin 1882; Petrov and Boy 2004). With OCE, the deformations are caused by ocean bottom pressure, which is mainly influenced by three effects: ocean water redistribution by atmospheric circulation, in- and outflow of ocean water, and changes in the total atmospheric mass over the oceans (van Dam et al. 2012). Due to the connection with atmospheric pressure, it is important to note the common inverted barometer hypothesis (IBH, compare van Dam and Wahr 1987). The IBH assumes that an increase in atmospheric pressure over an ocean site is compensated by an equivalent decrease in sea level at this very position and hence a decrease in ocean bottom pressure of equal size. This hypothesis is supposed to be adequate only “for periods longer than 5–20 days” (Petrov and Boy 2004, p. 3), and its postulation is mostly relevant for sites located close to a coast, as the corresponding ATM displacements would be larger without the offsetting effect of the IBH (Sun et al. 1995). Finally, the relevant pressure for HYD is determined by the temporal variation of land water storage (LWS). It comprises soil moisture, snow coverage, or river water flows, for example (Dill and Dobslaw 2013; Eriksson and MacMillan 2014).

The transformation of surface pressure anomalies, i.e. deviations from a mean pressure, into local horizontal ($\varDelta N$, $\varDelta E$) and vertical ($\varDelta U$) displacements at a particular site is based on Farrell (1972). It involves a two-dimensional integration over the Earth’s surface, where all pressure anomalies are weighted by a Green’s function of the angular distance between the chosen site and the position of the anomaly. The details can be found in Petrov and Boy (2004), for example.

The transformation further depends on the applied TRF and its origin, which could be the centre of Earth’s figure (CF), the centre of mass of the solid Earth (CE), or the centre of mass of the total Earth system (CM, including the fluid envelope of atmosphere and water) (compare Blewitt (2003)). As a consequence, there are different Green’s functions and site displacements depending on the chosen frame (see Blewitt 2003; Tregoning and van Dam 2005a, for example), and one must pick the version that corresponds to the geodetic space technique under investigation. For VLBI, in particular, the frame is mostly irrelevant, as the observable is depending on the difference vector (the baseline ${\varvec{B}}_{12}$) between each two observing stations at positions ${\varvec{S}}_1$ and ${\varvec{S}}_2$ (compare Sovers et al. 1998; Eriksson and MacMillan 2014). For example, if ${\varvec{T}}_{CF}^{CM}(t)$ is the translation vector between CF and CM at epoch $t$, then the displaced baseline is given by

$$\begin{aligned} {\varvec{B}}^{\varDelta }_{12}(t)= & {} \left( {\varvec{S}}_2(t) + {\varvec{\varDelta }}_2^{CM}(t) \right) - \left( {\varvec{S}}_1(t) + {\varvec{\varDelta _1}}^{CM}(t) \right) \nonumber \\= & {} \left( {\varvec{S}}_2(t) + \left[ {\varvec{\varDelta }}_2^{CF}(t) + {\varvec{T}}_{CF}^{CM}(t) \right] \right) \nonumber \\&- \left( {\varvec{S}}_1(t) + \left[ {\varvec{\varDelta }}_1^{CF}(t) + {\varvec{T}}_{CF}^{CM}(t) \right] \right) \nonumber \\= & {} \left( {\varvec{S}}_2(t) + {\varvec{\varDelta }}_2^{CF}(t) \right) - \left( {\varvec{S}}_1(t) + {\varvec{\varDelta }}_1^{CF}(t) \right) , \end{aligned}$$

(1)

where ${\varvec{\varDelta }}_i^{CF}$ and ${\varvec{\varDelta }}_i^{CM}$ are the site displacements at station $i$ in the CF- and CM-frame, respectively. Hence, the translation is cancelled (except for minor effects related to the line of sight at each station), and this situation holds as long as the site displacements are applied at the observation or the normal equation level. If they are applied at the solution level, however, i.e. to the final estimated station positions, then the displacements must be taken from the same frame that the stations have been aligned to. We plan to return to this issue in a follow-up paper.

The actual and mean pressure values for the computation of site displacements are usually taken from numerical (weather) models for regular latitude and longitude grids. The two displacement providers in our study use different models with different spatial and temporal resolutions for the three parts of non-tidal loading. Their properties are summarized in Table 1. More providers can be found at the web page of the IERS Global Geophysical Fluid Center (GGFC³). Since ATM, OCE, and HYD are interrelated, it is desirable that the underlying models are consistent with each other and that the global mass is conserved.

Table 1 Numerical models used to derive pressure anomalies for the computation of site displacements from non-tidal loading. The temporal and spatial resolutions refer to the original mass values of the models. If the resolution for the resampled pressure anomalies differs, it is given in brackets

Earth-System-Modelling group at GFZ

The first provider, the Earth-System-Modelling group at the Deutsches GeoForschungsZentrum (GFZ) in Potsdam (ESMGFZ⁴), basically follows the Green’s functions approach to compute site displacements from non-tidal loading. However, a patched version is used to significantly reduce the computation time. The patch consists of applying a high spatial resolution for nearby pressure contributions and a lower spatial resolution for contributions far away, in connection with fast interpolation techniques (Dill and Dobslaw 2013; Dill et al. 2018). ESMGFZ supplies a software for interpolating the displacements in local horizontal coordinates for any site from regular $0.5 ^{\circ }\times 0.5 ^{\circ }$ spatial grids, with temporal resolutions depending on the loading part (compare Table 1). We used this software to obtain non-tidal atmospheric, non-tidal oceanic, and hydrological site displacements for the years 1984 to 2017 and all VLBI stations observing in the corresponding sessions. The data are available for both the CF- and the CM-frame, and we decided to use the CM-related displacements, as we plan to combine VLBI with SLR solutions in the future (and the latter definitely need displacements in the CM-frame).

ESMGFZ provides only one underlying model for each loading part (also listed in Table 1), such that consistency can be ensured among them. For the global conservation of mass, a fourth component, the sea-level loading (SLEL), is available. It is derived from barystatic sea-level variations and given with the same resolution as the hydrological displacements. We have applied it together with all the other non-tidal loading parts in one scenario, but since the results did not differ significantly from the scenario where it was left out, and since there is no equivalent part available from the second provider, we will mostly not consider SLEL in this study. Only some of the tables will contain the corresponding results for comparison.

International mass loading service

The other provider, the International Mass Loading Service (IMLS⁵), has also augmented the Green’s function approach: as the two-dimensional integrations become computationally expensive with increasing spatial resolution of the geophysical models, a spherical harmonic transform approach is used (see Petrov 2015). The IMLS offers on-demand site displacements in local horizontal coordinates for any site in both the CF- and the CM-frame. Again, we requested non-tidal atmospheric, non-tidal oceanic, and hydrological loading displacements in the CM-frame for all VLBI stations taking part in our analysis. In contrast to ESMGFZ, there are several geophysical models per loading part to choose from, but we selected only the ones for which the full period from 1984 to 2017 was available. Their details are listed in Table 1, and at least for ATM and HYD we might assume consistency, since they are both based on the MERRA-2 model.

Comparison of site displacements

The properties of site displacements generated from non-tidal loading have been listed by various authors. For all three loading parts, the vertical displacements are generally significantly larger (peak-to-peak variation of $10$ to $20$ mm) than the horizontal ones ($2$ to $5$ mm) and hence the estimated station heights will be affected most (compare, for example, Schuh et al. 2003; van Dam et al. 2012; Eriksson and MacMillan 2014). According to Böhm and Schuh (2013), Tregoning and van Dam (2005b) and Dill and Dobslaw (2013), for example, atmospheric pressure varies strongly at mid-latitudes and continental sites, while the fluctuation is less pronounced close to the sea, also due to the IBH (Schuh et al. 2003). Most naturally, the displacements generated from ocean bottom pressure reveal their largest values at coastal or island sites, even though the effect of non-tidal oceanic loading is generally small (van Dam et al. 2012; Schuh et al. 2003). Eriksson and MacMillan (2014, p. 677) note that “the hydrologic variation is the largest within a $40 ^{\circ }$ latitude band about the equator in South America, South Asia, and Africa”. Additional sites with dominating hydrological loading are lake- and riversides, as well as the eastern part of the Rocky Mountains (see Dill and Dobslaw 2013).

Fig. 1

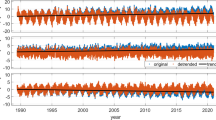
The changes in the length of the corresponding baseline after the addition of site displacements generated from non-tidal atmospheric (top), oceanic (middle), or hydrological loading (bottom) to the VLBI stations WETTZELL (Germany) and FORTLEZA (Brazil). The displacements were taken from ESMGFZ (blue) and IMLS (red)

Fig. 2

Root mean square (RMS) errors of the differences between the combined site displacements of ESMGFZ and IMLS per baseline, separated by Cartesian station coordinates and non-tidal loading part

Schuh et al. (2003) highlight important signals with periods of approximately two weeks and approximately one month for the time series of ATM and OCE, respectively. Furthermore, van Dam et al. (2012) state that the annual signal is the most powerful one for ocean bottom pressure, i.e. non-tidal oceanic loading. The site displacements for these two parts generally vary quite strongly, with a broad range of relevant frequencies. In contrast to that, there are basically only two dominant signals for hydrological loading: the semi-annual and the annual one (see Dill and Dobslaw 2013; Eriksson and MacMillan 2014).

As the differences between the displacements applied at two stations are most important for VLBI, we will present the comparison of ESMGFZ and IMLS data at the baseline level according to Eq. (1). In Fig. 1, we show the change in the length of the baseline WETTZELL–FORTLEZA after application of non-tidal atmospheric, oceanic, and hydrological loading at the observation level for both providers. In this example, and as we generally observed, for both ATM and OCE the displacements are very similar among the two data centres. This is in line with the results of Roggenbuck et al. (2015), who compare site displacements generated by the GSFC and l’Université de Luxembourg (ULux⁶) and also obtain rather small differences between the corresponding displacement time series for ATM and OCE.

The displacements computed from the two hydrological models, however, can deviate quite significantly (compare the bottom panel of Fig. 1). The amplitudes and also phases of the time series show considerable discrepancies between the two providers for many VLBI stations and hence for the displaced baselines, too. The continental water storage of the LSDM comprises soil moisture, the accumulation of snow, seasonal glacier run-off, and surface water in rivers and lakes, for example (see Dill and Dobslaw 2013). In contrast to this, the validation report of the MERRA-2 model (Reichle et al. 2017) highlights soil moisture, snow coverage, streamflow, and observation-based precipitation. There seem to be more serious modelling differences for HYD than for ATM, which was also reported in the study by Roggenbuck et al. (2015). Figure 2 confirms this situation by showing the root mean square (RMS) errors of the differences between the combined site displacements of ESMGFZ and IMLS for a large subset of VLBI baselines. While the data of the two providers agree very well for ATM and OCE (sub-mm RMS), the most critical choice is that of the hydrological model (average RMS of about 2–3 mm).

Fig. 3

Changes in the lengths of sample baselines after individual (red) and joint (blue) application of site displacements (to the a priori station coordinates) corresponding to the three non-tidal loading parts. For each baseline, a different part is dominant: ATM (top), OCE (middle), or HYD (bottom)

The operational analysis centres (AC) of the IVS are asked to provide solutions containing corrections for non-tidal atmospheric loading only. However, ATM not necessarily is the most relevant non-tidal loading part, as Fig. 3 suggests. Each subplot shows the change $\varDelta L$ in baseline length following the application of an individual loading part on top of the change following the joint application of all parts. We observe that the major contribution can originate from either ATM, OCE, or HYD, dependent on the respective stations which are involved. The dominant loading part at a station can even change per coordinate (East, North, or Up, not shown here), and it is sometimes different for ESMGFZ and IMLS (Fig. 3 only contains examples for the former). Consequently, one should take all three non-tidal loading effects into account when longing for an improvement of the VLBI solutions.

Finally, these figures confirm that the time series of site displacements derived from hydrological loading indeed is much smoother than those of ATM and OCE, as mostly semi-annual and annual signals exist for HYD. This will be a distinguishing feature when the application at normal equation level is considered.

Application levels

In the classic Gauss–Markov model (see Koch 1999), the normal equation

$$\begin{aligned} A^T P \, A \, {\varvec{\varDelta x}} \, = \, A^T P \, {\varvec{l}} \end{aligned}$$

(2)

is solved for ${\varvec{\varDelta x}} \in \mathbb {R}^n$, the vector of corrections to a priori values $x^0_j$ of particular parameters $x_j$, $j=1,\ldots ,n$. The latter are used within a functional model $f$ to approximate $m>> n$ real observations ${\varvec{b}} \in \mathbb {R}^m$. ${\varvec{l}} \in \mathbb {R}^m$ is the vector of observed minus computed (OMC) values

$$\begin{aligned} l_i \, = \, b_i - f(i,{\varvec{x^0}}) \quad (i=1,\ldots ,m), \end{aligned}$$

(3)

and $A \in \mathbb {R}^{m \times n}$ is the Jacobi matrix of $f$ with respect to the $x_j$.

$$\begin{aligned} P \, := \, \sigma _0^2 \, \, \left[ \, diag \left( \sigma ^2_1, \, \ldots , \, \sigma ^2_m \right) \, \right] ^{-1} \, \, \in \mathbb {R}^{m \times m} \end{aligned}$$

(4)

is a weight matrix, with $\sigma _0^2$ being a common a priori variance factor and the $\sigma _i$ being the standard deviations (formal measurement errors) of the observations $b_i$ for $i=1,\ldots ,m$. The constituents of (2) are labelled normal equation matrix

$$\begin{aligned} N \, := \, A^T P \, A \, \, \in \mathbb {R}^{n \times n} \end{aligned}$$

(5)

and right-hand side

$$\begin{aligned} {\varvec{y}} \, := \, A^T P \, {\varvec{l}} \, \, \in \mathbb {R}^n. \end{aligned}$$

(6)

Its outcome ${\varvec{\varDelta x}}$ solves the observation equation

$$\begin{aligned} A \, {\varvec{\varDelta x}} \, = \, {\varvec{l}} \, + \, {\varvec{v}}, \quad {\varvec{v}} \in \mathbb {R}^m, \end{aligned}$$

(7)

such that the weighted sum of squared observation residuals, ${\varvec{v}}^T P \, {\varvec{v}}$, is minimized.

In general geodetic applications, the matrix $N$ is singular and cannot be inverted, unless certain conditions are applied. The most important ones are the datum conditions, which align the estimated station and source coordinates to their a priori networks (compare Angermann et al. 2004). The corresponding no-net-translation (NNT, for stations) and no-net-rotation (NNR, for stations and sources) equations are provided in a matrix $N_D \in \mathbb {R}^{n \times n}$, while we assume that all other conditions are already contained in the matrices $A$ and $N$ as pseudo-observations. Then, the vector of best parameter estimates is finally given by

$$\begin{aligned} {\varvec{x}} \, \, = \, \, {\varvec{x^0}} \, + \, {\varvec{\varDelta x}} \, \, = \, \, {\varvec{x^0}} \, + \, \left( N + N_D \right) ^{-1} {\varvec{y}}. \end{aligned}$$

(8)

Its statistical properties will be discussed in Sect. 4.2. In the following, the above notations refer to an estimation process without any non-tidal loading applied.

Observation level

Let ${\varvec{\delta x}}(t) \in \mathbb {R}^n$ be the vector of site displacements computed from non-tidal loading for each parameter $x_j$ ($j=1,\ldots ,n$) at epoch $t$. As the coordinates of the observing stations are the only estimated parameters which are fixed to the Earth’s crust, $\delta x_j = 0$ for all other parameters. When applying non-tidal loading at the observation level (OBS), this means changing the functional model,

$$\begin{aligned} f(i,{\varvec{x^0}}) \, \mapsto \, \tilde{f}(i,{\varvec{x^0}},{\varvec{\delta x}}(t_i)), \end{aligned}$$

(9)

i.e. using the site displacements of each distinct observation epoch $t_i$, $i=1,\ldots ,m$. Since the temporal resolution of the displacements generally is not as fine as the observation epoch grid, an interpolation routine has to be defined as well. In the end, the Jacobi matrix and the OMC vector change:

$$\begin{aligned} A\mapsto & {} \tilde{A} \nonumber \\ l_i\mapsto & {} {\tilde{l}}_i \, = \, b_i \, - \, \tilde{f}(i,{\varvec{x^0}},{\varvec{\delta x}}(t_i)) \quad (i=1,\ldots ,m), \end{aligned}$$

(10)

which leads to a new observation equation with new residuals

$$\begin{aligned} \tilde{A} \, {\varvec{\varDelta }} \tilde{{\varvec{x}}} \, = \, \tilde{{\varvec{l}}} \, + \, \tilde{{\varvec{v}}}. \end{aligned}$$

(11)

The partial derivatives in $\tilde{A}$ differ from those in $A$ only to a very small extent (we plan to present the theoretical details in the follow-up paper). The best solution to Eq. (11) is again obtained by the corresponding normal equation

$$\begin{aligned} \tilde{N} \, {\varvec{\varDelta }} \tilde{{\varvec{x}}} \, = \, \tilde{{\varvec{y}}}, \end{aligned}$$

(12)

where

$$\begin{aligned} \tilde{N}= & {} \tilde{A}^T P \, \tilde{A}, \nonumber \\ \tilde{{\varvec{y}}}= & {} \tilde{A}^T P \, \tilde{{\varvec{l}}}. \end{aligned}$$

(13)

As before, we need to add the datum conditions in $N_D$ to invert the normal matrix. Then, we finally get the formula for parameter corrections with non-tidal loading applied at the observation level,

$$\begin{aligned} {\varvec{\varDelta }} \tilde{{\varvec{x}}} \, = \, (\tilde{N} + N_D)^{-1} \, \tilde{{\varvec{y}}}. \end{aligned}$$

(14)

Normal equation level

Analysis solutions are often exchanged in the form of datum-free normal equations only. Usually, they do not contain non-tidal loading, and there is no possibility to recover the functional model and apply the corresponding displacements at the observation level, either. However, there is an alternative way to correct these equations for non-tidal loading. It is referred to as the application at normal equation level (NEQ) and described by Seitz et al. (2020), who use this approach to generate the DTRF2014.

To derive NEQ, we start with the OMC vector $\tilde{{\varvec{l}}}$ for the application at observation level in Eq. (10),

$$\begin{aligned} \tilde{{\varvec{l}}} \, = \, {\varvec{b}} - \tilde{{\varvec{f}}}, \end{aligned}$$

(15)

where the components of $\tilde{{\varvec{f}}}$ are computed with the distinct displacement vectors ${\varvec{\delta x}}(t_i)$ for each observation epoch $t_i$ ($i=1,\ldots ,m$). Then, we define a vector ${\varvec{\delta \bar{x}}} \in \mathbb {R}^n$ of mean displacements per parameter $x_j$ ($j=1,\ldots ,n$), which could be the displacements interpolated at the mid-epoch of the session (as employed by Böhm et al. (2009)), or the averages of each parameter’s displacements during the whole session (this work). First, this mean vector replaces the distinct displacement vectors,

$$\begin{aligned} {\varvec{\delta x}}(t_i) \, \equiv \, {\varvec{\delta }} \bar{{\varvec{x}}} \quad \text {for } i=1,\ldots ,m. \end{aligned}$$

(16)

Second, we use the vector to linearly approximate the functional model $\tilde{{\varvec{f}}}$ of OBS,

$$\begin{aligned} \tilde{{\varvec{f}}} \, \approx \, {\varvec{f}} + A \, {\varvec{\delta }} \bar{{\varvec{x}}}, \end{aligned}$$

(17)

such that the OMC vector $\bar{{\varvec{l}}}$ for the application at normal equation level becomes

$$\begin{aligned} \bar{{\varvec{l}}} \, := \, {\varvec{b}} - \left( {\varvec{f}} + A \, {\varvec{\delta }} \bar{{\varvec{x}}} \right) . \end{aligned}$$

(18)

This approach leads to a simple amendment of the right-hand side ${\varvec{y}}$, ensuring that we can actually apply non-tidal loading although we are only provided with the normal equation. The modified right-hand side $\bar{{\varvec{y}}}$ of NEQ per session is given by

$$\begin{aligned} \bar{{\varvec{y}}}:= & {} A^T P \, \bar{{\varvec{l}}} \nonumber \\= & {} A^T P \, \left( {\varvec{b}} - \left( {\varvec{f}} + A \, {\varvec{\delta }} \bar{{\varvec{x}}} \right) \right) \nonumber \\= & {} A^T P \, ({\varvec{b}} - {\varvec{f}}) \, - \, A^T P \, A \, {\varvec{\delta }} \bar{{\varvec{x}}} \nonumber \\= & {} A^T P \, {\varvec{l}} \, - \, N \, {\varvec{\delta }} \bar{{\varvec{x}}} \nonumber \\= & {} {\varvec{y}} \, - \, N \, {\varvec{\delta }} \bar{{\varvec{x}}}. \end{aligned}$$

(19)

With the datum conditions $N_D$, the formula of the parameter corrections for the application of non-tidal loading at the normal equation level is finally given by

$$\begin{aligned} {\varvec{\varDelta }} \bar{{\varvec{x}}} \, = \, (N + N_D)^{-1} \, \bar{{\varvec{y}}}. \end{aligned}$$

(20)

To summarize, we are modifying the theoretical observations for NEQ by three simplifications:

• 1. The removal of temporal variation in site displacements during the VLBI session (or other observation period) in Eq. (16).

• 2. The linear approximation of the change in the functional model after the application of site displacements in Eq. (17).

• 3. The assumption of invariance of the Jacobi matrix $A$ and hence the normal matrix $N$ to the application of site displacements in the functional model, i.e. $\tilde{A} \approx A$ and $\tilde{N} \approx N$.

We investigated the individual impact of these three items in the analysis of VLBI observations (and plan to also present these results in the follow-up paper). We came to the conclusion that the introduction of mean displacements is much more significant than the linearization of the theoretical signal delay and the changes in the Jacobi matrix. If the temporal variations of the site displacements are small during a session, we can hence expect the results for OBS and NEQ to be quite similar. Böhm et al. (2009, p. 1112) support the concept of a mean displacement: “the intra-day variation of atmospheric loading corrections is - at the present accuracy level - not critical for the analysis of VLBI observations”. While this is encouraging, quite some progress in measuring and modelling has been made recently, and the current situation might be different, especially since we are also considering the other non-tidal loading effects.

Table 2 Parametrization of the estimated variables in the analysis of VLBI sessions with DOGS-RI

Table 3 Models and a priori data used for the analysis of VLBI sessions with DOGS-RI. This reference set-up (REF) does not yet include any non-tidal loading data

Solution level

The parameter corrections ${\varvec{\varDelta }} \hat{{\varvec{x}}}$ for the application at solution level (SOL) are obtained by

$$\begin{aligned}&{\varvec{\varDelta x}} \, = \, {\varvec{\varDelta }} \hat{{\varvec{x}}} \, + \, {\varvec{\delta }} \hat{{\varvec{x}}} \end{aligned}$$

(21)

$$\begin{aligned} \Leftrightarrow&{\varvec{\varDelta }} \hat{{\varvec{x}}} \, = \, {\varvec{\varDelta x}} \, - \, {\varvec{\delta }} \hat{{\varvec{x}}}, \end{aligned}$$

(22)

i.e. by simply subtracting the mean displacements

$$\begin{aligned} {\varvec{\delta x}}(t_i) \, \equiv \, {\varvec{\delta }} \hat{{\varvec{x}}} \quad \text {for } i=1,\ldots ,m, \end{aligned}$$

(23)

from the original parameter corrections without non-tidal loading (compare Williams and Penna 2011, for example). It becomes clear that the TRF used to derive the site displacements is important at this level: the difference between CF- and CM-displacements is fully transferred to the new coordinate estimates, and hence the correct choice depends on the frame of the latter.

Since $\delta x_j = 0$ for parameters other than station coordinates, these are not modified at SOL. With respect to single VLBI sessions or other geodetic experiments, this leads to inconsistencies between the station coordinates and the other parameters like the EOP, as these have been estimated in connection with the original coordinate corrections in ${\varvec{\varDelta x}}$. The consistency can be restored if the modified coordinates are used for the estimation of new EOP in the context of a long-term TRF, for example.

SOL will not be treated in this work. Böhm et al. (2009), who focused on atmospheric loading, conclude that the a posteriori correction of station coordinates is not appropriate in real VLBI analysis. The authors attribute the degradation observed in their station height repeatabilities to network effects: they claim that un-modelled loading is to some extent distributed between the stations, especially when the corresponding networks only consist of few antennas. Adding site displacements to the final estimates results in a partly redundant consideration of non-tidal loading. (In our follow-up paper, we will analyse the difference between the application of displacements during and after the estimation process in VLBI analysis in more detail.)

Impact of non-tidal loading

We examine the effect of non-tidal loading on geodetic parameters derived from VLBI observations with our DGFI Orbit and Geodetic parameter estimation Software (DOGS, see Gerstl et al. 2000). The component DOGS-RI (Radio Interferometry) establishes the theoretical model and provides datum-free normal equations according to the Gauss–Markov model (compare Sect. 3). For each VLBI session, we estimate constant station and source coordinates, the full set of Earth orientation parameters (EOP), as well as parameters modelling the station clocks and the tropospheric delay. Details about the temporal resolutions and the functional representations are found in Table 2.

The geophysical models used in the estimation process are those of the IERS Conventions 2010 (Petit and Luzum 2010). Table 3 provides the corresponding overview for our reference set-up (REF), where all conventional station displacements are applied. Any displacements referring to non-tidal loading are only considered in subsequent set-ups. First, this happens at the observation level (OBS), i.e. distinct displacements are applied at their corresponding observation epoch within the theoretical delay function. For each non-tidal loading scenario, DOGS-RI generates a separate set of datum-free normal equations, which contain conditions for clock and tropospheric parameters as pseudo-observations. These equations are forwarded to the component DOGS-CS (Combination and Solution), where no-net-translation (NNT, for station coordinates) and no-net-rotation (NNR, for station and source coordinates) conditions are added in the form of separate normal matrices (compare Angermann et al. 2004). The parameter estimates for each scenario and VLBI session are finally obtained by inversion of their respective normal equation as shown in Eq. (14).

With the normal equation level (NEQ), only the datum-free normal equations of the reference set-up are forwarded to DOGS-CS. For each non-tidal loading scenario, the right-hand sides of the normal equations are modified with the vector of average site displacements per station coordinate for the corresponding session. Afterwards, the same NNT and NNR conditions as for OBS are added, and the parameter estimates for NEQ are again obtained by inversion.

Fig. 4

In each scenario other than REF, one data provider, one non-tidal loading part, and one observation level are chosen

In the following, we investigate the changes in the estimated parameters when moving from REF to one of the non-tidal loading scenarios: ATM—atmospheric only, OCE—oceanic only, HYD—hydrological only, ALL—atmospheric plus oceanic and hydrological. In each case, the application levels OBS and NEQ as well as the providers ESMGFZ and IMLS have been considered. On overview of the choices is presented in Fig. 4.

WRMS of station positions

We want to analyse whether the site displacements computed from non-tidal loading are appropriate for explaining parts of the sub-daily station motions, i.e. whether their application is able to reduce the variation in the time series of session-wise positions. The differences between OBS and NEQ will give an impression of the significance of the sub-daily displacement resolution.

Fig. 5

Change in the WRMS of the local station coordinates when applying different non-tidal loading corrections at distinct levels (top subplot: OBS, bottom subplot: NEQ). The corresponding site displacements are provided by ESMGFZ

Fig. 6

Change in the WRMS of the vertical station coordinates when applying different non-tidal loading parts (top: ATM, middle: OCE, bottom: HYD) at distinct levels (OBS, NEQ) and with data from different providers (ESMGFZ, IMLS)

In Fig. 5, we plot the changes in the weighted root mean square (WRMS) values of the local station coordinates (East, North, Up) for the distinct non-tidal loading scenarios with ESMGFZ data. The time series of coordinates ranges from 1984 to 2017, and we considered every session that was analysed at DGFI-TUM during that period. If the stations participated in at least 100 sessions, they are listed on the x-axis, and they are ordered descending by the number of such sessions. The leftmost station, WETTZELL, for example, made observations in 3,323 sessions, while the rightmost one, DSS65, only participated in 111 sessions.

As expected, the change in WRMS values is generally largest for the Up component (bottom panel in each subplot), irrespective of the application level. Furthermore, the majority of changes for the Up component is negative, which means that the WRMS is generally improved when applying non-tidal loading. The maximum improvement is $-\,1.83$ mm ($-\,1.86$ mm) for the VLBI station GILCREEK when the sum of all site displacements is applied at OBS (NEQ). Across the listed stations, the average improvement is about $-\,0.39$ mm for both levels in the ALL scenario, which is equivalent to a relative average improvement of $-\,4.0$%. For ATM, OCE, and HYD, the averages are about $-\,0.23$ mm ($-\,2.4$%), $-\,0.04$ mm ($-\,0.4$%), and $-\,0.12$ mm ($-\,1.3$%), respectively. For the horizontal components, the tendency is less obvious. The statistics (minimum, mean, median, maximum, portion of improved cases) of the relative changes in WRMS values for all local coordinates and non-tidal loading parts are listed in Table 5 of the Appendix. It also contains the scenario ALL including SLEL and reveals that the corresponding results are close to that of the original ALL scenario. Compared to the relative improvements which are obtained for GNSS (see Tregoning et al. 2009; Dach et al. 2010; van Dam et al. 2012, for example), our values are rather small. However, the behaviour is systematic, and the WRMS of station heights is larger for VLBI (1–2 cm) than for GNSS ($< 1$ cm).

If only a single non-tidal loading part is applied at OBS, for 25 out of the 41 listed stations the reduction in WRMS is largest for the atmospheric one (Up component). However, for 13 stations the greatest improvement is obtained with the exclusive application of hydrological loading. And even though the corresponding changes in WRMS are very small, there are three stations which benefit the most from non-tidal oceanic loading. Hence, all non-tidal loading parts are worth considering.

The largest reduction in WRMS per station is not necessarily given in the scenario which applies its dominant non-tidal loading part. The total site displacements of FORTLEZA, for example, are mainly composed of hydrological loading (due to its location near the equator; compare also Fig. 3), while the station’s WRMS value hardly improves in the HYD scenarios ($-\,0.072$ mm to $-\,0.089$ mm). The reason for this behaviour is that the stations cannot be examined in isolation, but they have to be considered as being part of session-wise observation networks. Hydrological loading might be sufficient for FORTLEZA, but this does not hold for all of the other stations. As mentioned by Böhm et al. (2009), the missing displacements are transferred between the stations in the adjustment if non-deforming global datum conditions (i.e. NNR and NNT conditions) are used. This leads to adverse station motions and consequently the results for FORTLEZA deteriorate as well. This effect is present in all single non-tidal loading scenarios, and the overall impact depends on how much loading information is absent from the network. The best approach would be to apply all non-tidal loading parts together (under the assumption that all loading effects are modelled correctly).

The corresponding plots for IMLS look very alike, with similar values for the average improvements of the WRMS (see Table 6 of the Appendix for the statistics). To highlight the similarities and differences, we present the IMLS results only for the vertical coordinates, and we plot the associated changes in the WRMS values next to those of ESMGFZ in Fig. 6. In Sect. 3.2, we mentioned that the main discrepancy between OBS and NEQ is the loss of temporal resolution. Hence, for HYD, where the time series of site displacements hardly contains any intra-session variation, the results for OBS and NEQ should be almost identical. Eriksson and MacMillan (2014) make a corresponding observation when applying session-wise average hydrology corrections in their study, and we can confirm this by looking at the bottom panel of Fig. 6. The reduction in WRMS values in the HYD scenario matches very well for both levels with the same data provider. On the other hand, the reductions are generally not of similar size for the same application level but different data providers. This again emphasizes the discrepancies between the two hydrology models LSDM and MERRA-2.

For ATM (top panel of Fig. 6), we observe the opposite behaviour. The site displacements generated from ECMWF and MERRA-2 are quite similar to each other, but characterized by a high sub-daily variability. Hence, the approximation by an average displacement per session is potentially worse than for HYD, and the reductions in WRMS values for OBS and NEQ need not match very well (compare stations WETTZ13N or YEBES40M, for example). On the other hand, the difference between the two levels is much smaller than the difference to REF for most stations. Consequently, like for HYD, the approximation of OBS by NEQ is generally appropriate as far as the reduction of station position variability is concerned. For single sessions with large intra-day variations in the site displacements, however, there can still be significant differences.

A summary of the relative changes in the WRMS of baseline lengths (baseline length repeatability, BLR) is also provided in Tables 5 and 6 of the Appendix. The picture is similar to that for station heights: for at least two-thirds of the baselines with more than 100 observations, the BLR is reduced after the application of any non-tidal loading. The largest improvements (about $-\,3.0$% on average) are again obtained for the ALL scenario, followed by ATM (about $-\,1.6$%) and HYD (about $-\,1.0$%). The statistics for OBS and NEQ are very close, and the differences between ESMGFZ and IMLS are largest for HYD, where there are less extreme changes for IMLS.

Standard deviations

The variance–covariance matrix of the estimated parameters is given by

$$\begin{aligned} C \, = \, \breve{\sigma }_0^2 \, (A^T P \, A \, + \, N_D)^{-1} \end{aligned}$$

(24)

(see Koch 1999). When applying site displacements at the normal equation level, $A$, $P$, and $N_D$ are not modified. When applying them at the observation level, $P$ and $N_D$ stay constant as well, and the changes in $A$ are negligible (compare Sect. 3.2). Hence, the only variable is the common a posteriori variance factor

$$\begin{aligned} \breve{\sigma }_0^2 \, = \, \frac{{\varvec{v}}^T P {\varvec{v}}}{m+m_c-n}, \end{aligned}$$

(25)

where $m_c$ is the number of pseudo-observations (conditions).

Since the number of (pseudo-)observations and parameters is not altered between the scenarios, $\breve{\sigma }_0^2$ only depends on their weighted sums of squared observation residuals. As a consequence, the standard deviations vary proportionally to the square root of ${\varvec{v}}^T P \, {\varvec{v}}$. In the top panel of Fig. 7, we plot the relative changes of this weighted sum with respect to REF for each VLBI session in the ALL scenario. For most sessions, the changes are less than $1\%$. Furthermore, they are basically equally distributed around $0$. Hence, the impact on the standard deviations is small and has no clear direction (i.e. improvement or deterioration). Regarding the application level, NEQ provides fewer extreme results, but in general the relative changes are similar to those of OBS.

Fig. 7

Top panel: the relative change in the weighted sum of squared observation residuals (${\varvec{v}}^T P \, {\varvec{v}}$) per session, when all non-tidal loading parts are applied simultaneously at the observation (blue dots) or at the normal equation level (red dots). Bottom panel: the number of stations in the corresponding networks

A striking property, however, is the sharp and persistent increase in the relative change in ${\varvec{v}}^T P \, {\varvec{v}}$ at the end of 2011. The reason is not yet fully clarified, but we think this is related to the extension of the Australian–New Zealand network at this time, i.e. the introduction of the stations YARRA12M, KATH12M, and WARK12M. Almost simultaneously, the number of network stations—and hence baselines—per session increased (compare the bottom panel of Fig. 7). Furthermore, in the Continuous VLBI Campaign 2017 (CONT17⁷), where two networks processed daily 24-h sessions for 15 consecutive days, it is noticeable that almost all sessions of the XB network have a relative change of more than $1\%$ (and up to $12\%$), while those of the XA network are close to zero. The XA network has only one station in the Southern Hemisphere, and most baselines are directed from East to West. In contrast to that, the XB network consists of five Southern Hemisphere stations and NYALES20 in the far North, so there are many more North–South baselines. Opposite seasonal effects of non-tidal loading on the two hemispheres might induce a larger impact for this direction.

Anyway, in terms of ${\varvec{v}}^T P \, {\varvec{v}}$, we observe a growing significance of non-tidal loading in the last decade. But the effect of the un-modelled site displacements appears to already be distributed among the station coordinates or the other estimated parameters, which is why the weighted sum of observation residuals is not necessarily improved. The plots for ATM, OCE, and HYD look very similar to Fig. 7.

Fig. 8

Spectral analyses of the time series of scale parameters estimated in a 7-parameter Helmert transformation with respect to the DTRF2014. The site displacements for the distinct non-tidal loading scenarios generated by ESMGFZ have been applied at the normal equation level

Helmert transformation: scale

Vertical station positions experience the greatest impact by non-tidal loading. As VLBI stations are globally distributed, alterations in the stations’ height will influence the scale of the used TRF. This is also supported by Böhm et al. (2009, p. 1112), who mention that “the network-scale parameter of a VLBI network [...] is significantly affected by un-modeled atmospheric loading corrections at the stations”. We perform 7-parameter (three translation values, three rotation angles, and the scale parameter) Helmert transformations for all of our scenarios to investigate the impact on the scale. For each session, the transformation is computed with respect to the DTRF2014, which consists of linear representations of station motions via offsets and drifts (Seitz et al. 2020). Since there is a lot of noise in the resulting scale parameters for sessions before 2000, we restrict ourselves to the period from 2000 to 2017. Furthermore, we eliminate scales with an absolute value greater than 6 cm as outliers (less than $2\%$ of the data). The remaining series is interpolated to a regular 1-day time grid, before we finally perform a frequency analysis.

The amplitude pattern for the scale time series in non-tidal loading scenarios with displacements by ESMGFZ applied at NEQ is provided in Fig. 8. For REF, where no non-tidal loading is considered, the most striking observation is the dominant annual signal with an amplitude of about $1.7$ mm. As many authors report (Petrov and Boy 2004; van Dam et al. 2012; Eriksson and MacMillan 2014, for example), the 365-day period is also dominant for the site displacements themselves. Hence, we might expect that the application of the latter could dampen the annual variation in the station heights and, consequently, in the scale parameter. According to Fig. 8, this is partly true (compare the black box): the annual signal

• hardly changes, when only OCE is applied.

• slightly increases, when only ATM is applied.

• significantly decreases to about $0.9$ mm, when only HYD or all non-tidal loading parts (ALL) are applied.

The same behaviour is observed for both the IMLS and OBS (not shown here), so the approximation at NEQ preserves these properties.

Since the impact of OCE is very small for most VLBI stations, its minor effect on the scale parameter is no surprise. But it is rather counter-intuitive that the annual amplitude gets larger in the ATM scenario, even though this was noticed by van Dam and Herring (1994) and Petrov and Boy (2004) for OBS already. An actual reduction of the annual signal in the scale was only observed by Seitz et al. (2020), who applied ATM and HYD together at the normal equation level. Here, we discover that HYD is the relevant part: it reduces the amplitude to almost the same extent as when all non-tidal loading parts are used jointly (ALL).

Fig. 9

The amplitude of the annual signal in the time series of station heights as obtained in various non-tidal loading scenarios with site displacements by ESMGFZ applied at the normal equation level

To investigate the origin of this behaviour, we take a look at the annual signals of the time series of station heights in Fig. 9, which have also been computed with ESMGFZ site displacements at NEQ. We only show stations that are part of the NNT / NNR conditions and hence relevant for the Helmert transformation. Furthermore, they must participate in at least 500 sessions during the period 2000–2017 to ensure a reliable spectral analysis. For about half of these stations, the amplitude of the annual signal in the ATM scenario is actually greater than the amplitude in the REF scenario. Likewise, the amplitudes for OCE are quite similar to those of REF for most stations. And finally, for 9 out of the 12 listed stations, the annual amplitude for HYD is (in parts significantly) smaller than that for REF. Since the respective figure looks very alike for OBS, this is in line with MacMillan and Boy (2004), who find a reduction in annual vertical amplitude for 70% of their VLBI stations after the application of HYD at the observation level. This property most probably causes the corresponding mitigation of the annual signal in the scale.

Table 4 WRMS values of the differences between the EOP of each non-tidal loading scenario and those of the reference scenario without non-tidal loading. The units are $[\mu as]$ for polar motion and the celestial pole offsets, $[\mu as/d]$ for the polar motion rates, $[\mu s]$ for $\varDelta UT1$, and $[\mu s/d]$ for $LOD = - \partial \varDelta UT1/\partial t$

Earth orientation parameters

When applying all non-tidal loading parts, the absolute changes with respect to the reference scenario are generally below 100 $\mu$as for polar motion, below 3 $\mu$s for $\varDelta UT1$, and below 10 $\mu$as for the celestial pole offsets. If the authors analysed the particular EOP, these are the same orders of magnitude as reported in Roggenbuck et al. (2015) and Männel et al. (2019). (We were able to produce plots very similar to their Figures 5 and 13, respectively, which contain the changes after introduction of non-tidal loading.) The mean formal errors of polar motion, $\varDelta UT1$, and celestial pole offsets reported in the IERS Bulletins B⁸ are about 30–60 $\mu$as, 10–20 $\mu$s, and 50-100 $\mu$as, respectively. Hence, the impact of non-tidal loading is often below the measurement precision, but it can be relevant for polar motion.

In Table 4, we present a summary of how the EOP are affected when non-tidal loading is applied. We computed WRMS values for the differences between the parameters estimated in each loading scenario and those of REF, and the following properties are revealed:

• The largest impact for all EOP is given with the ALL scenario.

• For ATM and OCE, the WRMS values for ESMGFZ and IMLS are matching very well, while there is more deviation for HYD and (consequently) ALL.

• The application level is most relevant for all rates and the celestial pole offsets, while it has much less influence on polar motion and $\varDelta UT1$.

• Of all parts, HYD has the largest effect on polar motion (offsets), but the smallest effect on the celestial pole offsets.

The first two observations are in line with our previous statements. The third observation can be explained with the high sensitivity of the EOP rates to sub-daily variations in the site displacements. As the latter are only preserved at OBS, the impact on the rates is much smaller at NEQ. When rates are estimated, the application at observation level should hence be preferred. Only for HYD, where the temporal variation is low at both levels, the WRMS values for OBS and NEQ are of similar (small) size. The same behaviour holds for $\varDelta X_{CIP}$ and $\varDelta Y_{CIP}$, because the celestial pole offsets are periodically highly correlated with the rates of polar motion. If the latter were not estimated at all, there would be no impact on nutation by non-tidal loading, either. In general, the EOP (i.e. Earth rotation) are more affected by the horizontal than by the vertical site displacements.

Table 4 also contains the ALL scenarios including the mass conserving component SLEL of ESMGFZ. As indicated in Sect. 2.2, the results are very close to those of the original ALL scenario, with a striking (small) impact on polar motion only.

Fig. 10

Changes in clock correction (top panels) and zenith wet delay (bottom panels) parameters for the VLBI stations FORTLEZA (left), BADARY (middle), and NYALES20 (right), with respect to their values in REF when applying non-tidal atmospheric (blue dots), oceanic (red dots), or hydrological loading (yellow dots) at the observation level. The site displacements have been generated by ESMGFZ

Tropospheric and clock parameters

As shown in Table 2, the clock correction terms as well as the zenith wet delays (ZWD) are estimated once per hour during a 24-h session in DOGS-RI. These parameters are significantly correlated with the station heights (compare van Dam and Herring 1994; Nothnagel et al. 2002, for example), which are most affected by non-tidal loading. Hence, if the corresponding site displacements are applied, there is a potential impact on the clock corrections and the ZWD. And as the latter have a high temporal resolution, they might be more capable of dealing with sub-daily variations. (The same holds for the tropospheric gradients, but since their temporal resolution is lower, we will focus on the other parameter types here.)

Exemplary, in Fig. 10 the site displacements for ATM, OCE, and HYD (generated by ESMGFZ) have been applied at the observation level, and respective parameter changes are depicted for three VLBI stations. The changes are very small for both clock corrections and ZWD: they represent only a tiny fraction of the differences between two parameters estimated at distinct epochs during a session. This corresponds to the findings of Böhm et al. (2009, p. 1284), who say that “there is hardly any effect on the estimated ZWD because the estimated heights account for the atmospheric loading effect”.

Even though the changes are small, we can derive certain properties from Fig. 10. Each dot refers to one estimated ZWD or clock correction term, and dots that appear to lie on a vertical line belong to the same session. The average spread of changes per session is about $\pm \, 0.3$ mm for ATM and OCE, depending on the magnitude of the corresponding site displacements at a VLBI station. For HYD, however, the spread is significantly smaller (about $\pm \, 0.1$ mm), even for VLBI stations with dominant hydrological loading (like FORTLEZA). The reason is the (missing) temporal variation of the associated site displacements during a session, as Fig. 11 indicates. There, we compare the changes in clock corrections and zenith wet delays for ATM at the two distinct application levels. At NEQ (as with HYD in general), only a constant displacement is applied, and this can be taken care of by the constant station coordinates. At OBS, on the other hand, the full temporal resolution of displacements is utilized, which cannot be accounted for by the constant corrections to the station coordinates alone. Hence, the remaining sub-daily variation is propagated into the supporting station parameters with finer resolution. Compared to their values in REF, the clock corrections and ZWD thus differ more for OBS (blue dots in Fig. 11) than for NEQ (red dots), and the degree of variation per session is directly proportional to the variation of the corresponding site displacements (grey dots).

As long as station coordinates (heights) are estimated, the overall effect of non-tidal loading on the supporting parameters is small. However, if one is mainly interested in estimating tropospheric delays with a high resolution, the impact becomes more significant and OBS should be used.

Fig. 11

Changes in clock correction (top panel) and zenith wet delay (bottom panel) parameters for the VLBI station BADARY, Russia, with respect to their values in REF when applying non-tidal atmospheric loading at the observation (blue dots) or the normal equation level (red dots). The corresponding vertical site displacements generated by ESMGFZ are also provided (grey dots) in their original resolution

Conclusions

For VLBI, we have investigated the impact of the application of different non-tidal loading effects at the normal equation level (NEQ) in contrast to the observation level (OBS). The two main differences for NEQ are the linearization of the functional model with respect to the site displacements generated from non-tidal loading and the removal of temporal variation of these displacements during a session. The linearization error is rather small for VLBI, so the main influence is given by the introduction of average displacement values.

Three different loading parts were applied both separately and jointly: non-tidal atmospheric (ATM), non-tidal oceanic (OCE), and hydrological loading (HYD). For HYD, the time series of site displacements is sufficiently smooth to be almost perfectly approximated by the session average, and hence the results for OBS and NEQ are nearly identical. But also for ATM, OCE, and the sum of all parts (ALL), we found that the approximation of OBS by NEQ is quite appropriate in most cases.

The overall impact of non-tidal loading is rather small at both application levels. The weighted sum of squared residuals and the formal errors of the estimates hardly change, since un-modelled displacements are already distributed between the parameters in the least-squares adjustment. Most of the displacements are shifted between the station coordinates themselves, but a minor part is also absorbed by the clock and tropospheric parameters. Due to their greater temporal resolution, and their significant correlation with the station heights, they are able to partly account for the sub-daily variation in the site displacements. Since there is no such variation at NEQ, some of the most striking differences between the application levels are observed for these parameters of station clocks and troposphere.

The same holds for EOP rates and celestial pole offsets: they are strongly affected by sub-daily variations, and hence we obtain greater differences between the results of OBS and NEQ than for the polar motion offsets. However, the impact of non-tidal loading is generally largest for the latter, with HYD representing the most dominant part.

Regarding the station positions, we found that the exclusive application of ATM or HYD is able to reduce the WRMS values with respect to long-term linear station motions by up to $-\,12$% for the vertical coordinate. Since the displacements for OCE are comparatively small, there is little reduction in the corresponding WRMS values, either (about $-\,0.4$% on average). The greatest improvement is obtained when all loading parts are applied jointly (up to $-\,21.0$% and about $-\,4.0$% on average), as there are different dominant parts at each station. These values are approximately equal for both application levels, and most importantly, we could show that the reduction in WRMS values is systematic across the VLBI stations.

We used site displacements from two providers: ESMGFZ and IMLS. Their data are quite similar, at least for ATM and OCE. The time series show significant differences only for HYD, and the reason are discrepancies in the underlying models for land water storage (LSDM and MERRA-2, respectively). However, both time series basically consist of a characteristic annual signal, and their application is capable of decreasing the corresponding signal for many stations’ heights and the scale parameter of a 7-parameter Helmert transformation between the DTRF2014 and the networks of the various VLBI sessions. If ATM and OCE are applied separately, this reduction is not observed, but the behaviour of the annual signals is independent from the application level.

In total, the considered models for non-tidal loading make a valuable contribution. Furthermore, HYD was found to be as important as ATM. However, given the differences between LSDM and MERRA-2, the particular choice of the hydrological model is a crucial issue. From our results, it is hard to tell which model provides the better displacements. It is probably more relevant to long for consistency with the models for ATM and OCE and for global mass conservation (which is achieved with the component SLEL by ESMGFZ, for example).

Table 5 Statistics of the relative changes in WRMS (in [%]) for local station coordinates (East, North, Up) and baseline lengths (BLR) after application of individual and total site displacements provided by ESMGFZ. Negative values represent improvements, and “improv. portion” is the percentage of improved vs. total cases

Table 6 Statistics of the relative changes in WRMS (in [%]) for local station coordinates (East, North, Up) and baseline lengths (BLR) after application of individual and total site displacements provided by IMLS. Negative values represent improvements, and “improv. portion” is the percentage of improved vs. total cases

We leave the effect on source coordinates for future research. It would also be interesting to investigate the impact on global station solutions (i.e. TRFs) or to examine the distinct application levels in connection with the other geodetic space techniques. The relevance of non-tidal loading in VLBI analysis might also further increase as soon as more error sources are removed, like the gravitational deformation of the VLBI antennas.

Appendix

See Tables 5 and 6.