A vision-aided automation system for destructive web thickness measurement of microdrills

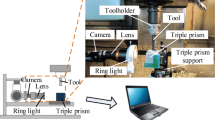
Abstract

Microdrills are fundamental cutting tools used in mechanical microdrilling. The web thickness of a microdrill is an important design parameter in balancing drill rigidity and chip removal ability. Conventional destructive method for measuring the web thickness is currently adopted by some microdrill manufactures. The conventional method must be carried out manually by experienced inspectors and thus lacks sufficient efficiency and accuracy. To improve the drawbacks of the conventional method, a vision-aided automation system for performing the destructive web thickness measurement is introduced in this paper. Based on the integration of motion and logic control, machine vision, and image processing techniques, an automated measuring process is then established. Experiments to measure the web thickness of microdrill samples were conducted to test the feasibility and effectiveness of the presented automation system and automated measuring process. The experimental results showed that the presented vision-aided automation system, in combination with the automated measuring process, could be an efficient and precise manner for replacing the conventional manual procedure in performing the destructive web thickness measurement of certain microdrills.

Appendix

The method used to determine common tangent circles of two regular planar curves is described below. Considering two planar curves Λ _P and Λ _Q represented in a Cartesian coordinate system O_F–X_FY_F, as shown in Fig. 16, their parametric vector equations can be referred to Eqs. (20) and (21), respectively. When a point P _Λ on curve Λ _P is determined by Eq. (20) with a given value of variable w ₁, there must be a circle C _Λ commonly tangent to curves Λ _P and Λ _Q , while point P _Λ and another point Q _Λ on curve Λ _Q are the common tangent points. Assuming curves Λ _P and Λ _Q and circle C _Λ are boundary contours of three rigid bodies, through the concept of simulated higher-pair contact analysis [33–36], circle C _Λ can be determined numerically. By denoting O _Λ and r _Λ as the center and radius of circle C _Λ , respectively, the necessary condition for the contact between curve Λ _P and circle C _Λ is that point P _Λ on curve Λ _P and a point C _P on circle C _Λ must be coincide, that is,

Fig. 16

Schematic diagram of a common tangent circle of two regular planar curves

$$ {\mathbf{P}}_{\varLambda }={\mathbf{C}}_P\kern1em \mathrm{for}\kern1em \left\{\begin{array}{l}{\mathbf{P}}_{\varLambda }={\boldsymbol{\Lambda}}_P\left({w}_1\right)=\left\{\begin{array}{c}\hfill {P}_{\varLambda x}\left({w}_1\right)\hfill \\ {}\hfill {P}_{\varLambda y}\left({w}_1\right)\hfill \end{array}\right\}\\ {}{\mathbf{C}}_P={\mathbf{O}}_{\varLambda }+{\mathbf{O}}_{\varLambda }{\mathbf{C}}_P=\left\{\begin{array}{c}\hfill {O}_{\varLambda x}\hfill \\ {}\hfill {O}_{\varLambda y}\hfill \end{array}\right\}+\left\{\begin{array}{c}\hfill {r}_{\varLambda } \cos {\theta}_P\hfill \\ {}\hfill {r}_{\varLambda } \sin {\theta}_P\hfill \end{array}\right\}\end{array}\right. $$

(25)

where O _Λx and O _Λy are the X_F- and Y_F-directional components of point O _Λ , and θ _P is the angle of vector O _Λ C _P measured from the +X_F-direction counterclockwise. The sufficient condition for the contact between curve Λ _P and circle C _Λ is that the normal vector to point P _Λ , denoted by N _P , must be collinear with vector O _Λ C _P , in other words, the cross-product of vectors N _P and O _Λ C _P must be zero:

$$ \begin{array}{c}\hfill {\mathbf{N}}_P\left({w}_1\right)\times {\mathbf{O}}_{\varLambda }{\mathbf{C}}_P=\left\{\begin{array}{c}\hfill -{P}_{\varLambda y}^{\prime}\left({w}_1\right)\hfill \\ {}\hfill {P}_{\varLambda x}^{\prime}\left({w}_1\right)\hfill \end{array}\right\}\times \left\{\begin{array}{c}\hfill {r}_{\varLambda } \cos {\theta}_P\hfill \\ {}\hfill {r}_{\varLambda } \sin {\theta}_P\hfill \end{array}\right\}\hfill \\ {}\hfill =-{r}_{\varLambda}\left[{P}_{\varLambda x}^{\prime}\left({w}_1\right) \cos {\theta}_P+{P}_{\varLambda y}^{\prime}\left({w}_1\right) \sin {\theta}_P\right]\mathbf{k}=\mathbf{0}\hfill \end{array} $$

(26)

where P ^′ _Λx (w ₁) = dP _Λx (w ₁)/dw ₁ and P ^′ _Λy (w ₁) = dP _Λy (w ₁)/dw ₁ are the X_F- and Y_F-components of the tangent vector to point P _Λ , and k is the unit vector of the Z_F-axis. Likewise, the necessary condition for the contact between curve Λ _Q and circle C _Λ is that point Q _Λ on curve Λ _Q and a point C _Q on circle C _Λ must be coincide, that is,

$$ {\mathbf{Q}}_{\varLambda }={\mathbf{C}}_Q\kern1em \mathrm{for}\kern1em \left\{\begin{array}{l}{\mathbf{Q}}_{\varLambda }={\boldsymbol{\Lambda}}_Q\left({w}_2\right)=\left\{\begin{array}{c}\hfill {Q}_{\varLambda x}\left({w}_2\right)\hfill \\ {}\hfill {Q}_{\varLambda y}\left({w}_2\right)\hfill \end{array}\right\}\\ {}{\mathbf{C}}_Q={\mathbf{O}}_{\varLambda }+{\mathbf{O}}_{\varLambda }{\mathbf{C}}_Q=\left\{\begin{array}{c}\hfill {O}_{\varLambda x}\hfill \\ {}\hfill {O}_{\varLambda y}\hfill \end{array}\right\}+\left\{\begin{array}{c}\hfill {r}_{\varLambda } \cos {\theta}_Q\hfill \\ {}\hfill {r}_{\varLambda } \sin {\theta}_Q\hfill \end{array}\right\}\end{array}\right. $$

(27)

where θ _Q is the angle of vector O _Λ C _Q measured from the +X_F-direction counterclockwise. The sufficient condition for the contact between curve Λ _Q and circle C _Λ is that the normal vector to point Q _Λ , denoted by N _Q , must be collinear with vector O _Λ C _Q , in other words, the cross-product of vectors N _Q and O _Λ C _Q must be zero:

$$ \begin{array}{c}\hfill {\mathbf{N}}_Q\left({w}_2\right)\times {\mathbf{O}}_{\varLambda }{\mathbf{C}}_Q=\left\{\begin{array}{c}\hfill -{Q}_{\varLambda y}^{\prime}\left({w}_2\right)\hfill \\ {}\hfill {Q}_{\varLambda x}^{\prime}\left({w}_2\right)\hfill \end{array}\right\}\times \left\{\begin{array}{c}\hfill {r}_{\varLambda } \cos {\theta}_Q\hfill \\ {}\hfill {r}_{\varLambda } \sin {\theta}_Q\hfill \end{array}\right\}\hfill \\ {}\hfill =-{r}_{\varLambda}\left[{Q}_{\varLambda x}^{\prime}\left({w}_2\right) \cos {\theta}_Q+{Q}_{\varLambda y}^{\prime}\left({w}_2\right) \sin {\theta}_Q\right]\mathbf{k}=\mathbf{0}\hfill \end{array} $$

(28)

where Q ^′ _Λx (w ₂) = dQ _Λx (w ₂)/dw ₂ and Q ^′ _Λy (w ₂) = dQ _Λy (w ₂)/dw ₂ are the X_F- and Y_F-components of the tangent vector to point Q _Λ . Therefore, from Eqs. (25) to (28), a nonlinear system of equations can be obtained as:

$$ \left\{\begin{array}{l}{P}_{\varLambda x}\left({w}_1\right)-{O}_{\varLambda x}-{r}_{\varLambda } \cos {\theta}_P=0\\ {}{P}_{\varLambda y}\left({w}_1\right)-{O}_{\varLambda y}-{r}_{\varLambda } \sin {\theta}_P=0\\ {}{Q}_{\varLambda x}\left({w}_2\right)-{O}_{\varLambda x}-{r}_{\varLambda } \cos {\theta}_Q=0\\ {}{Q}_{\varLambda y}\left({w}_2\right)-{O}_{\varLambda y}-{r}_{\varLambda } \sin {\theta}_Q=0\\ {}{P}_{\varLambda x}^{\prime}\left({w}_1\right) \cos {\theta}_P+{P}_{\varLambda y}^{\prime}\left({w}_1\right) \sin {\theta}_P=0\\ {}{Q}_{\varLambda x}^{\prime}\left({w}_2\right) \cos {\theta}_Q+{Q}_{\varLambda y}^{\prime}\left({w}_2\right) \sin {\theta}_Q=0\end{array}\right. $$

(29)

When the value of w ₁ is given, the nonlinear system of equations has six unknowns w ₂, O _Λx , O _Λy , r _Λ , θ _P , and θ _Q that must be solved simultaneously. By applying the well-known Newton–Raphson method [30, 38], the six unknowns can be solved numerically. For a given range of w ₁, a group of common tangent circles {C _Λ } and their radii {r _Λ } can be determined. When curves Λ _P and Λ _Q represent the concave flute contours of a cross-sectional plane of a microdrill, a minimum common tangent circle Č _Λ among all determined common tangent circles {C _Λ } exists such that its radius ř _Λ is the minimum radius among radii {r _Λ }, that is,

$$ \exists !{\check{C}}_{\varLambda}\in \left\{{\mathbf{C}}_{\varLambda}\right\}:{\check{r}}_{\varLambda }= \min \left(\left\{{\mathbf{r}}_{\varLambda}\right\}\right) $$

(30)

Hence, the cross-sectional web thickness w _(MC) is accordingly obtained by:

$$ {w}_{\left(\mathrm{MC}\right)}={\check{D}}_{\varLambda }=2{\check{r}}_{\varLambda } $$

(31)

in which, the value of w _(MC) is the diameter of the minimum common tangent circle Č _Λ .