1 Introduction

Development of ductile fracture criteria is an important issue for structural integrity and safety requirements. In various tests, it has been shown that increase in inelastic deformations in ductile metals can lead to fracture. Many research activities are documented in the literature of the past decades to detect fracture processes in ductile metals at a wide range of stress states. For example, in the range of high stress triaxialities fracture is the result of nucleation, growth and coalescence of voids on the micro-level, whereas small positive or negative stress triaxialities lead to formation and growth of micro-shear-cracks. Combination of these basic damage and fracture modes on the microscale occur for moderate positive stress triaxialities and for high negative stress triaxialities no fracture has been observed in experiments with ductile metals. Therefore, detailed experimental and numerical investigations of these stress-state-dependent failure processes are needed to develop and to validate accurate fracture models.

Information on stress-state-dependent damage and fracture mechanisms are taken from numerical studies on the micro-level examining deformation behavior of micro-defect-containing unit cells [6, 9, 13, 14, 17, 19, 28, 37]. Based on these numerical analyses individual behavior of micro-defects in unit cells under wide ranges of loading conditions have been investigated and the effects of their coalescence resulting in macro-cracks have been studied in detail. Systematic unit cell studies enable detection of stress-state-dependent damage and fracture processes which have not been revealed by experiments alone.

On the other hand, extensive experimental programs have been performed to investigate the influence of different stress states, often with focus on the role of the shear stress on ductile fracture. In particular, uniaxial tension tests with unnotched and pre-notched specimens have been performed to analyze stress-state-dependent inelastic deformation behavior as well as damage and fracture modes [3, 4, 9, 11, 21]. However, based on corresponding numerical simulations it has been shown that these tests with uniaxially loaded specimens only cover a small range of stress states and, thus, further tests with newly designed specimens have been developed by different research groups. For example, experiments with butterfly specimens have been discussed [2, 22, 32] which are uniaxially loaded in different directions using special experimental equipment and, thus, these tests are able to cover a wide range of stress triaxialities. Alternatively, two-dimensional experiments with different biaxially loaded specimens have been developed to investigate stress-state-dependent deformation, damage and fracture behavior [10, 15, 16, 23]. Corresponding numerical simulations have shown that these specimens cover a wide range of stress states allowing examination of different damage and fracture processes on the micro-level.

Furthermore, in the literature [3, 20, 27, 33, 36] the accumulated plastic strain to fracture is proposed to be an adequate measure to predict onset of fracture in a large number of engineering models and its stress state dependence is investigated by various experiments and numerical simulations. For example, a stress-triaxiality-dependent fracture strain criterion has been presented [26] based on micro-mechanical analysis of void growth [31, 34] and additional experimental data. This fracture strain equation has been extended [27] to numerically simulate failure behavior of smooth and differently notched tensile specimens [5]. A more sophisticated fracture strain criterion [3, 33, 38] is based on a series of experiments and corresponding numerical simulations to reveal the effect of stress triaxiality on the onset of fracture. In addition, alternative engineering fracture strain approaches depending on the stress triaxiality and the Lode parameter have been discussed [20, 36].

However, the engineering fracture approaches discussed above are only based on consideration of elastic–plastic behavior leading to fracture and ignore the damage mechanisms occurring in complexly loaded ductile metals before fracture happens. Therefore, alternative models have been presented using critical values of scalar damage variables predicting onset of ductile fracture. For example, formulations using critical micro-defect volume fractions [12, 39] or micro-defect area fractions [4, 29, 30] have been presented to identify onset of ductile fracture. On the other hand, the stress-state-dependent damage behavior is anisotropic and, thus, a simple scalar damage variable does not seem to adequately characterize the fracture behavior.

Therefore, a more detailed numerical analysis on the microscale investigating onset of macro-cracking caused by anisotropic growth and coalescence of micro-defects has been discussed and a fracture criterion taking into account critical values of damage strain tensors has been proposed [14]. This criterion is reconsidered in the present paper and modified based on experimental data from different biaxially loaded specimens.

In the present paper the continuum damage and fracture model is briefly discussed in Sect. 2. In Sect. 3 experimental and numerical results of biaxial tests with different specimens for two ductile metals, the aluminum alloy AlCuMg1 and the low carbon steel X5CrNi18-10, are presented. Based on these experimental and numerical data a fracture criterion for ductile metals is developed in Sect. 4. In Sect. 5 the main aspects of the paper are summarized.

2 Continuum damage and fracture model

The basic ideas of the thermodynamically consistent continuum damage model [7, 8] analyzing anisotropic damage in ductile metals are briefly presented. The phenomenological framework is based on a kinematic description of damage caused by stress-state-dependent evolution of micro-defects. The micro-defect volume fraction

$$\begin{aligned} f= \frac{\mathrm{d}V_\mathrm{d}}{\mathrm{d}V} \end{aligned}$$
(1)

has been proposed [25] as a continuous damage variable characterizing the current state of damage. It is directly given by the geometry of micropores where \(\mathrm{d}V_\mathrm{d}\) represents the differential volume of the micro-defects and \(\mathrm{d}V\) denotes the differential volume of the representative damaged volume element. However, this scalar damage variable f (Eq. (1)) only models isotropic damage behavior and, therefore, a kinematic concept to describe anisotropic damage behavior has been proposed [7, 13]. The trace of the damage strain tensor

$$\begin{aligned} \mathrm{tr} \mathbf{A}^\mathrm{da} = \mathrm{ln} \frac{\mathrm{d}V}{\mathrm{d}V - \mathrm{d}V_\mathrm{d}} = \mathrm{ln} (1 - f )^{-1} \end{aligned}$$
(2)

is introduced as a function of the void volume fraction f and models the volumetric increase in macroscopic strains caused by isotropic growth of micro-voids. Since \(\mathbf{A}^\mathrm{da}\) is a macroscopic irreversible strain tensor corresponding to nucleation, growth and coalescence of micro-defects it can be seen as a bridge between the micro- and the macro-level. In addition, the rate of the macroscopic volumetric damage strain rate tensor

$$\begin{aligned} {\dot{\mathbf{H}}}^\mathrm{da}_\mathrm{vol} = \frac{1}{3} (1 - f)^{-1} {\dot{f}} \mathbf{1} \end{aligned}$$
(3)

is introduced corresponding to the rate of growth of micropores. Motivated by the volumetric parts of the strains (3) and the strain rates (3) caused by isotropic growth of voids on the micro-level (characterized by the void volume fraction f) these tensors \(\mathbf{A}^\mathrm{da}\) and \({\dot{\mathbf{H}}}^\mathrm{da}\) are generalized in the present framework to model irreversible kinematic behavior caused by stress-state-dependent evolution of micropores and micro-shear-cracks leading to anisotropic damage. Thus, the damage strain and strain rate tensors are defined modeling micro-failure-induced degradation of ductile material properties in a phenomenological macroscopic way.

In the continuum damage model [7, 8] the strain rate tensor is additively decomposed into the elastic, \({\dot{\mathbf{H}}}^\mathrm{el}\), the effective plastic, \({\dot{\bar{\mathbf{H}}}}^\mathrm{pl}\), and the damage, \({\dot{\mathbf{H}}}^\mathrm{da}\), parts. Respective constitutive equations have to be formulated to compute these different strain rate tensors.

Plastic behavior of ductile metals is characterized by the yield condition

$$\begin{aligned} f^\mathrm{pl} \left( {\bar{I}}_1, {\bar{J}}_2 , c\right) \, = \, \sqrt{{\bar{J}}_2} \, - \, c \, \left( 1 \, - \, \frac{a}{c} {\bar{I}}_1\right) \, = \, 0 \; , \end{aligned}$$
(4)

where \({\bar{I}}_1 = \mathrm{tr} {\bar{\mathbf{T}}}\) and \({\bar{J}}_2 = \frac{1}{2} \, \mathrm{dev} {\bar{\mathbf{T}}} \, {\varvec{\cdot }} \, \mathrm{dev} {\bar{\mathbf{T}}}\) are the first and second deviatoric invariants of the effective Kirchhoff stress tensor \({\bar{\mathbf{T}}}\), c is the equivalent stress measure and a denotes the hydrostatic stress coefficient characterizing the effect of hydrostatic stress on plastic yielding. In addition, the rate of the isochoric plastic strain tensor

$$\begin{aligned} {\dot{\bar{\mathbf{H}}}}^\mathrm{pl} \, = \, {\dot{\gamma }} \, {\bar{\mathbf{N}}} \; \end{aligned}$$
(5)

models formation of plastic deformations taking into account the normalized deviatoric stress tensor \({\bar{\mathbf{N}}} \, = \, \frac{1}{\sqrt{2 \; {\bar{J}}_2}} \; \mathrm{dev} {\bar{\mathbf{T}}}\) and the equivalent plastic strain rate measure \({\dot{\gamma }} \, = \, {\bar{\mathbf{N}}} {\varvec{\cdot }} {\dot{\bar{\mathbf{H}}}}^\mathrm{pl}\).

Furthermore, onset of damage is described by the damage condition

$$\begin{aligned} f^\mathrm{da} = \alpha I_1 + \beta \sqrt{J_2} - \sigma = 0 \end{aligned}$$
(6)

where the stress invariants \(I_1 = \mathrm{tr} {\tilde{\mathbf{T}}}\) and \(J_2 = \frac{1}{2} \, \mathrm{dev} {\tilde{\mathbf{T}}} \, {\varvec{\cdot }} \, \mathrm{dev} {\tilde{\mathbf{T}}}\) (\({\tilde{\mathbf{T}}}\) is work conjugate to \({\dot{\mathbf{H}}}^\mathrm{da}\) and simply related to the Kirchhoff stress tensor, see [7] for further details) have been used and \(\sigma \) represents the equivalent damage stress measure. The additional stress-state-dependent parameters \(\alpha \) and \(\beta \) are based on different damage and failure mechanisms and have been identified by numerical investigations on the micro-level [13, 17]. The stress state dependence is here characterized by the stress triaxiality

$$\begin{aligned} \eta = \frac{\sigma _m}{\sigma _{eq}} = \frac{I_1}{3 \sqrt{3 J_2}} \end{aligned}$$
(7)

with the mean stress \(\sigma _m = I_1 / 3\) and the equivalent von Mises stress \(\sigma _{eq} = \sqrt{3 J_2}\) as well as with the Lode parameter

$$\begin{aligned} \omega = \frac{2 {\tilde{T}}_2 - {\tilde{T}}_1 - {\tilde{T}}_3}{{\tilde{T}}_1 - {\tilde{T}}_3} \; \; \; \mathrm{with} \; {\tilde{T}}_1 \ge {\tilde{T}}_2 \ge {\tilde{T}}_3 \end{aligned}$$
(8)

expressed in terms of the principal components of the Kirchhoff stress \({\tilde{T}}_1\), \({\tilde{T}}_2\) and \({\tilde{T}}_3\).

In addition, the rate of the damage strain tensor

$$\begin{aligned} {\dot{\mathbf{H}}}^{\mathrm{da}} = {\dot{\mu }} \left( \frac{{\bar{\alpha }}}{\sqrt{3}} \mathbf{1} + \frac{{\bar{\beta }}}{\sqrt{2}} \mathbf{N} + {\bar{\delta }} \mathbf{M} \right) \end{aligned}$$
(9)

predicts the increase in macroscopic strains caused by damage and failure processes on the microscale. In Eq. (9), \({\dot{\mu }}\) represents the equivalent damage strain rate, whereas \(\mathbf{N} = \frac{1}{\sqrt{2 {J}_2}} \mathrm{dev} {\tilde{\mathbf{T}}}\) and \(\mathbf{M} = \frac{\text{ dev } \tilde{\mathbf{S}}}{\left\| \text{ dev } \tilde{\mathbf{S}}\right\| }\) are the normalized stress-related deviatoric tensors with

$$\begin{aligned} \mathrm{dev}{\tilde{\mathbf{S}}} = \mathrm{dev}{\tilde{\mathbf{T}}}\,\, \mathrm{dev}{\tilde{\mathbf{T}}} - \frac{2}{3} J_2 \mathbf{1} \; . \end{aligned}$$
(10)

The parameters \({\bar{\alpha }}\), \({\bar{\beta }}\) and \({\bar{\delta }}\) in Eq. (9) are kinematic parameters which are identified by results of numerical simulations on the microscale [13, 17]. The evolution equation (9) can be seen as an anisotropic generalization of Eq. (3) because only the first term is the volumetric part of the damage strain rate tensor, whereas the second and third terms are anisotropic kinematic contributions corresponding to anisotropic growth and coalescence of micro-defects.

Moreover, critical accumulation of growing micro-defects will lead to macro-cracks and the onset of this macroscopic fracture process is modeled by the fracture criterion

$$\begin{aligned} f^\mathrm{fr} ( \mathbf{A}^\mathrm{da}, \, a_\mathrm{fr} ) = 0 \end{aligned}$$
(11)

expressed in terms of the damage strain tensor \(\mathbf{A}^\mathrm{da}\) taking into account the current amount and orientation of anisotropic damage and of the fracture threshold \(a_\mathrm{fr}\). This criterion is analyzed in the present paper by examining results of a number experiments with differently biaxially loaded specimens to propose a function for ductile metals.

3 Experimental and numerical results

Many experiments with different biaxially loaded specimens and corresponding numerical simulations have been performed by the group of the corresponding author during the last years [10, 15, 16, 18, 23, 24]. Some experimental and numerical results are reconsidered in the present paper and are used to propose a new fracture criterion. The experiments have been performed in a biaxial test machine containing four individually driven cylinders loading the specimens in perpendicular axes. After the tests fracture surfaces of the specimens are analyzed by scanning electron microscopy (SEM) showing different damage and fracture modes depending on the stress state. In addition, the finite element program ANSYS enhanced by a user-defined material subroutine based on the proposed continuum damage model has been used to numerically simulate the biaxial experiments. These corresponding analyses deliver information on stress states in critical regions of the specimens where fracture is expected to occur. It should be noted that different stress states (i.e., combinations of different stress triaxialities and Lode parameters) are obtained due to different boundary conditions and geometries of the specimens leading to a widespread database. In addition, the components of the damage strain tensors are numerically predicted which are used to propose the fracture criterion based on critical damage values and to identify the corresponding fracture parameters.

Fig. 1
figure 1

Range of stress triaxialities \(\eta \) covered by the Z-specimen (blue), X0-specimen (red) and H-specimen (green) for AlCuMg1 and X5CrNi18-10 (color figure online)

Full size image

With the newly developed geometries of the biaxially loaded specimens [23] it is possible to investigate different damage and fracture processes depending on the stress state in the material. For example, Fig. 1 shows the ranges of the stress triaxialities \(\eta \) (7) reached by the Z-, X0- and H-specimen for the aluminum alloy AlCuMg1 and the low carbon steel X5CrNi18-10.

Loading of the Z-specimen in 2-direction leads to shear behavior in the central part which can be superimposed by loading in direction 1 causing additional tension or compression. With different load ratios the wide band of stress triaxialities \(-\,0.6< \eta < 1.0\) has been reached. With the X0-specimen a range of positive stress triaxialities are possible for tensile loading in direction 2 superimposed by different tensile or compressive loads in direction 1. With variation of load ratios the stress triaxialities \(0.0< \eta < 0.8\) have been reached. Loading of the H-specimen in 2-direction leads to shear behavior in the central part which can be superimposed by loading in direction 1 causing additional tension or compression. With different load ratios the stress triaxialities \(-\,0.3< \eta < 0.7\) have been reached.

Fig. 2
figure 2

a Stress triaxialities \(\eta \) and Lode parameters \(\omega \) and b SEM pictures of the fracture surfaces for load ratios 1 \(F_1{:}F_2 = 0{:}1\), 2 \(F_1{:}F_2 = -\,4{:}1\), 3 \(F_1{:}F_2 = -\,8{:}1\) (Z-specimen, aluminum alloy AlCuMg1)

Full size image

The numerically predicted stress states in the notched areas of the specimens are investigated in detail for selected loading conditions and are compared with pictures of the fracture surfaces taken from SEM. In particular, for the Z-specimen manufactured from thin sheets of the aluminum alloy AlCuMg1 the stress triaxiality \(\eta \) and the Lode parameter \(\omega \) in the center of the specimen are shown in Fig. 2 for the load ratios \(F_1{:}F_2 = 0{:}1\), \(F_1{:}F_2 = -4{:}1\) and \(F_1{:}F_2 = -8{:}1\), respectively. For \(F_1{:}F_2 = 0{:}1\) in the center of the notch \(\eta = 0.0\) and \(\omega = 0.0\) are reached (Fig. 2a1) which are typical for shear loading. The corresponding damage and fracture modes on the micro-level are nucleation of few voids and formation of micro-shear-cracks. This can be seen in the SEM picture (Fig. 2b1) where few small and slightly sheared voids can be seen which are superimposed by remarkable micro-shear-effects then leading to shear fracture. Decrease in the stress triaxiality can be observed for the load ratio \(F_1{:}F_2 = -4{:}1\). In the center of the notch \(\eta = -\,0.4\) and \(\omega = 0.0\) are numerically predicted and the distribution of the Lode parameter is less homogeneous, see Fig. 2a2. This shear-compression loading condition leads to compression and shearing of micropores which can be clearly seen in Fig. 2b2. In addition, remarkable formation of micro-shear-cracks is also shown in the SEM picture (Fig. 2b2). This superimposed shear behavior then leads to macroscopic shear cracks. Further increase in the compressive load in the axis 1 up to \(F_1{:}F_2 = -8{:}1\) leads in the center of the notch to the remarkably high negative stress triaxiality \(\eta = -\,0.55\) and the corresponding Lode parameter \(\omega = 0.0\) (Fig. 2a3). In this case, the shear mechanisms are superimposed by high compression. Therefore, preexisting micropores are completely compressed and only shear effects can be seen in the SEM picture (Fig. 2b3). This leads to additional remarkable opening of a macro-crack perpendicular to the plane fracture surface caused by the compressed contact between these surfaces during the fracture process.

Fig. 3
figure 3

a Stress triaxialities \(\eta \) and Lode parameters \(\omega \) and b SEM pictures of the fracture surfaces for load ratios 1 \(F_1{:}F_2 = 1{:}1\), 2 \(F_1{:}F_2 = -\,0.5{:}1\), 3 \(F_1{:}F_2 = -\,1{:}1\) (X0-specimen, aluminum alloy AlCuMg1)

Full size image

In addition, for the aluminum alloy AlCuMg1 the X0-specimen has been analyzed for different loading conditions. The stress triaxiality \(\eta \) and the Lode parameter \(\omega \) for the load ratio \(F_1{:}F_2 = 1{:}1\) are shown in Fig. 3a1. In the center of the notched part the stress triaxiality reaches \(\eta = 0.83\) and the corresponding Lode parameter is \(\omega = -\,0.5\), both with inhomogeneous distributions in the notch area. The high stress triaxiality in the center leads to nucleation and growth of voids on the microscale. The SEM picture (Fig. 3b1) shows remarkable large voids which grew during the loading process as well as smaller micropores which nucleated later caused by the large strains occurring in this critical part of the specimen. In addition, dimples on the fracture surface can be seen in the SEM picture which are typical for fracture modes for high tensile loading conditions. The load ratio \(F_1{:}F_2 = -\,0.5{:}1\) leads to shear-tension behavior. The corresponding stress parameters are \(\eta = 0.2\) and \(\omega = -\,0.2\) with more homogeneous distributions over the notch area (Fig. 3a2). In this case, on the micro-level nucleation of voids as well as formation of micro-shear-cracks takes place. During the loading process the voids grow and are sheared leading to elliptical pores shown in the SEM picture (Fig. 3b2). In addition, the micro-shear cracks grow causing shear fracture mechanisms leading to plane fracture surfaces. For the load ratio \(F_1{:}F_2 = -1{:}1\) shear behavior occurs with micro-shear-cracks and few sheared voids in the notches of the X0-specimen. Figure 3a3 shows the stress triaxiality \(\eta = 0.0\) and the Lode parameter \(\omega = 0.0\) in the center of the notch and very homogeneous distribution over the notch area. For this stress state nucleation and growth of few voids superimposed by remarkable formation of micro-shear-cracks is predicted leading to shear fracture in the notches of the specimen. This behavior is illustrated in the corresponding SEM picture showing remarkable micro-shear-crack behavior, see Fig. 3b3.

Fig. 4
figure 4

a Stress triaxialities \(\eta \) and Lode parameters \(\omega \) and b SEM pictures of the fracture surfaces for load ratios 1 \(F_1{:}F_2 = 1{:}0\), 2 \(F_1{:}F_2 = 1{:}1\), 3 \(F_1{:}F_2 = -\,1{:}1\) (H-specimen, aluminum alloy AlCuMg1)

Full size image
Fig. 5
figure 5

a Stress triaxialities \(\eta \) and Lode parameters \(\omega \) and b SEM pictures of the fracture surfaces for load ratios 1 \(F_1{:}F_2 = 1{:}1\), 2 \(F_1{:}F_2 = 0.5{:}1\), 3 \(F_1{:}F_2 = -\,0.5{:}1\) (X0-specimen, steel X5CrNi18-10)

Full size image

Furthermore, H-specimens have been manufactured from the aluminum alloy sheets and have been tested under different loading conditions. For the load ratio \(F_1{:}F_2 = 1{:}0\) the stress triaxiality reaches \(\eta = 0.71\) in the center of the notch and the corresponding Lode parameter is \(\omega = -\,0.5\), see Fig. 4a1. This tensile loading leads to predominant nucleation and growth of voids, whereas formation of micro-shear-cracks is marginal. In the neighborhood of large micropores additional smaller voids can be seen in the SEM picture (Fig. 4b1) which nucleated later during the loading process. The fracture mode is characterized by dimples on the fracture surface which are typical for fracture under high stress triaxialities. Combination of shear and tensile behavior occurs in the notch of the specimen for the load ratio \(F_1{:}F_2 = 1{:}1\). As can be seen in Fig. 4a2 this leads to the stress parameters \(\eta = 0.3\) and \(\omega = -\,0.5\) in the center of the notch. For these moderate stress triaxialities combination of growth of voids and formation of micro-shear-cracks is predicted. The corresponding SEM picture shows small sheared voids combined with micro-shear-cracks leading to shear fracture mode (Fig. 4b2). For the load ratio \(F_1{:}F_2 = -1{:}1\) shear behavior with superimposed compression appears in the notches of the H-specimen leading to the stress triaxiality \(\eta = -\,0.27\) and the Lode parameter \(\omega = 0.3\) in its center, as shown in Fig. 4a3. In the corresponding SEM picture only few small compressed and sheared voids are visible and predominant micro-shear-cracks are shown in Fig. 4b3 leading again to shear fracture mode.

Moreover, the damage and failure behavior of the X0-specimen taken from ductile steel X5CrNi18-10 has been examined in the experimental program. Figure 5a1 shows the stress triaxiality and the Lode parameter in the notch area and in the center they reach \(\eta = 0.68\) and \(\omega = -\,0.4\) for the load ratio \(F_1{:}F_2 = 1{:}1\). This leads to nucleation and growth of micropores and at the end of the load step remarkably large voids in the fracture surface visualized by SEM, see Fig. 5b1. In addition, dimples can be seen which are typical for fracture under high stress triaxialities. For the load ratio \(F_1{:}F_2 = 0.5{:}1\) smaller stress parameters are numerically predicted and in the center of the notch they reach \(\eta = 0.60\) and \(\omega = -\,0.7\), see Fig. 5a2. On the fracture surface again many voids can be seen which nucleated and grew during the loading process. In the SEM picture (Fig. 5b2) these voids are slightly sheared and the fracture mode is again characterized by dimples. The stress parameters for the load ratio \(F_1{:}F_2 = -\,0.5{:}1\) are shown in Fig. 5a3 with values in the center of the notch of \(\eta = 0.15\) and \(\omega = -\,0.4\). This leads to shear-tension effects which can be seen in Fig. 5b3: voids grow and are sheared during the loading process in combination with some micro-shear-cracks leading to shear fracture with superimposed dimples.

Fig. 6
figure 6

a Stress triaxialities \(\eta \) and Lode parameters \(\omega \) and b SEM pictures of the fracture surfaces for load ratios 1 \(F_1{:}F_2 = 1{:}0\), 2 \(F_1{:}F_2 = 1{:}1\), 3 \(F_1{:}F_2 = -\,0.5{:}1\) (H-specimen, steel X5CrNi18-10)

Full size image

In addition, the H-specimens of steel X5CrNi18-10 have been tested under different loading conditions. For the load ratio \(F_1{:}F_2 = 1{:}0\) the numerically predicted stress parameters are \(\eta = 0.68\) and \(\omega = -\,0.4\) in the center of the notch, see Fig. 6a1. This tensile loading behavior leads to similar failure mechanisms as shown for the X0-specimen with \(F_1{:}F_2 = 1{:}1\) (Fig. 5b1) with remarkable growth of voids and formation of dimples on the fracture surface as can be seen in the SEM pictures shown in Fig. 6b1. The load ratio \(F_1{:}F_2 = 1{:}1\) leads to the stress triaxiality \(\eta = 0.3\) and the Lode parameter \(\omega = -\,0.7\) in the center of the notch (Fig. 6a2). For this stress state simultaneous growth of voids and formation of micro-shear-cracks is predicted. During loading of the specimens the voids are superimposed by shear processes leading to elliptical pores on the micro-level. Thus, in the corresponding SEM picture in Fig. 6b2 small sheared voids as well as micro-shear-cracks can be seen. For the alternative load ratio \(F_1{:}F_2 = -\,0.5{:}1\) the stress parameters are \(\eta = 0.0\) and \(\omega = 0.2\) in the center of the notch, see Fig. 6a3. This leads to nucleation and slight growth of voids which are compressed and sheared during the loading path leading to elliptical micropores. As shown in the SEM picture (Fig. 6b3) the fracture surface is nearly plane due to coalescence of micro-shear-cracks with few craters around the voids.

4 Fracture criterion for ductile metals

Based on the continuum damage model the numerical analysis of the biaxial experiments delivers damage quantities which can be used to formulate an appropriate fracture criterion. Following the basic ideas of formulation of yield conditions or damage criteria [1, 35] the fracture criterion (11) is expressed in terms of the invariants of the damage strain tensor:

$$\begin{aligned} f^\mathrm{fr} ( \mathbf{A}^\mathrm{da}, \, a_\mathrm{fr} ) = {\tilde{\alpha }} \; I_1^\mathrm{da} + {\tilde{\beta }} \; \sqrt{J_2^\mathrm{da}} - a_\mathrm{fr} = 0 \end{aligned}$$
(12)

with the first and second deviatoric invariants of the damage strain tensor, \({I}_1^\mathrm{da} = \mathrm{tr} \mathbf{A}^\mathrm{da}\) and \({J}_2^\mathrm{da} = \frac{1}{2} \, \mathrm{dev} \mathbf{A}^\mathrm{da} \, {\varvec{\cdot }} \, \mathrm{dev} \mathbf{A}^\mathrm{da}\), and the stress-state-dependent parameters \({\tilde{\alpha }}\) and \({\tilde{\beta }}\). Thus, these invariants are determined in critical points of all investigated specimens and the results for both materials are shown in Fig. 7. For negative and small positive stress triaxialities the first invariant \({I}_1^\mathrm{da} = 0\) is numerically predicted. This indicates that there is no volumetric damage strain. This agrees well with the pictures from SEM where no growth of voids and only formation of micro-shear-cracks has been observed for these stress states. On the other hand, with increasing stress triaxiality a remarkable increase in \({I}_1^\mathrm{da} > 0\) is shown in Fig. 7a. This also corresponds to the observation from SEM pictures where growth of voids was the predominant failure mechanism leading to increase in volumetric damage strains with increasing stress triaxiality. The second deviatoric invariant \(J_2^\mathrm{da}\) corresponds to damage strains caused by isochoric change in shape of micro-defects. As can be seen in Fig. 7b it is small for negative stress triaxialities where only micro-shear-cracks and few sheared micropores have been shown in the pictures of SEM. With increasing stress triaxiality the invariant \(J_2^\mathrm{da}\) also remarkably increases. This corresponds to the change in shape of the voids from spherical to elliptical ones which can be also seen in the respective SEM pictures. It can be concluded that the numerically predicted invariants of the macroscopic damage strain tensor nicely corresponds to the damage and fracture processes on the micro-level visualized by SEM.

Fig. 7
figure 7

Invariants of the damage strain tensor versus stress triaxiality

Full size image

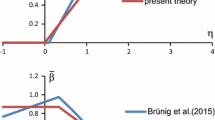
Using the invariants shown in Fig. 7 the parameters of the fracture criterion (12) are identified. In the present investigation, the fracture mode parameters \({\tilde{\alpha }}\) and \({\tilde{\beta }}\) in Eq. (12) are taken to be stress-state-dependent functions, whereas the fracture threshold \(a_\mathrm{fr}\) is assumed to be a material constant. For the aluminum alloy the experiment with the Z-specimen loaded by \(F_1{:}F_2 = -4{:}1\) is chosen as the reference test where the invariants of the damage strain tensor are \({I}_1^\mathrm{da} = 0\) and \(\sqrt{J_2^\mathrm{da}} = 0.01\). In this point the fracture mode parameters are taken to be \({\tilde{\alpha }} (\eta = -\,0.3; \omega = 0.0) = 0.0\) and \({\tilde{\beta }} (\eta = -\,0.3; \omega = 0.0) = 1.0\) which leads to the constant fracture threshold \(a_\mathrm{fr}^\mathrm{Al} = 0.01\) for the aluminum alloy AlCuMg1. With this chosen material constant the parameters \({\tilde{\alpha }}\) and \({\tilde{\beta }}\) are determined considering the critical damage strain quantities predicted for all experiments, see Fig. 8. Based on the available test results only dependence of the parameters on the stress triaxiality could be found out and the additional dependence on the Lode parameter could not be determined. As can be seen in Fig. 8 the chosen parameters \({\tilde{\alpha }}\) and \({\tilde{\beta }}\) fit the values for both materials and, thus, the stress triaxiality dependent functions

$$\begin{aligned} {{\tilde{\alpha }}} (\eta ) = \left\{ \begin{array}{ll} 0 &{}\quad \text{ for } \; \; \;\eta \le 0.13 \\ 2.05 \, \eta - 0.2665 &{}\quad \text{ for } \; \; \;0.13< \eta \le 0.32 \\ 4.29 \, \eta - 0.6737 &{}\quad \text{ for } \; \; \;0.32< \eta \le 0.43 \\ -\,5.6821 \, \eta + 3.6143 &{}\quad \text{ for } \; \; \;0.43 < \eta \le 0.63 \\ -\,0.01 \eta + 0.06925 &{}\quad \text{ for } \; \; \;\eta > 0.63 \end{array} \right. \end{aligned}$$
(13)

and

$$\begin{aligned} {{\tilde{\beta }}} (\eta ) = \left\{ \begin{array}{ll} \eta + 1.53 &{}\quad \text{ for }\; \; \;\eta \le -\,0.14 \\ 5 \, \eta + 2.13 &{}\quad \text{ for } \; \; \; -\,0.14< \eta \le 0.07 \\ 38 \, \eta + 0.15 &{}\quad \text{ for } \; \; \; 0.07< \eta \le 0.13 \\ -\,21.05 \, \eta + 7.236 &{}\quad \text{ for } \; \; \; 0.13< \eta \le 0.33 \\ -\,1.852 \, \eta + 1.0926 &{}\quad \text{ for } \; \; \; 0.33 < \eta \le 0.59 \\ 0 &{}\quad \text{ for }\; \; \; \eta > 0.59 \end{array} \right. \end{aligned}$$
(14)

seem to be valid for a wide class of ductile metals. Based on these functions the fracture threshold for the steel X5CrNi18-10 is identified to be \(a_\mathrm{fr}^\mathrm{St} = 0.006\).

Fig. 8
figure 8

Stress-state-dependent functions \({\tilde{\alpha }}\) and \({\tilde{\beta }}\) versus stress triaxiality

Full size image

5 Conclusions

A fracture criterion for ductile metals has been proposed. It takes into account invariants of the damage strain tensor as well as stress-state-dependent fracture mode parameters. The criterion is based on a series of biaxial experiments performed with different specimens and corresponding numerical simulations. In critical regions of the specimens the stress states as well as components of the damage strain tensors are determined and pictures of the fracture surfaces taken from scanning electron microscopy are shown revealing different stress-state-dependent damage and failure modes. Based on these data the fracture criterion is formulated in terms of the first and second deviatoric invariants of the damage strain tensor as well as of stress-triaxiality-dependent fracture mode parameters, whereas the fracture threshold is taken to be a material constant which is identified for both investigated ductile materials, the aluminum alloy AlCuMg1 and the low carbon steel X5CrNi18-10.

The proposed fracture criterion is validated for two different ductile metals and its applicability for other ductile materials should be examined in further studies. In addition, more experimental data for other stress states are desired to analyze the possible additional dependence of the parameters on the Lode parameter.