1 Introduction

Aging water distribution networks (WDN) are associated with increasing levels of losses through background leakage and frequent interruptions to customer supply. As a result, reducing pressure-induced pipe stress and leakage while improving network resilience, i.e., the ability of a WDN to maintain continuous customer supply, represents a critical challenge for water utilities.

This study investigates the design-for-control (DfC) problem which consists in simultaneously installing candidate valves (CNV) and pipes (CNP) in existing WDNs, and optimizing the controls of new and existing pressure control valves for the joint minimization of leakage and maximization of resilience at minimum cost. We adopt a steady-state hydraulic model, where flows and head differences across links and pressure heads at nodes are represented by continuous variables, subject to the conservation of mass and energy. The selection of CNVs and CNPs, on the other hand, is represented by binary variables, resulting in a non-convex multi-objective mixed-integer non-linear program (MOMINLP).

The solution of the multi-objective DfC problem requires identifying the non-dominated set of trade-offs for which one objective cannot be improved without worsening another. However, obtaining a complete description of the non-dominated set (or Pareto front) of MOMINLPs, which may be composed of disconnected segments and isolated points (Das 2000), is impractical. As a result, while global solution methods have been investigated for the single-objective design, control, and DfC of WDNs (Sherali et al. 1999; Gleixner et al. 2012; Pecci et al. 2018), multi-objective problems have mainly been solved using general-purpose evolutionary algorithms (Maier et al. 2014) or local deterministic methods (Pecci et al. 2017), which do not provide guarantees on the quality of the returned solutions.

On the other hand, both scalarization (Fernández and Tóth 2007; Ehrgott and Gandibleux 2007) and multi-objective branch-and-bound (De Santis et al. 2020; Niebling and Eichfelder 2019; Eichfelder et al. 2021) approaches have been investigated to extend (single-objective) guarantees of global optimality to convex multi-objective mixed-integer problems or non-convex multi-objective continuous problems. These methods return a set of feasible solutions and a guarantee of their non-dominance in the form of an enclosure of the Pareto front.

In Ulusoy et al. (2021), the authors first approximated the Pareto front of a bi-objective WDN design-for-control problem with global bounds using the method of \(\epsilon\)-constraints. More recently, Eichfelder et al. (2022) proposed a general branch-and-bound (BB) framework for non-convex MOMINLPs, the performance of which depends, in practice, on the choice of adequate branching and lower bounding strategies by the user. The framework also relies on the availability of attainable solutions which, for WDN design-for-control problems, can be hard to identify. In this study, we investigate the implementation of a multi-objective BB algorithm with tailored spatial branching, lower bounding and additional upper bounding strategies to efficiently approximate the Pareto front of WDN design-for-control problems with global bounds of \(\epsilon\)-non-dominance.

The structure of the paper is as follows. In Sect. 2, we describe the formulation of the considered WDN design-for-control problem. Section 3 then presents a multi-objective branch-and-bound (BB) algorithm based on tailored branching, lower bounding and upper bounding strategies. The proposed approach is applied to the DfC of two case study networks in Sect. 4, extending previous studies to investigate the trade-off between operational objectives and design cost. The performance of the proposed algorithm is also compared to the Non-Dominated Sorting Genetic Algorithm (NSGA-II) metaheuristic (Deb et al. 2002) and the scalarization approach presented in Ulusoy et al. (2021), and the conclusions of our work are summarized in Sect. 5.

2 Problem formulation

We consider a steady-state hydraulic model of a WDN, represented by a directed graph G with \(n_n + n_0\) nodes (including \(n_n\) demand nodes or junctions and \(n_0\) water sources) and \(n_p\) links (including \(n_{\text {V}}\) existing pressure control valves, \(n_{\text {CNV}}\) candidate pressure control valves, and \(n_{\text {CNP}}\) candidate pipes for installation). We denote by E the set of network links, and by \(E_{\text {V}}\), \(E_{\text {CNV}},\) and \(E_{\text {CNP}} \subset E\) the index subsets corresponding to existing control valves, CNVs and CNPs, respectively. Moreover, we consider that the physical characteristics (length, diameter, material) and locations of CNVs and CNPs are defined based on preliminary analyses (Fig. 1, for instance, illustrates the CNV and CNP locations considered for the optimal expansion of pescara in Sect. 4.1).

Fig. 1
figure 1

Example of WDN design-for-control problem: expansion of the modified pescara network (Ulusoy et al. 2021)

Full size image

We consider the problem which consists in determining the discrete design variables \({z \in \{0,1\}^{(n_{\text {CNV}}+n_{\text {CNP}})}}\) representing the installation of CNVs and CNPs, and the continuous control variables \(\eta _j^k\) representing additional head losses across valves \({j \in E_{\text {V}} \cup E_{\text {CNV}}}\) at time steps \(k=1,\dots ,n_t\) (\(n_t\) represents the number of considered loading conditions). Hydraulic conditions at time step k are represented by the continuous state variables \({h^k \in \mathbbm {R}^{n_n}}\) (hydraulic heads) and \({q^k \in \mathbbm {R}^{n_p}}\) (flows) which, given the vectors of known water demands and source heads \(d^k \in \mathbbm {R}^{n_n}\) and \({h_0^k \in \mathbbm {R}^{n_0}}\), are uniquely determined by the decision variables z and \(\eta ^k\) (see Sect. 2.1). The objective is to find z and \(\eta ^k\), for all \({k=1,\dots ,n_t}\), corresponding to hydraulically feasible conditions \(h^k\) and \(q^k\) jointly minimizing pressure-induced leakage, maximizing network resilience, and minimizing design cost (see Sect. 2.2).

2.1 Constraints

At time step k, the operation of a WDN is subject to the energy and mass conservation constraints:

$$\begin{aligned}&A_{12}h^k + A_{10}h^k_0 + \theta ^k + \eta ^k = 0, \end{aligned}$$
(1a)
$$\begin{aligned}&A_{12}^T q^k - d^k = 0, \end{aligned}$$
(1b)
$$\begin{aligned}&\theta ^k = \phi (q^k), \end{aligned}$$
(1c)

where \(A_{12} \in \mathbbm {R}^{n_p \times n_n}\) and \(A_{10} \in \mathbbm {R}^{n_p \times n_0}\) are the link-node incidence matrices for demand nodes and water sources, respectively, \({\phi (q^k)=[\phi _1(q_1^k) \dots \phi _{n_p}(q_{n_p}^k) ]^T}\) represents the vector of friction head losses associated with link flows \({q^k= [q_1^k \dots q_{n_p}^k ]^T}\) and the vector of auxiliary variables \(\theta ^k\) is introduced to isolate the non-convex potential-flow coupling constraints.

Friction head losses are commonly described by the Darcy–Weisbach (D-W) or Hazen–Williams (H-W) equations. However, a common approach in the literature (Eck and Mevissen 2015; Pecci et al. 2018; Zamzam et al. 2019) consists in using the quadratic approximation \({\phi _j(q^k_j) = q^k_j(a_j \mid q^k_j \mid +b_j)}\), where positive coefficients \((a_j,b_j) \in (\mathbbm {R}_+)^2\) depend on the physical characteristics and range of operational flows considered for link j. Appendix B shows that, for the considered problem instances, the use of a quadratic approximations of the friction head loss models does not affect the feasibility of the computed design-for-control solutions.

Moreover, the status of CNVs and CNPs \({j \in E_{\text {CNV}} \cup E_{\text {CNP}}}\) is represented by the binary design variables \(z_{l_j} \in \{0,1\}\), \({l_j \in \{1 \dots n_{\text {CNV}}+n_{\text {CNP}}\}}\). For \(j \in E_{\text {CNV}}\), either \(z_{l_j}=1\) and link j is selected for valve installation and modeled as a pressure control valve, or \(z_{l_j}=0\) and link j is modeled as an open pipe. For \({j \in E_{\text {CNP}}}\), on the other hand, the candidate location j is modeled as an open pipe if \(z_{l_j}=1\), and a closed pipe if \(z_{l_j}=0\). This is represented by the big-M constraints (13) on variables \(q^k\), \(\theta ^k\), \(\eta ^k\) and z defined in Appendix A.

Finally, infeasible designs are modeled by combinatorial constraints on the binary variables z:

$$\begin{aligned} \begin{aligned}{} & {} &Az \le b \end{aligned} \end{aligned}$$
(2)

where A and b are a matrix and vector of fixed entries. We define the overall vector of variables \({x=(x_{\mathcal {C}},x_{\mathcal {I}})}\), with subscripts \(\mathcal {I}\) and \(\mathcal {C}\) referring, respectively, to the vectors of integer (design) and continuous (control and state) variables, z and \((q,h,\eta ,\theta )\), where \({q=(q^k)_{k=1,\dots ,n_t}}\), \({h=(h^k)_{k=1,\dots ,n_t}}\), \({\eta =(\eta ^k)_{k=1,\dots ,n_t}}\) and \({\theta =(\theta ^k)_{k=1,\dots ,n_t}}\).

2.2 Objectives

We investigate the joint minimization of pressure-induced background leakage, maximization of resilience, and minimization of design cost.


Pressure-induced background leakage

In this study, we use the average zone pressure (AZP) as a surrogate measure of pressure-induced background leakage:

$$\begin{aligned} \begin{aligned} \text {AZP} = \frac{1}{n_{t}W} \sum _{k=1}^{n_t} w^T (h^k-\zeta ), \end{aligned} \end{aligned}$$
(3)

where \(w \in \mathbbm {R}_+^{n_n}\) is the vector of AZP weights (Wright et al. 2015) and \(W = \sum _{i=1}^{n_n}w_i\).


Resilience


Direct measures of WDN resilience, which rely on the simulation of a wide range of failure events, suffer from combinatorial limitations. As a result, surrogate measures depending on the performance of the network under normal operating conditions, such as the resilience index \(I_r\) (Todini 2000):

$$\begin{aligned} \begin{aligned} I_r = \frac{\sum _{k=1}^{n_t} ( (d^k)^T h^k - (d^k)^T h^{\min } )}{\sum _{k=1}^{n_t} \left( (-A_{10} h_0^k)^T q^k - (d^k)^T h^{\min } \right) }, \end{aligned} \end{aligned}$$
(4)

(where \({h^{\min} \in \mathbbm{R}^{n_n}}\) represents the vector of minimum hydraulic heads) are generally preferred for the formulation of WDN optimization problems. Since both the numerator and denominator in (4) are affine functions of h and q, respectively, \(I_r\) is, in general, a linear fractional function of x.


Cost


Finally, the cost of a solution is defined as a linear function of the integer design variables \(x_{\mathcal {I}}=z\):

$$\begin{aligned} \begin{aligned} \text {cost} = c^Tz, \end{aligned} \end{aligned}$$
(5)

where, for \({l_j=1,\dots ,n_{\text {CNV}}+n_{\text {CNP}}}\), \(c_{l_j}\) represents the cost of installing a pressure control valve on link j, if \(j \in E_{\text {CNV}}\), or a pipe, if \(j \in E_{\text {CNP}}\).

Let \(X_0 \in \mathbb {R}^{n_{\mathcal {C}}+ n_{\mathcal {I}}}\) be the polyhedral set defined by the linear constraints (1a), (1b), (2), upper and lower bounds (12), and the big-M constraints (13)—see Appendix A. For any polyhedral set \({X \in \mathbb {R}^{n_{\mathcal {C}}+ n_{\mathcal {I}}}}\), we define the corresponding non-convex set \(X^{g,\mathcal {I}}\) such that \({X^{g,\mathcal {I}} = X^{g} \cap X^{\mathcal {I}}}\), where

$$\begin{aligned} \begin{aligned}&X^{g} = \{x \in X \mid g(x) \le 0\}, \\&X^{\mathcal {I}} =\{x \in X \mid x_\mathcal {I} \in \{0,1\}^{n_{\text {CNV}}+n_{\text {CNP}}} \}, \end{aligned} \end{aligned}$$
(6)

and \({g(x) \le 0}\) represents non-convex potential-flow coupling constraints (1c). The design-for-control problem with the objectives of jointly minimizing cost and AZP and maximizing \(I_r\) can then be written in compact form, for \(X=X_0\), as the non-convex multi-objective mixed-integer non-linear program  \(\text {MOMINLP}(X)\):

$$\begin{aligned} \begin{aligned}&\underset{x}{\text {minimize}}{} & {} f(x) \\&\text {subject to}{} & {} x \in X^{g,\mathcal {I}}, \end{aligned} \qquad \qquad \qquad (\text {MOMINLP}(X)) \end{aligned}$$

where \(f_j\), \({j=1,\dots ,m}\), represent the AZP (3), \(-I_r\) (4), and cost (5) objective functions.

We also introduce the sets \({X^{\hat{g},\mathcal {I}}= X^{\hat{g}} \cap X^{\mathcal {I}}}\), where \(X^{\hat{g}}\) is a polyhedral relaxation of \(X^{g}\) (see Appendix C), and \(X^{g,\hat{x}_{\mathcal {I}}} = X^{g} \cap X^{\hat{x}_{\mathcal {I}}}\), where, for \(\hat{x} \in X^{\mathcal {I}}\), \({X^{\hat{x}_{\mathcal {I}}} = \{x \in X \mid x_{\mathcal {I}} = \hat{x}_{\mathcal {I}} \}}\). Finally, let \(\text {MINLP}_{f_j}(X)\) be the single-objective problem minimizing \(f_j\) over \(X^{g,\mathcal {I}}\) and, for any non-linear objective function \(f_j\), \(j=1,\dots ,m\), let \(\hat{f}^X_j\) be a linear relaxation of \(f_j\) such that \({\hat{f}^X_j(x) \le f_j(x)}\) for all \(x \in X\) (see Appendix C).

3 Solution of \(\text {MOMINLP}(X)\)

Solving \(\text {MOMINLP}(X)\) requires identifying the set of solutions which represent the best trade-offs between the objective functions \(f_j\), \({j=1,\dots ,m}\), also called non-dominated set. As identifying the complete non-dominated set of non-convex MOMINLPs is generally intractable, it can be approximated with good feasible solutions, called potentially non-dominated solutions, and global bounds on their quality, or non-dominance.

3.1 Preliminary definitions

In order to solve \(\text {MOMINLP}(X)\), we are interested in identifying the set of non-dominated solutions representing the best trade-offs between the objectives \(f_j\), \({j=1,\dots ,m}\).

Definition 1

The image \(f(x^*)\) of a feasible solution \(x^*\) of \(\text {MOMINLP}(X)\) is non-dominated if there is no \(x \in X^{g,\mathcal {I}}\) such that \({f(x) \ne f(x^*)}\) and \({f_j(x) \le f_j(x^*)}\) for all \({j=1,\dots ,m}\). The set of non-dominated solutions is called non-dominated set or Pareto front of \(\text {MOMINLP}(X)\).

For two vectors \(y_1\) and \(y_2\) in \(\mathbbm {R}^m\), we say that \(y_1\) dominates \(y_2\) if \(y_1 \le y_2\), where the inequality sign is defined component-wise. Let \(Y_N\) denote the non-dominated set of \(\text {MOMINLP}(X)\), as given by Definition 1. In general, identifying the exact non-dominated set of a multi-objective problem is intractable. Instead, \(Y_N\) can be approximated with a subset of potentially non-dominated solutions.

Definition 2

(De Santis et al. (2020)) A finite subset \(\mathcal {F}\) of \(f(X^{g,\mathcal {I}})\) is a potentially non-dominated set of \(\text {MOMINLP}(X)\) if no element of \(\mathcal {F}\) dominates any other element of \(\mathcal {F}\).

A set where no element dominates any other element is called stable, and, by Defintion 2, any finite, stable subset of \(f(X^{g,\mathcal {I}})\) is a potentially non-dominated set of \(\text {MOMINLP}(X)\). To provide a good approximation of \(Y_N\), we are interested in computing a potentially non-dominated set with guarantees of \(\epsilon\)-non-dominance, where \(\epsilon > 0\) is a user-defined tolerance:

Definition 3

(Eichfelder et al. 2022) The point \(f(x^*)\) is \(\epsilon\)-non-dominated for \(\text {MOMINLP}(X)\), for \({x^* \in X^{g,\mathcal {I}}}\) and \(\epsilon > 0\), if there is no \(x \in X^{g,\mathcal {I}}\) such that \({f(x) \ne f(x^*)}\) and \(f(x) \le f(x^*) - \epsilon e\), where \(e=\mathbbm {1}^m\) denotes the m-by-1 vector of all ones.

Guarantees of \(\epsilon\)-non-dominance are derived by extending the global optimization notion of optimality bounds to bounding sets of \(Y_N\).

Definition 4

Let \({LB,UB \in \mathbbm {R}^m}\) be two non-empty, compact sets. We say LB and UB are lower and upper bounding sets of the non-dominated set \(Y_N\) of \(\text {MOMINLP}(X)\), respectively, if

$$\begin{aligned} Y_N \subset (LB+\mathbbm {R}^m_+) \cap (UB-\mathbbm {R}^m_+). \end{aligned}$$

Moreover, the width \(w^{UB}(LB)\) of the enclosure defined by LB with respect to UB is given by

$$\begin{aligned} \begin{aligned} \underset{y,t}{\max }\ \{t \in \mathbbm {R}_+ \mid y, y+te \in (LB+\mathbbm {R}^m_+) \cap (UB-\mathbbm {R}^m_+) \}. \end{aligned} \end{aligned}$$

We note that, given a potentially non-dominated set \(\mathcal {F}\) and a sufficiently large box \({Z = [\underline{z}, \bar{z} ]}\), such that \({\underline{z}< f(x) < \bar{z}}\) for all \({x \in X^{g,\mathcal {I}}}\) (where the inequality is defined component-wise), the uniquely determined local upper bounding set \({\text {lub}(\mathcal {F}) \subset Z}\) associated with \(\mathcal {F}\) (Eichfelder et al. 2021) represents an upper bounding set for \(Y_N\).

For \(\epsilon > 0\), \(\text {MOMINLP}(X)\) can then be solved to \(\epsilon\)-non-dominance by computing a potentially non-dominated set \(\mathcal {F}\) as well as a lower bounding set LB for the true Pareto front \(Y_N\) such that

$$\begin{aligned} \begin{aligned}&w^{\text {lub}(\mathcal {F})}(LB) < \epsilon . \end{aligned} \end{aligned}$$
(7)

By definition of LB and \(\text {lub}(\mathcal {F})\), condition (7) guarantees that there exists no solution \(f(x) \in Y_N\) such that \({f(x) \le f(x^*) - \epsilon e}\), \({\forall f(x^*) \in \mathcal {F}}\).

3.2 Multi-objective BB algorithm

In this section, we present a multi-objective BB algorithm to approximate the Pareto front of \(\text {MOMINLP}(X)\) with global guarantees of \(\epsilon\)-non-dominance. In particular, we propose an implementation of the general framework proposed by Eichfelder et al. (2022), where branching and lower bounding rules are defined based on successful strategies for the single-objective design-for-control of WDNs. Moreover, we describe an explicit procedure to update the potentially non-dominated and upper bounding sets \(\mathcal {F}\) and \(\text {lub}(\mathcal {F})\) as, due to the complex structure of the feasible set of \(\text {MOMINLP}(X)\), attainable solutions f(x), \({x \in X^{g,\mathcal {I}}}\), are generally not available otherwise.

Algorithm 1
figure a

Multi-objective BB algorithm

Full size image

The first step of the proposed algorithm consists in initializing the potentially non-dominated set \(\mathcal {F}\) and a list of active nodes \(\mathcal {L}_W\) such that, for \({(X,LB^X) \in \mathcal {L}_W}\), \(LB^X\) is a lower bounding set for the Pareto front of the subproblem \(\text {MOMINLP}(X)\) defined on X (Sect. 3.2.1). Then, while

  • the list of active nodes \(\mathcal {L}_W\) is not empty,

  • the time limit and/or maximum number of iterations have not been exceeded,

  • and the width of any active node in \(\mathcal {L}_W\) with respect to the incumbent set \(\mathcal {F}\) is greater than the user-defined tolerance \(\epsilon\),

the active node \((X,LB^{X})\) associated with the largest width \(w^{\text {lub}(\mathcal {F})}(LB^{X})\) is removed from \(\mathcal {L}_W\) (Sect. 3.2.2) and the polyhedral set X is split into subsets \(X_1\) and \(X_2\) (Sect. 3.2.3). The lower bounding sets for the Pareto fronts of the subproblems corresponding to the children nodes \((X_l,LB^{X_l})\), \(l=1,2\), are updated with respect to the incumbent set \(\mathcal {F}\) (Sect. 3.2.4). If \(LB^{X_l}\) is not dominated by \(\mathcal {F}\) (Sect. 3.2.5), integer feasible solutions computed during the lower bounding step are used to update the potentially non-dominated set (Sect. 3.2.6) and \((X_l,LB^{X_l})\) is stored in the list of active nodes, \(\mathcal {L}_W\). After verification of any of the termination conditions above, a last check removes from \(\mathcal {L}_W\) all active nodes \((X,LB^{X})\) dominated by the incumbent potentially non-dominated set \(\mathcal {F}\). The proposed framework is summarized by Algorithm 1, which includes references to the individual steps described in Sects. 3.2.1 to 3.2.6.

3.2.1 Initialization

To initialize the potentially non-dominated and lower bounding sets \(\mathcal {F}\) and \(LB^{X_0}\), we apply a single-objective spatial branch-and-bound algorithm (Pecci et al. 2018) to compute feasible solutions with global optimality bounds for the problems \(\text {MINLP}_{f_j}(X_0)\), minimizing the AZP, \(-I_r\) , and cost objectives \(f_j\). If \(\text {MINLP}_{f_j}(X_0)\) is infeasible for any \({j=1,\dots ,m}\), then \(\text {MOMINLP}(X_0)\) is infeasible and we have that \(\mathcal {F} = \emptyset\) and \(\mathcal {L}_W = \emptyset\). Otherwise, the solution of the single-objective problems returns the incumbent solutions \(x^*_{f_j} \in X_0^{g,\mathcal {I}}\), as well as lower bounds \(\underline{f}_j = f_j(\hat{x}^*_{f_j})\) over the feasible set \(X_0^{g,\mathcal {I}}\) such that \(\hat{x}^*_{f_j} \in X_0^{\hat{g},\mathcal {I}}\) and, for all \(j=1,\dots ,m\) and \(x \in X_0^{g,\mathcal {I}}\), \(\underline{f}_j \le f_j(x)\).

Solving the single-objective problems \(\text {MINLP}_{-f_j}(X_0)\) maximizing the AZP, \(-I_r\) , and cost objectives, we can also derive upper bounds \(\bar{f}_j\) on \(f_j\) such that, for all \({x \in X_0^{g,\mathcal {I}}}\), \(f_j(x) \le \bar{f}_j\). In the rest of this study, we consider the multi-objective WDN design-for-control problem \(\text {MOMINLP}(X)\) defined for the normalized AZP, \(-I_r\) , and cost objective functions \(f_j\):

$$\begin{aligned} f_j(x) {:}{=}\frac{f_j(x)-(\underline{f}_j-\delta _j)}{(\bar{f}_j+\delta _j)-(\underline{f}_j-\delta _j)}, \end{aligned}$$
(8)

where, for \(j=1,\dots ,m\), \(\delta _j\) is an arbitrarily small positive value guaranteeing that \({f_j(X_0^{g,\mathcal {I}}) \subseteq \text {int}([0, 1 ])}\). Note that the existence of a box \(Z \subset \mathbbm {R}^m\) such that \({f(X_0^{g,\mathcal {I}}) \subseteq \text {int}(Z)}\) is required to construct the local upper bounding sets \(\text {lub}(\mathcal {F})\) associated with a potentially non-dominated set \(\mathcal {F}\) (Eichfelder et al. 2021). The normalized objective values of the solutions \(x^*_{f_j}\), \({j=1,\dots ,m}\), are used to initialize the potentially non-dominated set \(\mathcal {F}\) while a lower bounding set for the Pareto front is given by \({LB^{X_0}=\delta \left( \mathbbm {R}^m_+ \right) }\), where \({\delta \left( \mathbbm {R}^m_+ \right) }\) represents the boundary of \(\mathbbm {R}^m_+\). The list of active nodes \(\mathcal {L}_W\) of the multi-objective BB algorithm can then be initialized with \((X_0,LB^{X_0})\). (This approach is adopted for the solution of the bi-objective problem instances presented in Sects. 4.1.1 and 4.2.1.)

In addition, any available information about the nature of problem \(\text {MOMINLP}(X)\) \(\text {MOMINLP}(X)\) or the structure of its Pareto front can be used to initialize \(\mathcal {F}\) and/or \(\mathcal {L}_W\) and improve the convergence of Algorithm 1 to a set of \(\epsilon\)-non-dominated solutions. For example, in each instance of the design-for-control problems considered in Sects. 4.1.2 and 4.2.2, there is a single integer solution with a minimum cost objective of \(0 \$\), i.e., \(x_{\mathcal {I}} = \mathbb {0}^{n_{\mathcal {I}}}\). Since big-M constraints (13) are tight for a fixed design \({x_{\mathcal {I}} \in X_0^{\mathcal {I}}}\), initializing the working list \(\mathcal {L}_W\) as

$$\begin{aligned} \mathcal {L}_W := \{ (X_0^*,LB^{X_0}),\ (X_0^{\mathbb {0}^{n_{\mathcal {I}}}},LB^{X_0}) \}, \end{aligned}$$
(9)

where \(X_0^* = \{ x \in X_0 \mid (\mathbb {1}^{n_{\mathcal {I}}})^T x_{\mathcal {I}} \ge 1 \}\), results in tighter non-dominance bounds on the non-dominated set of \(\text {MOMINLP}(X)\).

3.2.2 Node selection rule

Given a list of active nodes \(\mathcal {L}_W\) and set of potentially non-dominated solutions \(\mathcal {F}\), we define the width \(w^{\text {lub}(\mathcal {F})}(LB^{X})\) of a node \({(X,LB^{X}) \in \mathcal {L}_W}\) with respect to the local upper bounding set \(\text {lub}(\mathcal {F})\) as

$$\begin{aligned} \underset{(p,t) \in \text {lub}(\mathcal {F}) \times \mathbbm {R}_+}{\max } \{t \mid p-te \in (LB^{X}+\mathbbm {R}^m_+) \}. \end{aligned}$$
(10)

At any stage of the BB algorithm, the non-dominance gap with respect to \(\mathcal {F}\) associated with the current working list \(\mathcal {L}_W\) is then given by

$$\begin{aligned} \text {gap}\ = {\underset{(X,LB^{X}) \in \mathcal {L}_W}{\max } w^{\text {lub}(\mathcal {F})}(LB^{X})}. \end{aligned}$$
(11)

As a result, while \(\text {gap} \ge \epsilon\), the BB algorithm moves on to selecting and processing the active node \((X,LB^{X}) \in \mathcal {L}_W\) with the largest width \(w^{\text {lub}(\mathcal {F})}(LB^{X})\).

3.2.3 Branching and domain reduction

To ensure that the linear relaxations of \(\text {MOMINLP}(X_l)\) result in tight lower bounding sets \(LB^{X_l}\) for the children nodes \((X_l,LB^{X_l})\), \(l=1,2\), we adapt the successful spatial branching rule implemented by Pecci et al. (2018) to the multi-objective design-for-control of WDNs.

Given an active node \((X,LB^{X}) \in \mathcal {L}_W\), the corresponding lower bounding set \(LB^{X}\) is, by construction, an intersection of supporting hyperplanes of the Pareto front of \(\text {MOMINLP}(X)\) (see Sect. 3.2.4). As a result, for any local upper bound \(p \in \text {lub}(\mathcal {F})\), there exists a lower bounding hyperplane \(H^{\lambda _p,\hat{f}(\hat{x}_p)}\) defined by \(\lambda _p \in \mathbbm {R}^m\) and a vector \({\hat{x}_p=(\hat{z}_p,\hat{q}_p,\hat{h}_p,\hat{\eta }_p,\hat{\theta }_p) \in X^{\hat{g}}_0}\) such that

$$\begin{aligned} \begin{aligned}&\lambda _p^T (\ p - w^{p}(LB^{X})\ e\ ) = \lambda _p^T \hat{f}(\hat{x}_p). \end{aligned} \end{aligned}$$
(12)

In particular, the vector \(\hat{x}_p\) defining the distance \(w^{p}(LB^{X})\) between p and the lower bounding set \(LB^X\), which belongs to the set \(X_0^{\hat{g}}\), is not required to verify the non-convex potential-flow coupling constraints (1c). To efficiently tighten the relaxations of sets \(X_l^{g}\), \(l=1,2\), the polyhedral set X is split along the flow variable \(\hat{q}_{p^*}\) whose value in \(\hat{x}_{p^*}\) is associated with the largest violation of (1c), where \(p^* \in \text {lub}(\mathcal {F})\) is given by

$$\begin{aligned} w^{p^*}(LB^{X}) = w^{\text {lub}(\mathcal {F})}(LB^{X}). \end{aligned}$$
(13)

To further tighten the relaxations of the resulting children sets \(X_l^{g}\), \(l=1,2\), we also implement the optimization-based bound tightening procedure described in (Pecci et al. 2018,Algorithm 1).

3.2.4 Lower bounding

After branching on the polyhedral set X, the lower bounding sets of the children nodes \((X_l,LB^{X_l})\) are initialized to \(LB^{X}\). The next step then consists in tightening \(LB^{X_l}\), \({l=1,2}\). As the performance of the BB algorithm depends on the choice of an adequate lower bounding procedure, we propose to extend successful strategies implemented for the single-objective design-for-control of WDNs. Moreover, the adopted lower bounding procedure does not rely on ideal point estimates but directly makes use of the cuts proposed for convex MOMINLPs to speed up the search.

For a given node \((X,LB^X)\), De Santis et al. (2020) propose to tighten the lower bounding set \(LB^{X}\) with respect to local upper bounds \({p \in \text {lub}^{LB^X}(\mathcal {F}) = \text {lub}(\mathcal {F})} \cap (LB^{X}+\mathbbm {R}^m_+)\). However, for a given tolerance \(\epsilon\), only local upper bounds p such that \({w^{\{p\}}(LB^{X}) \ge \epsilon }\) prevent the BB algorithm from terminating with guarantees of \(\epsilon\)-non-dominance on the incumbent potentially non-dominated set \(\mathcal {F}\). Moreover, every lower bounding set update requires solving a relaxed LP and MILP (see below). To prevent redundant lower bound updates when the set \(\text {lub}(\mathcal {F})\) grows too large, we define the subset \(\text {lub}^{LB^X}(\mathcal {F})\) of local upper bounds with respect to which the lower bounding set \(LB^X\) is to be updated such that

$$\begin{aligned} \begin{aligned}&w^{\{p\}}(LB^{X}) \ge \epsilon \quad \text {and}\\&w^{\{p\}}(LB^{X}) \ge w^{\{p'\}}(LB^{X}),\\&\forall p' \in (\text {lub}(\mathcal {F}) \setminus \{p\}): \Vert p - p' \Vert _2 \le \delta _{LB}, \end{aligned} \end{aligned}$$
(14)

\(\forall p \in \text {lub}^{LB^X}(\mathcal {F})\), where \(\delta _{LB} \in [0,1 ]\) is a user-defined threshold representing the trade-off between the size of the BB search tree and the tightness of lower bounding set updates at every iteration. The best value for \(\delta _{LB}\) depends, in part, on the geometry of the Pareto front: in the case of a “flat" front, for instance, many redundant lower bounding set updates can be avoided by choosing a large value of \(\delta _{LB}\). In the numerical experiments presented in Sect. 4, we use a value of \(\delta _{LB} = 0.3\).

The lower bounding set \(LB^{X}\) is then first updated by solving the continuous problems:

$$\begin{aligned} \begin{aligned}&\underset{t,x}{\text {minimize}}{} & {} t \\&\text {subject to}{} & {} \hat{f}^X(x) \le p + t{\textbf {e}}, \\{} & {} &t \in \mathbbm {R},\ x \in X^{\hat{g}}, \\ \end{aligned}\qquad \qquad \qquad (\text {LP}_p(X)) \end{aligned}$$

parametrized by \({p \in \text {lub}^{LB^X}(\mathcal {F})}\). Let \((t_p,\hat{x}_p)\) be a (globally) optimal solution of \(\text {LP}_p(X)\) and \(\lambda _p\) the corresponding Lagrange multiplier associated with the constraint \({\hat{f}^X(x) \le p+te}\). The hyperplane \(H^{\lambda _p,\hat{f}^X(\hat{x}_p)}\) defined by

$$\begin{aligned} H^{\lambda _p,\hat{f}^X(\hat{x}_p)}=\{ y \in \mathbbm {R}^m \mid \lambda _p^T y = \lambda _p^T \hat{f}^X(\hat{x}_p) \} \end{aligned}$$
(15)

is a supporting hyperplane of \(f(X^{g,\mathcal {I}})\) (Löhne et al. 2014; Niebling and Eichfelder 2019). If \({t_p \ge 0}\) or if \(\hat{x}_p\) is integer feasible, \(H^{\lambda _p,\hat{f}(\hat{x}_p)}\) can be added to \(LB^{X}\) to improve the lower bounding set:

$$\begin{aligned} LB^{X} {:}{=}\delta \left( (LB^{X} + \mathbbm {R}^m_+) \cap (H^{\lambda _p,\hat{f}^X(\hat{x}_p)} + \mathbbm {R}^m_+) \right) . \end{aligned}$$
(16)

If \(t_p < 0\) and the solution \(\hat{x}_p\) of \(\text {LP}_p(X)\) is not integer feasible, however, tighter lower bounds can be derived by solving the mixed-integer linear program \(\text {MILP}_{\lambda _p}(X)\) parameterized by \(\lambda _p \in \mathbbm {R}^m\):

$$\begin{aligned} \begin{aligned}&\underset{x}{\text {minimize}}{} & {} \lambda _p^T \hat{f}^X(x)\\&\text {subject to}{} & {} x \in X^{\hat{g},\mathcal {I}}, \end{aligned}\qquad \qquad \qquad \qquad (\text {MILP}_{\lambda _p}(X)) \end{aligned}$$

If \(\text {MILP}_{\lambda _p}(X)\) is feasible, the lower bounding set \(LB^{X}\) can be improved by including the hyperplane \(H^{\lambda _p,\hat{f}^X(\hat{x}_p)}\), where \(\hat{x}_p = \text {argmin}\) \(\text {MILP}_{\lambda _p}(X)\), and integer feasible solutions \(\hat{x}_p \in X^{\hat{g},\mathcal {I}}\) are stored in \(\hat{\mathcal {X}}\). On the other hand, if either of the relaxed problems \(\text {LP}_p(X)\) or \(\text {MILP}_{\lambda _p}(X)\) is infeasible, node \((X,LB^{X})\) can be discarded. The lower bounding step is summarized by Algorithm 2 in Appendix D.

Note that, in order to compute a supporting hyperplane of the non-dominated set of \(\text {MOMINLP}(X)\), lower bounding problems \(\text {LP}_p(X)\) and \(\text {MILP}_{\lambda _p}(X)\)are defined over relaxations of the feasible set \(X^{g,\mathcal {I}}\) which do not require the verification of the potential-flow coupling constraints (1c). In particular, compared to the approach presented in De Santis et al. (2020), an explicit upper bounding procedure is required to compute feasible solutions of the WDN design-for-control problem and update the potentially non-dominated set \(\mathcal {F}\)—see Sect. 3.2.6.

3.2.5 Discarding test

Consider a set of potentially non-dominated solutions \(\mathcal {F}\) and an active node \({(X,LB^{X}) \in \mathcal {L}_W}\). Node \((X,LB^{X})\) can be discarded if

$$\begin{aligned} Y_N \cap \left( f(X^{g,\mathcal {I}})+ \mathbbm {R}_+^m \right) = \emptyset . \end{aligned}$$
(17)

However, condition (17) is hard to verify for \(\text {MOMINLP}(X)\), as \(X^{g,\mathcal {I}}\) is defined by mixed-integer and non-convex constraints. Instead, it is sufficient to check whether (Eichfelder et al. 2021)

$$\begin{aligned} \text {lub}(\mathcal {F}) \cap \left( LB^{X}+ \mathbbm {R}_+^m \right) = \emptyset . \end{aligned}$$
(18)

Condition (18), which consists in verifying whether the linear inequalities \({\lambda ^T p < \lambda ^T \hat{f}^X(\hat{x})}\) hold for all \({p \in \text {lub}(\mathcal {F})}\) and \(H^{\lambda ,\hat{f}^X(\hat{x})}\) in \(LB^X\), provides a more tractable discarding test. After branching on \((X,LB^X) \in \mathcal {L}_W\) and updating the lower bounding sets \(LB^{X_l}\), \(l=1,2\), children nodes \((X_l,LB^{X_l})\) for which condition (18) is not verified are added to the working list \(\mathcal {L}_W\).

3.2.6 Upper bounding

Previous global BB methods rely on the availability of attainable solutions to update the potentially non-dominated set \(\mathcal {F}\) (De Santis et al. 2020; Eichfelder et al. 2021, 2022). For non-convex problems with complex feasible sets such as \(\text {MOMINLP}(X)\), however, identifying an attainable solution can be hard. We implement a procedure (summarized in Appendix D by Algorithm 3) inspired by the leaf node solution presented in Cacchiani and D’Ambrosio (2017) to explicitly compute feasible solutions \({x \in X^{g,\mathcal {I}}}\). Instead of approximating the entire Pareto front of a leaf node by solving a sequence of scalarized problems given by a pre-defined distribution of weights, Algorithm 3 focuses on regions of the objective space where lower bounds \(LB^X\) on the potentially non-dominated set \(\mathcal {F}\) are loose.

Consider a node \((X,LB^X)\) with updated lower bounding set \(LB^X\) and the corresponding set of integer feasible solutions \(\hat{\mathcal {X}}\). If the lower bounding set \(LB^{X}\) is not dominated by the incumbent potentially non-dominated set \(\mathcal {F}\) and \(\hat{\mathcal {X}} \ne \emptyset\), the upper bounding procedure first solves, for each integer feasible solution \(\hat{x} \in \hat{\mathcal {X}}\) and objective function \(f_j\), \({j=1,\dots ,m}\), the non-convex problem \(\text {NLP}_{f_j,\hat{x}}(X)\) minimizing \(f_j\), subject to \({x \in X^{g,\hat{x}_{\mathcal {I}}}}\). In particular, let \(x^*_{f_j}\) be a (locally) optimal solution of \(\text {NLP}_{f_j,\hat{x}}(X)\).

For all local upper bounds p in the restricted set \(\text {lub}^{\hat{x}_\mathcal {I}}(\mathcal {F})\) defined such that

$$\begin{aligned}&f_j(x_{f_j}^*) \le p_j,\ \forall j=1,\dots ,m,\end{aligned}$$
(19a)
$$\begin{aligned}&w^{\{p\}}(LB) \ge \epsilon \quad \text {and}\end{aligned}$$
(19b)
$$\begin{aligned}&w^{\{p\}}(LB) > w^{\{p'\}}(LB),\nonumber \\&\forall p' \in (\text {lub}(\mathcal {F}) \setminus \{p\}): \Vert p - p' \Vert _2 \le \delta _{UB}, \end{aligned}$$
(19c)

where \(\delta _{UB} \in [0, 1 ]\) is a user-defined tolerance, the upper bounding procedure then solves the non-convex problem:

$$\begin{aligned} \begin{aligned}&\underset{t,x}{\text {minimize}}{} & {} t\\&\text {subject to}{} & {} f(x) \le p + t{\textbf {e}},\\{} & {} &t \in \mathbbm {R},\ x \in X^{g,\hat{x}_{\mathcal {I}}}. \end{aligned}\qquad \qquad \qquad \qquad (\text {NLP}_{p,\hat{x}}(X)) \end{aligned}$$

In particular, condition (19c) aims to prevent redundant updates when \(\text {lub}(\mathcal {F})\) grows too large. Unlike lower bounding set updates, however, an upper bounding set update only requires solving a non-linear program to local optimality. As a result, we use a value of \(\delta _{UB}=0.1\) in the numerical experiments presented in Sect. 4.

Finally, the locally optimal solutions \(x^*_{f_j}\), obtained for \(\text {NLP}_{f_j,\hat{x}}(X)\), \(j=1,\dots ,m\), and \(x^*_p\), obtained for \(\text {NLP}_{p,\hat{x}}(X)\), \(p \in \text {lub}^{\hat{x}_{\mathcal {I}}}(\mathcal {F})\), are iteratively compared to the incumbent potentially non-dominated set \(\mathcal {F}\). If they are dominated by any point in \(\mathcal {F}\), they are disregarded. Otherwise, they are added to \(\mathcal {F}\) (and all dominated points in \(\mathcal {F}\) are removed). The local upper bounding set \(\text {lub}(\mathcal {F})\) is updated accordingly, following the procedure described in Klamroth et al. (2015).

4 Application and results

The formulation proposed in Sect. 2 accommodates a wide range of design-for-control problems. In this section, we apply the proposed BB algorithm to the expansion of pescara (4.1) and the redesign of Net25 (4.2). We first consider the bi-objective problem for the minimization of AZP and maximization of \(I_r\), before investigating the joint minimization of cost. The BB algorithm is implemented in Matlab R2022a using a 2.60-GHz Intel® Core™ i7-10750 H CPU, with 16 GB of RAM and a 64-bit operating system. Continuous problems are solved using IPOPT (v3.12.9) (Wachter and Biegler 2006), called from the Matlab interface (Currie et al. 2012), and mixed-integer problems are solved using GUROBI.

In the absence of general-purpose solvers, we compare the BB algorithm against the scalarization approach proposed in Ulusoy et al. (2021) which, for an appropriate choice of settings (see Appendix E), can be shown to approximate the Pareto front of \(\text {MOMINLP}(X)\) with guarantees of \(\epsilon\)-non-dominance. The proposed algorithm is also compared against NSGA-II, which is commonly applied to WDN design and control problems (Maier et al. 2014). In this work, we use the Matlab function gamultiobj, called with a population size of 200 and for a maximum time of 18, 000s (5 hours). Moreover, the value of ParetoFraction is modified for every problem instance to ensure gamultiobj returns the same number of Pareto solutions as the BB algorithm.

All methods are initialized using anchor points computed with a tailored single-objective spatial branch-and-bound algorithm (Pecci et al. 2018). (The remaining individuals of the GA population are generated by the default gacreationuniform.) Finally, fitness and non-linear constraint evaluations in gamultiobj are performed using a null space solver (Abraham and Stoianov 2016) and a quadratic approximation of the H-W friction head loss equation. This ensures the solutions returned by NSGA-II and the proposed BB algorithm are comparable and eliminates the overhead associated with calls to the simulation tool EPANET (Rossman 2000)—see Jenks et al. (2023).

4.1 Expansion of pescara

The pescara network represents the reduced WDN of an Italian medium-size city (Bragalli et al. 2008). The original network model, defined for a single loading condition, counts 71 junctions, 3 reservoirs, and 99 pipes. Friction head losses are modeled according to the H-W equation. In this section, we investigate the network expansion problem which consists in simultaneously selecting valves and pipes for installation at candidate locations represented in Fig. 1, and optimizing the control settings of newly installed valves. In particular, 3 CNPs, with diameters 100, 150, and 200mm are considered for installation at each candidate link location and combinatorial constraints (2) limit the selection of CNPs to 1 per location. (The reader is referred to Ulusoy et al. (2021) or Appendix G for the physical characteristics, locations, and costs of individual CNVs and CNPs.)

4.1.1 Bi-objective problem

Fig. 2
figure 2

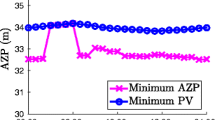
\(\epsilon\)-non-dominated (\(\epsilon =5 \cdot 10^{-2}\)) Pareto front approximation obtained with the proposed BB algorithm 1 and Pareto points returned by NSGA-II for the bi-objective expansion of pescara

Full size image

We first consider the network expansion problem for the joint minimization of AZP and maximization of \(I_r\). We approximate the Pareto front of the bi-objective problem with global bounds of \(\epsilon\)-non-dominance using the algorithm presented in Sect. 3.2.3. For the sake of brevity, we refer to Ulusoy et al. (2021) and Appendix F for a detailed discussion of the trade-off between AZP and \(I_r\), represented in Fig. 2.

Table 1 CPU time (in s) required to compute an \(\epsilon\)-non-dominated approximation of the Pareto front of \(\text {MOMINLP}(X)\) for the joint minimization of AZP and maximization of \(I_r\)
Full size table

The results in Table 1 show that, for the bi-objective expansion of pescara, the BB algorithm is 4–5 times faster than the scalarization method presented in Ulusoy et al. (2021). This is explained by the fact that the scalarization method requires to independently solve to global optimality a sequence of \(n_{\epsilon }=\lceil \frac{1}{\epsilon } \rceil\) problems (see Appendix E) which, despite sharing very similar structures, cannot make use of any previously derived lower bounding information. We note that, given the absence of steep segments or disconnected branches in the Pareto front represented in Fig. 2, more advanced approaches relying on adaptive parameter distributions (Kim and De Weck 2005) or grid generation techniques (Burachik et al. 2017, 2019) are unlikely to improve the performance of the scalarization method on this problem instance.

Next, we apply gamultiobj to the bi-objective network expansion problem. Figure 2 shows that the Pareto solutions returned by NSGA-II are similar to the set of \(\epsilon\)-non-dominated solutions computed using the BB algorithm for \({\epsilon =5\cdot 10^{-2}}\). While this is explained, in part, by the anchor points provided to initialize the GA population, we also expect the performance of the metaheuristic to benefit from specific properties of the problem instance, such as the small number of variables representing continuous control settings.

Finally, a posteriori analysis of the potentially non-dominated solutions in Fig. 2 shows that, at nearly \(173,000 \$\), the network configuration minimizing AZP is the most expensive solution of the Pareto front approximation, while the cheapest stands at just under \(99,000 \$\). In comparison, the cost of installation of a CNV in pescara ranges between \(17,500 \$\) and \({23,750 \$}\). In the next section, we investigate the trade-off between the operational objectives and the cost of design-for-control solutions.

4.1.2 Tri-objective problem

Next, we apply the proposed BB algorithm to solve the network expansion problem for the joint optimization of AZP and \(I_r\) and the minimization of cost. The marked knee in the resulting \(\epsilon\)-non-dominated Pareto front approximation (\({\epsilon = 10^{-1}}\)), represented in Fig. 3, shows that satisfactory trade-offs between the performance objectives can be achieved at much lower design cost than suggested by the results in 4.1.1. Consider, for instance, the solution associated with an AZP of 24.0m, a resilience index value of \(38 \%\) , and a design cost of over \(91,000\$\). Its performance is comparable to another which, at just under \(14,000\$\), allows to achieve AZP and resilience index values of 24.0m and \(37 \%\), respectively.

Fig. 3
figure 3

\(\epsilon\)-non-dominated (\(\epsilon =10^{-1}\)) Pareto front approximation obtained with the proposed BB algorithm for the tri-objective expansion of pescara (in 1615 s)

Full size image

Next, the BB algorithm is compared against gamultiobj. (Note that, in the tri-objective case, we cannot evaluate the performance of the scalarization method proposed in Ulusoy et al. (2021), since its generalization to problems with more than 2 objectives is not straightforward.) The lower bounding set LB returned by the proposed BB algorithm results in a \(28.9 \%\) non-dominance gap with respect to the Pareto points computed by NSGA-II, as the metaheuristic algorithm fails to explore the region of the objective space corresponding to low AZP values and design costs—see Fig. 8a and c in Appendix F.

While the parametrization of NSGA-II has not been extensively investigated in the WDN optimization literature and is not the focus of this study, Wang et al. (2019) suggest that population size is the single most important parameter when solving WDN design problems. Numerical experiments show that increasing the population size from 200 (twice the default value for mixed-integer problems in gamultiobj) to 500, however, does not significantly improve the spread of solutions returned by NSGA-II. This highlights the advantages of computing Pareto front approximations with global non-dominance bounds, as the Pareto optimal solutions returned by NSGA-II could lead a decision-maker to incorrectly believe, for instance, that the AZP in pescara cannot be reduced below 24m for less than \(61,250\$\) (while Fig. 3 shows that AZP values as low as 18m can be achieved for less than \(55,000\$\)).

4.2 DMA aggregation in Net25

Network sectorization, which consists in closing off boundary valves (BV) between district metered areas (DMA) to facilitate pressure management and leakage monitoring, is widespread in England and Wales. However, the practice affects the resilience of operational WDNs. In this section, we investigate a cost-efficient solution to improve the resilience of sectorized networks, which consists in aggregating DMAs by reopening closed BVs (Wright et al. 2015). The DMA aggregation problem is illustrated on the modified case study network Net25, which counts 3 reservoirs, 17 nodes, and 26 links, including 15 pipes, 3 existing PCVs, and 8 closed BVs, represented, in \(\text {MOMINLP}(X)\), by CNPs. In order to preserve the structure of the network, the aggregation of DMAs is limited to pairs by constraint (2)—see (Ulusoy et al. 2019, Appendix A). Finally, we consider 24 time steps representative of a day of operation and friction head losses are modeled by the H-W formula.

4.2.1 Bi-objective problem

Fig. 4
figure 4

\(\epsilon\)-non-dominated (\(\epsilon =5 \cdot 10^{-2}\)) Pareto front approximation obtained with the proposed BB algorithm 1 and Pareto points returned by NSGA-II for the bi-objective aggregation of DMAs in Net25

Full size image

First, we consider the DMA pairing problem for the joint minimization of AZP and maximization of \(I_r\), for which we compute a Pareto front approximation with bounds of \(\epsilon\)-non-dominance using the proposed BB algorithm. We refer to Ulusoy et al. (2021) and Appendix F for a detailed discussion of the trade-off between AZP and \(I_r\), represented, for \(\epsilon =5 \cdot 10^{-2}\), in Fig. 4.

We evaluate the performance of the proposed BB algorithm against the scalarization method proposed by Ulusoy et al. (2021). Table 1 shows that, while both methods efficiently compute an \(\epsilon\)-non-dominated set of the bi-objective problem for \({\epsilon =10^{-1}}\), the BB algorithm is nearly 4 times faster for \(\epsilon =5\cdot 10^{-2}\). Moreover, the lower bounding set returned by the proposed BB algorithm for \(\epsilon =5\cdot 10^{-2}\) results in a \(8.9\%\) non-dominance gap with respect to the Pareto points returned by gamultiobj (see Fig. 4), which are all dominated by the computed \(\epsilon\)-non-dominated set. (No improvement is observed after increasing the size of the GA population from 200 to 500 individuals.)

The performance of gamultiobj might be affected, in part, by the larger number of continuous decision variables involved in the formulation of the DMA aggregation problem, which requires deriving control settings for 3 PRVs over 24 different time steps. The size of the resulting search space represents a significant challenge for the application of evolutionary algorithms such as NSGA-II (Maier et al. 2014).

4.2.2 Tri-objective problem

Next, we approximate the Pareto front of the DMA aggregation problem for the joint optimization of AZP and \(I_r\) and minimization of cost with guarantees of \(\epsilon\)-non-dominance (\({\epsilon = 10^{-1}}\)) using the proposed BB algorithm. We assume all closed BVs require the same amount of resources to reopen and we use the number of selected CNPs as a surrogate measure of cost.

Fig. 5
figure 5

\(\epsilon\)-non-dominated (\(\epsilon =10^{-1}\)) Pareto front approximation obtained with the proposed BB algorithm for the tri-objective aggregation of DMAs in Net25 (in 159 s)

Full size image

While Fig. 5 shows that reopening BVs allows to increase \(I_r\) for a given AZP value by creating more efficient pathways, limited improvements are observed beyond 1 new CNP. The absence of more “expensive" non-dominated solutions in the range of lower AZP values, in particular, suggests that reopening more than 1 BV could have a detrimental effect on pressure management by reducing pressure control capabilities. As for the expansion of pescara, the Pareto front approximation guarantees that satisfactory trade-offs between the performance objectives can be achieved in Net25 at minimum cost.

Moreover, the lower bounding set LB computed by Algorithm 1 results in a \(18.7\%\) non-dominance gap with respect to the solutions returned by gamultiobj, which suggests a more linear trade-off between the network performance objectives—see Fig. 10a and b in Appendix F. For instance, consider the solution, returned by gamultiobj, which requires reopening 2 BVs to achieve an AZP value of 32.3m and a resilience index of \(63.7\%\). In comparison, the proposed BB algorithm identifies a solution requiring the creation of a single DMA pair which allows to reduce the AZP by nearly 2m while maintaining a resilience index of \(63.8\%\).

While additional heuristics and alternative settings might improve the performance of gamultiobj, the results highlight important limitations of NSGA-II, which can struggle to find representative sets of Pareto solutions for problems involving continuous variables. The proposed BB algorithm, on the other hand, provides global bounds on the true Pareto front of multi-objective WDN design-for-control problems, guaranteeing the \(\epsilon\)-non-dominance of computed Pareto front approximations.

5 Conclusion

This study investigates the solution of the DfC problem which consists in simultaneously installing new valves and/or pipes in existing WDNs and optimizing the control of new and existing valves. We consider the objectives of jointly minimizing pressure-induced leakage, maximizing network resilience, and minimizing design cost, resulting in the (non-convex) multi-objective mixed-integer non-linear program \(\text {MOMINLP}(X)\) for which, to the best of our knowledge, currently available solvers cannot return a Pareto front approximation with global bounds.

This study presents a BB algorithm based on the framework proposed by Eichfelder et al. (2022) to approximate the Pareto front of \(\text {MOMINLP}(X)\) with global bounds of \(\epsilon\)-non-dominance. In particular, we present tailored branching and lower bounding procedures based on successful strategies developed for the single-objective design-for-control of WDNs. Moreover, as feasible solutions of \(\text {MOMINLP}(X)\) can be hard to identify, we propose a procedure to efficiently update the upper bounding set which searches for feasible solutions in regions of the objective space where lower bounds on the potentially non-dominated set are looser.

The proposed algorithm is applied to the DfC of two case study networks, extending previous bi-objective formulations to investigate the trade-off between network resilience (\(I_r\)), pressure-induced leakage (AZP), and design cost. The marked knee in the Pareto front enclosures computed for the tri-objective problems guarantees that satisfactory network performance is achieved at a fraction of the cost of previously identified solutions for the bi-objective problems jointly minimizing AZP and maximizing \(I_r\).

Finally, the numerical experiments show that the proposed algorithm efficiently computes \(\epsilon\)-non-dominated approximations of the Pareto fronts of WDN design-for-control problems with 2 or more objectives, converging in less than 3 min in 3 out of 4 problem instances for \({\epsilon = 10^{-1}}\). These results suggest that the BB algorithm can be applied to the multi-objective DfC of large-scale operational WDNs. Even when convergence is not achieved, the algorithm provides global bounds allowing to identify gaps in the computed potentially non-dominated set. In comparison, NSGA-II can fail to return representative approximations of the Pareto front, while computing equivalent global guarantees with the scalarization method proposed in Ulusoy et al. (2021) is associated with up to a fivefold increase in computational effort.