Global optimality bounds for the placement of control valves in water supply networks

Abstract

This manuscript investigates the problem of optimal placement of control valves in water supply networks, where the objective is to minimize average zone pressure. The problem formulation results in a nonconvex mixed integer nonlinear program (MINLP). Due to its complex mathematical structure, previous literature has solved this nonconvex MINLP using heuristics or local optimization methods, which do not provide guarantees on the global optimality of the computed valve configurations. In our approach, we implement a branch and bound method to obtain certified bounds on the optimality gap of the solutions. The algorithm relies on the solution of mixed integer linear programs, whose formulations include linear relaxations of the nonconvex hydraulic constraints. We investigate the implementation and performance of different linear relaxation schemes. In addition, a tailored domain reduction procedure is implemented to tighten the relaxations. The developed methods are evaluated using two benchmark water supply networks and an operational water supply network from the UK. The proposed approaches are shown to outperform state-of-the-art global optimization solvers for the considered benchmark water supply networks. The branch and bound algorithm converges to good quality feasible solutions in most instances, with bounds on the optimality gap that are comparable to the level of parameter uncertainty usually experienced in water supply network models.

1 Introduction

The efficient management of hydraulic pressure in pipes results in reduction of leakage (Lambert 2000; Wright et al. 2015) and risk of pipe failure (Lambert and Thornton 2011), and it is therefore one of the main operational challenges in water supply networks (WSNs). Here we consider pressure management using pressure control valves, which regulate pressure at their outlet. We investigate the problem of simultaneously optimizing the placement and operational settings of control valves in WSNs, where the objective is to minimize average zone pressure (AZP). AZP is used as a surrogate measure for leakage. The problem formulation includes flows across network links and hydraulic heads at nodes as continuous decision variables. In addition, binary variables are introduced to model the placement of valves. Mass and energy conservation laws are enforced as optimization constraints, resulting in a nonconvex mixed integer nonlinear program (MINLP). The solution of process network optimization problems frequently relies on the solution of MINLPs. Some examples include synthesis of heat exchanger networks (Zamora and Grossmann 1998), multi-period blending (Kolodziej et al. 2013), optimal design and operation of gas networks (Pfetsch et al. 2015; Humpola and Fügenschuh 2015), and water supply networks (DAmbrosio et al. 2015). In the framework of WSNs, MINLP formulations are ubiquitous and employed in a variety of applications, ranging from optimal network design (Bragalli et al. 2012; Sherali et al. 1999) to pump scheduling (Menke et al. 2015; Gleixner et al. 2012).

Both heuristic and mathematical optimization methods were applied in previous work to solve the problem of optimal valve placement in water networks. Heuristic approaches based on genetic algorithms (GAs) have been widely used for solving the considered problem—see Reis et al. (1997), Araujo et al. (2006), Nicolini and Zovatto (2009), Liberatore and Sechi (2009), Ali (2015), De Paola et al. (2017). However, they present some limitations. Firstly, they can not guarantee optimality of the computed solutions, not even local optimality. Moreover, the number of objective function evaluations and hydraulic simulations required by these approaches grows rapidly with the size of the network, precluding the application of GAs when large operational water network are considered. Previous work has also investigated the application of mathematical optimization methods for the solution of the problem of optimal valve placement in WSNs—see Hindi and Hamam (1991), Eck and Mevissen (2012), Dai and Li (2014), Pecci et al. (2017a, b). Since the considered problem is nonconvex, approaches implemented in previous literature do not provide theoretical guarantees on the global optimality of the computed valve configuration.

This paper investigates mathematical optimization methods to generate a certified bound on the optimality gap of the computed solutions for the problem of optimal valve placement in WSNs, guaranteeing $\varepsilon$-sub-optimality. We formulate a branch and bound method, which is a common approach in global optimization. To the best of the authors knowledge, global optimization methods have not been previously applied to the problem of optimal valve placement in WSNs. Previous literature has investigated global optimization techniques for optimal design of WSNs (Sherali et al. 1999; Raghunathan 2013). However, when pipe diameters are fixed, hydraulic heads and flow rates are uniquely determined and can be found by solving a strictly convex optimization problem (Raghunathan 2013). As a result, in the case of optimal WSN design, it is sufficient to focus the branch and bound on integer decision variables. On the contrary, when optimal operation of water supply networks is considered, spatial branch and bound is needed (Gleixner et al. 2012). In the present manuscript, we consider the problem of optimal valve placement in WSNs, where locations and operational settings of the control valves need to be simultaneously optimized. Therefore, branching is required on both continuous and integer variables.

The implemented branch and bound algorithm relies on a sequence of lower and upper bounds to the optimal value of the nonconvex MINLP in study—for a general review see Tawarmalani and Sahinidis (2002). Since all convex constraints within the problem formulation for optimal valve placement are linear, it is particularly convenient to generate lower bounds using linear relaxations of the nonconvex constraints (Tawarmalani and Sahinidis 2002, Chapter 4). The nonconvexity of MINLPs arising in the framework of water networks is due to the absolute power functions representing friction energy losses within the system’s conservation laws—see Eq. (2a). Analogous nonconvex expressions have previously been studied in other engineering frameworks, where linear relaxations were formulated—see Humpola and Fügenschuh (2015), Gleixner et al. (2012), Liberti and Pantelides (2003), Tawarmalani and Sahinidis (2002), Udell and Boyd (2015), Vigerske (2012). We define linear relaxations of the nonconvex equality constraints considered here by extending the formulation proposed in Liberti and Pantelides (2003) for monomials of odd degree. Such linear relaxations define an outer approximation of the convex envelopes of the nonconvex equality constraints. We investigate the use of different number of linearizations for the outer approximation. The strength of the linear relaxations depends on the diameter of the decision variables’ domain (Puranik and Sahinidis 2017). Therefore, we implement a domain reduction procedure, based on the solution of a series of linear programs (LPs). The proposed approach takes advantage of the underlying network structure to reduce the number of linear programming solves. Benefits and limitations of the developed methods are evaluated using two benchmark water networks, and a large-scale operational network from the UK. Moreover, the numerical results show that the proposed approach outperforms state-of-the-art global optimization solvers for the considered benchmark water networks. The branch and bound framework has enabled the convergence to $\varepsilon$-sub-optimal solutions for the problem of optimal valve placement, with bounds on the optimality gap comparable to the order of parameter and data uncertainties inherent in operational network models.

2 Problem formulation

A water supply network with $n_0$ water sources, $n_n$ demand nodes and $n_p$ pipes, is modelled as a directed graph with $n_n+n_0$ nodes and $n_p$ edges. The operation of a network is considered under $n_l$ different demand conditions during the diurnal cycle. The nodal demands are denoted by $d^t \in {\mathbb {R}}^{n_n}$, while known hydraulic heads at water sources are indicated by $h_0^t \in {\mathbb {R}}^{n_0}$, for each $t=1,\ldots ,n_l$. Furthermore, the vector of node elevations is represented by $\zeta \in {\mathbb {R}}^{n_n}$. Given $t \in \{1,\ldots ,n_l\}$, we consider hydraulic heads $h^t \in {\mathbb {R}}^{n_n}$ and flow rates $q^t \in {\mathbb {R}}^{n_p}$ as continuous decision variables. Moreover, vector $\eta ^t \in {\mathbb {R}}^{n_p}$ is included to model the unknown head loss introduced by the action of pressure control valves. We introduce auxiliary variables $\theta ^t \in {\mathbb {R}}^{n_p}$ to isolate the nonconvex terms representing the friction head losses occurring within the pipes of a network. These can be expressed by either the Hazen-Williams (HW) or Darcy-Weisbach (DW) formulae. Since both friction head loss formulae involve non-smooth nonconvex terms, it is convenient to use smooth quadratic approximations, computed over a range of flow (Pecci et al. 2017c). When a suitable quadratic approximation has been determined, it can be written as $\phi _j(q^t_j)=q_j^t(a_j|q_j^t|+b_j)$, with $a_j \ge 0$ and $b_j\ge 0$, for all $j=1,\ldots ,n_p$ and $t=1,\ldots ,n_l$—see also Eq. (28) in Appendix 1.

In this work, we investigate the optimal placement and operation of pressure control valves to minimize average zone pressure (AZP), defined as:

$$\begin{aligned} \frac{1}{{n}_{l}W}\sum _{t=1}^{n_l}w^T (h^{t}-\zeta ) \end{aligned}$$

(1)

where $w_i:=\sum _{j \in I_{(i)}}\frac{L_j}{2}$ and I(i) is the set of indices for links incident at node i, $L_j$ is the length of pipe j and $W =\sum _{i=1}^{n_n}w_i$ is a normalisation factor.

The optimization of valve placement and operation to minimize AZP is primarily subject to conservation energy (2b) and mass (2c) laws:

$$\begin{aligned} \theta ^t&=\varPhi (q^t), \quad t=1,\ldots n_l, \end{aligned}$$

(2a)

$$\begin{aligned} A_{12}h^t+A_{10}h^t_0+\eta ^t+\theta ^t&=0, \quad t=1,\ldots ,n_l \end{aligned}$$

(2b)

$$\begin{aligned} A_{12}^Tq^t-d^t&=0, \quad t=1,\ldots , n_l, \end{aligned}$$

(2c)

where matrices $A_{12} \in {\mathbb {R}}^{n_p \times n_n}$ and $A_{10} \in {\mathbb {R}}^{n_p\times n_0}$ are edge-node incidence matrices for unknown and known head nodes, respectively. Moreover, we define the vector of friction head losses as $\varPhi (q^t):=[\phi _1(q^t_1) \ldots \phi _{n_p}(q^{t}_{n_p})]^T$.

We consider vectors of binary variables $z^+, z^- \in \{0,1\}^{n_p}$ with the following properties:

• $z^+_j=1 \Leftrightarrow$ there is a valve on link j in the assigned positive flow direction

• $z^-_j=1 \Leftrightarrow$ there is a valve on link j in the assigned negative flow direction

• $z^+_j=z^-_j=0 \Leftrightarrow$ there is no valve on link j

• $z^+_j+z^-_j \le 1$ prevents the placement of two valves on the same link.

The placement of control valves in a WSN is modelled by big-M constraints, ensuring that additional head losses have the same direction as flows and friction head losses across the valves. The following constant vectors and matrices are used to formulate the big-M constraints. Given a vector of maximum allowed velocities across network pipes $v^{\text {max}} \in {\mathbb {R}}^{n_p}$, let $q_L^t=-Sv^{\text {max}}$, and $q^t_U=Sv^{\text {max}}$, where $S:=\mathbf{diag }({\pi D_1^2}/{4},\ldots ,{\pi D_{n_p}^2}/{4})$, with $D \in {\mathbb {R}}^{n_p}$ vector of pipe diameters. Let $Q^t_L:=\mathbf{diag }(q^t_L)$, and $Q^t_U:=\mathbf{diag }(q^t_U)$. Moreover, set $\theta ^t_L:=\varPhi (q^t_L)$, $\theta ^t_U:=\varPhi (q^t_U)$, $\varTheta ^t_L:=\mathbf{diag }(\theta ^t_L)$, and $\varTheta ^t_U:=\mathbf{diag }(\theta ^t_U)$. Minimum and maximum allowed hydraulic heads at nodes are specified by $h^t_{\text {min}},h^t_{\text {max}} \in {\mathbb {R}}^{n_n}$, respectively. Define $\eta ^t_L \in {\mathbb {R}}^{n_p}$ ad $\eta ^t_U \in {\mathbb {R}}^{n_p}$ as follows:

$$\begin{aligned} \begin{aligned} (\eta ^t_L)_k&:=(h^t_{\text {min}})_i - (h^t_{\text {max}})_j, \quad \forall i\xrightarrow {k} j \\ (\eta ^t_U)_k&:=(h^t_{\text {max}})_i - (h^t_{\text {min}})_j, \quad \forall i\xrightarrow {k} j \end{aligned} \end{aligned}$$

(3)

and set $N^t_L:=\mathbf{diag }(\eta ^t_L)$, $N^t_U:=\mathbf{diag }(\eta ^t_U)$. We formulate the following constraints:

$$\begin{aligned} \eta ^t- N_U^t z^+&\le 0, \quad t=1,\ldots , n_l \end{aligned}$$

(4a)

$$\begin{aligned} -\eta ^t + N_L^t z^-&\le 0,\quad t=1,\ldots , n_l \end{aligned}$$

(4b)

$$\begin{aligned} -q^t -Q^t_L z^+&\le -q^t_L, \quad t=1,\ldots , n_l\end{aligned}$$

(4c)

$$\begin{aligned} q^t+Q^t_U z^-&\le q^t_U, \quad t=1,\ldots , n_l \end{aligned}$$

(4d)

$$\begin{aligned} -\theta ^t - \varTheta ^t_Lz^+&\le -\theta ^t_L, \quad t=1,\ldots , n_l\end{aligned}$$

(4e)

$$\begin{aligned} \theta ^t + \varTheta ^t_Uz^-&\le \theta ^t_U, \quad t=1,\ldots ,n_l. \end{aligned}$$

(4f)

Let $n_v$ be the number of valves to be installed. The desired properties of the binary variables are enforced by the linear constraints:

$$\begin{aligned}&z^+ + z^-\le {\mathbf {1}}_{{n_p}\times 1} \end{aligned}$$

(5a)

$$\begin{aligned}&\sum _{j=1}^{{n_p}} (z^+_j+z^-_j) = n_v\end{aligned}$$

(5b)

$$\begin{aligned}&z^+,z^- \in \{0,1\}^{n_p}. \end{aligned}$$

(5c)

Finally, physical and operational bounds on all continuous variables are enforced by the following constraints:

$$\begin{aligned} q^t_L&\le q^t \le q^t_U, \quad t=1,\ldots ,n_l \end{aligned}$$

(6a)

$$\begin{aligned} \theta ^t_L&\le \theta ^t \le \theta ^t_U, \quad t=1,\ldots ,n_l \end{aligned}$$

(6b)

$$\begin{aligned} \eta ^t_L&\le \eta ^t \le \eta ^t_U, \quad t=1,\ldots ,n_l \end{aligned}$$

(6c)

$$\begin{aligned} h^t_{\text {min}}&\le h^t \le h^t_{\text {max}},\quad t=1,\ldots ,n_l. \end{aligned}$$

(6d)

The valve placement optimization problem can be written in a compact form as:

$$\begin{aligned} \text {minimize}&\quad \frac{1}{n_lW}\sum _{t=1}^{n_l}w^T (h^t-\zeta )\\ \text {subject to}&\quad {\theta ^t-\varPhi (q^t) =0, \quad \forall t \in \{1,\ldots ,n_l\} \quad (2a)} \\&\quad (q,h,\eta ,\theta ,z^+,z^-)\in \text {F}(Q), \qquad \qquad \qquad \qquad \qquad (\text {MINLP}(Q)) \end{aligned}$$

where $q:=(q^t)_{t=1,\ldots ,n_l}$, $h:=(h^t)_{t=1,\ldots ,n_l}$, $\eta :=(\eta ^t)_{t=1,\ldots ,n_l}$, $\theta :=(\theta ^t)_{t=1,\ldots ,n_l}$. Furthermore, $\text {F}(Q) \subset {\mathbb {R}}^{n_ln_p} \times {\mathbb {R}}^{n_ln_n} \times {\mathbb {R}}^{n_ln_p} \times {\mathbb {R}}^{n_l n_p} \times \{0,1\}^{n_p} \times \{0,1\}^{n_p}$ is the set defined by (2b)–(6d), which depends on $Q:=\{q^t_L,q^t_U\}_{t=1,\ldots ,n_l}$. Problem $\text {MINLP}(Q)$ is a mixed integer nonlinear program (MINLP). Furthermore, the equality constraints (2a) are nonconvex, hence the problem formulation results in a nonconvex MINLP.

3 Solution method

The nonconvexity of $\text {MINLP}(Q)$ is due to the presence of functions $(\phi _j(\cdot ))_{j=1,\ldots ,n_p}$ within equality constraints (2a). Since the other constraints (2b)–(6d) are linear, it is convenient to consider linear relaxations of constraints (2a). Polyhedral relaxations for similar nonconvex expressions have been previously studied by Humpola and Fügenschuh (2015), Gleixner et al. (2012), Liberti and Pantelides (2003), Tawarmalani and Sahinidis (2002), Udell and Boyd (2015), Vigerske (2012). In this paper, linear relaxations developed in Liberti and Pantelides (2003) for monomials of odd degree are extended to the nonconvex equality constraints within the problem formulation for optimal valve placement in WSNs.

We implement a branch and bound method that relies on the generation of a sequence of lower and upper bounds to the optimal value. The present work takes a similar approach to Misener and Floudas (2013, 2014) and compute lower bounds solving Mixed Integer Linear Programming (MILP) relaxations of $\text {MINLP}(Q)$. As discussed in Smith and Pantelides (1999), MILP relaxations result in tighter lower bounds then relaxed linear programs (LPs) and the algorithm is expected to converge in less iterations. However, they also require an higher computational effort for each branch and bound iteration. Nonetheless, as shown in the numerical results reported in Sect. 4, the implementation of state-of-the-art MILP solvers (e.g. Gurobi Optimization 2017) have enabled the application of the considered method to large problem instances.

3.1 Lower bounding MILP

Let $Q'=\{(q^t_L)',(q^t_U)'\}_{t=1,\ldots ,n_l}$ such that $q^t_L \le (q^t_L)' \le (q^t_U)' \le q^t_U$, for all $t \in \{1,\ldots ,n_l\}$. We consider the following restriction of $\text {MINLP}(Q)$:

$$\begin{aligned} \text {minimize}&\quad \frac{1}{n_lW}\sum _{t=1}^{n_l}w^T (h^t-\zeta )\\ \text {subject to}&\quad \theta ^t-\varPhi (q^t) =0, \quad \forall t \in \{1,\ldots ,n_l\} \\&\quad (q,h,\eta ,\theta ,z^+,z^-)\in \text {F}(Q'), \qquad \qquad \qquad \qquad (\text {MINLP}(Q')) \end{aligned}$$

where $\text {F}(Q') \subset {\mathbb {R}}^{n_ln_p} \times {\mathbb {R}}^{n_ln_n} \times {\mathbb {R}}^{n_ln_p} \times {\mathbb {R}}^{n_l n_p} \times \{0,1\}^{n_p} \times \{0,1\}^{n_p}$ is the set defined by (2b)–(6d) using the bounds in $Q'$. Let $y^*(Q')$ be the optimal value of $\text {MINLP}(Q')$. In the following, we formulate a MILP relaxation of $\text {MINLP}(Q')$, which yields a lower bound $\text {L}(Q') \le y^*(Q')$.

A detailed derivation of linear relaxations of (2a) is presented in Appendix 1, where the formulation for monomials of odd degree proposed by Liberti and Pantelides (2003) is extended to functions $(\phi _j(\cdot ))_{j\in \{1,\ldots ,n_p\}}$. Such linear relaxations can be written as

$$\begin{aligned} R^t q^t + E^t \theta ^t \le r^t, \quad t=1,\ldots ,n_l \end{aligned}$$

(7)

for suitable matrices $R^t$ and $E^t$, and vectors $r^t$, which depend on $(q^t_L)'$, $(q^t_U)'$, and a parameter $N_c \ge 0$ used to control the number of linearizations for the outer approximation of the convex envelopes of constraints (2a)—see Appendix 1. In Section 4, we investigate the effect of different number of linearizations on the convergence properties of the branch and bound algorithm. Using the above linear relaxations, it is possible to define the following MILP relaxation of $\text {MINLP}(Q')$:

$$\begin{aligned} \text {minimize}&\quad \frac{1}{n_lW}\sum _{t=1}^{n_l}w^T (h^t-\zeta )\\ \text {subject to}&\quad R^tq^t + E^t\theta ^t \le r^t, \quad \forall t \in \{1,\ldots ,n_l\}\\&\quad (q,h,\eta ,\theta ,z^+,z^-)\in \text {F}(Q'),\qquad \qquad \qquad \qquad (\text {MILP}(Q')) \end{aligned}$$

Let $\text {L}(Q')$ be the optimal value of $\text {MILP}(Q')$. If $\text {MILP}(Q')$ is infeasible, then $\text {MINLP}(Q')$ is infeasible and we have $\text {L}(Q')=y^*(Q')=+\infty$. Otherwise, the solution of $\text {MILP}(Q')$ yields a lower bound $\text {L}(Q') \le y^*(Q')$. Moreover, if the current best lower bound $\text {LB}$ is available, set $\text {L}(Q')\leftarrow \max (\text {L}(Q'),\text {LB})$.

3.2 Generation of upper bounds

Let $Q'=\{(q^t_L)',(q^t_U)'\}_{t=1,\ldots ,n_l}$ a set of bounds on flow variables as in Sect. 3.1. Recall that $y^*(Q')$ denotes the optimal value of $\text {MINLP}(Q')$. If $\text {MILP}(Q')$ is infeasible, then set $U(Q'):=+\infty$. Otherwise, let ${\hat{z}}^+,{\hat{z}}^- \in \{0,1\}^{n_p}$ be solution of $\text {MILP}(Q')$. We compute an upper bound to $y^*(Q')$ by fixing $z^+={\hat{z}}^+$ and $z^-={\hat{z}}^-$ in $\text {MINLP}(Q')$. The resulting optimization problem is a nonconvex nonlinear program (NLP):

$$\begin{aligned} \text {minimize}&\quad \frac{1}{n_lW}\sum _{t=1}^{n_l}w^T (h^t-\zeta )\\ \text {subject to}&\quad \theta ^t-\varPhi (q^t) =0, \quad \forall t\in \{1,\ldots ,n_l\}\\&\quad (q,h,\eta ,\theta ,{\hat{z}}^+,{\hat{z}}^-) \in \text {F}(Q'). \qquad \qquad \qquad \qquad \qquad (\text {NLP}(Q')) \end{aligned}$$

If $\text {NLP}(Q')$ is infeasible, set $\text {U}(Q'):=+\infty$. On the contrary, any (local) solution yields an upper bound $\text {U}(Q')\ge y^*(Q')$.

The generation of a valid upper bound via the (local) solution of a nonlinear program is often computationally expensive, particularly when large problem instances are considered. However, $\text {NLP}(Q')$ presents a high level of sparsity, that is retained by constraints (2b) and (2c) from the sparse structure of water supply networks. As a consequence, sparse NLP solvers offer scalable solution approaches for $\text {NLP}(Q')$—see the interior point method introduced in Waechter and Biegler (2006).

3.3 Domain reduction

The strength of the MILP relaxations is expected to have a significant impact on the convergence properties of branch and bound schemes (Belotti et al. 2009). This is confirmed by the numerical results reported in Sect. 4. As discussed in Appendix 1, in the case considered here, smaller ranges of flows lead to tighter relaxations. Therefore, we investigate pre-processing strategies to reduce the domains of the flow variables, focusing on Optimization Based Bound Tightening (OBBT), which relies on the solution of a series of optimization problems to tighten upper and lower bounds on selected variables—for a recent review on variable bound tightening approaches see Puranik and Sahinidis (2017).

In order to highlight the separable structure of the feasible set of $\text {MINLP}(Q)$ with respect to the time indices, we introduce the time indexed sets $\{G^t(Q)\}_{t=1,\ldots ,n_l}$ such that $G^t(Q) \in {\mathbb {R}}^{n_p} \times {\mathbb {R}}^{n_n} \times {\mathbb {R}}^{n_p} \times {\mathbb {R}}^{n_p}\times \{0,1\}^{n_p}\times \{0,1\}^{n_p}$ is defined by

$$\begin{aligned} (q^t,h^t,\eta ^t,\theta ^t,u_1^t,u_2^t) \in G^t(Q) \, \forall t \in \{1,\ldots ,n_l\} \, \Leftrightarrow (q,h,\eta ,\theta ,z^+,z^-) \in F(Q) \end{aligned}$$

(8)

where $z^+=u_1^t$ and $z^-=u_2^t$, for all $t \in \{1,\ldots ,n_l\}$, and $q=(q^t)_{t=1,\ldots ,n_l}$, $h=(h^t)_{t=1,\ldots ,n_l}$, $\eta =(\eta ^t)_{t=1,\ldots ,n_l}$, $\theta =(\theta ^t)_{t=1,\ldots ,n_l}$. By definition of $\{G^t(Q)\}_{t=1,\ldots ,n_l}$, the feasible set of $\text {MINLP}(Q)$ is equivalent to the feasible set of the following problem:

$$\begin{aligned} \text {minimize}&\quad \frac{1}{n_lW}\sum _{t=1}^{n_l}w^T (h^t-\zeta ) \nonumber \\ \text {subject to}&\quad \theta ^t - \varPhi (q^t) =0, \quad \forall t \in \{1,\ldots ,n_l\}\nonumber \\&\quad \left( q^t,h^t,\eta ^t,\theta ^t,u_1^t,u_2^t\right) \in G^t(Q), \quad \forall t \in \{1,\ldots ,n_l\}\nonumber \\&\quad u_1^t-z^+={\mathbf {0}}_{{n_p}\times 1}, \quad \forall t \in \{1,\ldots ,n_l\}\nonumber \\&\quad u_2^t-z^-={\mathbf {0}}_{{n_p}\times 1}, \quad \forall t \in \{1,\ldots ,n_l\}. \end{aligned}$$

(9)

Let ${\sigma \in \{-1,1\}}$, $t \in \{1,\ldots ,n_l\}$, and $j \in \{1,\ldots ,n_p\}$. Consider the mixed integer linear program:

$$\begin{aligned} \text {minimize}&\quad \sigma q^t_j\nonumber \\ \text {subject to}&\quad R^lq^l + E^l\theta ^l \le r^l, \quad \forall l \in \{1,\ldots ,n_l\}\nonumber \\&\quad \left( q^l,h^l,\eta ^l,\theta ^l,u_1^l,u_2^l\right) \in G^l(Q), \quad \forall l \in \{1,\ldots ,n_l\} \nonumber \\&\quad u_1^l-z^+={\mathbf {0}}_{{n_p}\times 1}, \quad \forall l \in \{1,\ldots ,n_l\}\nonumber \\&\quad u_2^l-z^-={\mathbf {0}}_{{n_p}\times 1}, \quad \forall l \in \{1,\ldots ,n_l\}. \end{aligned}$$

(10)

where $R^l$, $E^l$ and $r^l$ represent the linear relaxations of (2a) computed using the flow bounds in Q as described in Appendix 1. The feasible set of Problem (10) is a relaxation of the set of feasible solutions of Problem (9). Tightening upper and lower bounds on the flow variables would require the solution of $2n_ln_P$ mixed integer linear programs analogous to (10). Mixed integer linear programs can be solved by state-of-the-art MILP solvers (Gurobi Optimization 2017). However, the dimension of Problem (10) and the number of problems to be solved can pose significant computational challenges when considering large-scale water networks. Therefore, the remainder of this section investigates tailored strategies to reduce the computational effort required by the considered domain reduction procedure.

Firstly, Problem (10) is converted into a linear program (LP) by replacing $G^t(Q)$ with a valid polyhedral relaxation $\widehat{G^t(Q)}$. Furthermore, the resulting LP can be decoupled with respect to the time indices $l \in \{1,\ldots ,n_l\}$, omitting the consistency constraints in Problem (10). For each $t \in \{1,\ldots ,n_l\}$ and $j \in \{1,\ldots ,n_p\}$, we consider the following relaxation of Problem (10):

$$\begin{aligned} \text {minimize}&\quad \sigma q^t_j\\ \text {subject to}&\quad R^tq^t + E^t\theta ^t \le r^t \\&\quad (q^t,h^t,\eta ^t,\theta ^t,u_1^t,u_2^t) \in \widehat{G^t(Q)}\qquad \qquad \qquad \qquad \qquad (\text {LP}_{Q}^{\sigma ,t,j}) \end{aligned}$$

The OBBT method solves $\text {LP}_{Q}^{1,t,j}$ to compute a new lower bound $(q^t_L)_j^{'}\ge {q^t_L}_j$, and $\text {LP}_{Q}^{-1,t,j}$ to obtain $(q^t_U)_j^{'} \le {q^t_U}_j$. If $Q'$ is the resulting set of bounds, then $\text {MINLP}(Q')$ and $\text {MINLP}(Q)$ have the same optimal solution. Further domain reductions are achieved by iteratively applying the described process. In order to reduce the number of flow variables whose bounds are tightened through the solution of linear programs, we exploit the underlying network (graph) structure of $\text {LP}_{Q}^{\sigma ,t,j}$. In what follows, few graph-theoretical definitions for WSNs are reviewed. The degree of an unknown head node in a WSN graph is defined as the number of links connected to the node. We define a tree in a WSN graph as an acyclic connected subgraph such that at least one of its unknown head nodes has degree one, and only one of its nodes is connected to either a looped part of the network or to a fixed head node (Deuerlein 2008). Such a unique node of a given tree is called its root node. The forest of a water network is defined as the disjoint union of all trees in the network (Deuerlein 2008). The part of the network which is not contained in the forest but includes the roots of all the trees is called core. If a link belongs to the forest of a network graph, its flow is uniquely determined by the demand assigned to the adjacent forest nodes (Elhay et al. 2014). As a consequence, flows across forest links do not depend from the optimization process and their values are fixed. The forest-core decomposition of a WSN graph can be implemented using the algorithm presented in Elhay et al. (2014).

In the bound tightening approach proposed here, upper and lower bounds on flow variables corresponding to forest links are set a priori. Then, let core links $j_1$ and $j_2$ be connected in series through a node i. For each $t \in \{1,\ldots ,n_l\}$, flow variables in $\text {LP}_{Q}^{\sigma ,t,j}$ are subject to the following mass conservation laws:

$$\begin{aligned} A_{12}(j_1,i)q^t_{j_1}+A_{12}(j_2,i)q^t_{j_2}=d^t_i, \quad \forall t \in \{1,\ldots ,n_l\}. \end{aligned}$$

(11)

Hence:

$$\begin{aligned} {q^t_{j_2}=A_{12}(j_2,i)d^t_i-A_{12}(j_2,i)A_{12}(j_1,i)q^t_{j_1}}, \quad \forall t \in \{1,\ldots ,n_l\}. \end{aligned}$$

(12)

Given a sequence of core links connected in series, it is possible to select one link as representative and derive relations analogous to (12) for all other links in the sequence, proceeding by substitution. Let ${\mathscr {C}} \subset \{1,\ldots ,n_p\}$ be a subset of indices corresponding to network’s links belonging to the core, where a unique representative for each sequence of links have been selected. An illustrative example of the definition of ${\mathscr {C}}$ for a simple network model is included in Appendix 2.

The proposed strategy is to perform OBBT only for those flow variables whose indices are in ${\mathscr {C}}$ and then propagate the bounds to the remaining core links using relations analogous to (12). Algorithm 1 is implemented for iterative domain reduction on the flow variables in $\text {MINLP}(Q)$. Such iterative method can fail to converge to a fixed point in finite time (Puranik and Sahinidis 2017). Therefore, Algorithm 1 is terminated when the progress in the domain reduction is not significant or when the maximum number of iterations is reached. Given a possible choice of lower and upper bounds $Q'=\{(q^t_L)',(q^t_U)'\}$, define:

$$\begin{aligned} \mathbf{diam} (Q'):= \max _{\begin{array}{c} t=1,\ldots ,n_l \\ j=1,\ldots ,n_p \end{array}}((q^t_U)'_j-(q^t_L)'_j). \end{aligned}$$

(13)

The analytical study of the number of iterations required to generate tight variable bounds represents an open research problem (Puranik and Sahinidis 2017). Therefore, the maximum number of iterations in Algorithm 1 is set to 10 based on empirical experience. The number of linear programming solves at each iteration of Algorithm 1 is $2n_l|{\mathscr {C}}|$, where $|{\mathscr {C}}|$ is expected to be significantly smaller than $n_p$ when operational water networks with a relatively low number of loops are considered. Furthermore, the for-loops within Algorithm 1 can be executed in parallel, as each iteration does not depend from the others.

3.4 Branch and bound algorithm

Let $Q^{\text {init}}$ be the set of initial lower and upper bounds on flow variables. It can either be $Q^{\text {init}}=Q$ or $Q^{\text {init}}=Q^{\text {tight}}$, where $Q^{\text {tight}}$ represents tightened lower and upper bounds on flow variables resulting from Algorithm 1. We denote by $y^*=y^*(Q)$ the optimal value of $\text {MINLP}(Q)$. Then, by definition, $y^*=y^*(Q^{\text {init}})$. The branch and bound method iteratively generates a hierarchy of optimization problems, starting from $\text {MINLP}(Q^{\text {init}})$, represented by a binary tree named branch and bound tree. In particular, the algorithm creates a partition of $\text {F}(Q^{\text {init}})$ given by $\{\text {F}(Q') \; | \; Q' \in {\mathscr {Q}} \}$ such that

$$\begin{aligned} \min _{Q' \in {\mathscr {Q}}} \text {L}(Q') \le y^* \le \min _{Q' \in {\mathscr {Q}}} \text {U}(Q') \end{aligned}$$

(14)

As standard in branch and bound methods, the proposed algorithm starts by computing lower and upper bounds to $y^*$—this is iteration 0. Then, the root problem $\text {MINLP}(Q^{\text {init}})$ is branched into two optimization problems—see Sect. 3.5. After branching, the algorithm computes lower and upper bounds on the two descendant problems as outlined in Sects. 3.1 and 3.2, respectively. The best upper and lower bounds are updated as necessary. Finally, a new problem from the branch and bound tree is selected for branching and the iteration is repeated. The method stops when a termination criterion is met and its implementation is described in Algorithm 2. The output of the algorithm is either an $\varepsilon$-sub-optimal solution to $\text {MINLP}(Q)$ or a feasible solution with a certified bound on the optimality gap greater than $\varepsilon$.

The computed optimality gaps should be considered within the range of uncertainties that are inherent in modelling of operational water networks. As discussed in Wright et al. (2015), pressure control in operational water networks is subject to multiple sources of data and modelling errors. These include the stochastic nature of customer demand, uncertainty in the hydraulic model parameters, network connectivity, measurements accuracy, and factors affecting the physical operation of control and isolation valves.

Remark 1

If $Q' \in {\mathscr {Q}}$ is such that $\text {L}(Q')>\text {UB}$, then the global optimum cannot belong to $\text {F}(Q')$ and $\text {MINLP}(Q')$ can be pruned from the branch and bound tree. However, the selection strategy implemented in Algorithm 2 implies that the branch and bound iterations will terminate before $Q'$ is selected for branching. Therefore, the method does not explicitly implement a pruning procedure.

3.5 Branching strategy

Let $\text {MINLP}(Q^b)$ be a problem in the branch and bound tree such that

$$\begin{aligned} \text {L}(Q^b)=\min _{Q' \in {\mathscr {Q}}}\text {L}(Q') \end{aligned}$$

(15)

Branching $\text {MINLP}(Q^b)$ into two descendant problems $\text {MINLP}(Q^{\text {left}})$ and $\text {MINLP}(Q^{\text {right}})$ is equivalent to partitioning $\text {F}(Q^b)$ into two sets $\text {F}(Q^{\text {left}})$ and $\text {F}(Q^{\text {right}})$. A good branching strategy should aim to improve the lower bound (i.e. $\text {L}(Q^{\text {left}})\ge \text {L}(Q^b)$ and $\text {L}(Q^{\text {right}})\ge \text {L}(Q^b)$), and maintain a balanced branch and bound tree (Belotti 2013, Section 5.3.1). A branch and bound tree is said balanced if all problems in the tree are similarly difficult to solve. In this work, the following branching rule is implemented.

Branching rule Let $Q^b:=\{(q^t_L)^b,(q^t_U)^b\}_{t=1,\ldots ,n_l}$ and $({\hat{q}},{\hat{h}},{\hat{\eta }},{\hat{\theta }},{\hat{z}}^+,{\hat{z}}^-)\in \text {F}(Q^b)$ be a solution of $\text {MILP}(Q^b)$. Define indices $(l,k) \in \{1,\ldots ,n_l\}\times \{1,\ldots ,n_p\}$ such that

$$\begin{aligned} {\hat{\theta }}^{l}_{k}-\phi _{k}\left( {\hat{q}}^{l}_{k}\right) =\max _{\begin{array}{c} t=1,\ldots ,n_l \\ j=1,\ldots ,n_p \end{array}}|{\hat{\theta }}^t_j-\phi _j({\hat{q}}^t_j)|. \end{aligned}$$

(16)

Let $Q^{\text {left}}:=\{(q^t_L)^{\text {left}},(q^t_U)^{\text {left}}\}_{t=1,\ldots ,n_l}$ and $Q^{\text {right}}:=\{(q^t_L)^{\text {right}},(q^t_U)^{\text {right}}\}_{t=1,\ldots ,n_l}$ be as follows:

$$\begin{aligned} \left( q^t_L\right) ^{\text {left}}_j&:=(q^t_L)^b_j, \quad \forall (t,j) \in \{1,\ldots ,n_l\} \times \{1,\ldots ,n_p\} \end{aligned}$$

(17)

$$\begin{aligned} \left( q^t_U\right) ^{\text {left}}_j&:=(q^t_U)^b_j, \quad \forall (t,j) \in \{1,\ldots ,n_l\} \times \{1,\ldots ,n_p\} \setminus (l,k)\end{aligned}$$

(18)

$$\begin{aligned} \left( q^t_L\right) ^{\text {right}}_j&:=(q^t_L)^b_j, \quad \forall (t,j) \in \{1,\ldots ,n_l\} \times \{1,\ldots ,n_p\} \setminus (l,k)\end{aligned}$$

(19)

$$\begin{aligned} \left( q^t_U\right) ^{\text {right}}_j&:=(q^t_U)^b_j, \quad \forall (t,j) \in \{1,\ldots ,n_l\} \times \{1,\ldots ,n_p\} \end{aligned}$$

(20)

$$\begin{aligned} \left( q^{l}_U\right) ^{\text {left}}_{k}&:={\hat{q}}^{l}_{k} \quad \; \; \; \end{aligned}$$

(21)

$$\begin{aligned} \left( q^{l}_L\right) ^{\text {right}}_{k}&:={\hat{q}}^{l}_{k}\quad \; \; \; \end{aligned}$$

(22)

Then, define of $\text {F}(Q^{\text {left}})$ and $\text {F}(Q^{\text {right}})$ using the bounds on flow variables contained in $Q^{\text {left}}$ and $Q^{\text {right}}$.

The above branching strategy improves the lower bound, by definition of the linear relaxations given in Appendix 1. In fact, the formulation of $\text {MILP}(Q^{\text {left}})$ and $\text {MILP}(Q^{\text {right}})$ requires the inclusion of linear inequalities corresponding to the polyhedral relaxations computed with the new bounds on variable $q^{l}_{k}$. Such refined linear relaxations are exact at ${\hat{q}}^{l}_{k}$ resulting in tighter MILP relaxations. If ${\hat{q}}^l_k$ is too close to either $(q^l_L)^b_k$ or $(q^l_U)^b_k$, the implemented branching strategy can result in an unbalanced branch and bound tree. However, the relaxation error $|{\hat{\theta }}^t_j-\phi _j({\hat{q}}^t_j)|$ is larger the more distant ${\hat{q}}^t_j$ is from $(q^t_L)^b_j$ and $(q^t_U)^b_j$, see Fig. 11. As a result, in most cases, ${\hat{q}}^l_k$ is expected to be closer to the middle point of the interval $[(q^t_L)^b_k,(q^t_U)^b_k]$ than to its extremes.

4 Results and discussion

In this section, the developed methods are evaluated using two benchmark network models, and a large operational water supply network from the UK. The corresponding problem sizes are reported in Table 1. All experiments presented below were conducted within MATLAB 2016b-64 bit for Windows 7, installed on a 2.50 GHz Intel Xeon(R) CPU E5-2640 0 with 12 Cores and 12 GB of RAM. The MILPs and LPs involved in Algorithms 1 and 2 are solved using GUROBI (v7.5) (Gurobi Optimization 2017), which is accessed via its MATLAB interface. In addition, all iterations in Algorithm 1 were executed in series, and GUROBI was forced to operate on a single-thread; all other parameters in GUROBI are set to their default values. Local solutions to the upper bounding NLPs considered in Sect. 3.2 are computed using IPOPT (v.3.12.6) (Waechter and Biegler 2006), accessed in MATLAB via an interface of the OPTI Toolbox (Currie and Wilson 2012). In the implementation of IPOPT, sparse gradients and Jacobians are directly supplied to the solver, in order to take advantage of the very sparse structure of our problem. The global optimization solvers BARON (v18.8.23) (Klnç and Sahinidis 2018) and SCIP (v3.2.1) (Gamrath et al. 2016) were implemented for the direct solution of the considered nonconvex MINLPs. The solver SCIP is accessed in MATLAB via an interface provided by OPTI Toolbox and relies on SoPLEX (v221) as linear solver and IPOPT (v3.12.6) as nonlinear solver. In our implementation, we accessed BARON via its MATLAB interface, and used IBM ILOG CPLEX (v12.8) as linear solver, while BARON was allowed to select the nonlinear solver according to its dynamic strategy (Sahinidis 2018). Finally, we set $\varepsilon =10^{-6}$, $\text {MaxIter}=+\infty$, and define $\texttt{Gap}:=100\cdot \frac{UB-LB}{LB}$.

Table 1 Problem size of the 3 case studies

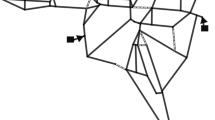
Firstly, we consider PescaraNet, a reduced model of the water supply network for the city of Pescara (Bragalli et al. 2012). The network’s layout is presented in Fig. 1a. This network model has 68 demand nodes, 99 pipes and 3 water sources. Moreover, friction head losses are modelled using the HW formula. In this case, the formulation of $\text {MINLP}(Q)$ includes a single demand condition and results in a relatively small size nonconvex MINLP whose characteristics are reported in Table 1. This water network has been already considered in Eck and Mevissen (2013) where a local optimization method was applied for computing optimal valve locations in PescaraNet. However, Eck and Mevissen (2013) did not include details on upper and lower bounds of flow variables, which precludes a direct comparison with the solutions obtained here. In the present implementation, maximum allowed velocity in each pipe is set to 2 (m/s) and minimum required pressure at each node to 19 (m). For every link $j \in \{1\ldots ,n_p\}$, a quadratic head loss approximation $\phi _j(\cdot )$ is defined as in Pecci et al. (2017c).

Fig. 1

Benchmark network models. a Layout of PescaraNet. b Layout of Net25

The second case study is named Net25. This benchmark network model has been used to evaluate solution approaches for optimal valve placement problems in previous literature using heuristics (Reis et al. 1997; Araujo et al. 2006; Liberatore and Sechi 2009; Nicolini and Zovatto 2009; Ali 2015; De Paola et al. 2017) and mathematical optimization methods (Eck and Mevissen 2012; Dai and Li 2014; Pecci et al. 2017a, b). The results presented in this section allow the quantification of the level of sub-optimality of valve configurations for Net25 previously computed using heuristics and local optimization methods. The network has 22 nodes, 37 pipes and 3 reservoirs—see Fig. 1b. Details on pipes’ characteristics, nodal demands and reservoirs’ levels are presented in Jowitt and Xu (1990) and Dai and Li (2014). The hydraulic model of Net25 uses the HW formula to model friction head losses. We observe that Net25 has a smaller dimension with respect to PescaraNet; nonetheless, it results in a larger nonconvex MINLP as the problem formulation considers 24 demand conditions, one for each hour of the day—see Table 1. Moreover, we set the maximum allowed velocity in each pipe to 1 (m/s) and the minimum pressure at each node to 30 (m). Analogously to what done for PescaraNet, for each link j, a quadratic approximation of the friction losses $\phi _j(\cdot )$ is computed as proposed in Pecci et al. (2017c).

The developed methods are tested for optimizing the placement of 1 to 5 control valves in both PescaraNet and Net25, where the objective to be minimized is AZP. In these experiments, we set a time limit of 7200 (s). Given $\delta >0$, let $\rho (\delta )$ be the percentage of problems with remaining $\texttt {Gap}$ smaller or equal than $\delta$, defined as

$$\begin{aligned} \rho (\delta ):= 100 \frac{\Big \{\# \text { instances with }{} \texttt {Gap} \le \delta \text { at termination}\Big \}}{\# \text { test problems}}. \end{aligned}$$

(23)

For the purpose of this numerical study, we consider a uniform distribution of values of $\delta$ between 0 and 100, spaced by $10^{-4}$. Let $N_c \ge 0$ be the parameter controlling the number of linearizations for the outer approximation of the convex envelopes of constraints (2a) - see Appendix 1. In the following, the symbol $\text {BB}_{N_c}$ indicates the implementation of Algorithm 2 where the polyhedral relaxations (7) are computed as detailed in Appendix 1. When Algorithm 1 is implemented as pre-processing routine to reduce the domain of the flow variables, the combination of Algorithms 1 and 2 is denoted by $\text {dBB}_{N_c}$. Moreover, in order to ensure a total maximum computational time of 7200 (s), the value of $T_{\max }$ in Algorithm 2 is adjusted to account for the time spent in Algorithm 1.

Initially, we evaluate the performance of $\text {BB}_{N_c}$ with $N_c \in \{0,1,3,5\}$. The complete numerical results are reported in Tables 2, 3, 4, 5, 6, 7, 8, and 9 of Appendix 3. When no domain reduction is applied, the solutions computed after 7200 (s) by $\text {BB}_{N_c}$ are within $10\%$ of optimality, for all $N_c \in \{0,1,3,5\}$. However, in the case of Net25, the obtained valve placements for $n_v \in \{3,4,5\}$ differ from the best-known solutions for the case study, with respect to those reported in Eck and Mevissen (2012), Dai and Li (2014), Pecci et al. (2017a), Pecci et al. (2017b). As shown in Fig. 2a, the inclusion of more linearizations for the outer approximation of the convex envelope of (2a) improves the convergence properties of the branch and bound algorithm with respect to $\text {BB}_0$. In addition, we observe that algorithms $\text {BB}_{1}$, $\text {BB}_3$, and $\text {BB}_5$ had similar performances. However, only $\text {BB}_1$ terminated in all instances with a Gap smaller than $7 \%$.

Fig. 2

Comparison of different number of linearizations for the outer approximation of the convex envelopes of (2a), with and without the application of domain reduction. a Performance of the branch and bound algorithm for different values of $N_c \in \{0,1,3,5\}$. b Performance of the branch and bound algorithm with the application of domain reduction for different values of $N_c \in \{0,1,3,5\}$

We investigate the implementation of algorithms $\text {dBB}_{N_c}$, with $N_c \in \{0,1,3,5\}$, for solving the considered optimal valve placement problems in PescaraNet and Net25. Firstly, Algorithm 1 was applied to tighten the flow variable bounds, for each $N_c \in \{0,1,3,5\}$. When considering PescaraNet, the implementation of Algorithm 1 required the solution of 656 LPs in the case of $n_v=1$ and $N_c=0$. In comparison, the domain reduction procedure required the solution of 492 LPs in all the other cases. The average computational time required to run Algorithm 1 in PescaraNet is 18 (s)—see Tables 10, 12, 14, 16 for more details. The application of Algorithm 1 as domain reduction procedure for Net25 required the solution of 5568 LPs for each $n_v \in \{1,\ldots ,5\}$ and $N_c \in \{0,1,3,5\}$, and an average computational time of 58 (s)—see Tables 11, 13, 15, 17. Algorithm 2 was then applied to the problem formulations with tightened bounds on the flow variables. The results are summarised in Tables 10, 11, 12, 13, 14, 15,  16, 17. As shown in Fig. 2b, in most instances, the solutions computed by $\text {dBB}_{N_c}$ are within $5\%$ of optimality, for all $N_c \in \{0,1,3,5\}$. Moreover, all the computed feasible solutions for Net25 equal the best-known valve locations obtained for the considered case study with respect to those reported in Eck and Mevissen (2012), Dai and Li (2014), Pecci et al. (2017a, b). According to these numerical results, the implementations of $\text {dBB}_{N_c}$ with $N_c >0$ have better computational performance than $\text {dBB}_0$.

In order to further investigate the effect of the domain reduction procedure on the convergence properties of Algorithm 2, we compare the implementation of the branch and bound algorithm with and without tightening the bounds on flow variables. As shown in Figs. 3, the domain reduction procedure significantly improved the performance of the branch and bound method for the considered problems of optimal valve placement in PescaraNet and Net25, irrespectively of the number of linearizations used. Furthermore, as shown in Fig. 4, the implementation of $\text {dBB}_0$ achieves better performance than the direct applications of branch and bound algorithm with $N_c \in \{1,3,5\}$. These results suggest that, for these benchmark water networks, increasing the number of linearizations improves the branch and bound ability to reduce the optimality gap, but not as much as the implementation of the developed domain reduction procedure. Furthermore, all the numerical experiments show rapid convergence of the algorithms to the final feasible solution and the associated optimality gap. As examples, Fig. 5 reports the progress of $\text {dBB}_0$ and $\text {dBB}_1$ when solving the problems of optimal placement of 3 valves on PescaraNet and Net25, respectively. In particular, it shows that good quality (if not optimal) solutions are computed early in the algorithm, while the remaining iterations are mostly used to improve the lower bounds.

Fig. 3

Comparisons between implementations of the branch and bound algorithm with and without the application domain reduction as pre-solving routine

Fig. 4

Comparison between the combination of Algorithms 1 and 2 with $N_c=0$, and the direct implementation of Algorithm 2 with $N_c \in \{1,3,5\}$

Fig. 5

Progress of $\text {dBB}_0$ and $\text {dBB}_1$ when applied to the problems of optimal placement of 3 valves in PescaraNet and Net25. a Progress of $\text {dBB}_0$ on PescaraNet for $n_v=3$. b Progress of $\text {dBB}_1$ on PescaraNet for $n_v=3$. c Progress of $\text {dBB}_0$ on Net25 for $n_v=3$. d Progress of $\text {dBB}_1$ on Net25 for $n_v=3$

In conclusion, we compare the performance of $\text {dBB}_5$ with state-of-the-art global optimization solvers SCIP and BARON for the solution of the considered nonconvex MINLPs. A time limit of 7200 (s) was set for all solvers. All other options in BARON and SCIP are set to their default values. As reported in Tables 18 and 19, BARON failed to produce a feasible solution in all instances except one. These results are in line with the numerical experiments reported in Misener and Floudas (2014), where both SCIP (v3.0) and BARON (v12.7.2) failed to generate feasible solutions for the majority of test problems related to optimal design of WSNs—see Tables 40 and 41 in the supplementary material to Misener and Floudas (2014). Tables 20 and 21 show that SCIP has failed to find a feasible solution only for the problem of optimal placement of 5 valves in Net25. However, in most instances, SCIP resulted in a $\texttt {Gap}$ larger than $5\%$. Furthermore, the majority of the feasible solutions computed by SCIP differ from the best-known solutions for Net25, which are reported in Pecci et al. (2017a) and were computed by the convex MINLP solver BONMIN (Bonami et al. 2008). Results reported in Tables 16, 17, 18, 19, 20, 21 show that the lower bounds computed by $\hbox {dBB}_5$ are tighter than those obtained by BARON and SCIP, in all instances. As illustrated in Fig. 6, after two hours of computations, the developed branch and bound method consistently results in smaller optimality gaps than the two state-of-the-art solvers.

Fig. 6

Comparison between the combination of Algorithms 1, and 2 with $N_c=5$ and two state-of-the-art global optimization solvers

4.1 Case study 3: BWFLnet

Finally, the proposed global optimization method for optimal valve placement has been applied to BWFLnet, the network model of the Smart Water Network Demonstrator (Field Lab) operated by Bristol Water, InfraSense Labs at Imperial College London and Cla-Val (Wright et al. 2014). This water supply network consists of 2310 nodes, 2369 pipes and 2 inlets (with fixed known hydraulic heads); its graph is presented in Fig. 7. The HW formula is used to model friction losses within BWFLnet.

Fig. 7

Layout of BWFLnet

The size of BWFLnet is two orders of magnitude larger than the other considered benchmark WSNs. In BWFLnet, the network’s operator has already installed three automatic pressure control valves and two boundary control valves, which are optimally controlled in order to minimize AZP (Wright et al. 2015). In the problem formulation for optimal valve placement in BWFLnet, we model the three pressure control valves as open smooth pipes. Moreover, details on the operation of the two boundary valves have been provided by the valves’ manufacturer. The daily demand profiles in BWFLnet include 96 different demand conditions, one every 15 minutes. However, the problem of optimal valve placement and operation in BWFLnet under 96 different demand conditions would result in a large MINLP with 227, 424 nonconvex constraints. In order to limit the problem size, $\text {MINLP}(Q)$ is formulated on BWFLnet using only three most relevant demand conditions, which were selected to capture network’s typical daily operational conditions at low night time demand, morning peak demand, and afternoon dip—see Fig. 8a. The AZP values computed using a problem formulation restricted to these 3 demand conditions are expected to be close to those obtained for a full set of 96 different demand conditions—this is confirmed to be the case for BWFLnet, as shown in Tables 24 and 26.

Fig. 8

Total network demand pattern and maximum velocities achieved in simulation in BWFLnet. a Total demand profile for BWFLnet. The circles correspond to the three time steps selected in this study. b Maximum velocity achieved in simulation across each link

Note that the highest impact in terms of AZP reduction will be achieved by controlling pressure through pipes carrying large quantity of water, hence links with small diameters are not likely to be good candidates for control valve placement. As a consequence, links in BWFLnet whose diameter is smaller than 100 (mm) are discarded from the set of candidate valve locations. The minimum allowed pressure at all demand nodes is set to 18 (m), while this value is relaxed to zero for nodes with no demand. A quadratic approximation of friction losses is computed as discussed in Pecci et al. (2017c). The size of the resulting MINLP is shown in Table 1.

Multiple simulations of BWFLnet, with no installed valves, under different demand conditions, show that the maximum velocities achieved across network pipes do not exceed 3 (m/s)—see Fig. 8b. In view of Fig. 8b, for most pipes, feasible velocities are expected to be significantly smaller than 3 (m/s). As a consequence, when upper and lower bounds on the flow variables are based on a maximum allowed velocity of 3 (m/s) for all pipes, the polyhedral relaxations (7) are not expected to be tight, leading to loose MILP relaxations—see also the discussion in Appendix 1. In order to tighten the polyhedral relaxations (7) and avoid unnecessarily large flow bounds, we define a tailored maximum allowed velocity for each link. It is known that the placement of control valves can result in velocity changes across network links (Abraham et al. 2018). In order to limit the possibility of discarding optimal solutions from the feasible set, we implement the following heuristic. Given a link $j \in \{1,\ldots ,n_p\}$, let $\nu ^{\text {sim}}_j$ be the maximum velocity achieved in simulation under multiple demand conditions. If $\nu ^{\text {sim}}_j\le 1 \, (\frac{m}{s})$, then the optimized velocities across link j are allowed to exceed $\nu ^{\text {sim}}_j$ by at least a factor of two. In comparison, for links where the simulated velocities achieved higher rates, the allowed increment is more limited. The implemented strategy is detailed in the following:

$$\begin{aligned} v^\text {max}_j:={\left\{ \begin{array}{ll} 1 &{} \text {if }0 \le \nu ^{\text {sim}}_j<0.5\\ 2 &{} \text {if } 0.5 \le \nu ^{\text {sim}}_j<1.0\\ 2.5 &{} \text {if } 1.0 \le \nu ^{\text {sim}}_j<2.0\\ 3 &{} \text {if } 2.0 \le \nu ^{\text {sim}}_j <3.0,\\ \end{array}\right. } \end{aligned}$$

(24)

Then, $\text {MINLP}(Q)$ was formulated on BWFLnet using tailored maximum velocities to define upper and lower bounds on flow variables Q. We consider the optimal placement of 1 to 5 control valves in BWFLnet. In the numerical experiments reported in this section, we set a time limit $T_{\max }=86{,}400$ (s) (1 day). We investigate the direct application of Algorithm 2 with $N_c \in \{0,3\}$, without implementing the domain reduction procedure. The results are summarised in Tables 22 and 23. In the case of $N_c=0$, the relative optimality gap obtained for $n_v \in \{1,2,3\}$ are larger than $30 \%$. No feasible solution was found after a day of computations for $n_v \in \{4,5\}$. Including more linearizations for the outer approximation of the convex envelopes of (2a) results in small improvements for the cases of $n_v\in \{1,2\}$, while no feasible solution was obtained when $n_v \in \{3,4,5\}$—see Table 23.

Then, the domain reduction procedure described in Algorithm 1 was applied as pre-processing reoutine to tighten the flow variable bounds within the formulation of $\text {MINLP}(Q)$ on BWFLnet. In this case, the fraction of links involved in LP solves corresponds to less than the $10\%$ of the whole set of network links. Such reduction is due to the structure of BWFLnet, a typical water network from the United Kingdom, where a considerable portion of links belongs to the forest. Moreover, hydraulic models of operational networks often present sequences of links connected in series, used to model the existence of different customer connections along network pipes. As a result, the proposed graph-theory based decomposition has significantly reduced the computational cost associated with Algorithm 1, which required the solution of 2532 LPs for each case of $n_v=1,\ldots ,5$. In the numerical experiments reported here, such LPs were solved sequentially. As a result, Algorithm 1 required roughly one hour of CPU time, in all instance—see Tables 24 and 25. However, as previously observed, the LPs solved at each iteration of Algorithm 1 do not depend on each other. Therefore, in a practical implementation, they can be solved in parallel, exploiting the existence of multiple computational cores.

Algorithm 1 was then applied to $\text {MINLP}(Q^{\text {tight}})$, with $N_c \in \{0,3\}$—see Tables 24 and 25. When $N_c=0$, the bounds on the absolute optimality gaps obtained for $n_v\in \{1,2,3\}$ are between 3 and 5 (m)—see also Fig. 9. Optimality bounds of such magnitude are comparable to the order of uncertainty affecting pressure control in BWFLnet (Wright et al. 2015). Hence, the quality of the computed feasible solutions is considered to be acceptable. Again, in the cases of $n_v \in \{4,5\}$, no feasible solution was found before reaching the time limit. Similar optimality gaps were obtained when $N_c=3$, but the algorithm failed to compute a feasible solution for $n_v \in \{3,4,5\}$. These results suggest that the inclusion of different number of linearizations for the outer approximation of the convex envelopes of (2a) did not improve the performance of the branch and bound algorithm for solving the problem of optimal valve placement in BWFLnet.

We observe that the feasible solutions computed with and without domain reduction are the same. However, as shown in Fig. 9, the application of Algorithm 1 has significantly improved the quality of the lower bounds computed by the branch and bound algorithm. Nonetheless, the optimality gaps reported in Table 24 are too wide to be reduced within the prescribed time limit, even if the domain reduction routine is applied. The numerical results show that, in all problem instances, most pipes in BWFLnet experience low velocities, which are significantly smaller than their expected maximum velocities, despite the implemented heuristic to tailor maximum allowed velocities. As a consequence, the polyhedral relaxations of Eq. (2a) corresponding to these pipes are not sufficiently tight—see also the discussion in Appendix 1.

Fig. 9

Upper and lower bounds for the solution of $\text {MINLP}(Q)$ on BWFLnet. a Upper and lower bounds computed by Algorithm 2, with $N_c=0$. b Upper and lower bounds computed by the combination of Algorithm 1 and 2, with $N_c=0$

Next, given optimal valve locations for $n_v \in \{1,2,3\}$, computed with Algorithm 2, we have formulated a nonconvex nonlinear program to optimize valve operation under the complete set of 96 demand conditions. Such NLP is obtained from the formulation of $\text {MINLP}(Q)$ by fixing the values of the binary variables corresponding to optimized valve locations, and it is equivalent to the problem of optimizing the actuators operation. Algorithm 1 is applied to tighten the bounds on flow variables, and Algorithm 2 is subsequently implemented to solve the nonconvex NLP with tightened variable bounds. Lower and upper bounds computed at the root of the branch and bound tree are reported in Table 26, for $n_v \in \{1,2,3\}$. As expected, the upper bounds to the AZP values computed considering the full set of multiple demand conditions are close to those obtained for the restriction to three demand conditions. Moreover, in this case, the domain reduction procedure has resulted in considerably tighter lower bounds, without performing any branching operation. In contrast, the results reported in Table 24 indicate that that inclusion of valve locations as unknowns significantly reduces the ability of Algorithm 1 to compute tight estimates of flow variable domains. This situation has an interpretation from the hydraulic application perspective. In fact, appropriate changes in network topology induced by valves closures can result in increased flow velocities across some pipes (Abraham et al. 2018).

In conclusion, we observe that the average computational cost associated with the solution of a single MILP relaxation for BWFLnet is considerably higher than for Net25 and PescaraNet. In fact, solving the MILP relaxation at the root of the branch and bound tree for BWFLnet required 2–6 orders of magnitude more computational time than what experienced for Net25 and PescaraNet. This behaviour is predictable, as the problem of optimal valve placement and operation in BWFLnet results in a MINLP whose size is one to two orders of magnitude larger than the size of the problem formulation on Net25 and PescaraNet—see Table 1. It is known that computational effort required to solve a mixed-integer program grows combinatorially with the size of the problem. These numerical experiments were conducted on a single computational thread of a desktop machine, using a standard implementation of GUROBI for the solution of the MILP relaxations. The availability of additional computational capability and the use of a tailored MILP solver could speed-up the optimization process.

All three case studies show that good quality solutions are often computed at the root node of the branch and bound tree (i.e. iteration 0). This is in accordance with the work by Diamond et al. (2018), presenting a number of examples where good quality solutions to nonconvex optimization problems are recovered from the solution of suitable convex relaxations. The results suggest that Algorithm 2 can be early terminated to generate good quality solutions of $\text {MINLP}(Q)$, by opportunely setting time limit or maximum number of iterations. Moreover, observe that Algorithm 2 provides more information than local optimization methods for optimal valve placement in WSNs studied in previous work. In fact, the algorithm always generates a certified bound on the optimality gap of the computed solution. Local optimization methods can be implemented before starting Algorithm 2, in order to rapidly generate good quality feasible solutions.

5 Conclusions and future work

In this manuscript, we have investigated the application of branch and bound strategies to compute $\varepsilon$-sub-optimal solutions for the problem of optimal valve placement and operation in water supply networks. The implemented algorithm relies on the solution of MILP relaxations of the original nonconvex MINLP. Furthermore, a tailored domain reduction procedure was implemented to tighten the MILP relaxations. In contrast to previously published solution methods for optimal valve placement in water networks, the presented algorithm terminates with a certified bound on the optimality gap of the computed solution, thus providing additional information to support the design and operation of water supply networks.

The proposed branch and bound method has successfully generated good quality feasible solutions in two benchmark water networks and a large water supply network, after few iterations, with bounds on the optimality gap comparable to the order of uncertainty usually experienced in pressure control of water supply networks. Furthermore, the results suggest that the proposed domain reduction strategy is more effective in improving the convergence properties of the algorithm, than simply increasing the number of linearizations used to define the polyhedral relaxations. Moreover, the results reported in this manuscript show that, for the considered benchmark water networks, the proposed branch and bound algorithms outperform state-of-the-art global optimization solvers SCIP and BARON. These results highlight the challenges of applying off-the-shelf global solvers to the problem in study.

However, the lower bounds generated by the algorithm experience slow progress, as shown in Fig. 5. They can be improved by performing Algorithm 1 on $Q^{\text {left}}$ and $Q^{\text {right}}$, so that the new bounds on the branching variable can be propagated to the remaining flow variables. Recall that, at each iteration of Algorithm 1, the required solutions of the $2n_l|{\mathscr {C}}|$ linear programs can be computed in parallel. As a consequence, if enough computational cores are available, the outlined bound propagation strategy can be applied at each branch and bound iteration, without dramatically increasing the overall computational time. Furthermore, future work should investigate the inclusion of additional valid linear inequalities in the formulation of $\text {MILP}(Q')$. A possible strategy is to use the locally optimal solutions generated at each stage of the branch and bound method, following an approach similar to Humpola et al. (2016). In addition, when large operational water networks are considered, tailored solvers for the relaxed MILPs can be designed using suitable decomposition strategies, following ideas discussed in Vigerske (2012, Chapters 3 and 4).

Although the present work has focused on the minimization of AZP, other convex objective functions can be minimized within the same framework, with little modifications to the discussed formulation. In particular, if the objective function is nonlinear, the generation of lower bounds requires the solution convex MINLPs. Furthermore, optimal design (Bragalli et al. 2012), optimal valve control (Wright et al. 2015), and optimal pump scheduling (Menke et al. 2015) problems result in optimization problems involving nonconvex constraints like (2a). As a consequence, using suitable linear relaxations and NLP sub-problems, Algorithms 1 and 2 can be applied to guarantee the optimality of the solution found, or a bound on the optimality gap, for such nonconvex optimization problems.

Appendices

Appendix 1: Polyhedral relaxations of nonconvex head loss constraints

We look for polyhedral relaxations of constraints

$$\begin{aligned} \theta ^t_j-\phi _j(q^t_j)=0, \quad t=1,\ldots ,n_l, \; j=1,\ldots {n_p}\end{aligned}$$

These will be written as

$$\begin{aligned} R^t q^t + E^t \theta ^t \le r^t, \quad t=1,\ldots ,n_l \end{aligned}$$

(25)

for suitable matrices $R^t$ and $E^t$ and constant vectors $r^t$ that depend on $q^t_L$ and $q^t_U$. Moreover, the present appendix demonstrates that the strength of the relaxations depends on the tightness of the bounds on the flow variables.

In the following, the indices t and j are omitted as the mathematical derivation does not depend on them. Consider the set

$$\begin{aligned} \Big \{ (q,\theta ) \;\Big | \;\theta =\phi (q), \quad \forall q \in [q_L,q_U] \Big \} \end{aligned}$$

(26)

A convex relaxation is given by

$$\begin{aligned} \Big \{ (q,\theta ) \; \Big | \; {\underline{\phi }}(q) \le \theta \le {\bar{\phi }}(q), \quad \forall q \in [q_L,q_U]\Big \} \end{aligned}$$

(27)

where ${\underline{\phi }}(\cdot )$ and ${\bar{\phi }}(\cdot )$ are suitable convex and concave functions, respectively. Analytical expressions for ${\underline{\phi }}(\cdot )$ and ${\bar{\phi }}(\cdot )$ can be derived following a similar procedure to the one illustrated in Liberti and Pantelides (2003) for monomials of odd degree. Recall that $\phi (\cdot )$ is defined as

$$\begin{aligned} \phi (q):=q(a|q|+b) \quad q \in [q_L,q_U], \quad a \ge 0, \quad b \ge 0. \end{aligned}$$

(28)

We can assume that $a>0$, otherwise $\phi (\cdot )$ is a linear function and relaxations are not needed. Let $q_L \le 0 \le q_U$ be upper and lower bounds on flow q. We look for ${\bar{q}} \le 0$ such that the line from $({\bar{q}},\phi ({\bar{q}}))$ to $(q_U,\phi (q_U))$ is tangent to the curve $\phi (\cdot )$ at $({\bar{q}},\phi ({\bar{q}}))$. This is represented by the equation:

$$\begin{aligned} \frac{\phi ({\bar{q}})-\phi (q_U)}{{\bar{q}}-q_U}=\phi ^\prime ({\bar{q}}). \end{aligned}$$

(29)

Multiplying by $({\bar{q}}-q_U)$ on both sides of the previous equation yields:

$$\begin{aligned} {\bar{q}}(a|{\bar{q}}|+b)-q_\text {U}(a|q_U|+b)-(2a|{\bar{q}}|+b)({\bar{q}}-q_U)=0. \end{aligned}$$

(30)

Since $a>0$, ${\bar{q}}\le 0$ and $q_U \ge 0$, we finally obtain

$$\begin{aligned} -{\bar{q}}^2+q_U^2+2{\bar{q}}q_U=0. \end{aligned}$$

(31)

Thus ${\bar{q}}:=(1-\sqrt{2})q_U$. Analogously, the unique point ${\underline{q}} \ge 0$ such that the line from $({\underline{q}},\phi (\underline{q}))$ to $(q_L,\phi (q_L))$ is tangent to $\phi (\cdot )$ in $({\underline{q}},\phi (\underline{q}))$ is defined as ${\underline{q}}:=(1-\sqrt{2})q_L$.

Fig. 10

Convex envelopes of nonconvex constraints $\theta =\phi (q)$. a$q_L< {\bar{q}}< 0< {\underline{q}} < q_U$. b${\bar{q}} \le q_L< 0< {\underline{q}} < q_U$. c$q_L< {\bar{q}}< 0 < q_U \le {\underline{q}}$. d$0 \le q_L < q_U$. e$q_L < q_U \le 0$.

If $q_L< {\bar{q}}< 0< {\underline{q}} < q_U$, we have the following convex over and under estimators (see Fig. 10a):

$$\begin{aligned} {\overline{\phi }}(q)= & {} {\left\{ \begin{array}{ll} \phi (q), &{}q_L \le q \le {\bar{q}} \\ \phi (q_U)+\frac{\phi ({\bar{q}})-\phi (q_U)}{{\bar{q}}-q_U}(q-q_U), &{}{\bar{q}}\le q \le q_U \end{array}\right. } \end{aligned}$$

(32)

$$\begin{aligned} {\underline{\phi }}(q)= & {} {\left\{ \begin{array}{ll} \phi (q_L)+\frac{\phi ({\underline{q}})-\phi (q_L)}{{\underline{q}}-q_L}(q-q_L) &{} q_L \le q \le {\underline{q}} \\ \phi (q) &{} {\underline{q}} \le q \le q_U \end{array}\right. } \end{aligned}$$

(33)

When ${\bar{q}} \le q_L$, it is necessary to modify the definition of ${\overline{\phi }}(\cdot )$ as follows (see Fig. 10b):

$$\begin{aligned} {\overline{\phi }}(q)=\phi (q_L)+\frac{\phi (q_U)-\phi (q_L)}{q_U-q_L}(q-q_L), \forall q \in [q_L,q_U]. \end{aligned}$$

(34)

Analogously, if ${\underline{q}} \ge q_U$ set (see Fig. 10c)

$$\begin{aligned} {\underline{\phi }}(q)=\phi (q_L)+\frac{\phi (q_U)-\phi (q_L)}{q_U-q_L}(q-q_L), \forall q \in [q_L,q_U]. \end{aligned}$$

(35)

Now, assume that $0 \le q_L < q_U$. In this case, the convex envelope (see Fig. 10d) is given by

$$\begin{aligned} {\underline{\phi }}(q)&=\phi (q) \end{aligned}$$

(36)

$$\begin{aligned} {\overline{\phi }}(q)&=\phi (q_L)+\frac{\phi (q_U)-\phi (q_L)}{q_U-q_L}(q-q_L) \end{aligned}$$

(37)

Analogously, if $q_L < q_U \le 0$, set (see Fig. 10e)

$$\begin{aligned} {\underline{\phi }}(q)&=\phi (q_L)+\frac{\phi (q_U)-\phi (q_L)}{q_U-q_L}(q-q_L) \end{aligned}$$

(38)

$$\begin{aligned} {\overline{\phi }}(q)&=\phi (q) \end{aligned}$$

(39)

In this manuscript, our aim is to apply a branch and bound method to the nonconvex problem $\text {MINLP}(Q)$. At each step of the algorithm, a solution of a convex MINLP relaxation of $\text {MINLP}(Q)$ will yield a lower bound on the optimal objective function value. Observe that, with the exception of (2a), all the other constraints in $\text {MINLP}(Q)$ are linear. Therefore, it is convenient to study polyhedral relaxations of the nonconvex set in (26), which will result in a Mixed Integer Linear Programming (MILP) relaxation of $\text {MINLP}(Q)$—for a general review, see Tawarmalani and Sahinidis (2002, Chapter 4). Let $N_c \ge 0$ be a parameter used to control the number of linearizations for the outer approximation of the convex envelopes in Fig. 10.

Assume $q_L< {\bar{q}}< 0< {\underline{q}} < q_U$. Let $N_c>0$, and $q_L< q^M_1< \cdots< q^M_{N_c}<{\bar{q}}$ and ${\underline{q}}<q^S_1<\cdots<q^S_{N_c}<q_U$ be sequences of equidistant points, where ${\bar{q}}$ and ${\underline{q}}$ are the tangential points defined above. A polyhedral relaxation is given by the following linear inequalities (see Figs. 11a, 12a) :

$$\begin{aligned} \phi (q_L)+\frac{\phi ({\underline{q}})-\phi (q_L)}{{\underline{q}}-q_L}(q-q_L)&\le \theta \end{aligned}$$

(40)

$$\begin{aligned} \phi (q_U)+\frac{\phi ({\bar{q}})-\phi (q_U)}{{\bar{q}}-q_U}(q-q_U)&\ge \theta \end{aligned}$$

(41)

$$\begin{aligned} \phi (q_U)+\phi ^\prime (q_U)(q-q_U)&\le \theta \end{aligned}$$

(42)

$$\begin{aligned} \phi (q_L)+\phi ^\prime (q_L)(q-q_L)&\ge \theta \end{aligned}$$

(43)

$$\begin{aligned} \phi (q^S_i)+\phi ^\prime (q^S_i)(q-q^S_i)&\le \theta , \quad \forall i \in \{1,\ldots N_c\} \end{aligned}$$

(44)

$$\begin{aligned} \phi (q^M_i)+\phi ^\prime (q^M_i)(q-q^M_i)&\ge \theta , \quad \forall i \in \{1,\ldots N_c\} \end{aligned}$$

(45)

If $N_c=0$, the polyhedral relaxation is defined only by constraints (40)–(43).

Now, let ${\bar{q}} \le q_L< 0< {\underline{q}} < q_U$. Assume that $N_c>0$, and let ${\underline{q}}<q^S_1<\cdots<q^S_{N_c}<q_U$ be sequence of equidistant points. In this case, we consider the linear relaxation given by (see Figs. 11b, 12b):

$$\begin{aligned} \phi (q_L)+\frac{\phi ({\underline{q}})-\phi (q_L)}{{\underline{q}}-q_L}(q-q_L)&\le \theta \end{aligned}$$

(46)

$$\begin{aligned} \phi (q_L)+\frac{\phi (q_U)-\phi (q_L)}{q_U-q_L}(q-q_L)&\ge \theta \end{aligned}$$

(47)

$$\begin{aligned} \phi (q_U)+\phi ^\prime (q_U)(q-q_U)&\le \theta \end{aligned}$$

(48)

$$\begin{aligned} \phi (q^S_i)+\phi ^\prime (q^S_i)(q-q^S_i)&\le \theta , \quad \forall i \in \{1,\ldots ,N_c\} \end{aligned}$$

(49)

If $N_c=0$, the corresponding polyhedral relaxation is defined only by constraints (46)–(48).

Analogously, if $q_L< {\bar{q}}< 0 < q_U \le {\underline{q}}$ and $N_c>0$, let $q_L<q^M_1<\cdots<q^M_{N_c}<{\bar{q}}$ be a sequence of equidistant points. We have (see Figs. 11c, 12c):

$$\begin{aligned} \phi (q_L)+\frac{\phi (q_U)-\phi (q_L)}{q_U-q_L}(q-q_L)&\le \theta \end{aligned}$$

(50)

$$\begin{aligned} \phi (q_U)+\frac{\phi ({\bar{q}})-\phi (q_U)}{{\bar{q}}-q_U}(q-q_U)&\ge \theta \end{aligned}$$

(51)

$$\begin{aligned} \phi (q_L)+\phi ^\prime (q_L)(q-q_L)&\ge \theta \end{aligned}$$

(52)

$$\begin{aligned} \phi (q^M_i)+\phi ^\prime (q^M_i)(q-q^M_i)&\ge \theta , \quad \forall i\in \{1,\ldots ,N_c\} \end{aligned}$$

(53)

When $N_c=0$, the polyhedral relaxation is defined by constraints (50)–(52).

Assume $0 \le q_L < q_U$. Let $N_c>0$ and consider a sequence of equidistant points $q_L<q^S_1<q^S_{N_c}<q_U$. We define (see Fig. 11d, 12d):

$$\begin{aligned} \phi (q_L)+\frac{\phi (q_U)-\phi (q_L)}{q_U-q_L}(q-q_L)&\ge \theta \end{aligned}$$

(54)

$$\begin{aligned} \phi (q_L)+\phi ^\prime (q_L)(q-q_L)&\le \theta \theta \end{aligned}$$

(55)

$$\begin{aligned} \phi (q_U)+\phi ^\prime (q_U)(q-q_U)&\le \theta \theta \end{aligned}$$

(56)

$$\begin{aligned} \phi (q^S_i)+\phi ^\prime (q^S_i)(q-q^S_i)&\le \theta , \quad \forall i \in \{1,\ldots ,N_c\} \theta \end{aligned}$$

(57)

If $N_c=0$, the polyhedral relaxation is defined only by constraints (54)–(56).

Finally, if $q_L < q_U \le 0$ and $N_c>0$, let $q_L<q^M_1<\cdots<q^M_{N_c}<q_U$ be a sequence of equidistant points. A linear relaxation is given by (see Figs. 11e, 12e):

$$\begin{aligned} \phi (q_L)+\frac{\phi (q_U)-\phi (q_L)}{q_U-q_L}(q-q_L)&\le \theta \end{aligned}$$

(58)

$$\begin{aligned} \phi (q_U)+\phi ^\prime (q_U)(q-q_U)&\ge \theta \end{aligned}$$

(59)

$$\begin{aligned} \phi (q_L)+\phi ^\prime (q_L)(q-q_L)&\ge \theta \end{aligned}$$

(60)

$$\begin{aligned} \phi (q^M_i)+\phi ^\prime (q^M_i)(q-q^M_i)&\ge \theta , \quad \forall i \in \{1,\ldots ,N_c\} \end{aligned}$$

(61)

When $N_c=0$, the polyhedral relaxation is defined only by constraints (58)–(60).

The polyhedral relaxations of (26) defined above are illustrated in Figs. 11 and 12. Observe that their strength depends on $q_L$ and $q_U$. Smaller ranges for $q_U-q_L$ lead to tighter linear relaxations. In conclusion, it is possible to write polyhedral relaxations of constraints (2a) as

$$\begin{aligned} R^t q^t + E^t \theta ^t \le r^t, \quad \forall t=1,\ldots ,n_l \end{aligned}$$

(62)

for suitable matrices $R^t$ and $E^t$ and vectors $r^t$ that depend on $q^t_L$ and $q^t_U$.

Fig. 11

Polyhedral relaxations of nonconvex constraints $\theta =\phi (q)$, with $N_c=0$. a$q_L< {\bar{q}}< 0< {\underline{q}} < q_U$. b${\bar{q}} \le q_L< 0< {\underline{q}} < q_U$. c$q_L< {\bar{q}}< 0 < q_U \le {\underline{q}}$. d$0 \le q_L < q_U$. e$q_L < q_U \le 0$

Fig. 12

Polyhedral relaxations of nonconvex constraints $\theta =\phi (q)$, with $N_c=3$. a$q_L< {\bar{q}}< 0< {\underline{q}} < q_U$. b${\bar{q}} \le q_L< 0< {\underline{q}} < q_U$. c$q_L< {\bar{q}}< 0 < q_U \le {\underline{q}}$. d$0 \le q_L < q_U$. e$q_L < q_U \le 0$.

Appendix 2: An illustrative example

In this appendix, we illustrate the graph decomposition routine outlined in Sect. 3.3 to compute the index set ${\mathscr {C}}$ corresponding to links considered by the domain reduction procedure in Algorithm 1.

Consider the network ToyNet, whose layout is presented in Fig. 13.

Fig. 13

ToyNet

This network includes one fixed-head node $H_0$, and six unknown-head nodes. Moreover, node $V_6$ is the only node in the network with degree one. In this case, there is a unique tree, which is composed by links $P_6$ and $P_7$, and nodes $V_3$, $V_5$, and $V_6$. Node $V_3$ is the root of the tree. Following the notation introduced in Sect. 2, the operation of ToyNet is considered under $n_l$ different demand conditions.

Let $t \in \{1,\ldots ,n_l\}$. Equation (2c) at $V_6$ implies that $q^t_{P_7}=d^t_{V_6}$, where $d^t_{V_6}$ denotes the demand at node $V_6$ and time t. Therefore, flow across link $P_7$ is known a priori, and upper and lower bounds on flow variables corresponding to link $P_7$ are equal. Furthermore, Eq. (2c) imply that $q^t_{P_6}=d_{V_5} + d_{V_6}$. Hence, also the flow across link $P_6$ is known a priori. Furthermore, we observe that links $P_2$, $P_4$ and $P_5$ are connected in series. Equation (2c) yield that

$$\begin{aligned} q^t_{P_2}&=q^t_{P_4}+d^t_{V_2} \end{aligned}$$

(63)

$$\begin{aligned} q^t_{P_5}&=q^t_{P_4}-d^t_{V_4} \end{aligned}$$

(64)

As a result, it is possible to select link $P_4$ as representative and derive bounds on variables $q_{P_2}$ and $q_{P_5}$ using (63). In conclusion, the optimization based bound tightening described in Algorithm 1 is performed only for flow variables corresponding to links in ${\mathscr {C}}:=\{P_1,P_4,P_3\}$.

Appendix 3: Supplementary material: tables with numerical results

See Tables 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,  16, 17, 18, 19, 20, 21, 22, 23, 24, 25 and 26.

Table 2 Results obtained by Algorithm 2 with $N_c=0$ for PescaraNet

Table 3 Results obtained by Algorithm 2 with $N_c=0$ for Net25

Table 4 Results obtained by Algorithm 2 with $N_c=1$ for PescaraNet

Table 5 Results obtained by Algorithm 2 with $N_c=1$ for Net25

Table 6 Results obtained by Algorithm 2 with $N_c=3$ for PescaraNet

Table 7 Results obtained by Algorithm 2 with $N_c=3$ for Net25

Table 8 Results obtained by Algorithm 2 with $N_c=5$ for PescaraNet

Table 9 Results obtained by Algorithm 2 with $N_c=5$ for Net25

Table 10 Results obtained by Algorithms 1 and 2 with $N_c=0$ for PescaraNet

Table 11 Results obtained by Algorithms 1 and 2 with $N_c=0$ for Net25

Table 12 Results obtained by Algorithms 1 and 2 with $N_c=1$ for PescaraNet

Table 13 Results obtained by Algorithms 1 and 2 with $N_c=1$ for Net25

Table 14 Results obtained by Algorithms 1 and 2 with $N_c=3$ for PescaraNet

Table 15 Results obtained by Algorithms 1 and 2 with $N_c=3$ for Net25

Table 16 Results obtained by Algorithms 1 and 2 with $N_c=5$ for PescaraNet

Table 17 Results obtained by Algorithms 1 and 2 with $N_c=5$ for Net25

Table 18 Results obtained by BARON (v18.8.23) for PescaraNet

Table 19 Results obtained by BARON (v18.8.23) for Net25

Table 20 Results obtained by SCIP (v3.2.1) for PescaraNet

Table 21 Results obtained by SCIP (v3.2.1) for Net25

Table 22 Results obtained by Algorithm 2 with $N_c=0$ for BWFLnet

Table 23 Results obtained by Algorithm 2 with $N_c=3$ for BWFLnet

Table 24 Results obtained by Algorithms 1 and 2 with $N_c=0$ for BWFLnet

Table 25 Results obtained by Algorithms 1 and 2 with $N_c=3$ for BWFLnet

Table 26 Lower and upper bounds at the root of the branch and bound tree obtained by Algorithm 2 with $N_c=0$ for BWFLnet, with fixed valve locations, considering 96 different demand conditions. Algorithm 1 was applied as pre-solving routine