Alternating optimization of design and stress for stress-constrained topology optimization

Abstract

Handling stress constraints is an important topic in topology optimization. In this paper, we introduce an interpretation of stresses as optimization variables, leading to an augmented Lagrangian formulation. This formulation takes two sets of optimization variables, i.e., an auxiliary stress variable per element, in addition to a density variable as in conventional density-based approaches. The auxiliary stress is related to the actual stress (i.e., computed by its definition) by an equality constraint. When the equality constraint is strictly satisfied, an upper bound imposed on the auxiliary stress design variable equivalently applies to the actual stress. The equality constraint is incorporated into the objective function as linear and quadratic terms using an augmented Lagrangian form. We further show that this formulation is separable regarding its two sets of variables. This gives rise to an efficient augmented Lagrangian solver known as the alternating direction method of multipliers (ADMM). In each iteration, the density variables, auxiliary stress variables, and Lagrange multipliers are alternatingly updated. The introduction of auxiliary stress variables enlarges the search space. We demonstrate the effectiveness and efficiency of the proposed formulation and solution strategy using simple truss examples and a dozen of continuum structure optimization settings.

1 Introduction

Design of structures with local stresses upper-bounded by a critical stress value is of paramount importance in engineering. To this end, the incorporation of stress constraints has been an important field of study in topology optimization of continuum structures (Duysinx and Sigmund 1998). Over the past two decades, three computational challenges have been recognized (Le et al. 2010; Holmberg et al. 2013), and solutions for some of them have been proposed:

• The “singularity” problem — the feasible design space contains degenerate sub-spaces of a lower dimension (Kirsch 1990; Rozvany 2001). The globally optimal solution, which often locates in the degenerate sub-spaces, is not accessible to nonlinear programming algorithms. It has been shown that the problem of degenerate sub-spaces can be alleviated by relaxing the stress constraints, i.e., the 𝜖-relaxation originally developed for trusses (Cheng and Guo 1997) and its variants for continuum structures (Duysinx and Bendsøe 1998; Bruggi 2008; Le et al. 2010).

• The local nature of stress constraints — the stress limit applies to every material point in the domain. This results in a large number of constraints. An often used solution strategy is to approximate these local constraints by a global one which can then be more efficiently addressed, e.g., the p-norm (Duysinx and Sigmund 1998) and Kreisselmeier-Steinhauser (KS) function (Yang and Chen 1996).

• The highly nonlinear dependence of stress on design variables. Especially at stress concentration regions, stresses are sensitive to density changes in neighborhoods. This leads to convergence problems: a large number of iterations, fluctuations in the objective and constraints, and a suboptimal objective value which potentially could be further reduced.

This last challenge is coupled with solutions of the first two. For instance, the aggregation for reducing the number of constraints may further exacerbate the nonlinearity. It is found in the literature that research has been mostly focusing on the first two challenges by reformulating the optimization problem, and effective alternative approaches have been proposed, e.g., Verbart et al. (2016, 2017), Wang and Qian (2018).

Stress-constrained topology optimization problems (and more general structural optimization) are typically solved by using sequential convex programming. Notable algorithms include the Convex Linearization method (CONLIN) (Fleury 1989), the Method of Moving Asymptotes (MMA) (Svanberg 1987) and its globally convergent version GCMMA (Svanberg 2002). These algorithms make use of (first order) approximations of objective and constraint functions. An assessment of these optimization algorithms, as well as general methods such as the primal-dual interior point methods (Forsgren and Gill 1998) and Sequential Quadratic Programming (SQP) (Boggs and Tolle 1995), is presented by Rojas-Labanda and Stolpe (2015). The benchmark problems in the comparative study include compliance/volume minimization and mechanism design. Unfortunately stress constraints are not included.

An alternative solution strategy to stress-constrained topology optimization is to incorporate local stress constraints in the objective function using an augmented Lagrangian formulation (Pereira et al. 2004). It has been used for topology optimization based on density (Fancello 2006; da Silva and Cardoso 2017; da Silva et al. 2019) and level sets (James et al. 2012; Emmendoerfer and Fancello 2014). Very recently (da Silva et al. 2020) demonstrated that this formulation allows handling very large problems in 3D manufacturing-tolerant topology optimization, with hundreds of millions of stress constraints. Also aiming for 3D large scale optimization, Senhora et al. (2020) proposed to modify both the penalty and objective function terms of the augmented Lagrangian function, leading to consistent solutions under mesh refinement and driving the mass minimization towards black and white solutions. Giraldo-Londoño and Paulino (2020) applied this to handle multiple classical failure criteria with a unified yielding function.

In this paper we introduce an interpretation of local stresses as optimization variables, using an augmented Lagrangian formulation. We consider auxiliary stresses as optimization variables, in addition to the design variables (i.e., densities) representing the material distribution. The stress limit is then imposed upon the auxiliary stresses as an upper bound. Given a material distribution and boundary conditions, the actual stress is computed by a finite element analysis. The auxiliary stress is related to the actual stress by an equality constraint. This equality constraint is then incorporated into the objective function as linear and quadratic terms using an augmented Lagrangian form.

This reformulation offers some conceptual benefits. Firstly, thanks to the extra set of optimization variables, it opens a larger space for the optimization to search. It even allows the optimization to explore the infeasible region in the conventional formulation — the actual stress could be larger than the prescribed stress limit. This can be beneficial for rapid convergence at the beginning iterations. Secondly, the stress limit is regarded as side or bound constraints for the auxiliary stress variables, and bound constraints are readily handled by optimization algorithms.

To efficiently solve the optimization problem with two sets of variables, we show that the formulation is separable regarding the auxiliary stresses and structural variables (i.e., densities). This gives rise to a variant of augmented Lagrangian solvers known as Alternating Direction Method of Multipliers (ADMM). Within each iteration, the structural variables, stress variables, and Lagrangian multipliers are alternatingly updated. This solver converges rapidly at the first few iterations. Our tests on continuum structures demonstrate reduced objective values in comparison with using the MMA family for solving the conventional formulation.

ADMM algorithms have provable convergence for solving convex optimization problems (Boyd et al. 2011). Their applicability to nonconvex problems has also been investigated, e.g., Diamond et al. (2018). For nonconvex problems, while ADMM is not guaranteed to converge, in practice it can often find a reasonable objective value with small computational cost (Kanno and Kitayama 2018). It has been recently applied in structural optimization for problems with a few or hundreds of design variables. Kanno and Kitayama (2018) used ADMM as an effective heuristic for mixed-integer nonlinear structural optimization. Palanduz and Groenwold (2020) analyzed the applicability of a subset of ADMM-type algorithms for optimal structural design, in combination with a novel scaling method and quadratic approximations of the primal problem. Eckstein and Bertsekas (1992) pointed out that ADMM is an application of the Douglas-Rachford splitting algorithm (Douglas and Rachford 1956), which is in turn an instance of the proximal point algorithm. Recently, Evgrafov and Sigmund (2020) proposed to split stress variables into positively and negatively semi-definite parts, and applied this splitting for compliance minimization in the vanishing volume ratio limit. In this paper we adopt ADMM to solve stress-constrained problems with a large number of variables and constraints, and compare its performance with conventional formulations and solvers.

Our main contributions in this work include the following: (i) an interpretation of local stresses as optimization variables, and (ii) an extensive comparison of different solution strategies for stress-constrained topology optimization. This intuitive interpretation leads to equations that turn out to be mathematically equivalent to those from the augmented Lagrangian formulation (e.g., Giraldo-Londoño and Paulino 2020). Using simple truss examples, we validate that the augmented Lagrangian formulation allows reaching the global optimum that is located in the degenerate sub-space, similarly to a unified aggregation and relaxation approach (Verbart et al. 2017). Tested on continuum structures, our comparison reveals that the augmented Lagrangian formulation can achieve superior solutions in terms of the objective value. Furthermore, we propose a hybrid approach which based on our comparison is most favorable regarding the objective value and computational efficiency.

2 Alternating optimization of design and stress

We start with a conventional density-based formulation for stress-constrained topology optimization (Section 2.1). We then introduce an interpretation of stresses as optimization variables (Section 2.2). An optimization strategy to this reformulation is explained in Section 2.3.

2.1 Stress-constrained compliance minimization

Using a finite element discretization of the design domain, the density distribution is represented by a vector, ρ. Let σ_e denote the stress tensor for generic element e when the structure is under a constant external load, F. We introduce a variable, α_e, to indicate a scalar measure of the stress tensor, i.e.,

$$ \alpha_{e} = \tilde{{\sigma}}_{e}. $$

(1)

The stress-constrained compliance minimization is then written as

$$ \begin{array}{@{}rcl@{}} &&(\mathcal{Q}_{0})\quad \underset{{\rho}}{\min} f_{c}({\rho}) = {F}^{\mathsf{T}}{U}({\rho}), \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} &&\text{s.t.} \quad V({\rho}) = {\rho}^{\mathsf{T}} {v} \le \gamma {1}^{\mathsf{T}}{v}, \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} &&\alpha_{e} \le \sigma_{\lim}, \forall e, \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} && 0 \le \rho_{e} \le 1, \forall e. \end{array} $$

(5)

This conventional formulation is denoted as $\mathcal {Q}_{0}$ to differentiate from a reformulation to be introduced soon. In the objective, U(ρ) represents the displacement vector. In (3), vector v is composed of the volume per element, and γ is a prescribed volume ratio. The stress constraint is encoded by (4), where $\sigma _{\lim }$ is a prescribed limit on the scalar stress measure. At last, (5) restricts the pseudo density of each element to between 0 (empty) and 1 (solid).

The displacement vector, U(ρ), is computed by solving a static equilibrium equation,

$$ {K} ({\rho}) {U} = {F}, $$

(6)

where K(ρ) is the assembled stiffness matrix. The element stiffness matrix is calculated using the Solid Isotropic Material with Penalization (SIMP) model,

$$ \begin{array}{@{}rcl@{}} &&{K}_{e} (\rho_{e}) = E_{e}(\rho_{e}) {K}_{0}, \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} &&E_{e}(\rho_{e}) = E_{\min} + {\rho_{e}^{k}}(E_{0}-E_{\min}), \end{array} $$

(8)

where K₀ is the stiffness matrix of a solid element with Young’s modulus E₀. E_e is the interpolated Young’s modulus. E_min is a small value to prevent the assembled stiffness matrix (K) from becoming singular. k is a penalization parameter (k = 3).

2.2 Interpreting stresses as optimization variables

An innovative aspect of our approach is to interpret stress α_e as an auxiliary optimization variable, and consequently (1) as an equality constraint rather than a definition. To efficiently handle the equality constraint, the objective function is updated by incorporating an augmented Lagrangian form of the equality constraint,

$$ L_{\mu}({\rho}, {\alpha}, {\lambda}) = f_{c}({\rho}) + {\lambda}^{\mathsf{T}} ({\alpha} - \tilde{{\sigma}}) + \frac{\mu}{2} \| {\alpha} - \tilde{{\sigma}} \|_{2}^{2}, $$

(9)

where λ is a Lagrange multiplier and μ is a penalty parameter. The conventional optimization problem is reformulated as

$$ \begin{array}{@{}rcl@{}} (\mathcal{Q}_{1}) \quad \underset{{\rho},{\alpha}}{\min} \underset{{\lambda}}{\max} & \quad L_{\mu}({\rho}, {\alpha}, {\lambda}), \\ \quad \text{s.t.} &\quad (3),~(4)~\text{and}~(5). \end{array} $$

Intuitively, interpreting stresses as optimization variables enlarges the optimization space, giving extra flexibility for searching an optimal solution. It relaxes the stress constraint in the sense that it permits, at the beginning of the optimization process, the actual stress (i.e., $\tilde {\sigma }_{e}$, computed from ρ) being larger than the upper bound. This is beneficial for a rapid decrease of the objective at the onset of the optimization process.

The augmented Lagrangian formulation can be solved by simultaneously optimizing the two sets of variables, by using for instance, MMA. To efficiently solve this formulation, in the following we introduce a method to decouple the two sets of optimization variables.

2.3 Alternating optimization

While two sets of optimization variables are employed, the objective, f_c(ρ), and inequality constraints, i.e., (3), (4) and (5), involve either ρ or α, but not both. In other words, each of these functions can be separated into two parts: one part that is dependent on ρ, and the other part that is dependent on α. In each of these functions, one of these two parts is null.

This so-called separability is essential for a variant of augmented Lagrangian methods, known as the alternating direction method of multipliers or ADMM. ADMM uses partial updates for the variables, similar to the Gauss-Seidel method for solving linear equations. This partial update scheme allows an efficient search of the optimal solution in the enlarged optimization space.

By making use of the separability, the density and stress variables are updated alternatingly. ADMM consists of the iterations

$$ \begin{array}{@{}rcl@{}} \begin{array}{ccccccc}{\rho}^{[i]} = & \underset{{\rho}}{\arg\min} &&L_{\mu}({\rho}, {\alpha}^{[i-1]},{\lambda}^{[i-1]}), \\ &\quad s.t. && (3)~\text{and}~(5). \end{array} \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} \begin{array}{cccccc}{\alpha}^{[i]} = & \underset{{\alpha}}{\arg\min} &&L_{\mu}({\rho}^{[i]}, {\alpha},{\lambda}^{[i-1]}), \\ &\quad s.t. && (4). \end{array} \end{array} $$

(11)

This is followed by updating the Lagrange multiplier,

$$ {\lambda}^{[i]} = {\lambda}^{[i-1]}+\mu({\alpha}^{[i]} - \tilde{{\sigma}}({\rho}^{[i]})). $$

(12)

Each of the two sub-problems itself is an optimization problem. In initialization, we set the density equal to the prescribed volume ratio, i.e., $\rho ^{[0]}_{e}=\gamma , \forall e$, and compute ${\alpha }^{[0]} = \tilde { {\sigma }}( {\rho }^{[0]})$. The initial value of Lagrange multipliers is ${\lambda }^{[0]}_{e} = 1, \forall e$. In the first sub-problem, the density variables are updated, while the stress variables and Lagrange multipliers are fixed. We solve this sub-problem by using MMA. Alternatingly, in the second sub-problem, the stress variables are optimized with updated densities (ρ^[i]) and Lagrange multipliers from the last iteration (λ^[i− 1]). In fact, (11) is a quadratic programming problem with respect to α, and can be reformulated as

$$ \begin{array}{@{}rcl@{}} \underset{{\alpha}}{\min} & \quad \frac{1}{2}\|{\alpha}-(\Tilde{{\sigma}}({\rho}^{[i]})-\frac{{\lambda}^{[i-1]}}{\mu})\|^{2}_{2}. \end{array} $$

(13)

Considering the bound constraint, the solution of the second sub-problem is

$$ {\alpha_{e}} = \min \{\tilde{{\sigma_{e}}}({\rho}^{[i]})-\frac{{\lambda_{e}}^{[i-1]}}{\mu},\sigma_{\lim}\}. $$

(14)

3 Test on a two-bar truss example

Before we proceed to the implementation details of continuum structure optimization, let us examine the validity of the proposed approach on a simple two-bar truss optimization problem. The example is illustrated in Fig. 1 (Stolpe 2003; Verbart et al. 2017). The problem is to minimize its mass subjected to a stress limit, $\sigma _{\lim }$. The design variables are the cross-sectional areas A = [A₁,A₂]^T. The cross-sectional area is upper bounded by $A_{\max \limits }=2$. Both members have a Young’s modulus E. ρ_j and L_j denote the density and length of member j, respectively. The stress in the members is calculated by

$$ \sigma_{1} = \frac{FL_{2}}{A_{1}L_{2}+A_{2}L_{1}},\quad \sigma_{2} = -\frac{FL_{1}}{A_{1}L_{2}+A_{2}L_{1}}. $$

(15)

Fig. 1

A two-bar truss example (Stolpe 2003) is used to validate the proposed approach. The optimization problem is to minimize the total mass by varying the cross-sectional areas, A₁ and A₂, under stress limit $\sigma _{\lim }$

The initial problem formulation, denoted by $\mathcal {P}_{0}$, is written as,

$$ \begin{array}{@{}rcl@{}} (\mathcal{P}_{0})\quad \underset{{A}}{\min} \quad m({A})=\rho_{1}A_{1}L_{1}+\rho_{2}A_{2}L_{2}, \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} \text{s.t.} \quad g_{j} = \frac{|\sigma_{j}|}{\sigma_{\lim}}-1 \leq 0, \quad j\in \{1,2\}, \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} 0 \le A_{j} \le A_{\max}, \quad j\in \{1,2\}. \end{array} $$

(18)

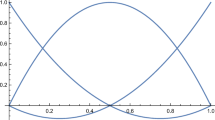
Figure 2a illustrates the solution space of the problem. It is composed of the polygon region BCDEF and the line segment EG, with the global optimum located at G. The global optimum is located in a 1-dimensional sub-space within the 2-dimensional solution space. Without special treatments, the optimization reaches a local minimum in the polygon region BCDEF.

Fig. 2

Solution space of the two-bar truss problem in Fig. 1, corresponding the initial formulation $\mathcal {P}_{0}$ (a) and the p-mean aggregated formulation $\mathcal {P}_{0}^{M}$ (b)

The unified approach proposed by Verbart et al. (2017) is included here as a reference for addressing the singularity problem. The optimization problem is modified as

$$ \begin{array}{@{}rcl@{}} (\mathcal{P}_{0}^{M})\quad \underset{{A}}{\min} & \quad m({A}) = \rho_{1}A_{1}L_{1}+\rho_{2}A_{2}L_{2}, \end{array} $$

(19)

$$ \begin{array}{@{}rcl@{}} \text{s.t.} \quad G^{L}(\bar{{g}}; p) \leq 0, \quad \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} 0 \le A_{j} \le A_{\max}, \quad j\in \{1,2\}. \end{array} $$

(21)

Here, G^L denotes the aggregated constraint, based on the p-mean function

$$ G^{L} = \left( \frac{1}{N}\sum\limits_{i=1}^{N}(\bar{g}_{i}+1)^{p}\right)^{1/p}-1, $$

(22)

with

$$ \bar{g}_{j} = \frac{A_{j}}{A_{\max}}\left( \frac{|\sigma_{j}|}{\sigma_{\lim}}-1\right), \quad j\in \{1,2\}. $$

(23)

Illustrated in Fig. 2b, the p-mean aggregated formulation, $\mathcal {P}_{0}^{M}$, enlarges the solution space to additionally include the shaded region $E\widetilde {FG}$. Curve $\widetilde {FG}$ corresponds to the boundary obtained when p = 8 in the p-mean function (Verbart et al. 2017).

3.1 Augmented Lagrangian formulation and alternating optimization

Following Section 2.2, we introduce an auxiliary variable α_j, and relate it to the stress by α_j = σ~_j, with $\Tilde {\sigma }_{j} = \frac {A_{j}}{A_{\max \limits }}\frac {\sigma _{j}}{\sigma _{\lim }}$¹. The equality constraint α_j = σ~_j is then incorporated in the objective using an augmented Lagrangian form,

$$ L_{\mu}({A},{\alpha},{\lambda}) = m({A}) + {\lambda}^{\mathsf{T}}({\alpha} -{\Tilde{\sigma}})+\frac{\mu}{2}\|{\alpha} - {\Tilde{\sigma}}\|^{2}. $$

(24)

The optimization problem is reformulated as

$$ \begin{array}{@{}rcl@{}} (\mathcal{P}_{1}) \quad \underset{{A},{\alpha}}{\min} \underset{{\lambda}}{\max} \quad L_{\mu}({A},{\alpha},{\lambda}), \end{array} $$

(25)

$$ \begin{array}{@{}rcl@{}} \text{s.t.} \quad 0 \le A_{j} \le A_{\max}, \quad j\in\{1,2\}, \end{array} $$

(26)

$$ \begin{array}{@{}rcl@{}} -\frac{A_{j}}{A_{\max}} \leq \alpha_{j} \leq \frac{A_{j}}{A_{\max}}, \quad j\in \{1,2\}. \end{array} $$

(27)

ADMM consists of alternatingly solving two sub-problems, i.e.,

$$ \begin{array}{@{}rcl@{}} \begin{array}{cccccc}{{A}}^{[i]} = & \underset{{A}}{\arg\min} L_{\mu}({A}, {\alpha}^{[i-1]},{\lambda}^{[i-1]}), \\ \end{array} \end{array} $$

(28)

s.t. (26).

$$ \begin{array}{@{}rcl@{}} {\alpha}^{[i]} = \underset{{\alpha}}{\arg\min} L_{\mu}({A}^{[i]}, {\alpha},{\lambda}^{[i-1]}), \end{array} $$

(29)

s.t. (27).

And the Lagrange multiplier is updated by

$$ {\lambda}^{[i]} = {\lambda}^{[i-1]}+\mu({\alpha}^{[i]} - {{\Tilde{\sigma}}}({A}^{[i]})). $$

(30)

In our test, we initialize λ^[0] = (1,1)^T and μ = 0.5. μ is multiplied by 1.05 after every 5 iterations.

3.2 Results and discussion

We compare six solution strategies for solving three formulations, $\mathcal {P}_{0}$, $\mathcal {P}_{0}^{M}$, and $\mathcal {P}_{1}$. The results are shown in Fig. 3. In all cases, the initial values of A₁ and A₂ equal to $A_{\max \limits }=2$, corresponding to C in the solution space. The global optimum is located at G(1,0). Using MMA to solve $\mathcal {P}_{0}$ leads to a local minimum point F(0,1) in the polygon region (Fig. 3a). With the p-mean aggregated formulation $\mathcal {P}_{0}^{M}$, both MMA and GCMMA are able to converge to the global optimum (Fig. 3b and c). Figure 3d and e show results of solving the augmented Lagrangian formulation $\mathcal {P}_{1}$ using MMA and ADMM, respectively. Lastly, Fig. 3f shows the results of a hybrid approach: we use ADMM to solve $\mathcal {P}_{1}$, and, after five iterations, switch to MMA for solving $\mathcal {P}_{0}^{M}$.

Fig. 3

Comparison of convergence histories. The optimization starts at point C(2,2). Except in (a) where MMA is used to solve $\mathcal {P}_{0}$, in other cases the global optimum, G(1,0), is reached

From Fig. 3, it can be observed that the global optimum (G) is correctly identified using the aggregated constraint formulation $\mathcal {P}_{0}^{M}$ and the augmented Lagrangian formulation $\mathcal {P}_{1}$. This is also confirmed in Table 1. The minimal mass is 0.60. In the plots of the augmented Lagrangian formulation (Fig. 3d and e), the path leading to the global optimum travels beyond the feasible region. This is not unexpected since the equality constraint ${\alpha }= {\tilde {\sigma }}$ is transformed to penalty terms in the objective, and thus the stress constraint is not strictly enforced during the process. Yet, as the process converges, the equality condition and consequently the stress constraint are satisfied.

Table 1 Statistics in solving the two-bar truss optimization problem

Discussion

The augmented Lagrangian formulation reduces constraints into a single scalar value. On this regard, it plays the role of constraints aggregation. The augmented Lagrangian formulation is also able to achieve what constraint aggregation schemes can offer, i.e., allowing an expansion of the search space and thus making the global optimum accessible (Verbart et al. 2017). We refer to Verbart et al. (2017) for a clever use of constraint aggregation schemes for stress-constrained optimization.

The convergence of the total mass is plotted in Fig. 4. ADMM is capable of rapidly reducing the objective at the first few iterations. As it approaches the final solution, it progresses slowly and leads to more iterations. This behavior is known and has been discussed, for instance, in Boyd et al. (2011). This motivates the hybrid approach which uses ADMM to quickly find a good start solution. The computation time is summarized in Table 1. It suggests that the hybrid approach, ADMM ($\mathcal {P}_{1}$) + MMA ($\mathcal {P}_{0}$), is promising in terms of the number of iterations and wall-clock time.

Fig. 4

The convergence of the total mass using different solution strategies

In the context of continuum structure optimization which is highly nonlinear and involves a large number of design variables, as will be shown in later sections, the augmented Lagrangian formulation demonstrates not only benefit in the computation time but more importantly in the optimality of the optimized solution.

4 Implementation of stress-constrained continuum structure optimization

4.1 Density operations

We adopt density operations that are commonly applied in density-based approaches, i.e., a smoothing operator to avoid checkerboard patterns (i.e., regions of alternating solid and empty elements), and a smoothed Heaviside operator for improving convergence towards black-and-white designs (Guest et al. 2004; Wang et al. 2011).

4.1.1 Density smoothing

Instead of taking ρ as the design variable, a new variable, ϕ ∈ [0,1], is introduced as the design variable. A smoothed version of ϕ is obtained by computing the weighted average,

$$ \tilde{\phi}_{e} = \frac{{\sum}_{i\in S_{e}}\omega_{e}(x_{i},r)v_{i}\phi_{i}}{{\sum}_{i\in S_{e}}\omega_{e}(x_{i},r)v_{i}}, \forall e, $$

(31)

where v_i is the volume of an element, and the weighting function is defined as

$$ \omega_{e}(x_{i},r) = r-\|x_{i}-x_{e}\|, $$

(32)

where r is a predefined filter radius, x_e and x_i are respectively the centroid of element e and an element (i) that is in close vicinity, i ∈ S_e = {i|∥x_i − x_e∥≤ r}.

4.1.2 Heaviside projection

The smoothed Heaviside projection is written as

$$ \rho_{e} = \bar{\tilde{\phi}}_{e} = \frac{\tanh(\beta\eta)+\tanh(\beta(\tilde{\phi}_{e}-\eta))}{\tanh(\beta\eta)+\tanh(\beta(1-\eta))}, $$

(33)

where β controls the sharpness of the step function and η is a projection threshold (η = 0.5). To avoid numerical instability, we start with β = 1 and double its value every 50 iterations.

4.2 Stress relaxation

We follow the qp-relaxation scheme proposed by Le et al. (2010) to resolve the stress singularity problem. The scalar measure of per element stress is computed by

$$ \tilde{\sigma}_{e} = {\rho_{e}^{q}}\bar{{\sigma}}_{e}, \\ $$

(34)

where q is a relaxation parameter (q = 0.5). $\bar {\sigma }_{e}$ refers to the von Mises stress of element e, defined by

$$ \bar{{\sigma}}_{e} = ({\sigma}_{e}^{\mathsf{T}}{V}{\sigma}_{e})^{\frac{1}{2}}, $$

(35)

where V is a symmetric matrix

$$ {V} = \left[ \begin{array}{ccc} 1 & -\frac{1}{2} & 0 \\ -\frac{1}{2} & 1 & 0 \\ 0 & 0 & 3 \end{array} \right], $$

(36)

and σ_e is the Voigt notation of a stress tensor, calculated by

$$ {\sigma}_{e} = {D}_{0}{B}_{c}{u}_{e}. $$

(37)

Here, D₀ is the elasticity tensor in the Voigt notation for a solid element, B_c is the strain-displacement matrix of the element centroid and u_e is the displacement vector of element e.

4.3 Sensitivity analysis

We present the derivatives of the augmented Lagrangian form, L_μ(ρ,α,λ), regarding density variables (ϕ_e). Since α and λ are not functions of the density variables, $\frac {\partial L_{\mu }( {\rho }, {\alpha }, {\lambda })}{\partial \phi _{e}}$ is computed by

$$ \begin{array}{@{}rcl@{}} \frac{\partial L_{\mu}}{\partial \phi_{e}} = \frac{\partial f_{c}({\rho})}{\partial \phi_{e}} - {\lambda}^{\mathsf{T}}\frac{\partial {\tilde{\sigma}}}{\partial \phi_{e}}-\mu({\alpha}-{\tilde{\sigma}})^{\mathsf{T}}\frac{\partial {\tilde{\sigma}}}{\partial \phi_{e}}. \end{array} $$

(38)

Detailed sensitivity analysis is presented in Appendix 1.

4.4 Algorithm

Algorithm 1 details the process of using ADMM to solve the augmented Lagrangian form. The algorithm takes the prescribed volume fraction (γ) and stress limit ($\sigma _{\lim }$) as input parameters. The output is the material distribution (ρ). We prescribe the maximum number of ADMM iterations I_ADMM = 1000 or I_ADMM = 20. The later is used in the hybrid solution which uses ADMM for $\mathcal {Q}_{1}$, followed by using MMA for $\mathcal {Q}_{0}$ (see Appendix 2 for solving $\mathcal {Q}_{0}$).

5 Results and discussion

The proposed method is implemented using MATLAB 2018b, and tested on a desktop PC with an Inter(R) Xeon(R) W-2123 CPU @3.60GHz and 64GB RAM. The material model has a Young’s modulus of E = 1.0 and Poisson’s ratio of ν = 0.3. Bi-linear square elements are used for stress analysis. The solution strategies for the conventional and the augmented Lagrangian formulation for compliance minimization are quantitatively compared using ten examples. The same termination criteria are applied: the maximum change in design variables in successive iterations is smaller than a threshold, 𝜖 = 10^− 2, and that both the volume and stress constraints are satisfied, or the maximum number of iterations (1000) is reached. For each solution strategy, all examples use the same parameters, which are selected empirically based on multiple tests using the L-shaped beam. Important parameters in MMA include move, asyincr, and asydecr. Based on tests, move = 0.1, asyincr = 1.2 and asydecr = 0.7 are selected.

5.1 L-shaped beam

The first example is an L-shaped beam as depicted in Fig. 5 (left). The design domain is specified by DH = DW = 150, Dh = Dw = 90. The top edge of the domain is fixed while a distributed force (F = 1) is applied downwards on the right, over a short span of 4 elements horizontally. Figure 5 (right) visualizes the von Mises stress distribution of a compliance minimized structure which is optimized without stress constraints, under volume ratio γ = 0.3. The visualization indicates a stress concentration at the corner. The maximum stress is 1.35. In the test of stress-constrained optimization, we set a stress limit of $\sigma _{\lim }=0.5$.

Fig. 5

Design domain of the L-shaped beam (left) and visualization of the von Mises stress distribution of a structure optimized without stress constraints (right)

The stress-constrained optimization problem is solved using two formulations, in total six algorithms. Fig. 6 illustrates the optimized structural layouts and the corresponding von Mises stress distributions. The first row is obtained using the conventional formulation with densities as design variables ($\mathcal {Q}_{0}$), while the second row corresponds to the proposed formulation with two sets of optimization variables ($\mathcal {Q}_{1}$). Note that in the last approach, ADMM ($\mathcal {Q}_{1}$) + MMA ($\mathcal {Q}_{0}$), we use MMA to solve the conventional formulation rather than the new formulation which has a doubled number of variables.

Fig. 6

Optimized structural layouts and stress distributions on the L-shaped beam using different optimization methods

Table 2 summarizes the statistics of using different optimization methods. The methods are grouped into two categories according to the formulation of the optimization problem, $\mathcal {Q}_{0}$ and $\mathcal {Q}_{1}$. The methods are comparable in terms of constraints on the total volume, V, and maximum stress, $\max \limits (\tilde { {\sigma }})$. Of interest here are the objective value and computation time of these six solution strategies, which are visualized using bar graphs in Fig. 7. In the former category, GCMMA leads to a smaller compliance than MMA (296.61 vs 301.53), at the price of a longer computing time (1464.6 vs 759.6). GCMMA requires a smaller number of iterations than MMA. However, on average a GCMMA iteration is more costly than an MMA iteration. GCMMA involves an inner loop which requires solving the state equation. The last row (# Solves) indicates how many times the state (and adjoint) equation is solved. The hybrid approach of GCMMA and MMA achieves a comparable compliance (295.91).

Table 2 Statistics of minimizing the compliance of an L-shaped beam. In the last row, #Solves refers to the number of solving the linear systems, including both the state equation and adjoint analysis

Fig. 7

Bar graph of the objective value and computation time for minimizing compliance of the L-shaped beam. The numbers 1 to 6 represent the different solution strategies in the order as they appear in Table 2, i.e., MMA ($\mathcal {Q}_{0}$), GCMMA ($\mathcal {Q}_{0}$), GCMMA ($\mathcal {Q}_{0}$)+MMA ($\mathcal {Q}_{0}$), MMA ($\mathcal {Q}_{1}$), ADMM ($\mathcal {Q}_{1}$), ADMM ($\mathcal {Q}_{1}$)+MMA ($\mathcal {Q}_{0}$)

The objectives from the category of $\mathcal {Q}_{1}$ outperform those from the conventional formulation $\mathcal {Q}_{0}$. ADMM ($\mathcal {Q}_{1}$) achieves a compliance of 281.99, which is 6.48% smaller than that by MMA ($\mathcal {Q}_{0}$). On the last column, the hybrid approach arrives at a slightly larger compliance, with a reduced total computation time.

Figure 8 plots the convergence of the volume and stress constraint ($\max \limits (\tilde { {\sigma }})-\sigma _{\lim }$) over iteration. It is found that ADMM is able to quickly meet the volume constraint, in less than 50 iterations. The stress constraints are gradually satisfied, since the penalty term increases during the optimization progress. MMA in general exhibits less severe fluctuations compared ADMM. This motivates the hybrid approach, ADMM ($\mathcal {Q}_{1}$) + MMA ($\mathcal {Q}_{0}$). The convergence in compliance for all six solutions is plotted together in Fig. 9. A few fluctuations in these plots are due to the continuation of the projection parameter (β) in (33).

Fig. 8

Plots of convergence of the volume and stress constraint ($\max \limits (\tilde { {\sigma }})-\sigma _{\lim }$) for optimizing the L-shaped beam

Fig. 9

Plots of compliance convergence for optimizing the L-shaped beam

5.2 Step-shaped structure

The second set of experiments is performed on a step-shaped structure shown in Fig. 10 (left). The design domain is descried by DH = DW = 150 and Dh = Dw = 50. A horizontally distributed force is applied on the top of 4 elements in the top right of the domain. Figure 10 (right) visualizes the von Mises stress distribution of a compliance-minimized structure optimized in the absence of stress constraints, with a target volume ratio of γ = 0.25. Three stress concentration regions can be observed. The maximum von Mises stress is 1.16. For this example, we test three stress limits: $\sigma _{\lim }\in \{0.6, 0.7, 0.8\}$.

Fig. 10

Design domain of a step-shaped structure (left) and visualization of the von Mises stress distribution of a structure optimized in the absence of stress constraints (right)

Table 3 summarizes the statistics of tests on this example. In all cases, the constraints on the total volume and maximum stress are satisfied. From the top block to the bottom one, as the allowed maximum stress increases, the objective value decreases. This trend in compliance is better visualized from the bar graphs in Fig. 11. There is however no clear pattern in the computation time for different stress limits.

Table 3 Data statistics for optimizing a step-shaped structure under three different stress limits

Fig. 11

Bar graph of the objective value and computation time for minimizing compliance of the step-shaped structure. The numbers 1 to 6 represent the different solution strategies in the order as they appear in Table 3, i.e., MMA ($\mathcal {Q}_{0}$), GCMMA ($\mathcal {Q}_{0}$), GCMMA ($\mathcal {Q}_{0}$)+MMA ($\mathcal {Q}_{0}$), MMA ($\mathcal {Q}_{1}$), ADMM ($\mathcal {Q}_{1}$), ADMM ($\mathcal {Q}_{1}$)+MMA ($\mathcal {Q}_{0}$). The triple indicates the increasing stress limits, from left to right, 0.6, 0.7 and 0.8

Comparing the final objectives from the six algorithms, it is observed that the augmented Lagrangian formulation in general results in smaller compliance values. ADMM is able to reduce the compliance value from MMA ($\mathcal {Q}_{0}$) by 8.78% ($\sigma _{\lim }=0.6$), 7.73% ($\sigma _{\lim }=0.7$) and 3.16% ($\sigma _{\lim }=0.8$), while for the hybrid strategy, ADMM ($\mathcal {Q}_{1}$) + MMA ($\mathcal {Q}_{0}$), the reduction is 7.06%, 6.44% and 4.57%, respectively. This reduction in objective is in agreement with results from the previous example. In these tests, the hybrid approach have comparable to slightly reduced computation time than that of MMA ($\mathcal {Q}_{0}$).

As a side note, we noticed that GCMMA was sensitive to the stress limit. As the stress limit became smaller, the constraints were not satisfied after 1000 iterations under a default setting. A parameter in GCMMA was thus modified for achieving satisfactory results. The optimization framework of GCMMA consists of “outer” and “inner” iterations. Within each outer iteration, depending on whether the approximation function is conservative or not, a number of inner iterations are carried out. The more inner iterations, the more conservative the approximation function. We found that an increase of the inner iterations in GCMMA from 5 to 20 was able to cope with the tight stress limit in our example.

Figure 12 shows the optimized structural layouts and stress distributions using different solvers, under the stress limit $\sigma _{\lim }=0.6$. The overall layouts are similar. In all cases, smooth geometry is developed around the sharp corners in the design domain, alleviating stress concentration. Interestingly, comparing (d)–(f) with (a), we find that the vertical substructure near the stress concentration region on the bottom corner (indicated by an arrow in (a)) is closer to the domain boundary in (d)–(f) than in (a). Note that in the structure optimized without stress constraints, shown in Fig. 10 (right), the vertical substructure conforms to the domain boundary with no gap. Similar trend can be observed in the L-shaped designs (Fig. 6).

Fig. 12

Optimized structural layouts and stress distributions in the step-shaped design domain using different optimization methods

5.3 Parameters and discussion

5.3.1 More examples

In addition to the four tests above, six other examples are tested. The specifications and detailed statistics can be found in Appendix 3. To compare results of different examples, we take MMA ($\mathcal {Q}_{0}$) as a reference, and normalize the compliance and computation time from other solution strategies by that of the reference. The average and standard deviation of the ten examples are summarized in Fig. 13. From the left, it is observed that ADMM ($\mathcal {Q}_{1}$) on average attains the smallest compliance, followed by the hybrid approach, ADMM ($\mathcal {Q}_{1}$) + MMA ($\mathcal {Q}_{0}$). On the right, the comparison shows that the computation time of the hybrid approach is marginally smaller than that of MMA ($\mathcal {Q}_{0}$).

Fig. 13

Comparison of the different solution strategies using the average and standard deviation from 10 examples. The numbers 1 to 6 represent the solution strategies in the order as they appear in other comparison figures and tables, i.e., MMA ($\mathcal {Q}_{0}$), GCMMA ($\mathcal {Q}_{0}$), GCMMA ($\mathcal {Q}_{0}$)+MMA ($\mathcal {Q}_{0}$), MMA ($\mathcal {Q}_{1}$), ADMM ($\mathcal {Q}_{1}$), ADMM ($\mathcal {Q}_{1}$)+MMA ($\mathcal {Q}_{0}$)

5.3.2 Lagrange multiplier λ and penalty parameter μ

Augmented Lagrangian formulation involves two parameters: the Lagrange multiplier λ and the penalty parameter μ in (9). These two parameters effectively control the discrepancy between α and $\tilde { {\sigma }}$. To achieve a smooth convergence process, in general it is beneficial to start with small λ and μ, and thus in the beginning iterations the combined objective is dominated by the compliance. We choose λ_e = 1 and μ = 0.5, such that the compliance (f_c(ρ)) accounts for more than 99.9% of the objective (L_μ(ρ,α,λ)) after the very first iteration. To penalize the discrepancy, μ is multiplied by 1.05 after every 5 iterations.

The evolution of the Lagrange multiplier is depicted in Fig. 14 (right) for three iterations. The actual stress and stress design variable are visualized in the second and third column, respectively. The magnitude of the Lagrange multiplier is large in regions where the stress design variable significantly deviates from the actual stress. As the optimization converges, the Lagrange multiplier takes values close to zero (see (f)).

Fig. 14

Visualization of the material distribution (ρ), actual stress ($\tilde {\sigma }$), stress design variable (α) and Lagrange multiplier λ at three different iterations

5.3.3 Initial iteration number

In the ADMM ($\mathcal {Q}_{1}$) + MMA ($\mathcal {Q}_{0}$) approach, a fixed number of ADMM iterations is performed. This value is chosen based on analyzing the stability in the compliance history. We use the relative standard deviation (RSD) of the compliance value over a period of five iterations as an index for evaluating stability,

$$ \begin{array}{@{}rcl@{}} RSD = \left( \frac{1}{4}\sum\limits_{i=j-2}^{j+2}(f_{i}-\bar{f_{j}})^{2}\right)^{\frac{1}{2}} / \bar{f_{j}}, \quad j > 2, \end{array} $$

(39)

with $\bar {f_{j}} = \frac {1}{5}{\sum }_{i=j-2}^{i=j+2}{f_{i}}$. From a number of tests we found that it took 12 to 25 iterations for the relative standard deviation to become less than 0.2%. Thus in our examples we chose to run 20 ADMM iterations.

In both examples the maximum stress is of the same magnitude to the range of density variables. We have performed additional tests by increasing the external forces by two orders of magnitude. Consequently the density variables and the stress variables are no longer of the same magnitude. In these tests, solving the new formulation by alternating optimization of design and stress (ADMM) is able to converge, while simultaneously solving for both sets of variables (MMA ($\mathcal {Q}_{1}$)) does not work well. Some scaling of the variables, possibly problem-dependent, might be needed for the simultaneous optimization.

5.3.4 Mass minimization

Augmented Lagrangian formulation for stress-constrained mass minimization has been studied in multiple recent works targeting 3D large scale optimization (da Silva et al. 2020; Senhora et al. 2020). We also performed a number of tests using different solution strategies for mass minimization. The optimized layout and stress distribution of the L-shape beam are shown in Fig. 15, while the statistics are reported in Table 4. In this example, ADMM achieves a slightly smaller volume fraction. However we note that this involves empirically selecting parameters, and the same set of parameters does not necessarily lead to consistent advantages in other examples. The objective of augmented Lagrangian formulation is written as

$$ L_{\mu}({\rho}, {\alpha}, {\lambda}) = \kappa {\rho}^{\mathsf{T}}{v} + {\lambda}^{\mathsf{T}} ({\alpha} - \tilde{{\sigma}}) + \frac{\mu}{2} \| {\alpha} - \tilde{{\sigma}} \|_{2}^{2}. $$

(40)

It consists of three terms, a scaled mass, the Lagrangian term, and the penalty term. The scaling factor κ is introduced to balance the three terms, following Senhora et al. (2020). The best set of parameters that fits different examples in the context of mass minimization remains to be found. We leave this as important future work.

Fig. 15

Final layouts of L-shaped structure on stress-based mass minimization topology optimization

Table 4 Statistics of stress-constrained mass minimization on the L-shaped beam. γ is the volume ratio, i.e., γ = ρ^Tv/1^Tv

6 Conclusion

In this paper, we have presented an interpretation of local stresses as optimization variables. The introduction of auxiliary stress variables enlarges the optimization space. It leads to an augmented Lagrangian formulation which can be solved by the alternating direction method of multipliers. Using simple truss examples, we have validated that the augmented Lagrangian formulation allows reaching the global optimum that is located in the degenerate sub-space. Numerical results on continuum structures suggest that the augmented Lagrangian formulation, solved using different solution strategies, leads to compliance values that are up to 9.1% smaller than that from the conventional formulation. In particular, using ADMM for solving the augmented Lagrangian formulation continued by MMA for the conventional formulation is most favorable in terms of both the objective and computation time.

The departure point of our approach is to introduce a second set of optimization variables corresponding to local (stress) constraints. We envision this is applicable to other topology optimization problems with local constraints, such as the minimum feature scale (Zhou et al. 2015) and porosity (Wu et al. 2018). The computational benefit for reformulating such problems is yet to be investigated.

Appendices

Appendix 1. Sensitivity analysis

The first term on the right-hand side in (38), $\frac {\partial f_{c}( {\rho })}{\partial \phi _{e}}$, is the same as in conventional density approaches (e.g., Wang et al. 2011), and thus is left out here. The second and third terms involves $\frac {\partial \tilde { {\sigma }}}{\partial \phi _{e}}$. Consider element i. Using the chain rule, $\frac {\partial \tilde {\sigma }_{i}}{\partial \phi _{e}}$ is calculated by

$$ \begin{array}{@{}rcl@{}} \frac{\partial \tilde{\sigma}_{i}}{\partial \phi_{e}} =\sum\limits_{j\in {S}_{e}} \frac{\partial \tilde{\sigma}_{i}}{\partial \rho_{j}} \frac{\partial \rho_{j}}{\partial \tilde{\phi}_{j}} \frac{\partial \tilde{\phi}_{j}}{\partial \phi_{e}}. \end{array} $$

(A1.1)

$\frac {\partial \tilde {\phi }_{j}}{\partial \phi _{e}}$ and $\frac {\partial \rho _{j}}{\partial \tilde {\phi }_{j}}$ are derived from (31) and (33), respectively,

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial \tilde{\phi}_{j}}{\partial \phi_{e}}= \frac{\omega_{j}(x_{e},r)v_{e}}{{\sum}_{i\in {S}_{j}} \omega_{j}(x_{i},r)v_{i}}, \end{array} $$

(A1.2)

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial \rho_{j}}{\partial \tilde{\phi}_{j}} =\beta\frac{1-\tanh^{2}(\beta(\eta-\tilde{\phi}_{j}))}{\tanh(\beta\eta)+\tanh(\beta(1-\eta))}. \end{array} $$

(A1.3)

With the definition of $\tilde {\sigma }_{e}$ given by (34), the derivative $\frac {\partial \tilde {\sigma }_{i}}{\partial \rho _{j}}$ has two cases,

$$ \frac{\partial \tilde{\sigma}_{i}}{\partial \rho_{j}}=\left\{ \begin{aligned} &{\rho_{i}^{q}}\big(\frac{\partial \bar{\sigma}_{i}}{\partial {\sigma}_{i}}\big)^{\mathsf{T}} \frac{\partial {\sigma}_{i}}{\partial \rho_{j}}, \quad & i \neq j;\\ &q \rho_{i}^{q-1} \bar{\sigma}_{i}+{\rho_{i}^{q}}\big(\frac{\partial \bar{\sigma}_{i}}{\partial {\sigma}_{i}}\big)^{\mathsf{T}} \frac{\partial {\sigma}_{i}}{\partial \rho_{j}}, \quad& i = j. \end{aligned} \right. $$

(A1.4)

1.1 Derivative of the von Mises stress w.r.t. the stress components

The von Mises stress $\bar {\sigma }_{i}$ is computed from the Voigt notation of stress tensor σ_i = [σ_i,x,σ_i,y,τ_i,xy]^T by (35) and (36). Thus, the derivative of the von Mises stress with respect to its stress components is

$$ \begin{array}{@{}rcl@{}} \frac{\partial \bar{\sigma}_{i}}{\partial {\sigma}_{i}} = [\frac{\partial \bar{\sigma}_{i}}{\partial \sigma_{i,x}}, \frac{\partial \bar{\sigma}_{i}}{\partial \sigma_{i,y}},\frac{\partial \bar{\sigma}_{i}}{\partial \tau_{i,xy}}]^{\mathsf{T}}, \end{array} $$

(A1.5)

where

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial \bar{\sigma}_{i}}{\partial \sigma_{ix}} = \frac{1}{2\bar{\sigma}_{i}}(2\sigma_{ix}-\sigma_{iy}),\\ &&\frac{\partial \bar{\sigma}_{i}}{\partial \sigma_{iy}} = \frac{1}{2\bar{\sigma}_{i}}(2\sigma_{iy}-\sigma_{ix}),\\ &&\frac{\partial \bar{\sigma}_{i}}{\partial \tau_{ixy}} = \frac{3\tau_{ixy}}{\bar{\sigma}_{i}}. \end{array} $$

1.2 Derivative of the stress components w.r.t. the density

From the stress form, (37), the derivative of stress is given by

$$ \begin{array}{@{}rcl@{}} \frac{\partial {\sigma}_{i}}{\partial \rho_{j}} = {D}_{0}{B}_{c}\frac{\partial {u}_{i}}{\partial \rho_{j}}. \end{array} $$

(A1.6)

It requires the derivative of the displacement field regarding the density. This is obtained by differentiating (6),

$$ \begin{array}{@{}rcl@{}} \frac{\partial {K}}{\partial \rho_{j}} {U} + {K} \frac{\partial {U}}{\partial \rho_{j}} = \frac{\partial {F}}{\partial \rho_{j}}. \end{array} $$

(A1.7)

Since the load vector F is assumed to be constant, the above equation leads to

$$ \begin{array}{@{}rcl@{}} \frac{\partial {U}}{\partial \rho_{j}} = -{K}^{-1} \frac{\partial {K}}{\partial \rho_{j}}{U}, \end{array} $$

(A1.8)

where $\frac {\partial {K}}{\partial \rho _{j}}$ is derived from the function of K in (7). By substituting (A1.8) into (A1.6), we get

$$ \begin{array}{@{}rcl@{}} \frac{\partial {\sigma}_{i}}{\partial \rho_{j}} = -{D}_{0}{B}_{c}({K}^{-1} \frac{\partial {K}}{\partial \rho_{j}}{U})_{i}, \end{array} $$

(A1.9)

where the subscript ()_i indicates extracting the entries that correspond to the degrees of freedom of element i.

1.3 Adjoint method

The adjoint method is used to avoid solving (A1.9) for each combination of i and j. The last two terms on the right in (38), $-( {\lambda }^{\mathsf {T}}\frac {\partial {\tilde {\sigma }}}{\partial \phi _{e}} + \mu ( {\alpha }- {\sigma })^{\mathsf {T}}\frac {\partial {\tilde {\sigma }}}{\partial \phi _{e}})$, expands as,

$$ \begin{array}{@{}rcl@{}} &&({\lambda}+\mu({\alpha}-{\sigma}))^{\mathsf{T}}\frac{\partial {\tilde{\sigma}}}{\partial \phi_{e}} = \sum\limits_{i=1}^{N}(\lambda_{i}+\mu(\alpha_{i}-\sigma_{i}))\frac{\partial \tilde{\sigma}_{i}}{\partial \phi_{e}} \end{array} $$

(A1.10)

$$ \begin{array}{@{}rcl@{}} && = \sum\limits_{i=1}^{N}(\lambda_{i}+\mu(\alpha_{i}-\sigma_{i}))\Big(\sum\limits_{j\in {S}_{e}}\frac{\partial \tilde{\sigma}_{i}}{\partial \rho_{j}}\frac{\partial \rho_{j}}{\partial \tilde{\phi}_{j}}\frac{\partial \tilde{\phi}_{j}}{\partial \phi_{e}}\Big) \\ && = \sum\limits_{j\in {S}_{e}}\Big(\sum\limits_{i=1}^{N}(\lambda_{i}+\mu(\alpha_{i}-\sigma_{i}))\frac{\partial \tilde{\sigma}_{i}}{\partial \rho_{j}}\Big)\frac{\partial \rho_{j}}{\partial \tilde{\phi}_{j}}\frac{\partial \tilde{\phi}_{j}}{\partial \phi_{e}}. \end{array} $$

(A1.11)

Let Θ_j denote ${\sum }_{i=1}^{N}(\lambda _{i}+\mu (\alpha _{i}-\sigma _{i}))\frac {\partial \tilde {\sigma }_{i}}{\partial \rho _{j}}$. Substituting (A1.6) in (A1.4) and then (A1.4) in Θ_j, we obtain

$$ \begin{array}{@{}rcl@{}} {\varTheta}_{j} &= &\sum\limits_{i=1}^{N}(\lambda_{i}+\mu(\alpha_{i}-\tilde{\sigma}_{i})){\rho_{i}^{q}}\Big(\frac{\partial \bar{\sigma}_{i}}{\partial {\sigma}_{i}}\Big)^{\mathsf{T}}{D}_{0}{B}_{c}\frac{\partial {u}_{i}}{\partial \rho_{j}} \end{array} $$

(A1.12)

$$ \begin{array}{@{}rcl@{}} &&+(\lambda_{j}+\mu(\alpha_{j}-\tilde{\sigma}_{j}))q\rho_{j}^{q-1}\bar{\sigma}_{j}, \end{array} $$

(A1.13)

with $\frac {\partial {u}_{i}}{\partial \rho _{j}} = (- {K}^{-1} \frac {\partial {K}}{\partial \rho _{j}} {U})_{i}$. Introducing an adjoint vector δ and solving

$$ \begin{array}{@{}rcl@{}} {K}{\delta} = -\underset{i=1}{\overset{N}{\mathrm{A}}}(\lambda_{i}+\mu({\alpha_{i}}-{\tilde{\sigma_{i}}})){\rho_{i}^{q}}{B}_{c}^{T}{D}_{0}^{T}\Big(\frac{\partial \bar{\sigma}_{i}}{\partial {\sigma}_{i}}\Big), \end{array} $$

(A1.14)

where A indicates matrix assembly, (A1.13) is calculated by

$$ \begin{array}{@{}rcl@{}} {\varTheta}_{j} = {\delta}_{j}^{\mathsf{T}}\frac{\partial {K}_{j}}{\partial \rho_{j}}{u}_{j}+(\lambda_{j}+\mu({\alpha_{j}}-{\tilde{\sigma_{j}}}))q\rho_{j}^{q-1}\bar{\sigma}_{j}, \end{array} $$

(A1.15)

where vector δ_j extracts entries in the adjoint vector δ that correspond to degrees of freedom of element j.

Appendix 2. Solving the conventional formulation

Maximum stress approximation

In ADMM the stress constraint is an upper bound on the optimization variable α. This renders commonly used aggregation schemes unnecessary. However, in the second part of the hybrid approach, aggregation schemes are needed for the MMA solver.

The stress constraint (4) is equivalent to

$$ \max({\alpha}) \le \sigma_{\lim}, $$

(A2.1)

where α = (α₁,α₂,⋯ ,α_n), with n being the number of elements. $\alpha _{e}=\tilde {\sigma }_{e}, \forall e$. It is calculated by (34). We use the p-norm to approximate the maximum function, i.e.,

$$ {\alpha}_{PN} = \left( \sum\limits_{i=1}^{N} {\alpha}_{i}^{p}\right)^{\frac{1}{p}}. $$

(A2.2)

The p-norm approaches the maximum as the positive p increases. p = 8 is used in our examples. It has been shown that a scaling based on the approximation quality in previous iterations improves the approximation accuracy (Le et al. 2010). This is implemented here as

$$ \max({\alpha}) \approx c^{[i]} \cdot {\alpha}^{[i]}_{PN} $$

(A2.3)

The scaling factor c^[i] accounts for the discrepancy between the actual maximum ${\alpha }_{\max \limits }$ and approximated maximum α_PN in previous iterations,

$$ c^{[i]} = \xi \frac{{\alpha}^{[i]}_{\max}}{{\alpha}^{[i]}_{PN}}+(1-\xi)c^{[i-1]}, \quad i \ge 1, $$

(A2.4)

where the weighting factor ξ = 0.5 is chosen and the scaling factor is initialized with c^[0] = 1.

Sensitivity analysis

The derivative of the maximum stress regarding to ϕ_e is stated below:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \max({{\alpha}})}{\partial \phi_{e}} \approx \frac{\partial c\cdot{{\alpha}}_{PN}}{\partial \phi_{e}} = c\sum\limits_{j\in {S}_{e}} \frac{\partial {{\alpha}}_{PN}}{\partial \rho_{j}}\frac{\partial \rho_{j}}{\partial \tilde{\phi}_{j}}\frac{\partial \tilde{\phi}_{j}}{\partial \phi_{e}}. \end{array} $$

(A2.5)

where $\frac {\partial \rho _{j}}{\partial \tilde {\phi }_{j}}$ and $\frac {\partial \tilde {\phi }_{j}}{\partial \phi _{e}}$ are given in (A1.3) and (A1.2), respectively. We use the chain rule to calculate $\frac {\partial {{\alpha }}_{PN}}{\partial \rho _{j}}$:

$$ \begin{array}{@{}rcl@{}} \frac{\partial {{\alpha}}_{PN}}{\partial \rho_{j}} = \sum\limits_{k=1}^{N}\frac{\partial {{\alpha}}_{PN}}{\partial {\alpha_{k}}} \frac{\partial {\alpha_{k}}}{\partial \rho_{j}}, \end{array} $$

(A2.6)

with $\frac {\partial {{\alpha }}_{PN}}{\partial {\alpha _{k}}} = ({\sum }_{i=1}^{N} {\alpha _{i}}^{p})^{\frac {1}{p}-1}{\alpha _{k}}^{p-1}$, and $\frac {\partial {\alpha _{k}}}{\partial \rho _{j}}$, i.e., $\frac {\partial \tilde {\sigma }_{k}}{\partial \rho _{j}}$, is given in (A1.4).

Appendix 3. More examples

The design domain and boundary conditions of six more tests are illustrated in Fig. 16 on the left of each example. The three C-shaped structures share the same design domain but with different boundary conditions. The concentrated forces are applied over a short span of 4 elements horizontally. Fixations are applied either to the entire boundary edge or ten elements. In (d) and (f), a distributed force with a sum of F = 5 is applied on the top edge. Figure16, on the right of each example, shows the stress distribution in the structural layout optimized without stress constraints. The stress limits used in stress-constrained compliance minimization are 0.4, 0.4, 0.4, 0.4, 2.5, 2, respectively. The results of different solution strategies are summarized in Table 5, while the optimized structures are shown in Figs. 17, 18, 19, 20, 21 and 22.

Fig. 16

In each example, from left to right: illustration of the design domain and boundary conditions, the optimized material distribution without stress constraints, and the corresponding stress distribution

Table 5 Statistics for optimizing six different structures/boundary conditions

Fig. 17

Optimized structural layouts and stress distributions in the C-shaped structure 1 using different solution strategies

Fig. 18

Optimized structural layouts and stress distributions in the C-shaped structure 2 using different solution strategies

Fig. 19

Optimized structural layouts and stress distributions in the C-shaped structure 3 using different solution strategies

Fig. 20

Optimized structural layouts and stress distributions in the O-shaped structure using different solution strategies

Fig. 21

Optimized structural layouts and stress distributions in the P-shaped structure using different solution strategies

Fig. 22

Optimized structural layouts and stress distributions in the S-shaped structure using different solution strategies