An optimal control method for time-dependent fluid-structure interaction problems

Abstract

In this article, we derive an adjoint fluid-structure interaction (FSI) system in an arbitrary Lagrangian-Eulerian (ALE) framework, based upon a one-field finite element method. A key feature of this approach is that the interface condition is automatically satisfied and the problem size is reduced since we only solve for one velocity field for both the primary and adjoint system. A velocity (and/or displacement)-matching optimisation problem is considered by controlling a distributed force. The optimisation problem is solved using a gradient descent method, and a stabilised Barzilai-Borwein method is adopted to accelerate the convergence, which does not need additional evaluations of the objective functional. The proposed control method is validated and assessed against a series of static and dynamic benchmark FSI problems, before being applied successfully to solve a highly challenging FSI control problem.

1 Introduction

Fluid-structure interactions (FSI) are ubiquitous throughout natural and industrial flow systems. In the human body, for example, almost all fluid-conveying vessels are flexible with even small changes in internal fluid pressure inducing strong FSI which can determine a vessel’s biological function or dysfunction (Grotberg and Jensen 2004). Important physiological examples include pulse-wave propagation in arteries, wheezing during exhalation and flow-induced deformation and ultimate rupture of arterial and cerebral aneurysms (Heil and Hazel 2011). Industrial examples are equally common, and the motion of fluid through a domain with elastic boundaries is extremely important in, for example, the adhesion of elastic elements and in hydraulic fracturing for shale-gas production (Box et al. 2018). Aeroelastic phenomena are also extremely important in aviation, and in particular FSI determine whirl flutter instabilities associated with rotorcraft and propeller systems, buffet responses and dynamic responses of aero-structures in gusts (Beran et al. 2017).

Computational FSI has developed rapidly and reached a significant level of maturity, with broad applications including aerodynamics (Bazilevs et al. 2013; Tezduyar and Sathe 2007; Davidson et al. 2012), biomechanics (Moireau et al. 2012; Bazilevs et al. 2010a, 2010b) and ocean mechanics (Bai and Taylor 2009; Finnegan and Goggins 2012; Calderer et al. 2014). A general FSI system has a solid surrounded by a fluid (such as aeroplane) or a solid surrounding a fluid (such as for blood vessels). The interface between the fluid and solid of a FSI system is an unknown of the coupled system, which can be solved by imposing continuity conditions through the interface, such as continuity of velocity and normal stress. Numerical methods for FSI problem have been intensively studied during the past decades. Based upon mesh types, the FSI numerical methods can be broadly categorised into fitted-mesh methods (Heil 2004; Hecht and Pironneau 2017; Tanaka and Kashiyama 2006) and unfitted-mesh methods (Peskin 2002; Zhang et al. 2004; Baaijens 2001; Boffi and Gastaldi 2016; Kreissl and Maute 2012); based upon solving strategies, these numerical methods include partitioned/segregated methods (Küttler and Wall 2008; Degroote et al. 2009, 2013; Bazilevs et al. 2013) and monolithic/fully coupled methods (Heil 2004, 2008; Muddle et al. 2012; Wang et al. 2017, 2020); and based upon solving variables, there are one-field (one velocity) methods (Wang et al. 2017, 2019a, 2019b; Hecht and Pironneau 2017) and multi-field (velocity, displacement and Lagrange multiplier) methods (Muddle et al. 2012; Boffi et al. 2015, 2016). In a recent study (Wang et al. 2020), we proposed an energy-stable one-field monolithic method based on an ALE fitted mesh, which is adopted to derive the optimality condition for the FSI control formulation in this article.

Optimal control is a classical theory which seeks solutions for a stationary or dynamical system such that an objective function can be optimised (Tröltzsch 2010). Adjoint-based methods have solid mathematical foundations which can efficiently compute the gradient of a function, and have been widely adopted to solve optimal control problems. Optimal flow control has been fully developed in the past decades, including distributed control (Gunzburger 2003; Abergel and Temam 1990; Hinze et al. 2012): solution existence of a static flow control by a distributed force is analysed in Abergel and Temam (1990) and a piecewise optimal control method for dynamical case has been presented at the same time; a distributed flow control method is implemented by the multigrid method in Hinze et al. (2012). Optimal flow control also includes shape optimisations from pioneering work (Pironneau 1973; 1974; Glowinski and Pironneau 1975; Mohammadi and Pironneau 2010) to recent developments in Montenegro-Johnson and Lauga (2015), Henrot and Privat (2010), Dapogny et al. (2018), and Jenkins and Maute (2016): the first-order optimality condition is derived for the Stokes flow (Pironneau 1973) and Navier-Stokes flow (Pironneau 1974) by a variational approach, and a numerical algorithm is presented in Glowinski and Pironneau (1975); a different minimum-drag profile of Stokes flow has been derived in Montenegro-Johnson and Lauga (2015) given a fixed surface, which has a slender shape compared with the classical results in Pironneau (1973, 1974) given a fixed volume; the classical optimisation of a solid surrounded by a fluid has been extended to the case of a solid surrounding a fluid in Henrot and Privat (2010), in which the authors prove that a cylindrical pipe is not the optimal shape for minimising the viscous dissipation of its inside flow, and a useful implementation of this method using FreeFEM++ is presented in Dapogny et al. (2018). However, few studies of optimal FSI control, in particular time-dependent FSI problems, have appeared in the literature to date and there is no recognised benchmark solution for comparison. Although there has been some progress reported in Heners et al. (2018), Chirco and Manservisi (2020), Failer and Richter (2020), and Wick and Wollner (2020), these are still very challenging both analytically and numerically. The problem falls into the category of inverse FSI problems of moving shape control (Moubachir and Zolesio 2006). The main challenges are summarised below.

A particular challenge in achieving optimal FSI control is to formulate the coupling conditions on the fluid-structure interface into the optimality system (Chirco et al. 2017; Failer et al. 2016). For example, Failer et al. (2016) enforce the coupling condition weakly to analyse optimal control for a linear FSI problem, whereas Chirco and Manservisi (2020) and Chierici et al. (2019) introduce an auxiliary mesh displacement in the solid domain to enforce the coupling condition. In Failer and Richter (2020) and Wick and Wollner (2020), the authors solve both solid velocity and displacement, together with fluid velocity and pressure using a monolithic Newton solver. In our previous work, we formulated the FSI problem using a one-field FEM scheme (Wang et al. 2017, 2019a) and solved it in a fully coupled system, so that the interface conditions are satisfied automatically in the primal FSI equations and are therefore not present in the adjoint FSI equations. As a result, both the primal and adjoint FSI system may be solved in the same manner as a fluid-only problem.

Another difficulty in the optimal dynamic control, of either fluid or FSI problems, is that the adjoint equations are coupled with the primal equations in both time and space (Hinze et al. 2012; Abergel and Temam 1990). A major challenge in the time coupling arises because the adjoint problem is propagated backwards in time, which uses the solution of the primal problem as initial conditions. The space coupling challenge is due to the non-linear terms in the primal equations, which introduce the solution of the primal equations to the adjoint equations. In Degroote et al. (2013), a multigrid is used to solve a single space-time discretisation of the primal problem. Alternatively, one may apply the piecewise-in-time optimal control approach, i.e. approximating the dynamic control by a sequence of local steady-state problems (Abergel and Temam 1990). The time-coupled primal and adjoint problems can also be decoupled and solved in an iterative manner as done in Heners et al. (2018), which also solves the FSI sub-problems using a partitioned/decoupled method. In this article, we decouple the primal and adjoint equations in time; however, we solve both the FSI system and the adjoint FSI system using a one-field monolithic approach (Wang et al. 2020).

Finally, efficiently selecting a step size for a minimisation algorithm, such as the gradient descent (GD) method, is usually costly. The Armijo rule is widely used in the context of the GD algorithm (Mohammadi and Pironneau 2010; Gerdes et al. 2014); however, this is computationally expensive for dynamic control problems because one needs several evaluations of the objective function, consequently several computations of the state equations. A constant step size (Heners et al. 2018) does not need evaluation of the objective functional; however, this is typically quite inefficient since it may need many iterations in order to reduce the objective sufficiently. In this article, we adopt a stabilised Barzilai-Borwein (BB) method to accelerate the iteration (Burdakov et al. 2019), which saves significant numerical effort and guarantees the quality of step size at the same time.

The original contributions of the paper are summarised as follows: (1) we consider general boundary and initial conditions, consider a complete coupling between the adjoint FSI velocity and the velocity of configuration, and derive the optimality conditions for optimal control of dynamic FSI problems in an arbitrary Lagrangian-Eulerian (ALE) formulation; (2) we formulate the whole control system using one velocity field, and consequently reduce the number of degrees of freedom of the FSI problem. This one-field formulation is very similar to a pure fluid-control formulation, which allows us to do similar analysis as a fluid control method (Abergel and Temam 1990); (3) we adopt a stabilised BB method to select the step size, which does not need additional evaluations of the objective, and has the same cost as using a constant step size but converges faster. Because of the above features, we demonstrate that it is computationally feasible to solve extremely challenging optimal FSI problems, by solving tens (at most hundreds) of CFD simulations.

The paper is organised as follows. In Section 2, the control equations for the FSI problem are introduced in an ALE framework. In Section 3, the optimisation problem is introduced, followed by gradient descent method in Section 4. The main derivation of the optimality system using the Lagrange multiplier method is presented in Section 5. Discretisation and implementation are considered in Section 6. Numerical results are reported in Section 7, with conclusions drawn in Section 8.

2 PDE for the FSI system in an ALE formulation

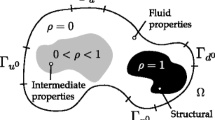
We introduce the FSI system using a benchmark test, sketched in Fig. 1, which was first proposed in Turek and Hron (2006) (named FSI3). Let ${{\varOmega }_{t}^{f}}\subset \mathbb {R}^{d}$ and ${{\varOmega }_{t}^{s}}\subset \mathbb {R}^{d}$ be the fluid and solid domain, respectively (which are time-dependent regions), and ${\varGamma }_{t}=\overline {{\varOmega }}_{t}^{f} \cap \overline {{\varOmega }}_{t}^{s}$ is the moving interface between the fluid and solid, where the superscripts f and s denote fluid and solid, respectively, and the subscript t explicitly highlights when regions are time dependent. ${\varOmega }=\overline {{\varOmega }}_{t}^{f} \cup \overline {{\varOmega }}_{t}^{s}$ is a fixed domain with an outer boundary ${\varGamma }_{in}+{\varGamma }_{w_{1}}+{\varGamma }_{N}$ and inner boundary ${\varGamma }_{w_{0}}$ (the circle, as shown in Fig. 1). For notational convenience, denote by ${\varGamma }_{w}={\varGamma }_{w_{0}}+{\varGamma }_{w_{1}}$ the wall boundaries, Γ_D = Γ_in + Γ_w on which the Dirichlet boundary condition (BC) is imposed, and Γ = Γ_D + Γ_N all the boundaries with Γ_N being the Neumann boundary on which the zero-normal stress is enforced. In this case, an ALE frame of reference is convenient to describe the FSI system, because it can track the fluid-solid interface Γ_t and move arbitrarily elsewhere.

Fig. 1

Diagram of the FSI benchmark from Turek and Hron (2006) (not in scale), with ${\varGamma }_{t}=\overline {{\varOmega }}_{t}^{f} \cap \overline {{\varOmega }}_{t}^{s}$

In this article, we consider both an incompressible fluid and an incompressible hyperelastic isotropic solid. We shall only solve for one velocity field in the whole domain, and the conservation of momentum and conservation of mass take the same form in the fluid and solid (just differing in the specific expressions of the stress tensor). Therefore, it is convenient to introduce an indicator function 1_ω(x) = 1 if x ∈ ω and 1_ω(x) = 0 otherwise. Let $\rho =\rho ^{f}\textit {1}_{{{\varOmega }_{t}^{f}}}+\rho ^{s}\textit {1}_{{{\Omega }_{t}^{s}}}$, $\textbf {u}=\textbf {u}^{f}\textit {1}_{{{\varOmega }_{t}^{f}}}+\textbf {u}^{s}\textit {1}_{{{\varOmega }_{t}^{s}}}$, ${ {\sigma }}={ \sigma }^{f}\textit {1}_{{{\varOmega }_{t}^{f}}}+{ \sigma }^{s}\textit {1}_{{{\varOmega }_{t}^{s}}}$ denote the density, velocity vector and stress tensor respectively. The control partial differential equations, with initial and boundary conditions, for the FSI problem can then be expressed as follows.

$$ \begin{array}{@{}rcl@{}} \text{Momentum equation:} && \rho\frac{\partial\textbf{u}}{\partial t} +\rho\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\textbf{u}\\ &&-\nabla \cdot {\sigma} =\textbf{f}\textit{1}_{{{\varOmega}_{t}^{s}}}, \end{array} $$

(1)

$$ \begin{array}{@{}rcl@{}} \text{Continuity equation:} && \nabla \cdot \textbf{u}=0, \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} \text{ALE equation:} && \rho\frac{\partial\textbf{w}}{\partial t}-\nabla\cdot(\mu\mathrm{D}\textbf{w}\\&&+\lambda\left( \nabla\cdot\textbf{w}\right)\textbf{I})=0, \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} \text{Initial condition:} && \left. \textbf{u}\right|_{t=0}=\textbf{u}_{0}, \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} \text{Dirichlet BC:} && \left.\textbf{u}\right|_{{\varGamma}_{D}}=\bar{\textbf{u}}\textit{1}_{{\varGamma}_{in}}, \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} \text{Neumann BC:} && \left.{ \sigma}\textbf{n}\right|_{{\varGamma}_{N}}=\bar{\textbf{h}}, \end{array} $$

(6)

$$ \begin{array}{@{}rcl@{}} \text{ALE initial condition:} && \left. \textbf{w}\right|_{t=0}=\textbf{w}_{0}, \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} \text{ALE Dirichlet BC:} && \left.\textbf{w}\cdot\textbf{n}\right|_{{\varGamma}-{\varGamma}_{w_{0}}}\\&&=0, \quad \left.\textbf{w}\right|_{{\varGamma}_{w_{0}}}=\textbf{0}, \end{array} $$

(8)

$$ \begin{array}{@{}rcl@{}} \text{ALE Neumann BC:} && \left.\textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}\right)\cdot\right.\\&&\left. {\tau}\right|_{{\varGamma}-{\varGamma}_{w_{0}}}=0, \end{array} $$

(9)

$$ \begin{array}{@{}rcl@{}} \text{Continuity of velocity:} && \left.\left( \textbf{u}^{s}-\textbf{u}^{f}\right)\right|_{{\varGamma}_{t}}=\textbf{0}, \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} \text{Continuity of ALE velocity:} && \left.\left( \textbf{w}-\textbf{u}\right)\right|_{{\varGamma}_{t}}=\textbf{0}, \end{array} $$

(11)

$$ \begin{array}{@{}rcl@{}} \text{Continuity of normal stress:} && \left.\left( {\sigma}^{s}-{\sigma}^{f}\right)\textbf{n}^{s}\right|_{{\varGamma}_{t}}=\textbf{0}. \end{array} $$

(12)

In the above, w is the velocity vector of the ALE frame, f is a distributed control variable, μ and λ are artificial Lamé constants for the ALE equation (Richter and Wick 2010), and n and τ are the normal and tangential direction of the outer boundary, respectively, as shown in Fig. 1. The stress tensor of an incompressible Newtonian flow is expressed as:

$$ {\sigma}^{f}=\mu^{f}\mathrm{D}\textbf{u}^{f}-p^{f}\textbf{I}, $$

(13)

with D(⋅) = ∇(⋅) + ∇^T(⋅), and μ^f being the viscosity parameter (which is unrelated to the artificial Lamé constant μ used in the ALE (3)). The stress tensor of an incompressible neo-Hookean solid is expressed as Hecht and Pironneau (2017):

$$ {\sigma}^{s}=c_{1}\left( \mathrm{D}\textbf{d}-\nabla^{T}\textbf{d}\nabla\textbf{d}\right)-p^{s}\textbf{I}, $$

(14)

with d being the solid displacement, and c₁ being the elasticity parameter. Notice that although the solid stress tensor is expressed as a function of displacement d, we shall not solve for d as an independent variable. Instead we view it as a function of velocity, and solve the whole FSI problem based upon a one-field-velocity method, which uses an ALE description for both the fluid and solid equations. When solving the mesh equation, the mesh velocity follows the fluid velocity only at the interface. Afterwards, both the fluid and solid meshes are updated based on the mesh velocity, and this can improve the mesh quality for the fluid as well as the solid (Wang et al. 2020).

3 The optimisation problem

Let L²(ω) be the square integrable functions in domain ω with inner product $\left (u,v\right )_{\omega }=\left ({\int \limits }_{\omega } uvdx\right )$, ∀u,v ∈ L²(ω), and the induced norm $\|v\|_{L^{2}\left (\omega \right )}=\left (v,v\right )_{\omega }^{1/2}$, ∀v ∈ L²(ω). For a vector function v ∈ L²(ω)^d, the norm is defined component-wise as $\|\textbf {v}\|_{L^{2}\left (\omega \right )^{d}}^{2}={\sum }_{i=1}^{d}\|v_{i}\|_{L^{2}\left (\omega \right )}^{2}$. Then, let $H^{1}(\omega )=\left \{v: v, \nabla v\in L^{2}(\omega )^{d}\right \}$, and denote by $H_{u\left ({\varGamma }\right )}^{1}(\omega )$ the subspace of H¹(ω), which has the boundary data u on Γ. We also denote by ${L_{0}^{2}}({\varOmega })$ the subspace of L²(Ω) whose functions have zero mean values.

We consider the following optimisation problem: reducing the discrepancy between the state velocity u (and/or displacement d) and the goal velocity u_g (and/or displacement d_g) profile, in a control region ${\varOmega }^{c}\subseteq {\varOmega }$ (and/or ${{\varOmega }_{t}^{s}}$), by controlling a distributed body force f.

Problem 1

Given an objective velocity profile u_g and a time interval ${\Theta }=\left [0, T\right ]$,

$$ \underset{\textbf{f}\in L^{2}\left( {{\varTheta}\times{\varOmega}}\right)^{d}}{\text{minimise}} \quad \hat{J}(\textbf{u}\left( \textbf{f}\right)) =J(\textbf{u}\left( \textbf{f}\right))+\frac{\theta}{2}\|\textbf{f}\|_{L^{2}({\varTheta}\times{\varOmega})^{d}}^{2}, $$

(15)

with

$$ \begin{array}{lll} & J(\textbf{u}\left( \textbf{f}\right)) = \frac{\beta_{1}}{2}\|\textbf{u}-\textbf{u}_{g}\|_{L^{2}({\varTheta}\times{\varOmega}^{c})^{d}}^{2} +\frac{\beta_{2}}{2}\|\textbf{d}-\textbf{d}_{g}\|_{L^{2}({{\varTheta}\times{\varOmega}_{t}^{s}})^{d}}^{2} \\ &+\frac{\gamma_{1}}{2}\|\textbf{u}(T) - \textbf{u}_{g}(T)\|_{L^{2}({\varOmega}^{c})^{d}}^{2} +\frac{\gamma_{2}}{2}\|\textbf{u}(T)-\textbf{u}_{g}(T)\|_{L^{2}({{\varOmega}_{t}^{s}})^{d}}^{2}, \end{array} $$

(16)

subject to (1)–(12), where f are the control variables, β₁ and β₂ are the weights of controlling velocity and displacement, respectively, and γ₁ and γ₂ are the weights in order to control the final velocity profile in Ω^c and ${{\varOmega }_{t}^{s}}$ respectively. The first term J(⋅) in (15) is the real objective to be minimised, and the second term is a regularisation term with a regularisation parameter θ. If θ is too large then the real objective is not achieved accurately, whereas if θ is too small, this may cause convergence issues for the numerical scheme.

4 The gradient descent algorithm

A general method of iteratively solving the optimisation Problem 1 is to use, from an initial point f⁰, the Taylor expansion to expand $J\left (\textbf {u}\left (\textbf {f}\right )\right )$ around f^k:

$$ \hat{J}\left( \textbf{u}\left( \textbf{f}\right)\right) \approx \hat{J}\left( \textbf{u}\left( \textbf{f}^{k}\right)\right) +\delta \hat{J}\left( \textbf{u}\left( \textbf{f}^{k}\right)\right)[\delta\textbf{f}], $$

(17)

with $\delta \hat {J}\left (\textbf {u}\left (\textbf {f}^{k}\right )\right )[\delta \textbf {f}]$ being the Gâteaux variation (see Rall (2014) or A) with respect to f (NOT u) at point f^k along the direction δf:

$$ \delta \hat{J}\left( \textbf{u}\left( \textbf{f}^{k}\right)\right)[\delta\textbf{f}] =\left.\frac{d}{d\epsilon}\hat{J}\left( \textbf{u}\left( \textbf{f}^{k}+\epsilon\delta\textbf{f}\right)\right)\right|_{\epsilon=0}. $$

(18)

The gradient descent with a line search algorithm seeks a direction ∥δf^k∥ = 1 such that:

• 1. It is a descent: $\delta \hat {J}\left (\textbf {u}\left (\textbf {f}^{k}\right )\right )[\delta \textbf {f}^{k}]<0$;

• 2. It is the negative gradient: $\delta \textbf {f}^{k} = \underset {\|\delta \textbf {f}\|=1}{\text {argmax}} |\delta \hat {J}(\textbf {u}(\textbf {f}^{k}))[\delta \textbf {f}]|$;

• 3. And it is the steepest: $\alpha ^{k}=\underset {\alpha }{\text {argmin}}\hat {J}\left (\textbf {u}\left (\textbf {f}^{k}+\alpha \delta \textbf {f}^{k}\right )\right )$.

Then, f is updated as:

$$ \textbf{f}^{k+1}=\textbf{f}^{k}+\alpha^{k}\delta\textbf{f}^{k}, \quad k=0,1,2,\ldots $$

(19)

The exact line search for the step size α^k is costly. In this paper, we use a stabilised Barzilai-Borwein (BB) method proposed in Burdakov et al. (2019) to optimise analytical functions (k > 0):

$$ \alpha^{k}= \begin{cases} min\left( {\alpha_{1}^{k}},{\alpha_{3}^{k}}\right) \quad {\alpha_{1}^{k}}>0 \\ min\left( {\alpha_{2}^{k}},{\alpha_{3}^{k}}\right) \quad {\alpha_{1}^{k}}<0 \end{cases} , $$

(20)

where

$$ {\alpha_{1}^{k}}=\frac{\left( \textbf{f}^{k}-\textbf{f}^{k-1}, \delta\textbf{f}^{k-1}-\delta\textbf{f}^{k}\right)_{L^{2}\left( {\varTheta}\times\omega\right)}}{\|\delta\textbf{f}^{k}-\delta\textbf{f}^{k-1}\|_{L^{2}\left( {\varTheta}\times\omega\right)}^{2}}, $$

(21)

$$ {\alpha_{2}^{k}}=\frac{\|\textbf{f}^{k}-\textbf{f}^{k-1}\|_{L^{2}\left( {\varTheta}\times\omega\right)}}{\|\delta\textbf{f}^{k}-\delta\textbf{f}^{k-1}\|_{L^{2}\left( {\varTheta}\times\omega\right)}^{2}}, $$

(22)

and

$$ {\alpha_{3}^{k}}=\frac{\|\textbf{f}^{k}-\textbf{f}^{k-1}\|_{L^{2}\left( {\varTheta}\times\omega\right)}}{\|\delta\textbf{f}^{k}\|_{L^{2}\left( {\varTheta}\times\omega\right)}^{2}}. $$

(23)

In the above, (21) is the original BB formula (Fletcher 2005; Dai et al. 2006). Formula (22) is an improvement for non-convex functions if ${\alpha _{1}^{k}}<0$ (Dai et al. 2015), and formulae (20) and (23) are introduced in Burdakov et al. (2019) in order to avoid too large a step size.

Notice that formula (20) does not specify how to compute α⁰ which is used to start the iteration. In this paper, we manually choose a relatively small α⁰ so that $\hat {J}\left (\textbf {u}\left (\textbf {f}^{0}+\alpha ^{0}\delta \textbf {f}^{0}\right )\right )$ $<\hat {J}\left (\textbf {u}\left (\textbf {f}^{0}\right )\right )$ to start off — the magnitude of α⁰ can be determined by $\textbf {f}^{0}+\alpha ^{0}\delta \textbf {f}^{0}\sim \rho ^{s}\frac {\partial \textbf {u}}{\partial t}$. In order to compute $\delta \hat {J}(\cdot )[\delta \textbf {f}]$, we introduce the Lagrange multiplier method in the following section.

5 The Lagrange multiplier method

The constraints for the optimisation Problem 1 can be eliminated by introducing the Lagrange multipliers $\hat {\textbf {u}}, \hat {p}, \hat {\textbf {w}}$ as follows:

$$ \begin{array}{ll} & L\left( \textbf{u}, p, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}}\right) = \hat{J}\left( \textbf{u}\right) \\ +&{\int}_{{\varTheta}\times{\varOmega}}\left( \rho\frac{\partial\textbf{u}}{\partial t} +\rho\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\textbf{u} -\nabla \cdot {\sigma} -\textbf{f}\textit{1}_{{{\varOmega}_{t}^{s}}}\right) \cdot \hat{\textbf{u}} \\ +&{\int}_{{\varTheta}\times{\varOmega}}\left( \rho\frac{\partial\textbf{w}}{\partial t}-\nabla\cdot\left( \mu\mathrm{D}\textbf{w}+\lambda\left( \nabla\cdot\textbf{w}\right)\textbf{I}\right) \right)\cdot \hat{\textbf{w}} \\ \end{array} $$

$$ \begin{array}{ll} -&{\int}_{{\varTheta}\times{\varOmega}} \hat{p} \nabla \cdot \textbf{u} +{\int}_{{\varOmega}}\left( \textbf{u}(0)-\textbf{u}_{0}\right)\cdot\hat{\textbf{u}}\\ +&{\int}_{{\varTheta}\times{\varGamma}_{D}}\left( \textbf{u}-\bar{\textbf{u}}\textit{1}_{{\varGamma}_{in}}\right)\cdot\hat{\textbf{u}} +{\int}_{{\varOmega}}\left( \textbf{w}(0)-\textbf{w}_{0}\right)\cdot\hat{\textbf{w}} \\ +&{\int}_{{\varTheta}\times{\varGamma}_{N}}\left( {\sigma}\textbf{n}-\bar{\textbf{h}}\right)\cdot\hat{\textbf{u}} + {\int}_{{\varTheta}\times{\varGamma}_{w_{0}}}\textbf{w}\cdot\hat{\textbf{w}} \\ +&{\int}_{{\varTheta}\times\left( {\varGamma}-{{\varGamma}_{w_{0}}}\right)}\left( \textbf{w}\cdot\textbf{n} \right)\left( \hat{\textbf{w}}\cdot\textbf{n}\right) +{\int}_{{\varTheta}\times{\varGamma}_{t}}\left( \textbf{w}-\textbf{u}\right)\cdot\hat{\textbf{w}} \\ +&{\int}_{{\varTheta}\times{\varGamma}_{t}}\left( {\sigma}^{s}-{\sigma}^{f}\right)\textbf{n}^{s}\cdot\hat{\textbf{u}} +{\int}_{{\varTheta}\times\left( {\varGamma}-{{\varGamma}_{w_{0}}}\right)} \textbf{n}\\&\cdot\left( \mu\mathrm{D}\textbf{w}\right)\cdot{\tau}\left( \hat{\textbf{w}}\cdot{\tau}\right). \end{array} $$

(24)

Notice that the condition of velocity continuity (10) is not included in the above Lagrangian functional, because it is automatically satisfied by treating the FSI system as a one-field velocity problem (Wang et al. 2019a). The following Karush-Kuhn-Tucker (KKT) conditions are the first-order necessary conditions to minimise (24):

$$ \begin{array}{@{}rcl@{}} \delta{L}\left( \textbf{u}, {p}, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}} \right)\left[\delta\hat{\textbf{u}}, \delta \hat{p}, \delta\hat{\textbf{w}}\right]=0, \end{array} $$

(25)

$$ \begin{array}{@{}rcl@{}} \delta{L}\left( \textbf{u}, {p}, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}} \right)\left[\delta\textbf{u}, \delta p, \delta\textbf{w}\right]=0. \end{array} $$

(26)

These equations will be solved in order to further compute $\delta {L}(\cdot )\left [\delta \textbf {f}\right ]\equiv \delta {\hat {J}}(\cdot )\left [\delta \textbf {f}\right ]$ due to the arbitrariness of $\hat {\textbf {u}}, \hat {p}, \hat {\textbf {w}}$ in the Lagrangian functional (24). Notice that the fluid domain ${{\varOmega }_{t}^{f}}$, solid domain ${{\varOmega }_{t}^{s}}$ and the fluid-solid interface Γ_t are all functions of the ALE velocity w, so these shape variations should be considered when taking variation with respect to w. We will compute the shape variation in the Hadamard form (Schmidt and Schulz 2010; Mohammadi and Pironneau 2010), i.e.

$$ {\int}_{{\delta{\varOmega}_{t}^{f}}}(\cdot)={\int}_{{\varGamma}_{t}}(\delta\textbf{w}\cdot\textbf{n}^{f})(\cdot), \quad {\int}_{{\delta{\varOmega}_{t}^{s}}}(\cdot)={\int}_{{\varGamma}_{t}}(\delta\textbf{w}\cdot\textbf{n}^{s})(\cdot), $$

(27)

and

$$ {\int}_{\delta{\varGamma}_{t}}\left( \cdot\right) ={\int}_{{\varGamma}_{t}}\left( \delta\textbf{w}\cdot\textbf{n}^{s}\right)\left[\nabla_{\textbf{n}^{s}}\left( \cdot\right) +\left( \nabla_{{\varGamma}_{t}}\cdot\textbf{n}^{s}\right)\left( \cdot\right)\right], $$

(28)

where $\nabla _{\textbf {n}^{s}}$ is the normal gradient operator, and $\nabla _{{\varGamma }_{t}}$ is the tangential gradient operator on Γ_t, with the tangential divergence being defined as:

$$ \nabla_{{\varGamma}_{t}}\cdot\textbf{v} =\nabla\cdot\textbf{v}-\left( \textbf{n}^{s}\cdot\nabla\right)\textbf{v}\cdot\textbf{n}^{s}, $$

(29)

for a given function v. Note that replacing n^s by n^f = −n^s in (28) does not change the sign of ${\int \limits }_{\delta {\varGamma }_{t}}\left (\cdot \right )$.

Notice that if we apply the domain variation (27) to the momentum (1), which is a term in (24), its shape variation is zero.

5.1 State equation

Taking Gâteaux variation of (24) with respect to the Lagrange multipliers $\hat {\textbf {u}}$, $\hat {p}$ and $\hat {\textbf {w}}$ gives the state equations in a weak formulation (see Appendix A for more details):

Problem 2

Given u₀ in (4) and w₀ in (7), for t ∈ (0,T], find $\textbf {w}\in H_{D_{1}}^{1}({\varOmega })^{d}$, $\textbf {u}\in H_{D_{2}}^{1}({\varOmega })^{d}$ and $p\in {L_{0}^{2}}({\varOmega })$, such that $\forall \delta \hat {\textbf {w}}\in {H}_{D_{1}}^{1}({\varOmega })^{d}$, $\forall \delta \hat {\textbf {u}}\in {H}_{0\left ({\varGamma }_{D}\right )}^{1}({\varOmega })^{d}$ and $\forall \delta \hat {p}\in L^{2}({\varOmega })$:

$$ \begin{array}{ll} &\rho{\int}_{{\varOmega}}\frac{\partial\textbf{u}}{\partial t}\cdot\delta\hat{\textbf{u}} +\rho{\int}_{{\varOmega}}\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\textbf{u}\cdot\delta\hat{\textbf{u}}\\ +&\frac{\mu^{f}}{2}{\int}_{{{\varOmega}_{t}^{f}}}\mathrm{D}\textbf{u}:\mathrm{D}\delta\hat{\textbf{u}} -{\int}_{{\varOmega}}p\nabla\cdot \delta\hat{\textbf{u}} -{\int}_{{\varOmega}} \delta\hat{p}\nabla \cdot \textbf{u}\\ + & c_{1}{\int}_{{{\varOmega}_{t}^{s}}}\left( \mathrm{D}\textbf{d}-\nabla^{T}\textbf{d}\nabla\textbf{d}\right):\nabla\delta\hat{\textbf{u}} \\ =&{\int}_{{\varGamma}_{N}}\bar{\textbf{h}}\cdot\delta\hat{\textbf{u}} +{\int}_{{{\varOmega}_{t}^{s}}}\textbf{f}\cdot\delta\hat{\textbf{u}}, \end{array} $$

(30)

and

$$ \begin{array}{ll} &\rho{\int}_{{\varOmega}}\frac{\partial\textbf{w}}{\partial t}\cdot\delta\hat{\textbf{w}} +\frac{\mu}{2}{\int}_{{\varOmega}}\mathrm{D}\textbf{w}:\mathrm{D}\delta\hat{\textbf{w}} \\ +&\lambda{\int}_{{\varOmega}}\left( \nabla\cdot\textbf{w}\right)\left( \nabla\cdot\delta\hat{\textbf{w}}\right) +{\int}_{{\varGamma}_{t}}\left( \textbf{w}-\textbf{u}\right)\cdot\delta\hat{\textbf{w}} =0, \end{array} $$

(31)

where $H_{D_{1}}^{1}({\varOmega })^{d}$ and $H_{D_{2}}^{1}({\varOmega })^{d}$ are the subspaces of H¹(Ω)^d, with boundary conditions (8) and (5) being satisfied respectively.

5.2 Adjoint equation

Taking G${\hat {\text {a}}}$teaux variation of (24) with respect to the variables u, p and w, we have

$$ \begin{array}{ll} &\delta{L}\left( \textbf{u}, {p}, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}} \right)\left[\delta\textbf{u}, \delta p\right] \\ =&\beta_{1}{\int}_{{\varTheta}\times{\varOmega}^{c}}\left( \textbf{u}-\textbf{u}_{g}\right)\cdot\delta\textbf{u} +\beta_{2}{\int}_{{{\varTheta}\times{\varOmega}_{t}^{s}}}\left( \textbf{d}-\textbf{d}_{g}\right)\cdot\delta\textbf{d} \\ +&\gamma_{1}{\int}_{{\varOmega}^{c}}\left( \textbf{u}(T)-\textbf{u}_{g}(T)\right)\cdot\delta\textbf{u}(T) \\&+\gamma_{2}{\int}_{{{\varOmega}_{t}^{s}}}\left( \textbf{u}(T)-\textbf{u}_{g}(T)\right)\cdot\delta\textbf{u}(T)\\ -&\rho{\int}_{{\varTheta}\times{\varOmega}}\frac{\partial \hat{\textbf{u}}}{\partial t}\cdot\delta\textbf{u} +{\int}_{{\varOmega}}\left( \hat{\textbf{u}}(T)\cdot\delta\textbf{u}(T)-\hat{\textbf{u}}(0)\cdot\delta\textbf{u}(0)\right)\\ +&\rho{\int}_{{\varTheta}\times{\varOmega}}\left( \delta\textbf{u}\cdot\nabla\right)\textbf{u}\cdot\hat{\textbf{u}} +\rho{\int}_{{\varTheta}\times{\varOmega}}\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\delta\textbf{u}\cdot\hat{\textbf{u}}\\ +&\frac{\mu^{f}}{2}{\int}_{{{\varTheta}\times{\varOmega}_{t}^{f}}}\mathrm{D}\delta\textbf{u}:\mathrm{D}\hat{\textbf{u}} -{\int}_{{\varTheta}\times{\varOmega}} \delta{p}\nabla \cdot \hat{\textbf{u}} -{\int}_{{\varTheta}\times{\varOmega}} \hat{p}\nabla \cdot \delta\textbf{u} \\ +& c_{1}{\int}_{{{\varTheta}\times{\varOmega}_{t}^{s}}}\delta\left( \mathrm{D}\textbf{d}-\nabla^{T}\textbf{d}\nabla\textbf{d}\right)\left[\delta\textbf{u}\right]:\nabla\hat{\textbf{u}} -{\int}_{{\varTheta}\times{\varGamma}} {\delta({{\sigma}})\textbf{n}}\cdot\hat{\textbf{u}} \\ +&{\int}_{{\varOmega}}\delta\textbf{u}(0)\cdot\hat{\textbf{u}}(0) +{\int}_{{\varTheta}\times{\varGamma}_{D}}\delta\textbf{u}\cdot\hat{\textbf{u}} +{\int}_{{\varTheta}\times{\varGamma}_{N}}\delta({\sigma})\textbf{n}\cdot\hat{\textbf{u}} \\ -&{\int}_{{\varTheta}\times{\varGamma}_{t}}\delta\textbf{u}\cdot\hat{\textbf{w}}=0, \end{array} $$

(32)

and

$$ \begin{array}{ll} &\delta{L}\left( \textbf{u}, {p}, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}} \right)\left[\delta\textbf{w}\right] \\ =&\frac{\beta_{2}}{2}{\int}_{{\varTheta}\times{\varGamma}_{t}}\left( \delta\textbf{w}\cdot\textbf{n}^{s}\right) \|\textbf{d}-\textbf{d}_{g}\|_{L^{2}\left( {{\varOmega}_{t}^{s}}\right)}^{2} \\ +& \frac{\gamma_{2}}{2}{\int}_{{\varGamma}_{t}}\left( \delta\textbf{w}(T)\cdot\textbf{n}^{s}\right) \|\textbf{u}(T)-\textbf{u}_{g}(T)\|_{L^{2}\left( {{\varOmega}_{t}^{s}}\right)}^{2}\\ -& \rho{\int}_{{\varTheta}\times{\varOmega}}\frac{\partial\hat{\textbf{w}}}{\partial t}\cdot\delta\textbf{w} +{\int}_{{\varOmega}}\left( \hat{\textbf{w}}(T)\cdot\delta\textbf{w}(T)-\hat{\textbf{w}}(0)\cdot\delta\textbf{w}(0)\right)\\ +&\frac{\mu}{2}{\int}_{{\varTheta}\times{\varOmega}}\mathrm{D}\hat{\textbf{w}}:\mathrm{D}\delta\textbf{w} +\lambda{\int}_{{\varTheta}\times{\varOmega}}\left( \nabla\cdot\hat{\textbf{w}}\right)\left( \nabla\cdot\delta\textbf{w}\right) \\ -&{\int}_{{\varTheta}\times{\varGamma}}\textbf{n}\cdot\left( \mu\mathrm{D}\delta\textbf{w}+\lambda\nabla\cdot\delta\textbf{w}\textbf{I}\right)\cdot\textbf{n} \left( \hat{\textbf{w}}\cdot\textbf{n}\right) \\ -&{\int}_{{\varTheta}\times{{\varGamma}_{w_{0}}}} \textbf{n}\cdot\left( \mu\mathrm{D}\delta\textbf{w}\right)\cdot{\tau}\left( \hat{\textbf{w}}\cdot{\tau}\right)\\ -&\rho{\int}_{{\varTheta}\times{\varOmega}}\left( \delta\textbf{w}\cdot\nabla\right)\textbf{u}\cdot\hat{\textbf{u}} +{\int}_{{\varOmega}}\delta\textbf{w}(0)\cdot\hat{\textbf{w}}(0) \\&+{\int}_{{\varTheta}\times{{\varGamma}_{w_{0}}}}\delta\textbf{w}\cdot\hat{\textbf{w}} \\ +&{\int}_{{\varTheta}\times\left( {\varGamma}-{{\varGamma}_{w_{0}}}\right)} \left( \delta\textbf{w}\cdot\textbf{n} \right)\left( \hat{\textbf{w}}\cdot\textbf{n}\right) +{\int}_{{\varTheta}\times{\varGamma}_{t}}\delta\textbf{w}\cdot\hat{\textbf{w}} =0. \end{array} $$

(33)

In the above, we adopt the integration (in time) by parts to obtain

$$ {\int}_{{\varTheta}\times{\varOmega}}\frac{\partial}{\partial t}\delta\textbf{u}\cdot\hat{\textbf{u}} ={\int}_{{\varOmega}}\left.\left( \hat{\textbf{u}}\cdot\delta\textbf{u}\right)\right|_{0}^{T} -{\int}_{{\varTheta}\times{\varOmega}}\frac{\partial \hat{\textbf{u}}}{\partial t}\cdot\delta\textbf{u}, $$

(34)

and similarly for ${\int \limits }_{{\varTheta }\times {\varOmega }}\frac {\partial }{\partial t}\delta \textbf {w}\cdot \hat {\textbf {w}}$. We also integrate the stress-tensor term by parts (in space) and eliminate the normal-stress term on Γ_t using the interface condition (12). In addition, notice that the shape variation ${\int \limits }_{{\varTheta }\times \delta {\varGamma }_{t}}\left (\textbf {w}-\textbf {u}\right )\cdot \hat {\textbf {w}}=0$ due to the interface condition (10) using (28).

If we choose the initial condition for $\hat {\textbf {u}}$ at time t = T (notice that the adjoint equation is solved backwards in time) as

$$ \hat{\textbf{u}}(T)=-\gamma_{1}\left( \textbf{u}(T)-\textbf{u}_{g}(T)\right)\textit{1}_{{\varOmega}^{c}}-\gamma_{2}\left( \textbf{u}(T)-\textbf{u}_{g}(T)\right)\textit{1}_{{{\varOmega}_{t}^{s}}}, $$

(35)

and the boundary condition

$$ \left.\hat{\textbf{u}}\right|_{{\varGamma}_{D}}=\textbf{0}, $$

(36)

rearrange and integrate the convection terms by parts:

$$ \begin{array}{ll} &{\int}_{{\varOmega}}\left( \delta\textbf{u}\cdot\nabla\right)\textbf{u}\cdot\hat{\textbf{u}} +{\int}_{{\varOmega}}\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\delta\textbf{u}\cdot\hat{\textbf{u}}\\ =&{\int}_{{\varOmega}}\left( \hat{\textbf{u}}\cdot\nabla\textbf{u}\right)\cdot\delta\textbf{u} +{\int}_{{\varGamma}_{N}}\left( \textbf{u}\cdot\textbf{n}\right)\left( \hat{\textbf{u}}\cdot\delta\textbf{u}\right)\\ -&{\int}_{{\varOmega}}\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\hat{\textbf{u}}\cdot\delta\textbf{u} +{\int}_{{\varOmega}}\left( \nabla\cdot\textbf{w}\right)\left( \hat{\textbf{u}}\cdot\delta\textbf{u}\right), \end{array} $$

(37)

and if we also choose the initial condition for $\hat {\textbf {w}}$ at time t = T as

$$ \hat{\textbf{w}}(T)=-\frac{\gamma_{2}}{2}\|\textbf{u}(T)-\textbf{u}_{g}(T)\|_{L^{2}\left( {{\varOmega}_{t}^{s}}\right)}^{2}\textit{1}_{{\varGamma}_{t}}\textbf{n}^{s}, $$

(38)

and boundary condition

$$ \left.\hat{\textbf{w}}\right|_{{\varGamma}}=\textbf{0}, $$

(39)

then the adjoint-ALE-FSI equation for $(\hat {\textbf {u}}, \hat {p}, \hat {\textbf {w}})$ is given by:

Problem 3

Given $\hat {\textbf {u}}(T)$ in (35) and $\hat {\textbf {w}}(T)$ in (38), for t ∈ [0,T), find $\hat {\textbf {w}}\in H_{0\left ({{\varGamma }}\right )}^{1}({\varOmega })^{d}$, $\hat {\textbf {u}}\in H_{0\left ({\varGamma }_{D}\right )}^{1}({\varOmega })^{d}$ and $\hat {p}\in {L_{0}^{2}}({\varOmega })$, such that $\forall \delta \textbf {w}\in {H}_{0\left ({{\varGamma }}\right )}^{1}({\varOmega }_{t})^{d}$, $\delta \textbf {u}\in {H}_{0\left ({\varGamma }_{D}\right )}^{1}({\varOmega }_{t})^{d}$ and $\forall \delta {p}\in L^{2}({\varOmega }_{t})$:

$$ \begin{array}{ll} &-\rho{\int}_{{\varOmega}}\frac{\partial}{\partial t}\hat{\textbf{u}}\cdot\delta\textbf{u} +\rho{\int}_{{\varOmega}}\left( \hat{\textbf{u}}\cdot\nabla\textbf{u}\right)\cdot\delta\textbf{u} \\ &-\rho{\int}_{{\varOmega}}\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\hat{\textbf{u}}\cdot\delta\textbf{u} +\rho{\int}_{{\varOmega}}\left( \nabla\cdot\textbf{w}\right)\left( \hat{\textbf{u}}\cdot\delta\textbf{u}\right) \\ &+\frac{\mu^{f}}{2}{\int}_{{{\varOmega}_{t}^{f}}}\mathrm{D}\hat{\textbf{u}}:\mathrm{D}\delta\textbf{u} -{\int}_{{\varOmega}} \delta{p}\nabla \cdot \hat{\textbf{u}} -{\int}_{{\varOmega}} \hat{p}\nabla \cdot \delta\textbf{u} \\ &+c_{1}{\int}_{{{\varOmega}_{t}^{s}}}\left( \mathrm{D}\delta\textbf{d}-\nabla^{T}\delta\textbf{d}\nabla\textbf{d}-\nabla^{T}\textbf{d}\nabla\delta\textbf{d}\right)\left[\delta\textbf{u}\right]:\nabla\hat{\textbf{u}}\\ &+\beta_{1}{\int}_{{\varOmega}^{c}}\left( \textbf{u}-\textbf{u}_{g}\right)\cdot\delta\textbf{u} +\beta_{2}{\int}_{{{\varOmega}_{t}^{s}}}\left( \textbf{d}-\textbf{d}_{g}\right)\cdot\delta\textbf{d} \\ -&{\int}_{{\varGamma}_{t}}\hat{\textbf{w}}\cdot\delta\textbf{u} +{\int}_{{\varGamma}_{N}}\left( \textbf{u}\cdot\textbf{n}\right)\left( \hat{\textbf{u}}\cdot\delta\textbf{u}\right) =0, \end{array} $$

(40)

and

$$ \begin{array}{ll} -&\!\rho{\int}_{{\varOmega}}\frac{\partial}{\partial t}\hat{\textbf{w}}\cdot\delta\textbf{w} +\frac{\mu}{2}{\int}_{{\varOmega}}\mathrm{D}\hat{\textbf{w}}:\mathrm{D}\delta\textbf{w} \\&+\lambda{\int}_{{\varOmega}}\left( \nabla\cdot\hat{\textbf{w}}\right)\left( \nabla\cdot\delta\textbf{w}\right) \\ -&\!\rho{\int}_{{\varOmega}}\left( \delta\textbf{w}\cdot\nabla\right)\textbf{u}\cdot\hat{\textbf{u}} +{\int}_{{\varGamma}_{t}}\hat{\textbf{w}}\cdot\delta\textbf{w} \\&+\frac{\beta_{2}}{2}{\int}_{{\varGamma}_{t}}\left( \delta\textbf{w}\cdot\textbf{n}^{s}\right)\|\textbf{d}-\textbf{d}_{g}\|^{2} =0. \end{array} $$

(41)

Remark 1

We give the Dirichlet boundary condition in (36) for Problem 3 in the weak form, where the Neumann boundary condition has been included. If the stress term is integrated by parts in (40), we would have the Neumann boundary condition ${ \sigma }\left (\hat {\textbf {u}},\hat {p}\right )\textbf {n}+\left (\textbf {n}\cdot \textbf {u}\right )\hat {\textbf {u}}=0$ on Γ_N for the corresponding problem in the PDE (partial differential equation) form.

5.3 Gradient descent direction

Taking Gâteaux variation of (24) with respect to f, we have

$$ \begin{array}{@{}rcl@{}} \delta{L}(\cdot)\left[\delta\textbf{f}\right] &=&-{\int}_{{\varTheta}\times{\varOmega}}\delta\textbf{f}\cdot{\hat{\textbf{u}}}\textit{1}_{{{\varOmega}_{t}^{s}}} +\theta{\int}_{{\varTheta}\times{\varOmega}}\delta\textbf{f}\cdot\textbf{f} \\&&=-{\int}_{{\varTheta}\times{\varOmega}}\delta\textbf{f}\cdot\left( {\hat{\textbf{u}}}\textit{1}_{{{\varOmega}_{t}^{s}}} -\theta\textbf{f}\right). \end{array} $$

(42)

From which it can be seen the gradient descent direction is $\delta \textbf {f}\textit {1}_{{{\varOmega }_{t}^{s}}}=\hat {\textbf {u}}-\theta \textbf {f}$.

6 Discretisation for the FSI control system

We discretise the time interval [0,T] as t₀ = 0,t₁,t₂,…, t_M = T with t_n+ 1 − t_n = Δt (n = 0,1,…,M), and then discretise the displacement using the backward Euler scheme:

$$ \textbf{d}_{n+1}=\tilde{\textbf{d}}_{n}+{\Delta} t\textbf{u}_{n+1}, \quad \tilde{\textbf{d}}_{n}=\textbf{d}_{n}\circ\mathcal{A}_{t_{n},t_{n+1}}^{-1}, $$

(43)

where $\mathcal {A}_{t_{n},t_{n+1}}$ is the ALE mapping from state ${\varOmega }_{t_{n}}$ to ${\varOmega }_{t_{n+1}}$: x_n↦x_n + Δtu_n+ 1. At the same time, we have δd = Δtδu. The state equations (30) and (31) can then be discretised forward in time, and the adjoint equations (40) and (41) can be discretised backward in time below in Problems 4 and 5 respectively.

Problem 4

Given u_n and w_n, find $\textbf {w}_{n+1}\in H_{D_{1}}^{1}({\varOmega })^{d}$, $\textbf {u}_{n+1}\in H_{D_{2}}^{1}({\varOmega })^{d}$ and $p_{n+1}\in {L_{0}^{2}}({\varOmega })$, such that $\forall \delta \hat {\textbf {w}}\in {H}_{D_{1}}^{1}({\varOmega }_{t})^{d}$, $\forall \delta \hat {\textbf {u}}\in {H}_{0\left ({\varGamma }_{D}\right )}^{1}({\varOmega }_{t})^{d}$ and $\forall \delta \hat {p}\in L^{2}({\varOmega }_{t})$:

$$ \begin{array}{ll} &\rho{\int}_{{\varOmega}}\frac{\textbf{u}_{n+1}-\textbf{u}_{n}}{\Delta t}\cdot\delta\hat{\textbf{u}} +\rho{\int}_{{\varOmega}}\left( \left( \textbf{u}_{n+1}-\textbf{w}_{n+1}\right)\cdot\nabla\right)\textbf{u}_{n+1}\cdot\delta\hat{\textbf{u}}\\ +&\frac{\bar{\mu}}{2}{\int}_{{\varOmega}}\mathrm{D}\textbf{u}_{n+1}:\mathrm{D}\delta\hat{\textbf{u}} -{\int}_{{\varOmega}}p_{n+1}\nabla\cdot \delta\hat{\textbf{u}} -{\int}_{{\varOmega}} \delta\hat{p}\nabla \cdot \textbf{u}_{n+1}\\ -&{\Delta} tc_{1}{\int}_{{\varOmega}_{t_{n+1}}^{s}}\left( \nabla^{T}\textbf{u}_{n+1}\nabla\tilde{\textbf{d}}_{n}+\nabla^{T}\tilde{\textbf{d}}_{n}\nabla\textbf{u}_{n+1}\right):\nabla\delta\hat{\textbf{u}} \\ =&{\int}_{{\varOmega}_{t_{n+1}}^{s}}\textbf{f}_{n+1}\cdot\delta\hat{\textbf{u}} +{\int}_{{\varGamma}_{N}}\bar{\textbf{h}}\cdot\delta\hat{\textbf{u}} \\&-c_{1}{\int}_{{\varOmega}_{t_{n+1}}^{s}}\left( \mathrm{D}\tilde{\textbf{d}}_{n}-\nabla^{T}\tilde{\textbf{d}}_{n}\nabla\tilde{\textbf{d}}_{n}\right):\nabla\delta\hat{\textbf{u}} , \end{array} $$

(44)

and

(45)

with $\bar {\mu }=\mu ^{f}1_{{{\varOmega }_{t}^{f}}}+{\Delta } tc_{1}1_{{{\varOmega }_{t}^{s}}}$, and ${\varOmega }_{t_{n+1}}^{s}=\{\textbf {x}: \textbf {x}=\textbf {x}_{n}+$ ${\Delta } t\textbf {u}_{n+1},\forall \textbf {x}_{n}\in {\varOmega }_{t_{n}}^{s}\}$.

Remark 2

Coupling between u_n+ 1 and w_n+ 1: the contribution of u_n+ 1 to w_n+ 1 is through ${\varGamma }_{t_{n+1}}$ in the boxed term in (45). In practice we may replace u_n+ 1 by u_n in this boxed term, decouple (44) and (45), solve them one by one.

Problem 5

Given $\hat {\textbf {u}}(t_{n+1})$ and $\hat {\textbf {w}}(t_{n+1})$, find $\hat {\textbf {w}}_{n}\in H_{0\left ({{\varGamma }}\right )}^{1}$ (Ω)^d, $\hat {\textbf {u}}_{n}\in H_{0\left ({\varGamma }_{D}\right )}^{1}({\varOmega })^{d}$ and $\hat {p}_{n}\in {L_{0}^{2}}({\varOmega })$, such that $\forall \delta \textbf {w}\in {H}_{0\left ({{\varGamma }}\right )}^{1}({\varOmega }_{t})^{d}$, $\forall \delta \textbf {u}\in {H}_{0\left ({\varGamma }_{D}\right )}^{1}({\varOmega }_{t})^{d}$ and $\forall \delta {p}\in L^{2}({\varOmega }_{t})$:

(46)

and

$$ \begin{array}{ll} &\rho{\int}_{{\varOmega}}\frac{\hat{\textbf{w}}_{n}-\hat{\textbf{w}}_{n+1}}{\Delta t}\cdot\delta\textbf{w} +\frac{\mu}{2}{\int}_{{\varOmega}}\mathrm{D}\hat{\textbf{w}}_{n}:\mathrm{D}\delta\textbf{w} \\&+\lambda{\int}_{{\varOmega}}\left( \nabla\cdot\hat{\textbf{w}}_{n}\right)\left( \nabla\cdot\delta\textbf{w}\right) \\ +&{\int}_{{\varGamma}_{t_{n}}}\hat{\textbf{w}}_{n}\cdot\delta\textbf{w} =\rho{\int}_{{\varOmega}}\left( \hat{\textbf{u}}_{n}\cdot\nabla\textbf{u}_{n}\right)\cdot\delta\textbf{w} \\&-\frac{\beta_{2}}{2}{\int}_{{\varGamma}_{t_{n}}}\left( \delta\textbf{w}\cdot\textbf{n}^{s}\right)\|\textbf{d}_{n}-\textbf{d}_{g}\|^{2}. \end{array} $$

(47)

Remark 3

Coupling between $\hat {\textbf {u}}_{n}$ and $\hat {\textbf {w}}_{n}$: the only contribution of $\hat {\textbf {w}}_{n}$ to $\hat {\textbf {u}}_{n}$ is through the boxed term in (46). In practice we may replace $\hat {\textbf {w}}_{n}$ by $\hat {\textbf {w}}_{n+1}$ in this boxed term, decouple equations (46) and (47) and solve them one by one. We have numerically investigated the boxed term in (46), and plotted its values for tests 7.3, 7.4 and 7.6. We find that this term is very small and can be neglected, which means it is not necessary to solve (47).

The optimality condition (42) gives the update of the control variable:

$$ \textbf{f}_{n+1}^{k+1}=\textbf{f}_{n+1}^{k}+\alpha^{k}\left( \hat{\textbf{u}}_{n+1}-\theta\textbf{f}_{n+1}^{k}\right), \quad k=0,1,2,\ldots $$

(48)

with α^k being computed using the modified Barzilai-Borwein method (20).

We use a standard Taylor-Hood finite element (Q₂/Q₁) for the velocity-pressure pair to discretise (44) and (46), and Q₂ element for the mesh velocity to discretise (45) and (47). Finally the whole algorithm is summarised in Algorithm 1.

Remark 4

For time-dependent control problems, the classic piecewise static control method cannot guarantee a global optimisation solution (Abergel and Temam 1990). In the proposed algorithm, if we just run the algorithm in one time step, the algorithm would be one step of the piecewise static control.

7 Numerical experiments

Considering the complicated features of the control problems, we discuss in this article, namely time-dependent, fluid-structure interaction problems with finite solid deformations, there are limited cases considered in literature. Therefore, in Section 7.1, we first validate the proposed optimal control method against an existing fluid-control result, obtained using a different approach to ours. We then test the proposed method using three dynamic FSI problems in the rest of this section: test 7.3 is a modification of the fluid problem 7.1, which shows that the control variable, the body force f, is feasible; test 7.4 is a static FSI control problem from the literature, for which we use our dynamic control method and show that the FSI control is also tractable. Finally, test 7.6 is a dynamic FSI problem involving complicated solid oscillations, which does not have a steady-state solution, and we show that it is controllable using the proposed methodology.

7.1 Lid-driven cavity flow — forcing a Navier-Stokes flow to a Stokes flow

In this example, we reproduce published results for control of a dynamic cavity pure fluid flow, which has been studied in Failer and Richter (2020) using a space-time multigrid method. We show that the proposed scheme, requiring only a relatively small number of CFD simulations, can achieve equivalent results to those reported in Hinze et al. (2012). To achieve this in our algorithm, we turn off the solid part of the proposed scheme, remove the integration in the solid domain, set the ALE velocity w = 0 and apply the control force f in the whole domain (fluid only in this case). Specifically speaking, we only solve (44) and (46) without terms of integration on ${\varOmega }_{t_{n}}^{s}$, ${\varOmega }_{t_{n+1}}^{s}$ and ${\varGamma }_{t_{n}}$.

The cavity flow is defined in domain Ω = [0,1] × [0,1], with velocity being prescribed as u = (1, 0) at the top of the boundary and u = (0, 0) at all the other boundaries. The fluid’s density and viscosity are ρ^f = 1.0 and μ^f = 0.01 respectively. We use 30 × 30 Q₂/Q₁ elements, and a fully developed Navier-Stokes (NS) and Stokes flow are shown in Fig. 2a and b respectively. In this flow control test, we choose the fully developed NS flow as the initial flow and determine the body force distribution needed to create the fully developed Stokes flow as the target flow (we run the simulation up to t = 10 using Δt = 0.01), and solve Problem 1 with Ω^c = Ω, T = 1, β₁ = 1, β₂ = 0, γ₁ = 1 and γ₂ = 0.

Fig. 2

Vertical velocity of fully developed NS and Stokes flow

We first test the influence of the regularisation parameter θ as shown in Fig. 3a, from which it can be seen that larger θ stops the objective decreasing at a earlier stage. We then compare the BB method against gradient descent using a constant step size, and the convergence of the objective functional J(⋅) is shown in Fig. 3b, from which it can be seen that the BB method is not sensitive to the initial step size and converges slightly faster. It may also be seen that a constant step size α = 4 does not converge, while starting from a different initial step size (α⁰ = 1, 2 or 4) presents similar convergence for the BB method. Overall, the BB method reduces the objective by over 80% after 10 iterations. We also report the L² norm of the control force and the gradient descent direction in Fig. 4. Notice that this problem has a steady-state solution and we have a control for the final velocity profile (γ₁ = 1); this is why the control force tends to a δ −function at t = 0 and t = T (see Remark 5). Figure 5 depicts the controlled flow and the control force at different times, from which we can see the two main vortices quickly “push” the NS flow to the Stokes flow. These results are very similar to Figure 2 in Hinze et al. (2012).

Fig. 3

Convergence of the objective functional J(⋅)

Fig. 4

L² nor/m of the control force f(t) (left) and the gradient descent direction δf(t) (right)

Fig. 5

Vertical velocity of the controlled flow (left) and the control force (right)

Remark 5

If the control problem has a steady-state solution, then the inertia tends to 0 as time involves. In this case, we know that (1) becomes a stationary PDE equation, which naturally holds without any initial conditions or control force. Therefore, if we want $\left .\textbf {u}\right |_{t=0}=\textbf {u}_{0}$ (initial condition (4)), we expect a control force f that tends to a δ −function at t = 0 in order to balance this initial condition. If we also want $\left .\textbf {u}\right |_{t=T}=\textbf {u}_{g}(T)$ (objective in (16)), we also expect the control force f tends to a δ −function at t = T.

7.2 Cavity flow with an initial pulse — forcing a Navier-Stokes flow to a predefined time-dependent fluid field

In this example, we consider again a fluid-control problem but with a different objective: steering the velocity to be a complicated predefined velocity profile with vortices, which is taken from Hou and Yan (1997). The computational domain and mesh are exactly the same as the test in Section 7.1. We use a wall boundary condition for all four sides of the cavity, and the fluid with ρ^f = 1 and μ^f = 0.1 is initially driven by:

$$ \begin{array}{@{}rcl@{}} \textbf{u}_{0}(x, y)&=&\left( \left( cos(2\pi x)-1\right)sin(2\pi y),\right.\\&&\left. sin(2\pi x)\left( 1-cos(2\pi y)\right)\right). \end{array} $$

(49)

The goal velocity

$$ \textbf{u}_{g}(x, y, t)=\left( \frac{\partial}{\partial y}{\varPsi}(x,y,t), -\frac{\partial}{\partial x}{\varPsi}(x,y,t)\right), $$

(50)

is derived from the following stream function:

$$ {\varPsi}(x, y, t)=\psi(x,t)\psi(y,t), $$

(51)

with

$$ \psi(s,t)=\left( 1-s\right)^{2}\left( 1-cos(4\pi st)\right), \quad s\in [0, 1]. $$

(52)

We use a time step of Δt = 0.01, run the simulation from t = 0 to 1, and compute the control force f(x,y,t) in the whole fluid domain. We compare the goal velocity and the controlled velocity in Fig. 6, from which it can be seen the four vortices have been clearly captured, and the L² error has the same magnitude reported in Figure 10 of Hou and Yan (1997). We test three different regularisation parameter θ, and its influence on the objective reduction may be observed from Fig. 7, from which we see again that the BB method performs better than a constant step method (Fig. 8).

Fig. 6

Velocity field of the goal and controlled flow at t = 1, ∥u −u_g∥ = 0.1041

Fig. 7

Convergence of the objective

Fig. 8

L² norm of the control force f(t)

7.3 Lid-driven cavity flow with an elastic solid wall — reducing the solid deformation

The next problem increases in complexity to consider the case of lid-driven cavity flow with a deformable solid as considered by Zhang et al. (2012), which has the same geometry as the above test in Section 7.1. However, there is a rectangular solid at the bottom of this square as shown in Fig. 9 (l = 1 and h = 0.25). In this case, there is no interior boundary ${\varGamma }_{w_{0}}$ as shown in Fig. 1. However, this would not change (4) to (47) that we solve. The fluid and solid properties are ρ^f = ρ^s = 1, μ^f = 0.01 and c₁ = 0.2. The purpose of this test is to demonstrate the feasibility of using the proposed algorithm to reduce the solid deformation/displacement. Using the one-field monolithic algorithm, there is little difference (compared with the NS flow in Section 7.1) from the computational point of view. We can use the same boundary conditions, the same mesh and time step Δt = 0.01 as used for the NS flow in Section 7.1. We first run the forward simulation up to t = 10 in order to get a steady-state solution: the vertical velocity and the deformed solid mesh are shown in Fig. 10. We then compute a distributed force, and enforce it on the solid to reduce the solid displacement. This is to say we solve Problem 1 by setting d_g = 0, β₁ = 0, β₂ = 1, and γ₁ = γ₂ = 0.

Fig. 9

Computational domain for test 7.3

Fig. 10

The steady-state vertical velocity and the deformed solid mesh

We compare again gradient descent using a constant step size and using the BB method to compute a step size. The BB method still performs better than a constant step size as shown in Fig. 11, while it is as cheap as the constant step size: using formula (20) to compute the step size. It can be seen from Fig. 11 that the objective is reduced by more than 70% at 30 iterations, although the convergence becomes slow afterwards. Figure 11 also shows the influence of regularisation parameter θ, and we can see that using a smaller θ allows a greater reduction of the objective to be achieved. However, we have observed numerical instability using θ = 10^− 5 for this test. The fluid-solid interface is plotted in Fig. 12, from which it can be seen that the additional iterations from 31 to 120 mainly contribute to changing to another mode, with only slight reductions in the magnitude of the displacement. Notice that the objective (15) has an integration through the time and space domain, so it is not a point-wise reduction of the displacement for this example. We also test this example using a finer mesh (40 × 40), and it can be seen from Figs. 11 and 12 that both the objective the FSI interface show very similar performance when using these two different meshes. For this example, the problem has a steady-state solution and we have no control for the final velocity profile (γ₁ = γ₂ = 0), so we observe that the control force tends to a δ −function at t = 0 as shown in Fig. 13. This is consistent with Remark 5. Finally, we investigate the boxed term in (46) in Fig. 14, from which it can be seen that this term is very small. We have tested the case of neglecting this term and found that all the results were identical.

Fig. 11

Convergence of the objective

Fig. 12

Steady-state displacement at the FSI interface

Fig. 13

L² norm of the control force f(t)

Fig. 14

Boxed term in (46)

7.4 Channel flow interacting with two flexible beams — minimising the velocity discrepancy in a specified region

This example is taken from Cerroni et al. (2016) which solves a quasi-static problem. Here we solve the full dynamic FSI problem and show that it also converges to the same stationary solution as reported in Cerroni et al. (2016). The computational geometry is shown in Fig. 15 which is symmetric about the x-axis. For this example, there is no interior boundary ${\varGamma }_{w_{0}}$. However, this would not change (4) to (47) that we solve. A parabolic velocity profile is prescribed at the inlet Γ_in:

$$ \bar{u}_{x}=4(0.5+y)(0.5-y). $$

(53)

Fig. 15

Computational domain for the oscillating beams

The fluid and solid parameters are ρ^f = ρ^s = 1, μ^f = 0.01, and c₁ = 66.67. We use 1210 Q₂/Q₁ elements with 5019 nodes as shown in Fig. 16, and a converged time step size of Δt = 0.1. We run the forward FSI simulation up to t = 50 until a steady-state flow is obtained, with the flow field and the solid displacement being displayed in Fig. 16, which is consistent with Fig. 3 in Cerroni et al. (2016). We then use this solution for the control problem: increasing the velocity by 20% for all t = 0 to T in a control region Ω^c (see Fig. 15) by controlling a distributed force on the solid. This is to say we solve Problem 1 with β₁ = 1, β₂ = 0 = γ₁ = γ₂ = 0 and $\textbf {u}_g = \left (1.2u_x(t),u_y(t)\right )$ in Ω_c, where (u_x(t),u_y (t)) is the solution (from t = 0 to t = 50) of this forward FSI problem without control (notice that the solution converges to a steady state at t = 50). It can be seen from Fig. 17 that the BB method still performs better than the constant step method, and reducing the regularisation parameter θ from 0.01 to 0.001 allows us to reduce the objective more (Fig. 18). It can also be seen from Fig. 19 that the control force converged to a complicated time-dependent distributed force for this FSI control problem (Fig. 20). The final converged velocity is reported in Fig. 21, and the final controlled velocity matches the target velocity well as plotted in Fig. 18. Finally, we plot the boxed term in (46) in Fig. 20, from which it can be seen that this term is negligible.

Fig. 16

Uncontrolled flow: vertical displacement in the solid domain, and flow field in the fluid domain

Fig. 17

Convergence of the objective for the two oscillating beams

Fig. 18

Horizontal velocity profile at the boundary Γ_N (point A to B in Fig. 15) at t = T

Fig. 19

L² norm of the control force f(t)

Fig. 20

Boxed term in (46)

Fig. 21

Controlled flow: deformed solid and horizontal velocity in the fluid domain

7.5 Oscillating leaflet oriented across the flow direction — forcing the solid to match a time-dependent displacement

We consider an oscillating leaflet in a fluid channel, which has been widely studied in the FSI literature (Baaijens 2001; Heil 2004; Wang et al. 2017; Chierici et al. 2019). The computational domain is a L × H channel with a h × w leaflet located across it as sketched in Fig. 22, and L = 4.0m, H = 1.0m, w = 0.1m and h = 0.8m in this example. A periodic flow condition is prescribed on the inlet and outlet boundaries, given by $\bar {u}_{x}=15y\left (2-y\right )sin\left (2\pi t\right )$. The fluid and solid properties are $\rho ^{f}=\rho ^{s}=100\left .kg\right /{m^{3}}$, $\mu ^{f}=10\left .N\cdot s\right /{m^{2}}$ and $c_{1}=10^{8}\left .N\right /{m^{2}}$.

Fig. 22

Computational domain and boundary conditions for the test of an oscillating leaflet

Simulation of the forward FSI problem can be achieved by solving the state equations (Problem 4) without control. We use a 80 × 20 uniform mesh and time step Δt = 0.01 and solve the forward problem from t = 0 to t = 1 (around one period of the leaflet’s oscillation). The velocity norm (when leaflet reaches its maximal deformation) and the horizontal displacement of the leaflet tip are presented in Figs. 23a and 24 (dashed green curve) respectively. Let $\left (d_x(t), d_y(t)\right )$ denote the solid displacement of the solution of this uncontrolled problem. For the control problem, we target to increase the leaflet’s deflection by 50%, i.e. we solve Problem 1 with $\textbf { d}_g=\left (1.5d_x(t), d_y(t)\right )$, γ₁ = γ₂ = β₁ = 0 and β₂ = 10⁵. The whole control is tractable, which can be seen from the convergence of the objective function as depicted in Fig. 25 for three different regularisation parameters θ. It can be seen from Fig. 23b that the leaflet’s deformation has be dramatically increased, and the deflection of the leaflet is very close to the target as shown in Fig. 24. We also investigate the control force, and it can be seen from Fig. 26 that the magnitude of the control force is a periodic function which converges to a fixed function of time. The norm of the gradient descent direction δf and the increment of the control force (αδf) are plotted in Fig. 27, from which it can be seen that the BB method cam successfully compute a varying iteration step α so that the increment of the control force converges, and consequently the control force converges as well.

Fig. 23

Velocity norm at t = 0.32

Fig. 24

Horizontal displacement at the tip of the leaflet

Fig. 25

Convergence of the objective for the oscillating leaflet

Fig. 26

L² norm of the control force f(t) for the oscillating leaflet (θ = 10^− 7)

Fig. 27

L² norm of the gradient descent direction (left) and the increment of the control force (right) for the oscillating leaflet (θ = 10^− 7)

7.6 Oscillating flag oriented along the flow direction — reducing the solid deflection

In this section, we consider the FSI control problem of an oscillating flag attached to a cylinder, where the goal is to minimise the solid deflection through the controlled application of a force. The computational domain is a rectangle (L × H) with a cut hole of radius r and centre (c,c) as shown in Fig. 28. A leaflet of size l × h is attached to the boundary of the hole (the mesh of the leaflet is fitted to the boundary of the hole, see the solid mesh in Fig. 29). The geometry parameters are L = 2.5, H = 0.41, l = 0.35, h = 0.02, c = 0.2 and r = 0.05. The fluid and solid parameters are as follows: ρ^f = ρ^s = 10³, μ^f = 1 and c₁ = 2.0 × 10⁶. The inlet flow is prescribed as:

$$ \bar{u}_x=\frac{12y}{H^2}\left( H-y\right),\quad \bar{u}_y=0. $$

(54)

Fig. 28

Computational domain and boundary conditions for the oscillating flag

Fig. 29

A snap shot of the velocity norms at t = 4.9 when the flag is maximally deformed

We use a mesh of 10, 054 nodes and 2448 biquadratic elements as shown in Fig. 29, and a converged time step of Δt = 10^− 3. The simulation results are first validated against the data provided in Turek and Hron (2006) through the oscillation period and amplitude at the tip of the flag as shown in Fig. 30, with the period and amplitude being around 0.526 and 0.035 respectively. These figures have a good agreement with the reference values given in Turek and Hron (2006) with a period and amplitude being 0.530 and 0.034 respectively. We note here that although our neo-Hookean solid model is different from the Saint Venant-Kirchhoff model in Turek and Hron (2006), however, these two models are equivalent when applying to solving this FSI benchmark problem (Kadapa et al. 2018; Hecht and Pironneau 2017; Wang et al. 2020), in the sense that they present the same numerical results as first presented in Turek and Hron (2006).

Fig. 30

Vertical displacement at the flag tip as a function of time

We now extend the analysis to consider the control of this FSI system, using the results of this fully converged FSI system as initial conditions. We use the results of t = 6 as initial values and run the simulation from t = 0 to 0.05. The aim of the control problem is to reduce the oscillation amplitude by solving Problem 1 with d_g = 0, β₁ = 0, β₂ = 10⁶, and γ₁ = γ₂ = 0. The BB method converges rapidly and reduces the objective by 60% as shown in Fig. 31, which is also faster than using a constant step size. It can also be seen from Fig. 31 that θ = 10^− 8 and 10^− 9 presents similar convergence for the objective functional J, but θ = 10^− 7 stops the reduction of J at an earlier stage, with the magnitude of the control force being plotted in Fig. 32. For a long-term control, such as from t = 0 to t = 0.40 (about one oscillation period), we insert 8 control points at t = 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35 and 0.40, and continuously solve Problem 1: the following control results use the results of the previous time as initial values for the next time (Fig. 33). We then patch together all these piecewise-in-time results as shown in Fig. 34 from which it can be seen that the oscillation magnitude has been dramatically reduced. Notice that our objective is to reduce the solid deflection by a time-dependent body force, and the solution (body force) of this problem is generally not unique or periodic. Therefore, after applying the control force, we would not expect (as observed in Fig. 34) an oscillation of fixed period and amplitude of the flag. For this problem, we also test a case of applying the control force only at the tip (x > 0.57) of the flag, and we find that the whole control is still tractable as shown in Fig. 34. We patch together the control force in Fig. 35 after gradually solving eight control problems by using the previous results as initial conditions for the following one. Although the continuity of the control force cannot be guaranteed, the displacement is still continuous in the whole time domain. The control force gradually decreases to zero in one phase of control, and then flips its direction (see Fig. 36) in the following phase and gradually decreases to zero again. It can be seen from Fig. 35 that the magnitude of the overall control force decreases as the solid deflection is reduced. Notice again that the control force is not unique, different piecewise control results would lead to different distributions of the control force, although they all may be able to successfully reduce the solid deformation. Finally, we investigate the boxed term in (46) in Fig. 33, and we find that it is negligible again.

Fig. 31

Convergence of the objective and displacement profile for the oscillating flag

Fig. 32

L² norm of the control force f(t)

Fig. 33

Boxed term in (46)

Fig. 34

Convergence of the piecewise control, with reduction of the oscillation magnitude being around 80%. “At the tip” means the control force is only applied at the tip (x > 0.57) of the flag

Fig. 35

Magnitude of the control force applied at the tip (x > 0.57) of the flag

Fig. 36

Distribution of the control force at different control points: t = 0, t = 0.05, t = 0.1, t = 0.15, t = 0.2, t = 0.25, t = 0.3, t = 0.35 (left to right, top to bottom)

8 Conclusion and future work

Time-dependent FSI control problems with large solid deformations are very challenging to solve and very few examples have appeared in the literature. This paper has made a number of original contributions to this area, including (1) derivation of the optimality condition for optimal control of time-dependent FSI problems in an ALE formulation; (2) formulation of the whole control system using one velocity field, thereby reducing the size of the FSI problem; and (3) adopting a stabilised Barzilai-Borwein (BB) method to select the gradient descent step size, which does not need additional evaluations of the objective, and has the same cost as using a constant step size but converges faster.

Gradient descent methods are widely used in the context of the adjoint-optimal control, with either the Armijo rule (Mohammadi and Pironneau 2010; Gerdes et al. 2014) or constant (Heners et al. 2018) step size typically being adopted; however, the former is costly and the latter is inefficient when applied to time-dependent control problems. In this paper, we use a stabilised BB method to accelerate the iteration which has the same cost as a constant step size and does not need additional evaluations of the objective function.

The proposed optimal control method is validated and assessed by six numerical tests: two pure fluid-control problems, two FSI problems which have steady-state solutions, and two dynamic FSI problems with complicated solid oscillation. It is shown that the complex FSI control systems can be solved using the proposed numerical method. More generally, the above features mean that it is now computationally feasible to solve extremely challenging optimal FSI problems, by solving as few as tens (at most hundreds) of CFD simulations.

In the future work, we shall consider minimising other objectives, such as the drag force, and apply this FSI control method to dynamic shape optimisation problems, such as morphing structure in aerospace engineering.

Appendices

Appendix 1. Gâteaux variation

Definition 1

The 1st-order Gâteaux variation of a functional $\mathcal {F}(\textbf {q})$ in the direction Δq is defined by (Bazilevs et al. 2013; Rall 2014)

$$ \delta\mathcal{F}(\textbf{q})[{\varDelta}\textbf{q}]=\left.\frac{d}{d\epsilon}\mathcal{F}\left( \textbf{q}+\epsilon{\Delta}\textbf{q}\right)\right|_{\epsilon=0}, $$

(55)

The following properties of Gâteaux variation are straightforward to obtain from the above definition.

• 1. For two arbitrary functionals $\mathcal {F}(\cdot )$ and $\mathcal {G}(\cdot )$:

  $$ \delta\left( \mathcal{F}\mathcal{G}\right) =\left( \delta\mathcal{F}\right)\mathcal{G} +\mathcal{F}\left( \delta\mathcal{G}\right). $$

  (56)

• 2. For a linear functional ${\mathscr{L}}(\cdot )$ and an arbitrary functional $\mathcal {F}(\cdot )$:

  $$ \delta\left( \mathcal{L}\circ\mathcal{F}\right)=\mathcal{L}\circ\delta\mathcal{F}. $$

  (57)

• 3. For the linear functional ${\mathscr{L}}(\textbf {q})=\textbf {q}$, taking the 1st variation in direction Δq:

  $$ \delta\mathcal{L}=\delta\textbf{q}={\varDelta}\textbf{q}. $$

  (58)

• 4. For a constant functional $\mathcal {F}(\textbf {q})=\textbf {c}$:

  $$ \delta\mathcal{F}=0. $$

  (59)

Remark 6

It is notationally convenient to omit the direction of a variation if it refers to an arbitrary direction δq, i.e. $\delta \mathcal {F}\left (\textbf {q}\right )=\delta \mathcal {F}(\textbf {q})[\delta \textbf {q}]$. One may further omit the independent variable q if it is not a specified point (such as q⁰, $\bar {\textbf {q}}$ or $\tilde {\textbf {q}}$). This is consistent with the differentiation of a scalar function $f\left (x\right )$: $df=f^{\prime } dx$. The terminology arbitrary δq is also consistent with the finite element arbitrary test function.

Appendix 2. Variation to the Lagrange multipliers

Taking Gâteaux variation of (24) with respect to the Lagrange multiplier $\hat {\textbf {u}}$ in an arbitrary direction $\delta \hat {\textbf {u}}$, using properties (57) and (58), gives:

$$ \begin{array}{ll} & \delta L\left( \textbf{u}, p, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}}\right)[\delta\hat{\textbf{u}}] \\ =&{\int}_{{\varTheta}\times{\varOmega}}\left( \rho\frac{\partial\textbf{u}}{\partial t} +\rho\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\textbf{u} -\nabla \cdot {\sigma} -\textbf{f}\textit{1}_{{{\varOmega}_{t}^{s}}}\right) \cdot \delta\hat{\textbf{u}} \\ +&{\int}_{{\varOmega}}\left( \textbf{u}(0)-\textbf{u}_{0}\right)\cdot\delta\hat{\textbf{u}} +{\int}_{{\varTheta}\times{\varGamma}_{D}}\left( \textbf{u}-\bar{\textbf{u}}\textit{1}_{{\varGamma}_{in}}\right)\cdot \delta\hat{\textbf{u}} \\ +&{\int}_{{\varTheta}\times{\varGamma}_{N}}\left( {\sigma}\textbf{n}-\bar{\textbf{h}}\right)\cdot\delta\hat{\textbf{u}} +{\int}_{{\varTheta}\times{\varGamma}_{t}}\left( {\sigma}^{s}-{\sigma}^{f}\right)\textbf{n}^{s}\cdot\delta\hat{\textbf{u}}. \end{array} $$

(60)

Integrating the stress term by parts;

$$ \begin{array}{ll} & \delta L\left( \textbf{u}, p, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}}\right)[\delta\hat{\textbf{u}}] \\ =&{\int}_{{\varTheta}\times{\varOmega}}\left( \rho\frac{\partial\textbf{u}}{\partial t} +\rho\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\textbf{u} -\textbf{f}\textit{1}_{{{\varOmega}_{t}^{s}}}\right) \cdot \delta\hat{\textbf{u}} \\ +& {\int}_{{{\varTheta}\times{\varOmega}_{t}^{f}}} {\sigma}^{f}:\nabla{\delta\hat{\textbf{u}}} -{\int}_{{{\varTheta}\times\partial{\varOmega}_{t}^{f}}}{\sigma}^{f}\textbf{n}^{f}\cdot\delta\hat{\textbf{u}} \\ +& {\int}_{{{\varTheta}\times{\varOmega}_{t}^{s}}} {\sigma}^{s}:\nabla{\delta\hat{\textbf{u}}} -{\int}_{{{\varTheta}\times\partial{\varOmega}_{t}^{s}}}{\sigma}^{s}\textbf{n}^{s}\cdot\delta\hat{\textbf{u}} \\ +&{\int}_{{\varOmega}}\left( \textbf{u}(0)-\textbf{u}_{0}\right)\cdot\delta\hat{\textbf{u}} +{\int}_{{\varTheta}\times{\varGamma}_{D}}\left( \textbf{u}-\bar{\textbf{u}}\textit{1}_{{\varGamma}_{in}}\right)\cdot \delta\hat{\textbf{u}} \\ +&{\int}_{{\varTheta}\times{\varGamma}_{N}}\left( {\sigma}\textbf{n}-\bar{\textbf{h}}\right)\cdot\delta\hat{\textbf{u}} +{\int}_{{\varTheta}\times{\varGamma}_{t}}\left( {\sigma}^{s}-{\sigma}^{f}\right)\textbf{n}^{s}\cdot\delta\hat{\textbf{u}}. \end{array} $$

(61)

Noticing that n^s = − n^f on the interface Γ_t, and the whole inner and outer boundary $\partial {\varOmega }={\varGamma }={\varGamma }_{D}+{\varGamma }_{N}=\left ({\partial {\varOmega }_{t}^{f}} - {\varGamma }_{t}\right ) + \left ({\partial {\varOmega }_{t}^{s}} - {\varGamma }_{t}\right )$, (61) can be further expressed as:

$$ \begin{array}{ll} & \delta L\left( \textbf{u}, p, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}}\right)[\delta\hat{\textbf{u}}] \\ =&{\int}_{{\varTheta}\times{\varOmega}}\left( \rho\frac{\partial\textbf{u}}{\partial t} +\rho\left( \left( \textbf{u}-\textbf{w}\right)\cdot\nabla\right)\textbf{u} -\textbf{f}\textit{1}_{{{\varOmega}_{t}^{s}}}\right) \cdot \delta\hat{\textbf{u}} \\ +& {\int}_{{\varTheta}\times{\varOmega}} {\sigma}:\nabla{\delta\hat{\textbf{u}}} -{\int}_{{\varTheta}\times{\varGamma}_{D}}{\sigma}\textbf{n}\cdot\delta\hat{\textbf{u}} \\ +&{\int}_{{\varOmega}}\left( \textbf{u}(0)-\textbf{u}_{0}\right)\cdot\delta\hat{\textbf{u}} +{\int}_{{\varTheta}\times{\varGamma}_{D}}\left( \textbf{u}-\bar{\textbf{u}}\textit{1}_{{\varGamma}_{in}}\right)\cdot \delta\hat{\textbf{u}} \\ -&{\int}_{{\varTheta}\times{\varGamma}_{N}}\bar{\textbf{h}}\cdot\delta\hat{\textbf{u}}. \end{array} $$

(62)

Similarly, taking Gâteaux variation of (24) with respect to the Lagrange multiplier $\hat {p}$ in an arbitrary direction $\delta \hat {p}$ gives:

$$ \delta L\left( \textbf{u}, p, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}}\right)[\delta\hat{p}] = -{\int}_{{\varTheta}\times{\varOmega}} \delta\hat{p} \nabla \cdot \textbf{u}. $$

(63)

Noticing the initial and boundary conditions stated in Problem 2, and also the space of test functions (in which $\left .\delta \hat {\textbf {u}}\right |_{{\varGamma }_{D}}=\textbf {0}$), we have (30) after letting both (62) and (63) be zero based on the optimality condition (25).

Taking Gâteaux variation of (24) with respect to the Lagrange multiplier $\hat {\textbf {w}}$ in an arbitrary direction $\delta \hat {\textbf {w}}$, using properties (57) and (58), gives:

$$ \begin{array}{ll} & \delta L\left( \textbf{u}, p, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}}\right)[\delta\hat{\textbf{w}}] \\ =&{\int}_{{\varTheta}\times{\varOmega}}\left( \rho\frac{\partial\textbf{w}}{\partial t}-\nabla\cdot\left( \mu\mathrm{D}\textbf{w}+\lambda\left( \nabla\cdot\textbf{w}\right)\textbf{I}\right) \right)\cdot \delta\hat{\textbf{w}} \\ +&{\int}_{{\varOmega}}\left( \textbf{w}(0)-\textbf{w}_{0}\right)\cdot \delta\hat{\textbf{w}} + {\int}_{{\varTheta}\times{\varGamma}_{w_{0}}}\textbf{w}\cdot \delta\hat{\textbf{w}} \\ +&{\int}_{{\varTheta}\times\left( {\varGamma}-{{\varGamma}_{w_{0}}}\right)}\left( \textbf{w}\cdot\textbf{n} \right)\left( \delta\hat{\textbf{w}}\cdot\textbf{n}\right) +{\int}_{{\varTheta}\times{\varGamma}_{t}}\left( \textbf{w}-\textbf{u}\right)\cdot\delta\hat{\textbf{w}} \\ +&{\int}_{{\varTheta}\times\left( {\varGamma}-{{\varGamma}_{w_{0}}}\right)} \textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}\right)\cdot{\tau}\left( \delta\hat{\textbf{w}}\cdot{\tau}\right), \end{array} $$

(64)

which may be further expressed as follows after integrating by parts.

$$ \begin{array}{ll} & \delta L\left( \textbf{u}, p, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}}\right)[\delta\hat{\textbf{w}}] \\ =&\rho{\int}_{{\varTheta}\times{\varOmega}}\frac{\partial\textbf{w}}{\partial t}\cdot\delta\hat{\textbf{w}} +\frac{\mu}{2}{\int}_{{\varTheta}\times{\varOmega}}\mathrm{D}\textbf{w}:\mathrm{D}\delta\hat{\textbf{w}} \\&+\lambda{\int}_{{\varTheta}\times{\varOmega}}\left( \nabla\cdot\textbf{w}\right)\left( \nabla\cdot\delta\hat{\textbf{w}}\right) \\ -&{\int}_{{\varTheta}\times\partial{\varOmega}} \textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}+\lambda\left( \nabla\cdot\textbf{w}\right)\textbf{I}\right) \cdot \delta\hat{\textbf{w}} \\ +&{\int}_{{\varOmega}}\left( \textbf{w}(0)-\textbf{w}_{0}\right)\cdot \delta\hat{\textbf{w}} + {\int}_{{\varTheta}\times{\varGamma}_{w_{0}}}\textbf{w}\cdot \delta\hat{\textbf{w}} \\ +&{\int}_{{\varTheta}\times\left( {\varGamma}-{{\varGamma}_{w_{0}}}\right)}\left( \textbf{w}\cdot\textbf{n} \right)\left( \delta\hat{\textbf{w}}\cdot\textbf{n}\right) +{\int}_{{\varTheta}\times{\varGamma}_{t}}\left( \textbf{w}-\textbf{u}\right)\cdot\delta\hat{\textbf{w}} \\ +&{\int}_{{\varTheta}\times\left( {\varGamma}-{{\varGamma}_{w_{0}}}\right)} \textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}\right)\cdot{\tau}\left( \delta\hat{\textbf{w}}\cdot{\tau}\right). \end{array} $$

(65)

Because

$$ \begin{array}{ll} &\textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}+\lambda\left( \nabla\cdot\textbf{w}\right)\textbf{I}\right) \cdot \delta\hat{\textbf{w}} \\ =&\textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}+\lambda\left( \nabla\cdot\textbf{w}\right)\textbf{I}\right)\cdot\textbf{n} \left( \delta\hat{\textbf{w}}\cdot\textbf{n}\right) \\&+\textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}+\lambda\left( \nabla\cdot\textbf{w}\right)\textbf{I}\right)\cdot{\tau} \left( \delta\hat{\textbf{w}}\cdot{\tau}\right) \\ =&\textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}+\lambda\left( \nabla\cdot\textbf{w}\right)\textbf{I}\right)\cdot\textbf{n} \left( \delta\hat{\textbf{w}}\cdot\textbf{n}\right) \\&+\textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}\right)\cdot{\tau} \left( \delta\hat{\textbf{w}}\cdot{\tau}\right), \end{array} $$

(66)

(65) can also be expressed as:

$$ \begin{array}{ll} & \delta L\left( \textbf{u}, p, \textbf{w}, \textbf{f}, \hat{\textbf{u}}, \hat{p}, \hat{\textbf{w}}\right)[\delta\hat{\textbf{w}}] \\ =&\rho{\int}_{{\varTheta}\times{\varOmega}}\frac{\partial\textbf{w}}{\partial t}\cdot\delta\hat{\textbf{w}} +\frac{\mu}{2}{\int}_{{\varTheta}\times{\varOmega}}\mathrm{D}\textbf{w}:\mathrm{D}\delta\hat{\textbf{w}} \\&+\lambda{\int}_{\Theta\times{\Omega}}\left( \nabla\cdot\textbf{w}\right)\left( \nabla\cdot\delta\hat{\textbf{w}}\right) \\ -&{\int}_{{\varTheta}\times\partial{\varOmega}} \textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}+\lambda\left( \nabla\cdot\textbf{w}\right)\textbf{I}\right)\cdot\textbf{n} \cdot \left( \delta\hat{\textbf{w}}\cdot\textbf{n}\right) \\ -&{\int}_{{\varTheta}\times{{\varGamma}_{w_{0}}}} \textbf{n}\cdot\left( \mu\mathrm{D}\textbf{w}\right)\cdot{\tau}\left( \delta\hat{\textbf{w}}\cdot{\tau}\right) \\ +&{\int}_{{\varOmega}}\left( \textbf{w}(0)-\textbf{w}_{0}\right)\cdot \delta\hat{\textbf{w}} + {\int}_{{\varTheta}\times{\varGamma}_{w_{0}}}\textbf{w}\cdot \delta\hat{\textbf{w}} \\ +&{\int}_{{\varTheta}\times\left( {\varGamma}-{{\varGamma}_{w_{0}}}\right)}\left( \textbf{w}\cdot\textbf{n} \right)\left( \delta\hat{\textbf{w}}\cdot\textbf{n}\right) +{\int}_{{\varTheta}\times{\varGamma}_{t}}\left( \textbf{w}-\textbf{u}\right)\cdot\delta\hat{\textbf{w}}. \end{array} $$

(67)

Noticing the finite element spaces we use in Problem 2, in which both the trial and test functions satisfy boundary condition (8), we have (31), based upon the optimality condition (25) and the initial condition w(0) = w₀ stated in Problem 2 as well.