Penalty regulation of overhang in topology optimization for additive manufacturing

Abstract

Several filter approaches that introduce additive manufacturing-related overhang constraints in topology optimization exist. However, a drawback of these is that exact satisfaction of overhang constraints produces sharp inward corners resulting in stress singularities. The present paper therefore modifies such filter approaches by a penalty formulation, where the choice of penalty factor regulates how closely the overhang constraint is satisfied. By appropriately choosing certain weight factors in the penalty function, the cost of support structures is also reflected in the formulation in a simple and computationally inexpensive way. The method is demonstrated by parameter studies using the classical MBB beam, using both structured and unstructured meshes.

1 Introduction

Topology optimization (TO) and additive manufacturing (AM) constitute an unusually striking match of design and manufacturing method, sharing the possibility of very general shapes and forms (see Liu et al. (2018) for a recent overview). However, certain constraints related to the manufacturing method will still be present and need to be explicitly taken into account by the TO formulation. In particular, the overhang constraint, implying that the angle a surface tangent makes to the AM build direction should be below a certain value, is of prime importance. Several methods and formulations that in various ways take such a constraint into account have been suggested. A direct strategy is to modify topology-optimized structures simply from geometrical considerations (Leary et al. 2014; Hu et al. 2015) without considering optimality of the modified structure. A more complete approach is to include the geometric overhang constraints in the TO problem. This has been done in two somewhat different, but related, ways: Qian (2017), and also Garaigordobil et al. (2018), used an average of the constrained angle in an explicit constraint, whiley Langelaar (2016, 2017, 2018) and Gaynor and Guest (2016) introduced filters that control the presence of support material at each point of the optimal structure. Another filter approach based on calculating arrival times of a front propagating the design domain and whose speed depends on the overhang was presented by van de Ven et al. (2018). Moreover, Allaire et al. (2017) introduced an implicit overhang constraint in the form of additional elasticity problems that need to be solved for partly manufactured designs, while they also presented numerical test on the average geometric constraint in Qian (2017). Mass and Amir (2017) imposed the overhang constraint implicitly by making the optimized continuum model adhere to a previously optimized truss structure satisfying the constraint. The method described by Guo et al. (2017) consists essentially of converting the TO problem into a shape optimization problem with explicit control over parameters describing the boundary, thus offering a way to control the overhang directly via constraints on the parameters.

However, all of these approaches have certain drawbacks: The direct inclusion of the geometric constraints into the TO formulation, as in Qian (2017) and Mezzadri et al. (2018), gives unwanted shapes that show a “dripping effect” (as named in Allaire 2017) and also seems to produce formulations with many local optima. The physical constraints of Allaire et al. (2017) do not show the “dripping effect,” but on the other hand, is very computationally demanding (calculation times of weeks are reported), and the method does not seem to eliminate all overhang. The methods described by Mass and Amir (2017) and Guo et al. (2017) put additional restrictions on the design space besides the overhang. The two slightly different filter approaches of Langelaar (2016, 2017) and Gaynor and Guest (2016) also do not show the “dripping effect,” but still produce designs that have a tendency to have a rugged appearance with inward corners that in linear elasticity will be associated with singular stress states. Such inward corners are in Hoffarth et al. (2017) removed by a post processing step where a smooth iso-surface defines the structure. In Wang et al. (2018), inward corners are smoothed algorithmically by accepting solutions as convergent when slight violation of the overhang constraint is present. The present contribution on the other hand builds the smoothing into the actual formulation of the optimization problem. Note that small rounded corners are accepted in AM structures, even though a strict overhang constraint is violated: AM design rules include expressions for allowable short overhang regions (see, e.g., Adam and Zimmer (2014), Kranz et al. (2015), and Mirzendehdel and Suresh (2016)).

The present formulation uses a modification to unstructured meshes, indicated by Hoffarth et al. (2017), of the filter approach of Langelaar (2016, 2017) to produce an overhang free design, but this design is not the final physical design. Rather, the overhang free design is compared to the physical design and a penalty term is added to the objective function of the TO problem, which implies a cost for deviation between the physical design and the overhang free design. This takes away the sharp corners present in original method of Langelaar, a feature that should be necessary when, e.g., stress constraints are included in TO. Depending on the value of the penalty parameter, different length of overhang will typically remain in the optimal design. Thus, at least for small values of this parameter, the aim of the method is to limit the amount of support structure, not removal of all such additional structure. Methods that somehow include the cost of support structure have been presented in Langelaar (2018) and Mirzendehdel and Suresh (2016). The present method implicitly includes such cost. In particular, a certain choice of weight factors in the penalty term makes overhang far from the base plates more costly, thus less preferable in an optimal solution, than overhang close to the base plate. It should be noted, however, that the method does not include a precise specification of, e.g., what length of overhang is allowed or what rounding is obtained at corners. Parameters of the formulation are not directly connected to such precise features of an optimal design. Therefore, as it is usual in TO, the suggested optimized designs should be seen as conceptual designs that need refinement and further analysis.

2 General setting and sensitivity

An overhang free design produced by Laangelaar’s filter is denoted $\boldsymbol {\rho }^{\text {of}}=(\rho _{i}^{\text {of}},\ldots ,\rho _{n}^{\text {of}})^{T}$ and the physical design is denoted ρ = (ρ_i,…,ρ_n)^T. As it is now standard in density-based TO, the physical design is a function of the optimization variable x = (x_i,…,x_n)^T through the use of a density filter, i.e., ρ = ρ(x), and a linear such filter is used in this paper (Bourdin 2001). The usual setting of one variable per finite element is used, so n represents the number of such elements. For comparison to Langelaar (2016, 2017), the physical variables are somewhat related to what Langelaar calls blue-print variables, but a difference in our approach is that these variables are used for calculating stiffness and are taken as the actual physical design. Moreover, Langelaar considers structured meshes only and the calculation is done layer by layer. Here, we extend this method to unstructured meshes, following Hoffarth et al. (2017). The details are given in Section 3, while in this section, we only need to realize that it means considering implicit functions of the form

$$ \rho_{i}^{\text{of}}=L_{i}(\boldsymbol{\rho},\boldsymbol{\rho}^{\text{of}}), i = 1,\ldots, n, $$

(1)

where the functions L_i will eventually be formed from smoothed max and min operators. These functions can in principle be solved for ρ^of, resulting in

$$ \boldsymbol{\rho}^{\text{of}}=\boldsymbol{B}(\boldsymbol{\rho}), $$

(2)

where B = (B_i,…,B_n)^T is a vector-valued function.

The objective function will depend on the physical design and is written f(ρ). A penalty term P representing the cost of deviating from an AM-preferred overhang free design is added to form an augmented objective

$$f^{a}(\boldsymbol{\rho},\boldsymbol{\rho}^{\text{of}})=f(\boldsymbol{\rho})+P(\boldsymbol{\rho}-\boldsymbol{\rho}^{\text{of}}). $$

A general formulation of an optimization problem is then

$$(\mathbb{P})\quad\min\limits_{\boldsymbol{x}\in \mathcal{X}} f^{a}(\boldsymbol{\rho}(\boldsymbol{x}),\boldsymbol{B}(\boldsymbol{\rho}(\boldsymbol{x}))), $$

where $\mathcal {X}$ is a set defined by the standard volume and box constrains of TO.

To calculate the sensitivity of the augmented objective function, we introduce a Lagrangian-like function

$$\mathcal{L}(\boldsymbol{\rho},\boldsymbol{\lambda})=f^{a}(\boldsymbol{\rho},\boldsymbol{B}(\boldsymbol{\rho}))+\sum\limits_{i = 1}^{n}\lambda_{i}(L_{i}(\boldsymbol{\rho},\boldsymbol{B}(\boldsymbol{\rho}))-{B}_{i}(\boldsymbol{\rho})), $$

where λ = (λ₁,…,λ_n)^T is a vector of Lagrangian multipliers. Since the bracket in the second term is zero for any Lagrangian multiplier, both the value and the sensitivity with respect to ρ are the same for $\mathcal {L}$ and f^a. Proceeding with a direct differentiation, omitting arguments, we get

$$\frac{\partial\mathcal{L}}{\partial\rho_{j}}=\frac{\partial f^{a}}{\partial \rho_{j}}+\sum\limits_{k = 1}^{n}\frac{\partial f^{a}}{\partial \rho_{k}^{\text{of}}}\frac{\partial B_{k}}{\partial \rho_{j}}+\sum\limits_{i = 1}^{n}\lambda_{i}\left( \frac{\partial L_{i}}{\partial \rho_{j}}+{\sum}_{k = 1}^{n}\frac{\partial L_{i}}{\partial \rho_{k}^{\text{of}}}\frac{\partial B_{k}}{\partial \rho_{j}}-\frac{\partial B_{i}}{\partial \rho_{j}}\right). $$

Rearranging terms, we get

$$\frac{\partial\mathcal{L}}{\partial\rho_{j}}=\frac{\partial f^{a}}{\partial \rho_{j}}+\sum\limits_{i = 1}^{n}\lambda_{i}\frac{\partial L_{i}}{\partial \rho_{j}}+\sum\limits_{k = 1}^{n}\left[\frac{\partial f^{a}}{\partial \rho_{k}^{\text{of}}}+\sum\limits_{i = 1}^{n}\lambda_{i}\left( \frac{\partial L_{i}}{\partial \rho_{k}^{\text{of}}}-\delta_{ik}\right)\right]\frac{\partial B_{k}}{\partial \rho_{j}}, $$

where δ_ij is Kronecker’s delta. Thus, by letting

$$ \lambda_{k}=\frac{\partial f^{a}}{\partial \rho_{k}^{\text{of}}}+\sum\limits_{i = 1}^{n}\lambda_{i}\frac{\partial L_{i}}{\partial\rho_{k}^{\text{of}}} $$

(3)

we obtain

$$ \frac{d f^{a}}{d\rho_{j}}=\frac{\partial\mathcal{L}}{\partial\rho_{j}}=\frac{\partial f^{a}}{\partial \rho_{j}}+\sum\limits_{i = 1}^{n}\lambda_{i}\frac{\partial L_{i}}{\partial \rho_{j}}. $$

(4)

The final sensitivity with respect to the optimization variable x is now obtained by the use of the chain rule.

Comparing the above formulation and sensitivity calculation with that of Langelaar (2016, 2017), we note that the latter is retrieved from the above by letting ρ approach ρ^of. The penalty term is then removed and the objective function becomes f(B(ρ(x))). The above sensitivity formulas (3) and (4) coincide with that of Langelaar (2016, 2017) if the term ∂f^a/∂ρ_j is removed. Thus, the present method involves no extra computational effort compared to the original AM filter in Langelaar (2016, 2017).

3 Overhang filter

For construction of the overhang free design ρ^of, we use a slightly extended version of the filter developed in Langelaar (2016, 2017). One of the limitations of the original formulation is that it is only defined for a structured mesh with equal sized elements, but this limitation can be lifted by introducing a mesh independent control volume in the form of a cone (denoted Θ_i below) as shown in Hoffarth et al. (2017). In the following, we give details of such an extension to unstructured meshes. To avoid the original method’s use of layers of elements, each element is given a height, h_i, by projecting the centroid of the element onto the build direction, i.e.,

$$h_{i}=\boldsymbol{x}_{i} \cdot {\boldsymbol{n}}, $$

where x_i is the centroid of element i and n is a unit vector in the build direction. A filtering application sequence is then determined by ordering the elements, and thereby the design variables, from lowest to highest in terms of h_i.

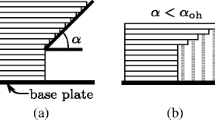
The cone control volume for element i is

$${\Theta}_{i} =\left\{j\in \{1,\ldots,n\} \ \left\vert \ -\frac{{\boldsymbol{n}}\cdot \boldsymbol{v}_{ij}}{|\boldsymbol{v}_{ij}|} \leq \cos{\phi_{max}}\right., 0 < |\boldsymbol{v}_{ij}| \leq H\right\}, $$

where v_ij = x_j −x_i, ϕ_max is the largest allowed overhang angle and H is the maximum distance to a supporting element. An illustration is given in Fig. 1, where the filter radius R of the linear density filter is also shown. With an appropriately chosen radius (H slightly larger than R), the linear density filter prevents the appearance of pathological situations where an element is not supported immediately below but only further down in the filter cone. Note that the discrete nature of the setting means that ϕ_max is an upper bound for the overhang angle, and as ϕ_max changes this actual overhang angle will change stepwise at certain values that depends on H. For the setting shown in Fig. 1 such steps will occur at tan− 10.5, tan− 11 and tan− 13. For unstructured coarse meshes, the actual angle will vary over the structure, depending on the local discretization. However, keeping R and H fixed, refining the mesh will improve the accuracy of the approximation of ϕ_max. Moreover, for a given mesh, one way to improve the approximation is to include additional points besides the centroids in the definition of Θ_i; cf. Johnson and Gaynor (2018).

Fig. 1

Illustration of the AM filter. R is the filter radius of the standard linear density filter. Other variables are defined in the text. The dots indicate the centroids of the elements

As a first step in calculating an overhang free design, we calculate what support exists in Θ_i; i.e., we calculate a tentative overhang free design as

$$\hat{\rho}_{i}^{\text{of}}=\max_{j\in {\Theta}_{i}}\rho_{j}^{\text{of}}. $$

Note that due to the ordering of elements, j ∈Θ_i is always less than i, which means that the right hand side is known if the calculation is done in the order of the numbering. Next, the possibility of filling an element with material, if indicated as a possibility by $\hat {\rho }_{i}^{\text {of}}= 1$, is utilized only if the physical design allows this; i.e., the overhang free design for element i is taken as

$$ \rho_{i}^{\text{of}}=\min\{\rho_{i},\hat{\rho}_{i}^{\text{of}}\}. $$

(5)

However, since the min and max operators are non-differentiable, smoothed versions of these need to be used, denoted smin and smax. That is, the functions L_i in (1) are defined as

$$ L_{i}(\boldsymbol{\rho},\boldsymbol{\rho}^{\text{of}})=\text{smin}\{\rho_{i},\text{smax}\{\rho_{j}^{\text{of}}|j\in{\Theta}_{i}\}\}, \quad i = 1,\dots,n. $$

(6)

Here, we use the approximations

$$\begin{array}{@{}rcl@{}} \text{smax}\{\rho_{j}^{\text{of}}|j\in{\Theta}_{i}\} &=& \left( \sum\limits_{j \in {\Theta}_{i}} (\rho_{j}^{\text{of}})^{P_{\rho}} \right)^{\frac{1}{Q}}, \\ \text{smin}(\rho_{i},\hat{\rho}_{i}^{\text{of}}) &=& \frac{1}{2}\left( \rho_{i}+\hat{\rho}_{i}^{\text{of}}-\left( (\rho_{i}-\hat{\rho}_{i}^{\text{of}})^{2}+\epsilon \right)^{\frac{1}{2}} + \sqrt[]{\epsilon} \right). \end{array} $$

The parameters P_ρ, Q, and 𝜖 determine the accuracy of the approximations and therefore the performance of the overhang filter. Based on the recommendations in Langelaar (2016), we use

$$\epsilon= 10^{-4}, \quad P_{\rho}= 40, \quad Q = P_{\rho} + \frac{\log{n_{\rho}}}{\log{\rho_{0}}}, $$

where ρ₀ = 0.5 and n_ρ = max{|Θ₁|,…,|Θ_n|}. Other values were not tested in the present work but finding the best performance in this respect is likely coupled to finite element refinement and parameters of the penalty function.

Note that for the functions L_i in (6) it holds that

$$\frac{\partial L_{i}}{\partial\rho_{j}^{\text{of}}}\not= 0 \text{ only if } i>j, $$

$$\frac{\partial L_{i}}{\partial\rho_{j}}\not= 0 \text{ only if } i=j, $$

which means that the sensitivity formulas (3) and (4) read

$$ \lambda_{k}=\frac{\partial f^{a}}{\partial \rho_{k}^{\text{of}}}+\sum\limits_{i=k + 1}^{n}\lambda_{i}\frac{\partial L_{i}}{\partial\rho_{k}^{\text{of}}} $$

$$ \frac{d f^{a}}{d\rho_{j}}=\frac{\partial\mathcal{L}}{\partial\rho_{j}}=\frac{\partial f^{a}}{\partial \rho_{j}}+\lambda_{j}\frac{\partial L_{j}}{\partial \rho_{j}}. $$

Therefore, the calculation of the multipliers can be done sequentially in the reversed order, from large number to low number.

4 Specification of optimization problem $(\mathbb {P})$

Assuming static linear elasticity, the equilibrium equation reads

$$ \boldsymbol{F}=\boldsymbol{K}(\boldsymbol{\rho})\boldsymbol{u}, $$

(7)

where the symmetric positive definite stiffness matrix K(ρ) depends on the physical design ρ. Here, u is the vector of nodal displacements and F is the corresponding force vector. Using the SIMP-method (Bendsøe and Sigmund 2002; Christensen and Klarbring 2009) to enforce black-and-white solutions, the explicit form of the stiffness matrix is

$$ \boldsymbol{K}(\boldsymbol{\rho})=\sum\limits_{i = 1}^{n}{\rho_{i}^{r}}{\boldsymbol{K}}_{i}, $$

(8)

where K_i is an element stiffness matrix for a unit value of the design variable ρ_i and r ≥ 1 is the SIMP exponent, here set to 3. The feasible set of the general problem $(\mathbb {P})$ is

$$\mathcal{X} = \{\boldsymbol{x}\in \mathbb{R}^{n}\mid\sum\limits_{i = 1}^{n} a_{i}\rho_{i}(\boldsymbol{x})\leq V, \varepsilon\leq{x}_{i}\leq 1, i = 1,\ldots,n\}, $$

where ε > 0 is a small value that, by being non-zero, has the effect of making K(ρ) non-singular assuming appropriate supports, a_i are positive constants, representing volumes of elements, and V is a specified volume bound. As an objective function, we take the standard compliance objective

$$f(\boldsymbol{\rho})=\frac{1}{2}\boldsymbol{F}^{T}\boldsymbol{u}(\boldsymbol{\rho}), $$

where u(ρ) is the solution of (7). The penalty function P is given by the following general form:

$$ P(\boldsymbol{\xi})=\gamma\left( \sum\limits_{i = 1}^{n}{\xi_{i}^{p}}w_{i}\right)^{\frac{1}{q}}, $$

(9)

where w_i > 0 are weight factors, γ > 0 is a penalty factor, p and q are positive constants that need to be chosen appropriately, and ξ is a vector with components $\xi _{i}=\rho _{i}-\rho _{i}^{\text {of}}$. The case p = q gives a p-norm that approaches the max-function as p approaches infinity. In the numerical calculations, we use a weak such approximation by taking p = 2. We also use the values p = 1 and q = 0.5, which gives a less localized penalty. These values give a proper penalty term since, by (5), $\rho _{i}^{\text {of}}\leq \rho _{i}$, implying ξ_i ≥ 0 in (9), i.e., P(ξ) = 0 implies ξ = 0. The weights w_i can be chosen to further achieve special features of the design. For instance, the heights h_i can be used to the define the weights as

$$ w_{i}=(h_{i}-h_{\min})/(h_{\max}-h_{\min}), $$

(10)

where h_min and h_max are the smallest and largest height values. With this choice of weight functions, elements far from the base plate, where h_i is near to h_max, are penalized to comply more closely to the overhang free design than elements closer to the base plate. This reflects the cost of support structure in a simple and computationally inexpensive way. In (10), the weights vary linearly with distance from the base plate, but obviously other variations could be considered.

5 Examples

The method is implemented in the program TRINITAS (Torstenfelt 2019) and tested for the classical MBB beam problem shown in Fig. 2.

Using symmetry, half of the beam is modelled. The numerical value of L is 0.2.¹ An isotropic material with Poisson’s ratio 0.3 and Young’s modulus 205 ⋅ 10⁹ is used. The applied force F is 10⁴. Note that magnitudes for Young’s modulus and the force does not effect the optimal topology in standard stiffness optimization, but since a penalty term is added in our method the value of the penalty coefficient γ needs to be compared to these values. The density filter radius is R = L/30, and the AM filter height is H = 1.2R. The volume bound V is 40% of the volume of the design domain. The problems are solved using MMA (Svanberg 1987) with default parameters and starting from a uniform density ρ_i = 0.25.

Fig. 2

The MBB beam used as test example, modeled using symmetry

5.1 Structured mesh

In this section, we use a structured mesh consisting of 10,800 (60 × 180) equally sized 4-node quadrilateral elements, implying that R = 2l, where l is the side length of an element. Calculations are run for for 650 iterations with no other stopping criteria. Run times are around 2 min on a standard PC.

Figure 3 shows a reference case where no AM filter or penalty is used. In the following, we will compare optimal compliances to this reference case and relative optimal compliance C will be specified. By definition, C = 1 for the design in Fig. 3.

In Fig. 4, the same beam is optimized using Langelaar’s AM filter. The build direction is in the positive y-direction and the maximum overhang angle is set to 46^∘ (which in practice means 45^∘ due to the structured grid). The relative optimal compliance of the beam in Fig. 4 is C = 1.11.

No boundaries with overhang exist in Fig. 4, but an unavoidable result of complete satisfaction of such a constraint is that sharp inward corners, where linear elasticity predicts stress singularities, are produced. The penalty approach makes it possible to obtain a compromise between the design in Fig. 3 and the overhang free design in Fig. 4. Figure 5 shows the result of this approach using a penalty term with p = q = 2, w_i = 1 and four values of γ. In principle, when γ changes from zero to infinity, we interpolate between, on the one hand, a standard stiffness optimization problem where we do not take overhang constraints into account and, on the other hand, a strict satisfaction of overhang constraints. However, the actual visual change of topology and geometry seems to take place for a rather small range of values. Presently, we find this range simply by manual interval halving. In practical applications, an engineer would likely want to generate a range of different designs with different γ to find an acceptable compromise between AM printability and performance.

Fig. 3

Reference case without AM filtering, structured mesh, C = 1

Fig. 4

The MBB beam using Langelaar’s AM filter, C = 1.11. Note the sharp corners where overhang constrained boundaries meet

Fig. 5

The MBB beam using the penalty approach with p = q = 2, w_i = 1 and γ equal 0.005, 0.01, 0.015, and 0.02 from top to bottom. Corresponding relative optimal compliances C are 1.03, 1.09, 1.12, and 1.14. In the upper picture, sections that violate the 45^∘ constraint are shown in red

The beam in the top picture in Fig. 5 has extensive overhang, that need support structure if manufactured by AM, but the penalization has produced more structural members in the print direction than the reference beam in Fig. 3. More specifically, the horizontal upper member has large unsupported spans, while the inclined members, with some exceptions, satisfy the 45^∘ constraint. Portions of the design where the constraint is not satisfied are indicated in red. As we move downwards in Fig. 5, the penalty term increases printability of design at the cost of stiffness performance. In the lower three figures, some rounding of sharp corners can be seen but no extensive overhang exists and inclined members closely satisfy the 45^∘ constraint, as can be verified by use of an angle hook. Clearly, the rounding varies not only as we move downwards, increasing the penalty, in Fig. 5, but also with position within each plot. This is because the penalty term only measures the average deviation between an overhang free design and the physical design. The fact that the relative optimal compliance is slightly higher in the designs at the bottom of Fig. 5 than in Fig. 4 is likely a result of local optimality. However, starting the calculation from a different initial design may induce small changes in topologies and compliance values.

In Fig. 6, we solve a problem with the same setting as in the lower picture of Fig. 5, except that the maximum overhang angle is set to 30^∘. We have also tested the angle 60^∘, but in accordance with the discussion in Section 3, the actual angle and solution then becomes the same as in Fig. 5.

Fig. 6

The same problem as in the lower picture of Fig. 5, except that the maximum overhang angle is changed from 46^∘ to 30^∘. The relative optimal compliance C = 1.13

A similar sequence of designs as in Fig. 5 but for p = 1 and q = 0.5 is shown in Fig. 7. As indicated in Section 4, this choice of parameters gives a penalty which is less local than the p-norm and corners are somewhat more rounded, even though a rather sharp corner to the right in the lower picture is observed.

Fig. 7

The MBB beam using the penalty approach with p = 1, q = 0.5, w_i = 1, and γ equal to 10^− 7, 5 ⋅ 10^− 7, and 10^− 5 from top to bottom. Corresponding relative optimal compliances C are 1.03, 1.07, and 1.08

In Fig. 8, we have solved the MBB beam using penalty and the weights defined in (10) with p = 1, q = 0.5, and γ = 10^− 5. The effect seen here is that some structural members close to the base are allowed a large angle, reflecting that the cost of support structure is smaller than for overhang with larger distance to the base plate.

Fig. 8

The MBB beam using the penalty approach with p = 1, q = 0.5, γ = 10^− 5 and weights defined in (10). The build direction is shown by an arrow. The corresponding relative optimal compliance C = 1.10

Finally, in Fig. 9, we have plotted the overhang free design ρ^of in the upper picture and the corresponding physical design ρ in the lower picture. The penalty parameter γ is chosen as 0.004 to give a low penalization, resulting in a clearly distinguishable difference between the two designs. Note that since the physical design ρ is the one used for calculating the stiffness matrix, there is no incentive for ρ^of to define a stiff structure. This is clearly seen in the plot of ρ^of, where the overhang constraint is satisfied at the expense of removing material at critical positions.

Fig. 9

Comparison of the overhang free design ρ^of in the upper picture and the corresponding physical design ρ in the lower picture

5.2 Unstructured mesh

We have also tested the method with unstructured meshes. A rather more fine mesh than for structured meshes turned out to be necessary for good satisfaction of the overhang angle. We use 102,808 3-node linear triangular elements, while other values such as filter radii are the same. The number of iterations was also raised to 3000, again without any other convergence criteria.

Figure 10 shows a reference case without AM filter. The relative optimal compliance for the reference case is again C = 1.

Figure 11 shows the MBB beam using Langelaar’s filtering for the unstructured mesh. The overhang angle is specified to 45.5^∘. The relative compliance is C = 1.176. Note the overall relatively large difference in appearance from Fig. 4, which turns out to be less using the penalty modification.

Fig. 10

Reference case for the unstructured mesh without AM filtering, C = 1

Fig. 11

The MBB beam using Langelaar’s AM filter, unstructured mesh, C = 1.18

Fig. 12

The MBB beam for an unstructured mesh using the penalty approach with p = q = 2, w_i = 1 and γ equal 0.003, 0.0035, 0.004, and 0.005 from top to bottom. Corresponding relative optimal compliances C are 1.096, 1.118, 1.122 and 1.131

A sequence of designs, gradually changing γ, similar to those in Fig. 5, is shown for the unstructured mesh in Fig. 12.

5.3 Stress calculation

We consider stiffness optimization in this paper and stresses are not explicitly involved in the problem formulation. However, since a motivation for developing the penalty approach is to avoid optimal geometrical shapes that are unfavorable from a stress point of view, we present in this section a typical stress distribution for an optimal solution. However, some issues first have to be clarified. Firstly, it is a matter of what is the correct stress in a region of the design where the physical density is less than the maximum value 1. We then refer to the classical paper by Duysinx and Bendsøe (1998), where it is indicated that, in case of SIMP penalization, the natural choice of local stress is obtained by scaling the standard stress by the same factor as the elasticity modulus, i.e., by ${\rho _{i}^{r}}$, r = 3, where the standard stress is calculated from the displacements without considering density scaling. From this local stress, we calculate the von Mises scalar stress. Secondly, a comparison between a solution using Langelaar’s filter and the present approach is not useful, since we expect the former to have sharp inward corners where theoretically the stress is infinity but in practice is a function of the mesh refinement. This being clarified, we show the von Mises stress distribution for a solution using a structured mesh that is denser than in Section 5.1. We use four times the number of elements used in Section 5.1, i.e., 43,200 elements. The penalty coefficient is γ = 0.005 and the penalty function coefficients are p = q = 2. The optimal topology is shown in the upper picture of Fig. 13 and the stress levels are plotted in the lower picture. Note that since the stress levels are less than 10% of the maximum stress in some parts of the optimal structure these parts are not seen in the stress plot. Note also that the two largest stress peaks occur at the application of the force in the lower right hand corner and due to the boundary conditions at the upper left corner, both of which are not related to the overhang filter.

Fig. 13

Upper picture: an optimal topology obtained using 43,200 4-node quadrilateral elements, γ = 0.005 and p = q = 2. Lower picture: von Mises stress distribution. Missing parts corresponds to stress less than 10% of maximum stress

6 Conclusions and discussion

Strict satisfaction of overhang constraints that emanate from additive manufacturing results in topology optimized designs that have sharp inward corners. Linear elasticity dictates stress singularities at such corners, meaning unwanted bad strength and fatigue properties. In order to relieve this problem, we suggest an approach where a penalty function, representing cost for designs that deviate from an overhang free design, is added. By changing a penalty parameter, families of solutions gradually approaching satisfaction of the overhang constraint can be generated. It is also possible to choose certain weight factors to reflect the cost of support structure needed when the overhang constraint is not fully satisfied.

The method is demonstrated for standard stiffness-based optimization, but can be used together with any objective or constraint functions. In particular, the removal of inward corners should be essential when stress is introduced as such functions.