On preventing the dripping effect of overhang constraints in topology optimization for additive manufacturing

Abstract

This article falls within the scope of topology optimization for Additive Manufacturing processes and proposes an alternative strategy to prevent the phenomenon known as the Dripping Effect. The Dripping Effect is when an overhang constraint is imposed on topology optimization processes for Additive Manufacturing and is defined as the formation of oscillatory contour trends within the prescribed threshold angle. Although these drop-like formations constitute local minimizers of the constraint function, they do not provide a printable feature, and, therefore, they neither eliminate the need to form temporary support structures. So far, there has been no general agreement on how to prevent the Dripping Effect, so this work aims to introduce a strategy that effectively prevents it, and that at the same time may be easy to extrapolate to other types of geometric overhang restrictions. This paper provides a study of the origin of the Dripping Effect and gives detailed instructions on how the proposed prevention strategy is applied. In addition, several benchmark examples where the Dripping Effect is prevented are shown.

1 Introduction

Additive Manufacturing (AM) is the process of joining material to make objects from 3D model data, usually layer upon layer, as opposed to subtractive manufacturing methodologies, such as traditional machining (ASTM International 2012). Usually, the input of these manufacturing techniques is constituted by a Computer-Aided Design (CAD) model, usually supplied under the form of a surface mesh that after a slicing process is converted into a series of two-dimensional layers. During the manufacturing process, these layers are individually assembled one on top of the other until they form a solid representation of the object.

The generation of 3D objects adding material layer by layer gave AM unprecedented power, so its introduction entailed a complete revolution of the fabrication capacities (Gibson et al. 2015). Namely, they put the complex geometries that were previously unattainable within the reach of designers and boosted design freedom. This power rapidly fell into the attention of designers, who started to combine the new fabrication capacities with the very well-established topology optimization processes. The binomial turned to be quite promising, and several high-performance novel designs can endorse it (EOS Aerospace 2018).

However, and despite their many assets, additive processes are not fully mature and suffer from several drawbacks: lack of scalability, anisotropy of the properties of the built part, and stair stepping or limit of the part size among others (Tofail et al. 2018; Bikas et al. 2019; Gao et al. 2015; Abdulhameed et al. 2019). Closer to the scope of the present work is the difficulty that additive processes experience when it comes to completing parts that have unsupported members, namely, large overhanging limbs with non-printable slopes. The minimum overhang angle is the smallest manufacturable overhang angle and typically amounts to 45° in Selective Laser Melting (Thomas 2009). This value is still a general convention, and it depends on the parameters of the process (Wang et al. 2013). If the part to be built includes such features, it can either collapse, distort, or break during the manufacturing process. These types of problems during the printing process can be avoided by introducing supports, but this solution entails further post-processing and greater material expenses.

Another alternative to solve these manufacturing problems is to address the overhang limitation of AM processes during the design stage, which in recent years was referred to as Design for Additive Manufacturing (DfAM). Some authors worked on the idea of optimizing the support structures needed to make the part printable (Vanek et al. 2014; Mirzendehdel and Suresh 2016; Calignano 2014; Leary et al. 2014), others introduced strategies to minimize the amount of support material by finding the optimal build direction of the part (Morgan et al. 2016). Alternatively, many authors developed strategies to effectively introduce an overhang constraint as a manufacturing constraint within the topology optimization problem formulation (Guo et al. 2017; Wang et al. 2021; de Ven et al. 2020).

Roughly, the different strategies that address the overhang issue during the topology optimization problem can be classified into additive manufacturing filters (Zhang et al. 2019; Gaynor and Guest 2016; Langelaar 2017, 2016; Zou et al. 2021; van de Ven et al. 2018) and geometric overhang constraints (Qian 2017; Garaigordobil et al. 2019, 2018; Garaigordobil and Ansola 2019; Garaigordobil 2018; Allaire et al. 2017). The former group of methods analyses layer by layer whether the solid elements have enough support material underneath, while the latter explores the design domain looking for the contours of the structure, analyzing their inclination, and correcting those who are below a threshold overhang angle.

However, many authors have reported an erratic contour formation, especially, when the overhang was controlled by geometric means (Qian 2017; Allaire et al. 2017). This contour pattern was later known as the Dripping Effect and consists of the formation of drops of solid material that gives the contours the appearance of oscillating within the prescribed threshold angle (Fig. 1). This work evolves in this line of work and studies the Dripping Effect in geometric overhang constraints.

Fig. 1

Design of an MBB beam with oscillatory contours

Concisely, this article aims to provide an effective procedure to prevent the formation of oscillatory contours. The specific contributions of the present paper can be listed as a novel strategy to suppress the Dripping Effect or oscillatory contour trend, and the introduction of the sigmoid function to get linearized and differentiable forms of the developed equations.

The article is organized as follows. Section 2 introduces the edge detection algorithm used in this work along with the overhang constraint that was developed in previous works. Section 3 discusses the Dripping Effect and explains how the new prevention method is applied. Section 4 introduces the filtering and projection schemes, and section 5 shows the formulation of the problem and its derivatives. Then, section 6 proposes several benchmark examples and analyzes the performance of the new approach. Finally, section 7 presents the conclusions reached.

2 Edge detection and overhang constraint

The overhang situation of any part is determined by the number, inclination, and length of the overhanging members present in it; therefore, a first step to attempt to address the overhang problem is to develop an algorithm that can recognize shapes and detect contours and their inclination. For that reason, this work resorts to the field of Digital Image Processing (DIP) and adopts the ideas of the Smallest Univalue Segment Assimilating Nucleus (SUSAN) algorithm (Smith and Brady 1997)

Once the contours are detected, an easy rule that considers their inclination determines whether these are supported or unsupported, which in turn allows obtaining a representative magnitude of the global overhang situation of the current topology. Eventually, the topology optimization algorithm interprets this magnitude to finally obtain a completely self-supported design. This section introduces the contour and boundary detection procedure, along with a quick overview of the overhang constraint developed in Garaigordobil et al. (2018, 2019) and Garaigordobil (2018)

2.1 Contour evaluation algorithm

The SUSAN is used in DIP as a solid tool to detect image contours. It works by simultaneously sweeping the domain with a mask while analyzing the intensity gradient of the pixels covered by the mask. At each position, the operator counts the value that characterizes the similarities between each pixel of the image and its neighborhood. Note that the positioning of the mask should allow its nucleus to match a pixel. The method has already been proven effective and reliable in the field of image processing, and it is fast when applied to optimization systems based on iterative evaluation of functions (Fymbo and Rasmussen 2001), and it is applicable to 3D domains and unstructured meshes (Walter et al. 2009b, 2009c; Walter et al. 2009a).

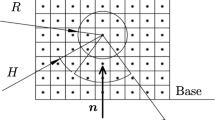
The design domain of a topology optimization problem does not contain pixels with intensity levels, but it is formed by finite elements with different gray levels, which, in any case, are very similar sets. Only a few modifications are needed to integrate the SUSAN algorithm within the framework of a topology optimization method, which is very straightforward, as simply requires replacing pixels by elements, while gray levels (or density values) substitute intensity levels. Alternatively, a square mask that fits all the corners of the domain, see Fig. 2, substitutes the circular mask. This approach showed to be convenient and effective even with the initial blurry intermediate designs.

Fig. 2

Domain sweeping process with a square mask

2.1.1 Edge detection

Based on the idea of SUSAN, the modified version of the method evaluates the gray levels of the neighborhoods of elements covered in the different positions of the mask and obtains a contour vector for each of these positions. The contour vector ${{\varvec{v}}}_{{\varvec{c}}{\varvec{g}}}$ originates from the center of the mask and passes through its center of gravity; therefore, it is always normal to the detected contour. In addition, the angle $\alpha$ formed between this vector and the building direction is equivalent to that formed by the contour and the build plate of the 3D printing machine, Fig. 3. This information is essential to determine whether a contour can be safely printed or not. The building direction can be any, but to formalize the formulation, from now on and in the rest of the paper, a building direction parallel to the vertical y axis is considered.

Fig. 3

Representation of a contour vector and the detected contour

In the modified version of the algorithm, the contour vector ${{\varvec{v}}}_{{\varvec{c}}{\varvec{g}}}$, Eq. (1), is formed by its components, ${q}_{x}$ and ${q}_{y}$, the static moments of the set of elements covered by the mask, calculated through Eqs. (2) and (3).

$${{\varvec{v}}}_{{\varvec{c}}{\varvec{g}}}=({q}_{x} ,{ q}_{y}),$$

(1)

$${q}_{x}=\sum_{i=1}^{n}{x}_{i}\cdot {\rho }_{i},$$

(2)

$${q}_{y}=\sum_{i=1}^{n}{y}_{i}\cdot {\rho }_{i},$$

(3)

where ${x}_{i}$ and ${y}_{i}$ are the coordinates of the ${i}^{th}$ element covered by the mask on a local $xy$ reference system with the origin at the nucleus of the mask, and ${\rho }_{i}$ is the density of that element. Finally, $n$ is the number of elements covered by the mask.

Based on the above formulation, it is said that the mask detects a contour when the length of the contour vector is non-zero. Considering that the contours formed in the optimization problem are inter-pixel contours, the static moments are at their maximum when the nucleus of the mask is placed right on the contour. Therefore, the closer the mask is from an interface, the longer the vector is, while for one-phase neighborhoods, all ${q}_{x}$, ${q}_{y}$, and $\left|{{\varvec{v}}}_{{\varvec{c}}{\varvec{g}}}\right|$ are zero, which suggests the presence of no interface.

For the inclination of the contour, it can be easily computed with the following rule:

$$tan(\alpha )=\frac{{q}_{x}}{{q}_{y}}.$$

(4)

2.1.2 Contour classification

According to their inclination and the defined overhang limit angle, the contours are classified into supported and unsupported. We say that a contour is supported when its inclination is above the limit overhang angle ψ, that is, any contour that complies with $\alpha \ge \psi$ is considered as a supported contour and, therefore, can be safely printed. All other contours are unsupported and require sacrificial support material (scaffold structures) to prevent their collapse during the AM process.

Alternatively, the rule for classifying contours developed by the authors in previous works compares the component of the contour vector parallel to the building direction, ${q}_{y}$, with a threshold value computed for that specific vector, ${{q}_{y}}^{\psi }$, see Fig. 4. Then, all supported contours comply with ${q}_{y}\le {{q}_{y}}^{\psi }$, while unsupported contours obey ${q}_{y}> {{q}_{y}}^{\psi }$. The value obtained in this comparison is gathered as ${\stackrel{\sim }{\varphi }}_{m}\left({\varvec{\rho}}\right)$, and Eqs. (5) and (6) control the thresholding process.

Fig. 4

Physical meaning of the contour classification equation. A supported contour ${{v}_{cg}}^{(1)}$ and an unsupported contour ${{v}_{cg}}^{(2)}$

$$ \mathop \varphi \limits^{\sim } _{m} \left( \rho \right) = \frac{{q_{y} }}{{q_{y} ^{\psi } }} - 1 = \left\{ {\begin{array}{*{20}c} {if\;\mathop \varphi \limits^{\sim } _{m} \left( \rho \right) > 0{\mkern 1mu} \;unsuported\;{\mkern 1mu} contour} & {} \\ {if\;\mathop \varphi \limits^{\sim } _{m} \left( \rho \right) \le 0{\mkern 1mu} \;supporter\;{\mkern 1mu} contour} & {} \\ \end{array} } \right. $$

(5)

$${{q}_{y}}^{\psi }=\frac{{|q}_{x}|}{tg(\uppsi )}.$$

(6)

The above presented Eq. (5) provides an easy expression to classify contours, but it is conflicted by the zero values of ${q}_{x}$, which is common in one-phase neighborhoods. In Garaigordobil et al. (2018, 2019) and Garaigordobil and Ansola (2019), Eq. (5) is evolved to a new expression that avoided the issue with the zero values of ${q}_{x}$, but the new form was, however, non-linear. The present paper introduces a new formulation of the contour classification equation, a linearized and differentiable form obtained by integrating the sigmoid function:

$${\varphi }_{m}\left({\varvec{\rho}}\right)={q}_{y}\cdot \mathrm{sin}\left(\uppsi \right)-\left(\frac{2}{k}\cdot \mathrm{ln}\left(\frac{1+{e}^{k\cdot {q}_{x}}}{2}\right)-{q}_{x}\right)\cdot \mathrm{cos}(\uppsi ),$$

(7)

where $k$ is a constant parameter that adjusts the equation and $m$ refers to the ${m}^{th}$ position of the mask.

The overhang situation of each detected contour is finally determined by the value of Eq. (7). The rule for the new contour classification equation is similar to the original, with positive and negative values corresponding to unsupported and supported contours, respectively. Once the contours are classified, the algorithm proceeds to quantify the unsupported and supported sets using Eqs. (8) and (9):

$${\varphi }_{unsupported}\left({\varvec{\rho}}\right){=\varphi }^{+}\left({\varvec{\rho}}\right)={\sum }_{m=1}^{M}{\varphi }_{m}\cdot (\frac{1}{1+{e}^{-\mu \cdot {\varphi }_{m}}}),$$

(8)

$${\varphi }_{supported}\left({\varvec{\rho}}\right){=\varphi }^{-}\left({\varvec{\rho}}\right)={\sum }_{m=1}^{M}{(-\varphi }_{m})\cdot (\frac{1}{1+{e}^{\mu \cdot {\varphi }_{m}}}).$$

(9)

The latter equations are also the linearized and differentiable/smoothed versions of the equations in the references (Garaigordobil et al. 2018, 2019; Garaigordobil and Ansola 2019), where M is the number of positions that the mask takes to sweep the domain and $\mu$ is a constant parameter that adjusts these equations. In this work, the parameters to adjust the equations are given values of $\mu =100$ and $k=100$.

2.2 Overhang constraint

The process of eliminating the volume of sacrificial support material by constraining the overhang angle can be performed elementwise; however, it would generate an unaffordable amount of local constraints. Therefore, rather than defining local overhangs, the authors proposed a magnitude that is representative of the global overhang situation of the structure, $\phi \left({\varvec{\rho}}\right)$ (Garaigordobil et al. 2018). This magnitude is calculated as the contribution of the set of supported contours concerning the total contribution as described in Eq. (10).

$$\phi \left({\varvec{\rho}}\right)=\frac{{\varphi }^{-}}{{\varphi }^{-}+{\varphi }^{+}}$$

(10)

This equation can give values in the range of [0–1], where $\phi =0$ denotes a completely unsupported design and $\phi =1$ is representative of a self-supporting structure. For the values in between, there will be some supported and some unsupported contours.

For the task at hand, the overhang situation of the structure should ideally be $\phi =1$; however, the authors found that this is not truly the case. Slightly lower values of $\phi$ allow the formation of smooth connections between downward-facing contours as small fillets that violate the constraint but that due to their short length can be safely printed. Taking that into account, the constraint, Eq. (11), is written so that the overhang situation of the optimized design can have any value in the range of [0–1].

$$g({\varvec{\rho}})=\frac{{\phi }_{0}}{\phi }-1\le 0$$

(11)

In this equation, ${\phi }_{0}$ is the control parameter that allows the different values of $\phi$ and can take values in the range of [0–1]. This way, the constraint is active when $\phi ={\phi }_{0}$, and inactive when $\phi >{\phi }_{0}$.

The role of the control parameter is to allow overhang situations that are below the unit. This definition gives the chance to avoid sharp edges and allow the formation of unsupported, yet printable, short overhanging contours when the control parameter is slightly below the unit. A zero value of ${\phi }_{0}$ supposes that the overhang constraint is already satisfied for any value of $\phi$ and $\psi$, which is similar to having no overhang constraint. On the other hand, intermediate values lead to what the authors call “partially supported designs”, which are topologies halfway between the unconstrained problem and the supported design. In other words, the control parameter offers the opportunity to get non-constrained, partially supported, or completely self-supported topologies with or without rounded overhanging fillets. The reader is referred to the studies (Garaigordobil et al. 2019; Garaigordobil 2018) for extended information on the control parameter.

3 Dripping effect

3.1 The problem with the oscillatory boundaries

The Dripping Effect is the formation of oscillatory contours within the prescribed threshold overhang angle. These drop-like formations are reported in many publications, see for example (Allaire et al. 2017; Qian 2017; Zhang et al. 2019), and the following section is focused on analyzing the formation of these drop-like regions.

To begin with, the following case of an MBB beam is considered. Because of the small overhanging angles and the near-horizontal solid member in the upper part, the conventional optimized topology can hardly be 3D printed without supporting structures with the building direction depicted in Fig. 5. What a geometric overhang constraint does when these solid members start to nucleate, is to form support paths that connect the overhanging interfaces with other solid members or the build plate. Ideally, over the course of iterations, these support members would be integrated into the main structure and evolve into a self-supported, optimized topology. However, collected data suggest that if the geometric constraint evaluates the overhang in very small neighborhoods, it can lead to numerous and very thin paths of support material that can easily tear due to the filtering and projection of densities, provoking the characteristic triangular shape of the drops (see Fig. 6).

Fig. 5

Conventional topology optimization results of a half MBB. Unsupported contours in red color

Fig. 6

The process of formation and iteration wise evolution of oscillatory boundaries in a half MBB

The reason for what they are formed and not erased over the course of iterations is because oscillatory contours constitute local minimizers of the constraint and only violate the overhang constraint in the cusps of the drops, leading to dramatic decreases of the constraint functional. Besides, in terms of compliance, the drops do not have any significant impact on the mechanical performance of the structure. Therefore, the algorithm would rather form oscillating boundaries than degrade the structural performance of the part by rearranging the large horizontal bars, especially in those members that bear great load.

3.2 A strategy to prevent the Dripping Effect

Although no general agreement has been proposed yet, a few proposals to suppress the formation of oscillatory contours can be found. In Allaire et al. (2017), the authors concluded that geometric overhang constraints were not sufficient to effectively constraint the overhang because they cannot ensure oscillatory contour-free topologies. They suggested that additional constraints have to be introduced in the problem in the form of perimeter or mechanical constraints. Another strategy (Zhang et al. 2019) proposed the introduction of a horizontal minimum member size constraint that avoided the formation of drops. Alternatively, Qian (2017) proposed several guidelines to avoid the Dripping Effect and concluded that larger filter sizes, combined with a grayness constraint and Heaviside filtering, could be used to suppress the Dripping Effect.

The common factor of these strategies is the introduction of additional design constraints to control the formation of drops. This work presents an alternative strategy that is easy to implement and builds on the idea that the Dripping Effect is the consequence of an excessively local evaluation of the overhang.

The drops appear after the density filtering and projection step (see section 4) tears the thin support material paths formed while the density field is still non-binary (see Fig. 6). The latter means that the formation of excessive support members must be discouraged to prevent the formation of the drops, which is achieved by increasing the size of the areas where the overhang is evaluated. In this way, the problem of oscillatory boundaries could be avoided by increasing the size of the mask that sweeps the domain.

On the other hand, evaluating the overhang in larger neighborhoods could be ineffective to prevent unsupported members. Due to its bigger size, the mask could cover several contours at the same time, so the generated contour vector would not be representative of any of them. Hence, there is a compromise between preventing the formation of excessive material support paths and good prevention of unsupported boundaries.

To tackle both situations, this work proposes a continuation scheme that slowly decreases the size of the mask. Concisely, the behavior of the proposed strategy can be resumed as follows. In the early stages of the optimization problem, while the domain is still populated by gray densities, this strategy avoids the formation of excessive support material paths by evaluating the overhang in larger neighborhoods. This way, the fewer support members that nucleate are thick and soon become part of the main structure. Once the density field is binary enough, the local inclination of the overhanging members is more rigorously controlled with small masks so that the structure becomes self-supporting. Note that the proposed strategy will be formulated for regular-orthogonal discretization; however, the formulation can be extended to unstructured meshes and non-unit-size elements, by adapting the edge detection algorithm as in Walter et al. (2009b).

4 Density filtering and Heaviside projection

To eliminate checkerboard patterns, mesh dependency, and implicitly introduce a minimum length scale, this work adopts a density filtering and projection routine. This strategy generates a cascade of variables ${\varvec{\rho}}\to \widehat{{\varvec{\rho}}}\to \overline{{\varvec{\rho}} }$, where $\widehat{{\varvec{\rho}}}$ is the vector of filtered independent design variables ${\varvec{\rho}}$ (Bourdin 2001; Bruns and Tortorelli 2001), and $\overline{{\varvec{\rho}} }$ is the vector of projected $\widehat{{\varvec{\rho}}}$ (F. Wang et al. 2011). In the first approaches to overhang constraints, the authors studied alternative filtering strategies, and the above routine proved to be very effective.

The initial filtering step consists of the weighted average of the independent design variable (Bruns and Tortorelli 2001; F. Wang et al. 2011):

$${\widehat{\rho }}_{e}=\frac{{\sum }_{i\epsilon {S}_{e}}{v}_{i}\cdot {w}_{ei}\cdot {\rho }_{i}}{{\sum }_{i\epsilon {S}_{e}}{{v}_{i}\cdot w}_{ei}},$$

(12)

where ${v}_{i}$ is the volume of element $i$, ${w}_{ei}$ is the weight factor, and ${S}_{e}$ is the set of $i$ elements in the domain of influence of element $e$, that is, the set where the center-to-center distance to the element $e$ is smaller than the filter radius ${r}_{min}$:

$${w}_{ei}={r}_{min}-\left|dist\left(e,i\right)\right|$$

(13)

The smoothing operation above limits the space of possible designs and solves the mesh dependency problem but also introduces gray transition zones at the interface between solid and void phases. To avoid transition areas, a density projection step that projects the intermediate densities, $\widehat{{\varvec{\rho}}}$, onto the physical field, $\overline{{\varvec{\rho}} }$, is added to the problem formulation. The projection is performed through a continuous approximation of the Heaviside function based on the hyperbolic tangent function, where the values of ${\widehat{\rho }}_{e}$ below the threshold $T$ are projected to zero and the values above are projected to one (Wang et al. 2011):

$${\overline{\rho }}_{e}=\frac{\mathrm{tanh}\left(\beta \cdot T\right)+\mathrm{tanh}(\beta \cdot ({\widehat{\rho }}_{e}-T))}{\mathrm{tanh}\left(\beta \cdot T\right)+\mathrm{tanh}(\beta \cdot (1-T))}.$$

(14)

In Eq. (14), $\beta$ is a scaling parameter that controls the steepness of the continuous approximation of the Heaviside function. The projected densities $\overline{{\varvec{\rho}} }$ are referred to as the physical densities and will be presented as the solution to the optimization problem. Similarly, the objective and constraint functions will be computed as functions of $\overline{{\varvec{\rho}} }$, given that this field is a function of the design variables.

5 Problem formulation and sensitivity analysis

5.1 Problem formulation

In the problem formulation presented in this work, the design domain is discretized with finite elements that are given an initial uniform value of material density, which, in turn, forms the vector of independent design variables ${\varvec{\rho}}={({\rho }_{1,} {\rho }_{2},\dots ,{\rho }_{N})}^{T}$. Since the relaxation of the problem allows any density value in the range of [0,1], the material properties of the elements are interpolated with the modified SIMP method (Bendsøe 1989; Rozvany et al. 1992) according to

$${E}_{e}({\overline{\rho }}_{e})={E}_{min}+{{\overline{\rho }}_{e}}^{p}\cdot ({E}_{0}-{E}_{min}),$$

(15)

where ${E}_{e}$ is the Young modulus of the ${e}^{th}$ finite element, ${\overline{\rho }}_{e}$ is the physical density of the ${e}^{th}$ element, and ${E}_{0}$ is the Young modulus of the solid isotropic material, with unit value in this work. The minimum ${E}_{e}$ is given a value of ${E}_{min}={10}^{-9}$. Finally, $p$ is the penalization factor.

The minimum compliance topology optimization problem with overhang constraints for AM is formulated as follows:

$$\begin{array}{c}min:\\{\varvec{\rho}}\end{array} c\left(\overline{{\varvec{\rho}} }\right)={{\varvec{U}}}^{{\varvec{T}}}\cdot {\varvec{K}}\cdot {\varvec{U}}={\sum }_{e=1}^{N}{E}_{e}\left({\overline{\rho }}_{e}\right)\cdot {{{\varvec{u}}}_{{\varvec{e}}}}^{{\varvec{T}}}\cdot {{\varvec{k}}}_{0}\cdot {{\varvec{u}}}_{{\varvec{e}}},$$

(16)

$$Subjected to: {\varvec{F}}={\varvec{K}}\cdot {\varvec{U}},$$

(17)

$$\frac{V\left(\overline{{\varvec{\rho}} }\right)}{{V}_{0}\cdot f}-1\le 0,$$

(18)

$$g(\overline{{\varvec{\rho}} })\le 0,$$

(19)

$$0\le {\rho }_{e}\le 1.$$

(20)

The compliance of the structure, $c\left(\overline{{\varvec{\rho}} }\right)$, is set as the objective function to be minimized, where ${\varvec{U}}$ is the displacement vector and ${\varvec{K}}$ is the global stiffness matrix. The displacement vector of the ${e}^{th}$ element is ${{\varvec{u}}}_{{\varvec{e}}}$, and ${{\varvec{k}}}_{0}$ is the stiffness matrix of an element with unit Young modulus. ${\varvec{F}}$ is the load vector, and Eq. (18) denotes the conventional volume fraction constraint, where $V\left(\overline{{\varvec{\rho}} }\right)$ is the volume of the current design point, ${V}_{0}$ is the volume of the design domain, and $f$ is the upper bound of the volume fraction. Equation (19) denotes the overhang constraint introduced in the problem, and Eq. (20) describes the set of admissible values for the design variables. In the results that are going to be presented, both volume fraction and overhang constraints are active.

The optimization problem is solved using the MMA method (Svanberg 1987). At this point, it must be considered that the sensitivities of the problem may be increasingly ill conditioned for high values of the scale parameter $\beta$. A sharp approximation to the step function may generate aggressive oscillations in the default MMA approach, whereby the distance of the asymptotes from the current point is modified in terms of $\beta$ as proposed in (Guest et al. 2011). In addition, a continuation scheme is introduced for $\beta$ and the penalization factor $p$ of the SIMP parametrization.

5.2 Sensitivity analysis

The sensitivity analysis of the functions involved in the problem is presented in this section. Considering that the independent design variable is still ${\varvec{\rho}}$, but the problem is, nonetheless, formulated in terms of $\overline{{\varvec{\rho}} }$, the partial derivative of any function $f\left(\overline{{\varvec{\rho}} }\right)$ involved in the problem concerning a design variable ${\rho }_{e}$ is calculated with the chain rule (F. Wang et al. 2011):

$$\frac{\partial f\left(\overline{{\varvec{\rho}} }\right)}{\partial {\rho }_{e}}=\sum_{j\in {S}_{e}}\frac{\partial f\left(\overline{{\varvec{\rho}} }\right)}{\partial {\overline{\rho }}_{j}}\cdot \frac{\partial {\overline{\rho }}_{j}}{\partial {\widehat{\rho }}_{j}}\cdot \frac{\partial {\widehat{\rho }}_{j}}{\partial {\rho }_{e}}.$$

(21)

The second and third terms on the right side of the equality are common for any function $f\left(\overline{{\varvec{\rho}} }\right)$ and are calculated with Eqs. (22) and (23), (Jansen et al. 2013).

$$\frac{\partial {\overline{\rho }}_{j}}{\partial {\widehat{\rho }}_{j}}=\frac{\beta \cdot [1-{tanh}^{2}\left(\beta \cdot \left({\widehat{\rho }}_{j}-T\right)\right)]}{\mathrm{tanh}\left(\beta \cdot T\right)+\mathrm{tanh}\left(\beta \cdot (1-T)\right)},$$

(22)

$$\frac{\partial {\widehat{\rho }}_{j}}{\partial {\rho }_{e}}=\frac{{w}_{je}}{{\sum }_{i\in {S}_{j}}{w}_{ji}}.$$

(23)

The derivative of the first term on the right-hand side of Eq. (21) varies according to the function $f\left(\overline{{\varvec{\rho}} }\right)$ that is being considered. That derivative is well known for the objective function $c\left(\overline{{\varvec{\rho}} }\right)$ and is given as follows (Martin P. Bendsøe and Sigmund 2004):

$$\frac{\partial c\left(\overline{{\varvec{\rho}} }\right)}{\partial {\overline{\rho }}_{j}}=-p\cdot {{\overline{\rho }}_{j}}^{p-1}\cdot \left({E}_{0}-{E}_{min}\right)\cdot {{{\varvec{u}}}_{{\varvec{j}}}}^{{\varvec{T}}}\cdot {{\varvec{k}}}_{0}\cdot {{\varvec{u}}}_{{\varvec{j}}}.$$

(24)

In the case of the volume fraction constraint, the derivative for the physical density is

$$\frac{\partial \left(\frac{V\left(\overline{{\varvec{\rho}} }\right)}{{V}_{0}\cdot f}-1\right)}{\partial {\overline{\rho }}_{j}}=\frac{{V}_{j}}{{V}_{0}\cdot f},$$

(25)

where ${V}_{e}$ is the volume of the finite element $e$.

The overhang constraint $g(\overline{{\varvec{\rho}} })$ is the last remaining function that is derived with respect to the physical density. In this case, we start by setting out the derivatives of Eq. (11):

$$\frac{\partial (g(\overline{{\varvec{\rho}} }) )}{\partial {\overline{\rho }}_{j}}=\frac{\partial \left(\frac{{\phi }_{0}}{\phi }-1\right)}{\partial {\overline{\rho }}_{j}}={\phi }_{0}\cdot \frac{\partial \left(\frac{1}{\phi }\right)}{\partial {\overline{\rho }}_{j}}={\phi }_{0}\cdot \frac{\partial \left(\frac{{\varphi }^{-}+{\varphi }^{+}}{{\varphi }^{-}}\right)}{\partial {\overline{\rho }}_{j}}$$

(26)

We now develop the last term in parenthesis of Eq. (26) that results in Eq. (27). It is seen there that the process requires the computation of the derivatives of the supported and unsupported sets.

$$\frac{\partial \left(\frac{{\varphi }^{-}+{\varphi }^{+}}{{\varphi }^{-}}\right)}{\partial {\overline{\rho }}_{j}}=\frac{1}{{{(\varphi }^{-})}^{2}}\cdot \left(\left.\frac{\partial {(\varphi }^{+})}{\partial {\overline{\rho }}_{j}}\cdot {\varphi }^{-}-\frac{\partial ({\varphi }^{-})}{\partial {\overline{\rho }}_{j}}\cdot {\varphi }^{+}\right)\right.$$

(27)

The latter expression is developed by taking derivatives in Eqs. (8) and (9).

$$\frac{\partial ({\varphi }^{+})}{\partial {\overline{\rho }}_{j}}={\sum }_{m=1}^{M}\frac{1}{{\left(1+{e}^{-\mu \cdot {\varphi }_{m}}\right)}^{2}}\cdot \left(1+{e}^{-\mu \cdot {\varphi }_{m}}\cdot (1+\mu \cdot {\varphi }_{m}\right))\cdot \frac{\partial {\varphi }_{m}}{\partial {\overline{\rho }}_{j}},$$

(28)

$$\frac{\partial ({\varphi }^{-})}{\partial {\overline{\rho }}_{j}}={\sum }_{m=1}^{M}\frac{(-1)}{{\left(1+{e}^{\mu \cdot {\varphi }_{m}}\right)}^{2}}\cdot \left(1+{e}^{\mu \cdot {\varphi }_{m}}\cdot (1-\mu \cdot {\varphi }_{m}\right))\cdot \frac{\partial {\varphi }_{m}}{\partial {\overline{\rho }}_{j}}.$$

(29)

Finally, it is necessary to compute the derivatives of the contour classification equation, Eq. (7), for substitution in the above Eqs. (28) and (29). These derivatives are obtained as follows:

$$\frac{\partial ({\varphi }_{m})}{\partial {\overline{\rho }}_{j}}={y}_{j}\cdot \mathrm{sin}\left(\uppsi \right)-\left(2\cdot \frac{{e}^{k\cdot {q}_{x}}}{1+{e}^{k\cdot {q}_{x}}}-1\right)\cdot {x}_{j}\cdot \mathrm{cos}(\uppsi ).$$

(30)

Equations (26, 27, 28, 29, 30) can be gathered all together to obtain a single expression for the derivatives on the overhang constraint with respect to the physical density.

$$\frac{\partial g(\overline{{\varvec{\rho}} }) }{\partial {\overline{\rho }}_{j}}=\frac{{\phi }_{0}}{{{(\varphi }^{-})}^{2}}\left({\sum }_{m=1}^{M}\left(\frac{{\varphi }^{-}}{{\left(1+{e}^{-\mu {\cdot \varphi }_{m}}\right)}^{2}}\left(1+{e}^{-\mu \cdot {\varphi }_{m}}\cdot (1+\mu {\cdot \varphi }_{m}\right))+\frac{{\varphi }^{+}}{{\left(1+{e}^{\mu \cdot {\varphi }_{m}}\right)}^{2}}\left(1+{e}^{\mu {\cdot \varphi }_{m}}(1-\mu {\cdot \varphi }_{m}\right))\right)\frac{\partial {\varphi }_{m}}{\partial {\overline{\rho }}_{j}}\right).$$

(31)

6 Numerical examples

This section introduces two topology optimization examples where the presented overhang constraint is applied according to the proposed methodology. As it was previously introduced, the optimization problems are parameterized using the SIMP method and solved with the MMA. In all cases, solid isotropic material with Young modulus ${E}_{0}=1$ and avoid material with Young modulus ${E}_{min}={10}^{-9}$ are considered.

A continuation scheme is applied to the Heaviside parameter $\beta$ and the SIMP penalization parameter $p$. The update of the mask size is also integrated into this continuation scheme, so all three parameters are updated at the same time. The continuation scheme updates the three parameters every 50 iterations or every time the convergence criterion is met. Parameters $\beta$ and $p$ start at 5, and every time they are updated they increase their value by 3 units up to a maximum value of at least 23 for $\beta$ and ${p}_{max}=11$. The maximum value of $\beta$ depends on the length of the mask size continuation scheme. The authors note that the initial SIMP penalty magnitude is larger than typically used. This is because the design progression shown by the algorithm in the first iterations is slower when lower values are used. The overhang constrained problem may give rise to large gray density areas to provide artificial support to the material above. To avoid them, the authors found that an initial penalization factor slightly greater than the usual value of 3 resulted in a more effective initialization of the problem, and $p$ = 5 showed to be a good starting value. Besides, the authors studied the possibilities of maintaining a constant value of the penalization or defining a continuation scheme on it. Both alternatives resulted in successful designs, but finally, the authors opted for the last strategy to keep consistency with the work previously done.

For the mask, this is given an initial size, and every time it updates, that size is reduced by 2 × 2 elements until the mask reaches a size of 3 × 3. The reason for using a final size of 3 × 3 is because that is the minimum size and the one that most finely detects and corrects the overhang. For the Heaviside threshold parameter, it is set to $T=0.5$ in all the examples, and the filter radius is set to ${r}_{min}=5$. The limit overhang angle is 45º and ${\phi }_{0}=0.99$. Unless otherwise stated, the upper bound of the volume fraction is 0.5. Finally, the problem is assumed to converge when the change of the objective function in two successive iterations is lower than ${10}^{-3}$.

6.1 MBB beam

This example includes several MBB optimization cases where the initial size of the mask is varied. The design domain presented in Fig. 7 takes advantage of symmetry and is discretized with 312 × 104 unit square finite elements. Roller supports are placed in the left side nodes, as well as in the lower right side node, and a vertical unit force is applied in the left upper node. The mask size continuation scheme is applied in all of the studied cases, decreasing the mask in 2 × 2 elements every time it is updated. The initial mask sizes are given in the caption of the corresponding Fig. 8.

Fig. 7

Design domain of a half MBB beam

Fig. 8

Continuation scheme of the mask size. Initial mask size: a 3 × 3, b 5 × 5, c 7 × 7, d 9 × 9, e 11 × 11, f 13 × 13, g 15 × 15, h 17 × 17, i 19 × 19, and j 21 × 21

It can be seen that excessively local overhang evaluation can lead to an important amount of oscillating boundaries, Fig. 8a–c, while bigger initial masks reduce the number of drops, Fig. 8d–f. On the other hand, when an adequate initial mask size is defined, the Dripping Effect can be completely avoided, as seen in Fig. 8g–j.

To discuss why larger initial mask sizes can prevent the formation of oscillating contours, consider Fig. 9, where the evolution of the overhang restriction and objective function for some cases of the MBB problem are superimposed. It can be observed that during the initial stages of the optimization process, the values of the constraint function are lower when the overhang evaluation area is larger. This is not because the smaller mask does not correct the overhanging contours but quite the opposite. The smaller mask is very severe during the initial stages, where the geometry is not yet defined and the domain is populated with gray densities. Because of that, thin material paths nucleate to give support, in these cases, to the upper horizontal member that bears a great part of the load. Alternatively, we may as well say that bigger initial mask sizes provide a more relaxed start to the constrained problem.

Fig. 9

Evolution of the overhang constraint, g, and objective function, c, for the different optimization cases of the MBB problem

Consider Fig. 10 where the different geometries obtained during the optimization process of Fig. 8h are depicted. It is noticeable that the support material paths that nucleate in the initial iterations of the problem are not as numerous as they are in Fig. 6 and they soon became thick solid members (see Fig. 10a). By studying the results, it can be observed that larger overhang evaluation areas are more permissive with the topology and allow the formation of small unsupported contours. As the problem progresses and the mask gradually becomes smaller, the initially small unsupported contours begin to correct their slope and the intersection points of the hanging members become sharper. Finally, the 3 × 3 size mask corrects the inclination of all the contours in finer detail and the topology becomes self-supporting.

Fig. 10

Topologies obtained during the optimization process. a Iteration 50, 17 × 17. b Iteration 100, 15 × 15. c Iteration 113, 13 × 13. d Iteration 116, 11 × 11. e Iteration 136, 9 × 9. f Iteration 157, 7 × 7. g Iteration 207, 5 × 5. h Iteration 245, 3 × 3. i Iteration 259, 3 × 3. j Iteration 276, 3 × 3

In the following, the different behavior of the overhang constraint with and without the proposed strategy is studied. Figure 11 depicts the evolution of the overhang constraint and the relative mask sizes (dashed line). Besides, the graph includes a parallel and more accurate evaluation of the constraint on constant 3 × 3 neighborhoods that plays no role in the optimization problem (solid line), and whose sole purpose is to be a benchmark for comparison.

Fig. 11

Evolution of the overhang constraint. Solid line: Accurate overhang constraint evaluated with a 3 × 3 mask. Dashed line: Relaxed overhang constraint evaluation evaluated with decreasing mask sizes

The different behavior of the constraint when evaluating the same topologies with both strategies is visible, and the separation between the two lines during the initial iterations shows the implicit relaxation of the constraint introduced by bigger initial mask sizes. Over the course of iterations, as the mask size is gradually reduced, both lines start to converge and finally meet when the mask size is reduced to 3 × 3. Note that the dashed line describes several peaks that coincide with the update of the size of the mask.

6.2 Cantilever beam

The following example proposes the optimization case of a cantilever beam; see Fig. 12. The domain is discretized with 260 × 130 unit square finite elements, the left side of the domain is clamped, and a vertical unit force is applied in the center of the right contour.

Fig. 12

Design domain of a cantilever beam

The mask size continuation scheme is applied proceeding in the same way as with the MBB case. The results obtained for different initial mask sizes are provided in Fig. 13, and the corresponding mask sizes are given in the caption of the figure.

Fig. 13

Continuation scheme of the mask size. Initial mask size: a 3 × 3, b 5 × 5, c 7 × 7, d 9 × 9, e 11 × 11, f 13 × 13, g 15 × 15, h 17 × 17, i 19 × 19, and j 21 × 21

Just as we could expect, the evaluation of the overhang in overly narrow neighborhoods leads to oscillatory contour patterns. Equally, as the initial evaluation area becomes larger, the number of drops is reduced up to the point that they eventually disappear. In short, the choice of the initial mask size turned again critical for preventing the Dripping Effect.

To further extend the study in this work, the cantilever case is proposed as a test case for a comparative review between the printable results obtained in (Garaigordobil 2018) and the present work. In the benchmark work, the overhang was evaluated in fixed 3 × 3 elements neighborhoods, and the formation of printable results was not always guaranteed. In that sense, the following study may be of interest to evaluate what impact the prevention strategy proposed in these lines may have on the material layout and the mechanical behavior of the emerging topologies.

The cantilever beam is discretized with 260 × 130 unit square finite elements, the overhang angle is constrained to 45°, and three different volume fractions are studied. The reason for varying the volume fraction is that low-volume problems are especially critical for overhang constraints, as the optimization algorithm may not have enough material to form stiff self-supporting structures. Low-volume problems may leave oscillatory boundary formation or extreme distortion of the material part as the only possible solutions to the optimization problem.

The results from both works are gathered in Fig. 14, where the first row depicts the results obtained with the conventional unconstrained formulation, the second row depicts the results obtained in (Garaigordobil 2018), and the third contains the results obtained in this work.

Fig. 14

Optimized cantilever beam. Unconstrained cases a f = 0.35, b f = 0.5, c f = 0.65. Results from (Garaigordobil 2018). d f = 0.35, e f = 0.5, f f = 0.65. Results obtained in this work. g f = 0.35, h f = 0.5, i f = 0.65

In Fig. 14d–f, it can be noted that the upper horizontal member is distorted and describes a characteristic slope. This effect can also be seen in the references (Gaynor and Guest 2016; Qian 2017; Guo et al. 2017; Zhang et al. 2019). Nevertheless, it is not the pattern seen in the conventional topologies which rather extend the upper horizontal member so that it can bear a greater load, as seen in Fig. 14a–c. In that sense, the new results (Fig. 14g–i) suggest that the relaxation of the overhang constraint during the initial iterations of the optimization problem generates geometries that are closer to the unconstrained problem, even avoiding the distortion of the part in low-volume problems.

On the other hand, and despite the divergence of their geometries, the compliance of medium- and high-volume designs is quite similar (Fig. 15). It can be blamed on the overhang constraint not being so demanding when enough material is available. In low-volume cases; however, a significant difference arises when the new approach is used. The compliance of the part decreases by 12.8%. Of course, this improvement cannot be extrapolated to other cases, but it shows that the mechanical behavior can improve when the prevention strategy introduced in these lines is added to the overhang restriction process presented in (Garaigordobil 2018).

Fig. 15

Comparison of the normalized compliance

7 Conclusions

The present paper introduces a novel strategy to deal with the Dripping Effect generated when geometric overhang constraints are introduced within topology optimization algorithms. It is in the early stages of the optimization process that the algorithm is more prone to generate thin support members, especially if the overhang is evaluated in very small neighborhoods. This problem is addressed by introducing bigger evaluation areas during the initial iterations, since this way, fewer support members nucleate, and those that appear are thick and soon become part of the main structure. In addition, unsupported small boundaries are permitted during that time, which, as the optimization process progresses and the overhang is more rigorously evaluated in smaller neighborhoods, are progressively corrected so that the topology eventually becomes self-supporting.

The effects of the strategy on the mechanical behavior of the resulting designs are also studied. Medium- and high-volume problems, although they look visually more appealing when the prevention strategy is applied, seem not to be affected and show similar compliance values. In the presented low volume problem, on the other hand, the obtained geometry is much closer to the unconstrained one when the Dripping Effect prevention strategy is applied, and there is a clear improvement of the objective function.

Summarizing, the algorithm presented in these lines has been shown to eliminate the Dripping Effect on the problems studied. These results (and possibly more) hint that the method could be effective at eliminating the Dripping Effect in other problems and consistently.