QR-patterns: artefacts in multiresolution topology optimization

Abstract

Recent multiresolution topology optimization (MTO) approaches involve dividing finite elements into several density cells (voxels), thereby allowing a finer design description compared to a traditional FE-mesh-based design field. However, such formulations can generate discontinuous intra-element material distributions resembling QR-patterns. The stiffness of these disconnected features is highly overestimated, depending on the polynomial order of the employed FE shape functions. Although this phenomenon has been observed before, to be able to use MTO at its full potential, it is important that the occurrence of QR-patterns is understood. This paper investigates the formation and properties of these QR-patterns, and provides the groundwork for the definition of effective countermeasures. We study in detail the fact that the continuous shape functions used in MTO are incapable of modeling the discontinuous displacement fields needed to describe the separation of disconnected material patches within elements. Stiffness overestimation reduces with p-refinement, but this also increases the computational cost. We also study the influence of filtering on the formation of QR-patterns and present a low-cost method to determine a minimum filter radius to avoid these artefacts.

1 Introduction

In the traditional density-based topology optimization (TO) approaches, an element-wise constant density distribution is assumed. Some authors have explored decoupled design and analysis discretizations with the aim of reducing the number of design variables used to describe the material distribution in the domain (e.g. de Ruiter and van Keulen 2004; Guest and Genut 2010).

Since the computational cost associated with TO is mainly controlled by the finite element analysis (FEA), Nguyen et al. (2010) proposed to use the strategy of decoupled design and analysis discretizations to obtain high-resolution designs at low analysis costs. A coarse analysis mesh is used and each finite element is divided into several density cells (voxels), which allows a finer density representation. This approach also allows to have material boundaries which are not necessarily aligned with the finite elements. Since different density resolutions are permitted for the same analysis mesh, Nguyen et al. (2010) referred to the approach as multiresolution topology optimization (MTO). Since then, various variants have been proposed (e.g. Nguyen et al. 2012, 2017; Parvizian et al. 2012; Wang et al.2014), and these have been used on several TO problems, e.g. for 3D TO in interactive hand-held devices (Nobel-Jørgensen et al. 2015), and designing thermoelectric generators (Takezawa and Kitamura 2012), phononic materials (Vatanabe and Silva 2013), patient-specific 3D printed craniofacial implants (Sutradhar et al. 2016), etc. In this paper, we use the term MTO to refer to all those approaches which involve decoupling of the analysis and design discretizations with the goal of reducing the modeling related computational costs.

The MTO-based optimized designs are visually appealing, but it is also important to determine whether the coarse analysis used in MTO approaches is capable of accurately modeling the high resolution material distributions. The methods proposed by Nguyen et al. (2010, 2012) used linear shape functions (p = 1) to interpolate the displacement field within the analysis elements. Here and henceforth, p denotes the polynomial order of the shape functions used for analysis. Filtering (density projection) is used in these methods to impose a restriction on minimum feature size and avoid checkerboard patterns. With large filter radii r_min, designs which were visually appealing and comprised of smooth (but gray) boundaries were obtained. However, it is important to note that the use of large filter radii restricts the design field from expressing a high order material distribution. As a downside, fine structural features and crisp boundaries cannot appear in the solution. Methods such as Heaviside projection (Guest et al. 2004) can help to improve the crispness of the design (Groen et al. 2017). However, the added computational cost associated with such schemes is not preferable for MTO, and it would be of great interest if smaller filter sizes can be used.

Wang et al. (2014) adaptively reduced the filter-size in their MTO approach. However, some of the optimized structures reported in that study consisted of artificially stiff regions, resembling the QR-patterns. Based on numerical experiments, Groen et al. (2017) hypothesized that these numerical artefacts observed in MTO schemes are caused due to inappropriate modeling scheme choices. Our investigation results (presented later in this paper) are aligned with the observations of Groen et al. (2017), and we show that these QR-patterns are indeed formed due to the limitations of the modeling scheme used.

Besides the formation of QR-patterns, MTO approaches can suffer from nonuniqueness in the solution of the design field (Gupta et al. 2017). For a high resolution design representation, it is important that the difference in optimized designs is also reflected in the analysis results. If not, different designs may show similar performance resulting in non-unique optima and instability issues (Jog and Haber 1996; Gupta et al. 2017). In Gupta et al. (2017), a rigorous study of this issue in the context of MTO is provided and mathematical bounds are presented to prevent non-uniqueness.

Parvizian et al. (2012) proposed a finite-cell method (FCM) based MTO approach. In FCM, higher-order shape functions and numerical integration schemes are used and a high-resolution design field is permitted. The design field is used to describe the material distribution in the domain. Studies related to FCM-based modeling have shown that shape functions of low polynomial order are incapable of accurately modeling material discontinuities (Joulaian and Düster 2013a, b). A computationally effective solution to overcome such limitations is the local enrichment strategy in FCM. Joulaian and Düster (2013b) presented the hp-d local enrichment strategy, which could very accurately model the solution field at the material discontinuities with the addition of only a few degrees of freedom. It has been shown that the hp-d version of the FCM can model the material discontinuities for non-matching discretizations (Kollmannsberger et al. 2015; Zander et al. 2015). Contrary to the extended finite element scheme (Moës et al. 1999) where new degrees of freedom need to be introduced in all finite elements requiring enrichment, their approach used an overlay mesh with higher-order enrichments to improve the solution of the base mesh. Nevertheless, the extended finite element method as well as enrichment-based FCM require knowledge of the location of material discontinuities in the domain. However, this is not generally available in TO, where the design changes at every iteration, and the boundary descriptions are not known beforehand.

For TO, the simplest solution is to use shape functions of higher polynomial order. With the use of high polynomial degree shape functions (e.g. p = 10) in TO, the QR-patterns as well as the non-uniqueness related issues can be avoided to a certain extent and physically reasonable structures can be obtained (Parvizian et al. 2012; Groen et al. 2017; Gupta et al. 2017). However, with configurations using very high p values, the computational advantage over traditional TO could be lost. Based on numerical experiments, Groen et al. (2017) inferred that by density filtering (Bruns and Tortorelli 2001), even relatively low values of p could be used. However, this solution comes with the same disadvantages as discussed previously for low-order MTO. Application of a minimal filter radius is often preferred, and values have been suggested based on full-scale numerical tests by previous studies (Groen et al. 2017; Nguyen et al. 2017).

As per our investigations, the filter radii choices for various MTO configurations, as described in Nguyen et al. (2017), seem to result in reasonably correct designs. However, it is of considerable interest to explore the full potential of MTO, which motivates us to investigate whether filter radii smaller than those proposed in Nguyen et al. (2017) can also be used. As mentioned earlier, a limiting factor is the occurrence of QR-patterns (Fig. 1), which leads us to study the QR-patterns in a more detailed manner. The minimum cost MTO configuration that can achieve a certain desired design resolution and is capable of avoiding these artefacts would be the one where the full capability of MTO is efficiently utilized. In general, the QR-patterns have been observed in several previous studies, however, a systematic study focused on the formation of QR-patterns as well as measures to suppress them is still missing.

Fig. 1

Design obtained in MTO compliance minimization of a cantilever beam subjected to a distributed load. The domain is discretized using 20 × 10 finite elements with shape functions of polynomial degree 3 and 4 × 4 design voxels per element. A composite integration scheme with 4th order Gauss quadrature rule is used in each voxel

The aim of this paper is to study the QR-patterns, and explain their formation in an MTO context. This can subsequently help to define suitable countermeasures. For this, we investigate whether for a given design resolution, there exists a certain minimum value of p for which the formation of QR-patterns can be avoided. The capability of the continuous shape functions in modeling the discontinuous displacement fields, that should arise at disconnected material patches within elements, is assessed. Also, an understanding of the applicability and limitations of filtering in MTO is presented.

The structure of the remainder of this paper is as follows. First, the MTO concept is explained and a numerical MTO example is presented for which the QR-patterns are prominent (Section 2). Next, through several elementary test cases, an understanding of these artefacts is presented (Section 3). Parameter studies on the influence of both polynomial degree and filter radius, on various test geometries and loadcases, are performed and an explanation on the formation of QR-patterns is presented in Sections 3 and 4. Discussions related to MTO and conclusions are presented in Sections 5 and 6, respectively.

2 Artificially stiff features in MTO

2.1 MTO concept

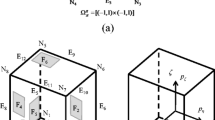
In MTO approaches, the design and analysis discretizations are decoupled, such that a finer density field can be expressed on a coarse analysis mesh (Nguyen et al. 2010 2017; Parvizian et al. 2012). Figure 2 shows an MTO element that uses 4 analysis nodes and 9 design voxels. In this example, bilinear shape functions are used for the interpolation of the displacement field within the element. Unlike traditional TO, where only one design voxel would be used, here the finite element is divided into 9 voxels. A density variable is associated with every design voxel and the density is assumed to be constant inside the voxel. Similar to traditional TO, this density represents the volume fraction of the voxel filled with certain material and can vary from 0 to 1.

Fig. 2

MTO element with 4 analysis nodes and 9 design voxels using a composite numerical integration scheme of 2 × 2 Gauss quadrature rule for every design voxel

Based on the density distribution inside the element, the corresponding element stiffness matrix K_e is constructed as

$$ \mathbf{K}_{e} = \sum\limits_{i = 1}^{n_{v}}\left( {\rho_{i}^{q}} \sum\limits_{j = 1}^{n_{g}}\mathbf{K}_{ij}w_{ij} \right), $$

(1)

where K_ij and w_ij are the stiffness matrix contribution evaluated at the j th integration point and the associated Gaussian weight, respectively of the i th design voxel and ρ_i is its density value. The parameters n_v and n_g refer to the number of voxels and Gauss integration points, respectively and q is the penalization power used for material interpolation (Bendsøe 1989). The order of the integration rule is chosen in a way that the voxel stiffness matrix can be accurately integrated. For the example shown in Fig. 2, n_v is set to 9, and a 2 × 2 Gaussian quadrature rule (n_g = 4) is used for numerical integration inside every design voxel.

2.2 Occurrence of QR-patterns

QR-patterns are artificially stiff regions in the design which can lead to erroneous compliance values for the structure. For example, the compliance accuracy $\mathcal {J}/\mathcal {J}^{*}$ for the design shown in Fig. 1 is 3.6 × 10^− 7. Here $\mathcal {J}$ is the calculated compliance value and $\mathcal {J}^{*}$ is the compliance obtained on a finer reference mesh. Such a low value of $\mathcal {J}/\mathcal {J}^{*}$ implies that the compliance of the structure has been tremendously underestimated by the employed modeling scheme. During the optimization process, this modeling flaw has been exploited by the formation of the QR-pattern, with characteristic disconnected material patches.

The design shown in Fig. 1 has been optimized for minimum compliance subjected to a distributed load and the domain is discretized using 20 × 10 finite elements with 4 × 4 design voxels per element. Shape functions of polynomial degree 3 are used and 4th order Gaussian quadrature rule is used for numerical integration in each voxel. The order of the design field is chosen to satisfy the element- as well as system-level bounds stated in Gupta et al. (2017). No filtering is employed here, a value of 3 is used for the penalization power q and a volume constraint of 30% is used. The reference mesh consists of 80 × 40 elements with elementwise constant density field and polynomial degree p = 3.

Figure 3 shows magnified versions of 3 elements from the optimized design shown in Fig. 1. All the 3 elements consist of disconnected or almost disconnected material parts along the horizontal as well as vertical directions. Such disconnected features can be seen in various regions of the design (Fig. 1). Note that unlike the infamous checkerboard patterns observed in traditional TO, these artefacts occur within the elements. In the presence of such disconnected features, the design appears far from optimal. However, since the QR-patterns obtained using MTO approaches are artificially stiff, erroneous compliance is reported by the used model and a low value of the error indicator $\mathcal {J}/\mathcal {J}^{*}$ is obtained.

Fig. 3

Magnified view of 3 finite elements from the optimized cantilever design shown in Fig. 1. These elements have been chosen arbitrarily from among finite elements with disconnected material features in the non-void regions of the domain

From the example presented above, it is clear that there are certain limitations of MTO, and to be able to fully harness the capabilities of this method, the limitations need to be known. The erroneous patterns may not always be so apparent as in this example. This can lead to deceptive results, where erroneous objective values are obtained and the structure may incorrectly be interpreted as a well performing one. As has been shown in Groen et al. (2017) and Nguyen et al. (2017), filtering may help to reduce this error. In both these studies, minimum filter sizes have been recommended for various shape function orders and design resolutions, and the authors have shown that acceptable designs are obtained. It is observed that the filter sizes proposed by Nguyen et al. (2017) are more conservative than those mentioned in Groen et al. (2017).

As stated earlier, it is of interest to see whether even smaller filter sizes can be used which can produce well performing artefact-free-designs. The first step in this direction would be to gain a better understanding of the QR-patterns, and identify the possible reason for their formation. Thus, through several small-scale studies, first we investigate the origin of QR-patterns more closely in the next section.

3 Origin of QR-patterns

3.1 Study of elementary cases

For a better insight in QR-patterns, we examine elementary cases where the material distribution inside a single element is optimized for minimum compliance. Figure 4 shows three plane stress test cases consisting of one square finite element of unit size subjected to axial, biaxial and shear loading. A volume constraint of 30% is chosen for all the cases. Each finite element is divided into 8 × 8 voxels, Lagrange polynomials based shape functions of p = 6 are used and no filtering is applied. A 5th order Gaussian quadrature rule is used for numerical integration of the voxel stiffness matrices. Here and throughout this paper, unless otherwise mentioned, the Young’s moduli of the material and the void are chosen to be 1 and 10^− 9 Nm^− 2, respectively, and the Poisson ratio is set to 0.3. A modified SIMP formulation (Bendsøe 1989) with penalization power q = 3 is used for material interpolation for intermediate density values. As an initial design for optimization purposes, we used a uniform density distribution with slight perturbation in the density of the voxel at the top-rightmost corner. The perturbation was needed because a uniform density distribution leads to equal sensitivities for all the design variables which was not suited for optimization.

Fig. 4

Numerical test cases with different loading conditions (F = 1 Nm^− 1). For modeling, the design domain for each case is discretized using a single finite element with shape functions of polynomial order 6, and 8 × 8 design voxels are used

The optimized designs as well as the deformed shapes for the three cases are shown in Fig. 5. For all the three cases, the compliance accuracy $\mathcal {J}/\mathcal {J}^{*}$ values are extremely low, which means that the chosen model strongly underestimates the compliance of the optimized designs. Here, the reference compliance $\mathcal {J}^{*}$ is calculated on an elementwise constant density based mesh with 8 × 8 finite elements with shape functions of polynomial order 3. Similar to Fig. 3, it can be seen that all the optimized designs consist of QR-patterns and possess material parts which are completely disconnected. There are structural features subjected to the distributed load that can freely float along the vertical or horizontal directions, which implies that with accurate modeling, large displacements should be anticipated. This in turn should lead to high compliance objective values for all the cases.

Fig. 5

Optimized designs (left) and respective deformed shapes (right, scaled for visualization) under various loading conditions obtained for a single finite element obtained using an MTO scheme with p = 6 and 8 × 8 voxels

However, the low values of $\mathcal {J}/\mathcal {J}^{*}$ imply that these designs are erroneously interpreted as stiff ones. In fact, their stiffness is overestimated by a factor of 10⁸. The artificial stiffness is evident from the deformed shapes of these structures for the corresponding exerted loads (Fig. 5). We see that the freely floating solid features also get deformed, which means that considerable load is transferred through the voids. Also, contrary to the fact that the voids should be significantly deformed due to their negligible stiffness, we see that the deformations in the void areas are quite comparable to those of the solid parts. This means that as per the employed modeling scheme, the voids possess certain artificial stiffness, making them less compliant.

From these test cases, it is evident that the reason for the formation of these QR-patterns is linked to the limitations of the finite element model used here. From our numerical experiments with various shape functions, we observed that by using higher values of p, these artificially stiff regions could be reduced. These observations are aligned with the previous studies related to FCM-based modeling, where it has been shown that the material discontinuities cannot be accurately mapped using low-order elements in an FCM setting (Joulaian and Düster 2013a, b). One approach to reduce the modeling error is to use higher-order elements, however, such an approach is not advantageous in terms of the added computational cost. Joulaian and Düster (2013b) and Kollmannsberger et al. (2015) used an hp-d variant of FCM, where local enrichments are introduced through an overlay mesh to improve the modeling accuracy in heterogeneous parts of the domain.

In the context of TO, artefacts arising due to the limitations of low order shape functions in an MTO setting have been reported by Parvizian et al. (2012), Groen et al. (2017) and Nguyen et al. (2017). In line with these studies, the link between the polynomial functions and the QR-patterns are studied in the following sections. Shape functions of higher polynomial degree can better represent the displacement solution. Thus, in Section 3.3, we investigate whether the QR-patterns arise due to misrepresentation of the displacement field. Also, we explore whether there exist certain polynomial orders of the shape functions for which these QR-patterns can be eliminated at a reasonable computational cost.

3.2 Gap modeling with polynomial shape functions

To investigate the role of polynomial order of the shape functions in the formation of QR-patterns, we employ a simple elementary test where thin strips of void are modeled. The choice of this test is motivated from the patterns seen in Fig. 5, where the void appears to bear load. For problems only related to modeling, the loads are applied on the solid parts of the domain, thus the void does not need to be modeled correctly. However, in the context of TO, it is possible that during the course of optimization, thin strips of void arise in the domain. For such scenarios, either the applied load needs to become zero, or the chosen shape function should be able to correctly model the gap.

For the test problem chosen here (Fig. 6), the load is fixed, and the modeling accuracy is investigated. A single square finite element of unit dimensions is constrained from three sides and loaded in tension by a uniform distributed load. The element is filled with two material phases, i.e. solid and void. The domain is divided into 10 × 10 design voxels and a composite integration scheme (as stated in (1) is used to integrate the element stiffness matrix. The order of the integration scheme is chosen based on the polynomial order of the shape functions used to model the displacement solution.

Fig. 6

An axially loaded finite element (F = 1 Nm^− 1) filled with solid and void parts

Several values of p are used and the compliance $\mathcal {J}$ of the structure is calculated. Since we seek the values of p for which the QR-patterns can be eliminated in general, it is important that the chosen p works for various feature resolutions. To take this into account, the height of the void layer (h_v) is varied. To assess the correctness of $\mathcal {J}$, the analytical solution $\mathcal {J}_{0}$ is also calculated. The ratio $\mathcal {J}/\mathcal {J}_{0}$ indicates the compliance accuracy, with an ideal value of 1.

Figure 7 shows $\mathcal {J}/\mathcal {J}_{0}$ for different values of p and h_v. A general observation is that the for low p values, e.g. 2 or 3, accuracy is poor for all feature sizes. This means that the shape functions of lower polynomial order are not able to represent the displacement solution arising from such discontinuous material fields. With increasing p, the accuracy of the model improves, however, the feature resolution h_v plays a significant role here. For a large gap of h_v = 0.9, a shape function order of 4 proves sufficient to model the large compliance of the structure. However, for smaller gaps, increasingly high values of p are needed to properly represent the displacement field and prevent artificial stiffness. The case with h_v = 0.1 is still not adequately modeled with p = 12. This observation is investigated further in the next section.

Fig. 7

Compliance accuracy ($\mathcal {J}/\mathcal {J}_{0}$) versus the shape function order (p) for different void-feature resolutions obtained using a single finite element (as shown in Fig. 6) comprising 10 × 10 density voxels. Here, $\mathcal {J}$ is the compliance obtained using the MTO setting, and $\mathcal {J}_{0}$ denotes the analytical solution

In general, it is observed that the feature-size plays an important role in choosing the correct value of p. Thus, for full-scale multiresolution topology optimization problems, very high-order polynomials are needed to ensure that even the finest features are modeled correctly. However, the use of very high order polynomials comes at significantly increased computational costs, which limits the efficiency of such an MTO setting.

3.3 Displacement solution accuracy

In Section 3.2, it has been shown that higher p values can help to eliminate the QR-patterns. As stated earlier, the reason is that with higher-order polynomials, the displacement solution for a discontinuous material distribution can be more accurately represented. To study this in more detail, we use a simple 1D example where a bar is axially loaded at one end and fixed at the other (Fig. 8a). The bar consists of solid and void material phases in equal proportions (h_v = 0.5). Figure 8b shows the calculated displacement solutions along the length of the bar for the two phases calculated for several values of p. As a reference to measure the correctness of the solution, the exact piecewise linear displacement solution has been calculated analytically and is shown in Fig. 8b (on log scale).

Fig. 8

Displacement fields obtained for shape functions of various polynomial orders and the analytical solution for a 1D bar example. The Young’s moduli of the solid and the void are denoted by E₁ and E₂, respectively, and h_v denotes the width of the void

The first observation is that even shape functions of polynomial order 10 are incapable of accurately representing the displacement field. The continuous polynomials cannot represent a nonsmooth displacement field arising for the chosen material distribution. For lower values of p, the displacements in the void part of the domain are severely underestimated. Similar to the results shown in Fig. 7, the design tends to be artificially stiff. With increasing p values, a better representation of the displacement field can be obtained in the void part, however, large oscillations are generated in the solid part. Although this is incorrect, the deviation from the exact solution in the solid phase is negligible compared to that in the void part. Thus, although the displacement solution in the solid part does not match well with the exact solution, the nodal displacement predicted by higher order polynomials matches well.

Another important thing to note is that although the error in the displacement solution at the top end of the bar reduces significantly with high-order polynomials, the mismatch in the rest of the domain is quite high. The displacement field can become negative in the solid region, and resulting stresses and strains will be highly incorrect. For certain problems, e.g. compliance minimization with nodal loads, using high-order polynomials would be fine in an MTO setting. However, for other objective functionals, involving also response quantities within the elements, e.g. stress minimization, even the solution obtained with high values of p could lead to incorrect results.

In Section 3.2, it was found that the required shape function order depends on the feature resolution. Larger voids allow lower polynomial order of the shape functions for accurate analysis. Figure 9 provides a better insight into this aspect. In this figure, the displacement fields calculated in the void areas are provided for void widths (h_v) equal to 0.1 and 0.9 and shape functions of polynomial orders 4 and 12 are used. These parameters are chosen based on the observations in Fig. 7 that for h_v = 0.9, p = 4 is sufficient, while for h_v = 0.1, even p = 12 may not be accurate. We see that for h_v = 0.9, the displacement curve with even p = 4 reaches close to the analytical solution and with p = 12, it improves further. However, for h_v = 0.1, even with p = 12, the displacements are poorly predicted compared to the analytical solution. This is due to the limitation of polynomial shape functions in representing the drastic change in displacement close to the material discontinuity. The polynomial shape functions increase gradually over an interval of y to represent such a jump. This behavior is more prominent for lower order shape functions. Thus, for h_v = 0.9, the displacement at the end of the bar is significantly higher than that for h_v = 0.1. Consequently, for larger gaps, even lower order polynomials are acceptable. Based on this, controlling feature sizes presents a mechanism to prevent configurations that yield analysis inaccuracy. This aspect is explored further in Section 4.

Fig. 9

Displacement field u(y) (on a log scale) in the void region for the 1D bar example shown in Fig. 8a. The log scale has been used due to large differences in the displacements for different values of p

3.4 Role of penalization and design-uniqueness

The numerical tests presented in this paper thus far demonstrated the role of shape functions in the formation of QR-patterns. Due to the weakness of the analysis model, the optimizer prefers to exploit designs consisting of artificially stiff-regions. However, it has been observed that shape function order is not the only factor driving the formation of QR-patterns. Penalization of intermediate density values, as introduced conventionally by, e.g., the SIMP approach, turns out to promote the formation of QR-patterns. In addition to the artificial stiffness caused by the continuous shape functions, penalization gives the black-white QR-patterns an additional advantage over more continuous intermediate density material distributions.

This hypothesis has been numerically validated on the cantilever beam design problem presented in Fig. 1. Figure 10b, c and d show 3 optimized designs obtained using penalization powers q = 1, 1.1 and 2.0, respectively in the modified SIMP formulation and the corresponding compliance accuracies are reported. A finite element domain of 20 × 10 elements is used with 8 × 8 voxels in each element and shape functions of polynomial degree 6 are used. For q = 1, the intermediate densities are not penalized due to which the optimized design consists of gray areas throughout the domain and is free from QR-patterns. From the value of $\mathcal {J}/\mathcal {J}^{*}$, it can be inferred that the model is very accurate. However, for q = 1.1 or 2.0, the smooth design is unfavorable and the optimizer creates more solid-void design. Designs largely consisting of QR-patterns are obtained, with even void voxels on the upper edge where the distributed load is applied. Clearly these parts would be very compliant in reality. However, the chosen MTO scheme cannot model the response properly and extremely low compliance accuracy is obtained.

Fig. 10

Optimized designs for a cantilever beam subjected to a distributed load obtained using various penalization powers q in the modified SIMP formulation. The domain consists of 20 × 10 finite elements with 8 × 8 voxels per element

An interesting result is obtained with shape functions of polynomial degree 1. For this case, even with no penalization, the design consists of QR-patterns and low compliance accuracy is obtained (Fig. 10d). Similar to the checkerboard patterns, it is possible that these patterns always perform better than the ones with intermediate densities (Díaz and Sigmund 1995), due to which they appear in the final design. A remedy to remove them would be to employ filtering that bans these patterns from the design space. Alternatively, it is possible that the optimizer converges to this solution due to the non-uniqueness of the design field (Gupta et al. 2017). Thus, it is important that the shape function orders are chosen in a way that the uniqueness bounds proposed in Gupta et al. (2017) are satisfied.

4 Filtering in MTO

4.1 Role of filtering

Existing MTO approaches use filtering of voxel densities, which prevents the formation of QR-patterns. Filtering was originally employed in traditional TO to avoid the formation of checkerboard patterns and impose a minimum feature size. Some of the frequently used filtering methods are sensitivity filtering (Sigmund 1997), density filtering (Bruns and Tortorelli 2001), density filtering with projection (Guest et al. 2004), etc.

Density filters can be understood as regularization functions that smoothen the density field by taking weighted contributions from the neighboring density values located within a certain radius. Thus, in a filtered density field, the density gradients are reduced. In traditional TO, where the density is constant inside every element, the use of filters prohibits large contrasts in densities between two adjacent elements. Since checkerboard patterns feature large density contrasts between adjacent elements, they are eliminated by the use of filters.

Unlike checkerboard patterns, QR-patterns obtained in MTO are intra-element artefacts. In traditional TO, a filter radius slightly larger than the minimal element size is sufficient to eliminate the checkerboard patterns. In line with this observation, in MTO approaches, the smallest effective filter size should be slightly larger than the size of a density voxel. However, QR-patterns in MTO require stronger regularization of the density field, hence the smallest filter size to eliminate QR-patterns needs to be considerably larger than the voxel width. Although QR patterns differ on these aspects from checkerboard patterns, Groen et al. (2017) and Nguyen et al. (2017) have shown that with the use of filters, acceptable designs could be obtained.

4.2 Effect of filtering and limitations

Here, we investigate using an elementary example the extent to which the use of filters can help to suppress the QR-patterns in MTO. As stated earlier, filters reduce the density contrast between the adjacent elements, which consequently reduces the extent of non-smoothness of the displacement solution. In this section, we study the role of density filters by varying the filter radius r_min and observing the effect on the accuracy of the calculated compliance solution. The tensile test problem shown in Fig. 6 is used and the domain is assumed to consist of solid and void parts in equal proportions prior to filtering. The original density field is smoothened using density filters to obtain the filtered design. The domain is discretized using one finite element consisting of 8 × 8 design voxels.

Figure 11 shows compliance accuracy $\mathcal {J}/\mathcal {J}^{*}$ for various filter radii, as a function of polynomial degree p. The filter radius r_min is expressed in terms of voxel length. The reference compliance $\mathcal {J}^{*}$ is calculated on a domain of 8 × 8 finite elements of elementwise constant density and shape functions of polynomial order 3 are used. For the case without filter, the design is free from intermediate density values, and a solid-void boundary is modeled. From Fig. 11, it is seen that for such a configuration, polynomial degree of 8 or higher will be needed to model the displacement field. For shape functions of low polynomial degree p, the non-smooth displacement field at the solid-void boundary cannot be accurately modeled and poor compliance accuracy is obtained.

For high values of p, the displacement field can be better approximated and the compliance accuracy improves. At the same time, increasing the filter radius smoothens the density field, due to which the displacement solution becomes smoother and it should be possible to approximate it with shape functions of lower polynomial order (p). However, from Fig. 11 we observe that under the influence of density filtering, contrary to expectation, higher values of p are needed. For r_min equal to 2.4 voxels, a value of 10 or higher is required for p. Moreover, it is seen that even p = 12 is not sufficient if the design is filtered using r_min equal to 3.6 voxels. This happens because although under the influence of filtering, the displacement solution becomes smoother, the size of the gap reduces as well (Fig. 12b). As seen in Section 3.2, smaller void regions cannot be modeled with low values of p. Thus, for the case presented here, filtering does not have the desired effect, rather it raises the need for higher-order polynomials and is counterproductive in terms of required computational costs.

Fig. 11

Compliance accuracy $\mathcal {J}/\mathcal {J^{*}}$ versus the shape function order p for various filter radii $r_{{\min }}$ (in terms of voxel-length) obtained using a single finite element comprising 8 × 8 design voxels. The unfiltered density field consists of solid and void parts in equal proportions

Fig. 12

Unfiltered density field and its filtered versions obtained using density filters with $r_{{\min }}$ equal to 3.6 and 7.0 voxels. The domain consists of 1 finite element with 8 × 8 voxels

However, for r_min values of 5.0 and 7.0 voxels, low values of p are already sufficient and the error is significantly reduced. This is because with such filter sizes, there is no void part left in the filtered design and the element becomes stiffer. For a better understanding, consider Fig. 12 where the unfiltered design and its two filtered versions are shown which are obtained using density filtering with r_min equal to 3.6 and 7.0 voxels. Since the density is constant in the horizontal direction, each row of voxels can be considered as an elastic layer of certain stiffness. The design, along the vertical direction, can be interpreted as multiple elastic layers connected in series, with different Young’s moduli reflected by the respective density values. The equivalent stiffness of the whole structure along the vertical direction is controlled mainly by the weakest layer.

For r_min equal to 3.6 voxels, there exists a void of size 1.0 voxel in the filtered design (Fig. 12b) due to which the design is highly compliant. For such a scenario, a nonsmooth displacement solution arises which cannot be correctly modeled by low values of p. However, with r_min set to 7.0 voxels (Fig. 12c) or even 5.0 voxels, no void region exists. This means the equivalent stiffness of the element is higher and the extent of nonsmoothness in the displacement solution is significantly lower.

This example shows that for cases where void features exist in the filtered design and play an important role in an element’s response, increasing the filter radius can increase the analysis error. Once the filter radius is large enough to remove such void regions from the filtered field, the opposite is observed and the required value of p decreases significantly. Thus, even in the presence of filters, it is possible that the displacement field cannot be modeled correctly in an MTO setting.

To understand the influence of this modeling inaccuracy on the optimization process, we study the axial load case presented in Fig. 4. The design domain for this case is modeled using the initial density fields and filter radii shown in Fig. 12, and the corresponding optimized designs are shown in Fig. 13. It is observed that when no filter is used, a disconnected final design is obtained (Fig. 13a). Clearly, the strips of void that exist in the optimized design were inaccurately modeled as connected parts, due to which the design was falsely interpreted as a well-performing one. When filtering is used, it is observed that the final design is well connected and numerically correct (Fig. 13b and c). Thus, for the compliance minimization problem chosen here, although the models are inaccurate during the intermediate stages of optimization, an accurate final design is obtained when filtering is used.

Fig. 13

Optimized designs obtained for Case I, as shown in Fig. 4, obtained by optimizing the density distributions from Fig. 12

To study the effect of the void strip on the convergence of the optimization process, we look at the convergence plots (Fig. 14) obtained by optimizing the designs shown in Fig. 12. Further, for comparison purpose, we also show in Fig. 14 the convergence plots obtained when a uniform initial design is chosen. When a uniform initial design is used and a filter is employed, well connected designs are obtained. For the case with no filter, QR-patterns are formed, similar to those shown in Fig. 5a. From the plots shown in Fig. 14, it is found that the convergence of the optimization process is very different when the design comprises a void strip. For all the cases, the initial compliance of the layout with a strip of void is clearly worse than the design with uniform density distribution. Comparing the final objectives, it is observed that the disconnected design obtained in Fig. 13a is suboptimal. The artificially stiff pattern is a local optimum, but one that the optimization process remains trapped in. Also in the convergence plot of the optimization process for the design shown in Fig. 13a, we see repeated stagnation, followed by evolution to better, but still clearly inferior local optima. When the design contains a void strip, it takes over 10 iterations before a noticeable decrease of the high initial objective value is realized. This is remarkable given the clear superiority in the objective of the connected designs. It is possible that the artificial stiffness that is caused by the inadequate modeling of the void strip competes with real design improvements in the initial stage. Once a connected design is formed, the convergence is rapid. In general, the optimization process for the disconnected design required approximately 50% more iterations than a homogeneous initial design to reach the same objective value.

Fig. 14

Convergence plots for optimizing the designs shown in Fig. 12, augmented with three cases where we optimize a uniform initial design using no filter, and filter sizes of 3.6 and 7.0 voxels

Although the results presented above indicate that the possibility exists for the optimization process to get trapped in local minima consisting of disconnected patterns, for this case sufficiently filtering opens a path to superior designs that are fully connected. However, it is evident that the presence of the studied thin strips of void has an influence on the convergence of the optimization process. For compliance minimization, the impact of void strips is found to be very limited in the presence of sufficiently large filters. However, in an optimization process in general, whether or not an optimizer will exploit these configurations is hard to predict and problem dependent and the possibility cannot be ruled out. Additionally, since the filters impose a minimum feature restriction, the desired high resolution of the design is also reduced.

From these observations it can be argued whether density filters are really the solution to eliminate QR-patterns. As a matter of fact, the choice of correct filter radius depends on the material distribution in the unfiltered design as well as the loading condition and chosen shape function order. As per our present understanding, the optimal filter radius can only be determined by computationally expensive trial and error. Fortunately, for various linear structural problems, use of filters has helped to design reasonably optimal MTO designs (Groen et al. 2017). In the next section, we study one of these problems and present a numerical approach towards efficiently finding a suitable filter radius.

4.3 Choosing the filter radius

From the tests presented in the preceding section, it is clear that the choice of filter radius r_min can significantly affect the accuracy of the optimized solution. However, a general theory to determine the minimum filter radius that gives reasonably correct solutions is not yet available. Here, we examine the possibility of finding an appropriate value of r_min based on numerical experiments conducted for the 3 test cases shown in Fig. 4. These 3 cases represent elementary loading conditions that may occur at element level in a full-scale topology optimization mesh. Since the optimization problems for the 3 test cases are computationally very cheap compared to the actual design problem, these tests can be run a priori to choose r_min for a given set of associated parameters.

The choice of an optimal filter size depends on the fact that small filter radii lead to inaccurate modeling and QR-patterns, while large filter size leads to undesirable loss of resolution and crispness. For several values of r_min, the error indicator $\mathcal {J}/\mathcal {J}^{*}$ is examined on a domain of 8 × 8 voxels with shape functions of polynomial degree 6 and the results are shown in Fig. 15. To calculate the reference solution $\mathcal {J}^{*}$, an analysis mesh of 8 × 8 finite elements is used and the polynomial order of the shape functions is set to 3.

Fig. 15

Compliance accuracy $\mathcal {J}/\mathcal {J}^{*}$ for various filter radii $r_{{\min }}$ obtained for the three test cases presented in Fig. 4. For all the cases, a single finite element is used with shape functions of polynomial order 6 and 8 × 8 design voxels

An interesting observation here is that for all values of r_min, the compliance accuracy is higher for axial loading compared to the biaxial and shear loading conditions. One of the possible reasons is that for the axial load, there is only one direction along which the material discontinuities affect the accuracy of the model. For choosing optimal r_min, we assume that a compliance accuracy of close to 90% or even higher is acceptable and from Fig. 15, it is seen that this holds true for r_min equal to 2.6 voxels for all the 3 cases. Figure 16 shows the optimized designs for the 3 cases obtained using r_min = 2.6 voxels. Due to the use of large filters, designs are significantly gray, however, it is clearly evident that they are free from QR-patterns.

Fig. 16

Optimized designs for the three elementary test cases shown in Fig. 6 obtained using a filter radius of 2.6 voxels. The domain consists of 1 finite element with 8 × 8 voxels and shape functions of polynomial degree 6

Next, the value of 2.6 is used for r_min during the optimization of material distribution for the problem shown in Fig. 1. The domain is discretized using 20 × 10 finite elements, each comprising 8 × 8 voxels and shape functions of polynomial order 6. Figure 17a shows the optimized design obtained for r_min = 2.6 voxels. With this filter radius, the compliance accuracy of the design is 0.98, which means the model meets the chosen accuracy level and the design is free from artificially stiff regions. Here also, the reference compliance $\mathcal {J}^{*}$ is calculated on an elementwise constant density mesh of 160 × 80 finite elements with p = 3. For comparison, Fig. 17b shows the optimized cantilever design obtained with r_min = 1.4 voxels. QR-patterns are very prominent in this design and the compliance accuracy of the design is low. For both the designs, intermediate density areas are seen in some parts of the domain, which could not be resolved using the MTO scheme.

Fig. 17

Optimized designs for cantilever beam subjected to distributed load (as in Fig. 1) for two different filter radii. The domain is discretized using 20 × 10 finite elements with shape functions of polynomial degree 6 and 8 × 8 design voxels per element

Thus, we find that the r_min value obtained from Fig. 15 works well for this problem. We observe that the compliance accuracy for the cantilever problem is higher compared to the 3 test cases from which the optimal value of r_min was derived. In terms of closeness, the compliance accuracy values for this design are closest to that of Case I, i.e. axial loading. This is indeed as expected since for a single load case compliance minimization, the optimized design tends to form members loaded in tension/compression.

It is important to note that this choice of r_min = 2.6 voxels cannot be generalized. There are several parameters that can affect the appropriate choice of filter radius, e.g., polynomial degree of shape functions, number of voxels, material volume fraction, loading conditions, etc. Among these, we study the effect of various shape functions and number of voxels on the optimal filter radius obtained using the 3 element test cases (Fig. 4). For ease of comparison, the filter radius for the further study will be defined in terms of element length (h). For example, for a square finite element comprising 5 × 5 voxels, a filter radius of 2 voxels will be referred as 0.4h. In addition, the number of voxels along the x- or y-direction will be denoted by d.

Table 1 shows the optimal filter radii found for various choices of p and d when compliance accuracy of around 90% or higher is assumed to be acceptable. The value 90% is chosen based on the fact that with the resultant filter radii, compliance accuracies of 98% or higher were obtained for several full-scale TO problems of compliance minimization. Clearly with the same method, filter radii limits can be found for other target accuracies. For this study, filter radii of 0.05h to 1.0h are tested at an interval of 0.05h. The dark gray region refers to the infeasible combinations of p and d as per the uniqueness bounds proposed in Gupta et al. (2017). The symbol × denotes that a discretization using only one finite element is not sufficient for the respective combinations of p and d, as far as QR-patterns are concerned. When the design is optimized without filtering for single element test cases comprising 2 × 2 voxels and 3 × 3 voxels, very inaccurate solutions are obtained. Clearly, for a very low design resolution, the single element test cases do not seem to work. This happens because with a very low design resolution, the optimization problem is quite restricted. Starting from a uniform distribution, it is observed that designs hardly change during the course of optimization. The unfiltered design itself is well connected and no filtering is needed.

Table 1 Choice of filter radius (in terms of element size h) for various choices of polynomial degree of the shape functions p and number of design voxels along the x- and y-direction (denoted by d), to obtain compliance accuracies $\mathcal {J}/\mathcal {J}^{*}$ of around 90% or higher for the three element test cases shown in Fig. 4

Table 2 presents the optimal filter radii for various choices of p and d obtained on a mesh of 2 × 2 finite elements. Only values related to the tensile case are reported, since for the one-element tests, this case was found to be controlling the choice of minimum filter radii. With an increase in the number of elements, the design freedom is increased, and optimal filter radii values can be obtained for low values of d as well.

Table 2 Choice of filter radius (in terms of element size h) for various choices of polynomial degree of the shape functions p and number of design voxels along the x- and y-direction (denoted by d), to obtain compliance accuracies $\mathcal {J}/\mathcal {J}^{*}$ of around 90% or higher for the tensile test case shown in Fig. 4

A general observation is that for obtaining very fine features, the filter radius needs to be very small. From Table 1, it is observed that for a filter radius of 0.2h, very high values of p and d are needed. Lowering p leads to the need for a larger filter radius. Lower values of d restrict the design resolution and also require a large filter radius. It is observed that these values of filter radius are slightly higher compared to the results reported in Groen et al. (2017), and the reason could be that the element test cases used in this study are more restrictive. Comparing the values of Tables 1 and 2, we observe that with a finer discretization, the optimal filter radii values decrease slightly for low values of p and d. However, for higher values, the minimum required filter radii to achieve the desired solution accuracy are equal.

To investigate how this method of determining an optimal filter radius extends to 3D, a preliminary study has been performed using only the tensile test. Similar to Case I shown in Fig. 4, a 3D cube of unit dimensions is considered and the top surface is subjected to a distributed load of 1 Nm^− 2. Apart from vertical displacements, motion is restricted along the other two spatial dimensions for the vertical surfaces of the cube, and the bottom surface is entirely fixed. The optimal filter radii for different values of p and d for this case are shown in Table 3. The observations are similar to those obtained from Tables 1 and 2. An interesting observation is that for 3D cases, the required filter radii are slightly lower than those obtained for 2D cases.

Table 3 Choice of filter radius (in terms of element size h) for various choices of polynomial degree of the shape functions p and number of design voxels along the x-, y- and z-direction (denoted by d), to obtain compliance accuracies $\mathcal {J}/\mathcal {J}^{*}$ of around 90% or higher for the tensile test case shown in Fig. 4

A general observation from Tables 1, 2 and 3 is that the required filter radius to guarantee reasonably accurate results only decreases slowly with p. For example, from Table 1, we see that with d = 4 and elements with cubic shape functions (p = 3), a filter radius of 0.7h is required, resulting in a feature size of 2r_min = 1.4h. To decrease this feature size by a factor 2 (i.e. allow r_min = 0.35h), polynomial shape functions of order 6 or higher are needed with d = 6. It is questionable whether this is advantageous in terms of computational cost compared to realizing a similar feature size reduction in conventional TO, which would give a similar increase in DOFs but a sparser stiffness matrix contribution. This finding indicates that in the present MTO scheme, increased level of detail is associated with a considerable increase in computational cost, due to which the advantage of MTO could be lost over the traditional TO approach.

5 Discussion

In this paper, the disconnected material distributions observed in MTO formulations, denoted as QR-patterns, are investigated using several numerical experiments. From the presented results, it can be inferred that these patterns cannot be correctly modeled by the employed modeling scheme. They form as artefacts in compliance minimization as their stiffness is strongly overestimated. In general, the use of large numbers of design voxels allows the representation of high resolution designs which in turn leads to material features that require shape functions of very high polynomial degree to be correctly modeled.

Density filtering has been used to eliminate the QR-patterns and has been successful for various instances, however, as shown in this work, the use of density filters can have a negative impact and can raise the polynomial order of the shape functions desired for accurate modeling, thereby leading to even higher computational costs. Filtering imposes a restriction on the minimum feature size. The native design resolution given by the voxel size is lost, and without additional measures, blurred design boundaries are formed. Furthermore, given the aim of reaching an optimal ratio between design resolution and analysis costs through MTO, imposing larger minimum feature sizes on the design through filtering is counterproductive.

The single-element tests presented in Section 4.2 show that void strips give strongly overestimated stiffness. However, these do not always appear during optimization, and seem to be fully suppressed when a sufficiently large filter radius is used. One of the reasons that these thin strips of void are not formed could be that the optimization process converges to different local optima, and these thin strips are not easily encountered. Moreover, the QR-patterns observed in unfiltered designs consist of quickly spatially-varying material patterns, and filtering removes such design patterns from the solution space. Although the thin strips of void can still be formed, the gradual density transition zone caused by density filtering make them less favorable in term of absolute stiffness compared to the connected designs. For example, we observed that for compliance minimization, the connected designs are preferred over the ones comprising void strips when filtering is used. Nevertheless, the relative stiffness overestimation is still observed. When filtering is combined with Heaviside projection, the artefacts reappear (Groen et al. 2017). This issue can be overcome for most of the cases using the modified Heaviside projection method (Sigmund 2007), however, this approach cannot be guaranteed to work and should be used with caution (Groen et al. 2017).

Although with suitable filtering, the thin strips of void are not observed in the designs optimized for minimal compliance, it cannot be guaranteed that such issues will not be encountered for other more complex TO problems. In this study, as well as most other studies, the application of MTO has focused on compliance minimization problems. Groen et al. (2017) also studied the application of MTO in a compliant mechanism optimization. Currently an incomplete understanding exists of the applicability of MTO to different optimization problems, and further research is required to support the generalization of MTO approaches. Of interest are for example problems involving eigenfrequencies or stress constraints, where it is yet unknown what interaction the multiresolution modeling will have with the optimization process. As a protective measure, such scenarios should be avoided in general. In this paper, the MTO approach has been studied from a more conservative point of view. The extreme limitations of MTO are explored, so that the highest permissible design resolution can be achieved without encountering any artefacts.

There are additional aspects that need to be investigated further so as to assess the full capability of the MTO concept. A measure of benefit-versus-cost for increasing the polynomial order of the shape functions can be defined to determine whether the use of high p values for certain MTO configurations is beneficial or not. Groen et al. (2017) have presented an empirical measure based on several numerical experiments. It would be of interest to explore further in this direction on a wider variety of MTO problems, and also look into theoretical aspects of the problem to establish more rigorous criteria. Another possible direction to look into could be to investigate the role of adaptive p-refinement in MTO. Locally increasing the value of p can reduce the artefacts while limiting the additional computational burden. For such methods, well defined refinement indicators are needed which can easily locate the regions at risk of developing QR-patterns.

For a certain MTO configuration in 2D, to determine the minimum filter radius that avoids the QR-pattern, we used three load cases (axial, biaxial and shear). For the problems studied in this paper, axial loading controls the choice of filter radius and only this case was used to determine filter choices for 3D problems. It is possible that for 3D problems, some additional load cases need to be considered. Moreover, for other problems, which are not covered in this study, these choices of loading might not be sufficient and a different case is needed. Thus, it would be of interest to investigate which load cases would be critical for 3D problems as well as problems involving other objective functionals.

In this paper, we have studied in detail the fact that the QR-patterns in MTO originate from the known incapability of the polynomial shape functions in modeling the displacement field that accompanies a discontinuous material distribution. Methods such as XFEM, GFEM, etc. are well-established techniques that use enrichment functions to accurately model such nonsmooth or discontinuous displacement fields (Moës et al. 1999; Strouboulis and Copps 2001). XFEM has successfully been used in the context of TO (e.g., Kreissl and Maute 2012). However, the significantly high complexity of this approach restricts its attractiveness, and how to combine XFEM with MTO is an open research question. It may nevertheless present a way to rigorously prevent QR-patterns without sacrificing design resolution.

6 Conclusions

In this paper, numerical artefacts arising in multiresolution topology optimization (MTO), denoted as QR-patterns, have been thoroughly studied and an explanation on their formation has been presented. Through several numerical tests, we observed that elements with discontinuous internal material distributions can show artificially low compliance when shape functions of insufficient polynomial degree are used. This deficiency of the finite element model has been observed before in higher-order multiresolution methods. It can be exploited during optimization, leading to unrealistic QR-patterns. While shape functions of very high polynomial degree can eliminate these artefacts, it is observed that the computational advantage of MTO over traditional TO could be lost due to the additional DOFs introduced. Further, the role of density filtering in MTO is investigated. It is shown that although filtering can reduce the QR-patterns for certain cases, it may not always be the solution to eliminate these artefacts and can sometimes be counterproductive.

Based on the investigations presented in this work, we conclude that while density filtering with a sufficiently large radius can prevent the occurrence of QR-patterns in the studied problems, it decreases the design resolution, and consequently, the efficiency of MTO. Furthermore, dedicated studies into particular problem types and other responses are needed to gain a better understanding on whether the filtering presents a universal remedy. An alternative research direction is to address the issue from the analysis side, and find formulations that properly represent the performance of disconnected designs. It is expected that our findings will serve as the groundwork to define effective countermeasures to eliminate QR-patterns and help to achieve the goal of obtaining high resolution designs at low computational cost.