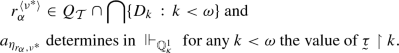Abstract
We consider a version of \(\kappa \)-Miller forcing on an uncountable cardinal \(\kappa \). We show that under \(2^{<\kappa } = \kappa \) this forcing collapses \(2^\kappa \) to \(\omega \) and adds a \(\kappa \)-Cohen real. The same holds under the weaker assumptions that \({{\,\mathrm{cf}\,}}(\kappa ) > \omega \), \(2^{2^{<\kappa }}= 2^\kappa \), and forcing with \(([\kappa ]^\kappa , \subseteq )\) collapses \(2^\kappa \) to \(\omega \).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many of the tree forcings on the classical Baire space have various analogues for higher cardinals. Here we are concerned with Miller forcing [4]. In the classical case, a Miller condition is a superperfect subtree of \(\omega ^{<\omega }\). The subtree is ordered by the end-extension relation on \(\omega ^{<\omega }\). The forcing order is simply \(\subseteq \). A tree is superperfect if each node has an extension that has infinitely many immediate tree successors. Such a node is called a splitting node. We can assume that each node has just one direct successor or infinitely many.
For a \(\kappa \)-version of Miller forcing, superperfectness and splitting are usually interpreted as follows: Above each node \(t \in p \subseteq \kappa ^{<\kappa }\) there is a node splitting node s. The common interpretation of “s is a splitting node of p” is:
In order to gain (\(<\kappa \))-closure of the notion of forcing, in addition to the club version of superperfectness one usually requires for conditions that (see, e.g., [2, Section 5.2]) limits of length less than \(\kappa \) of splitting nodes be splitting nodes as well.
In this paper we investigate a version of \(\kappa \)-Miller forcing where the conditions on superperfectness and (\(<\kappa \))-closure of splitting nodes are kept and the definition of “s is a splitting node of p” is weakened to
We show: If \({{\,\mathrm{cf}\,}}(\kappa ) > \omega \), \({{\,\mathrm{cf}\,}}(\kappa ) = \kappa \) or \({{\,\mathrm{cf}\,}}(\kappa ) < 2^{{{\,\mathrm{cf}\,}}(\kappa )} \le \kappa \), \(2^{2^{<\kappa }} = 2^\kappa \), and there is a \(\kappa \)-mad family of size \(2^\kappa \), then this variant of Miller forcing is related to the forcing \(([\kappa ]^\kappa , \subseteq )\) and collapses \(2^\kappa \) to \(\omega \). In particular, if \(\omega<\kappa ^{<\kappa } = \kappa \), then our four premises are fulfilled. Thus we provide some mathematical justification of the customary choice of higher Miller forcing.
Throughout the paper we let \(\kappa \) be an uncountable cardinal. We do not make the general assumption that \(2^{<\kappa } = \kappa \), nor do we assume that \(\kappa \) is regular.
We denote forcing orders in the form \(({\mathbb {P}},\le _{{\mathbb {P}}})\) and let \(q \le _{\mathbb {P}}p\) mean that q is stronger than p.
If \({{\,\mathrm{dom}\,}}(t), i \) are ordinals, we write \(t \,\hat{} \,\langle i\rangle \) for the concatenation of t with the singleton function \(\{(0,i)\}\), i.e., \(t \,\hat{} \,\langle i\rangle =t \cup \{({{\,\mathrm{dom}\,}}(t), i)\}\). For cardinals \(\kappa \), \(\lambda \), we write \({}^{<\lambda } \kappa \) for the set of functions \(f :\alpha \rightarrow \kappa \) for some \(\alpha < \lambda \). For \(s, t \in \kappa ^{<\lambda }\) we write \(s \trianglelefteq t\) if \(s = t \restriction {{\,\mathrm{dom}\,}}(s)\), and the corresponding strict order is written as \(\triangleleft \). The domain \(\alpha \) of f is also called the length of f. The set of subsets of \(\kappa \) of size \(\kappa \) is denoted by \([\kappa ]^\kappa \).
Definition 1.1
-
(1)
\({\mathbb {Q}}_\kappa ^1\) is the forcing \(([\kappa ]^\kappa , \subseteq )\).
-
(2)
\({\mathbb {Q}}_\kappa ^2\) is the following version of \(\kappa \)-Miller forcing: Conditions are trees \(T \subseteq {}^{\kappa > } \kappa \) that are \(\kappa \) superperfect: for each \(s \in T\) there is \(s \trianglelefteq t\) such that t is a \(\kappa \)-splitting node of T. A node \(t \in T\) is called a \(\kappa \)-splitting node if
$$\begin{aligned} {{\,\mathrm{set}\,}}_p(t) = \{\alpha < \kappa \, : \,t \,\hat{} \,\langle \alpha \rangle \in T\} \end{aligned}$$has size \(\kappa \). The set of splitting nodes of T is denoted by \({{\,\mathrm{spl}\,}}(T)\).
We furthermore require for \(p \in {\mathbb {Q}}^2_\kappa \) that the limit of an \(\triangleleft \)-increasing sequence of length less than \(\kappa \) of \(\kappa \)-splitting nodes is a \(\kappa \)-splitting node if it has length less than \(\kappa \).
For \(p,q \in {\mathbb {Q}}_\kappa ^2\) we write \(q \le _{{\mathbb {Q}}^2_\kappa } p\) if \(q \subseteq p\). So subtrees are stronger conditions.
-
(3)
For \(p \in {\mathbb {Q}}_\kappa ^2\) and \(\eta \in p\) we let \({{\,\mathrm{suc}\,}}_p(s) = \{t \in {}^{\kappa >} \kappa \, : \,(\exists \alpha < \kappa ) (t= s \,\hat{} \,\langle \alpha \rangle \in p)\}\).
-
(4)
Let \(s \in p \in {\mathbb {Q}}^2_\kappa \). We let \(p^{\langle s \rangle } = \{t\in p \, : \,t \trianglelefteq s \vee s \trianglelefteq t\}\).
-
(5)
For \(a, b \subseteq \kappa \) we write \(a \subseteq ^*_\kappa b\) if \(|a \setminus b|< \kappa \).
Each of the two forcing orders \({\mathbb {P}}\) has a weakest element, denoted by \(1_{{\mathbb {P}}}\). Namely, \({\mathbb {Q}}^1_\kappa \) has as a weakest element \(1_{{\mathbb {Q}}^1_\kappa } = \kappa \), and \({\mathbb {Q}}^2_\kappa \) has as a weakest element the full tree \({}^{\kappa >} \kappa \). We write \({\mathbb {P}}\Vdash \varphi \) if the weakest condition forces \(\varphi \).
2 Results about \({\mathbb {Q}}^1_\kappa \)
In this section we consider \({\mathbb {Q}}^1_\kappa \). The purpose is to provide standardised \({\mathbb {Q}}^1_\kappa \)-names for collapses. Later these particular \({\mathbb {Q}}^1_\kappa \)-names shall be translated to \({\mathbb {Q}}^2_\kappa \)-names.
Definition 2.1
A family \({\mathcal {A}}\subseteq [\kappa ]^\kappa \) is called a \(\kappa \)-almost disjoint family if for \(A \ne B \in {\mathcal {A}}\), \(|A \cap B|<\kappa \).
Observation 2.2
If \(2^{<\kappa } = \kappa \), there is a \(\kappa \)-ad family \({\mathcal {A}}\subseteq [\kappa ]^\kappa \) of size \(2^\kappa \).
Proof
We let \(f :{}^{\kappa >} 2 \rightarrow \kappa \) be an injection. We assign to each branch b of \({}^{\kappa >}2\) a set \(a_b=\{f(s) \, : \,s \in b\}\). The resulting family \(\{a_b \, : \,b \text{ branch } \text{ of } {}^{\kappa >} 2\}\) is \(\kappa \)-ad. \(\square \)
Observation 2.3
If \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\omega \), then there is a \(\kappa \)-ad family of size \(2^\kappa \).
Proof
\({\mathbb {Q}}^1_\kappa \) cannot have the \(2^\kappa \)-c.c. Hence there is an antichain of size \(2^\kappa \). Since \(p \perp _{{\mathbb {Q}}^1_\kappa } q\) means \(|p \cap q| < \kappa \), the antichain is a \(\kappa \)-ad family. \(\square \)
We will apply the following result for \(\chi = 2^\kappa \).
Theorem 2.4
[5, Theorem 0.5] Suppose that there is an antichain in \({\mathbb {Q}}^1_\kappa \) of size \(\chi \). Then the following holds.
-
(1)
Forcing with \({\mathbb {Q}}^1_\kappa \) collapses \(\chi \) to \(\aleph _0\) if \(\aleph _0 < {{\,\mathrm{cf}\,}}(\kappa ) = \kappa \) or if \(\aleph _0< {{\,\mathrm{cf}\,}}(\kappa ) < 2^{{{\,\mathrm{cf}\,}}(\kappa )} \le \kappa \).
-
(2)
Forcing with \({\mathbb {Q}}^1_\kappa \) collapses \(\chi \) to \(\aleph _1\) in the case of \(\aleph _0 = {{\,\mathrm{cf}\,}}(\kappa )<\kappa \).
Now we start defining tree structures from \({\mathbb {Q}}^1_\kappa \)-names for collapsing functions. Those trees will later be used to define dense suborders \(Q_{{\mathcal {T}}}\) of \({\mathbb {Q}}^2_\kappa \). The idea of \(Q_{{\mathcal {T}}}\) is that the sets \({{\,\mathrm{set}\,}}_p(t)\), \(t \in {{\,\mathrm{spl}\,}}(p)\), for \(p \in Q_{{\mathcal {T}}}\) will be sufficiently strong \({\mathbb {Q}}^1_\kappa \) conditions.
Lemma 2.5
Suppose that \({\mathbb {Q}}_\kappa ^1\) collapses \(2^\kappa \) to \(\omega \). Then there is a \({\mathbb {Q}}^1_\kappa \)-name  for a surjection, and there is a labelled tree \({{\mathcal {T}}}= \langle (a_\eta , n_\eta , \varrho _\eta ) \, : \,\eta \in {}^{\omega >}(2^\kappa )\rangle \) with the following properties
for a surjection, and there is a labelled tree \({{\mathcal {T}}}= \langle (a_\eta , n_\eta , \varrho _\eta ) \, : \,\eta \in {}^{\omega >}(2^\kappa )\rangle \) with the following properties
-
(a)
\(a_{\langle \rangle } = \kappa \) and for any \(\eta \in {}^{\omega >}(2^\kappa )\), \(a_\eta \in [\kappa ]^\kappa \).
-
(b)
\(\eta _1 \triangleleft \eta _2\) implies \(a_{\eta _1} \supseteq a_{\eta _2}\).
-
(c)
\(n_\eta \in [{{\,\mathrm{dom}\,}}(\eta )+1, \omega )\).
-
(d)
If \(a \in [\kappa ]^\kappa \) then there is some \(\eta \in {}^{\omega >} (2^\kappa )\) such that \(a \supseteq a_\eta \).
-
(e)
If \(\eta \,\hat{} \,\langle \beta \rangle \in T\) then \(a_{\eta \,\hat{} \,\langle \beta \rangle }\) forces
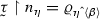 for some \(\varrho _{\eta \,\hat{} \,\langle \beta \rangle } \in {}^{n_\eta } (2^\kappa )\), such that the \(\varrho _{\eta \,\hat{} \,\langle \beta \rangle }\), \(\beta \in 2^\kappa \), are pairwise different. Hence for any \(\eta \in {}^{\omega >}(2^\kappa )\), the family \(\{a_{\eta \,\hat{} \,\langle \alpha \rangle } \, : \,\alpha < 2^\kappa \}\) is a \(\kappa \)-ad family in \([a_\eta ]^\kappa \).
for some \(\varrho _{\eta \,\hat{} \,\langle \beta \rangle } \in {}^{n_\eta } (2^\kappa )\), such that the \(\varrho _{\eta \,\hat{} \,\langle \beta \rangle }\), \(\beta \in 2^\kappa \), are pairwise different. Hence for any \(\eta \in {}^{\omega >}(2^\kappa )\), the family \(\{a_{\eta \,\hat{} \,\langle \alpha \rangle } \, : \,\alpha < 2^\kappa \}\) is a \(\kappa \)-ad family in \([a_\eta ]^\kappa \).
Proof
Let  be a \({\mathbb {Q}}^1_\kappa \)-name such that
be a \({\mathbb {Q}}^1_\kappa \)-name such that  is onto. For \(\alpha < 2^\kappa \) let \(AP_\alpha \) be the set of objects \({\bar{m}}\) satisfying
is onto. For \(\alpha < 2^\kappa \) let \(AP_\alpha \) be the set of objects \({\bar{m}}\) satisfying
- \((*)_1\):
-
(1.1) \({\bar{m}} = (T,{\bar{a}},{\bar{n}},{\bar{\varrho }}) = (T_{{\bar{m}}}, {\bar{a}}_{{\bar{m}}}, {\bar{n}}_{{\bar{m}}}, {\bar{\varrho }}_{{\bar{m}}})\).
(1.2) T is a subtree of \(({}^{\omega >} (2^\kappa ), \triangleleft )\) of cardinality \(\le |\alpha | + \kappa \) and \(\langle \rangle \in T\).
(1.3) \({\bar{a}} = \langle a_\eta \, : \,\eta \in T\rangle \) fulfils \(\eta \triangleleft \nu \rightarrow a_\nu \subseteq a_\eta \) and \( a_{\langle \rangle } = \kappa \) and \(a_\eta \in [\kappa ]^{\kappa }\).
(1.4) \({\bar{n}} = \langle n_\eta \, : \,\eta \in T \rangle \) fulfils \({{\,\mathrm{dom}\,}}(\varrho _{\eta \,\hat{} \,\langle \beta \rangle }) = n_\eta > {{\,\mathrm{dom}\,}}(\eta )\) for any \(\eta \,\hat{} \,\langle \beta \rangle \in T\).
(1.5) If \(\eta \,\hat{} \,\langle \beta \rangle \in T\), then \(a_{\eta \,\hat{} \,\langle \beta \rangle }\) forces a value to
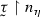 , called \(\varrho _{\eta \,\hat{} \,\langle \beta \rangle }\), and for \(\beta \ne \gamma \) we have \(\varrho _{\eta \,\hat{} \,\langle \beta \rangle } \ne \varrho _{\eta \,\hat{} \,\langle \gamma \rangle }\). Hence for any \(\eta \,\hat{} \,\langle \beta \rangle \), \(\eta \,\hat{} \,\langle \gamma \rangle \in T_{{\bar{m}}}\), \(\beta \ne \gamma \) implies \(a_{\eta \,\hat{} \,\langle \beta \rangle } \cap a_{\eta \,\hat{} \,\langle \gamma \rangle } \in [\kappa ]^{<\kappa }\).
, called \(\varrho _{\eta \,\hat{} \,\langle \beta \rangle }\), and for \(\beta \ne \gamma \) we have \(\varrho _{\eta \,\hat{} \,\langle \beta \rangle } \ne \varrho _{\eta \,\hat{} \,\langle \gamma \rangle }\). Hence for any \(\eta \,\hat{} \,\langle \beta \rangle \), \(\eta \,\hat{} \,\langle \gamma \rangle \in T_{{\bar{m}}}\), \(\beta \ne \gamma \) implies \(a_{\eta \,\hat{} \,\langle \beta \rangle } \cap a_{\eta \,\hat{} \,\langle \gamma \rangle } \in [\kappa ]^{<\kappa }\).(1.6) For \(\eta \in T_{{\bar{m}}}\), we let

and require that the latter has cardinality \(2^\kappa \).
In the next items we state some properties of \(AP_\alpha \) that are derived from \((*)_1\).
- \((*)_2\):
-
\(AP = \bigcup \{AP_\alpha \, : \,\alpha < 2^\kappa \}\) is ordered naturally by \(\le _{AP}\), which means end extension.
- \((*)_3\):
-
(a) \(AP_\alpha \) is not empty and increasing in \(\alpha \).
(b) For infinite \(\alpha \), \(AP_\alpha \) is closed under unions of increasing sequences of length \(< |\alpha |^+\).
- \((*)_4\):
-
Let \(\gamma < 2^\kappa \). If \({\bar{m}} \in AP_\gamma \) and \(\eta \in T_{{\bar{m}}}\) and \(\eta \,\hat{} \,\langle \alpha \rangle \not \in T_{{\bar{m}}}\) then there is \({\bar{m}}' \in AP_\gamma \) such that \({\bar{m}} \le _{AP} {\bar{m}}'\) and \(T_{{\bar{m}}'} = T_{{\bar{m}}} \cup \{\eta \,\hat{} \,\langle \alpha \rangle \}\).
Proof: For \(\eta \in T_{{\bar{m}}}\),
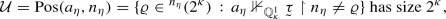
whereas
$$\begin{aligned} \Lambda _\eta = \{ \varrho _{\eta \,\hat{} \,\langle \beta \rangle } \restriction n_\eta \, : \,\beta \in 2^\kappa \wedge \eta \,\hat{} \,\langle \beta \rangle \in T_{{\bar{m}}}\} \end{aligned}$$is of size \(\le |T_{{\bar{m}}}| \le |\gamma | + \kappa \). Hence we can choose \(\varrho _*\in {\mathcal {U}}\setminus \Lambda _\eta \) and \(b_*\in [a_\eta ]^\kappa \) such that
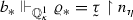 . We let \(\varrho _{\eta \,\hat{} \,\langle \alpha \rangle } = \varrho _*\). Since \(b_*\) forces a value of \(\tau \restriction n_\eta \) that is incompatible with the one forced by \(a_{\eta \,\hat{} \,\langle \beta \rangle }\) for any \(\eta \,\hat{} \,\langle \beta \rangle \in T_{{\bar{m}}}\), the set \(b_*\) is \(\kappa \)-almost disjoint from \( a_{\eta \,\hat{} \,\langle \beta \rangle }\) for any \(\eta \,\hat{} \,\langle \beta \rangle \in T_{{\bar{m}}}\). We take \(b_*= a_{{\bar{m}}', \eta \,\hat{} \,\langle \alpha \rangle } \subseteq a_{{\bar{m}},\eta }\).
. We let \(\varrho _{\eta \,\hat{} \,\langle \alpha \rangle } = \varrho _*\). Since \(b_*\) forces a value of \(\tau \restriction n_\eta \) that is incompatible with the one forced by \(a_{\eta \,\hat{} \,\langle \beta \rangle }\) for any \(\eta \,\hat{} \,\langle \beta \rangle \in T_{{\bar{m}}}\), the set \(b_*\) is \(\kappa \)-almost disjoint from \( a_{\eta \,\hat{} \,\langle \beta \rangle }\) for any \(\eta \,\hat{} \,\langle \beta \rangle \in T_{{\bar{m}}}\). We take \(b_*= a_{{\bar{m}}', \eta \,\hat{} \,\langle \alpha \rangle } \subseteq a_{{\bar{m}},\eta }\).
Since \({{\,\mathrm{cf}\,}}(2^\kappa ) > \aleph _0\) and since

there is an n such that

has cardinality \(2^\kappa \). We take the minimal one and let it be \(n_{\eta \,\hat{} \,\langle \alpha \rangle }\).
- \((*)_5\):
-
If \({\bar{m}} \in AP_\alpha \) and \(a \in [\kappa ]^\kappa \) then there is some \({\bar{m}}' \ge {\bar{m}}\), such that there is \(\eta \in T_{{\bar{m}}'}\) with \(a_{{\bar{m}}',\eta } \subseteq a\).
Let
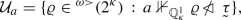
i.e.
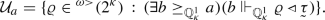
This set has cardinality \(2^\kappa \) because
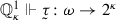 is onto. We take n minimal such that
is onto. We take n minimal such that 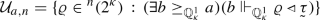
has size \(2^\kappa \). We let
$$\begin{aligned} {{\,\mathrm{set}\,}}_n^+({\bar{m}}) = \{ \varrho _{\eta } \, : \,\eta \in T_{{\bar{m}}}, {{\,\mathrm{dom}\,}}(\varrho _\eta ) \ge n\}. \end{aligned}$$Clearly \(|{{\,\mathrm{set}\,}}_n^+({\bar{m}})| \le |T_{{\bar{m}}}| \le |\gamma | + \kappa \). Thus we can take \(\varrho _a \in {\mathcal {U}}_{a,n}\) that is incompatible with every element of \({{\,\mathrm{set}\,}}^+_n({\bar{m}})\). We take some \(b_a \in [a]^\kappa \) such that
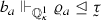 . The set $$\begin{aligned} \Lambda _a = \{ \eta \in T_{{\bar{m}}} \, : \,b_a \subseteq ^*_\kappa a_\eta \} \end{aligned}$$
. The set $$\begin{aligned} \Lambda _a = \{ \eta \in T_{{\bar{m}}} \, : \,b_a \subseteq ^*_\kappa a_\eta \} \end{aligned}$$is \(\triangleleft \)-linearly ordered by \((*)_1\) clauses 1.3 and 1.5 and \(\langle \rangle \in \Lambda _a\). Since \(b_a\) does not pin down
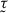 , \(\Lambda _a\) has a \(\triangleleft \)-maximal member \(\eta _a\). Now we take \(\alpha _*= \min \{\beta \, : \,\eta _a \,\hat{} \,\langle \beta \rangle \not \in T_{{\bar{m}}}\}\). For any \(\eta _a \,\hat{} \,\langle \beta \rangle \in T_{{\bar{m}}}\) we have \(\varrho _{\eta _a \,\hat{} \,\langle \beta \rangle } \) and \(\varrho _a\) are incompatible, and hence \(a_{\eta _a \,\hat{} \,\langle \beta \rangle } \cap b_a \in [\kappa ]^{<\kappa }\). Now we choose \(b_a^1 \in [b_a]^\kappa \) and \(\varrho ^*_a\) such that and \({{\,\mathrm{dom}\,}}(\varrho ^*_a) \ge n_{{\bar{m}},\eta _a}> {{\,\mathrm{dom}\,}}(\eta _a)\).
, \(\Lambda _a\) has a \(\triangleleft \)-maximal member \(\eta _a\). Now we take \(\alpha _*= \min \{\beta \, : \,\eta _a \,\hat{} \,\langle \beta \rangle \not \in T_{{\bar{m}}}\}\). For any \(\eta _a \,\hat{} \,\langle \beta \rangle \in T_{{\bar{m}}}\) we have \(\varrho _{\eta _a \,\hat{} \,\langle \beta \rangle } \) and \(\varrho _a\) are incompatible, and hence \(a_{\eta _a \,\hat{} \,\langle \beta \rangle } \cap b_a \in [\kappa ]^{<\kappa }\). Now we choose \(b_a^1 \in [b_a]^\kappa \) and \(\varrho ^*_a\) such that and \({{\,\mathrm{dom}\,}}(\varrho ^*_a) \ge n_{{\bar{m}},\eta _a}> {{\,\mathrm{dom}\,}}(\eta _a)\).We let
$$\begin{aligned} T_{{\bar{m}}'}= & {} T_{{\bar{m}}} \cup \{\eta _a \,\hat{} \,\langle \alpha _*\rangle \},\\ a_{\eta _a \,\hat{} \,\langle \alpha _*\rangle }= & {} b^1_a, \end{aligned}$$We let \(n_{\eta _a \,\hat{} \,\langle \alpha _*\rangle }\) be the minimal n such that \(|\mathrm{Pos}(b_a^1,n)| \ge 2^\kappa \). So \((*)_5\) holds.
Now we are ready to construct \({\mathcal {T}}\) as in the statement of the lemma. We do this by recursion on \(\alpha \le 2^{\kappa }\). First we enumerate \([\kappa ]^\kappa \) as \(\langle c_\alpha \, : \,\alpha < 2^\kappa \rangle \), and we enumerate \({}^{\omega >} (2^\kappa )\) as \(\langle \eta _\alpha \, : \,\alpha < 2^\kappa \rangle \) such that \(\eta _\alpha \triangleleft \eta _\beta \) implies \(\alpha < \beta \). We choose an increasing sequence \({\bar{m}}_\alpha \) by induction on \(\alpha <2^\kappa \). We start with the tree \(\{\langle \rangle \}\), \(a_{\langle \rangle }= \kappa \), \(\varrho _{\langle \rangle } = \emptyset \), \(n_{\langle \rangle }\) be minimal such that \(|\mathrm{Pos}(\kappa ,n)| = 2^\kappa \). In the odd successor steps we take \({\bar{m}}_{2\alpha +1} \ge _{AP} {\bar{m}}_\alpha \) so that \(a_\eta \subseteq c_\alpha \) for some \(\eta \in T_{2\alpha +1}\). This is done according to \((*)_5\). In the even successor steps we take \({\bar{m}}_{2\alpha +2} \ge _{AP} {\bar{m}}_{2\alpha +1}\) such that \(\eta _\alpha \in T_{2\alpha +2}\). Since all initial segments of \(\eta _\alpha \) appeared among the \(\eta _\beta \), \(\beta < \alpha \), \({\bar{m}}_{2\alpha +2}\) is found according to \((*)_4\). In the limit steps we take unions. Then \({{\mathcal {T}}}\) that is given by the last three components of \({\bar{m}}_{2^\kappa }\) has properties (a) to (e). \(\square \)
Since  is not in \(\mathbf {V}\), for any \({\mathcal {T}}\) as in Lemma 2.5, for any \(f \in {}^\omega (2^\kappa ) \cap {\mathbf {V}}\), the branch \(\langle (a_{f\restriction m},n_{f\restriction m}, \varrho _{f \restriction m}) \, : \,m \in \omega \rangle \) of \({\mathcal {T}}\) has a no \(\subseteq ^*_\kappa \)-lower bound for its first coordinate.
is not in \(\mathbf {V}\), for any \({\mathcal {T}}\) as in Lemma 2.5, for any \(f \in {}^\omega (2^\kappa ) \cap {\mathbf {V}}\), the branch \(\langle (a_{f\restriction m},n_{f\restriction m}, \varrho _{f \restriction m}) \, : \,m \in \omega \rangle \) of \({\mathcal {T}}\) has a no \(\subseteq ^*_\kappa \)-lower bound for its first coordinate.
3 Transfer to \({\mathbb {Q}}^2_\kappa \)
In this section we use the tree \({\mathcal {T}}\) from Lemma 2.5 for finding \({\mathbb {Q}}^2_\kappa \)-names. First we establish a dense subforcing \(Q_{{\mathcal {T}}}\) of \({\mathbb {Q}}^2_\kappa \). Then we construct \(Q_{{\mathcal {T}}}\)-names that are based on a \({\mathbb {Q}}^1_\kappa \)-name of a collapse and on the equation \(2^{2^{<\kappa }} = 2^\kappa \).
Definition 3.1
Let \(\mu , \lambda \) be cardinals. For \(\nu , \nu ' \in {}^{\lambda >}\mu \) we write \(\nu \perp \nu '\) if \(\nu \not \trianglelefteq \nu '\) and \(\nu ' \not \trianglelefteq \nu \).
Typical pairs \((\lambda , \mu )\) are \((\omega , 2^\kappa )\) and \((\kappa ,\kappa )\).
An important tool for the analysis of \({\mathbb {Q}}^2_\kappa \) is the following particular kind of fusion sequence \(\langle p_\alpha \, : \,\alpha< \kappa ^{<\kappa } \rangle \) in \({\mathbb {Q}}^2_\kappa \). Since we do not suppose \(\kappa ^{<\kappa } = \kappa \), a fusion sequence can be longer than \(\kappa \). An important property is that for each \(\nu \in {}^{\kappa >}\kappa \) there is at most one \(\alpha< \kappa ^{<\kappa }\) such that \({{\,\mathrm{set}\,}}_{p_\alpha }(\nu ) \supsetneq {{\,\mathrm{set}\,}}_{p_{\alpha +1}}(\nu )\).
Lemma 3.2
Let \(\langle \nu _\alpha \, : \,\alpha< \kappa ^{<\kappa } \rangle \) be an injective enumeration of \(\kappa ^{<\kappa }\) such that
Let \(\langle p_\alpha , \nu _\alpha , c_\alpha \, : \,\alpha< \kappa ^{<\kappa } \rangle \) be a sequence such that for any \(\alpha \le \lambda \) the following holds:
-
(a)
\(p _0 \in {\mathbb {Q}}^2_\kappa \).
-
(b1)
If \(\alpha = \beta +1< \kappa ^{<\kappa }\) and \(\nu _\beta \in {{\,\mathrm{spl}\,}}(p_\beta )\), then
$$\begin{aligned} \begin{aligned}&c_\beta \in [{{\,\mathrm{suc}\,}}_{p_\beta }(\nu _\beta )]^\kappa \text{ and } \\&p_{\alpha }= p_\beta (\nu _\beta , c_\beta ) := \bigcup \{p_\beta ^{\langle \nu _\beta \,\hat{} \,\langle i \rangle \rangle } \, : \,i \in c_\beta \} \cup \bigcup \{p_\beta ^{\langle \eta \rangle } \, : \,\eta \not \trianglelefteq \nu _\beta \wedge \nu _\beta \not \trianglelefteq \eta \} \end{aligned} \end{aligned}$$ -
(b2)
If \(\alpha = \beta +1< \kappa ^{<\kappa }\) and \(\nu _\beta \not \in {{\,\mathrm{spl}\,}}(p_\beta )\) then \(p_\alpha = p_\beta \).
-
(c)
\(p_\alpha = \bigcap \{p_\beta \, : \,\beta <\alpha \}\) for limit \(\alpha \le \kappa ^{<\kappa }\).
Then for any \(\lambda \le \kappa ^{<\kappa }\), \(p_\lambda \in {\mathbb {Q}}^2_\kappa \) and \(\forall \beta < \lambda \), \(p_\lambda \le _{{\mathbb {Q}}^2_\kappa } p_\beta \).
Proof
We go by induction on \(\lambda \). The case \(\lambda =0\) and the successor steps are obvious. So we assume that \(\lambda \le \kappa ^{<\kappa }\) is a limit ordinal and \(p_\alpha \in {\mathbb {Q}}^2_\kappa \) for \(\alpha < \lambda \). Since \(\emptyset \in p_\lambda \), \(p_\lambda \) is not empty, and \(p_\lambda \) clearly is a tree. Let \(t \in p_\lambda \). We show that there is \(t' \trianglerighteq t\) that is a splitting node in \(p_\lambda \).
We fix the smallest \(\alpha \) such that \(\nu _\alpha \trianglerighteq _{p_0} t\) is a splitting node in \(p_0\). Then in \(p_0\) there are no splitting nodes in \(\{s \, : \,t \trianglelefteq s \triangleleft \nu _\alpha \}\). Hence \(\nu _\alpha \in {{\,\mathrm{spl}\,}}(p_{\beta })\) for any \(\beta \in [0,\lambda ]\).
Now we show that the limit of splitting nodes in \(p_\lambda \) is a splitting node. Let \(\gamma < \lambda \) and let \(\langle \nu ^{i} \, : \,i < \gamma \rangle \) be an \(\triangleleft \)-increasing sequence of splitting nodes of \(p_\lambda \) with union \(\nu \in \kappa ^{<\kappa }\). Then \(\nu \) is a splitting node of each \(p_\alpha \), \(\alpha < \lambda \), and also in \(p_\lambda \) since \(\langle {{\,\mathrm{set}\,}}_{p_\alpha }(\nu ) \, : \,\alpha < \lambda \rangle \) has at most two entries and their intersection has size \(\kappa \). \(\square \)
We use yet another, richer type of fusion sequence.
Definition 3.3
Let \(p \in {\mathbb {Q}}^2_\kappa \) and let \(\nu \in {{\,\mathrm{spl}\,}}(p)\).
-
(1)
We say \(\eta \) is the shortest splitting node above \(\nu \) in p and write \(\eta = {{\,\mathrm{sucspl}\,}}_p(\nu )\) if \(\eta \) is the shortest splitting node in p such that \(\eta \supseteq \nu \). Equality is allowed and occurs if \(\nu \) is a splitting node.
-
(2)
We say \(F \subseteq p\) is the front of next splitting nodes above \(\nu \) in p, if
$$\begin{aligned} F = \{ \eta ' \in {{\,\mathrm{spl}\,}}(p) \, : \,\exists (\eta \in {{\,\mathrm{suc}\,}}_p(\nu ))(\eta ' = {{\,\mathrm{sucspl}\,}}_p(\eta ))\}. \end{aligned}$$
Lemma 3.4
Let \(\langle \nu _\alpha \, : \,\alpha< \kappa ^{<\kappa } \rangle \) be an injective enumeration of \(\kappa ^{<\kappa }\) such that
Let \(\langle p_\alpha , \nu _\alpha , c_\alpha , F_{\alpha } \, : \,\alpha< \kappa ^{<\kappa } \rangle \) be a sequence such that for any \(\alpha \le \lambda \) the following holds:
-
(a)
\(p _0 \in {\mathbb {Q}}^2_\kappa \).
-
(b1)
If \(\alpha = \beta +1< \kappa ^{<\kappa }\) and \(\nu _\beta \in sp(p_\beta )\), then \(c_\beta \in [{{\,\mathrm{suc}\,}}_{p_\beta }(\nu _\beta )]^\kappa \), \(F_{\beta }\) contains for each \(i \in c_\beta \) exactly one \(\eta \in {{\,\mathrm{spl}\,}}(p_\beta ^{\langle \nu _\beta \,\hat{} \,\langle i \rangle \rangle })\), and
$$\begin{aligned} \begin{aligned} p_{\alpha }= p_\beta (\nu _\beta , c_\beta , F_{\beta }) :=&\bigcup \{p_\beta ^{\langle \eta \rangle } \, : \,i \in c_\beta , \eta \in F_{\beta } \}\\&\cup \bigcup \{p_\beta ^{\langle \eta \rangle } \, : \,\eta \not \trianglelefteq \nu _\beta \wedge \nu _\beta \not \trianglelefteq \eta \}. \end{aligned} \end{aligned}$$Note that this implies that \(F_\beta \) is the front of next splitting nodes of \(p_\alpha \) above \(\nu _\beta \).
-
(b2)
If \(\alpha = \beta +1< \kappa ^{<\kappa }\) and \(\nu _\beta \not \in {{\,\mathrm{spl}\,}}(p_\beta )\) then \(p_\alpha = p_\beta \).
-
(c)
\(p_\alpha = \bigcap \{p_\beta \, : \,\beta <\alpha \}\) for limit \(\alpha \le \kappa ^{<\kappa }\).
Then for any \(\lambda \le \kappa ^{<\kappa }\), \(p_\lambda \in {\mathbb {Q}}^2_\kappa \) and \(\forall \beta < \lambda \), \(p_\lambda \le _{{\mathbb {Q}}^2_\kappa } p_\beta \).
Proof
We go by induction on \(\lambda \). The case \(\lambda =0\) and the successor steps are obvious. So we assume that \(\lambda \le \kappa ^{<\kappa }\) is a limit ordinal and \(p_\alpha \in {\mathbb {Q}}^2_\kappa \) for \(\alpha < \lambda \). Since \(\emptyset \in p_\lambda \), \(p_\lambda \) is not empty, and \(p_\lambda \) clearly is a tree. Let \(t \in p_\lambda \). We show that there is \(t' \trianglerighteq t\) that is a splitting node in \(p_\lambda \).
We fix the smallest \(\alpha \) such that \(\nu _\alpha \trianglerighteq _{p_0} t\) is a splitting node in \(p_0\). Then in \(p_0\) there are no splitting nodes in \(\{s \, : \,t \trianglelefteq s \triangleleft \nu _\alpha \}\). Hence \(\nu _\alpha \in {{\,\mathrm{spl}\,}}(p_{\beta })\) for any \(\beta \in [0,\lambda ]\).
Now we show that the limit of splitting nodes in \(p_\lambda \) is a splitting node. Let \(\gamma < \lambda \) and let \(\langle \nu ^{i} \, : \,i < \gamma \rangle \) be an \(\triangleleft \)-increasing sequence of splitting nodes of \(p_\lambda \) with union \(\nu \in \kappa ^{<\kappa }\). Then \(\nu \) is a splitting node of each \(p_\alpha \), \(\alpha < \lambda \), and also in \(p_\lambda \) since \(\langle {{\,\mathrm{set}\,}}_{p_\alpha }(\nu ) \, : \,\alpha < \lambda \rangle \) has at most two entries and their intersection has size \(\kappa \). \(\square \)
In the special case \(F_\beta = \{\nu _\beta \,\hat{} \,\langle j \rangle \, : \,j \in c_\beta \}\), the construction of Lemma 3.4 coincides with the simpler construction from Lemma 3.2.
Definition 3.5
We assume \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\omega \). Let  and \({{\mathcal {T}}} = \langle (a_\eta ,n_\eta ,\varrho ) \, : \,\eta \in {}^{\omega >}(2^\kappa )\rangle \) be as in Lemma 2.5. Now let \(Q_{{\mathcal {T}}}\) be the set of \(\kappa \)-Miller trees p such that for every \(\nu \in {{\,\mathrm{spl}\,}}(p)\) there is \(\eta _{p,\nu } = \eta _\nu \in {}^{\omega >} (2^\kappa )\) such that
and \({{\mathcal {T}}} = \langle (a_\eta ,n_\eta ,\varrho ) \, : \,\eta \in {}^{\omega >}(2^\kappa )\rangle \) be as in Lemma 2.5. Now let \(Q_{{\mathcal {T}}}\) be the set of \(\kappa \)-Miller trees p such that for every \(\nu \in {{\,\mathrm{spl}\,}}(p)\) there is \(\eta _{p,\nu } = \eta _\nu \in {}^{\omega >} (2^\kappa )\) such that
By the properties of \({\mathcal {T}}\), the node \(\eta _{p,\nu }\) is unique.
Lemma 3.6
Assume that \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\omega \), let \({\mathcal {T}}\) be chosen as in Lemma 2.5, and let \(Q_{{\mathcal {T}}}\) be defined from \({\mathcal {T}}\) as above. Then \(Q_{{\mathcal {T}}}\) is dense in \({\mathbb {Q}}^2_\kappa \).
Proof
Let \(p_0 = T \in {\mathbb {Q}}^2_\kappa \). Let \(\langle \nu _\alpha \, : \,\alpha<\kappa ^{<\kappa } \rangle \) be an injective enumeration of \(\kappa ^{<\kappa }\) with property (3.1). We now define fusion sequence \(\langle p_\alpha ,\nu _\alpha , c_\alpha \, : \,\alpha \le \kappa ^\kappa \rangle \) according to the pattern in Lemma 3.2 in order to find \(p_{\kappa ^{<\kappa }} \ge T\) such that \(p_{\kappa ^{<\kappa }} \in Q_{{\mathcal {T}}}\).
Suppose that \(p_\alpha \) and \(\nu _\alpha \) are given. If \(\nu _\alpha \) is not in \(p_\alpha \) or is not a splitting node in \(p_\alpha \), then we let \(p_{\alpha +1} = p_\alpha \). If \(\nu _\alpha \in {{\,\mathrm{spl}\,}}(p_\alpha )\), then according to Lemma 2.5 clause (d) there is \(\eta \in {}^{\omega >} (2^\kappa )\) such that \({{\,\mathrm{suc}\,}}_{p_\alpha }(\nu _\alpha ) \supseteq a_\eta \). We choose such an \(\eta \) of minimal length and call it \(\eta (\alpha )\).
Then we strengthen \(p_\alpha \) to
Now we have that
For limit ordinals \(\lambda \le \kappa ^{<\kappa }\), we let \(p_\lambda = \bigcap \{p_\beta \, : \,\beta < \lambda \}\). Since the sequence \(\langle p_\alpha , \nu _\alpha , c_\alpha \, : \,\alpha \le \kappa ^{<\kappa } \rangle \) matches the pattern in Lemma 3.2, we have \(p_{\kappa ^{<\kappa }} \in {\mathbb {Q}}^2_\kappa \). By construction, for any \(\alpha< \kappa ^{<\kappa }\) for any \(\delta \in [\alpha +1,\kappa ^{<\kappa })\), \(\nu _\alpha \in {{\,\mathrm{spl}\,}}(p_\delta )\) implies
Hence the condition \(p=p_{\kappa ^{<\kappa }}\) fulfils Equation (3.3) in its splitting node \(\nu _\alpha \) with witness \(\eta _{p,\nu _\alpha }= \eta (\alpha )\). Since all nodes are enumerated, we have \(p_{\kappa ^{<\kappa }} \in Q_{{\mathcal {T}}}\). \(\square \)
We use only the inclusion \({{\,\mathrm{set}\,}}_p(\nu ) \subseteq a_{\eta _\nu }\) from Definition 3.5.
Definition 3.7
We assume that \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\omega \) and the \({{\mathcal {T}}}\) is as in Lemma 2.5. For \(T \in Q_{{\mathcal {T}}}\) and a splitting node \(\nu \) of T we set \(\varrho _{T,\nu } := \varrho _{\eta _{T,\nu }} \in {}^{\omega >} (2^\kappa )\). Recall \(\eta _{T,\nu }\) is defined in Def. 3.5, and \(\varrho \) is a component of \({{\mathcal {T}}}\).
For \(p \in Q_{{\mathcal {T}}}\), the relation \(\nu \trianglelefteq \nu ' \in p\) does neither imply \(\eta _{\nu } \trianglelefteq \eta _{\nu '}\) nor \(\varrho _\nu \trianglelefteq \varrho _{\nu '}\). However, \(\eta _\nu \triangleleft \eta _{\nu '}\) implies \(a_{\eta _\nu } \supset a_{\eta _{\nu '}}\) and \( \varrho _\nu \triangleleft \varrho _{\nu '}\).
Observation 3.8
We assume that \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\omega \). Let \(p_1, p_2 \in Q_{{\mathcal {T}}}\). If \(p_1 \le _{{\mathbb {Q}}^2_\kappa } p_2\) then for \(\nu \in {{\,\mathrm{spl}\,}}(p_2)\) we have \(\nu \in {{\,\mathrm{spl}\,}}(p_1)\) and \(\varrho _{p_1,\nu } \trianglelefteq \varrho _{p_2,\nu }\).
We introduce dense sets:
Definition 3.9
We assume that \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\omega \). Let \(n \in \omega \).
\(D_n\) is open dense in \(Q_{{\mathcal {T}}}\) and the intersection of the \(D_n\) is empty.
Recall, by Lemma 3.6 we can work with the dense subforcing \(Q_{{\mathcal {T}}}\) of \({\mathbb {Q}}^2_\kappa \). The following technical lemma is the next step of a transformation of a \({\mathbb {Q}}^1_\kappa \)-name of a surjection from \(\omega \) onto \(2^\kappa \) into a \(Q_{{\mathcal {T}}}\)-name of such a surjection. The coordinate \({\bar{\gamma }}_\alpha \) and the clauses (d), (e), (f) are used for a counting argument in the induction steps. Later, only the coordinates \(p_\alpha \), \(n_\alpha \), and clauses (a), (b), (c) and Remark 3.11 will be used.
Lemma 3.10
We assume that \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\omega \), \({{\,\mathrm{cf}\,}}(\kappa ) > \omega \) and \(2^{(\kappa ^{<\kappa })} = 2^\kappa \). Let \(\langle T_{\alpha } \, : \,\alpha < 2^\kappa \rangle \) enumerate \({\mathbb {Q}}^2_\kappa \) such that each Miller tree appears \(2^\kappa \) times. There is \(\langle (p_\alpha , n_\alpha , {\bar{\gamma }}_\alpha ) \, : \,\alpha < 2^\kappa \rangle \) such that
-
(a)
\(n_\alpha < \omega \),
-
(b)
\(p_\alpha \in D_{n_\alpha } \subseteq Q_{{\mathcal {T}}}\) and \(p_\alpha \ge T_\alpha \).
-
(c)
If \(\beta < \alpha \) and \(n_\beta \ge n_\alpha \) then \(p_\beta \perp p_\alpha \).
-
(d)
\({\bar{\gamma }}_\alpha = \langle \gamma _{\alpha ,\nu } \, : \,\nu \in {{\,\mathrm{spl}\,}}(p_\alpha )\rangle \).
-
(e)
\((\forall \nu \in {{\,\mathrm{spl}\,}}(p_\alpha )) (a_{\eta _{p_\alpha ,\nu }} \Vdash _{{\mathbb {Q}}^1_\kappa } \gamma _{\alpha ,\nu } \in {{\,\mathrm{range}\,}}(\varrho _{p_\alpha ,\nu }))\).
-
(f)
\(\gamma _{\alpha ,\nu } \in 2^\kappa \setminus W_{<\alpha ,\nu }\) with
$$\begin{aligned} W_{<\alpha ,\nu } = \bigcup \{{{\,\mathrm{range}\,}}(\varrho _{p_\beta ,\nu }) \, : \,\beta < \alpha , \nu \in {{\,\mathrm{spl}\,}}(p_\beta )\}. \end{aligned}$$
Proof
Assume that \(\langle (p_\beta , n_\beta , {\bar{\gamma }}_\beta ) \, : \,\beta < \alpha \rangle \) has been defined and we are to define \((p_\alpha ,n_\alpha , {\bar{\gamma }}_\alpha )\). Note that the \(p_\beta \) need not be increasing in strength.
- \((\oplus )_1\):
-
The choice of the \(a_\eta \) in Lemma 2.5 and the choice \(Q_{{\mathcal {T}}}\) and of \(\eta _{p_\beta ,\nu }\) for \(\nu \in {{\,\mathrm{spl}\,}}(p_\beta )\), \(\beta < \alpha \), imply that the set \(W_{<\alpha ,\nu }\) is well defined and of cardinality \(\le |\alpha | + \aleph _0 < 2^\kappa \). Hence we can choose \(\gamma _{\alpha ,\nu } \in 2^\kappa \setminus W_{<\alpha ,\nu }\).
- \((\oplus )_2\):
-
With the fusion Lemma 3.2 we choose \(q_\alpha \ge T_\alpha \), \(q_\alpha \in Q_{{\mathcal {T}}}\), such that
$$\begin{aligned} (\forall \nu \in {{\,\mathrm{spl}\,}}(q_\alpha ))(a_{\eta _{q_\alpha ,\nu }} \Vdash _{{\mathbb {Q}}^1_\kappa } \gamma _{\alpha ,\nu } \in {{\,\mathrm{range}\,}}(\varrho _{q_\alpha ,\nu })). \end{aligned}$$ - \((\oplus )_3\):
-
Let \(q \in {\mathbb {Q}}^2_\kappa \). For \(n \in \omega \) and \(\nu \in {{\,\mathrm{spl}\,}}(q)\) we let
$$\begin{aligned} {\mathcal {U}}_{\alpha ,\nu ,n}(q) = \{ \beta < \alpha \, : \,n_\beta = n , \nu \in {{\,\mathrm{spl}\,}}(p_\beta ) \wedge |{{\,\mathrm{set}\,}}_{q}(\nu ) \cap {{\,\mathrm{set}\,}}_{p_\beta }(\nu ) | = \kappa \}. \\ {\mathcal {U}}_{\alpha , \nu }(q) = \bigcup \{{\mathcal {U}}_{\alpha ,\nu ,n}(q) \, : \,n \in \omega \}. \end{aligned}$$ - \((\oplus )_4\):
-
(a) If \(n \in \omega \) and \( \nu \in {{\,\mathrm{spl}\,}}(q_\alpha )\) then
$$\begin{aligned} \beta \in {\mathcal {U}}_{\alpha ,\nu }(q_\alpha ) \rightarrow \varrho _{p_\beta ,\nu } \trianglelefteq \varrho _{q_\alpha ,\nu }. \end{aligned}$$This is seen as follows. We let \(a= {{\,\mathrm{set}\,}}_{p_\beta }(\nu ) \cap {{\,\mathrm{set}\,}}_{q_\alpha }(\nu )\). Since \(\beta \in {\mathcal {U}}_{\alpha ,\nu }(q_\alpha )\), \(a \in [\kappa ]^\kappa \). Clearly
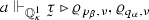 . So either \(\varrho _{p_\beta ,\nu } \triangleleft \varrho _{q_\alpha ,\nu }\) or \(\varrho _{p_\beta ,\nu } \trianglerighteq \varrho _{q_\alpha ,\nu }\). However, since \(\gamma _{\alpha ,\nu } \in {{\,\mathrm{range}\,}}(\varrho _{q_\alpha ,\nu }) \setminus W_{<\alpha ,\nu }\), only \(\varrho _{q_\alpha ,\nu } \triangleright \varrho _{p_\beta ,\nu }\) is possible.
. So either \(\varrho _{p_\beta ,\nu } \triangleleft \varrho _{q_\alpha ,\nu }\) or \(\varrho _{p_\beta ,\nu } \trianglerighteq \varrho _{q_\alpha ,\nu }\). However, since \(\gamma _{\alpha ,\nu } \in {{\,\mathrm{range}\,}}(\varrho _{q_\alpha ,\nu }) \setminus W_{<\alpha ,\nu }\), only \(\varrho _{q_\alpha ,\nu } \triangleright \varrho _{p_\beta ,\nu }\) is possible.(b) So for \(\nu \in {{\,\mathrm{spl}\,}}(q_\alpha )\), the set \(\{ \varrho _{p_\beta ,\nu } \, : \,\beta \in {\mathcal {U}}_{\alpha ,\nu }(q_\alpha )\}\) has at most \({{\,\mathrm{dom}\,}}(\varrho _{q_\alpha ,\nu })\) elements.
(c) The assigment \(\beta \mapsto \varrho _{p_\beta ,\nu }\) is is defined between \({\mathcal {U}}_{\alpha ,\nu }(q_\alpha )\) and \(\{ \varrho _{p_\beta ,\nu } \, : \,\beta \in {\mathcal {U}}_{\alpha ,\nu }(q_\alpha )\}\). According to properties (e) and (f) in the induction hypothesis, the assigment is injective, and hence
\(|{\mathcal {U}}_{\alpha ,\nu }(q_\alpha ) |\le {{\,\mathrm{dom}\,}}(\varrho _{q_\alpha ,\nu })\).
(d) We state for further use that \({\mathcal {U}}_{\alpha ,\nu }(q_\alpha )\) is finite and for any \(q \le q_\alpha \), \({\mathcal {U}}_{\alpha ,\nu }(q) \subseteq {\mathcal {U}}_{\alpha ,\nu }(q_\alpha )\).
- \((\oplus )_5\):
-
We look at the cone above \(q_\alpha \) and show:
$$\begin{aligned} \begin{aligned}&(\forall q \ge q_\alpha )(\forall \nu \in {{\,\mathrm{spl}\,}}(q)) (\exists r_{\alpha ,\nu }\le _{{\mathbb {Q}}^2_\kappa } q)\\&(\exists c \in [{{\,\mathrm{set}\,}}_q(\nu )]^\kappa )(\exists F \subseteq \{\eta \in {{\,\mathrm{spl}\,}}(q) \, : \,\eta \triangleright \nu \})\\&\bigl (r_{\alpha ,\nu } = q(\nu ,c,F) \wedge (\forall \beta \in {\mathcal {U}}_{\alpha ,\nu }(q_\alpha )) (r^{\langle \nu \rangle }_{\alpha ,\nu } \perp p_\beta ^{\langle \nu \rangle } \vee p_\beta ^{\langle \nu \rangle } \ge r^{\langle \nu \rangle }_{\alpha ,\nu })\bigr ). \end{aligned} \end{aligned}$$(3.5)
How do we find \(r_{\alpha ,\nu }= r_{\alpha ,\nu }(q)\)? Given \(q \le _{{\mathbb {Q}}^2_\kappa } q_\alpha \), \(\nu \in {{\,\mathrm{spl}\,}}(q)\) we enumerate \({\mathcal {U}}_{\alpha ,\nu }(q_\alpha )\) as \(\beta _0\), ..., \(\beta _{k-1}\). We let \(r_{0} = q\) and by induction on \(i \le k\) we define \(r_i\), increasing in strength, with \(\nu \in {{\,\mathrm{spl}\,}}(r_i)\) and \(c_i = {{\,\mathrm{set}\,}}_{r_i}(\nu )\). Thus the \(c_i\) are \(\subseteq \)-decreasing sets of size \(\kappa \). Given \(r_i\), we distinguish cases:
First case: \(\beta _i \not \in {\mathcal {U}}_{\alpha ,\nu }(r_i)\). Then there is \(c_{i+1} \in [{{\,\mathrm{set}\,}}_{r_i}(\nu )]^\kappa \), \(c_{i+1} \cap {{\,\mathrm{set}\,}}_{p_{\beta _i}}(\nu ) = \emptyset \). We let \(r_{i+1} = r_i(\nu , c_{i+1})\) and thus have \(r_{i+1}^{\langle \nu \rangle } \perp p_{\beta _i}\).
Second case: \(\beta _i \in {\mathcal {U}}_{\alpha ,\nu }(r_i)\). We let
If \(c_{i,1} = \{j \in {{\,\mathrm{set}\,}}_{r_i}(\nu ) \, : \,r_i^{\langle \nu \,\hat{} \,\langle j \rangle \rangle } \le p_{\beta _i}^{\langle \nu \,\hat{} \,\langle j \rangle \rangle }\} \) has size \(\kappa \), then we let \(c_{i+1} = c_{1,i}\) and \(r_{i+1} = r_i(\nu ,c_{i+1})\) and thus get \(r_{i+1}^{\langle \nu \rangle } \ge p_{\beta _i}\).
If \(|c_{i,1}|< \kappa \), then \(c_{i,2} = \{j \in {{\,\mathrm{set}\,}}_{r_i}(\nu ) \, : \,r_i^{\langle \nu \,\hat{} \,\langle j \rangle \rangle } \not \le p_{\beta _i}^{\langle \nu \,\hat{} \,\langle j \rangle \rangle }\} \) has size \(\kappa \), and we let \(c_{i+1} = c_{i,2}\). For \(j \in c_{i+1}\), \(r_i^{\langle \nu \,\hat{} \,\langle j \rangle \rangle } \not \le p_{\beta _i}^{\langle \nu \,\hat{} \,\langle j\rangle \rangle }\). Thus we can find a node in the \(r_i^{\langle \nu \,\hat{} \,\langle j \rangle \rangle }\setminus p_{\beta _i}^{\langle \nu \,\hat{} \,\langle j\rangle \rangle }\) and above this node we find a splitting node of \(r_i\). We take this latter splitting node into \(r_{i+1}\) as the direct successor splitting node to \(\nu \,\hat{} \,\langle j \rangle \). Doing so for every \(j \in c_{i+1}\) we get \(F_{\nu ,i}\), a front strictly above \(\nu \) in \(r_{i+1}= r_i(\nu ,c_{i+1}, F_{\nu ,i})\). Again we get \(r_{i+1}^{\langle \nu \rangle } \perp p_{\beta _i}\).
In the end we let \(r_{\alpha ,\nu } = r_k\). There is a front F that contains for each \(j \in c_k\) the shortest splitting node of \(r_k\) above \(\nu \,\hat{} \,\langle j \rangle \). Thus we have \(r_k = r_{\alpha ,\nu }= q(\nu ,c_k, F)\) and \(r_{\alpha ,\nu }\) fulfils (3.5).
- \((\oplus )_6\):
-
Now we use \((\oplus )_5\) iteratively along all \(\nu \in \kappa ^{<\kappa } \) to find a fusion sequence \(\langle r_{\alpha ,\nu },\nu ,c_\nu , F_{\nu } \, : \,\nu< \kappa ^{<\kappa }\rangle \) with starting point \(q_\alpha = r_{0,\nu _0}\). In this sequence, \(r_{\alpha , \nu } \) is chosen as \(r_{\alpha ,\nu }(q)\) in \(\oplus _5\) for \(q = \bigcap _{\beta < \alpha } r_\beta \), if \(\nu \in {{\,\mathrm{spl}\,}}(q)\). If \(\nu \not \in {{\,\mathrm{spl}\,}}(q)\), then \(r_{\alpha ,\nu } = q\). Then we apply the fusion Lemma 3.4 and get an lower bound \(r_\alpha \) of \(r_{\alpha ,\nu }\), \(\nu \in {}^{\kappa >}\kappa \). Note \(r_\alpha ^{\langle \nu \rangle } \perp p_\beta \) iff \(r_\alpha ^{\langle \nu \rangle } \perp p_\beta ^{\langle \nu \rangle }\) and \(r_\alpha ^{\langle \nu \rangle } \le p_\beta \) iff \(r_\alpha ^{\langle \nu \rangle } \le p_\beta ^{\langle \nu \rangle }\). Hence \(r_\alpha \ge q_\alpha \) and
$$\begin{aligned} (\forall \nu \in {{\,\mathrm{spl}\,}}(r_\alpha ))( \forall \beta \in {\mathcal {U}}_{\alpha ,\nu }(q_\alpha )) (r_\alpha ^{\langle \nu \rangle } \perp p_\beta \vee p_\beta \ge r_\alpha ^{\langle \nu \rangle }). \end{aligned}$$ - \((\oplus )_7\):
-
Finally we choose \(n_\alpha \) and \(p_\alpha \). There are k and \(\nu \) such that \(n < \omega \) and \( \nu \in {{\,\mathrm{spl}\,}}(r_\alpha )\) such that \(p_\alpha = r_\alpha ^{\langle \nu \rangle }\) fulfils
$$\begin{aligned} (\forall \beta < \alpha )( n_\beta \ge k \rightarrow p_\alpha \perp p_\beta ). \end{aligned}$$Proof of existence. By induction on \(k \in \omega \) we try to find \(\langle \nu _k, \beta _k \, : \,k \in \omega \rangle \) such that
(a) \(\nu _k \in {{\,\mathrm{spl}\,}}(r_\alpha )\),
(b) \(\nu _k \triangleleft \nu _m\) for \(k <m\),
(c) \(\beta _k < \alpha \) and \(n_{\beta _k} \ge k\) and \(r_\alpha ^{\langle \nu _k \rangle } \le p_{\beta _k}\).
If we succeed, then \(\nu _*=\bigcup \{\nu _k \, : \,k \in \omega \} = \nu ^* \in {{\,\mathrm{spl}\,}}(r_\alpha )\) by Definition 1.1 (2). Here we use that \({{\,\mathrm{cf}\,}}(\kappa ) > \omega \). Hence
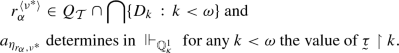
This is a contradiction.
So there is a smallest k such that \(\nu _k\) cannot be defined. We let \(n_\alpha = k\). We let \(p_\alpha \) be a strengthening of \(r_\alpha ^{\langle \nu _{k-1} \rangle }\) such that \(p_\alpha \in D_{n_\alpha }\). For finding such a strengthening we again invoke the fusion Lemma 3.2.
We show that \(p_\alpha \perp p_\beta \) for \(\beta < \alpha \) with \(n_\beta \ge k\). Otherwise, having arrived at \(r_\alpha ^{\langle \nu _{k-1}\rangle }\) we find some \(\beta _k , \alpha \) such that \(n_{\beta _k} \ge k\) and \(r_\alpha ^{\langle \nu _{k-1}\rangle } \) is compatible with \(p_{\beta _k}\). Then we can prolong \(\nu _{k-1}\) to a splitting node \(\nu _k \in {{\,\mathrm{spl}\,}}(p_{\beta _k}) \cap {{\,\mathrm{spl}\,}}(r_{\alpha })\). By the choice of \(r_\alpha \) the latter implies that \(r_{\alpha }^{\langle \nu _k \rangle } \le p_{\beta _k}\). However, now we would have found \(\nu _k, \beta _k\) as required in contradiction to the choice of k. \(\square \)
Remark 3.11
Conditions (a) to (c) of Lemma 3.10 yield: For any \(k <\omega \),
Proof
Let k and p be given. There is \(\alpha _0 \) such that \(T_{\alpha _0} \in D_0\) and \(T_{\alpha _0} \le _{{\mathbb {Q}}^2_\kappa } p\). Then \(p_{\alpha _0} \le T_{\alpha _0}\) and \(n_{\alpha _0}\ge 0\). Then there is \(\alpha _1> \alpha _0\) such that \(T_{\alpha _1} \le _{{\mathbb {Q}}^2_\kappa } p_{\alpha _0}\). Then \(p_{\alpha _1} \le T_{\alpha _1}\) and hence by condition (c), \(n_{\alpha _1} >n_{\alpha _0}\ge 0\). We can can repeat the argument \(k-1\) times. \(\square \)
Now we drop the component \({\bar{\gamma }}_\alpha \) from a sequence \(\langle p_\alpha , n_\alpha , {\bar{\gamma }}_\alpha \, : \,\alpha < 2^\kappa \rangle \) given by Lemma 3.10. Then we get a sequence with properties (a), (b), and a weakening (c) with the property stated in the remark. This sequence, combined with \(2^{(2^{<\kappa })} = 2^\kappa \), allows to define a \({\mathbb {Q}}^2_\kappa \)-name of a collapse.
Lemma 3.12
We assume that \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\omega \), \({{\,\mathrm{cf}\,}}(\kappa ) > \omega \) and \(2^{(2^{<\kappa })} = 2^\kappa \). Let \(\langle T_{\alpha } \, : \,\alpha < 2^\kappa \rangle \) enumerate all Miller trees that such each tree appears \(2^\kappa \) times. Assume that \(\langle (p_\alpha , n_\alpha ) \, : \,\alpha < 2^\kappa \rangle \) are such that
-
(a)
\(n_\alpha < \omega \),
-
(b)
\(p_\alpha \in D_{n_\alpha }\subseteq Q_{{\mathcal {T}}}\) and \(p_\alpha \ge T_\alpha \),
-
(c)
if \(\beta < \alpha \) and \(n_\beta = n_\alpha \) then \(p_\beta \perp p_\alpha \),
-
(d)
for any \(k \in \omega \), \(\{p_\alpha \, : \,n_\alpha \ge k\} \) is dense in \({\mathbb {Q}}^2_\kappa \).
Then there is a \({\mathbb {Q}}^2_\kappa \)-name  for a surjection of \(\omega \) onto \(2^\kappa \).
for a surjection of \(\omega \) onto \(2^\kappa \).
Proof
Let G be a \({\mathbb {Q}}^2_\kappa \)-generic filter over \({\mathbf {V}}\). We define  , a \({\mathbb {Q}}^2_\kappa \)-name by
, a \({\mathbb {Q}}^2_\kappa \)-name by  if \(p_\alpha \in G\) and \(n_\alpha = n\). The name
if \(p_\alpha \in G\) and \(n_\alpha = n\). The name  is a name of a function by (c). By (d), the domain of
is a name of a function by (c). By (d), the domain of  is forced to be infinite. For any \(p \in {\mathbb {Q}}^2_\kappa \) we let \(U_p = \{ \alpha \, : \,T_\alpha = p\}\). \(U_p\) is of size \(2^\kappa \), in particular for \(\alpha \in 2^\kappa \) we have \(|U_{p_\alpha }|= 2^\kappa \) and \(U_{p_\alpha } \) contains the antichain \(\{p_{\delta (\alpha ,i)} \, : \,i < 2^\kappa \}\). Hence there is \(f :2^\kappa \rightarrow 2^\kappa \) in \(\mathbf {V}[G]\) such that for any \(\gamma , \alpha \in 2^\kappa \) there is \( \beta = \delta (\alpha ,\gamma ) \in U_{p_\alpha }\) for some function \(\delta :2^\kappa \times 2^\kappa \rightarrow 2^\kappa \) with \(f(\beta ) = \gamma \) forced by \(p_{\delta (\alpha ,\gamma )}\). We let
is forced to be infinite. For any \(p \in {\mathbb {Q}}^2_\kappa \) we let \(U_p = \{ \alpha \, : \,T_\alpha = p\}\). \(U_p\) is of size \(2^\kappa \), in particular for \(\alpha \in 2^\kappa \) we have \(|U_{p_\alpha }|= 2^\kappa \) and \(U_{p_\alpha } \) contains the antichain \(\{p_{\delta (\alpha ,i)} \, : \,i < 2^\kappa \}\). Hence there is \(f :2^\kappa \rightarrow 2^\kappa \) in \(\mathbf {V}[G]\) such that for any \(\gamma , \alpha \in 2^\kappa \) there is \( \beta = \delta (\alpha ,\gamma ) \in U_{p_\alpha }\) for some function \(\delta :2^\kappa \times 2^\kappa \rightarrow 2^\kappa \) with \(f(\beta ) = \gamma \) forced by \(p_{\delta (\alpha ,\gamma )}\). We let

Next we show

Suppose \(p \in Q_{{\mathcal {T}}}\) and \(\gamma < 2^\kappa \) are given. By construction the sequence \(\{p_\beta \, : \,\beta < 2^\kappa \}\) is dense. Let \(p \le p_\alpha \). Then there is \(\beta =\delta (\alpha , \gamma ) \in U_{p_\alpha }\) \(p_{\delta (\alpha ,\gamma )} \le p_\gamma \), with \(f(\alpha ) = \gamma \). However, \(\delta (\alpha ,\gamma )=\beta \in U_{p_\alpha }\) means \(T_\beta = p_\alpha \ge p_\beta \) by construction. By the definition of  ,
,  , so
, so  . \(\square \)
. \(\square \)
So we can sum up:
Theorem 3.13
We assume that \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\omega \) and \({{\,\mathrm{cf}\,}}(\kappa ) > \omega \) and \(2^{(\kappa ^{<\kappa })} = 2^\kappa \). Then the forcing with \({\mathbb {Q}}_\kappa ^2\) collapses \(2^\kappa \) to \(\aleph _0\).
4 \(\kappa \)-Cohen reals and the Levy collapse
Many \(\kappa \)-tree forcings add a \(\kappa \)-Cohen real, sometimes even if their \(\omega \)-version does not add a Cohen real. Also our forcing \({\mathbb {Q}}^2_\kappa \) is of this kind. Classical Miller forcing preserves P-points and hence does not add a Cohen real. In this section we show that under the above conditions, \({\mathbb {Q}}^\kappa _2\) add a \(\kappa \)-Cohen real and is equivalent to the Levy collapse of \(2^\kappa \) to \(\aleph _0\).
Lemma 4.1
If \({\mathbb {Q}}^2_\kappa \) collapses \(2^\kappa \) to \(\aleph _0\), \({{\,\mathrm{cf}\,}}(\kappa ) > \aleph _0\), and \(2^{2^{<\kappa }} = 2^\kappa \), then \({\mathbb {Q}}_\kappa ^2\) adds a \(\kappa \)-Cohen real.
Proof
Let G be \({\mathbb {Q}}^2_\kappa \)-generic over \(\mathbf {V}\). Let \(f :\omega \rightarrow 2^{<\kappa }\) be a function in \(\mathbf{V}[G]\), such that \((\forall \eta \in 2^{<\kappa })(\exists ^\infty k f(k) = \eta )\). Such a function exists since \(2^{< \kappa } \le 2^\kappa \).
Since \(2^{2^{<\kappa }} = 2^\kappa \), we can enumerate all antichains in \({\mathbb {C}}(\kappa )\) in \(\alpha _*\le 2^\kappa \) many steps. In \(\mathbf {V}[G]\), \(\alpha _*\) is countable. We list it as \(\langle \alpha _n \, : \,n < \omega \rangle \). Now we choose \(\eta _n \in {\mathbb {C}}(\kappa )^{\mathbf {V}}\) by induction on n in \(\mathbf {V}[G]\): \(\eta _0 = \emptyset \). Given \(\eta _n\) we choose \(k_n\) such that \(f(k_n) = \eta _n\) and then we choose \(\eta _{n+1} \trianglerighteq \eta _n\), such that \(\eta _{n+1} \in I_{\alpha _n}\). Then \(\{\eta \, : \,(\exists n < \omega ) (\eta \trianglelefteq f(k_n))\}\) is a \({\mathbb {C}}(\kappa )\)-generic filter over \(\mathbf {V}\) and it exists in V[G], since it is definable from \(\{f(k_n) \, : \,n < \omega \}\). \(\square \)
Two forcings \({\mathbb {P}}_1\), \({\mathbb {P}}_2\) are said to be equivalent if their regular open algebras \({{\,\mathrm{RO}\,}}({\mathbb {P}}_i)\) coincide (for a definition of the regular open algebra of a poset, see, e.g., [3, Corollary 14.12]). Some forcings are characterised up to equivalence just by their size and their collapsing behaviour.
Lemma 4.2
[3, Lemma 26.7]. Let \((Q, <)\) be a notion of forcing such that \(|Q| = \lambda > \aleph _0\) and such that Q collapses \(\lambda \) onto \(\aleph _0\) , i.e.,
Then \(\mathrm{RO}(Q) = {{\,\mathrm{Levy}\,}}(\aleph _0,\lambda )\).
Lemma 4.3
If \({\mathbb {Q}}_\kappa ^1\) collapses \(2^\kappa \) to \(\aleph _0\), then \({\mathbb {Q}}_\kappa ^1\) is equivalent of \({{\,\mathrm{Levy}\,}}(\aleph _0, 2^\kappa )\).
Proof
\({\mathbb {Q}}^1_\kappa \) has size \(2^\kappa \). Hence Lemma 4.2 yields \(\mathrm{RO}({\mathbb {Q}}^1_\kappa )= \mathrm{Levy}(\aleph _0,2^\kappa )\). \(\square \)
Definition 4.4
A Boolean algebra is \((\theta ,\lambda )\)-nowhere distributive if there are antichains \({\bar{p}}^\varepsilon = \langle p^\varepsilon _\alpha \, : \,\alpha < \alpha _\varepsilon \rangle \) of \({\mathbb {P}}\) for \(\varepsilon < \theta \) such that for every \(p \in {\mathbb {P}}\) for some \(\varepsilon < \theta \)
Definition 4.5
Let B be a Boolean algebra. We write \(B^+ = B \setminus \{0\}\). A subset \(D \subseteq B^+\) is called dense if \((\forall b \in B^+)(\exists d \in D)(d \le b)\). The density of a Boolean algebra B is the least size of a dense subset of B. A Boolean algebra B has uniform density if for every \(a \in B^ +\), \(B \restriction a\) has the same density. The density of a forcing order \(({\mathbb {P}},\le _{{\mathbb {P}}})\) is the density of the regular open algebra \({{\,\mathrm{RO}\,}}({\mathbb {P}})\).
Lemma 4.6
[1, Theorem 1.15] Let \(\theta < \lambda \) be regular cardinals.
-
(1)
Suppose that \({\mathbb {P}}\) has the following properties (a) to (c).
-
(a)
\({\mathbb {P}}\) is a \((\theta ,\lambda )\)-nowhere distributive forcing notion,
-
(b)
\({\mathbb {P}}\) has density \(\lambda \),
-
(c)
in case \(\theta > \aleph _0\), \({\mathbb {P}}\) has a \(\theta \)-complete dense subset S. The latter means: \((\forall B \in [S]^{<\theta })(\exists s\in S)(\forall b \in B)(b \le _{{\mathbb {P}}} s)\).
-
(a)
Then \({\mathbb {P}}\) is equivalent to \({{\,\mathrm{Levy}\,}}(\theta ,\lambda )\).
-
(2)
Under (a) and (b) \({\mathbb {P}}\) collapses \(\lambda \) to \(\theta \) (and may or may not collapse \(\lambda \) to \(\aleph _0\)).
Proposition 4.7
If there is a \(\kappa \)-mad family of size \(2^\kappa \) the forcing \({\mathbb {Q}}^1_\kappa \) is \((\aleph _0,2^\kappa )\)-nowhere distributive.
Proof
Lemma 2.5 gives \({\mathcal {T}}\) such that \({\bar{p}}^n = \{ a_\eta \, : \,\eta \in {}^n (2^\kappa )\}\), \(n \in \omega \), witnesses \((\aleph _0,2^\kappa )\)-nowhere distributivity. \(\square \)
By Lemma 4.2 and Theorem 3.13 we get:
Proposition 4.8
If \({\mathbb {Q}}^1_\kappa \) collapses \(2^\kappa \) to \(\aleph _0\), \({{\,\mathrm{cf}\,}}(\kappa ) > \aleph _0\) and \(2^{(\kappa ^{<\kappa })} = 2^\kappa \) then \({\mathbb {Q}}^2_\kappa \) is equivalent to \(\mathrm{Levy}(\aleph _0,2^\kappa )\).
References
Bohuslav, B., Simon, P.: Disjoint refinement. In: Koppelberg, S., Monk, D. (eds.) Handbook of Boolean Algebras, vol. 2, pp. 333–388. North-Holland, Amsterdam (1989)
Brendle, J., Brooke-Taylor, A., Friedman, S.-D., Montoya, D.C.: Cichoń’s diagram for uncountable cardinals. Isr. J. Math. 225(2), 959–1010 (2018)
Jech, T.: Set Theory. The Third Millenium Edition, Revised and Expanded. Springer, Berlin (2003)
Miller, A.: Rational perfect set forcing. In: Baumgartner, J., Martin, D.A., Shelah, S. (eds.) Axiomatic Set Theory, Volume 31 of Contemporary Mathematics, pp. 143–159. Providence, American Mathematical Society (1984)
Shelah, S.: Power set modulo small, the singular of uncountable cofinality. J. Symb. Log. 72, 226–242 (2007). arxiv:math.LO/0612243
Acknowledgements
Open Access funding provided by Projekt DEAL. We thank Marlene Koelbing for pointing out a gap in an earlier version.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research, No. 1154 on the second author’s list, was partially supported by European Research Council Grant 338821.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mildenberger, H., Shelah, S. A version of \(\kappa \)-Miller forcing. Arch. Math. Logic 59, 879–892 (2020). https://doi.org/10.1007/s00153-020-00721-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00153-020-00721-y


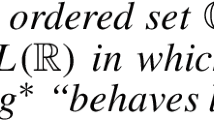

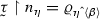 for some
for some 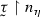 , called
, called 
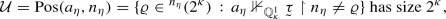
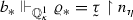 . We let
. We let 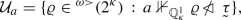
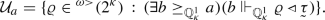
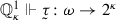 is onto. We take n minimal such that
is onto. We take n minimal such that 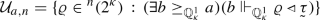
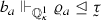 . The set
. The set 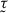 ,
, 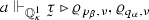 . So either
. So either