Sensitivity of Probabilistic Tsunami Hazard Assessment to Far-Field Earthquake Slip Complexity and Rigidity Depth-Dependence: Case Study of Australia

Abstract

Probabilistic Tsunami Hazard Assessment (PTHA) often proceeds by constructing a suite of hypothetical earthquake scenarios, and modelling their tsunamis and occurrence-rates. Both tsunami and occurrence-rate models are affected by the representation of earthquake slip and rigidity, but the overall importance of these factors for far-field PTHA is unclear. We study the sensitivity of an Australia-wide PTHA to six different far-field earthquake scenario representations, including two rigidity models (constant and depth-varying) combined with three slip models: fixed-area-uniform-slip (with rupture area deterministically related to magnitude); variable-area-uniform-slip; and spatially heterogeneous-slip. Earthquake-tsunami scenarios are tested by comparison with DART-buoy tsunami observations, demonstrating biases in some slip models. Scenario occurrence-rates are modelled using Bayesian techniques to account for uncertainties in seismic coupling, maximum-magnitudes and Gutenberg-Richter b-values. The approach maintains reasonable consistency with the historical earthquake record and spatially variable plate convergence rates for all slip/rigidity model combinations, and facilitates partial correction of model-specific biases (identified via DART-buoy testing). The modelled magnitude exceedance-rates are tested by comparison with rates derived from long-term historical and paleoseismic data and alternative moment-conservation techniques, demonstrating the robustness of our approach. The tsunami hazard offshore of Australia is found to be insensitive to the choice of rigidity model, but significantly affected by the choice of slip model. The fixed-area-uniform-slip model produces lower hazard than the other slip models. Bias adjustment of the variable-area-uniform-slip model produces a strong preference for ‘compact’ scenarios, which compensates for a lack of slip heterogeneity. Thus, both heterogeneous-slip and variable-area-uniform-slip models induce similar far-field tsunami hazard.

1 Introduction

Destructive tsunamis are most often generated by large subduction zone earthquakes (Grezio et al. 2017). Although the highest runup usually occurs near to the source, earthquake-generated tsunamis show strong directivity and can remain hazardous at trans-oceanic distances (Ben-Menahem and Rosenman 1972). This was illustrated by the far-field impacts of the 2004 Sumatra-Andaman tsunami (300 deaths in Somalia), the 1960 Chile tsunami (203 deaths in Hawaii and Japan), and the 1946 Aleutian tsunami (162 deaths in California, the Marquesas and Hawaii) (Okal et al. 2002; Fritz and Borrero 2006; Okal 2011). The latter sites range between 4000 and 17,000 km from the tsunami source. Probabilistic Tsunami Hazard Assessments (PTHAs) suggest far-field subduction earthquakes can contribute at first-order to the hazard even for sites exposed to near-field subduction sources, such as Crescent City (near Cascadia) and Napier (near the Hikurangi trench) (Gonzalez et al. 2009; Geist and Parsons 2016; Power et al. 2017).

A key challenge for earthquake-generated tsunami hazard assessments concerns representing earthquakes and their occurrence-rates given substantial uncertainties in the underlying science (Selva et al. 2016; Davies et al. 2017; Power et al. 2017). Most studies follow a computational approach which requires specifying each earthquake scenario’s location, moment magnitude $M_{w}$, focal mechanism, rupture extent, rigidity and spatial distribution of slip, and subsequently modelling the resulting tsunami (Grezio et al. 2017). The plausible variation of earthquake parameters and occurrence-rates is often very large; e.g., on the Kermadec-Tonga trench Berryman et al. (2015) suggested the maximum earthquake magnitude $M_{w,max}$ could be anywhere between [8.1–9.6], implying large uncertainty in potential far-field tsunami impacts. The representation of rupture area, spatial slip variability and rigidity is also not standardized, with different approaches potentially leading to first-order differences in the modelled tsunami size when $M_{w}$ is fixed (Geist and Bilek 2001; Gica et al. 2007; Davies et al. 2015; Mueller et al. 2015; Li et al. 2016; Butler et al. 2017; Mori et al. 2017). Compared with scenario based hazard assessments, Probabilistic Tsunami Hazard Assessment (PTHA) methodologies have the great advantage that such uncertainties can be explicitly integrated into the analysis, but the hazard calculations remain sensitive to choice of models and representation of uncertainties (Grezio et al. 2017). Competing models/parameters must be weighted appropriately to ensure limited weight is placed on unlikely models (which is often nontrivial to ensure in practice, as for Probabilistic Seismic Hazard Assessment, Bommer and Scherbaum 2008). Bayesian methods offer a useful approach to this problem, as initial weights can be updated based on the model’s consistency with data (Parsons and Geist 2009; Grezio et al. 2010, 2017; Selva et al. 2016; Davies et al. 2017). However testing and sensitivity analyses remain critical for informing PTHA modelling decisions, by focussing attention on the most significant model weaknesses and the most influential sources of uncertainty (Li et al. 2016; Sepúlveda et al. 2019; Volpe et al. 2019).

Currently there is no consensus regarding how earthquake rupture complexity (i.e. variability of fault dimensions and spatial slip distribution) should be represented for PTHA. Often rupture complexity is considered most important for near-field tsunamis and of limited significance at far-field sites (e.g. Geist 2002; Okal and Synolakis 2008), whereas other studies suggest it is important also for far-field tsunamis (i.e. more than 1000 km from the source, Gica et al. 2007; Li et al. 2016; Butler et al. 2017). In the near-field case, it is clear that if $M_{w}$ and the rupture-area are fixed then slip heterogeneity substantially influences modelled tsunami wave heights and inundation (Geist 2002; Mueller et al. 2015; Ruiz et al. 2015). However this does not necessarily imply that near-field tsunami hazard assessments must use heterogeneous-slip. An et al. (2018) found that if the rupture area and location were calibrated, then optimal uniform-slip scenarios matched near-field tsunami observations nearly as well as optimal heterogeneous-slip scenarios. Fewer studies have focussed on the far-field case. Okal and Synolakis (2008) compared the far-field tsunami radiation pattern of a uniform-slip scenario with a weakly heterogeneous scenario (slip within 80–120% of the mean). The far-field tsunami radiation pattern was similar in both cases; however, finite-fault inversions suggest historical earthquakes have much more than 20% slip variation (e.g. Poisson et al. 2011; Lay 2018) which may induce greater far-field effects. Li et al. (2016) compared PTHA calculations derived from uniform and heterogeneous-slip earthquakes on the Manila trench, finding slip heterogeneity substantially increased the peak nearshore tsunami amplitude at both near-field and far-field sites (e.g. $\simeq 35$% at 500 year average return interval (ARI)). Butler et al. (2017) modelled tsunamis in Hawaii due to a range of uniform-slip $M_{w}~8.6$ Aleutian Island earthquakes with varying length and width, finding a factor $\simeq 2$ variation in the modelled far-field tsunami size. Butler et al. (2017) also found $M_{w}~9.25$ Aleutian earthquakes with higher near-trench slip (and reduced deep slip) produced more inundation in Hawaii than similar uniform-slip scenarios, with some locations being more sensitive to shallow slip than others. Gica et al. (2007) studied the sensitivity of tsunami wave heights in Hawaii to variations in the dimensions of uniform-slip earthquakes in Chile, Japan, and the Aleutians. Their modelled wave heights varied by a factor $\simeq$ 2 due to doubling/halving the rupture length, width and slip (while preserving $M_{w}$). They also report that, along the main beam of tsunami energy, the sensitivity of the wave to the rupture dimensions did not decrease with increasing distance from the source, suggesting that rupture complexity influences even the far-field tsunami behaviour.

In addition to rupture complexity, PTHAs may be affected by the representation of the fault rigidity $\mu$. The rigidity mediates the relationship between $M_{w}$ and slip (and thus the tsunami size); all else being equal, lower $\mu$ implies higher slip for fixed $M_{w}$ and produces a larger offshore tsunami. In practice the rigidity of subduction zones is not very well constrained (Bilek and Lay 1999; Geist and Bilek 2001), but tsunami hazard studies often assume constant $\mu \simeq 3-6 \times 10^{10}$ Pa (e.g. Butler et al. 2017; Fukutani et al. 2018; Kalligeris et al. 2017). Despite this common practice, the use of depth-varying $\mu$ (with low near-trench values) appears necessary to simulate the large tsunamis observed historically following shallow ‘tsunami-earthquake’ events (e.g. Geist and Bilek 2001; Newman et al. 2011b; Hébert et al. 2012), albeit not in every such case (Newman et al. 2011a). For example, low rigidity was used to simulate near-field runup of up to 10 m resulting from the 2006 $M_{w} 7.7$ Java tsunami-earthquake (Hébert et al. 2012), an event which also produced the highest historically observed tsunami runup in Australia [7.9 m at Steep Point $\simeq 1800$ km from the source, Prendergast and Brown (2012)].

Even though the rigidity model is highly significant for interpreting such events, it remains unclear whether the overall tsunami hazard is sensitive to the choice of constant or depth-varying rigidity, assuming the modelled earthquake occurrence-rates are constrained with a combination of earthquake catalogue data and moment conservation methodologies (e.g. as in Kagan and Jackson 2013; Rong et al. 2014; Davies et al. 2017). The combination of these methodologies is desirable because earthquake catalogue data alone has limited power to constrain high $M_{w}$ exceedance-rates (Zöller 2013, 2017). Importantly, moment conservation arguments imply the time-integrated earthquake slip-rate should balance the seismically coupled fraction of the tectonic convergence-rate (e.g. Bird and Kagan 2004; Bird and Liu 2007), suggesting that for fixed $M_{w}$, low-rigidity high-slip earthquakes should occur less often than those with higher-rigidity and lower-slip. This would reduce the effect of low-rigidity tsunami-earthquake type events on the overall hazard. Thus to understand how the hazard is affected by the rigidity model, it is necessary to apply moment-conservation approaches in conjunction with both constant and depth-varying rigidity models. Compared with the constant-rigidity case, moment-conservation approaches are more complex to apply with depth-varying rigidity because there is no longer a one-to-one relation between the scenario $M_{w}$ and its spatially integrated slip.

This study considers the sensitivity of a PTHA to the representation of far-field earthquake scenarios and their occurrence-rates. The work was conducted as part of the 2018 Australian PTHA and the broader study is described in two detailed technical reports (Davies and Griffin 2018; Griffin and Davies 2018). In addition Davies (2019) tests the modelled tsunami scenarios against DART-buoy observations without consideration of scenario frequencies or hazard. The current study focusses on the hazard calculation for offshore sites, and its sensitivity to key modelling assumptions. Inundation hazard assessments can be developed on a site-by-site basis by combining an offshore PTHA with high-resolution inundation models (e.g. Lane et al. 2012), but for simplicity that step is not undertaken herein. Because the importance of earthquake rupture complexity for far-field tsunami hazard is unclear, the tests feature three alternative slip models with varying degrees of complexity. For all slip models, the sensitivity of the hazard to the rigidity representation is also examined by re-interpreting the scenario $M_{w}$ on the basis of either constant or depth-varying rigidity. To enable this the current study develops scenario occurrence-rate models which are applicable to multiple slip and rigidity representations. The approach generalises the global-scale methodology of Davies et al. (2017) which constrained scenario rates using earthquake catalogues and plate convergence rates, but was limited to scenarios with constant rigidity, uniform slip and a deterministic $M_{w}$-vs-area relation. As well as generalising to a range of slip and rigidity models, the new occurrence-rate methodology makes more efficient use of earthquake catalogue data, and leads to a better match between the modelled long-term earthquake-slip rates and spatial variations of tectonic convergence.

2 Earthquake-Tsunami Scenario Database

Below we present key features of the 2018 Australian PTHA earthquake-tsunami scenario database used in this study. Further details are provided in Davies and Griffin (2018).

2.1 Source-Zone Discretization

The database includes major Pacific and Indian Ocean earthquake source-zones, and minor sources close to Australia (Fig. 1a). Fault geometries were defined using SLAB 2.0 or SLAB 1.0 where possible (Hayes et al. 2012, 2018), and elsewhere were schematized using linear or parabolic profiles (Griffin and Davies 2018). The fault geometries extend between the trench and a maximum seismogenic depth estimated from Berryman et al. (2015) and Griffin and Davies (2018). Most source-zones were modelled with only thrust earthquake scenarios, which are by far the largest contributor to the computed hazard in Australia, and for brevity the treatment of non-thrust sources is not presented herein.

Two alternative rigidity models are tested, featuring constant-rigidity ($\mu = 30$ GPa) and depth-varying rigidity (Fig. 1b). The latter was fit to rigidity estimates for subduction earthquakes by Bilek and Lay (1999) (Fig. 1b). It exhibits low rigidities for shallow earthquakes (but always $\ge 10$ GPa), and transitions to the preliminary reference earth model (PREM) at greater depths (Dziewonski and Anderson 1981; Geist and Bilek 2001).

Each source-zone was discretized into unit-sources with dimensions of $\simeq 50\times 50$ km$^2$, although this varies to match the source-geometry (Fig. 1c–h). To better represent non-planar fault geometries the unit-sources were subdivided into a large number of rectangular ‘sub-unit-sources’ (Davies et al. 2017). The vertical co-seismic seabed deformation associated with 1 m of slip on each unit-source was computed using the homogeneous elastic half-space model (Okada 1985) integrated over sub-unit-sources. The ocean surface deformation was derived from this using a Kajiura filter (Kajiura 1963; Glimsdal et al. 2013). The resulting unit-source tsunami was modelled for 36 h with the linear shallow water equations on a 1-arc-min grid with elevation based on GEBCO14 and GA250 (Whiteway 2009; Weatherall et al. 2015). The tsunami model domain includes global longitudes $[-40,320]$, latitudes from $[-72,65]$, with boundary conditions being periodic (east–west) and reflective (north–south) (Davies and Griffin 2018).

Fig. 1

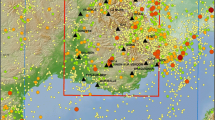
Overview of the earthquake-tsunami scenario database: a earthquake source-zones used in this study. Numbers show DART buoy locations. Black points along large source-zones denote segment boundary locations based on Berryman et al. (2015), which are given 50% weight in the scenario rate calculation (with 50% on an unsegmented model, Sect. 3.1); b Rigidity-vs-depth on subduction-zones using data from Bilek and Lay (1999), with the depth-dependent and constant-rigidity (30 GPa) models used here for thrust scenarios. The preliminary reference earth model (PREM) is also shown (Dziewonski and Anderson 1981); c, d example fixed-area-uniform-slip (FAUS) scenarios.; e, f example variable-area-uniform-slip (VAUS) scenarios; g, h example heterogeneous-slip (HS) scenarios. All examples c–h are on the Kurils–Japan source-zone

2.2 Earthquake-tsunami scenarios

Earthquake scenarios consist of linear combinations of unit-sources (Fig. 1c–h), with the associated tsunami being a linear combination of the unit-source tsunamis (Thio et al. 2007; Burbidge et al. 2008). On each source-zone the constant-rigidity earthquake scenarios were initially generated as detailed below, with magnitudes ranging from $7.2, 7.3, \ldots , 9.7, 9.8$ for computational convenience. Magnitudes above a source-zone specific $M_{w,max} < 9.8$ will later be assigned a rate of zero (Sect. 3.1), while in practice $M_{w}~7.2$ earthquakes will only generate small waves near Australia.

To understand how the hazard is affected by the earthquake representation, three different kinds of constant-rigidity scenarios were created (Fig. 1c–h):

• Fixed-area-uniform-slip (FAUS) scenarios have uniform-slip, with magnitude-dependent length and width based on the scaling relations of Strasser et al. (2010) ignoring the predictive uncertainty terms (Fig. 1c, d). For each magnitude the FAUS scenarios include a fixed number of unit-sources along-strike and down-dip (e.g. $16 \times 4$ for the examples in Fig. 1c, d, determined following Davies et al. (2017)) and the set of unit-sources is moved through all possible source-zone locations. By iterating over all magnitudes, the full set of FAUS scenarios is produced.

• Variable-area-uniform-slip (VAUS) scenarios also have uniform-slip, but account for $\pm \, 2 \sigma$ predictive uncertainties in the rupture length and width using the scaling relations of Strasser et al. (2010) (Fig. 1e, f). At least 15 VAUS scenarios were generated for each FAUS scenario, all having the same magnitude and a random length and width (with independent residuals). The VAUS scenario location is also random, but at least partially overlaps the ‘parent’ FAUS scenario. The number of ‘child’ VAUS scenarios per ‘parent’ FAUS scenario was increased to more than 15 if necessary, to ensure at least 200 VAUS scenarios on the source-zone at each magnitude. These numbers were found sufficient to obtain convergent hazard results at a range of sites around Australia, which was tested by splitting the scenario set into two equal groups and graphically comparing the tsunami maximum-stage vs return-period curves (Davies and Griffin 2018).

• Heterogeneous-slip (HS) scenarios are generated using the VAUS scenario’s rupture dimensions but have spatially non-uniform slip (Fig. 1g, h). The slip is randomly generated using a $k^{-2}$ type model, specifically the $S_{\text {NCF}}$ model of Davies et al. (2015). The $S_{\text {NCF}}$ model was chosen because it had the best performance among eight $k^{-2}$ type models tested by comparison with 66 finite-fault inversions (Davies et al. 2015). One HS scenario is generated per VAUS scenario. This implies a similar parent-child relationship exists between the FAUS (parent) scenarios and HS (child) scenarios, with 15 or more ‘children’ for each parent. Multi-site convergence tests indicate there are enough scenarios to support our hazard calculations (Davies and Griffin 2018).

Further implementation details are provided elsewhere (Davies and Griffin 2018; Davies 2019). A key concept is the parent-child relation between FAUS scenarios and the other scenario types, which will be exploited when assigning occurrence-rates to scenarios (Sect. 3.2) and for model testing (Sect. 2.3).

The effect of depth-varying rigidity is simulated by re-labelling the constant-rigidity scenario magnitudes, without otherwise changing their slip or area. Each unit-source is assigned a depth-dependent rigidity (Fig. 1b), assuming for simplicity the trench is 4 km below mean-sea-level, and these rigidities are used to re-compute each scenario’s magnitude. Scenarios in shallow, low-rigidity regions thus behave like constant-rigidity earthquakes with higher magnitude, and conversely for high-rigidity regions. It is necessary to adjust the scenario rate computations with depth-varying rigidity to maintain consistency with instrumental magnitude observations and tectonic constraints (Sect. 3.3), which affects the resulting hazard. This is not specific to our magnitude-relabelling approach; for example, Scala et al. (2019) propose a completely different treatment of depth-varying rigidity for PTHA which also requires scenario rate modifications.

2.3 Biases in Tsunami Scenarios

Scenario generation methods were tested by comparing random database scenarios with 18 earthquake-generated tsunamis observed at DART buoys in 2006–2016 (see two examples in Fig. 2a, b). Full details are reported elsewhere (Davies 2019); below we summarise key results that affect the scenario occurrence-rate modelling in this study. For each scenario generation method, each of the 18 observed tsunamis was compared with all database scenarios having ‘similar earthquake location and magnitude’. Scenarios are defined as having ‘similar earthquake location and magnitude’ as an observed event if their $M_{w}$ is within $\pm \, 0.15$ of the GCMT catalogue value, and their parent FAUS scenario includes unit-sources within half a scaling-relation length and width of the GCMT hypocenter (Davies 2019). This approach to testing was applied because in PTHA, scenario occurrence-rates are generally modelled as a function of the earthquake location and magnitude (e.g. Selva et al. 2016; Power et al. 2017; Davies et al. 2017); thus to avoid biases in the hazard, the ‘randomly generated tsunami waveforms’ should represent real tsunamis generated by earthquakes with similar location and magnitude. For each observed event, a weighted least-squares goodness-of-fit statistic was used to measure the agreement between the observed tsunami at DART buoys and all aforementioned scenarios (Davies 2019). The goodness-of-fit statistic includes an optimal time-offset (Lorito et al. 2008; Romano et al. 2016; Ho et al. 2019) to account for processes that can delay wave-propagation, but are not treated in our linear shallow water model (Watada et al. 2014; Allgeyer and Cummins 2014; Baba et al. 2017).

Figure 2a, b illustrates the best-fit FAUS, VAUS and HS database scenarios identified with the above procedure for 2 of the 18 test events; the 2014 $M_{w}~8.2$ Iquique (Chile) tsunami and the 2011 $M_{w}~9.1$ Tohoku tsunami (see Davies and Griffin 2018; Davies 2019 for other examples). For the 2014 event a reasonable agreement is obtained between observations and the best database scenario for every model type (FAUS, VAUS, HS) (Fig. 2a). In contrast, for the Tohoku event all FAUS scenarios produced long-period low-amplitude waves which poorly matched observations both near and far from the earthquake source, whereas the best VAUS and HS scenarios performed well (Fig. 2b). These visual observations are consistent with quantitative goodness-of-fit results (Davies 2019).

Fig. 2

a Example good-fitting database scenarios for the 2014/04/01 $M_{w}~8.2$ Iquique (Chile) earthquake-generated tsunami using the constant $\mu$ FAUS, VAUS and HS models. Each panel compares the tsunami observed at a DART buoy with the same three database scenarios (see Fig. 1 for DART locations). Vertical scale in meters. Modelled time-series are temporally offset by the optimum value determined in the goodness-of-fit calculation; b same as panel-A for the 2011/03/11 $M_{w}~9.1$ Tohoku tsunami, using the depth-varying $\mu$ scenarios. For brevity only 7 of the DART observations are shown; c magnitude vs mean-slip for the 5 best-fitting database scenarios for all 18 test events (constant $\mu$ case). The scaling relation mean-slip is inferred from the Strasser et al. (2010) length and width scaling relations assuming uncorrelated residuals. The ‘compact-uniform-slip’ curve was derived from the area scaling relation of An et al. (2018), $A=2.89\times 10^{-11} M_{0}^{2/3}$, assuming $\mu = 44$ GPa because they used PREM rigidities; d probability density for the maximum-slip percentile of good-fitting events. This is not applied to FAUS scenarios because by construction they have little variability

Analysis of the good-fitting earthquake scenarios was used to further assess model biases (Fig. 2c, d; Davies (2019)). If a model gives an unbiased representation of random tsunamis, then the properties of good-fitting earthquake scenarios should not differ systematically from random scenarios with similar location and magnitude, when considered over all 18 test events. Conversely if a model has some bias (e.g. producing too many low-slip, high-area scenarios), we may see statistical differences between good-fitting and random earthquake scenarios. Figure 2c, d suggests the good-fitting VAUS model scenarios most often have high slip relative to the scaling-relation used to construct them, which indicates bias in the VAUS model. In contrast, the good-fitting HS scenarios exhibit mean-slip variability within the expected $\pm \, 2\sigma$ range of random scenarios, without any strong preference for high or low values (Fig. 2c, d). The FAUS scenarios have little variability by construction and so their biases cannot be usefully quantified with this approach, but we emphasise that some historical events are not well modelled with FAUS scenarios (e.g. Tohoku, Fig. 2b).

The VAUS model biases are qualitatively consistent with the results of An et al. (2018). They simulated near-field tidal gauge and DART buoy observations for six tsunamis using both heterogeneous and uniform slip models, and found near-optimal results could consistently be obtained using compact uniform-slip earthquakes with a low aspect ratio ($L=W$) and high-slip (Fig. 2c). We infer the compact nature of good-fitting VAUS scenarios allows representation of rupture asperities, which have a dominant influence on the resulting tsunami. The HS model can simulate those asperities directly and so avoids similar biases (Davies 2019).

3 Scenario Rates

The scenario rate modelling methodology was designed to meet the following objectives:

• 1. Applicable to all earthquake-slip and rigidity models in Sect. 2.2.

• 2. On each source-zone the modelled magnitude-frequency distribution should be reasonably consistent with plate convergence rates and instrumental seismicity.

• 3. The method should treat uncertainties in the seismic coupling, maximum magnitudes and the Gutenberg-Richter b value.

• 4. Spatial variations in the scenario rates should reflect variations in plate convergence.

Our approach generalises that of Davies et al. (2017), because the latter is only applicable to FAUS type scenarios with constant rigidity (violating objective 1) and has some weaknesses regarding spatial variations in scenario rates (objective 4) that are addressed herein. Our new approach also makes more efficient use of earthquake catalogue data to constrain uncertainties (objective 3). The approach involves firstly modelling each source-zone’s magnitude-frequency distribution (Sect. 3.1), and secondly partitioning these rates among individual scenarios (Sect. 3.2). Possible segmentation of large source-zones (boundaries in Fig. 1) is treated by applying the model separately to: (A) the unsegmented source-zone, and; (B) the union of individual segments; with 50% weight on each interpretation. Ruptures are allowed to cross segment boundaries in any case (as occurred e.g. for the 2007 Solomons earthquake, Lorito et al. (2015a)) so the primary effect of segmentation is to enhance spatial variations in the source-zone’s magnitude-frequency distribution. The use of depth-varying-rigidity introduces additional complications which are addressed in Sect. 3.3. The results are tested in Sect. 3.4. The calculations which convert magnitude exceedance-rates to tsunami hazard metrics are described in Sect. 3.5.

3.1 Source-Zone Integrated Magnitude Exceedance-Rates

Seismicity on each source-zone is assumed to follow one of two Gutenberg-Richter (GR) type relations with different tail behaviour; a characteristic GR model (Kagan 2002):

$$\begin{aligned} GR(x) & = 10^{a - bx} \quad \text {for} \quad x \le M_{w,max} \nonumber \\&= {} 0 \quad \text {for} \quad x > M_{w,max} \end{aligned}$$

(1)

and a truncated GR model (Kagan 2002):

$$\begin{aligned} GR(x) & = {} 10^{a - bx} - 10^{a - bM_{w,max}} \quad \text {for}\quad x \le M_{w,max} \nonumber \\&= {} 0 \quad \text {for}\quad x > M_{w,max} \end{aligned}$$

(2)

For both models GR(x) gives the rate of earthquakes (events/year) with magnitude $\ge x$ as a function of three unknown parameters: a, b, and the maximum magnitude $M_{w,max}$.

Uncertainty in each source-zone’s magnitude-frequency distribution is represented using a logic-tree (Annaka et al. 2007). The logic-tree includes every combination of the GR model type and the parameters b, $M_{w,max}$, and the seismic coupling fraction c. The Gutenberg-Richter a value is derived from these via moment conservation arguments (Bird and Kagan 2004; Bird and Liu 2007; Davies et al. 2017). The individual parameters vary through a source-zone specific set of values with ‘prior weights’ described below. The prior weight of each parameter combination is defined as the product of its individual parameter prior weights. Some parameter combinations will predict unrealistic magnitude-frequency distributions compared with historical seismicity and this is dealt with by using earthquake catalogue data to update the weights via Bayes theorem (Davies et al. 2017).

The two GR models (Eqs. 1, 2) are assigned prior weights of 30% (characteristic) and 70% (truncated). The b parameter is assigned twenty equally spaced values between 0.7 and 1.2 (Berryman et al. 2015; Davies et al. 2017) with uniform prior weights. The coupling prior weights are a 50:50 combination of two different distributions. The first takes the lower, preferred and upper coupling values from Berryman et al. (2015) (with default values of 0.3, 0.5, 0.7 where no information is available) and assumes they define the lower limit, median and upper-limit of the prior coupling cumulative distribution function, with linear interpolation between these values. The second is a uniform distribution assigned to 20 coupling values in [0.1, 1.3]. This latter distribution is deliberately uninformative. The lower coupling limit ($c=0.1$) is conservative, to prevent source-zones with rapid convergence and limited historical seismicity from being assigned a very low coupling after the Bayesian weight-update. Considering the model herein cannot treat non-stationary seismicity, which could allow for longer time intervals between large earthquakes than expected under stationarity, such conservatism is warranted (Stirling and Gerstenberger 2018). The upper coupling limit ($c=1.3$) is also conservative and deliberately exceeds the physical limit ($c \le 1$). This was done because modelled seismicity depends on the product of c, the fault area $A_{T}$, and the mean horizontal tectonic convergence rate $\dot{s}$, but uncertainties in the geometry and convergence are not directly treated in our methodology. The $\dot{s}$ values are defined using the models of Bird (2003), Koulali et al. (2015, 2016) and Griffin and Davies (2018), averaged over the source-zone. If the convergence direction is oblique to the trench at any point then the component of convergence that maximises $\dot{s}$ is used, up to a maximum of 50$^\circ$ away from pure thrust. This allows oblique subduction as suggested for the Puysegur source-zone (Hayes and Furlong 2010). Although potentially enabling over-estimation of seismicity, this is counteracted by the Bayesian update which will down-weight high c values when inconsistent with observed seismicity (e.g. on ‘quiet’ source-zones with substantial convergence). By partially weighting the Berryman et al. (2015) coupling values the model can reflect the results of paleoseismic and geodetic analyses, which are informative for some source-zones (e.g. Cascadia) but not otherwise straightforward to include.

The maximum magnitude $M_{w,max}$ ranges between lower and upper limits. The lower limit reflects the largest earthquake thought to have occurred on the source-zone (based on Ekstrom et al. 2012; Storchak et al. 2012; Berryman et al. 2015), plus a small perturbation (0.05) to ensure it has non-zero rate according to the truncated GR model (Eq. 2). On the South-American trench, a lower limit $M_{w,max}=9.2$ is used to represent the 1960 Chile earthquake for consistency with tsunami and geodetic inversions (Moreno et al. 2009; Fujii and Satake 2013), even though seismic wave inversions suggest a higher magnitude ($\simeq 9.5$; Kanamori 1977; Engdahl and Villasenor 2002). The upper limit $M_{w,max}$ is defined using the minimum of two scaling-relation based constraints. Firstly $M_{w,max}$ is less than the magnitude of a ‘compact’ earthquake that fills the source zone according to the $M_{w}$-vs-area scaling relation of Strasser et al. (2010), where the area is evaluated at − 1 prediction standard-deviation to represent a ‘compact’ event. Secondly $M_{w,max}$ is less than the magnitude of a ‘narrow’ earthquake which fills the down-dip width of the source-zone, using the $M_{w}$-vs-width scaling relation of Strasser et al. (2010) with width evaluated at − 2 prediction standard deviations (representing a ‘narrow’ earthquake). Forty $M_{w,max}$ values are initially created with equal spacing between these lower and upper limits, and uniform prior weights. Finally all $M_{w,max}$ values are subsequently clipped to a maximum of 9.6, because scaling-relation based $M_{w,max}$ limits can be very high on large source-zones (Berryman et al. 2015; Davies et al. 2017).

The GR parameter a is derived from the above parameters using a fault-based seismic-moment conservation approach (Bird and Kagan 2004; Bird and Liu 2007; Davies et al. 2017). The relation between earthquake scenarios and tectonic convergence is:

$$\begin{aligned} \sum _{e \in E} r_{e} (SA)_{e} = \frac{A_{T} (c\dot{s}) \xi }{\cos (\overline{\delta })} \end{aligned}$$

(3)

Here e denotes an individual earthquake scenario within the set of modelled scenarios E, $r_{e}$ is its rate (events/year), and $(SA)_{e}$ is its spatially integrated slip ($\hbox {m}^3$). The full source-zone fault area is $A_{T}$ ($\hbox {m}^2$) with average coupled horizontal convergence rate $(c\dot{s})$ (m/year) and cosine of mean dip $\cos ({\overline{\delta }})$. See Meade and Loveless (2009) for justification of the latter factor in Eq. 3, which is not universally applied in moment balance approaches (e.g. Kagan and Jackson 2013); irrespective for our analysis its influence is largely offset when constraining the coupling coefficient (below). The factor $\xi \in [0-1]$ accounts for the convergence due to earthquakes with magnitude $< M_{w,min}$, which are not represented among the modelled events E. For the current study $M_{w,min}=7.2$, but given our scenario discretization this represents a bin of magnitudes $7.2\,\pm\, \Delta /2$ where $\Delta =0.1$ (Sect. 2.2). Assuming constant rigidity, the proportion of integrated slip due to the modelled scenarios is:

$$\begin{aligned} \xi = \frac{ \int _{(M_{w,min}-\Delta /2)}^{M_{w,max}} gr(x) M_{0}(x) dx }{ \int _{-\infty }^{M_{w,max}} gr(x) M_{0}(x) dx } \end{aligned}$$

(4)

where $M_{0}(x)$ is the seismic moment as a function of the magnitude x, and $gr(x) = -\frac{dGR}{dx}$ (technically we assume infinitesimal smoothing is applied to the GR models near $x=M_{w,max}$ so the derivative is well defined). Due to cancellation Eq. 4 is independent of a. Assuming constant rigidity, the a parameter can be derived from Eqs. 3 and 4 using $c, \dot{s}, A_{T}, \overline{\delta }, b$ and $M_{w,max}$ (known for each logic-tree branch). It is not necessary to know the individual scenario rates $r_{e}$ because with constant rigidity the spatially integrated slip $(SA)_{e}$ is a function of magnitude alone. This reasoning fails with depth-varying rigidity, necessitating a special treatment of that case (Sect. 3.3).

An extremely wide range of Gutenberg–Richter type models $GR_{i}$ result from these priors, as illustrated on the unsegmented Kermadec–Tonga source-zone (Fig. 3a). Both individual logic-tree branches and the prior-mean curve itself may deviate substantially from the observed seismicity rates. On all source-zones the observed seismicity is taken from the GCMT catalogue including events with $M_{w} > (M_{w,min}-\Delta /2) = 7.15$, hypocenter within 0.4$^\circ$ of the unit-sources, depth $< 71$ km, having at least one nodal plane with rake within 50$^\circ$ of pure thrust and strike within $50^\circ$ of the nearest unit-source’s strike.

Fig. 3

Source-zone magnitude-frequency modelling, using the unsegmented Kermadec-Tonga source as an example. a Magnitude-frequency curves prior to weight update. Note the individual logic-tree branches (thin grey curves) appear as a grey shading in much of the plot because there are many; b magnitude-frequency curves after weight update; c prior and posterior c weights; d prior and posterior $M_{w,max}$ weights; e prior and posterior b-value weights

To obtain better agreement between the rate models and aforementioned data, the prior weights are updated using Bayes theorem:

$$\begin{aligned} w_{i} = \frac{ w_{i}^{\prime } L(\text {data}| i) }{ \sum _{i} w_{i}^{\prime } L(\text {data}| i)} \end{aligned}$$

(5)

Here $w_{i}$ is the posterior weight of the i’th logic-tree branch, $w_{i}^{\prime }$ is the prior weight, and $L(\text {data}|i)$ is the likelihood of the data if the i’th logic-tree branch is true. The likelihood is calculated from the rate model and the assumption of stationary seismicity:

$$\begin{aligned} L(\text {data}|i) & =\, {} L_{\text {count}}(\text {data} | i) L_{\text {magnitude}}(\text {data}|i) \end{aligned}$$

(6)

$$\begin{aligned} L_{\text {count}}(\text {data}|i)=\, & {} \frac{ \exp (-\lambda _{i})(\lambda _{i})^{n} }{ n! } \end{aligned}$$

(7)

$$\begin{aligned} L_{\text {magnitude}}(\text {data}|i)= & {} \left( \frac{T}{\lambda _{i}} \right) ^{n} \prod _{l=1}^{n} \left( -\frac{dGR_{i}}{dx}(M_{w,l}) \right) \end{aligned}$$

(8)

Equation 7 is a standard model for observed counts from a Poisson process, where n is the number of events in the data which spans an observation time T (years), and $\lambda _{i} = GR_{i}(M_{w,min}-\Delta /2) T$ gives the mean number of events predicted by the i’th logic-tree branch in time T. Equation 8 was derived by converting $GR_{i}$ to a probability density for a random magnitude, with the likelihood being the product of the density at each observed magnitude $M_{w,l}$. The approach improves upon that of Davies et al. (2017) which ignored the observed magnitude distribution (i.e. $L_{\text {magnitude}} = 1$). In the special case with no observed events ($n=0$), the current study also assumes $L_{\text {magnitude}} = 1$. The observation of zero events is nonetheless informative because it suggests logic-tree branches which predict frequent events are unlikely to be correct, and Eq. 7 will down-weight such branches accordingly.

Bayesian updating has a dramatic impact on the modelled earthquake rates and their uncertainties (Fig. 3a, b). In general the mean rate becomes more consistent with historical observations, and uncertainties at low magnitudes are reduced (Fig. 3b). On the unsegmented Kermadec–Tonga source-zone, the results reflect that historical seismicity was relatively low compared to the prior model (Fig. 3a). In principle this could indicate low coupling, and/or that significant slip is released in higher magnitude earthquakes (in which case frequent low-magnitude earthquakes are not required to balance tectonic convergence). However the observations are unlikely if c is high and $M_{w,max}$ is low, because in this case more frequent low-magnitude earthquakes are required to balance tectonic convergence. As a result the Bayesian update shifts more weight onto lower c values, and higher $M_{w,max}$ values (Fig. 3c, d).

3.2 Partitioning the Source-Zone Integrated Exceedance-Rates Among Scenarios

For each logic-tree branch i, the individual scenario occurrence-rate $r_{e,i}$ (events/year) for any scenario e with magnitude $M_{w,e}$ must be consistent with the source-zone integrated exceedance-rate function $GR_{i}$. Supposing all scenarios have magnitudes arranged as $M_{w,min}, M_{w,min} + \Delta , M_{w,min} + 2\Delta , \ldots$ representing bins of width $\Delta$ (as for our constant rigidity scenarios where $\Delta =0.1$), this implies:

$$\begin{aligned} r_{e,i} = Pr(e | M_{w} = M_{w,e})\left( GR_{i}(M_{w,e} - \Delta /2) - GR_{i}(M_{w,e} + \Delta /2) \right) \end{aligned}$$

(9)

Here $Pr(e | M_{w} = M_{w,e})$ is the conditional probability that scenario e occurs, assuming some random scenario with the same magnitude occurs on the same source-zone. This will be modelled as independent of the logic-tree branch i.

Many studies assume uniform scenario conditional probabilities (e.g. Horspool et al. 2014; Løvholt et al. 2014; Lorito et al. 2015b):

$$\begin{aligned} Pr(e | M_{w} = M_{w,e}) \propto 1. \end{aligned}$$

(10)

Alternatively, the scenario conditional probability may be manipulated to make earthquakes more likely to occur on rapidly converging, wider parts of the source-zone. For the case of FAUS scenarios with constant rigidity Davies et al. (2017) proposed to represent this via:

$$\begin{aligned} Pr(e | M_{w} = M_{w,e}) \propto \left( \dot{s}_{e} / S_{e} \right) \end{aligned}$$

(11)

where $S_{e}$ is the scenario’s mean slip, and $\dot{s}_{e}$ is the average horizontal convergence rate where e occurs on the source-zone.

A problem with both Eqs. 10 and 11 is they artificially concentrate the time-integrated slip in the middle of the source zone (along-strike), even when the tectonic convergence and source-geometry is uniform. For illustration, consider a FAUS earthquake with $3 \times 2$ unit-sources which occurs on a uniform source-zone with $7 \times 2$ unit-sources (Fig. 4a). An earthquake of this size can occur in five different positions on the source-zone. Among those five scenarios, unit-sources at the along-strike edges will be included in only one, whereas unit-sources in the middle of the source-zone will be included in three scenarios (Fig. 4a). If all five scenarios have the same slip and occurrence-rate, the time-integrated slip rate would be 3 times greater in the interior of the source-zone than at the along-strike edges. This conflicts with the assumed uniform horizontal convergence and illustrates the ‘edge-effect’ bias.

Fig. 4

Edge-effect biases in time-integrated slip rates. a If a $3 \times 2$ earthquake is moved through all possible locations on a source-zone, then fewer scenarios will touch unit-sources at the along-strike extremities. If not explicitly treated, this concentrates time-integrated slip in the source-zone interior; b spatial distribution of the tectonic convergence rate prescribed for the Kurils–Japan source-zone. The modelled time-integrated slip rate should be similar to this; c modelled time-integrated slip rates using Eq. 12 to correct for edge-effects; d modelled time-integrated slip rates using Eq. 11, which does not include an edge-effect correction; e Modelled time-integrated slip rates using the ‘equal conditional probability’ approach without any edge-effect correction (Eq. 10)

The same edge-effect bias occurs in realistic applications which integrate over all scenarios. Figure 4b–e demonstrates this on the Kurils-Japan subduction-zone. All examples use constant rigidity FAUS scenarios, and $GR_{i}$ in Eq. 9 is replaced with the posterior mean magnitude exceedance-rate over all $GR_{i}$ in the logic-tree. Although the input tectonic convergence does not vary strongly in space (Fig. 4b), the time-integrated slip rate is concentrated in the middle of the source-zone using either Eq. 10 (Fig. 4e) or Eq. 11 (Fig. 4d) as the scenario conditional probability model. The results of these two approaches would differ more substantially if the source-zone had greater spatial variations in convergence, but clearly both approaches suffer the edge-effect bias.

To approximately correct for the edge-effect, FAUS scenarios which touch an along-strike edge unit-source should have a higher occurrence-rate. Herein this is achieved by modifying Eq. 11 to:

$$\begin{aligned} Pr(e | M_{w} = M_{w,e}) \propto \left( \dot{s}_{e} / S_{e} \right) (1+ kI_{e}). \end{aligned}$$

(12)

Here $I_{e} = 1$ for FAUS scenarios e which include unit-sources on the along-strike edge of the unsegmented source-zone (and $I_{e} = 0$ otherwise), and k is a source-zone specific constant. For each unsegmented source-zone, k is determined numerically to give the smallest least-squares difference between the spatial distribution of the horizontal tectonic convergence rate and the model’s time-integrated slip rate (using the posterior mean over all logic-tree branches). To account for the seismic coupling, which may lead to modelled slip rates being a fraction of the convergence rate, the variables are normalised (divided by their mean over all unit-sources) before computing k; thus only the spatial pattern of slip is considered. This approximation implies the conditional probability does not vary among logic-tree branches, a property shared by Eqs. 10 and 11. This simplifies some calculations and reduces the file-storage required for our analysis, although in-principle a more complex treatment of k could be developed. When modelling segmented source-zones the corresponding unsegmented k value is used, because scenarios can span multiple segments and receive a partial weight from each based on the fraction of their moment that occurs there. Equation 12 leads to better agreement between the spatial patterns of convergence in the input data and the model (Fig. 4b, c), as compared with the use of Eq. 10 (Fig. 4e) or Eq. 11 (Fig. 4d).

When source-zones include three or more unit-sources down-dip, a related edge-effect occurs in the down-dip direction. This reduces time-integrated slip rates in the deepest and shallowest row of unit-sources relative to the mid-depth unit-sources, which are included in more scenarios. The down-dip edge-effect is relatively small compared with the along-strike variant discussed above; for instance in Fig. 4c the shallow and deep unit-sources have modelled time-integrated slip rate on average 81% of the mid-depth sources. An approximate correction could be developed by adapting the above approach, but no attempt was made to do this in the current study because subduction-zone coupling is likely to be genuinely higher at mid-depths (e.g. Bilek and Lay 2018).

The arguments in this section thus far apply only to FAUS scenarios, because justification of Eqs. 11 and 12 requires that rupture area is a deterministic function of magnitude (Davies et al. 2017). To extend the approach to non-FAUS scenarios (Fig. 5) the occurrence-rate of each individual FAUS scenario is partitioned among its ‘child’ scenarios. Recall each FAUS scenario has at least 15 ‘child’ HS scenarios (and similarly for VAUS), all with the same magnitude and partial location overlap with their parent (Sect. 2.2). The simplest occurrence-rate partitioning method is to equally split the parent FAUS scenario’s occurrence-rate among its children. However an unequal partition is preferable to partially correct known model biases, such as those established earlier (most significantly for the VAUS model, Sect. 2.3). Thus in the current study an unequal partition is applied to each group of N child scenarios ($N \ge 15$), separately for VAUS and HS. Each scenario is assigned a local slip percentile ($100r/(N+1)$ where r is its maximum-slip rank among the other N scenarios), and the curves in Fig. 2d are applied to this percentile to define the unequal partition weights. Thus significantly more weight is placed on higher-slip VAUS scenarios, which show good-fit to observations more often (Sect. 2.3). In contrast the HS scenarios have relatively uniform weights (Fig. 2d) because good-fitting HS scenarios do not show strong preference for high or low slip.

Fig. 5

Comparison of modelled time-integrated slip rates (posterior mean over all logic-tree branches) on the Kermadec-Tonga source-zone, computed using the FAUS, VAUS and HS slip models

The occurrence-rate partitioning procedure does not affect the source-zone’s integrated magnitude-frequency distribution, so there is no difference in the frequency of earthquakes with FAUS, VAUS or HS. However the use of different earthquake slip models can lead to slight changes to the modelled spatial distribution of time-integrated slip on unit-sources, because the slip on a single FAUS scenario will not be spatially identical to the integrated slip on its child HS or VAUS scenarios. In practice these differences average out and are small enough to be ignored (Fig. 5). For instance at 95% of unit-sources in Fig. 5 the time-integrated slip rate of the HS and VAUS models differs by $< 10$% from the FAUS result.

3.3 Extension to Depth-Varying Rigidity

The arguments in Sects. 3.1 and 3.2 do not directly extend to the depth-varying rigidity case, because there is no longer a one-to-one relation between a scenario’s magnitude and its spatially integrated slip $(SA)_{e}$. This complicates the previously simple relation between magnitude and convergence, invalidating Eq. 4 and the associated a parameter calculation. It is also not obvious how to apply the scenario conditional probability model (Eqs. 9 and  12) to scenarios with variable-rigidity magnitudes, considering the latter are not arranged in a small set of discrete values $(7.2, 7.3, \ldots )$.

A key component of our solution to these problems is to parameterise the source-zone’s magnitude-frequency distribution as a function of the earthquake’s ‘constant rigidity magnitude’, even when the rigidity is modelled as depth-varying. Obviously the constant-rigidity magnitude then differs from the ‘true magnitude’. The difference between these quantities may be treated as a ‘perturbation of the magnitude’ (Fig. 6) and is explicitly treated below. The key point is that Eqs. 1, 2 are applied using the constant-rigidity magnitude for x, although the posterior logic-tree weights will differ in the constant and variable-rigidity cases. This GR re-parameterisation is reasonable given that the constant and variable rigidity magnitudes are heavily correlated (Fig. 6). Considering the modelled events are rare, we are unlikely to have sufficient data in the near future to distinguish the goodness-of-fit of either parameterisation.

Fig. 6

Constant rigidity magnitude vs depth-varying rigidity magnitude for HS scenarios on the Kermadec-Tonga source-zone

The great benefit of the GR re-parameterisation is that most reasoning in Sects. 3.1 and 3.2 can be applied directly to variable-rigidity scenarios, using constant rigidity magnitudes in Eqs. 1, 2, 3, 4, 9 and 12. The prior logic-tree weights are applied without modification, noting they are in any case very diffuse. However, adjustments are necessary when using magnitude observations to update the logic-tree weights (Eqs. 7, 8), because the $GR_{i}$ magnitude-frequency distribution now gives the exceedance-rate in terms of the ‘constant-rigidity’ magnitude $M_{w}^{c}$ rather than the ‘depth-varying-rigidity magnitude’ $M_{w}^{v}$ which is represented by observations. To enable the logic-tree weight update, the exceedance-rate function of $M_{w}^{v}$ (denoted $\Lambda _{i}(M_{w}^{v})$) is derived as detailed below, and then used in place of $GR_{i}$ in Eqs. 7 and 8. This ensures the logic-tree weight update treats the observed magnitudes as representing depth-varying rigidity earthquakes.

To derive $\Lambda _{i}$, consider the magnitude perturbation $m^{\prime }$ due to depth-varying rigidity:

$$\begin{aligned} m^{\prime } = M_{w}^{v} - M_{w}^{c}. \end{aligned}$$

(13)

For a random observed event e, we can consider $m^{\prime }_{e}$ as a random variable with distribution conditional on its unknown constant-rigidity magnitude (Fig. 6):

$$\begin{aligned} Pr(m_{e}^{\prime } \le X) = F(X | M_{w,e}^{c}) \end{aligned}$$

(14)

where $F(X | M_{w,e}^{c})$ is the cumulative distribution function of $m_{e}^{\prime }$ for a random scenario e with constant-rigidity magnitude $M_{w,e}^{c}$. Figure 6 highlights that for scenarios in our database, the variability of $m^{\prime }$ is magnitude dependent, with less variance at higher magnitudes because ruptures cover a larger area, averaging out the effect of rigidity variation. In the current study F is modelled empirically on each source-zone using the differences between $M_{w}^{v}$ and $M_{w}^{c}$ in the scenario database. It will be necessary to evaluate F at a continuous set of $M_{w}^{c}$ values, so interpolation is used in between the discrete scenario values $(7.2, 7.3, \ldots 9.8)$, while extrapolation outside this range uses the nearest boundary $M_{w}^{c}$ value (7.2 or 9.8). Finally, supposing that $GR_{i}(x)$ gives the source-zone’s exceedance-rate for $M_{w}^{c}$ on a particular logic-tree branch, the associated exceedance-rate for the variable-rigidity magnitudes is:

$$\begin{aligned} \Lambda _{i}(M_{w}^{v}) = \int _{-\infty }^{\infty } \left( 1 - F(M_{w}^{v} - x | x) \right) gr_{i}(x) dx \end{aligned}$$

(15)

where $gr_{i} = -\frac{dGR_{i}}{dx}$ (technically we assume infinitesimal smoothing of the GR models near $M_{w,max}$ so the derivative is well-defined). Notice the term in large parenthesis in the integrand gives the probability that the magnitude perturbation is large enough for the variable rigidity magnitude to exceed $M_{w}^{v}$ when the constant rigidity magnitude is x.

The $\Lambda _{i}$ exceedance-rate model is computed numerically from Eq. 15 and used in place of $GR_{i}$ for all calculations associated with Eqs. 7 and 8, thus treating the observed magnitudes as having depth-varying rigidity when defining the logic-tree weights. The individual scenario occurrence-rates are then computed as in the constant-rigidity case (Sect. 3.2), but using revised logic-tree weights.

3.4 Testing the Modelled Magnitude Exceedance-Rates

As a first test the modelled and observed seismicity are compared at the global scale (Fig. 7). Although this data was used to update the logic-tree weights and is thus not independent of the model, the comparison is useful because it may make model biases more obvious than tests at the individual source-zone level, where data sparsity permits a wide range of plausible magnitude-frequency curves (e.g. Fig. 3). The modelled mean magnitude exceedance-rates are in reasonable agreement with the GCMT observations using both constant and depth-varying $\mu$ (Fig. 7). The models give slightly higher exceedance-rates than empirical estimates, but are within 95% confidence intervals for the true exceedance-rate inferred from the data (Garwood 1936). At magnitudes $\gtrsim 8.4$ the depth-varying $\mu$ model predicts slightly greater exceedance-rates than the constant $\mu$ model (Fig. 7) because large earthquakes occur predominantly on wide, deep source-zones, where depth-varying rigidities on average exceed the constant value (30 GPa). For a fixed magnitude, higher rigidity implies less average slip, thus exceedance-rates should increase to produce the same horizontal convergence. This effect is partially offset by the Bayesian update of logic-tree weights using earthquake catalogue data, which constrains the exceedance-rates at commonly occurring magnitudes irrespective of the rigidity and convergence. Thus the globally-integrated exceedance-rates do not differ much at magnitudes $\lesssim \, 8.4$, irrespective of the rigidity model (Fig. 7).

Fig. 7

Comparison of globally integrated magnitude exceedance-rates model and the GCMT catalogue. The catalogue data combines all earthquakes used to update the source-zone logic-tree weights. The modelled exceedance-rates were derived by summing the mean scenario occurrence-rates. This leads to some artefacts in the depth-varying-rigidity curve at low magnitudes (around $M_{w,min}$), due to the use of a minimum magnitude combined magnitude-relabelling technique. However this is inconsequential for the hazard and is properly accounted for in the logic-tree weight update (Sect. 3.3)

To compare the models herein with other published magnitude exceedance-rates it is useful to restrict the analysis to some prescribed region (i.e. a subset of unit-sources that matches the region considered in other studies, Table 1). To do this, the modelled occurrence-rates for HS scenarios inside the prescribed region are summed to create a ‘local’ magnitude exceedance-rate curve. To account for the magnitude discretization, the local exceedance-rates are computed directly at magnitude bin-boundaries (i.e. $M_{w} \ge 7.15, 7.25, \ldots 9.75$), and linear interpolation of $M_{w}$ vs $\log _{10}(\text {exceedance-rate})$ is used to evaluate the ‘local’ exceedance-rate at other magnitudes. When HS scenarios have only part of their integrated slip in the prescribed region, they are included with proportionately down-weighted occurrence-rate. Credible intervals are derived by partitioning the full source-zones percentile uncertainties, using the same approach applied to the mean curve.

Table 1 Magnitude exceedance average-recurrence-interval (ARI, units of years) for sub-regions of some subduction zones

The constant and depth-varying $\mu$ models usually give similar magnitude exceedance-rates on subsets of subduction zones (Table 1). Differences reflect the source-zone’s maximum depth below the trench, as specified using the upper estimates of Berryman et al. (2015). On source-zones with relatively deep seismicity (Alaska, Chile, Japan, Sumatra—with modelled depths extending 45–55 km below the trench) the constant rigidity model predicts slightly lower exceedance-rates, as was observed for global seismicity due to the trade-off between higher rigidities and exceedance-rates under moment conservation constraints (Fig. 7). The converse applies for relatively shallow source-zones (Nankai and Cascadia, with modelled depths extending 25–30 km below the trench).

The modelled ARIs are generally comparable to the range of estimates in other studies using longer-term historical or paleo data, and/or alternative moment conservation techniques (Table 1). The credible intervals are wide, but this is also true of 95% intervals reported elsewhere (Table 1, Rong et al. 2014; Butler et al. 2016). The uncertainty is further emphasised by comparing ARIs from different studies at the same site (Table 1). For example on the relatively well studied Alaska megathrust (Kodiak to Prince William Sound), Wesson et al. (2007, 2008) drew on multi-site Holocene stratigraphy to infer an ARI $\simeq 650$ years for earthquakes like the 1964 event (which had $M_{w} ~9.2$), whereas Butler et al. (2016) estimated $M_{w} \ge 9$ ARI $\simeq$ 1403 (447–9800) years using an expanded set of paleo data. Recently Shennan et al. (2018) inferred the 1964 earthquake was the only event in the last 2000 years to rupture the entire region, by combining paleoseismic results at 22 sites. Our model’s results near Alaska are most similar to Butler et al. (2016), although the Wesson et al. (2007, 2008) ARI’s are within the 95% interval (Table 1). Wesson et al. (2007, 2008) assumed $M_{w} \ge 9$ earthquakes never occur further west (Semidi and Shumagin segments) whereas our model does not represent such fine-scale variations in seismicity. Thus if the latter segments are included in the prescribed region, our modelled $M_{w} \ge 9$ ARIs continue to reduce (Table 1).

Table 1 also highlights the diversity of ARIs estimated from moment-conservation type arguments (including our model). For example in the Tohoku region of Japan, Kagan and Jackson (2013) estimated that $M_{w} \ge 9$ events have ARI $\simeq$ 300–400 years by constraining the parameters of a tapered Gutenberg-Richter type model with tectonic convergence rates and earthquake catalogue data. In the same region Butler et al. (2016) obtained an ARI of 1148 (490–3448) using the ‘regionally scaled global moment rate’ (RSGR) method, whereas our method suggests ARIs intermediate between these two estimates (Table 1).

Systematic differences are expected between our model and the RSGR method used by Butler et al. (2016). The latter partitions global subduction seismicity among source-zones in proportion to their length and trench-normal convergence rate (Burbidge et al. 2008). It thus ignores variability in $M_{w,max}$, coupling, and the source-zone width, whereas these factors are included in our model, albeit with significant uncertainty (e.g. Fig. 3). Therefore compared with our model the RSGR method should predict more frequent earthquakes on narrow source-zones with apparently low coupling (e.g. Marianas trench), and conversely on wide source-zones with apparently high coupling (e.g. South America). This seems consistent with predictions of each model near Chile, Japan, Kamchatka and Sumatra (Table 1). However the relationship does not extend to the wide Alaskan megathrust, where both approaches give similar results (Table 1). This is because the Alaskan segment of our Alaska–Aleutian source-zone does not feature GCMT thrust earthquakes with $M_{w}>7.15$, causing the Bayesian weight update to prefer moderately low coupling (prior mean $c=0.75$; posterior mean $c=0.35$). The effect is moderated by the 50% weight assigned to the unsegmented Alaska-Aleutians source which exhibits more GCMT seismicity (prior mean $c=0.64$; posterior mean $c=0.49$). Nonetheless the lower overall coupling in our model effectively offsets the high width on the Alaskan megathrust, ultimately leading to results similar to the RSGR method.

Considering our model makes limited use of site-specific long-term data (to facilitate global application), our ARIs are not assumed to be more accurate than others in Table 1 at any particular site. However the fact that our results are comparable to a range of other studies, many of which employ much longer term observational data, gives some support to the method.

3.5 Maximum-Stage Exceedance-Rates at Hazard Points

For each earthquake-tsunami scenario, the maximum-stage (i.e. maximum simulated water-level above ambient sea level) is used to describe the tsunami size at any given location. In practice the tsunami model time-series are not stored at every grid cell due to file storage limitations; instead they are stored at a set of around 20,000 locations (termed ‘hazard points’) which are globally distributed but have much higher density near Australia (Davies and Griffin 2018). For each hazard point the tsunami maximum-stage exceedance-rates are derived from the earthquake magnitude-frequency models as described below.

First consider a single unsegmented source-zone (or an individual segment of a segmented source-zone). If the earthquake-slip and rigidity models are specified then each individual earthquake-tsunami scenario e on the source has an associated family of occurrence-rates $r_{e,i}$ which are derived by partitioning each logic-tree $GR_{i}$ curve among all scenarios on the source (Eqs. 9, 12). Each $GR_{i}$ and $r_{e,i}$ also have an associated Bayesian posterior weight $w_{i}$ (Sects. 3.2 and 3.3). For a given hazard point p and scenario e, denote the tsunami maximum-stage as $\eta _{e,p}$. Then for each $GR_{i}$ there is an associated maximum-stage exceedance-rate curve at p, given by:

$$\begin{aligned} \Upsilon _{i}^{p} (x) = & \sum\limits_{e} {r_{{e,i}} } {\mathcal{I}}(\eta _{{e,p}} > x) \\ = & \sum\limits_{e} {\left[ {\left( {GR_{i} \left( {M_{{w,e}} - \frac{\Delta }{2}} \right) - GR_{i} \left( {M_{{w,e}} + \frac{\Delta }{2}} \right)} \right)Pr(e|M_{w} = M_{{w,e}} ){\mathcal{I}}(\eta _{{e,p}} > x)} \right]} \\ \end{aligned}$$

(16)

where the second step simply expands $r_{e,i}$ using Eq. 9 and is useful below. Here $\Upsilon _{i}^{p}(x)$ gives the rate (average number of events per year) of earthquake-tsunamis with maximum-stage greater than x at point p, assuming that $GR_{i}$ is correct. The indicator function $\mathcal {I}()$ is defined to be unity if its argument is true, and zero otherwise. Equation 16 leads to a family of maximum-stage exceedance-rate curves at each hazard point for each unsegmented source-zone (or individual segment). To summarise the results it is natural to define the logic-tree-mean maximum-stage exceedance-rate curve $\Upsilon ^{p}(x)$ (events/year) as:

$$\begin{aligned} \Upsilon ^{p}(x)= & {} \sum _{i} w_{i} \Upsilon _{i}^{p}(x) \nonumber \\= & {} \sum _{e} \left[ \left( \overline{GR}(M_{w,e} - \frac{\Delta }{2}) - \overline{GR}(M_{w,e} + \frac{\Delta }{2}) \right) Pr(e | M_{w} = M_{w,e}) \mathcal {I}(\eta _{e,p} > x) \right] \end{aligned}$$

(17)

where $\overline{GR}$ is the posterior-mean magnitude exceedance-rate curve over all logic-tree branches. The second step follows from Eq. 16 and highlights that individual $\Upsilon _{i}^{p}(x)$ do not need to be calculated. This facilitates efficient computation, and is a benefit of the scenario conditional probability model being independent of i (Sect. 3.2). This logic-tree-mean maximum-stage exceedance-rate can be straightforwardly generalised to multiple source-zones by summation of their $\Upsilon ^{p}(x)$ values. On source-zones with segmentation 50% weight is placed on the union-of-segments interpretation, and the remainder on the unsegmented interpretation (as was done for the magnitude exceedance-rates).

Percentile maximum-stage exceedance-rate curves are also useful to indicate the uncertainty in the tsunami hazard (Power et al. 2017). For example, consider the 84th percentile maximum-stage exceedance-rate at point p, denoted $\Upsilon ^{p, 84}(x)$ with units (events/year) which is a function of the desired maximum-stage x. For the case of an unsegmented source-zone or single segment, $\Upsilon ^{p, 84}(x)$ is defined as the smallest number such that:

$$\begin{aligned} \sum _{i} \left( w_{i} \mathcal {I}\left( \Upsilon _{i}^{p}(x) \le \Upsilon ^{p, 84}(x) \right) \right) \ge 84/100 \end{aligned}$$

(18)

For a given maximum-stage x, this implies 84% of the logic-tree weight is assigned to maximum-stage exceedance-rates $\le \Upsilon ^{p, 84}(x)$. Eq. 18 directly generalises to other percentiles in the open interval (0, 100). Note a different definition was used in Davies and Griffin (2018) for computational expedience; in comparison Eq. 18 is more rigorous but relatively expensive to compute because all $\Upsilon _{i}^{p}(x)$ are required. Although Eq. 18 is used herein, the impact on our percentile uncertainty calculations is small; for instance the 84th percentile results in Sect. 4.2 differ from those of Davies and Griffin (2018) by less than 5% at 90% of hazard points.

The generalisation of exceedance-rate percentiles (Eq. 18) to multiple source-zones is more complex than for the logic-tree-mean (Eq. 17) because it depends on assumptions about the dependence of uncertainties between source-zones; we defer full discussion of this to Sect. 4.2. However note that for a possibly segmented source-zone, the maximum-stage exceedance-rate for a given percentile and maximum-stage is computed by summing the results of Eq. 18 on each individual segment (which prevents cancellation of uncertainties due to segmentation, and is consistent with the co-monotonic treatment discussed in Sect. 4.2). Given a 50% weight on both the ‘union-of-segments’ and ’unsegmented’ interpretations, the combined distribution of exceedance-rates for a given maximum-stage is a 50:50 mixture of the ‘union-of-segments’ and ‘unsegmented’ exceedance-rate distributions. The latter two distributions can be computed individually from their percentiles; it is then straightforward to derive the full mixture distribution and compute any desired percentiles directly.

4 Results

4.1 Sensitivity of Offshore Hazard to the Chosen Slip and Rigidity Model

The sensitivity analysis focusses on the ARI = 500 year tsunami maximum-stage at sites offshore of Australia (Fig. 8a). To compute this, for every source-zone the logic-tree-mean maximum-stage exceedance-rate (Eq. 17) is calculated at 100 maximum-stage values logarithmically spaced from 0.02 to 20 m; then for each maximum-stage the exceedance-rates are summed over all source-zones, and finally the ‘ARI = 500 year maximum-stage’ is defined as the maximum-stage that results in this summed exceedance-rate being 1/500, interpolating as required. Irrespective of the chosen slip or rigidity model, wave shoaling over the continental shelf leads to strong shore-normal gradients in tsunami size (Fig. 8a). This complicates interpretation at the continental scale, and so for subsequent analysis the results are normalised to 100 m depth using Green’s law (i.e. multiplied by $(\text {depth}/100)^{1/4}$). Normalisation greatly reduces the depth-dependence of the results and emphasises regional patterns in the offshore tsunami size (Fig. 8b).

Fig. 8

a Maximum-stage at ARI = 500 years, using the HS model with constant $\mu$ for illustration. b The same data normalised to a depth of 100 m using Green’s law (i.e. multiplied by $(\text {depth}/100)^{0.25}$), to reduce the effect of depth variations

For each combination of earthquake slip and rigidity model, the normalised ARI = 500 maximum-stage is depicted in Fig. 9. Comparison of models with constant $\mu$ (top row) and depth-varying $\mu$ (bottom row) indicates the choice of rigidity model has a minor effect on the results when the earthquake-slip model is fixed (Fig. 9). Switching between rigidity models typically leads to point-wise changes of a few percent, and while the difference varies from site to site it is always less than 10%.

Fig. 9

Maximum-stage at ARI = 500 years with Green’s law normalisation to 100 m depth, for all slip and rigidity models

The choice of earthquake slip model has a more substantial impact on the results (Fig. 9). The FAUS model produces smaller ARI = 500 tsunamis than both the VAUS and HS models (Fig. 9); for example the FAUS/VAUS ARI = 500 maximum-stage ratio is around 0.67 (median over all sites), with 90% of sites in (0.6–0.84) irrespective of the rigidity. Differences between the VAUS and HS models are much smaller (Fig. 9), with the VAUS/HS ARI=500 maximum-stage ratio $\simeq ~0.91$ (median over all sites), with 90% of sites in (0.85–0.96).

These differences reflect both the varying capacity of the earthquake slip models to produce large tsunamis, and our application of bias-adjustment via a non-uniform partition of the parent FAUS scenario occurrence-rates (Sect. 3.2). Recall bias-adjustment was not applied to the FAUS model because its scenarios have little variability by construction, so even though they poorly represent some observed tsunamis (Fig. 2b) no improvement can be obtained by preferentially weighting some subset of scenarios. Conversely, both the HS and VAUS models produce more variable scenarios that are amenable to bias adjustment. For the VAUS model this resulted in a strong preference for compact, high-slip scenarios (Fig. 2d), which tend to produce larger tsunamis than uniform-slip scenarios with similar magnitude but low or median slip. This is the key driver of differences between the VAUS and FAUS hazard results (Fig. 9). While the HS model was subject to a much smaller bias-adjustment, the similarity of the HS and VAUS results reflects that HS scenarios can simulate slip asperities directly without recourse to compact rupture area. Considering the VAUS model completely ignores earthquake slip heterogeneity, it is remarkable that the difference with a heterogeneous-slip model is only around 10% once a preference for compact ruptures is accounted for (Fig. 9).

4.2 Sensitivity of Offshore Hazard to Epistemic Uncertainty in the Magnitude-Frequency Distributions

Uncertainties in PTHA also result from the uncertain frequency of large-magnitude earthquakes (e.g. Fig. 3). It is important to understand the relative significance of this compared with the choice of slip and rigidity model, to help guide future improvements to PTHA methodologies (Sepúlveda et al. 2019). A complication arises because the site-specific hazard is often affected by multiple source-zones. Thus we must determine whether the uncertain earthquake frequencies on these source-zones are independent, or exhibit some kind of epistemic-uncertainty dependence. For example, the frequency of $M_{w} > 9$ earthquakes on the Kermadec-Tonga trench is highly uncertain due to poor constraints on $M_{w,max}$ (Fig. 3), but if future research demonstrated that $M_{w,max} > 9$ on the Tonga segment, we ask if this would influence our belief that $M_{w,max} > 9$ elsewhere (e.g. on the nearby Kermadec segment, or other source-zones)? If the answer to such questions is always ‘no’ then the uncertainties are independent, and otherwise they are dependent.

Dependence does not affect the mean hazard (because the mean of the sum of random variables is always equal to the sum of their means), but does affect percentile uncertainty calculations. If two source-zones show positive dependence in the magnitude-frequency epistemic-uncertainty, then the hazard uncertainty will increase at coastal sites affected by both. Although it is unclear how to best specify inter-source-zone epistemic-uncertainty dependence, in many situations independence seems unlikely. Source-zone parameters such as $M_{w,max}$, coupling coefficients and GR b-values are often hypothesised to be related to other physical properties of the source-zone (e.g. McCaffrey 1997; Scholz and Campos 2012; Nishikawa and Ide 2014; Bilek and Lay 2018), and if correct such theories imply epistemic-uncertainty dependence, because source-zones with similar properties will deviate similarly from the model (assuming those properties are not already accounted for). For example it has been hypothesised that subduction-zones with high down-dip curvature are less likely to host large earthquakes due to heterogeneities in shear strength (Bletery et al. 2016). This may or may not be correct, but if true it suggests the relatively high-curvature Solomon, New Hebrides, Kermadec-Tonga, Philippines, Marianas and Scotia subduction zones may host high-magnitude earthquakes infrequently compared with our model (which does not explicitly consider curvature). This possibility implies some epistemic-uncertainty dependence between these source-zones. A conflicting hypothesis is that $M_{w,max}$ is limited only by the source-zone size (McCaffrey 2008). This may or may not be correct, but if correct implies the true frequency of high magnitude earthquakes will be high relative to the model on most source-zones (i.e. wherever the model places significant weight on smaller $M_{w,max}$ values). The key point is that our model may have structural errors. This suggests some inter-source-zone epistemic-uncertainty dependence, albeit difficult to specify.

To robustly account for the unknown epistemic-uncertainty dependence structure, herein the multi-source-zone maximum-stage exceedance-rate percentile curves are computed assuming every source-zone simultaneously attains the same percentile (Fig. 10). This is termed ‘co-monotonic’ dependence (Deelstra et al. 2009). For instance the 16th-percentile panel in Fig. 10 is computed assuming that at each hazard point, the 16th percentile maximum-stage exceedance-rate curve is ‘true’ for all source-zones simultaneously, so for any maximum-stage these exceedance-rates may be summed to derive the multi-source-zone exceedance-rate (and similarly for the other percentiles). Co-monotonicity is widely used to robustly model dependence in economic theories of decision under risk and uncertainty (Deelstra et al. 2009) and prevents uncertainties on multiple source-zones from partially cancelling, as would occur under independence. Because most coastal sites are significantly affected by only a few source-zones, the site-specific maximum-stage exceedance-rate uncertainties are not reliant on the global correctness of the co-monotonic assumption, but rather that it describes the dependence of locally significant source-zones (Davies et al. 2017). The co-monotonic approach bypasses the need to fully describe this dependence structure, albeit at the expense of some conservatism.

Fig. 10

Percentile uncertainties in maximum-stage at ARI = 500 years with Green’s law normalisation to 100 m depth, due to epistemic-uncertainty in magnitude-frequency distributions. Results use the HS model with constant $\mu$

Compared with the choice of slip and rigidity model, epistemic uncertainty in the magnitude-frequency distributions leads to large uncertainty in the ARI = 500 maximum-stage (Fig. 10). Taking the HS model with constant $\mu$ for illustration, the 16th, 50th and 84th percentile values in Fig. 10 are respectively $\simeq$ 50%, 87% and 126% of the mean discussed earlier (top right-panel of Fig. 9). The latter ratios vary spatially, but mostly within $\pm\, 10$%. The dominance of magnitude-frequency related uncertainties in our model is qualitatively consistent with results of recent tsunami hazard assessments in the South China Sea (Li et al. 2016; Sepúlveda et al. 2019). They found the maximum-stage at ARIs $\simeq$ 100–1000 years changed by well over 100% due to the choice of magnitude-frequency model, as compared with changes $\simeq 20-60$% due to the earthquake slip representation.

4.3 Global Scale Results

Although our study is focussed on Australia, some results were stored globally to facilitate model testing and interpretation (Fig. 11). At the global level the model suggests large waves are most likely around major subduction zones. The South America and Kurils-Japan subduction-zones are particularly prominent because they are wide, converging relatively rapidly, definitely have $M_{w,max} > 9$, and their GCMT earthquake history leads the model to favour reasonably high coupling (posterior mean $c \simeq 0.77$ in both cases). The model also predicts substantial penetration of large waves into the central Pacific Ocean (Fig. 11). Noting that both the 1946 Aleutian and 1960 Chile earthquakes led to large far-field tsunami runup at central Pacific sites such as Hawaii, the Marquesas and Easter Island (NGDC 2018), this result seems qualitatively reasonable. Compared with the global results the hazard in Australia is moderate overall, except on the northwest coast which is directly exposed to tsunamis generated on the eastern Sunda Arc (Fig. 11).

It is illuminating to assess the FAUS, VAUS and HS model return periods corresponding to larger offshore waves observed near Japan during the 2011 Tohoku tsunami. During this event two GPS gauges near Iwate in Japan recorded maximum-stage values exceeding 6 m. They were located about 12 km offshore in 200 m depth and separated by 40 km (termed ‘Iwate M’ and ‘Iwate S’ in Satake et al. 2013, see the latter study for locations and observed time-series). Our nearest model point falls between these gauges but slightly further offshore (395 m depth). If the wave shoaling follows Green’s law then the corresponding maximum-stage is around 5.1 m at the model point, which has a modelled ARI of 970 years (HS), 1208 years (VAUS), and never occurs with the FAUS model (ARI $= \infty$). This further highlights the potential for FAUS scenarios to underestimate offshore wave-heights, and the tendency for comparable results to be obtained using either the (bias-adjusted) VAUS or HS scenarios.

Fig. 11

Maximum-stage (m) at ARI = 500 years, normalised to 100 m depth using a Green’s law factor $( (\text {depth}/100)^{0.25})$ to reduce the effect of depth variations. The HS model with constant $\mu$ was used

5 Conclusions

The framework in this paper facilitates a consistent treatment of earthquake-scenario rates for PTHA using different slip and rigidity models, while maintaining reasonable consistency with the historical earthquake record and tectonic constraints. It features a number of improvements relative to previous approaches for large-scale PTHA (e.g. Power et al. 2017; Davies et al. 2017):

• The edge-effect adjustment leads to a better match between modelled time-integrated slip rates and spatial variations in tectonic convergence

• Earthquake catalogue data is more efficiently used to control the logic-tree weights, in a manner that also accounts for the choice of rigidity model.

• Non-uniform scenario weights are used to partially offset biases in the earthquake slip models.

This provides a suitable basis to study the sensitivity of PTHA results to the choice of earthquake slip and rigidity model.

Within our framework the choice of rigidity model has a small effect on the offshore hazard. Although shallow low rigidity zones may permit surprisingly large tsunamis for their magnitude, tectonic constraints imply such events should occur less often than higher-rigidity events with similar magnitude and lower slip. A similar trade-off was identified by Scala et al. (2019) who used a completely different ‘slip-amplification’ approach to represent the effect of depth-varying rigidity on earthquake slip. Our ‘magnitude-relabelling’ approach implies the rigidity model affects the hazard by changing our interpretation of the integrated slip released by historical earthquakes (which in turn affects the logic-tree weights for the magnitude-frequency distributions). Compared with slip-amplification (Scala et al. 2019), the magnitude-relabelling approach has the practical advantage of not requiring any re-computation of tsunami waveforms. However it is not obvious whether one-or-other approach should be preferred on theoretical grounds, or the extent to which their results differ. This should be considered in future research.

Our results confirm that the representation of earthquake slip has a significant effect on PTHA, even in the far-field (Li et al. 2016). This is significant because PTHAs often employ FAUS-like uniform-slip scenarios with magnitude-dependent length and width based on a scaling relation (e.g. Løvholt et al. 2014; Roshan et al. 2016; Davies et al. 2017; Kalligeris et al. 2017). In our study some historical tsunamis were poorly represented with the FAUS approach, and it predicted significantly lower tsunami hazard in Australia than the other approaches. Thus we suggest the FAUS approach should not be used, even in the far-field. While the HS and VAUS scenarios showed better performance, there was a clear tendency for good-fitting VAUS scenarios to be ‘compact’ relative to the scaling-relation predictions. Once accounted for via bias-adjustment, the VAUS and HS scenarios produced similar ARI=500 maximum-stage estimates for Australia. This suggests both HS and VAUS can usefully represent earthquake-generated tsunamis for PTHA. For some hazard modelling applications the use of both scenario types could be beneficial to represent epistemic uncertainties in tsunami generation. In other cases the fewer degrees-of-freedom of VAUS scenarios may be exploited to reduce computational effort, as noted by An et al. (2018) in the context of tsunami early warning.

Although the representation of earthquake size and slip is important for producing realistic tsunami wave-forms, in this study the largest source of uncertainty remains the earthquake magnitude-frequency relations. Future work may reduce these uncertainties by more efficiently using paleo-seismic and long-term historical observations, coupled with appropriate treatment of the data uncertainties (Griffin et al. 2018). Refinements of the model’s structure should simultaneously be considered (e.g. allowing for non-Poissonion event times, Geist 2014; Moernaut et al. 2018) and are likely to become more important when additional data is used to constrain the model. In addition, the development of more refined representations of inter-source-zone epistemic-uncertainty dependence may allow the tsunami hazard uncertainty to be reduced at some sites affected by multiple source-zones, as compared with the co-monotonic treatment applied herein.