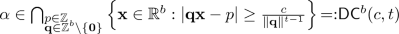Abstract
We consider separable 2D discrete Schrödinger operators generated by 1D almost Mathieu operators. For fixed Diophantine frequencies, we prove that for sufficiently small couplings the spectrum must be an interval. This complements a result by J. Bourgain establishing that for fixed couplings the spectrum has gaps for some (positive measure) Diophantine frequencies. Our result generalizes to separable multidimensional discrete Schrödinger operators generated by 1D quasiperiodic operators whose potential is analytic and whose frequency is Diophantine. The proof is based on the study of the thickness of the spectrum of the almost Mathieu operator and utilizes the Newhouse Gap Lemma on sums of Cantor sets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The almost Mathieu operator is the discrete Schrödinger operator \( H_{\lambda ,\alpha ,\omega } \) on \( \ell ^2(\mathbb {Z}) \) defined by
for every \( \psi \in \ell ^2(\mathbb {Z}),n\in \mathbb {Z} \). Here, \( \lambda \in \mathbb {R} \) is the coupling, \( \alpha \in \mathbb {R}/\mathbb {Z}{=}{:}\mathbb {T} \) is the frequency, and \( \omega \in \mathbb {T} \) is the phase. The operator has its origins in solid-state physics and the study of electrons. The operator also has a connection to the quantum Hall effect—a Nobel-prize-worthy discovery by K. von Klitzing, G. Dorda, and M. Pepper in 1980 [27]. The connection was made by D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs in 1982 [37]. For a discussion of discrete Schrödinger operators and the almost Mathieu operator, see the 2019 preprint by S. Jitomirskaya [24]. For more discussions, see [6, 9, 14, 22, 23, 28, 30, 36].
P. G. Harper in 1955 [19, 20] under the tutelage of R. E. Peierls established that electrons in a cubic lattice and under a magnetic field have nondiscrete nonevenly spaced broadened energy values. Harper used a tight-binding approximation now called the Harper model. The Schrödinger operator governing the spectrum of the Harper model is the almost Mathieu operator \( H_{\lambda ,\alpha ,\omega } \) with \( \lambda =1 \). Physicists sought to better understand the topological structure of the spectrum \( \Sigma _{\lambda ,\alpha ,\omega } \) of \( H_{\lambda ,\alpha ,\omega } \). M. Azbel in 1964 [5] conjectured and D. Hofstadter in 1976 [21] computationally supported that \( \Sigma _{\lambda ,\alpha ,\omega } \) has the characteristic of being either band-like for rational \( \alpha \) or fractal-like for irrational \( \alpha \). Decades later A. Avila and S. Jitomirskaya in 2009 [4] made the final contribution to the resolution of the Ten Martini Problem which sought to confirm the conjectured topological structure of \( \Sigma _{\lambda ,\alpha ,\omega } \). If \( \alpha =\frac{p}{q}\in \mathbb {T}\cap \mathbb {Q} \), then \( \Sigma _{\lambda ,\alpha ,\omega } \) is a disjoint union of at most q-many compact intervals. If \( \alpha \in \mathbb {T}{\setminus }\mathbb {Q} \), then \( \Sigma _{\lambda ,\alpha ,\omega } \) is a Cantor set. Also, \( \Sigma _{\lambda ,\alpha ,\omega } \) is independent of the phase \( \omega \) when the frequency \( \alpha \) is irrational. This last fact can be found in the 1982 review paper by B. Simon [36] (where the name of the almost Mathieu operator was introduced) and applies to operators with quasiperiodic potentials; the definition of quasiperiodic potentials can be found within Sect. 2.3. In general, phase independence of the spectrum for operators with quasiperiodic potentials follows from the fact that the underlying topological dynamical system \( (\mathbb {T}^b,\mathbb {Z}) \) is minimal [14].
Let \( d\ge 2 \) be a positive integer. We consider the d-dimensional analog operator \(\smash {\widehat{H}} \) generated by almost Mathieu operators. Specifically, \( \smash {\widehat{H}} \) is the discrete Schrödinger operator on \( \ell ^2(\mathbb {Z}^d) \) defined by
for every \( \psi \in \ell ^2(\mathbb {Z}^d),n\in \mathbb {Z}^d \); \( \left\{ e_1,\ldots ,e_d\right\} \) is the standard basis. The operator \( \smash {\widehat{H}} \) and the spectrum \( \smash {\widehat{\Sigma }}=\Sigma _{\lambda _1,\alpha _1,\omega _1}+\cdots +\Sigma _{\lambda _d,\alpha _d,\omega _d} \) are the main objects of study in this paper. The theory of the almost Mathieu operator provides insight into the theory of \( \smash {\widehat{H}} \). Consider the following theorem established by A. Avila and D. Damanik in 2008 [3]: If \( \lambda \ne 1 \) and \( \alpha \in \mathbb {T}{\setminus }\mathbb {Q} \), then the integrated density of states of the almost Mathieu operator is absolutely continuous. Along with a theorem by Steinhaus, which states that the sum of two sets with positive Lebesgue-measure contains an open interval, we immediately obtain the following proposition.
Proposition 1.1
Assume at least two among \( \lambda _1,\ldots ,\lambda _d \) are not equal to 1 and \( \alpha _1,\ldots ,\alpha _d\in \mathbb {T}{\setminus }\mathbb {Q} \). Then, \( \smash {\widehat{\Sigma }} \) has a dense interior.
More can be obtained in the small coupling and Diophantine frequency regime. This is the context of the main theorem in this paper.
Theorem 1.2
Assume \( \alpha _1,\ldots ,\alpha _d \) are irrational and satisfy a Diophantine condition. There exists \( \varepsilon =\varepsilon (\alpha _1,\ldots ,\alpha _d)>0 \) such that if \( 0<|\lambda _1|,\ldots ,|\lambda _d|<\varepsilon \), then \( \smash {\widehat{\Sigma }} \) is an interval.
We mention for comparison a theorem by J. Bourgain in 2002 [7].
Theorem 1.3
(J. Bourgain [7]) Assume \( \lambda _1,\ldots ,\lambda _d=\lambda >0 \). There exist positive Haar-measure sets \(A_{\lambda }^{(1)} ,\ldots , A_{\lambda }^{(d)} \subseteq \mathbb {T} \) such that if \( \alpha _1\in A_{\lambda }^{(1)},\ldots ,\alpha _d\in A_{\lambda } ^{(d)}\), then \({\widehat{\Sigma }} \) has gaps. Furthermore, \(A_{\lambda }^{(k)}\) can be chosen to be a subset of the Diophantine frequencies and lie within \( [0,\varepsilon ] \) for any \( \varepsilon >0 \).
We say a few words on the proof of Theorem 1.2. Observe \(\smash {\widehat{\Sigma }} \) is the sum of Cantor spectra \( \Sigma _1+\cdots +\Sigma _d \), where henceforth \( \Sigma _k{:}{=}\Sigma _{\lambda _k,\alpha _k,\omega _k} \). Indeed, the potential of \( \smash {\widehat{H}} \) is separable. In general, the spectra of separable multidimensional operators are sums of the spectra of 1D operators. This fact can be found within [12]. See also another proof involving the convolution of density of states measures within [13]. The Newhouse Gap Lemma may be utilized to guarantee that \( \Sigma _1+\cdots +\Sigma _d \) is an interval thereby establishing Theorem 1.2. The notion of thickness, which is a quantitative characterization of nonempty compact subsets K of \( \mathbb {R} \) often denoted \( \tau (K) \), was utilized by S. Newhouse in the 1970s [31,32,33] to prove the namesake Newhouse Gap Lemma. See also for a short proof Sect. 4.2 on page 63 within [34]. The definition of thickness can be found within Sect. 2.6. We abridge the Newhouse Gap Lemma: Let \( K_1 \) and \( K_2 \) be nonempty compact subsets of \( \mathbb {R} \). Assume the maximal-gap-lengths of \( K_1 \) and \( K_2 \) are sufficiently small relative to the diameters of \( K_1 \) and \( K_2 \), and \( 1\le \tau (K_1)\cdot \tau (K_2) \). Then, \( K_1+K_2 \) is an interval. S. Astels in 1999 [1, 2] generalized the Newhouse Gap Lemma to obtain the following; see Theorem 2.7 for the unabridged version.
Theorem 1.4
(S. Astels [1, 2]) Let \( K_1,\ldots ,K_d \) (\( d\ge 2 \)) be nonempty compact subsets of \( \mathbb {R} \). Assume the maximal-gap-lengths of \( K_1,\ldots ,K_d \) are sufficiently small relative to the diameters of \( K_1,\ldots ,K_d \), and \( 1\le \frac{\tau (K_1)}{\tau (K_1)+1}+\cdots +\frac{\tau (K_d)}{\tau (K_d)+1} \). Then \( K_1+\cdots +K_d \) is an interval.
Because \( \lambda _k \) is small, one can think of \( H_{\lambda _k,\alpha _k,\omega _k} \) as a perturbation of the discrete Laplacian whose spectrum is the interval \( [-2,2] \). Specifically, \( \Sigma _k \) converges to \( [-2,2] \) in the Hausdorff metric as \( \lambda _k\rightarrow 0 \). Also, the diameter of \( \Sigma _{k} \) converges to the diameter of \( [-2,2] \) as \( \lambda _k\rightarrow 0 \). Indeed, \( |\mathrm {diam}\,\sigma (A)-\mathrm {diam}\,\sigma (B)|\le 2\,\mathrm {dist}_{\mathsf {Haus}}(\sigma (A),\sigma (B))\le 2\left\Vert A-B\right\Vert \) for bounded self-adjoint operators A and B. Therefore, \( \Sigma _k \) has a small maximal-gap-length relative to the diameters of \( \Sigma _1,\ldots ,\Sigma _d \). As a result, to utilize the Newhouse Gap Lemma it is enough to establish that the thickness of the spectrum of the almost Mathieu operator approaches infinity as the coupling approaches zero.
Theorem 1.5
The spectrum of the almost Mathieu operator \( H_{\lambda ,\alpha ,\omega } \) with irrational frequency fixed and assumed to satisfy a Diophantine condition
has thickness approaching infinity as the coupling \( \lambda \) approaches zero, i.e.
Theorem 1.5 extends to 1D quasiperiodic operators whose potential is analytic and whose frequency is Diophantine; combine Theorem 2.4 and Theorem 2.5 and Lemma 4.1. As a result, Theorem 1.2 extends to separable multidimensional discrete Schrödinger operators generated by 1D quasiperiodic operators whose potential is analytic and whose frequency is Diophantine.
Theorem 1.6
For fixed Diophantine frequencies \( \alpha _1,\ldots ,\alpha _d \), the spectrum is an interval for separable d-dimensional discrete Schrödinger operators generated by 1D \( \alpha _k \)-quasiperiodic analytic operators \( H_k=\Delta +V_k \) with \( \alpha _k \)-dependent sufficiently small norms \( \Vert V_k\Vert \).
Theorem 1.6 is necessarily perturbative due to Theorem 1.3. Specifically, the smallness of the norm depends on the Diophantine frequency. We conclude this section with a few words on related mathematical results and questions. The definitions of limit-periodic and almost-periodic potential can be found within [15] and [36], respectively. It suffices to say that the collection of all almost-periodic potentials is a broad class of potentials which contains the periodic and limit-periodic and quasiperiodic potentials. The definitions of box-counting and Hausdorff dimension can be found within [16]. A Cantorval is a nonempty compact subset C of \( \mathbb {R} \) such that C has no isolated connected components and C has a dense interior; we mention for comparison that a Cantor set is a nonempty compact subset C of \( \mathbb {R} \) such that C has no isolated points and C has no interior points.
-
(a)
We establish a single-interval-characterization for the spectra of separable multidimensional discrete Schrödinger operators generated by 1D quasiperiodic analytic operators \( H_k=\Delta +V_k \) with Diophantine-frequency-dependent sufficiently small norms \( \Vert V_k\Vert \). The same characterization can be said about periodic \( V_k \) [18] and cannot be said about limit-periodic \( V_k \) [15].
-
(b)
R. Han and S. Jitomirskaya [18] proved that periodic (not necessarily separable) multidimensional discrete Schrödinger operators have interval spectra when the norm of the potential is small and at least one period is odd. This is the discrete analog of the L. Parnovski [35] resolution of the continuous Bethe–Sommerfeld Conjecture. Moreover, the resolution was extended to quasiperiodic (not necessarily separable) multidimensional continuous Schrödinger operators for almost-all frequencies [26]. This paragraph is the only place where continuous Schrödinger operators are mentioned, and it is done so to motivate the following question. Can one extend the [18, 26, 35] results to quasiperiodic (not necessarily separable) multidimensional discrete Schrödinger operators for almost-all frequencies? Specifically, can one remove the separability condition from Theorem 1.6? Moreover, can one remove the Diophantine condition from Theorem 1.6? For example, can the frequencies satisfy a Liouvillian condition? In a sense, this means that the irrational frequencies are well approximated by rational numbers.
-
(c)
D. Damanik, J. Fillman, and A. Gorodetski [15] proved that there exists a dense subset \( \mathcal {B} \) of 1D limit-periodic potentials such that \( \mathcal {B} \)-type operators have Cantor spectra with zero (lower) box-counting dimension. Furthermore, separable multidimensional discrete Schrödinger operators generated by \( \mathcal {B} \)-type operators have Cantor spectra with zero (lower) box-counting dimension. Is it true that the spectra of separable multidimensional discrete Schrödinger operators generated by 1D almost-periodic operators is either a finite union of disjoint intervals or a Cantor set or a Cantorval? In view of Proposition 1.1, does there exist \( \lambda _1,\ldots ,\lambda _d \) with at least two not equal to 1 and \( \alpha _1,\ldots ,\alpha _d\in \mathbb {T}{\setminus }\mathbb {Q} \) such that \( \smash {\widehat{\Sigma }} \) is a Cantorval?
-
(d)
D. Damanik and A. Gorodetski [12] proved that 1D Fibonacci Hamiltonians have Cantor spectra \( \Sigma _\lambda \) with Hausdorff dimension strictly between zero and one and with thickness strictly greater than zero, and \( \lim _{\lambda \rightarrow 0}\mathrm {dim}_{\mathsf {Haus}}(\Sigma _\lambda )=1 \) and \( \lim _{\lambda \rightarrow 0}\tau (\Sigma _\lambda )=+\infty \). Consequently, they establish a single-interval-characterization for the spectra of separable multidimensional discrete Schrödinger operators generated by 1D Fibonacci Hamiltonians with sufficiently small couplings.
-
(e)
For fixed \( s\in \mathbb {R}{\setminus }\left\{ -1,0,1\right\} \) and for fixed Diophantine frequency in the 2-torus M. Goldstein, W. Schlag, and M. Voda [17] proved that for sufficiently large couplings the 1D operators with 2-frequency quasiperiodic potential \( V_{\lambda ,s,\alpha }:\mathbb {Z}\rightarrow \mathbb {R}:n\mapsto \lambda (\cos (2\pi n\alpha _1)+s\cos (2\pi n\alpha _2)) \) must have an interval spectrum. This complements a result by J. Bourgain [8] establishing that for fixed small coupling the 1D operator with potential \( V_{\lambda ,1,\alpha } \) has gaps in its spectrum for some (positive measure) Diophantine frequencies.
-
(f)
The separable operator considered in Theorem 1.6 but with added background potential (so the resulting operator is not necessarily separable) has been studied by J. Bourgain and I. Kachkovskiy [10]. Similar but distinct quasiperiodic (not necessarily separable) operators have been studied by S. Jitomirskaya, W. Liu, and Y. Shi [25]. The [10, 25] results pertain to the spectral type but not the topological structure of the spectrum as a set.
In Sect. 2, we state the preliminaries. In Sect. 3, we prove the main theorem. In Sect. 4, we prove a lemma used in the proof of the main theorem.
2 Preliminaries
Let \( A:\mathcal {H}\rightarrow \mathcal {H} \) be a bounded operator. The spectrum of A is denoted \( \sigma (A) \). Note \( \sigma (A) \) is a nonempty compact subset of \( \mathbb {C} \). Also note, if A is self-adjoint, then \( \sigma (A)\subseteq \mathbb {R} \).
2.1 Potentials and Schrödinger Operators
A (d-dimensional lattice) potential is a bounded real-valued function V on \( \mathbb {Z}^d \). Moreover, V also denotes the bounded self-adjoint multiplication operator on \( \ell ^2(\mathbb {Z}^d)\) defined by \( [V\psi ](n)=V(n)\psi (n) \) for every \( \psi \in \ell ^2(\mathbb {Z}^d),n\in \mathbb {Z}^d \). The (d-dimensional lattice) Schrödinger operator with respect to a potential \( V:\mathbb {Z}^d\rightarrow \mathbb {R} \) is the bounded self-adjoint operator H on \(\ell ^2(\mathbb {Z}^d) \) defined by \( H=\Delta +V \), where \( \Delta =\Delta ^{(d)} \) is the (d-dimensional lattice) Laplacian defined by \([\Delta \psi ](n)=\sum _{m\in \left\{ e_1,\ldots ,e_d\right\} }\psi (n+m)+\psi (n-m) \) for every \( \psi \in \ell ^2(\mathbb {Z}^d),n\in \mathbb {Z}^d \); \( \left\{ e_1,\ldots ,e_d\right\} \) is the standard basis.
2.2 Separable Potentials and the Laplacian
Let \( V:\mathbb {Z}^d\rightarrow \mathbb {R} \) be a potential. Say V is separable if there exist (sub)potentials \( V_1,\ldots ,V_d:\mathbb {Z}\rightarrow \mathbb {R} \) such that \( V(n)=V_1(n_1)+\cdots +V_d(n_d) \) for every \( n\in \mathbb {Z}^d \). The proof of the following theorem can be found within [12].
Theorem 2.1
Let \( V:\mathbb {Z}^d\rightarrow \mathbb {R}:n\mapsto V_1(n_1)+\cdots +V_d(n_d) \) be a separable potential. Define \( H{:}{=}\Delta ^{(d)}+V \). For each k, define \( H_k{:}{=}\Delta ^{(1)}+V_k \). Then,
By the spectral mapping theorem,
By Theorem 2.1,
Here, \( U_m \) is the unitary operator from \( \ell ^2(\mathbb {Z}^d) \) to \( \ell ^2(\mathbb {Z}^d) \) defined by \( [U_m\psi ](n)=\psi (n-m) \) for every \( \psi \in \ell ^2(\mathbb {Z}^d),n\in \mathbb {Z}^d \). Also here, \( \Phi _A \) is the Borel functional calculus with respect to a bounded operator A.
2.3 Quasiperiodic Potentials and the Almost Mathieu Operator
Let \( V:\mathbb {Z}\rightarrow \mathbb {R} \) be a potential. Let b be a positive integer. Say V is (b-frequency) quasiperiodic if there exists \( v\in C(\mathbb {T}^b,\mathbb {R}) \) and there exist \( \alpha ,\omega \in \mathbb {T}^b \) such that v is nonconstant and \( \left\{ 1,\alpha _1,\ldots ,\alpha _b\right\} \) is independent over the rationals and \( V(n)=v(n\alpha +\omega ) \) for every \( n\in \mathbb {Z} \). The proof of the following theorem can be found within [36].
Theorem 2.2
Let \( V_\omega :\mathbb {Z}\rightarrow \mathbb {R}:n\mapsto v\big |_{\mathbb {T}^b}(n\alpha +\omega ) \) be a quasiperiodic potential with parameter \( \omega \). Let \( H_\omega \) be the Schrödinger operator. Then, \( \sigma (H_\omega )=\Sigma _{\omega }{=}{:}\Sigma \) is independent of \( \omega \). Furthermore, \( \Sigma \) is a nonempty compact subset of \( \mathbb {R} \) and \( \Sigma \) has no isolated points.
The potential of the almost Mathieu operator \( V_{\lambda ,\alpha ,\omega }:\mathbb {Z}\rightarrow \mathbb {R}:n\mapsto 2\lambda \cos (2\pi (n\alpha +\omega )) \) is 1-frequency quasiperiodic when \( \alpha \) is irrational. By the resolution of the Ten Martini Problem within [4], the spectrum \( \Sigma _{\lambda ,\alpha ,\omega } \) of the almost Mathieu operator is a Cantor set when \( \alpha \) is irrational.
2.4 Integrated Density of States
Let \( V_{\omega }:\mathbb {Z}\rightarrow \mathbb {R}:n\mapsto v\big |_{\mathbb {T}^b}(n\alpha +\omega ) \) be a quasiperiodic potential with parameter \( \omega \). Let \( H_{\omega } \) be the Schrödinger operator. The integrated density of states (IDS) is
Here, \( \mu \) is the normalized Haar measure on \( \mathbb {T}^b \). Note \( \mathfrak {N}\upharpoonright (-\infty ,\inf \Sigma ]\equiv 0 \) and \( \mathfrak {N}\upharpoonright [\sup \Sigma ,+\infty )\equiv 1 \). The proof of Theorem 2.3 can be found within [36] and of Theorem 2.4 can be found within [11].
Theorem 2.3
(Gap Labeling) Let \( V:\mathbb {Z}\rightarrow \mathbb {R}:n\mapsto v\big |_{\mathbb {T}^b}(n\alpha +\omega ) \) be a quasiperiodic potential. Let H be the Schrödinger operator. Let \( \mathfrak {N} \) be the IDS. Define \( \Sigma {:}{=}\sigma (H) \). Let \( \mathrm {Gap}_{\mathsf {b}}(\Sigma ) \) be the collection of all bounded gaps of \( \Sigma \).
-
(i)
\( \mathfrak {N} \) is monotone and continuous.
-
(ii)
\( \left\{ x\in \mathbb {R}:\left( \forall \varepsilon>0\right) [\mathfrak {N}(x+\varepsilon )-\mathfrak {N}(x-\varepsilon )>0]\right\} =\Sigma \).
-
(iii)
\( \left\{ \mathfrak {N}(x):x\in U\in \mathrm {Gap}_{\mathsf {b}}(\Sigma )\right\} \subseteq \{\mathbf {n}\alpha -\left\lfloor \mathbf {n}\alpha \right\rfloor :\mathbf {n}\in \mathbb {Z}^b\}{\setminus }\left\{ 0\right\} \).
-
(iv)
\( \left\{ \mathfrak {N}(x):x\in U\in \mathrm {Gap}_{\mathsf {b}}(\Sigma )\right\} \supseteq \{\mathbf {n}\alpha -\left\lfloor \mathbf {n}\alpha \right\rfloor :\mathbf {n}\in \mathbb {Z}^b\}{\setminus }\left\{ 0\right\} \) \( \implies \) \( \Sigma \) is a Cantor set.
Theorem 2.4
(Hölder Continuity) Let \( V_{\lambda ,v,\alpha ,\omega }:\mathbb {Z}\rightarrow \mathbb {R}:n\mapsto \lambda v\big |_{\mathbb {T}^b}(n\alpha +\omega ) \) be a quasiperiodic potential with parameters \( \lambda ,v,\alpha ,\omega \). Let \( H_{\lambda ,v,\alpha ,\omega } \) be the Schrödinger operator. Fix \( v,\alpha \). Let \( \mathfrak {N}_{\lambda } \) be the IDS. Assume the following:
-
(i)
\(\alpha \) satisfies a Diophantine condition:
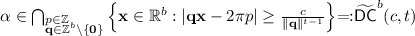 for some \( c>0,t>b \).
for some \( c>0,t>b \). -
(ii)
v satisfies a regularity condition: v is r-differentiable on \( \mathbb {T}^b \) for some \( r\ge 550t \).
There exist \( \lambda _0=\lambda _0(v,b,c,t,r)>0, C_{\mathsf {H}}=C_{\mathsf {H}}(b,c,t)>0 \) such that
for every \( \lambda _0\ge |\lambda |>0,x,y \).
2.5 Spectral Gaps
Let \( V:\mathbb {Z}\rightarrow \mathbb {R}:n\mapsto v\big |_{\mathbb {T}^b}(n\alpha +\omega ) \) be a quasiperiodic potential. Let H be the Schrödinger operator. Let \( \mathfrak {N} \) be the IDS. Define \( \Sigma {:}{=}\sigma (H) \). Let \( \mathrm {Gap}_{\mathsf {b}}(\Sigma ) \) be the collection of all bounded gaps of \( \Sigma \). Fix \( \mathbf {n}\in \mathbb {Z}^b{\setminus }\left\{ \mathbf {0}\right\} \). The \( \mathbf {n} \)-th spectral gap of \( \Sigma \) is either the element \( G^{(\mathbf {n})} \) in \( \mathrm {Gap}_{\mathsf {b}}(\Sigma ) \) such that \( \mathfrak {N}\upharpoonright \smash {\overline{G^{(\mathbf {n})}}}\equiv \mathbf {n}\alpha -\lfloor \mathbf {n} \alpha \rfloor \) or the empty set when such an element \( G^{(\mathbf {n})} \) does not exist. Moreover, \( (-\infty ,\inf \Sigma )\cup (\sup \Sigma ,+\infty ) \) is called the \( \mathbf {0} \)-th spectral gap of \( \Sigma \). The proof of the following theorem can be found within [29].
Theorem 2.5
(Gap Estimate) Let \( V_{v,\alpha ,\omega }:\mathbb {Z}\rightarrow \mathbb {R}:n\mapsto v\big |_{\mathbb {T}^b}(n\alpha +\omega ) \) be a quasiperiodic potential with parameters \( v,\alpha ,\omega \). Let \( H_{v,\alpha ,\omega } \) be the Schrödinger operator. Fix \( \alpha \). Fix \( r_0>r>0 \). Define \( \Sigma _{v}{:}{=}\sigma (H_{v,\alpha ,\omega }) \). For each \( \mathbf {n}\ne \mathbf {0} \), let \( G_{v} ^{(\mathbf {n})} =(E_{v}^{(\mathbf {n}){ -}}\), \( E_{v}^{(\mathbf {n}){+}}\)) be the \(\mathbf {n} \)-th spectral gap of \( \Sigma _{v} \). Assume the following:
-
(i)
\( \alpha \) satisfies a Diophantine condition:

for some \( c>0,t>b \).
-
(ii)
v satisfies a regularity condition: v is analytic on \( (\mathbb {T}+i(-r_0,r_0))^b \).
There exists \( \varepsilon =\varepsilon (b,c,t,r_0,r)>0 \) such that
for every \( \varepsilon \ge |v|_{r_0}>0,\mathbf {n}\ne \mathbf {0} \).
2.6 Thickness and Gap Lemmas
Let K be a nonempty compact subset of \( \mathbb {R} \). Henceforth \( K^{\scriptscriptstyle -}{:}{=}\inf K \) and \( K^{\scriptscriptstyle +}{:}{=}\sup K \). Let \( \mathrm {Gap}_{\mathsf {b}}(K) \) be the collection of all bounded gaps of K. Let U be a bounded gap of K. The left-plank of U, denoted \( \pi _{\scriptscriptstyle -}(K,U) \), is the length-maximal interval [a, b] contained in \( [K^{\scriptscriptstyle -},K^{\scriptscriptstyle +}] \) such that \( b\in \partial U \) and for each \( V\in \mathrm {Gap}_{\mathsf {b}}(K) \), if \( V\cap [a,b]\ne \varnothing \), then \( \mathrm {length}(V)< \mathrm {length}(U) \). The right-plank of U, denoted \( \pi _{\scriptscriptstyle +}(K,U) \), is the length-maximal interval [a, b] contained in \( [K^{\scriptscriptstyle -},K^{\scriptscriptstyle +}] \) such that \( a\in \partial U \) and for each \( V\in \mathrm {Gap}_{\mathsf {b}}(K) \), if \( V\cap [a,b]\ne \varnothing \), then \( \mathrm {length}(V)< \mathrm {length}(U) \). The (local) thickness of U is
The thickness of K is
Note \(\tau (K)=0 \) when K has an isolated point, \( \tau (K)=1 \) when K is the middle-thirds Cantor set, and \( \tau (K)=+\infty \) when K is an interval. The proof of Theorem 2.6 can be found within [12] and of Theorem 2.7 can be found within [1, 2]. The former theorem is the classical Gap Lemma, but we require the latter theorem which is a generalized version.
Theorem 2.6
(Gap Lemma) Let \( K_1 \) and \( K_2 \) be nonempty compact subsets of \( \mathbb {R} \). For each nonempty compact subset K of \( \mathbb {R} \), let \( \mathrm {Gap}_{\mathsf {b}}(K) \) be the collection of all bounded gaps of K. For each nonempty compact subset K of \( \mathbb {R} \), define \(\Gamma (K){:}{=}\sup \{\mathrm {length}(U):U\in \mathrm {Gap}_{\mathsf {b}}(K)\} \). Assume \( [K_{1}^{\scriptscriptstyle -},K_{1}^{\scriptscriptstyle +}]\cap [K_{2}^{\scriptscriptstyle -},K_{2}^{\scriptscriptstyle +}]\ne \varnothing \), \( \Gamma (K_2)\le \mathrm {diam}(K_1) \), \( \Gamma (K_1)\le \mathrm {diam}(K_2) \), and \( 1\le \tau (K_1)\cdot \tau (K_2) \). Then, \( K_1 \cap K_2\ne \varnothing \). Furthermore, \( K_1+K_2=[K_{1}^{\scriptscriptstyle -}+K_{2}^{\scriptscriptstyle -},K_{1}^{\scriptscriptstyle +}+K_{2}^{\scriptscriptstyle +}] \).
Theorem 2.7
(Gap Lemma) Let \( K_1,\ldots ,K_d \) (\( d\ge 2 \)) be nonempty compact subsets of \( \mathbb {R} \). For each nonempty compact subset K of \( \mathbb {R} \), let \( \mathrm {Gap}_{\mathsf {b}}(K) \) be the collection of all bounded gaps of K. For each nonempty compact subset K of \( \mathbb {R} \), define \(\Gamma (K){:}{=}\sup \{\mathrm {length}(U):U\in \mathrm {Gap}_{\mathsf {b}}(K)\} \). Assume
If \( 1\le \frac{\tau (K_1)}{\tau (K_1)+1}+\cdots +\frac{\tau (K_d)}{\tau (K_d)+1} \), then \( \tau (K_1+\cdots +K_d)=+\infty \) and
If \(\frac{\tau (K_1)}{\tau (K_1)+1}+\cdots +\frac{\tau (K_d)}{\tau (K_d)+1}<1\), then \( \tau (K_1+\cdots +K_d)\ge \frac{\frac{\tau (K_1)}{\tau (K_1)+1}+\cdots + \frac{\tau (K_d)}{\tau (K_d)+1}}{1-(\frac{\tau (K_1)}{\tau (K_1)+1}+\cdots +\frac{\tau (K_d)}{\tau (K_d)+1})} \).
3 Proof of Main Theorem
Lemma 3.1
Let \( A:\mathcal {H}\rightarrow \mathcal {H} \) and \( B:\mathcal {H}\rightarrow \mathcal {H} \) be bounded self-adjoint operators. Then,
Proof
Define \( \xi {:}{=}\min \sigma (A)-\min \sigma (B) \), \(\zeta {:}{=}\max \sigma (A)-\max \sigma (B) \). Define \( s\curlyvee t{:}{=}\sup \left\{ s,t\right\} \). Because
\( |\mathrm {diam}\,\sigma (A)-\mathrm {diam}\,\sigma (B)|=|\zeta -\xi |\le |\zeta |+|\xi |\le 2\,\mathrm {dist}_{\mathsf {Haus}}(\sigma (A),\sigma (B)) \le 2\left\Vert A-B\right\Vert \). \(\square \)
Lemma 3.2
Let \( H_{\lambda ,\alpha ,\omega }=\Delta +V_{\lambda ,\alpha ,\omega } \) be the almost Mathieu operator. Fix \( \alpha \in \mathbb {T}{\setminus }\mathbb {Q} \). Define \( \Sigma _\lambda {:}{=}\sigma (H_{\lambda ,\alpha ,\omega }) \). Assume \( \alpha \) satisfies a Diophantine condition:
Then, \( \lim _{\lambda \rightarrow 0}\tau (\Sigma _\lambda )=+\infty \).
The proof of Lemma 3.2 can be found within Sect. 4.
Theorem 3.3
(Main Theorem) Fix \( \alpha _1,\ldots ,\alpha _d,\omega _1,\ldots ,\omega _d\in [0,1]{=}{:}\mathbb {T} \). Let \( \smash {\widehat{H}} \) be the bounded self-adjoint operator \( \smash {\widehat{H}}:\ell ^2(\mathbb {Z}^d)\rightarrow \ell ^2(\mathbb {Z}^d) \) defined by
for every \( \psi \in \ell ^2(\mathbb {Z}^d),n\in \mathbb {Z}^d \); \( \left\{ e_1,\ldots ,e_d\right\} \) is the standard basis.
Let \( H_{\lambda ,\alpha ,\omega }=\Delta +V_{\lambda ,\alpha ,\omega } \) be the almost Mathieu operator. For each k, define \( \Sigma _k{:}{=}\sigma (H_{\lambda _k,\alpha _k,\omega _k}) \). Assume \( \alpha _1,\ldots ,\alpha _d \) (\( d\ge 2 \)) are irrational and satisfy a Diophantine condition:
There exists \( \varepsilon =\varepsilon (\alpha _1,\ldots ,\alpha _d)>0 \) such that if \( 0<|\lambda _1|,\ldots ,|\lambda _d|<\varepsilon \), then \( \sigma (\smash {\widehat{H}}) \), which is a sum of Cantor spectra \( \Sigma _1+\cdots +\Sigma _d \), is an interval.
Proof
For each nonempty compact subset K of \( \mathbb {R} \), let \( \mathrm {Gap}_{\mathsf {b}}(K) \) be the collection of all bounded gaps of K. For each nonempty compact subset K of \( \mathbb {R} \), define \(\Gamma (K){:}{=}\sup \{\mathrm {length}(U):U\in \mathrm {Gap}_{\mathsf {b}}(K)\} \). By Lemma 3.1, \(\lim _{\lambda \rightarrow 0}\mathrm {dist}_{\mathsf {Haus}}(\sigma (H_{\lambda ,\alpha ,\omega }),[-2,2])=0 \) and \( \lim _{\lambda \rightarrow 0}|\mathrm {diam}\,\sigma (H_{\lambda ,\alpha ,\omega })-4|=0 \). By Lemma 3.2, \( \lim _{\lambda \rightarrow 0}\tau (\sigma (H_{\lambda ,\alpha _k,\omega }))=+\infty \). As a result, there exists \( \varepsilon =\varepsilon (\alpha _1,\ldots ,\alpha _d)>0 \) such that if \( 0<|\lambda _1|,\ldots ,|\lambda _d|<\varepsilon \), then
By Theorem 2.7, \( \Sigma _1+\cdots +\Sigma _d \) is an interval. By Theorem 2.1, \( \sigma (\smash {\widehat{H}})=\Sigma _1+\cdots +\Sigma _d \). \(\square \)
4 Proof of Lemma 3.2
Lemma 4.1
Let \( V_{\lambda ,\alpha ,\omega }:\mathbb {Z}\rightarrow \mathbb {R}:n\mapsto \lambda v\big |_{\mathbb {T}^b}(n\alpha +\omega ) \) be a quasiperiodic potential with parameters \( \lambda ,\alpha ,\omega \). Let \( H_{\lambda ,\alpha ,\omega } \) be the Schrödinger operator. Fix \( \alpha \). Let \( \mathfrak {N}_{\lambda } \) be the IDS. Define \( \Sigma _{\lambda }{:}{=}\sigma (H_{\lambda ,\alpha ,\omega }) \). For each \( \mathbf {n}\ne \mathbf {0} \), let \(G_{\lambda }^{(\mathbf {n})} =(E_{\lambda }^{(\mathbf {n}){\scriptscriptstyle -}}, E_{\lambda } ^{(\mathbf {n}){\scriptscriptstyle +}})\) be the \( \mathbf {n} \)-th spectral gap of \(\Sigma _{\lambda }\). Assume the following:
-
(i)
\(\alpha \) satisfies a Diophantine condition:
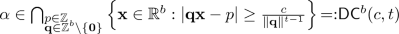
for some \( c>0,t>b \).
-
(ii)
There exist \( \lambda _0=\lambda _0(b,c,t)>0, C_{\mathsf {H}}=C_{\mathsf {H}}(b,c,t)>0,1\ge h=h(b,c,t)>0 \) such that
$$\begin{aligned} |\mathfrak {N}_\lambda (x)-\mathfrak {N}_\lambda (y)|\le C_{\mathsf {H}}|x-y|^{h} \end{aligned}$$for every \( \lambda _0\ge |\lambda |>0,x,y \).
-
(iii)
There exist \( \lambda _1=\lambda _1(b,c,t)>0, C(\lambda )=C(\lambda ,b,c,t)>0, C_{\mathsf {E}}=C_{\mathsf {E}}(b,c,t)>0 \) such that
$$\begin{aligned} |E_{\lambda }^{(\mathbf {n}){\scriptscriptstyle +}} - E_{\lambda }^{(\mathbf {n}){\scriptscriptstyle -}}|\le C(\lambda )e^{-C_{\mathsf {E}}\Vert \mathbf {n}\Vert } \end{aligned}$$for every \( \lambda _1\ge |\lambda |>0,\mathbf {n}\ne \mathbf {0} \) and \( \lim _{\lambda \rightarrow 0}C(\lambda )=0 \).
Then, \(\textstyle \lim _{\lambda \rightarrow 0}\tau (\Sigma _{\lambda })=+\infty \).
Proof
For each \( \mathbf {n}\ne \mathbf {0} \), let \( \pi (\Sigma _\lambda ,{G_{\lambda }^{(\mathbf {n})}})\) be a length-minimal plank of \({G_{\lambda }^{(\mathbf {n})}}\ne \varnothing \). Without loss of generality, assume
for some \( F_{\lambda }^{(\mathbf {n})}\in \Sigma _\lambda \). Observe
Because \( \Sigma _\lambda \) has no isolated points,
Temporarily, assume \({F_{\lambda }^{(\mathbf {n})}}=\sup \Sigma _{\lambda } \). Therefore,
By (i–iii), for sufficiently small \(\lambda \),
Temporarily, assume \(F_{\lambda }^{(\mathbf {n})}< \sup \Sigma _{\lambda } \). Therefore,
for some \(\mathbf {m}_\mathbf {n}\) such that \({G_{\lambda }^{(\mathbf {m}_\mathbf {n})}} \ne \varnothing \) and \(\mathrm {length}({G_{\lambda }^{(\mathbf {n})}}) <\mathrm {length}({G_{\lambda } ^{(\mathbf {m}_\mathbf {n})}})\) and \({F_{\lambda }^{(\mathbf {n})}}= { E_{\lambda }^{(\mathbf {m}_\mathbf {n}){\scriptscriptstyle -}}}\) and
where \( \mathrm {length}({G_{\lambda }^{(\mathbf {n})}}) =C(\lambda )e^{-C_{\mathsf {E}}\kappa _\lambda (\mathbf {n})}\). Because \(\Vert \mathbf {n}\Vert \le \kappa _\lambda (\mathbf {n})\), for sufficiently small \(\lambda \),
As a result,  . \(\square \)
. \(\square \)
The proof of Lemma 4.1 is a combination of three components. For simplicity, we restrict this discussion to the case \( b=1 \). The first component is that the frequency \( \alpha \) satisfies a Diophantine condition. Specifically, there exists \( c>0 \) and there exists \( t>1 \) such that
for every \( \frac{p}{q}\in \mathbb {Q} \). The second component is that the integrated density of states \( \mathfrak {N}_\lambda \) is Hölder continuous for small couplings. Specifically, there exists \( C_{\mathsf {H}}>0 \) and there exists \( h>0 \) such that
for sufficiently small \( \lambda \) and for every x, y and the constants \( C_{\mathsf {H}} \) and h are independent of the sufficiently small \( \lambda \). The existence of \( C_{\mathsf {H}} \) and h is established by A. Cai, C. Chavaudret, J. You, and Q. Zhou in 2019 [11]; see Theorem 2.4 for the unabridged statement. The third component is that the lengths of spectral gaps exponentially decay for large gap-labels. Specifically, there exists \( C(\lambda )>0 \) and there exists \( C_{\mathsf {E}}>0 \) such that
for sufficiently small \( \lambda \) and for every \( n\ne 0 \) and the constant \( C_{\mathsf {E}} \) is independent of the sufficiently small \( \lambda \) and the constant \( C(\lambda ) \) satisfies \( \lim _{\lambda \rightarrow 0}C(\lambda )=0 \). Here \( {G_{\lambda }^{(n)}}\) is a spectral gap satisfying \( \mathfrak {N}_{\lambda }\upharpoonright \overline{{G_{\lambda }^{(n)}}}\equiv n\alpha -\lfloor n\alpha \rfloor \) for every \( n\ne 0 \). The existence of \( C_{\mathsf {E}} \) and \( C(\lambda ) \) is established by M. Leguil, J. You, Z. Zhao, and Q. Zhou in 2017 [29]; see Theorem 2.5 for the unabridged statement. Then, we combine the three components to deduce
for every \( n\ne 0,E_\lambda ,F_\lambda \in \Sigma _\lambda \) with \( E_\lambda <F_\lambda \). If \({G_{\lambda }^{(n_1)}}\) is left-adjacent to \( [E_\lambda ,F_\lambda ] \) and \({G_{\lambda }^{(n_2)}}\) is right-adjacent to \( [E_\lambda ,F_\lambda ] \), then \( \mathfrak {N}_\lambda (E_\lambda )=n_1\alpha -\lfloor n_1\alpha \rfloor \) and \(\mathfrak {N}_\lambda (F_\lambda )=n_2\alpha -\lfloor n_2\alpha \rfloor \) and
and
Because the frequency is fixed and because the spectrum is the same for any phase, we define \( \Sigma _\lambda {:}{=}\Sigma _{\lambda ,\alpha ,\omega } \). The spectral-thickness \( \tau (\Sigma _\lambda ) \) is the infimum-length-ratio of planks over gaps; more details can be found within Sect. 2.6. Therefore, it can be similarly shown that

where \( \kappa _\lambda (n) \) is a positive real-valued function of n. Taking the limit as \( \lambda \) approaches zero concludes the proof of Lemma 4.1.
Theorem 4.2
(Lemma 3.2) Let \( H_{\lambda ,\alpha ,\omega }=\Delta +V_{\lambda ,\alpha ,\omega } \) be the almost Mathieu operator. Fix \( \alpha \in \mathbb {T}{\setminus }\mathbb {Q} \). Assume \( \alpha \) satisfies a Diophantine condition:
Then, \( \lim _{\lambda \rightarrow 0}\tau (\sigma (H_{\lambda ,\alpha ,\omega }))=+\infty \).
Proof
Observe \( \cos (z) \) is holomorphic on \( \mathbb {C} \). By Theorem 2.4 for \( b=1 \) and Theorem 2.5 for \( b=1 \) and Lemma 4.1 for \( b=1 \), \( \left( \forall \alpha \in \mathsf {DC}\right) [\textstyle \lim _{\lambda \rightarrow 0}\tau (\sigma (H_{\lambda ,\alpha ,\omega }))=+\infty ] \). \(\square \)
References
Astels, S.: Thickness measures for cantor sets. Elec. Res. Ann. Am. Math. Soc. 5, 108–111 (1999)
Astels, S.: Cantor sets and numbers with restricted partial quotients. Trans. Am. Math. Soc. 352, 133–170 (1999)
Avila, A., Damanik, D.: Absolute continuity of the integrated density of states for the almost Mathieu operator with non-critical coupling. Invent. Math. 172, 439–453 (2008)
Avila, A., Jitomirskaya, S.: The ten martini problem. Ann. Math. 170, 303–342 (2009)
Azbel, M.: Energy spectrum of a conduction electron in a magnetic field. Sov. Phys. JETP 19, 634–645 (1964)
Bellissard, J.: Schrödinger Operators with Almost Periodic Potential: An Overview. Mathematical Problems in Theoretical Physics, pp. 356–363. Springer, Berlin (1982)
Bourgain, J.: On the spectrum of lattice Schrödinger operators with deterministic potential. J. Anal. Math. 87, 37–75 (2002)
Bourgain, J.: On the spectrum of lattice Schrödinger operators with deterministic potential II. J. Anal. Math. 88, 221–254 (2002)
Bourgain, J.: Green’s Function Estimates for Lattice Schrödinger Operators and Applications. Annals of Mathematics Studies, vol. 158. Princeton University Press, Princeton (2005)
Bourgain, J., Kachkovskiy, I.: Anderson localization for two interacting quasiperiodic particles. Geom. Funct. Anal. 29, 3–43 (2019)
Cai, A., Chavaudret, C., You, J., Zhou, Q.: Sharp Hölder continuity of the Lyapunov exponent of finitely differentiable quasi-periodic cocycles. Math. Zeits. 291, 931–958 (2019)
Damanik, D., Gorodetski, A.: Spectral and quantum dynamical properties of the weakly coupled Fibonacci Hamiltonian. Commun. Math. Phys. 305, 221–277 (2011)
Damanik, D., Gorodetski, A., Solomyak, B.: Absolutely continuous convolutions of singular measures and an application to the square Fibonacci Hamiltonian. Duke Math. J. 164(8), 1603–1640 (2015)
Damanik, D.: Schrödinger operators with dynamically defined potentials. Ergod. Theory Dyn. Syst. 37, 1681–1764 (2017)
Damanik, D., Fillman, J., Gorodetski, A.: Multidimensional almost-periodic Schrödinger operators with cantor spectrum. Ann. Henri Poincaré 20, 1393–1402 (2019)
Falconer, K.: Fractal Geometry: Mathematical Foundations and Applications. Wiley, Hoboken (2014)
Goldstein, M., Schlag, W., Voda, M.: On the spectrum of multi-frequency quasiperiodic Schrödinger operators with large coupling. Invent. Math. 217, 603–701 (2019)
Han, R., Jitomirskaya, S.: Discrete Bethe–Sommerfeld conjecture. Commun. Math. Phys. 361, 205–216 (2018)
Harper, P.G.: Single band motion of conduction electrons in a uniform magnetic field. Proc. Phys. Soc. A 68, 874–878 (1955)
Harper, P.G.: The general motion of conduction electrons in a uniform magnetic field, with application to the diamagnetism of metals. Proc. Phys. Soc. A 68, 879–892 (1955)
Hofstadter, D.: Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976)
Jitomirskaya, S.: Ergodic Schrödinger operators (on one foot). Spectral theory and mathematical physics a festschrift in honor of Barry Simon’s 60th birthday. Proc. Sympos. Pure Math. 76(2), 613–647 (2007)
Jitomirskaya, S., Liu, W., Zhang, S.: Arithmetic spectral transitions: a competition between hyperbolicity and the arithmetics of small denominators (2019 preprint). https://www.math.uci.edu/~mathphysics/preprints/
Jitomirskaya, S.: Critical phenomena, arithmetic phase transitions, and universality: some recent results on the almost Mathieu operator (2019 preprint). https://www.math.uci.edu/~mathphysics/preprints/
Jitomirskaya, S., Liu, W., Shi, Y.: Anderson localization for multi-frequency quasi-periodic operators on ZD. Geom. Funct. Anal. 30, 457–481 (2020)
Karpeshina, Y.U., Parnovski, L., Shterenberg, R.: Bethe–Sommerfeld conjecture and absolutely continuous spectrum of multi-dimensional quasi-periodic Schrödinger operators (2020 preprint). https://arxiv.org/abs/2010.05881
von Klitzing, K., Dorda, G., Pepper, M.: New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys. Rev. Lett. 45(6), 494–497 (1980)
Last, Y.: Spectral theory of Sturm-Liouville operators on infinite intervals: a review of recent developments. In: Amrein, W.O., Hinz, A.M., Pearson, D.P. (eds.) Sturm-Liouville Theory: Past and Present, pp. 99–120. Basel, Birkhäuser (2005)
Leguil, M., You, J., Zhao, Z., Zhou, Q.: Asymptotics of spectral gaps of quasi-periodic Schrödinger operators (2017 preprint). https://arxiv.org/abs/1712.04700
Marx, C.A., Jitomirskaya, S.: Dynamics and spectral theory of quasi-periodic Schrödinger-type operators. Ergod. Theory Dyn. Syst. 37, 2353–2393 (2017)
Newhouse, S.: Nondensity of Axiom A(a) on S2. In: Global Analysis (Proc. Sympos. Pure Math., 1968), vol. 14, pp. 191–202. American Mathematical Society (1970)
Newhouse, S.: Diffeomorphisms with infinitely many sinks. Topology 12, 9–18 (1974)
Newhouse, S.: The abundance of wild hyperbolic sets and non-smooth stable sets for diffeomorphisms. Inst. Hautes Études Sci. Publ. Math. 50, 101–151 (1979)
Palis, J., Takens, F.: Hyperbolicity and Sensitive Chaotic Dynamics at Homoclinic Bifurcations. Cambridge University Press, Cambridge (1993)
Parnovski, L.: Bethe–Sommerfeld conjecture. Ann. Henri Poincaré 9, 457–508 (2008)
Simon, B.: Almost periodic Schrödinger operators: a review. Adv. Appl. Math. 3, 463–490 (1982)
Thouless, D.J., Kohmoto, M., Nightingale, M.P., den Nijs, M.: Quantized hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49(6), 405–408 (1982)
Acknowledgements
I want to thank Anton Gorodetski for his guidance and direction; this paper would not exist in its current form without the support. I want to thank David Damanik and Svetlana Jitomirskaya for their feedback which resulted in a more polished version of this paper. Along with the previous people mentioned, I want to thank Siegfried Beckus, Lingrui Ge, Ilya Kachovskiy, Abel Klein, and Wencai Liu for the mathematics-related discussions that in some form or another positively influenced me and positively influenced this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Anton Bovier.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The project was supported in part by the NSF grant DMS-1855541 (PI - A. Gorodetski).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Takase, A. On the Spectra of Separable 2D Almost Mathieu Operators. Ann. Henri Poincaré 22, 3747–3761 (2021). https://doi.org/10.1007/s00023-021-01080-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-021-01080-x



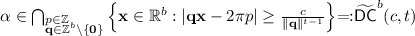 for some
for some