Abstract
This paper explores a delayed Nicholson-type system involving patch structure. Applying differential inequality techniques and the fluctuation lemma, we establish a new sufficient condition which guarantees the existence of positive asymptotically almost periodic solutions for the addressed system. The results of this article are completely new and supplement the previous publications.
Similar content being viewed by others
1 Introduction
As we all know, periodicity is important in real surroundings and the world, but almost periodicity is always more accurate, more realistic, and more general than periodicity when adding varied environmental factors. In comparison with periodic effects, almost periodic effects are more frequent in lots of real world applications [1–4]. In particular, the existence and global stability of almost periodic solutions for the famous scalar Nicholson’s blowflies equation
and the Nicholson’s blowflies systems with patch structure
have been extensively investigated in previous studies [5, 6] and [7], respectively. It is easy to know that scalar Nicholson’s blowflies Eq. (1.1) is a special case of Nicholson’s blowflies system (1.2), where \(x_{i}(t)\) denotes the density of the ith-population at time t, \(a_{ij}(t)\) (\(i\neq j\)) is the rate of the population moving from class j to class i at time t, \(a_{ii}(t)\) is the coefficient of instantaneous loss (which integrates both the death rate and the dispersal rates of the population in class i moving to the other classes), \(\beta _{ij}(t) x_{i}(t-\tau _{ij}(t))e^{-\gamma _{ij}(t)x_{i}(t- \tau _{ij}(t))}\) is the birth function, \(\beta _{ij}(t)\) is the birth rate for the species, \(\frac{1}{\gamma _{ij}(t)}\) is the ith-population reproducing at its maximum rate, and \(\tau _{ij}(t)\) is the generation time of the ith-population at time t. For the feedback function \(xe^{-x}\) and its derivative \(\frac{ 1-x}{e^{x}}\), the author in [8] pointed out that there exist two fixed positive numbers κ and κ̃ such that
It is worth noting that the global exponential stability of almost periodic solutions of (1.1) has been shown in [5, 6] under the restriction that the almost periodic solution exists in a small interval \([\kappa , \widetilde{\kappa }]\approx [0.7215355 , 1.342276]\), and the global exponential stability of (1.2) has been established in [7] where the authors adopted the restraint that the almost periodic solution exists in a small domain
Obviously, the above restriction and restraint do not accord with the biological significance of the population models.
On the other hand,
has been made as the crucial assumption in [5–7]. It should be mentioned that the stability of a class of delayed nonlinear density-dependent mortality Nicholson’s blowflies model has been investigated in [9–12] without assumption (1.5), when the maximum reproducing rate is not limited (i.e. \(\frac{1}{\gamma _{ij}(t)}\) maybe sufficiently large). However, there is no research work on the global exponential stability of almost periodic solutions for Nicholson’s blowflies Eq. (1.1) without assumption (1.5) and avoiding \([\kappa , \widetilde{\kappa }]\) as the existence interval for almost periodic solutions. In particular, to the best of our knowledge, there has not yet been research work on the global stability of almost periodic solutions of Nicholson’s blowflies systems with patch structure and nonlinear density-dependent mortality terms when the almost periodic solutions do not belong to the above domain (1.4).
Regarding the above discussions, in this paper, without adopting \(\underbrace{[\kappa , \widetilde{\kappa }] \times \cdots \times [\kappa , \widetilde{\kappa }]} _{n}\) as the existence domain of almost periodic solutions, we establish the existence and global exponential stability of positive almost periodic solutions for Nicholson’s blowflies systems involving patch structure and nonlinear density-dependent mortality terms. Our results improve and complement some existing ones in the recent publications [5–7, 12], and its effectiveness is demonstrated by some numerical examples.
This paper is organized as follows: In Sect. 2, some necessary definitions, lemmas, and assumptions are presented. In Sect. 3, the existence and global attractivity of positive asymptotically almost periodic solutions are demonstrated by virtue of some differential inequalities and analytic techniques. To verify our theoretical results, a numerical experiment is carried out in Sect. 4. Conclusions are drawn in Sect. 5.
2 Preliminary results
Throughout this paper, it will be assumed that
For \(x=(x_{1},\ldots ,x_{n}) \in \mathbb{R}^{n}\), define
Let \(\mathbb{R}^{+}=[0, +\infty )\) and \(C_{+}= \prod_{i=1}^{n}C([-\sigma _{i}, 0], \mathbb{R} ^{+})\). For \(\mathbb{J} ,\mathbb{J}_{1}, \mathbb{J}_{2}\subseteq \mathbb{R}\), denote
and let \(\operatorname{BC}(\mathbb{J}_{1},\mathbb{J}_{2} )\) be the set of bounded and continuous functions from \(\mathbb{J}_{1}\) to \(\mathbb{J}_{2} \).
Definition 2.1
A subset P of \(\mathbb{R}\) is said to be relatively dense in \(\mathbb{R}\) if there exists a constant \(l>0\) such that \([t, t+l]\cap P \neq \emptyset \) (\(t\in \mathbb{R}\)). \(u\in \operatorname{BC}(\mathbb{R},\mathbb{J} )\) is almost periodic on \(\mathbb{R}\) if, for any \(\epsilon >0\), the set \(T(u,\epsilon )= \{\delta : |u(t+\delta )-u(t) |<\epsilon , \forall t\in \mathbb{R}\}\) is relatively dense.
Definition 2.2
\(u \in C(\mathbb{R}^{+},\mathbb{J} )\) is asymptotically almost periodic if there exist an almost periodic function h and a continuous function \(g\in W_{0}(\mathbb{R}^{+}, \mathbb{J} ) \) such that \(u= h+g\).
For \(\mathbb{J} \subseteq \mathbb{R}\), we denote the set of almost periodic functions from \(\mathbb{R}\) to \(\mathbb{J} \) by \(\operatorname{AP}(\mathbb{R},\mathbb{J} )\). The set of asymptotic almost periodic functions will be represented by \(\operatorname{AAP}(\mathbb{R},\mathbb{J} )\). In addition, \(\operatorname{AP}(\mathbb{R},\mathbb{J} )\) is a proper subspace of \(\operatorname{AAP}(\mathbb{R},\mathbb{J} )\) [1, 2].
Remark 2.1
(see [1, p. 64, Remark 5.16])
The decomposition given in Definition 2.2 is unique.
Hereafter, let \(a_{ii}, \gamma _{ ij} \in \operatorname{AAP}(\mathbb{R}, (0, +\infty )) \), \(a_{ij}\) (\(i\neq j\)), \(\beta _{ ij}, \tau _{ ij} \in \operatorname{AAP}(\mathbb{R}, \mathbb{R}^{+})\), and
where \(a_{ii}^{h}, \gamma _{ ij}^{h} \in \operatorname{AP}(\mathbb{R}, (0, +\infty )) \), \(a_{ij}^{h}\) (\(i\neq j\)), \(\beta _{ ij}^{h}, \tau _{ ij}^{h} \in \operatorname{AP}(\mathbb{R}, \mathbb{R}^{+}) \), \(a^{g}_{ij}, \beta _{ ij}^{g}, \gamma _{i j}^{g}, \tau _{i j}^{g}\in W_{0}(\mathbb{R}^{+}, \mathbb{R}^{+} )\), \(\liminf_{t\rightarrow +\infty }\beta _{i j} (t)>0 \), and \(i\in Q\), \(j\in I\).
Then, we need to introduce a nonlinear almost periodic differential system
with the following admissible initial conditions:
where \(i \in Q \).
We set \(x(t; t_{0}, \varphi ) \) for a solution of (1.2) with initial value problem (2.4), and the maximal right-interval of existence of \(x(t; t_{0}, \varphi ) \) is marked by \([t_{0}, \eta (\varphi ))\). Then, the existence and uniqueness of \(x(t; t_{0}, \varphi )\) are easy to obtain from [8].
Lemma 2.1
(see [12, Lemma 2.1])
LetAandδbe constants and satisfy that
Then\(\delta A>\frac{1}{e}\).
Lemma 2.2
\(x (t; t_{0},\varphi )\)is positive and bounded on\([t_{0}, \eta (\varphi )) \), and\(\eta (\varphi )=+\infty \).
Proof
First, we state that
Otherwise, we can find \(i_{0}\in Q\) and \(\bar{t }_{i_{0}}\in (t_{0}, \eta (\varphi ))\) to satisfy that
From the facts that
we obtain
which is a contradiction and completes the above statement.
Now we evidence that \(\eta (\varphi )=+\infty \). For all \(t \in [t_{0},\eta (\varphi ))\), \(i \in Q\), we define \(y_{i}(t)=\max_{t_{0}-\sigma _{i} \leq s\leq t} x_{i}(s)\) and \(y(t)=\max_{i\in Q} y_{i}(t)\), we gain
and
which suggests that
Hence, by the Gronwall–Bellman inequality, we obtain
It follows from Theorem 2.3.1 in [13] that \(\eta (\varphi )=+\infty \), and then \(x_{i}(t) > 0\) for all \(t \in [t_{0}, +\infty )\).
Next, we demonstrate that \(x(t)\) is bounded on \([t_{0}, +\infty )\). For \(t\in [t_{0}-\sigma _{i}, +\infty ) \) and \(i\in Q\), we define
Suppose that \(x (t)\) is unbounded on \([t_{0}, +\infty )\). Then we can choose \(i^{*}\in Q\) and a strictly monotone increasing sequence \(\{\zeta _{n}\}_{n=1}^{+\infty }\) such that \(\lim_{n\rightarrow +\infty }\zeta _{n} =+\infty \),
and then
It follows that there exists \(n^{*}> 0 \) satisfying
for all \(n>n^{*}\).
According to the fact \(\sup_{u\geq 0}ue^{-u}=\frac{1}{e}\), it follows from (1.2) and (2.1) that, for all \(n>n^{*}\),
and
which contradicts (2.9) and suggests that \(x(t)\) is bounded on \([t_{0}, +\infty )\). □
Lemma 2.3
Assume that
and
hold. Then
whereκis defined in (1.3),
Proof
From Lemmas 2.1 and 2.2, we can designate \(i^{l}, i^{L}\in Q\) such that
By the fluctuation lemma [14, Lemma A.1], one can select a sequence \(\{t_{k}^{*}\}_{k=1}^{+\infty }\) satisfying
Now, we show that \(l>0\). By way of contradiction, we assume that
Let
for each \(t\geq t_{0} \). From (2.15), we can choose \(i^{**}\in Q\) and a strictly monotone increasing sequence \(\{\xi _{n}\}_{n=1}^{+\infty }\) such that \(\lim_{n\rightarrow +\infty }\xi _{n} =+\infty \),
and then
According to (2.17), one can find that there exists \(n^{**}>0\) such that, for \(n>n^{**}\) and \(j\in I\),
and
which together with (2.16) and the fact that \(\liminf_{t\rightarrow +\infty }\beta _{i^{**}j} (t)>0 \) gives
Note that
Letting \(n\rightarrow +\infty \), it follows from (2.10) and (2.18) that
which is a contradiction. Hence, \(l>0\).
Furthermore, from the asymptotically almost periodicity of (1.2), we can select a subsequence of \(\{ k \}_{k\geq 1} \) such that \(\lim_{k \rightarrow + \infty } a_{i^{L}j} (t_{k}^{* })\), \(\lim_{k \rightarrow + \infty } \beta _{i^{L}q} (t_{k}^{* })\), \(\lim_{k \rightarrow + \infty } \gamma _{i^{L}q} (t_{k}^{* })\), \(\lim_{k \rightarrow + \infty } x_{j}(t_{k}^{* } ) \), and \(\lim_{k \rightarrow + \infty } x_{i^{L}}(t_{k}^{* }-\tau _{i^{L} q} (t_{k}^{* })) \) exist for all \(j\in Q\), \(q\in I\). In addition, from (1.2) and (2.14), we have
which, together with the definitions of δ and A, entails that
Finally, we show that \(l >\frac{\kappa }{\gamma ^{-}}\). Again from the fluctuation lemma [14, Lemma A.1] and the asymptotically almost periodicity of (1.2), we can pick a sequence \(\{t_{k}^{**}\}_{k=1}^{+\infty }\) such that \(\lim_{k\rightarrow +\infty }t_{k}^{**}= +\infty \),
and \(\lim_{k \rightarrow + \infty } a_{i^{l}j} (t_{k}^{**})\), \(\lim_{k \rightarrow + \infty } \beta _{i^{l}q} (t_{k}^{**})\), \(\lim_{k \rightarrow + \infty } \gamma _{i^{l}q} (t_{k}^{**})\), \(\lim_{k \rightarrow + \infty } x_{j}(t_{k}^{**} ) \), \(\lim_{k \rightarrow + \infty } x_{i^{l}}(t_{k}^{**}-\tau _{i^{l} q} (t_{k}^{**})) \) exist for all \(j\in Q\), \(q\in I\).
From the fact that
one can see
Consequently, according to (2.20) and (2.21), we gain
If \(le^{-l}=\min \{le^{-l}, Le^{-L}\}\), (2.12) and (2.22) yield
If \(Le^{-L}=\min \{le^{-l}, Le^{-L}\}< le^{-l}\), (2.19) indicates that
together with (2.12) and (2.22), we obtain
This finishes the proof of Lemma 2.3. □
Lemma 2.4
Assume that all the assumptions adopted in Lemma 2.3are satisfied, and let\(x^{h}(t )= x^{h}(t; t_{0}, \varphi )\)be a solution of the initial value problem\((1.2)^{h}\)and (2.4). Then\(x ^{h}(t )\)is positive and bounded on\([t_{0}, +\infty ) \), \(\frac{\kappa }{\gamma ^{-}}< \liminf_{t\rightarrow +\infty }x_{i}^{h}(t) \leq \limsup_{t\rightarrow +\infty }x_{i}^{h}(t) < A\), and there is\(t _{\varphi }^{*}\in [t_{0}, +\infty )\)such that
Proof
From (2.1), (2.2), (2.10), (2.11), (2.12) and the definition of asymptotically almost periodic function, one can easily find that
and
Then, by applying a similar argument as Lemma 2.3, we can obtain
which proves Lemma 2.4. □
Lemma 2.5
Let assumptions adopted in Lemma 2.3hold, and\(x^{h}(t)= x^{h}(t; t_{0}, \varphi ) \)be a solution of equation\((1.2)^{h} \)and (2.4). Then, for any\(\epsilon > 0\), we can choose a relatively dense subset\(P_{\epsilon }\)of\(\mathbb{R}\)with the property that, for each\(\delta \in P_{\epsilon }\), there exists\(T=T(\delta )>0\)satisfying
Proof
According to the fact
we have
which implies that there exists a constant \(0<\varpi <\frac{\gamma ^{-}}{2} \) such that
From (2.1), (2.2), and Lemma 2.4, we can choose positive constants \(T_{1}>\max \{0, t_{\varphi }^{*}\}\) and ζ to satisfy that
and
This means there exist two constants \(\eta >0 \) and \(\lambda \in (0, 1]\) such that, for \(i\in Q\),
Define
and
In view of Lemma 2.4, one can see that \(x^{h}(t) \) and the right-hand side of \((1.2)^{h}\) are bounded. It follows from (2.27) that \(x^{h} (t)\) is uniformly continuous on \(\mathbb{R}\). Therefore, for any \(\epsilon >0\), we can choose a sufficiently small constant \(\epsilon ^{*}>0\) such that
follows that
where \(t\in \mathbb{R}\), \(i\in Q\), \(j\in I\).
Furthermore, for \(\epsilon ^{*}>0\), from the uniformly almost periodic family theory in [2, p. 19, Corollary 2.3], one can choose a relatively dense subset \(P_{\epsilon ^{*}}\) of \(\mathbb{R}\) such that
Denote \(P_{\epsilon }=P_{\epsilon ^{*}}\) for any \(\delta \in P_{\epsilon }\), from (2.29) and (2.30), we have
Let \(\varLambda _{0}\geq \max \{|t_{0}|+T_{1}+ \max_{i\in Q} \sigma _{i} , |t_{0}|+T_{1}+ \max_{i\in Q}\sigma _{i}- \delta \} \). For \(t\in \mathbb{R}\), denote
and
where \(i\in Q\). Let \(i_{t}\) be such an index that
Then, for all \(t\geq \varLambda _{0}\), we have
From (2.26), (2.33), and the inequality
we obtain
Let
It is obvious that \(e^{\lambda t} \|u (t) \| \leq E(t)\), and \(E(t)\) is nondecreasing.
Now, the remaining proof will be divided into two steps.
Step one. If \(E(t)> e^{\lambda t} \|u (t) \|\) for all \(t\geq \varLambda _{0}\), we assert that
In the contrary case, one can pick \(\varLambda _{1}> \varLambda _{0}\) such that \(E(\varLambda _{1})> E(\varLambda _{0})\). From the fact that
we can find that there exists \(\beta ^{*} \in (\varLambda _{0}, \varLambda _{1})\) such that
which contradicts the fact that \(E(\beta ^{*})>e^{\lambda \beta ^{*}} \|u (\beta ^{*}) \|\) and proves (2.36). Then we can select \(\varLambda _{2}>\varLambda _{0}\) satisfying
Step two. If there exists \(\varsigma \geq \varLambda _{0}\) such that \(E(\varsigma )= e^{\lambda \varsigma } \|u (\varsigma ) \| \), from (2.35) and the definition of \(E(t)\), we have
which leads to
For any \(t>\varsigma \) satisfying \(E(t )= e^{\lambda t } \|u (t ) \| \), by using the similar method to the proof of (2.39), we can get
Furthermore, if \(E(t )> e^{\lambda t } \|u (t ) \| \) and \(t>\varsigma \), one can pick \(\varLambda _{3}\in [\varsigma , t)\) such that
together with (2.39) and (2.40), we have
With a similar proof in step one, we can entail that
which together with (2.41) leads to
Finally, the above discussion infers that there exists \(\hat{\varLambda }>\max \{\varsigma , \varLambda _{0}, \varLambda _{2} \}\) obeying that
which finishes the proof of Lemma 2.5. □
3 Main result
Theorem 3.1
Assume that the assumptions in Lemma 2.3hold. Then system\((1.2)^{h}\)has exactly one positive almost periodic solution\(x^{*}(t)\), and every solution of (1.2) with initial condition (2.4) is asymptotically almost periodic on\(\mathbb{R}^{+}\)and converges to\(x^{*}(t)\)as\(t\rightarrow +\infty \).
Proof
Let \(v(t) \) be a solution of system \((1.2)^{h}\) with initial condition (2.4), and
We also define
where \(\{t_{q}\}_{q\geq 1}\subseteq \mathbb{R} \) is a sequence. Then
for all \(t+t_{q}\geq t_{0}\), \(i\in Q\). By using the proof similar to Lemma 2.5, we can choose \(\{t_{q}\}_{q\geq 1}\) such that
From Arzela–Ascoli lemma and the fact that the function sequence \(\{v(t+t_{q})\} _{q\geq 1} \) is uniformly bounded and equi-uniformly continuous, we can choose a subsequence \(\{t_{q_{j}}\}_{j\geq 1}\) of \(\{t_{q}\}_{q\geq 1}\) such that \(\{v(t+t_{q_{j}})\}_{j\geq 1}\) (for convenience, we still denote it by \(\{v(t+t_{q})\}_{q\geq 1}\)) uniformly converges to a continuous function \(x^{*}(t)=(x^{*}_{1}(t),x^{*}_{2}(t),\ldots ,x^{*}_{n}(t)) \) on any compact set of \(\mathbb{R}\). Then, from Lemma 2.4, we have
and
on any compact set of \(\mathbb{R}\), where “⇉” denotes “uniformly converge”. Thus, (3.2), (3.3), and (3.5) produce that \(\{v'_{i} (t+t_{q})\}_{q\geq 1}\) uniformly converges to
on any compact set of \(\mathbb{R}\). According to the properties of the uniform convergence function sequence, we obtain that \(x^{*}(t)\) is a solution of \((1.2)^{h}\) and
From Lemma 2.5, for any \(\epsilon >0\), we can choose a relatively dense subset \(P_{\epsilon }\) of \(\mathbb{R}\) with the property that, for each \(\delta \in P_{\epsilon }\), there exists \(T=T(\delta )>0\) satisfying
and
which implies that \(x^{*}(t)\) is a positive almost periodic solution of \((1.2)^{h}\).
Next, we show that all the solutions of (1.2) converge to \(x^{*}(t)\) as \(t\rightarrow +\infty \). Let \(x(t) \) be an arbitrary solution of system (1.2) with initial value (2.4). Define \(y(t)=x(t) -x^{*}(t)\) and \(x_{i}(t)\equiv x _{i}(t_{0}-\sigma _{i})\) for all \(t\in (-\infty , t_{0}-\sigma _{i}]\), let
Then
For any \(\epsilon >0\), in view of the global existence and uniform continuity of x and the fact that \(a_{ij}^{g}, \beta _{ ij}^{g}, \gamma _{i j}^{g}, \tau _{ ij}^{g} \in W_{0}(\mathbb{R}^{+}, \mathbb{R}^{+} )\), we can choose a constant \(T_{\varphi }^{**}>\max \{T_{1}, t_{\varphi }^{*}\}\) such that
Set
and let \(i_{t}\) be such an index that
According to (3.4) and Lemma 2.3, one can find \(T_{\varphi , x^{*} }>T_{\varphi }^{**}\) such that
Combined with (2.34) and (3.7), we gain
Then, from (2.26) and (3.8), by employing the argument of Lemma 2.5, we know that there is a constant \(\widetilde{T} \geq T_{\varphi , x^{*}}\) such that
which yields
It follows from the uniqueness of the limit function that \((1.2)^{h}\) has exactly one positive almost periodic solution \(x^{*}(t)\). The proof is complete. □
Then, we will establish the existence and global exponential stability of the almost periodic solution of \((1.2)^{h}\). To do this end, we first show the following proposition.
Proposition 3.1
Suppose that\(f(t)\)is an almost periodic function, then
Proof
We only need to validate the case that \(\limsup_{t\to +\infty }f(t)=\sup_{t\in \mathbb{R}}f(t)\), since the other case that \(\liminf_{t\to +\infty }f(t)=\inf_{t\in \mathbb{R}}f(t)\) can be proved similarly.
Define
It is easy to see that \(B\leq A\). We claim
Otherwise, \(B< A\), let \(\varepsilon _{0}=\frac{A-B}{8}\), from the definition of upper limit, there exists \(T=T(\varepsilon _{0})>0\) such that
According to the definition of the upper bound, one can take \(t_{0}\in R\) to satisfy that
Furthermore, there exists a constant \(l=l(\varepsilon _{0})>0\) such that, \(\forall [\alpha ,\alpha +l]\subset \mathbb{R}\) with \(\alpha \in \mathbb{R}\), one can pick \(\tau \in [\alpha ,\alpha +l]\) satisfying that
Letting \(\alpha =T-t_{0}\) and \(\tau \in [T-t_{0},T-t_{0}+l]\) leads to
which is contrary to the fact that \(f(t)< B+\varepsilon _{0}< A-2\varepsilon _{0}\) for all \(t\geq T \). This finishes the proof of Proposition 3.1. □
Theorem 3.2
Suppose that, for\(i\in Q\), \(j\in I\),
and
are satisfied. Then system\((1.2)^{h}\)has exactly one positive almost periodic solution\(x^{*}(t)\), which is global exponentially stable; in other words, the solution\(N(t;t_{0},\varphi )\)of\((1.2)^{h}\)with (2.4) converges exponentially to\(x^{*}(t)\)as\(t\rightarrow +\infty \).
Proof
From Proposition 3.1, (3.11)–(3.14) imply that the assumptions in Lemmas 2.4 and 2.5 hold. Then, by using the similar proof in Theorem 3.1, we can obtain that system \((1.2)^{h}\) has exactly one positive almost periodic solution \(x^{*}(t)\). It is sufficient to show the global exponential stability of \(x^{*}(t)\). Set \(N(t)=N(t;t_{0},\varphi )\) and \(y(t)=N(t)-x^{*}(t)\), then
It follows from Lemma 2.4 that there is \(M_{\varphi ,x^{*}}>t_{0}\) such that
Together with (3.11), we obtain
where \(i\in Q\), \(j\in I\).
With the help of (3.13), we can choose \(\lambda \in (0, 1]\) such that
Now, we define the Lyapunov functional as follows:
With the help of (3.16) and (3.18), we get
In the sequel, we prove that, for all \(t>M_{\varphi ,x^{*}}\),
Otherwise, there exist \(K^{*}>M_{\varphi ,x^{*}}\) and \(\hat{i}\in Q\) such that
It follows from (3.19), (3.20), and (3.22) that
which is a contradiction. Thus (3.21) holds, and it follows that
This completes the proof of Theorem 3.2. □
4 Some numerical simulations
In this section, we give two examples with simulations to demonstrate the feasibility and the validity of our theoretical results.
Example 4.1
Consider the following delayed Nicholson-type system involving patch structure and asymptotically almost periodic environments:
where \(t_{0}=0\).
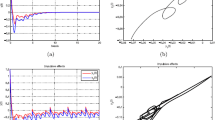
One can easily check that (2.1), (2.2), and (2.10)–(2.13) hold for system (4.1). From Theorem 3.1, we can obtain that every solution of (4.1) with initial value \(\varphi =(\varphi _{1}, \varphi _{2} ) \in C([-100, 0], \mathbb{R} ^{+}) \times C([-150, 0], \mathbb{R} ^{+})\) and \(\varphi _{i}(0)>0\) (\(i=1,2\)) is asymptotically almost periodic on \(\mathbb{R}^{+}\) and converges to the same almost periodic function as \(t\rightarrow +\infty \). The numeric simulations in Fig. 1 support this theoretical results.
Numerical solutions of (4.1) for initial value \((0.1,0.3)\), \((0.1,0.15)\), \((0.3,0.35)\)
Example 4.2
Consider the following delayed Nicholson-type system involving patch structure and almost periodic environments:
where \(t_{0}=0\).
Obviously, system (4.2) satisfies all the assumptions made in (3.11)–(3.15). Therefore, by Theorem 3.2, we obtain that system (4.2) has exactly one positive almost periodic solution \(x^{*}(t)\). In particular, the solution \(N(t;t_{0},\varphi )\) of (4.2) with initial value \(\varphi =(\varphi _{1}, \varphi _{2} ) \in C([-100, 0], \mathbb{R} ^{+}) \times C([-150, 0], \mathbb{R} ^{+})\) and \(\varphi _{i}(0)>0\) (\(i=1,2\)) converges exponentially to \(x^{*}(t)\) as \(t\rightarrow +\infty \). Figure 2 reveals the above consequences through numerical solutions of different initial values.
Numerical solutions of (4.2) for initial value \((1.1,1.3)\), \((1.1,1.15)\), \((1.3,1.35)\)
Remark 4.1
In the above examples, \(\limsup_{t\in \mathbb{R}}\gamma _{ij} (t ) \leq 0.91<1 \), \(i,j=1,2 \), does not satisfy assumption (1.5). Moreover, when \(\frac{\kappa }{\gamma }>1.5>\widetilde{\kappa }\), one can find that, in Theorems 3.1 and 3.2, the existence region of almost periodic solution and the attractive region of asymptotically almost periodic solutions are outside of \(\underbrace{[\kappa , \widetilde{\kappa }]\times \cdots \times [\kappa , \widetilde{\kappa }]}_{n}= \underbrace{[0.7215355 , 1.342276] \times \cdots \times [0.7215355 , 1.342276]}_{n}\). Therefore, it is not difficult to see that all the results in references [5–7] and [15–100] cannot be applied to show the almost periodic dynamics for system (4.1) and system (4.2).
5 Conclusions
In this paper, we combine the Lyapunov function method with the differential inequality method to establish some new criteria ensuring the existence and attractivity of positive asymptotically almost periodic solutions for a class of delayed Nicholson’s blowflies systems with patch structure. The assumptions adopted in this present paper are different from some previously known literature. Numerical simulations have been given to illustrate the obtained results. The approach presented in this article can be used as a possible way to study the asymptotically almost periodic patch structure population models such as neoclassical growth model, Mackey–Glass model, epidemical system or age-structured population model, and so on. We leave this as our future work.
References
Zhang, C.: Almost Periodic Type Functions and Ergodicity. Kluwer Academic, Beijing (2003)
Fink, A.M.: Almost periodic differential equations. Lect. Notes Math. 5(1), 167–181 (1974)
Al-Islam, N.S., Alsulami, S.M., Diagana, T.: Existence of weighted pseudo anti-periodic solutions to some non-autonomous differential equations. Appl. Math. Comput. 218, 6536–6548 (2012)
Diagana, T.: Weighted pseudo almost periodic functions and applications. C. R. Acad. Sci. Paris, Ser. I 343(10), 643–646 (2006)
Liu, B.: New results on global exponential stability of almost periodic solutions for a delayed Nicholson’s blowflies model. Ann. Polon. Math. 113(2), 191–208 (2015)
Xiong, W.: New results on positive pseudo-almost periodic solutions for a delayed Nicholson’s blowflies model. Nonlinear Dyn. 85, 563–571 (2016)
Wang, W., Liu, F., Chen, W.: Exponential stability of pseudo almost periodic delayed Nicholson-type system with patch structure. Math. Methods Appl. Sci. 42, 592–604 (2019)
Liu, B.: Global exponential stability of positive periodic solutions for a delayed Nicholson’s blowflies model. J. Math. Anal. Appl. 412, 212–221 (2014)
Xu, Y.: New stability theorem for periodic Nicholson’s model with mortality term. Appl. Math. Lett. 94, 59–65 (2019)
Doan, T.S., Le, V.H., Trinh, A.T.: Global attractivity of positive periodic solution of a delayed Nicholson model with nonlinear density-dependent mortality term. Electron. J. Qual. Theory Differ. Equ. 2019, 8, 1–21 (2019)
Huang, C., Zhang, H., Huang, L.: Almost periodicity analysis for a delayed Nicholson’s blowflies model with nonlinear density-dependent mortality term. Commun. Pure Appl. Anal. 18(6), 3337–3349 (2019). https://doi.org/10.3934/cpaa.2019150
Cao, Q., Wang, G., Qian, C.: New results on global exponential stability for a periodic Nicholson’s blowflies model involving time-varying delays. Adv. Differ. Equ. 2020, 43 (2020). https://doi.org/10.1186/s13662-020-2495-4
Hale, J.K., Verduyn Lunel, S.M.: Introduction to Functional Differential Equations. Springer, New York (1993)
Smith, H.L.: An Introduction to Delay Differential Equations with Applications to the Life Sciences. Springer, New York (2011)
Huang, C., Yang, Z., Yi, T., Zou, X.: On the basins of attraction for a class of delay differential equations with non-monotone bistable nonlinearities. J. Differ. Equ. 256, 2101–2114 (2014)
Huang, C., Zhang, H.: Periodicity of non-autonomous inertial neural networks involving proportional delays and non-reduced order method. Int. J. Biomath. 12(2), 1950016 (2019) (13 pages)
Chen, T., Huang, L., Yu, P., Huang, W.: Bifurcation of limit cycles at infinity in piecewise polynomial systems. Nonlinear Anal., Real World Appl. 41, 82–106 (2018)
Hu, H., Zou, X.: Existence of an extinction wave in the Fisher equation with a shifting habitat. Proc. Am. Math. Soc. 145(11), 4763–4771 (2017)
Duan, L., Fang, X., Huang, C.: Global exponential convergence in a delayed almost periodic Nicholson’s blowflies model with discontinuous harvesting. Math. Methods Appl. Sci. 41(5), 1954–1965 (2018)
Huang, C., Zhang, H., Cao, J., Hu, H.: Stability and Hopf bifurcation of a delayed prey–predator model with disease in the predator. Int. J. Bifurc. Chaos 29(7), 1950091, 23 pages (2019)
Huang, C., Yang, X., Cao, J.: Stability analysis of Nicholson’s blowflies equation with two different delays. Math. Comput. Simul. 171, 201–206 (2020). https://doi.org/10.1016/j.matcom.2019.09.023
Tan, Y., Huang, C., Sun, B., Wang, T.: Dynamics of a class of delayed reaction-diffusion systems with Neumann boundary condition. J. Math. Anal. Appl. 458(2), 1115–1130 (2018)
Wang, J., Chen, X., Huang, L.: The number and stability of limit cycles for planar piecewise linear systems of node-saddle type. J. Math. Anal. Appl. 469(1), 405–427 (2019)
Huang, C., Yang, L., Liu, B.: New results on periodicity of non-autonomous inertial neural networks involving non-reduced order method. Neural Process. Lett. 50, 595–606 (2019)
Long, X., Gong, S.: New results on stability of Nicholson’s blowflies equation with multiple pairs of time-varying delays. Appl. Math. Lett. 100, 10602 (2020). https://doi.org/10.1016/j.aml.2019.106027
Huang, C., Long, X., Cao, J.: Stability of anti-periodic recurrent neural networks with multi-proportional delays. Math. Methods Appl. Sci. 2020, 6350 (2020). https://doi.org/10.1002/mma.6350
Zhang, J., Huang, C.: Dynamics analysis on a class of delayed neural networks involving inertial terms. Adv. Differ. Equ. (2020). https://doi.org/10.1186/s13662-020-02566-4
Zhang, H.: Global large smooth solutions for 3-d hall-magnetohydrodynamics. Discrete Contin. Dyn. Syst. 39(11), 6669–6682 (2019)
Li, W., Huang, L., Ji, J.: Periodic solution and its stability of a delayed Beddington–DeAngelis type predator–prey system with discontinuous control strategy. Math. Methods Appl. Sci. 42(13), 4498–4515 (2019)
Hu, H., Yuan, X., Huang, L., Huang, C.: Global dynamics of an SIRS model with demographics and transfer from infectious to susceptible on heterogeneous networks. Math. Biosci. Eng. 16(5), 5729–5749 (2019)
Hu, H., Yi, T., Zou, F.: On spatial-temporal dynamics of Fisher-KPP equation with a shifting environment. Proc. Am. Math. Soc. 148, 213–221 (2020)
Huang, C., Long, X., Huang, L., Fu, S.: Stability of almost periodic Nicholson’s blowflies model involving patch structure and mortality terms. Can. Math. Bull. (2019). https://doi.org/10.4153/S0008439519000511
Qian, C., Hu, Y.: Novel stability criteria on nonlinear density-dependent mortality Nicholson’s blowflies systems in asymptotically almost periodic environments. J. Inequal. Appl. 2020, 13 (2020). https://doi.org/10.1186/s13660-019-2275-4
Xu, Y., Cao, Q., Guo, X.: Stability on a patch structure Nicholson’s blowflies system involving distinctive delays. Appl. Math. Lett. 105, 106340 (2020). https://doi.org/10.1016/j.aml.2020.106340
Cai, Z., Huang, J., Huang, L.: Periodic orbit analysis for the delayed Filippov system. Proc. Am. Math. Soc. 146, 4667–4682 (2018)
Li, J., Ying, J., Xie, D.: On the analysis and application of an ion size-modified Poisson–Boltzmann equation. Nonlinear Anal., Real World Appl. 47, 188–203 (2019)
Huang, C., Qiao, Y., Huang, L., Agarwal, R.P.: Dynamical behaviors of a food-chain model with stage structure and time delays. Adv. Differ. Equ. 2018, 186 (2018). https://doi.org/10.1186/s13662-018-1589-8
Li, X., Liu, Z., Li, J.: Existence and controllability for nonlinear fractional control systems with damping in Hilbert spaces. Acta Mech. Sin. Engl. Ser. 39(1), 229–242 (2019)
Zhu, K., Xie, Y., Zhou, F.: Pullback attractors for a damped semilinear wave equation with delays. Acta Math. Sin. Engl. Ser. 34(7), 1131–1150 (2018)
Zhao, J., Liu, J., Fang, L.: Anti-periodic boundary value problems of second-order functional differential equations. Bull. Malays. Math. Sci. Soc. 37(2), 311–320 (2014)
Iswarya, M., Raja, R., Rajchakit, G., Cao, J., Alzabut, J., Huang, C.: Existence, uniqueness and exponential stability of periodic solution for discrete-time delayed BAM neural networks based on coincidence degree theory and graph theoretic method. Mathematics 7(11), 1055 (2019). https://doi.org/10.3390/math7111055
Pratap, A., Raja, R., Alzabut, J., Cao, J., Rajchakit, G., Huang, C.: Mittag-Leffler stability and adaptive impulsive synchronization of fractional order neural networks in quaternion field. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.6367
Long, Z., Tan, Y.: Global attractivity for Lasota–Wazewska-type system with patch structure and multiple time-varying delays. Complexity 2020, 1947809 (2020). https://doi.org/10.1155/2020/1947809
Wang, F., Yao, Z.: Approximate controllability of fractional neutral differential systems with bounded delay. Fixed Point Theory 17, 495–508 (2016)
Wei, Y., Yin, L., Long, X.: The coupling integrable couplings of the generalized coupled Burgers equation hierarchy and its Hamiltonian structure. Adv. Differ. Equ. 2019, 58 (2019). https://doi.org/10.1186/s13662-019-2004-9
Zhang, J., Lu, C., Li, X., Kim, H., Wang, J.: A full convolutional network based on DenseNet for remote sensing scene classification. Math. Biosci. Eng. 16(5), 3345–3367 (2019)
Hu, H., Liu, L.: Weighted inequalities for a general commutator associated to a singular integral operator satisfying a variant of Hormander’s condition. Math. Notes 101(5–6), 830–840 (2017)
Huang, C., Liu, L.: Boundedness of multilinear singular integral operator with non-smooth kernels and mean oscillation. Quaest. Math. 40(3), 295–312 (2017)
Huang, C., Cao, J., Wen, F., Yang, X.: Stability analysis of SIR model with distributed delay on complex networks. PLoS ONE 11(8), e0158813 (2016). https://doi.org/10.1371/journal.pone.0158813
Li, X., Liu, Y., Wu, J.: Flocking and pattern motion in a modified Cucker–Smale model. Bull. Korean Math. Soc. 53(5), 1327–1339 (2016)
Xie, Y., Li, Q., Zhu, K.: Attractors for nonclassical diffusion equations with arbitrary polynomial growth nonlinearity. Nonlinear Anal., Real World Appl. 31, 23–37 (2016)
Xie, Y., Li, Y., Zeng, Y.: Uniform attractors for nonclassical diffusion equations with memory. J. Funct. Spaces 2016, 5340489 (2016). https://doi.org/10.1155/2016/5340489
Wang, F., Wang, P., Yao, Z.: Approximate controllability of fractional partial differential equation. Adv. Differ. Equ. 2015, 367 (2015). https://doi.org/10.1186/s13662-015-0692-3
Liu, Y., Wu, J.: Multiple solutions of ordinary differential systems with min–max terms and applications to the fuzzy differential equations. Adv. Differ. Equ. 2015, 379 (2015). https://doi.org/10.1186/s13662-015-0708-z
Yan, L., Liu, J., Luo, Z.: Existence and multiplicity of solutions for second-order impulsive differential equations on the half-line. Adv. Differ. Equ. 2013, 293 (2013). https://doi.org/10.1186/1687-1847-2013-293
Liu, Y., Wu, J.: Fixed point theorems in piecewise continuous function spaces and applications to some nonlinear problems. Math. Methods Appl. Sci. 37(4), 508–517 (2014)
Tong, D., Wang, W.: Conditional regularity for the 3D MHD equations in the critical Besov space. Appl. Math. Lett. 102, 106119 (2020). https://doi.org/10.1016/j.aml.2019.106119
Cai, Y., Wang, K., Wang, W.: Global transmission dynamics of a Zika virus model. Appl. Math. Lett. 92, 190–195 (2019)
Zhou, S., Jiang, Y.: Finite volume methods for N-dimensional time fractional Fokker–Planck equations. Bull. Malays. Math. Sci. Soc. 42(6), 3167–3186 (2019)
Liu, F., Feng, L., Vo, A., Li, J.: Unstructured-mesh Galerkin finite element method for the two-dimensional multi-term time-space fractional Bloch–Torrey equations on irregular convex domains. Comput. Math. Appl. 78(5), 1637–1650 (2019)
Li, J., Guo, B.: Divergent sqlution to the nonlinear Schrodinger equation with the combined power-type nonlinearities. J. Appl. Anal. Comput. 71(1), 249–263 (2017)
Huang, L.: Endomorphisms and cores of quadratic forms graphs in odd characteristic. Finite Fields Appl. 55, 284–304 (2019)
Huang, L., Lv, B., Wang, K.: Erdos–Ko–Rado theorem, Grassmann graphs and p(s)-Kneser graphs for vector spaces over a residue class ring. J. Comb. Theory, Ser. A 164, 125–158 (2019)
Li, Y., Vuorinen, M., Zhou, Q.: Characterizations of John spaces. Monatshefte Math. 188(3), 547–559 (2019)
Huang, L., Lv, B., Wang, K.: The endomorphisms of Grassmann graphs. Ars Math. Contemp. 10(2), 383–392 (2016)
Zhang, Y.: Right triangle and parallelogram pairs with a common area and a common perimeter. J. Number Theory 164, 179–190 (2016)
Zhang, Y.: Some observations on the Diophantine equation \(f(x)f(y)= f(z)^{2}\). Colloq. Math. 142(2), 275–283 (2016)
Gong, X., Wen, F., He, Z., Yang, J., Yang, X., Pan, P.: Extreme return, extreme volatility and investor sentiment. Filomat 30(15), 3949–3961 (2016)
Jiang, Y., Huang, B.: A note on the value distribution of f(l) (f((k))) (n). Hiroshima Math. J. 46(2), 135–147 (2016)
Huang, L., Huang, J., Zhao, K.: On endomorphisms of alternating forms graph. Discrete Math. 338(3), 110–121 (2015)
Peng, J., Zhang, Y.: Heron triangles with figurate number sides. Acta Math. Hung. 157(2), 478–488 (2019)
Liu, W.: An incremental approach to obtaining attribute reduction for dynamic decision systems. Open Math. 14, 875–888 (2016)
Huang, L., Lv, B.: Cores and independence numbers of Grassmann graphs. Graphs Comb. 33(6), 1607–1620 (2017)
Huang, L., Su, H., Tang, G., Wang, J.: Bilinear forms graphs over residue class rings. Linear Algebra Appl. 523, 13–32 (2017)
Lv, B., Huang, Q., Wang, K.: Endomorphisms of twisted Grassmann graphs. Graphs Comb. 33(1), 157–169 (2018)
Huang, L.: Generalized bilinear forms graphs and MRD codes over a residue class ring. Finite Fields Appl. 51, 306–324 (2018)
Li, L., Jin, Q., Yao, B.: Regularity of fuzzy convergence spaces. Open Math. 16, 1455–1465 (2018)
Cao, J., Ali, U., Javaid, M., Huang, C.: Zagreb connection indices of molecular graphs based on operations. Complexity 2020, Article ID 7385682 (2020). https://doi.org/10.1155/2020/7385682
Kumari, S., Chugh, R., Cao, J., Huang, C.: On the construction, properties and Hausdorff dimension of random Cantor one \(p^{th}\) set. AIMS Math. 55(4), 3138–3155 (2020)
Huang, C., Yang, L., Cao, J.: Asymptotic behavior for a class of population dynamics. AIMS Math. 54(4), 3378–3390 (2020)
Chen, D., Zhang, W., Cao, J., Huang, C.: Fixed time synchronization of delayed quaternion-valued memristor-based neural networks. Adv. Differ. Equ. 2020, 92 (2020). https://doi.org/10.1186/s13662-020-02560-w
Wang, J., Huang, C., Huang, L.: Discontinuity-induced limit cycles in a general planar piecewise linear system of saddle-focus type. Nonlinear Anal. Hybrid Syst. 33, 162–178 (2019)
Zhou, Y., Wan, X., Huang, C., Yang, X.: Finite-time stochastic synchronization of dynamic networks with nonlinear coupling strength via quantized intermittent control. Appl. Math. Comput. 376, 125157 (2020). https://doi.org/10.1016/j.amc.2020.125157
Yang, X., Wen, S., Liu, Z., Li, C., Huang, C.: Dynamic properties of foreign exchange complex network. Mathematics 7, 832 (2019). https://doi.org/10.3390/math7090832
Jin, Q., Li, L., Lang, G.: p-Regularity and p-regular modification in T-convergence spaces. Mathematics 7(4), 370 (2019). https://doi.org/10.3390/math7040370
Wang, W., Huang, C., Huang, C., Cao, J., Lu, J., Wang, L.: Bipartite formation problem of second-order nonlinear multi-agent systems with hybrid impulses. Appl. Math. Comput. 370, 124926 (2020). https://doi.org/10.1016/j.amc.2019.124926
Shi, M., Guo, J., Fang, X., Huang, C.: Global exponential stability of delayed inertial competitive neural networks. Adv. Differ. Equ. 2020, 87 (2020). https://doi.org/10.1186/s13662-019-2476-7
Li, L., Wang, W., Huang, L., Wu, J.: Some weak flocking models and its application to target tracking. J. Math. Anal. Appl. 480(2), 123404 (2019). https://doi.org/10.1016/j.jmaa.2019.123404
Li, X., Li, Y., Liu, Z., Li, J.: Sensitivity analysis for optimal control problems described by nonlinear fractional evolution inclusions. Fract. Calc. Appl. Anal. 21(6), 1439–1470 (2018)
Tan, Y., Liu, L.: Boundedness of Toeplitz operators related to singular integral operators. Izv. Math. 82(6), 1225–1238 (2018)
Zuo, Y., Wang, Y., Liu, X.: Adaptive robust control strategy for rhombus-type lunar exploration wheeled mobile robot using wavelet transform and probabilistic neural network. Comput. Appl. Math. 37(1), 314–337 (2018)
Tan, Y., Liu, L.: Weighted boundedness of multilinear operator associated to singular integral operator with variable Calderón–Zygmund Kernel. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 111(4), 931–946 (2017)
Wang, W., Chen, Y., Fang, H.: On the variable two-step IMEX BDF method for parabolic integro-differential equations with nonsmooth initial data arising in finance. SIAM J. Numer. Anal. 57(3), 1289–1317 (2019)
Tang, W., Sun, Y., Zhang, J.: High order symplectic integrators based on continuous-stage Runge–Kutta–Nystrom methods. Appl. Math. Comput. 361, 670–679 (2019)
Jiang, Y., Xu, X.: A monotone finite volume method for time fractional Fokker–Planck equations. Sci. China Math. 62(4), 783–794 (2019)
Chen, H., Xu, D., Zhou, J.: A second-order accurate numerical method with graded meshes for an evolution equation with a weakly singular kernel. J. Comput. Appl. Math. 356, 152–163 (2019)
Yu, B., Fan, H.Y., Chu, E.K.: Large-scale algebraic Riccati equations with high-rank constant terms. J. Comput. Appl. Math. 361, 130–143 (2019)
Wang, W.: Finite-time synchronization for a class of fuzzy cellular neural networks with time-varying coefficients and proportional delays. Fuzzy Sets Syst. 338, 40–49 (2018)
Huang, C., Wen, S., Li, M., Wen, F., Yang, X.: An empirical evaluation of the influential nodes for stock market network: Chinese A shares case. Finance Res. Lett. (2020). https://doi.org/10.1016/j.frl.2020.101517
Wang, W., Chen, W.: Stochastic Nicholson-type delay system with regime switching. Syst. Control Lett. 136, 104603 (2020). https://doi.org/10.1016/j.sysconle.2019.104603
Acknowledgements
We would like to thank the anonymous referees and the editor for very helpful suggestions and comments which led to improvements of our original paper.
Availability of data and materials
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Funding
This work was supported by the National Natural Science Foundation of China (Nos. 11861037, 11971076, 11771059, 51839002), the Hunan Provincial Natural Science Foundation of China (No. 2016JJ6104), and the Scientific Research Fund of Hunan Provincial Education Department (No. 17C1076).
Author information
Authors and Affiliations
Contributions
The three authors contributed equally to this work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, H., Cao, Q. & Yang, H. Asymptotically almost periodic dynamics on delayed Nicholson-type system involving patch structure. J Inequal Appl 2020, 102 (2020). https://doi.org/10.1186/s13660-020-02366-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-020-02366-0