Positive periodic solution for Nicholson’s blowfies systems with patch structure

Abstract

A generalized Nicholson blowfies system with patch structure is studied. Some existence and asymptotic stability results of the positive periodic solution to the considered system are obtained by coincidence degree theory and some analysis techniques. Finally, two examples are given to show the effectiveness of the results in the present paper.

1 Introduction

In 1980, Gurney et al. [1] studied the delayed Nicholson blowflies equation

$$ x'(t)=Px(t-\tau )e^{-\alpha x(t-\tau )}-\gamma x(t), $$

(1.1)

where $x(t)$ represents the population of mature adults at time t, $\frac{1}{\alpha }$ denotes the population size at which the complete population reproduces at its maximum rate, P denotes the maximum possible per capita egg production rate, $\tau >0$ is a delay term, $\gamma >0$ is the mortality rate. Consider the different practical conditions, model (1.1) is generalized to more general models. Berezansky et al. [2] considered a more general Nicholson blowflies equation with distributed delays and periodic coefficients and obtained rich dynamic properties including oscillation, permanence, local and global stability of solutions for the above models. Shu, Wang and Wu [3] changed Nicholson’s blowflies equation with natural death rate incorporated into the delay feedback case and regarded the delay as a bifurcation parameter and checked termination and the onset of Hopf bifurcations of periodic solutions coming from a positive solution. In very recent years, the stability of Nicholson’s blowfies equation with two different delays was investigated by the authors in [4].

On the other hand, the existence and stability of positive periodic solutions of population dynamic systems belong to the important issues in differential dynamic systems. Wang [5] studied a new fishery equation with a nonlinear mortality term, which is a generalization of the classical Nicholson blowflies equation. By the use of topology degree theory, some sufficient conditions are obtained to guarantee the existence of positive periodic solutions of the considered model. Chen [6] studied a class of new Nicholson’s blowflies equations with delays and periodic coefficients. Based on coincidence degree theory, the authors obtained some sufficient conditions for the existence of positive periodic solutions to the considered model. Li and Du [7] obtained the existence of positive periodic solutions for a Nicholson blowflies model with multiple delays by using the Krasnoselskii cone fixed point theorem. Chen and Liu [8] obtained the existence and dynamic properties of positive almost periodic solutions for the generalized Nicholson blowflies equation with multiple delays and derived some conditions to ensure that the solutions of the considered model converge locally exponentially to a unique equilibrium point. For more on periodic solutions of the differential system, see [9, 10].

Motivated by the above discussion, in the present paper, by the introduction of distinctive maturation and feedback delays, we study the generalized structure Nicholson blowflies system with multiple time-varying delays which can be described as follows:

$$ \begin{aligned}[b] x_{i}'(t)&=-a_{ii}(t)+b_{ii}(t)e^{-x_{i}(t)}+ \sum_{j=1,j\neq i}^{n}\bigl(a_{ij}(t)-b_{ij}(t)e^{-x_{j}(t)} \bigr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(t)x_{i}\bigl(t-\tau _{ij}(t) \bigr)e^{-\beta _{ij}(t)x_{i}(t- \gamma _{ij}(t))}, \end{aligned} $$

(1.2)

where $i\in I=\{1,2,\ldots ,n\}$, $j\in J=\{1,2,\ldots ,m\}$, $a_{ij}(t)$, $b_{ij}(t)$, $\beta _{ij}(t)$, $\tau _{ij}(t)$ and $\gamma _{ij}(t)$ are all positive T-periodic continuous functions and $\alpha _{ij}(t)\leq 0$ is for T-periodic continuous functions for any $t\in \mathbb{R}$, $i\in I$, $j\in J$. The ith path $a_{ii}(t)+b_{ii}(t)e^{-x_{i}(t)}$ is the nonlinear density-dependent mortality term; the time-dependent birth function $\alpha _{ij}(t)x_{i}(t-\tau _{ij}(t))e^{-\beta _{ij}(t)x_{i}(t- \gamma _{ij}(t))}$ contains two types of delays: maturation delays $\tau _{ij}(t)$ and feedback delays $\gamma _{ij}(t)$; the weight function $a_{ij}(t)-b_{ij}(t)e^{-x_{j}(t)}$ describes the population cooperative connection in ith patch and jth patch.

Remark 1.1

Recalling the research of Nicholson’s blowfies systems, when $\tau _{ij}(t)=\gamma _{ij}(t)$ for $t\in \mathbb{R}$, $i\in I$, $j\in J$ in (1.2), we find that a great deal of research has been done; see e.g. [11–15]. Few results for dynamic properties of system (1.2) have been derived. We only find that some stability results for the case $n=1$ in (1.2) are obtained in [16]. In this paper, we will continue to study the properties of positive periodic solution to system (1.2).

Throughout this paper, let

$$ f^{-}=\inf_{t\in \mathbb{R}}f(t), \qquad f^{+}=\sup _{t\in \mathbb{R}}f(t). $$

Lemma 1.1

([17])

Suppose that X and Y are two Banach spaces, and$L:D(L)\subset X\rightarrow Y$, is a Fredholm operator with index zero. Furthermore, $\varOmega \subset X$is an open bounded set and$N:\bar{\varOmega }\rightarrow Y$isL-compact onΩ̄. if all the following conditions hold:

• (1) $Lx\neq \lambda Nx$, $\forall x\in \partial \varOmega \cap D(L)$, $\forall \lambda \in (0,1)$,

• (2) $Nx\notin \operatorname{Im}L$, $\forall x\in \partial \varOmega \cap \operatorname{Ker}L$,

• (3) $\operatorname{deg}\{JQN,\varOmega \cap \operatorname{Ker}L,0\}\neq 0$,

where$J:\operatorname{Im}Q\rightarrow \operatorname{Ker}L$is an isomorphism. Then the equation$Lx=Nx$has a solution on$\bar{\varOmega }\cap D(L)$.

We organize the following sections as follows: Sect. 2 gives existence of positive periodic solutions for system (1.2). In Sect. 3, we give some sufficient conditions for the asymptotic behaviors of positive periodic solutions to system (1.2). In Sect. 4, two numerical examples are given to show the feasibility of our results. Finally, some conclusions and discussions are given for system (1.2).

2 Existence of positive periodic solutions for system (1.2)

Theorem 2.1

Suppose that the following conditions hold:

(H₁):

$\frac{1}{b_{ii}^{-}(a_{ii}^{+}+\sum_{j=1,j\neq i}^{n}b_{ij}^{+}+\sum_{j=1}^{m}|\alpha _{ij}|^{+})}>1$, $i \in I$, $j\in J$;

(H₂):

$\frac{b_{ii}^{+}}{a_{ii}^{-}-\sum_{j=1,j\neq i}^{n}a_{ij}^{+}}>1$, $i \in I$, $j\in J$.

Then system (2.1) has at least oneT-periodic solution, i.e., system (1.2) has at least one positiveT-periodic solution.

Proof

Let $x_{i}(t)=e^{y_{i}(t)}$, $i\in I$, $t\in \mathbb{R}$, then the positive T-periodic solution of system (1.2) is equivalent to the T-periodic solution of the following system:

$$ \begin{aligned}[b] y_{i}'(t)&=- \frac{a_{ii}(t)}{e^{y_{i}(t)}}+ \frac{b_{ii}(t)}{e^{y_{i}(t)+e^{y_{i}(t)}}}+\sum_{j=1,j\neq i}^{n} \biggl(\frac{a_{ij}(t)}{e^{y_{i}(t)}}- \frac{b_{ij}(t)}{e^{y_{i}(t)+e^{y_{j}(t)}}} \biggr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(t) \frac{e^{x_{i}(t-\tau _{ij}(t))}}{e^{y_{i}(t)+\beta _{ij}(t)e^{y_{i}(t-\gamma _{ij}(t))}}}. \end{aligned} $$

(2.1)

Let

$$ C_{T}=\bigl\{ x=\bigl(x_{1}(t),\ldots ,x_{n}(t) \bigr)^{\top }|x\in C\bigl(\mathbb{R}, \mathbb{R}^{n}\bigr), x(t+T)\equiv x(t), \forall t\in \mathbb{R}\bigr\} $$

with the norm

$$ \Vert x \Vert =\max_{t\in [0,T]} \bigl\vert x_{i}(t) \bigr\vert , \quad \forall x \in C_{T}, i \in I. $$

Let $X=Y=C_{T}$. Define a linear operator

$$ L:D(L)\subset X\rightarrow Y, \qquad (Ly) (t)=y'(t), \quad \forall t\in \mathbb{R}, $$

(2.2)

where

$$ (Ly) (t)=\bigl(y_{1}'(t),\ldots ,y_{n}'(t) \bigr)^{\top }. $$

Obviously, $\operatorname{Ker}L=\mathbb{R}^{n}$, $\operatorname{Im}L=\{y\in Y|\int _{0}^{T}y(s)\,ds=0\}$, ImL is a closed set in X and $\operatorname{dimKer}L=\operatorname{codimIm}L=n$. Hence L is a Fredholm operator with index zero. Define a nonlinear operator N by

$$\begin{aligned}& \begin{aligned} &N: X\rightarrow Y, \qquad (Ny) (t)=\bigl((Ny)_{1}(t), \ldots ,(Ny)_{n}(t)\bigr)^{\top }, \quad \forall t\in \mathbb{R}, \\ &(Ny)_{i}(t)=-\frac{a_{ii}(t)}{e^{y_{i}(t)}}+ \frac{b_{ii}(t)}{e^{y_{i}(t)+e^{y_{i}(t)}}}+\sum _{j=1,j\neq i}^{n} \biggl(\frac{a_{ij}(t)}{e^{y_{i}(t)}}- \frac{b_{ij}(t)}{e^{y_{i}(t)+e^{y_{j}(t)}}} \biggr) \\ &\hphantom{(Ny)_{i}(t)=}{}+\sum_{j=1}^{m}\alpha _{ij}(t) \frac{e^{y_{i}(t-\tau _{ij}(t))}}{e^{y_{i}(t)+\beta _{ij}(t)e^{y_{i}(t-\gamma _{ij}(t))}}}. \end{aligned} \end{aligned}$$

(2.3)

Define continuous projectors $\mathcal{P}$, $\mathcal{Q}$

$$ \mathcal{P}:X\rightarrow \operatorname{Ker}L, \qquad (\mathcal{P}x) (t)= \frac{1}{T} \int _{0}^{T}x(t)\,dt $$

and

$$ \mathcal{Q}:X\rightarrow X/\operatorname{Im}L, \qquad \mathcal{Q}y= \frac{1}{T} \int _{0}^{T}y(t)\,dt . $$

Hence

$$ \operatorname{Im}\mathcal{P}=\operatorname{Ker}L, \qquad \operatorname{Ker} \mathcal{Q}=\operatorname{Im}L. $$

Let

$$ L_{\mathcal{P}}=L|_{D(L)\cap \operatorname{Ker}\mathcal{P}}:D(L)\cap \operatorname{Ker}\mathcal{P} \rightarrow \operatorname{Im}L, $$

then

$$ {L}_{\mathcal{P}}^{-1}=K_{\mathcal{P}}:\operatorname{Im}L\rightarrow D(L)\cap \operatorname{Ker}\mathcal{P}. $$

From $\operatorname{Im}L\subset C_{T}$, then ${K}_{\mathcal{P}}$ is an embedding operator and $K_{\mathcal{P}}$ is a complete operator in ImL. In view of the definitions of projector $\mathcal{Q}$ and nonlinear operator N, it follows that $\mathcal{Q}N(\bar{\varOmega })$ is bounded on Ω̄, where Ω is a bounded open set on X. Hence the nonlinear operator N is L-compact on Ω̅.

Consider the following operator equation:

$$ Ly=\lambda Ny, \quad \lambda \in (0,1), $$

(2.4)

i.e.,

$$ (Ly)_{i}=\lambda (Ny)_{i}, \quad \lambda \in (0,1), i\in I, $$

(2.5)

where L and N are defined by (2.2) and (2.3), respectively. Let $y\in X$ be an arbitrary T-periodic solution of (2.4), then, by (2.5),

$$ \begin{aligned}[b] y_{i}'(t)&=-\lambda \frac{a_{ii}(t)}{e^{y_{i}(t)}}+\lambda \frac{b_{ii}(t)}{e^{y_{i}(t)+e^{y_{i}(t)}}}+\lambda \sum _{j=1,j\neq i}^{n} \biggl(\frac{a_{ij}(t)}{e^{y_{i}(t)}}- \frac{b_{ij}(t)}{e^{y_{i}(t)+e^{y_{j}(t)}}} \biggr) \\ &\quad{}+\lambda \sum_{j=1}^{m}\alpha _{ij}(t) \frac{e^{y_{i}(t-\tau _{ij}(t))}}{e^{y_{i}(t)+\beta _{ij}(t)e^{y_{i}(t-\gamma _{ij}(t))}}}. \end{aligned} $$

(2.6)

For such a solution $y_{i}(t)$ ($i\in I$) in (2.6), there are $\xi \in [0,T]$ and $\eta \in [0,T]$ such that

$$ y_{i}(\xi )=\min_{t\in [0,T]}y_{i}(t), \qquad y_{i}(\eta )=\max_{t\in [0,T]}y_{i}(t), $$

(2.7)

and

$$ y_{i}'(\xi )=y_{i}'(\eta )=0. $$

(2.8)

From (2.6)–(2.8), we have

$$ \begin{aligned}[b] 0&=-\frac{a_{ii}(\xi )}{e^{y_{i}(\xi )}}+ \frac{b_{ii}(\xi )}{e^{y_{i}(\xi )+e^{y_{i}(\xi )}}}+\sum _{j=1,j \neq i}^{n} \biggl(\frac{a_{ij}(\xi )}{e^{y_{i}(\xi )}}- \frac{b_{ij}(\xi )}{e^{y_{i}(\xi )+e^{y_{j}(\xi )}}} \biggr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(\xi ) \frac{e^{y_{i}(\xi -\tau _{ij}(\xi ))}}{e^{y_{i}(\xi )+\beta _{ij}(\xi )e^{y_{i}(\xi -\gamma _{ij}(\xi ))}}} \end{aligned} $$

(2.9)

and

$$ \begin{aligned}[b] 0&=-\frac{a_{ii}(\eta )}{e^{y_{i}(\eta )}}+ \frac{b_{ii}(\eta )}{e^{y_{i}(\eta )+e^{y_{i}(\eta )}}}+\sum _{j=1,j \neq i}^{n} \biggl(\frac{a_{ij}(\eta )}{e^{y_{i}(\eta )}}- \frac{b_{ij}(\eta )}{e^{y_{i}(\eta )+e^{y_{j}(\eta )}}} \biggr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(\eta ) \frac{e^{y_{i}(\eta -\tau _{ij}(\eta ))}}{e^{y_{i}(\eta )+\beta _{ij}(\eta )e^{y_{i}(\eta -\gamma _{ij}(\eta ))}}}. \end{aligned} $$

(2.10)

By (2.9), we get

$$ \begin{aligned}[b] a_{ii}(\xi )&=\frac{b_{ii}(\xi )}{e^{e^{y_{i}(\xi )}}}+\sum _{j=1,j \neq i}^{n} \biggl(a_{ij}(\xi )- \frac{b_{ij}(\xi )}{e^{e^{y_{j}(\xi )}}} \biggr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(\xi ) \frac{e^{y_{i}(\xi -\tau _{ij}(\xi ))}}{e^{\beta _{ij}(\xi )e^{y_{i}(\xi -\gamma _{ij}(\xi ))}}} \\ &\geq \frac{b_{ii}^{-}}{e^{e^{y_{i}(\xi )}}}-\sum_{j=1,j\neq i}^{n}b_{ij}^{+}- \sum_{j=1}^{m} \vert \alpha _{ij} \vert ^{+}. \end{aligned} $$

(2.11)

In view of (2.11) and assumption (H₁), we have

$$ y_{i}(\xi )\geq \ln \biggl(\ln \frac{1}{b_{ii}^{-}(a_{ii}^{+}+\sum_{j=1,j\neq i}^{n}b_{ij}^{+}+\sum_{j=1}^{m} \vert \alpha _{ij} \vert ^{+})} \biggr):=M_{1,i}. $$

(2.12)

By (2.10), we get

$$ \begin{aligned}[b] a_{ii}(\eta )&=\frac{b_{ii}(\eta )}{e^{e^{y_{i}(\eta )}}}+\sum _{j=1,j \neq i}^{n} \biggl(a_{ij}(\eta )- \frac{b_{ij}(\eta )}{e^{e^{y_{j}(\eta )}}} \biggr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(\eta ) \frac{e^{y_{i}(\eta -\tau _{ij}(\eta ))}}{e^{\beta _{ij}(\eta )e^{y_{i}(\eta -\gamma _{ij}(\eta ))}}} \\ &\leq \frac{b_{ii}^{+}}{e^{e^{y_{i}(\eta )}}}+\sum_{j=1,j\neq i}^{n}a_{ij}^{+}. \end{aligned} $$

(2.13)

In view of (2.13) and assumption (H₂), we have

$$ y_{i}(\eta )\leq \ln \biggl(\ln \frac{b_{ii}^{+}}{a_{ii}^{-}-\sum_{j=1,j\neq i}^{n}a_{ij}^{+})} \biggr):=M_{2,i}. $$

(2.14)

Thus,

$$ \Vert y \Vert =\max \bigl\{ \vert M_{1,i} \vert , \vert M_{2,i} \vert , i\in I\bigr\} :=M. $$

Take $\varOmega =\{y\in X: \|y\|\leq M+1\}$. Based on the above proof, the condition (1) of Lemma 1.1 holds. For $y\in \partial \varOmega \cap \operatorname{Ker}L$, then y is a constant vector in $\mathbb{R}^{n}$. For $i\in I$ there exists i such that $|y_{i}|=M$ and $|y_{j}|< M$ ($j\neq i$). We claim that

$$ QN_{i}(-M)>0 \quad \text{and} \quad QN_{i}(M)< 0\quad \text{for } i\in I. $$

(2.15)

Otherwise, if $QN_{i}(-M)\leq 0$ ($i\in I$), then, by (2.3) and the definition of Q, we have

$$ \begin{aligned}[b] QN_{i}(-M)&=\frac{1}{T} \int _{0}^{T} \Biggl[-\frac{a_{ii}(t)}{e^{-M}}+ \frac{b_{ii}(t)}{e^{-M+e^{-M}}}+\sum_{j=1,j\neq i}^{n} \biggl( \frac{a_{ij}(t)}{e^{-M}}-\frac{b_{ij}(t)}{e^{-M+e^{-M}}} \biggr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(t) \frac{e^{-M}}{e^{-M+\beta _{ij}(t)e^{-M}}} \Biggr]\,dt\\ &\leq 0. \end{aligned} $$

(2.16)

By (2.12) and (2.16), we have

$$ -M>\ln \biggl(\ln \frac{1}{b_{ii}^{-}(a_{ii}^{+}+\sum_{j=1,j\neq i}^{n}b_{ij}^{+}+\sum_{j}^{m} \vert \alpha _{ij} \vert ^{+})} \biggr)=M_{1,i}, \quad i\in I, $$

which is a contradiction to the definition of M. if $QN_{i}(M)\geq 0$ ($i\in I$), then, by (2.3) and the definition of Q, we have

$$ \begin{aligned}[b] QN_{i}(M)&=\frac{1}{T} \int _{0}^{T} \Biggl[-\frac{a_{ii}(t)}{e^{M}}+ \frac{b_{ii}(t)}{e^{M+e^{M}}}+\sum_{j=1,j\neq i}^{n} \biggl( \frac{a_{ij}(t)}{e^{M}}-\frac{b_{ij}(t)}{e^{M+e^{M}}} \biggr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(t) \frac{e^{M}}{e^{-M+\beta _{ij}(t)e^{M}}} \Biggr]\,dt\\ &\geq 0. \end{aligned} $$

(2.17)

By (2.14) and (2.17), we have

$$ M< \ln \biggl(\ln \frac{b_{ii}^{+}}{a_{ii}^{-}-\sum_{j=1,j\neq i}^{n}a_{ij}^{+}} \biggr):=M_{2,i}, \quad i \in I, $$

which is a contradiction to the definition of M. Thus the condition (2) of Lemma 1.1 is satisfied. It remains to verify the condition (3) of Lemma 1.1. In order to prove it, define the continuous function $H(y_{i},\mu _{i})$ ($i\in I$) as follows:

$$ \begin{aligned}[b] H(y_{i},\mu _{i})&=-(1-\mu _{i})y_{i}+\frac{\mu }{T} \int _{0}^{T} \Biggl[-\frac{a_{ii}(t)}{e^{y_{i}}}+ \frac{b_{ii}(t)}{e^{y_{i}+e^{y_{i}}}}+\sum_{j=1,j\neq i}^{n} \biggl( \frac{a_{ij}(t)}{e^{y_{i}}}-\frac{b_{ij}(t)}{e^{y_{i}+e^{y_{i}}}} \biggr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(t) \frac{e^{y_{i}}}{e^{y_{i}+\beta _{ij}(t)e^{y_{i}}}} \Biggr]\,dt, \quad \mu \in [0,1]. \end{aligned} $$

By (2.15), for $y_{i}\in \partial \varOmega \cap \operatorname{Ker}L$ and $\mu _{i}\in [0,1]$, we have $y_{i}H(y_{i},\mu _{i})\neq 0$ ($i\in I$). Using the homotopy invariance theorem, we have

$$ \begin{aligned}[b] \operatorname{deg}\{QN,\varOmega \cap \operatorname{Ker}L,0\}&=\operatorname{deg}\bigl\{ H( \cdot ,0),\varOmega \cap \operatorname{Ker}L,0\bigr\} \\ &=\operatorname{deg}\bigl\{ H(\cdot ,1),\varOmega \cap \operatorname{Ker}L,0\bigr\} \\ &=\operatorname{deg}\{-y_{i},\varOmega \cap \operatorname{Ker}L,0\} \\ &\neq 0. \end{aligned} $$

Therefore, by the use of Lemma 1.1, it is easy to see that the system (2.1) has at least one T-periodic solution, i.e., system (1.2) has at least one positive T-periodic solution. □

3 Globally asymptotic stability of positive periodic solutions

Definition 3.1

If $x^{*}(t)=(x^{*}_{1}(t),x^{*}_{2}(t),\ldots ,x^{*}_{n}(t))^{\top }$ is a periodic solution of system (1.2) and $x(t)=(x_{1}(t),x_{2}(t),\ldots ,x_{n}(t))^{\top }$ is any solution of system (1.2) satisfying

$$ \lim_{t\rightarrow +\infty }\sum_{i=1}^{n} \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert =0. $$

Then $x^{*}(t)$ is globally asymptotic stable.

By the theory of Hale [18] for functional differential equations, consider the following system with initial condition:

$$ \textstyle\begin{cases} x_{i}'(t)=-a_{ii}(t)+b_{ii}(t)e^{-x_{i}(t)}+\sum_{j=1,j\neq i}^{n}(a_{ij}(t)-b_{ij}(t)e^{-x_{j}(t)}) \\ \hphantom{x_{i}'(t)=}{}+\sum_{j=1}^{m}\alpha _{ij}(t)x_{i}(t-\tau _{ij}(t))e^{- \beta _{ij}(t)x_{i}(t-\gamma _{ij}(t))}, \\ x_{i}(t)=\phi _{i}(t), \quad t\in [-\tau ,0], i\in I, \end{cases} $$

(3.1)

where $\tau =\max \{\tau _{ij}(t), \gamma _{ij}(t), i\in I, j\in J\}$, $\phi _{i}(t) \in C([-\tau ,0],\mathbb{R})$. Let

$$ \begin{aligned}[b] f_{i}(t,\phi _{i})&=-a_{ii}(t)+b_{ii}(t)e^{-\phi _{i}(\cdot )}+ \sum_{j=1,j \neq i}^{n}\bigl(a_{ij}(t)-b_{ij}(t)e^{-\phi _{j}(\cdot )} \bigr) \\ &\quad{}+\sum_{j=1}^{m}\alpha _{ij}(t)\phi _{i}(\cdot )e^{-\beta _{ij}(t) \phi _{i}(\cdot )}, \quad i\in I. \end{aligned} $$

From Theorem 2.3 in [18], if $f_{i}(t,\phi _{i})$ ($i\in I$) is Lipschitzian for $\phi _{i}$ in $C([-\tau ,0],\mathbb{R})$, then for system (3.1) there exists a unique solution. In this section, $f_{i}(t,\phi _{i})$ ($i\in I$) always satisfies Lipschitz condition. For convenience of the proof, in this section we also assume that $x^{*}=0$ is unique solution of system (3.1).

Theorem 3.1

Under conditions of Theorem 2.1, assume further that

(H₃):

$a_{ii}^{-}-b_{ii}^{-}\sum_{j=1,j\neq i}^{n}a_{ij}^{+}>0$for$i\in I$, $j \in J$.

Then system (3.1) has a uniqueT-periodic solution$x^{*}(t)=0$which is globally asymptotic stable.

Proof

Suppose that $x(t)$ be any positive T-periodic solution of system (3.1). Let

$$ V_{i}(t)=\frac{1}{2}x_{i}^{2}(t), \quad i\in I. $$

Use the $x_{i}(t)>0$ and $\alpha _{ij}(t)\leq 0$ for $i\in I$, $j\in J$, derivation of it along the solution of system (3.1) and one obtains

$$ \begin{aligned}[b] V_{i}'(t)&=-a_{ii}(t)x_{i}(t)+b_{ii}(t)x_{i}(t)e^{-x_{i}(t)}+x_{i}(t) \sum_{j=1,j\neq i}^{n}\bigl(a_{ij}(t)-b_{ij}(t)e^{-x_{j}(t)} \bigr) \\ &\quad{}+x_{i}(t)\sum_{j=1}^{m} \alpha _{ij}(t)x_{i}\bigl(t-\tau _{ij}(t) \bigr)e^{- \beta _{ij}(t)x_{i}(t-\gamma _{ij}(t))} \\ &\leq - \Biggl(a_{ii}^{-}-b_{ii}^{-}\sum _{j=1,j\neq i}^{n}a_{ij}^{+} \Biggr)x_{i}(t). \end{aligned} $$

Take the Lyapunov functional for system (3.1) in the following form:

$$ V(t)=\sum_{i=1}^{n}V_{i}(t). $$

Use assumption (H₃), taking the derivation of it along the solution of system (3.1) one obtains

$$ V'(t)\leq -\sum_{i=1}^{n} \Biggl(a_{ii}^{-}-b_{ii}^{-}\sum _{j=1,j \neq i}^{n}a_{ij}^{+} \Biggr)x_{i}(t)< 0. $$

For sufficiently large positive constant $t_{0}$, integrating both sides of the above inequality from $t_{0}$ to +∞, we get

$$ V(t)+ \int _{t_{0}}^{\infty }\sum_{i=1}^{n} \Biggl(a_{ii}^{-}-b_{ii}^{-} \sum _{j=1,j\neq i}^{n}a_{ij}^{+} \Biggr)x_{i}(t)\,dt\leq V(0). $$

(3.2)

It follows by (3.2) and Barbalat’s lemma [19] that

$$ \lim_{t\rightarrow +\infty }\sum_{i=1}^{n}x_{i}(t)=0. $$

Then the solution $x^{*}=0$ of system (3.1) is globally asymptotic stable. □

Remark 3.1

From the proof of Theorem 3.1, it is easy to see that constructing a Lyapunov functional for system (3.1) is not difficult because of $x_{i}(t)>0$ ($i\in I$). If $x_{i}(t)$ is a variable sign solution of system (3.1), since system (3.1) contains e exponential functions, constructing a proper Lyapunov functional for system (3.1) becomes very difficult. By developing a new technique, we hope to study the stability of the general solution of the system (3.1) in the future.

4 Two numerical examples

This section gives two examples for system (1.2) that demonstrate the validity of our theoretical results.

Example 4.1

$$ \textstyle\begin{cases} x_{1}'(t)=-(4+\sin t)+\frac{2+\sin t}{40}e^{-x_{1}(t)}+ \frac{117-\cos 2t}{40}-\frac{2-\cos 2t}{20}e^{-x_{2}(t)} \\ \hphantom{x_{1}'(t)=}{}+(-2+\sin ^{2}t)x_{1}(t-\sin ^{2}\frac{\pi t}{2})e^{-(2+ \sin ^{2}t)x_{1}(t-\sin ^{2}\frac{\pi t}{2})} \\ \hphantom{x_{1}'(t)=}{}+(-2+\cos ^{2}t)x_{1}(t-\cos ^{2}\frac{\pi t}{2})e^{-(2+ \cos ^{2}t)x_{1}(t-\cos ^{2}\frac{\pi t}{2})}, \\ x_{2}'(t)=-(\frac{1}{60}+\frac{1}{60}\cos ^{2} t)+(2+\cos t)e^{-x_{2}(t)}+ \frac{2-\cos ^{2}t}{20}-\frac{2-\cos ^{2}t}{20}e^{-x_{1}(t)} \\ \hphantom{x_{2}'(t)=}{}+(-6+\cos ^{2}t)x_{2}(t-\sin ^{2}\frac{\pi t}{2})e^{-(3+ \sin ^{2}t)x_{2}(t-\sin ^{2}\frac{\pi t}{2})} \\ \hphantom{x_{2}'(t)=}{}+(-6+\cos ^{2}t)x_{2}(t-\cos ^{2}\frac{\pi t}{2})e^{-(3+ \cos ^{2}t)x_{2}(t-\cos ^{2}\frac{\pi t}{2})}, \end{cases} $$

(4.1)

where

$$\begin{aligned}& a_{11}(t)=4+\sin t, \qquad b_{11}(t)=\frac{2+\sin t}{40}, \\& a_{12}(t)= \frac{117-\cos 2t}{40}, \qquad b_{12}(t)= \frac{2-\cos 2t}{20}, \\& \alpha _{11}(t)=-2+\sin ^{2}t, \qquad \tau _{11}(t)=\sin ^{2} \frac{\pi t}{2}, \\& \beta _{11}(t)=2+\sin ^{2}t, \qquad \gamma _{11}(t)=\sin ^{2} \frac{\pi t}{2}, \\& \alpha _{12}(t)=-2+\cos ^{2}t, \qquad \tau _{12}(t)=\cos ^{2} \frac{\pi t}{2}, \\& \beta _{12}(t)=2+\cos ^{2}t, \qquad \gamma _{12}(t)=\cos ^{2} \frac{\pi t}{2}, \\& a_{21}(t)=\frac{1}{60}+\frac{1}{60}\cos ^{2} t, \qquad b_{21}(t)=2+\cos t, \\& a_{22}(t)= \frac{2-\cos ^{2}t}{20}, \qquad b_{22}(t)=\frac{2-\cos ^{2}t}{20}, \\& \alpha _{21}(t)=-6+\cos ^{2}t, \qquad \tau _{21}(t)=\sin ^{2} \frac{\pi t}{2}, \\& \beta _{21}(t)=3+\sin ^{2}t, \qquad \gamma _{21}(t)=\sin ^{2} \frac{\pi t}{2}, \\& \alpha _{22}(t)=-6+\cos ^{2}t, \qquad \tau _{22}(t)=\cos ^{2} \frac{\pi t}{2}, \\& \beta _{22}(t)=3+\cos ^{2}t, \qquad \gamma _{21}(t)=\cos ^{2} \frac{\pi t}{2}. \end{aligned}$$

Obviously, $\tau =\max \{\tau _{ij},\gamma _{ij}, i,j=1,2\}=1$, then for the initial values of system (4.1) one takes $x_{i}(t)=\phi _{i}(t)\in C([-1,0],\mathbb{R})$, $i=1,2$. After simple calculation, we have

$$\begin{aligned}& b_{11}^{-}=\frac{1}{40}, \qquad a_{11}^{+}=5, \qquad b_{12}^{+}=\frac{3}{20}, \qquad \vert \alpha _{11} \vert ^{+}= \vert \alpha _{12} \vert ^{+}=2,\\& \frac{1}{b_{11}^{-}(a_{11}^{+}+b_{12}^{+}+ \vert \alpha _{11} \vert ^{+}+ \vert \alpha _{12} \vert ^{+})}= \frac{800}{143}>1, \\& b_{22}^{-}=\frac{1}{20}, \qquad a_{22}^{+}= \frac{1}{10}, \qquad b_{21}^{+}=3, \qquad \vert \alpha _{21} \vert ^{+}= \vert \alpha _{22} \vert ^{+}=5,\\& \frac{1}{b_{22}^{-}(a_{22}^{+}+b_{21}^{+}+ \vert \alpha _{21} \vert ^{+}+ \vert \alpha _{22} \vert ^{+})}= \frac{200}{113}>1, \\& a_{11}^{-}=3, \qquad a_{12}^{+}= \frac{118}{40}, \qquad b_{11}^{+}=\frac{3}{40}, \qquad \frac{b_{11}^{+}}{a_{11}^{-}-a_{12}^{+}}=\frac{3}{2}>1, \\& a_{22}^{-}=\frac{1}{20}, \qquad a_{21}^{+}= \frac{1}{30}, \qquad b_{22}^{+}= \frac{1}{10}, \qquad \frac{b_{22}^{+}}{a_{22}^{-}-a_{21}^{+}}=6>1. \end{aligned}$$

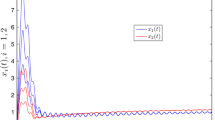
Hence, assumptions (H₁) and (H₂) of Theorem 2.1 hold and system (4.1) has at least one periodic solution. The numerical solutions with proper initial values are shown in Fig. 1 and Fig. 2.

Figure 1

State trajectories of system (4.1) for $x_{1}(t)$

Figure 2

State trajectories of system (4.1) for $x_{2}(t)$

Example 4.2

If $x(t)=0$ is a solution of system (1.2), then the coefficients of system (1.2) satisfy the following condition:

(H₄):

$-a_{ii}(t)+b_{ii}(t)+\sum_{j=1,j\neq i}^{n}(a_{ij}(t)-b_{ij})=0$, $i \in I$, $j\in J$.

Consider the following example:

$$ \textstyle\begin{cases} x_{1}'(t)=-(4+\sin t)+(4+\sin t)e^{-x_{1}(t)}+\frac{2-\sin t}{40}- \frac{2-\sin t}{40}e^{-x_{2}(t)} \\ \hphantom{x_{1}'(t)=}{}+(-2+\sin ^{2}t)x_{1}(t-\sin ^{2}\frac{\pi t}{2})e^{-(2+ \sin ^{2}t)x_{1}(t-\sin ^{2}\frac{\pi t}{2})} \\ \hphantom{x_{1}'(t)=}{}+(-2+\cos ^{2}t)x_{1}(t-\cos ^{2}\frac{\pi t}{2})e^{-(2+ \cos ^{2}t)x_{1}(t-\cos ^{2}\frac{\pi t}{2})}, \\ x_{2}'(t)=-(\frac{1}{60}+\frac{1}{60}\cos ^{2} t)+(\frac{1}{60}+ \frac{1}{60}\cos ^{2} t)e^{-x_{2}(t)}+\frac{2-\cos ^{2}t}{20}- \frac{2-\cos ^{2}t}{20}e^{-x_{1}(t)} \\ \hphantom{x_{2}'(t)=}{}+(-6+\cos ^{2}t)x_{2}(t-\sin ^{2}\frac{\pi t}{2})e^{-(3+ \sin ^{2}t)x_{2}(t-\sin ^{2}\frac{\pi t}{2})} \\ \hphantom{x_{2}'(t)=}{}+(-6+\cos ^{2}t)x_{2}(t-\cos ^{2}\frac{\pi t}{2})e^{-(3+ \cos ^{2}t)x_{2}(t-\cos ^{2}\frac{\pi t}{2})}, \end{cases} $$

(4.2)

where

$$\begin{aligned}& a_{11}(t)=4+\sin t, \qquad b_{11}(t)=4+\sin t, \\& a_{12}(t)= \frac{2-\cos 2t}{20}, \qquad b_{12}(t)= \frac{2-\cos 2t}{20}, \\& \alpha _{11}(t)=-2+\sin ^{2}t, \qquad \tau _{11}(t)=\sin ^{2} \frac{\pi t}{2}, \\& \beta _{11}(t)=2+\sin ^{2}t, \qquad \gamma _{11}(t)=\sin ^{2} \frac{\pi t}{2}, \\& \alpha _{12}(t)=-2+\cos ^{2}t, \qquad \tau _{12}(t)=\cos ^{2} \frac{\pi t}{2}, \\& \beta _{12}(t)=2+\cos ^{2}t, \qquad \gamma _{12}(t)=\cos ^{2} \frac{\pi t}{2}, \\& a_{21}(t)=\frac{1}{60}+\frac{1}{60}\cos ^{2} t, \qquad b_{21}(t)= \frac{1}{60}+\frac{1}{60}\cos ^{2} t, \\& a_{22}(t)= \frac{2-\cos ^{2}t}{20}, \qquad b_{22}(t)=\frac{2-\cos ^{2}t}{20}, \\& \alpha _{21}(t)=-6+\cos ^{2}t, \qquad \tau _{21}(t)=\sin ^{2} \frac{\pi t}{2},\\& \beta _{21}(t)=3+\sin ^{2}t, \qquad \gamma _{21}(t)=\sin ^{2} \frac{\pi t}{2}, \\& \alpha _{22}(t)=-6+\cos ^{2}t, \qquad \tau _{22}(t)=\cos ^{2} \frac{\pi t}{2}, \\& \beta _{22}(t)=3+\cos ^{2}t, \qquad \gamma _{21}(t)=\cos ^{2} \frac{\pi t}{2}. \end{aligned}$$

Obviously, $\tau =\max \{\tau _{ij},\gamma _{ij}, i,j=1,2\}=1$, then for the initial value of system (4.2) one takes $x_{i}(t)=\phi _{i}(t)\in C([-1,0],\mathbb{R})$, $i=1,2$. After simple calculation, assumption (H₄) holds and

$$\begin{aligned}& a_{11}^{-}=3, \qquad b_{11}^{-}=3, \qquad a_{12}^{+}=\frac{3}{20}, \qquad a_{11}^{-}-b_{11}^{-}a_{12}^{+}= \frac{51}{20}>0, \\& a_{22}^{-}=\frac{1}{20}, \qquad b_{21}^{-}= \frac{1}{60}, \qquad a_{21}^{+}= \frac{1}{30}, \qquad a_{22}^{-}-b_{21}^{-}a_{21}^{+}= \frac{89}{1800}>0. \end{aligned}$$

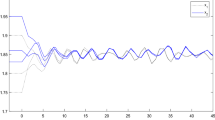
Hence, assumption (H₃) of Theorem 2.1 holds and $x^{*}=0$ of system (4.2) is globally asymptotic stable. The numerical solutions with proper initial values are shown in Fig. 3 and Fig. 4.

Figure 3

State trajectories of system (4.2) for $x_{1}(t)$

Figure 4

State trajectories of system (4.2) for $x_{2}(t)$

5 Conclusions and discussions

In the last past decades, Nicholson’s blowflies model has found successful applications in many areas, such as population dynamics, system control theory, biomathematics, and optimization problems. Hence, there is ongoing research interest on the dynamics of Nicholson’s blowflies model, including the existence, stability and oscillation which have occurred in the literature; see e.g. [1–4]. In this paper, we study a patch structure Nicholson blowflies model with multiple pairs of distinctive maturation and feedback delays and obtain existence and global asymptotic stability of the positive periodic solution. Two numerical examples are given to show the feasibility of our results.

The methods in this paper can be extended to the study of other types of differential dynamic systems such as stochastic differential equations, impulsive differential equations, and fractional differential equations. We hope other researchers can use the method provided in this article to do more in-depth research on various types of differential dynamic systems.