1 Introduction

Black holes are of the most important objects in the physics, which exhibit many interestingly physical consequences. Bekenstein and Hawking showed that the black holes are the thermodynamic systems whose entropy and temperature are determined by the area of the event horizon and the surface gravity at the event horizon, respectively [1,2,3,4,5]. Since their pioneering works, the thermodynamics of the black holes have been studied extensively. In 1983, Hawking and Page discovered a phase transition between Schwarzschild anti-de Sitter (AdS) black hole and thermal gas or thermal AdS space, well-known as the Hawking–Page transition in the literature [6]. According to AdS/CFT correspondence, the Hawking–Page transition can be explained as the gravitational dual of the confinement/deconfinement phase transition [7,8,9,10]. The AdS/CFT correspondence thus has motivated the study of the black holes and their thermodynamics in the AdS spacetime. Chamblin et al. found that the Reissner–Nordström AdS (RN-AdS) black hole can undergo a first-order phase transition which is similar to the liquid–gas phase transition [11, 12]. Recently, the cosmological constant was considered as the thermodynamic pressure associated with its conjugate variable which is the thermodynamic volume [13,14,15,16,17]. In the extended phase space, the black hole mass is most naturally the enthalpy, rather than the internal energy. Accordingly, many interesting phenomena of the black hole thermodynamics have been found, such as \(P-V\) criticality [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40], multiply reentrant phase transitions [41,42,43,44], the black holes as heat engines [45,46,47,48,49,50,51,52,53,54], or the Joule-Thomson expansion of the black holes [55,56,57,58,59,60].

The black hole solutions in general relativity (GR) have a central singularity surrounded by the event horizon [61]. It is widely believed that the black hole singularity does not exist in nature but shows the limitations of GR. On the other hand, it would be removed by a more fundamental theory of the gravitation, e.g. quantum gravity. However, a complete theory of quantum gravity has so far not been achieved. Thus, how to avoid the black hole singularity at the semi-classical level still gets many attentions. The regular black hole was first proposed by Bardeen [62], however, at that time what is the source leading to this regular black hole was not realized. In 2000, Ayon-Beato and Garcia reobtained the Bardeen black hole as a gravitational collapse of some magnetic monopole, in the scenario of Einstein gravity coupled to the non-linear electrodynamics [63]. Because the non-linear electrodynamics can lead to the regular black hole solutions, it has received many recent studies [19, 33, 39, 64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85].

Although GR predicts the graviton to be massless spin-2 particle with two degrees of freedom, it is natural to ask whether the graviton has mass. The recent direct observations of the gravitational waves by LIGO have constrained the graviton mass to \(m\le 1.2\times 10^{-22}\ \hbox {eV}\) [86]. This has made the question regarding the possibility of the massiveness of the graviton become more interesting. Theory of the massive gravity was first proposed by Fierz an Pauli (FP) [87]. In this theory, GR is extended by introducing a linear mass term in Fierz-Pauli form given as

$$\begin{aligned} S_{\text {FP}}=-\frac{m^2}{4}\int d^4x\left( h_{\mu \nu }h^{\mu \nu }-h^2\right) , \end{aligned}$$
(1)

where \(h_{\mu \nu }\) is a symmetric tensor field describing the massive graviton, \(h^{\mu \nu }=\eta ^{\mu \sigma }\eta ^{\nu \rho }h_{\sigma \rho }\), and \(h=\eta ^{\mu \nu }h_{\mu \nu }\). (Note that, any other combination of \(h_{\mu \nu }h^{\mu \nu }\) and \(h^2\) would lead to the appearance of the Boulware-Deser ghost [88]). Thus, this theory is well-known as the linear massive gravity theory. The massive graviton has 5 degrees of freedom which consist of two helicity-2 modes (or polarizations), two helicity-1 modes and one helicity-0 mode. The zero graviton mass limit of the linear massive or FP gravity theory is the massless gravity plus a massless vector and a massless scalar (the helicity-0 mode). The helicity-0 mode can couple to the trace of the stress-energy tensor and so it leads to extra contributions (for instance, to the Newtonian potential) which is responsible for the van Dam–Veltman–Zakharov (vDVZ) discontinuity [89, 90]. This problem was later resolved by Vainshtein, based on a well-known mechanism in a non-linear framework [91], at which the non-linear interactions screen the helicity-0 mode. In the non-linear framework, one introduces the interaction terms with no derivatives which reduces to FP mass term at quadratic order. Unfortunately, the non-linear massive gravity theory encounters another profound problem well-known as Boulware–Deser ghost in the literature [92]. Later, in 2010, de Rham, Gabadadze and Tolley (dRGT) proposed a new non-linear massive gravity theory which is ghost-free [93, 94]. It is notable to emphasize that the massive gravity has some significant phenomenological consequence such as the explanation of the accelerated expansion of the universe without invoking dark energy.

With the progress in the understanding of the massive gravity, various black hole solutions and their thermodynamics have been extensively studied in the presence of the graviton mass [32, 95,96,97,98,99,100,101,102,103,104,105,106,107,108,109]. In this paper, inspired by the non-linear electrodynamics, we would like to study the charged AdS black hole with the non-linear source in Einstein-dRGT gravity.

This paper is organized as follows. In Sect. 2, we introduce a system of Einstein-dRGT gravity coupled to the non-linear electromagnetic field in the four-dimensional AdS spacetime. Then, we derive a spherically-symmetric and static black hole solution of carrying magnetic charge and investigate the horizon properties of this black hole solution in details. In Sect. 3, we calculate the thermodynamic quantities and study the thermodynamic stability, phase transitions and \(P-V\) criticality. Finally, we make conclusions in the last section, Sect. 4. Note that, in this paper, we use units in \(G_N=\hbar =c=k_B=1\) and the signature of the metric \((-,+,+,+)\).

2 The black hole solution

Let us consider the coupling between the Einstein-massive gravity and the non-linear electromagnetic field in the background four-dimensional AdS spacetime. The action of this system is given as

$$\begin{aligned} S= & {} \int d^4x\sqrt{-g}\left\{ \phantom {\left. -\frac{1}{4\pi }\mathcal {L}(F)\right\} }\frac{1}{16\pi } \left[ R+\frac{6}{l^2}+m^2\sum ^4_{i=1}c_i \mathcal {U}_i(g,f)\right] \right. \nonumber \\&\left. -\frac{1}{4\pi }\mathcal {L}(F)\right\} , \end{aligned}$$
(2)

where R is the scalar curvature, l is the curvature radius of the background AdS spacetime, m is the graviton mass, \(c_i\) are the coupling parameters, f is a fixed symmetric tensor usually called the reference metric, \(\mathcal {U}_i\) are symmetric polynomials in terms of the eigenvalues of the \(4\times 4\) matrix \({\mathcal {K}^\mu }_\nu =\sqrt{g^{\mu \lambda }f_{\lambda \nu }}\) given as

$$\begin{aligned} \mathcal {U}_1= & {} [\mathcal {K}],\nonumber \\ \mathcal {U}_2= & {} [\mathcal {K}]^2-[\mathcal {K}^2],\nonumber \\ \mathcal {U}_3= & {} [\mathcal {K}]^3-3[\mathcal {K}][\mathcal {K}^2] +2[\mathcal {K}^3],\nonumber \\ \mathcal {U}_4= & {} [\mathcal {K}]^4-6[\mathcal {K}]^2[\mathcal {K}^2] +8[\mathcal {K}][\mathcal {K}^3]+3[\mathcal {K}^2]^2-6[\mathcal {K}^4],\nonumber \\ \end{aligned}$$
(3)

with \([\mathcal {K}]={\mathcal {K}^\mu }_\mu \), and \(\mathcal {L}(F)\) is a function of the invariant \(F\equiv F_{\mu \nu }F^{\mu \nu }/4\) with \(F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu \) to be the strength tensor of the non-linear electromagnetic field. The function \(\mathcal {L}(F)\) is a generalization of the Maxwell or linear electrodynamics at the region of the strong electromagnetic field corresponding to the short distances. But, \(\mathcal {L}(F)\) must reduce to the linear electrodynamics in the limit of the weak electromagnetic field. It is motivated to find a source leading to the regular black hole, in this work, we consider the non-linear electrodynamics defined by

$$\begin{aligned} \mathcal {L}(F)=Fe^{-\frac{k}{2Q}\left( 2Q^2F\right) ^{\frac{1}{4}}}. \end{aligned}$$
(4)

where k is a fixed characteristic parameter of the non-linear electrodynamics by which the charge Q and the mass M of the system are related as, \(Q^2=Mk\). Indeed, one can see that the Lagrangian (4) provides a suitable modification of the Maxwell or linear electrodynamics. As the characteristic parameter of the non-linear electrodynamics goes to zero, \(k\rightarrow 0\), the Lagrangian (4) should clearly approach the Maxwell one. Also, in the weak field region \(|Q^2F|\ll 1\), we can expand the Lagrangian (4) as

$$\begin{aligned} \mathcal {L}(F)=F\left[ 1-\frac{k}{2Q}\left( 2Q^2F\right) ^{\frac{1}{4}} +\cdots \right] . \end{aligned}$$
(5)

This means that the Maxwell electrodynamics is approximately restored in the weak field region.

Before proceeding, we stop here to more clarify the system described by the action (2) and indicate its suggestions. In this action, apart from considering the UV modification of the matter, we consider the modification of the gravity at the large distances or IR regime. Interestingly, at the short distances or UV regime, the gravity may obtain the corrections arising from a quantum theory of the gravity such as string theory. One of such UV modified gravity theories is the f(R) gravity where f(R) is a function of the scalar curvature R (see Ref. [110] for a review). Considering the modification of the gravity in both UV and IR regimes, corresponding to the f(R) nonlinear massive gravity, and its cosmological implications are studied in Refs. [111, 112]. In addition, in this work, the reference metric f is treated as a non-dynamical object. However, in general the reference metric f may be a dynamical object, and consequently we have a non-linear bimetric theory which consists of a massless spin-2 field coupling to a massive spin-2 field [113]. Therefore, it is significant to find the non-linear charged black hole solutions in the massive gravity with including the f(R) correction as well as considering the reference metric f to be a dynamical object. Also, an extension of the non-linear electrodynamics into the cosmology of the massive gravity [114,115,116,117,118,119] is expected to lead to interesting implications. All of these points will be studied in our future works.Footnote 1

We would like to consider the spherically-symmetric and static metric of the spacetime, given by the following ansatz

$$\begin{aligned} ds^2=-f(r)dt^2+f(r)^{-1}dr^2+r^2d\Omega ^2_2,\ \ f(r)=1-\frac{2m(r)}{r}. \end{aligned}$$
(6)

Following Ref . [97], we take the reference metric as

$$\begin{aligned} f_{\mu \nu }=\text {diag}(0,0,c^2,c^2\sin ^2\theta ), \end{aligned}$$
(7)

where c is a positive constant. With given spacetime and reference metrics, one can easily write explicitly the massive gravity term as

$$\begin{aligned} \mathcal {U}_1=\frac{2c}{r},\quad \mathcal {U}_2=\frac{2c^2}{r^2},\quad \mathcal {U}_3=\mathcal {U}_4=0. \end{aligned}$$
(8)

As a result, the equations of motion derived from the action (2) are

$$\begin{aligned}&G^\nu _\mu -\left[ \frac{3}{l^2}+m^2\left( \frac{cc_1}{r} +\frac{c^2c_2}{r^2}\right) \right] \delta ^\nu _\mu \nonumber \\&\quad =2\left[ \frac{\partial \mathcal {L}(F)}{\partial F} F_{\mu \rho }F^{\nu \rho } -\delta ^\nu _\mu \mathcal {L}(F)\right] , \end{aligned}$$
(9)
$$\begin{aligned}&\nabla _\mu \left( \frac{\partial \mathcal {L}(F)}{\partial F} F^{\nu \mu }\right) =0. \end{aligned}$$
(10)
$$\begin{aligned}&\nabla _\mu *F^{\nu \mu }=0. \end{aligned}$$
(11)

Now let us look for a black hole solution of the mass M and magnetic charge Q, with the ansatz of the magnetic field as

$$\begin{aligned} F_{\mu \nu }=\left( \delta ^\theta _\mu \delta ^\varphi _\nu -\delta ^\theta _\nu \delta ^\varphi _\mu \right) B(r,\theta ). \end{aligned}$$
(12)

It is notable that the magnetic charge Q is defined by

$$\begin{aligned} Q=\frac{1}{4\pi }\int _{S^\infty _2}{{\varvec{F}}}, \end{aligned}$$
(13)

with \({{\varvec{F}}}=\frac{1}{2}F_{\mu \nu }dx^\mu \wedge dx^\nu \) and \(S^\infty _2\) to be a two-sphere at the infinity. From Eqs. (10), (11) and (13), it can derive

$$\begin{aligned} B(r,\theta )=Q\sin \theta ,\ \ \longrightarrow \ \ F=\frac{Q^2}{2r^4}. \end{aligned}$$
(14)

Using this result, the (t, t) component of Eq. (9) reads

$$\begin{aligned} \frac{dm(r)}{dr}+\frac{3r^2}{2l^2}+\frac{m^2}{2}\left( cc_1r+c^2c_2\right) =\frac{Q^2}{2r^2}e^{-\frac{k}{2r}}. \end{aligned}$$
(15)

Integrating this equation with the integral constant M

$$\begin{aligned} \left[ m(r)+\frac{r^3}{2l^2}+\frac{m^2}{2} \left( \frac{cc_1r^2}{2}+c^2c_2r\right) \right] _{r\rightarrow \infty }=M, \end{aligned}$$
(16)

then substituting m(r) into f(r), we finally get

$$\begin{aligned} f(r)=1-\frac{2M}{r}e^{-\frac{k}{2r}}+\frac{r^2}{l^2} +m^2\left( \frac{cc_1r}{2}+c^2c_2\right) . \end{aligned}$$
(17)

Here, \(1+m^2c^2c_2\) can be understood as effective horizon curvature which can be positive, zero, or negative corresponding to the sphere, flat, or hyperbolic effective horizon. In the case of the massless graviton (\(m=0\)), it leads to the non-linear charged AdS black hole sourced by the non-linear electrodynamics (4). For \(M=Q=0\), we can derive the vacuum solution as

$$\begin{aligned} f(r)=1+\frac{r^2}{l^2}+m^2\left( \frac{cc_1r}{2}+c^2c_2\right) . \end{aligned}$$
(18)
Fig. 1
figure 1

We plot the curvature scalars R (left), \(R_{\mu \nu }R^{\mu \nu }\) (middle), and \(R_{\mu \nu \rho \lambda }R^{\mu \nu \rho \lambda }\) (right) in terms of r, for the different values of the characteristic parameter k of the non-linear electrodynamics, at \(l=M=1\) and \(m=0\). The blue, red, green and purple curves correspond to \(k=0.1\), 0.12, 0.14, 0.16, respectively

Full size image

Note that, the vacuum solution itself has a singularity at the origin \(r=0\) because the mass of the graviton is non-zero. In the limit \(k\rightarrow 0\), we have

$$\begin{aligned} f(r)=1-\frac{2M}{r}+\frac{r^2}{l^2}+m^2\left( \frac{cc_1r}{2}+c^2c_2\right) , \end{aligned}$$
(19)

which implies that the black hole becomes the 4D Schwarzschild-AdS black hole in the massive gravity. This is because, for \(k\rightarrow 0\), the squared charge \(Q^2\) of the black hole is extremely small compared to its mass M and thus the black hole could be considered to be electrically neutral. In the limit of the large distances \(k/r\ll 1\), we have the following approximation

$$\begin{aligned} f(r)\simeq 1-\frac{2M}{r}+\frac{Q^2}{r^2}+\frac{r^2}{l^2} +m^2\left( \frac{cc_1r}{2}+c^2c_2\right) , \end{aligned}$$
(20)

which suggests that the black hole behaves asymptotically like the 4D RN-AdS black hole in the massive gravity [97,98,99,100].

Now we would like to show that the source of the non-linear electrodynamics (4) leads to the regular black hole solution. In order to show this, let us consider the black hole in the background spacetime without any singularity corresponding to \(m=0\). For \(r\rightarrow 0\), one can find

$$\begin{aligned} f(r)=1+\frac{r^2}{l^2}, \end{aligned}$$
(21)

which means that the behavior of the black hole at the short distance looks like the AdS geometry and thus the singularity disappears. Also, we can check the curvature scalars R, \(R_{\mu \nu }R^{\mu \nu }\), and \(R_{\mu \nu \rho \lambda }R^{\mu \nu \rho \lambda }\) given as

$$\begin{aligned}&R=\frac{4m'(r)}{r^2}+\frac{2m''(r)}{r},\nonumber \\&R_{\mu \nu }R^{\mu \nu }=2\left[ \frac{2m'(r)}{r^2}\right] ^2 +2\left[ \frac{m''(r)}{r}\right] ^2,\nonumber \\&R_{\mu \nu \rho \lambda }R^{\mu \nu \rho \lambda }=3 \left[ \frac{4m(r)}{r^3}\right] ^2\nonumber \\&\quad -\frac{16m(r)}{r^3} \left[ \frac{4m'(r)}{r^2}-\frac{m''(r)}{r}\right] +2\left[ \frac{4m'(r)}{r^2}\right] ^2,\nonumber \\&\quad -\frac{16m'(r)m''(r)}{r^3}+\left[ \frac{2m''(r)}{r}\right] ^2, \end{aligned}$$
(22)

where

$$\begin{aligned} \frac{m(r)}{r^3}= & {} \frac{M}{r^3}e^{-\frac{k}{2r}}-\frac{1}{2l^2},\nonumber \\ \frac{m'(r)}{r^2}= & {} \frac{1}{2}\left( \frac{kM}{r^4}e^{-\frac{k}{2r}} -\frac{3}{l^2}\right) ,\nonumber \\ \frac{m''(r)}{r}= & {} \frac{kM(k-4r)}{4r^5}e^{-\frac{k}{2r}}-\frac{3}{l^2}. \end{aligned}$$
(23)

From these expressions, it can easily see that as r approaches zero we have

$$\begin{aligned} R\rightarrow -\frac{12}{l^2},\ \ R_{\mu \nu }R^{\mu \nu }\longrightarrow \frac{36}{l^4},\ \ R_{\mu \nu \rho \lambda }R^{\mu \nu \rho \lambda }\rightarrow \frac{24}{l^4}. \end{aligned}$$
(24)

In addition, as seen explicitly in Fig. 1, these curvature scalars are actually finite everywhere. Therefore, the non-linear charged AdS black hole is indeed regular.

We would like to analyze the horizon properties of the black hole solution. The equation of the horizon is given by, \(f(r_H)=0\), where \(r_H\) is denoted the horizon radius of the black hole. This equation leads to the relation between the black hole mass M and its horizon radius \(r_H\), as

$$\begin{aligned} M=\frac{r_H}{2}e^{\frac{k}{2r_H}}\left[ 1+\frac{r^2_H}{l^2} +m^2\left( \frac{cc_1r_H}{2}+c^2c_2\right) \right] . \end{aligned}$$
(25)

First let us consider the positive effective horizon curvature, \(1+m^2c^2c_2>0\). One can see that the mass M approaches infinite as \(r_H\rightarrow 0\) or \(r_H\rightarrow \infty \), and M is always larger than zero with the proper coupling parameter \(c_1\). This suggests that there actually exists the extremal black hole with the critical mass \(M_e\) below which there has no black hole. The extremal horizon radius \(r_e\) is a positive real root of the following equation

$$\begin{aligned}&12r^3_e-2\left( k-2l^2m^2cc_1\right) r^2_e+[4l^2\left( 1+m^2c^2c_2\right) \nonumber \\&\quad -kl^2m^2cc_1]r_e-2kl^2\left( 1+m^2c^2c_2\right) =0, \end{aligned}$$
(26)

which is derived from \(M'(r_e)=0\). Solving graphically this equation in order to derive the extremal radius and then the extremal mass is given in Fig. 2.

Fig. 2
figure 2

Plots of the extremal radius (left) and the extremal mass (right) in terms of the inverse squared curvature radius \(\frac{1}{l^2}\), for the different values of the characteristic parameter k of the non-linear electrodynamics, at \(m^2cc_1=m^2c^2c_2=1\). The blue, red, green and purple curves correspond to \(k=0.1, 0.15, 0.2, 0.25\), respectively

Full size image
Fig. 3
figure 3

The mass function, given at Eq. (25), is plotted in terms of the horizon radius for the different values of the characteristic parameter k of the non-linear electrodynamics, at \(l=m=c=c_1=1\). The blue, red, green and purple curves correspond to \(k=0.1, 0.15, 0.2, 0.25\), respectively. Left panel: \(c_2=1\). Right panel: \(c_2=-1\)

Full size image

This figure shows that the extremal radius and mass both should increase when the characteristic parameter k of the non-linear electrodynamics increases. And, for the curvature radius l of the AdS spacetime decreasing, the extremal radius should decrease, whereas the extremal mass should increase. The black hole with the mass \(M>M_e\) has two different horizons corresponding to the inner horizon and the event horizon, as shown in the left panel of Fig. 3.

The inner horizon radius \(r_-\) and event horizon one \(r_+\) correspond to the smaller and larger roots of the horizon equation, respectively, which are graphically solved in Fig. 4. With respect to the extremal black hole, these two horizons coincide together, \(r_-=r_+=r_e\).

Fig. 4
figure 4

We plot the inner horizon radius (left) and the event horizon radius (right) in terms of the black hole mass, for the different values of the characteristic parameter k of the non-linear electrodynamics, at \(l=m^2cc_1=m^2c^2c_2=1\). The blue, red, green and purple curves correspond to \(k=0.1, 0.15, 0.2\), 0.25, respectively

Full size image

For the zero effective horizon curvature, \(1+m^2c^2c_2=0\), the extremal black hole only exits if the coupling parameter \(c_1\) is positive, as seen in the right panel of Fig. 3. Here, we can easily get an analytical expression for the extremal horizon radius \(r_e\), by solving Eq. (26) with \(m^2c^2c_2=-1\), as

$$\begin{aligned} r_e=\frac{1}{12}\left( k-2l^2m^2cc_1+\sqrt{(k-2l^2m^2cc_1)^2 +12kl^2m^2cc_1}\right) . \end{aligned}$$
(27)

On the contrary, \(c_1<0\), we can see that the mass M approaches \(-\infty \) and \(+\infty \) as \(r_H\rightarrow 0\) and \(r_H\rightarrow \infty \), respectively. This means that there exits no the extremal black hole. But, the horizon radius of the black hole is bounded from below by

$$\begin{aligned} r_{b0}=-\frac{l^2m^2cc_1}{2}, \end{aligned}$$
(28)

which is independent on the characteristic parameter k of the non-linear electrodynamics and the coupling parameter \(c_2\). Also, with the proper parameters the black hole has possibly many inner horizons or does not have any inner horizon, as shown in Fig. 5. For the negative effective horizon curvature, \(1+m^2c^2c_2<0\), it is qualitatively the same as that of \(1+m^2c^2c_2=0\) and \(c_1<0\). However, in this case, the horizon radius of the black hole is bounded from below by

$$\begin{aligned} r_{b-}=\frac{1}{4}\left[ -l^2m^2cc_1+\sqrt{\left( l^2m^2cc_1\right) ^2 -16\left( 1+m^2c^2c_2\right) }\right] , \end{aligned}$$
(29)
Fig. 5
figure 5

The mass function is plotted in terms of the horizon radius, at \(k=0.1\) and \(m=c=-c_1=-c_2=1\). Left panel: \(l=1\). Right panel: \(l=0.1\)

Full size image

which is independent on the characteristic parameter k of the non-linear electrodynamics.

3 Thermodynamics and phase transitions

With the pressure defined as, \(P=\frac{3}{8\pi l^2}\), the mass function is reexpressed in terms of the event horizon radius, pressure and massive gravity parameters as

$$\begin{aligned} M=\frac{r_+}{2}e^{\frac{k}{2r_+}} \left[ 1+\frac{8\pi Pr^2_+}{3}+m^2 \left( \frac{cc_1r_+}{2}+c^2c_2\right) \right] . \end{aligned}$$
(30)

From this, we can write the first law of the black hole thermodynamics as

$$\begin{aligned} dM=TdS+VdP+\mathcal {C}_1dc_1+\mathcal {C}_2dc_2, \end{aligned}$$
(31)

at which there has naturally no the usual term \(\Phi dQ\). In general, the coupling parameters \(c_1\) and \(c_2\) can vary, thus we have treated them as the thermodynamic variables corresponding to the conjugating variables \(\mathcal {C}_1\) and \(\mathcal {C}_2\), respectively.

Using the surface gravity at the event horizon, we can identity the black hole temperature as

$$\begin{aligned} T= & {} \frac{f'(r_+)}{4\pi }=\left( 2r_+-\frac{k}{3}\right) P\nonumber \\&+\frac{(2r_+-k)}{8\pi r^2_+}\left[ 1+m^2 \left( \frac{cc_1r_+}{2}+c^2c_2\right) \right] +\frac{m^2cc_1}{8\pi }.\nonumber \\ \end{aligned}$$
(32)

As seen in Fig. 6, the behavior of the isobar curves is dependent on the coupling parameters \(c_{1,2}\), the characteristic one k, and the pressure.

Fig. 6
figure 6

Plots of the black hole temperature for the positive effective horizon curvature (left) and the zero one (right). Left panel: the blue, red, and green curves correspond to \(P=0.5\), 1.1353 \((P_c)\), 2, respectively, at \(m=c=c_1=c_2=1\) and \(k=0.1\). Right panel: the purple, blue and red curves correspond to \(P=1\), 2, 3, respectively, at \(m=c=-c_1=-c_2=1\) and \(k=\frac{1}{\pi }\). The dashed parts correspond to the regions that there has no the black hole solution

Full size image

For the positive effective horizon curvature, \(1+m^2c^2c_2>0\), with the proper pressure the isobar curves have one local maximum following one local minimum, denoted by \(T_{\text {max}}\) and \(T_{\text {min}}\), respectively. The corresponding event horizon radii \(r_{\text {max}}\) and \(r_{\text {min}}\) are smaller and larger positive roots of the following equation

$$\begin{aligned} 8\pi Pr^3_+- & {} \left( 1+m^2c^2c_2 -\frac{m^2cc_1k}{4}\right) r_+\nonumber \\+ & {} k\left( 1+m^2c^2c_2\right) =0, \end{aligned}$$
(33)

which is graphically solved in Fig. 7.

Fig. 7
figure 7

Plots of the radius \(r_{\text {max}}\) (top left), the radius \(r_{\text {min}}\) (top right), the temperature \(T_{\text {max}}\) (bottom left) and the temperature \(T_{\text {min}}\) (bottom right) in terms of the pressure for the different values of the characteristic parameter k of the non-linear electrodynamics, at \(m=c=c_1=c_2=1\). The blue, red, green, purple and pink curves correspond to \(k=0.1\), 0.11, 0.12, 0.13, 0.14, respectively

Full size image

From this equation one can see that, in order to have two different positive real roots, the following conditions have to be satisfied

$$\begin{aligned}&1+m^2c^2c_2-\frac{m^2cc_1k}{4}>0, \end{aligned}$$
(34)
$$\begin{aligned}&k^2\left( 1+m^2c^2c_2\right) ^2-\frac{1}{54\pi P}\left( 1+m^2c^2c_2 -\frac{m^2cc_1k}{4}\right) ^3<0.\nonumber \\ \end{aligned}$$
(35)

From (34), we obtain a critical value for the characteristic parameter k of the non-linear electrodynamics, with the parameters of the massive gravity fixed, as

$$\begin{aligned} k_c=\frac{4\left( 1+m^2c^2c_2\right) }{m^2cc_1}, \end{aligned}$$
(36)

above which the local maximum and minimum temperatures should disappear. Similarly, one can get a critical value for the pressure P from (35), with parameters of the massive gravity and non-linear electrodynamics fixed, as

$$\begin{aligned} P_c=\frac{\left( 1+m^2c^2c_2-m^2cc_1k/4\right) ^3}{54\pi k^2\left( 1+m^2c^2c_2\right) ^2}. \end{aligned}$$
(37)

If any of the above conditions is not satisfied, the isobar curves are the increasingly monotonic functions of the event horizon radius \(r_+\). For the zero effective horizon curvature, \(1+m^2c^2c_2=0\), we have the following cases:

  1. 1.

    If \(c_1>0\), the behavior of the isobar curves is qualitatively the same as that with \(1+m^2c^2c_2>0\) and \(P\ge P_c\) (or \(k\ge k_c\)).

  2. 2.

    If \(c_1<0\), the isobar curves should first decrease until a minimum and then increase when \(r_+\) increasing, where the minimum radius \(r_{\text {min}}\) and the minimum temperature \(T_{\text {min}}\) are given as

    $$\begin{aligned} r_{\text {min}}= & {} \frac{1}{4}\sqrt{-\frac{m^2cc_1k}{2\pi P}}, \end{aligned}$$
    (38)
    $$\begin{aligned} T_{\text {min}}= & {} -\frac{kP}{3}+\frac{m^2cc_1}{4\pi } +\sqrt{-\frac{m^2cc_1kP}{2\pi }}, \end{aligned}$$
    (39)

    with the conditions \(r_{\text {min}}>r_{b0}\) and \(T_{\text {min}}>0\).

  3. 3.

    If \(c_1<0\) and \(r_{\text {min}}<r_{b0}\), the isobar curves always increase in the increasing of the event horizon radius \(r_+\).

  4. 4.

    If \(c_1<0\), \(r_{\text {min}}>r_{b0}\), and \(T_{\text {min}}<0\), there are two temperature regions which are separated by a negative temperature region. (Note that, there has no the black hole with the event horizon radius corresponding to the negative temperature region). The first and second regions are the decreasingly and increasingly monotonous functions of the event horizon radius \(r_+\), respectively.

For the negative effective horizon curvature, \(1+m^2c^2c_2<0\), the behavior of the isobar curves is qualitatively the same as that with \(1+m^2c^2c_2=0\) and \(c_1<0\).

From the first law, the black hole entropy is obtained as

$$\begin{aligned} S= & {} \int \frac{1}{T}\left( \frac{\partial M}{\partial r_+}\right) dr_+,\nonumber \\= & {} \pi r^2_+\left( 1+\frac{k}{2r_+}\right) e^{\frac{k}{2r_+}}-\frac{\pi k^2}{4} \text {Ei}\left( \frac{k}{2r_+}\right) , \end{aligned}$$
(40)

where the function \(\text {Ei}(x)\) is defined as

$$\begin{aligned} \text {Ei}(x)=-\int _{-x}^{\infty }\frac{e^{-t}}{t}dt. \end{aligned}$$
(41)

It can easily see that only the non-linear electrodynamics affects the black hole entropy and that in particular it breaks the area law (\(S=\pi r^2_+\)). Indeed, if \(k\rightarrow 0\) or the non-linear electrodynamics approaches the usual Maxwell electrodynamics, then the area law of the black hole entropy should be recovered. In the regime of the large horizon radius \(k/r_+\ll 1\), we have the following expansion for the black hole entropy

$$\begin{aligned} S=\pi k^2\left[ \left( \frac{r_+}{k}\right) ^2+\frac{r_+}{k} +\frac{3-2\gamma }{8}-\frac{1}{4}\ln \left( \frac{k}{2r_+}\right) +\mathcal {O}\left( \frac{k}{r_+}\right) \right] , \end{aligned}$$
(42)

where \(\gamma \approx 0.577216\) is Euler’s constant. This expansion implies that only the first term is dominated whereas the remaining terms are approximately neglected. And, thus the black hole entropy satisfy approximately the area law in the regime of the large horizon radius.

Using the first law, one can obtain the thermodynamic volume V and the conjugating quantities \(\mathcal {C}_{1,2}\) as

$$\begin{aligned} V= & {} \left( \frac{\partial M}{\partial P}\right) _{S,c_1,c_2} =\frac{4\pi r^3_+}{3}e^{\frac{k}{2r_+}}, \end{aligned}$$
(43)
$$\begin{aligned} \mathcal {C}_1= & {} \left( \frac{\partial M}{\partial c_1}\right) _{S,P,c_2} =\frac{m^2cr^2_+}{4}e^{\frac{k}{2r_+}}, \end{aligned}$$
(44)
$$\begin{aligned} \mathcal {C}_2= & {} \left( \frac{\partial M}{\partial c_2}\right) _{S,P,c_1} =\frac{m^2c^2r_+}{2}e^{\frac{k}{2r_+}}. \end{aligned}$$
(45)

We would like to study the thermodynamic stability and the phase transitions of the black hole by investigating the behavior of the heat capacity \(C_P\) at constant pressure. The heat capacity \(C_P\) is defined as

$$\begin{aligned} C_P= & {} T\left( \frac{\partial S}{\partial T}\right) _P =\frac{\partial M}{\partial r_+}\left( \frac{\partial T}{\partial r_+}\right) ^{-1},\nonumber \\= & {} \frac{4\pi ^2r^2_+P}{3}\frac{h_1(r_+)}{h_2(r_+)}e^{\frac{k}{2r_+}}, \end{aligned}$$
(46)

where the functions \(h_1(r_+)\) and \(h_2(r_+)\) are defined by the left hand sides of Eqs. (26) and (33), respectively. The heat capacity is plotted in the event horizon radius, for the different cases of the effective horizon curvature and the different values of the pressure, in Fig. 8.

Fig. 8
figure 8

Plots of the heat capacity for the positive effective horizon curvature (left) and the zero one (right). Left panel: the blue, red and green curves correspond to \(P=0.5\), 1.1353 (\(P_c\)), 2, respectively, at \(m=c=c_1=c_2=1\) and \(k=0.1\). Right panel: the blue, red and green curves correspond to \(P=1\), 2, 3, respectively, at \(m=c=-c_1=-c_2=1\) and \(k=\frac{1}{\pi }\). Note that, the dashed parts correspond to the regions that there has no the black hole solution

Full size image
Fig. 9
figure 9

Plots of the Gibbs free energy for the positive effective horizon curvature (left) and the zero one (right). Left panel: the purple, blue, red and green curves correspond to \(P=0.3\), 0.5, 1.1353 \((P_c)\), 2, respectively, at \(m=c=c_1=c_2=1\) and \(k=0.1\). Right panel: the purple, blue and red curves correspond to \(P=1\), 2, 3, respectively, at \(m=c=-c_1=-c_2=1\) and \(k=\frac{1}{\pi }\). The dashed parts correspond to the regions that there has no the black hole solution

Full size image

For the positive effective horizon curvature, the heat capacity is always positive if \(P\ge P_c\) or \(k\ge k_c\), and thus the black hole is always stable thermodynamically. However, if \(P<P_c\) and \(k<k_c\), the heat capacity is positive only with respect to the small black holes of \(r_+<r_{\text {max}}\) and the large black holes of \(r_+>r_{\text {min}}\). Whereas, with respect to the intermediate black holes of \(r_{\text {max}}<r_+<r_{\text {min}}\), the heat capacity is negative. On the other hand, the small and large black holes are thermodynamically stable, whereas the intermediate black holes are thermodynamically unstable. Interestingly, we observe that the heat capacity suffers from discontinuities at the points \(r_{\text {max}}\) and \(r_{\text {min}}\). This suggests that the points \(r_{\text {max}}\) and \(r_{\text {min}}\) are the second-order phase transition points which correspond to the small-to-intermediate black hole transition and intermediate-to-large black hole transition, respectively. For the zero effective horizon curvature, we have the following cases:

  1. 1.

    If \(c_1>0\), the heat capacity is always positive, thus the black hole is thermodynamically stable.

  2. 2.

    If \(c_1<0\), \(r_{\text {min}}>r_{b0}\), and \(T_{\text {min}}>0\), the small black holes of \(r_+<r_{\text {min}}\) are thermodynamically unstable because of the negative heat capacity. Whereas, because of the positive heat capacity, the large black holes of \(r_+>r_{\text {min}}\) are thermodynamically stable. In particular, there occurs a second-order phase transition at \(r_{\text {min}}\) between the unstable small and stable large black holes.

  3. 3.

    If \(c_1<0\) and \(r_{\text {min}}<r_{b0}\), it is the same as the case of \(c_1>0\).

  4. 4.

    If \(c_1<0\), \(r_{\text {min}}>r_{b0}\), and \(T_{\text {min}}<0\), there have two different phases corresponding to the unstable small and stable large black holes. However, unlike the case 2, there has no phase transition between these two phases because of the presence of the forbidden region separating these two phases. In other words, if the black hole exits in one of these two phases, then it always exits in that phase and is impossible to undergo a phase transition to another phase.

For the negative effective horizon curvature, the thermodynamic stability and the phase transition of the black hole are qualitatively the same as that of \(1+m^2c^2c_2=0\) and \(c_1<0\).

Table 1 The numerical results for the radius \(r_{HP}\) and the temperature \(T_{HP}\) at the Hawking–Page phase transition, for the different values of the characteristic parameter k of the non-linear electrodynamics and the pressure, at \(m=c=c_1=c_2=1\)
Full size table

The Gibbs free energy G is defined as

$$\begin{aligned} G=M-TS, \end{aligned}$$
(47)

which is plotted in the temperature in Fig. 9.

For the positive effective horizon curvature, if \(P<P_c\) and \(k<k_c\) the Gibbs free energy exhibits a swallowtail structure which suggests the occurrence of a first-order phase transition between small and large black holes. This first-order phase transition should disappear when \(P\ge P_c\) or \(k\ge k_c\). In addition, we can point out the occurrence of the Hawking–Page phase transition between the thermal radiation and the black hole, at which the Gibbs free energy vanishes [6]. The radius \(r_{HP}\) and the temperature \(T_{HP}\), corresponding to the Hawking–Page phase transition, are numerically given in Table 1.

From Eq. (32), we can obtain the equation of state as

$$\begin{aligned} P= & {} \frac{T}{2r_+-k/3}\nonumber \\&+\frac{2\left( 1+m^2c^2c_2\right) (k-2r_+)+m^2cc_1r_+(k-4r_+)}{16\pi r^2_+(2r_+-k/3)},\nonumber \\ \end{aligned}$$
(48)

where \(r_+=r_+(V,k)\) is determined by Eq. (43). Note that, the pressure should be divergent when the event horizon radius \(r_+\) approaches \(\frac{k}{6}\), due to the fact that the black hole of \(r_+=\frac{k}{6}\) has the temperature independent on the pressure. On the other hand, the above equation of state is only defined for the black hole of \(r_+<\frac{k}{6}\) or that of \(r_+>\frac{k}{6}\). For the positive effective horizon curvature, a critical point occurs when the isotherm in the \(P-r_+\) diagram has an inflexion point, which is determined by

$$\begin{aligned} \left( \frac{\partial P}{\partial r_+}\right) _T=\left( \frac{\partial ^2P}{\partial r^2_+}\right) _T=0. \end{aligned}$$
(49)

From this, one can derive the critical radius \(r_c\) as

$$\begin{aligned} r_c=\frac{6k\left( 1+m^2c^2c_2\right) }{4\left( 1+m^2c^2c_2\right) -m^2cc_1k}, \end{aligned}$$
(50)

and the critical temperature \(T_c\) as

$$\begin{aligned} T_c= & {} \frac{13\left( 1+m^2c^2c_2\right) }{81\pi k}+\frac{37m^2cc_1}{216\pi }\nonumber \\&+\frac{(m^2cc_1)^2k\left( 1+m^2c^2c_2+m^2cc_1k/96\right) }{108\pi \left( 1+m^2c^2c_2\right) ^2}. \end{aligned}$$
(51)

For \(T<T_c\), there occurs a first-order phase transition between the small black hole of \(r_+>\frac{k}{6}\) and the large black hole, which is analogous to the van der Waals phase transition between the liquid and gas. More specifically, the behavior of the isotherms in the case of the positive effective horizon curvature is depicted in Fig. 10.

Fig. 10
figure 10

The pressure is plotted in terms of the event horizon radius \(r_+\), under the different values of the temperature, at \(m=c=c_1=c_2=1\) and \(k=0.1\). The blue, red, dashed green and purple curves correspond to \(T=0.9\), 1, 1.0764 (\(T_c\)), 1.2, respectively

Full size image

We find a universal constant as

$$\begin{aligned} \frac{P_cv_c}{T_c}=\frac{\left[ 32(1+m^2c^2c_2)+m^2cc_1k\right] \left[ 4(1+m^2c^2c_2)-m^2cc_1k\right] ^2}{16(1+m^2cc_2)^2 \left[ 104(1+m^2c^2c_2)+111m^2cc_1k\right] +(m^2cc_1k)^2 \left[ 96(1+m^2c^2c_2)+m^2cc_1k\right] }, \end{aligned}$$
(52)
Fig. 11
figure 11

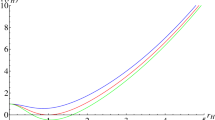
Plots of the universal constant \(\frac{P_cv_c}{T_c}\equiv \zeta \) in terms of the coupling parameter \(c_1\) or \(c_2\), for the different values of the characteristic parameter k of the non-linear electrodynamics, at \(m=c=1\). The blue, red, green and purple curves correspond to \(k=0.1\), 0.15, 0.2, 0.25, respectively. Left panel: \(c_1=0.1\). Middle panel: \(c_1=-0.1\). Right panel: \(c_2=1\)

Full size image

which is only dependent on the characteristic parameter k of the non-linear electrodynamics and the parameters of the massive gravity. Note that, \(v_c=2r_c-k/3\) is critical specific volume. Interestingly, in the case of the coupling parameter \(c_1=0\), the universal constant becomes

$$\begin{aligned} \frac{P_cv_c}{T_c}=\frac{4}{13}\approx 0.3077, \end{aligned}$$
(53)

which is independent on the remaining parameters. Also, the universal constant approaches this value, \(\frac{4}{13}\), as the characteristic parameter k of the non-linear electrodynamics approaches zero. In Fig. 52, we plot the universal constant with respect to the coupling parameter \(c_1\) or \(c_2\), under the different values of the characteristic parameter k of the non-linear electrodynamics.

This figure shows that, for fixed but negative coupling parameter \(c_1\), the universal constant should increase as the characteristic parameter k of the non-linear electrodynamics increases or as the coupling parameter \(c_2\) decreases. This happens to the contrary if \(c_1>0\). Whereas, for \(c_2\) fixed, the universal constant is an decreasingly monotonic function of \(c_1\) independently of the sign of \(c_2\).

4 Conclusion

In this paper, we have derived a solution of 4D non-linear charged AdS black hole, which is spherically-symmetric and static, in the context of the non-linear electrodynamics and the Einstein-massive gravity. The non-linear electrodynamics is characterized by a fixed parameter k by which the charge Q and the mass M of the system are related as, \(Q^2=Mk\). As the characteristic parameter k approaches zero, the Lagrangian of the non-linear electrodynamics should become the usual Maxwell one. In the massive gravity theory proposed by de Rham, Gabadadze and Tolley, the potential associated with the graviton mass consists of the four terms. However, in the four-dimensional spacetime, only two terms corresponding to the coupling parameters \(c_1\) and \(c_2\) appear in the black hole solution.

We have studied the horizon properties of the black hole, which are crucially dependent on the sign of both \(c_1\) and \(c_2\). Interesting, the presence of \(c_2\) yields an effective horizon curvature which can be positive, zero, or negative corresponding to the sphere, flat, or hyperbolic effective horizon. The extremal black hole only exists for the case of the positive effective horizon curvature or that of the zero effective horizon curvature and \(c_1>0\). On the contrary, the black hole solution can exist with arbitrary mass but its horizon radius is bounded from below. Also, with the proper parameters the black hole possibly has many inner horizons or does not have any inner horizon.

We have studied the thermodynamics, the thermodynamic stability and the phase transitions of the black hole. Interestingly, unlike the usual charged black hole, the usual term \(\Phi dQ\) disappears naturally in the first law of the present black hole. Also, the black hole entropy is affected only by the non-linear electrodynamics at which the area law is broken. But, the area law of the black hole entropy should be approximately restored in the regime of the large horizon radius. Based on the heat capacity at constant pressure, we studied the thermodynamic stability of the black hole and pointed to its second-order phase transitions which occur at the maximum temperature and the minimum one. Whereas, based on the Gibbs free energy, we pointed to a firs-order phase transition of the black hole and the Hawking–Page phase transition. In the case of the positive effective horizon curvature, we have also shown a critical point in the \(P-r_+\) diagram. For the temperature below the critical value, a first-order phase transition between the small and large black holes occurs, which is analogous to the van der Waals phase transition between the liquid and gas.