Behavior of quasinormal modes and Van der Waals-like phase transition of charged AdS black holes in massive gravity

Abstract

In this work, we utilize the quasinormal modes (QNMs) of a massless scalar perturbation to probe the Van der Waals-like small and large black holes (SBH/LBH) phase transition of charged topological Anti-de Sitter (AdS) black holes in four-dimensional massive gravity. We find that the signature of this SBH/LBH phase transition is detected in the isobaric as well as in the isothermal process. This further supports the idea that the QNMs can be an efficient tool to investigate the thermodynamical phase transition.

1 Introduction

Einstein’s general relativity introduces gravitons as massless spin-2 particles [1,2,3]. However, understanding the quantum behavior of gravity could be related to the possible mass of the graviton. This Einstein theory, modified at large distances in massive gravity, provides a possible explanation for the accelerated expansion of the Universe that does not require any dark energy. Actually, the massive gravity and its extensions, such as bimetric gravity, can yield cosmological solutions which do display late-time acceleration in agreement with observations [4,5,6,7]. Very recently, the LIGO collaboration reporting the discovery of gravitational waves asserted that [8] “assuming a modified dispersion relation for gravitational waves, our observations constrain the Compton wavelength of the graviton to be $\lambda _g>10^{13}\, \mathrm{km}$, which could be interpreted as a bound on the graviton mass $m_g<1.2\times 10^{-22}\,\mathrm{eV/c}^2$”. In order to have a massive graviton, the first attempt for constructing a massive theory was in the work of Fierz and Pauli [9], which was done in the context of linear theory. Unfortunately this theory possesses the so-called van Dam, Veltman and Zakharov discontinuity problem. The resolution to this problem was Vainshtein’s mechanism, which requires the system to be considered in a nonlinear framework. As is now well known, it usually brings about a Boulware–Deser ghost [10] by adding generic mass terms for the graviton on the nonlinear level. Subsequently, a nonlinear massive gravity theory was proposed by de Rham, Gabadadze and Tolley (dRGT) [11, 12], where the mass terms are added in a specific way to ensure that the corresponding equations of motion are at most second order differential equations so that the Boulware–Deser ghost is eliminated. Later, spherically symmetric black hole solutions were constructed in the dRGT massive gravity [13,14,15,16], including its extension in terms of electric charge [17,18,19], black string [20], BTZ like black holes [21, 22] and some other solutions with higher curvature correction terms [23, 24]. This program goes beyond solution constructions in the dRGT massive gravity and focuses on the investigation of holographic implications [25,26,27,28,29,30], discussing the thermodynamical properties [31,32,33,34] and calculating QNMs under massless scalar perturbations for the BTZ like black hole [35].

The thermodynamical phase transition of a black hole is always a hot topic in black hole physics. It may shed light on the understanding of the relation between gravity and thermodynamics. Recently, thermodynamics of AdS black holes has been generalized to the extended phase space where the cosmological constant is treated as the pressure of the black hole [36,37,38]. A particular emphasis has been put on the study of the black hole phase transitions in AdS spacetime in Ref. [39], which asserted the analogy between the Van der Waals liquid–gas system behavior and the charged AdS black hole. Subsequently a broad range of thermodynamic behaviors has been discovered, including reentrant phase transitions and more general Van der Waals behavior [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70]. Recently, some investigations of the thermodynamics of AdS black holes in massive gravity showed generalizations to the extended phase space [19, 71,72,73,74,75,76], including the higher curvature terms [23, 31, 32].

For a long time, thermodynamical phase transitions of the black hole are supposed to detect by some observational signatures. Considering that QNMs of dynamical perturbations are characteristic issues of black holes [77,78,79], it is expected that black hole phase transitions can be reflected in the dynamical perturbations in the surrounding geometries of black holes through frequencies and damping times of the oscillations. Moreover, the QNM frequencies of AdS black holes have direct interpretation in terms of the dual conformal field theory CFT [80,81,82,83,84,85]. A lot of discussions have been focused on this topic and more and more evidence has been found between thermodynamical phase transitions and dynamical perturbations. See for example [86,87,88,89,90,91,92,93,94,95,96]. In the extended phase space, we have recovered the deep relation between the dynamical perturbation and the Van der Waals-like SBH/LBH phase transition in the four-dimensional Reissner–Nordstr$\ddot{o}$m–Anti de Sitter (RN-AdS) black holes with spherical horizon $(k=1)$ [97]. Later, matters have been generalized to higher-dimensional RN-AdS black holes [98], including time-domain profiles [99], and higher-dimensional charged black holes in the presence of Weyl coupling [100].

It is necessary to point out that in four-dimensional dRGT massive gravity, there always exists a so-called Van der Waals-like SBH/LBH phase transition for the charged AdS black holes when the horizon topology is spherical $(k=1)$, Ricci flat $(k=0)$ or hyperbolic $(k=-1)$ [71]. In particular, this phenomenon rarely occurs, since this Van der Waals-like SBH/LBH phase transition was usually recovered in a variety of spherical horizon black hole backgrounds. Motivated by these results, in this paper we find it crucial and well justified to reconsider the charged topological AdS black hole in four-dimensional dRGT massive gravity. We further use the QNM frequencies of a massless scalar perturbation to probe the Van der Waals-like SBH/LBH phase transitions of charged topological black holes $(k=0, k=\pm 1)$, respectively.

This paper is organized as follows. In Sect. 2, we will review the Van der Waals-like SBH/LBH phase transition of charged topological AdS black holes in four-dimensional massive gravity. In Sect. 3, we will disclose numerically that the phase transition can be reflected by the QNM frequencies of dynamical perturbations. We end the paper with conclusions and discussions in Sect. 4.

2 Phase transition of charged topological AdS black hole in massive gravity

We start with the action of four-dimensional massive gravity in the presence of a negative cosmological constant [33],

$$\begin{aligned} \mathcal{I}= & {} \frac{1}{16\pi }\int {\mathrm{d}^4x\sqrt{-g}}\Biggl [R-2\Lambda -\frac{1}{4}F_{\mu \nu }F^{\mu \nu }\nonumber \\&+\,m^2\sum _i^{4}c_{i}\mathcal{U}_{i}(g,f)\Biggr ], \end{aligned}$$

(1)

where f is a fixed symmetric tensor usually called the reference metric, $c_i$ are constants, m is the mass parameter related to the graviton mass and $F_{\mu \nu }$ is the Maxwell field strength defined as $F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }$ with vector potential $A_{\mu }$. Moreover, $\mathcal{U}_{i}$ are symmetric polynomials of the eigenvalues of the $4\times 4$ matrix $\mathcal{K}^\mu _{\nu }\equiv \sqrt{g^{\mu \alpha }f_{\alpha \nu }}$,

$$\begin{aligned} \mathcal{U}_{1}= & {} [\mathcal K],\nonumber \\ \mathcal{U}_{2}= & {} [\mathcal{K}]^2-[\mathcal{K}^2],\nonumber \\ \mathcal{U}_{3}= & {} [\mathcal{K}]^3-3[\mathcal{K}][\mathcal{K}^2]+2[\mathcal{K}^3],\nonumber \\ \mathcal{U}_{4}= & {} [\mathcal{K}]^4-6[\mathcal{K}^2][\mathcal{K}]^2 +8[\mathcal{K}^3][\mathcal{K}]+3[\mathcal{K}^2]^2-6[\mathcal{K}^4].\nonumber \\ \end{aligned}$$

(2)

The square root in $\mathcal{K}$ is understood as the matrix square root, i.e., $(\sqrt{A})^{\mu }_{~\nu }(\sqrt{A})^{~\nu }_{\lambda }=A^\mu _{~\lambda }$, and the rectangular brackets denote traces $[\mathcal{K}]=\mathcal{K}^{\mu }_{~\mu }$.

The action admits a static black hole solution with metric

$$\begin{aligned} \mathrm{d}s^2=-f(r)\mathrm{d}t^2+\frac{1}{f(r)}\mathrm{d}r^2+r^2h_{ij}\mathrm{d}x^i\mathrm{d}x^j, \end{aligned}$$

(3)

where the coordinates are labeled $x^{\mu }=(t, r, x^1, x^2)$ and $h_{ij}$ describes the two-dimensional hypersurface with constant scalar curvature 2k. The constant k characterizes the geometric property of a hypersurface, which takes values $k=0$ for the flat case, $k=-1$ for negative curvature and $k=1$ for positive curvature, respectively. In a four-dimensional situation we have $\mathcal{U}_{3}=\mathcal{U}_{4}=0$. Then the solution of charged topological AdS black hole is given by [33]

$$\begin{aligned} f(r)=k+\frac{8\pi P r^2}{3}-\frac{m_0}{r}+\frac{q^2}{4r^2} +\frac{c_0c_1m^2r}{2}+c_0^2c_2m^2,\nonumber \\ \end{aligned}$$

(4)

where P equals $-\frac{\Lambda }{8\pi }$. Moreover, the parameters $m_0$ and q are related to mass and charge of black hole

$$\begin{aligned} M=\frac{V_2}{8\pi }m_0,\quad Q=\frac{V_2}{16\pi }q.\nonumber \end{aligned}$$

Here $V_2$ is the volume of space spanned by coordinates $x^i$. When $m\rightarrow 0$, the solution (4) reduces to the RN-AdS black hole.

The reference metric now can have a special choice

$$\begin{aligned} f_{\mu \nu }=\mathrm{diag}(0,0,c_0^2h_{ij}). \end{aligned}$$

(5)

Without loss of generality we have set $c_0=1$ in our following discussions.

In terms of the radius of the horizon $r_+$, the mass M, Hawking temperature T, entropy S and electromagnetic potential $\Phi$ of the black holes can be written as

$$\begin{aligned} M= & {} \frac{V_2 r_+}{8\pi }\left( k+c_{2}m^2+\frac{q^2}{4r_+^2}+\frac{8\pi P r_+^2}{3} +\frac{c_{1}m^2 r_{+}}{2}\right) ,\nonumber \\ T= & {} -\frac{q^2}{16\pi r_+^3}+\frac{k+c_2m^2}{4\pi r_+}+2 Pr_{+} +\frac{c_{1}m^2}{4\pi },\nonumber \\ S= & {} \frac{V_2}{4} r_+^2,\quad \Phi =\frac{q}{r_+} . \end{aligned}$$

(6)

In the extended phase space, the black hole mass M is considered as the enthalpy rather than the internal energy of the gravitational system [37].

From Eq. (6), the equation of state of the black hole can be obtained,

$$\begin{aligned} P=\frac{T}{2r_+}-\frac{c_{1}m^2}{8\pi r_+}-\frac{k+c_{2}m^2}{8\pi r_+^2} +\frac{q^2}{32\pi r_+^4}. \end{aligned}$$

(7)

To compare with Van der Waals fluid equation in four dimensions, we can translate the “geometric” equation of state to a physical one by identifying the specific volume v of the fluid with horizon radius of black hole as $v=2r_+$.

As usual, a critical point occurs when P has an inflection point,

$$\begin{aligned} \frac{\partial P}{\partial r_+}\Big |_{T=T_c, r_+=r_c} =\frac{\partial ^2 P}{\partial r_+^2}\Big |_{T=T_c, r_+=r_c}=0, \end{aligned}$$

(8)

which leads to

$$\begin{aligned} r_c= & {} \frac{\sqrt{6}q}{2\sqrt{k+c_{2}m^2}}, \quad T_c=\frac{2(k+c_{2}m^2)^{3/2}}{3\sqrt{6}\pi q} +\frac{c_{1}m^2}{4\pi },\nonumber \\ P_c= & {} \frac{(k+c_{2}m^2)^2}{24\pi q^2}. \end{aligned}$$

(9)

Evidently the critical behavior occurs when $k+c_{2}m^2>0$, which is a joint effect of horizon topology k and $c_2m^2$. Previous thermodynamical discussions for RN-AdS black holes show that the Van der Waals-like SBH/LBH only occurs for spherical horizon topology $k=1$. The graviton mass significantly modifies this behavior and a non-zero m admits that possibility of critical behavior for $k\ne 1$. In addition, it has been shown [33] that when $k+c_{2}m^2>0$, the small and large black hole phases are both locally thermodynamically stable because the corresponding heat capacities are always positive.¹

The equilibrium thermodynamics is governed by the Gibbs free energy, $G=G(T, P, q)$, which obeys the thermodynamic relation $G=M-TS$. For later discussions, it is convenient to rescale the Gibbs free energy in the following way: $g=\frac{4\pi }{V_2}G$. Then g reads

$$\begin{aligned} g=\frac{3q^2}{16r_+}+\frac{(k+c_{2}m^2)r_+}{4} -\frac{2\pi P r_+^3}{3}. \end{aligned}$$

(10)

Here $r_+$ is understood as a function of pressure and temperature, $r_+=r_+(P,T)$, via the equation of state (7).

3 Perturbations of charged topological AdS black hole in massive gravity

Now we study the evolution of a massless scalar field perturbation in the surrounding geometry of these charged topological AdS black holes.

A massless scalar field $\Psi (r,t,\Omega )=\phi (r)\mathrm{e}^{-i\omega t}Y_{lm}(\Omega )$, obeys the Klein–Gordon equation

$$\begin{aligned} \nabla _{\mu }^{2}\Psi (r,t,\Omega )=\frac{1}{\sqrt{-g}}\partial _\mu (\sqrt{ -g}g^{\mu \nu }\partial _\nu \Psi (r,t,\Omega ))=0,\nonumber \\ \end{aligned}$$

(11)

where $Y_{lm}(\Omega )$ is a normalizable harmonic function on the two-dimensional hypersurface. In particular, the Laplace operator on $\Omega$ yields

$$\begin{aligned} \nabla ^{2}_{\Omega }Y_{lm}(\Omega )=-\kappa ^2Y_{lm}(\Omega ). \end{aligned}$$

(12)

It is necessary to point out that the eigenvalue $\kappa ^2$ usually gets different values in consideration of different horizon topologies. For the spherical $(k=1)$ and flat $(k=0)$ topology, the eigenvalue $\kappa ^2$ can be zero. Then the radial function $\phi (r)$ obeys

$$\begin{aligned} \phi ''(r)+\left( \frac{f'(r)}{f(r)}+\frac{2}{r}\right) \phi '(r) +\frac{\omega ^2\phi (r)}{f(r)^2}=0, \end{aligned}$$

(13)

where  $\omega$  are complex numbers $\omega =\omega _r + i\omega _{im}$, corresponding to the QNM frequencies of the oscillations describing the perturbation. For the hyperbolic horizon topology$(k=-1)$, the eigenvalue $\kappa ^2$ of the Laplace operator on $\Omega$ cannot be zero [101,102,103,104], and is given by $\frac{1}{4}+\xi ^2$, where $\xi =L_{\Omega }(L_{\Omega }+1)$, $L_{\Omega }=0,1,2,...$ [105]. Then the radial function $\phi (r)$ obeys the following differential equation:

$$\begin{aligned} \phi ''(r)+\left( \frac{f'(r)}{f(r)}+\frac{2}{r}\right) \phi '(r) +\left( \frac{\omega ^2}{f(r)}-\frac{\kappa ^2}{r^2}\right) \frac{\phi (r)}{f(r)}=0.\nonumber \\ \end{aligned}$$

(14)

Here we define $\phi (r)$ as $\varphi (r)\exp [-i\int \frac{\omega }{f(r)}\mathrm{d}r]$, where the $\exp [-i\int \frac{\omega }{f(r)}\mathrm{d}r]$ asymptotically approaches the ingoing wave near the horizon, then Eqs. (13) and (14) become

$$\begin{aligned}&\varphi ''(r)+\varphi '(r)\left( \frac{f'(r)}{f(r)}-\frac{2i\omega }{f(r)}+\frac{2}{r}\right) \nonumber \\&\qquad \quad -\frac{2i\omega }{r f(r)}\varphi (r)=0,\quad k=0,1 , \end{aligned}$$

(15)

and

$$\begin{aligned}&\varphi ''(r)+\varphi '(r)\left( \frac{f'(r)}{f(r)}-\frac{2i\omega }{f(r)}+\frac{2}{r}\right) \nonumber \\&\qquad \quad -\left( 2i\omega +\frac{\kappa ^2}{r}\right) \frac{\varphi (r)}{r f(r)}=0,\quad k=-1. \end{aligned}$$

(16)

In this paper, we only consider $\xi =0$, namely $\kappa ^2=1/4$ for $k=-1$.

We are going to study whether the signature of Van der Waals-like SBH/LBH phase transition of charged topological AdS black holes can be reflected by the dynamical QNMs behavior in the massless scalar perturbation. For Eqs. (15) and (16), we have $\varphi (r)=1$ in the limit of $r\rightarrow r_+$. At the AdS boundary $(r\rightarrow \infty )$, we need $\varphi (r)=0$. Under these boundary conditions, we will numerically solve Eqs. (15) and (16) separately to find QNM frequencies by adopting the shooting method. In the context of the Van der Waals phase transition picture, the dynamical perturbations in the isobaric process and isothermal process will be discussed. In our following numerical computations we will set $q=2$, $m=1$, $c_1=0.05$ and $c_2=2$.

3.1 Isobaric phase transition

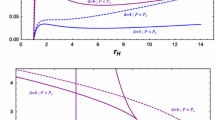
Due to the pressure P (or l) being fixed in this case, the black hole horizon $r_+$ is the only variable in the system. The behavior of an isobar with different horizon topologies is plotted in Fig. 1. For $P<P_c$, the oscillating part displays the occurrence of an SBH/LBH phase transition in the system and the Gibbs free energy depicts a swallow tail behavior, also signaling a first-order SBH/LBH phase transition. Here the intersection point indicates the coexistence of two phases in equilibrium. The critical pressure $P_c$ is obtained by $\frac{\partial T}{\partial r_+}=\frac{\partial ^2 T}{\partial r_+^2}=0$.

Fig. 1

The g–T (left panel) and T–$r_+$ (right panel) diagrams for $P<P_c$. The three lines correspond to $k=1$ (dashed line), $k=0$ (dotdashed line) and $k=-1$ (solid line)

In Table 1 (see the appendix), we further list the QNM frequencies of massless scalar perturbation around small and large black holes for a first order SBH/LBH phase transition. Fixing the pressure with $P=0.003$, we obtain the phase transition temperature $T_*\simeq 0.04567$, $T_*\simeq 0.06945$ and $T_*\simeq 0.08664$ in the cases of $k=-1$, 0 and 1, respectively, where the small and large black hole phases can coexist. With regard to a small black hole phase, the radius of the black hole becomes smaller and smaller when the temperature decreases from the phase transition temperature $T_*$. In this process the absolute values of the imaginary part of the QNM frequencies decrease, while the real part frequencies change very little. On the other hand, when the temperature for the large black hole phase increases from the phase transition temperature $T_*$, the black hole gets bigger. The QNM frequencies increase in the real and absolute value of imaginary parts. Consequently, the massless scalar perturbation outside the black hole gets more oscillations but it decays faster. These results are consistent with the overall discussions reported in [97, 98]. Figure 2 illustrates the QNM frequencies for small and large black hole phases. Increase in the black hole size is indicated by the arrows.

Fig. 2

The behavior of QNM frequencies for large and small black holes in the isobaric process. The arrow indicates the increase of the black hole horizon

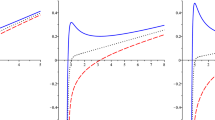
In addition, at the critical position $P=P_c$, with $P_c\simeq 0.0033157$ for $k=-1$, $P_c\simeq 0.0132629$ for $k=0$ and $P_c\simeq 0.0298416$ for $k=1$, a second-order phase transition occurs. The QNM frequencies of the small and large black hole phases are plotted in Fig. 3. We see that QNM frequencies of two black hole phases show the same behavior as the black hole horizon increases at the critical point.

Fig. 3

The behavior of QNM frequencies for large and small black holes in the isobaric process. The arrow indicates the increase of the black hole horizon

3.2 Isothermal phase transition

Fixing the black hole temperature T, the associated P–$r_+$ diagram of charged topological AdS black holes is displayed in the right part of Fig. 4. For $T<T_c$ there is an inflection point and the behavior is reminiscent of the Van der Waals liquid–gas system. Moreover, the behavior of the Gibbs free energy is plotted in the left panel of Fig. 4. Similarly to Fig. 1, characteristic first order SBH/LBH phase transition behavior shows up.

Table 2 (see the appendix) displays the QNM frequencies of small and large black hole phases at temperature $T=0.79T_c$ for different horizon topologies $(k=0,\pm 1)$ in the isothermal precess. Then the first order SBH/LBH phase transition happens at $P_*\approx 0.001728$ for $k=-1$, at $P_*\approx 0.007189$ for $k=0$ and at $P_*\approx 0.016215$ for $k=1$, where the small and large black holes possess the same Gibbs free energy and same pressure. The data above (below) the horizontal line are for the small (large) black hole phase, respectively. The drastically different QNM frequencies for small and large black hole phases are plotted in Fig. 5. From the figure we see different slopes of the QNM frequencies in the massless scalar perturbations revealing that small and large black holes are in different phases.

Fig. 4

The g–P (left panel) and P–$r_+$ (right panel) diagrams for $T<T_c$. The three lines correspond to $k=1$ (dashed line), $k=0$ (dot dashed line) and $k=-1$ (solid line)

Fig. 5

The behavior of QNM frequencies for large and small black holes in the isothermal process. The arrow indicates the increase of the black hole horizon

In the isothermal transition, the QNMs can be affected by the value of the pressure P(l) and the horizon radius $r_+$, which are related by a fixed temperature. To illustrate the effects of the two parameters, we list the influence of $r_+$ on the frequencies for small and large black holes by fixing P(l) in Table 3 (see the appendix) and QNM frequencies by fixing the black hole size $r_+$ in Table 4 (see the appendix). From Tables 3 and 4 one can see that there is competition between the pressure P and horizon radius $r_+$. Each of these parameters aims to overwhelm the other, which affects the decay rate of the field.

Fig. 6

The behavior of QNM frequencies for large and small black holes in the isothermal process. The arrow indicates the increase of the black hole horizon

In order to further discuss how these two factors affect the QNM frequencies, we perform a double-series expansion of the frequency $\omega (r_{+}+\Delta r_+,P+\Delta P)$

$$\begin{aligned} \omega (r_{+}+\Delta r_+,P+\Delta P)= & {} \omega (r_+,P)+\frac{\partial \omega }{\partial r_+}\Delta r_{+} +\frac{\partial \omega }{\partial P}\Delta P\nonumber \\&+\,\mathcal {O}(\Delta r_+^2,\Delta P^2,\Delta r_{+}\cdot \Delta P).\nonumber \\ \end{aligned}$$

(17)

Obviously, the changes of the QNM frequency are under two influences, one is from the change of the black hole size $r_+$ and the other is from the change of the pressure P (or AdS radius l). For simple discussions we define $\Delta _1\equiv \frac{\partial \omega }{\partial r_+}\Delta r_{+}$ and $\Delta _2\equiv \frac{\partial \omega }{\partial P}\Delta P$.

Note that the choice of the step of pressure $\Delta P$ in linear approximation is related to $\Delta r_+$, which is brought about by

$$\begin{aligned} \mathrm{d}P=\left( -\frac{T}{2r_+^2}+\frac{c_{1}m^2}{8\pi r_+}+\frac{k+c_{2}m^2}{4\pi r_+^3} -\frac{q^2}{8\pi r_+^5}\right) \mathrm{d}r_+ \end{aligned}$$

(18)

from the equation of state (7). In Table 5 (see the appendix), we list the QNM frequencies from the linear approximation for small and large black hole phase. One can see that the behavior of $\tilde{\omega }$ is in good agreement with the numerical computation results listed in Table 2. Comparing $\Delta _1$ and $\Delta _2$ in Table 5, the change of P (or l) in small black hole phase clearly wins over the change of the black hole size, which dominantly contributes to the behavior of QNM frequencies for small black hole phase. For the large black hole phase, the contributions of $\Delta _1$ and $\Delta _2$ on the real part of the QNM frequency are comparable. But the change of P (or l) wins out a little.

In addition, for the isothermal phase transition at $T=T_c$, the QNM frequencies for the small black hole and large black hole are plotted in Fig. 6, which shows the same behavior as the horizon radius increases.

4 Conclusions and discussions

We have calculated the QNMs of massless scalar field perturbation around small and large charged topological AdS black holes in four-dimensional dRGT massive gravity. When the Van der Waals-like SBH/LBH phase transition happens in the extended space, no matter whether in the isobaric process by fixing the pressure P or in the isothermal process by fixing the temperature T of the system, the slopes of the QNM frequencies change drastically being different in the small and large black hole phases as the horizon radius $r_+$ is increasing. This clearly shows the signature of the phase transition between small and large black holes. Moreover, we have also found that, at the critical isothermal and isobaric phase transitions, QNM frequencies for both small and large black holes have the same behavior, suggesting that QNMs are not appropriate to probing the black hole second order phase transition.

Comparing with the action of Eq. (1), Ref. [73] recently asserted the existence of a Van der Waals-like SBH/LBH phase transition with the massive potential $\mathcal{U}_{3}\ne 0$ in the five-dimensional case. Moreover, the charged black hole [23], the Born–Infeld black hole [32] and the black hole in the Maxwell and Yang–Mills fields [24] have recently been constructed in Gauss–Bonnet massive gravity. The Van der Waals-like SBH/LBH phase transition also appears in these models. It would be interesting to extend our discussion to these black hole solutions.

Appendix

Here we present the related QNM frequencies of the massless scalar perturbation around small and large black holes in the isobaric as well as in the isothermal process.

See Tables 1, 2, 3, 4 and 5.

Table 1 The QNM frequencies of massless scalar perturbation with the change of the black hole temperature in the isobaric process. The upper part above the horizontal line is for the small black hole phase, while the lower part is for the large black hole phase

Table 2 The QNM frequencies of massless scalar perturbation with the change of the black hole pressure in the isothermal process. The upper part, above the horizontal line, is for the small black hole phase, while the lower part is for the large black hole phase

Table 3 The QNM frequencies change as the black hole horizons $r_+$

Table 4 The QNM frequencies change as the pressure P

Table 5 $\tilde{\omega }$ is the QNM frequencies from the linear approximation. $\Delta _1$ and $\Delta _2$ represent corrections due to variation of the black hole size and pressure, respectively