1 Introduction

Since the original work of Vishveswara [2, 3] on quasinormal modes (QNMs), considered as solutions of a perturbed wave equation around black hole configuration, interest has been increasing in their study. Indeed the characteristic oscillations of the black holes play a prominent role in the dynamics of astrophysical black holes in the framework of general relativity [4, 5]. Last February, LIGO (Laser Interferometer Gravitational-Wave Observatory) announced for the first time the detection of gravitational waves from a cosmic event generated more than one billion year ago by the merger of two orbiting black holes [6]. The observation of these waves is an important landmark in the gravitational waves astronomy. The measure of the QNMs frequencies by various detectors such as LIGO [7], VIRGO [8], KAGRA [9, 10], can shed light on the main feature of the black holes such the mass and the angular momentum.

The properties of quasinormal modes have been tested in the context of the AdS/CFT correspondence [11,12,13], the investigation of the stability of AdS black holes becomes more appealing. The quasinormal frequencies of AdS black holes have direct interpretation in terms of the dual conformal field theory CFT, for details we refer to [14,15,16,17,18,19,20]. The QNMs can be used as a powerful tool to detect the extra dimensions of spacetime, in other words the brane-world scenarios assume the existence of extra dimensions, so that multidimensional black holes can be formed in a laboratory [21,22,23,24].

Recently, many efforts have been devoted to the study of the thermodynamical properties of black holes, in connection with higher dimensional supergravity models [25, 26]. These properties have been extensively studied via different methods including numerical computation using various codes [27]. In fact, several models based on mathematical methods have been explored to study critical behaviors of black holes with different geometrical configurations in arbitrary dimensions. A particular emphasis has been put on AdS black holes [28,29,30,31,32,33,34]. More precisely, a nice interplay between the behaviors of the RN–AdS black hole systems and the Van der Waals fluids has been discussed at length in [35,36,37,38,39,40,41,42,43].

In this context, several landmarks of statistical liquid-gas systems, such as the P–V criticality, the Gibbs free energy, the first-order phase transition and the behavior near the critical points have been derived. Also, in [1] the authors established a link between the Reissner-Nordström AdS black hole critical behavior and the quasinormal modes in \(d=4\), showing that QNM can be a dynamic probe of the thermodynamic phase transition. More precisely they find a drastic change in the slopes of the quasinormal frequencies in the small (SBH) and large (LBH) black holes near the critical point where the Van der Waals like thermodynamic phase transition occurs. Also in [44], the authors studied the quasinormal modes and P–V criticality for scalar perturbations in a class of dRGT massive gravity around Black Holes.

Motivated by these results we find it crucial and well justified to generalize these studies to high dimensional spacetime, since a higher dimension RN–AdS black hole also presents a Van der Waals like phase transition [35, 37].

Our paper is organized as follows. We briefly review the critical behavior of the charged-AdS black hole in arbitrary dimensional spacetime in Sect. 2. In Sect. 3 we develop the master equation for the massless scalar field perturbation in high dimensional RN–AdS spacetime. Sections 4 and 5 are devoted to the calculation of the quasinormal modes of scalar perturbation around the black holes and to show how their frequencies encode the signature of the first-order phase transition. Also we will see that the QNMs cannot reveal the second-order phase transition. In Sect. 6 we discus how the critical ratio affects the ability of the quasinormal modes frequencies to detect the phase transition. Finally, in the last section we summarize our results and draw the conclusion.

2 Critical behavior of RN–AdS black holes in higher dimension: a review

The Einstein–Maxwell–Anti-de Sitter action in higher dimensions d may be written as

$$\begin{aligned} I_\mathrm{EM}=-\frac{1}{16\pi }\int _M \mathrm{d}^dx\sqrt{-g}\left( R-F^2+\frac{(d-1)(d-2)}{l^2}\right) .\nonumber \\ \end{aligned}$$
(1)

The solution of the action (1) is the solution for a spherical d-dimensional charged AdS black hole with negative cosmological constant where \(d\ge 4\). It can be written in the static form

$$\begin{aligned}&\mathrm{d}s^2 = -f \mathrm{d}t^2 + \frac{\mathrm{d}r^2}{f} + r^{2} \mathrm{d}\omega _{d-2}^2,\nonumber \\&F=\mathrm{d}A,\quad A=-\sqrt{\frac{d-2}{2(d-3)}}\frac{q}{r^{d-3}}\mathrm{d}t. \end{aligned}$$
(2)

Here, the function f is given by

$$\begin{aligned} f = 1 - \frac{m}{r^{d-3}} + \frac{q^2}{r^{2(d-3)}} + \frac{r^2}{l^2}, \end{aligned}$$
(3)

and \(\mathrm{d}\omega _d^2\) is the metric of a d-dimensional unit sphere.

Fig. 1
figure 1

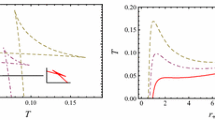
Top the Hawking temperature as a function of the black holes horizon \(r_H\) in \(d=4,6\). Bottom the Gibbs free energy as a function of the temperature T in \(d=4,6\). The two upper lines (purple) correspond to \(d=6\) while the lower one (blue) correspond to \(d=4\). The critical isobar \(P=P_c\) is denoted by the dashed lines, while the solid lines show the first-order transition \(P<P_c\)

Full size image
Table 1 The quasinormal frequencies of the massless scalar perturbation as a function of the black holes temperature. The upper part, above the horizontal lines is for the small black hole phase while the lower part is for the large one
Full size table
Fig. 2
figure 2

The behavior of the quasinormal modes for small and large black holes in the complex-\(\omega \) plane for \(4\le d\le 11\). The increase of the black hole size is shown by the arrows for the isobaric process

Full size image

The parameters m and q are related to the ADM mass M (in our set up, they are associated with the enthalpy of the system as we shall see later) and the charge Q of the black hole by [31]

$$\begin{aligned}&M=\frac{d-2}{16 \pi } \omega _{d-2} m, \nonumber \\&Q=\frac{\sqrt{2(d-2)(d-3)}}{8\pi }\,\omega _{d-2}\,q, \end{aligned}$$
(4)

with \(\omega _d\) being the volume of the unit d-sphere,

$$\begin{aligned} \omega _d=\frac{2\pi ^{\frac{d+1}{2}}}{\Gamma \left( \frac{d+1}{2}\right) }. \end{aligned}$$
(5)

It is worth to notice that the cosmological constant \(\Lambda = - \frac{(d-1)(d-2)}{2 l^2}\) is regarded as a variable and also identified with the thermodynamic pressure P [45,46,47],

$$\begin{aligned} P = - \frac{1}{8 \pi } \Lambda =\frac{(d-1)(d-2)}{16 \pi l^2}, \end{aligned}$$
(6)

in the geometric units \(G_{d}=\hbar =c=k_{B}=1\). The corresponding conjugate quantity, namely the thermodynamic volume, is given by [33]

$$\begin{aligned} V = \frac{\omega _{d-2} {r_H}^{d-1}}{d-1}, \end{aligned}$$
(7)

while the black hole temperature reads

$$\begin{aligned} T = \frac{f'(r_H)}{4 \pi } = \frac{d-3}{4 \pi r_{H}} \left( 1 - \frac{q^2}{r_H^{2(d-3)}} + \frac{d-1}{d-3}\frac{r_H^2}{l^2} \right) , \end{aligned}$$
(8)

where the position of the black hole event horizon, \(r_H\), is determined by solving the condition \(f(r=r_H)=0\) and we choose the largest real positive root. The electric potential \(\Phi \) measured at infinity with respect to the horizon while the black hole entropy S, was determined from the Bekenstein–Hawking formula \((S= \frac{A_{d-2}}{4})\) [48]. They are given by

$$\begin{aligned} \Phi= & {} \sqrt{\frac{d-2}{2(d-3)}}\frac{q}{r_H^{d-3}},\end{aligned}$$
(9)
$$\begin{aligned} S= & {} \frac{\omega _{d-2} r_H^{d-2}}{4}. \end{aligned}$$
(10)

All these quantities satisfy the Smarr formula

$$\begin{aligned} M=\frac{d-2}{d-3}TS+\Phi Q-\frac{2}{d-3} VP, \end{aligned}$$
(11)

where the black hole mass M is identified with the enthalpy rather than the internal energy of the gravitational system [30], so the first law of black hole thermodynamics reads [49, 50]

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+\Phi \mathrm{d}Q+V\mathrm{d}P. \end{aligned}$$
(12)

From Eq. (8), one can derive the following equation of state \(P=P(r_H,T)\) for a charged AdS black hole in arbitrary dimension d:

$$\begin{aligned} P = \frac{T(d-2)}{4 r_{H}} - \frac{(d-3)(d-2)}{ 16 \pi r_H^2} + \frac{q^2 (d-3) (d-2)}{ 16 \pi r_{H}^{2(d-2)}}.\nonumber \\ \end{aligned}$$
(13)

As usual, the critical points occur when P has an inflection point,

$$\begin{aligned} \left. \frac{\partial P}{\partial r_H}\right| _{T=T_c,r_H=r_c}= \left. \frac{\partial ^2 P}{\partial r_H^2}\right| _{T=T_c,r_H=r_c}=0, \end{aligned}$$
(14)

leading to

$$\begin{aligned} \begin{aligned} r_c&= \frac{2 \left( (d-2) (2 d-5) q^2\right) ^{\frac{1}{2 (d-3)}}}{d-2}, \\ T_c&= \frac{(d-3)^2 \left( (d-2) (2 d-5) q^2\right) ^{\frac{1}{6-2 d}}}{\pi (2 d-5)},\\ P_c&= \frac{(d-3)^2 \left( (d-2) (2 d-5) q^2\right) ^{\frac{1}{3-d}}}{16 \pi }. \end{aligned} \end{aligned}$$
(15)

As to the Gibbs free energy \(G=M-TS\) [48, 51, 52], for fixed charge, it reads [31]

$$\begin{aligned} G=G(P,T) = \frac{{\omega }_{d-2} }{16 \pi } \biggl (\!r_H^{d-3} - \frac{16\pi Pr_H^{d-1}}{(d-1)(d-2)} + \frac{(2d-5)q^2}{r_H^{d-3}}\biggl ).\ \ \end{aligned}$$
(16)

After having briefly introduced the main thermodynamical quantities and related phase transition, let us focus our attention in the next section on the derivation of the quasinormal frequencies of a scalar perturbation around a charged AdS black hole in high dimension spacetime.

3 Master equation in high dimension RN–AdS black hole spacetime

In the sequel, we study the evolution of a massless scalar field in the background of high dimensional charged AdS black hole. The radial part of the field, \(\Phi (r,t)=\phi (r) e^{-i \omega t}\), obeys the Klein–Gordon wave equation,

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu }\left( \sqrt{-g} g^{\mu \nu }\partial _{\nu }\Phi (t,r)\right) =0, \end{aligned}$$
(17)

where \(g_{\mu \nu }\) are the covariant metric components of the RN–AdS spacetime, \(g^{\mu \nu }\) are the contravariant metric components and g is the metric determinant. The radial functions \(\psi (r)\) obey the following differential equation:

$$\begin{aligned} \phi ''(r)+\left[ \frac{f'(r)}{f(r)}+\frac{d-2}{r}\right] \phi '(r)+\frac{\omega ^2 \phi (r)}{f(r)^2}=0, \end{aligned}$$
(18)

where \(\omega \) are complex numbers \(\omega =\omega _{r}+i \omega _{im}\), corresponding to the QNM frequencies of the oscillations describing the perturbation. Notice that the imaginary part \(\omega _{im}\) must be negative since the QNMs decay in time.

Defining \(\phi (r)\) as \(\psi (r) \exp [-i\int \frac{\omega }{f(r)}\mathrm{d}r]\), then in the vicinity of the black hole horizon \(r_H\), the exponential simplifies to

$$\begin{aligned} \exp \left[ -i\int \frac{\omega }{f(r)}\mathrm{d}r\right] \sim (r-r_H)^{-i \frac{\omega }{4\pi T}}, \end{aligned}$$
(19)

and the incoming waves behave as \(\psi (r)\sim (r-r_H)^{-i \frac{\omega }{4\pi T}}\), which means that \(\psi (r)\) is set to unity at the horizon [1]. Then we can reformulate Eq. (18) as

$$\begin{aligned} \psi ''(r)+\psi '(r) \left[ \frac{f'(r)}{f(r)}-\frac{2 i \omega }{f(r)}+\frac{d-2}{r}\right] - \psi (r)\frac{(d-2) i \omega }{r f(r)}=0. \end{aligned}$$
(20)

At this stage, for computation reasons, we use the coordinate transformation \(u=\left( \frac{r_H}{r}\right) ^{d-3}\), so the AdS boundary is located at \(u=0\), while the horizon is located at \(u=1\). In this case, Eq. (20) becomes

$$\begin{aligned}&\psi ''(u)+\left[ \frac{f'(u)}{f(u)}+\frac{2i\omega r_{H}}{(d-3)u^{\frac{d-2}{d-3}}f(u)}\right] \psi '(u)\nonumber \\&\quad -\frac{(d-2)i\omega r_{H}}{(d-3)^{2}u^{\frac{2d-5}{d-3}} f(u)}\psi (u) =0, \end{aligned}$$
(21)

with \(\psi (u)=0\) at the AdS limit \(u\rightarrow 0\). Thanks to the boundary conditions, we can solve numerically Eq. (21) and find out the frequencies of the quasinormal modes via the shooting method; see for example [53, 54].

The main purpose of the present paper is to show that the dynamical behavior of the quasinormal modes in the massless scalar perturbation encodes the signature of a thermodynamical first-order phase transition of high dimensions charged AdS black holes. The isobaric and the isothermal processes are used to perform this analysis in the context of the van der Waals phase transition picture.

4 QNM behaviors in the isobaric phase transition

Since the pressure P (or cosmological constant \(\Lambda \)) is fixed in an isobaric phase transition, the horizon radius \(r_H\) is the only variable in the system. Our subsequent analysis will take into account the spacetime dimension.

In Fig. 1, we show the behavior of this transformation in \((T,r_H)\)-diagram for \(d=4\) and \(d=6\).

Table 2 The quasinormal frequencies of the massless scalar perturbation as a function of the black holes temperature for the second phase transition. The upper part, above the horizontal lines is for the small black hole phase while the lower part is for the large one
Full size table

From the top panel of Fig. 1, we can see small–large black hole phase transitions under the critical regime \(P<P_c\) (solid lines) and at \(P=P_c\) (dashed lines), for which the coordinates of the critical point \((T_c,r_{H_{c}})\) are determined by the roots of the system: \(\frac{\partial T}{\partial r_H}= \frac{\partial ^2 T}{\partial r_H^2}=0\). The Gibbs free energy displays a characteristic swallow tail behavior, depicted in the bottom panel (solid lines), signaling a first-order SBH/LBH phase transition. The dashed line indicates the character of a second-order phase transition due a continuous variation of the free energy between SBH and LBH.

Table 1 lists the frequencies of the quasinormal modes of the massless scalar perturbation around small and large black holes for the first-order phase transition where the pressure is fixed at the value \(P=0.1P_c\).

One should keep in mind that, unlike the ordinary normal modes, the QNMs decay at certain rates. Hence, having complex frequencies, the real and imaginary parts can help to gain some insight in the oscillations and decays of the black hole. In the case of the small black hole phase, for any dimension, we note from Table 1 that the black hole becomes smaller and smaller when the temperature decreases from the phase transition critical point \(T_c\). In this process, the real part of the QNMs frequencies varies slightly, while the absolute value of the imaginary part decreases which indicates that the absorption performance of the black hole is reduced whatever the spacetime dimension d is. This result is consistent with the overall analysis reported in [1, 55].

For large black hole phase, for any dimension d, we see that by increasing the temperature from the critical value \(T_c\), the black hole becomes larger. In this case, the real part as well as the absolute value of the imaginary part of the quasinormal frequencies increases. Furthermore, the massless scalar perturbation outside the black hole performs more oscillations but decays faster. These observations are in agreement with the results found in [1, 56].

Fig. 3
figure 3

The behavior of the quasinormal modes for small (solid) and large (dashed) black holes in the isobaric second-order phase transition for a \(4\le d\le 11\). The increase of the black hole size is shown by the arrows

Full size image
Fig. 4
figure 4

Left panel pressure P as a function of the horizon radius \(r_H\) for isothermal process. Right panel Gibbs free energy as a function of the pressure for \(d=4,6\). The two upper lines (purple) correspond to \(d=6\) while the lower two lines (blue) correspond to \(d=4\). The critical isotherm \(T=T_c\) is denoted by the dashed lines, the solid lines shows the first-order transition \(T<T_c\)

Full size image

Using the results of Table 1, we illustrate in Fig. 2 the quasinormal frequencies for small and large black hole phases where the purple (blue) dots correspond to the results of the upper (lower) part, above the horizontal line in Table 1, respectively. The increase in the size of the black hole is indicated by the arrows. Notice here that Fig. 2 corresponds to the solid lines in Fig. 1.

From Fig. 2, we see different slopes of the quasinormal frequencies in the massless scalar perturbations with different phases of the small and large black holes. The SBH and LBH transform to each other through a phase transition. All these features revealed by dynamical perturbations are concording with the general picture of thermodynamic phase transitions between small-large RN–AdS black holes.

At the isobaric phase transition critical point \(P=P_c\), the situation is different. The values of the frequencies are shown in the Table 2.

The quasinormal frequencies for small and large black hole phases illustrated in Table 2 are plotted in Fig. 3 for \(4\le d \le 11\), at this level we must stress that this figure corresponds to the dashed lines in the Fig. 1.

We can see that when phase transitions are realized, the SBH and the LBH QNMs have the same behavior when the horizon increases, generalizing to higher spacetime dimensions the property found in \(d=4\) [1].

5 QNM behaviors in the isothermal phase transition

In this section, we fix the temperature T and made the study in the \((P,r_H)\)-diagram. In Fig. 4, we plot the pressure of the black hole in terms of the radius of event horizon and the Gibbs free energy.

The associated \((P,r_H)\)-diagram for \(d=4\) black hole is displayed in Fig. 4 (left panel). Obviously, for \(T < T_c\) there is a small-large black hole phase transition in the system. This qualitative behavior persists in higher dimensions, as illustrated for \(d= 6\). In the right panel the behavior of G for dimensions \(d=4\) and \(d=6\) is depicted in Fig. 4. Similarly to Fig. 1, the characteristic first-order phase transition behavior shows up.

Table 3 displays the frequencies of the quasinormal modes for small and large black hole phase in the isothermal process for different dimensions, with \(T=0.74T_c\). The data above (below) the horizontal line are for the small (large) black hole phase, respectively.

From Fig. 5, we can see that the behavior of the quasinormal modes in the isothermal process is not regular and depends on the spacetime dimension. Indeed:

  • For \(d=4\) and \(d=5\), we see that, for the SBH phase, the corresponding pressure P decreases with growing black hole horizon. In this process, the real part of the frequencies as well as the absolute imaginary part decrease. For the LBH case, the pressure also decreases when the black hole size increases. However, the real and the absolute values of the imaginary parts have opposite behaviors. Figure 5 shows the behaviors of the quasinormal modes for small and large holes where the arrows indicate increase of the black hole size. It is clear that the remarkable properties of the quasinormal frequencies are completely different in SBH and LBH phases, confirming the behavior seen in \(d=4\) [1], and providing a good measure to probe the black hole phase transitions.

  • For \(d \ge 6\), the behaviors of QNM in the two black hole phases are completely different: when the horizon radius grows the real and absolute value of the imaginary parts both decrease (increase) in the SBH phase (LBH phase), respectively. Therefore the QNM behavior is sensitive to the dimension d, which affects the correction induced by the variation of the horizon radius \(r_H\) and the pressure P, as can be seen from the master equation, Eq. (21).

In the isothermal transition, the quasinormal modes can be affected by the value of the pressure P(l) and the horizon radius \(r_H\). To illustrate the effect of these two parameters, we restrict our calculation here to only \(d=4\), \(d=5\) and \(d=6\). For higher dimensions, \(d>6\), the behavior is exactly similar to \(d=6\) as shown in Table 4. This feature can also be seen clearly in Fig. 6 where we notice a competition between the pressure P and horizon radius \(r_H\). Each of these parameters aims to overwhelm the other which affects the decay rate of the field, namely \(\omega _i\).

Table 3 The QNM frequencies of the massless scalar perturbation for black holes with different dimensions and sizes in the isothermal process
Full size table
Fig. 5
figure 5

The behavior of the quasinormal modes for small and large black holes for a \(4\le d\le 11\). The increase in the black hole size is shown by arrows in the case of the isothermal process

Full size image
Table 4 Left: the quasinormal frequencies as a function of the black hole horizon \(r_H\), for fixed pressure P. Right: quasinormal frequencies as a function of P, for fixed black hole horizons \(r_H\)
Full size table

To illustrate how these two factors affect the quasinormal frequencies, we perform a double-series expansion of the frequency \(\omega \left( r_{H}+\Delta r_{H},P+\Delta P\right) \) [1]:

$$\begin{aligned} \omega \left( r_{H}+\Delta r_{H},P+\Delta P\right)= & {} \omega \left( r_{H},P \right) +\frac{\partial \omega }{\partial r_{H}}\Delta r_{H}+\frac{\partial \omega }{\partial P}\Delta P \nonumber \\&+\, \mathcal {O}(\Delta r_{H}^{2},\Delta P^{2},\Delta r_{H}.\Delta P),\nonumber \\ \end{aligned}$$
(22)

with

$$\begin{aligned} \tilde{\omega }=\omega +\Delta _{r_{H}}+\Delta _{p}+ \mathcal {O}(\Delta r_{H}^{2},\Delta P^{2},\Delta r_{H}.\Delta P), \end{aligned}$$

where \(\Delta _{r_{H}}\) and \(\Delta _{p}\) represent corrections induced by variation of the black hole size and pressure, respectively. Recall here that the choice of the step of pressure \(\Delta P\) in a linear approximation is related to \(\Delta r_H\) via the relation

$$\begin{aligned} \mathrm{d}P= & {} \left( -\frac{(d-2) T}{4 r_H^2}+\frac{(3-d) (d-2)^2 r_H^{(3-2 d)}}{8 \pi }\right. \nonumber \\&\left. +\,\frac{(d-3) (d-2)}{8 \pi r_H^3}\right) \mathrm{d}r_H. \end{aligned}$$
(23)

Table 5 shows the evaluation of the quasinormal frequencies \(\tilde{\omega }\) from the linear approximation for small and large black hole phase (this evaluation is performed in a narrow range of \(r_H\) in order to preserve the linear approximation in Eq. (23)). One can see that the behaviors of \(\tilde{\omega }\) are consistent with the numerical computation. For example for a small black hole at \(d=5\) we obtain \(\tilde{\omega _{r}}<\omega _{r}\) and \(|\tilde{\omega }_{im}|<|\omega _{im}|\), which confirms the behavior shown in Fig. 5.

It is clear that, for the small black hole case and for all dimensions, the change of the pressure prevails over the change of the black hole size. We also notice that the imaginary part of the frequency is more sensitive to the pressure.

The quasinormal frequencies for small and large black hole phases are plotted in Fig. 7 for \(4\le d \le 11\). For the isothermal phase transition at \(T=T_c\), we can see that when phase transitions are realized, the SBH and the LBH QNMs have the same behavior as the horizon increases, which generalizes the result of [1] to higher dimensional spacetime.

6 Critical ratio and the detection efficiency

From the previous sections we can see that the quasinormal normal mode frequencies provide an efficient investigating tool to probe the signature of the black hole phase transition. The critical ratio parameter defined by \(\chi =\frac{P}{P_c}\) plays a prominent role in this detection. To illustrate how this parameter affects the way how quasinormal frequencies can be a good measure to probe different phases of the black hole, we present a brief analysis for several values of \(\chi \) parameter: we replot in Fig. 8 the quasinormal frequencies for small and large black hole phases for the isobaric transition using different values of \(\chi \).

Therein we can see that, for \(\chi =0.6,\; 0.9\), \(\omega _r-\omega _i\) plane does not show different slope in small and large black hole phases near the critical temperature. In large black hole phase, the quasinormal modes continue to have the same salient feature noticed in the previous sections. However, in the small black hole phase, we clearly observe a change of slope sign around the point dubbed \(\mathcal {T}\) in the figure.

In Table 6, we show the values of the temperature \(\mathcal {T}\) corresponding to the slope sign change in the small black hole phase for different values of the critical ratio \(\chi \) and for the spacetime dimension d.

Fig. 6
figure 6

The purple dashed plots show the quasinormal frequencies variation with the horizon \(r_H\), for fixed pressure P. The blue dots represent the quasinormal frequencies as a function of P, for fixed black hole horizons \(r_H\) (Table 4). The arrow indicates the increase of \(r_H\) (P) for fixed P (\(r_H\)), respectively

Full size image
Table 5 \(\tilde{\omega }\) is the quasinormal frequency from the linear approximation. \(\Delta _{r_{H}}\) and \(\Delta _{p}\) represent corrections due to variation of the black hole size and pressure, respectively
Full size table

Here, we need to highlight the following issue: when the critical ratio \(\chi \) becomes very small, \(\mathcal {T}\) tends to the critical temperature and the quantity \(\Delta T = T_c-\mathcal {T}\) becomes null. On the other hand, the quantity \(\Delta T\) increases when \(\chi \) becomes large and the quasinormal modes are not very efficient to probe the black hole phase transition. As in the case of the second phase transition we also should mention that, since the quantity \(\Delta T\) is sensitive to the spacetime dimension, d affects the efficiency of the quasinormal modes detection.

To close, we plot the real part of the quasinormal mode frequencies as a function of the temperature T, Fig. 9, in order to show the dashed region corresponding to the temperature interval where the quasinormal mode frequencies are able to reveal the phase transition.

Fig. 7
figure 7

The behavior of the quasinormal modes for small (solid) and large (dashed) black holes in the isothermal second-order phase transition for a \(4\le d\le 11\). The increase in the black hole size is shown by arrows

Full size image
Fig. 8
figure 8

The quasinormal frequencies in the \(\omega _{r}\)–\(\omega _{im}\) plane for \(\chi =0.6,\;0.9\). \(\mathcal {T}\) is the temperature corresponding to the slope sign change

Full size image

7 Conclusion

In this work, we have investigated the thermodynamical behaviors of d-dimensional charged AdS black holes and their phase transitions. Emphasis has been put on the calculation of the quasinormal modes frequencies of the massless scalar perturbation around small and large black holes. This study has been performed for an isobaric process as well as isothermal one.

Table 6 The temperature \(\mathcal {T}\) corresponding to the slope sign change
Full size table
Fig. 9
figure 9

The real part of the quasinormal modes frequencies as a function of the black hole temperature, with \(\chi =0.6 \) and \( d=4\)

Full size image

For the former, below the critical pressure, we found that, for any dimension d in the range \(4\le d\le 11\), the QNMs might well be an useful tool to probe the black hole phase transition, since the slopes of the quasinormal frequency change between small and large black holes, which can be affected by the value of the critical ratio \(\chi \). As to the latter process, for the phase transition below the critical point, we have shown that the spacetime dimension affects the behavior of QNMs. More precisely, we found that the change in QNM slopes occurs only for \(d=4\) and \(d=5\).

Finally we have also found that, at the critical isothermal and isobaric phase transitions, quasinormal frequencies of small and large black holes have the same behavior, suggesting that quasinormal modes are not appropriate to probe the black hole phase transition in the second order.