1 Introduction

Among generalizations of the Einstein action, Gauss–Bonnet (GB) gravity has some particular interests because it is ghost-free and emerges in the effective low-energy action of string theory [1, 2]. The effects of GB gravity on the speed of graviton propagation and appearance of potentially superluminal modes have been investigated in [3, 4] and recently the problem of its unusual causal structure has been solved [5]. In addition, the influences of GB gravity have been investigated as regards various physical phenomena such as superconductors [6–8], hydrodynamics [9, 10], LHC black holes [11], dark matter [12], dark energy [13, 14], and shear viscosity [15, 16].

Although one may consider the (Wald) entropy effect of GB gravity in four dimensions [17, 18], it is notable that the variation of GB Lagrangian is a total derivative in four dimension and therefore it does not affect the four-dimensional field equations as well as black hole solutions. Thus, in order to study the GB contributions, we may look for the five- and higher-dimensional solutions.

In addition to the higher derivative curvature terms, one would also expect to analyze the higher derivative gauge field contributions. The Born–Infeld (BI) nonlinear electrodynamics (NLED) is the first nonlinear higher derivative generalization of the Maxwell theory [19, 20] and its nonlinearity power is characterized by an arbitrary real positive parameter \(\beta \). Replacing the BI NLED with linear Maxwell theory in related topics, one can investigate the effects of nonlinearity on the physical consequences in electrodynamics [21–31].

Motivated by the recent results mentioned above, it is natural to investigate GB gravity in the presence of NLED [32–36]. For the first time, spherically symmetric black hole solutions of GB and GB–Maxwell gravity were, respectively, obtained in \(1985\) [37] and \(1986\) [38]. Then various properties of (charged) GB black holes were studied (for the very incomplete list of references, see [39–44]). Besides, coupling of the BI theory with general relativity have been derived by Hoffmann [45]. He removed the Reissner–Nordström divergency, but a conical singularity remained. Due to the complexity of the nonlinear field equations, BI theory has long been discarded. In \(1984\), Garcia and his colleagues could obtain a BI black hole solution without conical singularity [46]. Moreover, black hole solutions of GB gravity in the presence of NLED have been investigated in Refs. [32–36].

The objective of this paper is finding topological black hole solutions of the GB gravity coupled to new classes of NLED theory. It is worthwhile to mention that these models help us to improve our understanding of higher-dimensional black hole structures and also clarify some points of AdS/CFT correspondence [9, 21, 47–50]. In the present work, we discuss the thermodynamics of the asymptotically flat black holes with spherical horizon as well as asymptotically adS rotating black branes with flat-horizon and specially the role played by GB and NLED terms to stability of the solutions. Recently, one of us [51–53] considered other kinds of BI type Lagrangians to examine the possibility of black hole solutions. Although there are some analogies between the BI theory and logarithmic or exponential forms of NLED, there exist some differences between them as well.

For the sake of simplicity, we consider five-dimensional topological black holes and investigate the geometric as well as thermodynamic properties of the solutions. Appendix is devoted to the higher-dimensional generalization.

2 Equations of motion and topological black hole solutions

We are interested in the GB gravity coupled to a nonlinear \(U(1)\) gauge field. The action is

$$\begin{aligned} I_{G}=-\frac{1}{16\pi }\int _{\mathcal {M}}d^{n+1}x\sqrt{-g}\left[ R-2\Lambda +\alpha L_{GB}+L(\mathcal {F})\right] \end{aligned}$$
(1)

where \(\Lambda \) is the cosmological constant and \(\alpha \) is the GB coefficient. Furthermore, \(L_{GB}\) and \(L(\mathcal {F})\) are, respectively, the Lagrangians of GB and BI type theories, which can be defined as

$$\begin{aligned}&L_{GB}=R_{\mu \nu \gamma \delta }R^{\mu \nu \gamma \delta }-4R_{\mu \nu }R^{\mu \nu }+R^{2}, \end{aligned}$$
(2)
$$\begin{aligned}&L(\mathcal {F})=\left\{ \begin{array}{ll} \beta ^{2}\left( \exp (-\frac{\mathcal {F}}{\beta ^{2}})-1\right) , &{} \;~{ENEF } \\ -8\beta ^{2}\ln \left( 1+\frac{\mathcal {F}}{8\beta ^{2}}\right) , &{} \;~{LNEF} \end{array} \right. , \end{aligned}$$
(3)

where \(\beta \) is called the nonlinearity parameter, the Maxwell invariant \(\mathcal {F}=F_{\mu \nu }F^{\mu \nu }\) in which \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) is the Faraday tensor and \(A_{\mu }\) is the gauge potential. We should vary the action (1) with respect to \(g_{\mu \nu }\) and \(A_{\mu }\) to obtain the field equations

$$\begin{aligned}&G_{\mu \nu }+\Lambda g_{\mu \nu }-\alpha H_{\mu \nu }=\frac{1}{2}g_{\mu \nu }L(\mathcal {F})-2F_{\mu \lambda }F_{\nu }^{\;\lambda }L_{\mathcal {F}}, \end{aligned}$$
(4)
$$\begin{aligned}&\partial _{\mu }\left( \sqrt{-g}L_{\mathcal {F}}F^{\mu \nu }\right) =0, \end{aligned}$$
(5)

where \(G_{\mu \nu }\) is the Einstein tensor, \(L_{\mathcal {F}}=\frac{dL( \mathcal {F})}{d\mathcal {F}}\) and \(H_{\mu \nu }\) is the divergence-free symmetric tensor

$$\begin{aligned} H_{\mu \nu }&= 4R^{\rho \sigma }R_{\mu \rho \nu \sigma }-2R_{\mu }^{\ \rho \sigma \lambda }R_{\nu \rho \sigma \lambda }-2RR_{\mu \nu }+4R_{\mu \lambda }R_{\nu }^{\lambda }\nonumber \\&+\frac{L_{GB}}{2}g_{\mu \nu }. \end{aligned}$$
(6)

Now, we desire to obtain the five-dimensional black hole solutions of Eqs. (4) and (5) with the following line element:

$$\begin{aligned} ds^{2}=-f(r)dt^{2}+\frac{dr^{2}}{f(r)}+r^{2}d\Omega _{k}^{2}, \end{aligned}$$
(7)

where \(d\Omega _{k}^{2}\) represents the metric of a three-dimensional hypersurface at \(r=\)constant and \(t=\)constant with constant curvature \(6k\) and volume \(V_{3}\). We can write \(d\Omega _{k}^{2}\) in the following explicit forms:

$$\begin{aligned} d\Omega _{k}^{2}=\left\{ \begin{array}{l@{\quad }l} d\theta ^{2}+\sin ^{2}\theta \left( d\phi ^{2}+\sin ^{2}\phi d\psi ^{2}\right) &{} k=1 \\ d\theta ^{2}+\sinh ^{2}\theta \left( d\phi ^{2}+\sin ^{2}\phi d\psi ^{2}\right) &{} k=-1 \\ d\theta ^{2}+d\phi ^{2}+d\psi ^{2} &{} k=0 \end{array} \right. . \end{aligned}$$
(8)

Taking into account metric (7), we should consider a consistent gauge potential \(A_{\mu }\) with the following form:

$$\begin{aligned} A_{\mu }=h(r)\delta _{\mu }^{0}. \end{aligned}$$
(9)

where

$$\begin{aligned} h(r)=\left\{ \begin{array}{l@{\quad }l} \int \frac{q}{r^{3}}\exp \left[ \frac{-L_{W}}{2}\right] dr, &{} \text {ENEF} \\ 2\beta \int \sqrt{\frac{\Gamma -1}{\Gamma +1}}dr, &{} \text {LNEF} \end{array} \right. , \end{aligned}$$
(10)

and \(q\) is an integration constant which is related to the electric charge. In addition, \(\Gamma =\sqrt{1+\frac{q^{2}}{\beta ^{2}r^{6}}}\) and \(L_{W}=\mathrm{LambertW}(\frac{4q^{2}}{\beta ^{2}r^{6}})\) [54, 55]. We expand \(h(r)\) for large \(r\) to obtain the asymptotical behavior of the gauge potential

$$\begin{aligned} \left. h(r)\right| _{\text {Large }r}=-\frac{q}{2r^{2}}+\frac{\chi q^{3}}{ 32\beta ^{2}r^{8}}+O\left( \frac{q^{5}}{\beta ^{4}r^{14}}\right) , \end{aligned}$$
(11)

where \(\chi =8,1\) for ENEF and LNEF, respectively. Equation (11) shows that for large values of \(r\), the dominant (first) term of \(h(r)\) is the same as one in five-dimensional linear Maxwell theory.

Considering Eq. (9) with (10), we can solve the gravitational field equation (4). After some cumbersome calculations, we find that the nonzero (independent) components of the field equation (4) may be written as

$$\begin{aligned} e_{1}&= \left[ r^{2}-4\alpha \left( f-k\right) \right] f^{\prime }+2r\left( f-k\right) \nonumber \\&+\frac{2\Lambda r^{3}}{3}+\frac{8\beta ^{2}r^{3}}{3\chi }\Upsilon _{1}=0, \end{aligned}$$
(12)
$$\begin{aligned} e2&= \left[ r^{2}-4\alpha \left( f-k\right) \right] f^{\prime \prime }+4\left( r-\alpha f^{\prime }\right) f^{\prime }\nonumber \\&+2\left( f-k\right) +2\Lambda r^{2}+\beta ^{2}r^{2}\Upsilon _{2}=0 \end{aligned}$$
(13)

where the prime and double primes are, respectively, the first and second derivatives with respect to \(r\) and

$$\begin{aligned} \Upsilon _{1}&= \left\{ \begin{array}{l@{\quad }l} 1-\left( 1-L_{W}\right) e^{\frac{L_{W}}{2}}, &{} \text {ENEF}\\ \Gamma -1-\ln \left( \frac{\Gamma +1}{2}\right) , &{} \text {LNEF} \end{array} \right. , \end{aligned}$$
(14)
$$\begin{aligned} \Upsilon _{2}&= \left\{ \begin{array}{l@{\quad }l} 1-e^{\frac{L_{W}}{2}}, &{} \text {ENEF}\\ -\ln \left( \frac{\Gamma +1}{2}\right) , &{} \text {LNEF} \end{array} \right. . \end{aligned}$$
(15)

After some calculations, we find that \(\frac{de_{1}}{dr}=e_{2}\), so it is sufficient to solve \(e_{1}\) for each branch, yielding

$$\begin{aligned} f(r)=k+\frac{r^{2}}{4\alpha }\left( 1-\sqrt{\Psi (r)}\right) , \end{aligned}$$
(16)

where

$$\begin{aligned}&\Psi (r) =1+\frac{4\alpha }{3}\left( \Lambda +\frac{6m}{r^{4}}\right) + \frac{4\alpha \beta ^{2}}{3}\Upsilon , \end{aligned}$$
(17)
$$\begin{aligned}&\Upsilon =\left\{ \begin{array}{l@{\quad }l} \frac{1}{2}+\frac{4q}{\beta r^{4}}\int \left( \sqrt{L_{W}}-\frac{1}{\sqrt{ L_{W}}}\right) dr, &{} \text {ENEF}\\ 4\ln (2)-4+\frac{14}{r^{4}}\int r^{3}\left[ \Gamma -\ln \left( 1+\Gamma \right) \right] dr, &{} \text {LNEF} \end{array} \right. ,\nonumber \\ \end{aligned}$$
(18)

and \(m\) is an integration constant. In order to obtain the effect of nonlinearity parameter, one can expand the metric function for large values of \(\beta \). Calculations show that the series expansion of \(\Psi (r)\) for large values of \(\beta \) (or \(r\)) is

$$\begin{aligned} \Psi (r)=\Psi _{GBM}(r)+\frac{\chi \alpha q^{4}}{12\beta ^{2}r^{12}}+O\left( \frac{ 1}{\beta ^{4}}\right) , \end{aligned}$$
(19)

where the metric function of GB–Maxwell gravity is \(\Psi _{GBM}(r)=1+\frac{4\alpha }{3}\left( \Lambda +\frac{6m}{r^{4}}-\frac{ 2q^{2}}{r^{6}}\right) \).

As one can confirm, these solutions are asymptotically adS; the same as those in GB–Maxwell theory. The second term on the right hand side of Eq. (19) is the leading NLED correction to the GB–Maxwell black hole solutions.

Now, we want to compare the GB and NLED effects. As we know, the Maxwell theory, to a large extent in various physical scopes, has acceptable consequences. So, in the transition from the Maxwell theory to NLED, it is allowed to consider the effects of small nonlinearity variations, not strong effects.

Considering the fact that we are working in gravitational framework and GB gravity is a natural generalization of Einstein gravity (not a perturbation in general), the GB is dominant over nonlinear electrodynamics which should be considered as a perturbation to Maxwell field. Another reason for the majority of GB contributions is in the profound insight in the metric function. GB parameter is coupled with mass, cosmological constant and charge sector of the metric function and therefore its changing will be modified all sectors of the metric function, whereas modification of nonlinearity parameter of electrodynamics affects charge part of the solutions. Another way to see the majority of GB or NLED contributions is the series expansion of the metric function. One can consider GB and nonlinearity of the electrodynamics as corrections of Einstein–Maxwell black hole. Hence, we use a series expansion of metric function for small values of \( \alpha \) and also weak field limit of NLED (\(\beta \longrightarrow \infty \)) to obtain

$$\begin{aligned}&f(r)=f_{EM}+\frac{2(k-f_{EM})^{2}}{r^{2}}\alpha -\frac{\chi q^{4}}{ 96r^{10}\beta ^{2}}\nonumber \\&\qquad \quad +\frac{\chi q^{4}(k-f_{EM})}{24r^{12}}\frac{\alpha }{ \beta ^{2}}+O\left( \alpha ^{2},\beta ^{-4}\right) , \end{aligned}$$
(20)

where the metric function of Einstein–Maxwell gravity is \(f_{EM}=k-\frac{\Lambda r^{2}}{6}-\frac{m}{r^{2}}+\frac{q^{2}}{3r^{4}}\).

In Eq. (20), the second and third terms are, respectively the GB and NLED corrections and fourth term is the correction of coupling between NLED and higher derivative gravity.

Before proceeding, we should discuss about real solutions. Numerical evaluations show that depending on the metric parameters, the function \(\Psi (r)\) may be positive, zero or negative. In order to have real solutions we can use two methods. First, we can restrict ourselves to the set of the metric parameters, which lead to non-negative \(\Psi (r)\) for \(0\le r<\infty \). Second, we can focus on the \(r\) coordinate. One can define \(r_{0}\) as the largest root of \(\Psi (r=r_{0})=0\), in which \(\Psi (r)\) is positive for \( r>r_{0}\). One can use suitable coordinate transformation (\(r\longrightarrow r^{\prime }\)) to obtain real solutions for \(0\le r^{\prime }<\infty \) (see the last reference in [32–34] for more details). In this paper we use the first method.

Now, we should look for the black hole interpretation. We should make an analysis of the essential singularity(ies) and horizon(s). Calculations show that the Kretschmann scalar is

$$\begin{aligned} R_{\alpha \beta \gamma \delta }R^{\alpha \beta \gamma \delta }=f^{\prime \prime 2}+\frac{6f^{\prime 2}}{r^{2}}+\frac{12(f-k)^{2}}{r^{4}}. \end{aligned}$$
(21)

After some algebraic manipulation with numerical analysis, we find that the Kretschmann scalar (21) with metric function (16) diverges at \( r=0\) and is finite for \(r\ne 0\), and therefore there is a curvature singularity located at \(r=0\). Seeking possible black hole solutions, one may determine the real root(s) of \(g^{rr}=f(r)=0\) to find the of horizon(s).

Here, we should explain the effects of the nonlinearity on the event horizon. Taking into account the metric functions, we find that the nonlinearity parameter, \(\beta \), changes the value of the event horizon, \( r_{+}\). Furthermore, there is a critical nonlinearity, \(\beta _{c}\), in which for \(\beta <\beta _{c}\), the horizon geometry of nonlinear charged solutions behaves like Schwarzschild solutions (see Ref. [51–53] for more details). In addition, one can obtain the temperature of the black holes with the use of surface gravity interpretation in the following form:

$$\begin{aligned}&T=\frac{f^{\prime }(r_{+})}{4\pi }=\frac{6kr_{+}-2\Lambda r_{+}^{3}+\Upsilon ^{\prime }}{12\pi \left( r_{+}^{2}+4\alpha k\right) },\nonumber \\&\quad \Upsilon ^{\prime }=\left\{ \begin{array}{l@{\quad }l} 2q\beta L_{W_{+}}^{-1/2}\left( 1-L_{W_{+}}\right) -\beta ^{2}r_{+}^{3}, &{} \text {ENEF}\\ 8\beta ^{2}r_{+}^{3}\left[ 1-\Gamma _{+}+\ln (\frac{1+\Gamma _{+}}{2})\right] , &{} \text {LNEF} \end{array} \right. \!,\nonumber \\ \end{aligned}$$
(22)

which shows that the nonlinearity parameter, \(\beta \), and GB parameter can change the black hole temperature. As we discussed before, the singularity may be covered with two horizons for \(\beta >\beta _{c}\). Taking into account the metric (7) with a suitable local transformation, one can obtain the so-called Nariai spacetime [56, 57]. Following the work by Bousso–Hawking [58, 59], the Nariai solution may be found by coincidence of two horizons. In this extremal regime, the two horizons have the same temperature and they are in the thermal equilibrium. Using a suitable choice of boundary conditions one may discuss about anti-evaporation as it happens for Nariai anti-evaporating black holes [60–63].

3 Thermodynamics of asymptotically flat black hole solutions (\( \Lambda =0\), \(k=1\))

In this section, we set \(\Lambda =0\) and \(k=1\) to study the thermodynamic behavior of asymptotically flat solutions. It has been shown that we could not use the so-called area law [64–68] for higher derivative gravity [69, 70]. For asymptotically flat black hole solutions, one can use the Wald formula for calculating the entropy

$$\begin{aligned} S=\frac{1}{4}\int d^{3}x\sqrt{\gamma }\left[ 1+2\alpha \widetilde{R}\right] = \frac{V_{3}}{4}\left( 1+\frac{12\alpha }{r_{+}^{2}}\right) r_{+}^{3} \end{aligned}$$
(23)

where \(\widetilde{R}\) is the Ricci scalar for the induced metric \(\gamma _{ab}\) on the three-dimensional boundary. Equation (23) shows that, in GB gravity, asymptotically flat black hole with spherical horizon violates the area law. We should note that although the (nonlinear) electromagnetic source changes the values of inner and outer horizons of charged black objects, it does not alter the entropy formula and area law (see Ref. [71] for more details). In order to obtain the electric charge per unit volume \(V_{3}\) of the black hole, we use the flux of the electric field at infinity, yielding

$$\begin{aligned} Q=\frac{q}{8\pi }, \end{aligned}$$
(24)

which shows that the total charge does not depend on the nonlinearity of the electrodynamics. The mentioned static spacetime has a Killing vector \( \partial _{t}\) and therefore the electric potential \(\Phi \), measured at infinity (potential reference) with respect to the event horizon, is defined by

$$\begin{aligned} \Phi&= A_{\mu }\chi ^{\mu }\left| _{r \rightarrow \infty }-A_{\mu }\chi ^{\mu }\right| _{r=r_{+}} \nonumber \\&= \left\{ \begin{array}{ll} \frac{\beta r_{+}\sqrt{L_{W_{+}}}}{32}\left[ 8+3L_{W_{+}}F\left( [1],[\frac{7 }{3}],\frac{L_{W_{+}}}{6}\right) \right] , &{} \text {ENEF}\\ \frac{(1-\Gamma _{+})\beta ^{2}r_{+}^{4}}{2q}-\frac{3}{2}\left( \frac{q\beta ^{2}}{\Gamma _{+}}\right) ^{1/3}F\left( [\frac{1}{6},\frac{2}{3}],[\frac{7}{6 }],\frac{1}{\Gamma _{+}^{2}}\right) , &{} \text {LNEF} \end{array} \right. ,\nonumber \\ \end{aligned}$$
(25)

where

$$\begin{aligned} L_{W_{+}} =\mathrm{LambertW}\left( \frac{4q^{2}}{\beta ^{2}r_{+}^{6}}\right) , \; \; \; \mathrm{and} \; \; \; \Gamma _{+} =\sqrt{1+\frac{q^{2}}{\beta ^{2}r_{+}^{6}}}. \end{aligned}$$

The ADM (Arnowitt–Deser–Misner) mass of a black hole can be obtained by using the behavior of the metric at large \(r\) [72]. The mass per unit volume \(V_{3}\) of the black hole is

$$\begin{aligned} M=\frac{3m}{16\pi }=\frac{3}{16\pi }\left( r_{+}^{2}+2\alpha -\frac{\beta ^{2}r_{+}^{4}\left. \Upsilon \right| _{r=r_{+}}}{6}\right) . \end{aligned}$$
(26)

Equation (26) shows that both NLED and GB terms may be changed the finite mass of the asymptotically flat black hole solutions.

Now, we obtain the total mass \(M\) as a function of the extensive quantities \(Q\) and \(S\) to check the first law of thermodynamics. Using the expression for the entropy, the electric charge and the mass given in Eqs. (23), (24), and (26), one can obtain a Smarr-type formula:

$$\begin{aligned} M\left( S,Q\right) =\frac{3}{16\pi }\left[ r_{+}^{2}+2\alpha -\frac{\beta ^{2}r_{+}^{4}\Theta }{6}\right] , \end{aligned}$$
(27)
$$\begin{aligned} \Theta =\left\{ \begin{array}{l@{\quad }l} 7\left( \Gamma _{+}-1\right) +4\ln \left( \frac{2\beta ^{2}r_{+}^{6}}{q^{2}} \left( \Gamma _{+}-1\right) \right) -\frac{9q^{2}\mathcal {F}\left( \left[ \frac{1}{3},\frac{1}{2}\right] ,\left[ \frac{4}{3}\right] ,-\frac{q^{2}}{ \beta ^{2}r_{+}^{6}}\right) }{2\beta ^{2}r_{+}^{6}}, &{} \text {LNEF} \\ \frac{1}{2}-\frac{9q\sqrt{L_{W_{+}}^{3}}\mathcal {F}\left( \left[ 1\right] , \left[ \frac{7}{3}\right] ,\frac{L_{W_{+}}}{6}\right) }{16\beta r_{+}}-\frac{ q}{\beta r_{+}\sqrt{L_{W_{+}}}}\left( 1+\frac{L_{W_{+}}}{2}\right) , &{} \text { ENEF} \end{array} \right. \!. \end{aligned}$$

Now, we regard the parameters \(Q\) and \(S\) as a complete set of extensive parameters and define the intensive parameters conjugate to them. These quantities are the temperature and the electric potential,

$$\begin{aligned}&T=\left( \frac{\partial M}{\partial S}\right) _{Q}=\frac{\left( \frac{ \partial M}{\partial r_{+}}\right) _{Q}}{\left( \frac{\partial S}{\partial r_{+}}\right) _{Q}}, \end{aligned}$$
(28)
$$\begin{aligned}&\Phi =\left( \frac{\partial M}{\partial Q}\right) _{S}=\frac{\left( \frac{ \partial M}{\partial q}\right) _{r_{+}}}{\left( \frac{\partial Q}{\partial q} \right) _{r_{+}}}. \end{aligned}$$
(29)

Using Eqs. (23) and (24), one can show that the Eqs. (28) and (29) are equal to Eqs. (22) (with \(k=1\) and \( \Lambda =0\)) and (25), respectively, and hence we conclude that these quantities satisfy the first law of thermodynamics

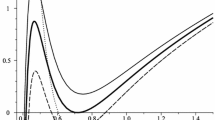
$$\begin{aligned} dM=TdS+\Phi dQ. \end{aligned}$$
(30)

It has been shown that small Lovelock black holes (including GB gravity) are, dynamically, unstable [73, 74]. In our case the mass \(M\) is a function of the entropy \(S\) and electric charge \(Q\). In order to obtain thermodynamical stable solutions, the heat capacity (\(C_{Q}=T_{+}/\left( \partial ^{2}M/\partial S^{2}\right) _{Q}\)) must be positive, a requirement usually referred to as canonical ensemble stability criterion. The canonical ensemble instability criterion for which the charge is a fixed parameter, is sufficiently strong to veto some gravity toy models. We should leave out the analytical result for reasons of economy and one cannot prove the positivity of the heat capacity, analytically. In order to investigate the effects of NLED and GB gravity, we plot Figs. 1, 2, and 3. It is notable that we plot the figures of \(C_{Q}\) for different ranges and scales for more clarifications and finding the roots of heat capacity. Figure 1 shows that there is a minimum value of the horizon radius, \(r_{0}\), for the physical black holes (positive temperature black holes). Also Figs. 2 and 3 show that small and large black holes are unstable. It means that there are two critical values \(r_{+\mathrm{min}}\) and \( r_{+\mathrm{max}}\) in which the asymptotically flat black hole solutions are stable for \(r_{+\mathrm{min}} < r_{+}< r_{+\mathrm{max}}\). Numerical calculations show that \( r_{0}=r_{+\mathrm{min}}\). Figures 1 and 3 confirm that although the GB parameter affects the value of the heat capacity and temperature, it does not change \(r_{+\mathrm{min}}\). This is due to the fact that the GB parameter appear in the denominator of \(T_{+}\) in Eq. (22). Also, Figs. 1 and 2 show that the nonlinearity parameter, \(\beta \), changes both \(r_{+\mathrm{min}}\) and \(r_{+\mathrm{max}}\). In other words, \(r_{+\mathrm{max}}\) decreases with increasing (decreasing) \(\beta \) (\(\alpha \)) and as the nonlinearity parameter, \(\beta \), increases, \(r_{+\mathrm{min}}\) decreases, too.

Fig. 1
figure 1

Asymptotically flat solutions (ENEF): \(T_{+}\) versus \(r_{+}\) for \( q=1\). Left \(\alpha =1\), and \(\beta =10\) (bold line), \(\beta =0.1\) (solid line) and \(\beta =0.01\) (dashed line). Right \(\beta =1\), and \(\alpha =1.2\) (bold line), \(\alpha =0.8\) (solid line), and \(\alpha =0.4\) (dashed line)

Full size image
Fig. 2
figure 2

Asymptotically flat solutions (ENEF): \(C_{Q}\) versus \(r_{+}\) for \( q=1\), \(\alpha =1\), and \(\beta =1\) (solid line), \(\beta =0.9\) (dotted line), and \(\beta =0.8\) (dashed line). “different ranges and scales”

Full size image
Fig. 3
figure 3

Asymptotically flat solutions (ENEF): \(C_{Q}\) versus \(r_{+}\) for \( q=1\), \(\beta =1\), and \(\alpha =1.5\) (solid line), \(\alpha =1\) (dotted line) and \(\alpha =0.5\) (dashed line). different ranges and scales

Full size image

Furthermore, we use series expansion of the heat capacity for large values of \(\beta \) and also small values of \(\alpha \) to see the effects of corrections. After some calculations, we find

$$\begin{aligned} C_{Q}\!=\! C_\mathrm{EinMax}\!+\!\alpha C_{GB}\!+\!\frac{C_\mathrm{NLED}}{\beta ^{2}}\!+\!C_\mathrm{coupled}\frac{ \alpha }{\beta ^{2}}\!+\!O\left( \frac{\alpha ^{2}}{\beta ^{4}}\right) ,\nonumber \\ \end{aligned}$$
(31)

where \(C_\mathrm{EinMax}\) is the heat capacity of the Einstein–Maxwell gravity and \( C_{GB}\), \(C_\mathrm{NLED}\), and \(C_\mathrm{coupled}\) are, respectively, the leading corrections of GB gravity, NLED theory and the nonlinear gauge–gravity coupling with the following explicit forms:

$$\begin{aligned} C_\mathrm{EinMax}&= -\frac{3\left( q^{2}-3r^{4}\right) r^{3}}{4\left( 5q^{2}-3r^{4}\right) }, \\ C_{GB}&= -\frac{3\left( 7q^{2}-9r^{4}\right) \left( q^{2}-3r^{4}\right) r}{ \left( 5q^{2}-3r^{4}\right) ^{2}}, \\ C_\mathrm{NLED}&= -\frac{9\chi \left( q^{2}-5r^{4}\right) q^{4}}{16r^{3}\left( 5q^{2}-3r^{4}\right) ^{2}}, \\ C_\mathrm{coupled}&= -\frac{27\chi \left( q^{2}-5r^{4}\right) \left( 3q^{2}-5r^{4}\right) q^{4}}{4r^{5}\left( 5q^{2}-3r^{4}\right) ^{3}}. \end{aligned}$$

4 Thermodynamics of asymptotically adS rotating black branes

In this section, we take into account zero curvature horizon with a rotation parameter. In order to add angular momentum to the metric (7), we perform the following boost:

$$\begin{aligned} t\mapsto \frac{t}{\sqrt{1+\frac{a^{2}}{l^{2}}}}-a\phi ,\phi \mapsto \frac{\phi }{\sqrt{1+\frac{a^{2}}{l^{2}}}}-\frac{a}{l^{2}}t. \end{aligned}$$
(32)

Applying the mentioned boost in Eq. (7) with \(k=0\), one obtains five-dimensional rotating spacetime with zero curvature horizon

$$\begin{aligned}&ds^{2} =-f(r)\left( \frac{dt}{\sqrt{1+\frac{a^{2}}{l^{2}}}}-ad\phi \right) ^{2}\nonumber \\&\quad \quad \,\,\,\, +\frac{r^{2}}{l^{4}}\left( adt-\frac{l^{2}d\phi }{\sqrt{1+\frac{a^{2}}{l^{2}}}}\right) ^{2}+\frac{dr^{2}}{f(r)}+r^{2}{{(d\theta ^{2}+d\psi ^{2})}},\qquad \nonumber \\ \end{aligned}$$
(33)

where the function \(f(r)\) is presented in Eq. (16). The consistent gauge potential for the rotating metric (33) is

$$\begin{aligned} A_{\mu }=h(r)\left( \sqrt{1+\frac{a^{2}}{l^{2}}}\delta _{\mu }^{0}-a\delta _{\mu }^{\phi }\right) , \end{aligned}$$
(34)

where the function \(h(r)\) is the same as Eq. (10). Now, we want to calculate the electric charge and potential of the solutions. Calculations show that the electric charge per unit volume \(V_{3}\) is

$$\begin{aligned} Q=\frac{q}{8\pi }\sqrt{1+\frac{a^{2}}{l^{2}}}. \end{aligned}$$
(35)

Considering the rotating spacetime (33), we find that the null generator of the horizon is \(\chi =\partial _{t}+\Omega \partial _{\phi }\). The electric potential \(\Phi \) for the rotating solutions may be written as

$$\begin{aligned} \Phi =\frac{\left. \Phi \right| _{\text {asymptotically flat case}}}{ \sqrt{1+\frac{a^{2}}{l^{2}}}}. \end{aligned}$$
(36)

In addition, one may use the analytic continuation of the metric with the regularity at the horizon to obtain the temperature and angular velocities in the following form:

$$\begin{aligned}&T=\frac{f^{\prime }(r_{+})}{4\pi \Xi }=\frac{-2\Lambda r_{+}^{3}+\Upsilon ^{\prime }}{12\pi \Xi r_{+}^{2}}, \end{aligned}$$
(37)
$$\begin{aligned}&\Omega =\frac{a}{\Xi l^{2}}. \end{aligned}$$
(38)

Now, we are in a position to calculate the mass and angular momentum of the solutions. We calculate the action and conserved quantities of the black brane solutions. In general the action and conserved quantities of the spacetime are divergent when evaluated on the solutions. One of the systematic methods for calculating the finite conserved charges of asymptotically adS solutions is the counterterm method inspired by the anti-de Sitter/conformal field theory (AdS/CFT) correspondence [75–77]. Considering two Killing vectors \(\partial /\partial t\) and \(\partial /\partial \phi \) and by using the Brown–York method [78], one can find that the conserved quantities associated with the mentioned Killing vectors are the mass and angular momentum with the following relations:

$$\begin{aligned}&\mathcal {M} =\frac{m}{16\pi }\left( \frac{4a^{2}}{l^{2}}+3\right) , \end{aligned}$$
(39)
$$\begin{aligned}&J =\frac{ma}{4\pi }\sqrt{1+\frac{a^{2}}{l^{2}}}, \end{aligned}$$
(40)

where \(m\) comes from the root of the metric function with the following form:

$$\begin{aligned} m=-\frac{r_{+}^{4}}{6}\left( \Lambda +\beta ^{2}\left. \Upsilon \right| _{r=r_{+}}\right) . \end{aligned}$$
(41)

Equation (41) shows that unlike the NLED, the GB term does not change the finite mass and angular momentum of the black hole solutions with zero curvature horizon.

The final step is devoted to the entropy calculation. Since the asymptotical behavior of the solutions is adS, we can use the Gibbs–Duhem relation to calculate the entropy

$$\begin{aligned} S=\frac{1}{T}(\mathcal {M}-\Gamma _{i}\mathcal {C}_{i})-I, \end{aligned}$$
(42)

where \(I\) is the finite action evaluated by the use of counterterm method, \( \mathcal {C}_{i}\) and \(\Gamma _{i}\) are the conserved charges and their associate chemical potentials, respectively. Surprisingly, calculations show that the entropy obeys the area law for our case where the horizon curvature is zero, i.e.

$$\begin{aligned} S=\frac{r_{+}^{3}}{4}\sqrt{1+\frac{a^{2}}{l^{2}}}. \end{aligned}$$
(43)

Conserved and thermodynamic quantities at hand, we can check the first law of thermodynamics. We regard the entropy \(S\), the electric charge \(Q\), and the angular momentum \(J\) as a complete set of extensive quantities for the mass \( M(S,Q,J)\), and we define the intensive quantities conjugate to them. These conjugate quantities are the temperature, electric potential and angular velocities

$$\begin{aligned} T&= \left( \frac{\partial \mathcal {M}}{\partial S}\right) _{Q,J}, \end{aligned}$$
(44)
$$\begin{aligned} \Phi&= \left( \frac{\partial \mathcal {M}}{\partial Q}\right) _{S,J}, \end{aligned}$$
(45)
$$\begin{aligned} \Omega&= \left( \frac{\partial \mathcal {M}}{\partial J}\right) _{S,Q}. \end{aligned}$$
(46)

Considering \(f(r=r_{+})=0\) with Eqs. (44), (45), and (46), and after some straightforward calculations, we find that the intensive quantities calculated by Eqs. (44), (45), and (46) are consistent with Eqs. (37), (36), and (38), respectively, and consequently one can confirm that the relevant thermodynamic quantities satisfy the first law of thermodynamics

$$\begin{aligned} dM=TdS+\Phi dQ+\Omega dJ. \end{aligned}$$
(47)

Now, our task is investigation of thermodynamic stability with respect to small variations of the thermodynamic coordinates. For rotating case the mass \(M\) is a function of the entropy \(S\), the angular momentum \(J\) and the electric charge \(Q\). As we mentioned before, in the canonical ensemble, the positivity of the heat capacity \(C_{Q,J}=T_{+}/ \left( \partial ^{2}M/\partial S^{2}\right) _{Q,J} \) is sufficient to ensure the thermodynamic stability.

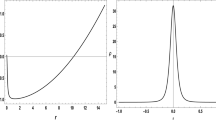
As we mentioned before, we may leave out the analytical result for reasons of economy and investigate the numerical calculations. We also plot Figs. 5 and 6 for more clarification. Figures 5 and 6 show that there is a critical value for the nonlinearity parameter, \(\beta _{c}\), in which for \(\beta >\beta _{c}\) there is a minimum value of the horizon radius (\(r_{+\mathrm{min}}\)) for physical black branes and the temperature is positive definite for \(\beta <\beta _{c}\) (see the left figure in Fig. 4 for more details). In addition, Figs. 5 and 6 indicate that rotating physical adS black branes are stable for \(\beta >\beta _{c}\). Also, for \(\beta <\beta _{c}\), although the solutions are physical for all values of \(r_{+}\), there is a minimum horizon radius for the stable adS black branes. Moreover, Fig. 5 confirms that for a fixed value of the rotation parameter, \( \beta \) affects the value of the \(r_{+\mathrm{min}}\). It means that for \( \beta >\beta _{c}\) (\(\beta <\beta _{c}\)), decreasing the nonlinearity parameter, \(\beta \), leads to decreasing (increasing) \(r_{+\mathrm{min}}\). Furthermore, Fig. 6 shows that, although for \(\beta >\beta _{c}\) the rotation parameter does not affect \(r_{+\mathrm{min}}\), it changes the minimum value of \(r_{+\mathrm{min}}\) for \( \beta <\beta _{c}\). In other words, for \(\beta <\beta _{c}\), increasing the rotation parameter leads to decreasing the value of \(r_{+\mathrm{min}}\).

Fig. 4
figure 4

Asymptotically adS rotating solutions (ENEF): \(T_{+}\) versus \(r_{+}\) for \(q=1\), \(\Lambda =-0.1\). Left \(\Xi =1.1\), and \(\beta =5\) (bold line), \(\beta =0.75\) (solid line), and \(\beta =0.5\) (dashed line). Right \(\beta =1\), and \(\Xi =1.01\) (bold line), \(\Xi =2\) (solid line), and \(\Xi =5\) (dashed line)

Full size image
Fig. 5
figure 5

Asymptotically adS rotating solutions (ENEF): \(C_{Q,J}\) and \(50T_{+} \) versus \(r_{+}\) for \(q=1\), \(\Lambda =-0.1\), and \(\Xi =1.1\). Left \(C_{Q,J}\): \(\beta =5\) (solid line), \(\beta =1\) (dotted line), and \(\beta =0.8\) (dashed line) and \(T_{+}\): \( \beta =5\) (solid-bold line), \(\beta =1\) (dotted-bold line), and \(\beta =0.8\) (dashed-bold line) Right \(C_{Q,J}\): \(\beta =0.7\) (solid line), \( \beta =0.6\) (dotted line), and \(\beta =0.5\) (dashed line) and \( T_{+}\) is positive definite

Full size image
Fig. 6
figure 6

Asymptotically adS rotating solutions (ENEF): \(C_{Q,J}\) and \(50T_{+} \) versus \(r_{+}\) for \(q=1\), \(\Lambda =-0.1\). Left \(C_{Q,J}\): \(\beta =1\), \(\Xi =1.01\) (solid line), \(\Xi =1.5\) (dotted line), and \(\Xi =3\) (dashed line) and \(T_{+}\): \( \beta =1\), \(\Xi =1.01\) (solid-bold line), \(\Xi =1.5\) (dotted-bold line), and \(\Xi =3\) (dashed-bold line) Right \(C_{Q,J}\): \(\beta =0.5\), \(\Xi =1.01\) (solid line), \(\Xi =1.5\) (dotted line), and \(\Xi =3\) (dashed line) and \(T_{+}\) is positive definite

Full size image

One finds that although \(C_{Q,J}\) does not depend on the GB parameter, it depends on the nonlinearity and rotation parameters. In order to check the nonlinearity effect, we can use the series expansion for large value of \( \beta \) to compare the mentioned \(C_{Q,J}\) with that of GB–Maxwell gravity. One finds

$$\begin{aligned} C_{Q,J}=C_\mathrm{EinMax}+\frac{C_\mathrm{NLED}}{\beta ^{2}}+O\left( \frac{1}{\beta ^{4}} \right) , \end{aligned}$$
(48)

where the heat capacity of the Einstein–Maxwell gravity, \(C_\mathrm{EinMax}\) (which is equal to the GB–Maxwell gravity for horizon-flat solutions) and its first nonlinear correction, \(C_\mathrm{NLED}\), are

$$\begin{aligned}&C_\mathrm{EinMax}\\&\quad =-\frac{4\left[ \Lambda ^{2}r^{12}(6\Xi ^{2}-5)+\Lambda q^{2}r^{6}\left( 6\Xi ^{2}-13\right) +2q^{4}(6\Xi ^{2}-1)\right] }{ r^{3}(q^{2}+\Lambda r^{6})(2q^{2}-\Lambda r^{6})(2\Xi ^{2}+1)\Xi }, \\&C_\mathrm{NLED}\\&\quad =\frac{3\chi q^{4}\left[ 2\Lambda ^{3}r^{18}-\Lambda ^{2}r^{12}q^{2}(6\Xi ^{2}+1)+4q^{4}\Xi ^{2}\left( \Lambda r^{6}+q^{2}\right) \right] }{r^{9}(q^{2}+\Lambda r^{6})^{2}(2q^{2}-\Lambda r^{6})^{2}(2\Xi ^{2}+1)\Xi } \end{aligned}$$

5 Closing remarks

In this paper we obtained five-dimensional black hole solutions of GB gravity in the presence of NLED with various horizon topology. We considered two classes of Maxwell modification, named logarithmic and exponential forms of NLED as source of gravity and found that for weak field limit (\(\beta \rightarrow \infty \)) all relations reduce to GB–Maxwell gravity.

At first, we investigated the thermodynamic properties of the asymptotically flat black holes. We found that although the NLED and GB gravity change some properties of the solutions such as entropy, mass, electric charge, and the temperature, all conserved and thermodynamic quantities satisfy the first law of thermodynamics. We analyzed the thermodynamic stability of the solutions and found that there is a minimum horizon radius, \(r_{+\mathrm{min}}\), in which the black holes have positive temperature for \(r_{+} > r_{+\mathrm{min}}\). Besides, we showed that there is an upper limit horizon radius for the stable black holes. It means that the asymptotically flat black hole solutions are stable for \(r_{+\mathrm{min}} < r_{+}< r_{+\mathrm{max}}\). In addition, we found that although the GB parameter affects the values of the heat capacity, the temperature and \(r_{+\mathrm{max}}\), it does not change \(r_{+\mathrm{min}}\). We also showed that \(\beta \) changes both \(r_{+\mathrm{min}}\) and \(r_{+\mathrm{max}}\).

Then we focused on the horizon-flat black hole solutions and obtained rotating adS black branes by use of a suitable local transformation. We used Gauss’ law, the counterterm method, and the Gibbs–Duhem relation to calculate the conserved and thermodynamic quantities. We found that these quantities satisfy the first law of thermodynamics. We investigated the effects of various parameters and found that although \(T_{+}\) and \(C_{Q,J}\) do not depend on the GB parameter, they depend on the \(\beta \) and the rotation parameter. Calculations showed that there is a critical value for the nonlinearity parameter, \(\beta _{c}\), in which for \(\beta >\beta _{c}\) there is a minimum value of the horizon radius (\(r_{+\mathrm{min}}\)) for physically stable adS black branes. We found that for \(\beta <\beta _{c}\), although the temperature is positive definite for all values of \(r_{+}\), there is a minimum horizon radius for the stable adS black branes. Also, we showed that for a fixed value of the rotation parameter and \(\beta >\beta _{c}\) (\(\beta <\beta _{c}\)), decreasing the nonlinearity parameter, \(\beta \), leads to decreasing (increasing) \(r_{+\mathrm{min}}\). Besides, we indicated that although for \(\beta >\beta _{c}\), the rotation parameter does not affect \(r_{+\mathrm{min}}\), it changes the minimum value of \(r_{+\mathrm{min}}\) for \(\beta <\beta _{c}\). More precisely, for \(\beta <\beta _{c}\), increasing the rotation parameter leads to decreasing the value of \(r_{+\mathrm{min}}\).

In this paper, we only considered static and rotating solutions. Therefore, it is worthwhile to use a suitable local transformation to obtain the so-called Nariai spacetime and investigate the anti-evaporation process. One more subject of interest for further study is regarding a model of time dependent FRW spacetime and investigate the effects of considering the NLED and fifth dimensions.