Three-dimensional charged black holes in Gauss–Bonnet gravity

Abstract

Using the zero-point length effect, we construct a new class of charged black hole solutions in the framework of three-dimensional Gauss–Bonnet (GB) gravity with Maxwell electrodynamics. The gravitational and electromagnetic potentials and the spacetime curvature are finite and regular everywhere; however, the computation of scalar curvature invariants suggests the presence of a singularity at the origin. We also explore the thermodynamics of the solutions obtained and reveal that the entropy of the black hole decreases due to the stringy effects. The thermodynamics and conserved quantities are computed, and the validity of the first law of thermodynamics on the black hole horizon is verified. Finally, the spinning black hole solution is reported.

1 Introduction

Black holes are among the most fascinating scientific discoveries. Predicted a century ago, their existence has only recently been confirmed through the detection of their gravitational waves as well as direct images of their shadows [1,2,3,4,5,6]. Black holes are entirely geometric objects but possess other enriched physical structures which connect different branches of physics including quantum gravity, thermodynamics, superconducting phase transition, paramagnetism–ferromagnetism phase transition, superfluids, condensed matter physics, spectroscopy, information theory, and holographic hypothesis. A massive black hole is usually formed through the relentless gravitational collapse of a supermassive star at the final stage of its life; for review, see [7]. However, the outcome of the collapse could be a naked singularity as well. According to the singularity theorems of Penrose and Hawking [8], the entire mass constituting the star eventually converges to a singular point, and a geometric surface called an event horizon is formed, which hides the singularity from view for all observers situated away from the black hole. It is generally believed that the singularities are nonphysical objects which are created by classical theories of gravity (ignoring quantum mechanical effects which would otherwise dominate over gravity near the Planck length scale) and that they do not exist in nature. In the literature, attempts have been made to study a black hole alongside a naked singularity and differentiate them using different astronomical observations [9,10,11,12,13]. Regular black holes are those that avoid singularity at their center [14,15,16]. In particular, the Bardeen solution [17] was later found to be an exact solution by incorporating a magnetic charge using nonlinear electrodynamics. However, some of the proposed black holes are not solutions of Einstein field equations, since the physical sources producing them are unknown. The best candidate today to produce singularity-free solutions, even at the classical level, due to its intrinsic non-locality, is string theory [18]. Regular black holes have been studied in the context of supergravity [19], conformal massive gravity [20], renormalization group approach [21, 22], and conformal field theory (CFT) [23]. A general procedure for constructing exact black hole solutions with electric or magnetic charges in Einstein gravity is presented in [24]. It was shown that in order to reproduce a regular black hole, one needs to take into account the nonlinear electrodynamics as the gauge field [24]. Other investigations on the regular black hole solutions are carried out in [25,26,27,28,29,30,31].

One of the most notable achievements in black hole physics is the discovery of three-dimensional solutions of general relativity in anti-de Sitter (AdS) spacetime known as the Banados–Teitelboim–Zanelli (BTZ) black hole [32] and Martinez–Teitelboim–Zanelli (MTZ) black hole [33, 34]. Later, these three-dimensional black holes were generalized via the Noether symmetry approach in f(R) gravity [35]. In fact, the $(2+1)$-dimensional solution of Einstein gravity provides a toy model to investigate conceptual issues such as black hole thermodynamics, quantum gravity, string and gauge/gravity duality, and holographic superconductors in the context of the $AdS_{3}/CFT_{2}$ [36,37,38,39,40,41,42]. It has been shown that the quasinormal modes in this spacetime coincide with the poles of the correlation function in the dual CFT. This gives quantitative evidence for $AdS_{3}/CFT_{2}$ [43]. Furthermore, BTZ black holes play a crucial role in improving our perception of gravitational interaction in low-dimensional spacetimes [44]. In particular, they may shed some light on quantum gravity in three dimensions. It was shown that the surface $r=0$ is not a curvature singularity but rather a singularity in the causal structure which is constant everywhere, and continuing beyond it would produce closed timelike curves [45]. The extension to include an electric charge in addition to the mass and angular momentum has been performed [46, 47]. The $(2+1)$-dimensional black holes also provide a powerful background to explore one-dimensional holographic superconductors [48,49,50,51,52]. In three-dimensional f(R) gravity, with a self-interacting scalar field non-minimally coupled to gravity, the hairy black hole solutions have already been derived and shown to be thermodynamically stable [53]. Black holes containing a magnetic charge and non-linearity parameter in Born–Infeld gravity were constructed in [54]. As a gravitational analogue, three-dimensional wormholes have also been derived and investigated thermodynamically [55]. In lower spatial dimensions, the spacetime topologies are simpler, making it possible to investigate the classical and quantum properties of black holes and wormholes in detail [56]. Extensive additional studies on $(2+1)$-dimensional black hole solutions of gravitational field equations have been reported in the literature (see e.g. [57,58,59,60,61,62,63,64,65,66,67,68,69]).

In the present work we investigate regular black hole solutions in $(2+1)$-dimensional GB gravity using the zero-point length effect. The study of lower-dimensional black hole solutions of GB gravity has received considerable attention in recent years [70,71,72]. These solutions indeed generalize the BTZ black hole from Einstein gravity to GB gravity and restore the three-dimensional BTZ solutions of Einstein gravity when the GB coupling goes to zero.

The remainder of this article is structured as follows. In Sect. 2, we construct three-dimensional black hole solutions of GB gravity with finite electrodynamics. In Sect. 3, we explore the thermodynamics of three-dimensional black holes in GB gravity. In Sect. 4, we express the Einstein field equation as a thermodynamics relation. The last section is devoted to conclusions and discussion. All Greek indices vary from 0, 1, 2. Units are chosen such that $c=1=G$.

2 3D black holes in GB gravity with Maxwell electrodynamics

Using the regularization factor $r \rightarrow \sqrt{r^2+l_0^2}$, where $l_0$ is the zero-point length [73], for the gravitational potential by means of the regularization factor in $(2+1)$ dimensions it was shown that [74]

$$\begin{aligned} \Phi (r)=k M \ln \left( \sqrt{r^2+l_0^2}\right) , \end{aligned}$$

(1)

where $\Phi (r)$ is the gravitational potential per unit mass and k is a constant of proportionality. By drawing upon concepts from string T-duality, it has been demonstrated that the zero-point length, denoted as $l_0$, assumes a role akin to that of the Planck length (see [92,93,94,95]). From the form of the last equation we observe that one has units of length inside the logarithm; however, one can add a normalization constant $r_0$ inside logarithmic terms. Hence, in general we have $\ln \left( \sqrt{r^2+l_0^2}/r_0\right)$. However, this constant will be omitted in all logarithmic terms in our paper. Using the gravitational potential mentioned above, we can solve Poisson’s equation in polar coordinates

$$\begin{aligned} \nabla ^2 \Phi (r)=2 \pi \rho , \end{aligned}$$

(2)

which easily yields the energy density as [74]

$$\begin{aligned} \rho (r)=\frac{k\,M\,l_0^2}{\pi (r^2+l_0^2)^2}. \end{aligned}$$

(3)

We can already see that when $l_0\rightarrow 0$, $\rho (r)$ reduces to zero, giving a point mass distribution. In contrast, due to the zero-point length, here we get a smeared matter distribution due to quantum gravity effects described by the quantum modified energy momentum tensor ${(T^\mu }_\nu )^\textrm{str} = \textrm{diag} \left( -\rho ,p_r,p_{\varphi }\right)$. It is interesting to note that this energy density can be reduced to the energy density given in Ref. [75], which also leads to a regular solution in Einstein gravity. For the electromagnetic potential in $(2+1)$-dimensions we have [74]

$$\begin{aligned} A_\mu =(-Q \ln (\sqrt{r^2+l_0^2}),0,0), \end{aligned}$$

(4)

where $A_{\mu }$ is the three-potential which is well defined even when $r \rightarrow 0$. For these reasons, we can refer to such a theory as finite electrodynamics, which is basically the Maxwell electrodynamics with a regular potential in the limit $r \rightarrow 0$. By comparing (1) and $A_t$ in (4), we note that $Q=-kM$. This is because both the gravitational force and electrostatic force, for example in 4D, have similar laws. In 3D, it is no surprise to see that the potentials are similar up to a sign difference due to the nature of the charge. A regularized GB theory has been shown to exist and it belongs to what is known as the scalar-tensor formulation described by the action [76,77,78]:

$$\begin{aligned} S= & {} \int _{\mathcal {M}} d^{D} x \sqrt{-g}\Big \{R-2\Lambda +\alpha \big [4 G^{\mu \nu } \nabla _{\mu } \phi \nabla _{\nu } \phi +\phi \mathcal {G}\nonumber \\{} & {} +\,4 \square \phi (\nabla \phi )^{2}+2(\nabla \phi )^{4}\big ] \Big \}+S_{EM}+S_{M}, \end{aligned}$$

(5)

where $\phi (x^\mu )$ is a real scalar field, $S_{EM}$ is the action for the electromagnetic field, $S_{M}$ is the matter action which arises due to the quantum gravity effects encoded in $l_0$, and finally, $\mathcal {G}=R_{\mu \nu \lambda \rho }R^{\mu \nu \lambda \rho }-4R_{\mu \nu }R^{\mu \nu }+R^2$ is the GB term. In fact, the action in the last equation is shown to be a special case of a more general well-defined action given in [79]

$$\begin{aligned} S= & {} \int d^D x\sqrt{-g}\Big \{R -2\Lambda +\alpha \Big (\phi \,\mathcal {G}+4G^{\mu \nu }\partial _\mu \phi \partial _\nu \phi \nonumber \\{} & {} -2\eta Re^{-2\phi }-4(\partial \phi )^2\Box \phi +2((\partial \phi )^2)^2\nonumber \\{} & {} -12\eta (\partial \phi )^2e^{-2\phi }-6\eta ^2e^{-4\phi }\Big )\Big \}. \end{aligned}$$

(6)

Here, $G^{\mu \nu }$ denotes the Einstein tensor. In this approach, one can use the Kaluza–Klein-like procedure to generate the limit of GB gravity by means of compactification. This action depends on a parameter $\eta$ which describes the curvature of the (maximally symmetric) internal space [79]

$$\begin{aligned} R_{\mu \nu \lambda \rho }= \eta (g_{\mu \lambda }g_{\nu \rho }-g_{\mu \rho }g_{\nu \lambda }). \end{aligned}$$

(7)

The equivalence is achieved for vanishing $\eta$. As was argued in [70, 71], there is no logical obstruction to consider a lower-dimensional GB gravity by setting $D = 3$ in the above action to obtain a $D = 3$ version of GB gravity. Note that $\mathcal {G}$ vanishes in $D = 3$ by construction or the choice of the metric. Also note that we are working with a regularized theory or a scalar–tensor theory of gravity. Vanishing $\mathcal {G}$ in the action (6) simplifies the computations but we still have an effect of $\alpha$. In what follows we shall consider this theory where $\mathcal {G}=0$ for $D = 3$. Following [70, 71], we can consider a static solution with

$$\begin{aligned} \textrm{d}s^2=-f_{GB}(r)\textrm{d}t^2+\frac{\textrm{d}r^2}{f_{GB}(r) h(r)}+r^2 \textrm{d}\varphi ^2. \end{aligned}$$

(8)

For the matter terms we have $S_{M}$, which encodes the effect of string corrections (terms containing zero-point length) given by

$$\begin{aligned} S_M=\int \textrm{d}^3x \sqrt{-g}\,\,\mathcal {L}_M. \end{aligned}$$

(9)

The simplest choice is to take $\mathcal {L}_M \sim \rho$. We do not yet have the full Lagrangian regarding the quantum gravity effects. In this direction it is also possible that the Einstein field equations might be modified. However, having the energy density, we can obtain the effective solution (along with the effective Einstein field equation), and one way of doing it is to identify $\mathcal {L}_M$ with the scalar $\rho$.

Fig. 1

Left panel: plot of $f_{GB}(r)$ as a function of r. We have set $M=1$, $Q=0.1$, $l=10$, $l_0=0.1$ and $\alpha =0.001$. This particular case shows the presence of the horizon; hence the solution describes a black hole. Right panel: plot of the energy density $\rho$ (given by Eq. (3)) as a function of r. We have set $M=1$ and $l_0=0.1$

If we solve (2) in the background metric (8), we get

$$\begin{aligned} \mathcal {L}_M=\frac{k M l_0^2 h(r)}{\pi (r^2+l_0^2)^2}+\frac{k h'(r) M r}{4 \pi (r^2+l_0^2)}, \end{aligned}$$

(10)

in which $\mathcal {L}_M$ encodes the smeared matter distribution due to stringy effects. The potential (1) corresponds to the virtual particle exchange obtained in flat spacetime, and in general, that means we can set $f(r)\rightarrow 1$ in metric (8). Although this is a good approximation, and can be justified from the equivalence principle $f(r)\rightarrow 1$, in our case we have a nontrivial metric due to the presence of h(r). With this information in hand, we solve $\nabla ^2\Phi =2 \pi \rho$, and as we see from the last equation, it contains (3) in the special case by setting $h(r)=1$ and $h'(r)=0$. The reason that we need these relations will be clear later on, since we need the equations of motion where we have to use a variation w.r.t. h. The finite electrodynamics are described by the action

$$\begin{aligned} S_{EM}=- \int \textrm{d}^3x \sqrt{-g}\mathcal {L}_{EM}, \end{aligned}$$

(11)

and one can evaluate the Faraday tensor $F_{\mu \nu }$ using Eq. (4) and then obtain the Lagrangian for the electromagnetic field given by [74]

$$\begin{aligned} \mathcal {L}_{EM}=\sigma F^{\mu \nu }F_{\mu \nu }= \sigma \,\frac{2\,Q^2\, r^2\,h(r)}{(r^2+l_0^2)^2}, \end{aligned}$$

(12)

where $\sigma$ is a constant of proportionality to be constrained via astronomical observations. Having in mind that the GB term vanishes in three dimensions, i.e. $\mathcal {G}=0$, and working with a vanishing $\eta$, for the total effective Lagrangian density we have

$$\begin{aligned} \mathcal {L}_\textrm{tot}= & {} R-2\Lambda +\alpha \big (4 G^{\mu \nu } \nabla _{\mu } \phi \nabla _{\nu } \phi + 4 \square \phi (\nabla \phi )^{2}+2(\nabla \phi )^{4}\big )\nonumber \\{} & {} +\mathcal {L}_{EM}+\mathcal {L}_{M}. \end{aligned}$$

(13)

Following [70, 71], one has to use the Euler–Lagrange equations and can obtain three equations of motion for the variables $f_{GB}, h, \phi$. It is worth noting that the equation of motion for the above Lagrangian retains the fundamental properties of GR and its extensions. As a result, the equation of motion of second order with respect to the metric and energy momentum tensor are conserved. In particular, focusing on the BTZ solutions that satisfy the condition $h = 1$, and fixing $\sigma =1/2$, the equation coming from the variation w.r.t. $f_{GB}$ reads

$$\begin{aligned} \alpha \left( \phi '^2+\phi ''\right) \left( r\phi '-1\right) =0, \end{aligned}$$

(14)

which has the solution $\phi (r)=\ln (r/l)$, with l being a constant of integration. On the other hand, the equation coming from variation w.r.t. h yields

$$\begin{aligned}{} & {} \frac{f_{GB}'(r)}{2r}+\frac{\alpha f_{GB}(r) f_{GB}'(r)}{r^3}-\frac{\alpha f_{GB}(r)^2}{r^4}\nonumber \\{} & {} \quad + \frac{M l_0^2 }{(r^2+l_0^2)^2} +\frac{ Q^2r^2}{(r^2+l_0^2)^2}-\frac{1}{l^2}=0. \end{aligned}$$

(15)

Solving the above equation and identifying the constant of integration with M, we find the following metric coefficient

$$\begin{aligned} f_{GB}(r)=-\frac{r^2}{2\alpha }\left( 1 \pm \sqrt{1+\frac{4\alpha }{r^2}f_E(r)}\right) , \end{aligned}$$

(16)

where

$$\begin{aligned} f_E(r)\equiv \frac{r^2}{l^2}-\frac{M r^2}{r^2+l_0^2}-\frac{ Q^2l_0^2}{r^2+l_0^2}- Q^2\ln (r^2+l_0^2). \end{aligned}$$

(17)

Note an interesting property of the above solution: if we use the transformation $r \rightarrow -r$, that does not generate a solution with negative mass but a replica of the same spacetime geometry. This fact can also be seen in the expression for the energy density in Eq. (3). In Fig. 1 (left-hand side), we show a plot of the function $f_{GB}(r)$ from which one can see the presence of the event horizon for this particular black hole and the plot for $\rho (r)$ (right-hand side). Another important aspect of our black hole solution is that it diverges at asymptote infinity. Namely, this can be seen from the presence of the first term $r^2/l^2$, but also the presence of last term $Q^2\ln (r^2+l_0^2)$ in Eq. (17). Eliminating these divergences (logarithmic and $r^2/l^2$ divergences) is beyond the scope of the present paper; however, one possibility is by using counter terms (see in particular [96]). But again, this requires further investigation of our solution. Usually in Gauss–Bonnet gravity we get two solutions, namely (16), which differ in the sign. The $+$ branch is not a physical solution in general. For example, we can have a $+$ sign before the mass term which signals a diverging mass for large radii. Moreover, the behavior of the core can be obtained if we analyze $r<l_0$. It turns out that core can behave as a de Sitter metric. This fact was explained in [74].

Fig. 2

Plot of the Ricci scalar and Kretschmann scalar. We have set $M=1$, $Q=0.1$, $l=10$, $l_0=0.1$, and $\alpha =0.001$. This particular case shows the presence of singularities

The above result is true provided the following conditions hold: (i) Consider the scalar-tensor limit of GB gravity such as [70, 71], coupled to additional matter. (ii) The matter considered has the property that $T_t^t = T_r^r$. (iii) Considering three-dimensional generalizations of the BTZ black hole, then (16) is true. Basically, it just needs to be the case that there is a single field equation for the gravitational sector. This was noted in [70]; one expects the form of Eq. (16) to remain valid for charged GB BTZ black holes even in any theory of nonlinear electrodynamics characterized by the action. The negative sign branch of the above admits a well-defined limit as $\alpha \rightarrow 0$, yielding

$$\begin{aligned} f_{GB}(r)=f_E-\frac{\alpha }{r^2}f_E^2+\cdots , \end{aligned}$$

(18)

in agreement with [74] in leading order terms. We can see that in the limit of $l_0\rightarrow 0$, the charged black hole solution in 3D GB gravity, reported in Ref. [70], is obtained

$$\begin{aligned} f_E(r)=\frac{r^2}{l^2}-M-2Q^2\ln (r). \end{aligned}$$

(19)

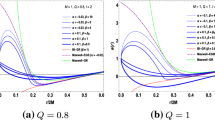
At the horizon we need $f_{GB}(r_+)=0$. This means that $1-\sqrt{1+4 \alpha f_E(r_+)/r_+^2}=0$, yielding $f_E(r_+)=0$, but so does $f_{GB}(r_+)=0$. It is interesting to note here that the solution presented in [74] is free from singularities; the solution (16) in the present paper is not. Specifically, one can show that the curvature scalar invariants such as the Ricci scalar and Kretschmann scalar diverge in the limit $r \rightarrow 0$; namely, $R=R_{\mu \nu } g^{\mu \nu }$ and $K=R_{\mu \nu \sigma \rho } R^{\mu \nu \sigma \rho }$ blow up to $-\infty$ and $+\infty$, respectively. We show the plot of the Ricci scalar and Kretschmann scalar in Fig. 2. In addition, the curvature is present for $\alpha <0$. This follows from the fact that the Kretschmann scalar is a function of the derivative of (16), where the inner-square term $1+4 \alpha f_E(r)/r$ should have a zero value (a curvature singularity), i.e., the solution should also have a zero value for $\alpha <0$.

3 Thermodynamics of 3D GB black holes

In this section we shall focus on the thermodynamics of the black hole solution (16). One can easily see that 3D charged GB black holes share the same horizon radius $r_+$ and the same temperature as in 3D general relativity. Hence we can write

$$\begin{aligned} T=\frac{f'(r)_{GB}}{4 \pi }|_{r_+}=\frac{f'(r)_{E}}{4 \pi }|_{r_+}. \end{aligned}$$

(20)

This means that their black hole thermodynamics will be identical. Following [70, 71], first we can define

$$\begin{aligned} \mathcal {M}=\frac{M}{8}, \end{aligned}$$

(21)

where the mass parameter is obtained from $f_E(r_+)=0$,

$$\begin{aligned} M=\frac{r_+^2}{l^2}+\frac{l_0^2}{l^2}-\frac{Q^2 (r_+^2+l_0^2)\ln (r_+^2+l_0^2)}{r_+^2}. \end{aligned}$$

(22)

Using the mass, it follows for the black hole temperature that

$$\begin{aligned} T= & {} \frac{r_+}{2 \pi l^2}+\frac{ l_0^2 Q^2 \ln (r_+^2+l_0^2)}{ 2 \pi r_+ (r_+^2+l_0^2) }\nonumber \\{} & {} -\frac{ Q^2 (r_+^2-l_0^2)}{2 \pi r_+(r_+^2+l_0^2)}-\frac{ l_0^2 r_+}{2 \pi (r_+^2+l_0^2) l^2}. \end{aligned}$$

(23)

From Eq. (22) we also see that

$$\begin{aligned} d\mathcal {M}= & {} \bigg (\frac{\partial \mathcal {M}}{\partial r_{+} }\bigg )_{Q,l_0}\textrm{d}r_{+}+\bigg (\frac{\partial \mathcal {M}}{\partial Q }\bigg )_{{r_+},l_0}\textrm{d}Q\nonumber \\{} & {} +\bigg (\frac{\partial \mathcal {M}}{\partial l_0 }\bigg )_{r_{+},Q}\textrm{d}l_0, \end{aligned}$$

(24)

where

$$\begin{aligned}{} & {} \bigg (\frac{\partial \mathcal {M}}{\partial r_{+} }\bigg )_{Q,l_0}=\frac{ r_+}{4l^2}+\frac{ l_0^2 Q^2 \ln (r_+^2+l_0^2)}{4r_+^3}-\frac{ Q^2 (r_+^2-l_0^2)}{4r_+^3},\\{} & {} \bigg (\frac{\partial \mathcal {M}}{\partial Q }\bigg )_{r_{+},l_0}=-\frac{ (l_0^2+r_+^2) Q \ln (r_+^2+l_0^2)}{4\,r_+^2}=\phi _e,\\{} & {} \bigg (\frac{\partial \mathcal {M}}{\partial l_0 }\bigg )_{r_{+},Q}=\frac{l_0}{4l^2}-\frac{ Q^2 l_0}{4r_+^2}-\frac{ l_0 Q^2 \ln (r_+^2+l_0^2)}{4r_+^2 }=\psi _{l_0}, \end{aligned}$$

where $\phi _e$ and $\psi _{l_0}$ are the potentials conjugate to Q and $l_0$, respectively. By using the fact that $\textrm{d}\mathcal {M}=T \textrm{d}S$ (keeping Q and $l_0$ constant), for the entropy we have

$$\begin{aligned} S= & {} \int \frac{1}{T} \bigg (\frac{\partial \mathcal {M}}{\partial r_{+} }\bigg )_{Q,l_0} \textrm{d}r_+; \end{aligned}$$

(25)

then, evaluating the last integral yields

$$\begin{aligned} S=\frac{\pi r_+}{2}-\frac{\pi l_0 \sqrt{14}}{56}\arctan \left( \frac{2 r_+ \sqrt{14}}{7 l_0} \right) . \end{aligned}$$

(26)

Fig. 3

Plot of the entropy given in Eq. (26) against $l_0$ and choosing $r_+=1$

From the last equation we see that the stringy effect suggests a decrease in the black hole entropy. From Fig. 3, we can see that the entropy remains non-negative. Note that this behavior of entropy is observed even for $|l_0|>2$. In the limit $l_0\rightarrow 0$, we get $\lim _{l_0 \rightarrow 0}S=\pi r_+/2$ [70, 71]. We should mention here that the presence of $l_0$ modifies the energy momentum tensor modifies the first law of thermodynamics, which leads to values of entropy that do not follow the area’s law. This was also the case for a regular black hole studied in Ref. [91]. The surface area of the black hole is

$$\begin{aligned} A=\int _0^{2 \pi } r_+ \textrm{d}\varphi =2 \pi r_+. \end{aligned}$$

(27)

Hence we see that for the classical case with no stringy effect, the Hawking–Bekenstein relation holds,

$$\begin{aligned} S=\frac{A}{4}. \end{aligned}$$

(28)

Let us note here that in the extended phase space, where the cosmological constant is interpreted as a thermal pressure, the mass of the black hole is no longer regarded as internal energy, rather it is identified with chemical enthalpy [80]. Adopting this picture, one can write $\mathcal {M}=E+PV$, with the potential given by

$$\begin{aligned} P= & {} \frac{1}{8 \pi l^2},\quad V=\pi r_+^2, \end{aligned}$$

(29)

we can write the first law for the black hole,

$$\begin{aligned} \textrm{d}\mathcal {M}=T\textrm{d}S+V\textrm{d}P+\phi _e \textrm{d}Q+\psi _{l_0} dl_0. \end{aligned}$$

(30)

4 Thermodynamic interpretation of the field equations

The thermodynamics–gravity conjecture has been well established through numerous investigations [81,82,83]. It has been confirmed that one can always rewrite the field equations of gravity in the form of the first law of thermodynamics. This connection has been confirmed for Einstein, GB, and more general Lovelock gravity [84,85,86,87]. For topological gravity, it has been shown that the gravitational field equations of $(n+1)$-dimensional topological black holes with constant horizon curvature, in cubic and quartic quasi-topological gravity, can be recast in the form of the first law of thermodynamics, $\textrm{d}E=T\textrm{d}S-P\textrm{d}V$, at the black hole horizon [90]. This connection was also shown in the framework of brane cosmology, where it was proved that the Friedmann equations describing the evolution of the universe can be written in the form of the first law of thermodynamics on the apparent horizon and vice versa [88, 89].

Here we would like to examine the connection between the field equations and first law of thermodynamics for regular GB black holes in three dimensions. To this end, let us rewrite the (rr)-component of the field equations in the presence of the cosmological constant at the horizon with the assumption that the equation also holds for $r=r_+$. We then obtain

$$\begin{aligned}{} & {} \frac{f_{GB}'(r_+)}{2r_+}+\frac{\alpha f_{GB}(r_+) f_{GB}'(r_+)}{r_+^3}-\frac{\alpha f_{GB}(r_+)^2}{r_+^4}-\frac{1}{l^2}\nonumber \\{} & {} \quad =8 \pi T^r_r|_{r_+}, \end{aligned}$$

(31)

where $T^r_r=P_r$ is the radial pressure of matter at the horizon [84]. In our case, it is given by

$$\begin{aligned} P_r|_{r_+}= - \frac{M l_0^2 }{8 \pi (r_+^2+l_0^2)^2}-\frac{ Q^2r_+^2}{8 \pi (r_+^2+l_0^2)^2}. \end{aligned}$$

(32)

Using the fact that at the horizon we need $f_{GB}(r_+)=0$, this means that $1=\sqrt{1+4 \alpha f_E(r_+)/r_+^2}=0$, yielding $f_E(r_+)=0$, but so does $f_{GB}(r_+)=0$. This implies that the second and third terms in the above equation vanish. Moreover, at the horizon, as we saw $f_{GB}(r_+)=f_{E}(r_+)$, this gives

$$\begin{aligned} \frac{f_{E}'(r_+)}{2r_+}-\frac{1}{l^2}=8 \pi P_r, \end{aligned}$$

(33)

which can also be rewritten as

$$\begin{aligned} \frac{f_{E}'(r_+)}{4 \pi }\textrm{d}\left( \frac{\pi r_+}{2}\right) -\frac{\textrm{d}\left( r_+^2\right) }{8\,l^2}=P_r \textrm{d}(\pi r_+^2). \end{aligned}$$

(34)

The second term on left side of the above equation is the change in mass. Using Eqs. (22 and 23), we can write

$$\begin{aligned}{} & {} \textrm{d}\left( \frac{r_+^2}{8l^2}\right) =\textrm{d} \mathcal {M}-\textrm{d} \left( \frac{l_0^2}{8 l^2}\right) \nonumber \\{} & {} \qquad \qquad \qquad +\textrm{d}\left( \frac{Q^2 (r_+^2+l_0^2)\ln (r_+^2+l_0^2)}{8r_+^2}\right) \end{aligned}$$

(35)

$$\begin{aligned}{} & {} \frac{f_{E}'(r_+)}{4 \pi }\textrm{d}S+\phi _e \textrm{d}Q+\psi _{l_0}\textrm{d}l_0-d\mathcal {M}=P_r \textrm{d}V, \end{aligned}$$

(36)

where $\phi _e$ and $\psi _{l_0}$ are the potentials conjugate to Q and $l_0$, respectively. Finally, we can express the total mass of the system as follows

$$\begin{aligned} \textrm{d}\mathcal {M}=T\textrm{d}S+\phi _e \textrm{d}Q+\psi _{l_0}\textrm{d}l_0-P_r\textrm{d}V, \end{aligned}$$

(37)

where $\textrm{d}V$ is the change in horizon volume, and the term $P_r \textrm{d}V$ corresponds to work done against the pressure. Note that this equation is obtained from a combination of the equations of motion at the horizon and the variation in parameters at the horizon. Hence, the field equations near the horizon of the 3D GB black hole can be expressed as a thermodynamic identity under the virtual displacement of the horizon. The effect of zero-point length is encoded in the third term. On the other hand, there is no effect of the GB parameter $\alpha$. This is because the solutions given by Eqs. (16 and 17) share the same horizon, and therefore the thermodynamic properties are the same.

5 Conclusion and discussion

In a framework of 3D regularized GB theory of gravity which belongs to a scalar-tensor formulation of gravity, we obtained an exact black hole solution using the zero-point length effect. The black hole solution is described by the mass, electric charge and the zero-point length $l_0$. The gravitational and electromagnetic potentials are finite and regular in the limit $r \rightarrow 0$; however, in general, the scalar curvature invariants show the presence of singularities at the origin. We investigated the thermodynamics of the black hole solution; in particular, we obtained the first law for the black hole thermodynamics relation. Using the thermodynamics-gravity conjecture, we showed that the field equations of the 3D GB black hole can be expressed as the first law of thermodynamics on the horizon. Due to the stringy effects, we found that the entropy of the black hole decreases. Finally, we briefly investigated a 3D rotating solution with zero-point length effect in GB gravity.

Appendix: Rotating black hole solutions

For the rotating black hole in three dimensions, it was found that [74]

$$\begin{aligned} \textrm{d}s^2= - N^2 \textrm{d}t^2 + r^2 \left( N^\varphi \textrm{d}t + \textrm{d}\varphi \right) ^2 + \frac{\textrm{d}r^2}{\hat{f}_E}, \end{aligned}$$

(38)

with

$$\begin{aligned}{} & {} N^2=\hat{f}_E=\frac{r^2}{l^2}-\frac{M r^2}{r^2+l_0^2}-\frac{ Q^2l_0^2}{r^2+l_0^2}- Q^2\ln (r^2+l_0^2)+{J^2 \over 4 r^2},\nonumber \\{} & {} N^{\varphi }(r) = -{J \over 2 r^2}. \end{aligned}$$

(39)

To obtain a rotating solution in the GB theory, we closely follow [71]. We have to perform the same type of boost used in the Einstein case, but modified to account for the fact that the higher-curvature corrections result in modifications to the AdS length scale of the theory:

$$\begin{aligned} t\rightarrow \Xi _{\textrm{eff}} t -a \varphi , \ \varphi \rightarrow \frac{a t}{\ell _{\textrm{eff}}^2} -\Xi _{\textrm{eff}} \varphi , \ \Xi _\textrm{eff}^2 = 1 + \frac{a^2}{\ell _{\textrm{eff}}^2},\nonumber \\ \end{aligned}$$

(40)

applied to our metric with

$$\begin{aligned} \ell _{\textrm{eff}}= \sqrt{ \frac{2 \alpha }{\sqrt{X_\alpha }-1}},\quad X_\alpha = 1+\frac{4\alpha }{\ell ^2}. \end{aligned}$$

(41)

This yields

$$\begin{aligned} \textrm{d}s^2= & {} -f_{GB}(\Xi _{\textrm{eff}} \textrm{d}t -a \textrm{d}\varphi )^2\!\nonumber \\{} & {} +\frac{r^2}{\ell _{\textrm{eff}}^4}(a\textrm{d}t-\Xi _{\textrm{eff}} \ell _{\textrm{eff}}^2 d\varphi )^2 +\frac{\textrm{d}r^2}{f_{GB}},\nonumber \\ \phi= & {} \ln (r/l), \end{aligned}$$

(42)

with $f_{GB}$ given by Eq. (16).