1 Introduction

Nonlinear field theories are of interest to different branches of mathematical physics because most physical systems are inherently nonlinear in the nature. The main reason to consider the nonlinear electrodynamics (NLED) comes from the fact that these theories are considerably richer than the Maxwell field and in special case they reduce to the linear Maxwell theory. Various limitations of the Maxwell theory, such as description of the self-interaction of virtual electron-positron pairs [1–3] and the radiation propagation inside specific materials [4–7], motivate one to consider NLED [8, 9]. Besides, NLED improves the basic concept of gravitational redshift and its dependency of any background magnetic field as compared to the well-established method introduced by standard general relativity. In addition, it was recently shown that NLED objects can remove both of the big bang and black hole singularities [10–15]. Moreover, from astrophysical point of view, one finds that the effects of NLED become indeed quite important in superstrongly magnetized compact objects, such as pulsars and particular neutron stars (also the so-called magnetars and strange quark magnetars) [16–18].

About 80 years ago Born and Infeld [19, 20] introduced an interesting kind of NLED in order to remove the divergence of the self-energy of a point-like charge. The first attempt to couple the NLED with gravity was made by Hoffmann [21]. After that the effects of Born–Infeld (BI) NLED coupled to the gravitational field have been studied for static black holes [22–46], rotating black objects [47–53], wormholes [54–57] and superconductors [58–63]. Also, BI NLED has acquired a new impetus, since it naturally arises in the low-energy limit of the open string theory [64–69]. Recently, two different BI types of NLED have been introduced, which can also remove the divergence of the electric field near the origin. One of them is Soleng NLED which is logarithmic form [70] and another one was proposed by Hendi with exponential form [71]. The Soleng field, like BI theory, removes divergency of the electric field, while the theory proposed by Hendi does not. It is notable to mention that although the exponential form of NLED does not cancel the divergency of the electric field but its singularity is much weaker than that in the Maxwell theory. Black object solutions coupled to these two nonlinear fields have been studied in literature (for e.g., see [57, 72–74]). The Lagrangian of mentioned BI type nonlinear theories, for weak nonlinearity, tends to the following form

$$\begin{aligned} L(\mathcal {F})=-\mathcal {F}+\alpha \mathcal {F}^{2}+O\left( \alpha ^{2}\right) , \end{aligned}$$
(1)

where \(\mathcal {F}=F_{\mu \nu }F^{\mu \nu }\) is the Maxwell invariant, in which \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) is the electromagnetic field tensor and \(A_{\mu }\) is the gauge potential. In addition, \(\alpha \) denotes nonlinearity parameter which is small and so the effects of nonlinearity should be considered as a perturbation (\(\alpha \) is proportional to the inverse value of nonlinearity parameter in BI-type theories). In this paper, we take into account the Eq. (1) as a NLED source and investigate the effects of nonlinearity on the properties of static and rotating black hole/brane solutions.

Here, it is necessary to focus on the basic motivation of considering the Lagrangian (1). At first, we should note that, regardless of a constant parameter, most of NLED Lagrangians reduce to Eq. (1) for the weak nonlinearity. Eventually, it is worthwhile to mention that although various theories of NLED have been created with different primitive motivations, only for the weak nonlinearity [Eq. (1)], they contain physical and experimental importances. As we know, using the Maxwell theory in various branches leads to near accurate or acceptable consequences. So, in transition from the Maxwell theory to NLED, the logical decision is to consider the effects of weak nonlinearity variations, not strong effects. This means that, one can expect to obtain precise physical results with experimental agreements, provided one regards the nonlinearity as a correction to the Maxwell field.

For the reasons mentioned above, there have been published some reasonable works by considering Eq. (1) as an effective Lagrangian of electrodynamics [1–3, 8, 9, 64–66, 75–81]. Heisenberg and Euler have shown that quantum corrections lead to nonlinear properties of vacuum [1–3, 8, 9, 75]. Also, as we mentioned before, it was proved that in the low-energy limit of heterotic string theory, a quartic correction of the Maxwell field strength tensor appears [64–66, 76–81]. So it is natural to consider Eq. (1) as an effective and suitable Lagrangian of electrodynamics instead of the Maxwell one.

The outline of our paper is as follows. In the next section, we consider the \((n+1)\)-dimensional topological static black hole solutions of Einstein gravity in presence of the mentioned NLED and investigate their properties. In Sect. 3, we calculate the conserved and thermodynamic quantities of asymptotically flat black holes, check the first law of thermodynamics and investigate the stability of the solutions in both canonical and grand canonical ensembles. Section 4 is devoted to introducing the rotating solutions with flat horizon and computing the conserved and thermodynamic quantities of the solutions. We also check the first law of thermodynamics and perform the stability analysis of the solutions both in the canonical and the grand canonical ensembles for the rotating solutions. We finish our paper with some concluding remarks.

2 Static topological black hole solutions

The \((n+1)\)-dimensional action of Einstein gravity with negative cosmological constant and in presence of NLED is

$$\begin{aligned} I_{G}&= -\frac{1}{16\pi }\int _{\mathcal {M}}\mathrm{d}^{n+1}x\sqrt{-g}\left[ R-2\Lambda +L(\mathcal {F})\right] \nonumber \\&-\frac{1}{8\pi }\int _{\partial \mathcal {M}}\mathrm{d}^{n}x \sqrt{-\gamma }\Theta \left( \gamma \right) \!, \end{aligned}$$
(2)

where \(R\) is the scalar curvature, \(\Lambda \) is the cosmological constant which is equal to \(-n\left( n-1\right) /2l^{2}\) for asymptotically anti-de Sitter (adS) solutions. In this action, \(L(\mathcal {F})\) is the Lagrangian of NLED presented in Eq. (1) and the second integral is the Gibbons–Hawking surface term which is chosen such that the variational principle will be well defined [82, 83]. In the second integral, \(\gamma \) and \(\Theta \) are, respectively, the trace of induced metric, \(\gamma _{ij}\), and the extrinsic curvature \(\Theta _{ij}\) on the boundary \(\partial \mathcal {M}\). Variation of the action (2) with respect to the metric tensor \(g_{\mu \nu }\) and the Faraday tensor \(F_{\mu \nu }\), leads to

$$\begin{aligned}&G_{\mu \nu }+\Lambda g_{\mu \nu }=\frac{1}{2}g_{\mu \nu } L(\mathcal {F})-2L_{\mathcal {F}}F_{\mu \lambda }F_{\nu }^{\lambda }, \end{aligned}$$
(3)
$$\begin{aligned}&\partial _{\mu }\left( \sqrt{-g}L_{\mathcal {F}}F^{\mu \nu }\right) =0, \end{aligned}$$
(4)

where \(G_{\mu \nu }\) is the Einstein tensor and \(L_{\mathcal {F}}=dL(\mathcal {F)}/d\mathcal {F}\).

Here, we want to obtain the \((n+1)\)-dimensional topological static black hole solutions. We take into account the metric of \((n+1)\)-dimensional spacetime with the following form

$$\begin{aligned} \mathrm{d}s^{2}=-f(r)\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{g(r)}+r^{2}\mathrm{d}\Omega _{n-1}^{2}, \end{aligned}$$
(5)

where \(f(r)\) and \(g(r)\) are two arbitrary functions of radial coordinate which should be determined and

$$\begin{aligned}&\mathrm{d}\Omega _{n-1}^{2}\nonumber \\&\quad =\left\{ \begin{array}{ll} \mathrm{d}\theta _{1}^{2}+\sum \limits _{i=2}^{n-1}\prod \limits _{j=1}^{i-1}\sin ^{2}\theta _{j}\mathrm{d}\theta _{i}^{2} &{}\quad k=1 \\ \mathrm{d}\theta _{1}^{2}+ \sinh ^{2}\theta _{1} \left( \mathrm{d}\theta _{2}^{2}+\sum \limits _{i=3}^{n-1}\prod \limits _{j=2}^{i-1}\sin ^{2}\theta _{j}\mathrm{d}\theta _{i}^{2}\right) &{}\quad k=-1 \\ \sum \limits _{i=1}^{n-1}\mathrm{d}\phi _{i}^{2} &{}\quad k=0 \end{array} \right. \!, \nonumber \\ \end{aligned}$$
(6)

represents the line element of an \(\left( n-1\right) \)-dimensional hypersurface with constant curvature \(\left( n-1\right) \left( n-2\right) k\) and volume \(V_{n-1}\). We should note that the constant \(k\) characterizes the hypersurface and indicates that the boundary of \(t=\mathrm{constant}\) and \(r=\mathrm{constant}\) can be a positive (elliptic), zero (flat) or negative (hyperbolic) constant curvature hypersurface.

Using Eq. (4) with the following radial gauge potential ansatz

$$\begin{aligned} A_{\mu }=h\left( r\right) \delta _{\mu }^{0}, \end{aligned}$$
(7)

we obtain the following differential equation

$$\begin{aligned}&E^{\prime }(r)\!+\!\frac{(n\!-\!1)E(r)}{r}\!+\!4E^{2}(r)\left( \frac{(n\!-\!1)E(r)}{r} \!+\!3E^{\prime }(r)\right) \alpha \nonumber \\&\quad =0, \end{aligned}$$
(8)

where \(E(r)=F_{tr}=h^{\prime }(r)\) is the nonzero component of electromagnetic field and prime denotes the derivative with respect to \(r\). Solving Eq. (8), one obtains

$$\begin{aligned} E(r)=\frac{3\left[ q\alpha ^{2}r^{2n+1}\left( 1+\sqrt{1+\frac{r^{2n-2}}{ 27\alpha q^{2}}}\right) \right] ^{2/3}-\alpha r^{2n}}{6\alpha r^{n}\left[ q\alpha ^{2}r^{2n+1}\left( 1+\sqrt{1+\frac{r^{2n-2}}{27\alpha q^{2}}}\right) \right] ^{1/3}}, \end{aligned}$$
(9)

where \(q\) is an integration constant which is related to the electric charge of the black hole. Now, we use the series expansion of \(E(r)\) for small values of \(\alpha \), and keep the first two terms to obtain

$$\begin{aligned} E(r)=\frac{q}{r^{n-1}}-4\left( \frac{q}{r^{n-1}} \right) ^3 \alpha +O\left( \left( \frac{q}{r^{n-1}} \right) ^5 \alpha ^{2}\right) , \end{aligned}$$
(10)

or correspondingly

$$\begin{aligned} h(r)\!=-\,\frac{q}{\left( n-2\right) r^{n-2}}\!+\!\frac{4q^{3}}{\left( 3n-4\right) r^{3n-4}}\alpha \!+\!O\left( \alpha ^{2}\right) .\quad \end{aligned}$$
(11)

It is easy to see that the second term in Eqs. (10) and (11) comes from the nonlinear correction and for vanishing \(\alpha \), one can reproduce the results of the Maxwell theory. Since we want to investigate the nonlinearity parameter as a (perturbative) correction, hereafter, we take into account the first correction term of nonlinearity parameter, \(\alpha \), and ignore \(\alpha ^{2}\) and higher power of nonlinearity parameter terms. To obtain the metric functions \(f\left( r\right) \) and \(g(r)\), one may use the nonzero components of Eq. (3). Straightforward calculations show that the nonzero components of Eq. (3) (up to the first order of \(\alpha \)) can be written as

$$\begin{aligned} e_{1}&= (n-1)rf^{\prime }(r)+(n-1)(n-2)\left[ f(r)-k\right] \nonumber \\&+2\Lambda r^{2}+ \frac{2q^{2}}{r^{2n-4}}-\frac{4q^{4}\alpha }{r^{4n-6}}+O\left( \alpha ^{2}\right) =0, \end{aligned}$$
(12)
$$\begin{aligned} e_{2}&= r^{2}f^{\prime \prime }(r)+2(n-2)rf^{\prime }(r)\nonumber \\&+(n-2)(n-3)\left[ f(r)-k\right] +2\Lambda r^{2}\nonumber \\&-\frac{2q^{2}}{r^{2n-4}}+\frac{12q^{4}\alpha }{r^{4n-6}}+O\left( \alpha ^{2}\right) =0. \end{aligned}$$
(13)

After some calculations, one can show that the solutions of Eqs. (12) and (13) can be written as

$$\begin{aligned} f(r)&= k-\frac{m}{r^{n-2}}-\frac{2\Lambda r^{2}}{n\left( n-1\right) }+\frac{ 2q^{2}}{\left( n-1\right) \left( n-2\right) r^{2n-4}} \nonumber \\&-\frac{4q^{4}}{\left[ 2\left( n-2\right) \left( n+2\right) +\left( n-3\right) \left( n-4\right) \right] r^{4n-6}}\alpha \nonumber \\&+O\left( \alpha ^{2}\right) , \end{aligned}$$
(14)
$$\begin{aligned} g(r)&= Cf(r), \end{aligned}$$
(15)

where \(m\) is an integration constant which is related to the mass of the black hole and the last term in Eq. (14) indicates the effect of nonlinearity. Hereafter, we set the constant \(C=1\) without loss of generality. It is notable to mention that, for \(\alpha =0\), this metric function reduces to Reissner–Nordström solution, as it should. The asymptotical behavior of the solution (14) is adS or dS provided \(\Lambda <0\) or \(\Lambda >0\) and the case of asymptotically flat solutions is permitted for \(\Lambda =0\) and \(k=1\).

Now we look for the singularities of the solutions. One can show that the metric (5) with the metric function (14) has an essential singularity at \(r=0\) by calculating the Kretschmann scalar, as

$$\begin{aligned} R_{\mu \nu \lambda \kappa }R^{\mu \nu \lambda \kappa }&= \frac{8\Lambda ^{2} }{n(n+1)}-\frac{16\Lambda q^{2}}{n(n+1)r^{2n}}\nonumber \\&\quad +\frac{\left( n^{2}-1\right) \left( n^{2}-2\right) m^{2}}{r^{2n+2}} \nonumber \\&\quad -\frac{8\left( 2n^{2}-n-2\right) mq^{2}}{r^{3n+1}}\nonumber \\&\quad +\left( \frac{96\Lambda \alpha }{n+1}+\frac{8\left( 8n^{2}-12n+3\right) }{n-1}\right) \frac{q^{4}}{ nr^{4n}} \nonumber \\&\quad +\frac{32\left( n-1\right) \left( 4n^{2}-n-2\right) m\alpha q^{4}}{\left( 3n-1\right) r^{5n+1}}\nonumber \\&\quad -\frac{32\left( 32n^{2}-32n+5\right) \alpha q^{6}}{ n\left( 3n-1\right) r^{6n}}+O\left( \alpha ^{2}\right) .\nonumber \\ \end{aligned}$$
(16)

From Eq. (16) it is obvious that Kretschmann scalar diverges at \(r=0\) and, like the asymptotically adS solutions, it reduces to \(8\Lambda ^{2}/n(n+1)\) for \(r\longrightarrow \infty \).

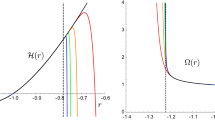
Figures 1, 2, 3 and 4 show that the singularity may be covered with horizon and, therefore, we can interpret the singularity as a black hole. In addition, these figures confirm that the nonlinearity parameter not only modify the electromagnetic part of solutions, but also the kind of horizons. For vanishing \(\alpha \), with suitable choice of parameters, metric function could acquire at most two horizons whereas, for this nonlinear theory (nonzero \(\alpha \)), it is possible to find three horizons. Figure 4 indicates that the nonlinearity parameter may considerably affect the existence, location and type of horizons. From Figs. 1, 2, 3 and 4 we find that, depending the values of metric parameters with suitable \(\alpha \), the horizons of the black hole solutions may be extreme or not.

Fig. 1
figure 1

Elliptic horizon solutions \(f(r)\) versus \(r\) for \(k=1\), \(n=4\), \(q=1\), \(\Lambda =-1\), \(\alpha =0.005\), and \(m=1.1\) (solid line), \(m=1.2\) (bold line) and \(m=1.3\) (dashed line); “dotted line is \(f(r)\) for the Maxwell case (\(\alpha =0\)) with \(m=1.3\)”

Full size image
Fig. 2
figure 2

Flat horizon solutions \(f(r)\) versus \(r\) for \(k=0\), \(n=4\) , \(q=1\), \(\Lambda =-1\), \(\alpha =0.02\), and \(m=0.4\) (solid line), \( m=0.5\) (bold line) and \(m=0.6\) (dashed line) ; “dotted line is \(f(r)\) for the Maxwell case (\(\alpha =0\)) with \(m=0.6\)”

Full size image
Fig. 3
figure 3

Hyperbolic horizon solutions \(f(r)\) versus \(r\) for \(k=-1\) , \(n=4\), \(q=5\), \(\Lambda =-1\), \(\alpha =0.1\), and \(m=0.1\) (solid line), \(m=0.7\) (bold line) and \(m=1.5\) (dashed line); “dotted line is \(f(r)\) for the Maxwell case (\(\alpha =0\)) with \(m=1.5\)”

Full size image
Fig. 4
figure 4

Elliptic horizon solutions \(f(r)\) versus \(r\) for \(k=1\), \( n=4\), \(q=1\), \(\Lambda =-1\), \(m=1.2\), and \(\alpha =0.007\) (solid line), \(\alpha =0.009\) (bold line) and \(\alpha =0.011\) (dashed line); “dotted line is \(f(r)\) for the Maxwell case (\(\alpha =0\)) with \(m=1.2\)”

Full size image

In order to study the conformal structure of the solutions, one may use the conformal compactification method to plot the Carter–Penrose (conformal) diagram (see Figs. 5, 6, 7). The Carter–Penrose diagrams and also the figures of the metric function (Figs. 1, 2, 3) confirm that, the singularity is spacelike such as that of Schwarzschild black holes. In other words, keeping the first order of nonlinearity parameter and ignoring the higher order of \(\alpha \), the timelike singularity of the Reissner–Nordström black holes (dotted line in Figs. 1, 2, 3) change to a spacelike singularity. Drawing the Carter–Penrose diagrams shows that the causal structure of the solutions are asymptotically well behaved.

Fig. 5
figure 5

Carter–Penrose diagram for the asymptotically flat (left figure) and the asymptotically adS (right figure) black holes when the metric function has one real positive root (\(r_{1}\)) (the same as Schwarzschild black hole)

Full size image
Fig. 6
figure 6

Carter–Penrose diagram for the asymptotically flat (left figure) and the asymptotically adS (right figure) black holes when the metric function has two real positive roots (\(r_{1}\) and \(r_{2}\)) (second root is an extreme root)

Full size image
Fig. 7
figure 7

Carter–Penrose diagram for the asymptotically flat (left figure) and the asymptotically adS (right figure) black holes when the metric function has three real positive roots (\(r_{1}\), \(r_{2}\) and \(r_{3}\))

Full size image

The temperature may be obtained through the use of regularity of the solutions at \(r=r_{+}\), yielding

(17)

The electric potential \(\Phi \), measured at infinity with respect to the horizon, is defined by [84, 85]

$$\begin{aligned} \Phi =A_{\mu }\chi ^{\mu }\mid _{r\rightarrow \infty }-A_{\mu }\chi ^{\mu }\mid _{r=r_{+}}, \end{aligned}$$
(18)

with the following explicit form

$$\begin{aligned} \Phi =\frac{q}{\left( n-2\right) r_{+}^{n-2}}-\frac{4q^{3}}{\left( 3n-4\right) r_{+}^{3n-4}}\alpha +O\left( \alpha ^{2}\right) . \end{aligned}$$
(19)

The last term in the right hand side of Eqs. (17) and (19) indicates the nonlinearity effect of the mentioned NLED.

3 Thermodynamics of asymptotically flat black hole (\(\Lambda =0, \, k=1 \))

At first, we calculate the conserved and thermodynamic quantities of the black hole for \(\Lambda =0\) and \(k=1\). Second, we obtain a Smarr-type formula for the mass as a function of the entropy and the electric charge of the solutions and finally check the first law of thermodynamics.

The first quantity which we are going to calculate is the entropy of the black hole. More than 30 years ago, Bekenstein argued that the entropy of a black hole in Einstein gravity is a linear function of the area of its event horizon, which is the area law [86, 87]. Therefore, the entropy per unit volume \(V_{n-1}\) of the presented black hole is equal to one-quarter of the area of the horizon

$$\begin{aligned} S=\frac{r_{+}^{n-1}}{4}. \end{aligned}$$
(20)

In order to obtain the electric charge per unit volume \(V_{n-1}\) of the black hole, we use the flux of the electric field at infinity, yielding

$$\begin{aligned} Q=\frac{q}{4\pi }, \end{aligned}$$
(21)

which shows that, this kind of nonlinearity does not change the electric charge. The Arnowitt–Deser–Misner (ADM) mass of black hole can be obtained by using the behavior of the metric at large \(r\). The mass per unit volume \(V_{n-1}\) of the black hole is

$$\begin{aligned} M=\frac{\left( n-1\right) m}{16\pi }, \end{aligned}$$
(22)

where we can obtain \(m\) from \(f(r=r_{+})=0\).

After calculating all of the conserved and thermodynamic quantities of the black hole solutions, we want to investigate the first law of thermodynamics. To do this, we obtain the total mass \(M\) as a function of the extensive quantities \(Q\) and \(S\). Using the expression for the entropy, the electric charge and the mass given in Eqs. (20), (21) and (22), and the fact that \(f(r=r_{+})=0\), one can obtain a Smarr-type formula as

$$\begin{aligned} M\left( S,Q\right) =\frac{\left( n-1\right) \Upsilon ^{n-2}}{16\pi }+\frac{2\pi Q^{2}}{\left( n-2\right) \Upsilon ^{n-2}}\nonumber \\ -\frac{64\pi ^{3}Q^{4}}{\left( 3n-4\right) \Upsilon ^{3n-4}}\alpha +O\left( \alpha ^{2}\right) , \end{aligned}$$
(23)

where \(\Upsilon =\left( 4S\right) ^{1/\left( n-1\right) }\).

Now, we regard the parameters \(Q\) and \(S\) as a complete set of extensive parameters and define the intensive parameters conjugate to them. These quantities are the temperature and the electric potential

$$\begin{aligned} T\!=\!\left( \frac{\partial M}{\partial S}\right) _{Q}\!&= \!\frac{n\left( n-1\right) \left( n-2\right) \Upsilon ^{n-2}}{16\pi n\left( n-1\right) S}-\frac{2\pi Q^{2}}{S\left( n-1\right) \Upsilon ^{n-2}}\nonumber \\&\quad +\frac{64\pi ^{3}Q^{4}}{S\left( n-1\right) \Upsilon ^{3n-4}}\alpha \!+\!O\left( \alpha ^{2}\right) , \end{aligned}$$
(24)
$$\begin{aligned} \Phi \!=\!\left( \frac{\partial M}{\partial Q}\right) _{S}&= \frac{4\pi Q}{\left( n-2\right) \Upsilon ^{n-2}}-\frac{256\pi ^{3}Q^{3}}{\left( 3n-4\right) \Upsilon ^{3n-4}}\alpha \nonumber \\&\quad +O\left( \alpha ^{2}\right) . \end{aligned}$$
(25)

Using Eqs. (20) and (21), one can show that the Eqs. (24) and (25) are equal to Eqs. (17) and (19), respectively. Thus, these quantities satisfy the first law of thermodynamics

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+\Phi \mathrm{d}Q. \end{aligned}$$
(26)

3.1 Stability of the solutions

In what follows, we want to investigate the local stability of the charged black hole solutions of Einstein gravity in the presence of NLED in the canonical and the grand canonical ensembles. In principle the local stability can be carried out by finding the determinant of the Hessian matrix of \(M(X_{i})\) with respect to its extensive variables \( X_{i}\), \(H_{X_{i}X_{j}}^{M}=\left[ \partial ^{2}M/\partial X_{i}\partial X_{j}\right] \) [84, 85]. In our case the mass \(M\) is a function of the entropy \(S\) and the charge \(Q\). The number of thermodynamic variables depends on the ensemble that is used. In the canonical ensemble, the positivity of the heat capacity \(C_{Q}=T_{+}/\left( \partial ^{2}M/\partial S^{2}\right) _{Q}\) is sufficient to ensure the local stability. Since \(T_{+}\) should be a positive definite quantity for physical black holes, it is sufficient to check the sign of \(\left( \partial ^{2}M/\partial S^{2}\right) _{Q}\)

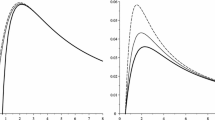
$$\begin{aligned} \left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}&= -\frac{(n-2)}{\pi \left( n-1\right) r_{+}^{n}}+\frac{2\left( 2n-3\right) q^{2}}{\pi \left( n-1\right) ^{2}r_{+}^{3n-4}}\nonumber \\&\quad -\frac{4\left( 4n-5\right) q^{4}}{\pi \left( n-1\right) ^{2}r_{+}^{5n-6}}\alpha +O\left( \alpha ^{2}\right) . \end{aligned}$$
(27)

Considering Eq. (27), we find that the first and second terms are related to the Einstein–Maxwell gravity and third one is related to the effect of nonlinearity. In order to find the effects of nonlinearity on the stability of the solutions, we plot Figs. 8 and 9. These figures show that there is a lower limit, \(r_{+\mathrm{min}}\), for the horizon radius of physical black holes (positive temperature). In addition, considering Figs. 8 and 9, one finds large physical black holes are not stable. In other words, one can obtain asymptotically flat stable black holes when the horizon radius satisfies \(r_{+\mathrm{min}}<r_{+}<r_{+\mathrm{max}}\), in which the values of \(r_{+\mathrm{min}}\) and \(r_{+\mathrm{max}}\) depend on \(n\), \(q\) and \(\alpha \). Although Fig. 8 shows that decreasing \(\alpha \) leads to increasing \(r_{+\mathrm{min}}\) (slightly increasing \(r_{+\mathrm{max}}\)), Fig. 9 indicates that decreasing \(q\) leads to decreasing both \(r_{+\mathrm{min}}\) and \(r_{+\mathrm{max}}\).

Fig. 8
figure 8

Asymptotically flat solutions: \(10^{-4} \times \left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}\) (thin lines) and \(T_{+}\) (bold lines) versus \(r_{+}\) for \(n=4\), \(q=0.01\), \(\alpha =10^{-5}\) (solid line), \(\alpha =5 \times 10^{-5}\) (dotted line) and \(\alpha =10 \times 10^{-5}\) (dashed line)

Full size image
Fig. 9
figure 9

Asymptotically flat solutions: \(\left( \frac{\partial ^{2}M}{ \partial S^{2}}\right) _{Q}\) (thin lines) and \(\frac{T_{+}}{10}\) (bold lines) versus \(r_{+}\) for \(n=4\), \(\alpha =10^{-4}\), and \(q=10\) (solid line), \(q=10.5\) (dotted line) and \(q=11\) (dashed line)

Full size image

In the grand canonical ensemble, after some algebraic manipulations, we obtain

$$\begin{aligned} H_{S,Q}^{M}&= \frac{1}{\left( n-1\right) ^{2}}\left\{ -\frac{4\left[ \left( n-1\right) \left( n-2\right) -2q^{2}r_{+}^{4-2n}\right] }{\left( n-2\right) r_{+}^{2n-2}} \right. \nonumber \\&\left. \quad + \frac{16q^{2}\left[ 3\left( n-1\right) \left( n-2\right) ^{2}r_{+}^{4-4n}-\left( 7n-8\right) q^{2}r_{+}^{8-6n}\right] \alpha }{\left( n-2\right) \left( 3n-4\right) }\right. \nonumber \\&\left. \quad +O(\alpha ^{2})\right\} , \end{aligned}$$
(28)

where the last term is the nonlinearity effect of NLED. Regardless of the values of \(n\), \(q\) and \(\alpha \), we can write

$$\begin{aligned} \left. H_{S,Q}^{M}\right| _{\text {Small }r_{+}}&= -\frac{16\left( 7n-8\right) q^{4}\alpha }{\left( n-2\right) \left( 3n-4\right) r_{+}^{6n-8}} <0, \end{aligned}$$
(29)
$$\begin{aligned} \left. H_{S,Q}^{M}\right| _{\text {Large }r_{+}}&= -\frac{4}{\left( n-1\right) r_{+}^{2n-2}}<0, \end{aligned}$$
(30)

which, in agreement with the canonical ensemble, confirm that the horizon radius of asymptotically flat stable black holes should satisfy \(r_{+\mathrm{min}}<r_{+}<r_{+\mathrm{max}}\).

4 Thermodynamics of asymptotically adS rotating black branes with flat horizon (\(k=0\))

Now, we want to endow our spacetime solutions (5) for \(k=0\) with global rotation parameters. In order to supplement angular momentum to the spacetime, we perform the following rotation boost in the \(t-\phi _{i}\) plane

$$\begin{aligned} \begin{array}{ll} t\longmapsto \Xi t-a_{i}\phi _{i},&\quad \phi _{i}\longmapsto \Xi \phi _{i}- \frac{a_{i}}{l^{2}}t. \end{array} \end{aligned}$$
(31)

Thus the metric of \((n+1)\)-dimensional asymptotically adS rotating spacetime with \(p\) rotation parameters can be written as

$$\begin{aligned} \mathrm{d}s^{2}&= -f(r)\left( \Xi \mathrm{d}t-\sum \limits _{i=1}^{p}a_{i}\mathrm{d}\phi _{i}\right) ^{2}\nonumber \\&\quad +\frac{r^{2}}{l^{4}}\sum \limits _{i=1}^{p}\left( a_{i}\mathrm{d}t-l^{2}\Xi \mathrm{d}\phi _{i}\right) ^{2} \nonumber \\&\quad +\,\frac{\mathrm{d}r^{2}}{f(r)}-\frac{r^{2}}{l^{2}}\sum \limits _{i=1}^{p}\left( a_{i}\mathrm{d}\phi _{j}-a_{j}\mathrm{d}\phi _{i}\right) ^{2}\nonumber \\&\quad +\,r^{2}\sum \limits _{i=p+1}^{n-1}\mathrm{d}x_{i}^{2}, \end{aligned}$$
(32)

where \(\Xi =\sqrt{1+\sum _{i=1}^{p}a_{i}^{2}/l^{2}}\). Using Eq. (4), one can show that the suitable gauge potential can be written as

$$\begin{aligned} A_{\mu }=h(r)\left( \Xi \delta _{\mu }^{0}-a_{i}\delta _{\mu }^{i}\right) \quad (\text {no sum on i}), \end{aligned}$$
(33)

where \(h(r)\) is the same as that in Eq. (11). Now, we want to obtain the metric function \(f(r)\) for the spacetime (32) by inserting Eqs. (32) and (33) into (3). After some simplifications, we find that the nonzero components of the gravitational field equations lead to four different differential equations \(e_{11}\), \(e_{22}\), \(e_{33}\) and \(e_{44}\) for the unknown function \(f(r)\), in which

$$\begin{aligned} e_{11}&= \left. e_{1}\left( \mathrm{static}\ \mathrm{case}\right) \right| _{k=0\!}, \end{aligned}$$
(34)
$$\begin{aligned} e_{33}&= \left. e_{2}\left( \mathrm{static}\ \mathrm{case}\right) \right| _{k=0}\!, \end{aligned}$$
(35)
$$\begin{aligned} e_{33}&= \left[ \left. e_{2}\left( \mathrm{static}\ \mathrm{case}\right) \right| _{k=0} \right] (\Xi ^{2}-1)\nonumber \\&\quad -l^{2} f(r) \Xi ^{2}\left[ \left. e_{1}\left( \mathrm{static}\ \mathrm{case}\right) \right| _{k=0}\right] , \end{aligned}$$
(36)
$$\begin{aligned} e_{44}&= \sqrt{\Xi ^{2}-1} \left\{ \left[ \left. e_{1} \left( \mathrm{static}\ \mathrm{case}\right) \right| _{k=0}\right] \frac{f(r)}{2r^{2}}\right. \nonumber \\&\quad \left. -\frac{1}{2l^{2}} \left[ \left. e_{2} \left( \mathrm{static}\ \mathrm{case}\right) \right| _{k=0}\right] \right\} . \end{aligned}$$
(37)

Considering Eqs. (34) and (37), we find that the metric function (14) with \(k=0\) satisfies all field equations. Straightforward calculations confirm that the mentioned rotating spacetime has a curvature singularity at \(r=0\), which may be covered with an event horizon. We can obtain the temperature and the angular velocity of the event horizon by analytic continuation of the metric function (32) and its regularity at the horizon \(r_{+}\). One obtains

$$\begin{aligned} T_{+}=\left. \frac{T_{+}\left( \mathrm{static}\ \mathrm{case}\right) }{\Xi }\right| _{k=0}, \end{aligned}$$
(38)

and

$$\begin{aligned} \Omega _{i}=\frac{a_{i}}{l^{2}\Xi }. \end{aligned}$$
(39)

Considering the fact that \(\chi =\partial _{t}+\sum _{i=1}^{p}\Omega _{i} \, \partial _{\phi _{i}}\) is the null Killing generator of the horizon and using Eq. (18), one can find the electric potential as

$$\begin{aligned} \Phi = \frac{\Phi \left( \mathrm{static}\ \mathrm{case}\right) }{\Xi }. \end{aligned}$$
(40)

Here, we calculate other conserved and thermodynamic quantities of the black brane solutions. Like previous section and with the same approaches, one can show that the entropy and the electric charge per unit volume \(V_{n-1}\) of the presented black branes are, respectively, given by

$$\begin{aligned} S=\frac{\Xi r_{+}^{n-1}}{4}, \end{aligned}$$
(41)

and

$$\begin{aligned} Q=\frac{q\Xi }{4\pi }. \end{aligned}$$
(42)

Now, we should calculate the finite mass. In general, the action \(I_{G}\), diverges when evaluated on the solutions, as the Hamiltonian and other associated conserved quantities. To compute the conserved charges of the asymptotically adS solutions of Einstein gravity, we use the counterterm method [88–94]. This method was inspired by the adS/conformal field theory correspondence and consists in adding suitable counterterm \(I_{\mathrm{ct}}\) to the action \(I_{G}\) in order to ensure the finiteness of the boundary stress tensor derived by the quasilocal energy definition [95]. For asymptotically adS solutions of Einstein gravity with flat boundary, the suitable counterterm \(I_{\mathrm{ct}}\) is given by

$$\begin{aligned} I_{\mathrm{ct}}=-\frac{1}{8\pi }\int _{\partial \mathcal {M}}\mathrm{d}^{n}x\sqrt{-\gamma } \left( \frac{n-1}{l}\right) . \end{aligned}$$
(43)

Varying the total action (\(I_{\mathrm{tot}}=I_{G}+I_{\mathrm{ct}}\)) with respect to the induced metric \(\gamma _{ab}\), we find the boundary stress-tensor as

$$\begin{aligned} T^{ab}=\frac{1}{8\pi }\left[ \Theta ^{ab}-\left( \Theta +\frac{n-1}{l} \right) \gamma ^{ab}\right] . \end{aligned}$$
(44)

Now, we choose a spacelike surface \(\mathcal {B}\) in \(\partial \mathcal {M}\) with metric \(\sigma _{ij}\), and write the boundary metric in ADM form

$$\begin{aligned} \gamma _{\mu \nu }\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }\!=\!-\!N^{2}\mathrm{d}t^{2}\!+\!\sigma _{ij}\left( \mathrm{d}\varphi ^{i}\!+\!V^{i}\mathrm{d}t\right) \left( \mathrm{d}\varphi ^{j}\!+\!V^{j}\mathrm{d}t\right) ,\nonumber \\ \end{aligned}$$
(45)

where the coordinates \(\varphi ^{i}\) are the angular variables parameterizing the hypersurface of constant \(r\) around the origin, and \(N\) and \(V^{i}\) are the lapse and shift functions, respectively. When there is a Killing vector field \(\xi \) on the boundary, then the quasilocal conserved quantities associated with the stress energy momentum tensor of Eq. (44) can be calculated as

$$\begin{aligned} Q\left( \xi \right) =\int _{\mathcal {B}}\mathrm{d}^{n-2}\varphi \sqrt{\sigma } T_{ab}n^{a}\xi ^{b}, \end{aligned}$$
(46)

where \(\sigma \) is the determinant of the metric \(\sigma _{ij}\), and \(n^{a}\) is the timelike unit normal vector to the boundary \(\mathcal {B}\). The conserved quantities associated to the timelike \(\xi =\partial _{t}\) and rotational \(\zeta =\partial _{\phi _{i}}\) Killing vector fields are

$$\begin{aligned} M&= \int _{\mathcal {B}}\mathrm{d}^{n-2}\varphi \sqrt{\sigma }T_{ab}n^{a}\xi ^{b}=\frac{V_{n-1}}{16\pi }m\left( n\Xi ^{2}-1\right) , \end{aligned}$$
(47)
$$\begin{aligned} J_{i}&= \int _{\mathcal {B}}\mathrm{d}^{n-2}\varphi \sqrt{\sigma }T_{ab}n^{a}\zeta ^{b}= \frac{V_{n-1}}{16\pi }n\Xi ma_{i}, \end{aligned}$$
(48)

which are the mass and the angular momentum of the system enclosed by the boundary \(\mathcal {B}\). To check the first law of thermodynamics, we obtain the total mass \(M\) as a Smarr-type formula

$$\begin{aligned} M\left( S,J,Q\right) =\frac{\left( nZ-1\right) J}{nl\sqrt{Z\left( Z-1\right) }}, \end{aligned}$$
(49)

where \(J_{i}=\sum _{i}J_{i}^{2}\) and \(Z=\Xi ^{2}\) is the positive real root of the following equation

$$\begin{aligned}&\frac{2\Lambda \Psi ^{-2}}{n\left( n-1\right) }+\frac{16\pi J\Psi ^{n-2}}{nl \sqrt{Z\left( Z-1\right) }}-\frac{32\pi ^{2}Q^{2}\Psi ^{2n-4}}{\left( n-1\right) \left( n-2\right) Z}\nonumber \\&\quad +\frac{1024\pi ^{4}Q^{4}\Psi ^{4n-6}}{\left( n-1\right) \left( 3n-4\right) Z^{2}}\alpha +O\left( \alpha ^{2}\right) =0, \end{aligned}$$
(50)

with \(\Psi =\left[ \sqrt{Z}\left( 4S\right) ^{-1}\right] ^{1/(n-1)}\). It is a matter of straightforward calculation to show that the conserved and thermodynamic quantities satisfy the first law of thermodynamics

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+\sum _{i}\Omega _{i} \mathrm{d}J_{i}+\Phi \mathrm{d}Q. \end{aligned}$$
(51)

In other words, the quantities \(T=\left( \frac{\partial M}{\partial S} \right) _{J,Q}\), \(\Omega _{i}=\left( \frac{\partial M}{\partial J_{i}} \right) _{S,Q}\) and \(\Phi =\left( \frac{\partial M}{\partial Q}\right) _{J,S}\) are the same as those calculated in Eqs. (38), (39) and (40), respectively.

4.1 Stability of the solutions

The final step is devoted to analyzing the local stability of charged rotating black brane solutions of Einstein gravity in the presence of NLED. We use the similar theoretical manner as was discussed in the Sect. (3) and investigate thermal stability in both the canonical and the grand canonical ensembles. In the canonical ensemble, the electric charge and the angular momenta are fixed parameters, and \(\left( \partial ^{2}M/\partial S^{2}\right) _{J,Q}\) at constant charge and angular momenta is

$$\begin{aligned} \left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{J,Q}&= \frac{C_{1}}{C_{2} }+\frac{C_{3}}{C_{4}}\alpha +O\left( \alpha ^{2}\right) , \end{aligned}$$
(52)
$$\begin{aligned} C_{1}&= -2\left\{ n\left[ 3(n-2)\Xi ^{2}-n+3\right] q^{4}r_{+}^{-3n+6} \right. \nonumber \\&+2\left[ 3(n-2)\Xi ^{2}-n^{2}+3\right] \Lambda q^{2}r_{+}^{-n+4} \nonumber \\&+\left. (n-2)\left[ (n+2)\Xi ^{2}-n-1\right] \Lambda ^{2}r_{+}^{n+2}\right\} ,\nonumber \\\end{aligned}$$
(53)
$$\begin{aligned} C_{2}&= (n-1)\pi \Xi ^{2}\left[ (n-2)\Xi ^{2}+1\right] \nonumber \\&\times \left[ (n-2)\Lambda r_{+}^{2n}-nq^{2}r_{+}^{2}\right] ,\end{aligned}$$
(54)
$$\begin{aligned} C_{3}&= -4q^{4}\left\{ n^{2}\left[ (17n^{2}-54n+40)\Xi ^{2}\right. \right. \nonumber \\&\left. \left. -n(5n-23)-20 \right] q^{4}r_{+}^{-5n+10}\right. \nonumber \\&-2n(n-2)\left[ (13n^{2}-50n+40)\Xi ^{2}\right. \nonumber \\&\left. -n(n-19)-20\right] \Lambda q^{2}r_{+}^{-3n+8} \nonumber \\&+\left. (n-2)^{2}\left[ (5n^{2}-42n+40)\Xi ^{2}\right. \right. \nonumber \\&\left. \left. +n(7n+11)-20\right] \Lambda ^{2}r_{+}^{-n+6}\right\} ,\end{aligned}$$
(55)
$$\begin{aligned} C_{4}&= (n-1)(3n-4)\pi \Xi ^{2}\left[ (n-2)\Xi ^{2}+1\right] \nonumber \\&\times \left[ (n-2)\Lambda r_{+}^{2n}-nq^{2}r_{+}^{2}\right] ^{2}, \end{aligned}$$
(56)

where in the Eq. (52) the first term is related to the Einstein–Maxwell gravity.

Fig. 10
figure 10

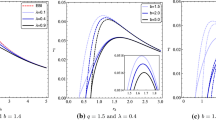
Asymptotically adS solutions: \(\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q,J}\) (thin lines) and \(\frac{T_{+}}{10}\) (bold lines) versus \(r_{+}\) for \(n=4\), \(q=100\), \(\Xi =1.1\) and \(\Lambda =-1\), and \(\alpha =0.001\) (solid line), \(\alpha =0.02\) (dotted line) and \(\alpha =0.05\) (dashed line)

Full size image
Fig. 11
figure 11

Asymptotically adS solutions: \(\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q,J}\) (thin lines) and \(\frac{T_{+}}{10}\) (bold lines) versus \(r_{+}\) for \(n=4\), \(q=100\) and \(\Lambda =-1\), \(\alpha =10^{-5}\) with \(\Xi =1.1\) (solid line), \(\Xi =1.2\) (dotted line) and \(\Xi =1.3\) (dashed line)

Full size image

Here, we plot Figs. 10 and 11 to investigate the nonlinearity as well as rotation effects. These figures show that for suitable fixed values of the metric parameters, there is an \(r_{+\mathrm{min}}\), in which for \(r_{+}>r_{+\mathrm{min}}\) we can obtain physical asymptotically adS rotating stable black brane solutions. In other words, we find that, unlike the asymptotically flat solutions, the asymptotically adS rotating large black brane solutions are stable. Considering Fig. 11, one may find the rotation parameter affects on the values of both \(T_{+}\) and \(\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{J,Q}\).

In the grand canonical ensemble, one can show that the determinant of the Hessian matrix has the following form

$$\begin{aligned} H_{S,Q,J}^{M}&= \frac{64\pi \left( q^{2}-\Lambda r_{+}^{2n-2}\right) }{B_{1}}\nonumber \\&\quad - \frac{B_{2}}{B_{1}(3n-4)\left[ nq^{2}-(n-2)\Lambda r_{+}^{2n-2}\right] r_{+}^{2n-2}}\alpha \nonumber \\&\quad +O\left( \alpha ^{2}\right) ,\end{aligned}$$
(57)
$$\begin{aligned} B_{1}&= l^{2}\Xi ^{6}\left[ \left( n-2\right) \Xi ^{2}+1\right] \left[ nq^{2}-(n-2)\Lambda r_{+}^{2n-2}\right] \nonumber \\&\quad \times r_{+}^{3n-4},\end{aligned}$$
(58)
$$\begin{aligned} B_{2}&= 256\pi q^{2}\left[ 3(n-2)^{2}\Lambda ^{2}r_{+}^{4n-4}+3n(n-1)q^{4}\right. \nonumber \\&\quad \left. -2(n-2)(3n-2)\Lambda q^{2}r_{+}^{2n-2}\right] , \end{aligned}$$
(59)

where in the Eq. (57) the first term is the determinant of Hessian matrix of Einstein–Maxwell gravity and the last term indicates the nonlinearity effect. Following the method of previous section and regardless of the values of \(n, \, q, \, \Lambda , \, \Xi \) and \(\alpha \), one finds

$$\begin{aligned}&\left. H_{S,Q,J}^{M}\right| _{\text {Small }r_{+}}\nonumber \\&\quad =-\frac{768\pi (n-1)q^{2}\alpha }{n(3n-4)l^{2}\Xi ^{6}\left[ \left( n-2\right) \Xi ^{2}+1\right] r_{+}^{5n-6}}<0, \end{aligned}$$
(60)
$$\begin{aligned}&\left. H_{S,Q,J}^{M}\right| _{\text {Large }r_{+}}\nonumber \\&\quad =\frac{64\pi }{(n-2)l^{2}\Xi ^{6}\left[ \left( n-2\right) \Xi ^{2}+1\right] r_{+}^{3n-4}}>0, \end{aligned}$$
(61)

which are in agreement with results of the canonical ensemble and confirm that large black branes are stable.

In order to analyze the correctness of our discussions for stability criterion of asymptotically flat and adS black objects, we should argue for the validity of numerical calculations. Regarding Eq. (10), we find that higher order terms of electric field can be formed by increasing \(j\) in \(\left( \frac{q}{r_{+}^{n-1}}\right) ^{(2j+1)}\alpha ^{j}\) (\(j=0,1,2,\ldots \)). Therefore, ignoring the higher order terms of \(\alpha \) makes sense, if increasing \(j\) leads to reasonable decreasing of \(\left( \frac{q}{r_{+}^{n-1} }\right) ^{(2j+1)}\alpha ^{j}\). In the following tables, we consider the numerical calculations of Figs. 8, 9, 10 and 11 (Table 1).

Table 1 Left table: asymptotically flat solutions and right table: asymptotically adS solutions
Full size table

Taking into account the numerical results of the tables, one can confirm that numerical calculations of stability conditions for both asymptotically flat and adS black objects are logical.

5 Conclusions

Motivated by the (quartic) string corrections of Maxwell field strength, at first, we obtained black hole solutions of Einstein-NLED gravity with various horizon topology and investigated their geometric properties. Then, we fixed \(\Lambda =0\) and \(k=1\) to calculate the conserved quantities of the asymptotically flat black holes. We obtained a Smarr-type formula for the mass as a function of the entropy and the electric charge of the solutions and checked the first law of thermodynamics. We studied the stability analysis of the asymptotically flat black holes both in the canonical and the grand canonical ensembles and investigated the effects of NLED. We found that for the fixed values of \(n\), \(q\) and \(\alpha \), small and large physical black holes are not stable. It means that obtained asymptotically flat black holes can be stable when the horizon radius satisfies \(r_{+\mathrm{min}}<r_{+}<r_{+\mathrm{max}}\), in which the values of \(r_{+\mathrm{min}}\) and \(r_{+\mathrm{max}}\) depend on the metric parameters. In addition, we found that although decreasing the nonlinearity parameter leads to increasing \(r_{+\mathrm{min}}\) (slightly increasing \(r_{+\mathrm{max}}\)), decreasing the charge parameter leads to decreasing both \(r_{+\mathrm{min}}\) and \(r_{+\mathrm{max}}\).

After that, we considered the horizon-flat solutions and used a suitable rotation boost to endow angular momentum to the asymptotically adS spacetime. Using the counterterm method, we obtained the conserved quantities of the asymptotically adS black branes. We also obtained a Smarr-type formula for the finite mass as a function of the other quantities and showed that they satisfy the first law of thermodynamics. Besides, we performed a stability analysis of the rotating solutions both in the canonical and the grand canonical ensembles. We showed that there is a lower limit, \(r_{+\mathrm{min}}\), for the physical solutions (positive temperature). Stability analysis of both ensembles confirmed that, unlike the asymptotically flat solutions with spherical horizon, the horizon-flat asymptotically adS rotating black brane solutions with large event horizon are stable. In other words, we showed that there is an \(r_{+\mathrm{min}}\) for suitable fixed values of the metric parameters, in which for \(r_{+}>r_{+\mathrm{min}}\), the asymptotically adS rotating black brane solutions are stable. Moreover, we fixed the values of \(n\), \(\Lambda \), \(\alpha \) and \(q\) to analyze the rotation’s effect on the stability conditions. We showed that although \(\Xi \) does not change the location of \(r_{+\mathrm{min}}\), it can change the values of the temperature, the heat capacity and the determinant of Hessian matrix.

It is notable that due to the negative temperature, the small black holes/branes are not physical and we should restrict the horizon radius to \( r_{+}>r_{+\mathrm{min}}\), while (in)stability of large ones is related to their horizon geometries. In other words, large black holes (branes) with \(k=1\) (\(k=0\)) are unstable (stable).

Finally, it was seen that the nonlinearity part not only modified electromagnetic part of the solutions, but also the kind of horizons and thermodynamics properties. In absence of of correction part, with suitable choices of parameters, metric function could acquire two horizons whereas, for this nonlinear theory, it is possible to find three horizons. This fact has some application regarding anti-evaporation of black holes/branes. The structure of black hole in presence of NLED is quite different comparing to the linear Maxwell theory and its phenomenology is also describing a more general case. In addition, it is worthwhile to mention that considering the first order effects of NLED changed the properties of the black objects at small distances. In other words, this generalization changed timelike singularity of Reissner–Nordström black holes to spacelike singularity. Hence, in order to recover the properties of the Reissner–Nordström black holes, it may be logical to keep terms only upto quadratic order of \(\alpha \) in the series expansions. Besides, it is notable that one can consider asymptotically adS black holes with spherical \((k=1)\) and hyperbolic topologies \((k=-1)\), to investigate \(P-V\) criticality in the extended phase space of the solutions by calculating the Gibbs free energy for various \(\Lambda \). These extensions are under examination.