The multi-level and multi-dimensional quantum wavelet packet transforms

Abstract

The classical wavelet packet transform has been widely applied in the information processing field. It implies that the quantum wavelet packet transform (QWPT) can play an important role in quantum information processing. In this paper, we design quantum circuits of a generalized tensor product (GTP) and a perfect shuffle permutation (PSP). Next, we propose multi-level and multi-dimensional (1D, 2D and 3D) QWPTs, including a Haar QWPT (HQWPT), a D4 QWPT (DQWPT) based on the periodization extension and their inverse transforms for the first time, and prove the correctness based on the GTP and PSP. Furthermore, we analyze the quantum costs and the time complexities of our proposed QWPTs and obtain precise results. The time complexities of HQWPTs is at most 6 on 2ⁿ elements, which illustrates high-efficiency of the proposed QWPTs. Simulation experiments demonstrate that the proposed QWPTs are correct and effective.

Introduction

With the rapid development in the fields of optical imaging, Internet technology, high performance calculation etc., the amount of data is increasing explosively, so that it is necessary to find new ways to store and process information. Quantum information processing (QIP)¹ as new technology of information processing, offers a potential solution to store and process massive visual data efficiently. QIP has two outstanding merits: (1) the unique computing performance of quantum coherence, entanglement and superposition [1], and (2) quantum storage capacity increasing exponentially. Models of quantum image representation^{2,3,4,5,6,7,8} have displayed the enormous storage capacity of QIP. Other popular quantum algorithms, such as the Shor’s discrete logarithms and integer-factoring algorithms⁹, the Deutsch’s parallel computing algorithm¹⁰ and the Grover’s quadratic speed up algorithm¹¹, have further shown that QIP is more efficient than its classical counterparts. In addition, many algorithms of QIP emerge continually, and these algorithms include quantum geometric transformation^12,13,14, quantum image encryption and decryption algorithms^15,16, quantum watermarking¹⁷, quantum image compression⁶, quantum edge detection¹⁸, and quantum image filtering¹⁹.

The classical wavelet packet transform (WPT) has been widely spread to the information processing field for image coding²⁰, pattern matching²¹ and fractional brownian motion decorrelation²². It indicates that the quantum wavelet packet transform (QWPT) plays an important role in QIP. Unfortunately, the research on QWPT is rare and still preliminary. For example, two important QWPTs, namely the Haar QWPT (HQWPT) and the D4 QWPT (DQWPT) proposed in^23,24,25,26, are still single level quantum wavelet transforms. Up to now, we have not yet found any implementation of a multi-level and multi-dimensional QWPT. Therefore, we believe that QWPTs deserve further research.

In this paper, we introduce the generalized tensor product (GTP) and the perfect shuffle permutation (PSP), and design quantum circuits for them. Then, we propose the iterations and implementation circuits of the multi-level and multi-dimensional QWPT and inverse QWPT (IQWPT). QWPTs and the inverse QWPTs being considered include HQWPT, DQWPT based on a periodization extension, the inverse HQWPT (IHQWPT), the inverse DQWPT (IDQWPT). In addition, we analyze the quantum costs and time complexities of the proposed circuits and prove that the multi-level and multi-dimensional HQWPT can be implemented with a complexity of O(1). Simulation experiments demonstrate that the proposed QWPTs are correct and effective.

The contributions of this paper are listed as follows.

• We analyze precisely the complexities of the simulated networks of controlled NOT gates with multi-control qubits. Comparing with the methods proposed in the reference²⁷, our proposed simulated networks are reduced by 50% approximately.

• We design the simplified circuits of the PSP and reduce time complexity to 6 for 2ⁿ elements.

• We present the multi-level and multi-dimensional QWPTs, including HQWPT, IHQWPT, DQWPT and IDQPT for the first time, and prove the correctness by theoretical derivations and simulation experiments.

• We design the circuits of the multi-level and multi-dimensional HQWPT with the complexity O(1), which has the overwhelming advantage over the classic Haar WPT.

The Quantum Implementation of GTP

Let A be an n × n matrix and B be an m × m matrix, then the tensor product $A\otimes B$ is an mn × mn block matrix in the following equation,

$$A\otimes B=[\begin{array}{ccc}{A}_{0,0}B & \cdots & {A}_{0,n-1}B\\ \vdots & \ddots & \vdots \\ {A}_{n-1,0}B & \cdots & {A}_{n-1,n-1}B\end{array}].$$

(1)

Thus, the tensor product of quantum states are defined as the tensor product of matrices: $|u\rangle \otimes |v\rangle ={[{u}_{0}\cdots {u}_{{2}^{n}-1}]}^{T}\otimes {[{v}_{0}\cdots {v}_{{2}^{n}-1}]}^{T}$, which is also written simply as $|u\rangle$ $|v\rangle$ or $|uv\rangle$.

Then, n fold tensor product $U\otimes U\otimes \cdots \otimes U$ is abbreviated as ${U}^{\otimes n}$. Similarly, the abbreviation of $|u\rangle \otimes |u\rangle \otimes \cdots \otimes |u\rangle$ is ${|u\rangle }^{\otimes n}$.

A larger vector space can be formed by putting vector spaces together. For instance, suppose that $|i\rangle$ is a basic state in a 2ⁿ dimensional Hilbert space for i = 0, 1, …, 2ⁿ − 1, the state $|i\rangle$ consists of the tensor products of the n computation basis states:

$$|i\rangle =|{i}_{n}\rangle \otimes |{i}_{n-1}\rangle \otimes \cdots \otimes |{i}_{1}\rangle =|{i}_{n}\rangle |{i}_{n-1}\rangle \cdots |{i}_{1}\rangle =|{i}_{n}{i}_{n-1}\ldots {i}_{1}\rangle ,$$

(2)

where $i={\sum }_{j=1}^{n}\,{i}_{j}\times {2}^{j-1}$ and i₁, i₂, …, i_n ∈ {0, 1}. Its dual state is

$$\langle i|=\langle {i}_{n}|\otimes \langle {i}_{n-1}|\otimes \cdots \otimes \langle {i}_{1}|=\langle {i}_{n}|\langle {i}_{n-1}|\cdots \langle {i}_{1}|=\langle {i}_{n}{i}_{n-1}\ldots {i}_{1}|.$$

(3)

There are some base gates and their corresponding symbols shown in Fig. 1. In the figure, the identity (I₂), Hadamard (H), Pauli-X (X) and Swap gates are well-known and can be found in the reference²⁸. The 2ⁿ × 2ⁿ identity matrix ${({I}_{2})}^{\otimes n}={I}_{{2}^{n}}$ denotes the circuit of n qubits. V and V⁺ are two specific examples of U gates where U corresponds to a unitary matrix and

$$V=\frac{1+i}{2}[\begin{array}{cc}1 & -i\\ -i & 1\end{array}],\,{V}^{+}=\frac{1-i}{2}[\begin{array}{cc}1 & i\\ i & 1\end{array}]\mathrm{.}$$

(4)

Figure 1

Notations for some base gates with their corresponding symbols.

A controlled gate is one of the most useful gates in quantum computing, and we define two controlled gates of (n + m)-qubits.

Definition 1.

Let ${U}_{{2}^{m}}$ be a 2^m × 2^m unitary matrix, ${I}_{{2}^{m}}$ be a 2^m × 2^m identity matrix. Then, controlled gates ${C}_{n}^{j}({U}_{{2}^{m}})$ and ${V}_{n}^{j}({U}_{{2}^{m}})$ with n control qubits and m target qubits are defined by

$${C}_{n}^{j}({U}_{{2}^{m}})=(|j\rangle \langle j|)\otimes {U}_{{2}^{m}}+\sum _{i=0,i\ne j}^{{2}^{n}-1}\,((|i\rangle \langle i|)\otimes {I}_{{2}^{m}}),$$

(5)

$${V}_{n}^{j}({U}_{{2}^{m}})=({U}_{{2}^{m}}\otimes |\,j\rangle \langle \,j|)+\sum _{i=0,i\ne j}^{{2}^{n}-1}\,({I}_{{2}^{m}}\otimes (|i\rangle \langle i|)),$$

(6)

where $|i\rangle =|{i}_{n}\,\cdots \,{i}_{2}{i}_{1}\rangle$ and $|j\rangle =|{j}_{n}\,\cdots \,{j}_{2}{j}_{1}\rangle$ are the basic states in a 2ⁿ dimensional Hilbert space shown in Eq. (2), and j ∈ {0, 1, …, 2ⁿ − 1}. The Notations of ${C}_{n}^{j}({U}_{{2}^{m}})$ and ${V}_{n}^{j}({U}_{{2}^{m}})$ are shown in (a) and (b) of Fig. 2. Furthermore, ${C}_{2}^{j}(X)$ and ${V}_{2}^{j}(X)$ are called Toffoli gates.

Figure 2

The (n + m) qubit controlled gates and the ${N}_{n+m}^{n}$ gate. The abbreviation notations are in the right parts of (a,b). The dashed box 1 and 2 in (c) implement ${C}_{n-1}^{j}(X)$ and ${C}_{n-1}^{j}(X)\otimes {I}_{{2}^{m-1}}$ where j = j_n−1 j_n−2 … j₁ and j_n−1, j_n−2, … j₁, j₀ ∈ {0, 1}.

Definition 2.

An (n + m) qubit controlled gate with n control qubits is named as an ${N}_{n+m}^{n}$ gate, when the X gate is in the target qubit of the controlled gate. An instance of an ${N}_{n+m}^{n}$ gate is shown in (c) of Fig. 2. In addition, the four ${N}_{2}^{1}$ gates shown in Fig. 3 are called controlled-NOT gates.

Figure 3

The four ${N}_{2}^{1}$ gates. The numbers 1 and 0 can be replaced by black and white points on control qubits.

A Swap gate can be simulated by three ${N}_{2}^{1}$ gates, that is, $Swap={C}_{1}^{0}(X){V}_{1}^{0}(X){C}_{1}^{0}(X)$.

Next, we introduce a perfect shuffle permutation. Let P_n,m be the mn × mn matrix of a perfect shuffle permutation, then P_n,m satisfies that (P_n,m)_k,l = δ_v,z′δ_z,v′ where k = vn + z, l = v′m + z′, 0 ≤ v, z′ < m, 0 ≤ v′, z < n, δ_x,y is the Kronecker delta function, that is, δ_x,y = 0 if x ≠ y, otherwise δ_x,y = 1. Therefore, P_n,m shuffles n packs of m cards into m packs of n cards.

As a useful tool for wavelet transforms, the GTP is defined as follows²⁹. Suppose that ${\mathscr{A}}=\{{A}^{0},{A}^{1},\ldots ,{A}^{m-1}\}$ and ${\mathcal B} =\{{B}^{0},{B}^{1},\ldots ,{B}^{n-1}\}$ are two sets of matrices, where Aⁱ is an n × n matrix, 0 ≤ i < m, and B^j is an m × m matrix, 0 ≤ j < n. Then, the generalized tensor product $C={\mathscr{A}}\otimes {\mathcal B}$ is an mn × mn matrix and can be calculated by

$$C={\mathscr{A}}\otimes {\mathcal B} ={P}_{m,n}Diag({\mathscr{A}}){P}_{n,m}Diag( {\mathcal B} ),$$

(7)

where $Diag({\mathscr{A}})=Diag({A}^{0},{A}^{1},\ldots ,{A}^{m-1})$ and $Diag( {\mathcal B} )=Diag({B}^{0},{B}^{1},\ldots ,{B}^{n-1})$ are block diagonal matrices.

Definition 3.

Let ${\mathscr{A}}=\{{A}^{0},{A}^{1},\ldots ,{A}^{m-1}\}$ and ${\mathscr{D}}=\{{D}^{0},{D}^{1},\ldots ,{D}^{m-1}\}$ be two sets of matrices where Aⁱ and Dⁱ are n × n matrices. Then, the generalized product is defined as ${\mathscr{A}}\times {\mathscr{D}}={\mathscr{A}}{\mathscr{D}}=\{{A}^{0}\times {D}^{0},{A}^{1}\times {D}^{1},\ldots ,{A}^{m-1}\times {D}^{m-1}\}$.

Definition 4.

The transpose, conjugate transpose and inverse of the matrix set ${\mathscr{A}}$ are defined as follows:

$$\{\begin{array}{l}{{\mathscr{A}}}^{T}=\{{({A}^{0})}^{T},{({A}^{1})}^{T},\ldots ,{({A}^{m-1})}^{T}\},\\ {{\mathscr{A}}}^{+}=\{{({A}^{0})}^{+},{({A}^{1})}^{+},\ldots ,{({A}^{m-1})}^{+}\},\\ {{\mathscr{A}}}^{-1}=\{{({A}^{0})}^{-1},{({A}^{1})}^{-1},\ldots ,{({A}^{m-1})}^{-1}\},\end{array}$$

where (Aⁱ)^T, (Aⁱ)⁺ and (Aⁱ)⁻¹ denote the transpose, conjugate transpose and inverse of matrix Aⁱ, respectively.

The following equations hold by using equation (7) and definitions 3 and 4.

$$\{\begin{array}{l}{({\mathscr{A}}\otimes {\mathcal B} )}^{T}={P}_{m,n}({ {\mathcal B} }^{T}\otimes {{\mathscr{A}}}^{T}){P}_{n,m},\\ {({\mathscr{A}}\otimes {\mathcal B} )}^{+}={P}_{m,n}({ {\mathcal B} }^{+}\otimes {{\mathscr{A}}}^{+}){P}_{n,m},\\ {({\mathscr{A}}\otimes {\mathcal B} )}^{-1}={P}_{m,n}({ {\mathcal B} }^{-1}\otimes {{\mathscr{A}}}^{-1}){P}_{n,m}.\end{array}$$

(8)

Let ${\mathscr{A}}$ and ${\mathscr{C}}$ be two sets of matrices containing m matrices with size n × n, ${\mathcal B}$ and ${\mathscr{D}}$ be two sets of matrices containing n matrices with size m × m, and I_m and I_n be m × m and n × n identity matrices, respectively. Then, the following equation holds²⁴:

$$({\mathscr{A}}\times {\mathscr{C}})\otimes ( {\mathcal B} \times {\mathscr{D}})=({\mathscr{A}}\otimes {I}_{m})\times ({\mathscr{C}}\otimes {\mathcal B} )\times ({I}_{n}\otimes {\mathscr{D}}),$$

(9)

and implies

$$\{\begin{array}{l}{\mathscr{A}}\otimes {\mathscr{D}}=({\mathscr{A}}\times {I}_{n})\otimes ({I}_{m}\times {\mathscr{D}})=({\mathscr{A}}\otimes {I}_{m})\times ({I}_{n}\otimes {\mathscr{D}}),\\ ({\mathscr{A}}\times {\mathscr{C}})\otimes {I}_{m}=({\mathscr{A}}\otimes {I}_{m})\times ({\mathscr{C}}\otimes {I}_{m}).\end{array}$$

(10)

Furthermore, calculating by the definition of a GTP, we can implement the following four GTPs using controlled gates:

$$\{\begin{array}{l}{I}_{2}\otimes \{{I}_{{2}^{n}},{U}_{{2}^{n}}\}=(|0\rangle \langle 0|)\otimes {I}_{{2}^{n}}+(|1\rangle \langle 1|)\otimes {U}_{{2}^{n}}={C}_{1}^{1}({U}_{{2}^{n}}),\\ {I}_{2}\otimes \{{U}_{{2}^{n}},{I}_{{2}^{n}}\}=(|0\rangle \langle 0|)\otimes {U}_{{2}^{n}}+(|1\rangle \langle 1|)\otimes {I}_{{2}^{n}}={C}_{1}^{0}({U}_{{2}^{n}})\\ \{{I}_{{2}^{n}},{U}_{{2}^{n}}\}\otimes {I}_{2}={I}_{{2}^{n}}\otimes (|0\rangle \langle 0|)+{U}_{{2}^{n}}\otimes (|1\rangle \langle 1|)={V}_{1}^{1}({U}_{{2}^{n}}),\\ \{{U}_{{2}^{n}},{I}_{{2}^{n}}\}\otimes {I}_{2}={U}_{{2}^{n}}\otimes (|0\rangle \langle 0|)+{I}_{{2}^{n}}\otimes (|1\rangle \langle 1|)={V}_{1}^{0}({U}_{{2}^{n}}).\end{array}$$

(11)

The Complexity Analysis of Quantum Circuits

The complexity analysis of quantsssum circuits

Since a quantum circuit can be simulated by basic operations referring to single-qubit gates, controlled-NOT gates, controlled-V and controlled-V⁺ gates^12,27,28,30, we introduce some definitions and lemmas. Furthermore, $\lfloor \rfloor$ and $\lceil \rceil$ are the symbols of round down and round up respectively, which are used in the following definitions and lemmas.

Definition 5.

The quantum cost of a quantum circuit can be regarded as the total number of basic operations which simulate the circuit, marked by ${\rm{C}}()$.

Definition 6.

The time complexity of a quantum circuit is defined by the total number of time steps. In a time step, only one basic operation is executed serially, but multiple ones can be performed in parallel. It is marked by ${{\rm{C}}}^{p}()$.

Lemma 1.

When n ≥ 6 and $m\in \{3,4,\ldots ,\lfloor n/2\rfloor \}$, an ${N}_{n}^{m}$ gate can be simulated by a network consisting of 2(m − 1) Toffoli gates and a basic operation.

For instance, ${C}_{m}^{0}({I}_{{2}^{n-m-1}}\otimes X)$ and ${V}_{m}^{0}(X\otimes {I}_{{2}^{n-m-1}})$ gates can be simulated by 2(m − 1) Toffoli gates and a basic operation, respectively. The form of the network is shown in (a) and (b) of Fig. 4.

Figure 4

The controlled gate ${N}_{n}^{m}$ illustrated for n = 10 and m ∈ {5, 6}.

Lemma 2.

For any n ≥ 6, $r=\lfloor n/2\rfloor$ and m ∈ {r + 1, r + 2, …, n − 2}, an ${N}_{n}^{m}$ gare can be simulated by two ${N}_{n}^{r}$ gates and two ${N}_{n}^{m-r+1}$ gates.

For instance, the simulated networks of ${C}_{6}^{0}({I}_{{2}^{3}}\otimes X)$ and ${V}_{6}^{0}(X\otimes {I}_{{2}^{3}})$ gates are shown in (c) and (d) of Fig. 4.

Lemma 3.

When n ≥ 5 and $m=\lceil n/2\rceil$, an ${N}_{n}^{m}$ gate can be simulated by a network consisting of 4(m − 2) Toffoli gates.

For instance, the simulated networks of ${C}_{m}^{0}({I}_{{2}^{n-m-1}}\otimes X)$ and ${V}_{m}^{0}(X\otimes {I}_{{2}^{n-m-1}})$ gates are shown in Fig. 5.

Figure 5

The controlled gate ${N}_{n}^{m}$ illustrated for n = 9 and m = 5.

Lemma 4.

For any SU(2) matrix D, there exist SU(2) matrices A, B, and C such that ABC = I₂ and AXBXC = D, and the gates ${C}_{1}^{0}(D)$ and ${V}_{1}^{0}(D)$ can be simulated by networks of the form shown in (a) and (b) Fig. 6. Here, SU(2) is the Lie group of 2 × 2 unitary matrices with determinant 1.

Figure 6

The simulated networks of the gates ${C}_{n-1}^{0}(D)$ and ${V}_{n-1}^{0}(D)$ with n ≥ 2.

More details of Lemmas 2, 3 and 4 are described in the reference²⁷. Next, we derive the following corollaries.

Corollary 1.

For any n ≥ 7, $r=\lfloor n/2\rfloor$ and m ∈ {r + 2, r + 3, …, n − 2}, an ${N}_{n}^{m}$ gate can be simulated by 4(m − 1) Toffoli gates and four basic operations.

Proof.

Applying Lemma 2, an ${N}_{n}^{m}$ gate can be simulated by two ${N}_{n}^{r}$ gates and two ${N}_{n}^{m-r+1}$ gates. Noting that $3\le r\le \lfloor \frac{n}{2}\rfloor$ and $3\le m-r+1\le \lfloor \frac{n}{2}\rfloor$, we apply lemma 1 so that the corollary holds.$\square$

Corollary 2.

For any n ≥ 6 and $r=\lfloor n/2\rfloor$, an ${N}_{n}^{r+1}$ gate can be simulated by (4r − 2) Toffoli gates and two basic operations when n is even, and 4(r − 1) Toffoli gates when n is odd.

Proof.

When n is odd, $r+1=\lceil n/2\rceil$. Then, applying Lemma 3, we have that an ${N}_{n}^{r+1}$ gate can be simulated by a network consisting of 4(r − 1) Toffoli gates.

When n is even, by applying Lemma 2, it is derived that an ${N}_{n}^{r+1}$ gate can be simulated by two ${N}_{n}^{r}$ gates and two Toffoli gates. Then, by applying Lemma 1, it is proved that one can use (4r − 2) Toffoli gates and two basic operations to simulate the ${N}_{n}^{r+1}$ gate.$\square$

From lemma 4, the following corollary holds.

Corollary 3.

For any SU(2) matrix D, there exist SU(2) matrices A, B, and C such that ABC = I₂ and AXBXC = D, and the gates ${C}_{n-1}^{0}(D)$ and ${V}_{n-1}^{0}(D)$ can be simulated by networks of the form shown in (c) and (d) of Fig. 6.

To analyze the complexities of the gates ${C}_{n-1}^{0}(X)$ and ${V}_{n-1}^{0}(X)$, we define three matrices:

$$\{\begin{array}{rcl}{R}_{z}(\theta ) & = & [\begin{array}{cc}{e}^{i\frac{\theta }{2}} & 0\\ 0 & {e}^{-i\frac{\theta }{2}}\end{array}],\\ {\rm{\Phi }}(\theta ) & = & [\begin{array}{cc}{e}^{i\theta } & 0\\ 0 & {e}^{i\theta }\end{array}],\\ {R}_{y}(\theta ) & = & [\begin{array}{cc}\cos \,\frac{\theta }{2} & \sin \,\frac{\theta }{2}\\ -\sin \,\frac{\theta }{2} & \cos \,\frac{\theta }{2}\end{array}].\end{array}$$

(12)

Lemma 5.

Let ${\delta }_{i}=\frac{\delta }{{2}^{i}}$, i ∈ {0, 1, 2, …, n}, E₀ = Φ(δ_n−1)R_z(δ_n−2). Then, the gates ${C}_{n-1}^{0}({\rm{\Phi }}(\delta ))$ and ${V}_{n-1}^{0}({\rm{\Phi }}(\delta ))$ can be simulated by networks of the form shown in Fig. 7.

Figure 7

The simulated networks of the gates ${C}_{n-1}^{0}({\rm{\Phi }}(\delta ))$ and ${V}_{n-1}^{0}({\rm{\Phi }}(\delta ))$.

Proof.

Note that

$${C}_{1}^{0}({\rm{\Phi }}(\delta ))=({\rm{\Phi }}(\frac{\delta }{2}){R}_{z}(\delta ))\otimes {I}_{2}=({\rm{\Phi }}({\delta }_{1}){R}_{z}({\delta }_{0}))\otimes {I}_{2},$$

(13)

$${V}_{1}^{0}({\rm{\Phi }}(\delta ))={I}_{2}\otimes ({\rm{\Phi }}(\frac{\delta }{2}){R}_{z}(\delta ))={I}_{2}\otimes ({\rm{\Phi }}({\delta }_{1}){R}_{z}({\delta }_{0})).$$

(14)

Then, we have that

$$\begin{array}{rcl}{C}_{n-1}^{0}({\rm{\Phi }}(\delta )) & = & {C}_{n-2}^{0}({C}_{1}^{0}({\rm{\Phi }}(\delta )))\\ & = & {C}_{n-2}^{0}(({\rm{\Phi }}({\delta }_{1}){R}_{z}({\delta }_{0}))\otimes {I}_{2})\\ & = & [{C}_{n-2}^{0}(({\rm{\Phi }}({\delta }_{1})){C}_{n-2}^{0}({R}_{z}({\delta }_{0}))]\otimes {I}_{2}.\end{array}$$

(15)

Similarly,

$${V}_{n-1}^{0}({\rm{\Phi }}(\delta ))={I}_{2}\otimes [{V}_{n-2}^{0}(({\rm{\Phi }}({\delta }_{1})){V}_{n-2}^{0}({R}_{z}({\delta }_{0}))].$$

(16)

Therefore, we have the simulated networks of the gates ${C}_{n-1}^{0}({\rm{\Phi }}(\delta ))$ and ${V}_{n-1}^{0}({\rm{\Phi }}(\delta ))$ as shown in Fig. 7.$\square$

Lemma 6.

The gates ${C}_{m}^{0}({R}_{z}(\delta ))$ and ${V}_{m}^{0}({R}_{z}(\delta ))$ can be simulated by networks of the form shown in Fig. 8.

Figure 8

The simulated networks of the gates ${C}_{m}^{0}({R}_{z}(\delta ))$ and ${V}_{m}^{0}({R}_{z}(\delta ))$.

Proof.

Due to ${R}_{z}(\frac{\delta }{2}){R}_{z}(\,-\frac{\delta }{2})={I}_{2}$ and ${R}_{z}(\frac{\delta }{2})X{R}_{z}(\,-\frac{\delta }{2})X={R}_{z}(\delta )$, the conclusion is obvious.$\square$

${C}_{2}^{i}(X)$ (i = 0, 1, 2, 3) can be simulated by five basic operations shown in Fig. 9, i.e., $C({C}_{2}^{i}(X))={C}^{p}({C}_{2}^{i}(X))=5$.

Figure 9

The simulated networks of the gates ${C}_{2}^{i}(X)$ (i = 0, 1, 2, 3).

Similarly, $C({V}_{2}^{i}(X))={C}^{p}({V}_{2}^{i}(X))=5$. Therefore, the complexity of Toffoli gates is 5. Thus, we obtain the complexity of ${C}_{n-1}^{0}(X)$ and ${V}_{n-1}^{0}(X)$ as described in theorem 1 below.

Theorem 1.

For any n ≥ 7, the gates ${C}_{n-1}^{0}(X)$ and ${V}_{n-1}^{0}(X)$ can be simulated by (3.5n² − 13n − 4) Toffoli gates and 7n − 4 basic operations when n is even, and by (3.5n² − 12n − 5.5) Toffoli gates and 7n − 3 basic operations when n is odd.

Proof.

Let δ = π/2, D = R_z(−π)R_y(π), A = R_z(−π)R_y(π), B = R_y(−π/2)R_z(π/2) and C = R_z(π/2). Then, D, A, B, C ∈ SU(2), ABC = I₂, AXBXC = D and Φ(δ)D = X.

Note that ${C}_{n-1}^{0}(X)={C}_{n-1}^{0}({\rm{\Phi }}(\delta )){C}_{n-1}^{0}(D)$. Then,

$$C({C}_{n-1}^{0}(X))=C({C}_{n-1}^{0}({\rm{\Phi }}(\delta )))+C({C}_{n-1}^{0}(D)).$$

(17)

From lemma 4 and corollary 3, we obtain

$$C({C}_{n-1}^{0}(D))=2C({N}_{n}^{n-2})+15.$$

(18)

By lemma 5 and lemma 6, $C({C}_{n-1}^{0}({\rm{\Phi }}(\delta )))$ can be computed by

$$C({C}_{n-1}^{0}({\rm{\Phi }}(\delta )))=\sum _{i=1}^{n-2}\,C({C}_{i}^{0}({R}_{z}({\delta }_{n-2-i})))+1=2\,\sum _{i=1}^{n-2}\,C({N}_{n}^{i})+2n-3.$$

(19)

Therefore,

$$C({C}_{n-1}^{0}(X))=\sum _{i=3}^{r}\,2C({N}_{n}^{i})+\sum _{i=r+2}^{n-3}\,2C({N}_{n}^{i})+4C({N}_{n}^{n-2})+2C({N}_{n}^{r+1})+2C({N}_{3}^{2})+2n+14,$$

(20)

where $r=\lfloor n/2\rfloor$ and ${N}_{3}^{2}$ is a Toffoli gate.

Applying lemma 1, corollary 1 and corollary 2, we obtain

$$C({C}_{n-1}^{0}(X))=\{\begin{array}{l}(3.5{n}^{2}-13n-4)C({N}_{3}^{2})+7n-4,\,{\rm{when}}\,{\rm{n}}\,{\rm{is}}\,{\rm{even}},\\ (3.5{n}^{2}-12n-5.5)C({N}_{3}^{2})+7n-3,\,{\rm{when}}\,{\rm{n}}\,{\rm{is}}\,{\rm{odd}}.\end{array}$$

(21)

Similarly, we obtain that $C({V}_{n-1}^{0}(X))=C({C}_{n-1}^{0}(X))$.$\square$

Comparing with the methods proposed in²⁷, the complexities of our proposed simulated networks of these gates ${N}_{n}^{i}\mathrm{(3}\le i\le n-\mathrm{1)}$ are reduced by 50% approximately.

The Quantum Circuits of PSP

The perfect shuffle permutation ${P}_{{2}^{n-1}\mathrm{,2}}$ and ${P}_{{\mathrm{2,2}}^{n-1}}$ can be expressed as

$$\{\begin{array}{l}{P}_{{2}^{n-1},2}=({P}_{{2}^{n-2},2}\otimes {I}_{2})\,({I}_{{2}^{n-2}}\otimes {P}_{2,2}),\\ {P}_{2,{2}^{n-1}}=({I}_{2}\otimes {P}_{2,{2}^{n-2}})\,({P}_{2,2}\otimes {I}_{{2}^{n-2}}),\end{array}$$

(22)

where P_2,2 is a Swap gate, and their implementation circuits are shown in Fig. 10.

Figure 10

The implement circuits of ${P}_{{2}^{n-1}\mathrm{,2}}$ and ${P}_{{\mathrm{2,2}}^{n-1}}$. The dotted boxes in (a,b) are the circuits of ${P}_{{2}^{n-2}\mathrm{,2}}$ and ${P}_{{\mathrm{2,2}}^{n-2}}$, respectively.

Applying ${P}_{{2}^{n-1}\mathrm{,2}}$ and ${P}_{{\mathrm{2,2}}^{n-1}}$ to the state $|{j}_{n}{j}_{n-1}\cdots {j}_{2}{j}_{1}\rangle$, we have

$$\{\begin{array}{l}{P}_{{2}^{n-1},2}|{j}_{n}{j}_{n-1}\cdots {j}_{2}{j}_{1}\rangle =|{j}_{1}{j}_{n}{j}_{n-1}\cdots {j}_{2}\rangle ,\\ {P}_{2,{2}^{n-1}}|{j}_{n}{j}_{n-1}\cdots {j}_{2}{j}_{1}\rangle =|{j}_{n-1}\cdots {j}_{2}{j}_{1}{j}_{n}\rangle .\end{array}$$

(23)

Let ${{\rm{\Gamma }}}_{{2}^{n}}={P}_{{2}^{n-1},2}({P}_{{2}^{n-2},2}\otimes {I}_{2})\ldots ({P}_{{2}^{2},2}\otimes {I}_{{2}^{n-3}})\,({P}_{2,2}\otimes {I}_{{2}^{n-2}})$, we have that ${({{\rm{\Gamma }}}_{{2}^{n}})}^{-1}=({P}_{2,2}\otimes {I}_{{2}^{n-2}})$ $({P}_{2,{2}^{2}}\otimes {I}_{{2}^{n-3}})\ldots ({P}_{2,{2}^{n-2}}\otimes {I}_{2}){P}_{2,{2}^{n-1}}$ and

$${{\rm{\Gamma }}}_{{2}^{n}}|{j}_{n}{j}_{n-1}{j}_{n-2}\cdots {j}_{2}{j}_{1}\rangle =|{j}_{1}{j}_{2}\cdots {j}_{n-2}{j}_{n-1}{j}_{n}\rangle ={({{\rm{\Gamma }}}_{{2}^{n}})}^{-1}|{j}_{n}{j}_{n-1}{j}_{n-2}\cdots {j}_{2}{j}_{1}\rangle $$

(24)

Therefore, we conclude that ${{\rm{\Gamma }}}_{{2}^{n}}={({{\rm{\Gamma }}}_{{2}^{n}})}^{-1}$ and design quantum circuits shown in Fig. 11.

Figure 11

The simplified quantum circuits of ${{\rm{\Gamma }}}_{{2}^{n}}$ and ${({{\rm{\Gamma }}}_{{2}^{n}})}^{-1}$.

The costs of the circuits of ${{\rm{\Gamma }}}_{{2}^{n}}$ and ${({{\rm{\Gamma }}}_{{2}^{n}})}^{-1}$ are

$$C({{\rm{\Gamma }}}_{{2}^{n}})=C({({{\rm{\Gamma }}}_{{2}^{n}})}^{-1})=3\times \lfloor \frac{n}{2}\rfloor .$$

(25)

By parallel computing, we redesign the circuits of ${{\rm{\Gamma }}}_{{2}^{n}}$ and ${({{\rm{\Gamma }}}_{{2}^{n}})}^{-1}$ shown in Fig. 12 and calculate time complexities by

$${C}^{p}({{\rm{\Gamma }}}_{{2}^{n}})={C}^{p}({({{\rm{\Gamma }}}_{{2}^{n}})}^{-1})=C(Swap)=3.$$

(26)

i.e., complexities of ${{\rm{\Gamma }}}_{{2}^{n}}$ and ${({{\rm{\Gamma }}}_{{2}^{n}})}^{-1}$ are O(1).

Figure 12

The parallel quantum circuits of ${{\rm{\Gamma }}}_{{2}^{n}}$ and ${({{\rm{\Gamma }}}_{{2}^{n}})}^{-1}$.

The iterations of ${{\rm{\Gamma }}}_{{2}^{n}}$ and ${({{\rm{\Gamma }}}_{{2}^{n}})}^{-1}$ are given by

$$\{\begin{array}{rcl}{{\rm{\Gamma }}}_{{2}^{n}} & = & {P}_{{2}^{n-1},2}({{\rm{\Gamma }}}_{{2}^{n-1}}\otimes {I}_{2}),\\ {({{\rm{\Gamma }}}_{{2}^{n}})}^{-1} & = & ({({{\rm{\Gamma }}}_{{2}^{n-1}})}^{-1}\otimes {I}_{2}){P}_{2,{2}^{n-1}}.\end{array}$$

(27)

Then, we obtain

$$\{\begin{array}{lcc}{P}_{{2}^{n-1},2} & = & {{\rm{\Gamma }}}_{{2}^{n}}({{\rm{\Gamma }}}_{{2}^{n-1}}\otimes {I}_{2}),\\ {P}_{2,{2}^{n-1}} & = & ({{\rm{\Gamma }}}_{{2}^{n-1}}\otimes {I}_{2}){{\rm{\Gamma }}}_{{2}^{n}}.\end{array}$$

(28)

Therefore, we design the simplified circuits of ${P}_{{2}^{n-1}\mathrm{,2}}$ and ${P}_{{\mathrm{2,2}}^{n-1}}$ as shown in Fig. 13.

Figure 13

The simplified circuits of ${P}_{{2}^{n-1}\mathrm{,2}}$ and ${P}_{{\mathrm{2,2}}^{n-1}}$. The rights of (a,b) correspond to the abbreviation notation of ${P}_{{2}^{n-1}\mathrm{,2}}$ and ${P}_{{\mathrm{2,2}}^{n-1}}$, respectively.

The complexities of ${P}_{{2}^{n-1}\mathrm{,2}}$ and ${P}_{{\mathrm{2,2}}^{n-1}}$ are

$$\{\begin{array}{rcl}C({P}_{{2}^{n-1},2}) & = & C({P}_{2,{2}^{n-1}})=3(n-1),\\ {C}^{P}({P}_{{2}^{n-1},2}) & = & {C}^{P}({P}_{2,{2}^{n-1}})=6.\end{array}$$

(29)

The reason that the abbreviation notations in Fig. 13 are the same except for the positions of black boxes is due to the fact that the circuit in Fig. 13(b) consists of the gates in Fig. 13(a) but rearranged in reverse order. We also adopt similar abbreviation notations to denote the circuits that are composed of the same quantum gates with reverse order in the following sections.

The iterations of ${P}_{{2}^{n}{\mathrm{,2}}^{m-1}}$ and ${P}_{{2}^{m-1}{\mathrm{,2}}^{n}}$ are given by

$$\{\begin{array}{l}{P}_{{2}^{n},{2}^{m-1}}=({P}_{2,{2}^{m-1}}\otimes {I}_{{2}^{n-1}})\,({I}_{2}\otimes {P}_{{2}^{n-1},{2}^{m-1}}),\\ {P}_{{2}^{m-1},{2}^{n}}=({I}_{2}\otimes {P}_{{2}^{m-1},{2}^{n-1}})\,({P}_{{2}^{m-1},2}\otimes {I}_{{2}^{n-1}}).\end{array}$$

(30)

According to (30), we design the implementation circuits of ${P}_{{2}^{m-1}{\mathrm{,2}}^{n}}$ and ${P}_{{2}^{n}{\mathrm{,2}}^{m-1}}$ in Fig. 14.

Figure 14

The quantum circuits of ${P}_{{2}^{m-1}{\mathrm{,2}}^{n}}$ and ${P}_{{2}^{n}{\mathrm{,2}}^{m-1}}$. The dotted boxes in (a,b) are the implement circuits of ${P}_{{2}^{m-1}{\mathrm{,2}}^{n-1}}$ and ${P}_{{2}^{n-1}{\mathrm{,2}}^{m-1}}$, respectively.

The complicities of the circuits in Fig. 14 are

$$\{\begin{array}{rcl}C({P}_{{2}^{m-1},{2}^{n}}) & = & C({P}_{{2}^{n},{2}^{m-1}})=3n(m-1),\\ {C}^{p}({P}_{{2}^{m-1},{2}^{n}}) & = & {C}^{p}({P}_{{2}^{n},{2}^{m-1}})=6n.\end{array}$$

(31)

The Implementation of QWPT

Let ${W}_{{2}^{n}}^{0}={W}_{{2}^{n}}$ be a wavelet kernel matrix. Then, the (k + 1)-th iteration of a discrete wavelet packet transform is defined by

$$\{\begin{array}{l}{Z}_{{2}^{n}}^{k}={W}_{{2}^{n}}^{k}{W}_{{2}^{n}}^{k-1}\ldots {W}_{{2}^{n}}^{1}{W}_{{2}^{n}}^{0},\\ {W}_{{2}^{n}}^{j}=Diag({W}_{{2}^{n-j}},{W}_{{2}^{n-j}},\ldots ,{W}_{{2}^{n-j}}),\end{array}$$

(32)

where j = 1, …, k and $Diag({W}_{{2}^{n-j}},{W}_{{2}^{n-j}},\ldots ,{W}_{{2}^{n-j}})$ is a matrix with 2^j blocks of ${W}_{{2}^{n-j}}$ on the main diagonal and zeros elsewhere.

The following equations

$$\{\begin{array}{l}{W}_{{2}^{n}}^{j}=Diag({W}_{{2}^{n-1}}^{j-1},{W}_{{2}^{n-1}}^{j-1}),\\ {Z}_{{2}^{n}}^{k}=Diag({Z}_{{2}^{n-1}}^{k-1},{Z}_{{2}^{n-1}}^{k-1}){W}_{{2}^{n}}\end{array}$$

(33)

can be derived by (32).

Since

$$\begin{array}{l}{Z}_{{2}^{n-1}}^{k-1}\otimes {I}_{2}={P}_{2,{2}^{n-1}}Diag({Z}_{{2}^{n-1}}^{k-1},{Z}_{{2}^{n-1}}^{k-1}){P}_{{2}^{n-1},2},\end{array}$$

(34)

the iteration equation of the QWPT is given by

$${Z}_{{2}^{n}}^{k}={P}_{{2}^{n-1},2}({Z}_{{2}^{n-1}}^{k-1}\otimes {I}_{2}){P}_{2,{2}^{n}}{W}_{{2}^{n}}$$

(35)

with the initial value ${Z}_{{2}^{n-k}}^{0}={W}_{{2}^{n-k}}$ and the implementation circuit shown in (a) of Fig. 15.

Figure 15

The implementation circuits of ${Z}_{{2}^{n}}^{k}$ and ${({Z}_{{2}^{n}}^{k})}^{-1}$.

Similarly, the inverse of ${Z}_{{2}^{n}}^{k}$ is

$${({Z}_{{2}^{n}}^{k})}^{-1}={({W}_{{2}^{n}})}^{-1}{P}_{{2}^{n-1},2}({({Z}_{{2}^{n-1}}^{k-1})}^{-1}\otimes {I}_{2}){P}_{2,{2}^{n-1}}$$

(36)

with the initial value ${({Z}_{{2}^{n-k}}^{0})}^{-1}={({W}_{{2}^{n-k}})}^{-1}$ and the implementation circuit of ${({Z}_{{2}^{n}}^{k})}^{-1}$ shown in (b) of Fig. 15.

Next, we describe the implementations of the Haar QWPT (HQWPT) and the D4 QWPT (DQWPT) in detail.

The implementation of HQWPT

Substituting the kernel matrix ${W}_{{2}^{n}}={P}_{{2}^{n-1},2}({I}_{{2}^{n-1}}\otimes H)$ into equations (35) and (36), the (k + 1)-th iteration of HQWPT and its inverse are

$$\{\begin{array}{rcl}{R}_{{2}^{n}}^{k} & = & {P}_{{2}^{n-1},2}({R}_{{2}^{n-1}}^{k-1}\otimes {I}_{2})\,({I}_{{2}^{n-1}}\otimes H),\\ {({R}_{{2}^{n}}^{k})}^{-1} & = & ({I}_{{2}^{n-1}}\otimes H)\,({({R}_{{2}^{n-1}}^{k-1})}^{-1}\otimes {I}_{2}){P}_{2,{2}^{n-1}}\end{array}$$

(37)

with the initial values

$$\{\begin{array}{rcl}{R}_{{2}^{n-k}}^{0} & = & {P}_{{2}^{n-k-1},2}({I}_{{2}^{n-k-1}}\otimes H),1\le k < n-1,\\ {R}_{2}^{0} & = & H,k=n-1,\\ {({R}_{{2}^{n-k}}^{0})}^{-1} & = & (H\otimes {I}_{{2}^{n-k-1}}){P}_{2,{2}^{n-k-1}},1\le k < n-1,\\ {({R}_{2}^{0})}^{-1} & = & H,k=n-1.\end{array}$$

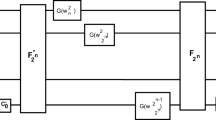
The quantum circuits of ${R}_{{2}^{n}}^{n-1}$ and ${R}_{{2}^{n}}^{k}$ (1 ≤ k < n − 1) are designed in Fig. 16.

Figure 16

The implementation circuits of ${R}_{{2}^{n}}^{n-1}$ and ${R}_{{2}^{n}}^{k}$ (1 ≤ k < n − 1). The dashed box 1 and box 3 implement ${R}_{{2}^{n-1}}^{n-2}$ and ${R}_{{2}^{n-1}}^{k-1}$, respectively.

Since ${P}_{{2}^{n-1},2}({P}_{{2}^{n-2},2}\otimes {I}_{2})\,\ldots \,({P}_{2,2}\otimes {I}_{{2}^{n-2}})={{\rm{\Gamma }}}_{{2}^{n}}$ and ${P}_{{2}^{n-1},2}({P}_{{2}^{n-2},2}\otimes {I}_{2})\,\ldots \,({P}_{{2}^{n-k-1},2}\otimes {I}_{{2}^{k}})={{\rm{\Gamma }}}_{{2}^{n}}({({{\rm{\Gamma }}}_{{2}^{n-k-1}})}^{-1}$ $\otimes {I}_{{2}^{k+1}})$ with 1 ≤ k < n − 2, the quantum circuit of ${R}_{{2}^{n}}^{k}$, ${R}_{{2}^{n}}^{n-2}$ and ${R}_{{2}^{n}}^{n-1}$ can be simplified and shown in Fig. 17.

Figure 17

The simplified circuits of ${R}_{{2}^{n}}^{k}$ 1 ≤ k < n − 2, ${R}_{{2}^{n}}^{n-2}$ and ${R}_{{2}^{n}}^{n-1}$.

Similarly, the quantum circuits of the inverses of ${R}_{{2}^{n}}^{k}$, ${R}_{{2}^{n}}^{n-2}$ and ${R}_{{2}^{n}}^{n-1}$ can be designed as shown in Fig. 18.

Figure 18

The simplified circuits of ${({R}_{{2}^{n}}^{k})}^{-1}$ 1 ≤ k < n − 2, ${({R}_{{2}^{n}}^{n-2})}^{-1}$ and ${({R}_{{2}^{n}}^{n-1})}^{-1}$.

The costs of HQWPT are

$$\{\begin{array}{rcl}C({R}_{{2}^{n}}^{k}) & = & C({({R}_{{2}^{n}}^{k})}^{-1})=3\lfloor \frac{n}{2}\rfloor +3\lfloor \frac{n\,-\,k\,-\,1}{2}\rfloor +k+1,\\ C({R}_{{2}^{n}}^{n-2}) & = & C({({R}_{{2}^{n}}^{n-2})}^{-1})=3\lfloor \frac{n}{2}\rfloor +n-1,\\ C({R}_{{2}^{n}}^{n-1}) & = & C({({R}_{{2}^{n}}^{n-1})}^{-1})=3\lfloor \frac{n}{2}\rfloor +n,\end{array}$$

(38)

where 1 ≤ k < n − 2. Since ${C}^{p}({R}_{{2}^{n}}^{k})={C}^{p}({({R}_{{2}^{n}}^{k})}^{-1})=6,1\le k < n-2$ and ${C}^{p}({R}_{{2}^{n}}^{k})={C}^{p}({({R}_{{2}^{n}}^{k})}^{-1})=4,n-2\le$ $k\le n-1$, the time complexity of the HQWPT is O(1).

The implementation of DQWPT

The kernel matrix of the D4 wavelet transform is defined by the reference³¹

$${D}_{{2}^{n}}=[\begin{array}{lllllllllll}{h}_{0} & {h}_{1} & {h}_{2} & {h}_{3} & 0 & 0 & \cdots & 0 & 0 & 0 & 0\\ {h}_{3} & -{h}_{2} & {h}_{1} & -{h}_{0} & 0 & 0 & \cdots & 0 & 0 & 0 & 0\\ 0 & 0 & {h}_{0} & {h}_{1} & {h}_{2} & {h}_{3} & \cdots & 0 & 0 & 0 & 0\\ 0 & 0 & {h}_{3} & -{h}_{2} & {h}_{1} & -{h}_{0} & \cdots & 0 & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & 0 & \cdots & {h}_{0} & {h}_{1} & {h}_{2} & {h}_{3}\\ 0 & 0 & 0 & 0 & 0 & 0 & \cdots & {h}_{3} & -{h}_{2} & {h}_{1} & -{h}_{0}\\ {h}_{2} & {h}_{3} & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & {h}_{0} & {h}_{1}\\ {h}_{1} & -{h}_{0} & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & {h}_{3} & -{h}_{2}\end{array}],$$

(39)

where ${h}_{0}=\frac{1+\sqrt{3}}{4\sqrt{2}}$, ${h}_{1}=\frac{3+\sqrt{3}}{4\sqrt{2}}$, ${h}_{2}=\frac{3-\sqrt{3}}{4\sqrt{2}}$ and ${h}_{3}=\frac{1-\sqrt{3}}{4\sqrt{2}}$.

${D}_{{2}^{n}}$ and ${({D}_{{2}^{n}})}^{-1}$ can be rewritten to

$$\{\begin{array}{rcl}{D}_{{2}^{n}} & = & ({I}_{{2}^{n-1}}\otimes {S}_{1}){Q}_{{2}^{n}}({I}_{{2}^{n-1}}\otimes {S}_{0}),\\ {Q}_{{2}^{n}} & = & (\{{Q}_{{2}^{n-1}},{I}_{{2}^{n-1}}\}\otimes {I}_{2}),\\ {({D}_{{2}^{n}})}^{-1} & = & ({I}_{{2}^{n-1}}\otimes {S}_{0})\,{({Q}_{{2}^{n}})}^{-1}({I}_{{2}^{n-1}}\otimes {S}_{1}),\\ {({Q}_{{2}^{n}})}^{-1} & = & (\{{({Q}_{{2}^{n-1}})}^{-1},{I}_{{2}^{n-1}}\}\otimes {I}_{2})\,({I}_{{2}^{n-1}}\otimes X),\end{array}$$

(40)

where

$$\{\begin{array}{rcl}{S}_{0} & = & [\begin{array}{ll}\sin (2\pi /3) & \cos (2\pi /3)\\ \cos (2\pi /3) & -\sin (2\pi /3)\end{array}]\\ {S}_{1} & = & [\begin{array}{ll}-\cos (\pi /12) & \sin (\pi /12)\\ \sin (\pi /12) & \cos (\pi /12)\end{array}]\\ {Q}_{2} & = & {({Q}_{2})}^{-1}=X,\end{array}$$

and the implementation circuits shown in Fig. 19.

Figure 19

The quantum circuits of the kernel matrix of the D4 wavelet transform.

In order to implement a multi-level DQWPT based on the periodization extension, a single-level DQWPT and its inverse are given by:

$$\{\begin{array}{rcl}{T}_{{2}^{n}} & = & {P}_{{2}^{n-1},2}{D}_{{2}^{n}}^{p},\\ {D}_{{2}^{n}}^{p} & = & {D}_{{2}^{n}}{({Q}_{{2}^{n}})}^{-1},\\ {({T}_{{2}^{n}})}^{-1} & = & {({D}_{{2}^{n}}^{p})}^{-1}{P}_{2,{2}^{n-1}},\\ {({D}_{{2}^{n}}^{p})}^{-1} & = & {Q}_{{2}^{n}}{({D}_{{2}^{n}})}^{-1}.\end{array}$$

(41)

The implement circuits of the above DQWPT are shown in Fig. 20. Substituting the kernel matrix ${W}_{{2}^{n}}$ with ${T}_{{2}^{n}}$ in (35) and (36), we obtain that the (k + 1)-th iterations of the DQWPT and its inverse based on the periodization extension are

$$\{\begin{array}{rcl}{A}_{{2}^{n}}^{k} & = & {P}_{{2}^{n-1},2}({A}_{{2}^{n-1}}^{k-1}\otimes {I}_{2}){D}_{{2}^{n}}^{p},\\ {({A}_{{2}^{n}}^{k})}^{-1} & = & {Q}_{{2}^{n}}{({D}_{{2}^{n}})}^{-1}({({A}_{{2}^{n-1}}^{k-1})}^{-1}\otimes {I}_{2}){P}_{2,{2}^{n-1}}\end{array}$$

(42)

with the initial values ${A}_{{2}^{n-k}}^{0}={T}_{{2}^{n-k}}$, ${({A}_{{2}^{n-k}}^{0})}^{-1}={({T}_{{2}^{n-k}})}^{-1}$, 1 ≤ k < n − 1 and their implementation circuits shown in Fig. 21.

Figure 20

The quantum circuits of the single-level DQWPT and its inverse based on the periodization extension.

Figure 21

The quantum circuits of ${A}_{{2}^{n}}^{k}$ and ${({A}_{{2}^{n}}^{k})}^{-1}$. The dashed boxes in (a,b) implement ${A}_{{2}^{n-1}}^{k-1}$ and ${({A}_{{2}^{n-1}}^{k-1})}^{-1}$, respectively.

Using ${{\rm{\Gamma }}}_{{2}^{n}}$, the quantum circuit of ${A}_{{2}^{n}}^{k}$ and ${({A}_{{2}^{n}}^{k})}^{-1}$ can be simplified and shown in Fig. 22.

Figure 22

The simplified circuits of ${A}_{{2}^{n}}^{k}$ and ${({A}_{{2}^{n}}^{k})}^{-1}$ with 1 ≤ k < n − 1.

We analyze the complexity of the above DQWPT and suppose $r=\lfloor n/2\rfloor$.

From Figs 19 and 20, we calculate the complexity of ${T}_{{2}^{n}}$ by

$${C}^{p}({T}_{{2}^{n}})={C}^{p}({({T}_{{2}^{n}})}^{-1})={C}^{P}({Q}_{{2}^{n}})+{C}^{p}({D}_{{2}^{n}})+{C}^{P}({P}_{{2}^{n-1},2})=\sum _{i=1}^{n-1}\,2C({N}_{n}^{i})+10.$$

(43)

Applying lemma 1, corollary 1, corollary 2 and theorem 1, we obtain

$${C}^{p}({T}_{{2}^{n}})={C}^{p}({({T}_{{2}^{n}})}^{-1})=\{\begin{array}{l}52.5{n}^{2}-216n+38,\,{\rm{n}}\,{\rm{is}}\,{\rm{even}},\\ 52.5{n}^{2}-201n+16.5,\,{\rm{n}}\,{\rm{is}}\,{\rm{odd}}.\end{array}$$

(44)

We calculate the quantum cost of ${T}_{{2}^{n}}$ by

$$C({T}_{{2}^{n}})=C({({T}_{{2}^{n}})}^{-1})=C({Q}_{{2}^{n}})+C({D}_{{2}^{n}})+C({P}_{{2}^{n-1},2})={C}^{p}({T}_{{2}^{n}})+3n-9.$$

(45)

Let ${\varphi }_{2}(k)=\{\begin{array}{l}3,k=n-2\\ 6,1\le k < n-2,\end{array}$ the time complexity of DQWPT is

$${C}^{p}({A}_{{2}^{n}}^{k})={C}^{p}({({A}_{{2}^{n}}^{k})}^{-1})=\sum _{i=1}^{n-k-1}\,2(k+1)C({N}_{n}^{i})+\sum _{i=n-k}^{n-1}\,2(n-i)C({N}_{n}^{i})+4(k+1)+{\varphi }_{2}(k).$$

(46)

For instance,

$${C}^{p}({A}_{{2}^{n}}^{n-2})={C}^{p}({({A}_{{2}^{n}}^{n-2})}^{-1})=\{\begin{array}{l}5{n}^{3}+21{n}^{2}-163.5n+63,\,{\rm{n}}\,{\rm{is}}\,{\rm{even}},\\ 5{n}^{3}+23.5{n}^{2}-168.5n+51,\,{\rm{n}}\,{\rm{is}}\,{\rm{odd}},\end{array}$$

(47)

and

$${C}^{p}({A}_{{2}^{n}}^{1})={C}^{p}({({A}_{{2}^{n}}^{1})}^{-1})=\{\begin{array}{l}70{n}^{2}-316n+115,\,{\rm{n}}\,{\rm{is}}\,{\rm{even}},\\ 70{n}^{2}-296n+85,\,{\rm{n}}\,{\rm{is}}\,{\rm{odd}}.\end{array}$$

(48)

The costs of ${A}_{{2}^{n}}^{k}$ and ${({A}_{{2}^{n}}^{k})}^{-1}$ are

$$C({A}_{{2}^{n}}^{k})=C({({A}_{{2}^{n}}^{k})}^{-1})={C}^{p}({A}_{{2}^{n}}^{k})-{\varphi }_{2}(k)+\lfloor \frac{n-k-1}{2}\rfloor +\lfloor \frac{n}{2}\rfloor .$$

(49)

The 2D and 3D QWPTs

Firstly, we briefly describe NASS to represent 2D images and 3D videos. The NASS state $|{\psi }_{2}\rangle$ of an image can be represented by

$$|{\psi }_{2}\rangle =\sum _{{x}_{m}=0}^{{2}^{m}-1}\,\sum _{{y}_{k}=0}^{{2}^{k}-1}\,{\theta }_{{x}_{m},{y}_{k}}|{x}_{m}\rangle |{y}_{k}\rangle ,$$

(50)

where $|{x}_{m}\rangle =|{i}_{n}\ldots {i}_{k+1}\rangle$ and $|{y}_{k}\rangle =|{i}_{k}\ldots {i}_{1}\rangle$ are the X-axis and Y-axis of the image, ${\theta }_{{x}_{m},{y}_{k}}$ represents the color of the pixel in the coordinate $|{x}_{m}\rangle$ $|{y}_{k}\rangle$, and n = m + k.

The NASS state $|{\psi }_{3}\rangle$ of a video can represented by

$$|{\psi }_{3}\rangle =\sum _{{x}_{m}=0}^{{2}^{m}-1}\,\sum _{{y}_{k}=0}^{{2}^{k}-1}\,\sum _{{t}_{h}=0}^{{2}^{h}-1}\,{\theta }_{{x}_{m},{y}_{k},{t}_{h}}|{x}_{m}\rangle |{y}_{k}\rangle |{t}_{h}\rangle ,$$

(51)

where $|{x}_{m}\rangle =|{i}_{n}\ldots {i}_{h+k+1}\rangle$, $|{y}_{k}\rangle =|{i}_{h+k}\ldots {i}_{h+1}\rangle$ and $|{t}_{h}\rangle =|{i}_{h}\ldots {i}_{1}\rangle$ are the X-axis, Y-axis and time-axis of a video, and n = m + k + h.

More details are shown in our previous work⁶. For instance, the NASS state

$$|{\psi }_{2}\rangle =\sum _{{x}_{3}=0}^{{2}^{3}-1}\,\sum _{{y}_{2}=0}^{{2}^{2}-1}\,{\theta }_{{x}_{3},{y}_{2}}|{x}_{3}\rangle |{y}_{2}\rangle ={\theta }_{0,0}|000\rangle |00\rangle +\cdots +{\theta }_{7,3}|111\rangle |11\rangle $$

(52)

represents the color image of 8 × 4 (height multiplies weight) as shown in (a) of Fig. 23.

Figure 23

The image and the video.

The NASS state

$$|{\psi }_{3}\rangle =\sum _{{x}_{2}=0}^{{2}^{2}-1}\,\sum _{{y}_{1}=0}^{1}\,\sum _{{t}_{2}=0}^{{2}^{2}-1}\,{\theta }_{{x}_{m},{y}_{k},{t}_{h}}|{x}_{2}\rangle |{y}_{1}\rangle |{t}_{2}\rangle ={\theta }_{0,0,0}|00\rangle |0\rangle |00\rangle +\cdots +{\theta }_{3,1,3}|11\rangle |1\rangle |11\rangle $$

(53)

represents the video with four frames as shown in (b) of Fig. 23, where each frame is a 4 × 2 image.

The same string can have different meanings corresponding to different data types in classic computers. For instance, a binary string 0100001 can represent a char ‘A’ or a number 65. Similarly, using the circuit in⁶, we can store an image (shown in (a) of Fig. 23) or a video (shown in (b) of Fig. 23) in the following state

$$|\psi \rangle =\sum _{i=0}^{{2}^{5}-1}\,{\theta }_{i}|i\rangle .$$

(54)

Meanwhile, the priori knowledge ‘x₃, y₂’ or ‘x₂, y₁, t₂’ is equivalent to a data type, implying an image or a video stored in the state $|\psi \rangle$.

A natural image with size of 2ⁿ × 2^m can be expressed as an angle matrix

$${{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}=[\begin{array}{cccc}{\theta }_{0,0} & {\theta }_{0,1} & \cdots & {\theta }_{0,{2}^{m}-1}\\ {\theta }_{1,0} & {\theta }_{1,1} & \cdots & {\theta }_{1,{2}^{m}-1}\\ \vdots & \vdots & \cdots & \vdots \\ {\theta }_{{2}^{n}-1,0} & {\theta }_{{2}^{n}-1,1} & \cdots & {\theta }_{{2}^{n}-1,{2}^{m}-1}\end{array}],$$

(55)

where θ_x,y is the color information of the pixel on the coordinate (x, y) and an example is shown in Fig. 23.

Thus, the 2D wavelet transform on ${{\rm{\Lambda }}}_{{2}^{n}{\mathrm{,2}}^{m}}$ is defined as

$$wt2({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}})={W}_{{2}^{n}}\times {{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}\times {W}_{{2}^{m}}^{T},$$

(56)

where ${W}_{{2}^{n}}$ and ${W}_{{2}^{m}}$ are 2ⁿ × 2ⁿ and 2^m × 2^m wavelet transforms, respectively

An image can be stored in the state NASS $|{\psi }_{2}\rangle$ in (50) by using a quantum circuit in the literature⁶. Suppose that the function $f(\,\cdot \,)$ is equivalent to the quantum circuit implementing the storage of the image ${{\rm{\Lambda }}}_{{2}^{n}{\mathrm{,2}}^{m}}$, that is,

$$f({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}})=|{\psi }_{2}\rangle =[\begin{array}{c}{B}_{0}^{T}\\ \vdots \\ {B}_{{2}^{n}-1}^{T}\end{array}],$$

(57)

where ${B}_{j}=[{\theta }_{j,0}\,{\theta }_{j,1}\,\cdots \,{\theta }_{j,{2}^{m}-1}]$ is the row vector of ${{\rm{\Lambda }}}_{{2}^{n}{\mathrm{,2}}^{m}}$ and 0 ≤ j ≤ 2ⁿ − 1.

Applying the function $f(\,\cdot \,)$ on ${{\rm{\Lambda }}}_{{2}^{n}{\mathrm{,2}}^{m}}\times {W}_{{2}^{m}}^{T}$, the result is

$$f({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}\times {W}_{{2}^{m}}^{T})=({I}_{{2}^{n}}\otimes {W}_{{2}^{m}})f({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}).$$

(58)

Using the perfect shuffle permutation ${P}_{{2}^{m}{\mathrm{,2}}^{n}}$, we obtain

$$f({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}})={P}_{{2}^{m},{2}^{n}}f({({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}})}^{T}).$$

(59)

Then, we have

$$f({W}_{{2}^{n}}{{\rm{\Lambda }}}_{{2}^{n},{2}^{m}})=({W}_{{2}^{n}}\otimes {I}_{{2}^{m}})f({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}),$$

(60)

$$f({W}_{{2}^{n}}{{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}{W}_{{2}^{m}}^{T})=({W}_{{2}^{n}}\otimes {W}_{{2}^{m}})f({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}).$$

(61)

Then, the 2D QWPT of ${{\rm{\Lambda }}}_{{2}^{n}{\mathrm{,2}}^{m}}$ is given by

$$f(wt2({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}))=({W}_{{2}^{n}}\otimes {W}_{{2}^{m}})|{\psi }_{2}\rangle .$$

(62)

A video of 2^p frames of size 2ⁿ × 2^m corresponds to the following angle matrix.

$${A}_{{2}^{n},{2}^{m},{2}^{p}}=({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}^{1},{{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}^{2},\cdots ,{{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}^{{2}^{p}}),$$

(63)

where the angle matrix ${{\rm{\Lambda }}}_{{2}^{n}{\mathrm{,2}}^{m}}^{k}$ is the k-th frame.

We firstly define the following DWPTs: ${W}^{x}(\,\cdot \,)$, ${W}^{y}(\,\cdot \,)$ and ${W}^{t}(\,\cdot \,)$.

$$\{\begin{array}{l}{W}^{x}({A}_{{2}^{n},{2}^{m},{2}^{p}})=({W}_{{2}^{n}}{{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}^{1},\,\cdots ,{W}_{{2}^{n}}{{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}^{{2}^{p}}),\\ {W}^{y}({A}_{{2}^{n},{2}^{m},{2}^{p}})=({{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}^{1}{W}_{{2}^{m}}^{T},\,\cdots ,{{\rm{\Lambda }}}_{{2}^{n},{2}^{m}}^{{2}^{p}}{W}_{{2}^{m}}^{T}),\\ {W}^{t}({A}_{{2}^{n},{2}^{m},{2}^{p}})=({C}_{{2}^{n},{2}^{m}}^{1},{C}_{{2}^{n},{2}^{m}}^{2},\,\cdots ,{C}_{{2}^{n},{2}^{m}}^{{2}^{p}}),\end{array}$$

(64)

with the row vectors

$$\{\begin{array}{l}[{C}_{x,y}^{1}\,{C}_{x,y}^{2}\,\cdots \,{C}_{x,y}^{{2}^{p}}]={u}_{x,y}\times {W}_{{2}^{m}}^{T},\\ {u}_{x,y}=[{\theta }_{x,y}^{1}\,{\theta }_{x,y}^{2}\,\cdots \,{\theta }_{x,y}^{{2}^{p}}],\end{array}$$

(65)

where ${C}_{x,y}^{j}$ and ${\theta }_{x,y}^{j}$ are the elements of the matrices ${C}_{{2}^{n}{\mathrm{,2}}^{m}}^{j}$ and ${{\rm{\Lambda }}}_{{2}^{n}{\mathrm{,2}}^{m}}^{j}$ on the position (x, y), respectively.

Next, the 3D DFPT of ${A}_{{2}^{n}{\mathrm{,2}}^{m}{\mathrm{,2}}^{p}}$ can be defined as

$$wt3({A}_{{2}^{n},{2}^{m},{2}^{p}})={W}^{t}({W}^{y}({W}^{x}({A}_{{2}^{n},{2}^{m},{2}^{p}}))).$$

(66)

Similarly, we utilize the equivalent function of the quantum circuit to create the NASS state of ${A}_{{2}^{n}{\mathrm{,2}}^{m}{\mathrm{,2}}^{p}}$

$$|{\psi }_{3}\rangle =f({A}_{{2}^{n},{2}^{m},{2}^{p}})={[{u}_{0,0}\cdots {u}_{0,{2}^{m}-1}{u}_{1,0}\cdots {u}_{1,{2}^{m}-1}\cdots {u}_{{2}^{n}-1,0}\cdots {u}_{{2}^{n}-1,{2}^{m}-1}]}^{T},$$

(67)

where the row vector u_x,y is shown in equation (65).

Applying the function $f(\,\cdot \,)$ on ${F}^{t}({A}_{{2}^{n}{\mathrm{,2}}^{m}{\mathrm{,2}}^{p}})$, ${F}^{y}({A}_{{2}^{n}{\mathrm{,2}}^{m}{\mathrm{,2}}^{p}})$ and ${F}^{x}({A}_{{2}^{n}{\mathrm{,2}}^{m}{\mathrm{,2}}^{p}})$ respectively, we have the following three equations.

$$\{\begin{array}{rcl}f({W}^{t}({A}_{{2}^{n},{2}^{m},{2}^{p}})) & = & ({I}_{{2}^{n+m}}\otimes {W}_{{2}^{p}})|{\psi }_{3}\rangle ,\\ f({W}^{y}({A}_{{2}^{n},{2}^{m},{2}^{p}})) & = & ({I}_{{2}^{n}}\otimes {W}_{{2}^{m}}\otimes {I}_{{2}^{p}})|{\psi }_{3}\rangle ,\\ f({W}^{x}({A}_{{2}^{n},{2}^{m},{2}^{p}})) & = & ({W}_{{2}^{n}}\otimes {I}_{{2}^{m}}\otimes {I}_{{2}^{p}})|{\psi }_{3}\rangle .\end{array}$$

(68)

Therefore, we derive the 3D QWPT of ${A}_{{2}^{n}{\mathrm{,2}}^{m}{\mathrm{,2}}^{p}}$

$$f(wt3({A}_{{2}^{n},{2}^{m},{2}^{p}}))=({W}_{{2}^{n}}\otimes {W}_{{2}^{m}}\otimes {W}_{{2}^{p}})|{\psi }_{3}\rangle .$$

(69)

Substituting our proposed 1D QWPT into equations (62) and (69), we obtain 2D HQWPT, 2D DQWPT, 3D HQWPT and 3D DQWPT. Furthermore, their circuits can be designed in Figs 24 and 25.

Figure 24

The quantum circuits of the 2D QWPT and IQWPT with 1 ≤ k ≤ min(m, n) − 1 in (e,f), 1 ≤ k ≤ min(m, n) − 2 in (f,h).

Figure 25

The quantum circuits of the 2D QWPT and IQWPT with 1 ≤ k ≤ min(m, n, p) − 1 in (e,f), 1 ≤ k ≤ min(m, n, p) − 2 in (f,h).

Simulation Experiments

In the absence of a quantum computer to implement our proposed QWPTs, experiments of quantum signals are simulated on a classical computer. The quantum signals are stored in quantum states (i.e., column vectors) and the QWPTs are implemented using unitary matrices in Matlab (the R2010bversion).

Simulation experiments of the 1D HQWPT and DQWPT

Consider a quantum state

$$|v\rangle =\frac{1}{\sqrt{\sum _{i=0}^{2047}{({v}_{i})}^{2}}}\,{[{v}_{0}{v}_{1}\cdots {v}_{2047}]}^{T}$$

(70)

as an input signal of the QWT, where v_k = d(k/2048), k = 0, …, 2047, and $d(t)=\sqrt{t(1-t)}\,\sin \,(\frac{2\pi \,\ast \,1.05}{t+0.05})$.

For simply, we can take a vector

$$S={[{v}_{0}{v}_{1}\cdots {v}_{2047}]}^{T}$$

(71)

as the input signal of simulation experiments, which is according with the state $|v\rangle$ without the normalized item.

For convenience, let the single-level HQWPT and DQWPT be

$${R}_{{2}^{11}}^{0}={P}_{{2}^{n-1},2}({I}_{{2}^{n-1}}\otimes H),{A}_{{2}^{11}}^{0}={T}_{{2}^{11}}.$$

(72)

Applying multi-level HQWPT ${R}_{{2}^{11}}^{k},k=0,1,\ldots 10$ and multi-level DQWPT ${A}_{{2}^{11}}^{k},k=0,1,\ldots 9$ to the input signal S in Eq. (71), the simulation results of the first 3 levels are shown in Fig. 26 with multi-windows. Table 1 shows the comparison of simulation experiments of our proposed QWPT and the function of the WPT in Matlab using the 2-norm function $norm()$. The symbols in this table are listed as follows:

$$\{\begin{array}{l}{M}_{1}^{k}={R}_{{2}^{11}}^{k}\times S,0\le k\le 10,\\ {M}_{2}^{k}={({R}_{{2}^{11}}^{k})}^{-1}\times {M}_{1}^{k},0\le k\le 10,\\ {M}_{3}^{k}={A}_{{2}^{11}}^{k}\times S,0\le k\le 9,\\ {M}_{4}^{k}={({A}_{{2}^{11}}^{k})}^{-1}\times {M}_{3}^{k},0\le k\le 9.\end{array}$$

(73)

Figure 26

The simulation results of the first 3 levels of HQWPT and DQWPT. The left number i refers to i-level QWT with 1 ≤ i ≤ 10, and i = 0 refers to the input signal.

Table 1 The simulation results of the HQWT, IHQWT and HWT.

The function $wpdec(S,k+1,^{\prime} db1^{\prime} )$ in Matlab performs a (k + 1)-level HWPT to return a wavelet packet tree. Next, we get the coefficients of the nodes of the wavelet packet tree using the function $wpcoef()$ to construct a vector ${M}_{5}^{k}$. similarly, we obtain a a vector ${M}_{6}^{k}$ of a (k + 1)-level DWPT based on the periodization extension by the $wpdec(S,k+1,^{\prime} db2^{\prime} )$ and $wpcoef()$.

Simulation experiments of the 2D HQWPT and DQWPT

An angle matrix Λ_g is given by

$${{\rm{\Lambda }}}_{g}=\frac{\pi {C}_{g}}{2\times {2}^{8}-2}{A}_{g},$$

(74)

where A_g is the 128 × 128 matrix of the gray-scale image shown in Fig. 27(a), and C_g is a constant corresponding to the image.

Figure 27

The simulation results of the first 2 levels of HQWPT and DQWPT.

The NASS state $|{\psi }_{2}\rangle =f({{\rm{\Lambda }}}_{g})$ can be regarded as a column vector, where the function $f(\,\cdot \,)$ is defined in equation (57). Applying the k + 1 level 2D HQWPT and DQWPT on the image A_g, respectively, the results are

$$\{\begin{array}{l}{Q}_{1}^{k}=\frac{2\times {2}^{8}-2}{\pi {C}_{g}}{f}^{-1}(({R}_{{2}^{7}}^{k}\otimes {R}_{{2}^{7}}^{k})|{\psi }_{2}\rangle ),\\ {Q}_{3}^{k}=\frac{2\times {2}^{8}-2}{\pi {C}_{g}}{f}^{-1}(({A}_{{2}^{7}}^{k}\otimes {A}_{{2}^{7}}^{k})|{\psi }_{2}\rangle ),\end{array}$$

(75)

where ${f}^{-1}(\,\cdot \,)$ is the inverse function of $f(\,\cdot \,)$, which converts a column vector into a 2-dimension matrix.

The simulation results are shown in Fig. 27 and Table 2. The rest symbols in Table 2 are: ${Q}_{2}^{k}=|{\psi }_{2}\rangle -$ $({({R}_{{2}^{7}}^{k})}^{-1}\otimes {({R}_{{2}^{7}}^{k})}^{-1})[({R}_{{2}^{7}}^{k}\otimes {R}_{{2}^{7}}^{k})|{\psi }_{2}\rangle ]$, ${Q}_{2}^{k}=|{\psi }_{2}\rangle -({({A}_{{2}^{7}}^{k})}^{-1}\otimes {({A}_{{2}^{7}}^{k})}^{-1})\,[({A}_{{2}^{7}}^{k}\otimes {A}_{{2}^{7}}^{k})|{\psi }_{2}\rangle ]$. Similarly with the 1D HQWPT and DQWPT, matrices ${Q}_{5}^{k}$ and ${Q}_{6}^{k}$ are created using the functions $wpdec2({A}_{g},k+1,^{\prime} db1^{\prime} )$, $wpdec2({A}_{g},k+1,^{\prime} db2^{\prime} )$ and $wpcoef()$, respectively.

Table 2 The simulation results of the 2D HQWT, IHQWT and HWT.

Simulation experiments of the 3D HQWPT and DQWPT

An angle matrix Λ_c is given by

$${{\rm{\Lambda }}}_{c}=\frac{\pi {C}_{c}}{2\times {2}^{8}-2}{V}_{t},$$

(76)

where V_t is the 64 × 64 × 4 matrix of the video shown in (a) of Fig. 28, and C_c is a constant corresponding to the video.

Figure 28

The simulation results of the first 2 levels of the 3D HQWPT and DQWPT.

The NASS state $|{\psi }_{3}\rangle =f({{\rm{\Lambda }}}_{c})$ can be regarded as a column vector, where the function $f(\,\cdot \,)$ is defined in equation (67). Applying the k + 1 level 3D HQWPT and DQWPT on the video V_t, respectively, the results are

$$\{\begin{array}{l}{V}_{1}^{k}=\frac{2\times {2}^{8}-2}{\pi {C}_{g}}{f}^{-1}(({R}_{{2}^{6}}^{k}\otimes {R}_{{2}^{6}}^{k}\otimes {R}_{{2}^{6}}^{k})|{\psi }_{3}\rangle ),\\ {V}_{3}^{k}=\frac{2\times {2}^{8}-2}{\pi {C}_{g}}{f}^{-1}(({A}_{{2}^{6}}^{k}\otimes {A}_{{2}^{6}}^{k}\otimes {A}_{{2}^{6}}^{k})|{\psi }_{3}\rangle ),\end{array}$$

(77)

where ${f}^{-1}(\,\cdot \,)$ converts a column vector into a 3-dimension matrix.

The simulation results are shown in Fig. 28 and Table 3. Since there are no functions of the 3D WPT, we realize wt3 in (66) using the functions $wpdec\mathrm{2()}$ and $wpdec()$ and note ${V}_{5}^{k}$ and ${V}_{6}^{k}$ as results of 3D HWPT and DWPT, respectively. The rest symbols in Table 2 are ${V}_{2}^{k}=|{\psi }_{3}\rangle -({({R}_{{2}^{6}}^{k})}^{-1}\otimes {({R}_{{2}^{5}}^{k})}^{-1}\otimes {({R}_{{2}^{3}}^{k})}^{-1})\,[({R}_{{2}^{6}}^{k}\otimes {R}_{{2}^{5}}^{k}\otimes {R}_{{2}^{3}}^{k})\,|{\psi }_{3}\rangle ]$ and ${V}_{4}^{k}=|{\psi }_{3}\rangle -({({A}_{{2}^{6}}^{k})}^{-1}\otimes {({A}_{{2}^{5}}^{k})}^{-1}\otimes {({A}_{{2}^{3}}^{k})}^{-1})\,[({A}_{{2}^{6}}^{k}\otimes {A}_{{2}^{5}}^{k}\otimes {A}_{{2}^{3}}^{k})\,|{\psi }_{3}\rangle ]$.

Table 3 The simulation results of the 3D HQWT, IHQWT and HWT.

Analyzing the above simulation experiments, we conclude that our proposed HQWPT, IHQWPT, DQWPT and IDQWPT can implement decompositions and reconstructions of the Haar wavelet and D4 wavelet, respectively. The simulation results of our proposed HQWPT and DQWPT, which are equal to the corresponding WPTs without consideration of truncation error on machine computing, show our proposed QWPTs are correct.

Conclusion and Future Works

This article has constructed the iteration equations of multi-level and multi-dimensional QWPTs by GTP and PSP. The iteration equations include HQWPT, DQWPT based on the periodization extension and their inverse transforms for the first time, which ensure the theoretical correctness of our proposed QWPTs. Next, we have designed circuits of the proposed QWPTs. The precise analysis of the quantum costs and the time complexities of circuits prove that our proposed QWPTs are of high-efficiency. For instance, the time complexities of the multi-level HQWPT and DQWPT at most are 6 and (5n³ + O(n²)) on 2ⁿ, respectively. In contrast, the classical fast WPTs need O(n2ⁿ) basic operations to implement the discrete wavelet transform^21,32. Thus, our proposed QWPT can exponentially speed up the computation of the wavelet transform in comparison to the one on a classical computer. The simulation results show that our proposed QWTs are correct and effective. In summary, the proposed QWPTS and IQWPTs can implement effective decompositions and reconstructions of 1D signals, 2D images and 3D vedio, respectively. Therefore, the article provide a feasible scheme for the WPT to be applied in QIP.

Studies of quantum wavelet packet are still in their infancy. Multi-level and multi-dimension wavelet transforms play an important role in classical image and signal processing, therefore, their quantum versions will be significant and core tool algorithms for quantum image and signal processing. Our future works are how to use these wavelet transforms to implement some complex operations, such as quantum image and signal compression, and quantum image and signal denoising.