Abstract
This research paper examines the characteristics of a two-dimensional steady flow involving an incompressible viscous Casson fluid past an elastic surface that is both permeable and convectively heated, with the added feature of slip velocity. In contrast to Darcy’s Law, the current model incorporates the use of Forchheimer’s Law, which accounts for the non-linear resistance that becomes significant at higher flow velocities. The accomplishments of this study hold significant relevance, both in terms of theoretical advancements in mathematical modeling of Casson fluid flow with heat mass transfer in engineering systems, as well as in the context of practical engineering cooling applications. The study takes into account the collective influences of magnetic field, suction mechanism, convective heating, heat generation, viscous dissipation, and chemical reactions. The research incorporates the consideration of fluid properties that vary with respect to temperature or concentration, and solves the governing equations by employing similarity transformations and the shooting approach. The heat transfer process is significantly affected by the presence of heat generation and viscous dissipation. Furthermore, the study illustrates and presents the impact of various physical factors on the dimensionless temperature, velocity, and concentration. From an engineering perspective, the local Nusselt number, the skin friction, and local Sherwood number are also depicted and provided in graphical and tabular formats. In the domains of energy engineering and thermal management in particular, these results have practical relevance in improving our understanding of heat transmission in similar settings. Finally, the thorough comparison analysis reveals a significant level of alignment with the outcomes of the earlier investigations, thus validating the reliability and effectiveness of our obtained results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Scientists have been studying the motion of non-Newtonian fluids within the boundary layer for the past few years. These fluids have important features that have several applications in technological and industrial operations, such as food, particular separation methods, paper production petroleum drilling, and more. Drilling muds, clay coatings, synthetic lubricants, biological fluids including blood, specific oils, sugar solutions, and paints are a few examples of non-Newtonian fluids [1, 2]. The fundamental Navier-Stokes equations are unable to completely describe the dynamic behaviour of non-Newtonian fluid flow because of the complex mathematical expressions involved in the flow problems. Because of this, these equations are unable to instantly portray all of the features of such fluid flow fields. To characterise the behavior of non-Newtonian fluids while taking into consideration their rheological characteristics, numerous models have been devised. Carreau, Williamson, Burger, Viscoelastic, Casson, Eyring-Powell, Micropolar, Seely, Hyperbolic, Oldroyd-B, Bulky, Oldroyd-A, Maxwell, Jeffrey, and more models are included in this group. Researchers can examine and comprehend the distinct rheological characteristics of non-Newtonian fluids by using the various perspectives that each model offers on the flow behavior of these fluids. The Casson model, which was first presented by Casson [3], is among the models that has the most bearing on our understanding of the characteristics of blood and suspensions in daily life. This model has become a crucial tool for researching these fluids’ characteristics and behaviours since it clearly addresses how they behave. A specific kind of plastic fluid model called the Casson model exhibits a number of distinguishing characteristics, such as shear thinning behaviour, a yield stress threshold, and high viscosity at high shear circumstances. When the applied shear stress is greater than the yield stress, the Casson fluid behaves physically in a way that resembles a solid. The Casson fluid, however, starts to deform as soon as the shear stress exceeds the yield stress. This phenomenon is discussed in detail by Rohni et al. [4]. Eldabe and Salwa [5] conducted a study to examine the flow characteristics of a Casson fluid in the region between two cylinders that were rotating. In their research, Pramanik [6] examined the effects of thermal radiation on the steady boundary layer flow and heat transfer of a Casson fluid over a stretching surface with exponential permeability. The research conducted by Rao et al. [7] suggests that when the Casson fluid model is subjected to extremely high wall shear stresses, it can be simplified and treated as a Newtonian fluid. The impact of Dufour and Soret mechanism on the magnetohydrodynamic flow of a Casson fluid was investigated by Hayat et al. in their work [8]. Mustafa et al. [9] conducted a study on the unsteady boundary layer flow and heat transfer of a Casson fluid over a moving flat plate with a parallel free stream. To tackle the issue analytically, they used the Homotopy analysis technique. Alali and Megahed [10] utilized a shooting numerical method to investigate the impact of mass heat transmission on the flow of a dissipative Casson nanofluid liquid film.
Fluid flow within a porous medium involves the movement of a fluid through a substance that has interconnected empty spaces. This can be seen in materials like soil, sand, or rock. The flow occurs because of differences in pressure or concentrations, and it is significant in various natural and human-made systems. The structure of the porous material affects how the fluid flows, including factors like the size of the empty spaces, how they connect, and their winding paths. The interaction between the fluid and the porous medium follows principles of fluid mechanics, particularly Darcy’s law [11], which explains the relationship between the fluid’s speed, pressure changes, and the permeability of the medium. Understanding and researching fluid flow in porous materials are crucial for fields like hydrogeology, gas-cleaning filtration, petroleum engineering, environmental science, and managing groundwater resources.
Dupuit [12] and Forchheimer [13] achieved a great advancement in the field of fluid flow through their empirical discoveries. They discovered that the resistance or drag a fluid encounters grows in a quadratic connection with the velocity of the fluid flow. In other words, when velocity increases, the drag force acting on the fluid quadratically increases. This finding has ramifications for a variety of engineering and scientific applications and offers important new insight into the behavior of fluid flow. In their investigation, Ali et al. [14] considered the Darcy–Forchheimer model to analyze the Casson nanofluid flow across a non-linearly diminishing surface. Their study’s goal was to look at how slip conditions and viscous dissipation affect flow behaviour. A considerable amount of researches [15,16,17,18,19,20,21] can be found in the literature regarding the Darcy model and the Forchheimer model in the context of fluid flow through porous media. The Darcy–Forchheimer model serves as a versatile and essential instrument in fluid dynamics, with its utility extending across fields such as groundwater hydrology, petroleum engineering, filtration processes, and more. Its capacity to precisely depict non-linear fluid flow through porous media renders it indispensable for comprehending and refining diverse engineering systems and operations in both natural and industrial settings. Therefore, the literature provides an extensive array of studies [22,23,24,25] that explore the uses, constraints, and improvements of both the Darcy and Forchheimer models concerning fluid flow through porous media.
It becomes clear from a careful review of the literature that there is a notable lack of scientific research examining the combined effects of heat generation, viscous dissipation, slip velocity, and variable fluid properties on the flow behavior of Casson fluids, as well as their related heat and mass transfer characteristics. The simultaneous influence of these elements has not yet been thoroughly investigated, indicating a large research gap in the area. In a Darcy–Forchheimer porous media, this work intends to investigate the hydrodynamic flow of a Casson fluid past a permeable stretched sheet with slip circumstances. A magnetic field, viscous dissipation, slip velocity, chemical reaction, and convective heating are among the additional aspects that the analysis takes into account. The main goal is to look at how these parameters collectively affect the Casson fluid system’s flow behaviour and heat transfer properties.
2 Flow Analysis
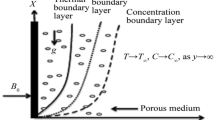
The study examines the properties of a Casson fluid flowing past a linearly stretching, convectively heated permeable surface in an incompressible, stable, two-dimensional laminar boundary layer. The physical flow concept is illustrated visually in Fig. 1 and the surface velocity is given as \(U_{w}=ax\), where a is a constant.
In this study, the x-axis is defined parallel to the direction of the plate, while the y-axis is perpendicular to it. Heat and mass transfer models are examined to account for the presence of chemical reaction, viscous dissipation and slip conditions. The velocity components in the x and y directions are represented by u and v, respectively. The analysis assumes that the boundary conditions of slip are present on the plate’s surface. The Casson temperature away the sheet is assumed to be \(T_{\infty }\), while the concentration of the fluid at the same location is assumed to be \(C_{\infty }\). Furthermore, in accordance with previous work [26], the equations governing the boundary layer flow through a Darcy–Forchheimer porous medium with heat and mass transfer of the Casson fluid are formulated as follows:
where \(\rho _{\infty }\) is the ambient fluid density, \(\beta \) is the Casson parameter, \(c_{p}\) is the specific heat at constant pressure, C represents the fluid concentration, k is the permeability of the porous medium, \(\kappa \) denotes the thermal conductivity of the Casson fluid and F is the Forchheimer drag force coefficient. It is noteworthy that as the parameter \(\beta \) tends towards infinity, our previously utilized non-Newtonian Casson model can be converted into a Newtonian model. \(K_{1}\) is the coefficient of chemical reaction, \(\sigma \) is the electrical conductivity, \(B_{0}\) is the magnetic field strength, D is the Brownian diffusion coefficient, \(\kappa (T)\) is the thermal conductivity of the Casson fluid and \(\mu (T)\) is the fluid viscosity. Additionally, the variable Q denotes the amount of heat produced (when \(Q>0\)) or consumption (when \(Q<0\)) per unit volume. The research carried out by Gomathy and Kumar [27] served as the basis for the particular expression for the term Q.
In the fluid system, the parameter \(\delta \) represents the temperature-dependent heat generation or absorption. When heat is generated, \(\delta \) is positive, and when heat is absorbed, \(\delta \) is negative. We consider the significant association between the fluid viscosity, designated as \(\mu (T)\), and the fluid temperature in our analysis as follows [28]:
where \(\alpha \) is the viscosity parameter, \(\mu _{\infty }\) is the ambient viscosity, \(T_{f}\) is the temperature of the convective fluid below the stretching sheet, which can be assumed to take the form \(T_{f}=T_{\infty }+nx^{2}\). Additionally, it is anticipated that the fluid’s thermal conductivity will follow the following relation [28]:
where \(\kappa _{\infty }\) represents the thermal conductivity of the fluid at the ambient and \(\varepsilon _{1}\) is the thermal conductivity parameter. Further, the fluid concentration is expressed in the following form [29]:
where \(\varepsilon _{2}\) represents the diffusion parameter and \(D_{\infty }\) is the ambient diffusivity.
The appropriate boundary conditions for the present problem are described as follows [29]:
Now, we presented a set of appropriate transformations in terms of a new similarity variable \(\eta \) that can be summarized as follows [29]:
It is important to note that with each \(\eta \) under consideration, a set of equations is developed, encompassing pertinent governing parameters. The selection of \(\eta \) serves the purpose of defining dimensionless parameters that govern the behavior of the reduced equation system. In the given context, f, \(\theta \), and \(\phi \) represent the stream function, the dimensionless temperature, and the dimensionless concentration, respectively. By applying the suitable transformation mentioned earlier (11)–(12), the partial differential equation that governs the proposed model (2)–(4) together with the given boundary conditions (9)–(10) is converted into an ordinary differential equation, as illustrated below:
With the following boundary condition:
Clearly that the factors denoting the parameters that influence the previously governing equations are diverse. These factors encompass a range of variables such as Forchheimer parameter \(F_{r}\), suction parameter S, magnetic parameter M, Darcy number \(D_{a}\), Eckert number Ec, chemical reaction parameter R, Biot number \(B_{i}\), Prandtl number \({\text {Pr}}\), Schmidt number Sc and the slip velocity parameter \(\lambda \), which are defined as follows:
3 Physical and Engineering Quantities
The drag coefficient \(Cf_{x}\), energy transfer rate \(Nu_{x}\), and mass transfer rate \(Sh_{x}\) are examples of the physical quantities associated with the system. These quantities can be expressed in a simplified, non-dimensional form as follows:
where \(Re_{x}=\frac{U_{w} x}{\nu _{\infty }}\) denotes the local Reynold number.
4 Shooting Method Algorithms
Due to the significant nonlinearity present in the system described by equations (13) through (15), it is imperative to employ numerical methods for obtaining solutions. Here, we have utilized the shooting method to accomplish this objective. The shooting technique for solving boundary value ordinary differential equations entails converting the initial boundary problem into an initial value problem, alongside transforming the set of ordinary differential equations into a system of first-order equations. Here is a concise overview of the algorithm:
-
1.
Initial Guess: Select an initial estimation for the values of the unknown parameters or initial conditions.
-
2.
Integrate ODEs: Numerically integrate the system of first-order ordinary differential equations using the provided initial guesses.
-
3.
Evaluate Residuals: Assess the residuals by comparing the acquired solution with the specified boundary conditions.
-
4.
Iteration: Iterate through the preceding steps until the solution approaches the designated boundary conditions within an acceptable tolerance.
-
5.
Convergence Check: Verify convergence by observing the variation in the solution across iterations. If the change falls within the predefined tolerance, deem the solution as converged.
-
6.
Final Solution: Upon reaching convergence, the determined values for the unknown parameters or initial conditions serve as the solution to the nonlinear system of boundary value ordinary differential equations.
Further, the efficacy of the shooting method hinges on the initial guess and convergence criteria. Runge–Kutta methods or similar numerical techniques are employed for integrating the ODEs. Iterative application of the algorithm continues until the solution satisfies the accuracy or convergence requirements.
5 Code Verification
To confirm the present-day outcomes and assess the reliability of the existing assessment, we conducted comparisons with available data on the skin friction coefficient for the proposed Casson fluid. In Table 1, we present a comparison between our findings of the skin friction coefficient and the results obtained by Mabood et al. [30]. During this comparison, we observe a significant agreement between our findings and those presented in the table. The results indicate that the skin friction coefficient exhibits an upward trend as the magnetic parameter M increases.
6 Discussion of Numerical Results
This study looked at how heat and mass transfer effect the motion of a non-Newtonian Casson fluid with heat generation. The porous media, whose characteristics vary has a permeable sheet through which the fluid flows. The impact of Forchheimer’s Law is also taken into account in the study. Mathematically, the equations (13)–(15) and the accompanying boundary conditions in equations (16)–(17) have been resolved by combining shooting and Runge–Kutta approaches. Graphs are used to represent the contributions of various flow parameters in the study, including the magnetic parameter M, suction parameter S, Casson parameter \(\beta \), chemical reaction parameter R, viscosity parameter \(\alpha \), Forchheimer parameter \(F_{r}\), Darcy number \(D_{a}\), Prandtl number \({\text {Pr}}\), Biot number \(B_{i}\), and others. These graphs illustrate the relationship between these parameters and their impact on the system. Figure 2 showcases the influence of the magnetic factor M on the velocity \(f'(\eta )\) and temperature \(\theta (\eta )\) profiles of the flow of Casson fluid. The effect of the magnetic factor on the temperature and fluid velocity profiles is depicted in this figure. The velocity is seen to decrease over the whole boundary layer as the magnetic factor values rise. The temperature, on the other hand, displays a distinct pattern, initially rising near the sheet’s surface then reversing to fall.
The magnitude of the Darcy number’s \(D_{a}\) influence on the flow rate or velocity \(f'(\eta )\) and temperature proportions \(\theta (\eta )\) is seen in Fig. 3. The Darcy number, in essence, signifies the relative magnitude of viscous forces compared to inertial forces within the flow of a porous medium. Generally speaking, an increase in the Darcy number causes a rise in fluid velocity and a fall in fluid temperature. This is so because the Darcy number identifies the proportion of inertial to viscous forces in a flow through a porous medium. Physically, an increase in the Darcy number signifies a greater influence of viscous forces relative to inertial forces. Consequently, the resistance to flow within the porous medium becomes more prominent compared to the fluid’s momentum. Consequently, the fluid velocity decreases as the flow encounters increased resistance, making it more challenging for the fluid to traverse through the porous medium.
Figure 4 illustrates how the concentration profile \(\phi (\eta )\) is influenced by variations in both the magnetic parameter M and the Darcy parameter \(D_{a}\). This figure demonstrates that an increase in the magnetic parameter leads to an enhancement of the dimensionless concentration profile and the boundary layer thickness, whereas the opposite effect is observed for the Darcy number.
Figure 5 showcases the effects of the Forchheimer parameter \(F_{r}\) on the velocity \(f'(\eta )\) and temperature \(\theta (\eta )\) profiles. From this figure, it is evident that increasing the values of the Forchheimer parameter leads to a reduction in velocity across the entire boundary layer region. However, the temperature profile near the surface of the sheet exhibits the opposite trend when influenced by the same parameter.
The temperature \(\theta (\eta )\) and velocity \(f'(\eta )\) profiles are also impacted by the slip velocity parameter \(\lambda \), as seen in Fig. 6. With a boost in the slip velocity parameter, as shown in this figure, both the temperature and the velocity profiles decline. Physically, the slip effect gets more noticeable as the slip velocity parameter rises, which speeds up the rate at which heat is transferred from the fluid to the solid. As more heat is transmitted to the solid surface as a result, the fluid’s temperature decreases.
Figure 7 illustrates the variations in the concentration profile for different values of both the Forchheimer parameter \(F_{r}\) and the slip velocity parameter \(\lambda \). The figure demonstrates that the concentration profile \(\phi (\eta )\) and the associated thickness of the boundary layer are slightly enhanced by the first parameter, but they experience a significant enhancement with the second parameter.
Figure 8 shows how the viscosity parameter \(\alpha \) affects both the velocity \(f'(\eta )\) and temperature \(\theta (\eta )\) curves. This figure demonstrates that the viscosity parameter has a decreasing relationship with both the temperature and velocity profiles. Higher viscosity physically translates to greater flow resistance, which causes more internal friction inside the fluid. The fluid’s temperature drops as a result of the enhanced heat dissipation that results from this.
Figure 9 visually represents the impact of the Casson parameter \(\beta \) on both the temperature and velocity curves. The Casson fluid flow’s temperature and the thickness of its thermal boundary layer both drop as the Casson parameter rises, as seen by the plot. Additionally, as the Casson parameter is improved, the fluid velocity away from the sheet also declines. Physically, the yield stress of the Casson fluid weakens as the Casson factor values rise, enhancing the plastic dynamic viscosity. As a result, the thermal boundary layer’s thickness in the flow temperature profile decreases.
Suction parameter S effects on temperature \(\theta (\eta )\) and velocity \(f'(\eta )\) profiles are shown in Fig. 10. The opposing relationship between the suction parameter’s uplifting values and the structures of the momentum boundary layer, Casson fluid velocity, and temperature distribution can be observed from Fig. 10. Physically, the rate of fluid removal from the boundary layer grows in direct proportion to the suction parameter. The thermal boundary layer’s thickness decreases as a result, and the amount of heat that is transferred from the fluid to the surface also diminishes. It follows that the temperature of the fluid drops.
The concentration field \(\phi (\eta )\) is influenced by the suction parameter S and chemical reaction parameter R, as depicted in Fig. 11. A drop in the concentration profile and the thickness of the related boundary layer has been seen when both the suction parameter and the concentration of the chemical reactive species are increased.
Figure 12 illustrates the relationship between the heat generation parameter \(\delta \) and the Biot number \(B_{i}\) in terms of the temperature distribution \(\theta (\eta )\). In physical terms, the Biot number \(B_{i}\) can be understood as the ratio between the internal thermal resistance at the surface of a body and the thermal resistance of the boundary layer. According to findings, thermal convection near the surface strengthens as the Biot number \(B_{i}\) increases, causing the fluid’s temperature distribution to accelerate. In other words, greater values of the Biot number \(B_{i}\) are related with thicker fluid boundary layers and higher temperature profiles. Similarly, the heat generation parameter \(\delta \) exhibits a similar effect on both the temperature field \(\theta (\eta )\) and the thickness of the thermal boundary layer.
Figure 13a shows how the thermal conductivity parameter \(\varepsilon _{1}\) affects the temperature profile \(\theta (\eta )\). This graph shows how, when the thermal conductivity parameter climbs, the temperature profile away the sheet and the thermal thickness rises as well. Figure 13b shows the diffusion parameter’s influence on the concentration field. A higher value of the diffusion parameter is observed to result in an increase in both the fluid concentration and the thickness of the boundary layer. The rate of diffusion physically increases with a bigger diffusion parameter. By spreading out and dispersing more equally throughout the system, this causes a more effective mixing of the fluid and enables molecules or particles to move about more freely. Because of this, when the diffusion parameter is greater, the fluid concentration tends to rise.
The skin friction coefficient \(Re_{x}^{\frac{1}{2}}Cf_{x}\), local Nusselt number \(Re_{x}^{\frac{-1}{2}} Nu_{x}\), and the local Sherwood number \(Re_{x}^{\frac{-1}{2}} Sh_{x}\) were calculated using fixed values \(Pr=6.2, Sc=0.9, \varepsilon _{1}=0.2, R=0.2\) and \(\varepsilon _{2}=0.2\), while considering the effects of different remaining governing factors such as magnetic parameter (\(M= 0.0, 0.5, 1.5\)), Darcy number (\(D_{a}=3, 7, 10\)), Forchheimer parameter (\(F_{r}=0.0, 1.5, 2.5\)), slip velocity parameter (\(\lambda =0.0, 0.2, 0.4\)), viscosity parameter (\(\alpha =0.0, 0.5, 1.5\)), Casson parameter (\(\beta = 0.0, 0.5, 1.0\)), suction parameter (\(S=0.0, 0.5, 1.5\)), Biot number (\(B_{i}=0.1, 0.3, 0.5\)) and heat generation parameter (\(\delta =0.0, 1.0, 2.5\)) in Table 2. This table shows that as the Darcy number, slip velocity parameter, viscosity parameter, and Casson parameter increase, the skin friction coefficient drops. In addition, as the magnetic, Forchheimer, viscosity, and heat generating parameters rise, the Nusselt number also falls. On the other hand, the Darcy number, slip velocity parameter, and suction parameter show the opposite pattern. The table also shows that, whereas the opposite tendency is seen for the other parameters, the Sherwood number enhances as the Darcy number and suction parameter rise.
7 Conclusion
This study’s objective was to look into the heat and mass transfer processes that occur when a Casson fluid flows across a permeable stretched sheet while being exposed to a steady magnetic field. The research considered the flow occurring within a porous medium, where the Forchheimer’s Law was followed. Additionally, the study examined the influences of heat generation, slip velocity, variable fluid properties, chemical reaction, and convection phenomenon. The authors employed similarity transformations and the shooting method to solve the governing equations in the research. Graphs and tables were included to facilitate the visual and quantitative analysis of the obtained results. The primary findings are summarized as follows:
-
1.
As the chemical reaction parameter increased, there was a degenerate in fluid concentration. However, the slip velocity parameter and the diffusion parameter showed an opposite trend, with their increase resulting in an increase in fluid concentration.
-
2.
Observations indicate that elevating the suction and chemical reaction parameters leads to a deterioration in fluid concentration.
-
3.
Increasing the slip velocity parameter results in a degradation of both the temperature and velocity of the Casson fluid.
-
4.
Large values of the magnetic and Forchheimer parameters are found to degenerate the velocity profile, whilst the Darcy number shows the opposite trend.
-
5.
Raising the Casson parameter causes the fluid flow near the sheet surface to have higher velocity profiles and lower temperature profiles.
-
6.
Future research avenues stemming from this study might involve exploring hybrid Casson nanofluids within non-Darcian porous medium under varied thermal property conditions, which stands out as a substantial area of interest.
Availability of data and materials
No data.
References
Abdelsalam Sara, I., Abbas, W., Megahed, A.M., Said, A.A.M.: A comparative study on the rheological properties of upper convected Maxwell fluid along a permeable stretched sheet. Heliyon 9, 1–10 (2023)
Abbas, W., Megahed, A.M., Ibrahim, M.A., Said, A.A.M.: Ohmic dissipation impact on flow of Casson-Williamson fluid over a slippery surface through a porous medium. Indian J. Phys. 97, 4277–4283 (2023)
Casson, N.: Flow equation for pigment oil suspensions of the printing ink type. In: Mill, C.C. (ed.) Rheology of Disperse Systems, pp. 84–102. Pergamon Press, Oxford (1959)
Rohni, A.M., Dero, S., Saaban, A.: Triple solutions and stability analysis of mixed convection boundary flow of Casson nanofluid over an exponentially vertical stretching/shrinking sheet. J. Adv. Res. Fluid Mech. Therm. Sci. 72, 94–110 (2020)
Eldabe, N.T.M., Salwa, M.G.E.: Heat transfer of MHD non-Newtonian Casson fluid flow between two rotating cylinder. J. Phys. Soc. Jpn. 64, 41–64 (1995)
Pramanik, S.: Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng. J. 5, 205–212 (2014)
Rao, A.S., Prasad, V.R., Reddy, N.B., Bég, O.A.: Heat transfer in a Casson rheological fluid from a semi-infinite vertical plate with partial slip. Heat Trans. Asian Res. 44, 272–291 (2015)
Hayat, T., Shehzadi, S.A., Alsaedi, A.: Soret and Dufour effects on magnetohydrodynamic (MHD) flow of Casson fluid. Appl. Math. Mech. Engl. 33, 1301–1312 (2012)
Mustafa, M., Hayat, T., Pop, I., Aziz, A.: Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate. Heat Transfer 40, 563–576 (2011)
Alali, E., Megahed, A.M.: MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nanotechnol. Rev. 11, 463–472 (2022)
Darcy, H.P.C.: Les Fontsines Publiques de la Ville de Dijon. Victor Dalmont, Paris (1856)
Dupuit, J.: Etudes Theoriques et Pratiques sur le Mouvement des Eaux. Dunod, Paris (1863)
Forchheimer, P.: Wasserbewegung durch Boden. VDI Z. 45, 1782–1788 (1901)
Ali, L., Omar, Z., Khan, I., Raza, J., Bakouri, M., Tlili, I.: Stability analysis of Darcy-Forchheimer flow of Casson type nanofluid over an exponential sheet: investigation of critical points. Symmetry 11, 412 (2019)
Khader, M.M., Megahed, A.M.: On the numerical solution for the flow and heat transfer in a thin liquid film over an unsteady stretching sheet in a saturated porous medium in the presence of thermal radiation. J. Appl. Mech. Tech. Phys. 53, 710–721 (2012)
Mahmoud, M.A.A., Megahed, A.M.: Thermal radiation effect on mixed convection heat and mass transfer of a non-Newtonian fluid over a vertical surface embedded in a porous medium in the presence of thermal-diffusion and diffusion-thermo. J. Appl. Mech. Tech. Phys. 54, 90–99 (2013)
Khader, M.M., Megahed, A.M.: Effect of viscous dissipation on the boundary layer flow and heat transfer past a permeable stretching surface embedded in a porous medium with a second-order slip using Chebyshev finite difference method. Transp. Porous Media 105, 487–501 (2014)
Yousef, N.S., Megahed, A.M., Ghoneim, N.I., Elsafi, M., Fares, E.: Chemical reaction impact on MHD dissipative Casson-Williamson nanofluid flow over a slippery stretching sheet through porous medium. Alex. Eng. J. 61, 10161–10170 (2022)
Elsaid Essam, M., Abedel-Aal, E.M., et al.: Darcy-Forchheimer flow of a nanofluid over a porous plate with thermal radiation and Brownian motion. J. Nanofluids 12, 55–64 (2023)
Shahzad, A., Imran, M., Tahir, M., Khan, S.A., Akgül, A., Abdullaev, S., Park, C., Zahran, H.Y., Yahia, I.S.: Brownian motion and thermophoretic diffusion impact on Darcy-Forchheimer flow of bioconvective micropolar nanofluid between double disks with Cattaneo-Christov heat flux. Alex. Eng. J. 62, 1–15 (2023)
Abbas, W., Attia, H.A., Abdeen, M.A.M.: Non-Darcy effect on non-Newtonian Bingham fluid with heat transfer between two parallel plates. Bull. Chem. Commun. 48, 497–505 (2016)
Rahman, S., Díaz, P.J., L., González J. R.: Analysis and profiles of travelling wave solutions to a Darcy–Forchheimer fluid formulated with a non-linear diffusion. AIMS Math. 7, 6898–6914 (2022)
Muhammad, T., Alsaedi, A., Hayat, T., Shehzad, S.A.: A revised model for Darcy-Forchheimer three-dimensional flow of nanofluid subject to convective boundary condition. Results Phys. 7, 2791–2797 (2017)
Díaz Palencia, J.L., Rahman, S.: Geometric perturbation theory and travelling waves profiles analysis in a Darcy-Forchheimer fluid model. J. Nonlinear Math. Phys. 29, 556–572 (2022)
Díaz Palencia, J.L.: A mathematical analysis of an extended MHD Darcy-Forchheimer type fluid. Sci. Rep. 12, 5228 (2022)
Oyelakin, I.S., Mondal, S., Sibanda, P.: Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alex. Eng. J. 55, 1025–1035 (2016)
Gomathy, G., Kumar, B.R.: Variable thermal conductivity and viscosity effects on thin film flow over an unsteady porous stretching sheet. J. Porous Media 14, 77–94 (2023)
Abbas, W., Megahed, A.M., Morsy, O.M., Ibrahim, M.A., Said, A.A.M.: Dissipative Williamson fluid flow with double diffusive Cattaneo-Christov model due to a slippery stretching sheet embedded in a porous medium. AIMS Math. 7, 20781–20796 (2022)
Abbas, W., Megahed, A.M., Ibrahim, M.A., Said, A.A.M.: Non-Newtonian slippery nanofuid flow due to a stretching sheet through a porous medium with heat generation and thermal slip. J. Nonlinear Math. Phys. (2023). https://doi.org/10.1007/s44198-023-00125-5
Mabood, F., Shateyi, S.: Multiple slip effects on MHD unsteady flow heat and mass transfer impinging on permeable stretching sheet with radiation. Mod. Simul. Eng. 2019, 1–12 (2019)
Acknowledgements
The researchers wish to extend their sincere gratitude to the Deanship of Scientific Research at the Islamic University of Madinah for the support provided to the Post-Publishing Program.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
The study’s conception and design involved the participation of all authors. SG, WA, and AAM conducted the material preparation. AM and EF were responsible for data collection and analysis. WA and AM wrote the initial draft of the manuscript, and all authors provided feedback on earlier versions. The final manuscript was read and approved by all authors.
Corresponding author
Ethics declarations
Conflict of interest
We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Elgendi, S.G., Abbas, W., Said, A.A.M. et al. Computational Analysis of the Dissipative Casson Fluid Flow Originating from a Slippery Sheet in Porous Media. J Nonlinear Math Phys 31, 19 (2024). https://doi.org/10.1007/s44198-024-00183-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s44198-024-00183-3