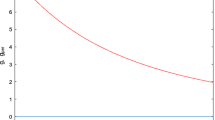
Abstract
The intention along the presented analysis is to develop existence, uniqueness and asymptotic analysis of solutions to a magnetohydrodynamic (MHD) flow saturating porous medium. The influence of a porous medium is provided by the Darcy–Forchheimer conditions. Firstly, the existence and uniqueness topics are developed making used of a weak formulation. Once solutions are shown to exist regularly, the problem is converted into the Travelling Waves (TW) domain to study the asymptotic behaviour supported by the Geometric Perturbation Theory (GPT). Based on this, analytical expressions are constructed to the velocity profile for the mentioned Darcy–Forchheimer flow. Afterwards, the approximated solutions based on the GPT approach are shown to be sufficiently accurate for a range of travelling waves speeds in the interval [2.5, 2.8].
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flow of materials saturating porous media is quite prevalent in geophysical and physiological processes. These processes in particular may include gall blander with stones, tumor growth dynamics, porous catalysis, nuclear reactors cooling, soil pollution, oil enhanced recovery, fuel cells, combustion technology, water movement in reservoirs, fermentation, grain storage etc. However, much attention in previous literature on this topic has been focused to the description of porous medium contribution by classical Darcy’s expression. It is obvious that Darcy’s law does not account the boundary and inertia effects in the flow. In addition, the porous media in most modern processes have been characterized via higher velocities where the corresponding Reynolds number is greater than one (see [1,2,3,4,5,6,7,8,9,10] and studies therein).
There exists a wide literature dealing with the Darcy–Forchheimer flow modelling and resolution with numerical means. In [24], the authors study a fluid flow across a bank of circular cylinders with Darcy–Forchheimer drag. To this end, a numerical technique is developed to account for the irregular domain studied. In [25], the authors analyze the flow motivated by a rotating disk with heat in a three-dimensional nanoliquid flow of Darcy–Forchheimer type. Firstly, the set of equations are converted into a system of ODEs and a shooting method is employed to support the construction of a numerical scheme. Note that these cited references have been selected on the basis of a representative set of examples in the field. Unlike the cited references and along the presented analysis in the coming sections, the intention is to explore solutions to a Darcy–Forchheimer model within the Travelling Waves (TW) scope. A travelling wave is a kind of wave that advances in a particular direction while retaining a fixed shape. Moreover, a travelling wave is associated with having a constant velocity throughout its course of propagation. Such waves are observed in many areas of science: For instance in combustion, which may occur as a result of a chemical reaction [11]. As well in mathematical biology to model the impulses that are apparent in a neural network [12]. Also, in conservation laws associated to problems in fluid dynamics, shock profiles are characterised as travelling waves [13]. Further, the structures in solid mechanics are typically modelled as standing waves [14].
Along the presented analysis, the relevant nonlinear flow equations are given by the following set of equations (refer to [20] for a modern derivation of typical fluids models, as Darcy and Forchheimer ones, under the scope of the Theory of Porous Media):
where P is the pressure field, \(\nu =\frac{\mu }{\rho }\) is the kinematic viscosity, F the nonuniform inertia coefficient in the porous medium, \(\rho \) the density, \(\mu \) the dynamic viscosity, \(\Phi \) the porosity, K the permeability of the medium, \(\sigma \) represents the charges distribution and \(B_0\) the intensity of an applied magnetic field. Firstly, differentiate (1.2) with regards to x:
After integration, we obtain the constant \(K_1 = -\frac{1}{\rho }\frac{\partial P}{\partial x}\).
The equation (1.2) becomes then
Along the following sections, we study existence and uniqueness in the solutions. Afterwards, we make use of the TW structures of solutions and the Geometric Perturbation Theory to build solutions in the proximity of the critical point.
It shall be noted that the theory of parabolic operators and non-linear reaction theory have been widely exposed in [21, 22] and [23] where existence and uniqueness general principles are exposed. Along the presented analysis, it is the intention to provide insights on existence and uniqueness of weak solutions due to the generalized initial condition \(u_{0}(y) \in L^\infty (\mathbb {R}) \cap L^1 (\mathbb {R})\).
2 Preliminaries
The following is a definition of a weak solutions to (1.2):
Definition 1
Admit a test function \(\phi\;\in\;C^{\infty }\;\left( \mathbb {R}\right) \), such that for \(0<\tau<t<T,\) the following weak solution to (1.2) holds:
3 Existence and Uniqueness of Solutions
Based on the weak solution defined, consider \(r = \vert y \vert>> r_{0}\) (where \(r_0\) is a finite arbitrary spatial value) and the domain \(B_r\) as a ball of radium r. Admit the following equation:
defined in \(B_{r}\times \left[ 0,T\right] ,\) so that along the border \(\partial B_r\) a semi-compact supported \(\phi \) function is given to control any possible global unexpected behaviour of solutions under the non-linear terms involved, i.e:
with the initial condition \(u\left( y,0\right) =u_{0}\left( y\right) \in L^\infty (\mathbb {R}) \cap L^1 (\mathbb {R})\).
Based on this defined problem with borders, the following existence theorem is shown:
Theorem 1
Given \(u_{0}(y) \in L^\infty (\mathbb {R}) \cap L^1 (\mathbb {R}) \), any solution u(y, t) is bounded for all \(\left( y,t\right) \in B_{r}\times \left[ 0,T\right] \) with \(r>>1.\)
Proof
The idea is to study solution bounds based on a weak formulation under potential irregular initial data under the functional space \( L^\infty (\mathbb {R}) \cap L^1 (\mathbb {R})\). To this end, a cut-off function, \(\psi \), is defined to control the variations along the borders of \(B_r\) inspired by an idea in [15]. To this end, consider \(\eta \in \mathbb {R}^{+}\), so that:
so that
Multiplying (3.1) by \(\psi _{\eta }\) and integrating in \(B_{r}\times \left[ \tau ,T\right] ,\) we obtain
The integral for the diffusive term reads
Then the equation (3.2)
Under the positive parabolic condition in the involved gaussian operator and for some large \(r>>r_{0}>1\), it is possible to make use of known results obtained to a generalized non-linear diffusion under regions with positive solutions. The spatial diffusion term \(\frac{\partial ^2 u}{\partial y^2}<< \frac{\partial ^2 u^m}{\partial y^2}\), for \(m>1\) and for an arbitrary big u, so that the following results from [15] hold
For \(m=2,\) we get
Then
Next, consider a test function \(\phi \) of the form
where \(g\left( s\right) >0\) for \(0<s<t,\) \(g\left( t\right) =0\) and \(\beta \) is chosen for convergence of (3.4). Therefore
For \(\beta >\frac{5}{2}\) and \(r\rightarrow \infty ,\) the right hand integrals above tend to zero. Then for any r, the right hand side term is finite with a bounding constant A. Then:
Considering (3.2) and \(K_1>>1\) together with the introduced positive condition \(u>0\) :
Note that the involved supporting function \(\phi \), \(\phi _t\) and \(\psi _\eta \) are positive, bounded and finite in \(\tau<s<t<T,\) then it is possible to conclude the theorem postulations on the boundness of solutions in \( B_{r}\times \left[ 0,T\right] \) for any pair of finite r, T, than can be considered sufficiently large. \(\square \)
The next intention is to show the uniqueness of solutions.
Theorem 2
Let \(u>0\) and \({\hat{u}}>0\) be a minimal and a maximal solution respectively to 1.3\(\mathbb {R}\times \left( 0,T\right) \). Then, the minimal u coincides with the maximal solution \({\hat{u}}\), i.e the solution is unique.
Proof
Let \({\hat{u}}\) be the maximal solution to (1.3) in \( \mathbb {R}\times \left( 0,T\right) \) defined as per evolution of the following initial condition:
with \(\epsilon >0\) arbitrary small. In addition, let define the minimal solution upon evolution of the initial condition \( u\left( y,0\right) =u_{0}\left( y\right) \).
Both the maximal and the minimal solutions satisfy the following set of equations
Considering the associated weak formulation for every test function \(\phi \in C^{\infty }\left( \mathbb {R}\right) ,\) the following expression holds after subs-traction:
Admit the test function
where \(K_{2}\) and \(\gamma \) are constants. Differentiate \(\phi \) with regards to t and y to obtain:
Then
where \(L_{1}=\max _{\mathbb {R}} \lbrace {\hat{u}} + u \rbrace \) is bounded as shown in Theorem 1. Since \(K_{2}\) is constant, a suitable value can be chosen considering:
so that
The expression (3.6) becomes
Admit the following order preserving differentiation with regards to t to obtain:
Let
then (3.7) becomes
with
After solving (3.8) by standard means, we get \(g\left( t\right) =\epsilon \rightarrow 0,\) i.e \( {\hat{u}}\rightarrow u,\) which shows the uniqueness postulation. \(\square \)
4 Travelling Waves Existence and Regularity
The TW profiles are defined as \(u\left( y,t\right) =f\left( \zeta \right) ,\) \(\zeta =y-at\in \mathbb {R},\) where a is the TW speed and \( f:\mathbb {R} \rightarrow \left( 0,\infty \right) \) belongs to \(L^{\infty }\left( \mathbb {R}\right) \) as per the boundness condition shown in Theorem 1. Then, the Eq. (1.3) is transformed to the TW domain as per:
with
We introduce the new variables:
so that, the following system holds
To determine the critical points \(X^{\prime }=0\) and \(Y^{\prime }=0,\) then:
So that the following are solutions:
Consequently, \(\left( X_{1},0\right) \) and \(\left( X_{2},0\right) \) are the system critical points. The intention, now, is to make use of the Geometric Perturbation Theory to characterize the obtained critical points and to determine the orbits close such critical conditions.
4.1 Geometric Perturbation Theory (GPT)
A singular geometric perturbation approach is employed in this section to show the asymptotic behaviour of a manifold defined to make simpler the assessment of a TW analytical profile.
For this purpose, define firstly the following manifold as:
under the flow (4.2) and with critical points \(\left( X_{1},0\right) ,\) \(\left( X_{2},0\right) .\) Admit the following perturbed manifold \( M_{\epsilon }\) close to \(M_{0}\) in the critical point \((X_1,0)\):
where \(\epsilon \) represents a perturbation close the equilibrium \((X_1,0)\) and B is a suitable constant obtained after root factorization. Now, let \(\hat{X_{2}}=X-X_{2}\). The intention is to use the Fenichel invariant manifold theorem [12] as formulated in [13] and [14] to determine the hyperbolic condition of \(M_\epsilon \). For this purpose, it is required to show that \(M_{0}\) is a normally hyperbolic manifold, i.e. the eigenvalues of \(M_{0}\) in the linearized frame close to the critical point, and transversal to the tangent space, have non-zero real part. This is shown based on the following equivalent flow associated to \(M_{0}:\)
The associated eigenvalues are both real \(\left( \pm \sqrt{B}\epsilon \right) .\) Hence \(M_{0}\) is a hyperbolic manifold. The next step is to show that the manifold \(M_{\epsilon }\) is locally invariant under the flow (4.2), so that the manifold \(M_{0}\) can be represented as an asymptotic approach to \(M_{\epsilon }\). For this purpose, consider the functions
which are \(C^{i}\left( \mathbb {R} \times \left[ 0,\delta \right] \right) \), \(i>0\), in the proximity of the critical point \(\left( X_{1},0\right) .\) In this case, \(\delta \) is determined based on the following flows that are considered to be measurable a.e. in \(\mathbb {R}\)
where \(\delta = B \Vert {\hat{X}}_2\Vert \) is finite given the boundness properties of solutions. The distance between the manifolds keeps the normal hyperbolic condition for \(\delta \in \left( 0,\infty \right) \) and for \(\epsilon \) sufficiently small close the critical point \((X_1, 0)\).
Now we take the following perturbed manifold \( M_{\beta }\) close to \(M_{0}\) in the critical point \((X_2,0)\):
where \(\beta \) is a perturbation close the equilibrium \((X_2,0)\) and A is a suitable constant obtained after root factorization. Now, let \(\hat{X_{1}}=X-X_{1}\), then the Fenichel invariant manifold theorem can apply in the same manner as for critical point \((X_1, 0).\) Note the following equivalent flow associated to \(M_{0}:\)
The associated eigenvalues are both real \(\left( \pm \sqrt{A}\beta \right) .\) Hence \(M_{0}\) is a hyperbolic manifold. In the same manner, the next intention is to show that the manifold \(M_{\beta }\) is locally invariant under the flow (4.2), so that the manifold \(M_{0}\) can be represented as an asymptotic approach to \(M_{\beta }\). For this purpose, consider the functions
which are \(C^{i}\left( \mathbb {R} \times \left[ 0,\gamma \right] \right) \), \(i>0\), in the proximity of the critical point \(\left( X_{2},0\right) .\) Note that \(\gamma \) is determined based on the following flows that are considered to be measurable a.e. in \(\mathbb {R}\)
where \(\gamma = A \Vert {\hat{X}}_1\Vert \) is finite given the boundness properties of solutions. The distance between the manifolds keeps the normal hyperbolic condition for \(\gamma \in \left( 0,\infty \right) \) and for \(\beta \) sufficiently small close the critical point \((X_2, 0)\).
Once we have shown that the manifold \(M_{0 }\) remains invariant with regards to manifolds \(M_{\epsilon }\) and \(M_{\beta }\) under the flow (4.2), the TW profiles can be obtained operating in the linearized perturbed manifolds close to \(M_{0 }.\)
4.2 Travelling Waves Profiles
Based on the normal hyperbolic condition in the manifold \(M_{0}\) under the flow (4.2), asymptotic TW profiles can be obtained. For this purpose, consider, firstly, (4.2) so that the following expression provides the family of trajectories in the phase plane \(\left( X,Y\right) \):
The intention is to determine a trajectory in the phase plane closed the equilibrium \((X_1, 0)\). This is shown based on a comparison with subsolutions for a sufficiently small and supersolutions for a sufficiently large together with a topological argument and the continuity of H. Admit \(a \rightarrow 0\) then it is possible to find a suitable value of \(K_1\) such that \(dY_1/dX_1 > 0\) while when \(a>> 0\), it is possible to conclude on a condition of the form \(\, dY_1/dX_1 < 0\) for suitable values in the involved constants. Given the continuity of H, it is possible, hence to conclude on the existence of a critical trajectory close the critical point \((X_1,0)\) of the form:
which implies that
Solving (4.3) by using separation of variables, we obtain
which implies that
close the critical point \((X_1,0)\).
Note that growing TW is obtained by replacing \((-\zeta )\) by the symmetric \((\zeta )\) and taking \(\frac{\rho K_{1}}{F}=1\), we get:
The same process shall be repeated to determine a trajectory in the phase plane closed the equilibrium \((X_2, 0)\). Admit \(a \rightarrow 0\) then it is possible to find a suitable value of \(K_1\) such that \(dY_2/dX_2 > 0\). Similarly, for \(a>> 0\), \(\, dY_2/dX_2 < 0\) for suitable values in the involved constants. Given the continuity of H, it is possible, hence to conclude on the existence of a critical trajectory close the critical point \((X_2,0)\) of the form:
which implies that
Solving (4.4) by using separation of variables, we obtain
which implies that
close the critical point \((X_2,0)\).
Note that growing TW is obtained by replacing \((-\zeta )\) by the symmetric \((\zeta )\) and taking \(\frac{\rho K_{1}}{F}=1\), we get:
5 Numerical Assessments
The intention along this section is to develop a numerical simulation to determine a suitable TW-speed for which the approximated TW solution obtained in the previous section can fit the actual solution. The numerical approach has been performed considering the following bullets:
-
The numerical simulation is executed with the Matlab function bvp4c. This function is based on a Runge–Kutta implicit approach with interpolant extensions [19]. The bvp4c collocation method requires to specify pseudo-boundary conditions. In this case, the left boundary is considered positive (for instance \(f(-\infty ) = 1\)) and the right boundary coincides with the stationary conditions \(X_1\) and \(X_2\). To simplify the numerical representations, the solutions are translated into the zero state by the standard vertical translation.
-
The interval for integration is assumed as \((-100, 100)\). It has been considered sufficiently large to avoid any impact of the boundary condition over the integration domain of interest.
-
The domain has been split into 100000 nodes with an absolute error of \(10^{-6}\) during the computation.
-
The involved constants related with fluid and porous medium properties (see expressions (1.3) and (4.1)) have been considered to have a value of one. Hence, the only variable for a parametric analysis is the TW-speed (a).
The results are compiled in Figs. 1, 2, 3, 4. It is possible to check that there exists a TW-speed (a) for which both, the approximated and simulated, solutions evolves closely. This speed has been sharply assessed to be in the interval [2.5, 2.8] (see Fig. 2). If the TW-speed is increased, both solutions diverges leading to a less accurate approximation. Note that the particular values considered for the involved parameters provide the described interval in the TW-speed. If any other combination is considered, then such assessed speed interval will be modified. Although, this is an important limitation, it is relevant to highlight that the numerical exercise has the intention of providing a validating proof for the involved analytical assessments. Hence, it is possible to conclude that the analytical paths are suitable and reproducible via a numerical scheme.
The blue line represents the numerical simulation to the system (4.2). The red line represents the approximated solution in the TW profile obtained in (4.5). Solutions on the left are provided for \(a = 1\) and solutions on the right for \(a= 1.5\). Both solutions have been translated into zero when \(\xi \rightarrow \infty \) for simplification purposes. It is possible to check the exponential behaviour of both the accurate and approximated solutions
The blue line represents the numerical simulation to the system (4.2). The red line represents the approximated solution in the TW profile obtained in (4.5). Solutions on the left are provided for \(a = 2.5\) and solutions on the right for \(a= 2.8\). Both solutions have been translated into zero when \(\xi \rightarrow \infty \) for simplification purposes. It is possible to check the exponential behaviour of both the accurate and approximated solutions. Note that for \(a = 2.5\), the simulated solution is above the approximated while for \(a = 2.8\) is below
The blue line represents the numerical simulation to the system (4.2). The red line represents the approximated solution in the TW profile obtained in (4.5). Solutions on the left are provided for \(a = 3\) and solutions on the right for \(a= 3.38\). Both solutions have been translated into zero when \(\xi \rightarrow \infty \) for simplification purposes. It is possible to check the exponential behaviour of both the accurate and approximated solutions
The blue line represents the numerical simulation to the system (4.2). The red line represents the approximated solution in the TW profile obtained in (4.5). Solutions on the left are provided for \(a = 10\) and solutions on the right for \(a= 100\). Both solutions have been translated into zero when \(\xi \rightarrow \infty \) for simplification purposes. It is possible to check the exponential behaviour of both the accurate and approximated solutions
6 Conclusions
Along the presented analysis, existence and uniqueness results have been provided to a Darcy–Forchheimer flow. Solutions have been explored in the TW domain and approximated solutions have been obtained making used of the GPT approach. Finally, the analytical conceptions followed have been validated with the use of a numerical simulation. Note that GPT solutions have been shown to evolve close the actual solution for a range of TW-speeds \(a \in [2.5,2.8]\). The numerical assessments have been done for particular values in the involved parameters, but it permits to validate the analytical solutions so that they can be used for other parametric values.
Data Availibility Statement
The authors declare that data can be made available upon request.
Abbreviations
- GPT:
-
Geometric perturbation theory
- TW:
-
Travelling wave(s)
References
Jawad, M., Shah, Z., Islam, S., Bonyah, E., Khan, A.Z.: Darcy–Forchheimer flow of MHD nanofluid thin film flow with Joule dissipation and Naviers partial slip. J. Phys. Commun. 2(11), 115014 (2018)
Rasool, G., Zhang, T., Chamkha, A.J., Shafiq, A., Tlili, I., Shahzadi, G.: Entropy generation and consequences of binary chemical reaction on MHD Darcy–Forchheimer Williamson nanofluid flow over non-linearly stretching surface. Entropy 22(1), 18 (2020)
Saif, R.S., Muhammad, T., Sadia, H.: Significance of inclined magnetic field in Darcy-Forchheimer flow with variable porosity and thermal conductivity. Phys. A Stati. Mech. Appl. 551, 124067 (2020)
Rasool, G., Shafiq, A., Khan, I., Baleanu, D., Nisar, K.S., Shahzadi, G.: Entropy generation and consequences of MHD in Darcy–Forchheimer nanofluid flow bounded by non-linearly stretching surface. Symmetry 12(4), 652 (2020)
Sadiq, M.A., Hayat, T.: Darcy–Forchheimer flow of magneto Maxwell liquid bounded by convectively heated sheet. Results Phys. 6, 884–890 (2016)
Sajid, T., Sagheer, M., Hussain, S., Bilal, M.: Darcy–Forchheimer flow of Maxwell nanofluid flow with nonlinear thermal radiation and activation energy. AIP Adv. 8(3), 035102 (2018)
Hayat, T., Rafique, K., Muhammad, T., Alsaedi, A., Ayub, M.: Carbon nanotubes significance in Darcy–Forchheimer flow. Results Phys. 8, 26–33 (2018)
Hayat, T., Haider, F., Muhammad, T., Alsaedi, A.: On Darcy–Forchheimer flow of carbon nanotubes due to a rotating disk. Int. J. Heat Mass Transfer 112, 248–254 (2017)
Saif, R. S., Hayat, T., Ellahi, R., Muhammad, T., Alsaedi, A.: Darcy–Forchheimer flow of nanofluid due to a curved stretching surface. Int. J. Numer. Methods Heat Fluid Flow (2019)
Kieu, T.: Existence of a solution for generalized Forchheimer flow in porous media with minimal regularity conditions. J. Math. Phys. 61(1), 013507 (2020)
Volpert, A.: Traveling wave solutions of parabolic systems
Murray, J.: Mathematical Biology Biomathematics. Springer, Berlin Heidelberg (2013)
Smoller, J.: Shock Waves and Reaction Diffusion Equations, vol. 258. Springer, Berlin (2012)
Champneys, A., Hunt, G., Thompson, J.: Localization and Solitary Waves in Solid Mechanics. Advanced Series in Nonlinear Dynamics, World Scientific, Singapore (1999)
De Pablo, A., Vázquez, J.L.: Travelling waves and finite propagation in a reaction diffusion equation. J. Differ. Equ. 93, 19–61 (1991)
Fenichel, N.: Persistence and smoothness of invariant manifolds for flows. Indiana Univ. Math. J. 21, 193–226 (1971)
Akveld, M.E., Hulshof, J.: Travelling wave solutions of a fourth-order semilinear diffusion equation. Appl. Math. Lett. 11(3), 115–120 (1998)
Jones, C.K.R.T., Geometric, C.K.: singular Perturbation Theory in Dynamical Systems. Springer, Berlín (1995)
Enright, H., Muir P.H.: A Runge-Kutta type boundary value ODE solver with defect control. In: Teh. Rep. 267/93, University of Toronto, Dept. of Computer Sciences. Toronto. Canada (1993)
Ehlers, W.: Darcy–Forchheimer. Brinkman and Richards: classical hydromechanical equations and their significance in the light of the TPM. Arch. Appl. Mech. (2021). https://doi.org/10.1007/s00419-020-01802-3
LadyZenskaja , O.A., Solonnikov, V.A. and Uralceva, N.N.: Linear and quasilinear equations of parabolic type. Translated from the Russian by S. Smith. Translations of Mathematical Monographs, Vol. 23. American Mathematical Society, Providence, R.I. (1968)
Ladyzhenskaya, O.A., Uraltseva, N.N.: Linear and Quasilinear Elliptic equations. Academic Press, New York (1973)
Oleĭnik, O.A., Kruzhkov, S.N.: Quasilinear second-order parabolic equations with many independent variables. Russ. Math. Surv. 0036-0279 16(5), 105–146 (1961)
Lee, S.L., Yang, J.H.: Modeling of Darcy–Forchheimer drag for fluid flow across a bank of circular cylinders. Int. J. Heat Mass Transfer 40(13), 3149–3155 (1997)
Zaka, U., Stefano, S. and Dumitru, B.: A Numerical simulation for Darcy–Forchheimer flow of nanofluid by a rotating disk with partial slip effects. Front. Phys. 7 (2020). https://doi.org/10.3389/fphy.2019.00219
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
JL and SR conceived the study and the overall manuscript design. JL and SR carried out the analytical studies. SR has performed the specific analytical assessment with the revision of JL. SR and JL have make a revision of the manuscript. JL has carried out the numerical simulations. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Consent for Publication
Authors declare the consent for manuscript publication.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Palencia, J.L.D., Rahman, S. Geometric Perturbation Theory and Travelling Waves profiles analysis in a Darcy–Forchheimer fluid model. J Nonlinear Math Phys 29, 556–572 (2022). https://doi.org/10.1007/s44198-022-00041-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s44198-022-00041-0