1 Introduction

The studying of the characteristics of flow and heat transfer over stretched surfaces was considerable interest by the researchers due to its importance in many applications of technology, industrial, and science such as fiber production, condensation process, and textiles machines plastic sheets and etc. [1]. Nadeem and Hussain [2] investigate the heat transmission of Williamson fluid flow passing on a porous stretched sheet. Megahed [3] studies the Powell-Eyring fluid flow and heat transfer over an exponentially stretched continuous porous surface with a growing temperature distribution of heat flux and changing thermal conductivity. The analysis of computational solution of viscosity and sloped Lorentz force effects on Williamson nanofluid flow passing on a stretching sheet is carried out by Khan et al. [4]. The nanofluid MHD (magnetohydrodynamics) flow which microstructure and micropolar with magnetic field on micropolar ferrofluid flow over stretching/shrinking sheet is inspected by Patel et al. [5]. Kumar et al. [6] researched the effects of mixed convection, viscous flow, and heat dissipation, on continuous nanofluid flow over a stretched sheet in a porous media. Humane et al. [7] investigates the Casson-Williamson fluid flow through a stretching, porous sheet under the influence of heat radiation, chemical processes, and an external magnetic field. Unsteady heat and mass transmission, magnetohydrodynamics (MHD) nanofluid flow via an extending sheet with Soret, Dufour, mixed convection and Variable thermal conductivity effects under nonlinear thermal radiation and viscous dissipation are investigated by Siddique et al. [8]. Additionally, various researchers looked at the fluid flow under flexible sheets with different thicknesses, as shown in the references ([9,10,11]).

Over the years, the non-Newtonian fluid flow has been widely interested by researchers for their numerous uses in industrial, Technological, and biomedical applications, such as polymers, nuclear systems, food processing, coal slurries, clay mixtures, lubricants, oil retrieval, etc. ([12, 13]). Numerous studies have examined this subject and its many applications. The effective thermal conductivity of oil in nanotube suspensions was measured by Choia et al. [14]. Mahmoud [15] investigated the impacts of radiation and variable conductivity on an electrically conducting non-Newtonian micropolar fluid flow with heat transfer passing on stretching varying temperature sheet. For non-Newtonian Williamson fluid flow, Khan et al. [16] investigated the steady boundary layer of Blasius, Sakiadis, stretching, and stagnation-point flows. Seth et al. ([17, 18]) investigated the unsteady magnetohydrodynamic Casson fluid flow through a non-Darcy porous vertical oscillating plate, with viscous dissipation, thermo-diffusion and Joule heating impacts. Hashim et al. [19] examined numerically the problem of flow and heat transfer of Williamson fluid with magnetic field due to a stretching sheet. Nanomaterials from Casson Carreau with nonlinear radiative microrotation in magnetohydrodynamics with Newtonian heating, homogenous and heterogeneous reactions was investigated by Shaw et al. [20]. Shafiq et al. [21] studied numerically and synthetic neural network modeling the unsteady hydromagnetic Williamson fluid flow in a permeable stretching sheet. The flow and heat transfer of third-grade fluid over a stretching sheet with a porous medium and magnetic field were studied by Abbas et al. [22]. Yousef et al. [23] reported the heat and mass transfer of a non-Newtonian Casson-Williamson nanofluid flow under the velocity slip, thermal radiation and viscous dissipation effects through a stretching sheet. The chemical reaction and thermal stratification phenomenon influence of Cross fluid flow past a stratified stretching sheet was created by Megahed and Abbas [24]. Further details, some scientists have been working on new advancements regarding the flow of hybrid and nanofluids beyond stretched sheets under different categories which may be highlighted in ([25,26,27,28]).

The foregoing studies provided the motivation for the current article. The novelty/originality of this article is in the theoretical and numerical study of the thermal conductivity characteristic that affected the steady-state slippery flow of a Casson-Williamson fluid across an impermeable stretched sheet with Ohmic dissipation. The article’s conclusion discusses the graphical and tabular results of a few significant physical quantities for several associated parameters. As a specific case of the current work, it is also computed to compare the current results with the earlier numerical results.

2 Basic governing equations

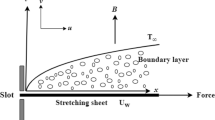
In this section, let’s simulate a non-Newtonian Casson-Williamson fluid flow that is incompressible and steady and is caused by a stretched surface. The fluid is thought to have a magnetic field with strength \(B_{0}\) and be electrically conductive. Induced magnetic effects are disregarded when a smaller magnetic Reynolds number is assumed. The fluid velocity components on a stretched sheet are u in the direction from the leading edge of the boundary layer and v in the perpendicular direction (Fig. 1).

Fig. 1
figure 1

Model of the boundary layer over a stretching sheet in physical terms [29]

Full size image

The linear variation in stretching sheet velocity is regarded as \(U_{w}=ax\), where a is a constant. According to these hypotheses and using the Boussinesq approximation, the following equations regulate the non-Newtonian Casson-Williamson fluid flow in this model [29]:

$$\begin{aligned}{} & {} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$
(1)
$$ \begin{aligned} u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} = & \nu \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial ^{2} u}}{{\partial y^{2} }} + \sqrt 2 \nu \Gamma \frac{{\partial u}}{{\partial y}}\frac{{\partial ^{2} u}}{{\partial y^{2} }} \\ & + \frac{\sigma }{\rho }\left( {E_{0} B_{0} - B_{0}^{2} u} \right) - \frac{\nu }{k}u, \\ \end{aligned} $$
(2)
$$ \begin{aligned} u\frac{{\partial T}}{{\partial x}} + v\frac{{\partial T}}{{\partial y}} = & \frac{1}{{\rho c_{p} }}\frac{\partial }{{\partial y}}\left( {\kappa \frac{{\partial T}}{{\partial y}}} \right) + \frac{\sigma }{{\rho c_{p} }}\left( {uB_{0} - E_{0} } \right)^{2} \\ & + \frac{\nu }{{c_{p} }}\left( {\left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial u}}{{\partial y}}} \right)^{2} } \right.\left. { + \frac{\Gamma }{{\sqrt 2 }}\left( {\frac{{\partial u}}{{\partial y}}} \right)^{3} } \right). \\ \end{aligned} $$
(3)

Here \(\rho \) is the fluid density, \(\nu \) is the kinematic viscosity, \(\mu \) is the fluid viscosity, k is the porous medium permeability, \(\sigma \) is the electrical conductivity of fluid, \(\beta \) is the Casson parameter, \(\kappa \) is the thermal conductivity, T is the temperature of fluid, \(E_{0}\) is the electric field, \(c_{p}\) is the specific heat, \(\nu \) is the kinematic viscosity and \(\Gamma \) is the time constant. The Newtonian model case in the prior system can be obtained if both \(\beta \) and \(\Gamma \) are dropped from the governing equations, as we must note. If \(\beta \rightarrow \infty \) and \(\Gamma =0\), then this is possible. The relevant boundary conditions are [23]:

$$\begin{aligned}{} & {} u=U_{w}+\lambda _{1}\left( \left( 1+\frac{1}{\beta }\right) \frac{\partial u}{\partial y}+\frac{\Gamma }{\sqrt{2}}\left( \frac{\partial u}{\partial y}\right) ^{2}\right) ,\nonumber \\{} & {} \quad v=0, \quad T=T_{w}, \quad \text{ at } y=0, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} u\rightarrow 0, \quad T \rightarrow T_{\infty }, \quad \text{ as } y \rightarrow \infty , \end{aligned}$$
(5)

we must highlight once more that the boundary condition’s first component Eq. (4) confirms that the slip phenomenon is taken into account, while the second component indicates that the sheet is impermeable. We next incorporate the following dimensionless variables as we continue with the analysis [23]:

$$\begin{aligned}{} & {} \eta = y\left( \frac{a}{\nu }\right) ^{\frac{1}{2}},\quad u=U_{w} f^{\prime }(\eta ), \quad v=-\left( a\nu \right) ^{\frac{1}{2}} f(\eta ), \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \theta (\eta )=\frac{T-T_{\infty }}{T_{w}-T_{\infty }}. \end{aligned}$$
(7)

The previous transformations result in the following set of governing equations:

$$ \begin{aligned} & \left( {1 + \frac{1}{\beta }} \right)f^{{\prime \prime \prime }} + W_{e} f^{{\prime \prime }} f^{{\prime \prime \prime }} + ff^{{\prime \prime }} \\ & - f^{{\prime 2}} + M^{2} \left( {E_{1} - f^{\prime } } \right) - \Delta f^{\prime } = 0, \\ \end{aligned} $$
(8)
$$\begin{aligned}{} & {} \theta ''(1+\varepsilon \theta )+\varepsilon \theta '^{2}+M^{2}Ec Pr\left( f^{\prime }-E_{1}\right) ^{2}+Pr f \theta ^{\prime }\nonumber \\{} & {} \quad +Ec Pr\left( \left( 1+\frac{1}{\beta }\right) f''^{2}+\frac{W_{e}}{2}f''^{3}\right) =0, \end{aligned}$$
(9)

with the following applicable boundary constraints:

$$\begin{aligned}{} & {} f(0)=0,\quad f'(0)=1+\lambda \left( \frac{W_{e}}{2}f''^{2}+\left( 1+\frac{1}{\beta }\right) f''\right) ,\nonumber \\{} & {} \quad \theta (0)=1, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} f'(\eta )\rightarrow 0,\quad \theta (\eta )\rightarrow 0,\quad \hbox {as}\,\,\eta \rightarrow \infty , \end{aligned}$$
(11)

where \(W_{e}=\Gamma x\sqrt{\frac{2a^{3}}{\nu }}\) is the local Weissenberg number, \(\lambda =\lambda _{1}\sqrt{\frac{a}{\nu }}\) is the slip velocity parameter, \(\Delta =\frac{\nu }{k a}\) is the porous parameter, \(E_{1}=\frac{E_{0}}{aB_{0}x}\) is the local electric parameter, \(M^{2}=\frac{\sigma B_{0}^{2}}{\rho a}\) is the magnetic number, \(Ec=\frac{U_{w}^{2}}{c_{p}(T_{w}-T_{\infty })}\) is the Eckert number and \(Pr=\frac{\mu \,c_{p}}{\kappa _{\infty }}\) is the Prandtl number.

Local skin-friction coefficient \(C_{f}\) and local Nusselt number \(Nu_{x}\), which have the following formulas, are the physical quantities of major relevance [23]:

$$ \begin{aligned} & C_{f} Re_{x}^{{\frac{1}{2}}} = - \left( {(1 + \frac{1}{\beta })f^{\prime\prime}(0) + \frac{{W_{e} }}{2}f^{{\prime \prime 2}} (0)} \right), \\ & Nu_{x} Re_{x}^{{\frac{{ - 1}}{2}}} = - (1 + \varepsilon )\theta ^{\prime}(0), \\ \end{aligned} $$
(12)

where \(Re_{x}=\frac{U_{w} x}{\nu }\) is the local Reynolds number. Additionally, after paying close attention to the form of the previous equation (12), we must point out that the Casson \(\beta \) and local Weissenberg \(W_{e}\) numbers have a direct impact on the local skin-friction coefficient, whilst the other factors have an indirect effect. Furthermore, the thermal conductivity parameter \(\varepsilon \) has a direct effect on the Nusselt number, while the other parameters have an indirect impact.

3 Results and discussion

In order to better comprehend the flow characteristics of the non-Newtonian fluid under study, numerical outcomes for the velocity distribution and temperature field are generated for different monitoring parameter values. First, a comparison of our numerical solution with previously published results in the literature is provided in Table 1, and both solutions are found to be in good concord.

Table 1 Comparison of \(-(1+\frac{1}{\beta })f''(0)\) with the results of Afify ([30]) when \(M=\Delta =W_{e}=0\)
Full size table

Figure 2 investigates the velocity and temperature variance caused by the local electric parameter \(E_{1}\). As the amount of \(E_{1}\) rises, more force is produced in the form of traction power in the direction of the fluid’s motion, as seen in this Fig. 2(a), which also indicates that the propagation of velocity and boundary layer thickness has increased. Similar to Fig. 2(a) and (b) investigates the thermal boundary layer temperature propagation rises with increasing the same parameter \(E_{1}\).

Fig. 2
figure 2

(a) \(f'(\eta )\) for chosen \(E_{1}\) (b) \(\theta (\eta )\) for chosen \(E_{1}\)

Full size image

The modification in velocity distribution caused by the porous parameter \(\Delta \) is seen in Fig. 3(a). This graph demonstrates how the velocity profile decreases as the porous parameter is raised. Additionally, it is showed that higher the viscosity value results in a thinner boundary layer. In addition, Fig. 3(b) demonstrates that raising the porous parameter improves the temperature fields, which increases the thermal boundary layer’s thickness. Physically, a high value of the porous parameter enhances the friction force in between liquid layers, reducing flow motion and enhancing temperature distribution.

Fig. 3
figure 3

(a) \(f'(\eta )\) for chosen \(\Delta \) (b) \(\theta (\eta )\) for chosen \(\Delta \)

Full size image

Figure 4 shows the effects of the Casson parameter \(\beta \) on velocity and temperature distributions. Figure 4(a) shows that when the Casson parameter \(\beta \) declines, the fluid velocity accelerates. Furthermore, Fig. 4(b) shows the temperature’s small increase in response to an increase in the Casson parameter. Thus, it is inferred that the process of rapid cooling requires the application of a non-Newtonian fluid with a minimum value of the Casson parameter.

Fig. 4
figure 4

(a) \(f'(\eta )\) for chosen \(\beta \) (b) \(\theta (\eta )\) for chosen \(\beta \)

Full size image

Figure 5 looks at how the local Weissenberg number \(W_{e}\) affects the distribution of velocity \(f'(\eta )\) and temperature \(\theta (\eta )\). The distribution of the velocity and the thickness of the momentum boundary layer is shown to be decreasing due to an increase in the local Weissenberg number as observed from Fig. 5(a). Further, as seen in Fig. 5 (b), larger values of the same parameter \(W_{e}\) are associated with a small rise in temperature \(\theta (\eta )\) and thermal boundary layer thickness.

Fig. 5
figure 5

(a) \(f'(\eta )\) for chosen \(W_{e}\) (b) \(\theta (\eta )\) for chosen \(W_{e}\)

Full size image

The velocity-slip factor’s \(\lambda \) impacts on velocity \(f'(\eta )\) and temperature profiles \(\theta (\eta )\) are seen in Fig. 6. Generally, the existence of a velocity slip factor tends to produce a flow-resistive force that is directed against the flow of the fluid. This force helps to lower the thickness of the boundary layer and slow down fluid travel along the sheet. Consequently, raises the thermal boundary layer’s fluid temperature. A high slip velocity value correlates physically with a high sheet roughness. As a result, enhanced roughness raises fluid motion resistance, which lowers fluid velocity and increases fluid temperature.

Fig. 6
figure 6

(a) \(f'(\eta )\) for chosen \(\lambda \) (b) \(\theta (\eta )\) for chosen \(\lambda \)

Full size image

Figure 7(a) illustrates how the thermal conductivity parameter \(\varepsilon \) affects the temperature distribution \(\theta (\eta )\). It has been observed that raising the thermal conductivity parameter causes the temperature to rise everywhere. This is because a larger fluid’s capacity for thermal conduction is implied by an increase in the thermal conductivity parameter, which raises the fluid’s temperature. Also, Fig. 7 (b) displays the temperature profile for the Eckert number Ec. It has been shown that a rise in the Eckert number contributes significantly to the regime’s temperature field and increases the thickness of the thermal boundary layer.

Fig. 7
figure 7

(a) \(\theta (\eta )\) for chosen \(\varepsilon \) (b) \(\theta (\eta )\) for chosen Ec

Full size image

Table 2 is now prepared to observe the behavior of variables impacting the skin-friction coefficient and the local Nusselt number. It is clear that the local electric parameter, the Casson parameter, the thermal conductivity parameter, and the slip velocity parameter all have an impact on the local Nusselt number’s magnitude, while the local Weissenberg number, the Eckert number, and the different values of the porous parameter all have a depressing effect. The skin-friction coefficient is shown by tabulated data to be decreased by the effects of the local electric parameter, Casson parameter, local Weissenberg number, and slip velocity parameter, while being increased by the porous parameter.

Table 2 Values for  \(C_{f}Re_{x}^{\frac{1}{2}}\) and \(Nu_{x}Re_{x}^{\frac{-1}{2}}\) for various values of \(E_{1}\), \(\Delta \), \(\beta \), \(W_{e}\), \(\lambda \), \(\varepsilon \) and Ec with \(Pr=2.0\) and \(M=0.2\)
Full size table

4 Conclusions

Discussion is had regarding steady non-Newtonian Casson-Williamson fluid flow over a stretching sheet in the presence of ohmic dissipation. An elastic rough sheet exposed to a magnetic field and immersed in a porous medium is stretched, which results in fluid motion. When fluid thermal conductivity is dependent on temperature and viscous dissipation occurs, the mechanism of heat transfer is examined. The governing equations are numerically resolved using the highly efficient shooting method. Some important conclusions from the current analysis show that when the porous parameter rises, the Nusselt number falls and the local skin-friction coefficient rises. Also, the slip parameter, the Casson parameter, and the local weissenberg number values should all be raised to lower the local skin-friction coefficient. Likewise, the local Weissenberg parameter, the slip parameter, and the porous parameter all have reverse impacts on the temperature and velocity fields. Further, the thickness of the momentum boundary layer was shown to rapidly diminish for large values of the slip, Casson, and porous parameters. On the other hand, the existence of the slip velocity improves the local Nusselt number but restricts fluid flow and raises fluid temperature. With the local electric parameter, both temperature and velocity fields have the same boosting behaviour. Further, by raising the Eckert number or thermal conductivity parameter, the temperature distribution is made more uniform with little change in the thermal boundary layer thickness. Finally, we want to use the homotopy analysis method in the future to numerically analyze how thermal slip and variable viscosity impact the flow model.