1 Introduction

Many implementations are found in conducted over the past twenty years nanotechnology has advanced to become the leading technology, science, and biomechanics, chemical of the twenty-first century [1]. Due to its many industrial, electronic, and medicinal uses, such as high-tech nuclear systems, solar collection, heat exchangers, engine cooling, and biological materials [2, 3]. The term of nanofluid was first introduced by Choi [4], he found that when added small nanoparticles in a base fluid increase the thermal conductivity. Earlier several researchers have carried out the studied the growth of nanofluid flow with heat and mass transfer under different physical conditions. Goyal and Bhargava [5] studied the non-newtonian nanofluid double diffusive boundary layer flow over a stretching sheet. Das et al. [6] investigated the heat and mass transfer of magnetohydrodynamics nanofluid flow over a vertical stretching sheet with non-uniform heat generation/absorption effect. Sulochana et al. [7] studied the effect of thermophoresis and Brownian motion on the heat and mass transmission over a stretching surface. Pal et al. [8] analyzed the Soret and Dufour effects on the mixed convection heat and mass transport of nanofluids over non-linear stretching and contracting sheets. The conjugate mixed convection heat and mass transfer with electrical magnetohydrodynamic and heat source/sink effects of nanofluid flow over a slip boundary stretching sheet surface was studied by Hsiao [9]. Khan et al. [10] investigated numerically the changing viscosity and angled Lorentz force effects on Williamson nanofluid flow across a stretching sheet. Pal et al. [11] discussed the combined impacts of non-linear thermal radiation, non-uniform heat source, and sink on the heat transfer of Casson nanofluid flow over a stretching surface. The flow and heat transfer for unsteady nanofluid past a moving rotating plate with Brownian, and thermophoresis diffusion impacts was studied by Abbas and Magdy [12]. The three-dimensional continuous thin film flow of tangent hyperbolic fluid past a stretching surface accompanied by nonlinear mixed convection flow and entropy formation was studied by Ibrahim and Gizewu [13]. Loganathan et al. [14] investigated analytically the effects of heat-absorbing viscoelastic nanofluidic flow through heated porous Riga plate with Cattaneo-Christov double flux. Shao et al. [15] investigated the significance of visco-elastic time dependent materials and electrically conductive motion over gravitationally affected cylindrical surface.

Several researchers have accomplished various types of study the characteristics of flow and heat transfer over stretched surfaces due to its significance in numerous technological, industrial, and scientific applications, including the production of fibre, the condensation process, textile machines, and plastic sheets [16]. Turkyilmazoglu [17] analyzed the heat and mass transfer characteristics of the magnetohydrodynamic viscous flow through a permeable stretched surface. The effects of velocity slip and heat generation/absorption on magnetohydrodynamic stagnation point flow and heat transfer over a contracting/expanding surface was investigated by Nandy et al. [18]. Gireesha et al. [19] examined the impact of nanoparticles on a steady magnetohydrodynamic of Eyring-Powell fluid flow with heat and mass transfer over a stretching sheet. The impacts of viscous dissipation, Joule heating and convective boundary condition of magnetohydrodynamics micropolar liquid flow past nonlinear stretched surface were presented by Waqas et al. [20]. Jena et al. [21] explored the Soret and Dufour effects on magnetohydrodynamics viscoelastic nanofluid flow over a porous vertical stretching sheet. The boundary layer viscous flow of nanofluids and heat transfer over a non-linearly stretching sheet in the presence of a magnetic field was demonstrated by Ramya et al. [22]. Mabood et al. [23] investigated numerically the thermal radiation, suction/injection, and multiple slip effects on MHD unsteady nanofluid flow with heat and mass transfer over a stretching sheet. The effect of the aligned magnetic field on Williamson’s nanofluid flow on a stretching surface with convective boundary conditions was investigated numerically by Srinivasulu et al. [24]. Megahed [25] addressed the steady MHD of non-Newtonian Maxwell fluid flow over an imbedded stretched sheet in a porous medium with convective boundary condition. The MHD free convective stagnation-point flow toward an inclined nonlinearly stretching sheet embedded in a porous medium was presented by Biswal et al. [26]. Alali et al. [27] investigated numerically the thin film flow and heat mass transfer for Casson nanofluid on a horizontal elastic sheet in presence of viscous dissipation, thermophoresis, and the slip velocity effects. The flow of a non-Newtonian Williamson fluid over stretched sheet embedded in a porous medium and combining with the Cattaneo-Christov model was studied numerically by Abbas et al. [28]. The literature review reveals several studies that discuss the feasibility of obtaining exact solutions for certain nonlinear models, as demonstrated in works by Yu-Hang Yin et al. [29] and Si-Jia Chen et al. [30]. However, our proposed model exhibits high nonlinearity, necessitating the utilization of numerical methods for solution determination.

Based on the research above and motivated by the possible technological applications regarding the nanofluid topic, the novelty of the proposed study can be emphasized by examining the combined effects of mixed convection and viscous dissipation phenomena on the flow of a Maxwell nanofluid over a stretching sheet embedded in a porous medium, considering the presence of slip velocity. The unique contribution and significance of this study lie in its unprecedented treatment of Maxwell nanofluids, offering novel insights that have not been explored previously. Further, the motivation for this study stems from several factors. Firstly, Maxwell fluids exhibit distinct rheological properties that differ from conventional Newtonian fluids. Gaining an understanding of the flow characteristics and heat transfer properties of these non-Newtonian fluids is essential for diverse industrial and engineering applications. Secondly, the inclusion of nanoparticles in slippery nanofluids offers the potential for significant enhancements in heat transfer performance. Exploring the flow and heat transfer behavior of these nanofluids is highly valuable in improving energy efficiency and thermal management across various systems. The findings reported here, according to the authors, have not been previously published and may fill in any gaps.

2 Formulation and Description for the Physical Model

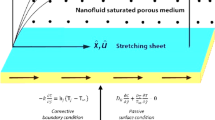
Let’s examine the two-dimensional, steady, mixed convective boundary layer flow caused by a vertically stretched sheet under the influence of non-uniform heat generation, as shown in Fig. 1, where the sheet velocity is \(U_{w}=ax\) and a is a constant. The assumption is that the nanoparticles are homogenous in size and shape. Choose a cartesian coordinate system where the \(x-\)axis is generally parallel to the sheet and the \(y-\)axis is orthogonal to the sheet. The sheet is also considered to be immersed in a porous medium. With regard to the fact that the current work adopts Buongiorno’s nanofluid model, which incorporates thermophoresis and Brownian motion impacts. It is assumed that there is a magnetic field with a strength of \(B_{0}\) in the \(y-\)direction. Due to the low Reynolds number, the induced magnetic field is disregarded.

Fig. 1
figure 1

Sketch of the physical fluid flow problem

Full size image

In this research, we assume that the suggested model is subject to an internal heat generation or absorption phenomenon that can be expressed by the term \(q^{\prime \prime \prime }\) and may be mathematically modelled as follows [31]:

$$\begin{aligned} q^{\prime \prime \prime }=\frac{\kappa U_{w}}{x \nu }\left( A^{*}(T_{w}-T_{\infty })\frac{u}{U_{w}}+B^{*}(T-T_{\infty }) \right) , \end{aligned}$$
(1)

where \(\nu _{\infty }\) is the kinematic viscosity of the nanofluid away from the sheet, \(T_{w}\) is the sheet temperature, \(T_{\infty }\) is the ambient temperature. Also, in our model, \(T_{w}\) is assumed to correlate with \(T_{\infty }\) according to the relation \(T_{w}=T_{\infty }+Ax\), where A is a constant. Likewise, \(\kappa\) is the nanofluid thermal conductivity which obey the following relation [25]:

$$\begin{aligned} \kappa =\kappa _{\infty }\left[ 1+\varepsilon _{1}\left( \frac{T-T_{\infty }}{T_{w}-T_{\infty }}\right) \right] , \end{aligned}$$
(2)

where \(\kappa _{\infty }\) is the ambient thermal conductivity and \(\varepsilon _{1}\) is the thermal conductivity parameter. Additionally, the following relationship is considered to affect the Maxwell nanofluid’s viscosity [25]:

$$\begin{aligned} \mu =\mu _{\infty }e^{-\alpha \left( \frac{T-T_{\infty }}{T_{w}-T_{\infty }}\right) }, \end{aligned}$$
(3)

where \(\alpha\) is the viscosity parameter and \(\mu _{\infty }\) is the ambient viscosity of the nanofluid. Also, the base fluid’s nanoparticle concentration is denoted as \(C_{w}\). Additionally, as y approaches infinity \(C_{\infty }\) exhibits a concentration of nanoparticles. Further, we assume that the motion of the nanoparticles in the base fluid is caused according to the Brownian diffusion coefficient \(D_{B}\) which obey the following relation [32]:

$$\begin{aligned} D_{B}(C)=d_{1}\left[ 1+\varepsilon _{2}\left( \frac{C-C_{\infty }}{C_{w}-C_{\infty }}\right) \right] , \end{aligned}$$
(4)

where \(\varepsilon _{2}\) is the mass diffusivity parameter and \(d_{1}\) is the reference mass diffusivity. Moreover, the movement of nanofluids exhibits a thermophoretic behavior with a thermophoretic diffusion coefficient \(D_{T}\), where the reactivity of the nanoparticles to temperature gradients is distinct. In fact, the suitable partial differential equations governing the aforementioned hypothesized MHD Maxwell nanofluid flow model are provided in terms of the following equations for mass, momentum, energy, and nanoparticles’ molar concentrations:

$$\begin{aligned}{} & {} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \begin{aligned} u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}&= \frac{1}{\rho _{\infty }}\frac{\partial }{\partial y}\left( \mu (T)\frac{\partial u }{\partial y }\right) -\lambda _{1}\left( u^{2} \frac{\partial ^{2} u}{\partial x^{2}}+v^{2} \frac{\partial ^{2} u}{\partial y^{2}}+2 u v \frac{\partial ^{2} u}{\partial x \partial y}\right) \\&\quad -\frac{\mu }{\rho _{\infty } K} u-\frac{\sigma B_{0}^{2}}{\rho _{\infty }} u \\&\quad +g\left[ \beta _{T}\left( T-T_{\infty }\right) +\beta _{C}\left( C-C_{\infty }\right) \right] , \end{aligned}\end{aligned}$$
(6)
$$\begin{aligned}{} & {} \begin{aligned} u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y}=\frac{1}{\rho _{\infty } c_{p}}\frac{\partial }{\partial y}\left( \kappa (T) \frac{\partial T}{\partial y} \right) +\tau \left[ D_{B}(C) \frac{\partial C}{\partial y} \frac{\partial T}{\partial y}+\frac{D_{T}}{T_{\infty }}\left( \frac{\partial T}{\partial y}\right) ^{2}\right] +\frac{q^{\prime \prime \prime }}{\rho _{\infty }c_{p}}, \end{aligned}\end{aligned}$$
(7)
$$\begin{aligned}{} & {} u \frac{\partial C}{\partial x}+v \frac{\partial C}{\partial y}=\frac{\partial }{\partial y}\left( D_{B}(C) \frac{\partial C}{\partial y}\right) +\frac{D_{T}}{T_{\infty }} \frac{\partial ^{2} T}{\partial y^{2}}, \end{aligned}$$
(8)

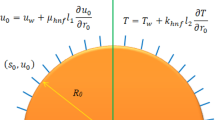
where u and v, respectively, stand for the velocity elements in the x and y directions. Maxwell’s parameter is \(\lambda _{1}\), the density of the ambient nanofluid is \(\rho _{\infty }\), the acceleration due to gravity is g, T is the nanofluid’s temperature, \(\beta _{C}\) is the concentration expansion coefficient, K is the permeability of the porous medium and the coefficient of thermal expansion is \(\beta _{T}\). Further,the boundary conditions for the temperature, velocity, and concentration distributions are as follows:

$$\begin{aligned}{} & {} \begin{aligned} u&=a x+\left(\frac{\delta _{0}}{\mu _{\infty }}\right) \left( \mu (T)\frac{\partial u}{\partial y}-\rho _{\infty }\lambda _{1}(2uv\frac{\partial u}{\partial x}+v^{2}\frac{\partial u}{\partial y})\right) ,\quad v=0,\\&\quad -\kappa \left( \frac{\partial T}{\partial y}\right) =h_{T}\left( T_{w}-T\right) , \quad C=C_{w}(x)=C_{\infty }+c x, \quad at \quad y=0, \end{aligned}\end{aligned}$$
(9)
$$\begin{aligned}{} & {} u\rightarrow 0, \quad T \rightarrow T_{\infty }, \quad C \rightarrow C_{\infty } \text{ as } y \rightarrow \infty , \end{aligned}$$
(10)

where a, c are constants, \(h_{T}\) is the coefficient of heat transfer and \(\delta _{0}\) is the factor of the slip velocity. Now, we begin the dimensionless variables in the formats listed below before creating the solution algorithm:

$$\begin{aligned} \eta= & {} \left( \frac{a}{\nu _{\infty }}\right) ^{\frac{1}{2}} y,\quad u=a x f^{\prime }(\eta ), \quad v=-\left( a\nu _{\infty }\right) ^{\frac{1}{2}} f(\eta ), \end{aligned}$$
(11)
$$\begin{aligned} \theta (\eta )= & {} \frac{T-T_{\infty }}{T_{w}-T_{\infty }}, \quad \phi (\eta )=\frac{C-C_{\infty }}{C_{w}-C_{\infty }}, \end{aligned}$$
(12)

where \(\theta\) is the non-dimensional fluid temperature, f is the non-dimensional stream function, \(\phi\) is the dimensionless concentration and \(\eta\) is the dimensionless similarity variable. We now see that the continuity equation Eq. (5) is quickly and easily satisfied once these transformations (11–12) have been applied. Additionally, employing the same non-dimensional transformations that were suggested earlier, we can obtain the following governing ordinary differential equations:

$$\begin{aligned}{} & {} \left( f^{\prime \prime \prime }-\alpha f^{\prime \prime } \theta '\right) e^{-\alpha \theta }+f f^{\prime \prime }-f^{\prime 2}+\beta \left( 2 f f^{\prime } f^{\prime \prime }-f^{2} f^{\prime \prime \prime }\right) \nonumber \\{} & {} \quad -\gamma e^{-\alpha \theta } f^{\prime }+\lambda (\theta +N \phi )-Mf^{\prime }=0, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \frac{1}{{\text {Pr}}}\left( \varepsilon _{1}\theta ^{\prime 2}+(1+\varepsilon _{1}\theta )\theta ^{\prime \prime }\right) +f \theta ^{\prime }-\theta f^{\prime }+Nb(1+\varepsilon _{2}\phi )\theta ^{\prime }\phi ^{\prime }+N t \theta '^{2}\nonumber \\{} & {} \quad +\left( \frac{1+\varepsilon _{1}\theta }{{\text {Pr}} e^{-\alpha \theta }}\right) \left( A^{*}f^{\prime }+B^{*}\theta \right) =0, \end{aligned}$$
(14)
$$\begin{aligned}{} & {} (1+\varepsilon _{2}\phi )\phi ^{\prime \prime }+\varepsilon _{2}\phi ^{\prime 2}+{\text {PrLe}}\left( f \phi ^{\prime }-\phi f^{\prime }\right) +\frac{N t}{N b} \theta ^{\prime \prime }=0. \end{aligned}$$
(15)

Additionally, with equivalent boundary conditions, the following is stated:

$$\begin{aligned}{} & {} f=0,\quad f'=1+\delta _{1}\left( e^{-\alpha \theta }f''+\beta (2f f'^{2}-f^{2}f'') \right) ,\nonumber \\{} & {} \quad \theta =\frac{\delta _{2}+\theta '}{\delta _{2}-\varepsilon _{1}\theta '},\quad \phi =1, \quad at \quad \eta =0, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} f'\rightarrow 0,\quad \theta \rightarrow 0,\quad \phi \rightarrow 0, \quad \hbox {as}\,\,\eta \rightarrow \infty , \end{aligned}$$
(17)

where \(M=\frac{\sigma B_{0}^{2}}{\rho _{\infty } a}\) is the magnetic parameter, \(\gamma =\frac{\nu _{\infty }}{a K}\) is the porous parameter, \(\beta =a \lambda _{1}\) is the Maxwell parameter, \(\delta _{1}=\delta _{0} \sqrt{\frac{a}{\nu _{\infty }}}\) is the slip velocity parameter, \(\lambda =\frac{g \beta _{T}\left( T_{w}-T_{\infty }\right) x}{U_{w}^{2}}\) is the mixed convection parameter, \(N=\frac{\beta _{c}\left( C_{w}-C_{\infty }\right) }{\beta _{T}\left( T_{w}-T_{\infty }\right) }\) is the buoyancy parameter for dimensionless concentration, \(\delta _{2}=\frac{h_{T}}{\kappa _{\infty }}\sqrt{\frac{\nu _{\infty }}{a}}\) is the thermal slip parameter, \(Nt=\frac{\tau D_{T}\left( T_{w}-T_{\infty }\right) }{ \nu _{\infty }T_{\infty }}\) is the thermophoresis parameter, \(N b=\frac{\tau d_{1}\left( C_{w}-C_{\infty }\right) }{\nu _{\infty }}\) is the Brownian motion parameter, \({\text {Pr}}=\frac{\mu _{\infty }c_{p}}{\kappa _{\infty }}\) is the Prandtl number and \(Le=\frac{\kappa _{\infty }}{d_{1}c_{p}\rho _{\infty }}\) is the Lewis parameter. Here in Eq. (16), it is important to note that the condition will physically represent the thermal slip phenomena, which is independent of thermal conductivity, if \(\varepsilon _{1}=0\). Additionally, when \(\beta =0\), our non-Newtonian nanofluid model can be transformed into a Newtonian one. The following are other significant physical factors for the drag force \(Cf_{x}\), heat transfer rate or the local Nusselt number \(Nu_{ x}\), and the rate of mass transfer or the local Sherwood number \(Sh_{ x}\):

$$\begin{aligned} \begin{aligned}&\frac{Cf_{x}}{2}Re_{x}^{\frac{1}{2}}=-\left[ e^{-\alpha \theta (0)}\,f''(0)-\beta\, (f''(0)\,f^{2}(0)-2f(0)\,f'^{2}(0)) \right] ,\\ {}&\frac{Nu_{x}}{\sqrt{Re_{x}} }=-\theta '(0),\quad \quad \quad \frac{Sh_{x}}{\sqrt{Re_{x}}}=-\phi '(0), \end{aligned}\end{aligned}$$
(18)

where \(Re_{x}=\frac{U_{w} x}{\nu _{\infty }}\) is the local Reynolds number.

3 Code Validation

Comparisons with the findings reported in the literature by Hayat et al. [33] for the Newtonian fluid situation for various values of slip velocity parameter \(\delta _{1}\) when \(\beta =\alpha =\gamma =M=\lambda =0\) are done in order to confirm the numerical results.

Table 1 Comparison of skin-friction coefficient \(-f^{\prime \prime }(0)\) with various \(\delta _{1}\) and the results of Hayat et al. [33] when \(\beta =\alpha =\gamma =M=\lambda =0\)
Full size table

Here, it is important to note that Hayat et al. [33] used a homotopy analysis method to examine the problem of viscous liquid flow past a stretching sheet under conditions of maintaining velocity and thermal slip as well as the presence of thermal radiation effects. Table 1 provides this comparison. This table demonstrates the great concordance between our findings and those reported in the literature. So we may certainly say that the data provided here is authentic.

4 Discussion of the Results

Using graphical and tabular representations, relevant numerical results are presented in this section. Numerous physical parameter values, including the magnetic parameter M, the porous parameter \(\gamma\), the Maxwell parameter \(\beta\), the slip velocity parameter \(\delta _{1}\), the mixed convection parameter \(\lambda\), the thermal slip parameter \(\delta _{2}\), the thermophoresis parameter Nt, the Lewis parameter Le and the Brownian motion parameter Nb, were computed. Figure 2 depicts how altering the Maxwell parameter \(\beta\) affects the nanofluid flow’s velocity \(f'(\eta )\), temperature \(\theta (\eta )\) and concentration \(\phi (\eta )\) fields. The velocity profile clearly exhibits a magnifying effect caused by the Maxwell parameter, which is in opposition to the temperature and concentration fields. In physical terms, a higher value of the Maxwell parameter indicates an increased resistance affecting the flow behavior. This heightened resistance exerts a stronger drag force on the fluid particles, leading to a decrease in velocity.

Fig. 2
figure 2

a \(f'(\eta )\) for picked \(\beta\). b \(\theta (\eta )\) and \(\phi (\eta )\) for picked \(\beta\)

Full size image

Figure 3 illustrates the relationship between the porous parameter \(\gamma\) and the temperature \(\theta (\eta )\), velocity \(f'(\eta )\), and concentration \(\phi (\eta )\) of the nanofluid. Because of the increased flow impedance caused by the presence of a porous medium, the flow velocity falls and the temperature and concentration of solutes rise. Furthermore, from a physical interpretation standpoint, this finding aligns with the observation that reducing the permeability of the porous medium decreases the drag force. As a consequence, this reduction in drag force leads to a decrease in the velocity of the flow.

Fig. 3
figure 3

a \(f'(\eta )\) for picked \(\gamma\). b \(\theta (\eta )\) and \(\phi (\eta )\) for picked \(\gamma\)

Full size image

Figure 4 shows how M varies with \(f'(\eta )\), \(\theta (\eta )\) and \(\phi (\eta )\). As M grows, the temperature and concentration profiles both rise, however the velocity behavior shows the opposite tendency. The Lorentz force causes the frictional drag to increase, which causes the temperature and concentration boundary layer thickness to boost and the velocity field to diminish. A magnetic parameter indicates a stronger magnetic field’s impact on the flow, leading to an increased Lorentz force that hampers the velocity. Additionally, the magnetic field promotes heat and mass transfer processes, resulting in elevated temperature and concentration. The magnetic forces induce enhanced mixing and facilitate the transportation of thermal energy and solute particles, consequently raising the temperature and concentration levels.

Fig. 4
figure 4

a \(f'(\eta )\) for picked M. b \(\theta (\eta )\) and \(\phi (\eta )\) for picked M

Full size image

The velocity \(f'(\eta )\) of the nanofluid, the temperature \(\theta (\eta )\) and the concentration of the nanoparticles \(\phi (\eta )\) are plotted against various viscosity parameter \(\alpha\) in Fig. 5. While a large values of the viscosity parameter causes the concentration and temperature fields to be amplified and the velocity field to be reduced, it is also seen that the parameter increases the thickness of the thermal boundary. Further, higher viscosity results in less heat being transferred to the surroundings, warming the flow and increasing both temperature and the concentration of nanoparticles.

Fig. 5
figure 5

a \(f'(\eta )\) for picked \(\alpha\). b \(\theta (\eta )\) and \(\phi (\eta )\) for picked \(\alpha\)

Full size image

As the slip velocity parameter \(\delta _{1}\) was increased, Fig. 6 showed how the motion of nanofluids \(f'(\eta )\), temperature distribution \(\theta (\eta )\), and the concentration \(\phi (\eta )\) of nanoparticles changed. This graph displayed the positive slip parameter values, which cause the nanofluids’ concentration and temperature to increase while slowing the flow of the fluid. Physically, a high slip velocity parameter signifies a substantial slip between the fluid and solid surface, resulting in increased momentum and mass transport. This heightened transport fosters improved heat and mass transfer processes. The amplified slip velocity encourages greater mixing and interaction among fluid particles, facilitating the movement of thermal energy and solute particles. Consequently, the temperature and concentration levels escalate within the flow region, indicative of the intensified heat and mass transfer arising from the larger slip velocity parameter.

Fig. 6
figure 6

a \(f'(\eta )\) for picked \(\delta _{1}\). b \(\theta (\eta )\) and \(\phi (\eta )\) for picked \(\delta _{1}\)

Full size image

In Figure 7, while keeping the other parameters unchanged, the influence of the mixed convection parameter \(\lambda\) is examined in relation to the distribution of velocity \(f'(\eta )\), temperature \(\theta (\eta )\), and nanoparticle concentration \(\phi (\eta )\). It is obvious that the mixed convection parameter only appears in the equation for the momentum boundary layer. As a result, it has a direct impact on the velocity field and a secondary impact on the temperature and concentration fields. In contrast to the temperature and concentration fields, which show a tendency in the opposite direction as the mixed convection parameter is increased, the velocity distribution is found to increase.

Fig. 7
figure 7

a \(f'(\eta )\) for picked \(\lambda\). b \(\theta (\eta )\) and \(\phi (\eta )\) for picked \(\lambda\)

Full size image

In Figure 8a, the impact of the thermal slip parameter \(\delta _{2}\) on the temperature distribution \(\theta (\eta )\) is examined while maintaining the other parameters at their constant values. It is discovered that as the thermal slip parameter’s increases up, both the sheet temperature \(\theta (0)\) and the nanofluid temperature within the boundary layer decrease. As a result, the thermal boundary layer will be thinner and the rate of heat transmission will be increased. The temperature field \(\theta (\eta )\) results are shown in Fig. 8b for the thermal conductivity parameter \(\varepsilon _{1}\). Due to the increased thermal conductivity of solid particles compared to base fluid, the volume of nanoparticles enhances the overall thermal conductivity of nanofluids. The thickening of the thermal boundary layer is caused by an increase in thermal conductivity. Therefore, the temperature as well as the thickness of the boundary layer grow as the overall thermal conductivity of nanofluids improves.

Fig. 8
figure 8

a \(\theta (\eta )\) for picked \(\delta _{2}\). b \(\theta (\eta )\) for picked \(\varepsilon _{1}\)

Full size image

The performance of the temperature profile \(\theta (\eta )\) in response to the space dependent heat source parameter \(A^{*}\) is depicted in Fig. 9a. The findings demonstrated that as the space based heat source parameter was altered, both the temperature distributions \(\theta (\eta )\) and the sheet temperature \(\theta (0)\) significantly increased. Further, Fig. 9b showed the Maxwell nanofluid temperature distribution characteristics as the thermally heat source parameter \(B^{*}\) was increased. It has been found that raising the values of the temperature-dependent heat source parameter raises both the temperature of the sheet \(\theta (0)\) and the temperature distribution \(\theta (\eta )\), which has an significant impact on the thermal thickness.

Fig. 9
figure 9

a \(\theta (\eta )\) for picked \(A^{*}\). b \(\theta (\eta )\) for picked \(B^{*}\)

Full size image

Figure 10a show how the thermophoresis parameter Nt impacts the thermal field \(\theta (\eta )\). The temperature and concentration boundary layer equations can be observed to contain the thermophoresis parameter. As we observe, it is connected with the temperature field and significantly affects the boundary layer’s heat transport and nanoparticle concentration. The increase in the thermophoresis parameter thus leads to an improvement in the thermal boundary layer thickness and temperature distributions for the flow of Maxwell nanofluids. Also, the properties of the thermal thickness of the boundary layer and the temperature distribution \(\theta (\eta )\) are affected by the Brownian motion parameter Nb, as shown in Fig. 10b. The presence of nanoparticles in nanofluid media enhances heat transmission capabilities through Brownian movement, which promotes heat conduction and increases the heat transfer surface area. The temperature distribution in the nanofluid flow, represented by \(\theta (\eta )\), is influenced by both the Brownian motion parameter and the sheet temperature, \(\theta (0)\). The Brownian motion parameter affects the dispersion and movement of nanoparticles, while the sheet temperature determines the initial conditions for the temperature distribution.

Fig. 10
figure 10

a \(\theta (\eta )\) for picked Nt. b \(\theta (\eta )\) for picked Nb

Full size image

The concentration patterns \(\phi (\eta )\) for various values of the mass diffusivity parameter \(\varepsilon _{2}\) are shown in Fig. 11a. When the mass diffusivity parameter is set to a significant value, the amount of nanoparticles present increases in concentration. Additionally, Fig. 11b depicts the behavior of the concentration distribution \(\phi (\eta )\) for the investigated range of Lewis number Le. In addition to describing the diffusivity relationship between heat and mass, Lewis number is a ratio of Schmidt number and Prandtl number.

Fig. 11
figure 11

a \(\phi (\eta )\) for picked \(\varepsilon _{2}\). b \(\phi (\eta )\) for picked Le

Full size image

It makes sense that when Le rises, kinematic viscosity falls to facilitate quicker mass transfer to the surroundings. The nanoparticle concentration decreases as you move farther away from the sheet, as seen by the flows in Fig. 11b.

When it comes to engineering and application, the forms of the velocity, temperature, and concentration profiles are frequently less important than the skin-friction coefficient \(\frac{Cf_{x}}{2}Re_{x}^{\frac{1}{2}}\) values or the heat \(\frac{Nu_{x}}{\sqrt{Re_{x}}}\) and mass transfer \(\frac{Sh_{x}}{\sqrt{Re_{x}}}\) mechanism. Table 2 shows that an increase in the Maxwell parameter, the porous parameter, the magnetic number, the viscosity parameter, and the velocity slip parameter causes a reduction in the Nusselt number or the rate of heat transfer at the boundary. Shear stress and the local Nusselt number grow along with the thermal slip parameter values, but they diminish when the slip velocity parameter values are elevated. The local Sherwood number is shown to have a falling function for the Maxwell parameter, porous parameter, magnetic number, viscosity parameter, and slip velocity parameter in the same table, but the opposite is seen for the mixed convection parameter and Browninan motion parameter.

Table 2 Values of \(\frac{Cf_{x}}{2}Re_{x}^{\frac{1}{2}}\), \(\frac{Nu_{x}}{\sqrt{Re_{x}}}\) and \(\frac{Sh_{x}}{\sqrt{Re_{x}}}\) for various values of \(\beta , \gamma , M, \alpha , \delta _{1}, \delta _{2}, A^{*}, B^{*}, Nb\) and Nt with \(Le=1.0\) and \(Pr=3.0\)
Full size table

5 Conclusive Remarks

To examine the impact of physical factors on the heat and mass transfer of a non-Newtonian Maxwell slippery nanofluid flow on a vertical stretched sheet, a mathematical and theoretical investigation was carried out. The stretching sheet is thought to be submerged in a porous medium. Studies are also done on the importance of Brownian motion, thermal slip, velocity, and non-uniform heat generation. In this study, the ability to vary thermal conductivity and diffusivity within the nanofluid flow is incorporated. The primary aim of this study is to investigate the influence of a magnetic field on the flow characteristics of a Maxwell nanofluid within a porous medium. Ordinary differential equations with suitable boundary conditions are created by simplifying the set of governing equations and the boundary condition using dimensionless transformations. In order to treat modelled equations numerically, the shooting method is used. The key findings of this contemporary research are listed below:

  1. 1.

    The wall heat transfer coefficient is shown to be significantly affected by the thermal slip parameter and the mixed convection parameter.

  2. 2.

    The velocity, temperature, and concentration profiles are found to be significantly affected by the influences of the slip velocity parameter and magnetic parameter.

  3. 3.

    When a porous media is available and a non-Newtonian Maxwell fluid is provided, the velocity is lower than it is when a Newtonian fluid is present and a porous medium is absent.

  4. 4.

    It has been discovered that the parameters that control slip velocity, viscosity, and magnetic field result in a thicker thermal and concentration boundary layer.

  5. 5.

    Skin-friction coefficients, the local Nusselt number, and the local Sherwood number are all affected by slip velocity parameter variations in a similar manner.

  6. 6.

    In future studies, there is potential to expand this research by incorporating the Jeffery nanofluid and investigating the impact of thermal and concentration slips.