1 Introduction

The scientific studies on the motion of vibrating dynamical systems have been increased during the last two centuries [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] due to its significance and applications in practical life like vibrating buildings, electric motors, airplanes, locomotive engines, and missiles. Such problems can be solved whether analytically or numerically according to the nature of the governing system of motion. The relevant vibrational movement of a heavy homogenous cylinder on a specified curve without slipping is investigated in [1]. In [2], the authors presented original research that employs analytical techniques to investigate the nonlinear characteristics displayed by various nonlinear phenomena. It is shown that, the asymptotic method and the MMS [20] are demonstrated to be an effective and understandable way to approach mechanics, and are applicable to fields throughout engineering and physics. In [3] the authors investigated a weakly nonlinear dynamical system with 2DOF. They have been observed that there’s a lot of energy transfer between vibrational modes. Moreover, resonance conditions are identified, in which the picked resonance case are analyzed. The generalization of this problem has been examined in [4], when the system is forced by an external excitation force in addition to the motion is considered to be on an elliptic trajectory.

The nonlinear oscillations of a 3DOF rigid body’s pendulum close to resonance is studied in [5], where its pivot point is restricted to be fixed. Whereas, the motion of the pivot point, of a damped elastic pendulum linked with rigid body, on various paths are investigated in [6,7,8,9]. The MMS is utilized to obtain the analytic solutions of the studied models. The resonance cases, the requirements of solvability, and the ME are achieved.

A simulation model of triple pendulum with three linked identical rods besides the existence of a horizontal frictionless barrier is investigated in [10], in which the first rod is forced harmonically by an excitation force. The authors presented numerical simulations of some examples related with the investigated model. The analytic solutions of a triple pendulum with three different lengths of its rods under the action of a normal excitation force on the direction of the last rod besides to the influence of harmonic moment at the pendulum’s piovt point are investigated in [11]. The approach of Routh-Hurwitz [21] for the nonlinear stability is utilized to study the stability of the investigated model. The numerical solutions of a vibrating rigid body’s pendulum close to the equilibrium locations are examined in [12, 13] using the Runge–Kutta algorithm [22], while the methods of small and large parameter [20] are used in [14, 15] to obtain the analytic solutions of a connected rigid body with pendlum, respectively. Whereas, the location of equilibrium of a vertical triple pendulum exposed to an asymmetric iterative force is investigated in [16]. The effects of periodic disturbance on a damped three-link pendulum are investigated in [17]. The results of time integration with those of the theoretical study for the frequency response are contrasted. Furthermore, a law explains the behavior of resonant frequency shifts is established. Moreover, the numerical and experimental study of a damped and forced triple pendulum is examined in [18, 19], respectively. In contrast, in [23, 24], the chaotic motion of a 2DOF weakly nonlinear elastic pendulum system for a stationary and moving suspension point is investigated to disclose their chaotic behaviors close to resonance regarding to the used parameters. The MMS has been used in [25] to study the stability of a nonlinear elastic pendulum, while the work is enhancemented in [26] when the pendulum is forced by an external harmonic force.

However, due to the great significance of absorber’s applications in engineering industries, the use of absorbers in the creation of various types of dynamical models has attracted the interest of numerous academics, such as [27,28,29,30]. The authors of [27] looked into the behavior of a 3DOF nonlinear spring pendulum, with fixed suspension, to see how a longitudinal absorber may stabilize and control the ship’s vibrational motion. Whereas, the estimation of the same model when the suspension point moving on the ellipse route has been studied in [28]. The steady-state’s solutions around the specified resonance case are analyzed using the equations of frequency response. In [29], the impact of a damped nonlinear elastic pendulum on the behavior of this problem is regulated. However, the stability a transverse absorber connected with this spring, based on the examination of three resonance cases is explored in [30]. The rolling motion of a heavy homogenous cylinder through unknown curve without slipping is investigated in [1, 31]. Equation of variation is solved to find and minimize a function of total rolling time. The parametric form of the quickest-descent directrix for the algebraic equation is obtained. On the other hand, the vibrational motion of a rolling cylinder in a circular curve is examined in [32]. The governing EOM are derived and solved using the MMS. In light of the physical parameters of the studied model, diagrams of these solutions are presented.

This main aim of this paper is to investigate the motion and the stability of a damped 2DOF auto-parametric dynamical system. The governing EOM are constructed in terms of generalized coordinates using Lagrange’s equations. The MMS is applied to generate the analytic solution up to the third-order of approximation. To investigate the solvability criteria of the motion and the associated ME, two resonance situations, namely the internal and primary external, are investigated together. By removing the modified phases, the ME are simplified to two algebraic equations in terms of parameters of detuning and amplitudes. The time histories graphs of the obtained solutions, as well as the amplitudes and adjusted phases, are given to portray the motion of the system at any given time. The stability requirements of Routh-Hurwitz are used to investigate and analysis the various stability zones. Since the employed method is applied to the investigated dynamical system, the results are considered to be new and original. Applications in a range of disciplines, including swaying structures and rotor dynamics, demonstrate the importance of the investigated system.

2 The model’s formulation

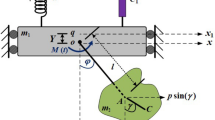
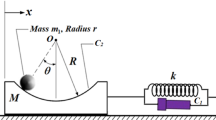
Consider a planar movement of a rolling cylinder with mass \(m_{1}\) and radius \(r\) across a circular surface with mass \(M\) and radius \(R\), in which this surface is connected with two damped nonlinear springs of stiffness \(k_{1}\) and \(k_{2}\), see Fig. 1. Let \(C\) and \(\varphi\) represent the damping coefficient and the angle between the radius \(R\) and the vertical at \(O_{3}\). The model is considered to be influenced by an external force \(F(t) = F_{1} \cos (\Omega_{1} t)\) in the vertical direction, where \(F_{1}\) and \(\Omega_{1}\) are its amplitude and frequency, respectively.

Fig. 1
figure 1

Description of the system

Full size image

Therefore, the model’s kinetic and potential energies \(T\) and \(V\) have the forms

$$\begin{aligned} & T = \frac{1}{2}(m_{1} + M)\dot{y}_{1}^{2} + \frac{1}{2}m_{1} \left[ {\frac{3}{2}(R - r)^{2} \dot{\varphi }^{2} + 2(R - r)\dot{\varphi }\dot{y}_{1} \sin \varphi } \right], \\ & V = \frac{1}{2}k_{1} y_{1}^{2} + \frac{1}{4}k_{2} y_{1}^{4} + (m_{1} + M)\,gy_{1} - m_{1} g[R - (R - r)\cos \varphi ]; \\ & y_{1} = y - \tilde{y}_{c} ,\,\,\,\,\,\,\,\,\,\tilde{y}_{c} = OO_{1} = y_{c} + y_{st} . \\ \end{aligned}$$
(1)

Here \(g\) is the gravitational acceleration, dots are time’s derivatives, \(y_{1}\) is the elongation or contraction in the height of the studied model, and \(y_{c}\), \(y_{st}\) are the natural lengths and static elongation of both springs, respectively.

The controlling EOM can be acquired using equations of Lagrange [33]

$$\begin{aligned} & \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{y}_{1} }}} \right) - \left( {\frac{\partial L}{{\partial y_{1} }}} \right) = F(t) - C\dot{y}_{1} , \\ & \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{\varphi }}}} \right) - \left( {\frac{\partial L}{{\partial \varphi }}} \right) = 0, \\ \end{aligned}$$
(2)

where \(L = T - V\) is the system’s Lagrangian, \((y_{1} ,\varphi )\) and \((\dot{y}_{1} ,\dot{\varphi })\) are the system’s generalized coordinates and velocities.

Taking a look at the dimensionless parameter listed below

$$\begin{aligned} & u = \frac{{y_{1} }}{R - r},\,\,\,\,\,\,m = \frac{{m_{1} }}{{(m_{1} + M)}},\,\,\,\,\,\,\omega_{1}^{2} = \frac{{k_{1} }}{{(m_{1} + M)}},\,\,\,\,\,\,\omega_{2}^{2} = \frac{2g}{{3(R - r)}}, \\ & f_{1} = \frac{{F_{1} }}{{(R - r)(m_{1} + M)}},\,\,\,\,\,\,\,\mu_{1} = \frac{C}{{2(m_{1} + M)}},\,\,\,\,\,\,\,\mu_{2} = \frac{{k_{2} (R - r)^{2} }}{{2(m_{1} + M)}},\,\,\,\,\,\,y_{st} = \frac{{(m_{1} + M)g}}{{k_{1} }}. \\ \end{aligned}$$
(3)

Substituting Eqs. (1) and parameters (4) into the second-order Eqs. (2), yields the EOM in its dimensionless form

$$\ddot{u} + \omega_{1}^{2} u + m(\ddot{\varphi }\sin \varphi + \dot{\varphi }^{2} \cos \varphi ) + \mu_{2} u^{3} + 2\mu_{1} \dot{u} = f_{1} \cos (\Omega_{1} t),$$
(4)
$$\ddot{\varphi } + (\omega_{2}^{2} + \frac{2}{3}\ddot{u})\sin \varphi = 0.$$
(5)

Therefore, the controlling EOM can be seen as a set second-order nonlinear ordinary differential equations (ODE) Eqs. (4) and (5) regarding to \(u\) and \(\varphi\).

3 The approach technique

The major goal of this research’s section is to use the MMS to acquire the solutions of the EOM (4) and (5) analytically, to categorize the cases of resonance, to obtain solvability requirements, and to generate the ME. Therefore, the trigonometric functions \(\sin \varphi\) and \(\cos \varphi\) in these equations can be approximated utilizing Taylor series till to the first two terms of their expansions. These approximations must be valid in a small area around the location of static equilibrium. Equations (4) and (5) are then transformed into

$$\ddot{u} + \omega_{1}^{2} u + m\left[ {\ddot{\varphi }\left( {\varphi - \frac{{\varphi^{3} }}{6}} \right) + \dot{\varphi }^{2} \left( {1 - \frac{{\varphi^{2} }}{2}} \right)} \right] + \mu_{2} u^{3} + 2\mu_{1} \dot{u} = f_{1} \cos (\Omega_{1} t),$$
(6)
$$\ddot{\varphi } + \left( {\omega_{2}^{2} + \frac{2}{3}\ddot{u}} \right)\left( {\varphi - \frac{{\varphi^{3} }}{6}} \right) = 0.$$
(7)

The vibrations’ amplitudes are supposed to be of a small parameter’s order \(0 < \varepsilon < < 1\). Consequently, we can characterize the functions \(u\) and \(\varphi\) as in terms \(\xi\) and \(\phi\) according to

$$u(\tau ) = \varepsilon \,\xi (\tau ;\varepsilon ),\,\,\,\varphi (\tau ) = \varepsilon \,\phi (\tau ;\varepsilon ).$$
(8)

Based on the procedure of MSM, the functions \(\xi\) and \(\phi\) we can sought in forms [20]

$$\begin{gathered} \xi = \sum\limits_{k = 0}^{2} {\varepsilon^{k} \xi_{k + 1} (\tau_{0} ,\tau_{1} ,\tau_{2} ) + } O(\varepsilon^{3} ), \hfill \\ \phi = \sum\limits_{k = 0}^{2} {\varepsilon^{k} \phi_{k + 1} (\tau_{0} ,\tau_{1} ,\tau_{2} )} + O(\varepsilon^{3} ), \hfill \\ \end{gathered}$$
(9)

where \(\tau_{0} = \tau\) stands as a quick time, while \(\tau_{1} = \varepsilon \tau\) and \(\tau_{2} = \varepsilon^{2} \tau\) are the slow ones. As a result, the below chain rule can be applied to convert the time derivatives regarding \(\tau\) to \(\tau_{0} ,\tau_{1} ,\) and \(\tau_{2}\) [20]

$$\begin{aligned} & \frac{{\text{d}}}{{{\text{d}}\tau }} = \frac{\partial }{{\partial \tau_{0} }} + \varepsilon \frac{\partial }{{\partial \tau_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial \tau_{2} }} + O(\varepsilon^{3} ), \\ & \frac{{{\text{d}}^{2} }}{{{\text{d}}\tau^{2} }} = \frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 2\varepsilon \frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{1} }} + \varepsilon^{2} \left( {\frac{{\partial^{2} }}{{\partial \tau_{1}^{2} }} + 2\frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{2} }}} \right) + O(\varepsilon^{3} ), \\ \end{aligned}$$
(10)

Based on the smallness of \(\varepsilon\), terms like \(O(\varepsilon^{3} )\) and higher have been ignored.

To follow the desired solutions, the amplitude \(f_{1}\) as well as the damping coefficient \(\mu_{1}\) can be defined follows

$$f_{1} = \varepsilon^{3} \tilde{f}_{1} ,\mu_{1} = \varepsilon^{2} \tilde{\mu }_{1} ,$$
(11)

where \(\tilde{f}_{1}\) and \(\tilde{\mu }_{1}\) are quantities of unity’s order.

Substituting (8)–(11) into (7) and (8), to obtain two second-order partial differential equations (PDE). Equaling the coefficients of similar powers of \(\varepsilon\) in both sides of the resulted equations to obtain the below sets according to these powers.

Order of \(\varepsilon\) :

$$\frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0}^{2} }} + \omega_{1}^{2} \xi_{1} = 0,$$
(12)
$$\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }} + \omega_{2}^{2} \phi_{1} = 0.$$
(13)

Order of \(\varepsilon^{2}\)

$$\frac{{\partial^{2} \xi_{2} }}{{\partial \tau_{0}^{2} }} + \omega_{1}^{2} \xi_{2} = - m\left( {\frac{{\partial \phi_{1} }}{{\partial \tau_{0} }}} \right)^{2} - 2\frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - m\phi_{1} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }},$$
(14)
$$\frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }} + \omega_{2}^{2} \phi_{2} = - 2\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \tau_{1} }} - \frac{2}{3}\phi_{1} \frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0}^{2} }}.$$
(15)

Order of \(\varepsilon^{3}\)

$$\begin{aligned} \frac{{\partial^{2} \xi_{3} }}{{\partial \tau_{0}^{2} }} + \omega_{1}^{2} \xi_{3} & = \tilde{f}_{1} \cos \Omega_{1} \tau_{0} - \frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{1}^{2} }} - 2\tilde{\mu }_{1} \frac{{\partial \xi_{1} }}{{\partial \tau_{0} }} - 2\left( {\frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} + \frac{{\partial^{2} \xi_{2} }}{{\partial \tau_{0} \partial \tau_{1} }}} \right) \\ & - 2m\left[ {\frac{{\partial \phi_{1} }}{{\partial \tau_{0} }}\frac{{\partial \phi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \phi_{1} }}{{\partial \tau_{0} }}\frac{{\partial \phi_{2} }}{{\partial \tau_{0} }} + \phi_{1} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \phi_{2} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }} + \phi_{1} \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }}} \right] + \mu_{2} \xi_{1}^{3} , \\ \end{aligned}$$
(16)
$$\begin{aligned} \frac{{\partial^{2} \phi_{3} }}{{\partial \tau_{0}^{2} }} + \omega_{2}^{2} \phi_{3} & = \frac{1}{6}\omega_{2}^{2} \phi_{1}^{3} - \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{1}^{2} }} - 2\left( {\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} + \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0} \partial \tau_{1} }}} \right) \\ & \, - \frac{4}{3}\phi_{1} \frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \frac{2}{3}\left( {\phi_{1} \frac{{\partial^{2} \xi_{2} }}{{\partial \tau_{0}^{2} }} + \phi_{2} \frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0}^{2} }}} \right). \\ \end{aligned}$$
(17)

A closer inspection of the above three sets of PDE demonstrates that the solutions the last two sets depend on the solutions of the first one, which means that they can be solved consecutively. Then, the general solutions of (13) and (14) can be written in an exponential form in terms of complex functions \({\rm A}_{j} \,\,(j = 1,\,2)\) hand their conjugates \(\overline{\rm A}_{j}\) as follows

$$\xi_{1} = {\rm A}_{1} e^{{i\omega_{1} \tau_{0} }} + \overline{\rm A}_{1} e^{{ - i\omega_{1} \tau_{0} }} ,$$
(18)
$$\phi_{1} = {\rm A}_{2} e^{{i\omega_{2} \,\tau_{0} }} + \overline{\rm A}_{2} e^{{ - i\,\omega_{2} \tau_{0} }} .$$
(19)

The substitution of these solutions into the second set of Eqs. (14) and (15) produces undesired secular terms [34]. Elimination of these terms demands that

$$\frac{{\partial {\rm A}_{1} }}{{\partial \tau_{1} }} = 0,$$
(20)
$$\frac{{\partial {\rm A}_{2} }}{{\partial \tau_{1} }} = 0.$$
(21)

Therefore, we can write the second-order solutions as follows

$$\xi_{2} = \frac{{2m\omega_{2}^{2} {\rm A}_{2}^{2} }}{{(\omega_{1}^{2} - 4\omega_{2}^{2} )}}e^{{2i\omega_{2} \tau_{0} }} - \frac{{m\omega_{2}^{2} {\rm A}_{2} \overline{\rm A}_{2} }}{{\omega_{1}^{2} }} + CC,$$
(22)
$$\phi_{2} = \frac{{2\omega_{1} {\rm A}_{1} {\rm A}_{2} }}{{3(\omega_{1} + 2\omega_{2} )}}e^{{i(\omega_{1} + \omega_{2} )\tau_{0} }} + \frac{{2\omega_{1} {\rm A}_{1} \overline{\rm A}_{2} }}{{3(\omega_{1} - 2\omega_{2} )}}e^{{i(\omega_{1} - \omega_{2} )\tau_{0} }} + CC.$$
(23)

The preceding terms’ complex conjugates are represented here by \(CC.\)

Other secular terms are produced by substituting the solutions (18), (19), (22), and (23) into Eqs. (17) and (18). The criteria for removing these phrases are outlined below

$$2i\omega_{1} \left( {\tilde{\mu }_{1} {\rm A}_{1} + \frac{{\partial {\rm A}_{1} }}{{\partial \tau_{2} }}} \right) + \frac{{4m\omega_{1}^{4} {\rm A}_{1} {\rm A}_{2} \overline{\rm A}_{2} }}{{3(\omega_{1}^{2} - 4\omega_{2}^{2} )}} + 3\mu_{2} {\rm A}_{2}^{2} \overline{\rm A}_{1} = 0,$$
(24)
$$2i\omega_{2} \frac{{\partial {\rm A}_{2} }}{{\partial \tau_{2} }} + \frac{{4\omega_{1}^{3} {\rm A}_{1} {\rm A}_{2} \overline{\rm A}_{1} }}{{9(\omega_{1} + 2\omega_{2} )}} + \frac{{\omega_{2}^{2} {\rm A}_{2}^{2} \overline{\rm A}_{2} }}{{6(\omega_{1}^{2} - 4\omega_{2}^{2} )}}[3\omega_{1}^{2} + 4\omega_{2}^{2} (4m - 3)] = 0.$$
(25)

Judging on the previous conditions, one can write the third-order solutions as follows

$$\begin{aligned} \xi_{3} & = \frac{{\tilde{f}_{1} e^{{i\Omega_{1} \tau_{0} }} }}{{2(\omega_{1}^{2} - \Omega_{1}^{2} )}} - \frac{{2m\omega_{1} (\omega_{1} + 2\omega_{2} )}}{{3[\omega_{1}^{2} - (\omega_{1} + 2\omega_{2} )^{2} ]}}{\rm A}_{1} {\rm A}_{2}^{2} e^{{i\tau_{0} (\omega_{1} + 2\omega_{2} )}} \\ & \,\, + \frac{{2m\omega_{1} (\omega_{1} - 2\omega_{2} )}}{{3[\omega_{1}^{2} - (\omega_{1} - 2\omega_{2} )^{2} ]}}{\rm A}_{1} \overline{\rm A}_{2}^{2} e^{{i\tau_{0} (\omega_{1} - 2\omega_{2} )}} + \frac{1}{{8\omega_{1}^{2} }}\mu_{2} {\rm A}_{1}^{3} \,e^{{3i\tau_{0} \omega_{1} }} + CC, \\ \end{aligned}$$
(26)
$$\begin{aligned} \phi_{3} & = - \frac{{[\omega_{1}^{2} + 4\omega_{2}^{2} ( - 1 + 4m)]{\rm A}_{2}^{3} }}{{48(\omega_{1}^{2} - 4\omega_{2}^{2} )}}e^{{2i\omega_{2} \tau_{0} }} - \frac{{4\omega_{1}^{3} {\rm A}_{1}^{2} {\rm A}_{2} e^{{i(2\omega_{1} + \omega_{2} )\tau_{0} }} }}{{9(\omega_{1} + 2\omega_{2} )[\omega_{2}^{2} - (2\omega_{1} + \omega_{2} )^{2} ]}} \\ & \,\,\,\,\,\,\,\,\, - \frac{{4\omega_{1}^{3} {\rm A}_{1}^{2} \overline{\rm A}_{2} e^{{i(2\omega_{1} - \omega_{2} )\tau_{0} }} }}{{9(\omega_{1} - 2\omega_{2} )[\omega_{2}^{2} - (2\omega_{1} - \omega_{2} )^{2} ]}} + CC. \\ \end{aligned}$$
(27)

The complex functions \({\rm A}_{j} \,\,(j = 1,\,2)\) can be determined according to the above four conditions of eliminating secular terms and by using the following initial conditions

$$\xi (0) = u_{01} ,\,\,\,\,\,\,\,\,\,\dot{\xi }(0) = u_{02} ,\,\,\,\,\,\,\,\,\,\phi (0) = u_{03} ,\,\,\,\,\,\,\,\,\,\dot{\phi }(0) = u_{04} ,$$
(28)

where \(u_{0s} \,\,(s = 1,2,3,4)\) represents known values.

4 Resonance requirements and modulation equations (ME)

This section classifies various cases of resonance, investigates two of them, and derives ME in the context of these cases. When the denominators of the foregoing approximate second or third orders solutions tend to zero, resonance cases can be distinguished [35]. Therefore, we can classify them as principal primary external and internal resonances which can be done when \(\Omega_{1} \approx \omega_{1}\) and \(\omega_{1} \approx 0,\) \(\omega_{2} \approx 0,\) \(\omega_{1} \approx \omega_{2} ,\) \(\omega_{1} \approx \pm 2\omega_{2} ,\) respectively. It’s interesting to note that the behavior of the researched system will be challenging if one of the aforementioned resonance cases is realized [36]. As a result, we’ll have to make some adjustments to the used technique. We’ll investigate both of two resonances simultaneously to remedy this problem, i.e., \(\Omega_{1} \approx \omega_{1}\) and \(\omega_{1} \approx 2\omega_{2}\), which mean that \(\Omega_{1}\) and \(\omega_{1}\) close to \(\omega_{1}\) and \(2\omega_{2}\), respectively.

It is critical to employ the dimensionless quantities \(\sigma_{j} \,\,(j = 1,2)\) which are known by detuning parameters, in which they measure the distances between the oscillations and the stern resonances [37]. Then, we’ll be able to write

$$\Omega_{1} = \omega_{1} + \sigma_{1} ,\,\,\,\,\,\omega_{1} = 2\omega_{2} + \sigma_{2} ;\,\,\,\,\,\sigma_{j} = \varepsilon \tilde{\sigma }_{j} (j = 1,2).$$
(29)

Substituting (29) into the sets of second and third-order of \(\varepsilon\), and then cancelling terms of the yield secular ones to obtain the solvability requirements in the forms

$$\begin{aligned} & \frac{{\partial {\rm A}_{1} }}{{\partial \tau_{1} }} = 0,\frac{{\partial {\rm A}_{2} }}{{\partial \tau_{1} }} = 0, \\ & 2i\omega_{1} \left( {\tilde{\mu }_{1} {\rm A}_{1} + \frac{{\partial {\rm A}_{1} }}{{\partial \tau_{2} }}} \right) + \frac{{4m\omega_{1}^{4} {\rm A}_{1} {\rm A}_{2} \overline{\rm A}_{2} }}{{3(\omega_{1}^{2} - 4\omega_{2}^{2} )}} + 3\mu_{2} {\rm A}_{2}^{2} \overline{\rm A}_{1} - \frac{{\tilde{f}_{1} }}{2}e^{{i\tilde{\sigma }_{1} \tau_{1} }} \, = 0,\, \\ & 2i\omega_{2} \frac{{\partial {\rm A}_{2} }}{{\partial \tau_{2} }} + \frac{{4\omega_{1}^{3} {\rm A}_{1} {\rm A}_{2} \overline{\rm A}_{1} }}{{9(\omega_{1} + 2\omega_{2} )}} + \frac{{\omega_{2}^{2} {\rm A}_{2}^{2} \overline{\rm A}_{2} }}{{6(\omega_{1}^{2} - 4\omega_{2}^{2} )}}[3\omega_{1}^{2} + 4\omega_{2}^{2} (4m - 3)] \\ & \quad + \frac{{4\omega_{1}^{3} {\rm A}_{1}^{2} \overline{\rm A}_{2} e^{{i\tau_{1} \tilde{\sigma }_{2} }} }}{{9(\omega_{1} - 2\omega_{2} )}} = 0. \\ \end{aligned}$$
(30)

These requirements clearly form a system of four nonlinear PDE regarding the functions \({\rm A}_{j} \,\,(j = 1,\,2)\) in which \({\rm A}_{j} = {\rm A}_{j} (\tau_{2} )\). As a result, one expresses them in the following polar forms

$$A_{j} = \frac{{\tilde{h}_{j} (\tau_{2} )}}{2}e^{{i\tilde{\psi }_{j} \tau_{2} }} ;h_{j} = \varepsilon \tilde{h}_{j} \,\,\,\,\,(j = 1,2),$$
(31)

where \(\tilde{h}_{j}\) and \(\psi_{j} (j = 1,2)\) refer real functions of amplitudes and phases for the functions \(\xi\) and \(\phi\) respectively.

According to the first two conditions of (30), the functions \(A_{j}\) are independent of \(\tau_{0}\) and \(\tau_{1}\). Then, we can write

$$\frac{{dA_{j} }}{d\tau } = \varepsilon^{2} \frac{{\partial A_{j} }}{{\partial \tau_{2} }};(j = 1,2).$$
(32)

Using the modified phases listed below [38], the above solvability requirements can be transformed from PDE to ordinary ones

$$\begin{gathered} \theta_{1} (\tau_{1} ,\tau_{2} ) = \tau_{1} \tilde{\sigma }_{1} - \psi_{1} (\tau_{2} ); \hfill \\ \theta_{2} (\tau_{1} ,\tau_{2} ) = \tau_{1} \tilde{\sigma }_{2} + 2[\psi_{1} (\tau_{2} ) - \psi_{2} (\tau_{2} )]. \hfill \\ \end{gathered}$$
(33)

Inserting (31)–(33) into conditions (30), and then separating the real and imaginary portions to obtain the next first-order ODE regarding to the amplitudes and adjusted phases \(h_{j}\) and \(\theta_{j} (j = 1,2)\)

$$\begin{aligned} & h_{1} \frac{{d\theta_{1} }}{d\tau } = h_{1} \sigma_{1} + \frac{{f_{1} }}{{2\omega_{1} }}\cos \theta_{1} - \frac{{m\omega_{1}^{3} h_{1} h_{2}^{2} }}{{6(\omega_{1}^{2} - 4\omega_{2}^{2} )}} - \frac{{3\mu_{2} h_{1}^{3} }}{{8\omega_{1} }}, \\ & \frac{{{\text{d}}h_{1} }}{{{\text{d}}\tau }} = \frac{{f_{1} }}{{2\omega_{1} }}\sin \theta_{1} - \mu_{1} h_{1} , \\ & h_{2} \frac{{{\text{d}}\theta_{2} }}{{{\text{d}}\tau }} = h_{2} (\sigma_{2} + 2\sigma_{1} ) - 2h_{2} \frac{{{\text{d}}\theta_{1} }}{{{\text{d}}\tau }} - \frac{{\omega_{1}^{3} h_{1}^{2} h_{2} }}{{9\omega_{2} (\omega_{1} + 2\omega_{2} )}} \\ & - \frac{{\omega_{2} h_{2}^{3} [3\omega_{1}^{2} + 4\omega_{2} (4m - 3)]}}{{24(\omega_{1}^{2} - 4\omega_{2}^{2} )}} - \frac{{\omega_{1}^{3} h_{1}^{2} h_{2} \cos \theta_{2} }}{{9\omega_{2} (\omega_{1} - 2\omega_{2} )}}, \\ & \frac{{{\text{d}}h_{2} }}{{{\text{d}}\tau }} = \frac{{\omega_{1}^{3} h_{1}^{2} h_{2} \sin \theta_{2} }}{{9\omega_{2} (\omega_{1} - 2\omega_{2} )}}. \\ \end{aligned}$$
(34)

These equations known as ME which can be solved numerically utilizing fourth-order Runge–Kutta method, whereby these solutions are graphed in Figs. 2 and 3 for various values of \(\omega_{j} (j = 1,2)\) according to the data listed below

$$\begin{aligned} & m_{1} = 2,\,\,\,\,\,\,M = 12,\,\,\,\,\,\,\,\,c = 0.01,\,\,\,\,\,\,\,\,\,\,\sigma_{1} = 0.00001,\, \\ & \sigma_{2} = 0.00003,\,\,\,\,\,\,\,\,f_{1} = 0.0000035,\,\,\,\,\,\,\,\,\,\Omega_{2} = \omega_{1} + \sigma_{1} . \\ \end{aligned}$$
Fig. 2
figure 2

Shows the amplitude’s modulation \(h_{1}\) and modified phase \(\theta_{1}\) at different values of \(\omega_{1}\) and \(\omega_{2}\)

Full size image
Fig. 3
figure 3

Sketches \(h_{2} {(}\tau {)}\) and \(\theta_{2} {(}\tau {)}\) when \(\omega_{1}\) and \(\omega_{2}\) have distinct values

Full size image

These figures represent the temporal histories of \(h_{j}\) and \(\theta_{j}\). However, they are graphed when \(\omega_{1} = (1.2,1.5,1.7)\) and \(\omega_{2} = (1.3,1.5,1.8)\) as shown in potions [(a), (b)] and [(c), (d)], respectively. The curves increase with time till the first quarter of the investigated time period and they have decay behavior till the end of this period as drawn in Fig. 2. Curves of Fig. 3 increase with \(h_{2} (\tau )\) or decrease with \(\theta_{2} (\tau )\) till to a specified time and then they have a steady manner. The conclusion that may be written here is \(h_{j}\) and \(\theta_{j}\) have a stable behavior.

The change of the obtained approximate solutions \(u(\tau )\) and \(\varphi (\tau )\) has been represented through the graphical plots of the curves of Figs. 4 and 5, keeping in mind the former values of the used parameters and when \(\omega_{j} (j = 1,2)\) have various values. It is obvious that the drawn curves have the forms of wave packets and have decay behaviors.

Fig. 4
figure 4

Explores \(u{(}\tau {)}\) and \(\varphi {(}\tau {)}\) when \(\omega_{1} ( = 1.2,1.5,1.7)\)

Full size image
Fig. 5
figure 5

Sketches the curves of \(u(\tau )\) and \(\varphi (\tau )\) at \(\omega_{2} ( = 1.3,1.5,1.8)\)

Full size image

The phase plane diagrams of the solutions \(h_{1}\) and \(\theta_{1}\) of the system of Eq. (34) are plotted in curves of Figs. 6 and 7 for different values of \(\omega_{1}\) and \(\omega_{2}\), respectively. Spiral curves are drawn and directed towards one red point as seen in portions (a), (b), and (c) of these figures; which assert that the solutions of this system are stable. Alternatively, Figs. 8 and 9 show the variation of \(h_{2} (\theta_{2} )\) at \(\omega_{1} = (1.2,1.5,1.7)\) and \(\omega_{2} ( = 1.3,1.5,1.8)\), respectively. Periodic standing waves are plotted in Fig. 8, whereby the vibrational modes of these waves grow as the value of the frequency \(\omega_{1}\) rises, while the oscillations’ number of remains steady. The change of \(h_{2}\) with \(\theta_{2}\) when \(\omega_{2}\) has distinct values is drawn as seen in parts Fig. 9, in which they have spiral forms.

Fig. 6
figure 6

Shows the amplitudes modulation of \(h_{1} (\theta_{1} )\): (a) at \(\omega_{1} = 1.7\), (b) at \(\omega_{1} = 1.5\), and (c) at \(\omega_{1} = 1.2\)

Full size image
Fig. 7
figure 7

Describes the amplitudes modulation of \(h_{1} (\theta_{1} )\): (a) at \(\omega_{2} = 1.3\), (b) at \(\omega_{2} = 1.5\), and (c) at \(\omega_{2} = 1.8\)

Full size image
Fig. 8
figure 8

Describes the behavior of \(h_{2} (\theta_{2} )\) at \(\omega_{1} = (1.2,1.5,1.7)\)

Full size image
Fig. 9
figure 9

Describes the behavior of \(h_{2} (\theta_{2} )\): (a) at \(\omega_{2} = 1.3\), (b) at \(\omega_{2} = 1.5\), and (c) at \(\omega_{2} = 1.8\)

Full size image

5 Oscillations at the case of steady-state

This section's main purpose is to look at the vibrations at steady-state of the studied system. This case is known to occur when transitory processes disappear owing to damping [39, 40]. Therefore, we evaluate the left sides in Eqs. (34) for their zero values, i.e., \(\frac{{{\text{d}}\theta_{j} }}{{{\text{d}}t}} = 0,\,\,\frac{{{\text{d}}h_{j} }}{{{\text{d}}t}} = 0\,\,\,(j = 1,\,2)\). Then, the below system of algebraic equations is simply constructed

$$\begin{aligned} & h_{1} \sigma_{1} + \frac{{f_{1} }}{{2\omega_{1} }}\cos \theta_{1} - \frac{{m\omega_{1}^{3} h_{1} h_{2}^{2} }}{{6(\omega_{1}^{2} - 4\omega_{2}^{2} )}} - \frac{{3\mu_{2} h_{1}^{3} }}{{8\omega_{1} }} = 0, \\ & \frac{{f_{1} }}{{2\omega_{1} }}\sin \theta_{1} - \mu_{1} h_{1} = 0, \\ & h_{2} (\sigma_{2} + 2\sigma_{1} ) - \frac{{\omega_{1}^{3} h_{1}^{2} h_{2} }}{{9\omega_{2} (\omega_{1} + 2\omega_{2} )}} - \frac{{\omega_{2} h_{2}^{3} [3\omega_{1}^{2} + 4\omega_{2} (4m - 3)]}}{{24(\omega_{1}^{2} - 4\omega_{2}^{2} )}} - \frac{{\omega_{1}^{3} h_{1}^{2} h_{2} \cos \theta_{2} }}{{9\omega_{2} (\omega_{1} - 2\omega_{2} )}} = 0, \\ & \frac{{\omega_{1}^{3} h_{1}^{2} h_{2} \sin \theta_{2} }}{{9\omega_{2} (\omega_{1} - 2\omega_{2} )}} = 0. \\ \end{aligned}$$
(35)

When the modified phases \(\theta_{1}\) and \(\theta_{2}\) are removed the previous Eq. (35), the following two algebraic equations for the amplitudes \(h_{j}\) and frequency are obtained, which are clarified by the parameters of detuning \(\sigma_{j} .\)

$$\begin{aligned} & f_{1}^{2} = 4\omega_{1}^{2} \left\{ {\left[ {h_{1} \sigma_{1} - \frac{{m\omega_{1}^{3} h_{1} h_{2}^{2} }}{{6(\omega_{1}^{2} - 4\omega_{2}^{2} )}} - \frac{{3\mu_{2} h_{1}^{3} }}{{8\omega_{1} }}} \right]^{2} + (\mu_{1} h_{1} )^{2} } \right\}, \\ &\qquad \frac{{\omega_{1}^{6} h_{1}^{4} h_{2}^{2} }}{{81\omega_{2}^{2} (\omega_{1} - 2\omega_{2} )^{2} }} = \left[ {h_{2} (\sigma_{2} + 2\sigma_{1} ) - \frac{{\omega_{1}^{3} h_{1}^{2} h_{2} }}{{9\omega_{2} (\omega_{1} + 2\omega_{2} )}} - \frac{{\omega_{2} h_{2}^{3} [3\omega_{1}^{2} + 4\omega_{2} ( - 3 + 4m)]}}{{24(\omega_{1}^{2} - 4\omega_{2}^{2} )}}} \right]^{2} . \\ \end{aligned}$$
(36)

The above Eqs. (36) are graphed as seen in Figs. 10, 11, 12 when the above data are considered to obtain the blue curve that describes the first equation in (36) and the red one which describing the second equation of (36). The points where these curves meet create fixed points. Figure 10 is drawn when \(\sigma_{1} = 0.00001\) and \(\sigma_{2} = - 0.00003\) and shows that there is no possible fixed points, while Fig. 11 is graphed at \(\sigma_{1} = 0.00001\) and \(\sigma_{2} = 0\) and contain four unstable fixed points. On the other hand, Fig. 12 is plotted at \(\sigma_{1} = 0.00001\) and \(\sigma_{2} = 0.00003\), in which it has four fixed points; two of them are stable and marked by a solid black circle while the others are unstable and denoted by hollow circle.

Fig. 10
figure 10

Shows no possible fixed points at \(\sigma_{1} = 0.00001\) and \(\sigma_{2} = - 0.00003\)

Full size image
Fig. 11
figure 11

Describes the unstable four fixed points at \(\sigma_{1} = 0.00001\) and \(\sigma_{2} = 0\)

Full size image
Fig. 12
figure 12

Describes the arising fixed points at \(\sigma_{1} = 0.00001\) and \(\sigma_{2} = 0.00003.\)

Full size image

Now, we’ll look at how a dynamical system behaves in a zone near to the fixed points for further stability’s examination. To achieve this purpose, consider the below substitutions in Eq. (34) for amplitudes and phases

$$\begin{aligned} & h_{1} = h_{10} + h_{11} ,\,\,\,\,h_{2} = h_{20} + h_{21} , \\ & \theta_{1} = \theta_{10} + \theta_{11} ,\,\,\,\theta_{2} = \theta_{20} + \theta_{21} , \\ \end{aligned}$$
(37)

where \(h_{10} ,h_{20} ,\theta_{10}\) and \(\theta_{20}\) are the steady-state’s solutions, while \(h_{11} ,h_{21} ,\theta_{11}\) and \(\theta_{21}\) are the perturbations that are considered to be very tiny. Then, Eq. (34) becomes

$$\begin{aligned} h_{10} \frac{{d\theta_{11} }}{d\tau } & = - \frac{{f_{1} }}{{2\omega_{1} }}\theta_{11} \sin \theta_{10} + h_{11} [\sigma_{1} - \frac{{m\omega_{1}^{3} h_{20}^{2} }}{{6(\omega_{1}^{2} - 4\omega_{2}^{2} )}} - \frac{{9\mu_{2} h_{10}^{2} }}{{8\omega_{1} }}] - \frac{{m\omega_{1}^{3} h_{10} h_{20} h_{21} }}{{3(\omega_{1}^{2} - 4\omega_{2}^{2} )}}, \\ \frac{{dh_{11} }}{d\tau } & & = \frac{{f_{1} }}{{2\omega_{1} }}\theta_{11} \cos \theta_{10} - \mu_{1} h_{11} , \\ h_{20} \frac{{{\text{d}}\theta_{21} }}{{{\text{d}}\tau }} & = h_{21} \left[ {\sigma_{2} + 2\sigma_{1} - \frac{{\omega_{1}^{3} h_{10}^{2} }}{{9\omega_{2} (\omega_{1} + 2\omega_{2} )}} + \frac{{h_{20}^{2} \omega_{2} [3\omega_{1}^{2} + 4\omega_{2} (4m - 3)]}}{{8(\omega_{1}^{2} - 4\omega_{2}^{2} )}}} \right. \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { - \frac{{\omega_{1}^{3} h_{10}^{2} \cos \theta_{20} }}{{9\omega_{2} (\omega_{1} - 2\omega_{2} )}}} \right] - 2h_{20} \frac{{{\text{d}}\theta_{11} }}{{{\text{d}}\tau }} - \frac{{2\omega_{1}^{3} }}{{9\omega_{2} }}\left[ {\frac{1}{{(\omega_{1} + 2\omega_{2} )}} + \frac{{\cos \theta_{20} }}{{(\omega_{1} - 2\omega_{2} )}}} \right]\,h_{20} h_{10} h_{11} , \\ \frac{{{\text{d}}h_{21} }}{{{\text{d}}\tau }} & = \frac{{\omega_{1}^{3} }}{{9\omega_{2} (\omega_{1} - 2\omega_{2} )}}(2h_{20} h_{10} h_{11} + h_{10}^{2} h_{21} )\sin \theta_{20} , \\ \end{aligned}$$
(38)

Remembering that \(h_{j1}\) and \(\theta_{j1} \,\,(j = 1,2)\) are unknown tiny perturbation functions. Therefore, we can phrase their solutions as a linear combination of \(k_{d} e^{\lambda \tau }\), where \(\lambda\) represents the eigenvalue of these perturbations and \(k_{d} \,\,\,\,(d = 1,2,3,4)\) are constants, which are counted from the roots real potions. In this context, if \(h_{j0}\) and \(\theta_{j0} \,\,(j = 1,2)\) are stable asymptotically, then the roots real portions of the next characteristic equation must therefore be negative [41]

$$\lambda^{4} + \Gamma_{1} \lambda^{3} + \Gamma_{2} \lambda^{2} + \Gamma_{3} \lambda + \Gamma_{4} = 0,$$
(39)

where

$$\begin{aligned} \Gamma_{1} & = \frac{{f_{1} \sin \theta_{10} }}{{2h_{10} \omega_{1} }} - \frac{{\omega_{1}^{3} h_{10}^{2} }}{{9\omega_{2} (\omega_{1} + 2\omega_{2} )}}\sin \theta_{20} + \mu_{1} , \\ \Gamma_{2} & = \frac{1}{{16h_{10} \omega_{1}^{2} }}\left\{ { - \frac{{16\omega_{1}^{3} h_{10}^{3} \sin \theta_{20} }}{{9\omega_{2} (\omega_{1} + 2\omega_{2} )}} + f\left[ {\frac{{4m\omega_{1}^{3} h_{20}^{2} \cos \theta_{10} }}{{3(\omega_{1}^{2} - 4\omega_{2}^{2} )}} + 8(\mu_{1} \sin \theta_{10} - \sigma_{1} \cos \theta_{10} )} \right.} \right. \\ & \,\,\,\,\,\,\left. {\left. { + \omega_{1} h_{10}^{2} \left( {9\mu_{2} \cos \theta_{10} - \frac{{8\omega_{1}^{3} \sin \theta_{10} \sin \theta_{20} }}{{9\omega_{2} (\omega_{1} + 2\omega_{2} )}}} \right)} \right]} \right\}, \\ \Gamma_{3} & = \frac{1}{{2592h_{10} h_{20} \omega_{2}^{2} (\omega_{1}^{2} - 4\omega_{2}^{2} )^{2} }}\{ h_{10} \omega_{1}^{2} \cos \theta_{20} (\omega_{1} + 2\omega_{2} )[ - 8h_{10}^{2} \omega_{1}^{4} (f_{1} \sin \theta_{10} \\ & \,\,\,\,\,\, + 2\mu_{1} h_{10} \omega_{1}^{2} ) + 8\omega_{1}^{2} (f_{1} \sin \theta_{10} (18\sigma_{1} + 9\sigma_{2} + 2h_{10}^{2} \omega_{1} )\mu_{1} + 2\mu_{1} h_{10} \omega_{1}^{2} (18\sigma_{1} \\ & \,\,\,\,\,\, + 9\sigma_{2} + 2(h_{10}^{2} - 3mh_{20}^{2} )\omega_{1} )]\omega_{2} + 27h_{20}^{2} \omega_{1}^{2} (f_{1} \sin \theta_{10} + 2\mu_{1} h_{10} \omega_{1}^{2} )\omega_{2}^{2} \, - 288(2\sigma_{1} \\ & \, + \sigma_{2} )(f_{1} \sin \theta_{10} + 2\mu_{1} h_{10} \omega_{1}^{2} )\omega_{2}^{3} + 36(4m - 3)h_{20}^{2} (f_{1} \sin \theta_{10} + 2\mu_{1} h_{10} \omega_{1}^{2} )\omega_{2}^{4} \\ & \,\,\, - 432f_{1} mh_{20}^{2} \omega_{2}^{4} [ - 6\mu_{1} \sin \theta_{10} (\omega_{1}^{2} - 4\omega_{2}^{2} ) + \cos \theta_{10} (mh_{20}^{2} \omega_{1}^{3} - 6\sigma_{1} (\omega_{1}^{2} - 4\omega_{2}^{2} ))]\} , \\ \Gamma_{4} & = \frac{{f_{1} \cos \theta_{20} \omega_{1}^{3} }}{{5184h_{20} \omega_{2}^{2} (\omega_{1} - 2\omega_{2} )^{3} (\omega_{1} + 2\omega_{2} )^{3} }}\{ - 3\omega_{2} [8(2\sigma_{1} + \sigma_{2} )\omega_{1}^{2} + 3h_{20}^{2} \omega_{1}^{2} \omega_{2} \\ & \,\,\,\,\,\, - 32(2\sigma_{1} + \sigma_{2} )\omega_{2}^{2} + 4(4m - 3)h_{20}^{2} \omega_{2}^{3} ][ - 6\mu_{1} \sin \theta_{10} (\omega_{1}^{2} - 4\omega_{2}^{2} ) + \cos \theta_{10} \\ & \,\,\,\,\,\, \times (mh_{10}^{2} \omega_{1}^{3} - 6\sigma_{1} (\omega_{1}^{2} - 4\omega_{2}^{2} ))] - 8h_{10}^{2} \omega_{1}^{3} (\omega_{1} - 2\omega_{2} )[2\mu_{1} \sin \theta_{10} (\omega_{1}^{2} - 4\omega_{2}^{2} ) \\ & \,\,\,\,\,\, + \cos \theta_{10} (mh_{10}^{2} \omega_{1}^{3} - 6\sigma_{1} (\omega_{1}^{2} - 4\omega_{2}^{2} ))]\} . \\ \end{aligned}$$

5.1 (40)

However, the essential prerequisites of the stability for specific solutions at the case of steady-state based on the Routh–Hurwitz criterion [42, 43] are

$$\begin{aligned} & \Gamma_{1} > 0, \\ & \Gamma_{3} (\Gamma_{1} \Gamma_{2} - \Gamma_{3} ) - \Gamma_{4} \Gamma_{1}^{2} > 0, \\ & \Gamma_{1} \Gamma_{2} - \Gamma_{3} > 0, \\ & \Gamma_{4} > 0. \\ \end{aligned}$$
(41)

Resonance response curves in parts (a) and (b) of Figs. 13 and 14 are calculated at \(\sigma_{2} = 0\) when \(\omega_{1} ( = 1.2,1.5,1.7)\) and \(\omega_{2} ( = 1.3,1.5,1.8)\) in addition to the above data of other parameters. Solid curves are used to indicate about the stability zones, while the unstable ones are depicted through dashed curves.

Fig. 13
figure 13

Sketches the frequency responses at \(\sigma_{2} = 0\) and \(\omega_{1} = (1.2,1.5,1.7)\): (a) \(h_{1} (\sigma_{1} )\) (b) \(h_{2} (\sigma_{1} )\)

Full size image
Fig. 14
figure 14

Portrays the frequency response at \(\sigma_{2} = 0\) and \(\omega_{2} = (1.3,1.5,1.8)\): (a) \(h_{1} (\sigma_{1} )\) (b) \(h_{2} (\sigma_{1} )\)

Full size image

Based on the plotted curves in portions of Fig. 13, we can see from part (a) that the stability zones and instability ones are found in the ranges \(\sigma_{1} < - 0.002\) and \(- 0.002 \le \sigma_{1}\), respectively. On the other hand, curves of Fig. 13b show that the stability areas are \(\sigma_{1} < 0.001\) and \(\sigma_{1} < 0.002\), while the unstable ones are \(0.001 \le \sigma_{1}\) and \(0.002 \le \sigma_{1}\) when \(\omega_{1} = 1.5\) and \(\omega_{1} = 1.7\).

The influences of \(\omega_{2}\) values on the frequency response curves are at \(\sigma_{2} = 0\) are shown in portions of Fig. 14, whereby the zones of stability and instability are located in the domains \(\sigma_{1} < - 0.003\) and \(- 0.003 \le \sigma_{1}\), respectively, see Fig. 14a. These zones are displaced slightly in portion (b) of Fig. 14 when \(\omega_{2} = 1.5\) and \(\omega_{2} = 1.8\) to be \(\sigma_{1} < 0.001\) and \(\sigma_{1} < 0.003\) for the stability areas, \(0.001 \le \sigma_{1}\) and \(0.003 \le \sigma_{1}\) for the instability areas. The locations of critical fixed points (CFP) and peaks fixed points (PFP) of the curves of portions of Figs. 13 and 14 are given in Tables 1 and 2, respectively.

Table 1 Demonstrates the positions of the PFP and the CFP for the response curves at \(\sigma_{2} = {0}\) and \(\omega_{1} = (1.2,1.5,1.7)\)for the curves of Fig. 13
Full size table
Table 2 Demonstrates the positions of the PFP and the CFP for the response curves at \(\sigma_{2} = {0}\)and \(\omega_{2} = (1.3,1.5,1.8)\) for the curves of Fig. 14
Full size table

6 Conclusion

The movement of a damped 2DOF auto-parametric dynamical system has been examined. In terms of generalized coordinates, Lagrange’s equations have been employed to derive the governing EOM. The new approximate solutions are obtained applying the MMS up to a higher order of approximation. The solvability requirements and the ME of the studied system have been obtained. The arising cases of resonance have been distinguished, with the internal and primary external cases are examined together. The stability and instability of the fixed points are checked. The time history graphs of the obtained solutions, as well as the amplitudes and adjusted phases have been analysed to study the system’s behavior at any given time. Applications of the examined system can be found in swaying structures and rotor dynamics which demonstrate the importance of the attained results.